2. ИНТЕГРАЛЫ ДВИЖЕНИЯ

Диагонализация гамильтониана облегчается, если известны интегралы движения. В самом деле, если Р есть такой интеграл, то операторы Р и Н коммутируют. Пусть матрица Р диагональна. Тогда

    (2.1)

В представлении, в котором матрица Р диагональна, гамильтониан Н имеет отличные от нуля матричные элементы лишь между состояниями с одним и тем же собственным значением Р. Иными словами, матрица Н разбивается на «блоки», связывающие только состояния с одним и тем же Р. Поскольку из симметрии задачи часто оказывается возможным найти диагональное представление для Р, то секулярное уравнение для собственных значений Н в значительной степени упрощается.

Пусть гамильтониан Н инвариантен по отношению к инверсии. Это заведомо имеет место для сферически симметричного потенциала и может быть справедливо также и для других потенциалов более общего вида. Тогда интегралом движения будет четность состояния. Для изолированных систем интегралом движения всегда будет полный момент количества движения J. Действительно, оператор J осуществляет бесконечно малые повороты, а мы предполагаем, что пространство изотропно.

Рассматривая бесконечно малые повороты, можно найти правила перестановки для компонент J

Эти равенства можно объединить в символической записи

Отсюда следует, что

и аналогично для у- и z-компонент J. Выберем представление, в котором операторы и диагональны, и будем обозначать строки и столбцы парами символов и . Тогда окажется, что собственные значения при фиксированном будут равны где меняется с единичным шагом от до Собственные значения для любого будут равны , где — положительное целое число или нуль.

Матричные элементы можно получить из матрицы , определяемой равенством

Единственный отличный от нуля матричный элемент имеет вид

Иначе говоря, для любого состояния

Сопряженный оператор обладает свойством

Операторы называются соответственно повышающим и понижающим операторами.

Представления соответствующие целочисленным значениям могут возникать при рассмотрении орбитального момента количества движения L. Последний определяется равенством

где — импульс частицы. Оператор L удовлетворяет правилам перестановки (2.2), а его собственные функции суть сферические гармоники. Для произвольной квантовой системы, например для атома, значение L не обязано сохраняться, ибо этот оператор осуществляет повороты только в пространстве координат; относительно

таких поворотов изолированная система не обязана быть инвариантной. Если оператор все же оказывается интегралом движения, то это вытекает из частных физических особенностей гамильтониана задачи, а не из общих геометрических свойств пространства. Например, значение сохраняется для центральносимметричного гамильтониана в отсутствие спин-орбитальной связи [1].

Спин

Частицы могут обладать собственным моментом количества движения, который нельзя выразить через классические координаты и импульс. Компоненты этого момента количества движения могут быть полуцелыми, так как представление для оператора J здесь неприменимо.

Спин не имеет аналога в классической механике. В частности, ранние модели электрона, вращающегося подобно волчку, совершенно бессмыслены. Рассматривая спин, мы будем заменять оператор J на S, j на s и на Каждая элементарная частица имеет определенный спин s, т. е.

где — нуль или положительное целое число, — единичный оператор в спиновом пространстве.

Поскольку для каждой частицы значение s фиксировано, то что указывает на отсутствие классического аналога для спина. Каково значение спина конкретных частиц — это вопрос опыта. (Хотя релятивистская теория Дирака и предсказывает для электронов спин но можно построить в равной мере последовательную теорию, которая предсказывает нулевой спин.) Электроны, нуклоны и -мезоны имеют спин ; -мезоны имеют спин 0; фотоны, в той мере, в какой их можно считать частицами, имеют спин 1. Очевидно, оператор S коммутирует с ; следовательно, если одночастичный гамильтониан не содержит спиновых членов, то S будет интегралом движения (см. также гл. 8),.

Функция, описывающая состояние частицы, должна зависеть от компонент спина. Вообще говоря, если гамильтониан сильно связывает пространственное и спиновое движения, то для характеристики такой частицы потребуется функций пространственных и спиновых координат . Если же названную связь можно игнорировать, то волновая функция факторизуется

Поскольку спиновое пространство состоит всего из точек, то функция полностью определяется числом. В качестве очевидно, можно взять набор собственных функций матриц Например, для случая

Для нас основной интерес представляют функции и спиновые матрицы для спина так как именно они описывают отдельные электроны. Полагая находим из общих выражений (2.6), (2.7) для ,

Матрицы называются спиновыми матрицами Паули. Легко проверить, что они удовлетворяют следующим соотношениям:

Для двух (или более) моментов количества движения мы можем составить оператор

Следовательно, если все компоненты коммутируют, то J вновь оказывается оператором момента количества движения. Поскольку спиновые операторы двух электронов коммутируют, то опять будет спиновым оператором. Четыре ортонормированные спиновые функции для пары электронов можно выбрать в виде . В этих произведениях спиновых функций действует только на первую спиновую функцию, — только на вторую. Указанные четыре спиновые функции отвечают соответственно следующим значениям . Так как оператор S описывает момент количества движения, то можно найти представление, в котором матрицы диагональны. Легко проверить, что произведения суть собственные функции Чтобы построить остальные собственные функции из произведений заметим, что функция симметрична и отвечает значениям Поэтому, применив к ней понижающий оператор мы получим волновую функцию, отвечающую получающаяся таким путем волновая функция также будет симметричной. В явном виде мы имеем

Четвертую собственную функцию можно найти, заметив, что единственная нормированная линейная комбинация ортогональная к выражению (2.13), ямеет антисимметричный вид

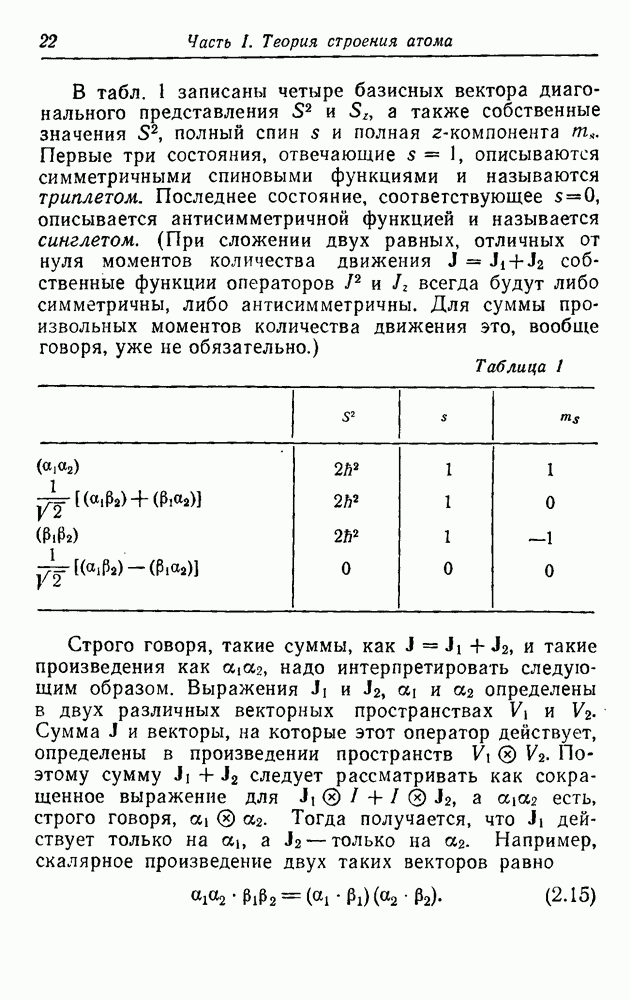
В табл. 1 записаны четыре базисных вектора диагонального представления а также собственные значения полный спин s и полная z-компонента . Первые три состояния, отвечающие описываются симметричными спиновыми функциями и называются триплетом. Последнее состояние, соответствующее описывается антисимметричной функцией и называется синглетом. (При сложении двух равных, отличных от нуля моментов количества движения собственные функции операторов всегда будут либо симметричны, либо антисимметричны. Для суммы произвольных моментов количества движения это, вообще говоря, уже не обязательно.)

Таблица 1

Строго говоря, такие суммы, как и такие произведения как надо интерпретировать следующим образом. Выражения определены в двух различных векторных пространствах . Сумма J и векторы, на которые этот оператор действует, определены в произведении пространств . Поэтому сумму следует рассматривать как сокращенное выражение для , а есть, строго говоря, . Тогда получается, что действует только на — только на . Например, скалярное произведение двух таких векторов равно