14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ

В гл. 12 мы нашли дифференциальное поперечное сечение для такого процесса, в котором атом поглощает излучение частоты и электрон переходит в непрерывный спектр. Именно таковы экспериментальные условия для фотоэффекта. Мы получили выражение

    (12.14)

где нижний индекс f означает конечное состояние. Рассмотрим теперь три метода вычисления этого интеграла для атома водорода в предположении, что начальное состояние является основным.

Борновское приближение

Возьмем вместо волновой функции конечного состояния плоскую волну . Это приближение разумно, если где — импульс в основном состоянии. Мы имеем

Сверх того, должно выполняться неравенство

Интеграл принимает вид

где . Пусть вектор поляризации А направлен вдоль оси , так что у вектора к отсутствует х-компонента. Проинтегрируем по частям, подставим явное

выражение для волновой функции основного состояния атома водорода и после некоторых простых алгебраических операций получим для дифференциального поперечного сечения следующее выражение:

Выражение (14.3) содержит угловые переменные двояким образом. Во-первых, множитель а показывает, что электрон вылетает преимущественно в направлении вдоль электрического поля волны падающего света (вдоль вектора поляризации). Если бы волновая функция начального состояния была анизотропной, тогда вместо множителя а появилось бы выражение вида .

Вторая угловая зависимость происходит от стоящей в знаменателе величины

На основании неравенства (14.1) можно заключить, что

где у — скорость выбитого электрона. Поскольку мы рассматриваем нерелятивистский случай, можно написать

Далее, . Следовательно, можно заменить величину на Замечая, что

находим окончательно

Угловую зависимость выражения (14.7) легко интерпретировать. Если пренебречь членом с что оправдано в нерелятивистском приближении, то окажется, что рассматриваемая величина пропорциональна и максимальна в направлении электрического поля падающей световой волны. Этот результат означает, что электрон из начального -состояния переходит в конечное состояние, для которого (если в качестве оси квантования выбрать направление поля, т. е. ось ). Это находится в соответствии с правилами отбора, установленными в гл. 13. По отношению к направлению распространения распределение имеет максимум в экваториальной плоскости, Если учесть теперь член, описывающий влияние отдачи и пропорциональный , то этот максимум сдвинется вперед приблизительно до угла

Множитель 4 здесь не имеет особого значения; он был бы иным для других начальных состояний.

Интегрируя выражение (14.7) по угловым переменным и пренебрегая членами порядка , получаем

С другой стороны, воспользовавшись дипольным приближением для выражения (12.14), мы пришли бы к следующему результату для :

так . Сравнивая этот результат с выражением (14.9), находим, что . Этот вывод

справедлив, если волновая функция конечного состояния нормирована на единичную амплитуду бы вместо этого была использована нормировка по шкале энергий, то появился бы лишний множитель число состояний в единичном интервале энергий вблизи . Так как дипольный матричный элемент при нормировке волновой функции конечного состояния на единичную энергию ведет себя при больших частотах о как

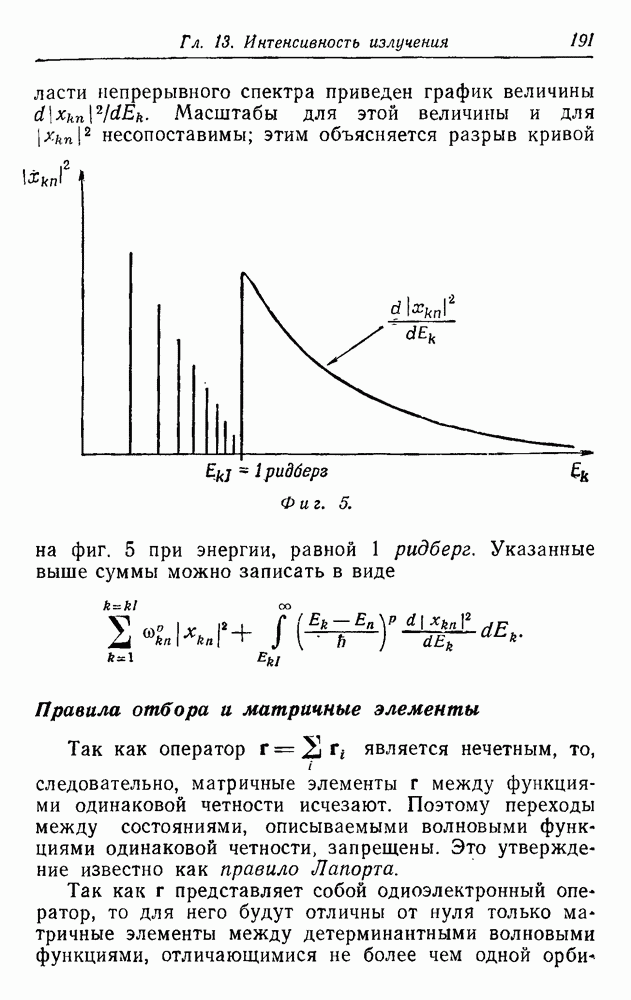
Это согласуется с нашим прежним выводом, полученным с помощью правила сумм (см. стр. 190).

Дипольное приближение

Во втором методе расчета фотоэлектрического эффекта полностью пренебрегают влиянием отдачи, но используют точные волновые функции непрерывного спектра. Подобный расчет описан, например, в книге [7]. Результат гласит:

В случае больших число становится малым и

Тогда

что совпадает с борновским приближением. Этого и следовало ожидать, так как при больших энергиях квантов света, когда , борновское приближение должно быть применимым, а при эффектами отдачи можно пренебречь, что фактически и было сделано при выводе

выражения (14.9). Вблизи границы фотоэлектрического эффекта и поэтому

Тогда

Так как при этом последнее выражение можно представить следующим образом:

    (14.15)

Появления множителей можно было ожидать просто из соображений размерности; численный множитель 31 мог быть получен только прямым расчетом. Ввиду того что этот множитель велик, в области энергий выше порога фотоэлектрического эффекта имеет место сильное поглощение рентгеновских лучей.

Грубая оценка

Третий, метод расчета поперечного сечения фотоэлектрического эффекта основан на весьма грубом приближении и полезен в тех случаях, когда о системе известно очень немного, например при рассмотрении неводородных атомов. Пусть волновая функция конечного состояния нормирована на -функцию от энергии, т. е.

Соответствующая сила осциллятора есть . В пренебрежении отдачей

В случае атома водорода можно положить

Эта величина выбрана таким образом, чтобы было выполнено условие

ибо такой, как мы знаем, должна быть полная сила осциллятора для перехода из состояния в непрерывный спектр. Зависимость от частоты выбрана в соответствии с эмпирическими данными по поглощению рентгеновских лучей, она является промежуточной между зависимостями . При формула (14.17) дает

    (14.18)

Это следует сравнить с точной формулой (14.15). Ошибка составляет 10%.