| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
§ 1. Равнораспределение энергии
Броуновское
движение открыл в 1827 г. ботаник Роберт Броун. Изучая жизнь под микроскопом,
он заметил, что мельчайшие частицы цветочной пыльцы пляшут в его поле зрения; в
то же время он был достаточно сведущ, чтобы понимать, что перед ним не живые
существа, а просто плавающие в воде соринки. Чтобы окончательно доказать, что
это не живые существа, Броун разыскал обломок кварца, внутри которого была
заполненная водой полость. Вода попала туда много миллионов лет назад, но и в
такой воде соринки все продолжали свою пляску. Казалось, что очень мелкие
частицы пляшут непрерывно. Позднее было доказано, что это один из эффектов
молекулярного движения и понять его качественно можно, представив себе, что мы
откуда-то издалека следим за игрой в пушбол. Мы знаем, что под большим мячом
движется толпа людей и каждый толкает мяч, куда хочет. Мы не видим отдельных
игроков, потому что поле очень далеко от нас, но мяч мы видим и замечаем, что
перемещается он очень беспорядочно. Мы уже знаем из разобранных в предыдущих
главах теорем, что средняя кинетическая энергия взвешенной в газе или жидкости
маленькой частицы равна ![]() , даже если эта частица гораздо
тяжелее молекул газа. Если она очень тяжела, то и движется она сравнительно
медленно, но на самом деле оказывается, что скорость частицы не так уж мала.
Конечно, заметить движение частицы не очень легко, потому что средняя
кинетическая энергия
, даже если эта частица гораздо
тяжелее молекул газа. Если она очень тяжела, то и движется она сравнительно
медленно, но на самом деле оказывается, что скорость частицы не так уж мала.
Конечно, заметить движение частицы не очень легко, потому что средняя
кинетическая энергия ![]() соответствует скорости около 1
мм/сек, если диаметр частицы равен 1-2 мк. Такое движение трудно заметить даже
под микроскопом, потому что частица постоянно меняет направление своего
движения и пойти в какую-нибудь определенную сторону не желает. В конце главы
мы посмотрим, далеко ли она может уйти. Этот вопрос впервые был разрешен
Эйнштейном в начале нашего столетия.
соответствует скорости около 1
мм/сек, если диаметр частицы равен 1-2 мк. Такое движение трудно заметить даже
под микроскопом, потому что частица постоянно меняет направление своего
движения и пойти в какую-нибудь определенную сторону не желает. В конце главы
мы посмотрим, далеко ли она может уйти. Этот вопрос впервые был разрешен
Эйнштейном в начале нашего столетия.
Между
прочим, когда говорят, что средняя кинетическая энергия частицы равна ![]() , то требуют,
чтобы этот результат был выведен из кинетической теории, т. е. из законов
Ньютона. Мы уже можем получать разные удивительные вещи с помощью кинетической
теории, самое интересное - что удается получить так много из столь малого.
Конечно, мы не хотим сказать, что законы Ньютона - это «малое», они на самом
деле дают все необходимое для решения задачи, просто нам пришлось потрудиться
совсем немного. Как же нам удалось так много получить? Просто мы постоянно
исходили из очень важного предположения, что если заданная система находится
при некоторой температуре в тепловом равновесии, то при той же температуре она
будет в равновесии с чем угодно. Скажем, нам хочется посмотреть, как движется
частица, если она сталкивается с водой.
, то требуют,
чтобы этот результат был выведен из кинетической теории, т. е. из законов
Ньютона. Мы уже можем получать разные удивительные вещи с помощью кинетической
теории, самое интересное - что удается получить так много из столь малого.
Конечно, мы не хотим сказать, что законы Ньютона - это «малое», они на самом
деле дают все необходимое для решения задачи, просто нам пришлось потрудиться
совсем немного. Как же нам удалось так много получить? Просто мы постоянно
исходили из очень важного предположения, что если заданная система находится
при некоторой температуре в тепловом равновесии, то при той же температуре она
будет в равновесии с чем угодно. Скажем, нам хочется посмотреть, как движется
частица, если она сталкивается с водой.
Для
этого представим, что, кроме воды и частицы, есть еще и газ, состоящий из
частиц еще одного сорта - маленьких дробинок, которые, как мы предполагаем, с
водой не взаимодействуют и только сильно ударяют по нашей частице. Предположим,
что частица ощетинилась острыми шипами и все дробинки наталкиваются на них. Об
этом воображаемом газе из дробинок при температуре ![]() нам известно все - это
идеальный газ. Вода – дело сложное, а идеальный газ - он попроще. И вот наша
частица находится в равновесии с газом из дробинок. Следовательно, среднее
движение частицы должно быть таким, каким ему следует быть вследствие
столкновений с атомами, потому что если бы частица двигалась относительно воды
с большей скоростью, чем положено, то дробинки, отняв у частицы часть ее
энергии, нагрелись бы больше, чем вода. Но ведь мы начали с равных температур и
предполагаем, что если равновесие однажды наступило, то оно таким и останется;
не может вдруг одна часть системы нагреться, а другая остыть.
нам известно все - это
идеальный газ. Вода – дело сложное, а идеальный газ - он попроще. И вот наша
частица находится в равновесии с газом из дробинок. Следовательно, среднее
движение частицы должно быть таким, каким ему следует быть вследствие
столкновений с атомами, потому что если бы частица двигалась относительно воды
с большей скоростью, чем положено, то дробинки, отняв у частицы часть ее
энергии, нагрелись бы больше, чем вода. Но ведь мы начали с равных температур и
предполагаем, что если равновесие однажды наступило, то оно таким и останется;
не может вдруг одна часть системы нагреться, а другая остыть.
Это
предположение справедливо и его можно доказать, используя законы механики, но
доказательство очень сложно и понять его можно, только хорошо зная механику. С
помощью квантовой механики доказать это гораздо легче, чем с помощью
классической. Впервые эту теорему доказал Больцман, а мы, приняв, что она
верна, можем утверждать, что если частица сталкивается с воображаемыми
дробинками, то ее энергия равна ![]() . Но этой же самой энергией она
должна обладать, если мы удалим дробинки и оставим частицу наедине с водой при
такой же температуре. Это странная, но правильная цепь рассуждений.
. Но этой же самой энергией она
должна обладать, если мы удалим дробинки и оставим частицу наедине с водой при
такой же температуре. Это странная, но правильная цепь рассуждений.
Кроме
движения коллоидных частиц, на которых и было впервые открыто броуновское
движение, имеется еще целый ряд других явлений, и не только в лабораторных, но
и в других условиях, позволяющих обнаружить броуновское движение. Если бы мы
смогли соорудить чрезвычайно тонкое измерительное устройство, скажем, крохотное
зеркальце, прикрепленное к тонкой кварцевой нити очень чувствительного
баллистического гальванометра (фиг. 41.1), то зеркальце не стояло бы на месте,
а непрерывно плясало бы, поэтому если бы мы осветили это зеркальце лучом света
и проследили за отраженным пятном, то потеряли бы надежду создать совершенный
измерительный инструмент, так как зеркальце все время пляшет. Почему? Потому
что средняя кинетическая энергия вращения зеркальца равна ![]() .
.

Фиг. 41.1. Чувствительный зеркальный гальванометр и образец записи шкалы как функция времени.
Пучок света из источника отражается от маленького зеркальца на шкале.
Чему
равен средний квадратичный угол качаний зеркальца? Предположим, что мы
определили период собственных колебаний зеркальца, стукнув слегка по одной его
стороне и наблюдая, как долго будет оно качаться взад и вперед, и пусть нам
также известен момент инерции ![]() . Формулу для кинетической энергии
вращения мы знаем, это равенство (19.8):
. Формулу для кинетической энергии
вращения мы знаем, это равенство (19.8): ![]() . А потенциальная энергия
пропорциональна квадрату угла отклонения, т. е.
. А потенциальная энергия
пропорциональна квадрату угла отклонения, т. е. ![]() . Но если мы знаем период колебаний
. Но если мы знаем период колебаний ![]() и можем вычислить
собственную частоту
и можем вычислить
собственную частоту ![]() , то можно и потенциальную энергию
записать в виде
, то можно и потенциальную энергию
записать в виде ![]() .
Мы знаем, что средняя кинетическая энергия равна
.
Мы знаем, что средняя кинетическая энергия равна ![]() , но поскольку перед нами
гармонический осциллятор, то средняя потенциальная энергия также равна
, но поскольку перед нами
гармонический осциллятор, то средняя потенциальная энергия также равна ![]() . Следовательно,
. Следовательно,
![]() ,
,
или
![]() . (41.1)
. (41.1)
Таким образом мы можем рассчитать колебания зеркальца гальванометра и тем самым найти предел точности нашего инструмента. Если нам нужно уменьшить колебания, то следует охладить зеркальце. Но здесь возникает интересный вопрос - в каком месте его охладить? Все зависит от того, откуда оно получает больше «пинков». Если в колебаниях повинна кварцевая нить, то охлаждать нужно ее верхний конец, если же зеркальце находится в газовой среде и раскачивается в основном за счет соударений с молекулами газа, то лучше охладить газ. Итак, практически, если известно, почему происходит затухание колебаний, то оказывается, что имеется всегда какой-то источник флуктуаций; к этому вопросу мы еще вернемся.
Те
же флуктуации работают, и довольно удивительным образом, в электрических цепях.
Предположим, что мы построили очень чувствительный, точный усилитель для
какой-нибудь определенной частоты и к его входу подключили резонансную цепь
(фиг. 41.2), настроенную на эту же частоту, наподобие радиоприемника, только
получше. Предположим, что мы захотели как можно точнее изучить флуктуации, для
этого мы сняли напряжение, скажем, с индуктивности и подали его на усилитель.
Конечно, во всякой цепи такого рода имеются некоторые потери. Это не идеальная
резонансная цепь, но все же очень хорошая цепь, и обладает она малым
сопротивлением (на схеме сопротивление показано, надо только помнить, что оно
очень мало). А теперь мы хотим узнать, как велики флуктуации падения напряжения
на индуктивности? Ответ: Нам известно, что «кинетическая энергия», запасенная
катушкой резонансной цепи, равна ![]() (см. гл. 25). Поэтому среднее
значение
(см. гл. 25). Поэтому среднее
значение ![]() равно
равно
![]() , это
дает нам среднее квадратичное значение тока, а отсюда можно определить и
среднее квадратичное значение напряжения. Если мы хотим знать падение
напряжения на индуктивности, нам пригодится формула
, это
дает нам среднее квадратичное значение тока, а отсюда можно определить и
среднее квадратичное значение напряжения. Если мы хотим знать падение
напряжения на индуктивности, нам пригодится формула ![]() , тогда средний квадрат
модуля падения напряжения на индуктивности равен
, тогда средний квадрат
модуля падения напряжения на индуктивности равен ![]() , а полагая
, а полагая ![]() , получаем
, получаем
![]() . (41.2)
. (41.2)
Итак, теперь мы можем рассчитать контур и предсказать, каким в нем будет так называемый шум Джонсона, т. е. шум, связанный с тепловыми флуктуациями!

Фиг. 41.2. Резонансная цепь с
большим ![]() .
.
а - реальная цепь при температуре
![]() ; б - искусственная
цепь с идеальным (бесшумным) сопротивлением и «генератором шума».
; б - искусственная
цепь с идеальным (бесшумным) сопротивлением и «генератором шума».
Но откуда же эти флуктуации берутся? А все из-за сопротивления, точнее говоря, в результате пляски электронов в сопротивлении. Ведь они находятся в тепловом равновесии с остальным материалом сопротивления, а это приводит к флуктуациям плотности электронов. Таким образом они порождают крошечные электрические поля, управляющие резонансной цепью.
Инженеры-электрики
объясняют все это иначе. Физически источником шумов служит сопротивление. Однако
можно заменить реальную цепь с честным сопротивлением, вызывающим шумы,
фиктивной цепью, содержащей маленький генератор, который якобы порождает шумы,
а сопротивление теперь будет идеальным - оно уже не шумит. Все шумы теперь
исходят от фиктивного генератора. Итак, если нам известны характеристики шума,
порождаемого сопротивлением, и у нас для этого имеется подходящая формула, то
можно рассчитать, как цепь реагирует на этот шум. Следовательно, нам нужна
формула для шумовых флуктуаций. Сопротивление одинаково хорошо порождает шумы
всех частот, поскольку оно само отнюдь не резонатор. Резонансная цепь, конечно,
«слышит» лишь часть этого шума вблизи определенной частоты, а в сопротивлении
заключено много и других частот. Силу генератора можно описать таким образом:
выделяемая на сопротивлении средняя мощность, если оно непосредственно
соединено с генератором шума, равна ![]() , где
, где ![]() - снимаемое с генератора напряжение.
Но теперь мы хотим знать подробнее о распределении мощности по частотам. Каждой
определенной частоте соответствует очень малая мощность. Пусть
- снимаемое с генератора напряжение.
Но теперь мы хотим знать подробнее о распределении мощности по частотам. Каждой
определенной частоте соответствует очень малая мощность. Пусть ![]() - мощность,
которую генератор посылает сопротивлению в интервале частот
- мощность,
которую генератор посылает сопротивлению в интервале частот ![]() . Тогда можно доказать (мы
докажем это для другого случая, но математика и там и тут одинакова), что
выделяемая мощность равна
. Тогда можно доказать (мы
докажем это для другого случая, но математика и там и тут одинакова), что
выделяемая мощность равна
![]() (41.3)
(41.3)
и, таким образом, не зависит от сопротивления.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
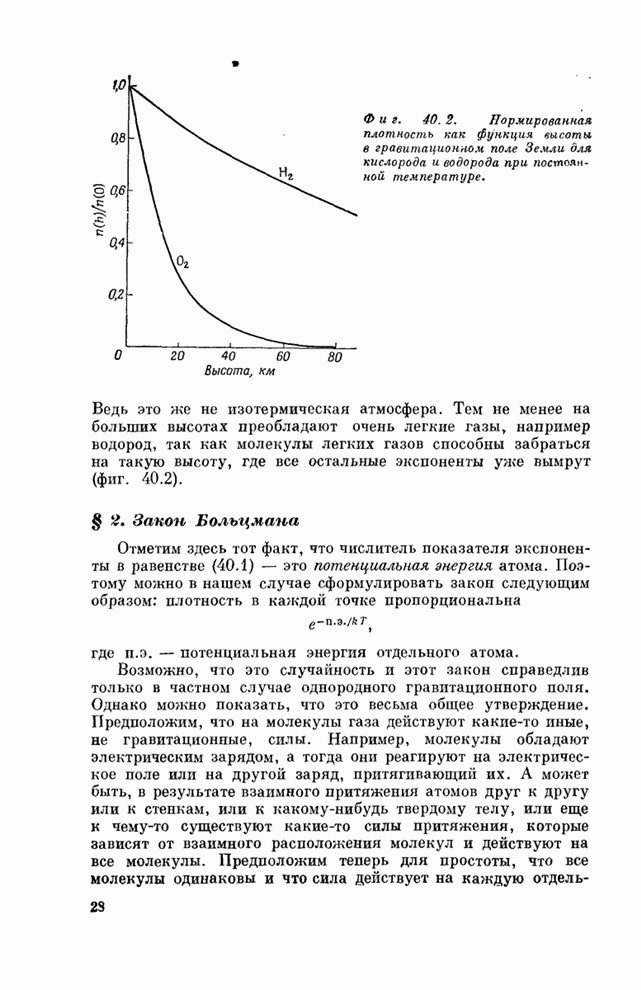
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
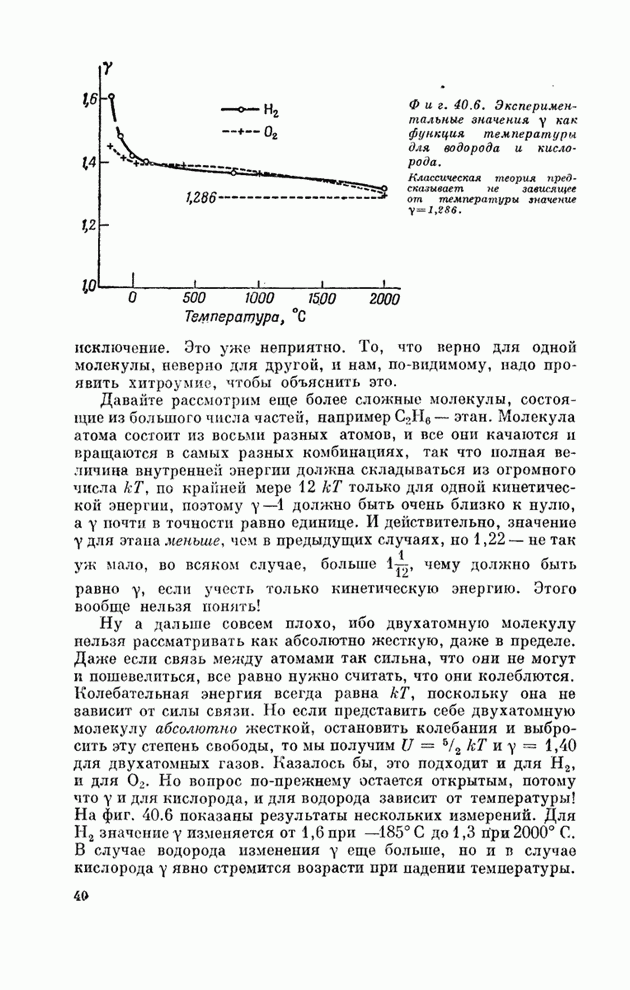
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
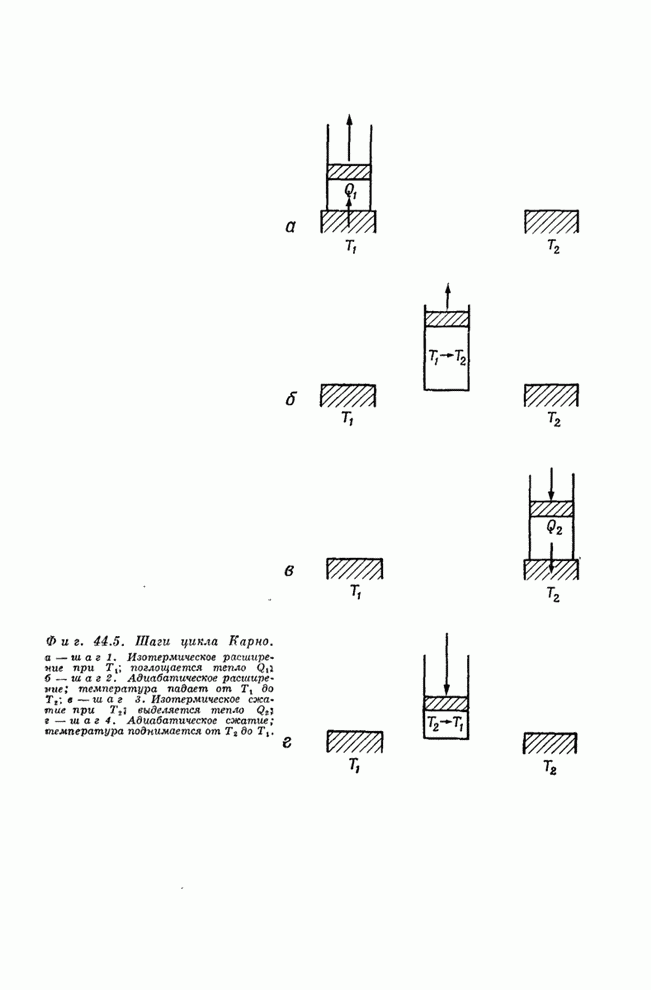
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
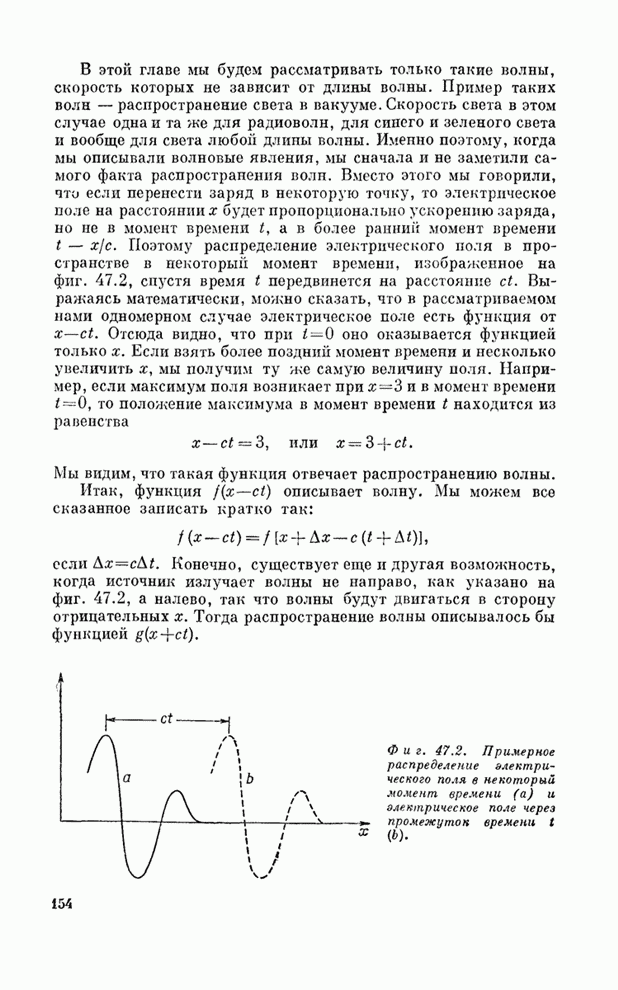
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия