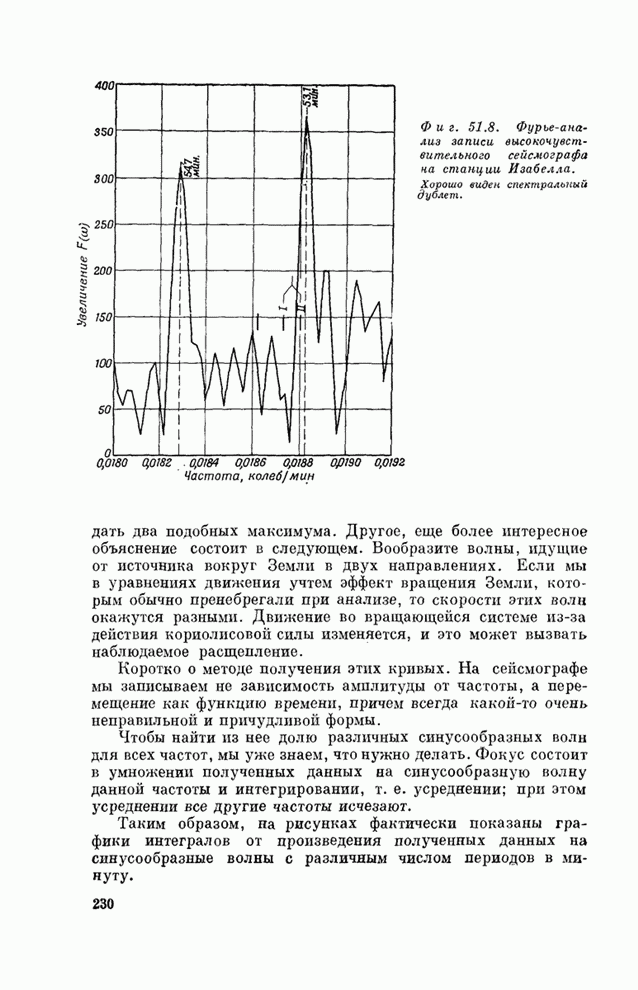
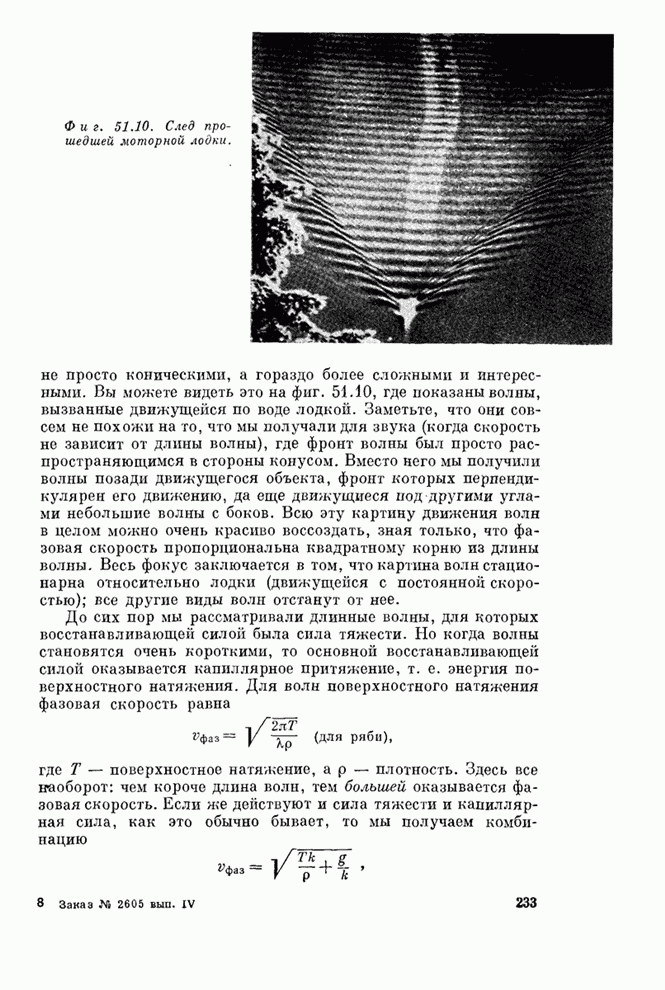
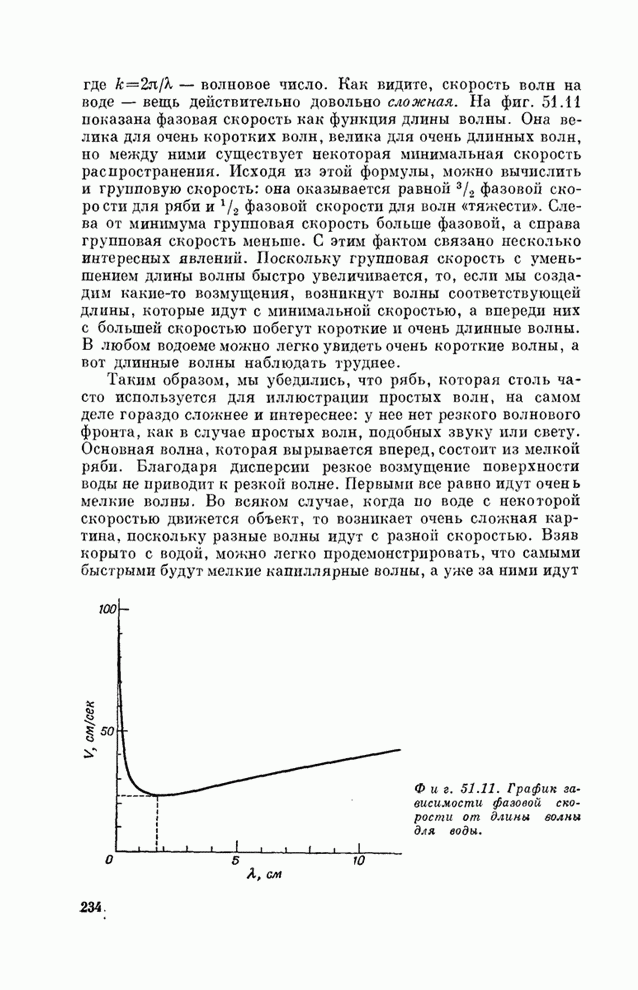
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Связанные маятники
Напоследок необходимо подчеркнуть, что гармоники возникают не только в сложных непрерывных системах, но и в очень простых механических системах. Хорошим примером этого служит рассмотренная в предыдущей главе система двух связанных маятников. Там мы показали, что общее движение этой системы можно рассматривать как суперпозицию двух типов гармонических движений с различными частотами, так что даже такую систему можно рассматривать с точки зрения собственных гармоник. В струне возбуждается бесконечное число собственных гармоник, у двумерной поверхности их тоже бесконечно много. В каком-то смысле здесь получается даже двойная бесконечность (если бы мы только знали, как работать с бесконечностями!). Но в простом механическом устройстве, обладающем только двумя степенями свободы и требующем для своего описания лишь двух переменных, возбуждаются всего две гармоники.
Попробуем
найти математически эти две гармоники для случая, когда длины маятников
одинаковы. Пусть отклонение одного маятника будет ![]() , а другого -
, а другого - ![]() , как это показано на фиг.
49.5. При отсутствии пружины сила тяжести, действующая на первый маятник,
пропорциональна его отклонению. Если бы здесь не было пружины, то для одного
маятника появилась бы некоторая собственная частота
, как это показано на фиг.
49.5. При отсутствии пружины сила тяжести, действующая на первый маятник,
пропорциональна его отклонению. Если бы здесь не было пружины, то для одного
маятника появилась бы некоторая собственная частота ![]() , а уравнение движения в
этом случае приобрело бы вид
, а уравнение движения в
этом случае приобрело бы вид
![]() . (49.13)
. (49.13)
Второй
маятник при отсутствии пружины качался бы точно так же, как и первый. Однако
при наличии пружины в дополнение к восстанавливающей силе, возникающей в
результате гравитации, появляется еще добавочная сила от пружины, которая
стремится «стянуть» маятники. Эта сила зависит от превышения отклонения ![]() над отклонением
над отклонением ![]() и пропорциональна
их разности, т. е. она равна некоторой постоянной, зависящей только от
геометрии, умноженной на
и пропорциональна
их разности, т. е. она равна некоторой постоянной, зависящей только от
геометрии, умноженной на ![]() . Та же сила, но в обратном
направлении действует на второй маятник. Поэтому уравнения движения, которые мы
должны решить, будут следующими:
. Та же сила, но в обратном
направлении действует на второй маятник. Поэтому уравнения движения, которые мы
должны решить, будут следующими:
 (49.14)
(49.14)
Чтобы
найти движение, при котором оба маятника колеблются с одинаковой частотой, мы
должны определить, насколько отклоняется каждый из них. Другими словами,
маятник ![]() и
маятник
и
маятник ![]() будут
колебаться с одинаковой частотой и с какими-то амплитудами
будут
колебаться с одинаковой частотой и с какими-то амплитудами ![]() и
и ![]() , отношение которых
фиксировано. Давайте проверим, насколько подходит такое решение:
, отношение которых
фиксировано. Давайте проверим, насколько подходит такое решение:
![]() . (49.15)
. (49.15)
Если подставить его в уравнения (49.14) и собрать подобные члены, то получим
 (49.16)
(49.16)
При
выводе этих уравнений мы сократили общий множитель ![]() и разделили все на
и разделили все на ![]() .
.

Фиг. 49.5. Два связанных маятника.
Теперь
мы видим, что получились два уравнения для, казалось бы, двух неизвестных. Однако
на самом деле здесь не два неизвестных, ибо общие масштабы движения нельзя
найти из этих уравнений. Они могут дать нам только отношение ![]() к
к ![]() , причем оба
уравнения должны дать одинаковую величину. Требование согласованности уравнений
друг с другом накладывает требование на частоту: она должна быть какой-то очень
специальной.
, причем оба
уравнения должны дать одинаковую величину. Требование согласованности уравнений
друг с другом накладывает требование на частоту: она должна быть какой-то очень
специальной.
Но найти частоту в этом частном случае довольно легко. Если перемножить оба уравнения, то мы получим
![]() . (49.17)
. (49.17)
В
обеих сторонах можно сократить произведение ![]() , за исключением тех случаев, когда
либо
, за исключением тех случаев, когда
либо ![]() ,
либо
,
либо ![]() равно
нулю, что означает отсутствие движения вообще. Но если движение есть, то должны
быть равны между собой и другие сомножители, что приводит к квадратному
уравнению. В результате получаются две возможные частоты:
равно
нулю, что означает отсутствие движения вообще. Но если движение есть, то должны
быть равны между собой и другие сомножители, что приводит к квадратному
уравнению. В результате получаются две возможные частоты:
![]() и
и
![]() . (49.18)
. (49.18)
Более
того, если подставить эти значения частот снова в уравнения (49.16), то для
первой частоты мы получим ![]() , т. е. пружина вообще не будет
растягиваться и оба маятника колеблются с частотой
, т. е. пружина вообще не будет
растягиваться и оба маятника колеблются с частотой ![]() , как если бы пружины
вообще не было. В другом решении, когда
, как если бы пружины
вообще не было. В другом решении, когда ![]() , пружина увеличивает
восстанавливающую силу и частота возрастает. Более интересен случай, когда
маятники имеют различные длины. Анализ этого случая, который очень похож на то,
что мы недавно проделали, рекомендуем в качестве упражнения провести самим
читателям.
, пружина увеличивает
восстанавливающую силу и частота возрастает. Более интересен случай, когда
маятники имеют различные длины. Анализ этого случая, который очень похож на то,
что мы недавно проделали, рекомендуем в качестве упражнения провести самим
читателям.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
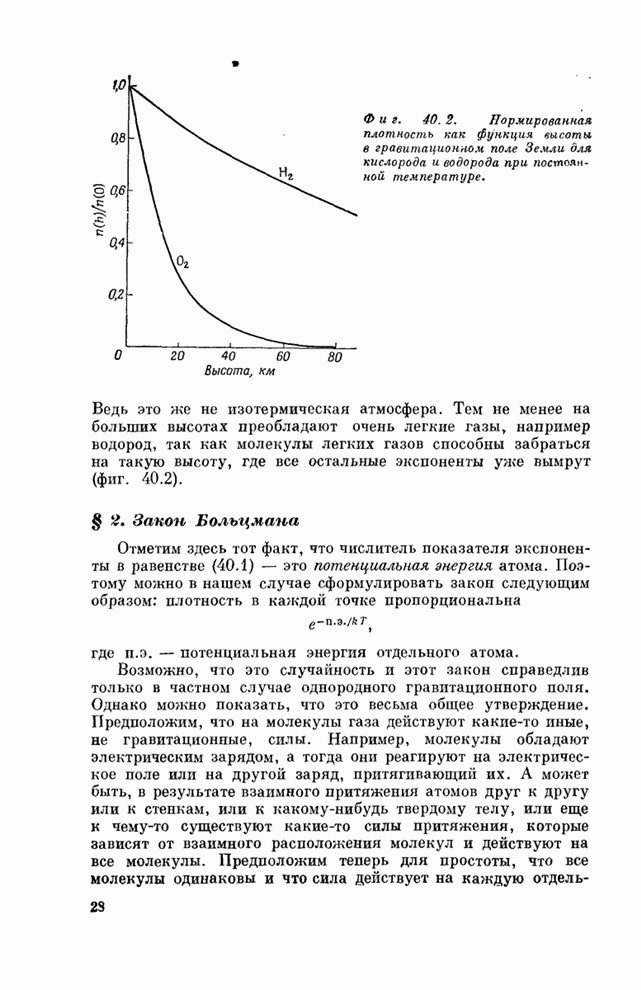
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
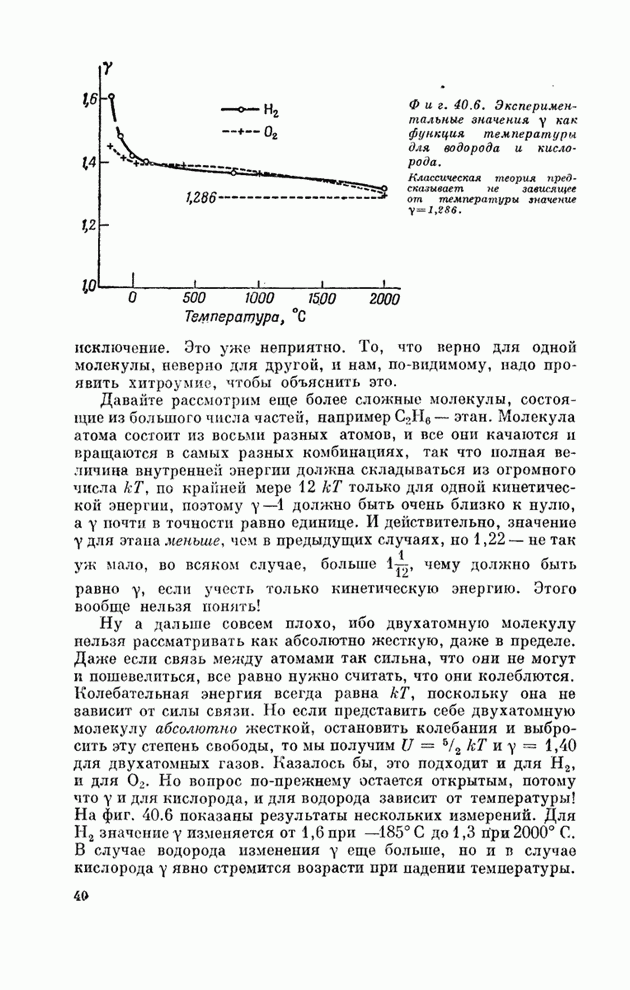
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
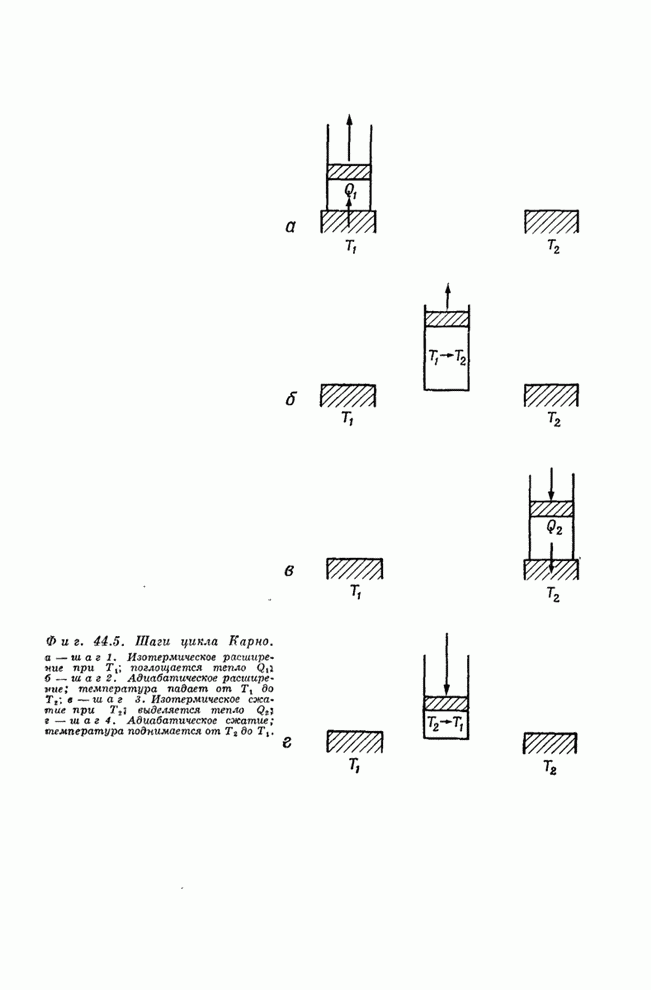
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
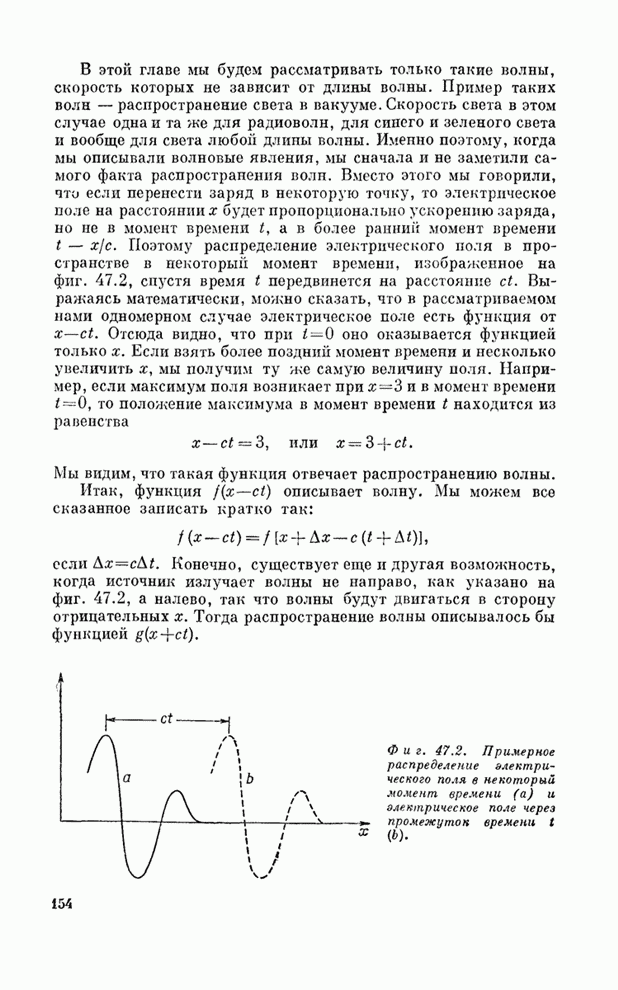
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
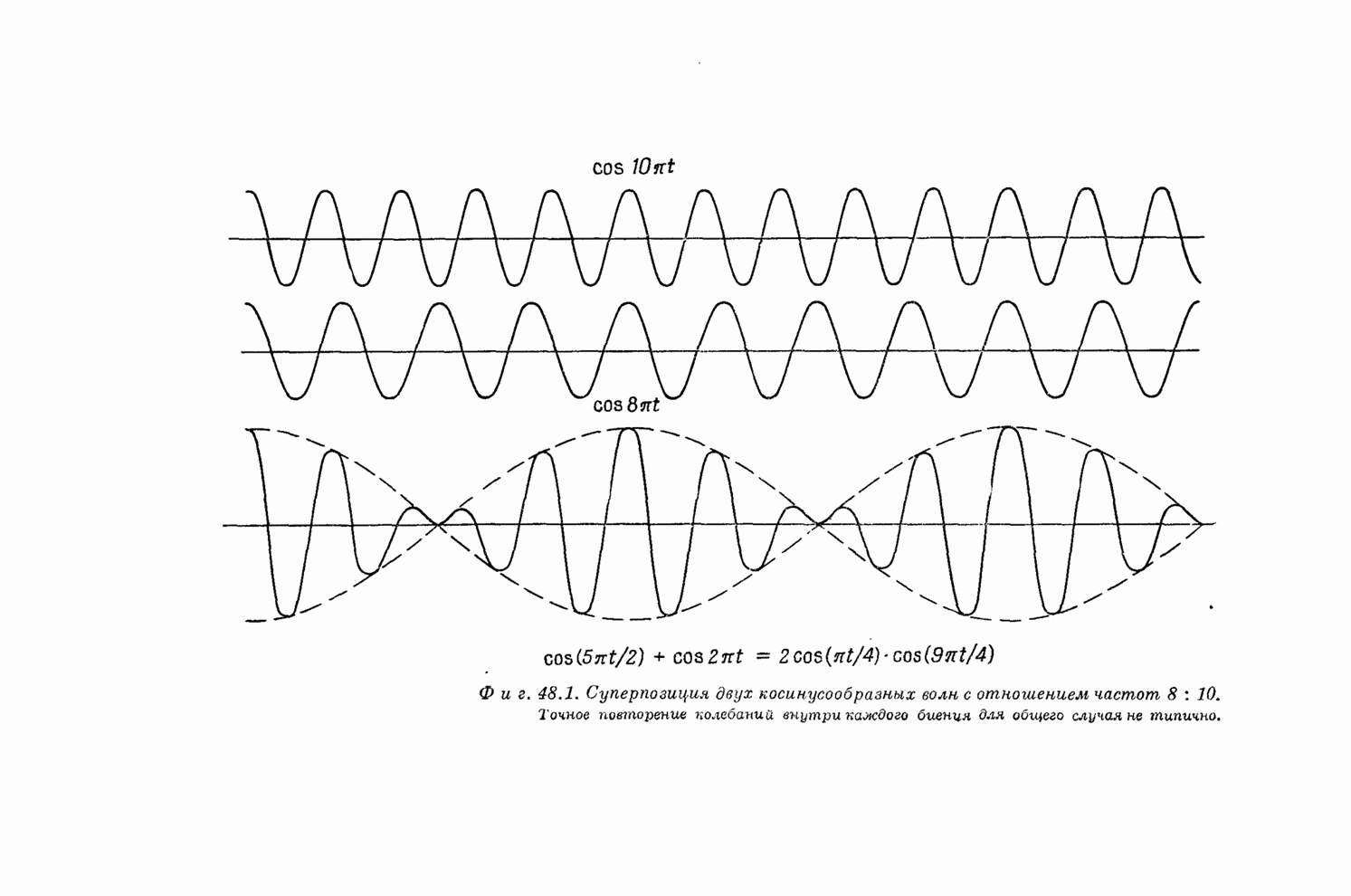
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
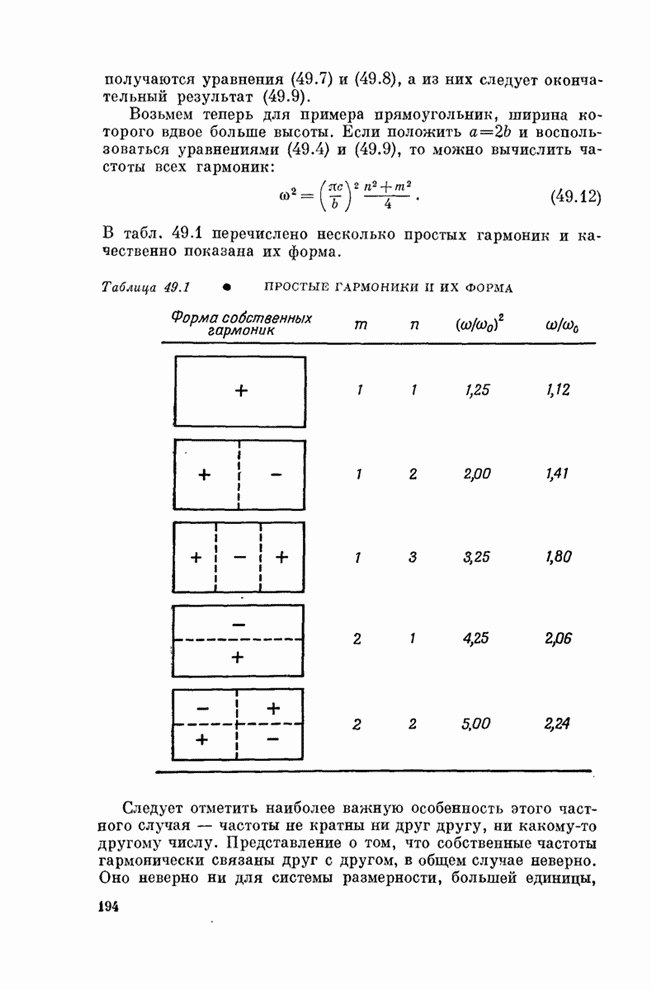
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
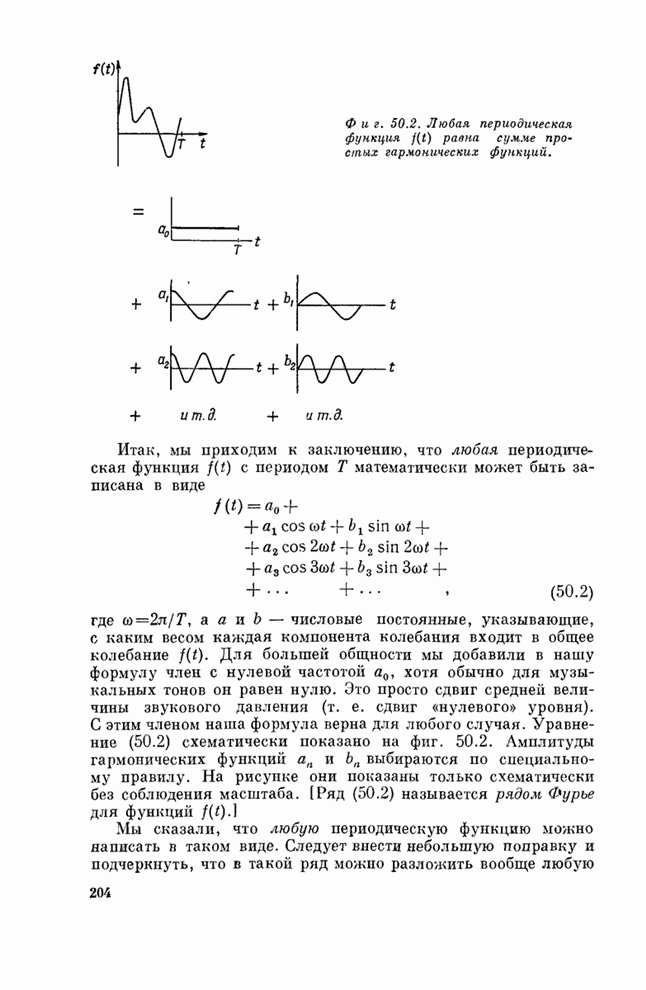
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
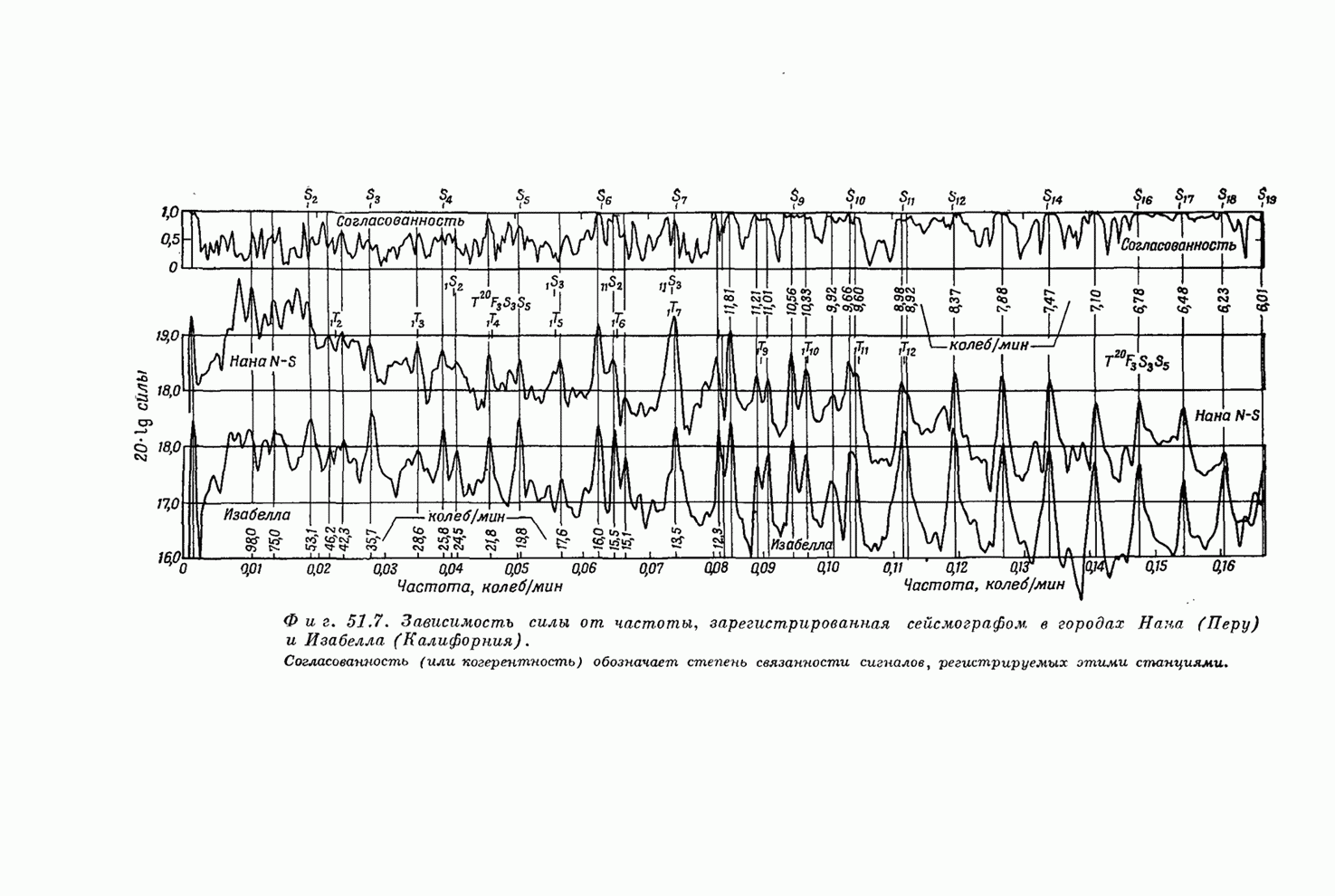
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия