| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Давление газа
Каждый знает, что газ оказывает давление. Но отчего? В этом надо разобраться как следует. Если бы наши уши были намного чувствительнее, чем они есть на самом деле, мы бы все время слышали страшный шум. Но природа позаботилась, чтобы наши уши не были столь восприимчивы, ведь они оказались бы для нас совершенно бесполезными - в них постоянно стоял бы дикий гул, похожий на шум от стартующей ракеты. Дело в том, что барабанные перепонки наших ушей соприкасаются с воздухом, а воздух состоит из великого множества беспорядочно движущихся молекул, которые, ударяясь о барабанные перепонки, создают такой шум, как будто сразу очень много барабанщиков отбивают беспорядочную дробь - бум, бум, бум... Однако мы не слышим этих звуков, потому что атомы очень малы, а уши наши недостаточно чувствительны. Беспорядочные удары молекул должны были бы собственно продавить барабанную перепонку, но ее непрестанно бомбардируют и с внутренней стороны, и в результате полная сила, действующая на перепонку, оказывается равной нулю. Если бы откачать воздух с одной стороны или хотя бы сделать разным его относительное количество с обеих сторон, то перепонка продавилась бы в ту или иную сторону, потому что бомбардировка с одной стороны оказалась бы гораздо сильнее. Мы иногда испытываем это неприятное ощущение, когда очень быстро поднимаемся в лифте или на самолете, а хуже всего, если мы еще при этом простужены (в этом случае распухшая слизистая оболочка закрывает каналы, соединяющие через носоглотку внутреннюю полость уха с внешним пространством, и таким образом оба давления не могут быстро уравняться.)
Чтобы
проанализировать это явление количественно, предположим, что газ находится в
ящике, одна стенка которого представляет собой поршень, способный перемещаться
(фиг. 39.1). Найдем силу, с которой действуют на поршень находящиеся внутри
ящика атомы. О поршень ударяются атомы, движущиеся внутри объема ![]() со всевозможными
скоростями. Предположим, что вне ящика ничего нет - сплошной вакуум. Что же
произойдет? Если предоставить поршень самому себе и не придерживать его, то с
каждым ударом молекулы он будет приобретать небольшой импульс и постепенно
будет вытолкнут совсем из ящика. Чтобы удержать его в ящике, придется приложить
силу
со всевозможными
скоростями. Предположим, что вне ящика ничего нет - сплошной вакуум. Что же
произойдет? Если предоставить поршень самому себе и не придерживать его, то с
каждым ударом молекулы он будет приобретать небольшой импульс и постепенно
будет вытолкнут совсем из ящика. Чтобы удержать его в ящике, придется приложить
силу ![]() .
Какова должна быть эта сила? Говоря о силе, мы будем относить ее к единице
площади: если площадь поршня равна
.
Какова должна быть эта сила? Говоря о силе, мы будем относить ее к единице
площади: если площадь поршня равна ![]() , то действующая на него сила будет
пропорциональна площади. Определим давление как величину, равную отношению
приложенной к поршню силы к площади поршня:
, то действующая на него сила будет
пропорциональна площади. Определим давление как величину, равную отношению
приложенной к поршню силы к площади поршня:
![]() . (39.1)
. (39.1)
Чтобы
лучше понять, для чего это делается, подсчитаем бесконечно малую работу ![]() , которую надо
затратить, чтобы протолкнуть поршень на бесконечно малое расстояние
, которую надо
затратить, чтобы протолкнуть поршень на бесконечно малое расстояние ![]() (позднее это
понадобится нам и для других целей); эта работа равна произведению силы на
расстояние или, согласно (39.1), произведению давления, площади поршня и
расстояния. Все это равно произведению давления на изменение объема, взятого с
обратным знаком:
(позднее это
понадобится нам и для других целей); эта работа равна произведению силы на
расстояние или, согласно (39.1), произведению давления, площади поршня и
расстояния. Все это равно произведению давления на изменение объема, взятого с
обратным знаком:
![]() . (39.2)
. (39.2)
(Произведение
площади ![]() на
изменение высоты
на
изменение высоты ![]() равно
изменению объема.) Знак минус в этом выражении возникает из-за того, что при
сжатии объем уменьшается; если принять это во внимание, то мы получим
правильный результат: чтобы сжать газ, надо затратить работу.
равно
изменению объема.) Знак минус в этом выражении возникает из-за того, что при
сжатии объем уменьшается; если принять это во внимание, то мы получим
правильный результат: чтобы сжать газ, надо затратить работу.

Фиг. 39. 1. Атомы газа в ящике, в котором движется поршень без трения.
Итак, с какой силой надо давить на поршень, чтобы уравновесить удары молекул? При каждом ударе поршню сообщается некий импульс. В каждую секунду поршень получает определенный импульс и начинает двигаться. Чтобы предотвратить это, приложенная нами сила за секунду должна сообщить поршню точно такой же импульс. Таким образом, сила равна импульсу, сообщенному поршню за 1 сек. Можно об этом сказать и иначе: если предоставить поршень самому себе, то он за счет бомбардировки наберет скорость и с каждым ударом будет подталкиваться и двигаться с ускорением. Быстрота изменения скорости поршня, или ускорение, пропорциональна действующей силе. Таким образом, сила, которую мы определили как произведение давления на площадь, равна импульсу, сообщенному поршню за 1 сек всеми молекулами внутри ящика.
Подсчитать импульс, передаваемый поршню за 1 сек, легко; мы сделаем это в два этапа: сначала определим импульс, переданный одним атомом при столкновении с поршнем, а потом умножим эту величину на число соударений атомов с поршнем за 1 сек. Сила и будет произведением этих двух величин.
Займемся теперь этими величинами: предположим сначала, что поршень - это идеальный «отражатель» атомов. Если это не так, то вся наша теория рухнет - поршень начнет нагреваться и произойдет много всяких событий, предсказать которые мы не в состоянии. Однако, когда снова установится равновесие, в результате окажется, что каждое столкновение будет эффективно упругим. В среднем энергия приходящих и уходящих частиц не изменяется. Таким образом, предположим, что газ находится в равновесии и поршень, будучи неподвижным, энергии не поглощает. В этом случае частица, подлетевшая к поршню с определенной скоростью, улетит от него с той же скоростью, причем масса частицы не изменится.
Если
![]() есть
скорость атома, a
есть
скорость атома, a ![]() - составляющая скорости вдоль оси
- составляющая скорости вдоль оси ![]() , то импульс «к
поршню» равен
, то импульс «к
поршню» равен ![]() ,
но раз частица «отражается», то импульс «от поршня» равен той же величине;
значит, за одно соударение поршню сообщается импульс
,
но раз частица «отражается», то импульс «от поршня» равен той же величине;
значит, за одно соударение поршню сообщается импульс ![]() .
.
Нужно
теперь подсчитать число соударений атома за 1 сек; для этого можно взять любой
промежуток времени ![]() , а потом разделить число соударений
на
, а потом разделить число соударений
на ![]() .
Много ли атомов попадает за это время в цель? Предположим, что в объеме
.
Много ли атомов попадает за это время в цель? Предположим, что в объеме ![]() заключено
заключено ![]() атомов, т. е. в
каждом единичном объеме имеется
атомов, т. е. в
каждом единичном объеме имеется ![]() атомов. Теперь заметим, что за время
атомов. Теперь заметим, что за время ![]() достигнут поршня не
все частицы, движущиеся к поршню с заданной скоростью, а только те, которые
оказались достаточно близко от него. Если частицы были очень далеко, то, хотя
они и стремятся к поршню, к сроку они не успеют. Таким образом, за время
достигнут поршня не
все частицы, движущиеся к поршню с заданной скоростью, а только те, которые
оказались достаточно близко от него. Если частицы были очень далеко, то, хотя
они и стремятся к поршню, к сроку они не успеют. Таким образом, за время ![]() о поршень ударятся
лишь те частицы, которые в начальный момент были не дальше чем на расстоянии
о поршень ударятся
лишь те частицы, которые в начальный момент были не дальше чем на расстоянии ![]() от него.
Следовательно, число соударений за время
от него.
Следовательно, число соударений за время ![]() равно числу атомов, находящихся на расстоянии,
не превышающем
равно числу атомов, находящихся на расстоянии,
не превышающем ![]() ,
а поскольку площадь поршня равна
,
а поскольку площадь поршня равна ![]() , то атомы, которые со временем
попадут в цель, занимают объем
, то атомы, которые со временем
попадут в цель, занимают объем ![]() . А число атомов, попавших в цель,
равно произведению объема на число атомов в единичном объеме
. А число атомов, попавших в цель,
равно произведению объема на число атомов в единичном объеме ![]() . Но нас, конечно,
интересует не число соударений за время
. Но нас, конечно,
интересует не число соударений за время ![]() , а мы хотим знать число соударений за
1 сек, поэтому мы делим на
, а мы хотим знать число соударений за
1 сек, поэтому мы делим на ![]() и получаем
и получаем ![]() . (Время
. (Время ![]() может быть взято очень
малым, для красоты можно писать
может быть взято очень
малым, для красоты можно писать ![]() и затем дифференцировать, но это все
одно и то же.)
и затем дифференцировать, но это все
одно и то же.)
Итак, мы нашли, что сила равна
![]() . (39.3)
. (39.3)
Обратите внимание, что если фиксировать плотность частиц, то сила оказывается пропорциональной площади! После этого давление найти очень просто:
![]() . (39.4)
. (39.4)
Теперь
надо исправить кое-какие неточности: прежде всего не все молекулы имеют одну и
ту же скорость и не все они движутся в одном направлении, так что нам
приходится иметь дело с разными ![]() ! Каждая молекула, ударяясь о поршень,
вносит свой вклад, поэтому надо взять среднее по всем молекулам. Сделав это, мы
получим
! Каждая молекула, ударяясь о поршень,
вносит свой вклад, поэтому надо взять среднее по всем молекулам. Сделав это, мы
получим
![]() . (39.5)
. (39.5)
А
не забыли ли мы множитель 2? Нет, потому что лишь половина атомов движется к
поршню. Другие летят в противоположную сторону, а усредняя по ![]() , мы усредняем как
по положительным, так и по отрицательным составляющим
, мы усредняем как
по положительным, так и по отрицательным составляющим ![]() .
.
Если
просто усреднить по ![]() , получится вдвое больший результат.
Среднее
, получится вдвое больший результат.
Среднее ![]() для
положительных
для
положительных ![]() равно
половине среднего
равно
половине среднего ![]() для всех
для всех ![]() .
.
Но
атомы прыгают в ящике как хотят, и поэтому ясно, что «![]() -направление» для них ничем
не отличается от любого другого; они движутся куда угодно: вправо - влево,
вверх - вниз, взад - вперед. Поэтому
-направление» для них ничем
не отличается от любого другого; они движутся куда угодно: вправо - влево,
вверх - вниз, взад - вперед. Поэтому ![]() (средний квадрат скорости движения в
одном направлении) равен среднему квадрату скорости в любом другом направлении
(средний квадрат скорости движения в
одном направлении) равен среднему квадрату скорости в любом другом направлении
![]() . (39.6)
. (39.6)
Используем это обстоятельство для небольшого математического трюка и обнаружим, что каждый из членов в (39.6) равен их сумме, деленной на три, а сумма - это квадрат величины скорости:
 . (39.7)
. (39.7)
Это очень хорошо, потому что теперь уже не надо заботиться о координатных осях, и формулу для давления можно записать в виде
 . (39.8)
. (39.8)
Мы
выделили множитель ![]() , потому что это кинетическая энергия
движения молекулы как целого. Итак, мы нашли
, потому что это кинетическая энергия
движения молекулы как целого. Итак, мы нашли
 . (39.9)
. (39.9)
Если мы будем знать скорость молекул, то очень быстро подсчитаем давление.
В
качестве простого примера можно описать такие газы, как гелий, пары ртути или
калия при достаточно высокой температуре или аргон; это одноатомные газы, для
которых можно считать, что их атомы не имеют внутренних степеней свободы. Если
нам попадется сложная молекула, то в ней могут быть всевозможные внутренние
движения, всякого рода колебания и т. д. Мы предполагаем, что можно не
принимать их в расчет; но можно ли это делать - вопрос сложный и мы к нему
вернемся; в действительности для нашего случая это окажется допустимым. Итак,
предположим, что внутреннее движение атомов можно не рассматривать, и поэтому
кинетическая энергия движения молекулы как целого восполняет всю энергию. Для
одноатомного газа кинетическая энергия - действительно полная энергия. Будем
обозначать полную энергию буквой ![]() (иногда ее называют полной внутренней
энергией, как-будто у газа может быть какая-то внешняя энергия), т. е. всю
энергию всех молекул газа или любого другого объекта.
(иногда ее называют полной внутренней
энергией, как-будто у газа может быть какая-то внешняя энергия), т. е. всю
энергию всех молекул газа или любого другого объекта.
В
случае одноатомного газа мы предположим, что полная энергия ![]() равна произведению числа
атомов на среднюю кинетическую энергию каждого из них, потому что мы
пренебрегли возможным возбуждением атомов или какими-то внутриатомными
движениями. Тогда
равна произведению числа
атомов на среднюю кинетическую энергию каждого из них, потому что мы
пренебрегли возможным возбуждением атомов или какими-то внутриатомными
движениями. Тогда
![]() . (39.10)
. (39.10)
Немного
задержимся и ответим на такой вопрос: предположим, что мы медленно сжимаем газ;
каким должно быть давление, чтобы сжать газ до заданного объема? Определить это
легко, так как давление есть энергия, деленная на объем. Но когда газ
сжимается, производится работа и поэтому энергия газа ![]() возрастает. Процесс сжатия
описывается неким дифференциальным уравнением. В начальный момент газ занимает
определенный объем и обладает определенной энергией, поэтому нам известно и
давление. Как только мы начинаем сжимать газ, энергия
возрастает. Процесс сжатия
описывается неким дифференциальным уравнением. В начальный момент газ занимает
определенный объем и обладает определенной энергией, поэтому нам известно и
давление. Как только мы начинаем сжимать газ, энергия ![]() возрастает, объем
возрастает, объем ![]() уменьшается, а как
изменяется давление, нам еще предстоит узнать.
уменьшается, а как
изменяется давление, нам еще предстоит узнать.
Итак, нам предстоит решить дифференциальное уравнение. Сейчас мы это сделаем. Однако подчеркнем сначала, что, сжимая газ, мы предполагаем, что вся работа уходит на увеличение энергии атомов газа. Вы спросите: «А необходимо ли на этом останавливаться? Куда же еще она может уйти?» Но оказывается, что затраченная работа может уйти и в другое место. Энергия может «вытечь» из ящика сквозь стенки: горячие (т. е. очень быстрые) атомы при бомбардировке будут нагревать стенки ящика и энергия выйдет наружу. Но мы предполагаем, что в нашем случае этого не происходит.
Сделаем
небольшое обобщение, хотя и в этом случае мы будем рассматривать лишь очень
частный случай: запишем вместо ![]()
![]() . (39.11)
. (39.11)
Энергия
![]() умножается
на
умножается
на ![]() для
удобства, потому что в дальнейшем нам придется иметь дело с газами, для которых
множитель перед
для
удобства, потому что в дальнейшем нам придется иметь дело с газами, для которых
множитель перед ![]() равен
не
равен
не ![]() , а
какому-то другому числу. Чтобы можно было описывать и такие случаи, запишем
этот множитель так, как его обозначают почти сто лет. Тогда в нашем случае
одноатомного газа, такого, как гелий,
, а
какому-то другому числу. Чтобы можно было описывать и такие случаи, запишем
этот множитель так, как его обозначают почти сто лет. Тогда в нашем случае
одноатомного газа, такого, как гелий, ![]() , потому что
, потому что ![]() .
.
Мы
уже говорили, что совершаемая при сжатии газа работа равна ![]() . Сжатие, при котором тепло
не поглощается и не выделяется, называется адиабатическим сжатием; это слово
образовано из трех греческих слов: а (не) + dia (сквозь) + bainein (проходить). (Слово
адиабатический употребляется в физике в разных смыслах, так что не всегда можно
понять, что между ними общего.) При адиабатическом сжатии вся затраченная
работа уходит на изменение внутренней энергии. Вот в этом и смысл, что нет
потерь энергии и, значит,
. Сжатие, при котором тепло
не поглощается и не выделяется, называется адиабатическим сжатием; это слово
образовано из трех греческих слов: а (не) + dia (сквозь) + bainein (проходить). (Слово
адиабатический употребляется в физике в разных смыслах, так что не всегда можно
понять, что между ними общего.) При адиабатическом сжатии вся затраченная
работа уходит на изменение внутренней энергии. Вот в этом и смысл, что нет
потерь энергии и, значит, ![]() . Но поскольку
. Но поскольку ![]() , то можно записать
, то можно записать
![]() . (39.12)
. (39.12)
Итак,
![]() или,
приводя подобные члены, получаем
или,
приводя подобные члены, получаем ![]() , или
, или
![]() . (39.13)
. (39.13)
Если
мы примем, что ![]() постоянна,
а это так в случае одноатомных газов, то уравнение интегрируется и мы получаем
постоянна,
а это так в случае одноатомных газов, то уравнение интегрируется и мы получаем ![]() , где
, где ![]() - постоянная
интегрирования. Переходя к степеням, мы получаем такой закон:
- постоянная
интегрирования. Переходя к степеням, мы получаем такой закон:
![]() (постоянная). (39.14)
(постоянная). (39.14)
Иначе
говоря, если выполнены условия адиабатичности, т. е. потерь энергии нет и газ
при сжатии нагревается, то в случае одноатомного газа произведение объема на
давление в степени ![]() есть величина постоянная! Этот
результат мы получили чисто теоретически, но опыт показывает, что и в
действительности все происходит именно так.
есть величина постоянная! Этот
результат мы получили чисто теоретически, но опыт показывает, что и в
действительности все происходит именно так.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
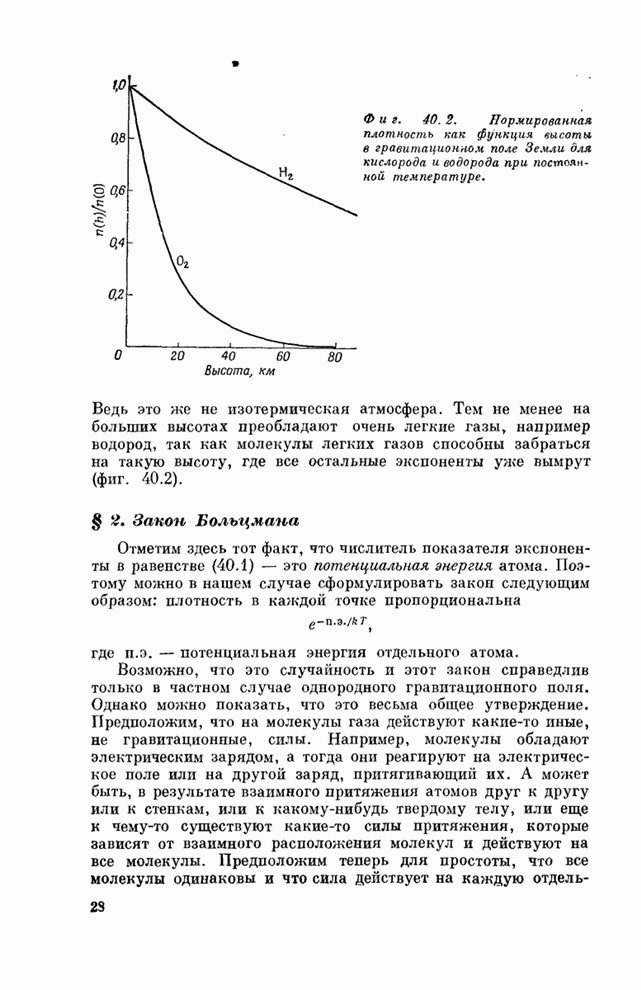
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
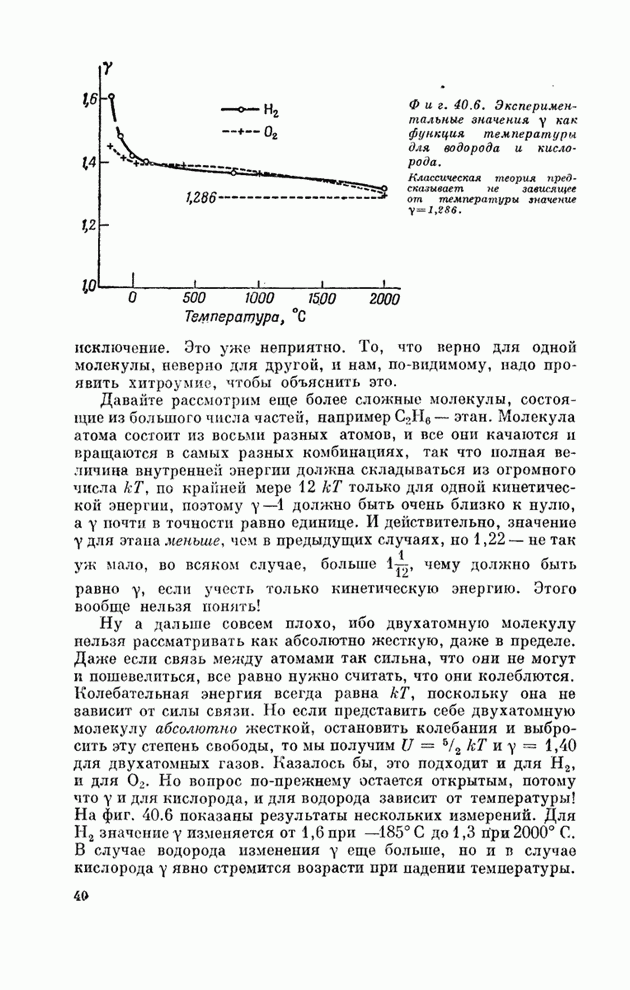
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
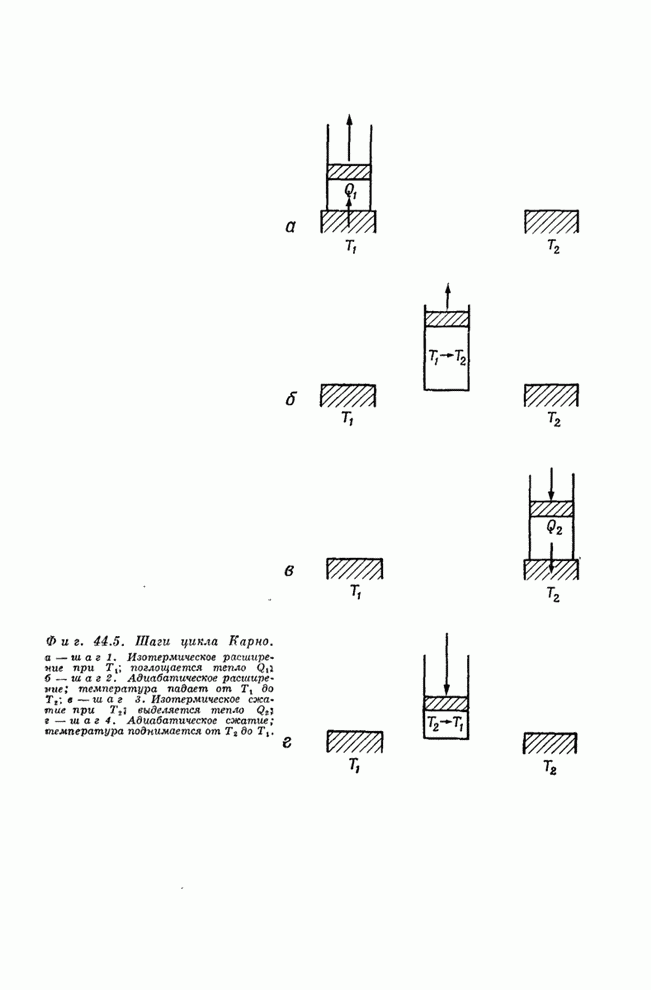
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
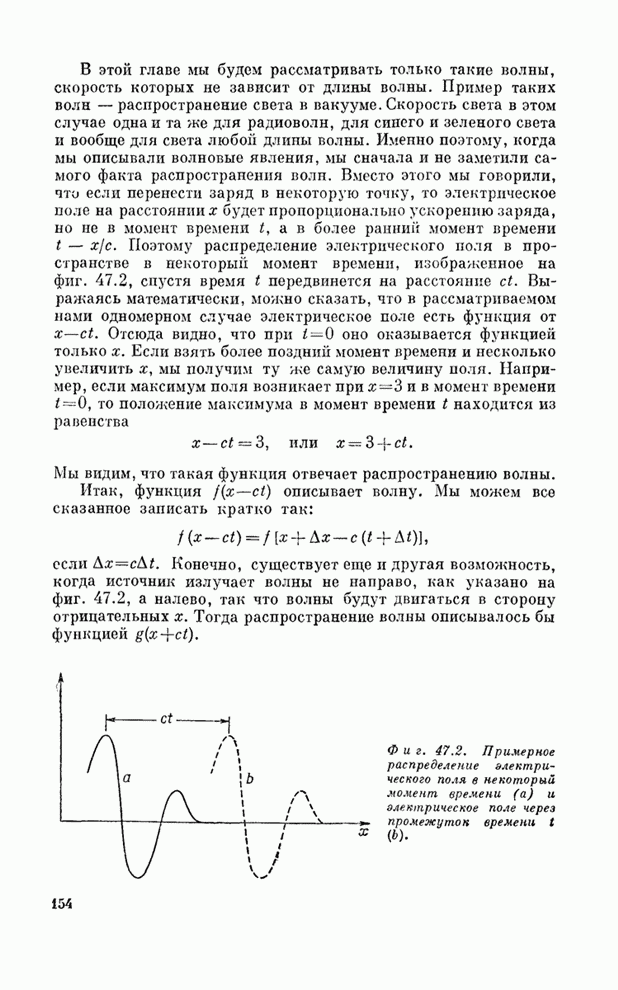
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия