| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Закон идеального газа
Теперь
можно подставить наше определение температуры в уравнение (39.9) и найти закон
зависимости давления газа от температуры: произведение давления на объем равно
произведению полного числа атомов на универсальную постоянную ![]() и температуру:
и температуру:
![]() . (39.22)
. (39.22)
Следовательно, при одинаковых температуре, давлении и объеме число атомов строго определено - это тоже универсальная постоянная! Таким образом, из законов Ньютона следует, что в равных объемах любых газов при одинаковых температуре и давлении содержится равное число молекул. Вот какой неожиданный вывод!
На
практике, когда имеешь дело с молекулами, приходится оперировать большими
числами, поэтому химики произвольно выбрали число, очень большое число, и
придумали ему специальное название. Они назвали его моль. Моль - это очень
искусственное число. Почему химики не приняли за единицу ![]() , чтобы вышло круглое число,
- это вопрос исторический.
, чтобы вышло круглое число,
- это вопрос исторический.
Случилось
так, что они для удобства выбрали стандартное число ![]() объектов и назвали это
число молем объектов. После этого, вместо того чтобы измерять число молекул в
штуках, они измеряют их в молях. Можно написать число молей (выражая их через
объектов и назвали это
число молем объектов. После этого, вместо того чтобы измерять число молекул в
штуках, они измеряют их в молях. Можно написать число молей (выражая их через ![]() ) и умножить его на
число атомов в моле, потом умножить на
) и умножить его на
число атомов в моле, потом умножить на ![]() , а затем, если захотим, выделить
произведение числа атомов в моле на
, а затем, если захотим, выделить
произведение числа атомов в моле на ![]() , тогда получится молярное значение
, тогда получится молярное значение ![]() ; для этой величины
выделим особую букву
; для этой величины
выделим особую букву ![]() . Молярное значение
. Молярное значение ![]() равно 8,317 дж:
равно 8,317 дж: ![]() . Таким образом мы
нашли газовый закон, выраженный в виде произведения числа молей (его обозначают
буквой
. Таким образом мы
нашли газовый закон, выраженный в виде произведения числа молей (его обозначают
буквой ![]() )
на
)
на ![]() , или
в виде произведения числа атомов на
, или
в виде произведения числа атомов на ![]() :
:
![]() . (39.23)
. (39.23)
Смысл
тот же самый, только единицы измерения разные. В качестве единицы мы используем
1, а химики используют ![]() !
!
Сделаем
еще одно замечание по поводу газового закона; оно касается вещей более сложных,
чем одноатомные молекулы. Пока мы имели дело только с движением одноатомного
газа в центре масс. А что если при этом учесть действие сил? Рассмотрим сначала
случай, когда поршень удерживается горизонтально расположенной пружинкой, на
которую действует сила. Взаимная встряска атомов и поршня в каждый данный
момент, конечно, не зависит от положения поршня. Условия равновесия остаются
прежними. Независимо от того, где находится поршень, от него требуется только,
чтобы скорость его движения была такой, чтобы он получал от молекул столько же
энергии, сколько отдавал им. Наличие пружинки не меняет дела. Скорость, с
которой движется поршень, в среднем та же. Таким образом, наша теорема о том,
что средняя кинетическая энергия в одном направлении равна ![]() , справедлива независимо от
того, есть силы или их нет.
, справедлива независимо от
того, есть силы или их нет.
Рассмотрим,
например, двухатомную молекулу, составленную из атомов с массами ![]() и
и ![]() . Нам удалось
доказать, что движение в центре масс части
. Нам удалось
доказать, что движение в центре масс части ![]() и части
и части ![]() таково, что
таково, что ![]() . Но как это может быть,
если отдельные части связаны друг с другом? Хотя они и связаны между собой, но
обмен энергией при взаимных вращениях, изменении расстояния и соударениях с
другими молекулами зависит только от того, как быстро они движутся. Только этим
определяется обмен энергией при соударениях. Сила в каждый отдельный момент не
имеет никакого значения. Следовательно, даже если между отдельными частями
молекулы действуют силы, верен тот же принцип.
. Но как это может быть,
если отдельные части связаны друг с другом? Хотя они и связаны между собой, но
обмен энергией при взаимных вращениях, изменении расстояния и соударениях с
другими молекулами зависит только от того, как быстро они движутся. Только этим
определяется обмен энергией при соударениях. Сила в каждый отдельный момент не
имеет никакого значения. Следовательно, даже если между отдельными частями
молекулы действуют силы, верен тот же принцип.
Докажем,
наконец, что газовый закон справедлив и в том случае, когда внутреннее движение
не учитывается. До сих пор нам не надо было включать внутреннее движение. Мы
просто рассматривали одноатомный газ. Но теперь мы покажем, что скорость центра
масс любого объекта, который можно рассматривать как тело массы ![]() , равна
, равна
![]() . (39.24)
. (39.24)
Иначе
говоря, можно рассматривать как отдельные части, так и всю молекулу в целом!
Посмотрим, почему это можно делать: масса двухатомной молекулы равна ![]() , а скорость центра
масс равна
, а скорость центра
масс равна ![]() .
Нам нужно теперь определить
.
Нам нужно теперь определить ![]() . Если возвести в квадрат
. Если возвести в квадрат ![]() , то получится
, то получится
![]() .
.
Умножив
это на ![]() и
усреднив, получим
и
усреднив, получим
![]() .
.
[Мы
воспользовались тем, что ![]() .] А чему равно
.] А чему равно ![]() ? (Хорошо бы, чтобы это было
равно нулю!) Чтобы найти это среднее, используем наше предположение, что
относительная скорость
? (Хорошо бы, чтобы это было
равно нулю!) Чтобы найти это среднее, используем наше предположение, что
относительная скорость ![]() не предпочитает какое-то одно определенное
направление остальным, т. е. средняя составляющая вдоль любого направления
равна нулю. Мы предполагаем, следовательно, что
не предпочитает какое-то одно определенное
направление остальным, т. е. средняя составляющая вдоль любого направления
равна нулю. Мы предполагаем, следовательно, что
![]() .
.
Но
что такое ![]() ?
Это скалярное произведение, равное
?
Это скалярное произведение, равное
![]() .
.
Далее,
поскольку ![]() ,
то первый и последний члены взаимно уничтожаются, и мы получаем
,
то первый и последний члены взаимно уничтожаются, и мы получаем
![]() .
.
Итак,
если ![]() , то
, то
![]() , а это
означает, что жесткому движению всей молекулы, рассматриваемой как одна частица
массы
, а это
означает, что жесткому движению всей молекулы, рассматриваемой как одна частица
массы ![]() ,
соответствует средняя кинетическая энергия, равная
,
соответствует средняя кинетическая энергия, равная ![]() .
.
Одновременно
мы доказали, что средняя кинетическая энергия внутреннего движения двухатомной
молекулы, если не учитывать движения центра масс, равна ![]() ! Ведь полная кинетическая
энергия отдельных частей молекулы равна
! Ведь полная кинетическая
энергия отдельных частей молекулы равна ![]() , а среднее ее значение - это
, а среднее ее значение - это ![]() , или
, или ![]() . Кинетическая
энергия движения центра масс равна
. Кинетическая
энергия движения центра масс равна ![]() , так что средняя кинетическая энергия
вращательного и колебательного движений двух атомов внутри молекулы - это
разность этих величин,
, так что средняя кинетическая энергия
вращательного и колебательного движений двух атомов внутри молекулы - это
разность этих величин, ![]() .
.
Теорема
о средней энергии центра масс - это весьма общая теорема: для каждого объекта,
рассматриваемого как единое целое, независимо от того, действуют на этот объект
силы или нет, средняя кинетическая энергия каждого независимого движения равна ![]() . Эти «независимые
направления движения» иногда называют степенями свободы системы. Число степеней
свободы молекулы, составленной из
. Эти «независимые
направления движения» иногда называют степенями свободы системы. Число степеней
свободы молекулы, составленной из ![]() атомов, равно
атомов, равно ![]() , потому что для определения
положения каждого атома нужны три координаты. Полную кинетическую энергию
молекулы можно представить либо как сумму кинетических энергий отдельных
атомов, либо как сумму кинетической энергии движения центра масс и кинетической
энергии внутренних движений. Последнюю иногда можно представить как сумму
кинетической энергии вращений и кинетической энергии колебаний, но это можно
сделать только приближенно. Наша теорема, если применить ее к
, потому что для определения
положения каждого атома нужны три координаты. Полную кинетическую энергию
молекулы можно представить либо как сумму кинетических энергий отдельных
атомов, либо как сумму кинетической энергии движения центра масс и кинетической
энергии внутренних движений. Последнюю иногда можно представить как сумму
кинетической энергии вращений и кинетической энергии колебаний, но это можно
сделать только приближенно. Наша теорема, если применить ее к ![]() -атомной молекуле,
гласит, что средняя кинетическая энергия молекулы равна
-атомной молекуле,
гласит, что средняя кинетическая энергия молекулы равна ![]() дж, из которых
дж, из которых ![]() - кинетическая
энергия движения молекулы как целого, а остаток
- кинетическая
энергия движения молекулы как целого, а остаток ![]() - это внутренняя кинетическая энергия
вращений и колебаний.
- это внутренняя кинетическая энергия
вращений и колебаний.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
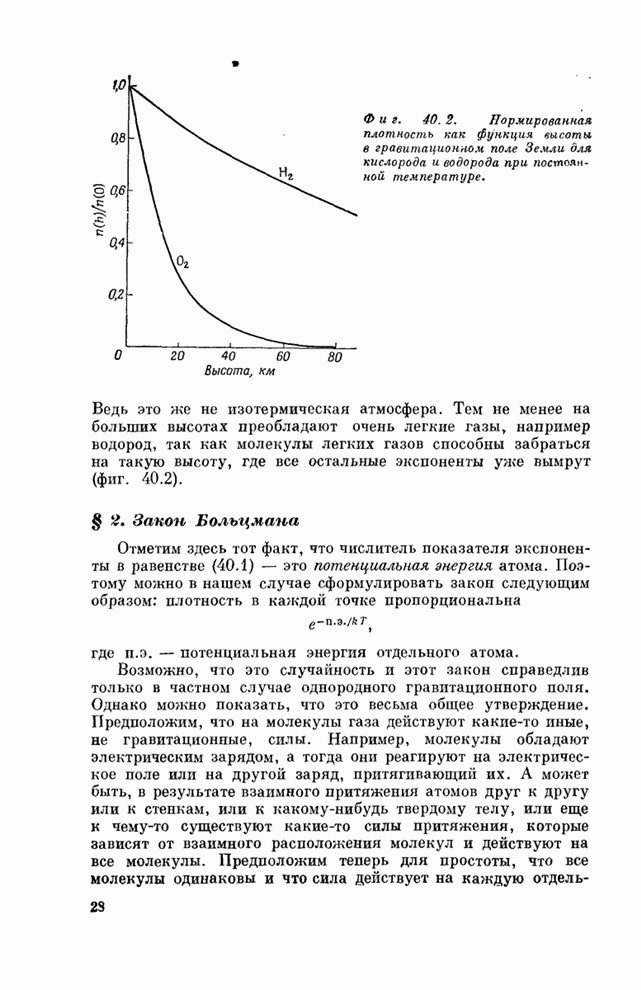
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
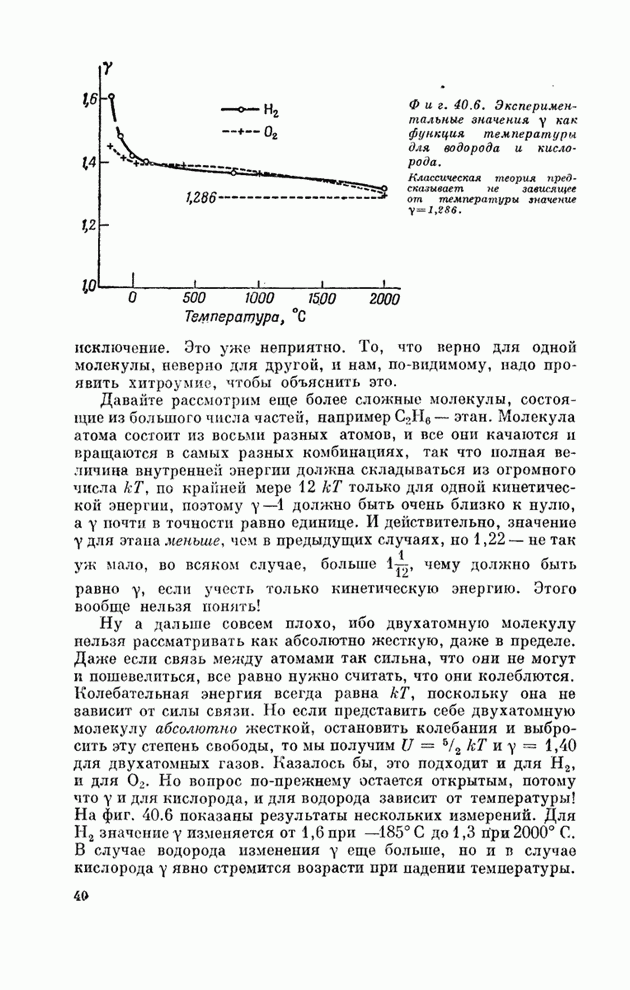
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
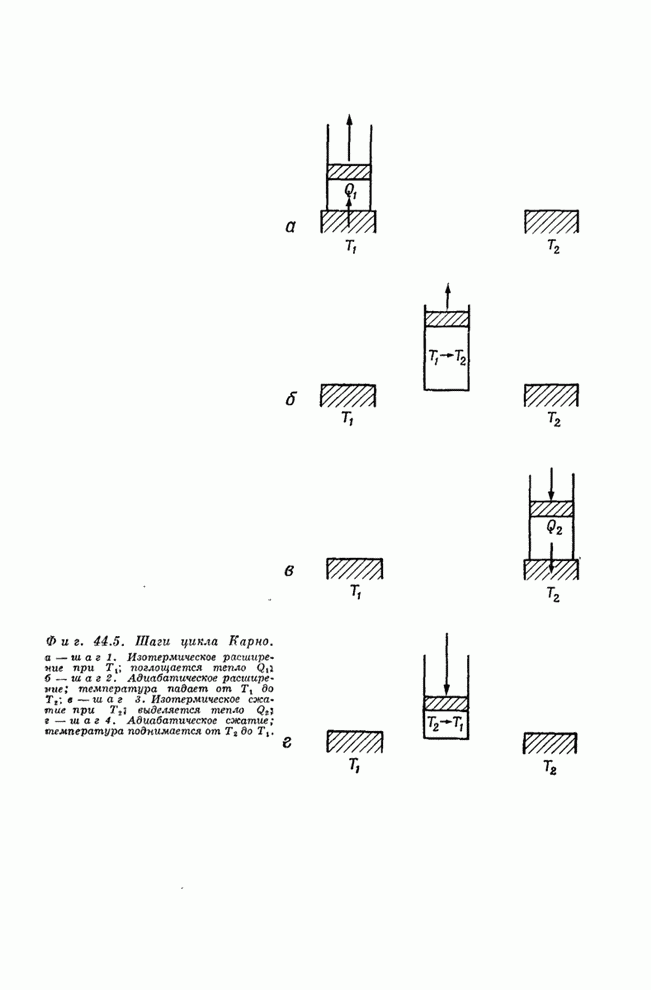
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
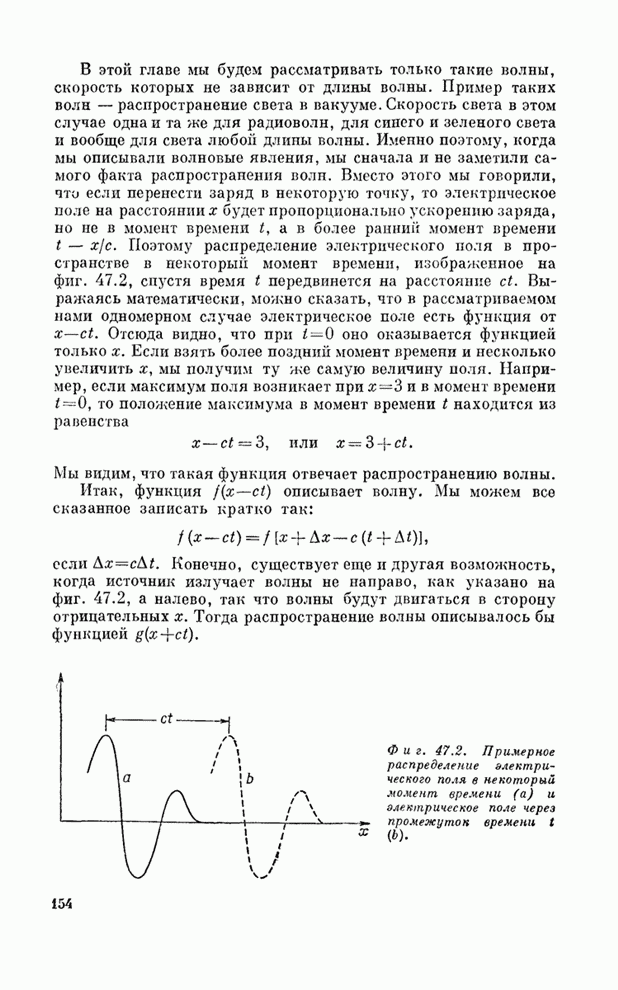
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия