| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Решения волнового уравнения
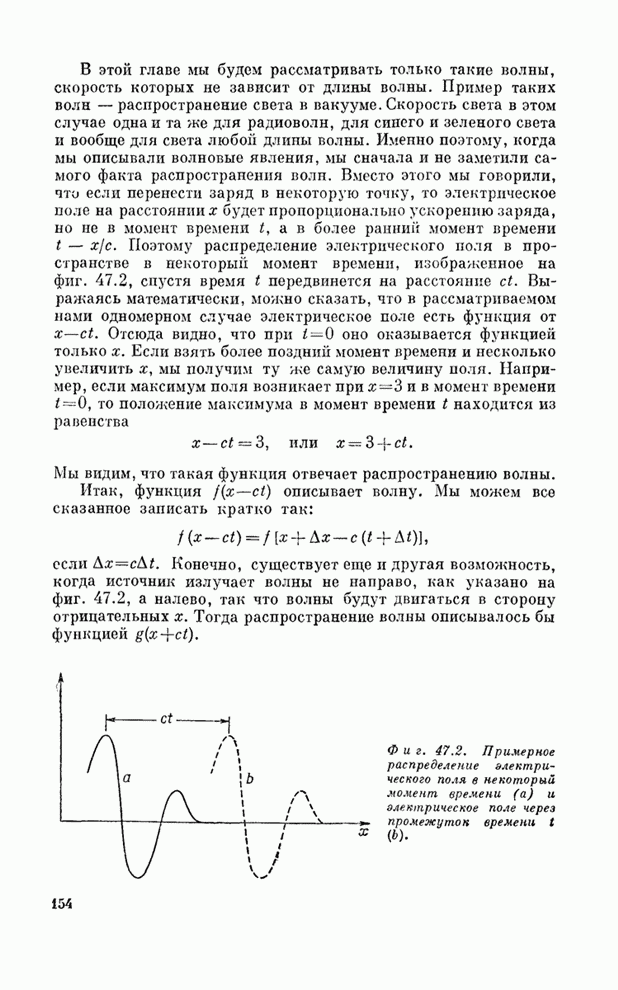
Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмущение, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно проходить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном уравнении.
Раньше
мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с
постоянной скоростью, записывается в виде ![]() . Посмотрим теперь, является ли
. Посмотрим теперь, является ли ![]() решением
волнового уравнения. Вычисляя
решением
волнового уравнения. Вычисляя ![]() , получаем производную функции
, получаем производную функции ![]() . Дифференцируя
еще раз, находим
. Дифференцируя
еще раз, находим
![]() . (47.15)
. (47.15)
Дифференцируя
эту же функцию ![]() по
по
![]() ,
получаем значение
,
получаем значение ![]() , умноженное на производную, или
, умноженное на производную, или ![]() ; вторая
производная по времени дает
; вторая
производная по времени дает
![]() . (47.16)
. (47.16)
Очевидно,
что ![]() удовлетворяет
волновому уравнению, если
удовлетворяет
волновому уравнению, если ![]() равно
равно ![]() .
.
Таким
образом, из законов механики мы получаем, что любое звуковое возмущение
распространяется со скоростью ![]() и, кроме того,
и, кроме того,
 ;
;
тем самым мы связали скорость звуковых волн со свойствами среды.
Легко
увидеть, что звуковая волна может распространяться и в направлении
отрицательных ![]() ,
т. е. звуковое возмущение вида
,
т. е. звуковое возмущение вида ![]() также удовлетворяет волновому
уравнению. Единственное отличие этой волны от той, которая распространялась
слева направо, заключается в знаке
также удовлетворяет волновому
уравнению. Единственное отличие этой волны от той, которая распространялась
слева направо, заключается в знаке ![]() , но знак
, но знак ![]() не зависит от выбора
не зависит от выбора ![]() или
или ![]() , потому что в эту
производную входит только
, потому что в эту
производную входит только ![]() . Отсюда следует, что решение
уравнения описывает волны, бегущие в любом направлении со скоростью
. Отсюда следует, что решение
уравнения описывает волны, бегущие в любом направлении со скоростью ![]() .
.
Особый
интерес представляет вопрос о суперпозиции решений. Допустим, мы нашли одно
решение, скажем ![]() .
Это значит, что вторая производная
.
Это значит, что вторая производная ![]() по
по ![]() равна второй производной
равна второй производной ![]() по
по ![]() , умноженной на
, умноженной на ![]() . И пусть есть
второе решение
. И пусть есть
второе решение ![]() ,
обладающее тем же свойством. Сложим эти два решения, тогда получается
,
обладающее тем же свойством. Сложим эти два решения, тогда получается
![]() . (47.17)
. (47.17)
Теперь
мы хотим удостовериться, что ![]() тоже представляет некую волну, т. е.
тоже представляет некую волну, т. е.
![]() тоже
удовлетворяет волновому уравнению. Это очень просто доказать, так как
тоже
удовлетворяет волновому уравнению. Это очень просто доказать, так как
![]() (47.18)
(47.18)
и вдобавок
![]() . (47.19)
. (47.19)
Отсюда
следует, что ![]() ,
так что справедливость принципа суперпозиции проверена. Само существование
принципа суперпозиции связано с тем, что волновое уравнение линейно по
,
так что справедливость принципа суперпозиции проверена. Само существование
принципа суперпозиции связано с тем, что волновое уравнение линейно по ![]() .
.
Теперь
естественно было бы ожидать, что плоская световая волна, распространяющаяся
вдоль оси ![]() и
поляризованная так, что электрическое поле направлено по оси
и
поляризованная так, что электрическое поле направлено по оси ![]() , тоже
удовлетворяет волновому уравнению
, тоже
удовлетворяет волновому уравнению
![]() , (47.20)
, (47.20)
где
![]() -
скорость света. Волновое уравнение для световой волны есть одно из следствий
уравнений Максвелла. Уравнения электродинамики приводят к волновому уравнению
для света точно так же, как уравнения механики приводят к волновому уравнению
для звука.
-
скорость света. Волновое уравнение для световой волны есть одно из следствий
уравнений Максвелла. Уравнения электродинамики приводят к волновому уравнению
для света точно так же, как уравнения механики приводят к волновому уравнению
для звука.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия