| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Температура и кинетическая энергия
До сих пор мы не имели дела с температурой; мы сознательно избегали разговоров на эту тему. Мы знаем, что если сжимать газ, энергия молекул возрастает, и мы обычно говорим, что газ при этом нагревается. Теперь надо понять, какое это имеет отношение к температуре. Нам известно, что такое адиабатическое сжатие, а как поставить опыт, чтобы можно было сказать, что он был проведен при постоянной температуре? Если взять два одинаковых ящика с газом, приставить их один к другому и подержать так довольно долго, то даже если вначале эти ящики обладали тем, что мы назвали различной температурой, то в конце концов температуры их станут одинаковыми. Что это означает? Только то, что ящики достигли того состояния, которого они в конце концов достигли бы, если бы их надолго предоставили самим себе! Состояние, в котором температуры двух тел равны - это как раз то окончательное состояние, которого достигают после длительного соприкосновения друг с другом.
Давайте
посмотрим, что случится, если ящик разделен на две части движущимся поршнем и
каждое отделение заполнено разным газом, как это показано на фиг. 39.2 (для
простоты предположим, что имеются два одноатомных газа, скажем, гелий и неон).
В отделении 1 атомы массы ![]() движутся со скоростью
движутся со скоростью ![]() , а в единице
объема их насчитывается
, а в единице
объема их насчитывается ![]() штук, в отделении 2 эти числа
соответственно равны
штук, в отделении 2 эти числа
соответственно равны ![]() ,
, ![]() и
и ![]() . При каких же условиях достигается
равновесие?
. При каких же условиях достигается
равновесие?

Фиг. 39.2. Атомы двух разных одноатомных газов, разделенных подвижным поршнем.
Разумеется,
бомбардировка слева заставляет поршень двигаться вправо и сжимает газ во втором
отделении, затем то же самое происходит справа и поршень ходит так взад и
вперед, пока давление с обеих сторон не сравняется, и тогда поршень
остановится. Мы можем устроить так, чтобы давление с обеих сторон было
одинаковым, для этого нужно, чтобы внутренние энергии, приходящиеся на
единичный объем, были одинаковыми или чтобы произведения числа частиц ![]() в единице объема
на среднюю кинетическую энергию было одинаковым в обоих отделениях. Сейчас мы
попытаемся доказать, что при равновесии должны быть одинаковы и отдельные
сомножители. Пока мы знаем только, что равны между собой произведения чисел
частиц в единичных объемах на средние кинетические энергии
в единице объема
на среднюю кинетическую энергию было одинаковым в обоих отделениях. Сейчас мы
попытаемся доказать, что при равновесии должны быть одинаковы и отдельные
сомножители. Пока мы знаем только, что равны между собой произведения чисел
частиц в единичных объемах на средние кинетические энергии
 ;
;
это следует из условия равенства давлений и из (39.8). Нам предстоит установить, что по мере постепенного приближения к равновесию, когда температуры газов сравниваются, выполняется не только это условие, а происходит и еще кое-что.
Чтобы
было яснее, предположим, что нужное давление слева в ящике достигается за счет
очень большой плотности, но малых скоростей. При больших ![]() и малых
и малых ![]() можно получить то же самое
давление, что и при малых
можно получить то же самое
давление, что и при малых ![]() и больших
и больших ![]() . Атомы, если они плотно
упакованы, могут двигаться медленно, или атомов может быть совсем немного, но
ударяют они о поршень с большей силой. Установится ли равновесие навсегда?
Сначала кажется, что поршень никуда не сдвинется и так будет всегда, но если продумать
все еще раз, то станет ясно, что мы упустили одну очень важную вещь. Дело в
том, что давление на поршень вовсе не равномерное, поршень-то раскачивается
точно также, как барабанная перепонка, о которой мы говорили в начале главы,
ведь каждый новый удар не похож на предыдущий. Получается не постоянное
равномерное давление, а скорее нечто вроде барабанной дроби - давление
непрерывно меняется, и наш поршень как бы постоянно дрожит. Предположим, что
атомы правого отделения ударяют о поршень более или менее равномерно, а слева
атомов меньше, и удары их редки, но очень энергичны. Тогда поршень то и дело
будет получать очень сильный импульс слева и отходить вправо, в сторону более
медленных атомов, причем скорость этих атомов будет возрастать. (При столкновении
с поршнем каждый атом приобретает или теряет энергию в зависимости от того, в
какую сторону движется поршень в момент столкновения.) После нескольких
столкновений поршень качнется, потом еще, еще и еще..., газ в правом отделении
будет время от времени встряхиваться, а это приведет к увеличению энергии его
атомов, и движение их ускорится. Так будет продолжаться до тех пор, пока не
уравновесятся качания поршня. А равновесие установится тогда, когда скорость
поршня станет такой, что он будет отбирать у атомов энергию так же быстро, как
и отдавать. Итак, поршень движется с какой-то средней скоростью, и нам
предстоит найти ее. Если нам это удастся, мы подойдем к решению задачи поближе,
потому что атомы должны подогнать свои скорости так, чтобы каждый газ получал
через поршень ровно столько энергии, сколько теряет.
. Атомы, если они плотно
упакованы, могут двигаться медленно, или атомов может быть совсем немного, но
ударяют они о поршень с большей силой. Установится ли равновесие навсегда?
Сначала кажется, что поршень никуда не сдвинется и так будет всегда, но если продумать
все еще раз, то станет ясно, что мы упустили одну очень важную вещь. Дело в
том, что давление на поршень вовсе не равномерное, поршень-то раскачивается
точно также, как барабанная перепонка, о которой мы говорили в начале главы,
ведь каждый новый удар не похож на предыдущий. Получается не постоянное
равномерное давление, а скорее нечто вроде барабанной дроби - давление
непрерывно меняется, и наш поршень как бы постоянно дрожит. Предположим, что
атомы правого отделения ударяют о поршень более или менее равномерно, а слева
атомов меньше, и удары их редки, но очень энергичны. Тогда поршень то и дело
будет получать очень сильный импульс слева и отходить вправо, в сторону более
медленных атомов, причем скорость этих атомов будет возрастать. (При столкновении
с поршнем каждый атом приобретает или теряет энергию в зависимости от того, в
какую сторону движется поршень в момент столкновения.) После нескольких
столкновений поршень качнется, потом еще, еще и еще..., газ в правом отделении
будет время от времени встряхиваться, а это приведет к увеличению энергии его
атомов, и движение их ускорится. Так будет продолжаться до тех пор, пока не
уравновесятся качания поршня. А равновесие установится тогда, когда скорость
поршня станет такой, что он будет отбирать у атомов энергию так же быстро, как
и отдавать. Итак, поршень движется с какой-то средней скоростью, и нам
предстоит найти ее. Если нам это удастся, мы подойдем к решению задачи поближе,
потому что атомы должны подогнать свои скорости так, чтобы каждый газ получал
через поршень ровно столько энергии, сколько теряет.
Очень
трудно рассчитать движение поршня во всех деталях; хотя все это очень легко
понять, оказывается, что проанализировать это несколько труднее. Прежде чем
приступить к такому анализу, решим другую задачу: пусть ящик заполнен
молекулами двух сортов с массами ![]() и
и ![]() , скоростями
, скоростями ![]() и
и ![]() и т. д.; теперь молекулы
смогут познакомиться поближе. Если сначала все молекулы №2 покоятся, то долго
это продолжаться не может, потому что о них будут ударять молекулы №1 и
сообщать им какую-то скорость. Если молекулы №2 могут двигаться значительно
быстрее, чем молекулы №1, то все равно рано или поздно им придется отдать часть
своей энергии более медленным молекулам. Таким образом, если ящик заполнен
смесью двух газов, то проблема состоит в определении относительной скорости
молекул обоих сортов.
и т. д.; теперь молекулы
смогут познакомиться поближе. Если сначала все молекулы №2 покоятся, то долго
это продолжаться не может, потому что о них будут ударять молекулы №1 и
сообщать им какую-то скорость. Если молекулы №2 могут двигаться значительно
быстрее, чем молекулы №1, то все равно рано или поздно им придется отдать часть
своей энергии более медленным молекулам. Таким образом, если ящик заполнен
смесью двух газов, то проблема состоит в определении относительной скорости
молекул обоих сортов.
Это тоже очень трудная задача, но мы все-таки решим ее. Сначала нам придется решить «подзадачу» (опять это один из тех случаев, когда, независимо от того как решается задача, окончательный результат запоминается легко, а вывод требует большого искусства). Предположим, что перед нами две сталкивающиеся молекулы, обладающие разными массами; во избежание осложнений мы наблюдаем за столкновением из системы их центра масс (ц. м.), откуда легче уследить за ударом молекул. По законам столкновений, выведенным из законов сохранения импульса и энергии, после столкновения молекулы могут двигаться только так, что каждая сохраняет величину своей первоначальной скорости, и изменить они могут только направление движения. Типичное столкновение выглядит так, как его изобразили на фиг. 39.3. Предположим на минутку, что мы наблюдаем столкновения, системы центра масс которых покоятся. Кроме того, надо предположить, что все молекулы движутся горизонтально. Конечно, после первого же столкновения часть молекул будет двигаться уже под каким-то углом к исходному направлению. Иначе говоря, если вначале все молекулы двигались горизонтально, то спустя некоторое время мы обнаружим уже вертикально движущиеся молекулы. После ряда других столкновений они снова изменят направление и повернутся еще на какой-то угол. Таким образом, если кому-нибудь и удастся сначала навести порядок среди молекул, то все равно они очень скоро разбредутся по разным направлениям и с каждым разом будут все больше и больше распыляться. К чему же это в конце концов приведет? Ответ: Любая пара молекул будет двигаться в произвольно выбранном направлении столь же охотно, как и в любом другом. После этого дальнейшие столкновения уже не смогут изменить распределения молекул.

Фиг. 39. 3. Столкновение двух неодинаковых молекул, если смотреть из системы центра масс.
Что имеется в виду, когда говорят о равновероятном движении в любом направлении? Конечно, нельзя говорить о вероятности движения вдоль заданной прямой – прямая слишком тонка, чтобы к ней можно было относить вероятность, а следует взять единицу «чего-нибудь». Идея заключается в том, что через заданный участок сферы с центром в точке столкновения проходит столько же молекул, сколько через любой другой участок сферы. В результате столкновений молекулы распределяются по направлениям так, что любым двум равным по площади участкам сферы будут соответствовать равные вероятности (т. е. одинаковое число прошедших через эти участки молекул).
Между
прочим, если мы будем сравнивать первоначальное направление и направление,
образующее с ним какой-то угол ![]() , то интересно, что элементарная
площадь на сфере единичного радиуса равна произведению
, то интересно, что элементарная
площадь на сфере единичного радиуса равна произведению ![]() на
на ![]() , или, что то же самое, на
дифференциал
, или, что то же самое, на
дифференциал ![]() .
Это означает, что косинус угла
.
Это означает, что косинус угла ![]() между двумя направлениями с равной
вероятностью принимает любое значение между
между двумя направлениями с равной
вероятностью принимает любое значение между ![]() и
и ![]() .
.
Теперь
нам надо вспомнить о том, что имеется на самом деле; ведь у нас нет
столкновений в системе центра масс, а сталкиваются два атома с произвольными
векторными скоростями ![]() и
и ![]() . Что происходит с ними? Мы поступим так:
снова перейдем к системе центра масс, только теперь она движется с «усредненной
по массам» скоростью
. Что происходит с ними? Мы поступим так:
снова перейдем к системе центра масс, только теперь она движется с «усредненной
по массам» скоростью ![]() . Если следить за столкновением из
системы центра масс, то оно будет выглядеть так, как это изображено на фиг.
39.3, только надо подумать об относительной скорости столкновения
. Если следить за столкновением из
системы центра масс, то оно будет выглядеть так, как это изображено на фиг.
39.3, только надо подумать об относительной скорости столкновения ![]() . Относительная
скорость равна
. Относительная
скорость равна ![]() .
Дело, следовательно, обстоит так: движется система центра масс, а в системе
центра масс молекулы сближаются с относительной скоростью
.
Дело, следовательно, обстоит так: движется система центра масс, а в системе
центра масс молекулы сближаются с относительной скоростью ![]() ; столкнувшись, они движутся
по новым направлениям. Пока все это происходит, центр масс все время движется с
одной и той же скоростью без изменений.
; столкнувшись, они движутся
по новым направлениям. Пока все это происходит, центр масс все время движется с
одной и той же скоростью без изменений.
Ну
и что же получится в конце концов? Из предыдущих рассуждений делаем следующий
вывод: при равновесии все направления ![]() равновероятны относительно
направления движения центра масс. Это означает, что в конце концов не будет
никакой корреляции между направлением относительной скорости и движением центра
масс. Если бы даже такая корреляция существовала вначале, то столкновения ее бы
разрушили и она в конце концов исчезла бы полностью. Поэтому среднее значение
косинуса угла между
равновероятны относительно
направления движения центра масс. Это означает, что в конце концов не будет
никакой корреляции между направлением относительной скорости и движением центра
масс. Если бы даже такая корреляция существовала вначале, то столкновения ее бы
разрушили и она в конце концов исчезла бы полностью. Поэтому среднее значение
косинуса угла между ![]() и
и ![]() равно нулю. Это значит, что
равно нулю. Это значит, что
![]() . (39.19)
. (39.19)
Скалярное
произведение ![]() легко
выразить через
легко
выразить через ![]() и
и
![]() :
:
 . (39.20)
. (39.20)
Займемся
сначала ![]() ;
чему равно среднее
;
чему равно среднее ![]() ? Иначе говоря, чему равно среднее
проекции скорости одной молекулы на направление скорости другой молекулы? Ясно,
что вероятности движения молекулы как в одну сторону, так и в противоположную
одинаковы. Среднее значение скорости
? Иначе говоря, чему равно среднее
проекции скорости одной молекулы на направление скорости другой молекулы? Ясно,
что вероятности движения молекулы как в одну сторону, так и в противоположную
одинаковы. Среднее значение скорости ![]() в любом направлении равно нулю.
Поэтому и в направлении
в любом направлении равно нулю.
Поэтому и в направлении ![]() среднее значение
среднее значение ![]() тоже равно нулю. Итак,
среднее значение
тоже равно нулю. Итак,
среднее значение ![]() равно
нулю! Следовательно, мы пришли к выводу, что среднее
равно
нулю! Следовательно, мы пришли к выводу, что среднее ![]() должно быть равно
должно быть равно ![]() . Это значит, что
средние кинетические энергии обеих молекул должны быть равны:
. Это значит, что
средние кинетические энергии обеих молекул должны быть равны:
![]() . (39.21)
. (39.21)
Если газ состоит из атомов двух сортов, то можно показать (и мы даже считаем, что нам удалось это сделать), что средние кинетические энергии атомов каждого сорта равны, когда газ находится в состоянии равновесия. Это означает, что тяжелые атомы движутся медленнее, чем легкие; это легко проверить, поставив эксперимент с «атомами» различных масс в воздушном желобе.
Теперь сделаем следующий шаг и покажем, что если в ящике имеются два газа, разделенные перегородкой, то по мере достижения равновесия средние кинетические энергии атомов разных газов будут одинаковы, хотя атомы и заключены в разные ящики. Рассуждение можно построить по-разному. Например, можно представить, что в перегородке проделана маленькая дырочка (фиг. 39.4), так что молекулы одного газа проходят сквозь нее, а молекулы второго слишком велики и не пролезают. Когда установится равновесие, то в том отделении, где находится смесь газов, средние кинетические энергии молекул каждого сорта сравняются. Но ведь в числе проникших сквозь дырочку молекул есть и такие, которые не потеряли при этом энергии, поэтому средняя кинетическая энергия молекул чистого газа должна быть равна средней кинетической энергии молекул смеси. Это не очень удовлетворительное доказательство, потому что ведь могло и не быть такой дырочки, сквозь которую пройдут молекулы одного газа и не смогут пройти молекулы другого.

Фиг. 39.4. Два газа в ящике, разделенном полупроницаемой перегородкой.
Давайте
вернемся к задаче о поршне. Можно показать, что кинетическая энергия поршня
тоже должна быть равна ![]() . Фактически кинетическая энергия
поршня связана только с его горизонтальным движением. Пренебрегая возможным
движением поршня вверх и вниз, мы найдем, что горизонтальному движению
соответствует кинетическая энергия
. Фактически кинетическая энергия
поршня связана только с его горизонтальным движением. Пренебрегая возможным
движением поршня вверх и вниз, мы найдем, что горизонтальному движению
соответствует кинетическая энергия ![]() . Но точно так же, исходя из
равновесия на другой стороне, можно показать, что кинетическая энергия поршня
должна быть равна
. Но точно так же, исходя из
равновесия на другой стороне, можно показать, что кинетическая энергия поршня
должна быть равна ![]() . Хотя мы повторяем предыдущее
рассуждение, возникают некоторые дополнительные трудности в связи с тем, что в
результате столкновений средние кинетические энергии поршня и молекулы газа
сравниваются, потому что поршень находится не внутри газа, а смещен в одну
сторону.
. Хотя мы повторяем предыдущее
рассуждение, возникают некоторые дополнительные трудности в связи с тем, что в
результате столкновений средние кинетические энергии поршня и молекулы газа
сравниваются, потому что поршень находится не внутри газа, а смещен в одну
сторону.
Если
вас не удовлетворит и это доказательство, то можно придумать искусственный
пример, когда равновесие обеспечивается устройством, по которому молекулы
каждого газа бьют с обеих сторон. Предположим, что сквозь поршень проходит
короткий стержень, на концах которого насажено по шару. Стержень может
двигаться сквозь поршень без трения. По каждому из шаров со всех сторон бьют
молекулы одного сорта. Пусть масса нашего устройства равна ![]() , а массы молекул газа, как
и раньше, равны
, а массы молекул газа, как
и раньше, равны ![]() и
и
![]() . В
результате столкновений с молекулами первого сорта кинетическая энергия тела
массы
. В
результате столкновений с молекулами первого сорта кинетическая энергия тела
массы ![]() равна
среднему значению
равна
среднему значению ![]() (мы уже доказали это). Точно так же,
столкновения с молекулами второго сорта заставляют тело иметь кинетическую
энергию, равную среднему значению
(мы уже доказали это). Точно так же,
столкновения с молекулами второго сорта заставляют тело иметь кинетическую
энергию, равную среднему значению ![]() . Если газы находятся в тепловом
равновесии, то кинетические энергии обоих шаров должны быть равны. Таким
образом, результат, доказанный для случая смеси газов, можно немедленно
обобщить на случай двух разных газов при одинаковой температуре.
. Если газы находятся в тепловом
равновесии, то кинетические энергии обоих шаров должны быть равны. Таким
образом, результат, доказанный для случая смеси газов, можно немедленно
обобщить на случай двух разных газов при одинаковой температуре.
Итак, если два газа имеют одинаковую температуру, то средние кинетические энергии молекул этих газов в системе центра масс равны.
Средняя
кинетическая энергия молекул - это свойство только «температуры». А будучи
свойством «температуры», а не газа, она может служить определением температуры.
Средняя кинетическая энергия молекулы, таким образом, есть некоторая функция
температуры. Но кто нам подскажет, по какой шкале отсчитывать температуру? Мы
можем сами определить шкалу температуры так, что средняя энергия будет
пропорциональна температуре. Лучше всего для этого назвать «температурой» саму
среднюю энергию. Это была бы самая простая функция, но, к несчастью, эту шкалу
уже выбрали иначе и вместо того, чтобы назвать энергию молекулы просто
«температурой», используют постоянный множитель, связывающий среднюю энергию
молекулы и градус абсолютной температуры, или градус Кельвина. Этот множитель: ![]() дж на каждый
градус Кельвина. Таким образом, если абсолютная температура газа равна
дж на каждый
градус Кельвина. Таким образом, если абсолютная температура газа равна ![]() , то средняя
кинетическая энергия молекулы равна
, то средняя
кинетическая энергия молекулы равна ![]() (множитель
(множитель ![]() введен только для удобства,
благодаря чему исчезнут множители в других формулах).
введен только для удобства,
благодаря чему исчезнут множители в других формулах).
Заметим,
что кинетическая энергия, связанная с составляющей движения в любом
направлении, равна только ![]() . Три независимых направления движения
доводят ее до
. Три независимых направления движения
доводят ее до ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
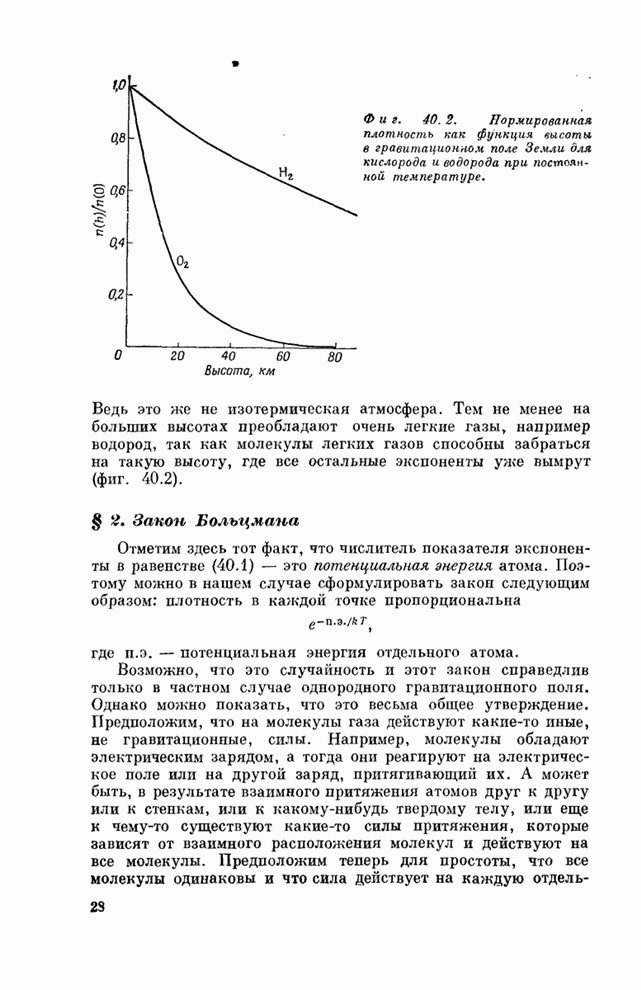
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
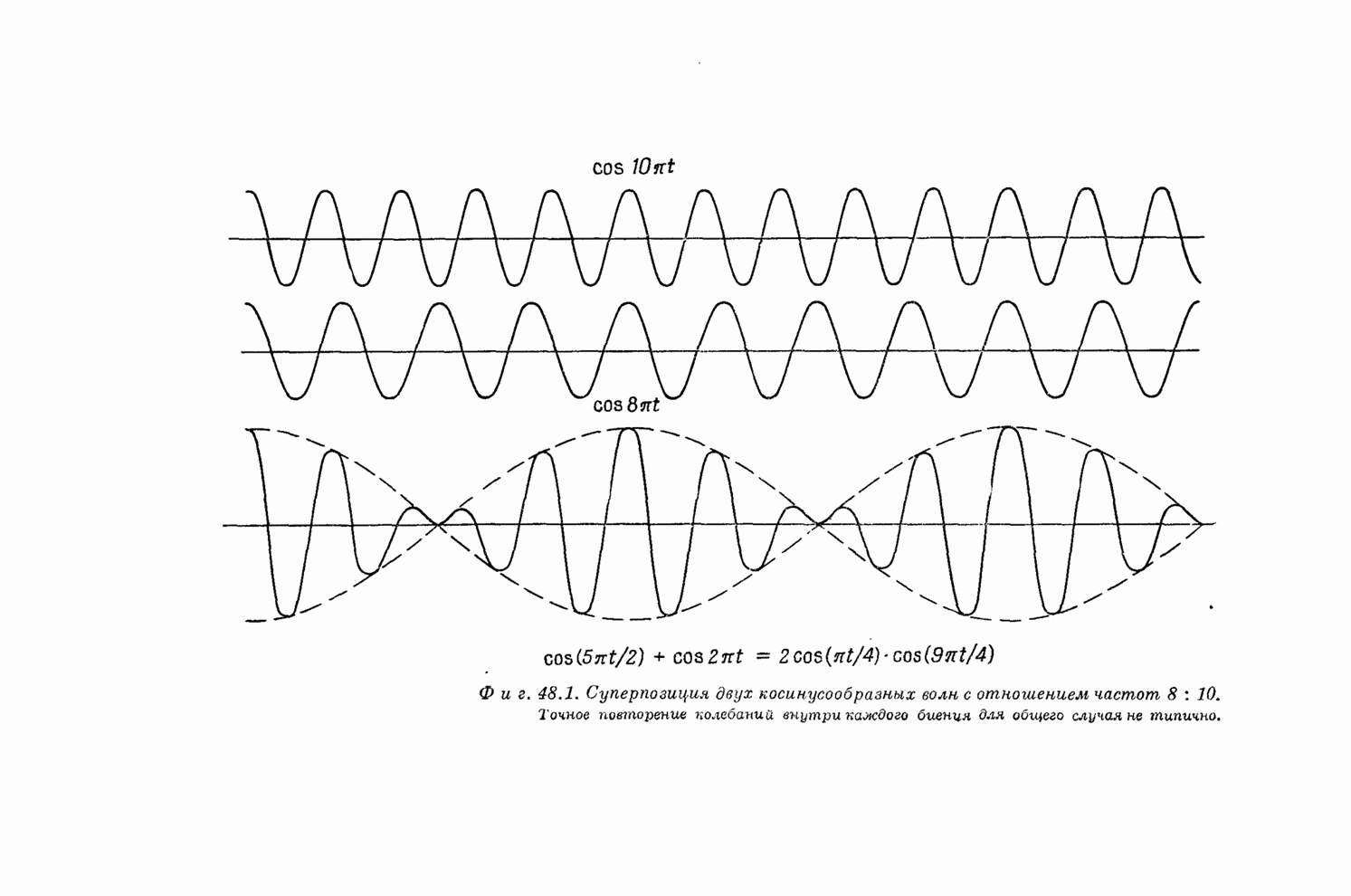
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
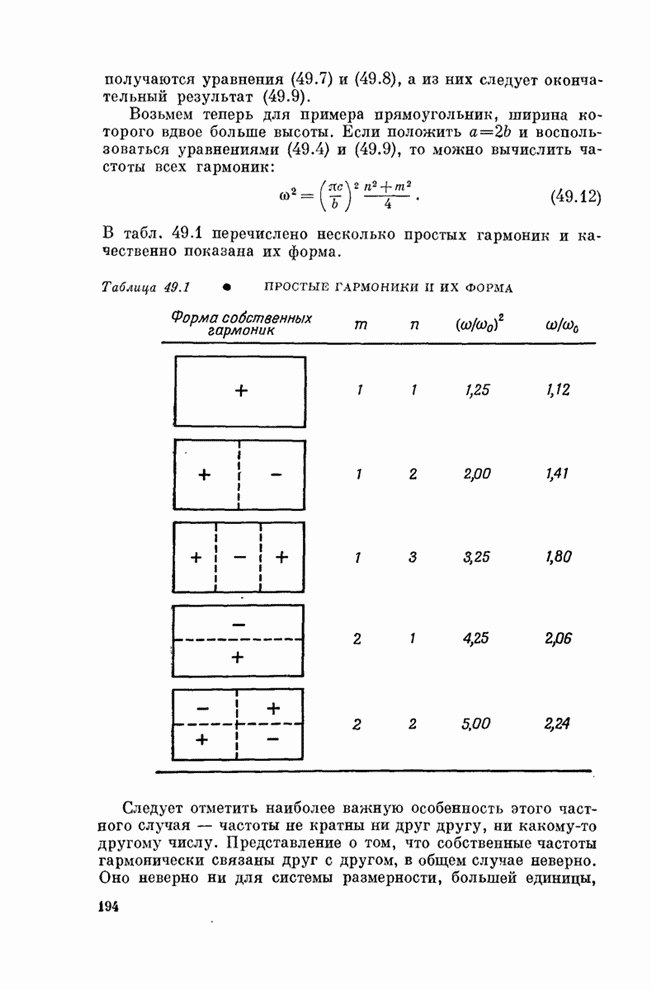
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
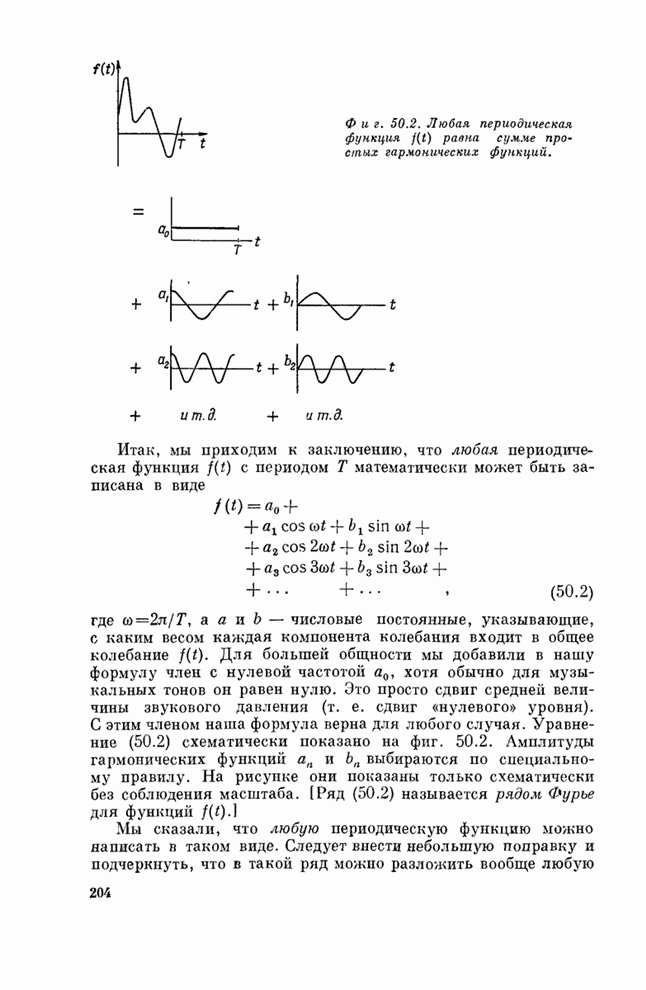
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
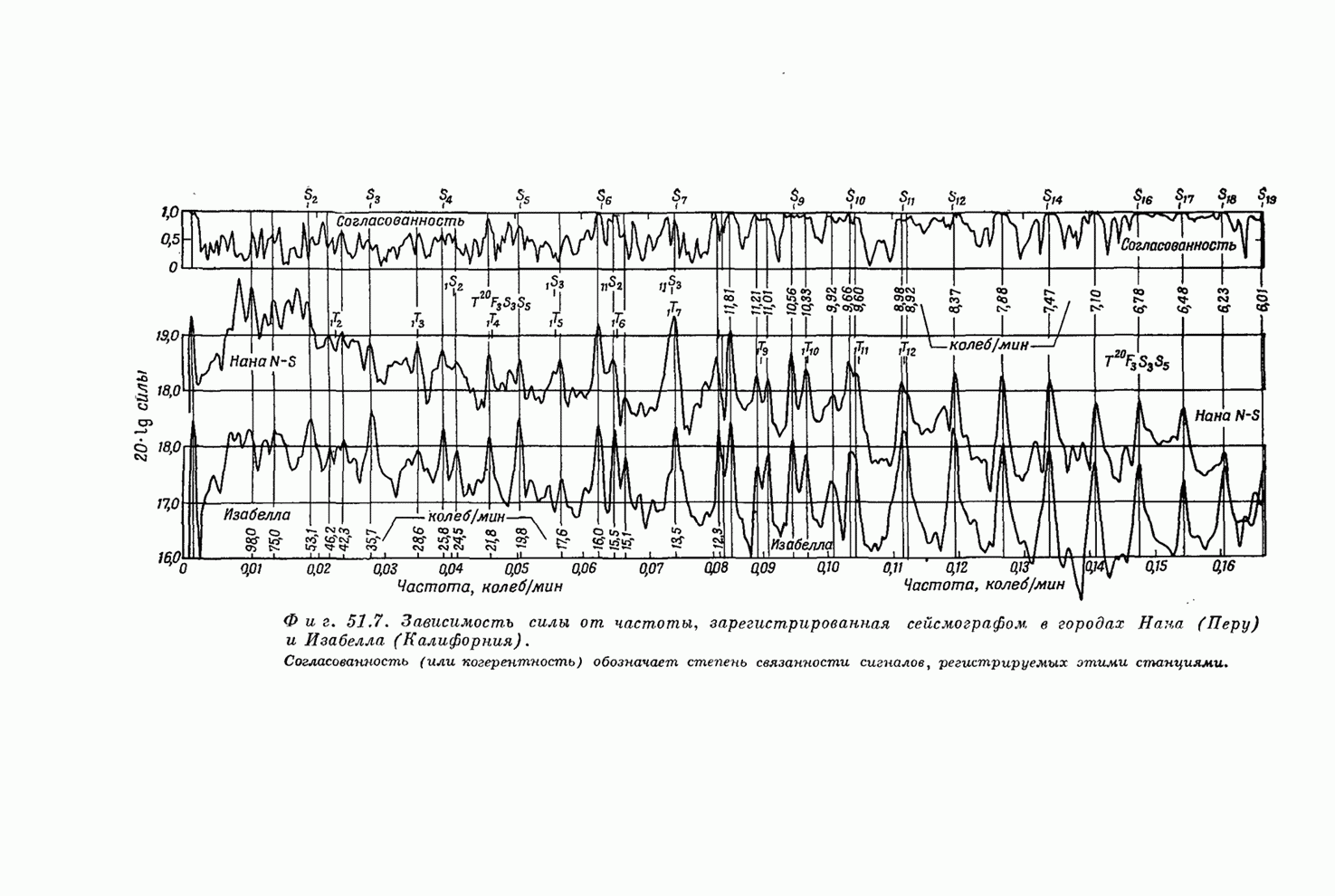
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия