| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Удельные теплоемкости газов
Посмотрим
теперь, как можно проверить теорию и оценить, насколько хороша классическая
теория газов. Мы уже говорили, что если ![]() - внутренняя энергия
- внутренняя энергия ![]() молекул, то
формула
молекул, то
формула ![]() иногда
и для некоторых газов может оказаться правильной. Мы знаем, что для
одноатомного газа правая часть равна 2/3 кинетической энергии движения центров
масс атомов. В случае одноатомного газа кинетическая энергия равна внутренней
энергии, поэтому
иногда
и для некоторых газов может оказаться правильной. Мы знаем, что для
одноатомного газа правая часть равна 2/3 кинетической энергии движения центров
масс атомов. В случае одноатомного газа кинетическая энергия равна внутренней
энергии, поэтому ![]() .
.
Но
предположим, что мы столкнулись с более сложной молекулой, которая может
вращаться и колебаться, и предположим (в классической механике это так), что
энергии внутренних движений также пропорциональны ![]() . Поэтому при заданной температуре
молекула, кроме кинетической энергии
. Поэтому при заданной температуре
молекула, кроме кинетической энергии ![]() , имеет внутреннюю энергию колебания
и вращения. Тогда полная энергия
, имеет внутреннюю энергию колебания
и вращения. Тогда полная энергия ![]() включает не только кинетическую
энергию, но и вращательную энергию и мы получаем другие значения
включает не только кинетическую
энергию, но и вращательную энергию и мы получаем другие значения ![]() . Наилучший способ
измерения
. Наилучший способ
измерения ![]() -
это измерение удельной теплоемкости, характеризующей изменение энергии при
изменении температуры. К этому способу мы еще вернемся, а пока предположим, что
нам удалось экспериментально определить
-
это измерение удельной теплоемкости, характеризующей изменение энергии при
изменении температуры. К этому способу мы еще вернемся, а пока предположим, что
нам удалось экспериментально определить ![]() с помощью кривой
с помощью кривой ![]() , соответствующей
адиабатическому сжатию.
, соответствующей
адиабатическому сжатию.
Попробуем
вычислить ![]() для
ряда частных случаев. Прежде всего для одноатомных газов полная энергия
для
ряда частных случаев. Прежде всего для одноатомных газов полная энергия ![]() есть не что иное,
как кинетическая энергия, и в этом случае, как мы уже знаем,
есть не что иное,
как кинетическая энергия, и в этом случае, как мы уже знаем, ![]() равно 5/3. В
качестве примера двухатомных газов рассмотрим кислород, водород, пары иода и т.
д. и предположим, что двухатомный газ можно представить как собрание пар
атомов, между которыми действуют силы, похожие на те, что изображены на фиг.
40.3. Можно также предположить, и оказывается, что это вполне законно, что при
температурах, обычных для диатомных газов, пары атомов стремятся удалиться друг
от друга на расстояние
равно 5/3. В
качестве примера двухатомных газов рассмотрим кислород, водород, пары иода и т.
д. и предположим, что двухатомный газ можно представить как собрание пар
атомов, между которыми действуют силы, похожие на те, что изображены на фиг.
40.3. Можно также предположить, и оказывается, что это вполне законно, что при
температурах, обычных для диатомных газов, пары атомов стремятся удалиться друг
от друга на расстояние ![]() (расстояние минимума потенциальной
энергии). Если бы это было не так, и вероятность не очень сильно зависела от
удаления от равновесной конфигурации, то мы обнаружили бы, что кислород есть
смесь сравнимых количеств
(расстояние минимума потенциальной
энергии). Если бы это было не так, и вероятность не очень сильно зависела от
удаления от равновесной конфигурации, то мы обнаружили бы, что кислород есть
смесь сравнимых количеств ![]() и одиночных атомов кислорода. А мы
знаем, что в кислороде присутствует очень мало одиночных атомов кислорода, а
это означает, что глубина потенциальной ямы значительно больше
и одиночных атомов кислорода. А мы
знаем, что в кислороде присутствует очень мало одиночных атомов кислорода, а
это означает, что глубина потенциальной ямы значительно больше ![]() , и это как раз мы
и предполагали. Но раз атомы, составляющие молекулу, прочно закреплены на расстоянии
, и это как раз мы
и предполагали. Но раз атомы, составляющие молекулу, прочно закреплены на расстоянии
![]() , то нам
понадобится лишь часть потенциальной кривой вблизи минимума, которую в этом
случае можно приближенно заменить параболой. Параболический потенциал
соответствует гармоническому осциллятору, и, в самом деле, отличной моделью
молекулы кислорода могут служить два соединенных пружинкой атома.
, то нам
понадобится лишь часть потенциальной кривой вблизи минимума, которую в этом
случае можно приближенно заменить параболой. Параболический потенциал
соответствует гармоническому осциллятору, и, в самом деле, отличной моделью
молекулы кислорода могут служить два соединенных пружинкой атома.
Но
чему же равна полная энергия молекулы при температуре ![]() ? Мы знаем, что
кинетическая энергия каждого из атомов равна
? Мы знаем, что
кинетическая энергия каждого из атомов равна ![]() , так что кинетическая энергия обоих
атомов равна
, так что кинетическая энергия обоих
атомов равна ![]() .
Можно распределить эту энергию иначе: тогда те же самые 3/2 плюс 3/2 будут
выглядеть как кинетическая энергия центра масс (3/2), кинетическая энергия
вращения (2/2) и кинетическая энергия колебаний (1/2). Известно, что на долю
кинетической энергии колебаний приходится 1/2, потому что это одномерное
движение, а каждой степени свободы соответствует
.
Можно распределить эту энергию иначе: тогда те же самые 3/2 плюс 3/2 будут
выглядеть как кинетическая энергия центра масс (3/2), кинетическая энергия
вращения (2/2) и кинетическая энергия колебаний (1/2). Известно, что на долю
кинетической энергии колебаний приходится 1/2, потому что это одномерное
движение, а каждой степени свободы соответствует ![]() . Обращаясь к вращениям, мы можем
выделить две оси вращения, что соответствует двум независимым движениям. Мы
представляем себе атомы в виде точек, которые не могут вращаться вокруг
соединяющей их линии. Но на всякий случай запомним о таком предположении,
потому что если мы упремся где-то в тупик, то, может быть, здесь обнаружится
корень зла. Нас должен интересовать еще и другой вопрос: чему равна
потенциальная энергия колебаний, велика ли она? Средняя потенциальная энергия
гармонического осциллятора равна средней кинетической энергии, т.е. также
. Обращаясь к вращениям, мы можем
выделить две оси вращения, что соответствует двум независимым движениям. Мы
представляем себе атомы в виде точек, которые не могут вращаться вокруг
соединяющей их линии. Но на всякий случай запомним о таком предположении,
потому что если мы упремся где-то в тупик, то, может быть, здесь обнаружится
корень зла. Нас должен интересовать еще и другой вопрос: чему равна
потенциальная энергия колебаний, велика ли она? Средняя потенциальная энергия
гармонического осциллятора равна средней кинетической энергии, т.е. также ![]() . Полная энергия
молекулы
. Полная энергия
молекулы ![]() ,
или
,
или ![]() на
атом. Это означает, что
на
атом. Это означает, что ![]() равно 9/7, а не 5/3, т. е.
равно 9/7, а не 5/3, т. е. ![]() .
.
Можно
сравнить эти числа с действительно измеренными значениями ![]() , приведенными в табл.
40.1. Взгляните сначала на гелий; это одноатомный газ, и значение
, приведенными в табл.
40.1. Взгляните сначала на гелий; это одноатомный газ, и значение ![]() очень близко к 5/3;
отклонение от этого значения, вероятно, есть просто следствие экспериментальных
неточностей, хотя при столь низких температурах между атомами могут появиться
силы взаимодействия. Криптон и аргон - еще два одноатомных газа - также дают
согласующиеся значения в пределах ошибки эксперимента.
очень близко к 5/3;
отклонение от этого значения, вероятно, есть просто следствие экспериментальных
неточностей, хотя при столь низких температурах между атомами могут появиться
силы взаимодействия. Криптон и аргон - еще два одноатомных газа - также дают
согласующиеся значения в пределах ошибки эксперимента.
Таблица
40.1 ИЗМЕРЕННЫЕ ЗНАЧЕНИЯ ![]() ДЛЯ РАЗЛИЧНЫХ ГАЗОВ
ДЛЯ РАЗЛИЧНЫХ ГАЗОВ
|
Газ |
|
|
Газ |
|
|
|
Не |
-180 |
1,660 |
HI |
100 |
1,40 |
|
Kr |
19 |
1,68 |
|
300 |
1,32 |
|
Аr |
15 |
1,668 |
|
185 |
1,30 |
|
|
100 |
1,404 |
|
15 |
1,310 |
|
|
100 |
1,399 |
|
15 |
1,22 |
Перейдем
к двухатомным газам. Тут же обнаружится, что значение ![]() для водорода, равное
1,404, не согласуется с теоретическим значением 1,286. Очень близкое значение
дает и кислород, 1,399, но с теоретическим это снова не согласуется. Для
йодистого водорода
для водорода, равное
1,404, не согласуется с теоретическим значением 1,286. Очень близкое значение
дает и кислород, 1,399, но с теоретическим это снова не согласуется. Для
йодистого водорода ![]() равно просто 1,40. Начинает
казаться, что мы нашли общий закон: для двухатомных молекул
равно просто 1,40. Начинает
казаться, что мы нашли общий закон: для двухатомных молекул ![]() равно 1,40. Но нет,
поглядите дальше. Для брома мы получаем 1,32, а для иода 1,30. Поскольку 1,30
довольно близко к 1,286, то можно считать, что экспериментальное значение
равно 1,40. Но нет,
поглядите дальше. Для брома мы получаем 1,32, а для иода 1,30. Поскольку 1,30
довольно близко к 1,286, то можно считать, что экспериментальное значение ![]() для иода
согласуется с теоретическим, а кислород представляет собой исключение. Это уже
неприятно. То, что верно для одной молекулы, неверно для другой, и нам,
по-видимому, надо проявить хитроумие, чтобы объяснить это.
для иода
согласуется с теоретическим, а кислород представляет собой исключение. Это уже
неприятно. То, что верно для одной молекулы, неверно для другой, и нам,
по-видимому, надо проявить хитроумие, чтобы объяснить это.
Давайте
рассмотрим еще более сложные молекулы, состоящие из большого числа частей,
например ![]() -
этан. Молекула атома состоит из восьми разных атомов, и все они качаются и
вращаются в самых разных комбинациях, так что полная величина внутренней
энергии должна складываться из огромного числа
-
этан. Молекула атома состоит из восьми разных атомов, и все они качаются и
вращаются в самых разных комбинациях, так что полная величина внутренней
энергии должна складываться из огромного числа ![]() , по крайней мере
, по крайней мере ![]() только для одной
кинетической энергии, поэтому
только для одной
кинетической энергии, поэтому ![]() должно быть очень близко к нулю, а
должно быть очень близко к нулю, а ![]() почти в точности
равно единице. И действительно, значение
почти в точности
равно единице. И действительно, значение ![]() для этана меньше, чем в предыдущих
случаях, но 1,22 - не так уж мало, во всяком случае, больше
для этана меньше, чем в предыдущих
случаях, но 1,22 - не так уж мало, во всяком случае, больше ![]() , чему должно быть равно
, чему должно быть равно ![]() , если учесть
только кинетическую энергию. Этого вообще нельзя понять!
, если учесть
только кинетическую энергию. Этого вообще нельзя понять!
Ну
а дальше совсем плохо, ибо двухатомную молекулу нельзя рассматривать как
абсолютно жесткую, даже в пределе. Даже если связь между атомами так сильна,
что они не могут и пошевелиться, все равно нужно считать, что они колеблются.
Колебательная энергия всегда равна ![]() , поскольку она не зависит от силы
связи. Но если представить себе двухатомную молекулу абсолютно жесткой,
остановить колебания и выбросить эту степень свободы, то мы получим
, поскольку она не зависит от силы
связи. Но если представить себе двухатомную молекулу абсолютно жесткой,
остановить колебания и выбросить эту степень свободы, то мы получим ![]() и
и ![]() для двухатомных
газов. Казалось бы, это подходит и для
для двухатомных
газов. Казалось бы, это подходит и для ![]() , и для
, и для ![]() . Но вопрос по-прежнему остается
открытым, потому что
. Но вопрос по-прежнему остается
открытым, потому что ![]() и для кислорода, и для водорода
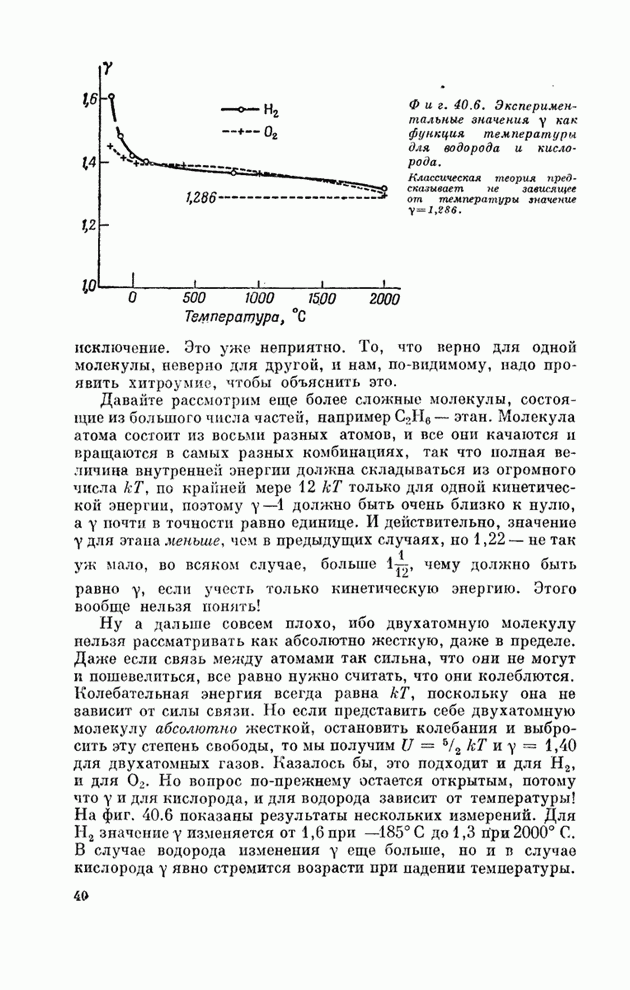
зависит от температуры! На фиг. 40.6 показаны результаты нескольких измерений.
Для
и для кислорода, и для водорода
зависит от температуры! На фиг. 40.6 показаны результаты нескольких измерений.
Для ![]() значение
значение
![]() изменяется
от 1,6 при -185°С до 1,3 при 2000°С. В случае водорода изменения
изменяется
от 1,6 при -185°С до 1,3 при 2000°С. В случае водорода изменения ![]() еще больше, но и
в случае кислорода
еще больше, но и
в случае кислорода ![]() явно стремится возрасти при падении
температуры.
явно стремится возрасти при падении
температуры.

Фиг. 40.6. Экспериментальные
значения ![]() как
функция температура для водорода и кислорода.
как
функция температура для водорода и кислорода.
Классическая теория предсказывает
не зависящее от температуры значение ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
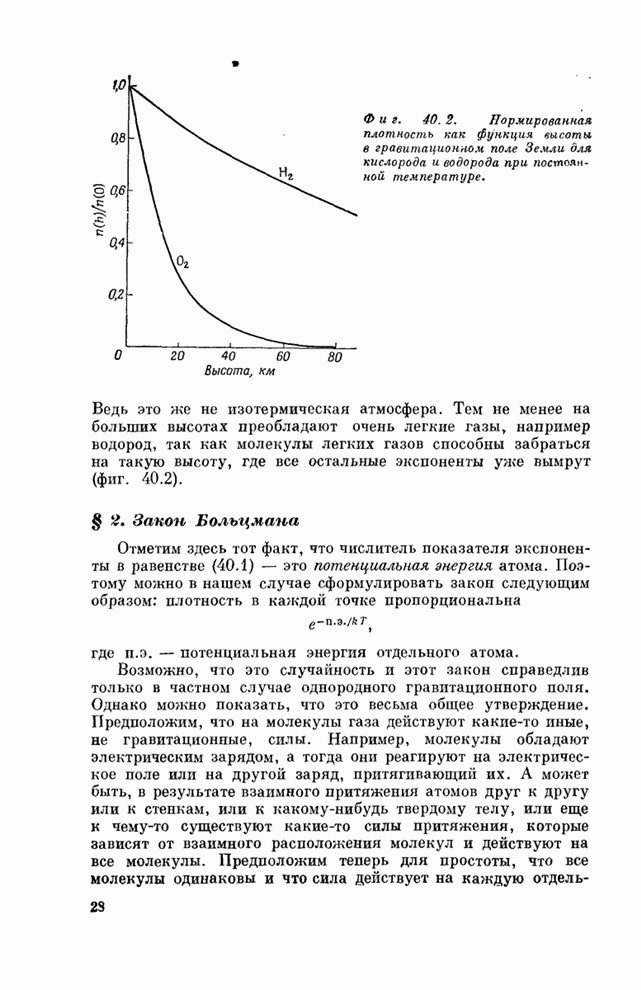
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
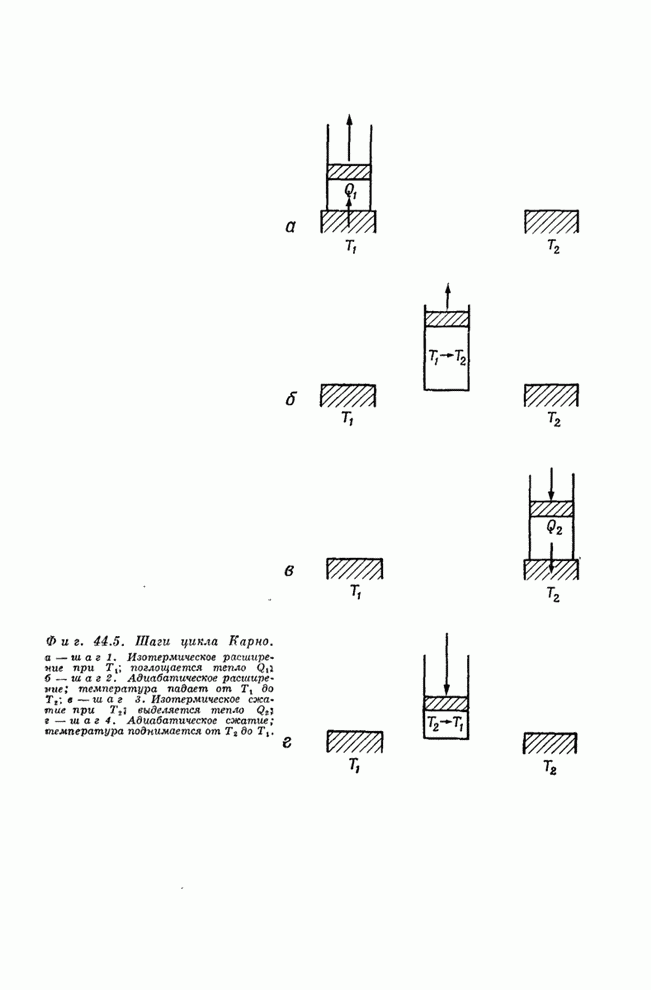
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
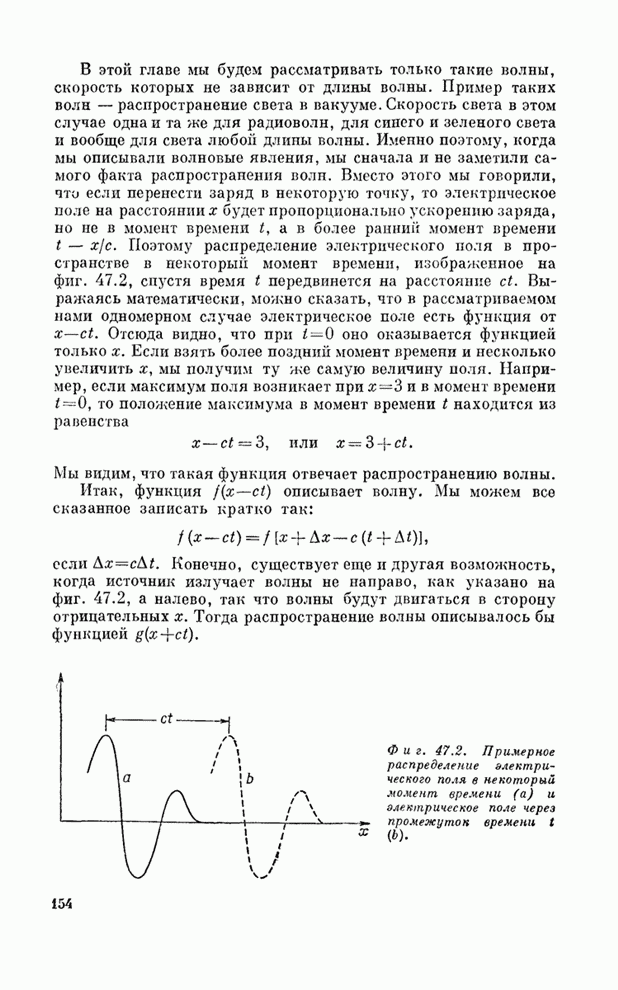
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия