| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Некоторые замечания о биениях и модуляции
Предположим теперь, что нас интересует интенсивность волны, описываемой уравнением (48.7). Чтобы найти ее, нужно взять квадрат абсолютной величины либо правой, либо левой части этого уравнения. Давайте возьмем левую часть. Интенсивность при этом будет равна
![]() . (48.8)
. (48.8)
Видите,
интенсивность возрастает и падает с частотой ![]() , изменяясь в пределах между
, изменяясь в пределах между ![]() и
и ![]() . Если
. Если ![]() , то минимальная
интенсивность не равна нулю.
, то минимальная
интенсивность не равна нулю.
Те
же результаты можно получить и другим путем - с помощью схем, подобных фиг.
48.2. Изобразим одну из волн в виде вектора длиной ![]() в комплексной плоскости,
вращающегося с угловой скоростью
в комплексной плоскости,
вращающегося с угловой скоростью ![]() . Вторую волну изобразим другим
вектором, длина которого
. Вторую волну изобразим другим
вектором, длина которого ![]() , а угловая скорость вращения
, а угловая скорость вращения ![]() . Если эти частоты
в точности равны между собой, то мы получим вращающийся вектор, длина которого
все время постоянна. Так что интенсивность в этом случае будет все время
постоянной фиксированной величиной. Если, однако, частоты хоть немного
отличаются одна от другой, то эти два вектора будут крутиться с различными
скоростями.
. Если эти частоты
в точности равны между собой, то мы получим вращающийся вектор, длина которого
все время постоянна. Так что интенсивность в этом случае будет все время
постоянной фиксированной величиной. Если, однако, частоты хоть немного
отличаются одна от другой, то эти два вектора будут крутиться с различными
скоростями.
На
фиг. 48.3 показано, как выглядит вся картина «с точки зрения» вектора ![]() . Мы видим, что
вектор
. Мы видим, что
вектор ![]() медленно
«отворачивается» от вектора
медленно
«отворачивается» от вектора ![]() , так что амплитуда, получаемая при
сложении этих векторов, сначала велика, а затем, когда второй вектор совсем
«отвернется» в другую сторону, т. е. когда угол между ними станет 180°, она
будет особенно мала, и т. д. Вектор крутится, амплитуда суммы векторов
становится то больше, то меньше, а интенсивность пульсирует. Идея сравнительно
простая, и ее можно реализовать множеством различных способов. Этот эффект
очень легко наблюдать экспериментально. Можно установить, например, два
громкоговорителя, каждый из которых связан со своим генератором колебаний и
может давать свой собственный тон. Таким образом, мы принимаем один сигнал от
первого источника, а другой сигнал от второго. Если частоты этих сигналов в
точности одинаковы, то в результате в каждой точке пространства получится
эффект определенной силы. Но если генераторы немного расстроить, то мы услышим
некоторые изменения интенсивности. Чем больше мы расстраиваем генераторы, тем
более быстрыми будут изменения силы звука. Однако уху становится трудно
уследить за изменениями, скорость которых превышает 10 колебаний в секунду или
что-то около этого.
, так что амплитуда, получаемая при
сложении этих векторов, сначала велика, а затем, когда второй вектор совсем
«отвернется» в другую сторону, т. е. когда угол между ними станет 180°, она
будет особенно мала, и т. д. Вектор крутится, амплитуда суммы векторов
становится то больше, то меньше, а интенсивность пульсирует. Идея сравнительно
простая, и ее можно реализовать множеством различных способов. Этот эффект
очень легко наблюдать экспериментально. Можно установить, например, два
громкоговорителя, каждый из которых связан со своим генератором колебаний и
может давать свой собственный тон. Таким образом, мы принимаем один сигнал от
первого источника, а другой сигнал от второго. Если частоты этих сигналов в
точности одинаковы, то в результате в каждой точке пространства получится
эффект определенной силы. Но если генераторы немного расстроить, то мы услышим
некоторые изменения интенсивности. Чем больше мы расстраиваем генераторы, тем
более быстрыми будут изменения силы звука. Однако уху становится трудно
уследить за изменениями, скорость которых превышает 10 колебаний в секунду или
что-то около этого.

Фиг. 48.3. Результат сложения двух комплексных векторов с различными частотами во вращающейся системе отсчета первого вектора.
Показаны девять последовательных положений медленно вращающегося вектора.
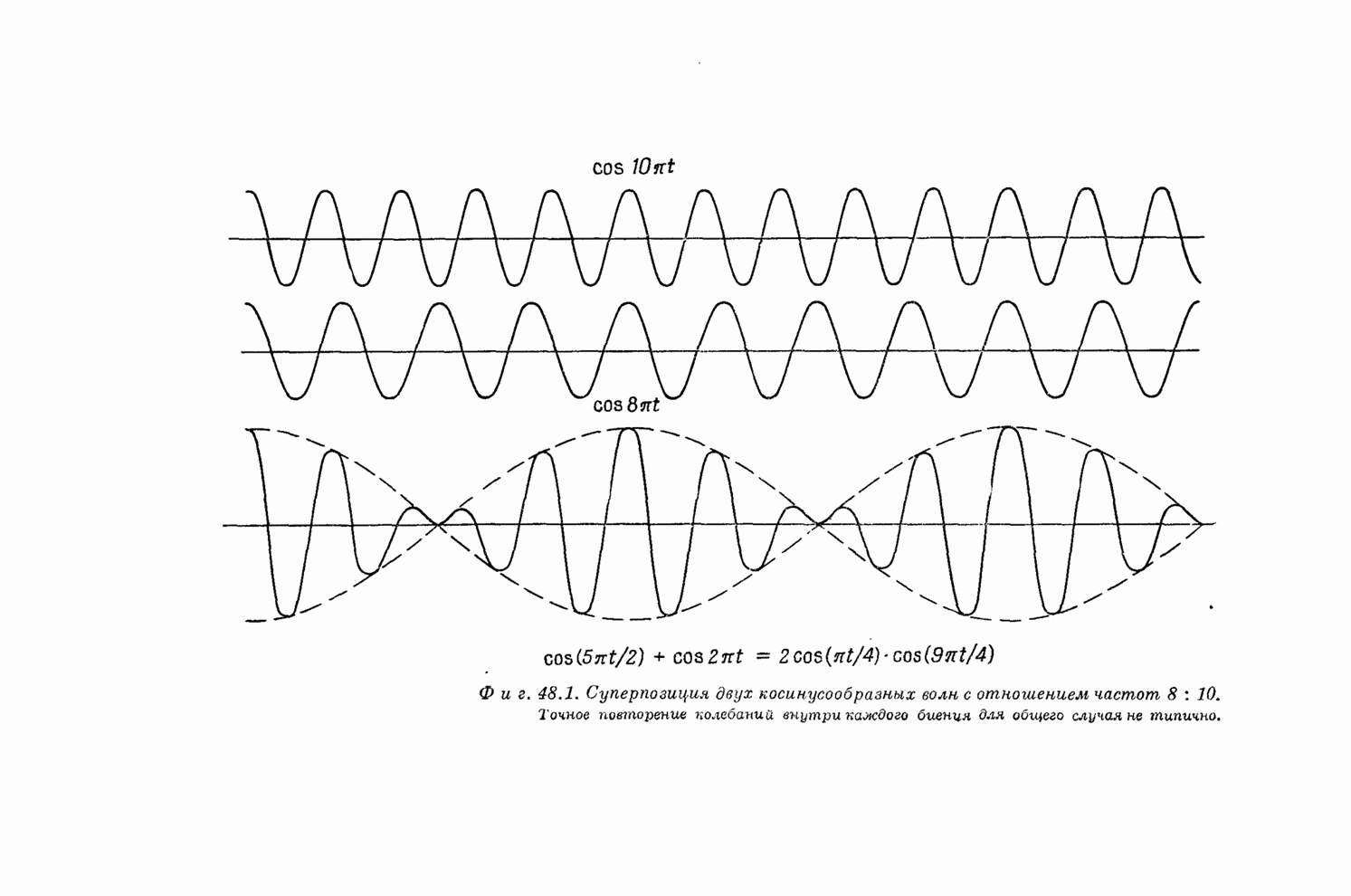
Тот же эффект можно наблюдать и на осциллографе, который просто показывает сумму токов двух генераторов. Если частота пульсаций сравнительно мала, то мы просто видим, как на экране перед нами проходят синусоидальные волны, амплитуда которых пульсирует, но если сделать пульсации более быстрыми, то мы увидим нечто похожее на то, что показано на фиг. 48.1. По мере увеличения разницы между частотами «вершины» сближаются все больше и больше. Если амплитуды не равны друг другу, если мы один сигнал сделаем слабее другого, то образуется волна, амплитуда которой, как это и ожидается, никогда не становится равной нулю. Все получается так, как нужно, независимо от того, электричество это или звук.
Но возможно и обратное явление! При радиопередаче используют так называемую амплитудную модуляцию (AM). Вот как это делается. Радиопередатчик возбуждает электрические колебания очень высокой частоты. Для радиовещания, например, используется частота 800 кгц. Если включен этот несущий сигнал, то передатчик будет излучать волны с частотой 800 000 колебаний в секунду, причем амплитуда их постоянна. Информация же (зачастую совершенно бесполезная, вроде того, какую марку автомобиля вам следует приобрести) передается следующим образом: когда кто-то говорит в микрофон, амплитуда несущего сигнала изменяется «в ногу» с колебаниями звука, приходящего в микрофон.
Возьмем простейший с точки зрения математики случай, когда певица берет безупречную ноту с безупречным синусоидальным колебанием голосовых связок, причем получается сигнал, сила которого меняется, как это показано на фиг. 48.4. Изменения слышимой частоты принимаются затем приемником; мы избавляемся от несущей волны и смотрим просто на «обертку», которая представляет собой колебания голосовых связок, или звук голоса певицы. Громкоговоритель же производит колебания той же частоты в воздухе, и в принципе слушатель не может обнаружить разницы между настоящим голосом певицы и передачей, слышимой по радио. В действительности же из-за некоторых искажений и других тончайших эффектов можно все же определить, слышим ли мы радио или «живой» голос певицы; в других же отношениях все происходит так, как мы описали.

Фиг. 48.4. Модуляция несущей волны.
На этом схематическом рисунке
отношение ![]() .
В настоящей радиоволне
.
В настоящей радиоволне ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
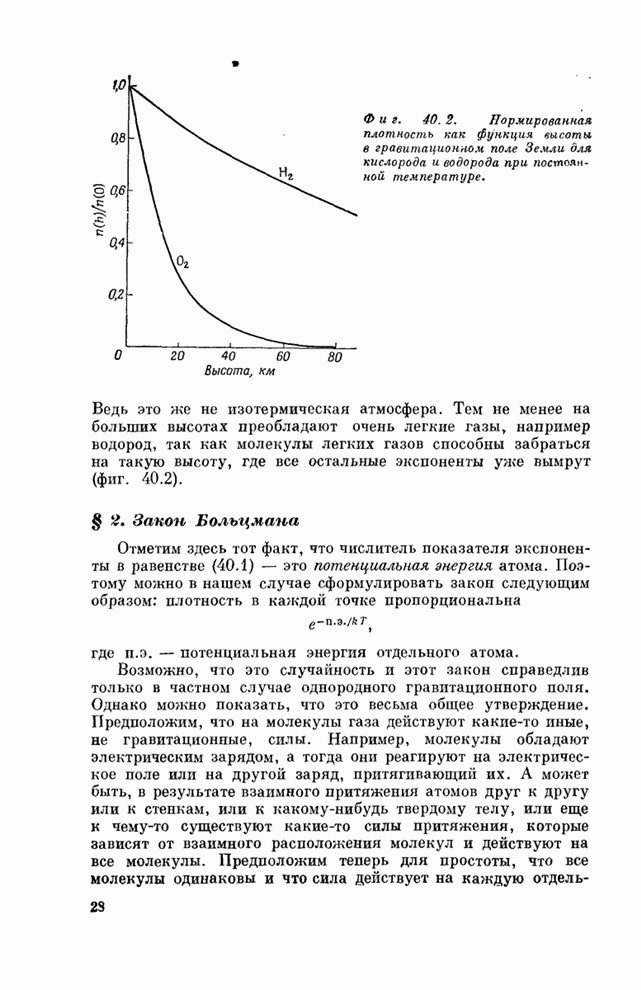
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
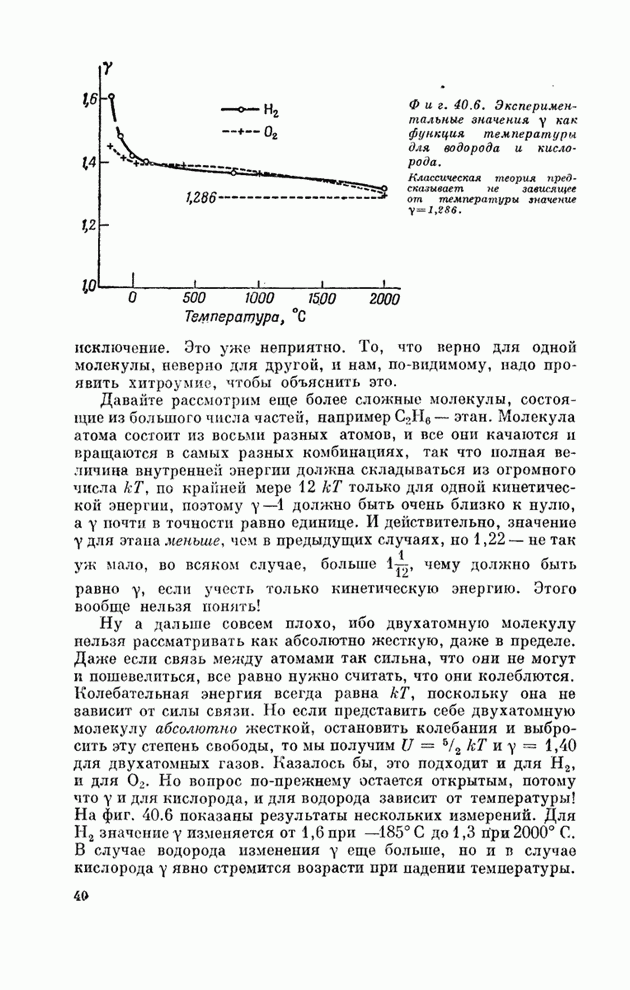
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
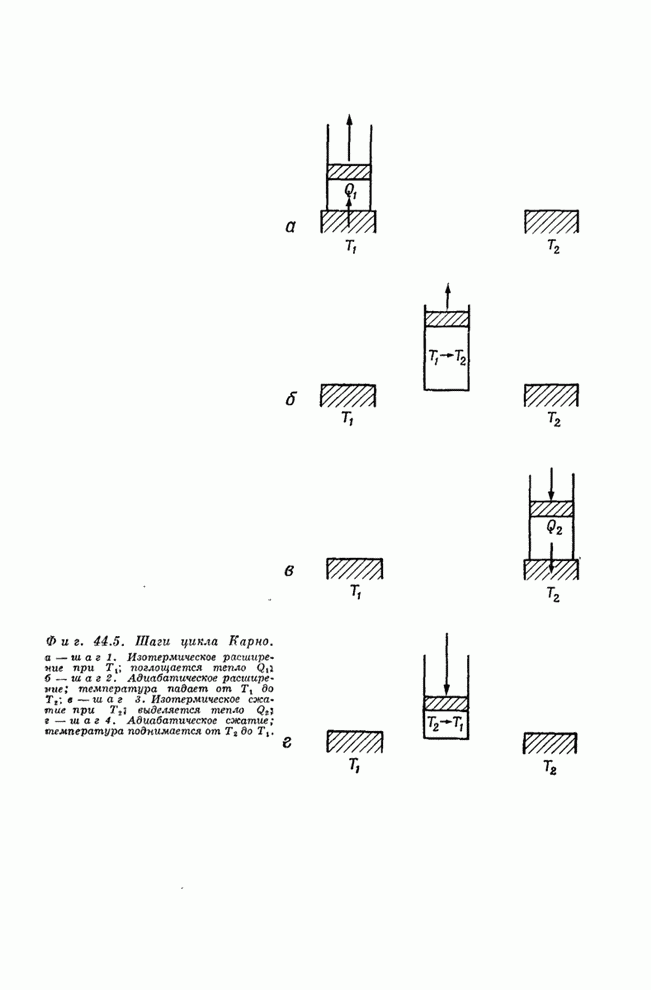
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
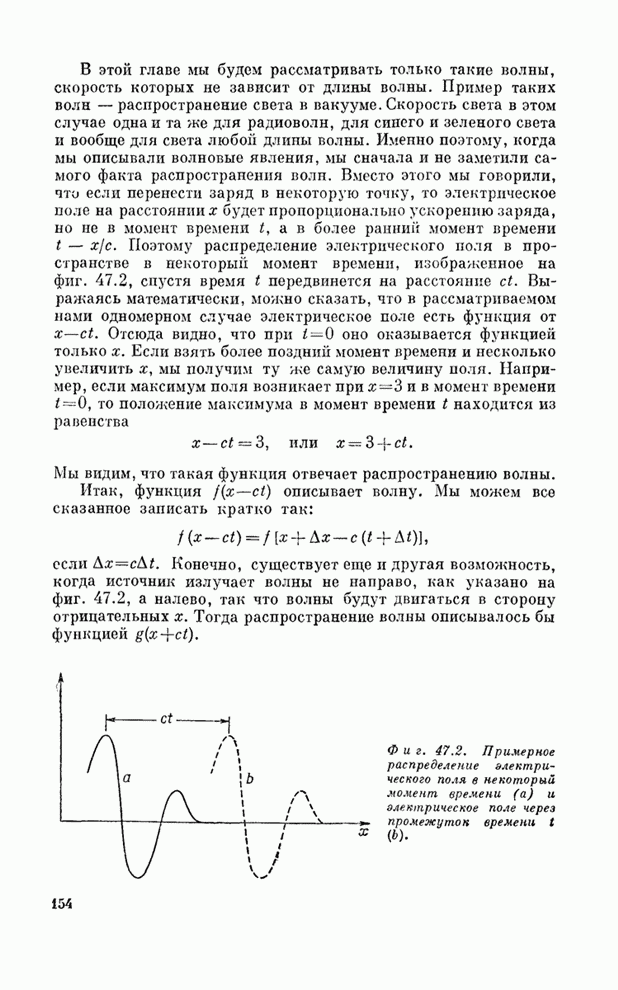
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
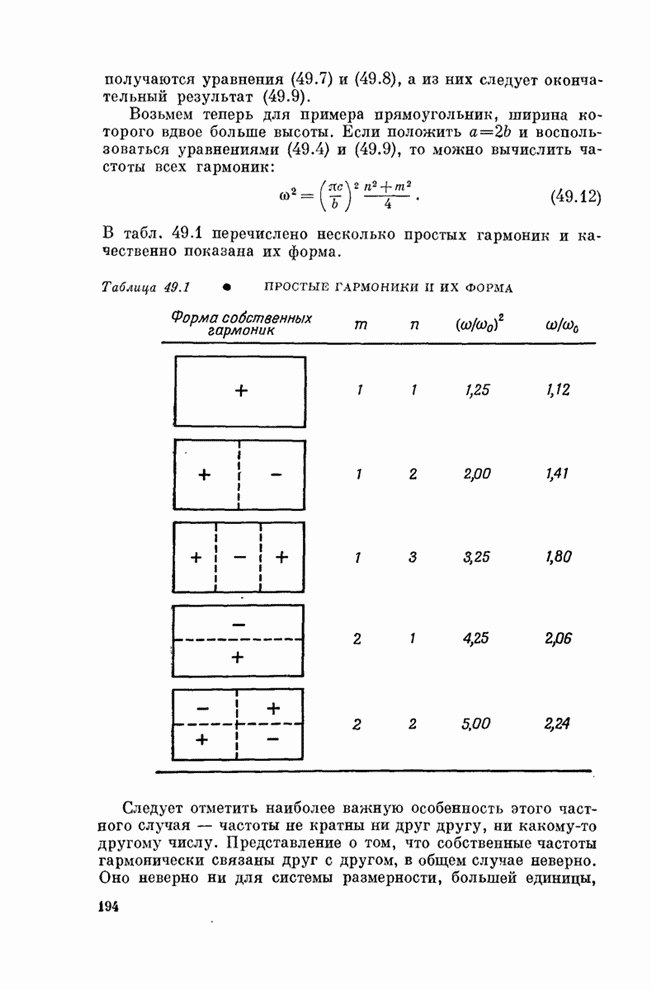
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
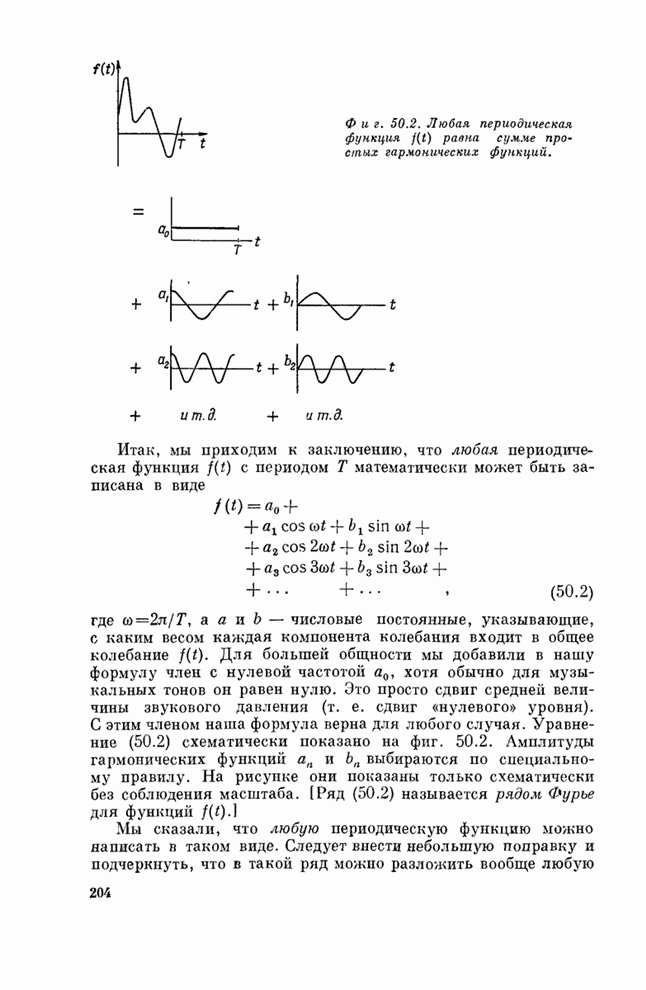
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия