| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Испарение жидкости
В
менее элементарной статистической механике пытаются решить следующую важную
задачу. Предположим, что имеется совокупность притягивающихся друг к другу
молекул и сила между любыми двумя молекулами, скажем ![]() -й и
-й и ![]() -й, зависит только от
расстояния между ними
-й, зависит только от
расстояния между ними ![]() , и может быть представлена в виде
производной от потенциальной энергии
, и может быть представлена в виде
производной от потенциальной энергии ![]() . На фиг. 40.3 показан возможный вид
такой функции. Если
. На фиг. 40.3 показан возможный вид
такой функции. Если ![]() , то при сближении молекул энергия
уменьшается, поэтому молекулы притягиваются; если же молекулы сближаются еще
теснее, энергия очень резко возрастает, значит, на малых расстояниях молекулы
сильно отталкиваются. Таково в общих чертах поведение молекул.
, то при сближении молекул энергия
уменьшается, поэтому молекулы притягиваются; если же молекулы сближаются еще
теснее, энергия очень резко возрастает, значит, на малых расстояниях молекулы
сильно отталкиваются. Таково в общих чертах поведение молекул.

Фиг. 40.3. Кривая потенциальной энергии для двух молекул.
Потенциальная энергия зависит только от расстояния.
Предположим
теперь, что мы заполнили этими молекулами какой-то ящик и хотим знать, как они
там уместятся в среднем. На это даст ответ выражение ![]() . В этом случае полная
потенциальная энергия, если предположить, что молекулы взаимодействуют только
попарно, равна сумме всех парных энергий (в более сложных случаях могут
встретиться и тройные силы, но электрические силы, например, парные). Поэтому
вероятность того, что молекулы образуют конфигурацию, характеризуемую заданными
комбинациями расстояний пропорциональна
. В этом случае полная
потенциальная энергия, если предположить, что молекулы взаимодействуют только
попарно, равна сумме всех парных энергий (в более сложных случаях могут
встретиться и тройные силы, но электрические силы, например, парные). Поэтому
вероятность того, что молекулы образуют конфигурацию, характеризуемую заданными
комбинациями расстояний пропорциональна
 .
.
Если
температура очень высока, так что ![]() , то экспонента почти всюду мала, и
вероятность найти молекулу в том или ином месте почти не зависит от расстояния
до других молекул. Рассмотрим случай двух молекул; в этом случае
, то экспонента почти всюду мала, и
вероятность найти молекулу в том или ином месте почти не зависит от расстояния
до других молекул. Рассмотрим случай двух молекул; в этом случае ![]() будет
вероятностью найти молекулы на расстоянии
будет
вероятностью найти молекулы на расстоянии ![]() друг от друга. Ясно, что вероятность
максимальна тогда, когда потенциал наиболее отрицателен, а когда потенциал
стремится к бесконечности, вероятность почти равна нулю (это происходит на
очень малых расстояниях). Это означает, что у атомов газа нет шансов
столкнуться друг с другом, уж очень сильно они отталкиваются. Но очень велики
шансы найти эти молекулы (если отнести вероятность к единичному объему) вблизи
точки
друг от друга. Ясно, что вероятность
максимальна тогда, когда потенциал наиболее отрицателен, а когда потенциал
стремится к бесконечности, вероятность почти равна нулю (это происходит на
очень малых расстояниях). Это означает, что у атомов газа нет шансов
столкнуться друг с другом, уж очень сильно они отталкиваются. Но очень велики
шансы найти эти молекулы (если отнести вероятность к единичному объему) вблизи
точки ![]() .
Здесь вероятность больше, чем в других точках, но насколько больше - это
зависит от температуры. Если температура очень велика по сравнению с разностью
энергий в точках
.
Здесь вероятность больше, чем в других точках, но насколько больше - это
зависит от температуры. Если температура очень велика по сравнению с разностью
энергий в точках ![]() и
и
![]() , то
экспонента всегда почти равна единице. Это случай, когда средняя кинетическая
энергия (она порядка
, то
экспонента всегда почти равна единице. Это случай, когда средняя кинетическая
энергия (она порядка ![]() ) значительно превосходит
потенциальную энергию. Силы тогда мало что значат. Но с падением температуры
вероятность найти молекулы на расстоянии, близком к
) значительно превосходит
потенциальную энергию. Силы тогда мало что значат. Но с падением температуры
вероятность найти молекулы на расстоянии, близком к ![]() , резко возрастает по
сравнению с вероятностью найти молекулы в любом другом месте; и в самом деле,
если
, резко возрастает по
сравнению с вероятностью найти молекулы в любом другом месте; и в самом деле,
если ![]() много
меньше
много
меньше ![]() ,
то около
,
то около ![]() экспонента
имеет довольно большой положительный показатель. Другими словами, при заданном
объеме молекулы предпочитают быть на расстоянии минимальной энергии, а не очень
далеко друг от друга. По мере падения температуры атомы сближаются, сбиваются в
кучу, объединяются в жидкости, в твердые тела и молекулы, а если их подогреть,
то они испаряются.
экспонента
имеет довольно большой положительный показатель. Другими словами, при заданном
объеме молекулы предпочитают быть на расстоянии минимальной энергии, а не очень
далеко друг от друга. По мере падения температуры атомы сближаются, сбиваются в
кучу, объединяются в жидкости, в твердые тела и молекулы, а если их подогреть,
то они испаряются.
Если
бывает необходимо точно описать, как происходит испарение, или вообще уточнить,
как молекулы ведут себя в данных обстоятельствах, то поступать следует так.
Прежде всего нужно как можно точнее узнать закон взаимодействия молекул ![]() . Как это сделать -
безразлично: можно вычислить потенциал с помощью квантовой механики или
установить закон взаимодействия экспериментально. Но если даже закон
взаимодействия молекул известен, нужно все же учесть, что дело идет о миллионах
молекул и нам еще придется хватить горя при изучении функции
. Как это сделать -
безразлично: можно вычислить потенциал с помощью квантовой механики или
установить закон взаимодействия экспериментально. Но если даже закон
взаимодействия молекул известен, нужно все же учесть, что дело идет о миллионах
молекул и нам еще придется хватить горя при изучении функции  . Все же
удивительно, что функция так проста и все как будто ясно, поскольку известен
точный потенциал взаимодействия, а дело это оказывается невероятно сложным:
трудность заключается в ужасающе большом числе переменных.
. Все же
удивительно, что функция так проста и все как будто ясно, поскольку известен
точный потенциал взаимодействия, а дело это оказывается невероятно сложным:
трудность заключается в ужасающе большом числе переменных.
Но вопрос захватывающе интересен. Это один из примеров того, что называют «задачей многих тел», и он содержит много поистине увлекательных вещей. Одна-единственная формула, которую мы получим, решив задачу, должна содержать все детали, например переход газа в твердое состояние или возможные кристаллические строения твердого тела. Многие пытались ее сосчитать, но математические трудности уж очень велики, и дело не в трудности вывода общего закона, а просто в том, чтобы справиться с огромным числом переменных.
Вот и все, что касается распределения частиц в пространстве. На этом, собственно, и кончается классическая статистическая механика, ибо если нам известны силы, то в принципе мы можем найти пространственное распределение, а распределение скоростей находится сразу на все случаи жизни, оно не будет меняться от случая к случаю. Основная задача состоит в получении более конкретной информации из нашего формального решения: это и является основным занятием классической статистической механики.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
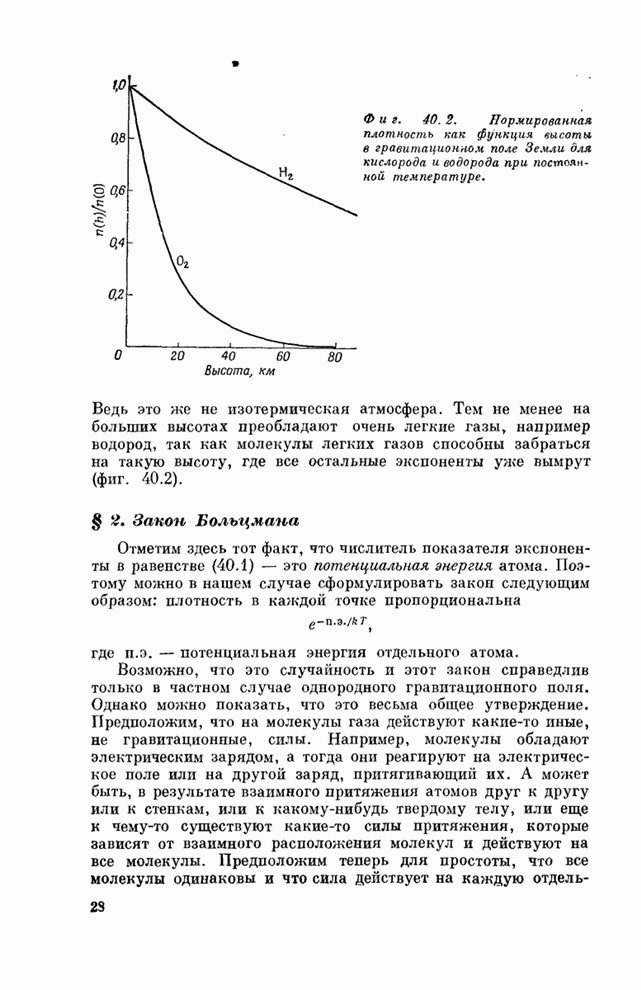
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия