| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Ряд Фурье
В
предыдущей главе мы познакомились с другой точкой зрения на колеблющуюся
систему. Мы видели, что в струне возникают различные собственные гармоники и
что любое частное колебание, которое только возможно получить из начальных
условий, можно рассматривать как составленную в надлежащей пропорции комбинацию
нескольких одновременно осциллирующих собственных гармоник. Для струны мы
нашли, что собственные гармоники имеют частоты ![]() . Поэтому наиболее общее движение
струны складывается из синусоидальных колебаний основной частоты
. Поэтому наиболее общее движение
струны складывается из синусоидальных колебаний основной частоты ![]() , затем второй
гармоники
, затем второй
гармоники ![]() ,
затем третьей гармоники
,
затем третьей гармоники ![]() и т. д. Основная гармоника
повторяется через каждый период
и т. д. Основная гармоника
повторяется через каждый период ![]() , вторая гармоника - через каждый
период
, вторая гармоника - через каждый
период ![]() ;
она повторяется также и через каждый период
;
она повторяется также и через каждый период ![]() , т. е. после двух своих периодов.
Точно таким же образом через период
, т. е. после двух своих периодов.
Точно таким же образом через период ![]() повторяется и третья гармоника. В
этом отрезке укладываются три ее периода. И снова мы понимаем, почему задетая
струна через период
повторяется и третья гармоника. В
этом отрезке укладываются три ее периода. И снова мы понимаем, почему задетая
струна через период ![]() полностью повторяет форму своего
движения. Так получается музыкальный звук.
полностью повторяет форму своего
движения. Так получается музыкальный звук.
До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное движением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей доски». Разные гармоники по-разному связаны с воздухом.
Если
для музыкального тона функция ![]() представляет давление воздуха в
зависимости от времени (скажем, такая, как на фиг. 50.1,б), то можно ожидать,
что
представляет давление воздуха в
зависимости от времени (скажем, такая, как на фиг. 50.1,б), то можно ожидать,
что ![]() записывается
в виде суммы некоторого числа простых гармонических функций от времени
(подобных
записывается
в виде суммы некоторого числа простых гармонических функций от времени
(подобных ![]() )
для каждой из различных гармонических частот. Если период колебаний равен
)
для каждой из различных гармонических частот. Если период колебаний равен ![]() , то основная
угловая частота будет
, то основная
угловая частота будет ![]() , а следующие гармоники будут
, а следующие гармоники будут ![]() и т. д.
и т. д.
Здесь
появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты
начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться
функциями типа ![]() .
Вместо этого, однако, проще использовать для каждой частоты как синус, так и
косинус. Напомним, что
.
Вместо этого, однако, проще использовать для каждой частоты как синус, так и
косинус. Напомним, что
![]() , (50.1)
, (50.1)
а
поскольку ![]() -
постоянная, то любые синусоидальные колебания с частотой
-
постоянная, то любые синусоидальные колебания с частотой ![]() могут быть записаны в виде
суммы членов, в один из которых входит
могут быть записаны в виде
суммы членов, в один из которых входит ![]() , а в другой -
, а в другой - ![]() .
.
Итак,
мы приходим к заключению, что любая периодическая функция ![]() с периодом
с периодом ![]() математически
может быть записана в виде
математически
может быть записана в виде
![]() , (50.2)
, (50.2)
где
![]() , а
, а ![]() и
и ![]() - числовые
постоянные, указывающие, с каким весом каждая компонента колебания входит в
общее колебание
- числовые
постоянные, указывающие, с каким весом каждая компонента колебания входит в
общее колебание ![]() .
Для большей общности мы добавили в нашу формулу член с нулевой частотой
.
Для большей общности мы добавили в нашу формулу член с нулевой частотой ![]() , хотя обычно для
музыкальных тонов он равен нулю. Это просто сдвиг средней величины звукового
давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для
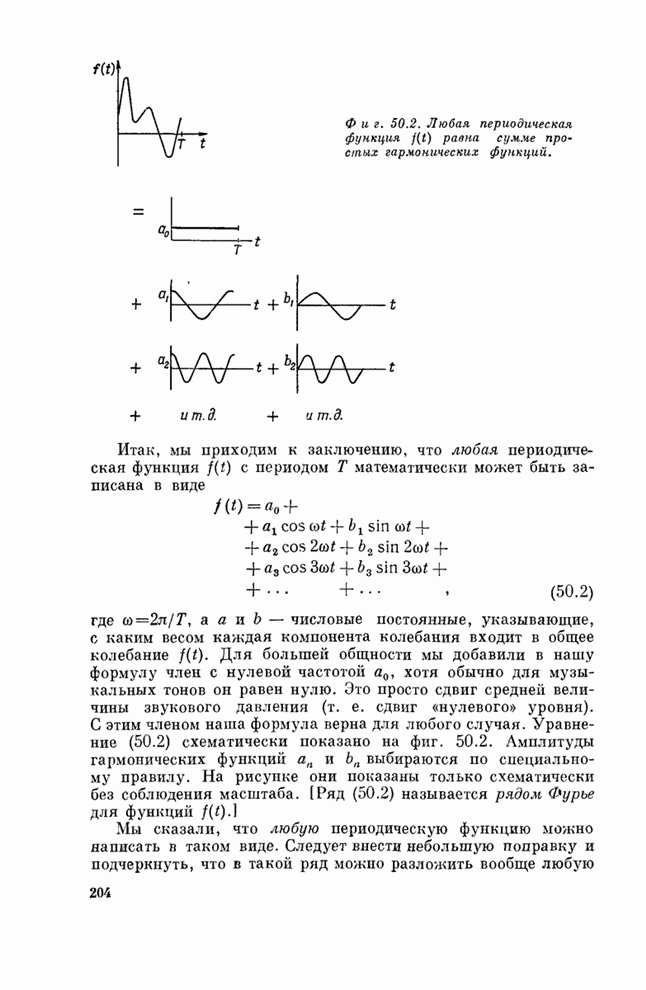
любого случая. Уравнение (50.2) схематически показано на фиг. 50.2. Амплитуды
гармонических функций
, хотя обычно для
музыкальных тонов он равен нулю. Это просто сдвиг средней величины звукового
давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для
любого случая. Уравнение (50.2) схематически показано на фиг. 50.2. Амплитуды
гармонических функций ![]() и
и ![]() выбираются по специальному правилу.
На рисунке они показаны только схематически без соблюдения масштаба. [Ряд
(50.2) называется рядом Фурье для функций
выбираются по специальному правилу.
На рисунке они показаны только схематически без соблюдения масштаба. [Ряд
(50.2) называется рядом Фурье для функций ![]() .]
.]

Фиг. 50.2. Любая периодическая функция
![]() равна
сумме простых гармонических функций.
равна
сумме простых гармонических функций.
Мы
сказали, что любую периодическую функцию можно написать в таком виде. Следует
внести небольшую поправку и подчеркнуть, что в такой ряд можно разложить вообще
любую звуковую волну или любую функцию, с которой мы сталкиваемся в физике.
Математики, конечно, могут придумать такую функцию, что ее нельзя будет
составить из простых гармонических (например, функцию, которая «заворачивает»
назад, так что для некоторых величин ![]() она имеет два значения!). Однако
здесь нам не стоит беспокоиться о таких функциях.
она имеет два значения!). Однако
здесь нам не стоит беспокоиться о таких функциях.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия