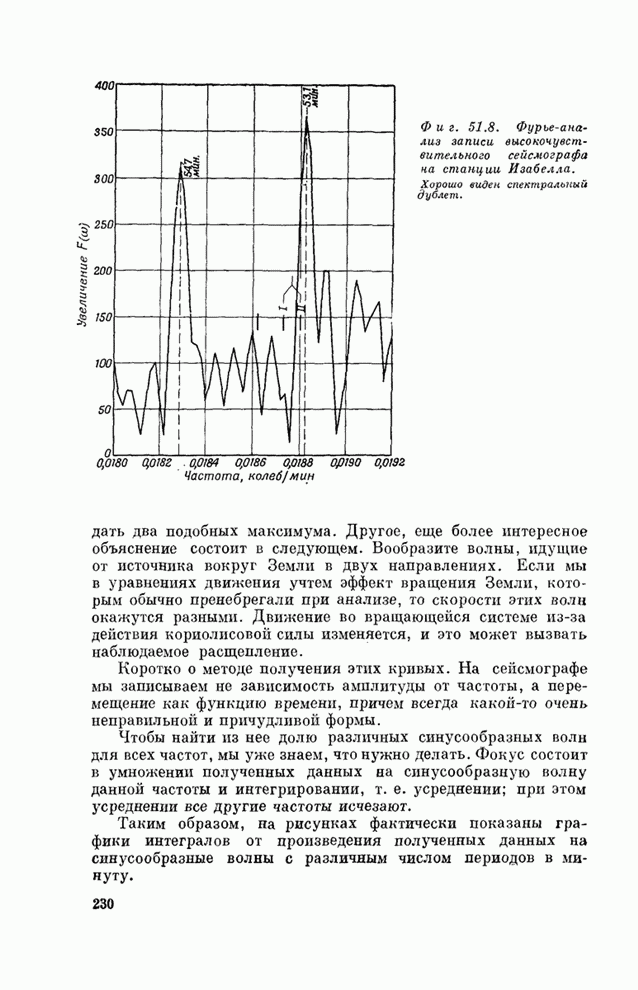
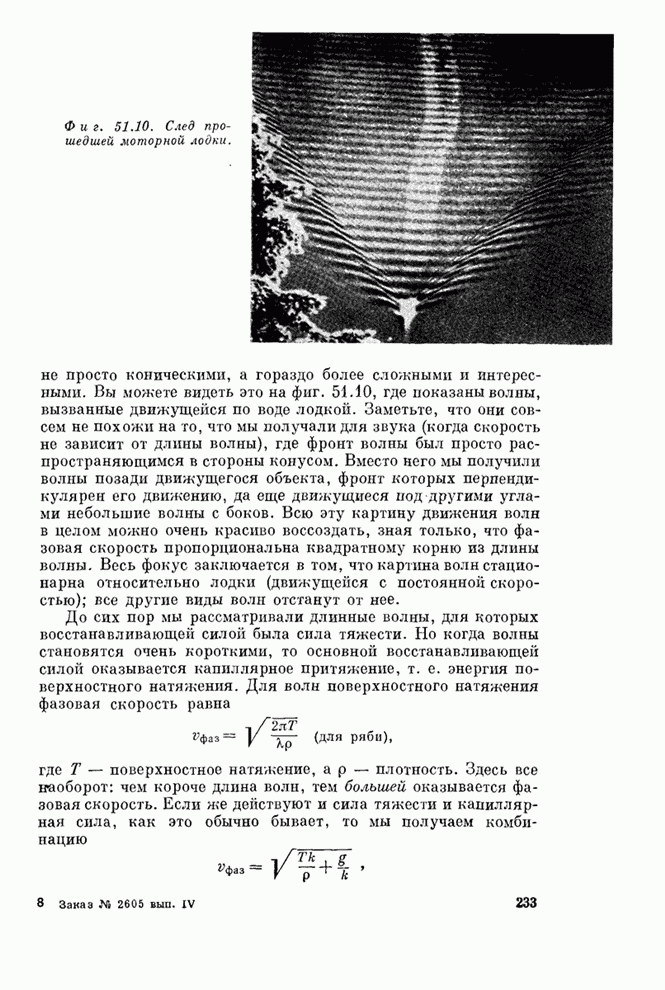
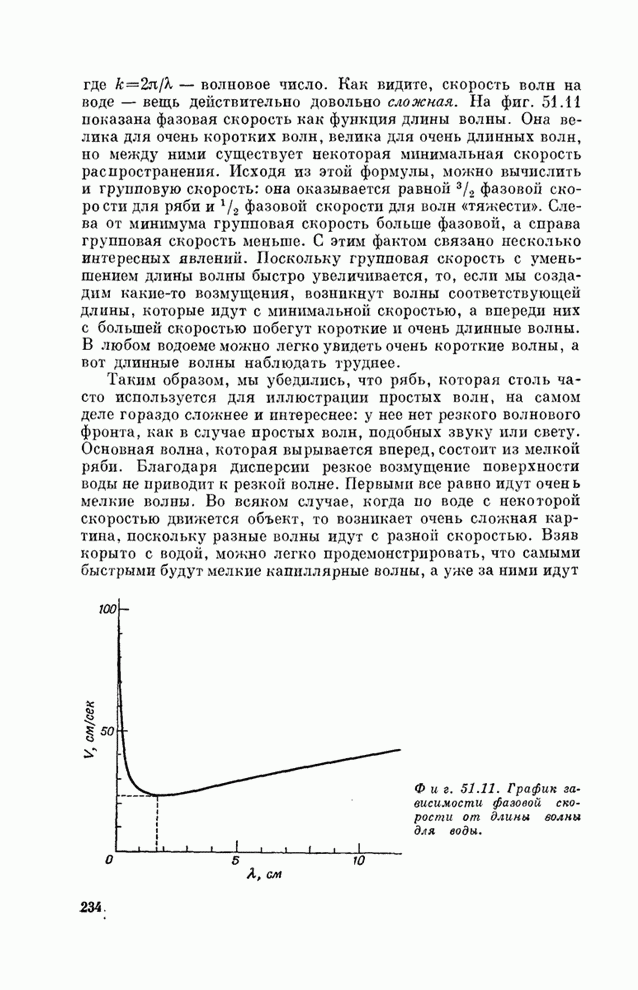
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Химическая кинематика
При
химических реакциях происходит нечто похожее на «ионизацию». Например, два
вещества ![]() и
и
![]() комбинируют
в основном веществе
комбинируют
в основном веществе ![]() ; тогда, подумав немного, мы можем
; тогда, подумав немного, мы можем ![]() назвать атомом (
назвать атомом (![]() - то, что мы
называем электроном, а
- то, что мы
называем электроном, а ![]() - то, что мы называем ионом). После
такой замены, как и раньше, можно написать уравнение равновесия
- то, что мы называем ионом). После
такой замены, как и раньше, можно написать уравнение равновесия
![]() . (42.9)
. (42.9)
Эта
формула, конечно, неточна, потому что «постоянная» ![]() зависит от того, в каком
объеме позволено объединяться
зависит от того, в каком
объеме позволено объединяться ![]() и
и ![]() и т. п., но, обратясь к
термодинамическим аргументам, можно придать смысл величине
и т. п., но, обратясь к
термодинамическим аргументам, можно придать смысл величине ![]() в экспоненциальном
множителе, и тогда окажется, что она тесно связана с энергией, необходимой для
реакции.
в экспоненциальном
множителе, и тогда окажется, что она тесно связана с энергией, необходимой для
реакции.
Попробуем
понять эту формулу как результат столкновений, приблизительно так же, как мы
постигали формулу испарения, подсчитывая электроны, вырывающиеся в пространство,
и те, которые возвращаются назад за единицу времени. Предположим, что при
столкновениях ![]() и
и
![]() иногда
образуют соединение
иногда
образуют соединение ![]() . И предположим еще, что
. И предположим еще, что ![]() - это сложная
молекула, которая участвует в общей пляске и по которой ударяют другие
молекулы, причем время от времени она получает энергию, достаточную для того,
чтобы взорваться и снова развалиться на части
- это сложная
молекула, которая участвует в общей пляске и по которой ударяют другие
молекулы, причем время от времени она получает энергию, достаточную для того,
чтобы взорваться и снова развалиться на части ![]() и
и ![]() .
.
Заметим,
что в химических реакциях дело обстоит так, что если сближающиеся атомы имеют
слишком малую энергию, то, хотя этой энергии и достаточно для реакции ![]() , факт соударения
атомов
, факт соударения
атомов ![]() и
и
![]() еще не
обязательно означает начало реакции. Обычно требуется, чтобы соударение было
более «жестким», «мягкого» соударения между
еще не
обязательно означает начало реакции. Обычно требуется, чтобы соударение было
более «жестким», «мягкого» соударения между ![]() и
и ![]() может оказаться недостаточно для
начала реакции, даже если в процессе освобождается достаточное для реакции
количество энергии. Предположим, что общей чертой химических реакций является
требование, по которому для объединения
может оказаться недостаточно для
начала реакции, даже если в процессе освобождается достаточное для реакции
количество энергии. Предположим, что общей чертой химических реакций является
требование, по которому для объединения ![]() и
и ![]() в
в ![]() недостаточно простого соударения, а
нужно, чтобы они столкнулись, имея определенное количество энергии. Эта энергия
называется энергией активации, т. е. энергия, нужная для «активации» реакции.
Пусть
недостаточно простого соударения, а
нужно, чтобы они столкнулись, имея определенное количество энергии. Эта энергия
называется энергией активации, т. е. энергия, нужная для «активации» реакции.
Пусть ![]() -
тот избыток энергии, который необходим, чтобы столкновения могли вызвать
реакцию. Тогда скорость
-
тот избыток энергии, который необходим, чтобы столкновения могли вызвать
реакцию. Тогда скорость ![]() , с которой
, с которой ![]() и
и ![]() порождают
порождают ![]() , должна содержать
произведение числа атомов
, должна содержать
произведение числа атомов ![]() и
и ![]() , умноженное на скорость, с которой
отдельный атом ударяется о некоторую площадку величиной
, умноженное на скорость, с которой
отдельный атом ударяется о некоторую площадку величиной ![]() , и на величину
, и на величину ![]() (вероятность
того, что атомы обладают достаточной энергией):
(вероятность
того, что атомы обладают достаточной энергией):
![]() . (42.10)
. (42.10)
Теперь
надо найти скорость обратного процесса ![]() . Есть некоторая вероятность, что
. Есть некоторая вероятность, что ![]() и
и ![]() снова разойдутся.
Чтобы разойтись, им недостаточно энергии
снова разойдутся.
Чтобы разойтись, им недостаточно энергии ![]() , которая обеспечит их раздельное
существование. Но раз молекулам нелегко соединиться, должен существовать некий
барьер, через который
, которая обеспечит их раздельное
существование. Но раз молекулам нелегко соединиться, должен существовать некий
барьер, через который ![]() и
и ![]() должны перевалить, чтобы
разлететься. Они должны запастись не только нужной для их существования
энергией, но и взять кое-что про запас. Получается что-то вроде подъема на холм
перед спуском в долину; сначала приходится вскарабкаться на высоту, потом
спуститься, и только после этого разойтись (фиг. 42.1). Таким образом, скорость
перехода
должны перевалить, чтобы
разлететься. Они должны запастись не только нужной для их существования
энергией, но и взять кое-что про запас. Получается что-то вроде подъема на холм
перед спуском в долину; сначала приходится вскарабкаться на высоту, потом
спуститься, и только после этого разойтись (фиг. 42.1). Таким образом, скорость
перехода ![]() в
в
![]() и
и ![]() пропорциональна
произведению
пропорциональна
произведению ![]() -
начальному числу молекул
-
начальному числу молекул ![]() на
на ![]() :
:
![]() . (42.11)
. (42.11)
Постоянная
![]() складывается
из объема атомов и частоты столкновений; ее можно получить, как и в случае
испарения, перемножая площадь и толщину слоя, но сейчас мы этого делать не
будем. Сейчас нас больше интересует тот факт, что, когда эти скорости равны, их
отношение равно единице. Это говорит о том, что, как и раньше,
складывается
из объема атомов и частоты столкновений; ее можно получить, как и в случае
испарения, перемножая площадь и толщину слоя, но сейчас мы этого делать не
будем. Сейчас нас больше интересует тот факт, что, когда эти скорости равны, их
отношение равно единице. Это говорит о том, что, как и раньше, ![]() , где
, где ![]() содержит сечения,
скорости и другие множители, не зависящие от чисел
содержит сечения,
скорости и другие множители, не зависящие от чисел ![]() .
.

Фиг. 42.1. Соотношение энергий в
реакции ![]() .
.
Интересно,
что скорость реакции по-прежнему изменяется как ![]() , хотя эта постоянная уже не имеет
никакого отношения к той, с которой мы встречались в задаче о концентрациях;
энергия активации
, хотя эта постоянная уже не имеет
никакого отношения к той, с которой мы встречались в задаче о концентрациях;
энергия активации ![]() сильно отличается от энергии
сильно отличается от энергии ![]() . Энергия
. Энергия ![]() регулирует
пропорции
регулирует
пропорции ![]() и
и
![]() , при
которых устанавливается равновесие, но если нам захочется узнать, быстро ли
, при
которых устанавливается равновесие, но если нам захочется узнать, быстро ли ![]() переходит в
переходит в ![]() , то это уже к
равновесию отношения не имеет, и появляется уже другая энергия, энергия
активации, которая с помощью экспоненты управляет скоростью реакции.
, то это уже к
равновесию отношения не имеет, и появляется уже другая энергия, энергия
активации, которая с помощью экспоненты управляет скоростью реакции.
Кроме
того, ![]() не
является фундаментальной постоянной, как
не
является фундаментальной постоянной, как ![]() . Предположим, что реакция происходит
на поверхности стены, или на какой-нибудь другой поверхности, тогда
. Предположим, что реакция происходит
на поверхности стены, или на какой-нибудь другой поверхности, тогда ![]() и
и ![]() могут растечься
по ней так, что объединение в
могут растечься
по ней так, что объединение в ![]() будет для них более легким делом.
Иначе говоря, сквозь гору можно прорыть «туннель» или срыть вершину горы. В
силу сохранения энергии, по какому бы пути мы ни шли, результат будет один: из
будет для них более легким делом.
Иначе говоря, сквозь гору можно прорыть «туннель» или срыть вершину горы. В
силу сохранения энергии, по какому бы пути мы ни шли, результат будет один: из ![]() и
и ![]() получится
получится ![]() , так что разность
энергий
, так что разность
энергий ![]() не
зависит от пути, по которому идет реакция, однако энергия активации
не
зависит от пути, по которому идет реакция, однако энергия активации ![]() очень сильно
зависит от этого пути. Вот почему скорости химических реакций столь
чувствительны к внешним условиям. Можно изменить скорость реакции, изменив
поверхность, с которой соприкасаются реактивы, можно изготовить «набор
бочонков» и подбирать с его помощью любые скорости, если они зависят от свойств
поверхности. Можно внести в среду, в которой происходит реакция, третий
предмет; это также может сильно изменить скорость реакции, такие вещества при
незначительном изменении
очень сильно
зависит от этого пути. Вот почему скорости химических реакций столь
чувствительны к внешним условиям. Можно изменить скорость реакции, изменив
поверхность, с которой соприкасаются реактивы, можно изготовить «набор
бочонков» и подбирать с его помощью любые скорости, если они зависят от свойств
поверхности. Можно внести в среду, в которой происходит реакция, третий
предмет; это также может сильно изменить скорость реакции, такие вещества при
незначительном изменении ![]() иногда чрезвычайно влияют на
скорость реакции; их называют катализаторами. Реакции может практически не быть
совсем, потому что
иногда чрезвычайно влияют на
скорость реакции; их называют катализаторами. Реакции может практически не быть
совсем, потому что ![]() слишком велика для заданной
температуры, но если добавить это специальное вещество - катализатор, то
реакция протекает очень быстро, потому что
слишком велика для заданной
температуры, но если добавить это специальное вещество - катализатор, то
реакция протекает очень быстро, потому что ![]() уменьшается.
уменьшается.
Между
прочим, эта реакция ![]() плюс
плюс ![]() , дающая
, дающая ![]() , доставляет немало
волнений. Ведь невозможно сохранить сразу и энергию, и импульс, пытаясь
подогнать два предмета друг к другу, чтобы сделать из них один более
устойчивый. Следовательно, необходим по крайней мере третий предмет
, доставляет немало
волнений. Ведь невозможно сохранить сразу и энергию, и импульс, пытаясь
подогнать два предмета друг к другу, чтобы сделать из них один более
устойчивый. Следовательно, необходим по крайней мере третий предмет ![]() и реальная
реакция выглядит гораздо сложнее. Скорость прямого процесса должна содержать
произведение
и реальная
реакция выглядит гораздо сложнее. Скорость прямого процесса должна содержать
произведение ![]() ,
и можно подумать, что наша формула становится неверной, но это не так! Если мы
начнем искать скорость развала
,
и можно подумать, что наша формула становится неверной, но это не так! Если мы
начнем искать скорость развала ![]() , то выясним, что этой молекуле еще
надо столкнуться с
, то выясним, что этой молекуле еще
надо столкнуться с ![]() , поэтому скорость обратной реакции
пропорциональна
, поэтому скорость обратной реакции
пропорциональна ![]() и
из формулы для равновесных концентраций
и
из формулы для равновесных концентраций ![]() выпадает. Правильность закона
равновесия (42.9), который мы написали прежде всего, абсолютно гарантирована
независимо от любого возможного механизма реакции!
выпадает. Правильность закона
равновесия (42.9), который мы написали прежде всего, абсолютно гарантирована
независимо от любого возможного механизма реакции!
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
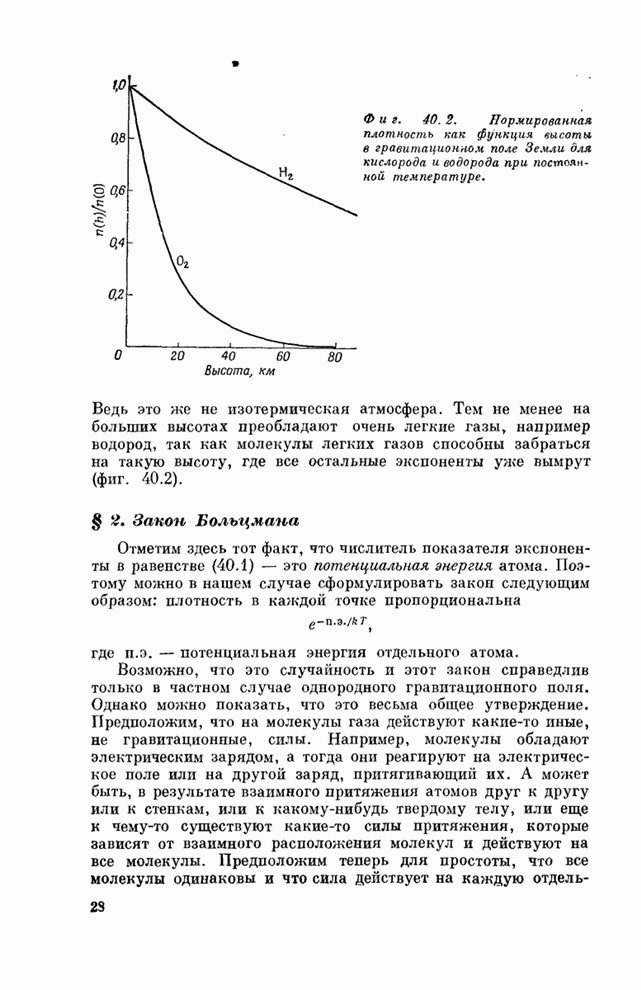
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
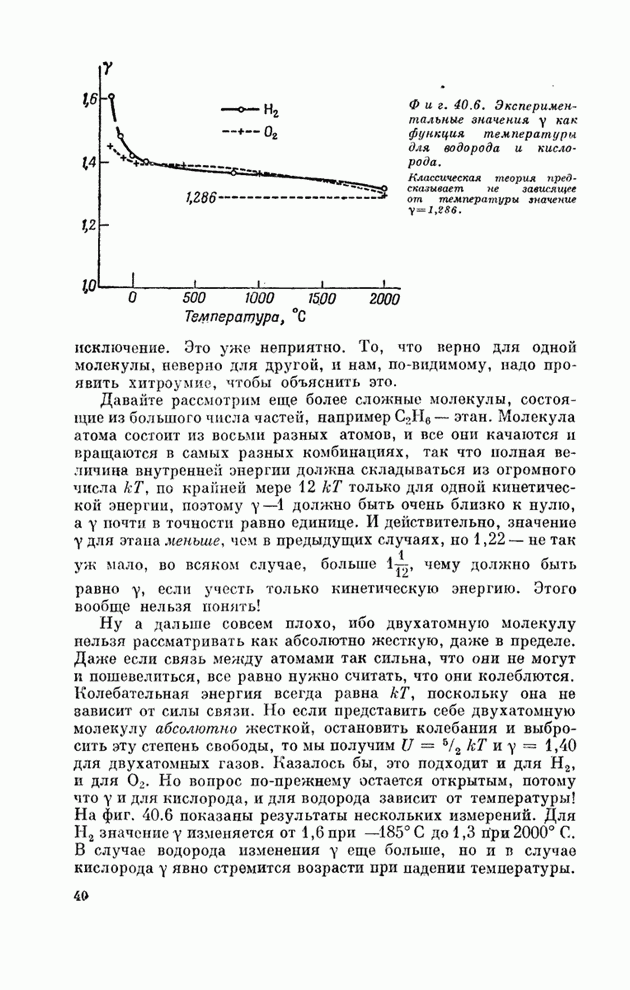
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
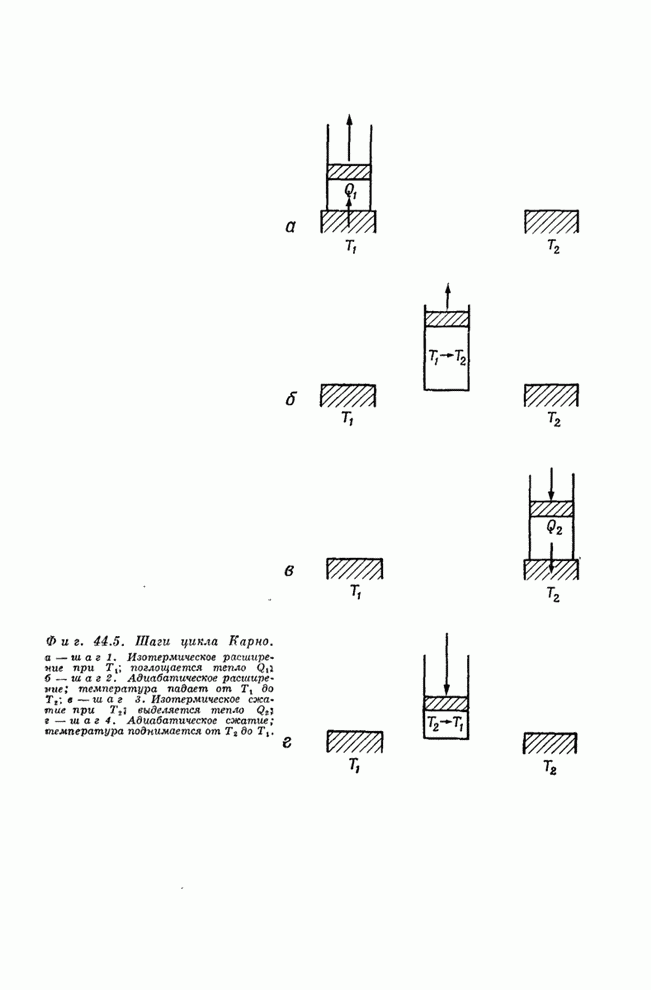
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
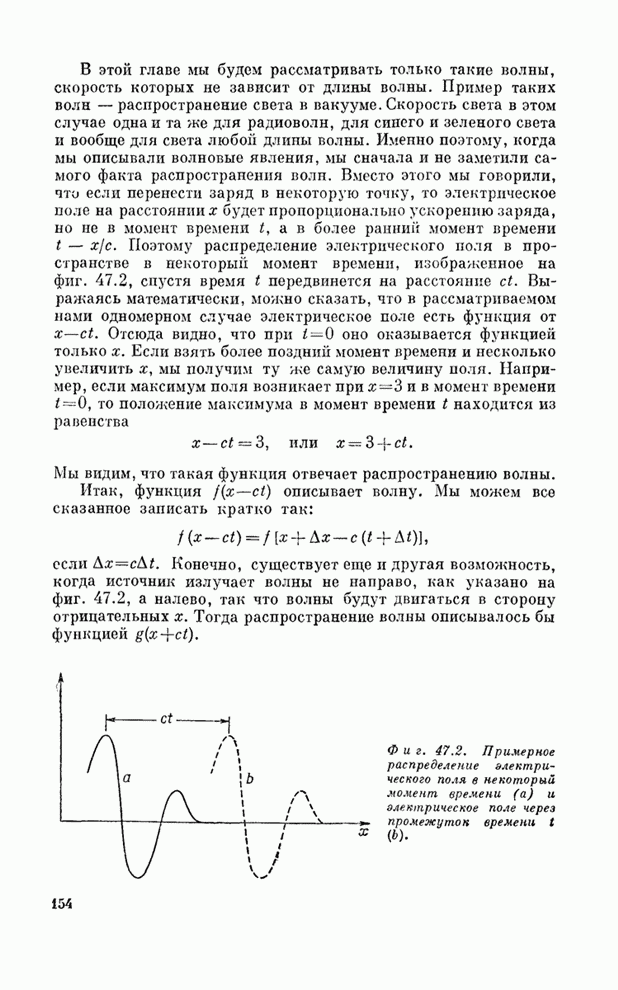
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
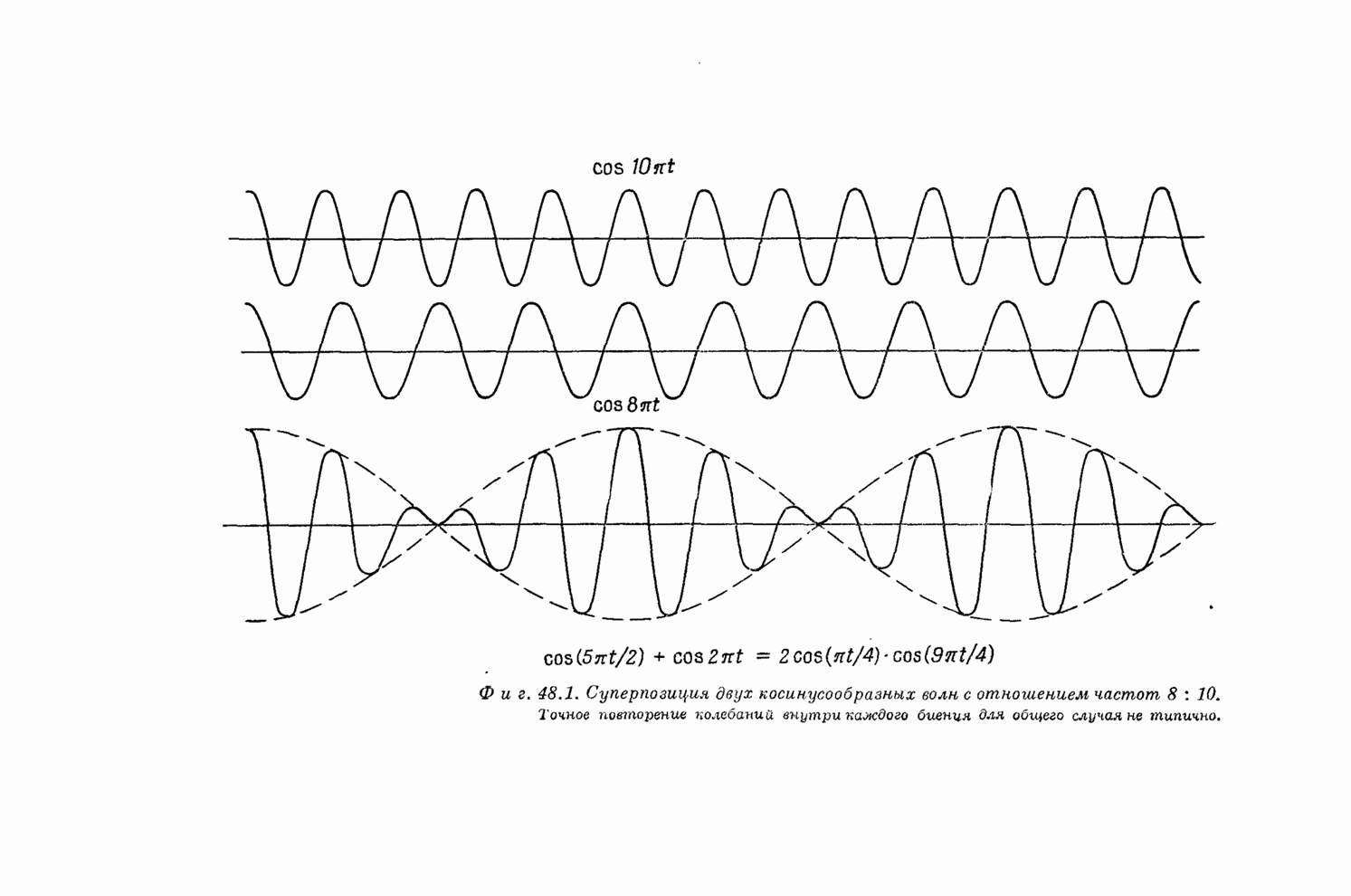
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
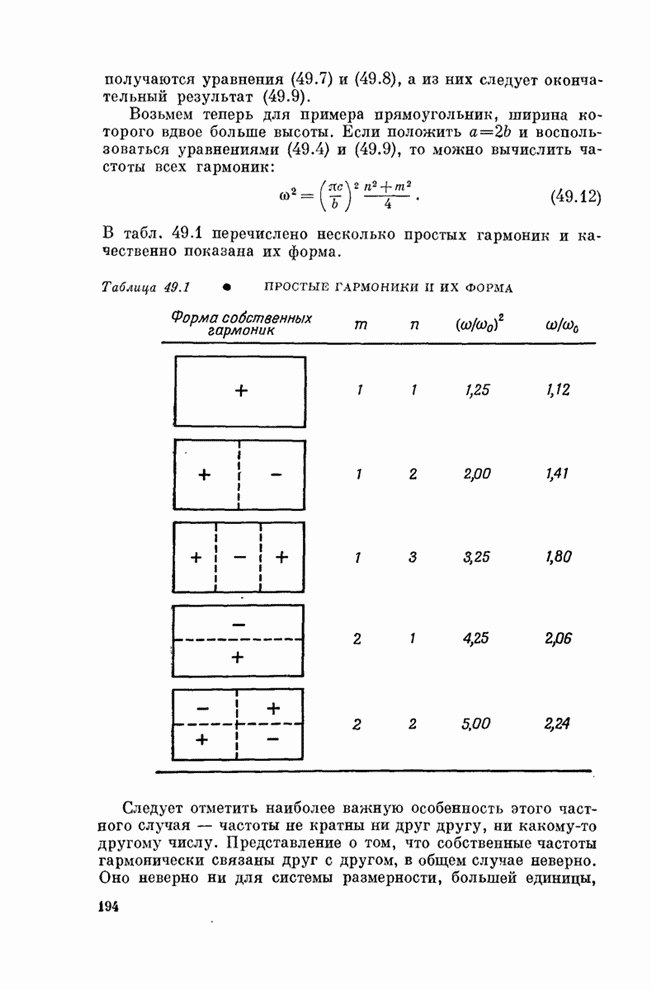
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
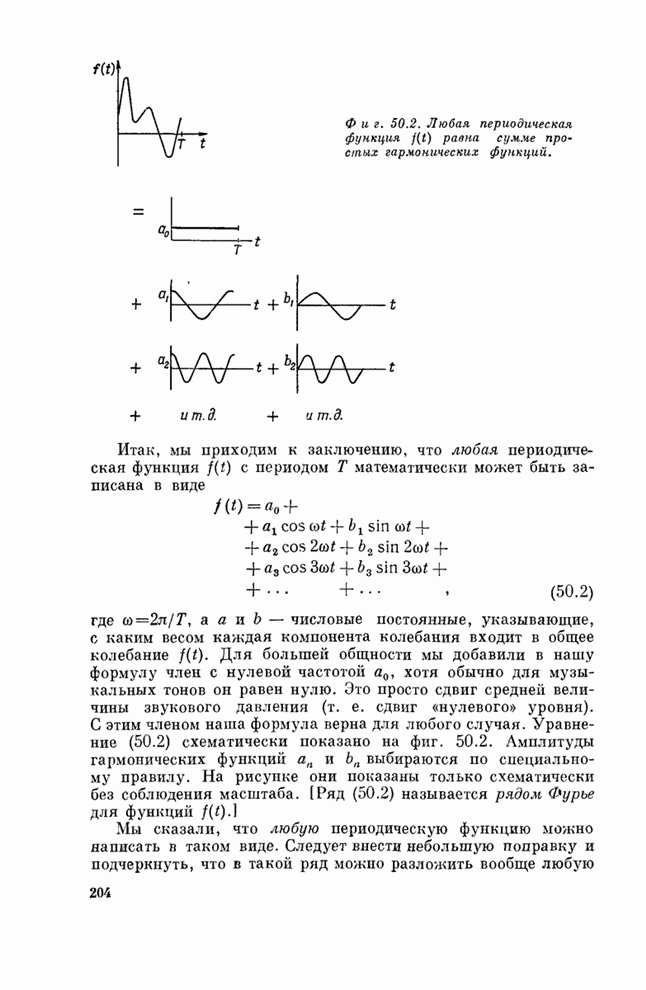
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия