| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Локализованный волновой пакет
Следующий
вопрос, который мы хотим обсудить, - это интерференция волн как в пространстве,
так и во времени. Предположим, что в пространстве распространяются две волны.
Вы, конечно, знаете, что распространение волны в пространстве, например
звуковой, можно описать с помощью экспоненты ![]() . Такая экспонента удовлетворяет
волновому уравнению при условии, что
. Такая экспонента удовлетворяет
волновому уравнению при условии, что ![]() , где
, где ![]() - скорость распространения волны. В
этом случае экспоненту можно записать в виде
- скорость распространения волны. В
этом случае экспоненту можно записать в виде ![]() , что является частным случаем общего
решения
, что является частным случаем общего
решения ![]() .
Такая экспонента должна описывать волну, распространяющуюся со скоростью
.
Такая экспонента должна описывать волну, распространяющуюся со скоростью ![]() , равной
, равной ![]() , и поэтому здесь
все в порядке.
, и поэтому здесь
все в порядке.
Давайте
теперь складывать две такие волны. Пусть первая волна распространяется с одной
частотой, а вторая волна - с какой-то другой. Случай неравных амплитуд
рассмотрите самостоятельно, хотя существенного отличия здесь нет. Таким
образом, мы хотим сложить ![]() . Это можно сделать с помощью
математики, аналогичной использованной нами при сложении двух сигналов. Если
скорости с обеих волн одинаковы, то сделать это очень легко; за исключением
того, что вместо
. Это можно сделать с помощью
математики, аналогичной использованной нами при сложении двух сигналов. Если
скорости с обеих волн одинаковы, то сделать это очень легко; за исключением
того, что вместо ![]() стоит
стоит
![]() , это
будет то же самое, что мы недавно проделали:
, это
будет то же самое, что мы недавно проделали:
![]() . (48.11)
. (48.11)
При этом, естественно, мы получаем точно такие же модуляции, как и раньше, которые, однако, движутся вместе с волной. Другими словами, если сложить две волны, которые не просто осциллируют, но и перемещаются в пространстве, то получившаяся волна также будет двигаться с той же скоростью.
Хотелось
бы обобщить это на случай волн, у которых отношение между частотой и волновым
числом ![]() не
столь просто, например распространение волн в веществе с некоторым показателем
преломления. В гл. 31 (вып. 3) мы уже изучали показатель преломления
не
столь просто, например распространение волн в веществе с некоторым показателем
преломления. В гл. 31 (вып. 3) мы уже изучали показатель преломления ![]() и выяснили, что
он связан с волновым числом следующим образом:
и выяснили, что
он связан с волновым числом следующим образом: ![]() . В качестве интересного примера мы
нашли показатель преломления
. В качестве интересного примера мы
нашли показатель преломления ![]() для рентгеновских лучей:
для рентгеновских лучей:
 . (48.12)
. (48.12)
На самом деле в гл. 31 мы получали и более сложные формулы, однако эта ничуть не хуже, так почему бы нам не взять ее в качестве примера.
Нам
известно, что даже в том случае, когда ![]() и
и ![]() не пропорциональны друг другу,
отношение
не пропорциональны друг другу,
отношение ![]() все
равно будет скоростью распространения данной частоты и данного волнового числа.
Это отношение называется фазовой скоростью, т. е. скоростью, с которой движется
фаза или узел отдельной волны:
все
равно будет скоростью распространения данной частоты и данного волнового числа.
Это отношение называется фазовой скоростью, т. е. скоростью, с которой движется
фаза или узел отдельной волны:
![]() . (48.13)
. (48.13)
Интересно,
что, например, для случая распространения рентгеновских лучей в стекле эта
фазовая скорость больше скорости света в пустоте [поскольку ![]() , согласно (48.12), меньше
единицы], а это несколько неприятно, ведь не думаем же мы, что можно посылать сигналы
быстрее скорости света!
, согласно (48.12), меньше
единицы], а это несколько неприятно, ведь не думаем же мы, что можно посылать сигналы
быстрее скорости света!
Обсудим
теперь интерференцию двух волн, у которых значения ![]() и
и ![]() связаны какой-то
определенной зависимостью. Например, написанная ранее формула для показателя
связаны какой-то
определенной зависимостью. Например, написанная ранее формула для показателя ![]() говорит, что
говорит, что ![]() есть определенная
известная функция частоты
есть определенная
известная функция частоты ![]() . Для большей определенности давайте
выпишем формулу зависимости
. Для большей определенности давайте
выпишем формулу зависимости ![]() и
и ![]() в данной частной задаче:
в данной частной задаче:
![]() , (48.14)
, (48.14)
где
![]() -
постоянная. Во всяком случае, мы хотим сложить такие две волны, у которых для
каждой частоты существует определенное волновое число.
-
постоянная. Во всяком случае, мы хотим сложить такие две волны, у которых для
каждой частоты существует определенное волновое число.
Давайте сделаем это точно так же, как и при получении уравнения (48.7):
![]() . (48.15)
. (48.15)
Таким образом, снова получается модулированная волна, распространяющаяся со средней частотой и средним волновым числом, однако сила ее меняется в соответствии с выражением, зависящим от разности частот и разности волновых чисел.
Рассмотрим
теперь случай, когда разности между двумя волнами относительно малы.
Предположим, что мы складываем две волны с приблизительно равными частотами,
при этом ![]() практически
равно каждой из частот
практически
равно каждой из частот ![]() . То же можно сказать и о
. То же можно сказать и о ![]() . Таким образом,
скорость волны, быстрых осцилляций, узлов действительно остается равной
. Таким образом,
скорость волны, быстрых осцилляций, узлов действительно остается равной ![]() . Но смотрите,
скорость распространения модуляций не та же самая! Как нужно изменить
. Но смотрите,
скорость распространения модуляций не та же самая! Как нужно изменить ![]() , чтобы
сбалансировать некоторую величину времени
, чтобы
сбалансировать некоторую величину времени ![]() ? Скорость этих модулирующих волн
равна
? Скорость этих модулирующих волн
равна
![]() . (48.16)
. (48.16)
Скорость движения модуляций иногда называют групповой скоростью. Если мы возьмем случай относительно малой разности между частотами и соответственно относительно малой разности между волновыми числами, то это выражение переходит в пределе в
![]() . (48.17)
. (48.17)
Другими словами, чем медленнее модуляции, тем медленнее и биения, и вот что самое удивительное - существует определенная скорость их распространения, которая не равна фазовой скорости волны.
Групповая
скорость равна производной ![]() по
по ![]() , а фазовая скорость равна отношению
, а фазовая скорость равна отношению ![]() .
.
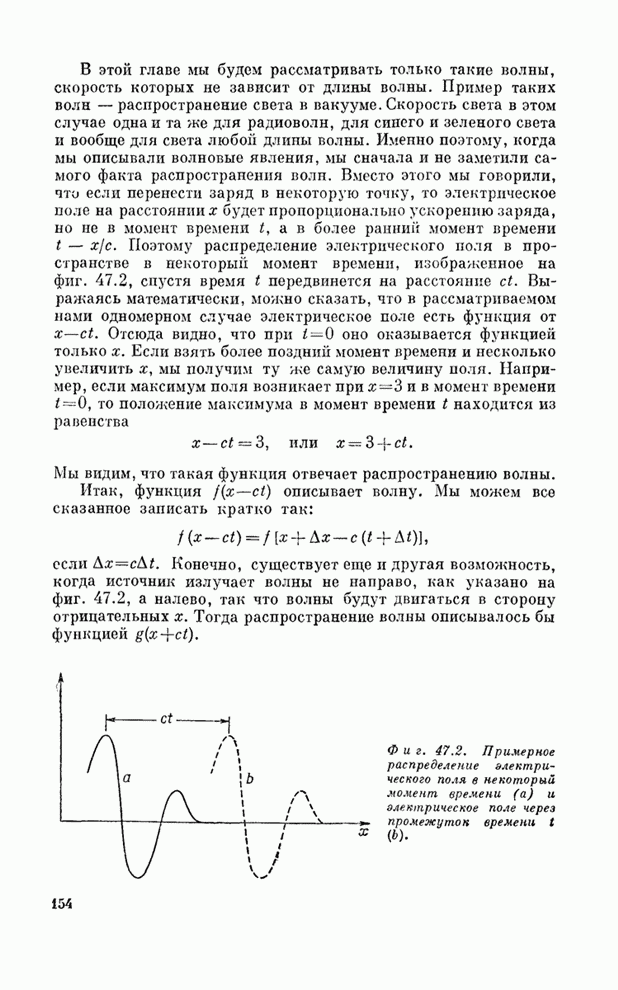
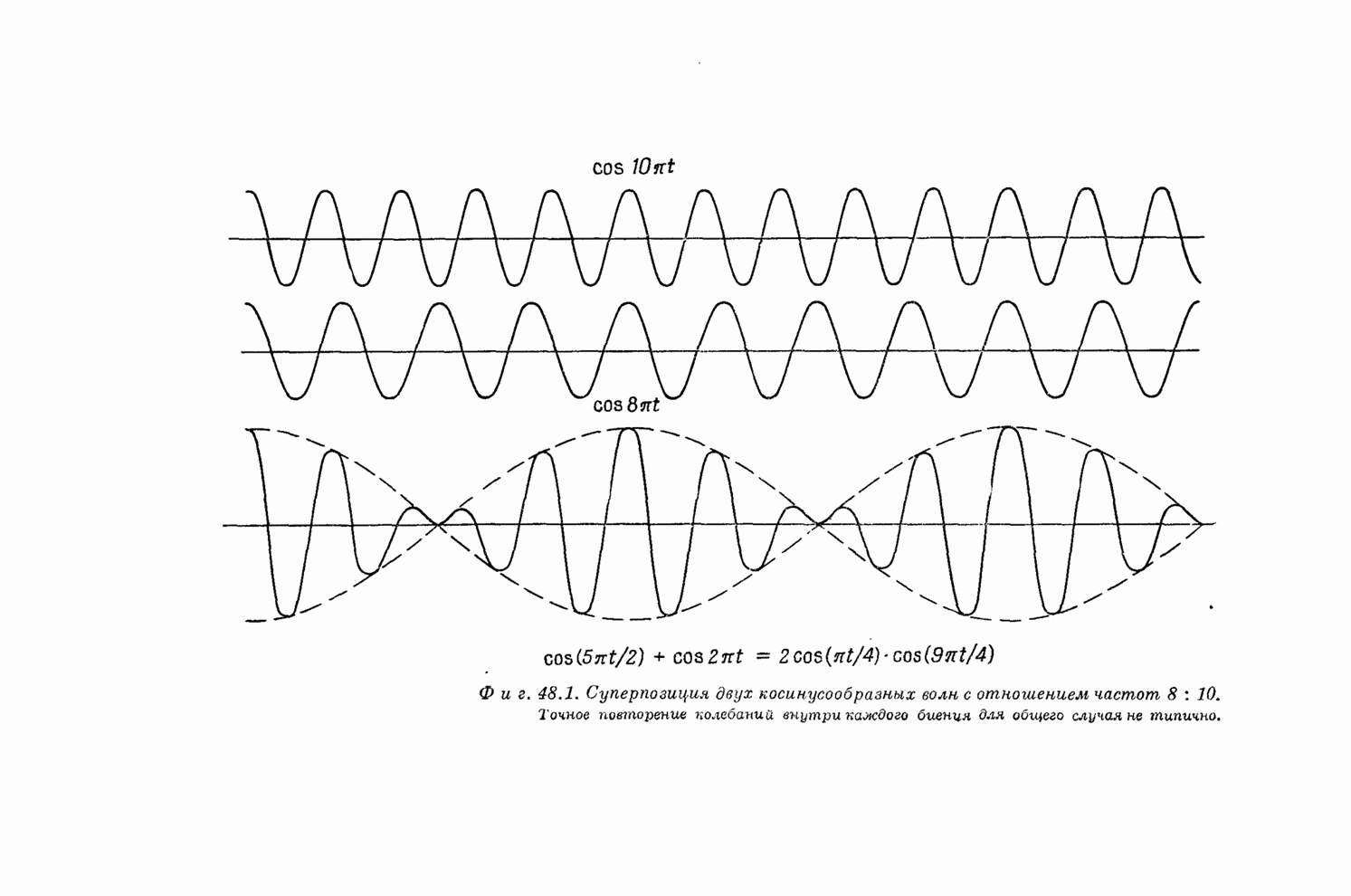
Посмотрим, можно ли понять, почему так происходит. Рассмотрим две волны с несколько различными длинами, как это показано на фиг. 48.1. Они то совпадают по фазе, то различаются, то снова совпадают и т. д. Однако теперь эти волны в действительности представляют волны в пространстве, распространяющиеся с немного различными скоростями. Но поскольку фазовая скорость, скорость узлов этих двух волн, не в точности одинакова, то происходит нечто новое. Предположим, что мы едем рядом с одной из волн и смотрим на другую. Если бы они двигались с одинаковой скоростью, то вторая волна оставалась бы относительно нас там же, где и была с самого начала, поскольку мы едем как бы на гребне одной волны и видим гребень второй прямо около себя. Однако в действительности скорости не равны. Частоты немного отличаются друг от друга, а поэтому немного отличаются и скорости. Из-за этой небольшой разницы в скоростях другая волна либо медленно обгоняет нас, либо отстает. Что же с течением времени происходит с узлом? Если чуть-чуть продвинуть одну из волн, то узел при этом уйдет на значительное расстояние вперед (или назад), т. е. сумма этих двух волн имеет какую-то огибающую, которая вместе с распространением волн скользит по ним с другой скоростью. Групповая скорость является той скоростью, с которой передаются модулирующие сигналы.
Если мы посылаем сигнал, т. е. производим какие-то изменения волны, которые могут быть услышаны и расшифрованы кем-то, то это является своего рода модуляцией, но такая модуляция при условии, что она относительно медленная, будет распространяться с групповой скоростью (быстрые модуляции значительно труднее анализировать).
Теперь
мы можем показать (наконец-то!), что скорость распространения рентгеновских
лучей в куске угля, например, не больше, чем скорость света, хотя фазовая
скорость больше скорости света. Чтобы сделать это, нужно найти соотношение ![]() , которое мы
вычислим дифференцированием формулы (48.14):
, которое мы
вычислим дифференцированием формулы (48.14): ![]() . А групповая скорость равна обратной
величине, т. е.
. А групповая скорость равна обратной
величине, т. е.
 , (43.18)
, (43.18)
что
меньше, чем ![]() !
Таким образом, хотя фазы могут бежать быстрее скорости света, модулирующие
сигналы движутся медленнее, и в этом состоит разрешение кажущегося парадокса! Разумеется,
в простейшем случае
!
Таким образом, хотя фазы могут бежать быстрее скорости света, модулирующие
сигналы движутся медленнее, и в этом состоит разрешение кажущегося парадокса! Разумеется,
в простейшем случае ![]() групповая скорость
групповая скорость ![]() тоже равна
тоже равна ![]() , т. е. когда все
фазы движутся с одинаковой скоростью, естественно, и групповая скорость будет
той же самой.
, т. е. когда все
фазы движутся с одинаковой скоростью, естественно, и групповая скорость будет
той же самой.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия