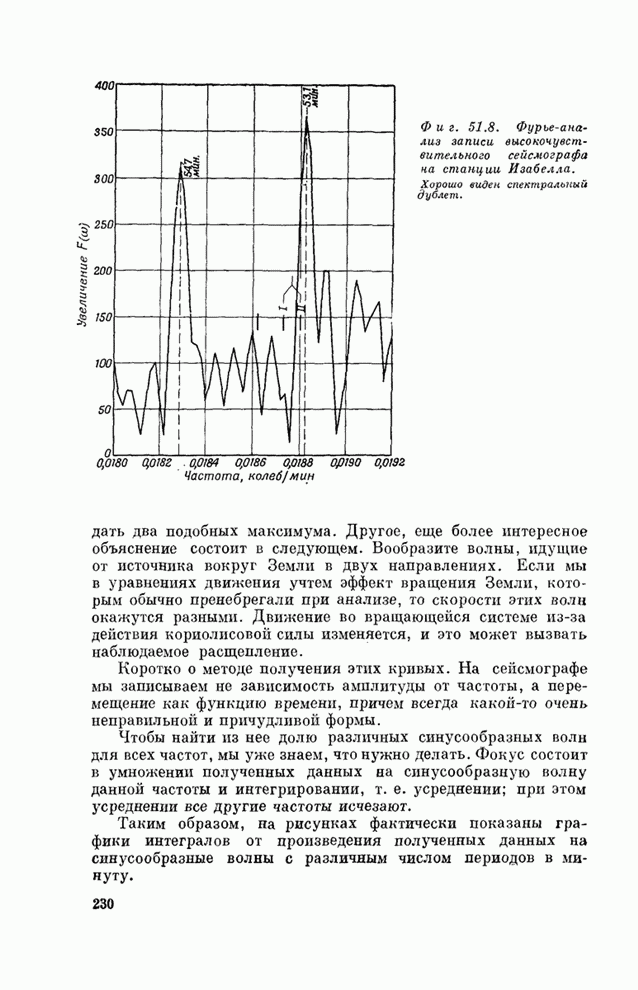
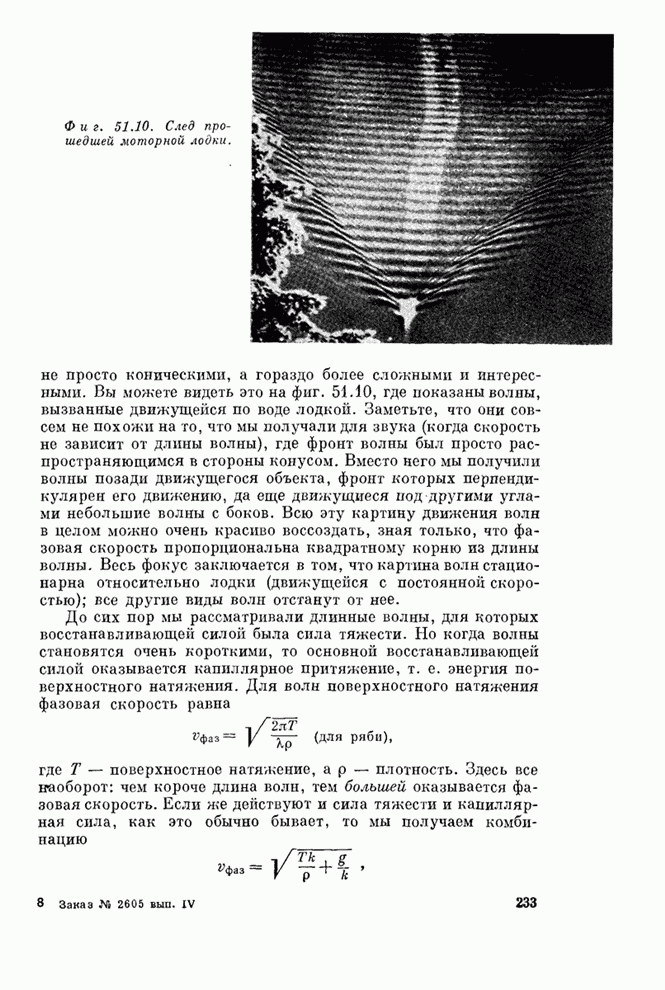
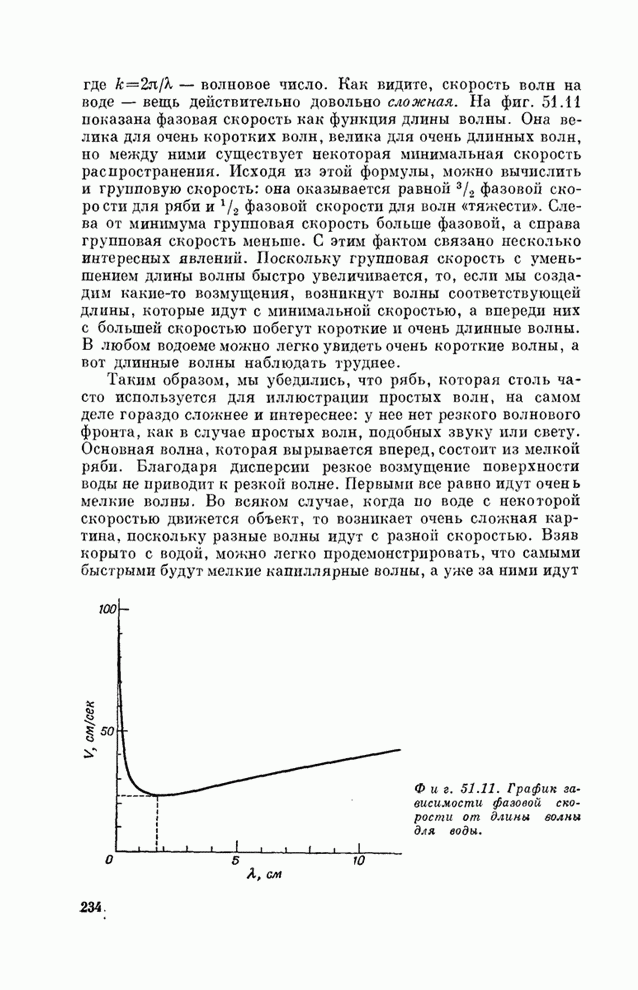
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Теорема об энергии
Энергия
волны пропорциональна квадрату ее амплитуды. Для сложной волны энергия за один
период пропорциональна  . Эту энергию можно связать с
коэффициентами Фурье.
. Эту энергию можно связать с
коэффициентами Фурье.
Напишем
 . (50.22)
. (50.22)
После
раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных
членов типа ![]() .
Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от
всех таких членов по одному периоду равны нулю, так что останутся только
квадратные члены, подобные
.
Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от
всех таких членов по одному периоду равны нулю, так что останутся только
квадратные члены, подобные ![]() . Интеграл от любого квадрата
косинуса или синуса по одному периоду равен
. Интеграл от любого квадрата
косинуса или синуса по одному периоду равен ![]() , так что получаем
, так что получаем
 . (50.23)
. (50.23)
Это уравнение называют «теоремой об энергии», которая говорит, что полная энергия волны равна просто сумме энергий всех ее Фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем
![]() ,
,
поскольку
![]() . Таким
образом мы узнали, что сумма квадратов обратных нечетных чисел равна
. Таким
образом мы узнали, что сумма квадратов обратных нечетных чисел равна ![]() . Точно так же,
выписав сначала ряд Фурье для функции и используя затем теорему об энергии,
можно доказать результат, понадобившийся нам в гл. 45, т. е. что
. Точно так же,
выписав сначала ряд Фурье для функции и используя затем теорему об энергии,
можно доказать результат, понадобившийся нам в гл. 45, т. е. что ![]() равно
равно ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 39. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 1. Свойства вещества
- § 2. Давление газа
- § 3. Сжимаемость излучения
- § 4. Температура и кинетическая энергия
- § 5. Закон идеального газа
- Глава 40. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
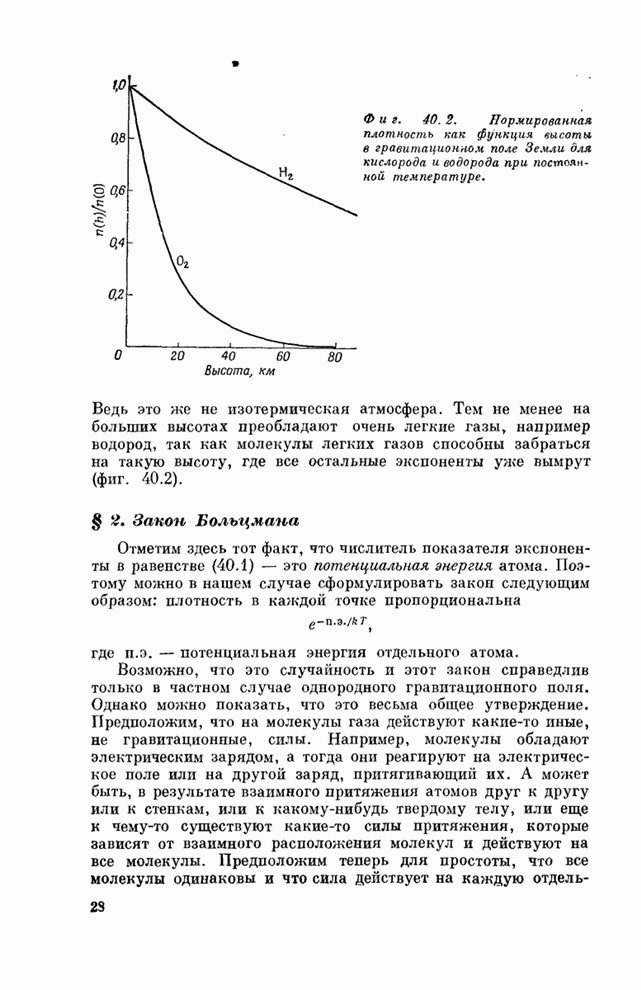
- § 1. Экспоненциальная атмосфера
- § 2. Закон Больцмана
- § 3. Испарение жидкости
- § 4. Распределение молекул по скоростям
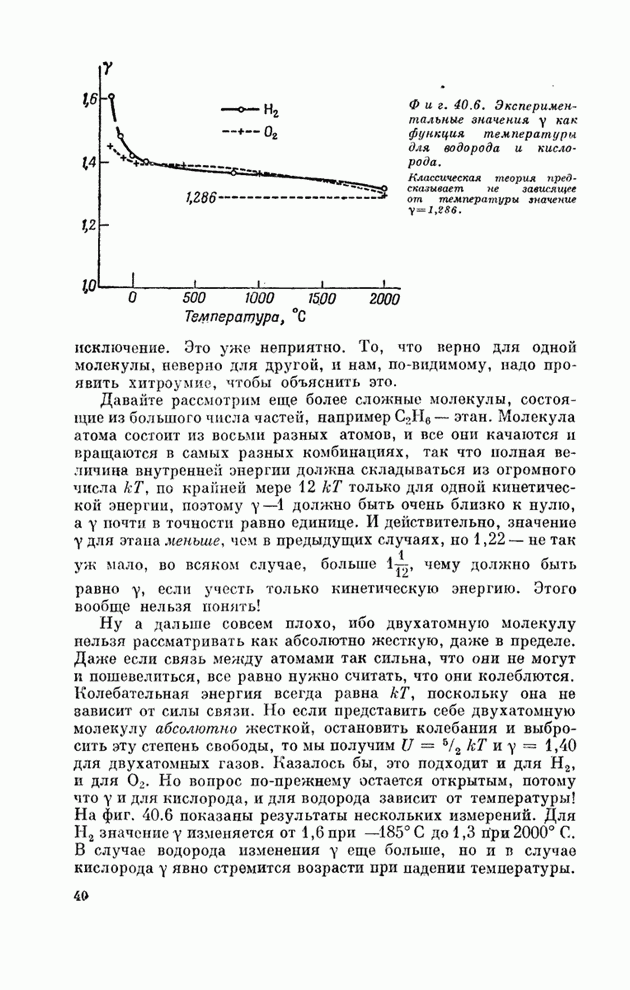
- § 5. Удельные теплоемкости газов
- § 6. Поражение классической физики
- Глава 41. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 1. Равнораспределение энергии
- § 2. Тепловое равновесие излучений
- § 3. Равномерное распределение и квантовый осциллятор
- § 4. Случайные блуждания
- Глава 42. ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 1. Испарение
- § 2. Термоионная эмиссия
- § 3. Тепловая ионизация
- § 4. Химическая кинематика
- § 5. Законы излучения Эйнштейна
- Глава 43. ДИФФУЗИЯ
- § 1. Столкновения молекул
- § 2. Средняя длина свободного пробега
- § 3. Скорость дрейфа
- § 4. Ионная проводимость
- § 5. Молекулярная диффузия
- § 6. Теплопроводность
- Глава 44. ЗАКОНЫ ТЕРМОДИНАМИКИ
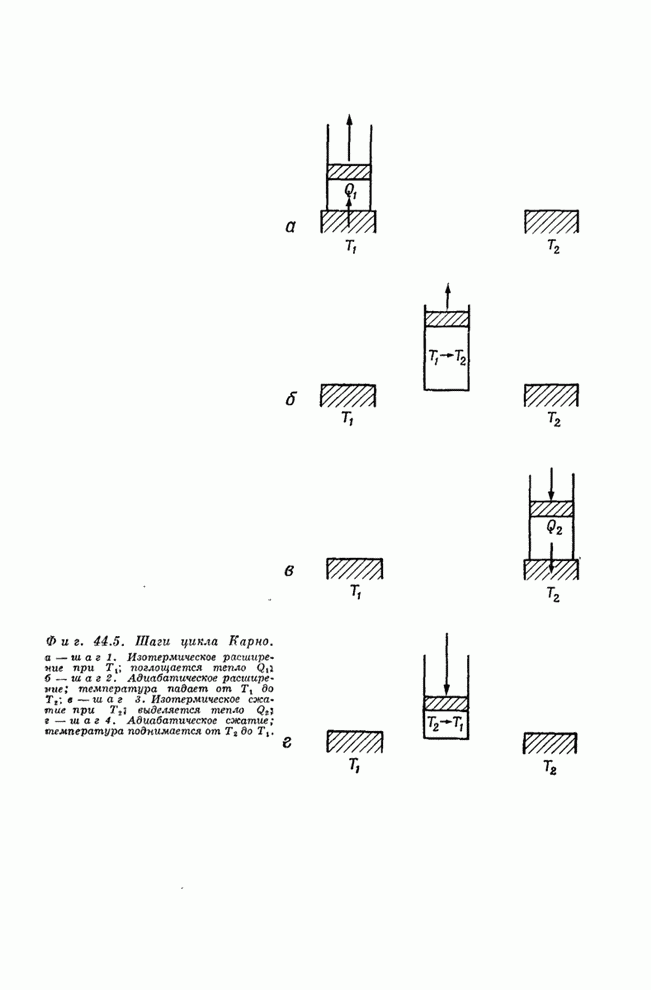
- § 1. Тепловые машины; первый закон
- § 2. Второй закон
- § 3. Обратимые машины
- § 4. Коэффициент полезного действия идеальной машины
- § 5. Термодинамическая температура
- § 6. Энтропия
- Глава 45. ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
- § 1. Внутренняя энергия
- § 2. Применения
- § 3. Уравнение Клаузиуса-Клайперона
- Глава 46. ХРАПОВИК И СОБАЧКА
- § 1. Как действует храповик
- § 2. Храповик как машина
- § 3. Обратимость в механике
- § 4. Необратимость
- § 5. Порядок и энтропия
- Глава 47. ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ
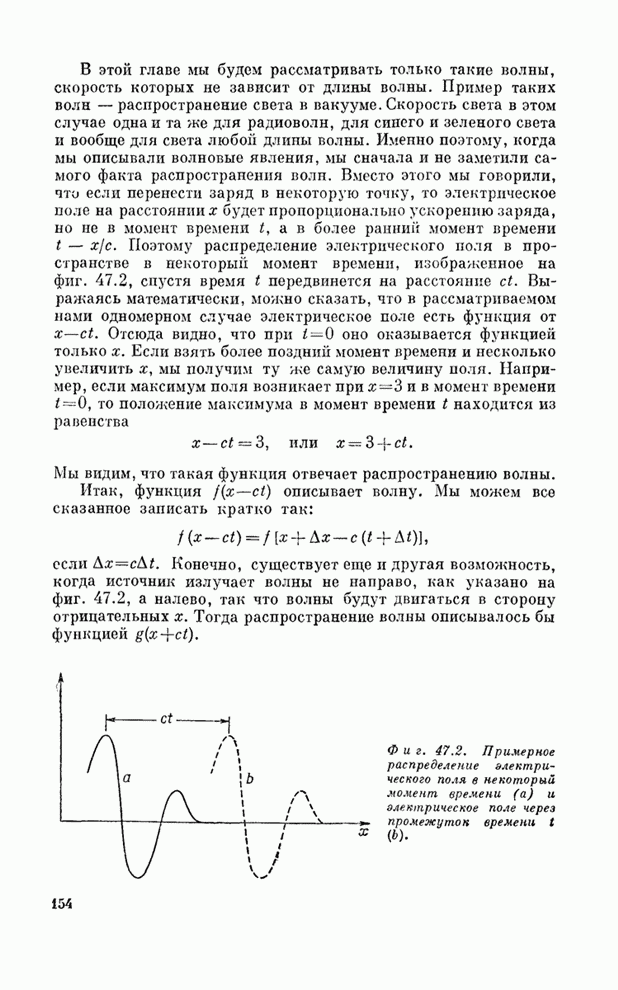
- § 1. Волны
- § 2. Распространение звука
- § 3. Волновое уравнение
- § 4. Решения волнового уравнения
- § 5. Скорость звука
- Глава 48. БИЕНИЯ
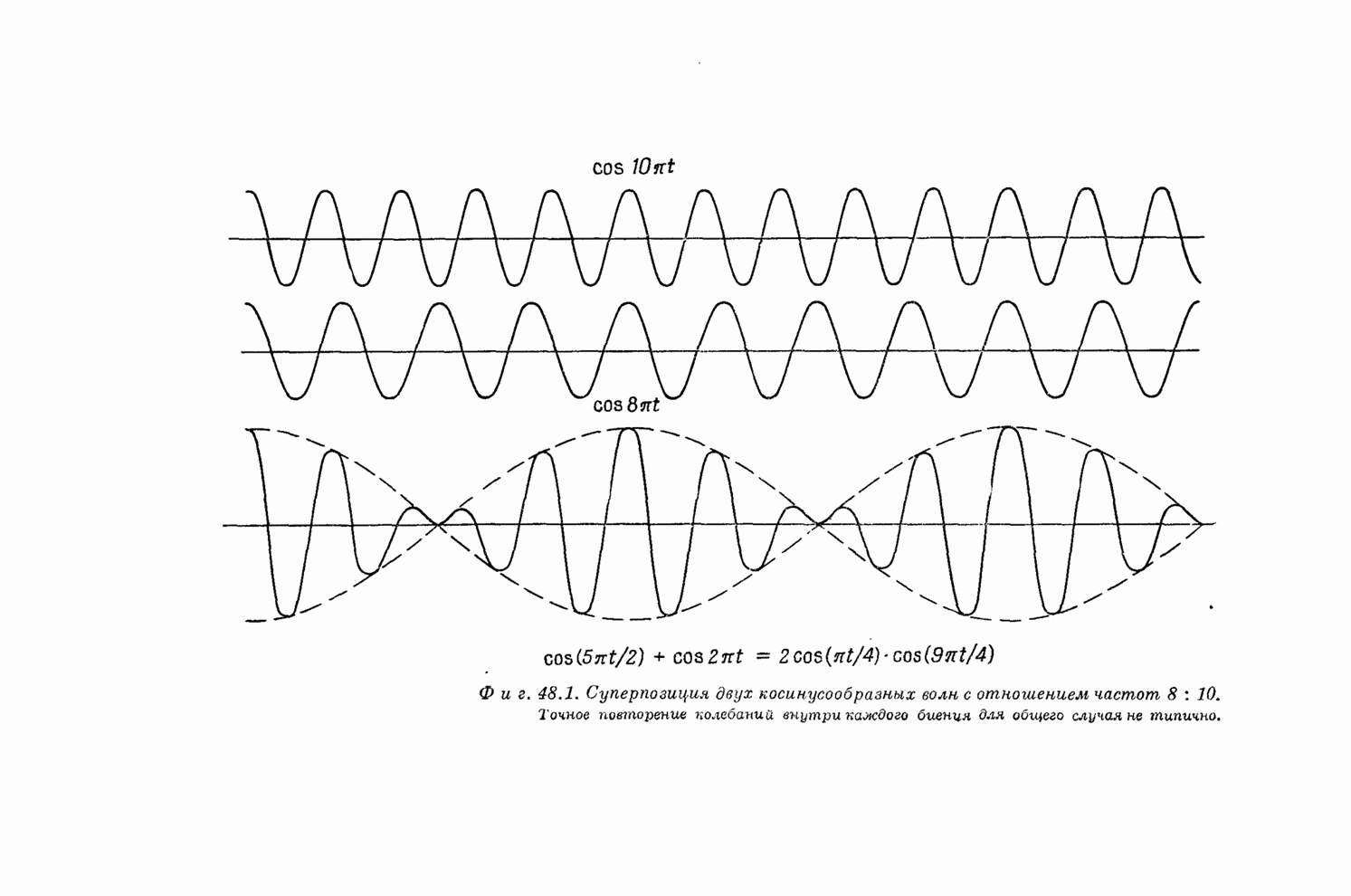
- § 1. Сложение двух волн
- § 2. Некоторые замечания о биениях и модуляции
- § 3. Боковые полосы
- § 4. Локализованный волновой пакет
- § 5. Амплитуда вероятности частиц
- § 6. Волны в пространстве трех измерений
- § 7. Собственные колебания
- Глава 49. СОБСТВЕННЫЕ КОЛЕБАНИЯ
- § 1. Отражение волн
- § 2. Волны в ограниченном пространстве и собственные частоты
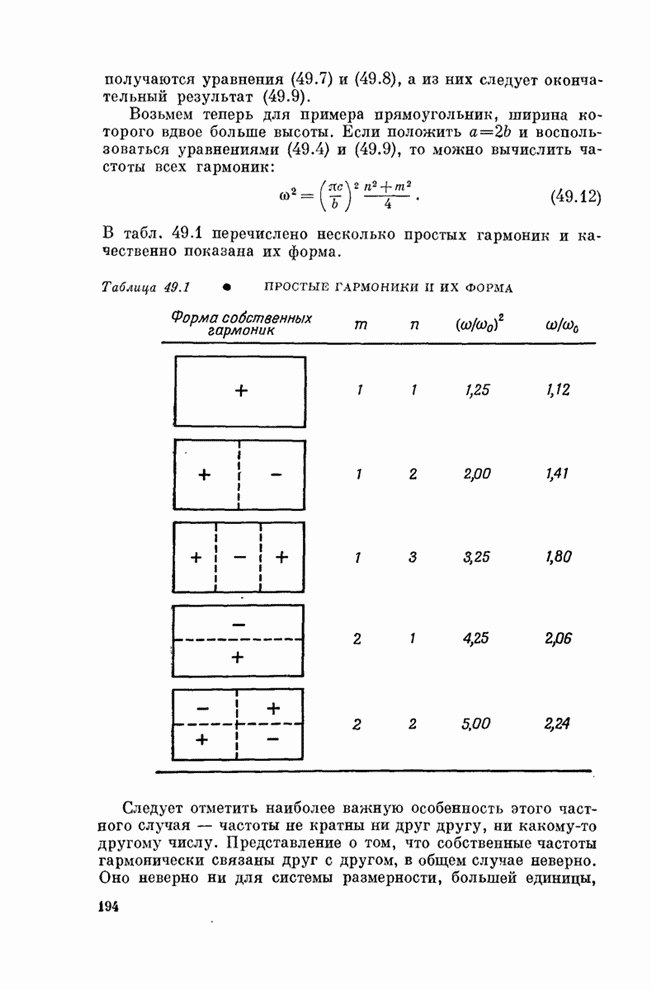
- § 3. Двумерные собственные колебания
- § 4. Связанные маятники
- § 5. Линейные системы
- Глава 50. ГАРМОНИКИ
- § 1. Музыкальные звуки
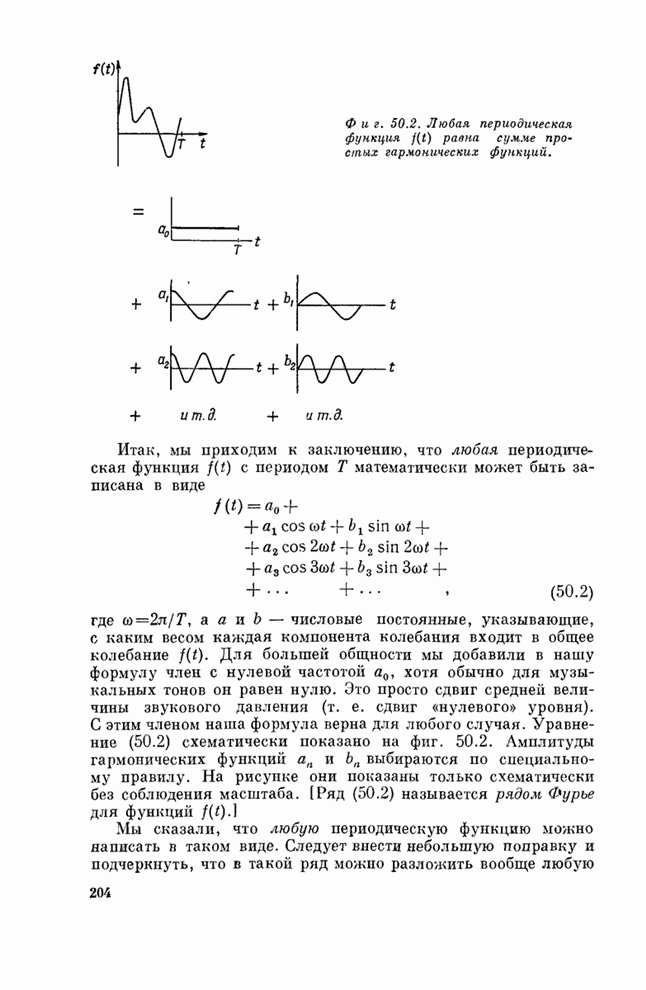
- § 2. Ряд Фурье
- § 3. Качество и гармония
- § 4. Коэффициенты Фурье
- § 5. Теорема об энергии
- § 6. Нелинейная реакция
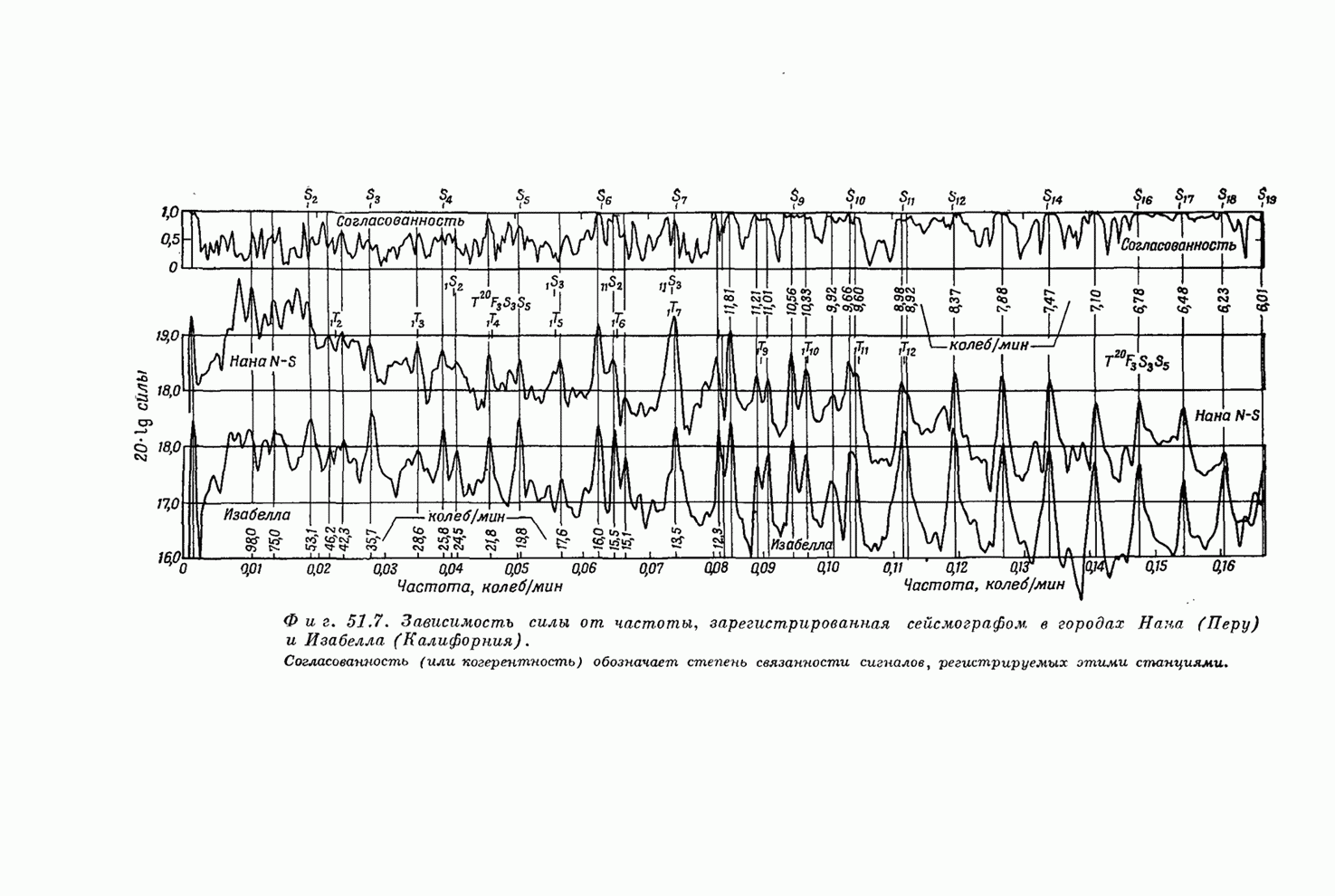
- Глава 51. ВОЛНЫ
- § 1. Волна от движущегося предмета
- § 2. Ударные волны
- § 3. Волны в твердом теле
- § 4. Поверхностные волны
- Глава 52. СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ
- § 1. Симметричные операции
- § 2. Симметрия в пространстве и времени
- § 3. Симметрия и законы сохранения
- § 4. Зеркальное отражение
- § 5. Полярный и аксиальный векторы
- § 6. Какая же рука правая?
- § 7. Четность не сохраняется!
- § 8. Антивещество
- § 9. Нарушенная симметрия