| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Математический аппарат, используемый в методах принятия решений
2.1. Вычисление главного собственного вектора примитивных матриц
Основы метода анализа иерархий базируются на классической теории матриц, изложенной в [9, 33, 60, 93, 94].
Матрицы парных сравнений МАИ представляют собой положительные обратносимметричные неприводимые матрицы, к которым предъявляется требование согласованности.
Квадратные матрицы  для которых
для которых  , называются положительными обратносимметричными матрицами.
, называются положительными обратносимметричными матрицами.
Положительные обратносимметричные матрицы  для элементов которых выполняется соотношение
для элементов которых выполняется соотношение  , являются согласованными.
, являются согласованными.
Квадратная матрица - неприводимая, если она не может быть представленалена в виде  , где
, где  - квадратные матрицы, 0 - нулевая матри
- квадратные матрицы, 0 - нулевая матри  . В противном случае матрицу называют приводимой. Заметим, что в некоторых работах такие матрицы называют неразложимыми [33].
. В противном случае матрицу называют приводимой. Заметим, что в некоторых работах такие матрицы называют неразложимыми [33].
Пример. Матрица  приводима.
приводима.
Граф, соответствующий этой матрице, имеет дугу из первой в первую и третью вершины и аналогично - из третьей в первую и третью вершины, но переход во вторую вершину невозможен (рис. 2.1). Из второй вершины можно перейти во все три вершины.

Рис. 2.1. Граф, иллюстрирующий матрицу
Таким образом, первая и третья вершины образуют неприводимую компоненту, а вторая связана с ними.
Заметим, что комплексная матрица А неприводима в том и только в том случае, если ее направленный граф D(А) - сильно связный.
Теорема. Квадратная матрица или неприводима, или не может быть приведена путем перестановок индексов к виду:

содержащему блок - диагональную матрицу с неприводимыми матрицами  на диагонали. При этом, по крайней мере, одна из матриц с двойным индексом в каждой строке, в которой они появляются, нулевая.
на диагонали. При этом, по крайней мере, одна из матриц с двойным индексом в каждой строке, в которой они появляются, нулевая.
МАИ позволяет вычислять приоритеты альтернатив  . Приоритетами альтернатив, полученными на основе матрицы их парных сравнений, служат нормализованные значения главного собственного вектора матрицы.
. Приоритетами альтернатив, полученными на основе матрицы их парных сравнений, служат нормализованные значения главного собственного вектора матрицы.
Векторы  для которых
для которых  называются собственными векторами, а соответствующие им числа
называются собственными векторами, а соответствующие им числа  - характеристическими, или собственными числами матрицы А.
- характеристическими, или собственными числами матрицы А.
Собственные числа матрицы А являются корнями характеристического уравнения матрицы  где I - единичная матрица. Как полиномиальное уравнение относительно
где I - единичная матрица. Как полиномиальное уравнение относительно  , оно имеет N корней. Каждому собственному значению ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя.
, оно имеет N корней. Каждому собственному значению ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя.
В теореме Фробениуса [33] утверждается, что неприводимая неотрицательная матрица А (в теореме Перрона, что положительная матрица А) всегда имеет действительное положительное простое собственное значение Лтах. Причем модули всех других характеристических чисел не превосходят Лтах.
Теорема (Перрон-Фробениуса) Пусть А > 0 - неприводимая матрица. Тогда:
1. А имеет действительное положительной простое (т.е. некратное) собственное значение Лтах, которое по модулю не меньше любого другого собственного значения матрицы А (некоторые из которых могут быть комплексными числами).
2. Собственный вектор А, соответствующий собственному значению  , имеет положительные компоненты и, по существу (с точностью до постоянного множителя), единственен.
, имеет положительные компоненты и, по существу (с точностью до постоянного множителя), единственен.
3. Число  (иногда называемое конем Перрона матрицы А) удовлетворяет условию
(иногда называемое конем Перрона матрицы А) удовлетворяет условию
 тттах-;
тттах-;  - произвольно.
- произвольно.

Следствие. Пусть  неприводима и пусть х > 0 произвольно. Тогда корень Перрона удовлетворяет условию
неприводима и пусть х > 0 произвольно. Тогда корень Перрона удовлетворяет условию

 называют главным собственным значением (в некоторых источниках корнем Перрона) матрицы А, а соответствующий ему собственный вектор w — главным собственным вектором.
называют главным собственным значением (в некоторых источниках корнем Перрона) матрицы А, а соответствующий ему собственный вектор w — главным собственным вектором.
Таким образом, вычислять приоритеты элементов (находить главный собственный вектор) возможно следующим образом: составляется характеристическое уравнение матрицы А, среди корней данного уравнения выбирается наибольшее, вычисляется соответствующий собственный вектор w, значения вектора нормализуются. Составление и решение такого рода уравнений для каждой матрицы в методе анализа иерархий - достаточно трудоемкий и сложный процесс.
В МАИ предложено использовать другие способы получения главного собственного вектора матрицы, один из которых опирается на следствие к теореме Перрона-Фробениуса, при этом матрицы должны удовлетворять условию примитивности.
Если неприводимая неотрицательная матрица имеет всего h характеристических чисел:  с максимальным модулем
с максимальным модулем  , то такая матрица называется примитивной при
, то такая матрица называется примитивной при  (главное собственное значение по модулю является единственным
(главное собственное значение по модулю является единственным  ), при
), при  матрица называется импримитивной (существуют характеристические корни матрицы, совпадающие по модулю с главным собственным значением). Т. Саати использует в качестве определения примитивной матрицы утверждение теоремы: неприводимая матрица
матрица называется импримитивной (существуют характеристические корни матрицы, совпадающие по модулю с главным собственным значением). Т. Саати использует в качестве определения примитивной матрицы утверждение теоремы: неприводимая матрица  является примитивной в том и
является примитивной в том и
только в том случае, когда  такое, что
такое, что  (некоторая степень матрицы А положительна).
(некоторая степень матрицы А положительна).
Основная теорема МАИ формулируется для примитивных матриц.
Теорема. Для примитивной матрицы  где с - постоянная, а w - собственный вектор, соответствующий
где с - постоянная, а w - собственный вектор, соответствующий  .
.
Используя следствие теоремы Перрона, получаем менее трудоемкий (при компьютерной поддержке) способ вычисления вектора приоритетов матрицы парных сравнений: матрица возводится в произвольно большие степени, вычисляются суммы элементов строк матрицы-результата, полученные суммы нормализуются. Такой подход предоставляет возможность находить главный собственный вектор матрицы А без использования характеристического уравнения, что намного облегчает процедуру его вычисления. Пример вычисления главного собственного вектора и классическим методом, и с использованием основной теоремы МАИ, рассмотрен нами в работе [20].
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
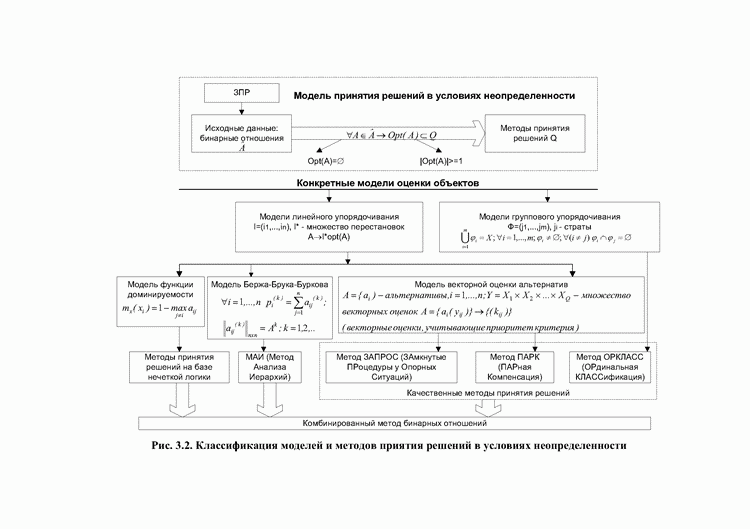
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
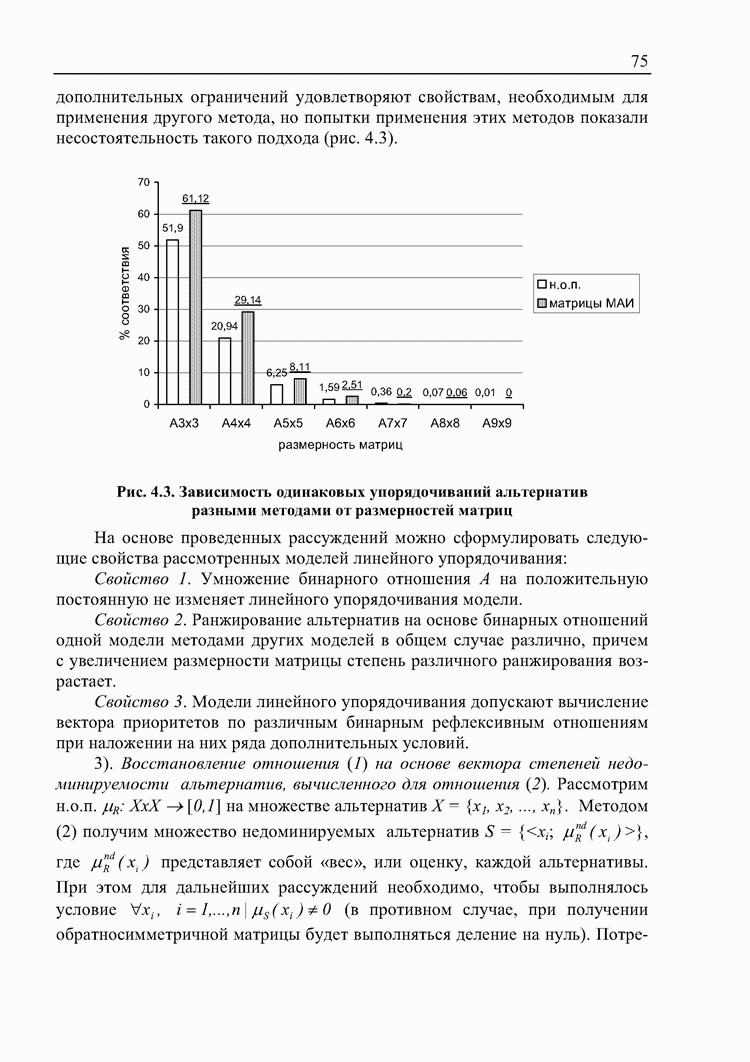
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список