| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Введение
Проблемы принятия решений, которые в широком плане можно рассматривать как проблемы анализа сложных систем, занимают все большее место в современной науке [69].
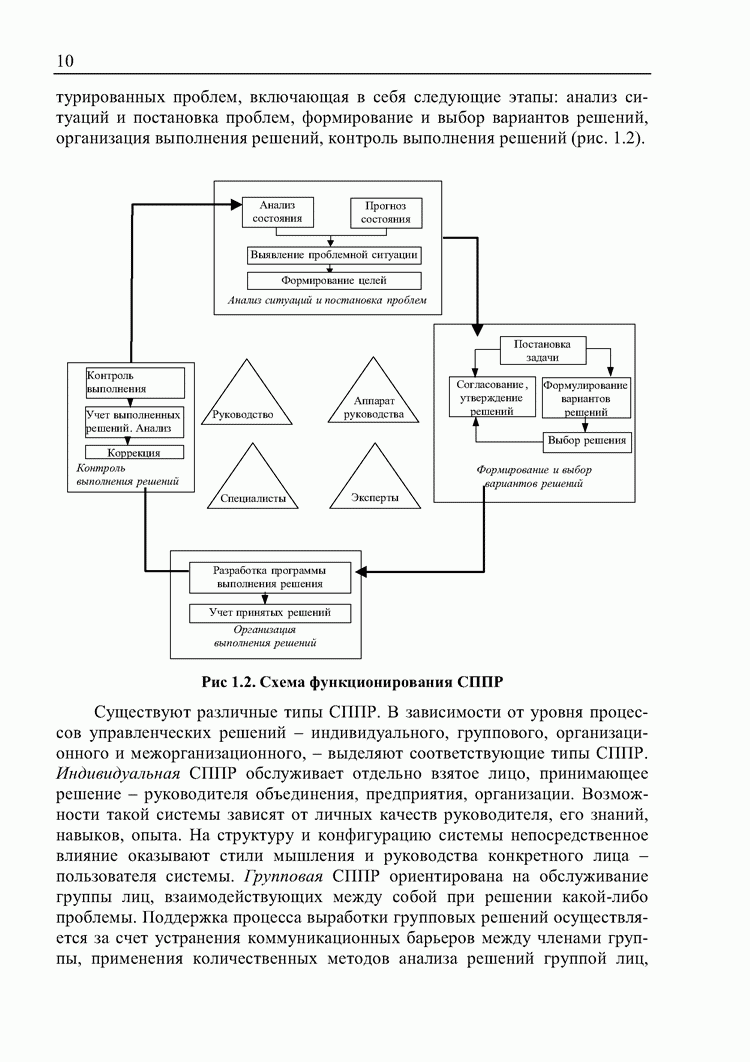
В той или иной степени системы поддержки принятия решений присутствуют в любой информационно-управляющей системе. По мере развития предприятия, упорядочения структуры организации и налаживания межкорпоративных связей, проблема разработки и внедрения системы поддержки принятия решений (СППР) становится особенно актуальной.
ИУС промышленного предприятия должна обладать возможностями и MIS (Manager Information System - ориентирована на обеспечение процесса управления необходимой информацией о прошлом, настоящем и будущем управляемой системы), и DSS (Decision Support System - ориентирована на интеллектуальное обеспечение процесса принятия решения и ставит своей целью поддержку данного процесса) систем, так как руководителю предприятия необходима не только конкретная информация для принятия управленческого решения, но и возможность поддержки решения. Возможной реализацией такого подхода является разработка и внедрение в существующую ИУС предприятия СППР как ее подсистемы.
Одним из главных вопросов разработки СППР является выбор математических моделей и методов принятия решений, составляющих основу ее функционирования. Принятие решений в системе управления промышленными предприятиями связано со сложностью системы, распределенностью ее подсистем, неопределенностью текущего состояния, необходимостью учитывать большое число различных факторов и критериев, характеризующих варианты решений. Поэтому при разработке СППР промышленного предприятия возникает проблема выбора адекватных математических методов, позволяющих отражать структуру сложной системы, для которой принимается решение, оперировать субъективными оценками экспертов, принимать во внимание качественный (вербальный) характер оценки специалистами вариантов решения проблемы, учитывать неясность, неточность данных средствами нечеткой логики.
Бурно развивавшаяся в последнее время математическая теория оптимизации создала совокупность методов, помогающих при компьютерной поддержке эффективно принимать решения при фиксированных и известных параметрах, характеризующих исследуемый процесс, а также в том случае, когда параметры - случайные величины. Однако основные трудности возникают в том случае, когда параметры оказываются неопределенными и когда они в то же время сильно влияют на результаты решения. Такие ситуации могут возникать как вследствие недостаточной изученности процессов, для
которых принимается решение, так и из-за участия в управление нескольких лиц, преследующих различные цели.
Приближенные, но в то же время эффективные способы анализа сложных, плохо определенных систем, не поддающихся точному математическому описанию, опираются на использование лингвистических переменных и нечетких алгоритмов. Основные приложения данного подхода относятся к областям экономики, управления производством, искусственному интеллекту, психологии, лингвистики, обработки информации, медицины, биологии.
Компьютеризация общества вызвала быстрое расширение сферы использования количественных методов анализа за счет их применения для анализа экономических, урбанистических, социальных, биологических и других систем. Большинство методов, используемых в настоящее время для анализа гуманистических систем, т.е. систем, в которых участвует человек, представляют собой модификации методов, которые в течение длительного времени создавались для механистических систем. Замечательные успехи, достигнутые с помощью этих методов, позволили объяснить многие природные явления и создавать все более и более совершенные устройства. Но эти же успехи вселили широко распространенное убеждение в том, что теми же методами или подобными им можно сравнительно эффективно исследовать и гуманистические системы. Так, например, успехи, достигнутые с помощью теории управления в конструировании космических навигационных систем высокой точности, стимулировали применение этой теории для анализа экономических и биологических систем. Успехи макроскопического анализа физических систем с помощью моделирования на ЭВМ привели к тому, что эконометрическое моделирование с помощью ЭВМ стали применять для решения задач прогнозирования, экономического планирования и управления производством.
По глубоко укоренившейся традиции научного мышления понимание явления отождествляют с возможностью его количественного анализа. Однако, по своей сути обычные количественные методы анализа систем непригодны для гуманистических систем и вообще любых систем, сравнимых по сложности с гуманистическими системами. В основе этого тезиса лежит то, что можно было бы назвать принципом несовместимости. Суть этого принципа можно выразить примерно так: чем сложнее система, тем менее мы способны дать точные и в то же время имеющие практическое значение суждения о ее поведении. Чем глубже мы анализируем реальную задачу, тем неопределеннее становится ее решение. Для систем, сложность которых превосходит некоторый пороговый уровень, точность и практический смысл становятся почти исключающими друг друга характеристиками. Именно в этом смысле точный количественный анализ поведения гуманистических систем не имеет, по-видимому, большого практического значения в реальных социальных, экономических и других задачах, связанных с участием одного человека или группы людей.
Представленная работа опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов [61-64, 69], для которых переход от «принадлежности к классу» к «непринадлежности» не скачкообразен, а непрерывен. И в самом деле, нечеткость, присущая процессу мышления человека, наводит на мысль о том, что в основе этого процесса лежит не традиционная двузначная или даже многозначная логика, а логика с нечеткой истинностью, нечеткими связями и нечеткими правилами вывода. Именно такая нечеткая логика играет основную роль в том, что может оказаться одной из наиболее важных сторон человеческого мышления - способности оценивать информацию, т.е. выбирать из разнообразия сведений те и только те, которые имеют отношение к анализируемой проблеме.
По своей природе оценка является приближением. Во многих случаях достаточна весьма приближенная характеризация набора данных, поскольку в большинстве основных задач, решаемых человеком, не требуется высокая точность. Человек использует допустимость такой неточности, кодируя информацию, «достаточную для решения задачи» элементами нечетких множеств, которые лишь приближенно описывают исходные данные. Поток информации, поступающей в мозг через органы зрения, слуха, осязания и др., суживается, таким образом, в тонкую струйку информации, необходимой для решения поставленной задачи с минимальной степенью точности. Способность оперировать нечеткими множествами и вытекающая из нее способность оценивать информацию является одним из наиболее ценных качеств человеческого разума, которое фундаментальным образом отличает человеческий разум от так называемого машинного разума, приписываемого вычислительным машинам.
Традиционные методы анализа систем недостаточно пригодны для анализа гуманистических систем именно потому, что они не в состоянии охватить нечеткость человеческого мышления и поведения. Поэтому для действенного анализа гуманистических систем нужны подходы, для которых точность, строгость и математический формализм не являются чем-то абсолютно необходимым и в которых используется методологическая схема, допускающая нечеткости и частичные истины. В работе, с одной стороны, проводится сравнительный анализ методов принятия решения в условиях неопределенности; с другой стороны, рассматривается возможность создания единого подхода к процессу принятия решений, что позволит специалисту конкретной предметной области не выбирать среди имеющихся методов адекватный для данной ситуации, а пользоваться универсальным алгоритмом, значительно упрощающим процедуру принятия решений.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
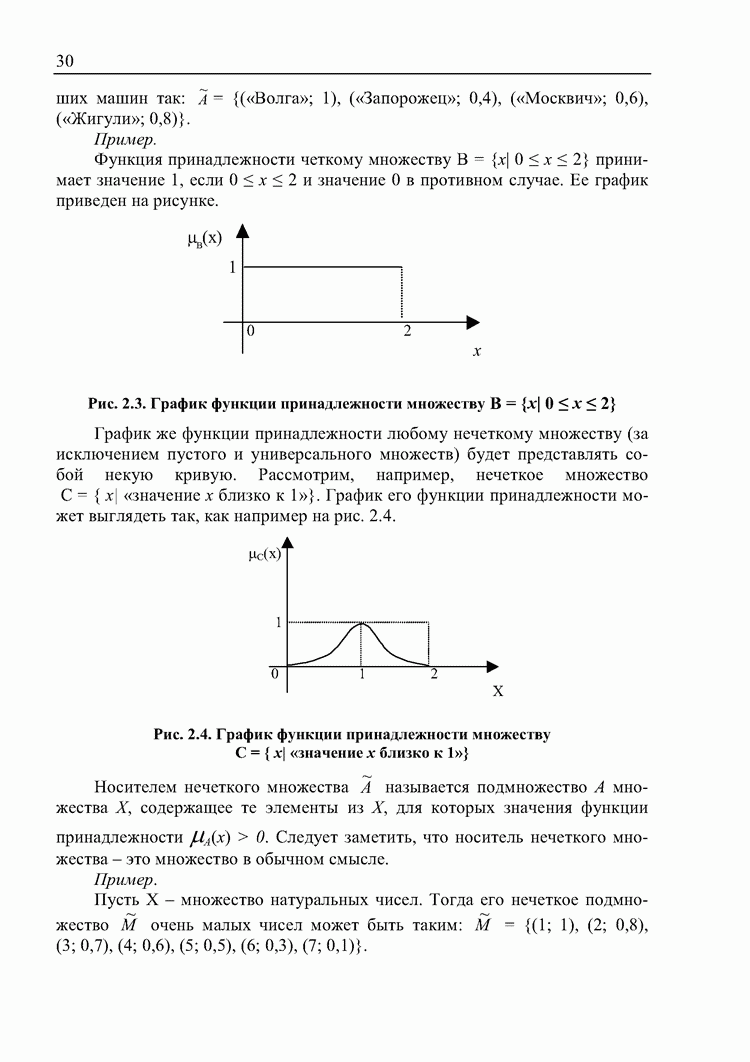
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
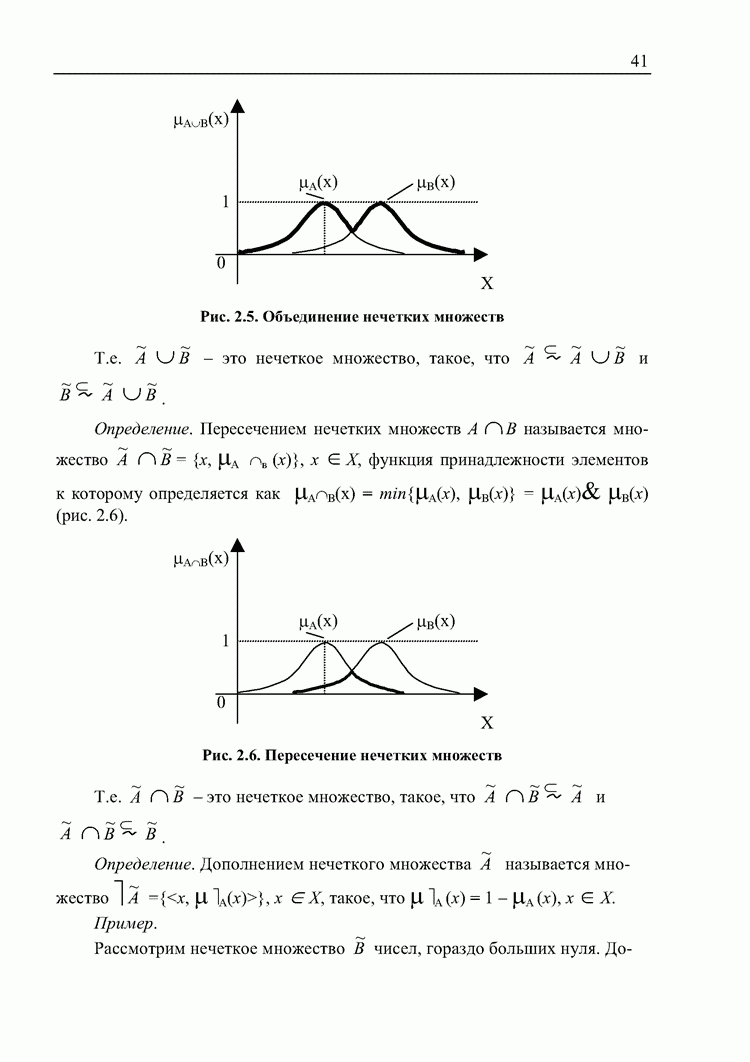
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
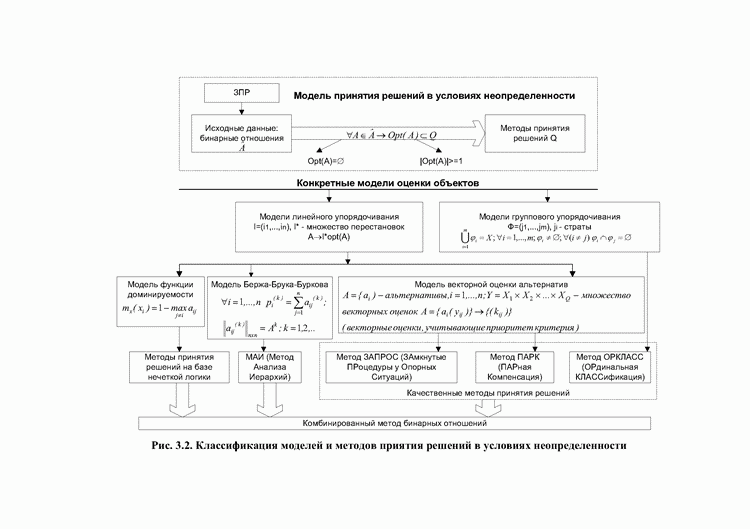
- 3.1. Классификация моделей и методов принятия решений
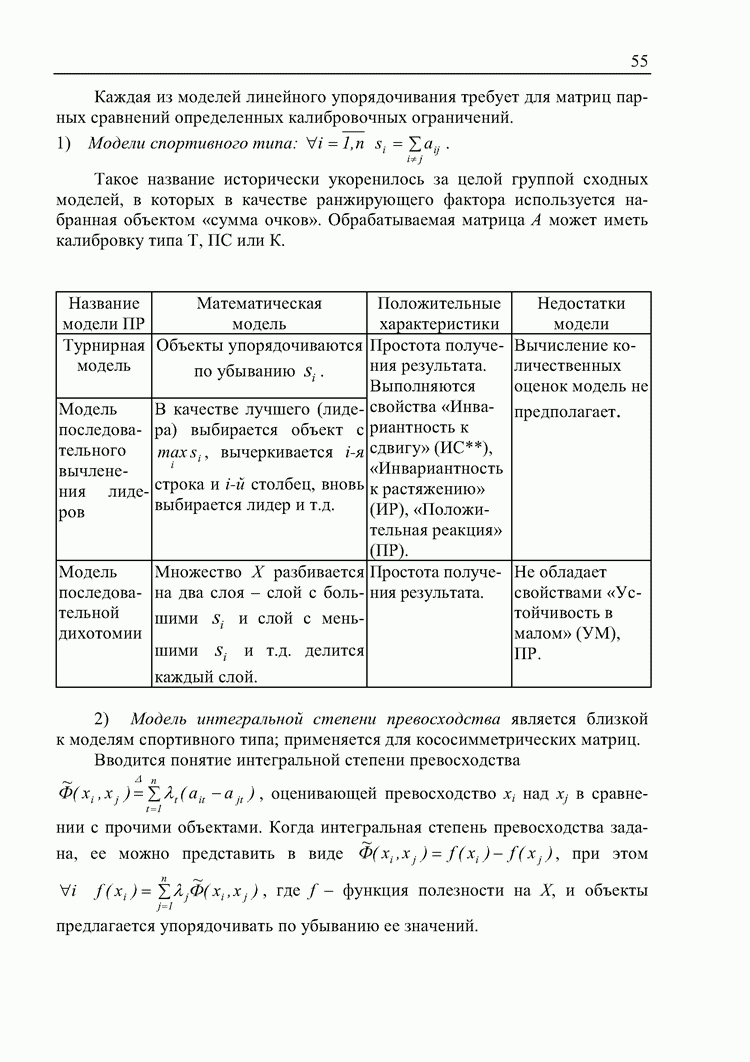
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
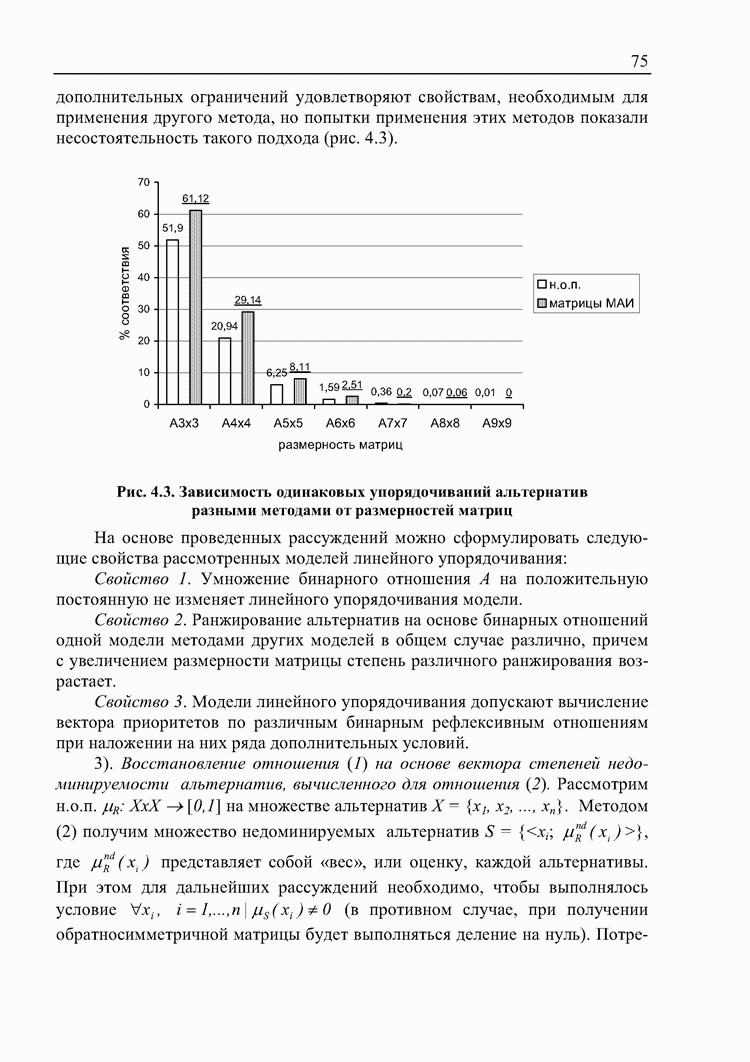
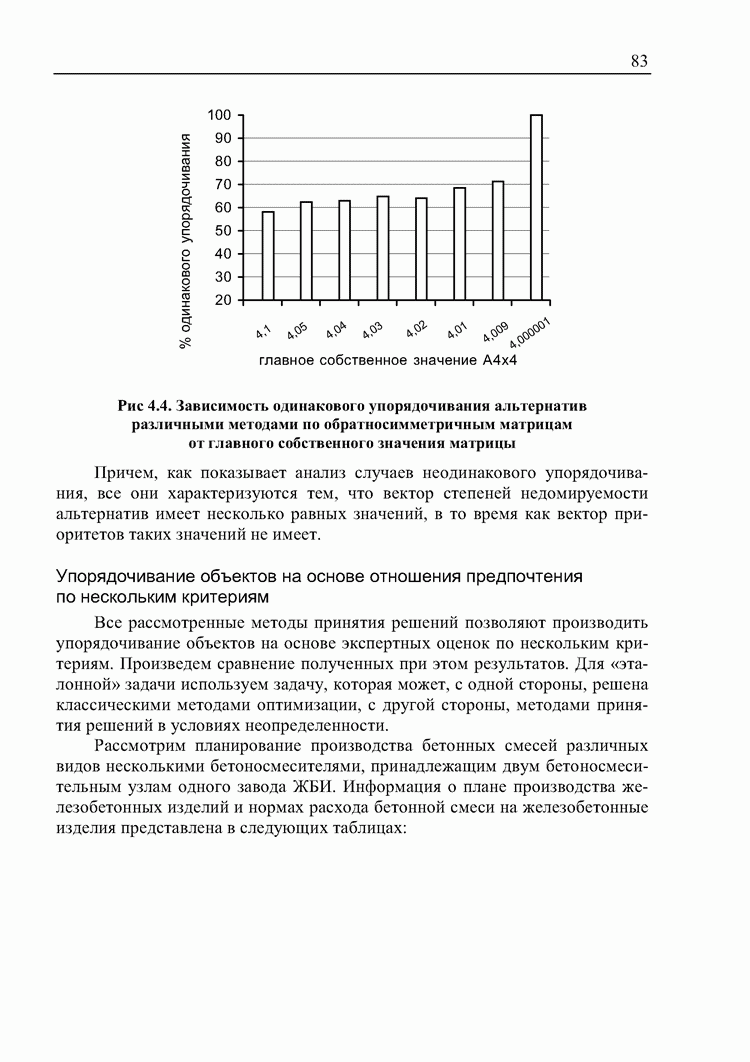
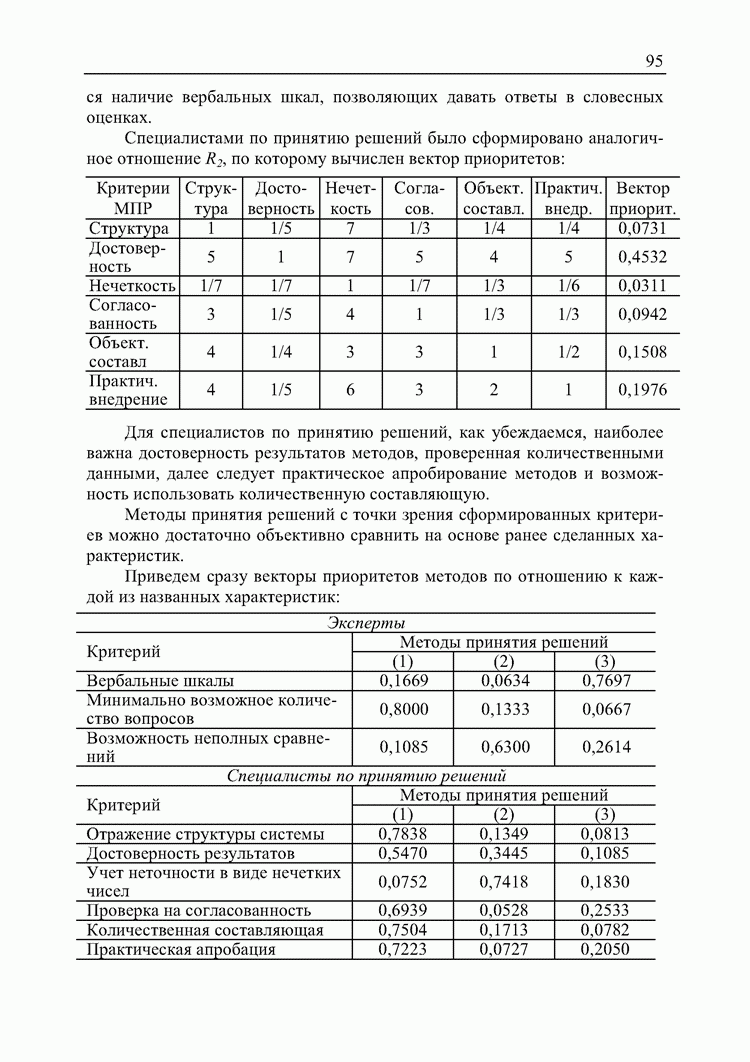
- 4.1. Сравнение результатов ранжирования альтернатив различными
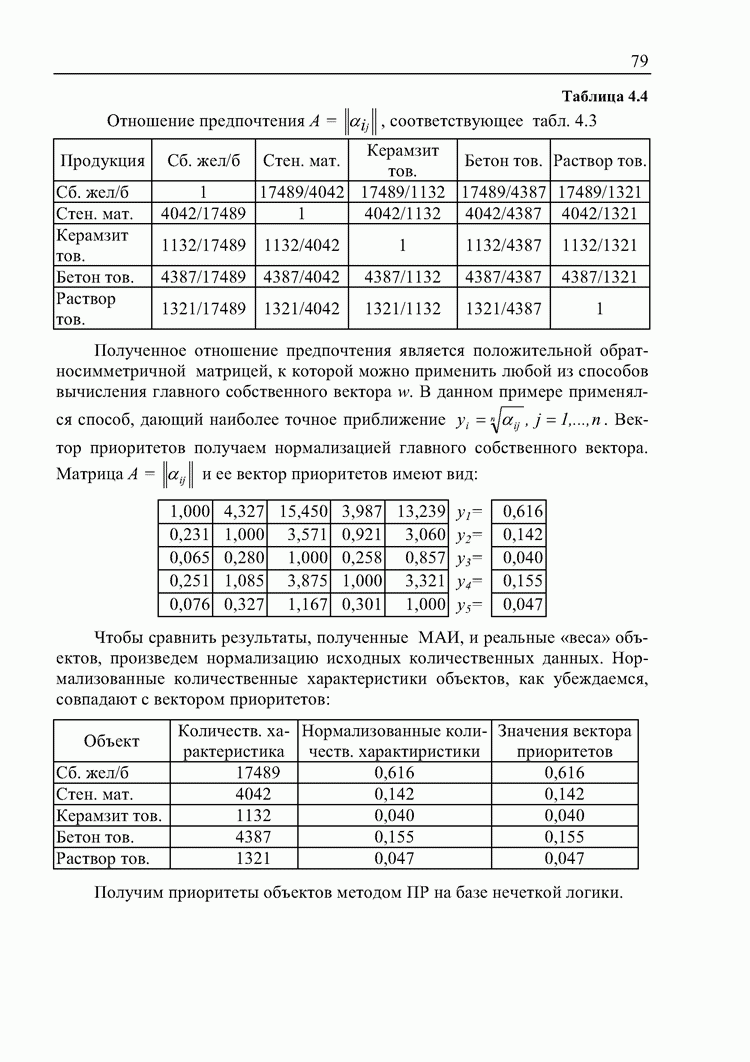
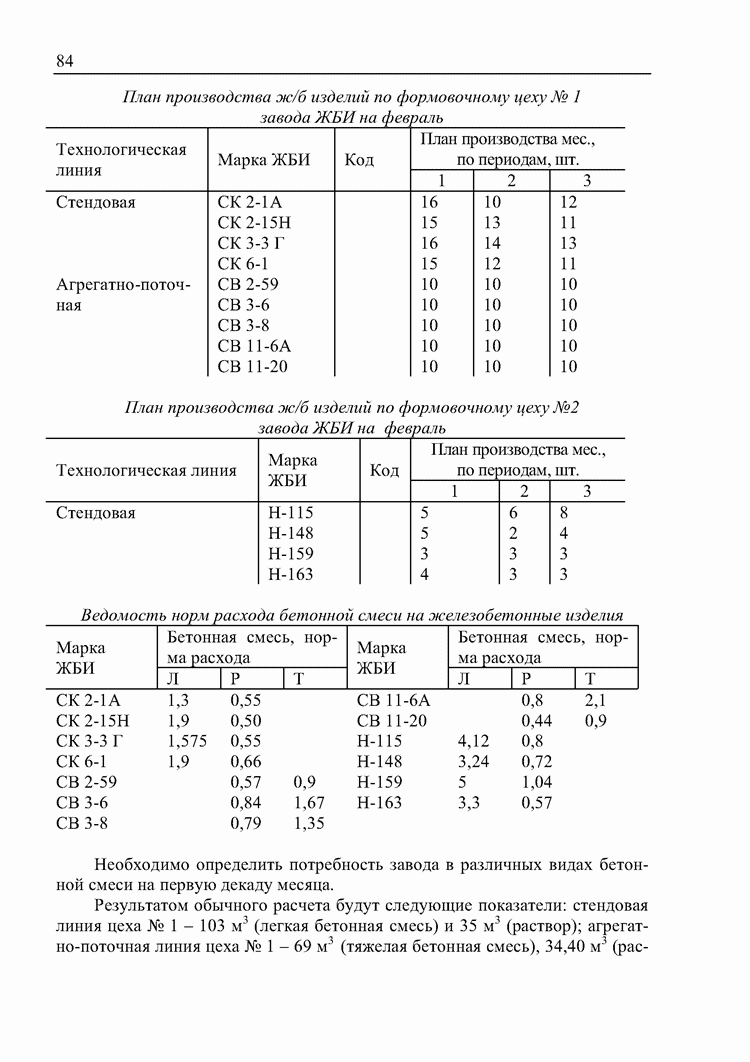
- 4.2. Применение методов принятия решений для анализа количественных данных
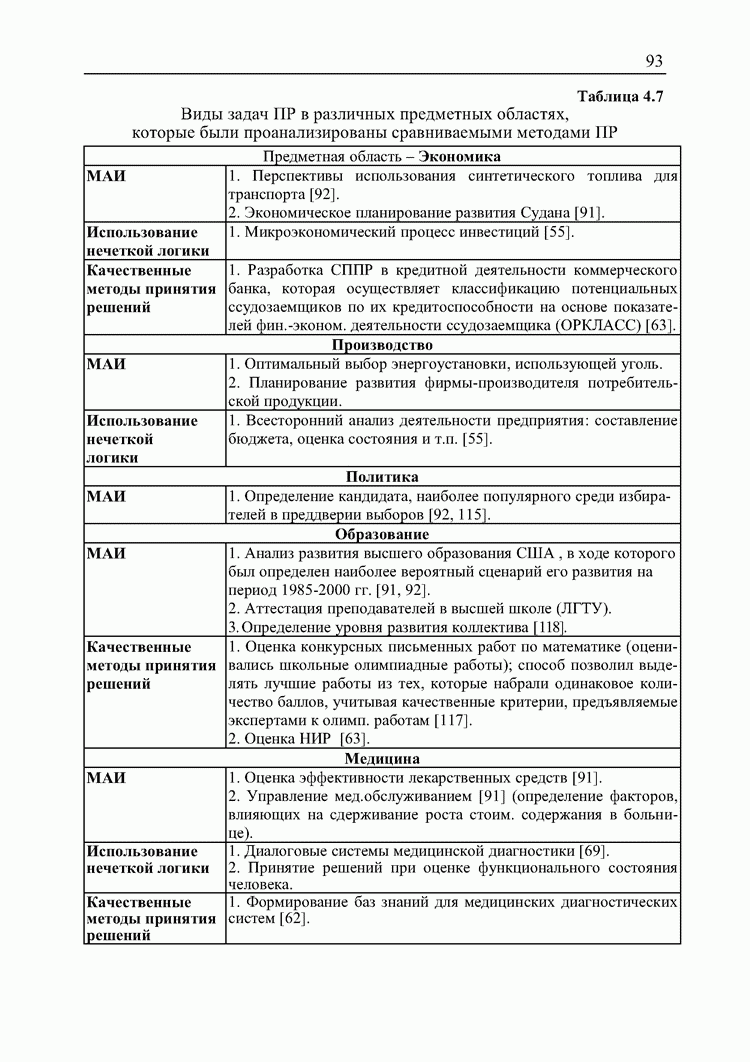
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
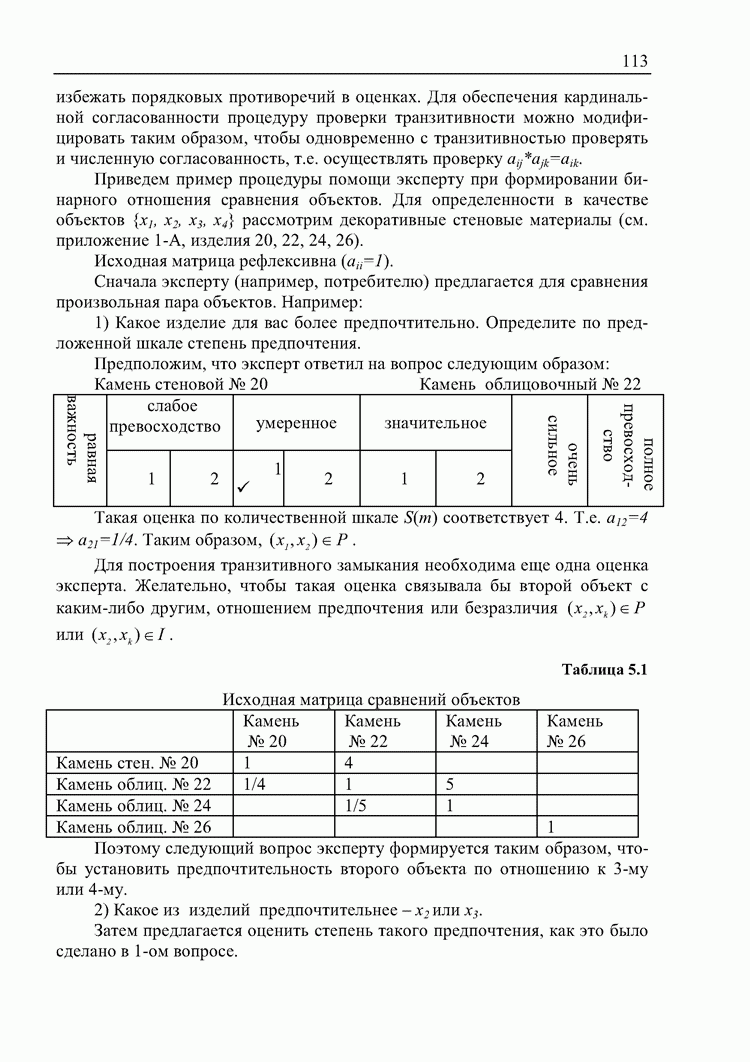
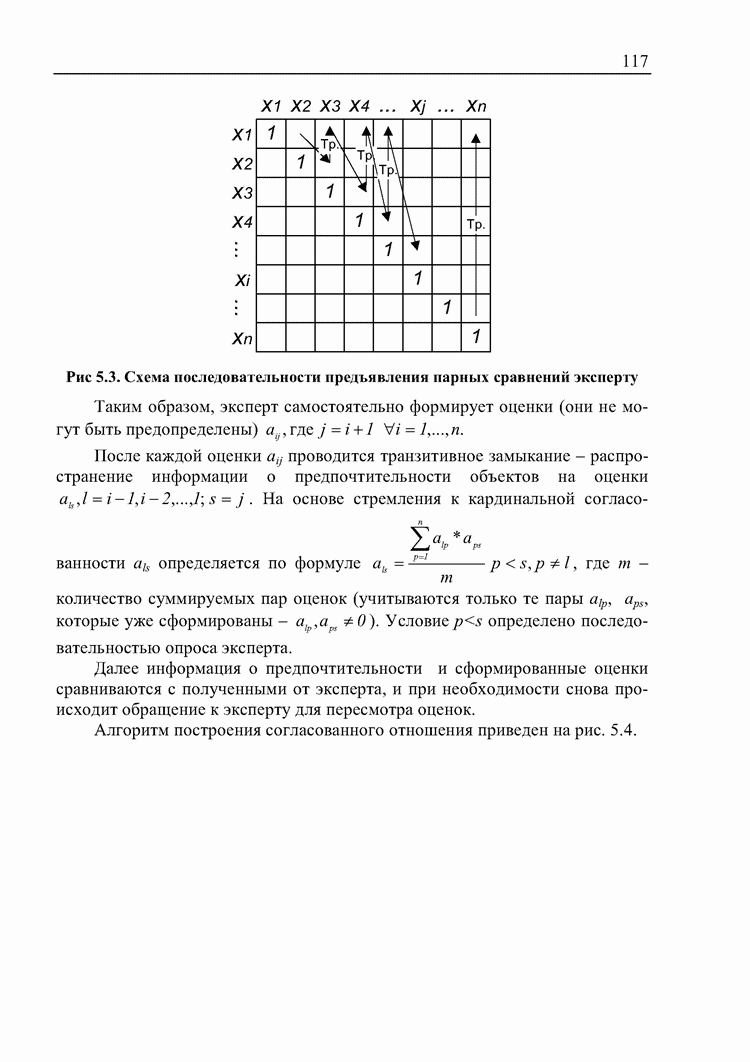
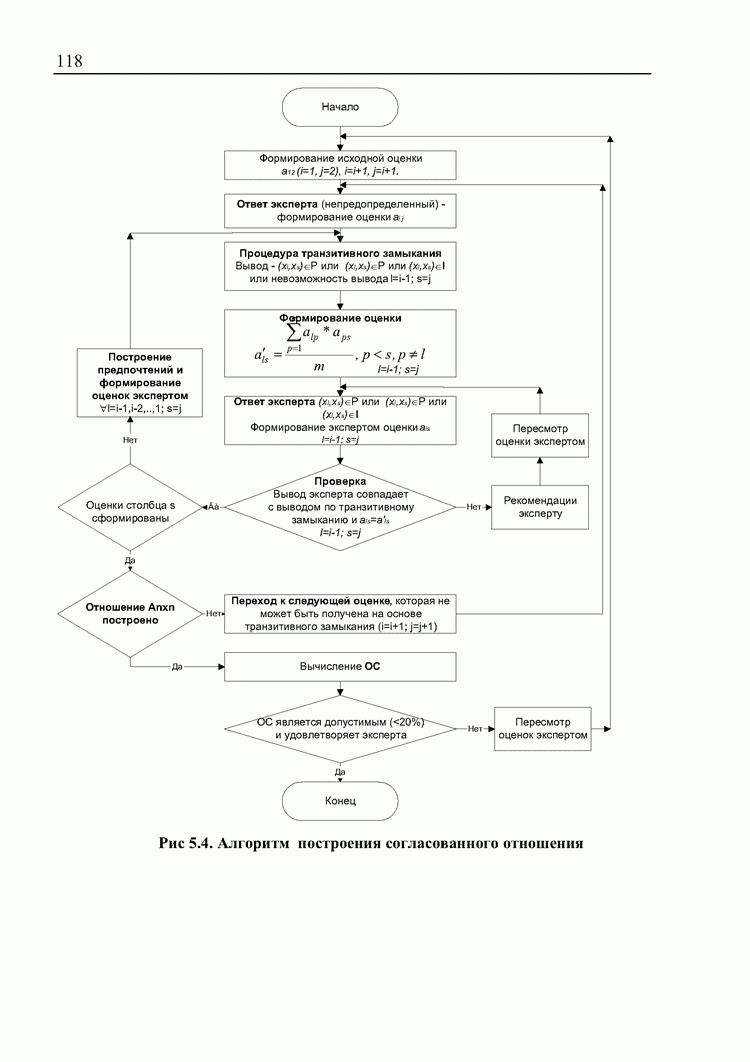
- 5.3. Выявление несогласованности суждений экспертов
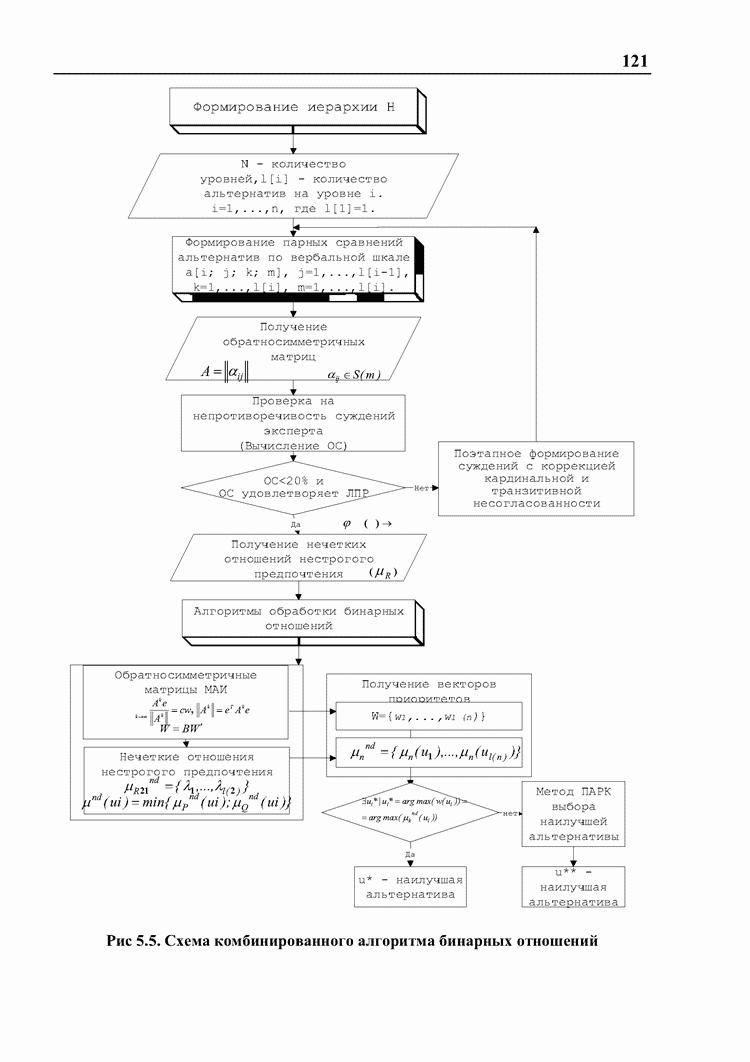
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список