| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Комплекты. Нечеткие множества. Нечеткие отношения
Четкие и нечеткие множества
Любые ситуации, требующие принятия решений, содержат, как правило, большое количество неопределенностей. В этом случае информация, на основе которой принимается решение, может быть выражена нечетко.
Начало развития понятий нечетких множеств связано с именем Л.А. Заде. Современные понятия нечеткой логики представлены в работах А.Н. Мелихова [70, 71], А.Н. Борисова [23, 24, 25, 26], С. А. Орловского [81], X. Райфа [89], А. Кофмана [56], В.Б. Кузьмина [57, 58], в работах [74, 78, 79, 87].
Множество А - четкое множество, если А - часть некоторого универсального для данной прикладной задачи множества U, характеризующегося условиями:
- все элементы множества четко различимы между собой, в множестве нет нескольких экземпляров некоторых элементов;
- относительно каждого элемента  можно четко определить, принадлежит он данному множеству или нет.
можно четко определить, принадлежит он данному множеству или нет.
Эти условия позволяют охарактеризовать четкое множество его характеристической функцией, заданной на универсальном множестве U и принимающей значения в множестве {0, 1}:

Отказ от первого условия приводит к более общему, чем множество, понятию комплекта, допускающего наличие нескольких экземпляров некоторых элементов. Комплект характеризуется функцией экземплярности, заданной на универсальном множестве U и принимающей значения в множестве неотрицательных целых чисел:  - число экземпляров элемента
- число экземпляров элемента  в комплекте А.
в комплекте А.
Отказ от второго условия приводит к более общему, чем множество, понятию нечеткого множества, допускающего определение лишь некоторой степени принадлежности элементов такому множеству.
Нечетким подмножеством  множества X называется совокупность пар вида
множества X называется совокупность пар вида  , где
, где  - функция принадлежности, ставящая в соответствие множеству X отрезок [0;1].
- функция принадлежности, ставящая в соответствие множеству X отрезок [0;1].
X - базовое множество, или базовая шкала. В множество  не включаются элементы, для которых
не включаются элементы, для которых  . Нечеткое множество 0 - пустое, если
. Нечеткое множество 0 - пустое, если  для каждого
для каждого  . Нечеткое множество X - универсальное,
. Нечеткое множество X - универсальное,
если  для каждого
для каждого  .
.
Функция принадлежности выбирается субъективно, зависит от субъекта, его настроения, цели построения множеств, решаемой задачи и т.д.
Пример.
Пусть X - множество отечественных машин. X = {«Волга», «Ока», «Москвич», «Жигули»}. Тогда можно определить нечеткое множество  хороших
хороших
машин так:  = {(«Волга»; 1), («Запорожец»; 0,4), («Москвич»; 0,6), («Жигули»; 0,8)}.
= {(«Волга»; 1), («Запорожец»; 0,4), («Москвич»; 0,6), («Жигули»; 0,8)}.
Пример.
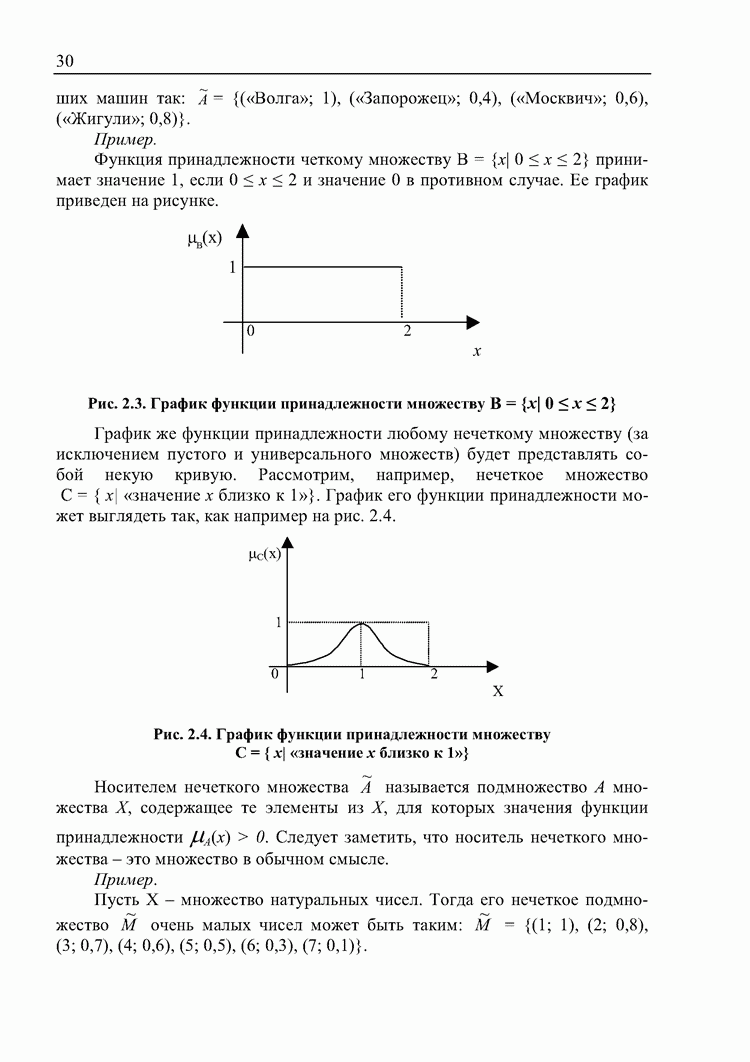
Функция принадлежности четкому множеству  принимает значение 1, если
принимает значение 1, если  и значение 0 в противном случае. Ее график приведен на рисунке.
и значение 0 в противном случае. Ее график приведен на рисунке.

Рис. 2.3. График функции принадлежности множеству 
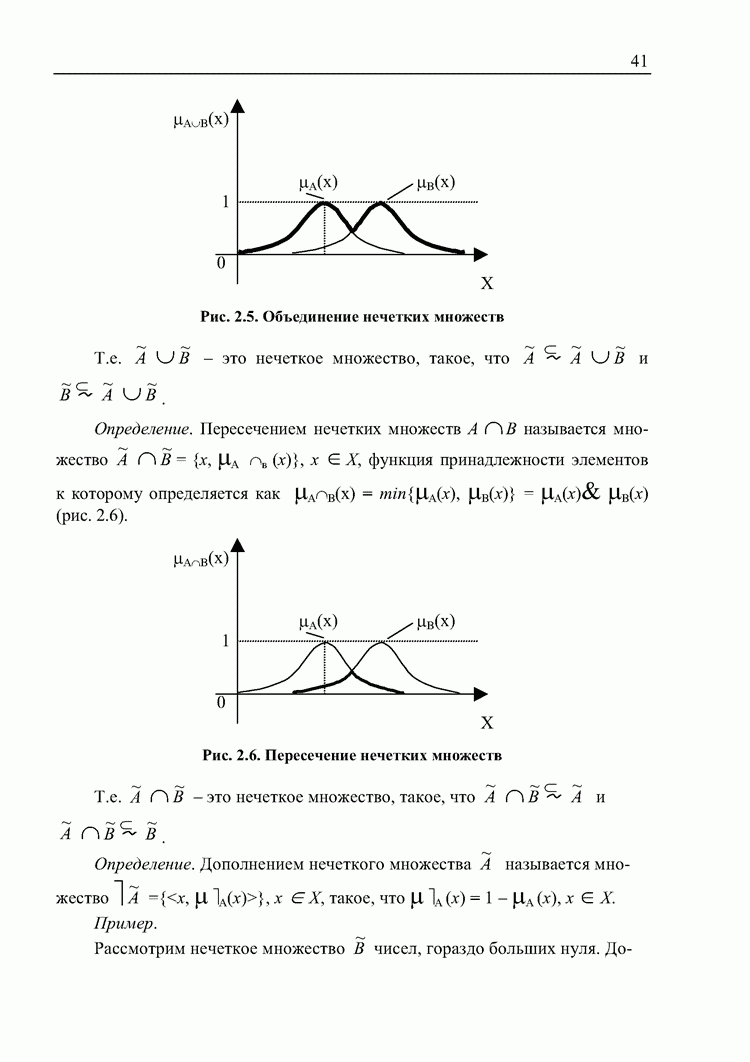
График же функции принадлежности любому нечеткому множеству (за исключением пустого и универсального множеств) будет представлять собой некую кривую. Рассмотрим, например, нечеткое множество  «значение
«значение  близко к
близко к  . График его функции принадлежности может выглядеть так, как например на рис. 2.4.
. График его функции принадлежности может выглядеть так, как например на рис. 2.4.

Рис. 2.4. График функции принадлежности множеству  «значение
«значение  близко к
близко к 
Носителем нечеткого множества  называется подмножество
называется подмножество  множества X, содержащее те элементы из X, для которых значения функции принадлежности
множества X, содержащее те элементы из X, для которых значения функции принадлежности  Следует заметить, что носитель нечеткого множества - это множество в обычном смысле.
Следует заметить, что носитель нечеткого множества - это множество в обычном смысле.
Пример.
Пусть X - множество натуральных чисел. Тогда его нечеткое подмножество М очень малых чисел может быть таким:  = {(1; 1), (2; 0,8), (3; 0,7), (4; 0,6), (5; 0,5), (6; 0,3), (7; 0,1)}.
= {(1; 1), (2; 0,8), (3; 0,7), (4; 0,6), (5; 0,5), (6; 0,3), (7; 0,1)}.
Носителем нечеткого множества  является множество М = {1, 2, 3, 4, 5, 6, 7}. Это обычное четкое подмножество множества X.
является множество М = {1, 2, 3, 4, 5, 6, 7}. Это обычное четкое подмножество множества X.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
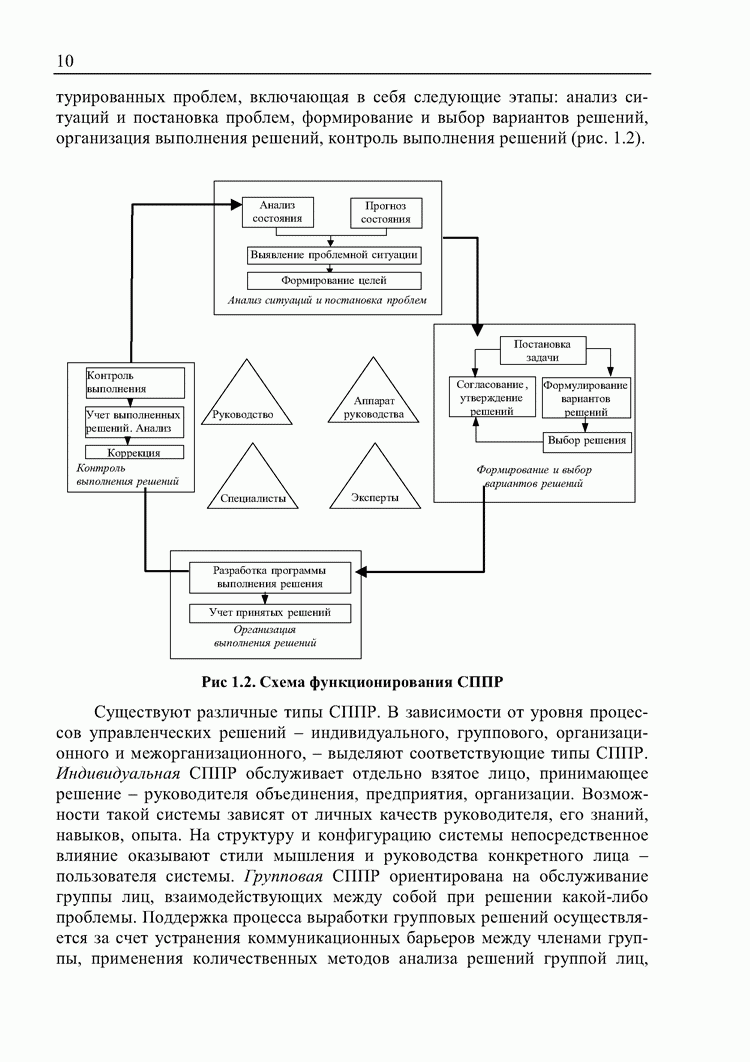
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
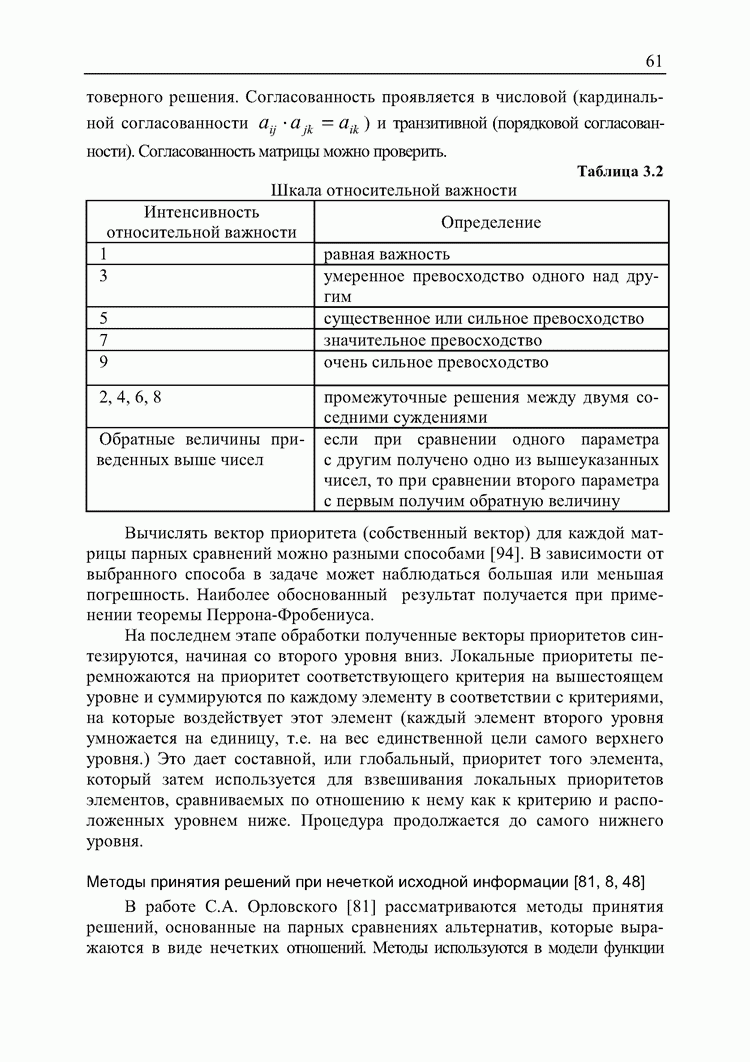
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
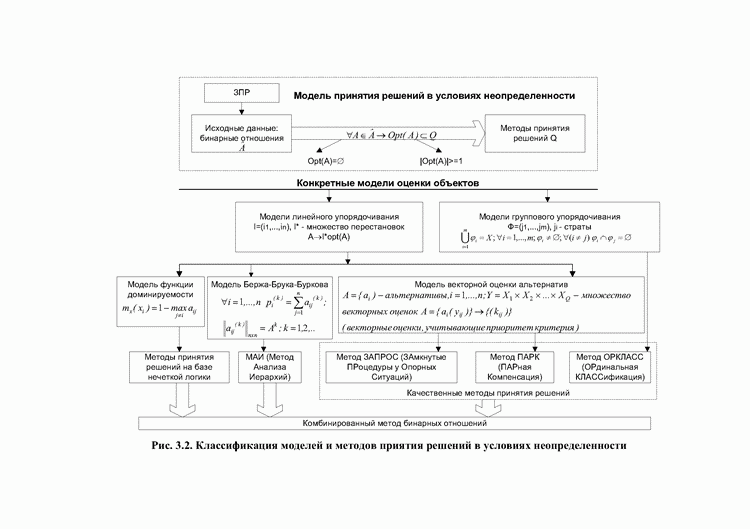
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
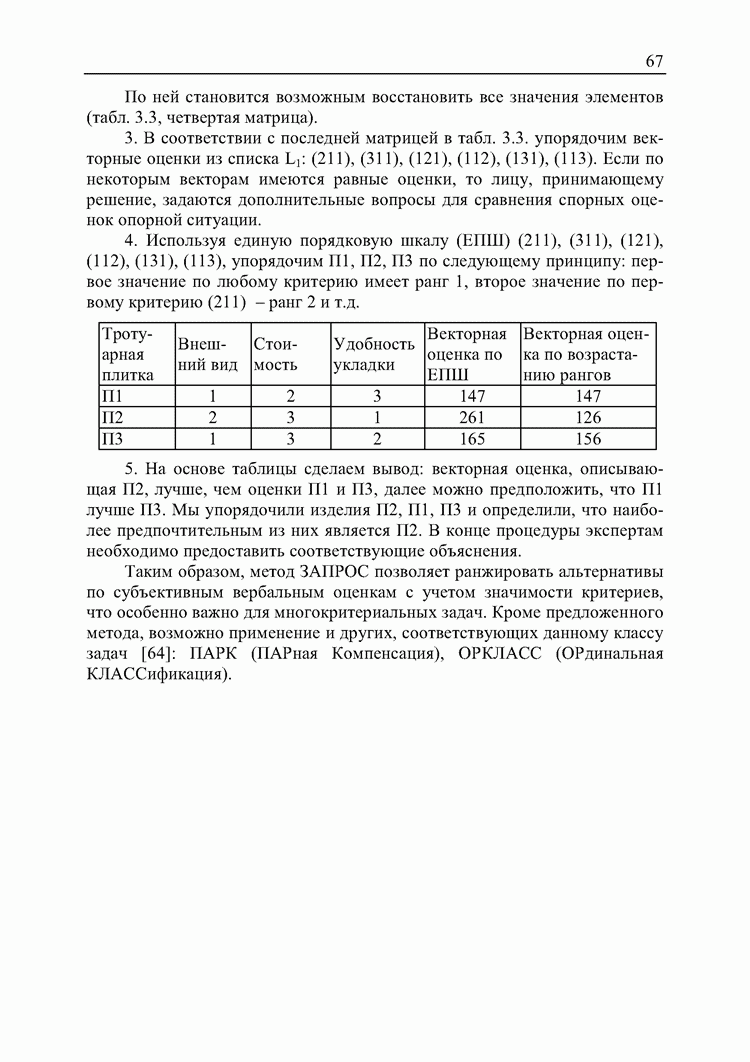
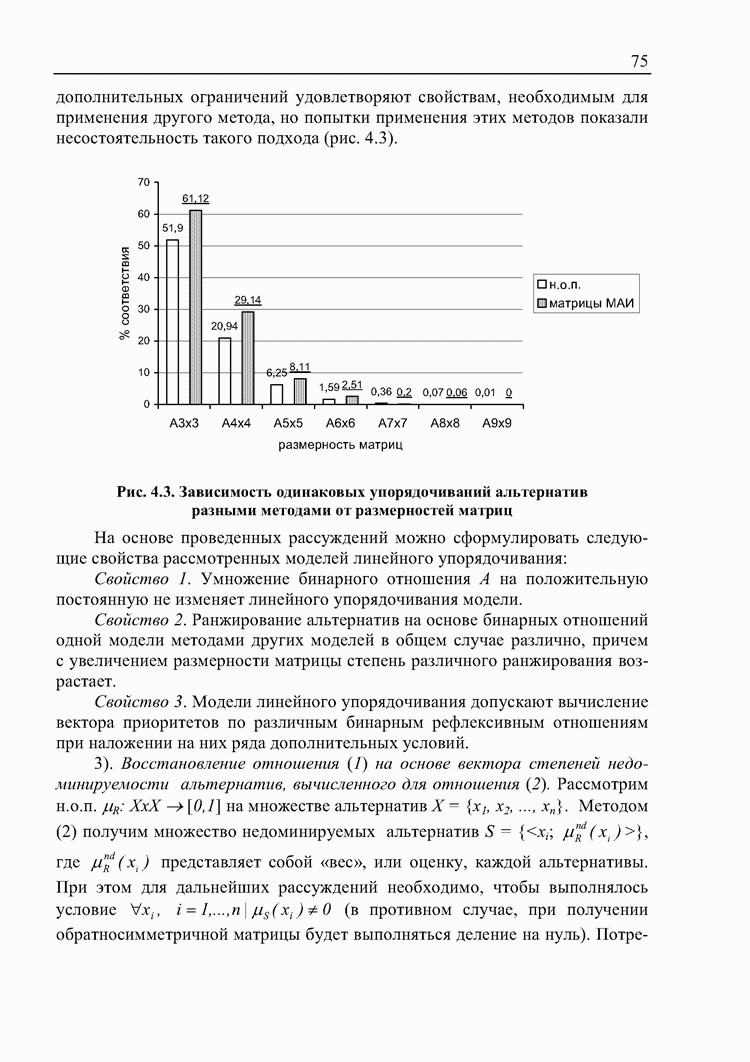
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список