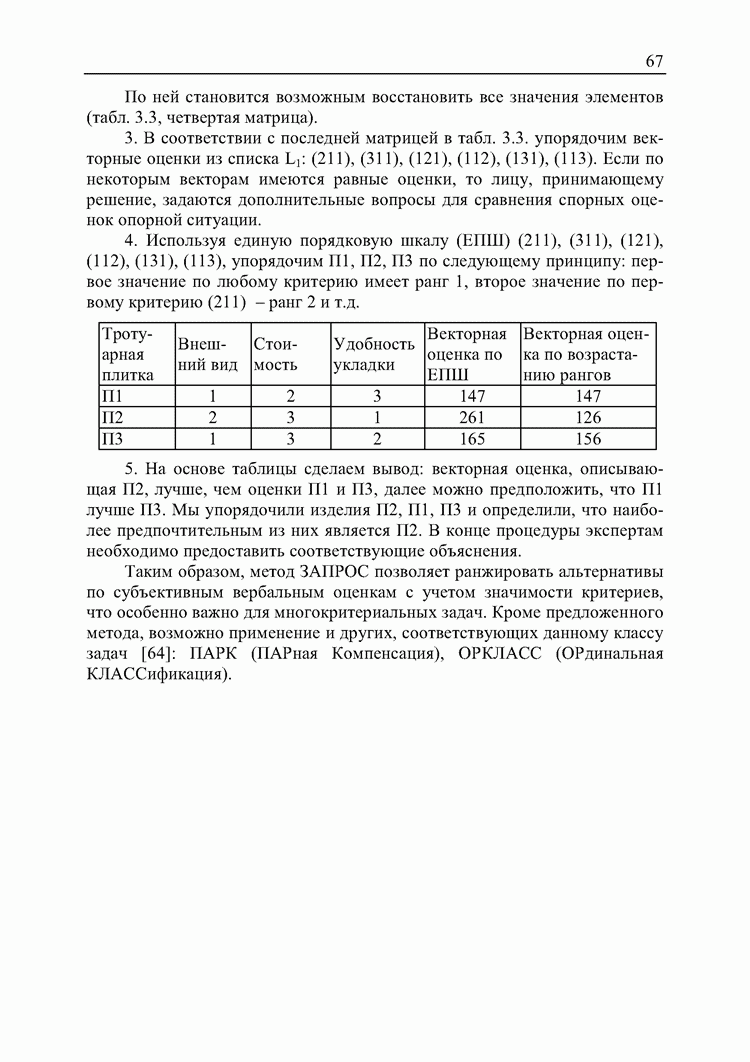
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
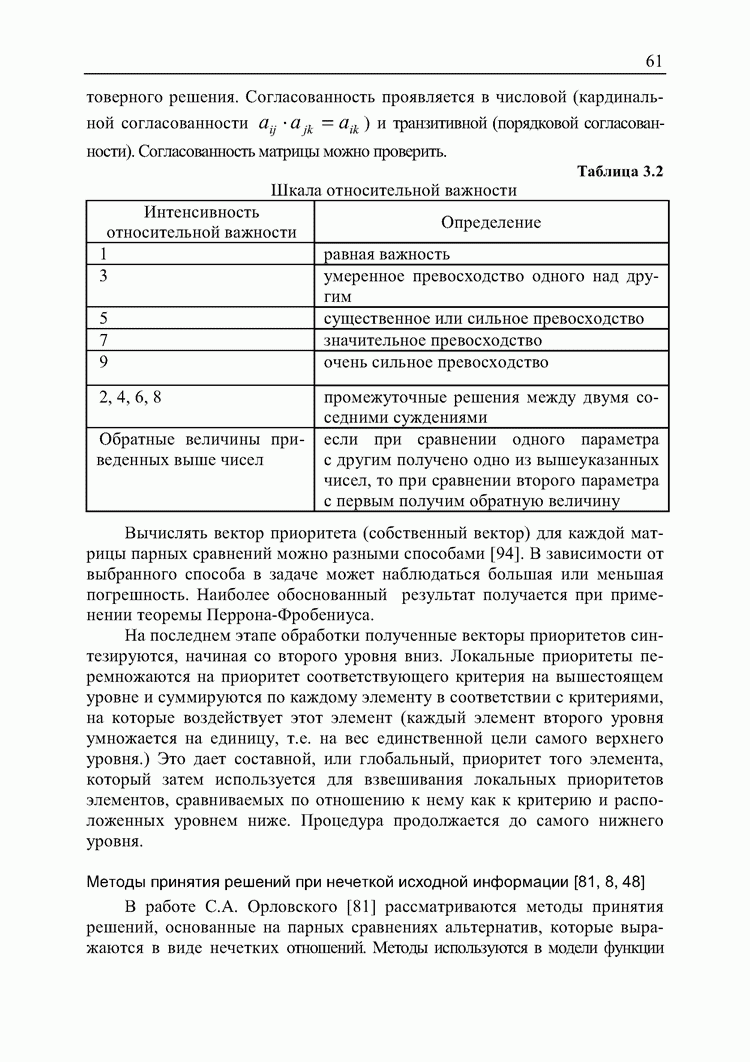
Базовая шкала метода анализа иерархий (1) может быть формализована в виде множества  , где
, где  . При
. При  при
при  и т.д. В частности, в МАИ
и т.д. В частности, в МАИ  .
.
Базовая шкала метода принятия решений при нечеткой исходной информации (2) представляет собой отрезок действительных чисел 
В качественных методах принятия решений (3) для нумерации оценок на порядковой шкале  критерия q используется ряд натуральных чисел. Количественную шкалу, в этом случае, можно формализовать как комплект
критерия q используется ряд натуральных чисел. Количественную шкалу, в этом случае, можно формализовать как комплект  целые числа
целые числа  .
.
Отрезок  , множество
, множество  комплект (базовые шкалы методов (1), (2), (3)) являются решетками и, в частности, цепями. Во множествах S и
комплект (базовые шкалы методов (1), (2), (3)) являются решетками и, в частности, цепями. Во множествах S и  имеют место операции
имеют место операции  .
.
Множество S(m) является дискретным и состоит из  элементов.
элементов.
Множество S - множество мощности континиум (как непрерывный отрезок действительных чисел).
Решетка является полной, если любое множество ее элементов имеет как точную верхнюю, так и точную нижнюю грани. Отрезок действительных чисел  является полной решеткой.
является полной решеткой.
Так как всякая конечная решетка полна, то множество S(m) как конечная решетка является полной решеткой.
Для возможности формирования количественных шкал, соответствующих различным методам принятия решений, необходимо установить правило перехода от одной из них к другой. В этом случае эксперту будет достаточно один раз вербально оценить предпочтительность объектов; при этом количественные шкалы, соответствующие каждому из методов принятия решений, будут сформированы автоматически.
Переход между шкалами возможен на основе их гомоморфного отображения друг в друга. Такой гомоморфизм возможно установить несколькими способами. Не каждый гомоморфизм позволит получать корректные результаты другим методом на основе полученной шкалы. Приведем некоторые из таких случаев.
Установим гомоморфизм решетки S в решетку  и наоборот. Отображение
и наоборот. Отображение  решетки L в решетку
решетки L в решетку  называется верхним [нижним] гомоморфизмом, если
называется верхним [нижним] гомоморфизмом, если  для любых
для любых
 . Гомоморфизм решетки L в решетку
. Гомоморфизм решетки L в решетку  определяется как отображение, являющееся верхним и нижним гомоморфизмом одновременно.
определяется как отображение, являющееся верхним и нижним гомоморфизмом одновременно.
Определим отображение  таким образом, что
таким образом, что

Пример. Пусть  , тогда
, тогда

Докажем, что так определенное отображение  является верхним гомоморфизмом.
является верхним гомоморфизмом.
Пусть  , тогда
, тогда  .
.
где  и
и  соответствуют представлению чисел a и b в виде
соответствуют представлению чисел a и b в виде  или
или  , где
, где  (для элемента
(для элемента  ),
),  где
где  (для элемента
(для элемента  ).
).
Требуется доказать, что  .
.
Действительно, по определению операции  в решетке
в решетке  .
.
Пусть  , тогда
, тогда  , т.е.
, т.е.  .
.
Пусть  тогда
тогда  , т.е.
, т.е.  .
.
Пусть  где
где  .
.
В этом случае  .
.
 при любых
при любых  , т.е.
, т.е.  .
.
То есть отображение  является верхним гомоморфизмом. Аналогично можно доказать, что для всех a и b выполняется
является верхним гомоморфизмом. Аналогично можно доказать, что для всех a и b выполняется  . Таким образом, отображение
. Таким образом, отображение  решетки
решетки  в решетку S является и верхним, и нижним гомоморфизмом одновременно, т.е. решетка
в решетку S является и верхним, и нижним гомоморфизмом одновременно, т.е. решетка  гомоморфна решетке S.
гомоморфна решетке S.
Определить отображение  можно различными способами. Например, отрезок
можно различными способами. Например, отрезок  разбить на
разбить на  интервалов, каждому интервалу поставить в соответствие элемент множества S(m) по следующему правилу:
интервалов, каждому интервалу поставить в соответствие элемент множества S(m) по следующему правилу:
Если  и т.д.
и т.д.
Для множества  , где
, где  отображение
отображение  представлено на рисунке:
представлено на рисунке:

В этом случае отображение  определим так:
определим так:

Например, в случае  :
:

Договоримся при  включать правый конец отрезка в промежуток, тогда при
включать правый конец отрезка в промежуток, тогда при  .
.
Очевидно, что изотонное отображение  является гомоморфизмом.
является гомоморфизмом.
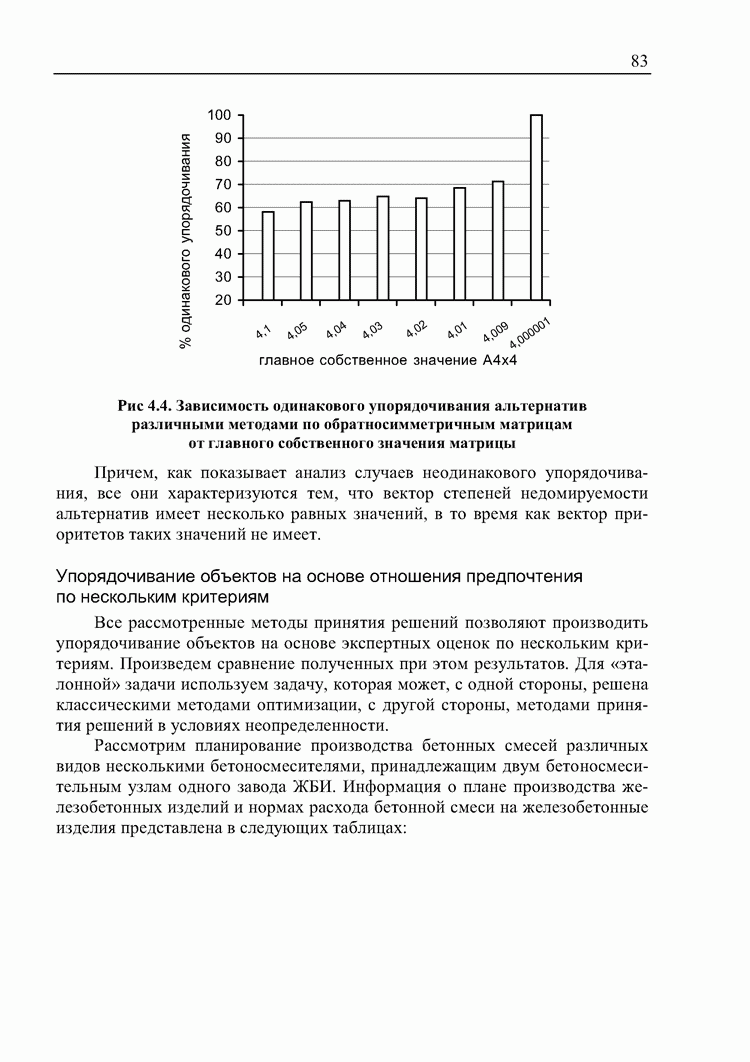
Проверим, действительно ли установленный гомоморфизм шкал позволят получать одинаковые результаты ранжирования альтернатив при переходе от одной шкалы к другой.
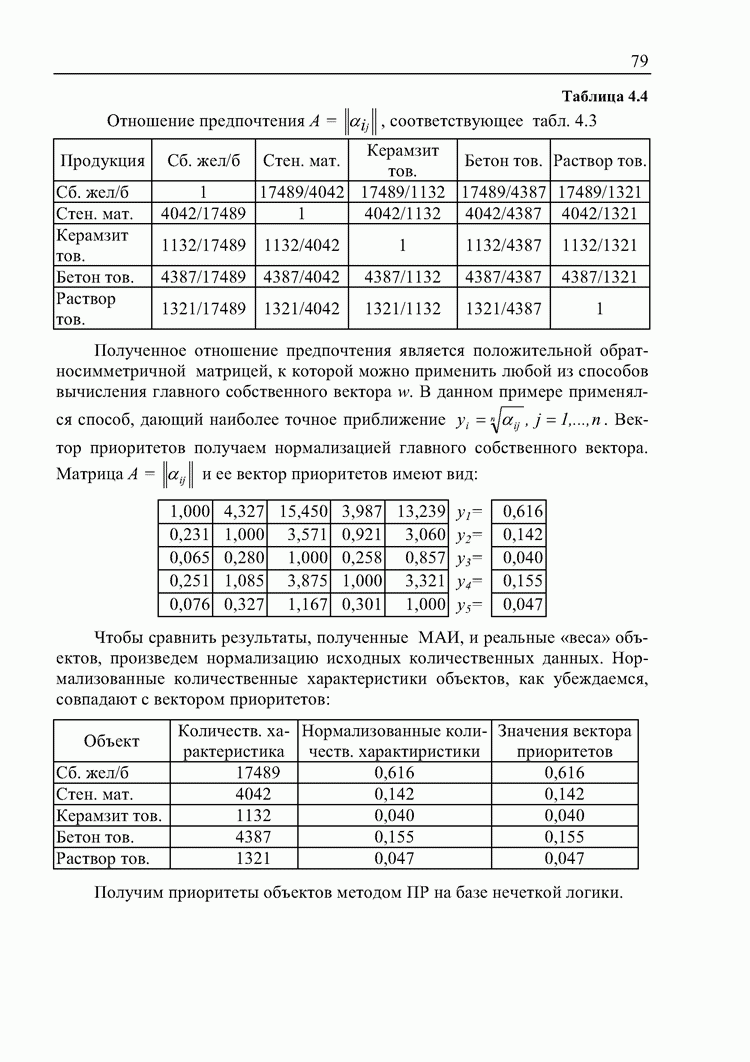
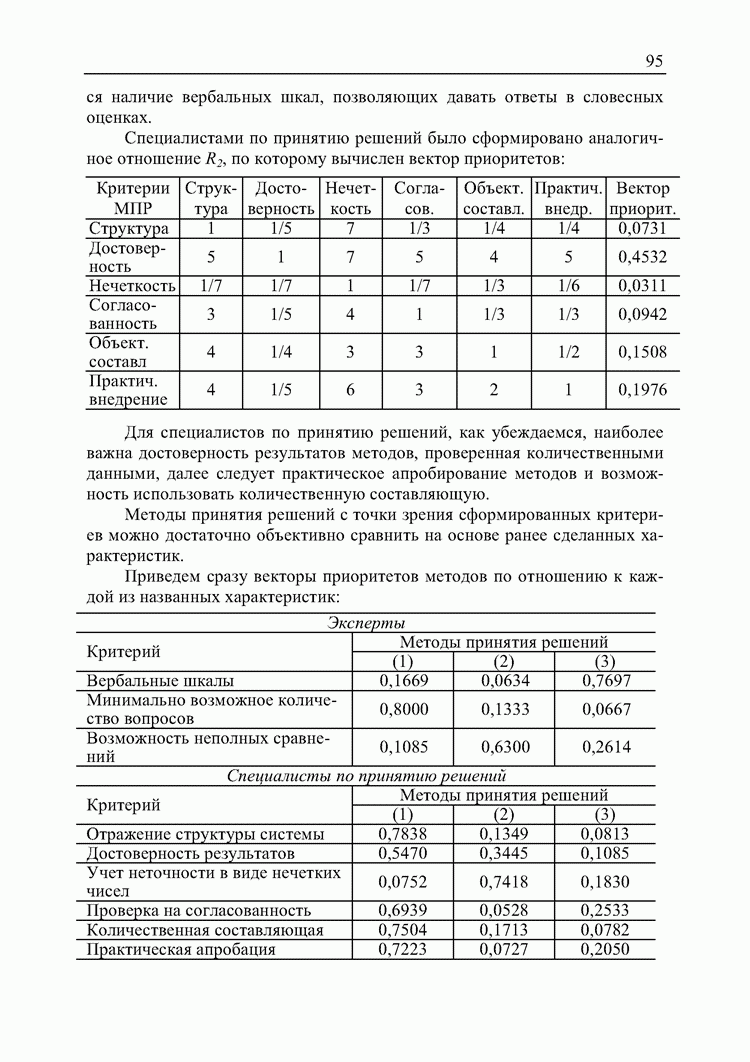
Пример. Обратносимметричная матрица МАИ имеет нормализованный главный собственный вектор (0,095; 0,654; 0,249).

Пользуясь установленным гомоморфизмом  определим для каждого элемента матрицы соответствующий ему элемент в S.
определим для каждого элемента матрицы соответствующий ему элемент в S.
Так как


В результате преобразований матрица будет иметь вид

Применяя к полученный матрице метод принятия решений при нечеткой исходной информации, получим вектор степеней недоминируемости альтернатив

Нормализуя этот вектор, получим

Получаем отличный от исходного результат.
Применим к матрице теорему Перрона-Фробениуса. Получим нормализованный собственный вектор, не совпадающий с исходным.

Значит, что при так установленном гомоморфизме матрица теряет свои свойства с точки зрения достоверности имеющейся в ней информации относительно исходных оценок.
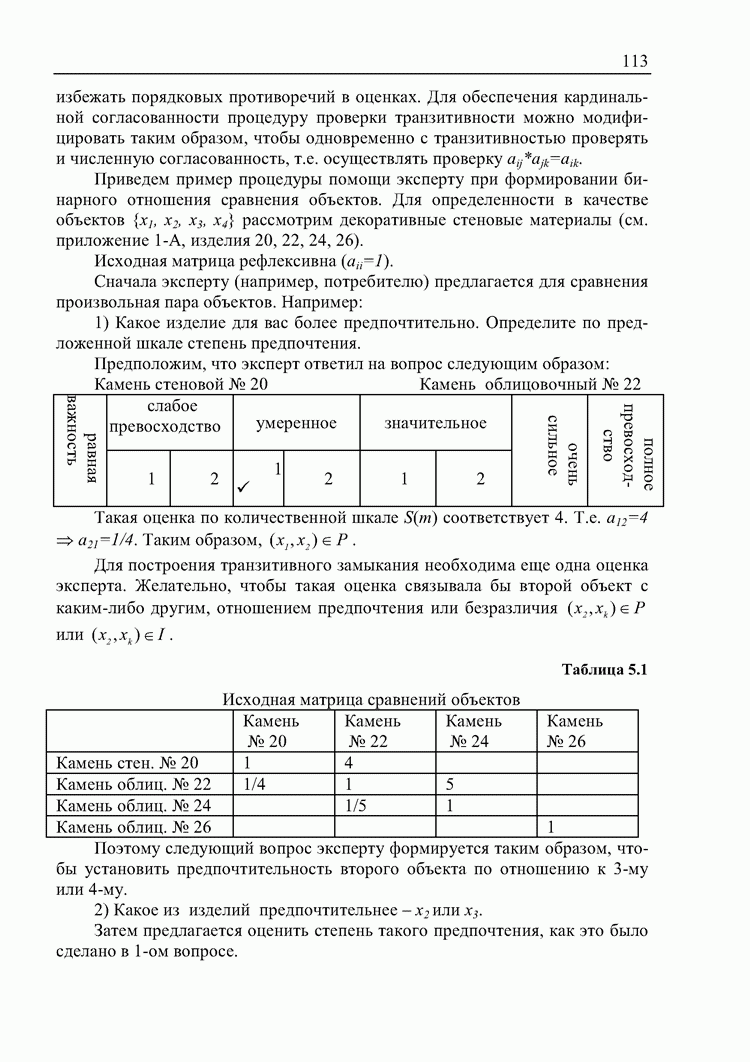
Пример. Нестрогое отношение нечеткого предпочтения имеет вид:

Вектор недоминируемых альтернатив, соответствующий н.о.п.,  = (0,9; 0,9; 0,7) (или, с учетом нормализации,
= (0,9; 0,9; 0,7) (или, с учетом нормализации,  ). Преобразуем на основе установленного гомоморфизма матрицу к виду
). Преобразуем на основе установленного гомоморфизма матрицу к виду

Применяя к такой матрице теорему Перрона-Фробениуса, получим вектор приоритетов:

не совпадающий с вектором степеней недоминируемости альтернатив.
Если произвести вычисление вектора степеней недоминируемости альтернатив по данной матрице, то получим вектор, также не совпадающий с исходным -

Таким образом, так установленные гомоморфизмы не позволяют получать одинаковые результаты ранжирования альтернатив при переводе одной количественной шкалы в другую.
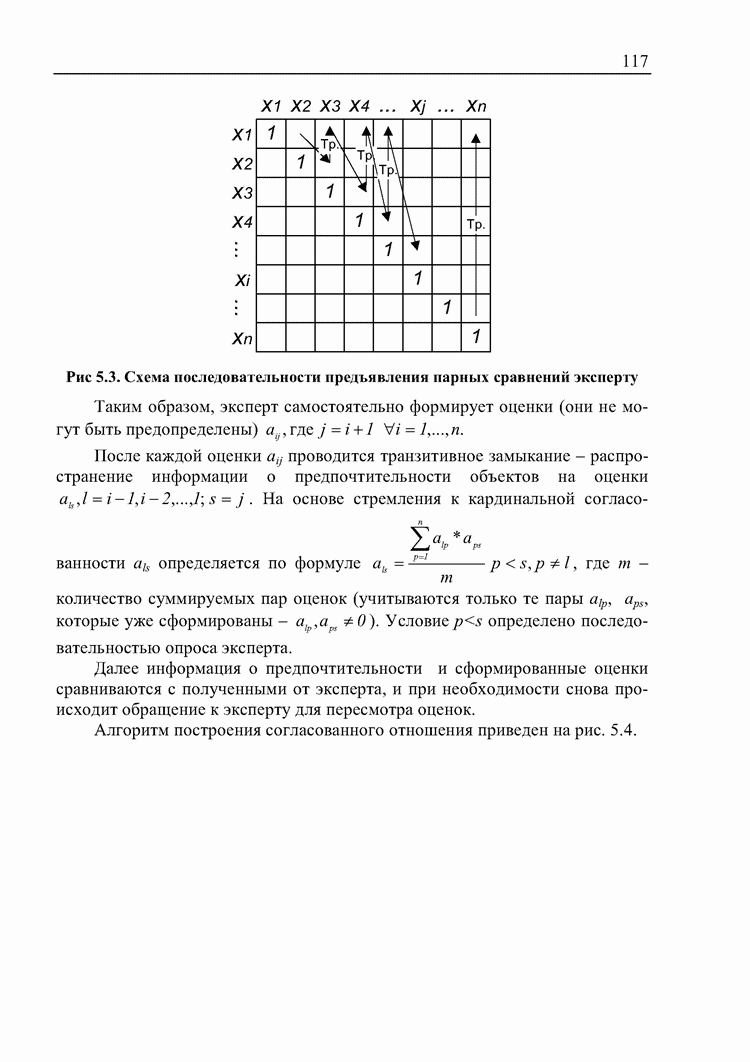
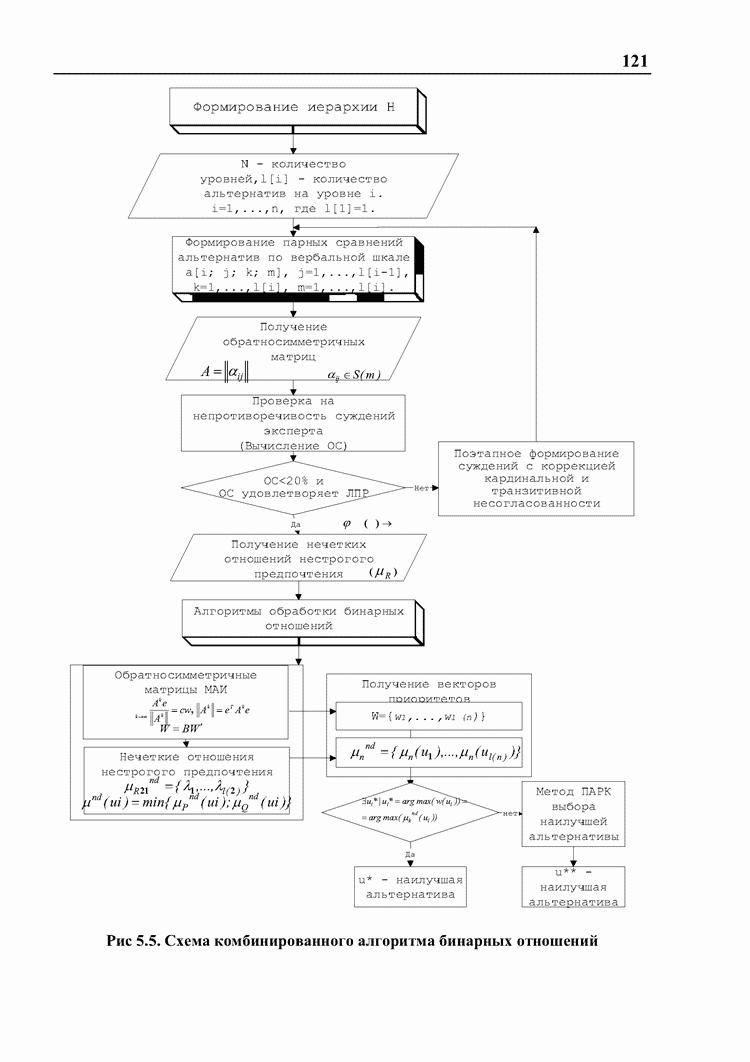
В комбинированном алгоритме поддержки принятия решений предлагается использовать для сравнения объектов качественную шкалу, вербальные оценки которой зависят от конкретного критерия, по которому происходит сравнение. Из двух предложенных объектов  сначала выбирается тот, который, с точки зрения эксперта, имеет большую значимость. Затем оценивается его предпочтительность по вербальной шкале. Шкала ориентирована на 8 дискретных оценок предпочтительности по аналогии со шкалой МАИ и методом принятия решений на базе нечеткой логики. В методах принятия решений при нечеткой исходной информации, хотя С.А. Орловским и предлагается непрерывная шкала [0/1], но фактически в рассмотренных примерах осуществляется прием дискретизации и используются 9 оценок предпочтительности - 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9.
сначала выбирается тот, который, с точки зрения эксперта, имеет большую значимость. Затем оценивается его предпочтительность по вербальной шкале. Шкала ориентирована на 8 дискретных оценок предпочтительности по аналогии со шкалой МАИ и методом принятия решений на базе нечеткой логики. В методах принятия решений при нечеткой исходной информации, хотя С.А. Орловским и предлагается непрерывная шкала [0/1], но фактически в рассмотренных примерах осуществляется прием дискретизации и используются 9 оценок предпочтительности - 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9.
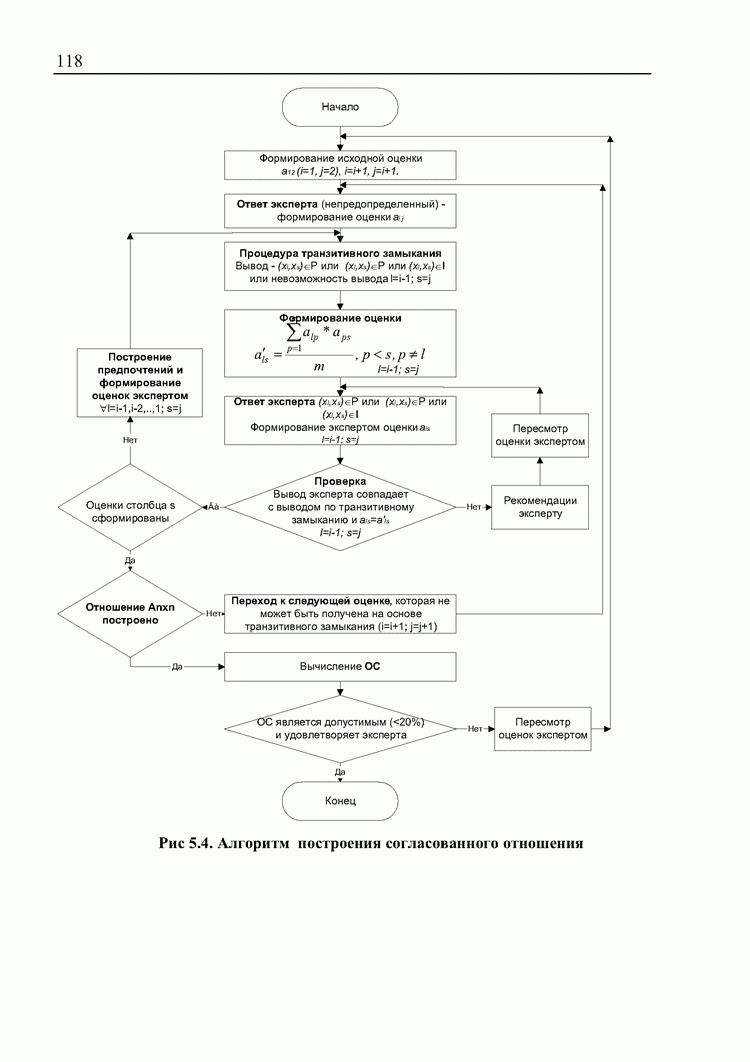
Пример возможной вербальной шкалы приведен на рис. 5.1.

Рис 5.1. Вербальная шкала сравнений объектов
Для слабого превосходства, умеренного и значительного указывается степень такого превосходства.
По выбранному значению лексической переменной из вербальной шкалы в соответствие ему ставится оценка МАИ -  соответственно. Если
соответственно. Если  , то
, то  .
.
Гомоморфизм  устанавливается следующим образом:
устанавливается следующим образом:

В этом случае  , то есть
, то есть  .
.
Так определенный гомоморфизм лишен самых существенных недостатков ранее приводившихся отображений - несовпадения результатов ранжирования по отношению предпочтения до гомоморфного отображения и после него одним и тем же способом вычисления вектора приоритетов. Это следует из того, что, умножение матрицы на постоянную не меняет ее нормализованного главного собственного вектора.
При так определенном гомоморфизме обратносимметричная матрица  отображается в нечеткое отношение
отображается в нечеткое отношение  Такое нечеткое отношение удовлетворяет методу принятия решений на базе нечеткой логики, хотя и не является рефлексивным.
Такое нечеткое отношение удовлетворяет методу принятия решений на базе нечеткой логики, хотя и не является рефлексивным.
Рефлексивность в определении  такому условию полученные нечеткие отношения не удовлетворяют. Но, как следует из метода принятия решения на базе нечеткой логики,
такому условию полученные нечеткие отношения не удовлетворяют. Но, как следует из метода принятия решения на базе нечеткой логики,  . В этом случае
. В этом случае  при любом
при любом  , т.е. полученное отношение является корректным для вычисления по нему вектора недоминируемых альтернатив.
, т.е. полученное отношение является корректным для вычисления по нему вектора недоминируемых альтернатив.
Обратносимметричная матрица при таком отображении станет толерантным нечетким отношением нестрогого предпочтения. Недостатком такого гомоморфизма является лишь невозможность осуществления неполных сравнений, что, впрочем, следует уже из ранее определенной вербальной шкалы.
Следует отметить, что полученное н.о.п.  - линейное, так как его функция принадлежности удовлетворяет условию
- линейное, так как его функция принадлежности удовлетворяет условию  для любых и.,
для любых и., 
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
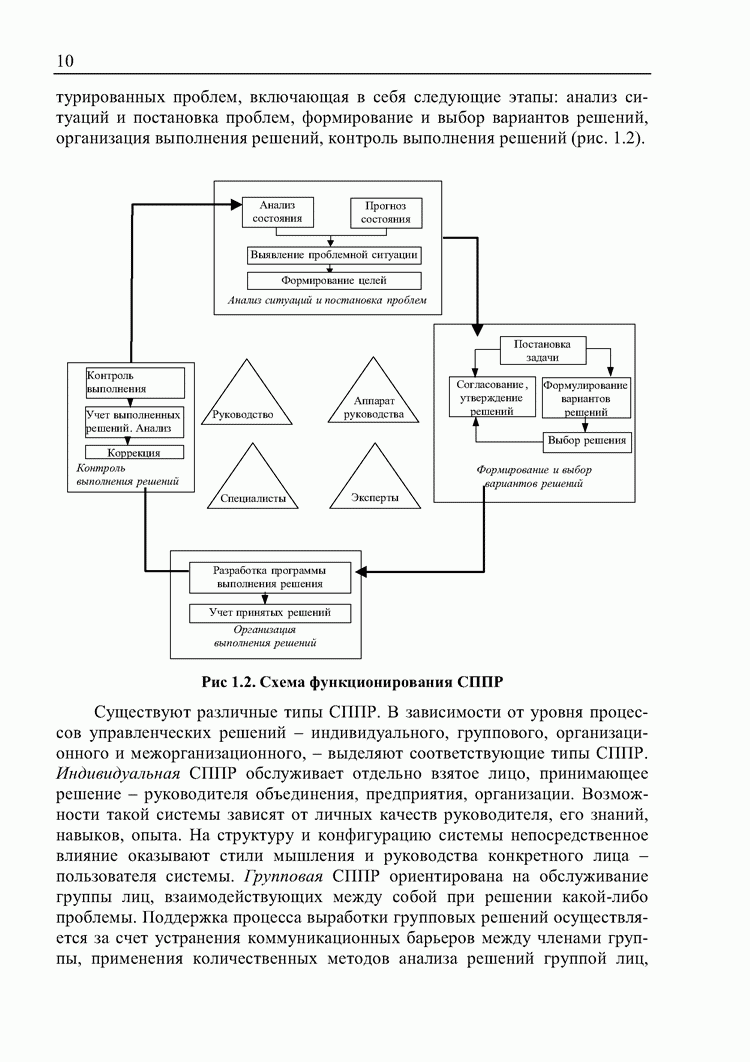
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
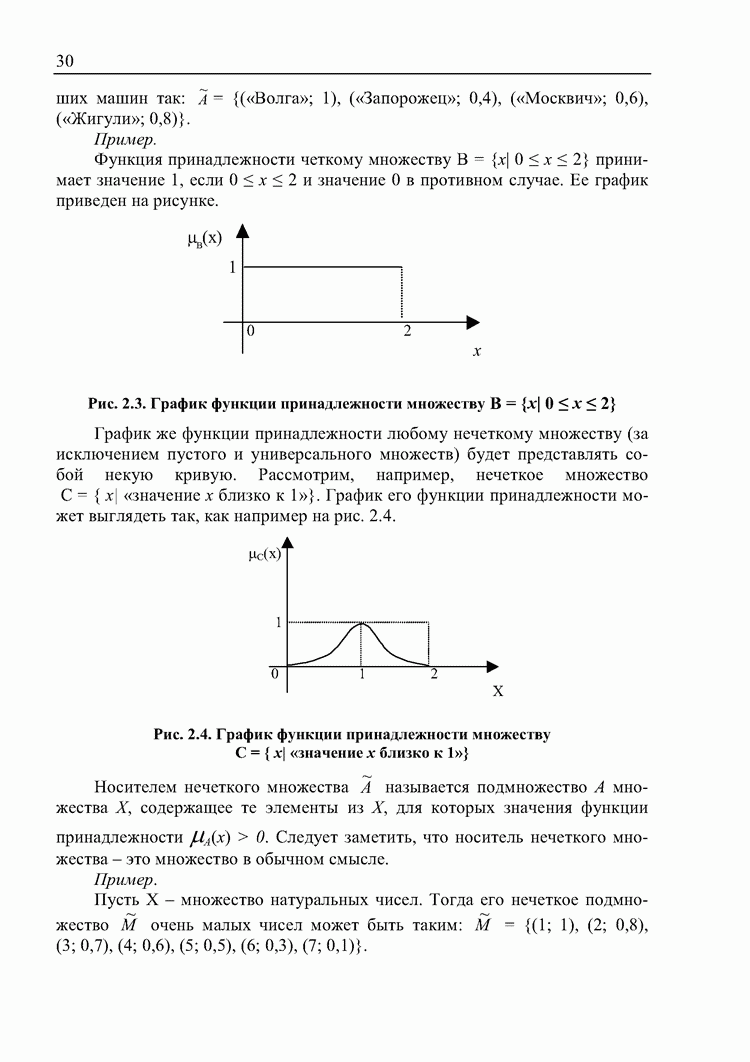
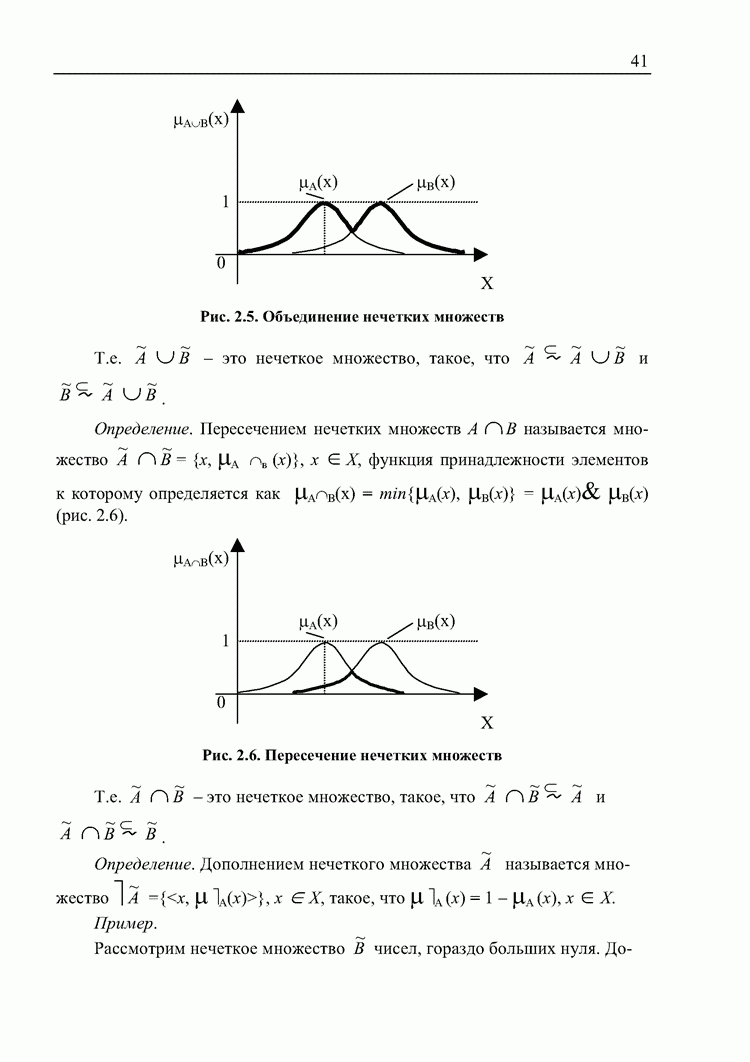
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
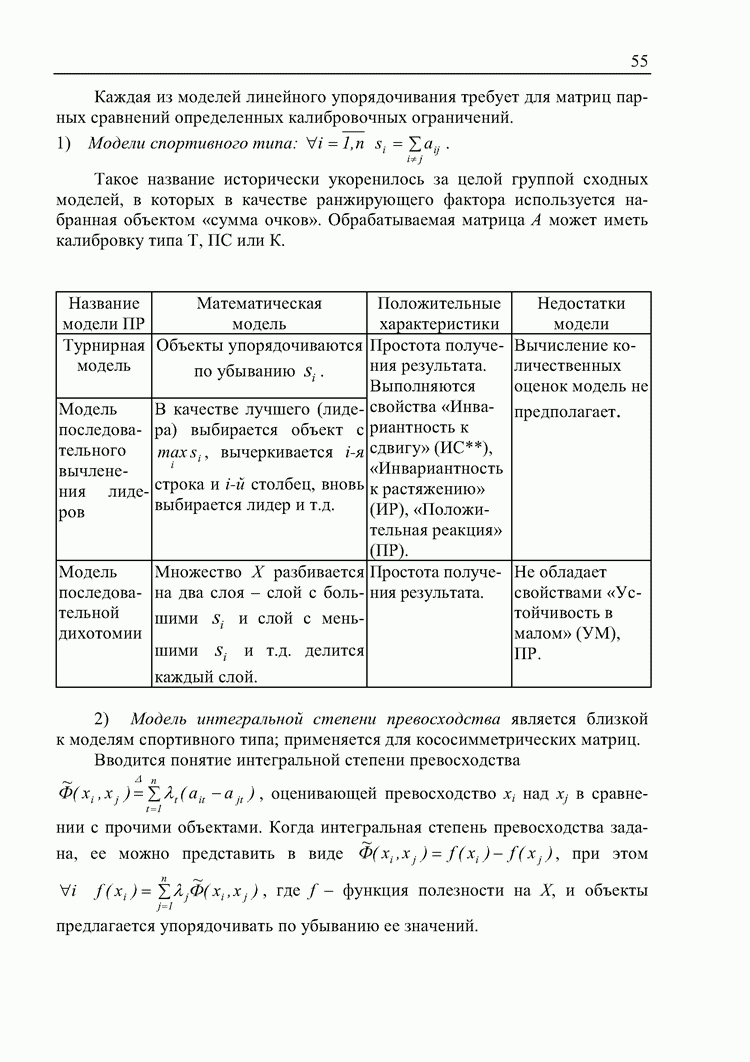
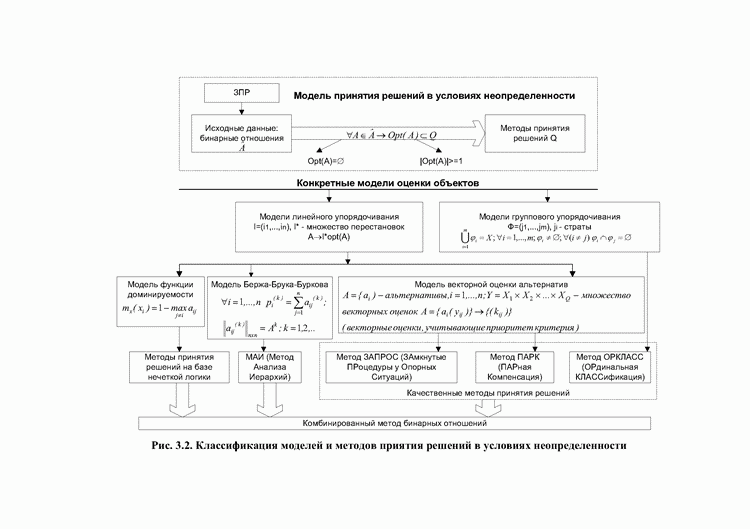
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
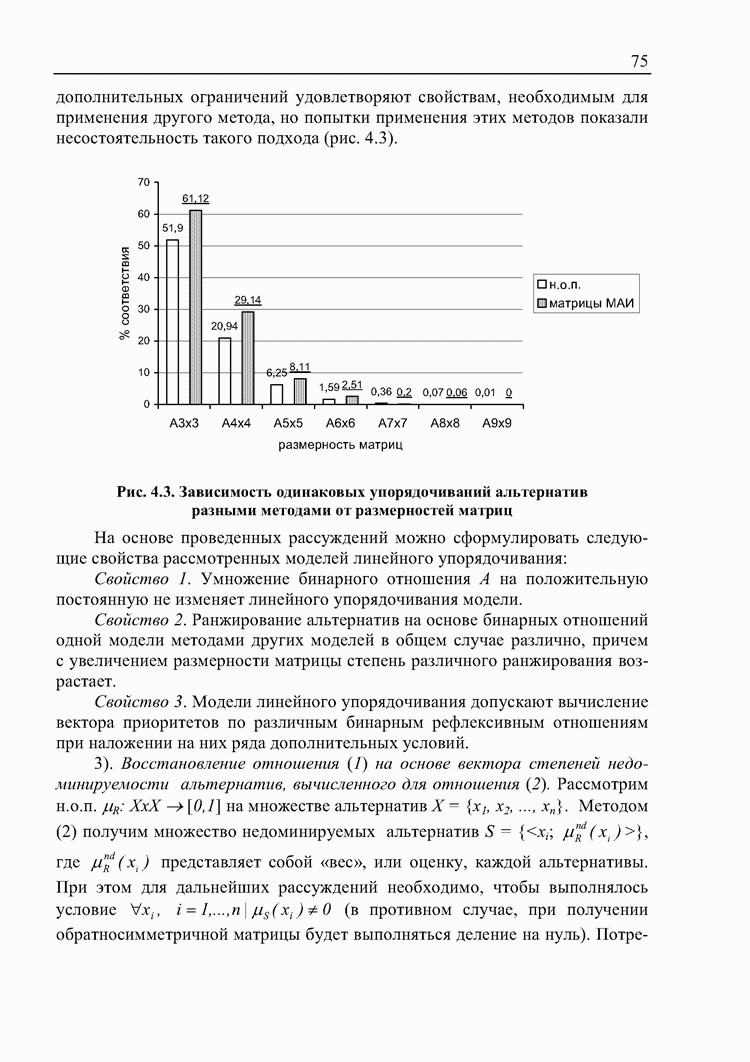
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список