| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Полные алгебраические решетки
Общие свойства решеток рассматриваются в работах Л.А. Скорнякова, С.К. Сагнаевой, М.Ш. Цаленко, Yi-Jia Tan [79, 95, 110, 124].
Частично упорядоченное множество L называется нижней [верхней] полyрешеткой, если каждое двухэлементное его подмножество имеет точную нижнюю [верхнюю] грань. Если частично упорядоченное множество является нижней и верхней полурешеткой одновременно, то оно называется решеткой.
Если L - решетка, то для любых элементов а и b можно ввести операции 
Решетка называется полной, если в ней существуют объединения и пересечения любых множеств элементов. Всякая конечная решетка полна.
Отображение  решетки L в решетку L называется верхним [нижним] гомоморфизмом, если
решетки L в решетку L называется верхним [нижним] гомоморфизмом, если  для любых
для любых  . Гомоморфизм решетки L в решетку L определяется как отображение, являющееся верхним и нижним гомоморфизмом одновременно. Взаимно-однозначный гомоморфизм называется изоморфизмом. Верхние и нижние гомоморфизмы являются изотонными отображениями.
. Гомоморфизм решетки L в решетку L определяется как отображение, являющееся верхним и нижним гомоморфизмом одновременно. Взаимно-однозначный гомоморфизм называется изоморфизмом. Верхние и нижние гомоморфизмы являются изотонными отображениями.
Непустое подмножество Н решетки L называется подрешеткой, если из  следует
следует  .
.
Пусть L - решетка.  Наибольший элемент
Наибольший элемент  , такой, что
, такой, что  называется относительным псевдодополнением элемента а относительно элемента b в решетке L. Если такой элемент существует, он определяется однозначно заданием а и b и обозначается через
называется относительным псевдодополнением элемента а относительно элемента b в решетке L. Если такой элемент существует, он определяется однозначно заданием а и b и обозначается через  . Решетка, в которой для любых
. Решетка, в которой для любых  определена операция
определена операция  , называется решеткой с относительными псевдодополнениями (или
, называется решеткой с относительными псевдодополнениями (или  решеткой).
решеткой).
Наименьший элемент  , такой, что а
, такой, что а  называется
называется  относительным псевдодополнением элемента а относительно элемента b. Решетка, в которой для любых
относительным псевдодополнением элемента а относительно элемента b. Решетка, в которой для любых  определена операция а b, называется
определена операция а b, называется  решеткой с относительными псевдодополнениями (или дyальной браyэровой решеткой).
решеткой с относительными псевдодополнениями (или дyальной браyэровой решеткой).
Решетка L называется  решеткой, если в ней выполняются тождества:
решеткой, если в ней выполняются тождества:  , называемые дистрибутивными законами. Решетка дистрибутивна уже тогда, когда в ней имеет место уже один из указанных законов.
, называемые дистрибутивными законами. Решетка дистрибутивна уже тогда, когда в ней имеет место уже один из указанных законов.
Решетка L называется бесконечно  решеткой, если для любого
решеткой, если для любого  и любых семейств элементов
и любых семейств элементов  где I - множество индексов элементов, выполняется:
где I - множество индексов элементов, выполняется:

Полная решетка является  если она бесконечно
если она бесконечно  -дистрибутивна, т.е. выполняется (17). Полная решетка является дуальной брауэровой решеткой, если она бесконечно
-дистрибутивна, т.е. выполняется (17). Полная решетка является дуальной брауэровой решеткой, если она бесконечно  -дистрибутивна, т.е. выполняется (18). Следовательно, полная решетка L - это брауэрова решетка и дуальная брауэрова решетка, если L - бесконечно дистрибутивна бесконечно
-дистрибутивна, т.е. выполняется (18). Следовательно, полная решетка L - это брауэрова решетка и дуальная брауэрова решетка, если L - бесконечно дистрибутивна бесконечно  -дистрибутивной, а значит, и брауэровой, решетки является любая конечная дистрибутивная решетка, отрезок [0;1].
-дистрибутивной, а значит, и брауэровой, решетки является любая конечная дистрибутивная решетка, отрезок [0;1].
Решетка L называется решеткой с относительными дополнениями, если для всякого элемента  из любого ее интервала
из любого ее интервала  найдется такой элемент d, что с
найдется такой элемент d, что с  при этом
при этом  Решетка L с нулем 0 и единицей 1 называется решеткой с дополнениями, если каждый ее элемент имеет дополнение в интервале [0;1]. Дополнения в интервале [0;1] называются просто дополнениями.
Решетка L с нулем 0 и единицей 1 называется решеткой с дополнениями, если каждый ее элемент имеет дополнение в интервале [0;1]. Дополнения в интервале [0;1] называются просто дополнениями.
Бyлевой решеткой называется дистрибутивная решетка с дополнениями, т.е. дистрибутивная решетка с 0 и 1. В булевой решетке В каждый элемент  имеет в точности одно дополнение
имеет в точности одно дополнение  , такое, что
, такое, что  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
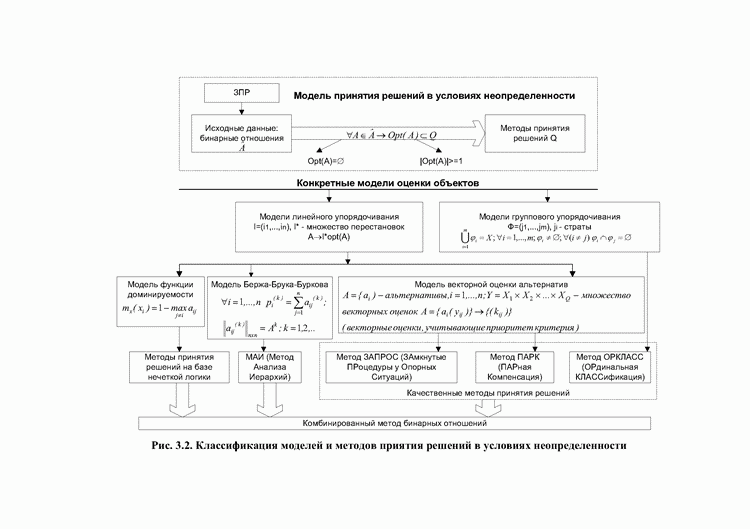
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список