| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
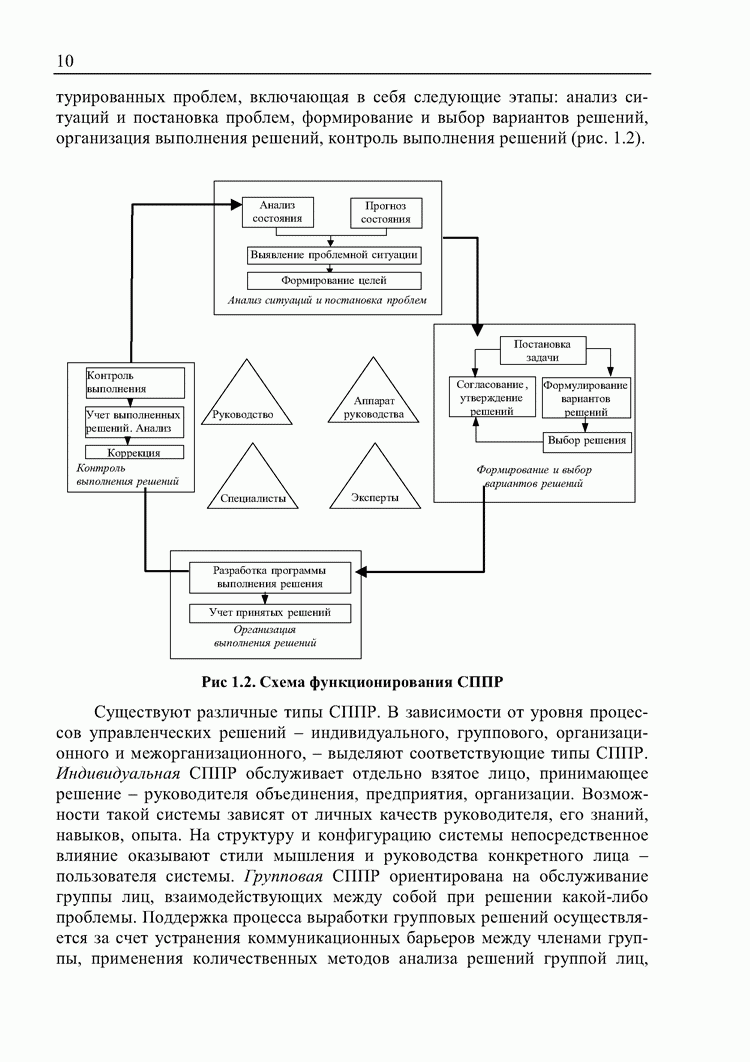
4.1. Сравнение результатов ранжирования альтернатив различными
методами принятия решений в условиях неопределенности
Модели принятия решений в условиях неопределенности применяются для выбора наиболее оптимальных альтернатив из имеющихся в ситуациях, характеризуемых неточностью, неполнотой информации. Осуществление ранжирования альтернатив в этом случае возможно производить различными прямыми методами. Для ЛПР важно, чтобы результаты применения методов предоставляли одинаковое ранжирование альтернатив. Возможны различные приоритеты альтернатив, определяемые разными методами, но упорядочивание их должно быть одинаковым. Проведем сравнение результатов ранжирования альтернатив МАИ и методом принятия решений при нечеткой исходной информации.
Пусть имеется множество  - альтернатив,
- альтернатив,  - бинарное отношение на множестве альтернатив. Требуется для каждой альтернативы определить ее оценку -
- бинарное отношение на множестве альтернатив. Требуется для каждой альтернативы определить ее оценку -  . В МАИ (в ходе дальнейшего изложения -
. В МАИ (в ходе дальнейшего изложения -  )
)  - вектор приоритетов, в методах принятия решений при нечеткой исходной информации (способ
- вектор приоритетов, в методах принятия решений при нечеткой исходной информации (способ  )
)  - вектор степеней недоминируемости альтернатив. Причем, в
- вектор степеней недоминируемости альтернатив. Причем, в  .
.
Бинарное отношение предпочтения альтернатив  задается в виде квадратной матрицы
задается в виде квадратной матрицы  , где
, где  - степень предпочтения
- степень предпочтения  альтернативы перед
альтернативы перед  Матрицы
Матрицы  сформированные
сформированные
в каждом способе в соответствии со шкалами (шкалой функции принадлежности (2) или шкалой относительной важности  и правилами формирования отношений в каждом из методов, будут обладать рядом общих и «индивидуальных» свойств.
и правилами формирования отношений в каждом из методов, будут обладать рядом общих и «индивидуальных» свойств.
В способе  представляет собой нечеткое отношение нестрогого предпочтения альтернатив:
представляет собой нечеткое отношение нестрогого предпочтения альтернатив:  , т.е.
, т.е.  - значения функции принадлежности
- значения функции принадлежности  . Матрицы
. Матрицы  неотрицательны,
неотрицательны,  , где
, где  , т.е.
, т.е.  рефлексивно.
рефлексивно.
Базовая шкала способа (2) представлена на рис. 4.1. Функция принадлежности  обладает следующими свойствами:
обладает следующими свойствами:
—  возрастает с возрастанием степени превосходства (силы, интенсивности) оценки превосходства альтернативы;
возрастает с возрастанием степени превосходства (силы, интенсивности) оценки превосходства альтернативы;
—  означает безусловное превосходство альтернативы
означает безусловное превосходство альтернативы  над
над 
—  означает либо полное отсутствие превосходства альтернативы
означает либо полное отсутствие превосходства альтернативы  над
над  , либо то, что i-тая альтернатива хуже j-той.
, либо то, что i-тая альтернатива хуже j-той.

Рис. 4.1. Базовая шкала метода ПР при нечеткой исходной информации
В способе  представляет собой положительную обратносимметричную матрицу, которую можно считать отношением предпочтения альтернатив
представляет собой положительную обратносимметричную матрицу, которую можно считать отношением предпочтения альтернатив  , т.е. а.
, т.е. а.  - значения функции принадлежности отношению предпочтения альтернатив, при этом
- значения функции принадлежности отношению предпочтения альтернатив, при этом  .
.
принимает значения в соответствии с базовой шкалой относительной важности, представленной на рис. 4.2. В (1)  являются:
являются:
- положительными;
- обратносимметричными (если  , то
, то  );
);
- неприводимыми;
- импримитивными;
- так же, как и в (2), бинарные отношения (1) являются рефлексивными,  , где
, где  .
.

Рис. 4.2. Базовая шкала МАИ
Функция принадлежности  обладает следующими свойствами:
обладает следующими свойствами:
—  возрастает с возрастанием надежности оценки превосходства альтернативы;
возрастает с возрастанием надежности оценки превосходства альтернативы;
—  означает равную важность альтернатив.
означает равную важность альтернатив.
Сравнение результатов ранжирования альтернатив можно произвести несколькими способами.
1). Соотнесение оценочных шкал. Чтобы сравнить результаты ранжирования альтернатив  , полученные в результате применения методов (1) и (2), необходимо вначале сформировать соответствующие этим способам н.о.п. для (2) и матрицу парных сравнений для (1) в соответствии с их базовыми шкалами. Очевидно, что эксперт не сможет заполнить для одной и той же группы альтернатив две матрицы, соответствующие способам (1) и (2), согласованные между собой, так, чтобы элементы матриц удовлетворяли перечисленным выше свойствам. Таким образом, процедуре сравнения результатов (1) и (2) должна предшествовать процедура соотнесения шкал (1) и (2). Процедура соотнесения шкал позволит по каждому «весу» критерия шкалы (1) получить «вес» критерия шкалы (2). Для соотнесения шкал рассматриваемых методов необходимо определить элементы шкал как гомоморфные алгебраические структуры, что будет сделано в главе 5.
, полученные в результате применения методов (1) и (2), необходимо вначале сформировать соответствующие этим способам н.о.п. для (2) и матрицу парных сравнений для (1) в соответствии с их базовыми шкалами. Очевидно, что эксперт не сможет заполнить для одной и той же группы альтернатив две матрицы, соответствующие способам (1) и (2), согласованные между собой, так, чтобы элементы матриц удовлетворяли перечисленным выше свойствам. Таким образом, процедуре сравнения результатов (1) и (2) должна предшествовать процедура соотнесения шкал (1) и (2). Процедура соотнесения шкал позволит по каждому «весу» критерия шкалы (1) получить «вес» критерия шкалы (2). Для соотнесения шкал рассматриваемых методов необходимо определить элементы шкал как гомоморфные алгебраические структуры, что будет сделано в главе 5.
2). Применение алгоритмов (1) и (2) к сформированным бинарным отношениям для одних и тех же альтернатив на основе базовых шкал данных методов. ЛПР формирует отношения на множестве одних и тех же альтернатив и для метода (1), и для метода (2), субъективно (имеется в виду, что он не ставит целью точное соотнесение оценок методов). Затем к каждому отношению применяется алгоритм (1) и (2).
Рассмотрим возможность применения МАИ к н.о.п. (2), т.е. возможность применить к н.о.п. теорему Перрона-Фробениуса: для примитивной
матрицы  , где с - постоянная, а w - собственный вектор, соответствующий
, где с - постоянная, а w - собственный вектор, соответствующий  .
.
Матрицы  являются неотрицательными
являются неотрицательными  как и матрицы парных сравнений в МАИ (1). Если на компоненты а. наложить дополнительное условие
как и матрицы парных сравнений в МАИ (1). Если на компоненты а. наложить дополнительное условие  (с точки зрения сравнения альтернатив это означает, что альтернативы не могут быть безразличны по отношению друг к другу), или, иначе, потребовать толерантности н.о.п. (нечеткое отношение толерантно, если оно рефлексивно и симметрично), то матрицы R заведомо удовлетворяют условиям теоремы Перрона-Фробениуса - являются примитивными. В этом случае возможна обработка матриц нечеткого отношения нестрогого предпочтения не только методом (2), но и на основе теоремы Перрона-Фробениуса (методом (1)). Однако, даже самый простой пример убеждает нас в различных результатах применяемых методов. Например, на основе матрицы
(с точки зрения сравнения альтернатив это означает, что альтернативы не могут быть безразличны по отношению друг к другу), или, иначе, потребовать толерантности н.о.п. (нечеткое отношение толерантно, если оно рефлексивно и симметрично), то матрицы R заведомо удовлетворяют условиям теоремы Перрона-Фробениуса - являются примитивными. В этом случае возможна обработка матриц нечеткого отношения нестрогого предпочтения не только методом (2), но и на основе теоремы Перрона-Фробениуса (методом (1)). Однако, даже самый простой пример убеждает нас в различных результатах применяемых методов. Например, на основе матрицы

с использованием метода (2) получим вектор  , тогда как применив теорему Перрона -
, тогда как применив теорему Перрона -  .
.
Проверим вывод о несовпадении w и  в общем случае на выборке случайных
в общем случае на выборке случайных  при помощи вычислительного эксперимента. Для этого для матриц всех размерностей до 9 создадим по 50 выборок (каждая выборка состоит из 400 матриц) и заполним случайными образом их элементы числами из шкалы (0;1] так, что
при помощи вычислительного эксперимента. Для этого для матриц всех размерностей до 9 создадим по 50 выборок (каждая выборка состоит из 400 матриц) и заполним случайными образом их элементы числами из шкалы (0;1] так, что  при
при  . Применим к каждому из полученных отношений алгоритмы (2) и (1) и подсчитаем количество отношений каждой размерности, для которых вектор приоритетов и функция недоминируемости предоставляют одинаковое ранжирование альтернатив (табл. 4.1). Из приведенной таблицы видно, что с увеличением размерности матрицы количество случаев одинакового упорядочивания альтернатив заметно уменьшается.
. Применим к каждому из полученных отношений алгоритмы (2) и (1) и подсчитаем количество отношений каждой размерности, для которых вектор приоритетов и функция недоминируемости предоставляют одинаковое ранжирование альтернатив (табл. 4.1). Из приведенной таблицы видно, что с увеличением размерности матрицы количество случаев одинакового упорядочивания альтернатив заметно уменьшается.
Таблица 4.1. Результаты соответствия упорядочивания альтернатив методами (1) и (2) по н.о.п.

Рассмотрим возможность применения метода принятия решения при нечеткой исходной информации с одним экспертом к обратносимметричным матрицам метода (1).
Матрицу  (1) можем представить в виде н.о.п. (2). Для этого от отношения
(1) можем представить в виде н.о.п. (2). Для этого от отношения  перейдем к отношению
перейдем к отношению  , где
, где  . Таким образом, мы получаем нечеткое отношение
. Таким образом, мы получаем нечеткое отношение  .
.
Утверждение. Деление каждого элемента матрицы (1) на максимальный элемент (умножение на любое положительное число в общем виде) не меняет ее вектора приоритета (главного собственного вектора). Действительно, по теореме Перрона-Фробениуса для примитивной матрицы А
 , где с - постоянная, а w - собственный вектор,
, где с - постоянная, а w - собственный вектор, 
соответствующий  . Получаем
. Получаем

где 
Отсюда следует, что для одного набора значений вектора приоритетов альтернатив в (1) существует бесконечно много отношений  , отличающихся друг от друга на постоянную.
, отличающихся друг от друга на постоянную.
Аналогичное утверждение можно сформулировать и для  Утверждение. Умножение отношения (2) на
Утверждение. Умножение отношения (2) на  не меняет его вектор степеней недоминируемости альтернатив.
не меняет его вектор степеней недоминируемости альтернатив.
Действительно, пусть имеется отношение R. Рассмотрим отношение  , где
, где  .
.
При построении нечеткого отношения строгого предпочтения  по
по 

При построении нечеткого отношения строгого предпочтения  по н.о.п.
по н.о.п. 

Если  т.е.,
т.е.,  .
.
Вторым этапом в алгоритме (2) формируется множество недоминируемых альтернатив  . Для
. Для  сформируем его следующим образом:
сформируем его следующим образом:  . Из определения
. Из определения  следует, что и для отношения
следует, что и для отношения  и для
и для  будет произведено одинаковое ранжирование альтернатив. Кроме того, если
будет произведено одинаковое ранжирование альтернатив. Кроме того, если  нормализуется (что в методе (2) в принципе не требуется), то и для
нормализуется (что в методе (2) в принципе не требуется), то и для  и для
и для  , векторы степеней недоминируемости альтернатив будут совпадать.
, векторы степеней недоминируемости альтернатив будут совпадать.
Отсюда следует, что фиксированному нормализованному вектору
 в (2) соответствует бесконечно много
в (2) соответствует бесконечно много  с точностью до постоянной. По данному утверждению, применяя алгоритм (2) к обратносимметричной матрице
с точностью до постоянной. По данному утверждению, применяя алгоритм (2) к обратносимметричной матрице  переход к отношению
переход к отношению  , где
, где  , в принципе необязателен.
, в принципе необязателен.
Но применение метода (2) к матрицам (1) не приводит к результату, который получается в МАИ.
Например, для обратносимметричной матрицы

по теореме Перрона-Фробениуса будет сформирован вектор приоритетов (0,095; 0,654; 0,249).
Если применить к данной матрице способ (2), то будет получен вектор степеней недоминируемости альтернатив (0,045; 0,909; 0,045), который представляет ранжирование альтернатив, отличное от метода (1).
Аналогично, как и в первом случае, проверим вывод о несовпадении 
на выборке случайных обратносимметричных матриц при помощи вычислительного эксперимента. Для этого для матриц всех размерностей до 9 создадим по 50 выборок (каждая выборка состоит из 400 матриц) и заполним случайными образом их элементы числами из шкалы МАИ так, что  при
при  . Применим к каждому из полученных отношений алгоритмы (2) и (1) и подсчитаем количество отношений каждой размерности, для которых вектор приоритетов и функция недоминируемости предоставляют одинаковое ранжирование альтернатив (табл. 4.2). Из приведенной таблицы видно, что с увеличением размерности матрицы количество случаев одинакового упорядочивания альтернатив заметно уменьшается.
. Применим к каждому из полученных отношений алгоритмы (2) и (1) и подсчитаем количество отношений каждой размерности, для которых вектор приоритетов и функция недоминируемости предоставляют одинаковое ранжирование альтернатив (табл. 4.2). Из приведенной таблицы видно, что с увеличением размерности матрицы количество случаев одинакового упорядочивания альтернатив заметно уменьшается.
Таблица 4.2. Результаты соответствия упорядочивания альтернатив методами (1) и (2) по обратносимметричной матрице

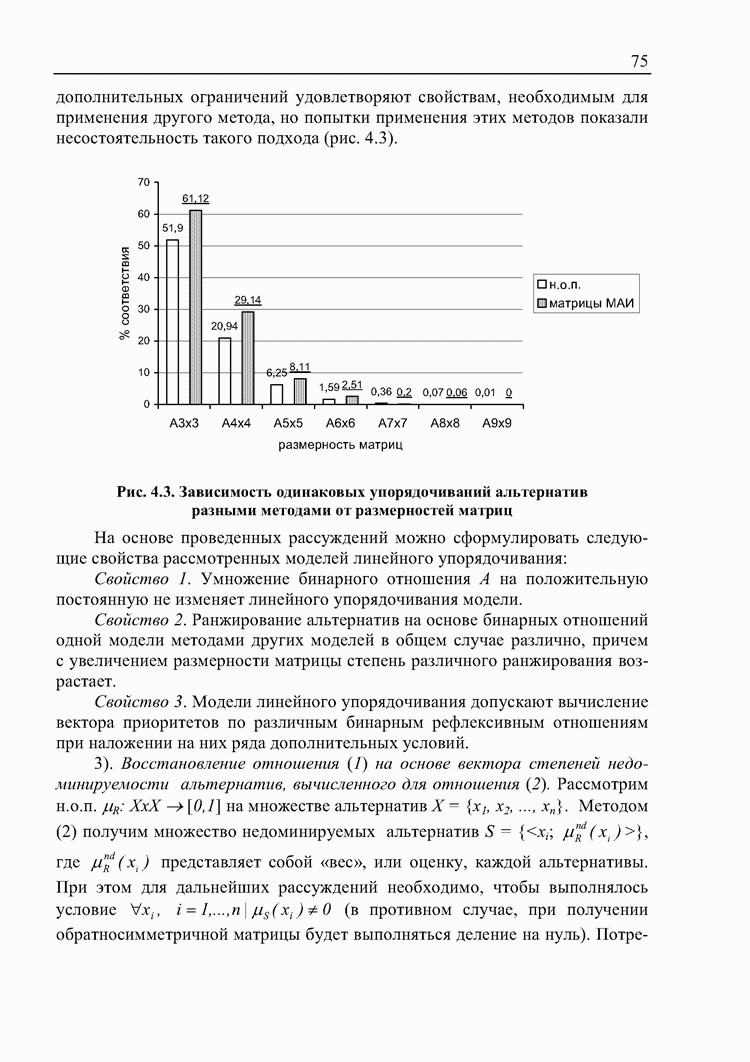
То есть, отношения сравнения альтернатив при наложении некоторых
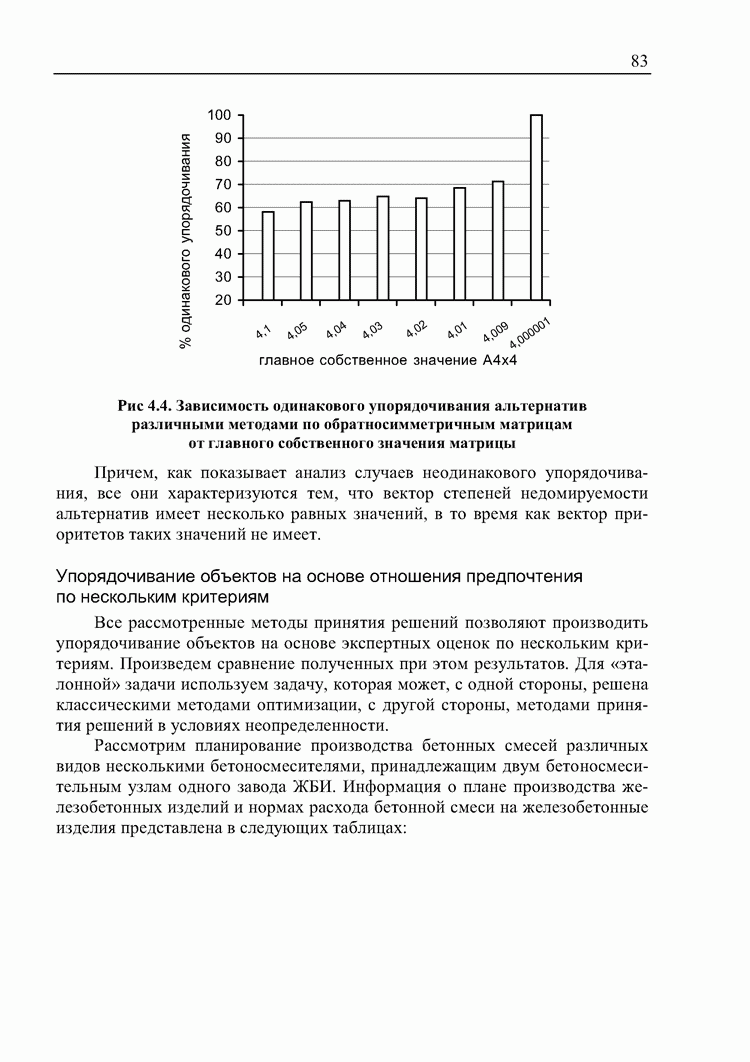
дополнительных ограничений удовлетворяют свойствам, необходимым для применения другого метода, но попытки применения этих методов показали несостоятельность такого подхода (рис. 4.3).

Рис. 4.3. Зависимость одинаковых упорядочиваний альтернатив разными методами от размерностей матриц
На основе проведенных рассуждений можно сформулировать следующие свойства рассмотренных моделей линейного упорядочивания:
Свойство 1. Умножение бинарного отношения А на положительную постоянную не изменяет линейного упорядочивания модели.
Свойство 2. Ранжирование альтернатив на основе бинарных отношений одной модели методами других моделей в общем случае различно, причем с увеличением размерности матрицы степень различного ранжирования возрастает.
Свойство 3. Модели линейного упорядочивания допускают вычисление вектора приоритетов по различным бинарным рефлексивным отношениям при наложении на них ряда дополнительных условий.
3). Восстановление отношения (1) на основе вектора степеней недоминируемости альтернатив, вычисленного для отношения (2). Рассмотрим  на множестве альтернатив
на множестве альтернатив  . Методом (2) получим множество недоминируемых альтернатив
. Методом (2) получим множество недоминируемых альтернатив  , где
, где  представляет собой «вес», или оценку, каждой альтернативы. При этом для дальнейших рассуждений необходимо, чтобы выполнялось условие
представляет собой «вес», или оценку, каждой альтернативы. При этом для дальнейших рассуждений необходимо, чтобы выполнялось условие  (в противном случае, при получении обратносимметричной матрицы будет выполняться деление на нуль).
(в противном случае, при получении обратносимметричной матрицы будет выполняться деление на нуль).
Потребуем, чтобы  (нормализуем полученный вектор). Степень принадлежности элементов отношению
(нормализуем полученный вектор). Степень принадлежности элементов отношению  будем определять посредством парных сравнений
будем определять посредством парных сравнений  (в виду этого условие
(в виду этого условие  можно считать избыточным). В результате получим примитив
можно считать избыточным). В результате получим примитив  обратносимметричную матрицу, обладающую свойством рефлексивности
обратносимметричную матрицу, обладающую свойством рефлексивности  при
при  , которая удовлетворяет условиям теоремы Перрона-Фробениуса. Вычислим для данной матрицы вектор приоритетов
, которая удовлетворяет условиям теоремы Перрона-Фробениуса. Вычислим для данной матрицы вектор приоритетов  и убедимся в том, что он совпадает с нормализованным вектором степеней недоминируемости альтернатив.
и убедимся в том, что он совпадает с нормализованным вектором степеней недоминируемости альтернатив.
Действительно, пусть дан вектор степеней недоминируемости альтернатив как результат метода  , такой, что
, такой, что  .
.
Обозначим через  . число, соответствующее значимости альтернативы
. число, соответствующее значимости альтернативы  по сравнению с
по сравнению с  . Матрицу, состоящую из этих чисел, обозначим через
. Матрицу, состоящую из этих чисел, обозначим через  . В нашем случае
. В нашем случае  . Поэтому
. Поэтому  . Тогда
. Тогда  . Следовательно,
. Следовательно,  Получаем
Получаем  . Или
. Или  . То есть,
. То есть,  - собственный вектор матрицы А с собственным значением n. С другой стороны, по теореме Перрона-Фробениуса (в методе МАИ) по матрице А будет вычислен вектор приоритетов
- собственный вектор матрицы А с собственным значением n. С другой стороны, по теореме Перрона-Фробениуса (в методе МАИ) по матрице А будет вычислен вектор приоритетов  ), который, как показано, и будет являться вектором степеней недоминируемости альтернатив
), который, как показано, и будет являться вектором степеней недоминируемости альтернатив  .
.
Например, для ранее рассмотренного н.о.п.

соответствующая данным результатам  матрица МАИ будет иметь вид:
матрица МАИ будет иметь вид:

Восстановление по вектору приоритетов (1) н.о.п. (2) с точностью до постоянной невозможно, так как одному w могут соответствовать несколько различных н.о.п.
Таким образом, в разделе 4.1 показано, что применение к произвольному н.о.п. модели функции доминируемости способа обработки данных (1) предоставляет результаты, отличные от тех, которые могут быть получены на основе модели (2). Такой же вывод был сделан и для обратносимметричных матриц (1).
В этом случае представляет интерес вопрос о том, как по вектору приоритетов, полученному при помощи одного из методов, восстановить бинарное отношение, удовлетворяющее условиям другого метода. Нами предложен способ восстановления матрицы (1) по вектору степеней недоминируемости альтернатив (2).
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
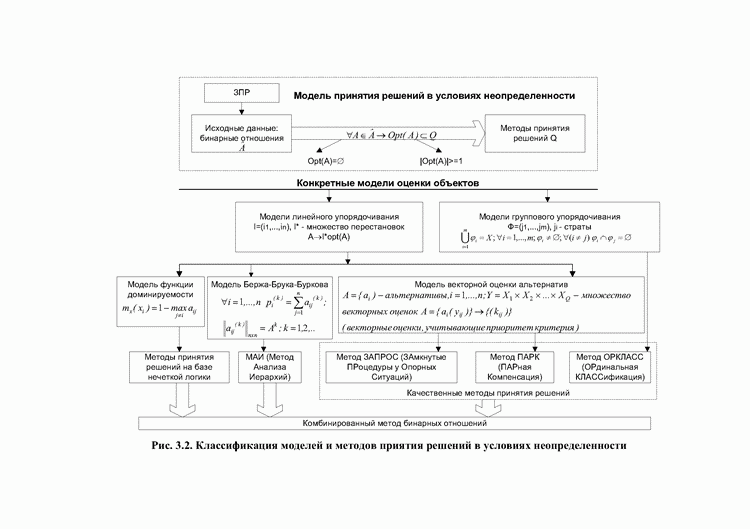
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
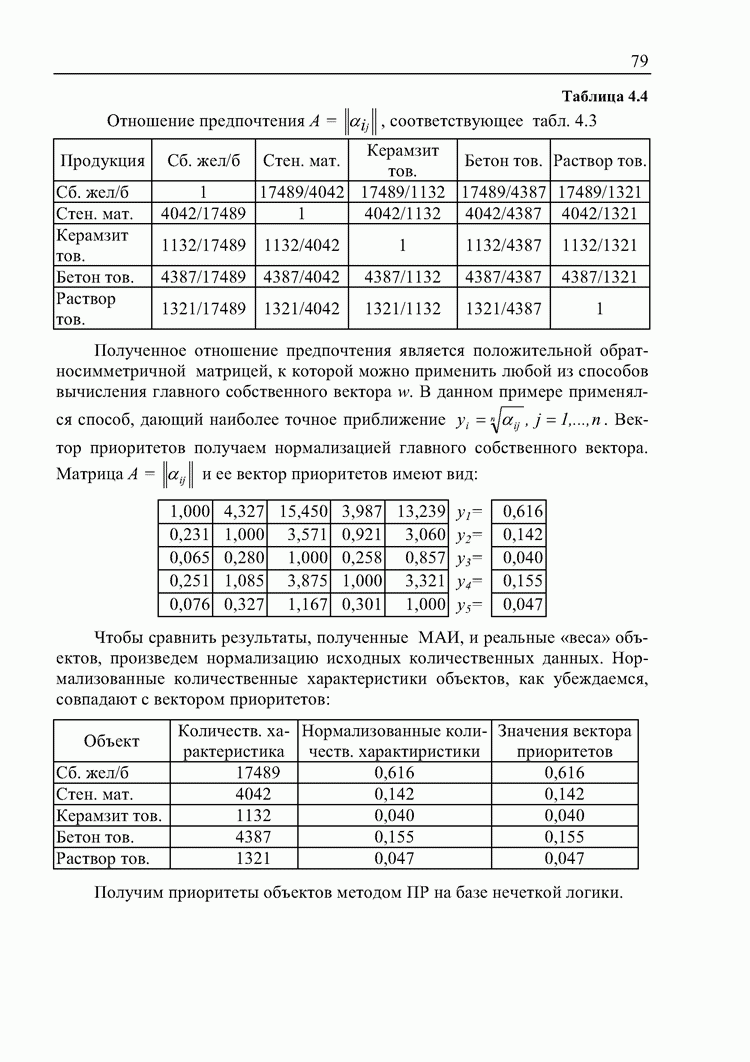
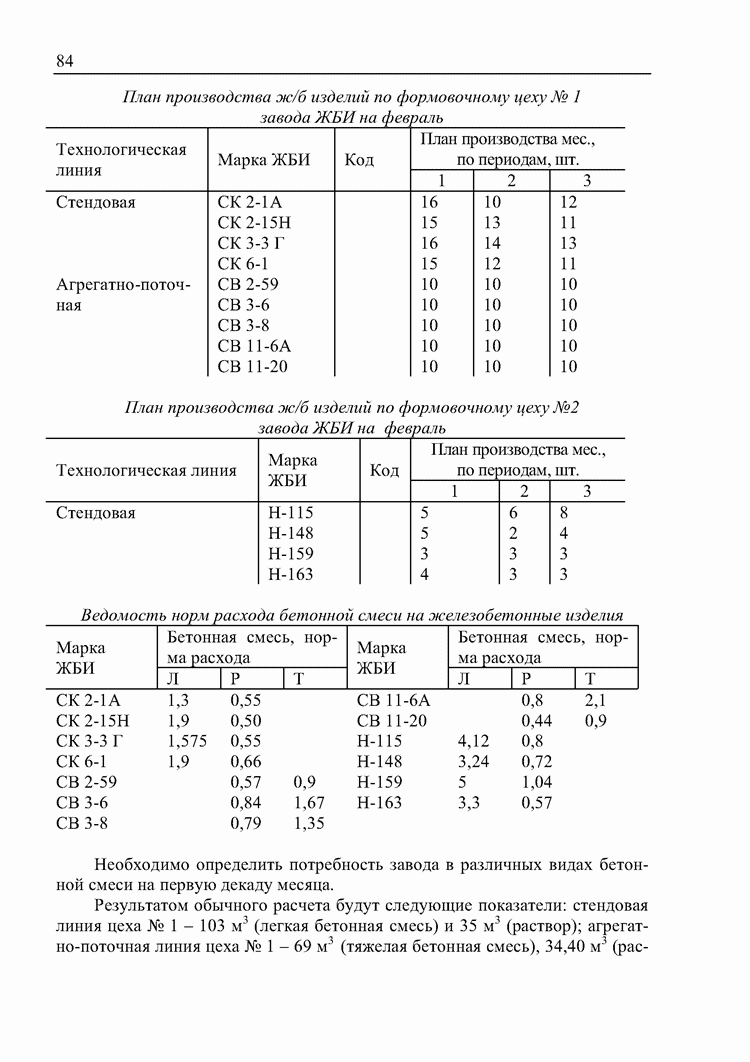
- 4.2. Применение методов принятия решений для анализа количественных данных
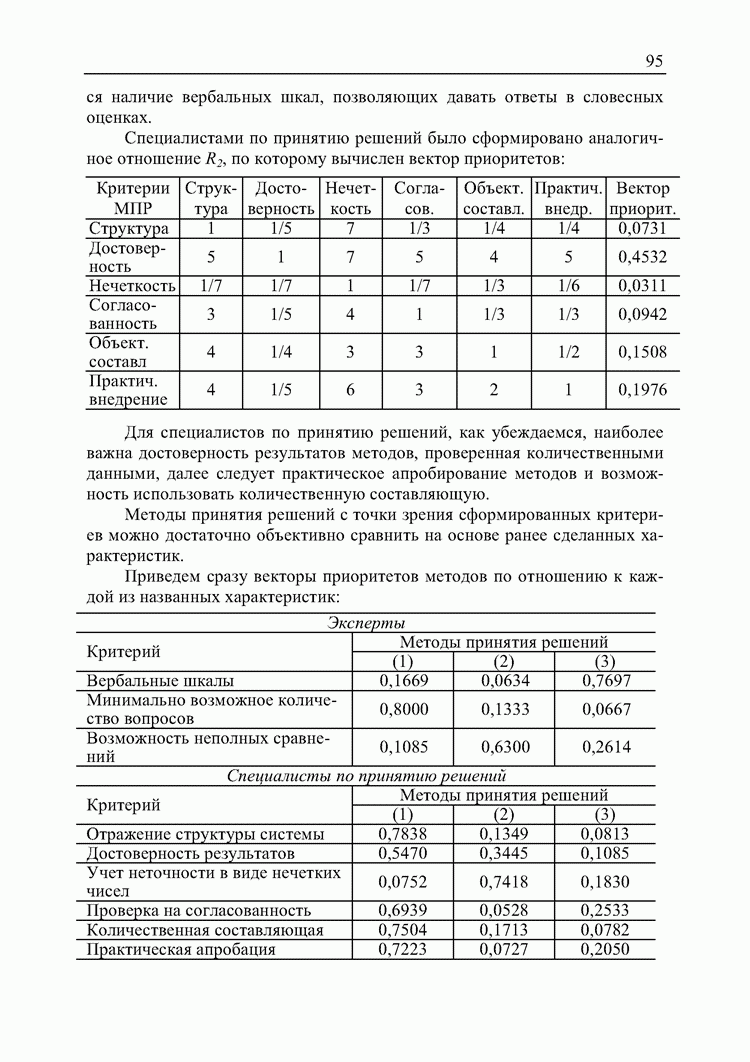
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список