| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Модели линейного упорядочивания
Используемые в практике модели линейного упорядочивания традиционно разделяются на две большие группы, различающиеся своим подходом к решению задачи упорядочивания объектов [8].
В моделях первой группы, использующих статистические методы, каждому объекту х, сопоставляется определенный интегральный показатель  , оценивающий итоги его сравнений с остальными объектами, а далее объекты просто упорядочиваются по убыванию значений этого ранжирующего фактора. В моделях второй группы, использующих комбинаторно-логические и теоретико-графовые методы, оцениваются показатели не отдельных объектов, а всего упорядочивания в целом и выбирается упорядочивание, максимизирующее некоторый функционал качества. Оценок важности при этом не делается. Рассмотрим некоторые модели первой группы.
, оценивающий итоги его сравнений с остальными объектами, а далее объекты просто упорядочиваются по убыванию значений этого ранжирующего фактора. В моделях второй группы, использующих комбинаторно-логические и теоретико-графовые методы, оцениваются показатели не отдельных объектов, а всего упорядочивания в целом и выбирается упорядочивание, максимизирующее некоторый функционал качества. Оценок важности при этом не делается. Рассмотрим некоторые модели первой группы.
Пусть задано некоторое фиксированное множество объектов  , которые сравниваются попарно с точки зрения их предпочтительности, желательности, важности и т.п., а результаты записываются в виде матрицы парных сравнений
, которые сравниваются попарно с точки зрения их предпочтительности, желательности, важности и т.п., а результаты записываются в виде матрицы парных сравнений  , отражающей возникающее бинарное отношение предпочтения/безразличия на множестве X. Симметричные элементы матрицы парных сравнений
, отражающей возникающее бинарное отношение предпочтения/безразличия на множестве X. Симметричные элементы матрицы парных сравнений  должны выбираться равными, если соответствующие объекты равноценны или несравнимы
должны выбираться равными, если соответствующие объекты равноценны или несравнимы  если же
если же  , то должно быть
, то должно быть  . Кроме того, на элементы матрицы А обычно накладываются дополнительные калибровочные ограничения, однозначно связывающие попарно симметричные элементы
. Кроме того, на элементы матрицы А обычно накладываются дополнительные калибровочные ограничения, однозначно связывающие попарно симметричные элементы  . Приведем основные типы калибровок.
. Приведем основные типы калибровок.
1) Простая структура (ПС).

Интерпретация:  - индикатор факта превосходства одного объекта над другим или их равноценности (несравнимости).
- индикатор факта превосходства одного объекта над другим или их равноценности (несравнимости).
2) Турнирная калибровка (Т).

Интерпретация:  - число очков, набранных игроком
- число очков, набранных игроком  во всех встречах с игроком
во всех встречах с игроком  ; число
; число  при этом может интерпретироваться как количество таких встреч. Нередко дополнительно постулируется целочисленность матрицы.
при этом может интерпретироваться как количество таких встреч. Нередко дополнительно постулируется целочисленность матрицы.
3) Кососимметрическая калибровка (К).

Интерпретация: объект х, превосходит в парном сравнении объект 
4) Степенная калибровка (С).

Интерпретация: объект  превосходит в парном сравнении объект
превосходит в парном сравнении объект  раз.
раз.
5) Вероятностная калибровка (В).

Интерпретация:  - вероятность превосходства
- вероятность превосходства  над
над 
Помимо калибровок  для полноты анализа можно ввести еще и произвольную взвешенную структуру (ВС), в рамках которой предполагается обычно только неотрицательность матрицы А, сами же ее элементы могут интерпретироваться по-разному.
для полноты анализа можно ввести еще и произвольную взвешенную структуру (ВС), в рамках которой предполагается обычно только неотрицательность матрицы А, сами же ее элементы могут интерпретироваться по-разному.
Переход от матрицы А, заданной в некоторой калибровке, к откалиброванной по-иному матрице В возможен не всегда, но лишь при соблюдении некоторых дополнительных содержательных условий и нередко сопряжен с потерей важной информации. Вопрос о возможности перехода к матрице с другой калибровкой и о путях такого перехода всякий раз должен рассматриваться с учетом содержательных особенностей задачи. Схемы и направления подобных переходов приведены в табл. 3.1.
Таблица 3.1. Реализация преобразований калибровки

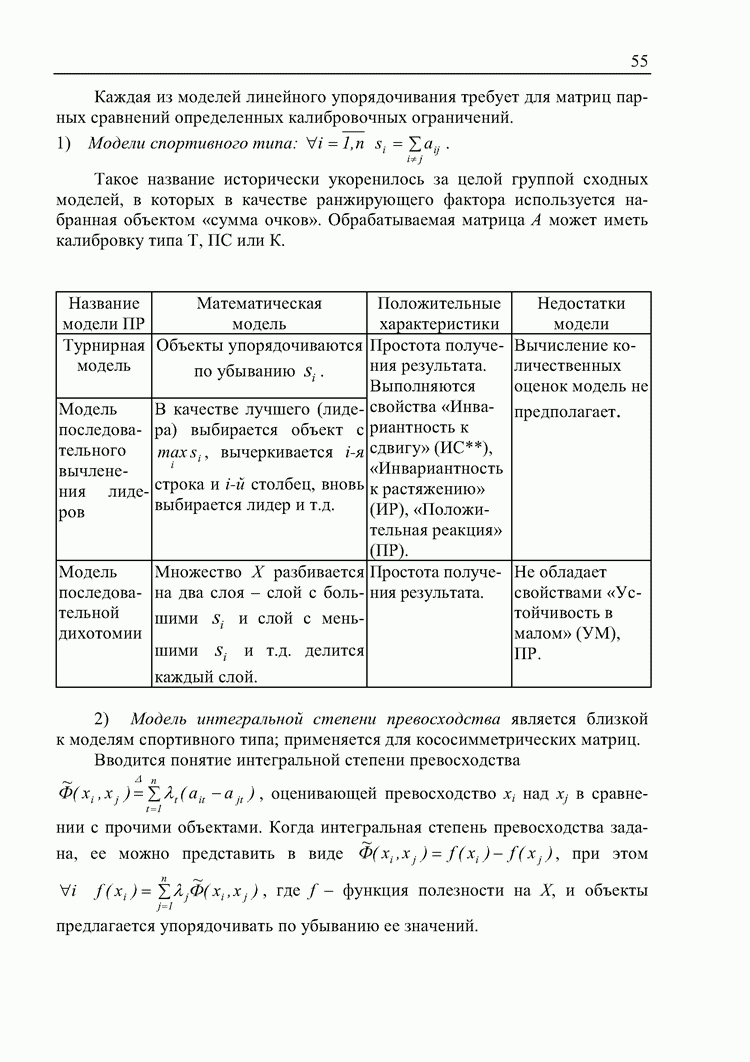
Каждая из моделей линейного упорядочивания требует для матриц парных сравнений определенных калибровочных ограничений.
1) Модели спортивного типа:  .
.
Такое название исторически укоренилось за целой группой сходных моделей, в которых в качестве ранжирующего фактора используется набранная объектом «сумма очков». Обрабатываемая матрица А может иметь калибровку типа Т, ПС или К.

2) Модель интегральной степени превосходства является близкой к моделям спортивного типа; применяется для кососимметрических матриц. Вводится понятие интегральной степени превосходства  , оценивающей превосходство
, оценивающей превосходство  над
над  в сравнении с прочими объектами. Когда интегральная степень превосходства задана, ее можно представить в виде
в сравнении с прочими объектами. Когда интегральная степень превосходства задана, ее можно представить в виде  при этом
при этом  , где f - функция полезности на X, и объекты предлагается упорядочивать по убыванию ее значений.
, где f - функция полезности на X, и объекты предлагается упорядочивать по убыванию ее значений.
К недостаткам модели можно отнести введение коэффициентов  — весов объектов, однако таких весов заранее задано быть не может. Модель сводится к турнирной и самостоятельного интереса не имеет.
— весов объектов, однако таких весов заранее задано быть не может. Модель сводится к турнирной и самостоятельного интереса не имеет.
3) Модель функции доминируемости ориентирована на обработку нечетких отношений предпочтения, т.е.  Применяется для калибровок Т, К.
Применяется для калибровок Т, К.
Функция доминируемости  характеризует максимальную силу, с которой объект
характеризует максимальную силу, с которой объект  доминируется остальными объектами множества X. При
доминируется остальными объектами множества X. При  - абсолютно не доминируется, при
- абсолютно не доминируется, при  - абсолютно доминируется, при
- абсолютно доминируется, при  - слабо доминируется. Объекты упорядочиваются по убыванию соответствующих значений функции
- слабо доминируется. Объекты упорядочиваются по убыванию соответствующих значений функции  . В [81] используются другие способы получения
. В [81] используются другие способы получения  .
.
Возможно использование значений  в качестве количественных оценок важности объектов. Модель обладает свойствами УМ, ПР, ИС, ИР.
в качестве количественных оценок важности объектов. Модель обладает свойствами УМ, ПР, ИС, ИР.
4) Модель Брэдли-Терри пригодна для простых структур без равноценных элементов и целочисленных турнирных матриц.
Каждому объекту сопоставляется его «сила»  , причем предполагается, что вероятность превосходства в парном сравнении
, причем предполагается, что вероятность превосходства в парном сравнении  прямо пропорциональна
прямо пропорциональна  . Для каждой пары
. Для каждой пары  проводится k независимых актов парных сравнений. Окончательно получается:
проводится k независимых актов парных сравнений. Окончательно получается: 
Система может быть решена итерационно. После вычисления всех s, объекты упорядочиваются по их убыванию.
Получаемые компоненты нормализованного вектора s могут служить количественными оценками важности объектов. Выполняются свойства ИС, ИР.
5) Модель Бэржа-Брука-Буркова применяется для обработки простых структур, матриц с турнирной и степенной калибровками.
Каждому объекту  ставится в соответствие цепочка так называемых интегрированных сил, в которой сила
ставится в соответствие цепочка так называемых интегрированных сил, в которой сила  порядка
порядка  определяется как сумма элементов
определяется как сумма элементов  строки в матрице
строки в матрице 

При  имеет место
имеет место  где нормализованный собственный вектор
где нормализованный собственный вектор  матрицы А отвечает максимальному по модулю собственному числу теоремы Перрона-Фробениуса.
матрицы А отвечает максимальному по модулю собственному числу теоремы Перрона-Фробениуса.
Модель обладает свойствами ИР, УМ; Т (при  ). Получаемые значения компонент собственного вектора могут служить оценкой важности объектов.
). Получаемые значения компонент собственного вектора могут служить оценкой важности объектов.
6) Стохастическая модель Ушакова предложена для обработки матриц, заданных в степенной и вероятностной калибровках.
Матрица А преобразуется в вероятностную матрицу Р, где  - вероятность превосходства
- вероятность превосходства  над
над 
При калибровке (23)  .
.
При калибровке (22)  .
.
Строится стохастическая матрица  .
.

где  - минор получаемый из
- минор получаемый из  вычеркиванием
вычеркиванием  столбца и i-той строки.
столбца и i-той строки.
Упорядочивание х, производится по  .
.
Обладает свойствами УМ, ПР. Получаемые компоненты финального распределения могут использоваться в качестве количественных оценок важности объектов.
Не обладает свойствами ИС, ИР.
7) Модель равномерного сглаживания применяется для положительных матриц с калибровкой Т или С.
По аксиоме Льюса для калибровки Т имеет место:  .
.
Обозначая  , получаем
, получаем  , так что матрица
, так что матрица  может быть восстановлена по любой строке.
может быть восстановлена по любой строке.
В данной модели от исходной матрицы А необходимо перейти к матрице Z и построить  различных матриц
различных матриц  полагая, что матрица
полагая, что матрица  порождается
порождается  строкой матрицы Z по формуле
строкой матрицы Z по формуле  , причем
, причем  . Проделав преобразования
. Проделав преобразования  в итоге получим
в итоге получим  .
.
Обладает свойствами ИР, Т, УМ, ПР. Получаемые коэффициенты можно использовать для количественной оценки важности объектов.
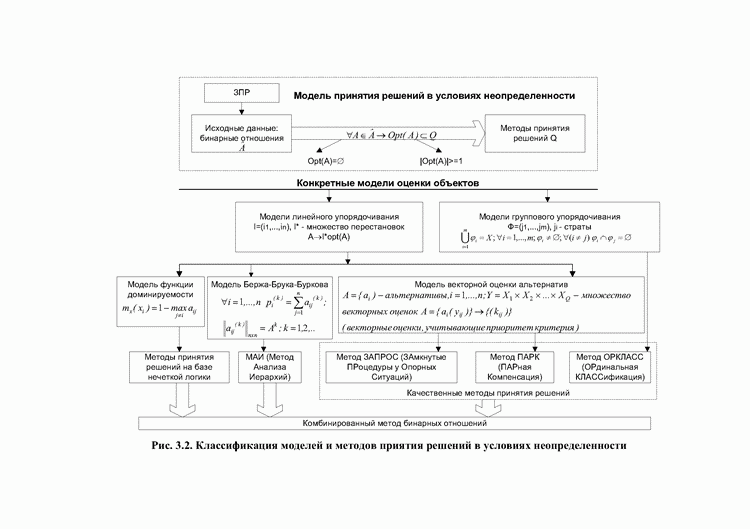
Выбор модели упорядочивания с теми свойствами, которые особенно желательны в данном конкретном случае, представляется весьма полезным в системах поддержки принятия решений [8]. Модели типа: модель функции доминируемости, Брэдли-Терри, Бержа-Брука-Буркова, стохастическая модель Ушакова, модель равномерного сглаживания предлагают гораздо более убедительные доводы в пользу соответствующих оптимальных упорядочиваний. Модель Брэдли-Терри пригодна для простых структур и целочисленных турнирных матриц, которые не учитывают неточность, неопределенность в оценках экспертов. Стохастическая модель Ушакова скорее ориентирована на вероятностный класс неопределенностей, в отличие от нее модель Бержа-Брука-Буркова и модель функции доминируемости позволяют учитывать неопределенность явлений, не поддающихся измерению со сколь угодно большой точностью и с учетом нечеткости соответственно. Модель равномерного сглаживания не обладает свойством ИС, что не позволяет экспертам производить неполные сравнения. В [8] утверждается, что модель Бержа-Брука-Буркова также не обладает свойством ИС, однако в [93] указан подход к выявлению приоритетов для неполной матрицы на основе данной модели. Таким образом, для линейного упорядочивания в условиях неопределенности предпочтительнее пользоваться моделями функции доминируемости и Бержа-Брука-Буркова. Рассмотрим методы ПР, ориентированные на выделенные модели. Кроме них, в монографии рассматриваются также качественные методы ПР, процедуры сравнения объектов в которых ориентированы на качественные оценки экспертов, что облегчает опрос экспертов, позволяя оперировать терминами, свойственными конкретной предметной области (рис. 3.2).
(см. скан)
Рис. 3.2. Классификация моделей и методов приятия решений в условиях неопределенности
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
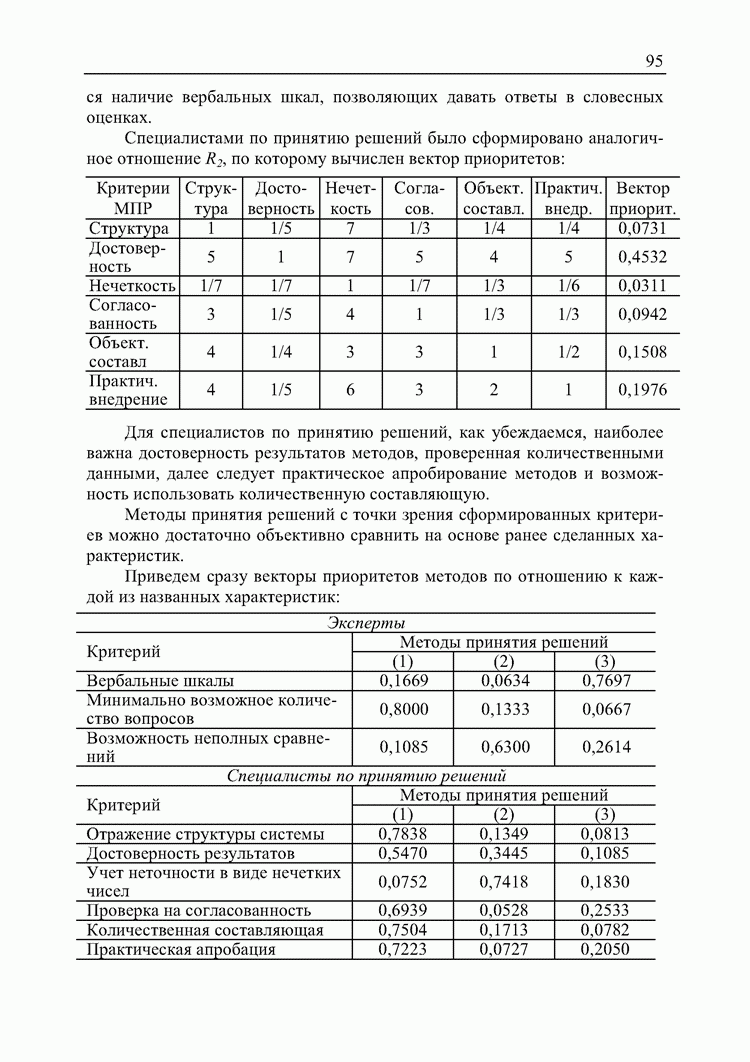
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
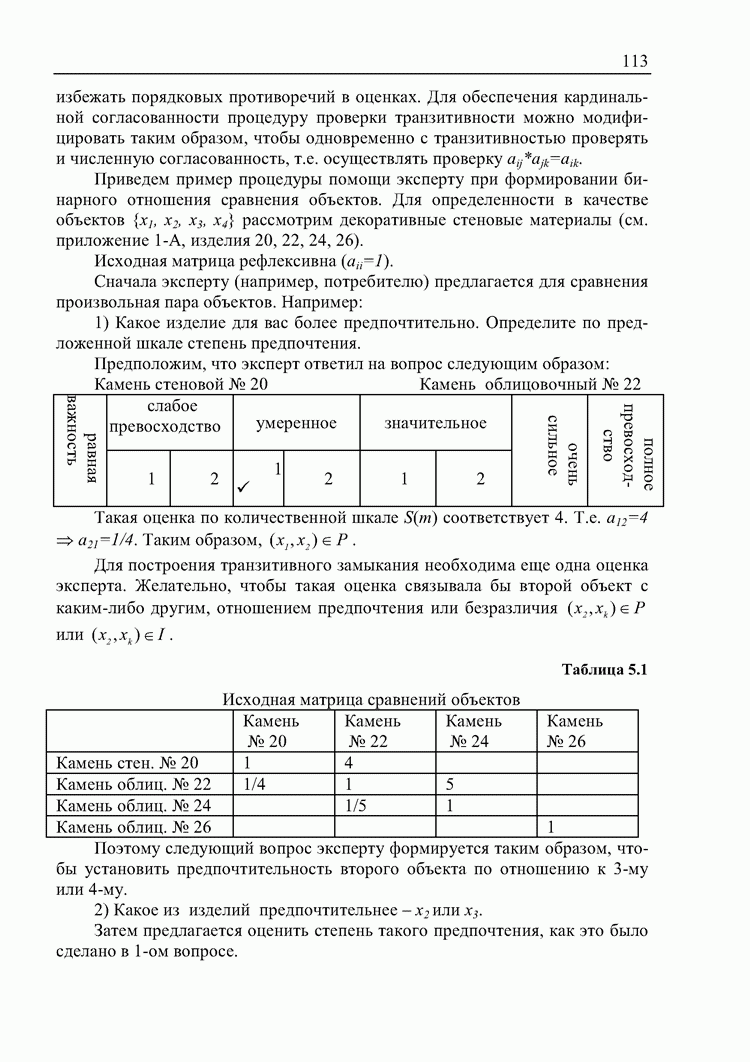
- 5.3. Выявление несогласованности суждений экспертов
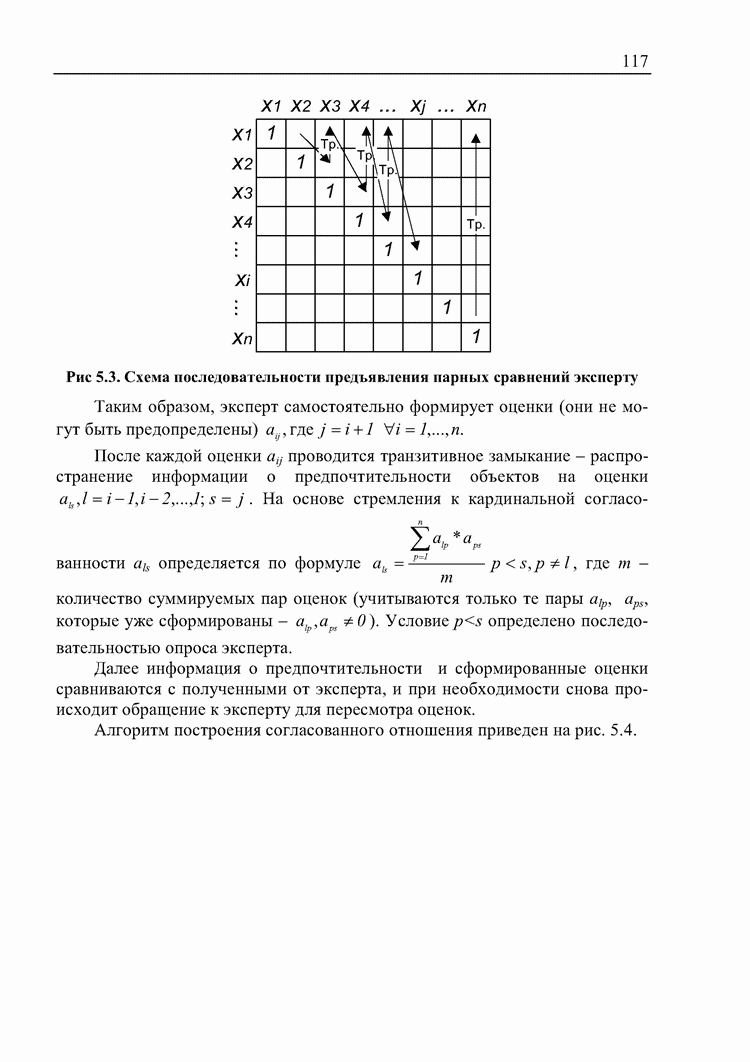
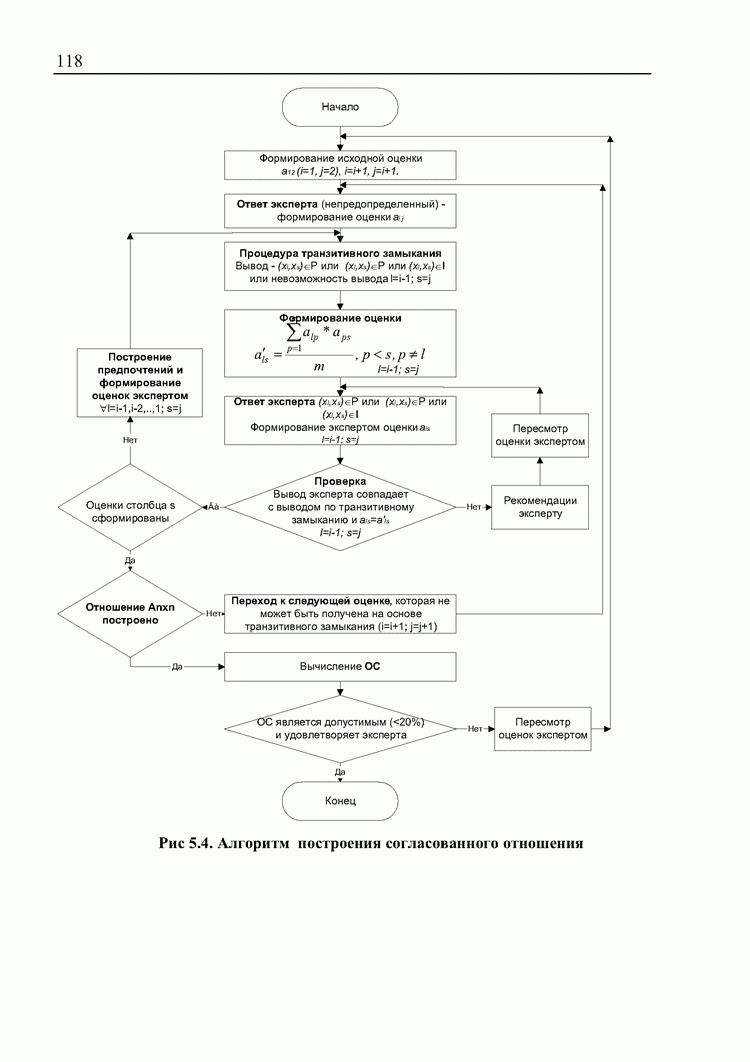
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список