| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Система аксиом

Эта система аксиом полна. Подалгебра ВХ тех элементов из X, для которых  (или, что равносильно
(или, что равносильно  ), является булевой алгеброй, в которой
), является булевой алгеброй, в которой  .
.
Связь с нечеткими множествами становится ясной после рассмотрения класса примеров таких алгебр, образованного множествами S действительных чисел между 0 и 1, удовлетворяющими условиям (двойные ++, -- обозначают
обычные арифметические операции):
Операции в S определяются следующим образом:
Без труда проверяется, что так определенная структура удовлетворяет приведенным аксиомам, но не аксиомам булевой алгебры. Сформулированным условиям 1-4 удовлетворяют различные конкретные множества, например,  ; S = {все рациональные числа между 0 и 1};
; S = {все рациональные числа между 0 и 1};  = - {все рациональные числа вида
= - {все рациональные числа вида  для некоторого фиксированного натурального
для некоторого фиксированного натурального  и целых
и целых  }, с операциями
}, с операциями  .
.
Нечеткое подмножество А универсального множества U может быть определено функцией принадлежности  , где X удовлетворяет требуемым аксиомам (традиционно
, где X удовлетворяет требуемым аксиомам (традиционно  );
);  . Операции над нечеткими множествами определяются в терминах их функций принадлежности и сводятся («поточечно») к операциям над значениями последних, то есть к операциям в X.
. Операции над нечеткими множествами определяются в терминах их функций принадлежности и сводятся («поточечно») к операциям над значениями последних, то есть к операциям в X.
Операции  в случае
в случае  и являются известными в теории нечетких множеств дополнением, граничными суммой и произведением, менее популярными, чем
и являются известными в теории нечетких множеств дополнением, граничными суммой и произведением, менее популярными, чем  , но находящими свое обоснование в новом контексте. Вне этого контекста (в частности, в рамках булевой алгебры) непосредственную связь между операциями
, но находящими свое обоснование в новом контексте. Вне этого контекста (в частности, в рамках булевой алгебры) непосредственную связь между операциями  и 1 над нечеткими множествами установить затруднительно.
и 1 над нечеткими множествами установить затруднительно.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
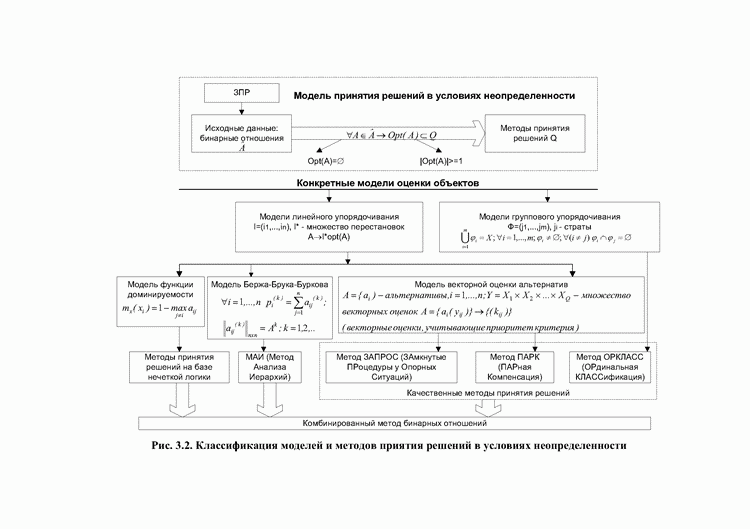
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
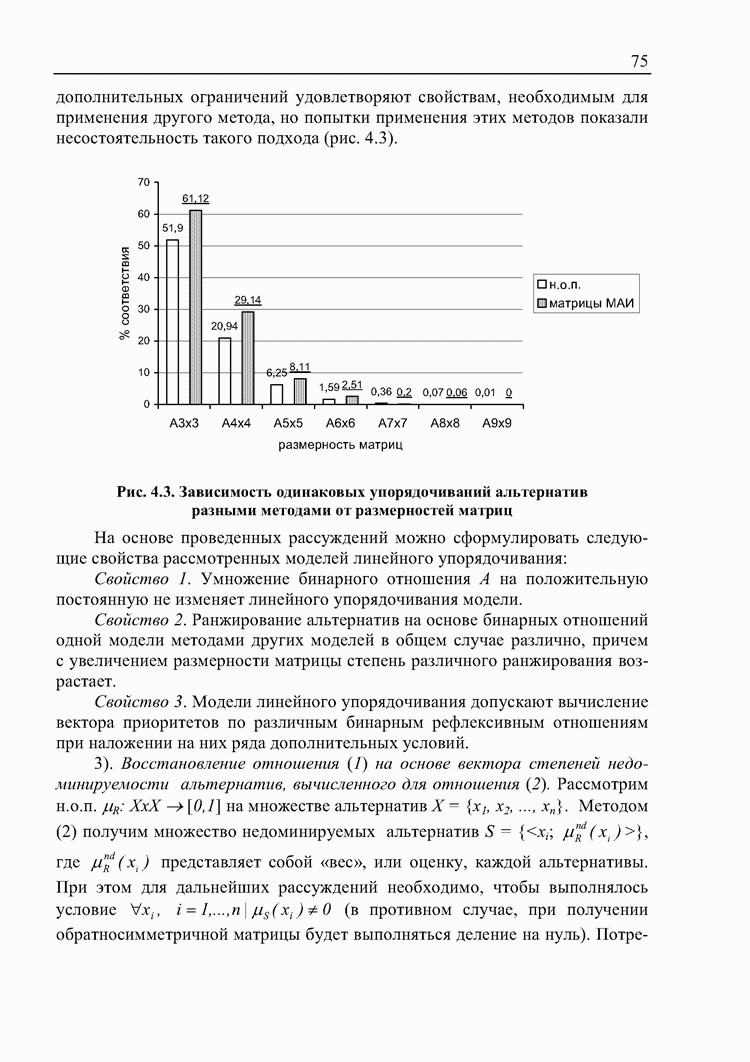
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список