| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Иерархии и приоритеты
Первым этапом МАИ является построение иерархии, отражающей процесс принятия решений. Иерархии рассматриваются в [93] как специальный тип упорядоченного множества или частный случай графа. Первая интерпретация выбрана в качестве основы формального определения, а вторая - в качестве иллюстрации. Изложим некоторые математические основы иерархий.
Частично упорядоченным множеством называется множество S с бинарным отношением  , которое удовлетворяет законам рефлексивности, антисимметричности и транзитивности:
, которое удовлетворяет законам рефлексивности, антисимметричности и транзитивности:
Рефлексивность: для всех  .
.
Антисимметричность: если  , то
, то  .
.
Транзитивность: если  , то
, то  .
.
Для любого отношения  такого типа можно определить
такого типа можно определить  , что означает
, что означает  .
.
Говорят, что у покрывает (доминирует)  если
если  и если
и если  невозможно ни для какого
невозможно ни для какого 
Упорядоченные множества с конечным числом элементов могут быть удобно представлены направленным графом. Каждый элемент системы представлен вершиной так, что дуга направлена от а к b, если 
Вполне упорядоченное множество (также называемое цепью) есть упорядоченное множество со следующим дополнительным свойством: если  , то или
, то или  или
или  .
.
Вводится обозначение  покрывает
покрывает  покрывает
покрывает  для любого элемента
для любого элемента  в упорядоченном множестве.
в упорядоченном множестве.
Пусть Н - конечное частично упорядоченное множество с наибольшим элементом b. Н есть иерархия, если выполняются следующие условия:
1. Существует разбиение Н на подмножества  где
где 
2. Из  следует, что
следует, что  .
.
3. Из  следует, что
следует, что 
Для каждого  существует весовая функция (сущность ее зависит от явления, для которого строится иерархия)
существует весовая функция (сущность ее зависит от явления, для которого строится иерархия)

Множества  являются уровнями иерархии, а функция
являются уровнями иерархии, а функция  есть функция приоритета элемента одного уровня относительно цели х.
есть функция приоритета элемента одного уровня относительно цели х.
Пример. Рассмотрим иерархию Н, построенную для задачи выбора руководителя из трех кандидатов. Элементами множества Н в данном случае являются цель задачи и факторы, на нее влияющие, а также кандидаты на должность руководителя.

Рис. 2.2. Иерархия задачи «Выбор руководителя»
Н = {руководитель, организационные способности, профессионализм, личная активность, коммуникабельность, внимание к подчиненным, авторитет среди подчиненных, кандидат 1, кандидат 2, кандидат 3}.
Для иерархии выполняются все условия определения.
1. Существует разбиение множества Н на подмножества  , где L1 = {Руководитель}, L2 = {организационные способности, профессионализм, личная активность, коммуникабельность, внимание к подчиненным, авторитет среди подчиненных}, L3 = {кандидат 1, кандидат 2, кандидат 3}.
, где L1 = {Руководитель}, L2 = {организационные способности, профессионализм, личная активность, коммуникабельность, внимание к подчиненным, авторитет среди подчиненных}, L3 = {кандидат 1, кандидат 2, кандидат 3}.
2. Рассмотрим  Руководитель
Руководитель  в этом случае
в этом случае  (аналогичные выводы справедливы и для всех других
(аналогичные выводы справедливы и для всех других  ).
).
3. Рассмотрим  кандидат 1
кандидат 1  в этом случае
в этом случае  (аналогичные выводы справедливы и для всех других
(аналогичные выводы справедливы и для всех других  ).
).
Определим весовую функцию для элемента  — Руководитель. Эта функция ставит в соответствие качествам руководителя (элементам уровня
— Руководитель. Эта функция ставит в соответствие качествам руководителя (элементам уровня  ) значения из отрезка [0, 1] и определяет приоритет этих качеств относительно
) значения из отрезка [0, 1] и определяет приоритет этих качеств относительно
цели - «Руководитель». Весовая функция задается субъективно экспертами. К примеру, она может быть такой:

Основная задача МАИ заключается в следующем: как определить для любого заданного элемента  и подмножества
и подмножества  функцию
функцию  чтобы она отражала свойства функций приоритетов
чтобы она отражала свойства функций приоритетов  на уровнях
на уровнях  . В частности, что это за функция
. В частности, что это за функция  .
.
В [93, 94] предлагается следующий метод решения основной задачи. Предположим, что  . Пусть также существует элемент
. Пусть также существует элемент  . Рассмотрим функции приоритетов
. Рассмотрим функции приоритетов

где  - количество объектов на к-ом уровне иерархии.
- количество объектов на к-ом уровне иерархии.
Обозначим  функцию приоритета элемента
функцию приоритета элемента  относительно цели
относительно цели  . В [93] такая функция задается в виде
. В [93] такая функция задается в виде  . То есть, происходит процесс взвешивания показателя влияния элемента у. на приоритет элемента
. То есть, происходит процесс взвешивания показателя влияния элемента у. на приоритет элемента  путем умножения этого показателя на важность элемента у. относительно z. Если из
путем умножения этого показателя на важность элемента у. относительно z. Если из  образовать матрицу В, положив
образовать матрицу В, положив  , то окончательная формула примет вид:
, то окончательная формула примет вид:  . Такое взвешивание производится для каждого уровня иерархии.
. Такое взвешивание производится для каждого уровня иерархии.
Рассматривая процесс взвешивания на всей иерархии, получаем формулу вектора приоритетов самого низкого уровня относительно цели  , где h - количество уровней в иерархии, W - приоритет элементов первого уровня иерархии (в большинстве случаев первый уровень состоит из одного элемента - цели процесса принятия решений, в этом случае W - скаляр).
, где h - количество уровней в иерархии, W - приоритет элементов первого уровня иерархии (в большинстве случаев первый уровень состоит из одного элемента - цели процесса принятия решений, в этом случае W - скаляр).
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
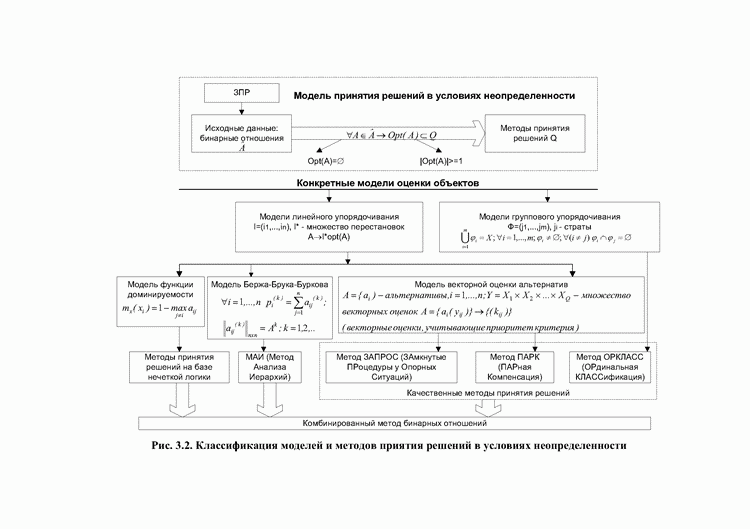
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
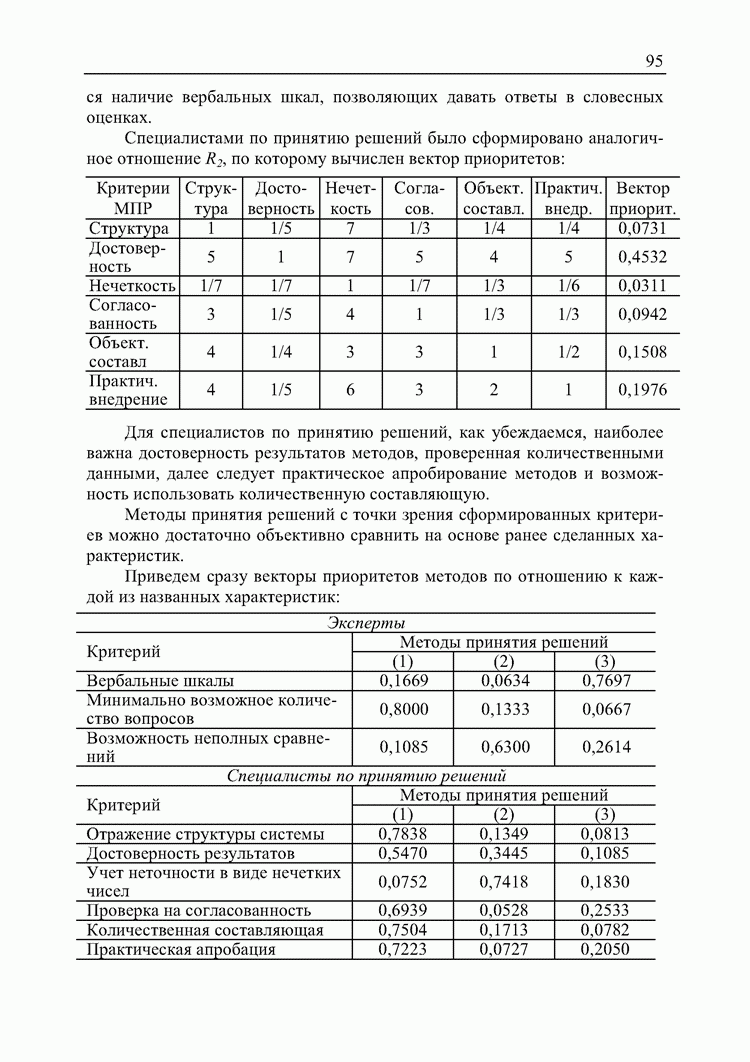
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
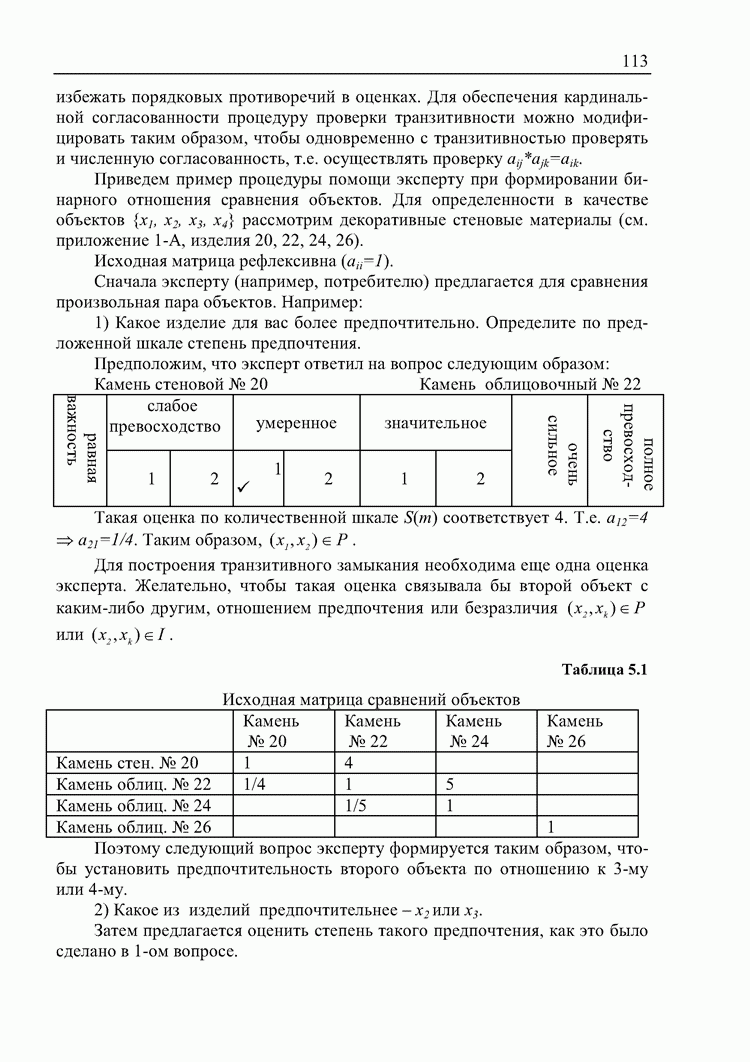
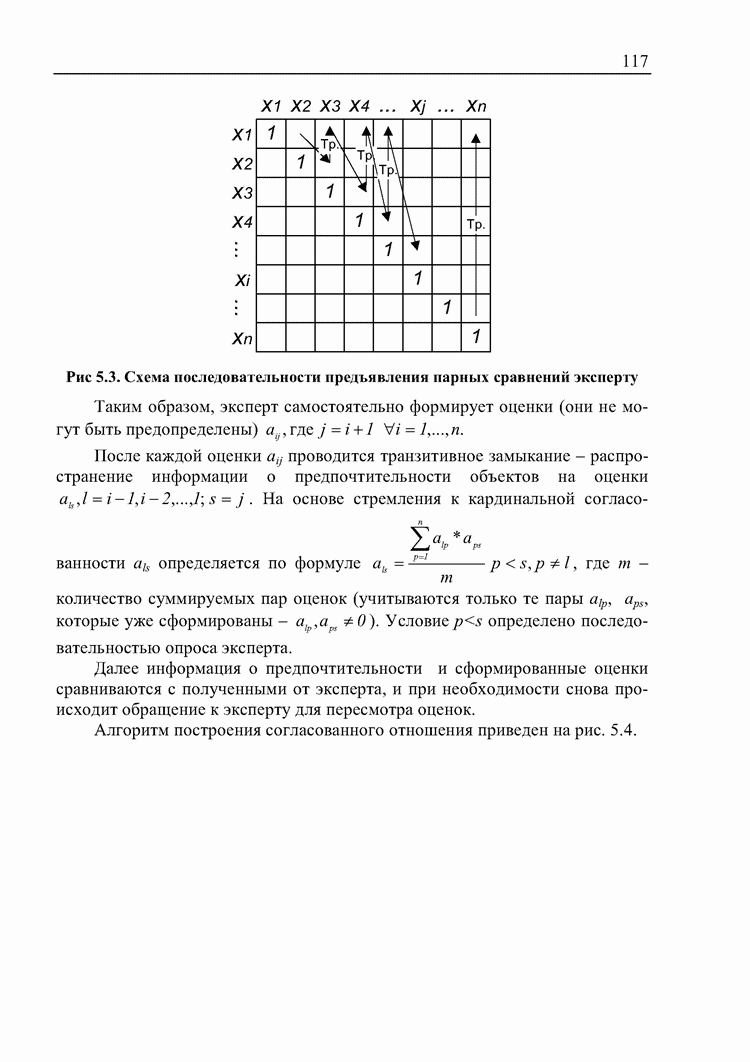
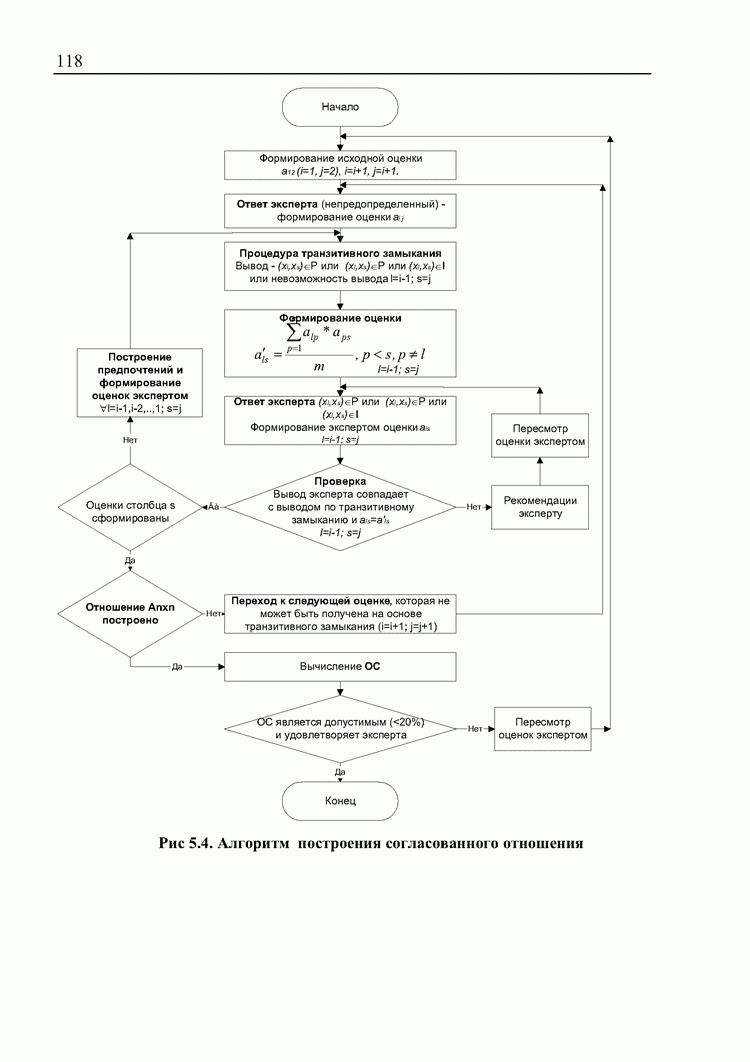
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список