| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Нечеткие логические формулы и их свойства
Определение. Нечеткая высказывательная переменная х. - это нечеткое высказывание, степень истинности которого может принимать произвольное значение из отрезка [0; 1].
Определение. Нечеткой логической формулой  называется:
называется:
а) любая нечеткая высказывательная переменная или константа из [0; 1],
б) выражение  полученное из нечетких логических формул
полученное из нечетких логических формул  применением к ним любого конечного числа логических операций.
применением к ним любого конечного числа логических операций.
В частности составные нечеткие высказывания также являются нечеткими логическими формулами, если рассмотреть образующие их простые нечеткие высказывания как нечеткие высказывательные переменные.
Определение. Степень равносильности формул  и
и  обозначается
обозначается  и определяется
и определяется 
Если степень равносильности нечетких логических формул  на всех определенных наборах степеней истинности высказывательных переменных больше или равна 0,5, то такие формулы будем называть нечетко близкими на этих наборах и обозначать
на всех определенных наборах степеней истинности высказывательных переменных больше или равна 0,5, то такие формулы будем называть нечетко близкими на этих наборах и обозначать  .
.
Если  , то формулы не являются нечетко близкими:
, то формулы не являются нечетко близкими:  .
.
Заметим, что при  формулы
формулы  одновременно являются и не являются нечетко близкими. Их называют взаимно индифферентными и обозначают
одновременно являются и не являются нечетко близкими. Их называют взаимно индифферентными и обозначают  .
.
Равносильность четких логических формул является частным случаем нечеткой близости.
Если  на одних и тех же наборах степеней истинности переменных принимают одни и те же значения степени истинности, то значение степени их равносильности всегда больше или равно 0,5, что является частным случаем нечеткой близости. То есть, нечеткие логические формулы, имеющие на одних и тех же наборах переменных одинаковые степени истинности не равносильны, а имеют некоторую степень равносильности
на одних и тех же наборах степеней истинности переменных принимают одни и те же значения степени истинности, то значение степени их равносильности всегда больше или равно 0,5, что является частным случаем нечеткой близости. То есть, нечеткие логические формулы, имеющие на одних и тех же наборах переменных одинаковые степени истинности не равносильны, а имеют некоторую степень равносильности  , но всегда
, но всегда  .
.
Пример.
Определить степень равносильности формул  , где
, где  принимает значение степени истинности из множества дискретных значений
принимает значение степени истинности из множества дискретных значений  из {0,3; 0,4}.
из {0,3; 0,4}.
Решение.
 . Выбирая все возможные наборы степеней истинности
. Выбирая все возможные наборы степеней истинности  , запишем
, запишем

Откуда следует, формулы  нечетко близки при заданных наборах степеней истинности.
нечетко близки при заданных наборах степеней истинности.
Если сделать такую же проверку, полагая, что  принимает значение из набора
принимает значение из набора  из
из  , то
, то  . И в этом случае формулы не являются нечетко близкими.
. И в этом случае формулы не являются нечетко близкими.
Определение. Если при всех определенных значениях степени истинности нечетких переменных  значение степени истинности нечеткой логической формулы
значение степени истинности нечеткой логической формулы  больше или равно 0,5, то формула является нечетко истинной на данных наборах переменных и обозначается через
больше или равно 0,5, то формула является нечетко истинной на данных наборах переменных и обозначается через  . Если значение степени истинности меньше или равно 0,5, то такую формулу будем называть нечетко ложной на данных наборах переменных и обозначим
. Если значение степени истинности меньше или равно 0,5, то такую формулу будем называть нечетко ложной на данных наборах переменных и обозначим 
Пусть  - некоторые нечетко истинные и нечетко ложные формулы на одних и тех же наборах переменных, тогда справедливы следующие соотношения.
- некоторые нечетко истинные и нечетко ложные формулы на одних и тех же наборах переменных, тогда справедливы следующие соотношения.

Если  - произвольные нечеткие логические формулы, то справедливы соотношения:
- произвольные нечеткие логические формулы, то справедливы соотношения:

где  определены на одних и тех же наборах переменных.
определены на одних и тех же наборах переменных.
Пример.
Приведем простейший пример нечетко истинных и нечетко ложных формул.

Это следует из определения операций отрицания, конъюнкции и дизъюнкции,  .
.
Тождества позволяют определить класс нечетко близких формул, не имеющих аналогов в нечеткой логике.
Соотношения, справедливые для любых наборов значений истинности нечетких переменных.
Пусть  - нечеткие логические формулы.
- нечеткие логические формулы.


Кроме того, пусть  - константы и
- константы и  , тогда
, тогда

Для доказательства каждого из выражений необходимо показать, что степень равносильности  образующих его формул
образующих его формул  больше или равно 0,5.
больше или равно 0,5.
Это возможно тогда, когда формулы  принимают одни и те же значения степени истинности на одинаковых наборах переменных либо имеют степень истинности одновременно меньше или равно 0,5 или больше или равно 0,5 на одинаковых наборах переменных.
принимают одни и те же значения степени истинности на одинаковых наборах переменных либо имеют степень истинности одновременно меньше или равно 0,5 или больше или равно 0,5 на одинаковых наборах переменных.
Докажем формулу (6)  обозначим
обозначим

Если  , тогда
, тогда  , т.е. при всех у степени истинности формул
, т.е. при всех у степени истинности формул  совпадают, откуда следует
совпадают, откуда следует  .
.
Если  , то
, то  , откуда следует
, откуда следует  .
.
Если  , то
, то  , откуда следует
, откуда следует  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
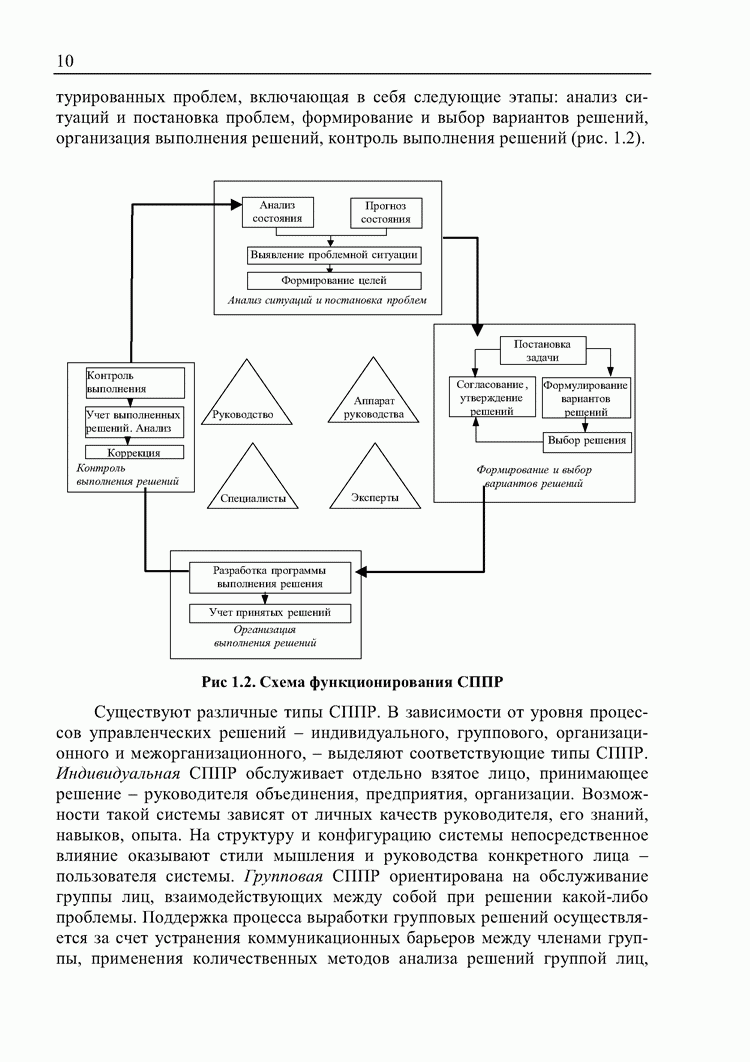
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
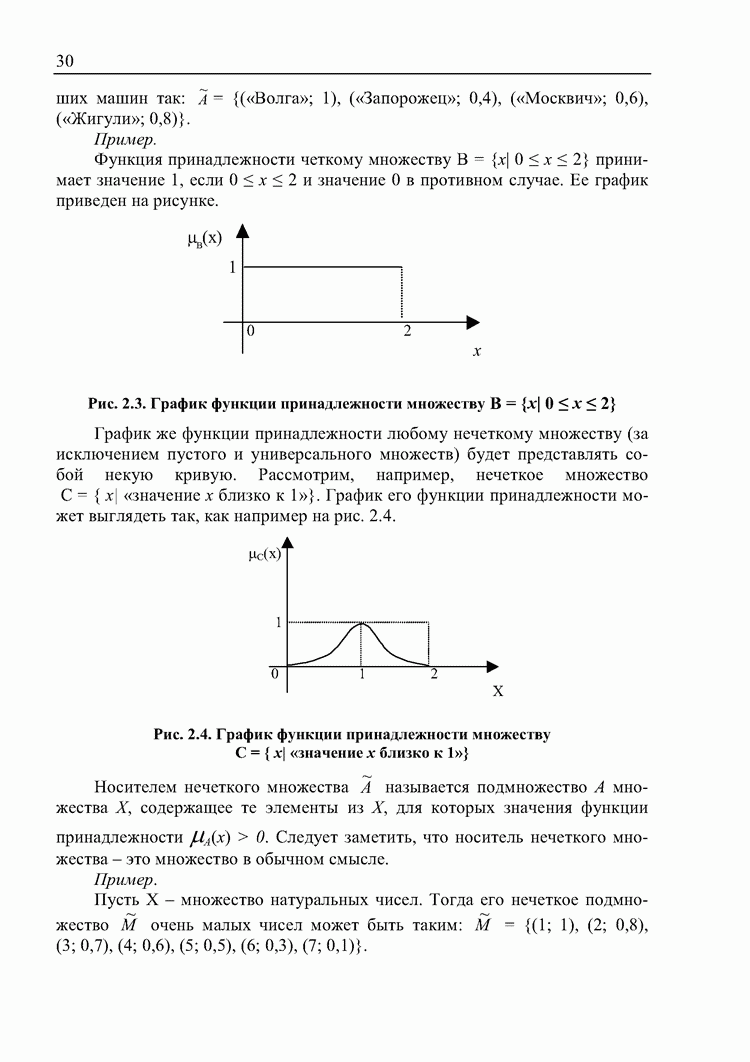
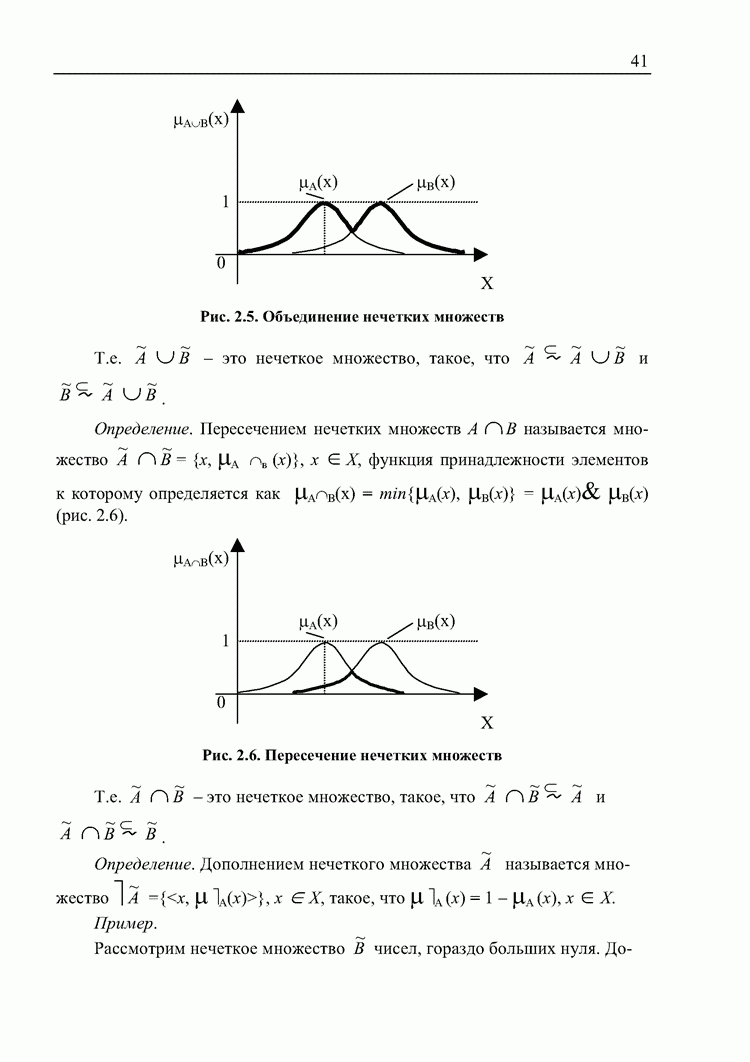
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
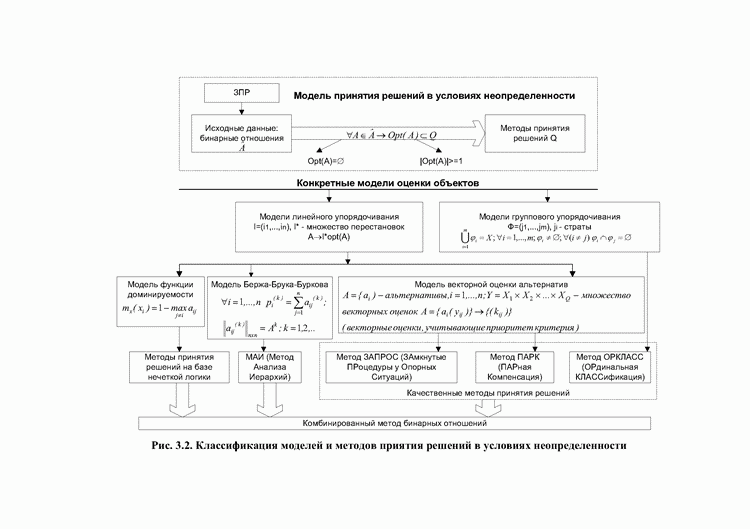
- 3.1. Классификация моделей и методов принятия решений
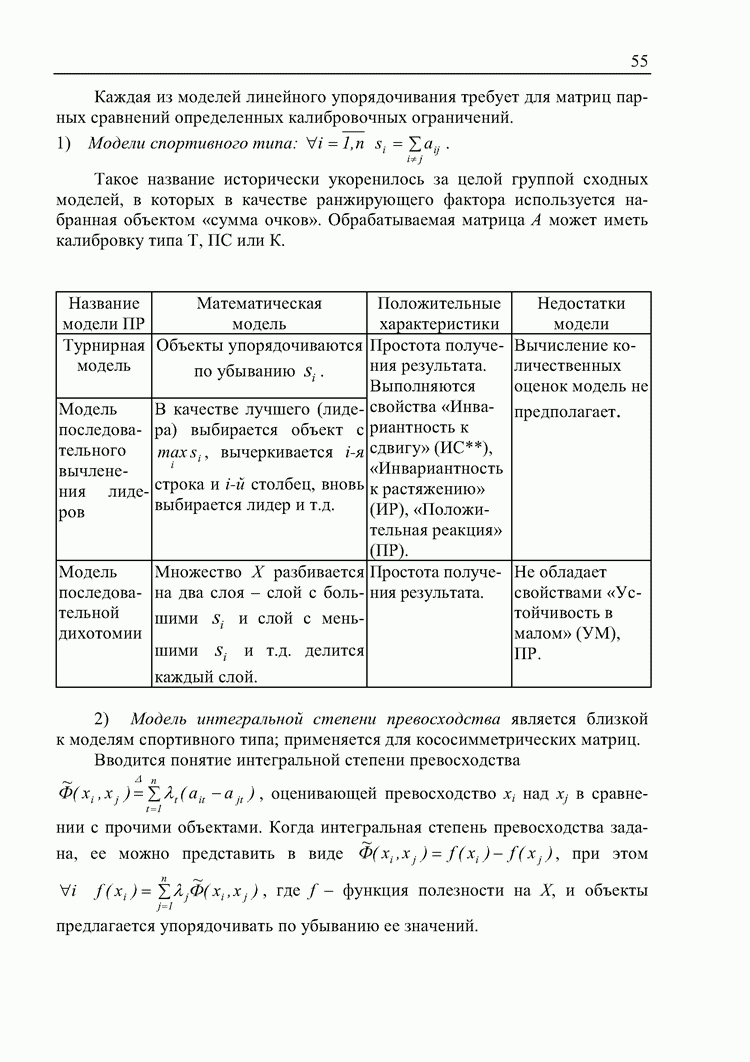
- 3.2. Модели линейного упорядочивания
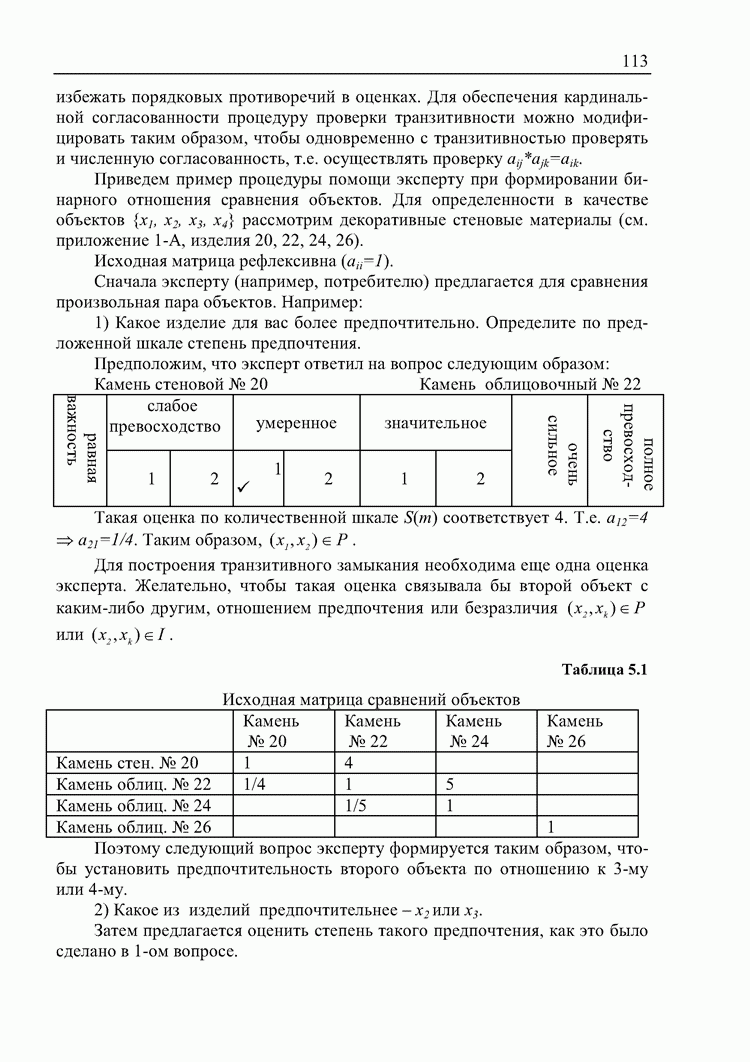
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
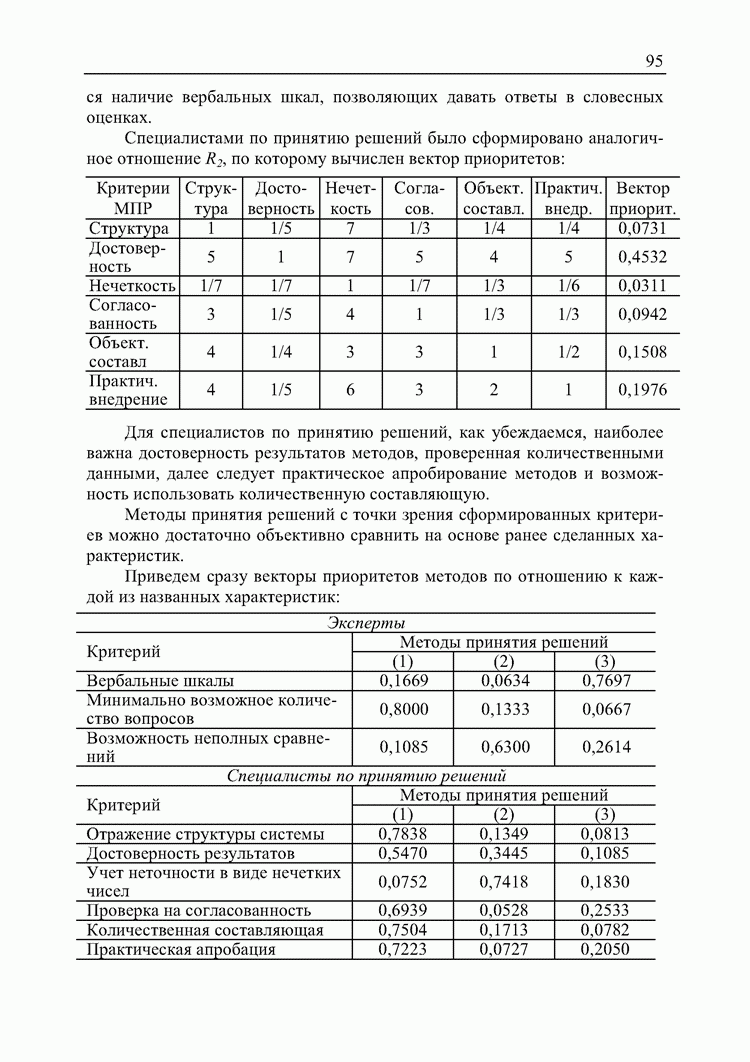
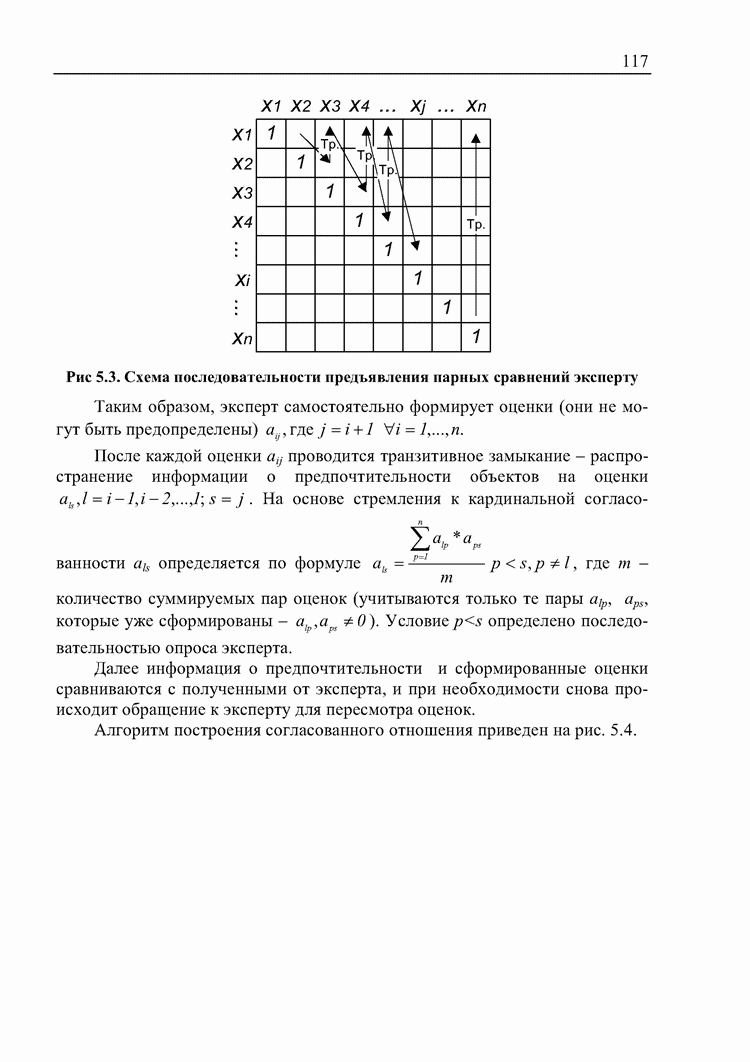
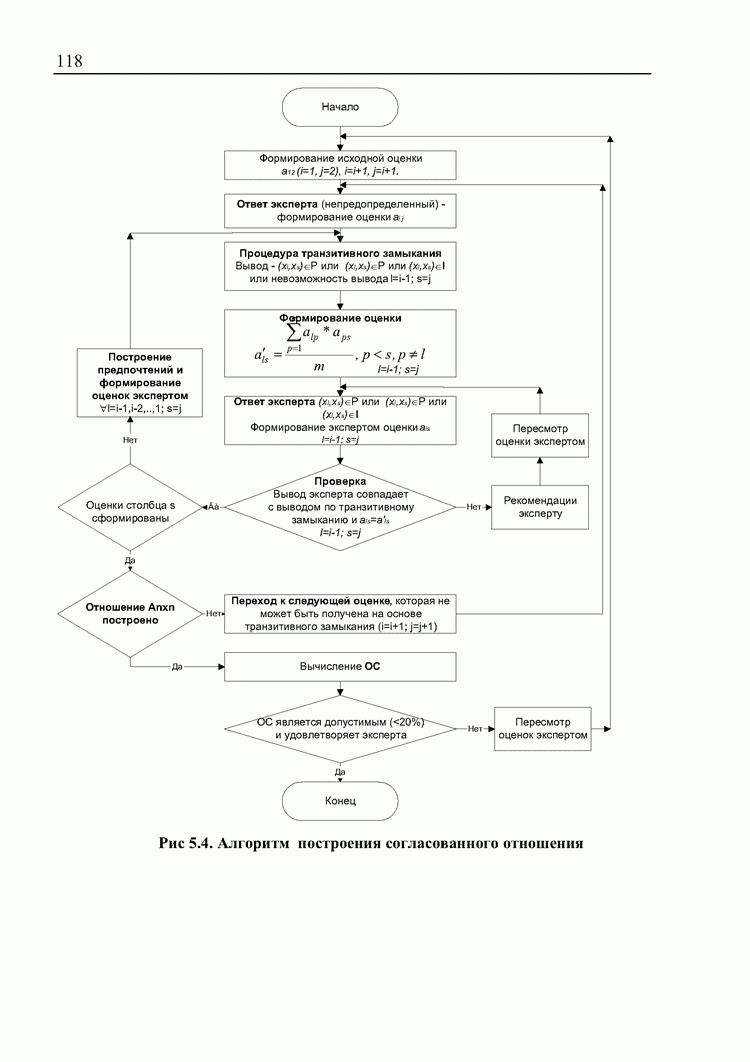
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
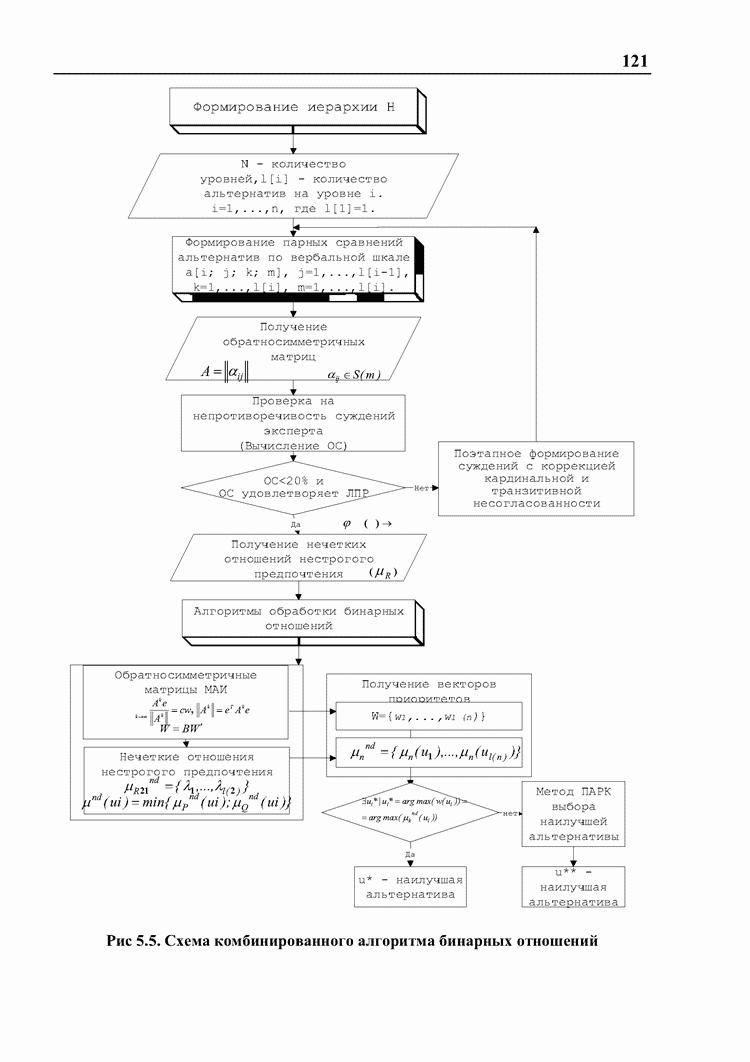
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список