| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Нечеткие соответствия и отношения
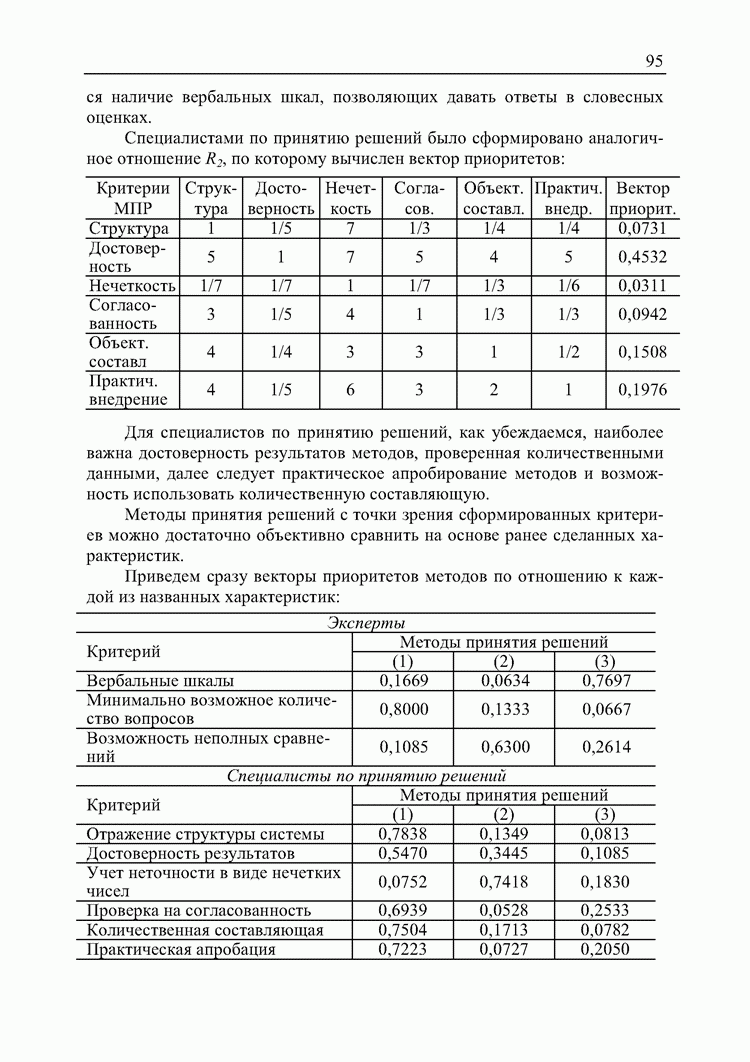
В методе принятия решений при нечеткой исходной информации [81] и в качественных методах принятия решений [64] существенно используются понятия соответствий, отношений, нечетких соответствий и отношений, операций над ними.
Нечетким соответствием между множествами X и Y называется и через  обозначается тройка множеств, в которой X, Y - произвольные четкие множества,
обозначается тройка множеств, в которой X, Y - произвольные четкие множества,  - нечеткое множество в
- нечеткое множество в  . Подобно названиям элементов четкого соответствия множество X называют областью отправления, множество Y - областью прибытия, а
. Подобно названиям элементов четкого соответствия множество X называют областью отправления, множество Y - областью прибытия, а  - нечетким графиком нечеткого соответствия.
- нечетким графиком нечеткого соответствия.
Назовем носителем нечеткого соответствия  соответствие
соответствие  , у которого график
, у которого график  является носителем нечеткого графика
является носителем нечеткого графика  .
.
Нечеткое соответствие может быть задано теоретико-множественно, графически и в матричном виде.
Для теоретико-множественного задания нечеткого соответствия необходимо перечислить элементы множеств X и Y и задать нечеткое множество  в
в  .
.
В матричном виде нечеткое соответствие  задается с помощью матрицы инциденций
задается с помощью матрицы инциденций  строки которой помечены элементами
строки которой помечены элементами  столбцы - элементами
столбцы - элементами  , а на пересечении строки
, а на пересечении строки  и столбца
и столбца  ставится элемент
ставится элемент  , где
, где  - функция принадлежности элементов из
- функция принадлежности элементов из  нечеткому графику.
нечеткому графику.
Нечеткое соответствие можно задать в виде ориентированного графа с множеством вершин  каждой дуге
каждой дуге  которого приписано значение
которого приписано значение  функции принадлежности.
функции принадлежности.
Пример.
Зададим некоторое нечеткое соответствие  , определив X и
, определив X и  как
как  .
.
Матрица инциденций  и граф нечеткого соответствия изображены на рис. 2.8.
и граф нечеткого соответствия изображены на рис. 2.8.

Рис. 2.8. Графическое и матричное задание нечеткого соответствия  .
.
Нечетким отношением на непустом множестве X называется и через  обозначается пара множеств, в которой
обозначается пара множеств, в которой  является нечетким подмножеством
является нечетким подмножеством  .
.
Множество X называется областью задания, а  - нечетким графиком отношения. Нечеткие отношения можно задавать теоретико-множественно, графически и в матричном виде. В методе принятия решений используется матричное задание нечетких отношений: отношение
- нечетким графиком отношения. Нечеткие отношения можно задавать теоретико-множественно, графически и в матричном виде. В методе принятия решений используется матричное задание нечетких отношений: отношение  задается с помощью матрицы смежности
задается с помощью матрицы смежности  на пересечении каждой
на пересечении каждой  строки
строки
и  столбца ставится элемент
столбца ставится элемент  , где
, где  - функция принадлежности элементов из
- функция принадлежности элементов из  нечеткому графику
нечеткому графику  . Свойства нечетких отношений [64, 81].
. Свойства нечетких отношений [64, 81].
Рефлексивность. Нечеткое отношение R на множестве X называется рефлексивным, если для любого  выполняется равенство
выполняется равенство  . Нечеткое отношение R на множестве X называется антирефлексивным, если для любого
. Нечеткое отношение R на множестве X называется антирефлексивным, если для любого  выполняется равенство
выполняется равенство  .
.
Связность. Нечеткое отношение R на множестве X называется связным, если для любого  выполняется неравенство
выполняется неравенство  или
или  .
.
Симметричность. Нечеткое отношение R на множестве X называется симметричным, если для любого  из
из 
Антисимметричность. Если для любых  , то такое отношение будет являться антисимметричным.
, то такое отношение будет являться антисимметричным.
Транзитивность. Если для любых  функция принадлежности нечеткого отношения R на множестве X удовлетворяет неравенству
функция принадлежности нечеткого отношения R на множестве X удовлетворяет неравенству  то такое отношение называется транзитивным.
то такое отношение называется транзитивным.
Отношение R называется транзитивным, если  таких, что
таких, что  следует
следует 
Квазипорядок. Отношение R называют квазипорядком, если оно рефлексивно и транзитивно.
Отношение R называют отношением строгого предпочтения, если оно антисимметрично и транзитивно.
Отношение R называют отношением безразличия, если оно симметрично и транзитивно.
Для получения матрицы композиции отношений используется максминное произведение соответствующих матриц. Если Т и S - нечеткие отношения, то их максминное произведение
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
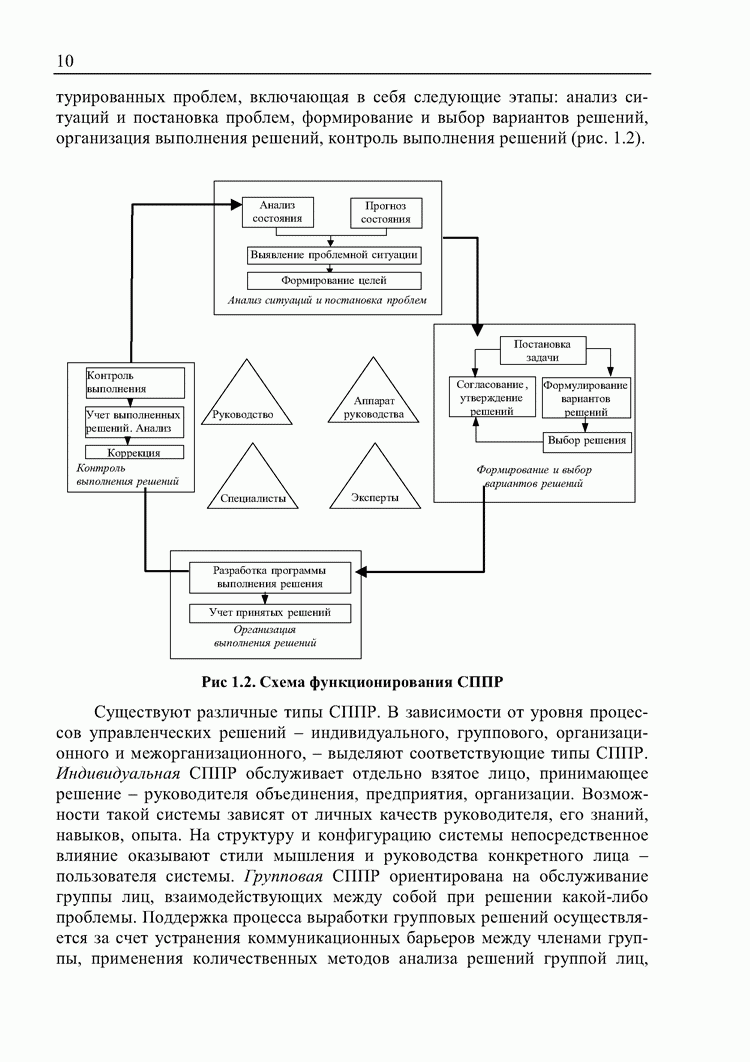
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
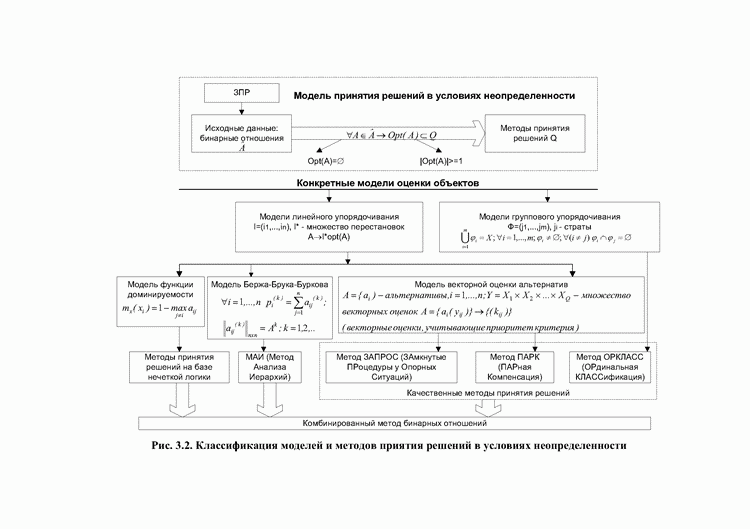
- 3.1. Классификация моделей и методов принятия решений
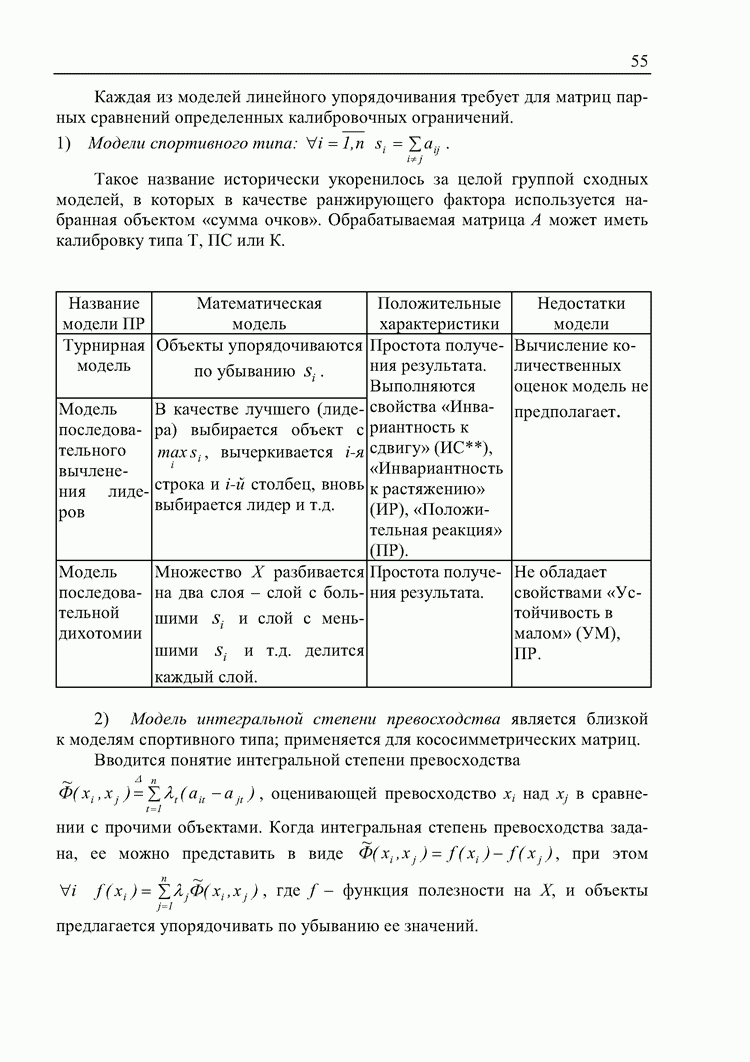
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
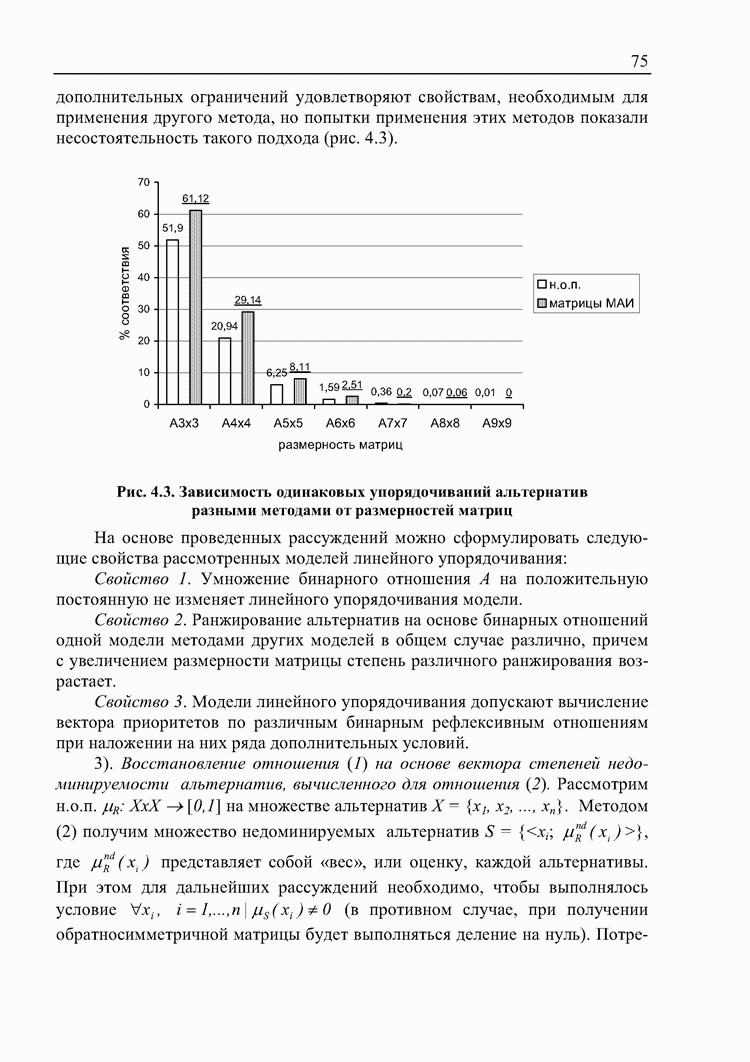
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
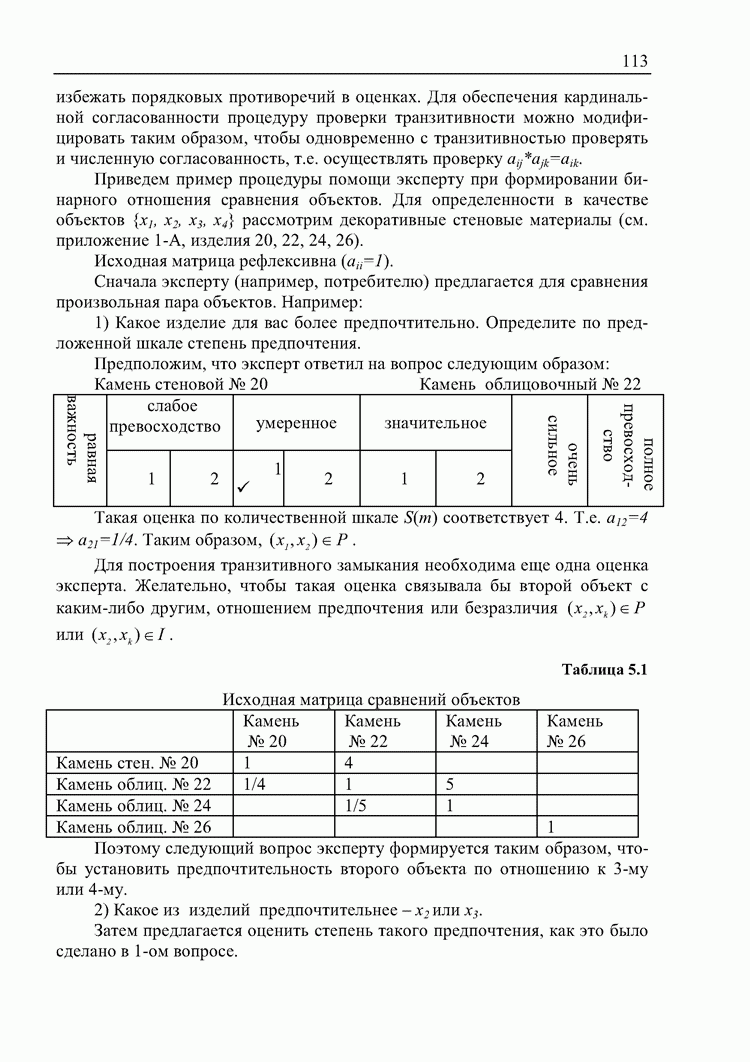
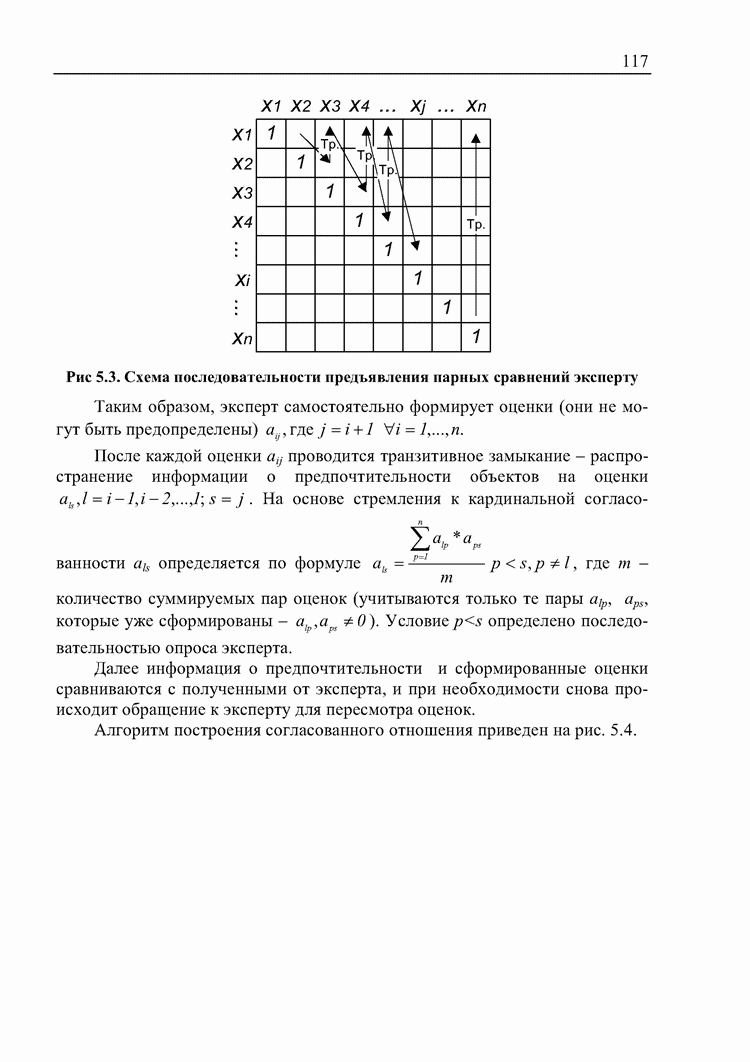
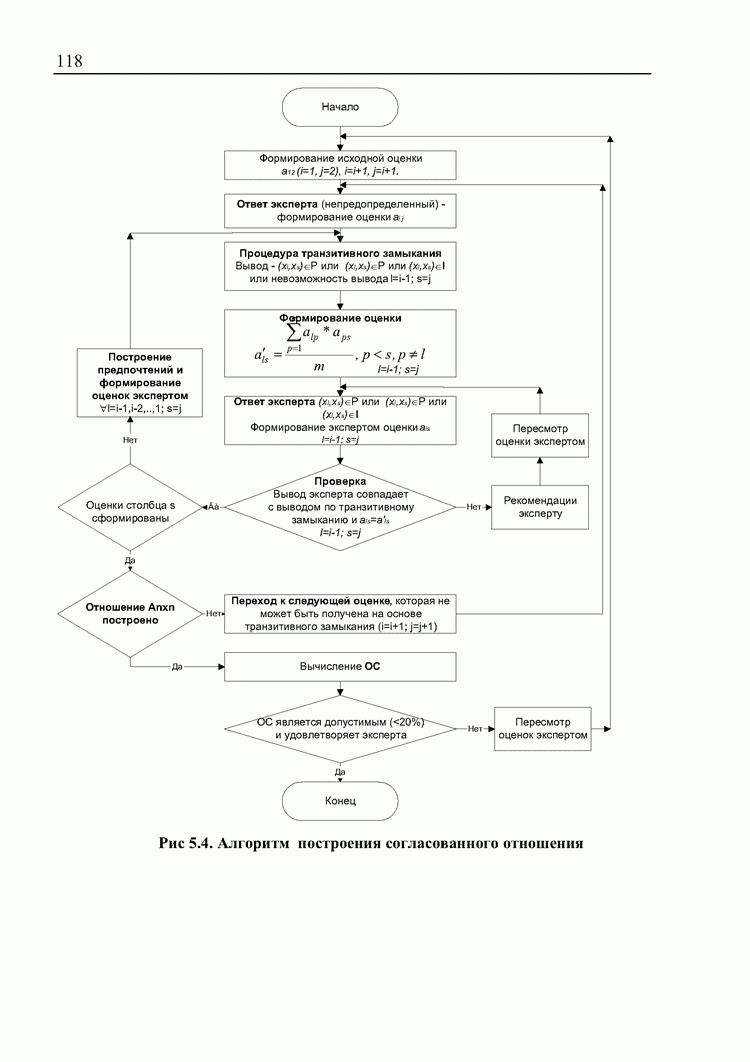
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список