| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Метод анализа иерархий [93, 94]
При принятии управленческих решений и прогнозировании возможных результатов лицо, принимающее решение, обычно сталкивается со сложной системой взаимозависимых компонент (ресурсы, желаемые исходы или цели, лица или группа лиц и т.д.), которую нужно проанализировать [93, 94]. МАИ развивает модель Бержа-Брука-Буркова [8].
Принимая решение, группа экспертов производит декомпозицию сложной проблемы - определяет ее компоненты и отношения между ними. Получается модель реальной действительности, построенная в виде иерархии. Вершина иерархии - общая цель, далее располагаются подцели, затем силы, которые влияют на эти подцели, люди, их цели, политики, стратегии, и, наконец, исходы, являющиеся результатами стратегий. На следующем этапе решения сравниваются уже отдельные компоненты иерархии между собой. В результате может быть выражена относительная степень интенсивности взаимодействия элементов в иерархии. Затем эти суждения выражаются численно. В завершении анализа проблемы МАИ включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Таким образом, основные этапы принятия решения с помощью МАИ следующие:
- построение иерархии рассматриваемой проблемы;
- парное сравнение компонент иерархии;
- математическая обработка полученных суждений.
В наиболее элементарном виде иерархия строится с вершины (целей -с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем альтернатив). Существуют несколько видов иерархий: доминантные, холлархии, китайский ящик и т.д. Наиболее часто применяется первый тип иерархий.
Парные сравнения проводятся в терминах доминирования одного из элементов над другим. Эти суждения затем выражаются в целых числах. Если элемент А доминирует над элементом Б, то ячейка матрицы, соответствующая строке А и столбцу Б, заполняется целым числом, а ячейка, соответствующая строке Б и столбцу А, заполняется обратным к нему числом (дробью). В МАИ предложена шкала относительной важности элементов иерархии (табл. 3.2).
Все матрицы в МАИ должны быть обратно симметричны, т.е.  По главной диагонали матрицы заранее ставятся единицы, т.к. альтернатива равноценна самой себе. Для заполнения каждой матрицы размером
По главной диагонали матрицы заранее ставятся единицы, т.к. альтернатива равноценна самой себе. Для заполнения каждой матрицы размером  достаточно произвести только
достаточно произвести только  суждения.
суждения.
Составление таких матриц проводится для всех уровней и групп в иерархии. Причем полученные матрицы должны быть согласованы для достоверного решения.
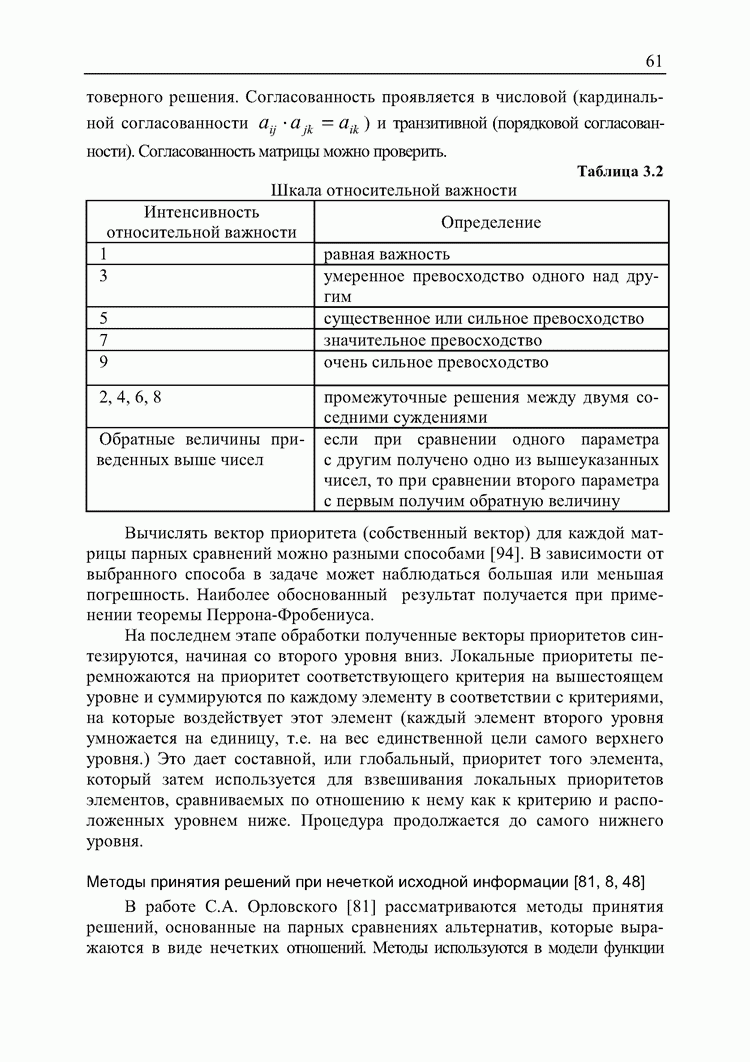
Согласованность проявляется в числовой (кардинальной согласованности  ) и транзитивной (порядковой согласованности). Согласованность матрицы можно проверить.
) и транзитивной (порядковой согласованности). Согласованность матрицы можно проверить.
Таблица 3.2. Шкала относительной

Вычислять вектор приоритета (собственный вектор) для каждой матрицы парных сравнений можно разными способами [94]. В зависимости от выбранного способа в задаче может наблюдаться большая или меньшая погрешность. Наиболее обоснованный результат получается при применении теоремы Перрона-Фробениуса.
На последнем этапе обработки полученные векторы приоритетов синтезируются, начиная со второго уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии с критериями, на которые воздействует этот элемент (каждый элемент второго уровня умножается на единицу, т.е. на вес единственной цели самого верхнего уровня.) Это дает составной, или глобальный, приоритет того элемента, который затем используется для взвешивания локальных приоритетов элементов, сравниваемых по отношению к нему как к критерию и расположенных уровнем ниже. Процедура продолжается до самого нижнего уровня.
Методы принятия решений при нечеткой исходной информации [81, 8, 48]
В работе С.А. Орловского [81] рассматриваются методы принятия решений, основанные на парных сравнениях альтернатив, которые выражаются в виде нечетких отношений. Методы используются в модели функции
недоминируемости [8]. В работе [48] произведена структуризация данных методов, в результате которой выделим следующие методы теории принятия решений при нечеткой исходной информации:
- методы принятия решений с одним экспертом;
- методы принятия решений с группой экспертов, характеризуемых весовыми коэффициентами;
- методы принятия решений с группой экспертов, характеризуемых нечетким отношением нестрогого предпочтения.
Задача принятия решения с одним экспертом
Задано множество возможных решений или альтернатив  и нечеткое отношение нестрогого предпочтения
и нечеткое отношение нестрогого предпочтения  на множестве U с функцией принадлежности
на множестве U с функцией принадлежности  - любое рефлексивное нечеткое отношение на U, так что
- любое рефлексивное нечеткое отношение на U, так что  задается обычно ЛПР в результате опроса экспертов, обладающих знаниями или представлениями о содержании или существе задачи, которые не были формализованы в силу чрезмерной сложности такой формализации или по другим причинам.
задается обычно ЛПР в результате опроса экспертов, обладающих знаниями или представлениями о содержании или существе задачи, которые не были формализованы в силу чрезмерной сложности такой формализации или по другим причинам.
Для любой пары альтернатив и,  значение
значение  понимается как степень предпочтения
понимается как степень предпочтения  не хуже
не хуже  в записи
в записи  . Равенство
. Равенство  может означать как то, что
может означать как то, что  то есть с положительной степенью выполнено «обратное» предпочтение
то есть с положительной степенью выполнено «обратное» предпочтение  , так и то, что и
, так и то, что и  , то есть альтернативы
, то есть альтернативы  несравнимы. Рефлексивность
несравнимы. Рефлексивность  отражает тот естественный факт, что любая альтернатива не хуже самой себя.
отражает тот естественный факт, что любая альтернатива не хуже самой себя.
Задача принятия решения заключается в рациональном выборе наиболее предпочтительных альтернатив из множества U, на котором задано нечеткое отношение предпочтения  .
.
Алгоритм решения задачи
1. Строится нечеткое отношение строгого предпочтения  ассоциированное с
ассоциированное с  , определяемое функцией принадлежности
, определяемое функцией принадлежности

Это отношение может быть представлено в виде  где
где  - «обратное» отношение (матрица отношений
- «обратное» отношение (матрица отношений  получается транспонированием матрицы отношений
получается транспонированием матрицы отношений  ).
).
2. Строится нечеткое подмножество  недоминируемых альтернатив, ассоциированное с
недоминируемых альтернатив, ассоциированное с  и включающее те альтернативы, которые
и включающее те альтернативы, которые
не доминируются никакими другими, определяемое функцией принадлежности

Для любой альтернативы  значение
значение  понимается как степень недоминируемости этой альтернативы, то есть степень, с которой
понимается как степень недоминируемости этой альтернативы, то есть степень, с которой  не доминируется ни одной из альтернатив множества
не доминируется ни одной из альтернатив множества  означает, что никакая альтернатива
означает, что никакая альтернатива  не может быть лучше
не может быть лучше  со степенью доминирования большей а; иначе говоря,
со степенью доминирования большей а; иначе говоря,  может доминироваться другими альтернативами, но со степенью не выше 1 - а. Рациональным естественно считать выбор альтернатив, имеющих по возможности большую
может доминироваться другими альтернативами, но со степенью не выше 1 - а. Рациональным естественно считать выбор альтернатив, имеющих по возможности большую
степень принадлежности множеству  .
.
3. Выбирается та альтернатива и, для которой значение  , максимально:
, максимально:

Она и дает решение задачи. Если наибольшую степень недоминируемости имеет не одна, а несколько альтернатив, то ЛПР может либо сам выбрать одну из них, исходя из каких-либо дополнительных соображений, либо расширить круг экспертов при формировании исходных данных задачи и повторить ее решение.
Задача принятия решения с группой экспертов, характеризуемых весовыми коэффициентами
На множестве всевозможных решений (альтернатив)  задано несколько
задано несколько  . Нечеткие отношения нестрогого предпочтения
. Нечеткие отношения нестрогого предпочтения  получены в результате опроса каждого эксперта и заполнении матрицы нечеткого отношения нестрогого предпочтения
получены в результате опроса каждого эксперта и заполнении матрицы нечеткого отношения нестрогого предпочтения  каждый элемент которой есть значение функции принадлежности
каждый элемент которой есть значение функции принадлежности  выражающее степень предпочтительности альтернативы
выражающее степень предпочтительности альтернативы  по сравнению с
по сравнению с  . При
. При  предпочтительнее, чем
предпочтительнее, чем  если же
если же  , то либо первая альтернатива хуже второй, либо они несравнимы. Лицо, принимающее решение, по-разному относится к экспертам, что находит отражение в весовых коэффициентах
, то либо первая альтернатива хуже второй, либо они несравнимы. Лицо, принимающее решение, по-разному относится к экспертам, что находит отражение в весовых коэффициентах  (где
(где  ), соответствующих каждому из них.
), соответствующих каждому из них.
Целью данной задачи является упорядочение совокупности альтернатив 
Алгоритм решения задачи
1. Строится свертка Р отношений как пересечение нечетких отношений нестрогого предпочтения экспертов  :
:
таким образом, получается новое нечеткое отношение нестрогого предпочтения. Далее с н.о.п. ассоциируется отношение строгого предпочтения  с функцией принадлежности
с функцией принадлежности  .
.

Далее определяется множество недоминируемых альтернатив  с функцией принадлежности
с функцией принадлежности

2. Строится выпуклая свертка Q отношений  , которая определяется как
, которая определяется как  . Она является новым
. Она является новым  с которым ассоциируются его отношение строгого предпочтения
с которым ассоциируются его отношение строгого предпочтения  и множество недоминируемых альтернатив
и множество недоминируемых альтернатив  . Множества
. Множества  и
и  несут дополняющую друг друга информацию о недоминируемости альтернатив.
несут дополняющую друг друга информацию о недоминируемости альтернатив.
3. Рассматривается пересечение полученных множеств  с функцией принадлежности
с функцией принадлежности  .
.
4. Выбирается та альтернатива и, для которой значение  максимально:
максимально:  .
.
Задача принятия решения с группой экспертов, характеризуемых нечетким отношением нестрого предпочтения между ними.
Можно рассмотреть задачу принятия решений с группой экспертов, характеризуемых не весовыми коэффициентами, а при помощи еще одного  заданного на множестве Е экспертов с функцией принадлежности
заданного на множестве Е экспертов с функцией принадлежности  , значения которой означают степень предпочтения эксперта по сравнению с экспертом
, значения которой означают степень предпочтения эксперта по сравнению с экспертом  .
.
Алгоритм решения задачи
1. С каждым  ассоциируются
ассоциируются  вводится обозначение
вводится обозначение  . Тем самым задается нечеткое соответствие Ф между множествами Е и
. Тем самым задается нечеткое соответствие Ф между множествами Е и 
2. Строится свертка Г в виде композиции соответствий  . Причем, результирующее отношение Г определяется как максминное произведение матриц
. Причем, результирующее отношение Г определяется как максминное произведение матриц  . То есть, получается единое результирующее отношение, полученное с учетом информации об относительной важности н.о.п.
. То есть, получается единое результирующее отношение, полученное с учетом информации об относительной важности н.о.п.  . С отношением Г ассоциируется отношение
. С отношением Г ассоциируется отношение  и множество
и множество  .
.
3. Корректируется множество  до множества U с функцией принадлежности
до множества U с функцией принадлежности  .
.
4. Выбирается та альтернатива, для которой значение функции принадлежности скорректированного нечеткого подмножества U недоминируемых альтернатив максимально.
Качественные методы принятия решений [61-64]
Качественные методы принятия решений разработаны О.И. Ларичевым и описываются в работе [64]. Методы могут использоваться в моделях линейного упорядочивания объектов на основе их векторов предпочтений. В качественных методах принятия решений используются только такие способы получения информации от экспертов и логические процедуры для построения выводов, которые, согласно данным психологических исследований, соответствуют возможностям человеческой системы переработки информации. Одним из таких способов, который может быть с успехом применен для решения неструктурированных проблем с качественными переменными - планирования научных исследований, конкурсного отбора проектов, проблем личного выбора - является метод упорядочивания многокритериальных альтернатив ЗАПРОС (замкнутые процедуры у опорных ситуаций).
Рассмотрим применение этого метода на примере ранжирования железобетонных изделий, а именно, некоторых видов тротуарных плиток, с точки зрения потребительского спроса. Предположим, что число видов изделий - три: П1 (плитка «Лепесток»), П2 (плитка «Катушка»), П3 (Плитка «Бабочка»). Выделим критерии их оценивания: внешний вид, стоимость, удобность укладки (количество альтернатив и критериев в общем случае может быть произвольным). Критериальное описание альтернативных изделий может быть сведено в таблицу:

В соответствии с критериальными оценками вербальная шкала каждого критерия сопоставляется с базовой (количественной) шкалой, при этом самая высокая оценка критерия условно принимается за единицу, следующая за ней оценивается как 2 и т.д. Например, по критерию «стоимость» базовая шкала может быть представлена в виде:

Исходя из этих данных, нам нужно сравнить векторы  , которые соответствуют П1, П2, П3.
, которые соответствуют П1, П2, П3.
1. Сформируем список векторных оценок у первой опорной ситуации  . Опорные ситуации - это векторные оценки, имеющие только лучшие или худшие значения по всем критериям (соответственно первая и вторая опорная ситуации). Список векторных оценок у опорных ситуации - подмножество векторных оценок, имеющих по всем критериям, кроме одного, те же значения, что и у данной опорной ситуации.
. Опорные ситуации - это векторные оценки, имеющие только лучшие или худшие значения по всем критериям (соответственно первая и вторая опорная ситуации). Список векторных оценок у опорных ситуации - подмножество векторных оценок, имеющих по всем критериям, кроме одного, те же значения, что и у данной опорной ситуации.  .
.
2. Сравним полученные векторные оценки первой опорной ситуации между собой. Для этого составим матрицу парных сравнений  , где n - количество векторов опорной ситуации,
, где n - количество векторов опорной ситуации,  - степень предпочтения
- степень предпочтения  оценки перед
оценки перед  . Если
. Если  , то элемент
, то элемент  предпочтительнее элемента
предпочтительнее элемента  равноценен
равноценен  предпочтительнее
предпочтительнее  при a
при a  элементы в строке и столбце не сравнены.
элементы в строке и столбце не сравнены.
В исходной матрице в некоторых ячейках уже имеются единицы, поставленные там на основе базовой шкалы (табл. 3.3). Далее в таблице приведена та же матрица, но после того, как было указано, что оценка (211) лучше, чем (121). Заметим, что сравнение (211) с (131) сделано на основе транзитивности ((211) лучше (121), а (121) лучше, чем (131) в исходной матрице). Полностью заполненная экспертами матрица приведена в таблице третьей.
Таблица 3.3

По ней становится возможным восстановить все значения элементов (табл. 3.3, четвертая матрица).
3. В соответствии с последней матрицей в табл. 3.3. упорядочим векторные оценки из списка L1: (211), (311), (121), (112), (131), (113). Если по некоторым векторам имеются равные оценки, то лицу, принимающему решение, задаются дополнительные вопросы для сравнения спорных оценок опорной ситуации.
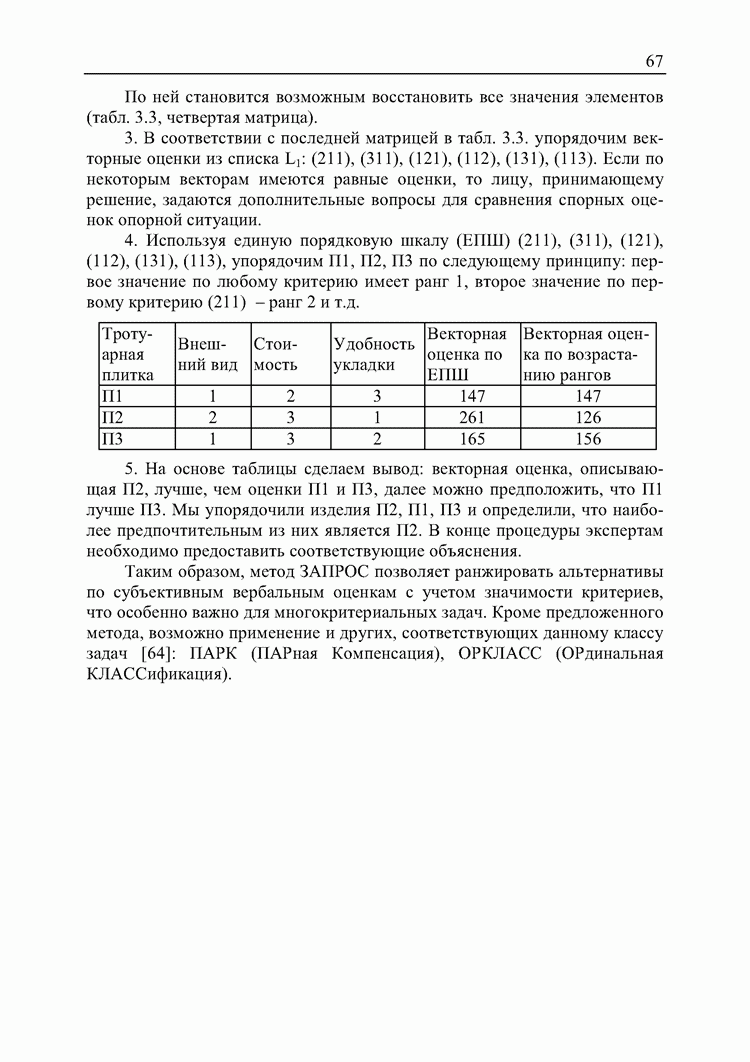
4. Используя единую порядковую шкалу (ЕПШ) (211), (311), (121), (112), (131), (113), упорядочим П1, П2, П3 по следующему принципу: первое значение по любому критерию имеет ранг 1, второе значение по первому критерию (211) - ранг 2 и т.д

5. На основе таблицы сделаем вывод: векторная оценка, описывающая П2, лучше, чем оценки П1 и П3, далее можно предположить, что П1 лучше П3. Мы упорядочили изделия П2, П1, П3 и определили, что наиболее предпочтительным из них является П2. В конце процедуры экспертам необходимо предоставить соответствующие объяснения.
Таким образом, метод ЗАПРОС позволяет ранжировать альтернативы по субъективным вербальным оценкам с учетом значимости критериев, что особенно важно для многокритериальных задач. Кроме предложенного метода, возможно применение и других, соответствующих данному классу задач [64]: ПАРК (ПАРная Компенсация), ОРКЛАСС (ОРдинальная КЛАССификация).
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
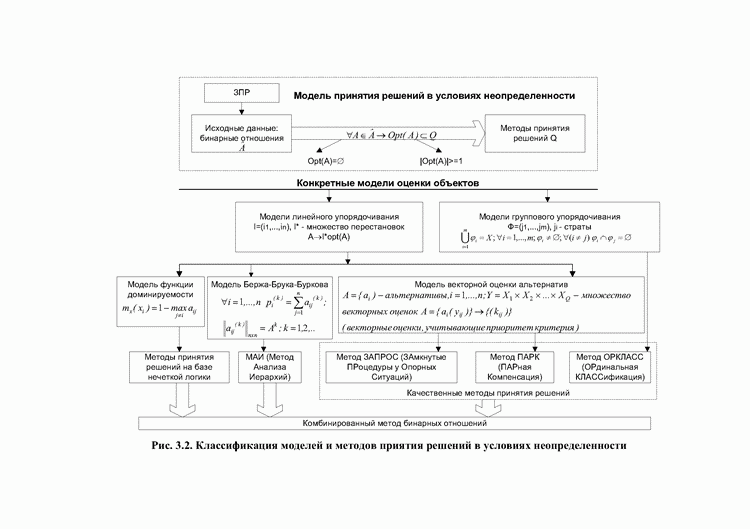
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
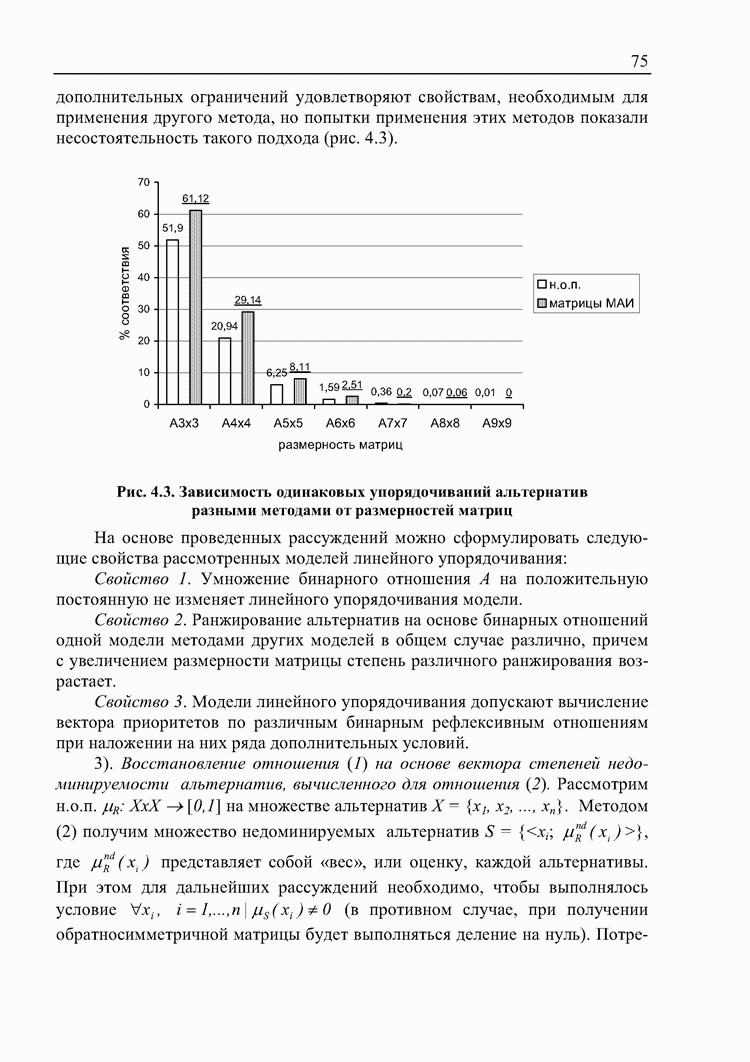
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список