| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Применение методов принятия решений для анализа количественных данных
Для сравнения результатов различных методов принятия решений с целью выявления их достоверности и объективности необходимо воспользоваться каждым из них при анализе одной и той же проблемной ситуации. В качестве такой задачи будем рассматривать задачу ранжирования объектов на основе их отношения предпочтения, сформированного ЛПР. Если при этом использовать субъективные оценки экспертов при парных сравнениях объектов, то результаты, зависящие от исходных данных каждого метода, заведомо будут различны, так как в каждом методе используется свой принцип парных сравнений объектов и количественная шкала. Поэтому в роли «эталонной» задачи может выступать только та задача, исходными данными которой являются парные сравнения объектов, основанные на их количественных характеристиках (а не на оценках экспертов).
Такой подход был реализован в [91] для иллюстрации адекватности МАИ реальному линейному упорядочиванию объектов.
В монографии рассматривается линейное упорядочивание объектов при помощи различных моделей принятия решений на основе количественных данных с целью выявления модели и метода, результаты которого наиболее точно соответствуют исходному ранжированию объектов и их количественным характеристикам.
Упорядочивание объектов на основе отношения предпочтения по одному критерию
Пусть имеет множество  объектов.
объектов.
 - количественные оценки объектов по критерию q.
- количественные оценки объектов по критерию q.
Необходимо сформировать нечеткие подмножества  соответствующие различному упорядочиванию наиболее предпочтительных по критерию q объектов различными методами ПР.
соответствующие различному упорядочиванию наиболее предпочтительных по критерию q объектов различными методами ПР.
В качестве реальных объектов и их количественных характеристик рассмотрим фактическую среднегодовую себестоимость основных видов продукции ОАО «КЗ ЖБИ» за 1998 г. (табл. 4.3). На основе моделей принятия решений необходимо в этом случае осуществить ранжирование изделий по возрастанию фактических затрат на их производство.
Таблица 4.3. Среднегодовая фактическая себестоимость ж/б продукции за 1998 г. по «КЗ ЖБИ»

Составим отношение предпочтения объектов  .
.
При этом, если w. - абсолютная характеристика (вес)  объекта, то
объекта, то  выражает степень предпочтения
выражает степень предпочтения  объекта перед
объекта перед  (табл. 4.4).
(табл. 4.4).  .
.
Так составленное отношение соответствует логике построения отношений в методе анализа иерархий (1) и в методах принятия решений при нечеткой исходной информации (2) и удовлетворяет степенной калибровке, приемлемой как для модели Бэржа-Брука-Буркова, так и модели функции доминируемости. Качественные методы принятия решений позволяют сравнивать объекты лишь по нескольким критериям; сравнение объектов на основе их предпочтения относительно какой-либо одной цели в этих методах не применяется (в этом случае будет получен простейший случай - модель спортивного типа), поэтому на их основе линейное упорядочивание объектов по одному критерию не производилось.
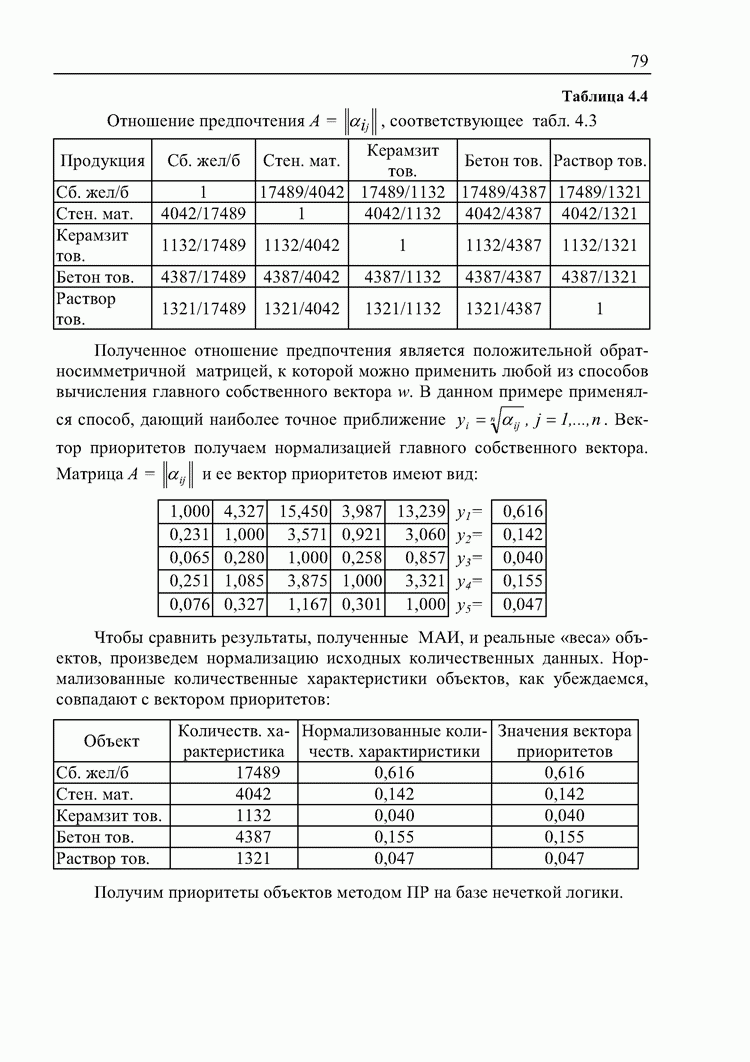
Таблица 4.4. Отношение предпочтения  соответствующее табл. 4.3
соответствующее табл. 4.3

Полученное отношение предпочтения является положительной обратносимметричной матрицей, к которой можно применить любой из способов вычисления главного собственного вектора w. В данном примере применялся способ, дающий наиболее точное приближение  . Вектор приоритетов получаем нормализацией главного собственного вектора. Матрица
. Вектор приоритетов получаем нормализацией главного собственного вектора. Матрица  и ее вектор приоритетов имеют вид:
и ее вектор приоритетов имеют вид:

Чтобы сравнить результаты, полученные МАИ, и реальные «веса» объектов, произведем нормализацию исходных количественных данных. Нормализованные количественные характеристики объектов, как убеждаемся, совпадают с вектором приоритетов:

Получим приоритеты объектов методом ПР на базе нечеткой логики.
Исходное бинарное отношение нестрогого предпочтения имеет вид:

Максимальный элемент отношения  . В дальнейшем это значение будет использовано как «единица» (наибольшее значение) отношения.
. В дальнейшем это значение будет использовано как «единица» (наибольшее значение) отношения.
Бинарное отношение строгого предпочтения, ассоциированное с  :
:

Множество недоминируемых альтернатив строится в данном случае по правилу  .
.
Например,  .
.
В итоге получим вектор степеней недоминируемости альтернатив

Нормализованные значения  не совпадают с вектором приоритетов, полученным нормализацией главного собственного вектора матрицы А, но предоставляют такое же ранжирование альтернатив. Несовпадение значений объясняется тем, что МАИ определяет в результате исходный «вес» каждого объекта, а метод (2) - степень недоминируемости. Действительно, фактическая себестоимость сборного железобетона не доминируется никакими другими изделиями со степенью недоминируемости
не совпадают с вектором приоритетов, полученным нормализацией главного собственного вектора матрицы А, но предоставляют такое же ранжирование альтернатив. Несовпадение значений объясняется тем, что МАИ определяет в результате исходный «вес» каждого объекта, а метод (2) - степень недоминируемости. Действительно, фактическая себестоимость сборного железобетона не доминируется никакими другими изделиями со степенью недоминируемости  , которая семантически выражает то, что объект может доминироваться другими, но со степенью доминирования не выше, чем
, которая семантически выражает то, что объект может доминироваться другими, но со степенью доминирования не выше, чем  Для стеновых
Для стеновых
материалов  , т. е. степень доминируемости
, т. е. степень доминируемости

(по бинарному отношению нестрогого предпочтения в этом легко убедиться).
Сравним полученные приоритеты (степень недоминируемости в методе (2) можно рассматривать как приоритет объекта, так как на основе вектора степеней недоминируемости делается вывод о ранжировании объектов) (табл. 4.5).
Таблица 4.5. Приоритеты объектов, полученные разными методами принятия решений

Полученные нормализованные приоритеты объектов каждого метода можно рассматривать как нечеткие подмножества  множества X, соответствующие методам (1) и (2) соответственно, где
множества X, соответствующие методам (1) и (2) соответственно, где

Нормализованные количественные характеристики объектов будем интерпретировать как нечеткое подмножество  .
.
В этом случае становится возможным определить степень равенства нечетких подмножеств  «эталонному» множеству
«эталонному» множеству  . Степень равенства определим различными способами.
. Степень равенства определим различными способами.
Степень равенства двух нечетких подмножеств, рассматриваемая А.Н. Мелиховым [69], определяется по формуле

Так как  , то
, то  (сравниваемые множества нечетко равны).
(сравниваемые множества нечетко равны).
Так как  , то сравниваемые множества нечетко не равны
, то сравниваемые множества нечетко не равны  Степень равенства
Степень равенства  , что свидетельствует о
, что свидетельствует о
предпочтительности результатов метода (1), рассматриваемых как количественные оценки важности объектов.
Хэммингово расстояние.

В этом случае 

Евклидово расстояние

При этом 

Таким образом, приоритеты, получаемые в МАИ, практически совпадают с «эталонными» значениями объектов по выбранному критерию. Метод (2) дает близкие значения к «эталону», но менее предпочтительные с точки зрения равенства исходным количественным характеристикам.
В отличие от разделе 4.1., результаты двух рассмотренных методов для количественных данных предоставляют как одинаковое ранжирование альтернатив, так и близость результатов к исходным данным. Такое достоверное упорядочивание методом (2) количественных данных и расхождение его результатов с результатами метода (1) в разделе 4.1. может быть объяснено несогласованностью произвольно выбранных матриц. Чем согласованнее матрица (1), тем ближе будут результаты методов (1) и (2) по ее обработке. Такое утверждение иллюстрирует следующий вычислительный эксперимент: случайным образом формируются 50 выборок по 100 обратносимметричных матриц  каждая (все элементы матрицы - случайные числа, соответствующие шкале МАИ), причем главное собственное значение каждой матрицы отличается от 4 (главного собственного значения полностью согласованной матрицы
каждая (все элементы матрицы - случайные числа, соответствующие шкале МАИ), причем главное собственное значение каждой матрицы отличается от 4 (главного собственного значения полностью согласованной матрицы  на
на  . С уменьшением
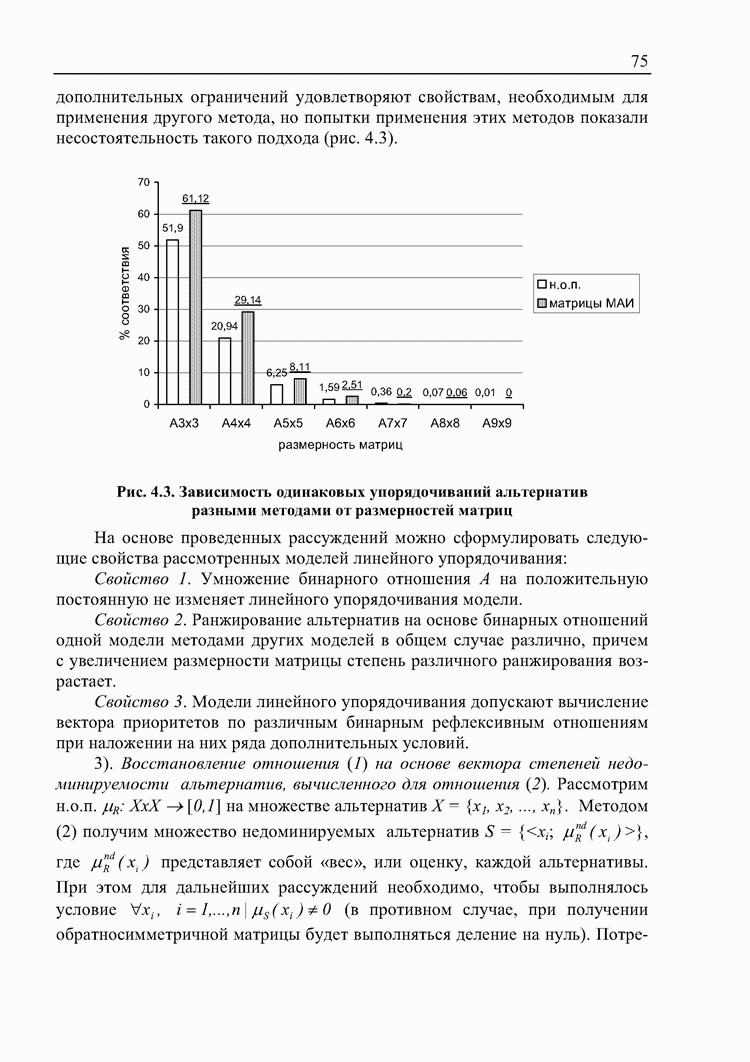
. С уменьшением  процент одинакового упорядочивания альтернатив различными методами возрастает (табл. 4.6, рис. 4.4).
процент одинакового упорядочивания альтернатив различными методами возрастает (табл. 4.6, рис. 4.4).
Таблица 4.6. Результаты упорядочивания альтернатив методами (1) и (2) по обратносимметричным матрицам  для которых
для которых 


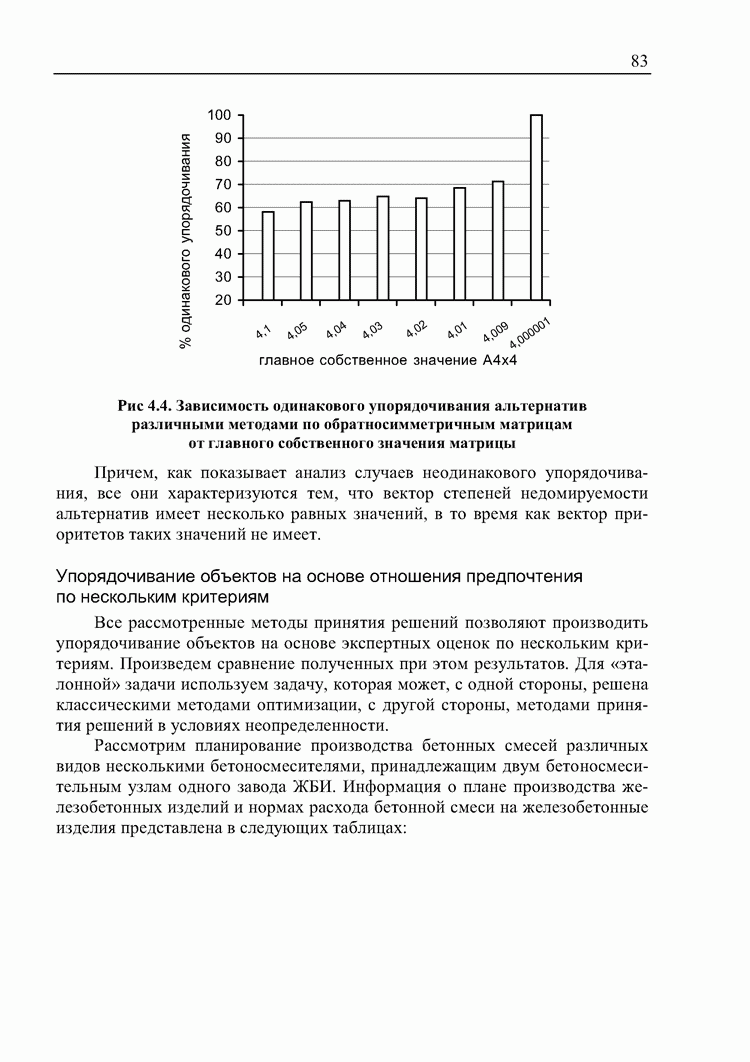
Рис 4.4. Зависимость одинакового упорядочивания альтернатив различными методами по обратносимметричным матрицам от главного собственного значения матрицы
Причем, как показывает анализ случаев неодинакового упорядочивания, все они характеризуются тем, что вектор степеней недомируемости альтернатив имеет несколько равных значений, в то время как вектор приоритетов таких значений не имеет.
Упорядочивание объектов на основе отношения предпочтения по нескольким критериям
Все рассмотренные методы принятия решений позволяют производить упорядочивание объектов на основе экспертных оценок по нескольким критериям. Произведем сравнение полученных при этом результатов. Для «эталонной» задачи используем задачу, которая может, с одной стороны, решена классическими методами оптимизации, с другой стороны, методами принятия решений в условиях неопределенности.
Рассмотрим планирование производства бетонных смесей различных видов несколькими бетоносмесителями, принадлежащим двум бетоносмесительным узлам одного завода ЖБИ. Информация о плане производства железобетонных изделий и нормах расхода бетонной смеси на железобетонные изделия представлена в следующих таблицах:
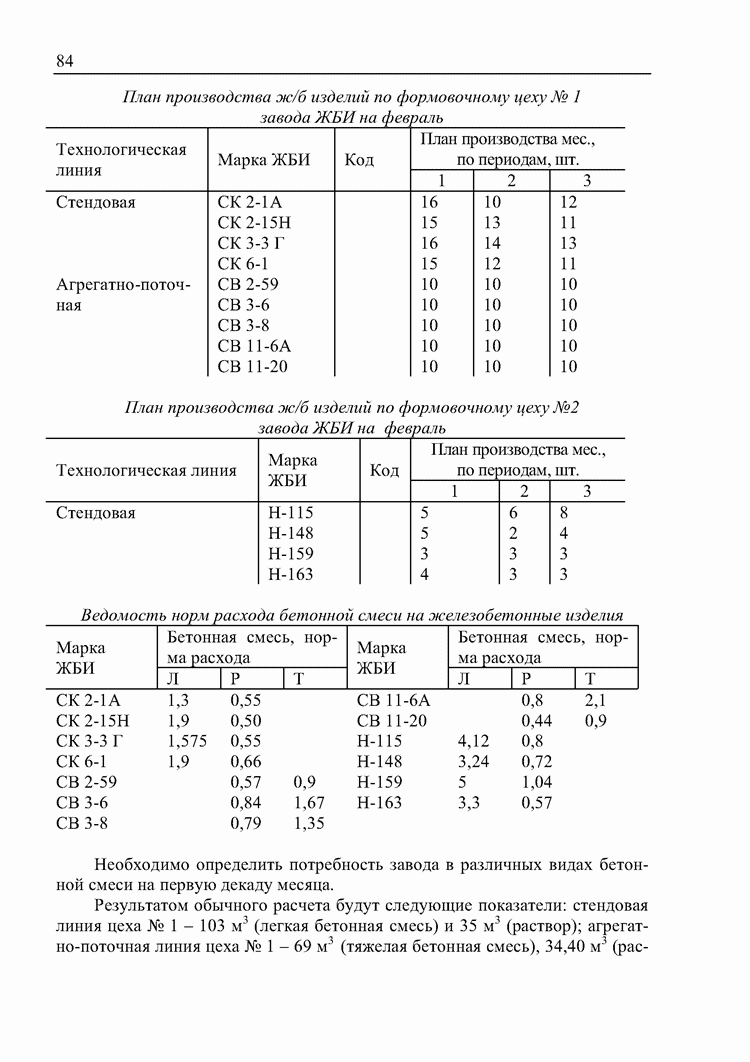
План производства ж/б изделий по формовочному цеху № 1 завода ЖБИ на февраль

План производства ж/б изделий по формовочному цеху № 2 завода ЖБИ на февраль

Ведомость норм расхода бетонной смеси на железобетонные изделия

Необходимо определить потребность завода в различных видах бетонной смеси на первую декаду месяца.
Результатом обычного расчета будут следующие показатели: стендовая линия цеха 103 м3 (легкая бетонная смесь) и 35 м3 (раствор); агрегатнопоточная линия цеха № 1 - 69 м3 (тяжелая бетонная смесь), 34,40 м3 (раствор);
стендовая линия цеха № 2 - 65 м3 (легкая бетонная смесь), 13 м3 (раствор). Всего необходимо выпустить легкой бетонной смеси  раствора 82,4 м3, тяжелой бетонной смеси - 69 м3.
раствора 82,4 м3, тяжелой бетонной смеси - 69 м3.
Применяя МАИ к поставленной задаче, проблему можно представить в виде четырехуровневой иерархии:

На каждом из уровней формируются матрицы парных сравнений объектов по отношению к каждому из объектов вышестоящего уровня, как это делалось для задачи ранжирования объектов по одному критерию.
По каждой из полученных матриц вычисляется вектор приоритетов. Как было показано в первом примере, нормализованный главный собственный вектор каждой из матриц будет состоять из нормализованных количественных значений объектов. Для вычисления обобщенных приоритетов объектов применяется процедура взвешивания, в процессе которой матрица весов видов бетонной смеси относительно изделий умножается на вектор приоритетов изделий: матрица

умножается на вектор-столбец весов изделий

В результате получим обобщенные (глобальные) веса видов бетонной смеси:
Вид бетонной смеси Приоритет МАИ Нормализованные количеств. оценки

Ранжирование объектов нижнего уровня иерархии оказалось таким же, как и при обычном способе вычисления.
Применяя к вычислению приоритетов объектов метод принятия решений при нечеткой информации, будем рассматривать проблему как задачу с несколькими заданными бинарными отношениями количественного превосходства видов бетонной смеси  по отношению к изделиям и еще одним бинарным отношением N количественного превосходства изделий.
по отношению к изделиям и еще одним бинарным отношением N количественного превосходства изделий.
Для каждого отношения  вычисляем функцию принадлежности
вычисляем функцию принадлежности  (которую будем рассматривать как нормализованные исходные количественные значения), по которым формируем матрицу Ф.
(которую будем рассматривать как нормализованные исходные количественные значения), по которым формируем матрицу Ф.
Свертку Г определяем как максминное произведение матриц  .
.

Множество недоминируемых альтернатив  определяется вектором:
определяется вектором:  , а скорректированное множество
, а скорректированное множество  которое представляет ранжирование альтернатив, не соответствующее действительному.
которое представляет ранжирование альтернатив, не соответствующее действительному.
Можно проанализировать задачу и методом принятия решений при нечеткой исходной информации в случае, когда критерии характеризуются весовыми коэффициентами. Составим отношения количественного превосходства изделий по группам, которые соответствуют используемым материалам. В первую группу включим изделия:  для изготовления которых используется легкая бетонная смесь и раствор. Для каждого из них составим отношение количественного превосходства видов используемой бетонной смеси. В качестве весов изделий будем использовать их нормализованные количества:
для изготовления которых используется легкая бетонная смесь и раствор. Для каждого из них составим отношение количественного превосходства видов используемой бетонной смеси. В качестве весов изделий будем использовать их нормализованные количества:  .
.
Свертки Р и Q отношений  определяются матрицами:
определяются матрицами:

Множества  определяются векторами:
определяются векторами:
Легкая бет. смесь Раствор

Откуда  .
.
Во вторую группу включим изделия: СВ 2-59, СВ 3-6, СВ 3-8, СВ 11-6, СВ 11-20, для изготовления которых используется тяжелая бетонная смесь
и раствор. В этом случае  . Произведя аналогичные вычисления, как и для первой группы изделий, получим:
. Произведя аналогичные вычисления, как и для первой группы изделий, получим:  . Обобщая полученные результаты, получим: легкая бетонная смесь - 22,335; раствор - 2,843; тяжелая бетонная смесь - 2,625. После нормализации: легкая бетонная смесь - 0,803; раствор - 0,102; тяжелая бетонная смесь - 0,094.
. Обобщая полученные результаты, получим: легкая бетонная смесь - 22,335; раствор - 2,843; тяжелая бетонная смесь - 2,625. После нормализации: легкая бетонная смесь - 0,803; раствор - 0,102; тяжелая бетонная смесь - 0,094.
При таком способе вычисления линейное упорядочивание объектов соответствует реальному.
Применить качественные методы принятия решений для анализа количественных данных не представляется возможным по целому ряду причин.
Например, при использовании в этих целях метода ЗАПРОС задача будет поставлена следующим образом:
Дано:  - множество критериев (в данной задаче изделий).
- множество критериев (в данной задаче изделий).  .
.
 - число оценок по критерию q для каждого объекта (вида бетонной смеси),
- число оценок по критерию q для каждого объекта (вида бетонной смеси),  .
.
 - шкала критерия q. Например
- шкала критерия q. Например 
 - множество векторных оценок
- множество векторных оценок 
В случае рассмотренной задачи  .
.
В методе ЗАПРОС ЛПР производит сравнение векторных оценок из опорных ситуаций; такие векторные оценки будут являться подмножеством множества Y. Вначале формируется список оценок у первой опорной ситуации  состоящий из всевозможных векторных оценок альтернатив, среди которых все, кроме одной, наилучшие. То есть, эксперту необходимо будет сравнивать векторные оценки, что намного психологически труднее, как показывает наш опыт применения данного метода, чем сравнивать непосредственно объекты (при таком сравнении эксперту приходится неявно еще и сравнивать сами критерии).
состоящий из всевозможных векторных оценок альтернатив, среди которых все, кроме одной, наилучшие. То есть, эксперту необходимо будет сравнивать векторные оценки, что намного психологически труднее, как показывает наш опыт применения данного метода, чем сравнивать непосредственно объекты (при таком сравнении эксперту приходится неявно еще и сравнивать сами критерии).
Кроме того, метод ориентирован на качественные оценки и качественные операции сравнения, которые к формальным количественным критериям могут и не быть правильно применены.
| << Предыдущий параграф | Следующий параграф >> |
- Список используемых сокращений
- Введение
- 1. Основные понятия теории принятия решений
- 1.1. Системы поддержки принятия решений и их место в информационно-управляющих системах
- 1.2. Компьютерная поддержка принятия решений
- 1.3. Участники процесса принятия решений
- 1.4. Цели и ресурсы
- 1.5. Альтернативы и критерии
- 1.6. Риски и неопределенности
- 1.7. Экспертное оценивание
- 2. Математический аппарат, используемый в методах принятия решений
- 2.2. Иерархии и приоритеты
- 2.3. Комплекты. Нечеткие множества. Нечеткие отношения
- Нечеткие высказывания и операции над ними
- Нечеткие логические формулы и их свойства
- Нечеткие предикаты и кванторы
- Операции над нечеткими множествами. Нечеткое включение и нечеткое равенство множеств
- Теоретико-множественные операции
- Система аксиом
- Нечеткие соответствия и отношения
- 2.4. Полные алгебраические решетки
- 3. Модели и методы принятия решений, основанные на парном сравнении альтернатив
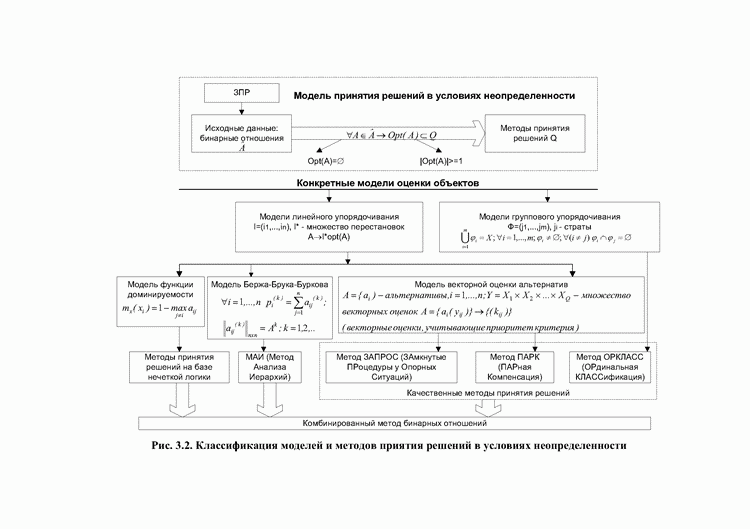
- 3.1. Классификация моделей и методов принятия решений
- 3.2. Модели линейного упорядочивания
- Метод анализа иерархий [93, 94]
- 4. Сравнительное исследование методов принятия решений в условиях неопределенности
- 4.1. Сравнение результатов ранжирования альтернатив различными
- 4.2. Применение методов принятия решений для анализа количественных данных
- 4.3. Оценка предпочтительности методов принятия решений с точки зрения участников процесса принятия решений
- 5. Комбинированный алгоритм поддержки принятия решений
- 5.1. Гомоморфизм шкал МАИ и метода принятия решений при нечеткой исходной информации
- 5.2. Отражение структуры сложной распределенной системы в методах принятия решений для этой системы
- 5.3. Выявление несогласованности суждений экспертов
- 5.4. Разработка СППР «Выбор» на основе комбинированного метода бинарных отношений
- Заключение
- Библиографический список