| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. Счетные множества
Множества, равномощные множеству всех натуральных чисел, называют счетными, остальные же бесконечные множества — несчетными. Следовательно, счетное множество — это такое бесконечное множество, все
элементы которого можно перенумеровать с помощью натуральных чисел таким образом, чтобы каждому элементу множества соответствовал определенный номер и чтобы каждый номер соответствовал определенному и единственному элементу множества. Другими словами, элементы счетного множества можно расположить в виде бесконечной последовательности

по порядковым номерам (индексам). Обратно, множество всех членов любой данной бесконечной последовательности (с различными членами) является счетным.
Очевидно, что часть счетного множества, если она не является конечным множеством, будет счетным множеством. Это следует из того, что элементы любой части множества (1) можно расположить в виде последовательности в порядке возрастания индексов. Например, множества всех нечетных чисел, всех простых чисел, всех чисел, являющихся квадратами натуральных чисел, — счетны. О существовании взаимно однозначного соответствия между натуральными числами и их квадратами знал уже Галилей в первой половине XVII века.
Если плоскость разбить на прилегающие один к другому квадраты, то множество этих квадратов будет счетно. Перенумеровать все эти квадраты можно следующим образом (рис. 1):

Рис. 1
Можно также доказать, что, разбив трехмерное пространство на равные кубы, мы получим счетное множество этих кубов. И в этом случае можно бы поочередно обходить кубы по ломаной, соединяющей центры смежных кубов.
Непустое множество мы называем конечным, если число его элементов может быть выражено каким-либо натуральным числом. Отсюда следует, что если данное множество  бесконечно, т. е. не является ни пустым, ни конечным, то для любого натурального числа
бесконечно, т. е. не является ни пустым, ни конечным, то для любого натурального числа  существует
существует  различных элементов, каждый из которых принадлежит
различных элементов, каждый из которых принадлежит  Доказать это можно по индукции. Указанное предложение справедливо для числа
Доказать это можно по индукции. Указанное предложение справедливо для числа  так как, поскольку множество
так как, поскольку множество  не пусто, в нем должен существовать какой-нибудь элемент
не пусто, в нем должен существовать какой-нибудь элемент  Допустим теперь, что наше утверждение справедливо для некоторого натурального числа
Допустим теперь, что наше утверждение справедливо для некоторого натурального числа  и что, следовательно, существует
и что, следовательно, существует  различных элементов
различных элементов  каждый из которых принадлежит множеству
каждый из которых принадлежит множеству  Если бы, кроме этих
Если бы, кроме этих  элементов, множество
элементов, множество  не содержало никаких других элементов, то оно имело бы только
не содержало никаких других элементов, то оно имело бы только  элементов и было бы конечно, что противоречит условию. Следовательно, в множестве
элементов и было бы конечно, что противоречит условию. Следовательно, в множестве  имеется какой-то элемент
имеется какой-то элемент  отличный от каждого из элементов
отличный от каждого из элементов  Мы имеем,
Мы имеем,
следовательно,  различных элементов, каждый из которых принадлежит множеству
различных элементов, каждый из которых принадлежит множеству  Утверждение иаше справедливо, следовательно, для числа
Утверждение иаше справедливо, следовательно, для числа  Отсюда по индукции заключаем о справедливости утверждения для любого натурального числа
Отсюда по индукции заключаем о справедливости утверждения для любого натурального числа 
Казалось бы, что подобное рассуждение приводит к заключению, что каждое бесконечное множество содержит счетное подмножество (счетную часть). Имея  разных элементов
разных элементов  множества
множества  мы можем извлечь из него новый элемент
мы можем извлечь из него новый элемент  отличный от каждого из элементов
отличный от каждого из элементов  что приводит к бесконечному ряду
что приводит к бесконечному ряду  различных элементов множества
различных элементов множества  т. е. к некоторому его счетному подмножеству.
т. е. к некоторому его счетному подмножеству.
Но этому рассуждению можно предъявить следующий упрек. Образуя последовательность  различных элементов множества
различных элементов множества  мы вынуждены
мы вынуждены  раз произвести выбор. Никто не сомневается в возможности осуществления любого конечного числа выборов. Но есть математики, которые считают, что нельзя производить бесконечно много выборов без указания закона или правила осуществления этих выборов (первым из таких математиков был Дж. Пеано). Без использования так называемой аксиомы выбора (сформулированной Э. Цермело) мы не сможем доказать ни то, что любое бесконечное множество содержит счетную часть, ни то, что каждое бесконечное множество равномощно некоторой своей правильной части.
раз произвести выбор. Никто не сомневается в возможности осуществления любого конечного числа выборов. Но есть математики, которые считают, что нельзя производить бесконечно много выборов без указания закона или правила осуществления этих выборов (первым из таких математиков был Дж. Пеано). Без использования так называемой аксиомы выбора (сформулированной Э. Цермело) мы не сможем доказать ни то, что любое бесконечное множество содержит счетную часть, ни то, что каждое бесконечное множество равномощно некоторой своей правильной части.
То, что каждое счетное множество равномощно некоторой своей правильной части, очевидно, так как множество (1) равномощио множеству, которое мы получим, удалив из него первый член  Но можно также доказать, не прибегая к аксиоме выбора, что каждое множество, равномощное некоторой своей правильной части, содержит счетное подмножество. Вот набросок этого доказательства. Допустим, что множество
Но можно также доказать, не прибегая к аксиоме выбора, что каждое множество, равномощное некоторой своей правильной части, содержит счетное подмножество. Вот набросок этого доказательства. Допустим, что множество  равномощно своей правильной части Т. Каждому элементу а множества
равномощно своей правильной части Т. Каждому элементу а множества  соответствует определенный элемент
соответствует определенный элемент  множества Т таким образом, что разным элементам множества
множества Т таким образом, что разным элементам множества  соответствуют различные элементы множества Т. Поскольку Т является правильной частью множества
соответствуют различные элементы множества Т. Поскольку Т является правильной частью множества  существует элемент а множества
существует элемент а множества  не принадлежащий Т. Теперь можно легко доказать, что члены бесконечной последовательности
не принадлежащий Т. Теперь можно легко доказать, что члены бесконечной последовательности

являются различными элементами множества  и, следовательно, образуют его счетное подмножество.
и, следовательно, образуют его счетное подмножество.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ ИЗДАТЕЛЬСТВА
- От редакции польского издания
- ГЛАВА I. О МНОЖЕСТВАХ И ИХ СВОЙСТВАХ
- 2. Равенство множеств
- 4. Пустое множество
- 5. Конечные множества
- 6. Равночисленные множества
- 7. Взаимно однозначное соответствие
- 8. Равномощные множества
- 9. Счетные множества
- 10. Сумма множеств
- 11. Несчетные множества
- 12. Континуум-гипотеза
- 13. Непересекающиеся множества
- 14. Сравнение мощностей бесконечных множеств
- 15. Аксиома выбора
- 16. Алгебра множеств
- 17. Упорядоченные множества
- 18. Подобные упорядоченные множества
- 19. Плотные упорядоченные множества. Сечения. Щели
- 20. Заполнение щелей
- 21. Вполне упорядоченные множества
- 22. Принцип трансфинитной индукции
- 23. Принцип математической индукции
- 24. Функции
- 25. Декартово произведение
- 26. Метрические пространства
- 27. Евклидовы пространства
- 28. Борелевские множества
- 29. Открытые и замкнутые множества
- 30. Производное множество и замыкание множества
- 31. Топология
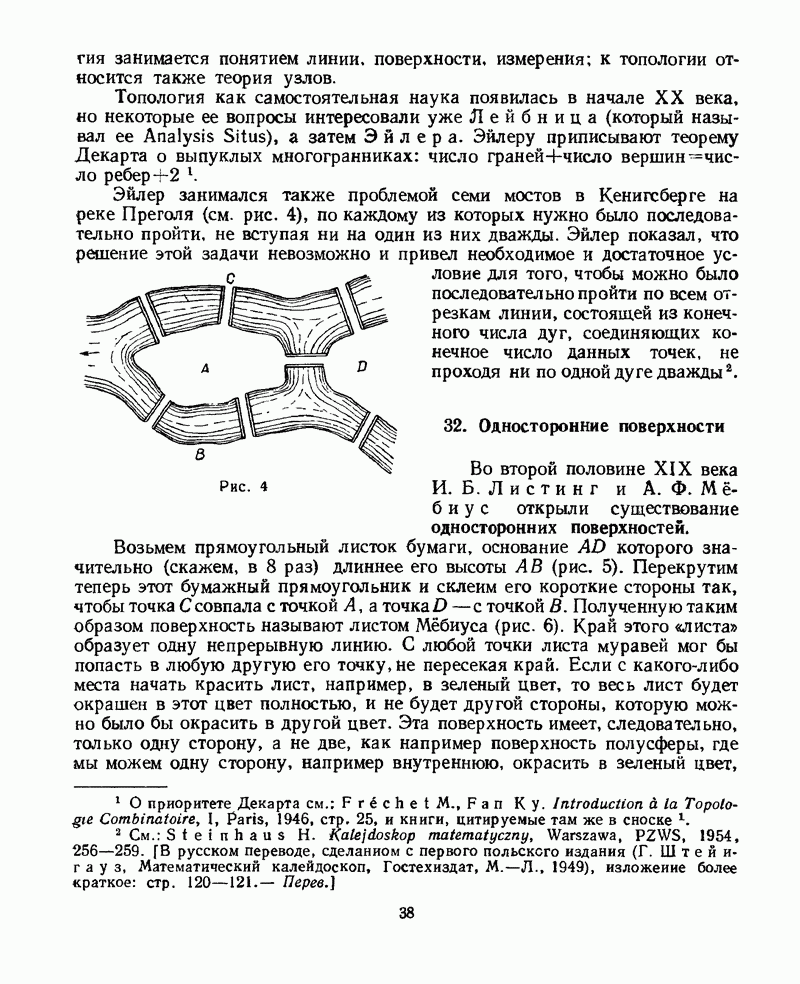
- 32. Односторонние поверхности
- 33. Проблема четырех красок
- ГЛАВА II. О КОНГРУЭНТНОСТИ МНОЖЕСТВ. КОНГРУЭНТНОСТЬ МНОЖЕСТВ ПРИ КОНЕЧНОМ РАЗБИЕНИИ
- 2. Движения множеств
- 3. Конгруэнтность множеств при конечном разбиении
- 4. Преобразования сжатия