| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА II. О КОНГРУЭНТНОСТИ МНОЖЕСТВ. КОНГРУЭНТНОСТЬ МНОЖЕСТВ ПРИ КОНЕЧНОМ РАЗБИЕНИИ
1. Конгруэнтность множеств
Конгруэнтность геометрических фигур хорошо известна из элементарной геометрии. Две геометрические фигуры, т. е. два множества точек, лежащих на прямой, на плоскости или в пространстве, конгруэнтны между собой, если они могут быть получены одно из другого путем переноса, поворота или зеркального отражения. Чтобы показать, что два множества А и В конгруэнтны, пишут  Необходимым и достаточным условием конгруэнтности множеств А и В является существование между их точками взаимно однозначного соответствия, сохраняющего расстояния, т. е. такого, что если
Необходимым и достаточным условием конгруэнтности множеств А и В является существование между их точками взаимно однозначного соответствия, сохраняющего расстояния, т. е. такого, что если  являются двумя произвольными точками множества А, а
являются двумя произвольными точками множества А, а  — соответствующими им точками множества В, то расстояние между точками
— соответствующими им точками множества В, то расстояние между точками  равно расстоянию между точками
равно расстоянию между точками  и
и
Преобразования множеств, сохраняющие расстояния, называют изометрическими. Вместо того, чтобы говорить конгруэнтные множества, можно сказать изометрические множества. Понятие изометрии может применяться не только к множествам точек в пространстве, одного или многих измерений, но и вообще к множествам в так называемых метрических пространствах, для которых определено расстояние между двумя любыми их точками. Существуют множества точек даже на прямой, конгруэнтные некоторому
своему собственному подмножеству (т. е. подмножеству, не совпадающему со всем множеством). Таким множеством является, например, множество всех точек полупрямой.
Множество точек называют мономорфным, если оно не конгруэнтно ни одному своему собственному подмножеству Множество точек называют ограниченным, если существует число, большее, чем расстояние между любыми двумя точками этого множества. Докажем, что имеет место
Теорема 1. Каждое ограниченное множество точек прямой мономорфно.
Доказательство. На прямой зеркальное отражение какого-либо множества относительно данной точки (как центра симметрии) совпадает с поворотом этого множества на 180° около той же точки Покажем сперва, что при повороте прямой на 180° вокруг какой-нибудь ее точки ни одно множество точек не может отобразиться в свое собственное подмножество. Допустим, что при таком повороте множество  точек прямой отображается в свое собственное подмножество
точек прямой отображается в свое собственное подмножество  . Пусть х — произвольная точка множества Е. При повороте она, следовательно, отображается в некоторую точку х множества
. Пусть х — произвольная точка множества Е. При повороте она, следовательно, отображается в некоторую точку х множества  . Очевидно также, что при этом повороте точка х (которая принадлежит
. Очевидно также, что при этом повороте точка х (которая принадлежит  , а следовательно, и Е) отображается в точку
, а следовательно, и Е) отображается в точку  Отсюда следует, что каждая точка множества Е принадлежит
Отсюда следует, что каждая точка множества Е принадлежит  . а это противоречит предположению о том, что
. а это противоречит предположению о том, что  является собственным подмножеством Е.
является собственным подмножеством Е.
Обозначим теперь для произвольного множества Е точек прямой и для произвольного данного Действительного числа а через  сдвиг множества
сдвиг множества  на длину а вдоль нашей прямой.
на длину а вдоль нашей прямой.  является, таким образом, множеством всех действительных чисел х, где х — точка множества Е. Очевидно, что если
является, таким образом, множеством всех действительных чисел х, где х — точка множества Е. Очевидно, что если  то
то  и что для каждого действительного числа
и что для каждого действительного числа 
Допустим, что множество  точек прямой ограничено. Тогда существует положительное (конечное) число
точек прямой ограничено. Тогда существует положительное (конечное) число  такое, что для любой пары
такое, что для любой пары  точек множества Е расстояние между
точек множества Е расстояние между  меньше
меньше  Если при сдвиге на длину
Если при сдвиге на длину  множество Е отображается на свою часть, или
множество Е отображается на свою часть, или  (выражение
(выражение  означает, что множество А является частью множества В), то мы имеем также
означает, что множество А является частью множества В), то мы имеем также  и, вообще,
и, вообще,  при
при  Если
Если  есть точка множества Е, то для любого натурального числа
есть точка множества Е, то для любого натурального числа  является точкой множества
является точкой множества  и, следовательно, также точкой множества Е Поскольку расстояние между точками
и, следовательно, также точкой множества Е Поскольку расстояние между точками  равно
равно  , то абсолютна» величина числа
, то абсолютна» величина числа  должна быть
должна быть  при
при  , что при
, что при  невозможно. Следовательно ограниченное множество точек прямой ни при каком сдвиге (на длину, отличную от нуля) не может отобразиться на свою правильную часть.
невозможно. Следовательно ограниченное множество точек прямой ни при каком сдвиге (на длину, отличную от нуля) не может отобразиться на свою правильную часть.
Теорема 1 доказана. Отметим, что для ограниченных множеств точек на плоскости аналогичное утверждение не имеет места. Для этого случая справедлива
Теорема 2. Существует ограниченное множество точек на плоскости, конгруэнтное некоторой своей правильной части.
Доказательство. Пусть а обозначает какой-либо угол, несоизмеримый с прямым углом. Возьмем произвольный отрезок прямой и повернем его вокруг одного конца на угол а в данном направлении. Будем затем поворачивать этот отрезок в том же направлении на углы  Мы получим таким образом бесконечную последовательность отрезков
Мы получим таким образом бесконечную последовательность отрезков  с общей точкой О. Если удалить точку О, то множество наших отрезков будет ограниченным множеством точек плоскости, конгруэнтным (при повороте на угол а) своей правильной части, а именно множество всех точек отрезков
с общей точкой О. Если удалить точку О, то множество наших отрезков будет ограниченным множеством точек плоскости, конгруэнтным (при повороте на угол а) своей правильной части, а именно множество всех точек отрезков  без точки О конгруэнтно множеству всех точек отрезков
без точки О конгруэнтно множеству всех точек отрезков  (также без точки О).
(также без точки О).
Отметим, что два множества, каждое  которых конгруэнтно части другого, могут быть не конгруэнтны между собой. Пусть, например, А есть множество всех точек прямой с неотрицательными абсциссами,
которых конгруэнтно части другого, могут быть не конгруэнтны между собой. Пусть, например, А есть множество всех точек прямой с неотрицательными абсциссами,  множество, которое мы получим из А, добавив к нему точку с абсциссой —1. Множество А есть часть множества В, а множество В при сдвиге вдоль прямой на длину 1 конгруэнтно части множества А. Однако множества
множество, которое мы получим из А, добавив к нему точку с абсциссой —1. Множество А есть часть множества В, а множество В при сдвиге вдоль прямой на длину 1 конгруэнтно части множества А. Однако множества  не конгруэнтны между собой, так как для любой точки
не конгруэнтны между собой, так как для любой точки  множества А существует другая точка этого множества, расстояние которой от точки
множества А существует другая точка этого множества, расстояние которой от точки  меньше -у, точка же множества В с абсциссой —1 таким свойством не обладает.
меньше -у, точка же множества В с абсциссой —1 таким свойством не обладает.
В связи с теоремой 1 отметим, что существуют множества (конечно, неограниченные) точек прямой, которые конгруэнтны множеству, образуемому из них удалением некоторой единственной точки. Таким является, например, множество всех точек прямой с абсциссами, равными натуральным числам, которое конгруэнтно множеству, образованному из него удалением точки с абсциссой 1.
Имеет место
Теорема 3. Всякое множество  точек прямой имеет не более одной точки
точек прямой имеет не более одной точки  такой, что по ее удалении из множества
такой, что по ее удалении из множества  получается множество, конгруэнтное
получается множество, конгруэнтное 
Доказательство. Допустим, что некоторое множество  точек прямой имеет две различные точки
точек прямой имеет две различные точки  и
и  такие, что по удалении из множества
такие, что по удалении из множества  какой-нибудь из них мы получим множество, конгруэнтное
какой-нибудь из них мы получим множество, конгруэнтное  Пусть
Пусть  множество, образованное удалением из множества
множество, образованное удалением из множества  точки
точки  множество, образованное удалением из множества
множество, образованное удалением из множества  точки
точки  Допустим, что множество
Допустим, что множество  конгруэнтно
конгруэнтно  при повороте прямой на 180° около некоторой ее точки, и пусть при этом повороте точка
при повороте прямой на 180° около некоторой ее точки, и пусть при этом повороте точка  отображается в точку
отображается в точку  . Поскольку точка
. Поскольку точка  принадлежит
принадлежит  точка
точка  будет принадлежать
будет принадлежать  и тем более,
и тем более,  Но при этом же повороте точка р, очевидно, отображается в точку
Но при этом же повороте точка р, очевидно, отображается в точку
р, а множество  отображается в множество
отображается в множество  Точка
Точка  принадлежала бы тогда множеству
принадлежала бы тогда множеству  что невозможно.
что невозможно.
Следовательно, множество  не может быть конгруэнтно множеству
не может быть конгруэнтно множеству  при повороте, и аналогично множество
при повороте, и аналогично множество  не может быть конгруэнтно множеству
не может быть конгруэнтно множеству  при повороте. Следовательно, множества
при повороте. Следовательно, множества  конгруэнтны множеству
конгруэнтны множеству  при сдвиге, иначе говоря, существуют действительные числа а и
при сдвиге, иначе говоря, существуют действительные числа а и  такие, что
такие, что 
Так как  то
то  принадлежит множеству
принадлежит множеству  и поэтому
и поэтому  принадлежит множеству
принадлежит множеству  Так как
Так как  то
то  поэтому
поэтому  и, следовательно,
и, следовательно,  принадлежит множеству
принадлежит множеству  откуда следует, что
откуда следует, что  принадлежит множеству
принадлежит множеству  из этого, в свою очередь, что
из этого, в свою очередь, что  принадлежит множеству
принадлежит множеству  и тем более множеству
и тем более множеству  следовательно,
следовательно,  принадлежит множеству
принадлежит множеству  что невозможно.
что невозможно.
Теорема 3 таким образом доказана. Как легкое следствие из нее получается
Теорема 4. Во всяком непустом множестве  точек прямой, существует точка
точек прямой, существует точка  , после удаления которой из множества
, после удаления которой из множества  получают множество, не конгруэнтное
получают множество, не конгруэнтное 
Доказательство. Теорема 4, очевидно, справедлива для множеств, состоящих из одной только точки. Если же множество  содержит по меньшей мере две разные точки
содержит по меньшей мере две разные точки  то, удаляя
то, удаляя  или
или  из множества
из множества  мы получим два множества, которые по теореме 3 не могут быть оба конгруэнтны
мы получим два множества, которые по теореме 3 не могут быть оба конгруэнтны 
Возникает вопрос, сохраняют ли силу теоремы  для множеств точек на плоскости и для множеств точек в трехмерном пространстве.
для множеств точек на плоскости и для множеств точек в трехмерном пространстве.
Э. Штраус (Е. Q. Straus) доказал» что теорема 3, а следовательно, и теорема 4 справедливы для множеств точек на плоскости, но доказательство этого является сложным.  Мыцельский (J. Mycielski) доказал, что теоремы 3 и 4 для множеств точек трехмерного пространства неверны.
Мыцельский (J. Mycielski) доказал, что теоремы 3 и 4 для множеств точек трехмерного пространства неверны.
С. Мазуркевич (S. Mazurkiewicz) и я доказали в 1914 г., что существует множество  точек на плоскости, состоящее из двух не имеющих общих точек частей, каждая из которых конгруэнтна множеству
точек на плоскости, состоящее из двух не имеющих общих точек частей, каждая из которых конгруэнтна множеству  Можно доказать, что таким свойством не обладает никакое множество точек на прямой.
Можно доказать, что таким свойством не обладает никакое множество точек на прямой.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ ИЗДАТЕЛЬСТВА
- От редакции польского издания
- ГЛАВА I. О МНОЖЕСТВАХ И ИХ СВОЙСТВАХ
- 2. Равенство множеств
- 4. Пустое множество
- 5. Конечные множества
- 6. Равночисленные множества
- 7. Взаимно однозначное соответствие
- 8. Равномощные множества
- 9. Счетные множества
- 10. Сумма множеств
- 11. Несчетные множества
- 12. Континуум-гипотеза
- 13. Непересекающиеся множества
- 14. Сравнение мощностей бесконечных множеств
- 15. Аксиома выбора
- 16. Алгебра множеств
- 17. Упорядоченные множества
- 18. Подобные упорядоченные множества
- 19. Плотные упорядоченные множества. Сечения. Щели
- 20. Заполнение щелей
- 21. Вполне упорядоченные множества
- 22. Принцип трансфинитной индукции
- 23. Принцип математической индукции
- 24. Функции
- 25. Декартово произведение
- 26. Метрические пространства
- 27. Евклидовы пространства
- 28. Борелевские множества
- 29. Открытые и замкнутые множества
- 30. Производное множество и замыкание множества
- 31. Топология
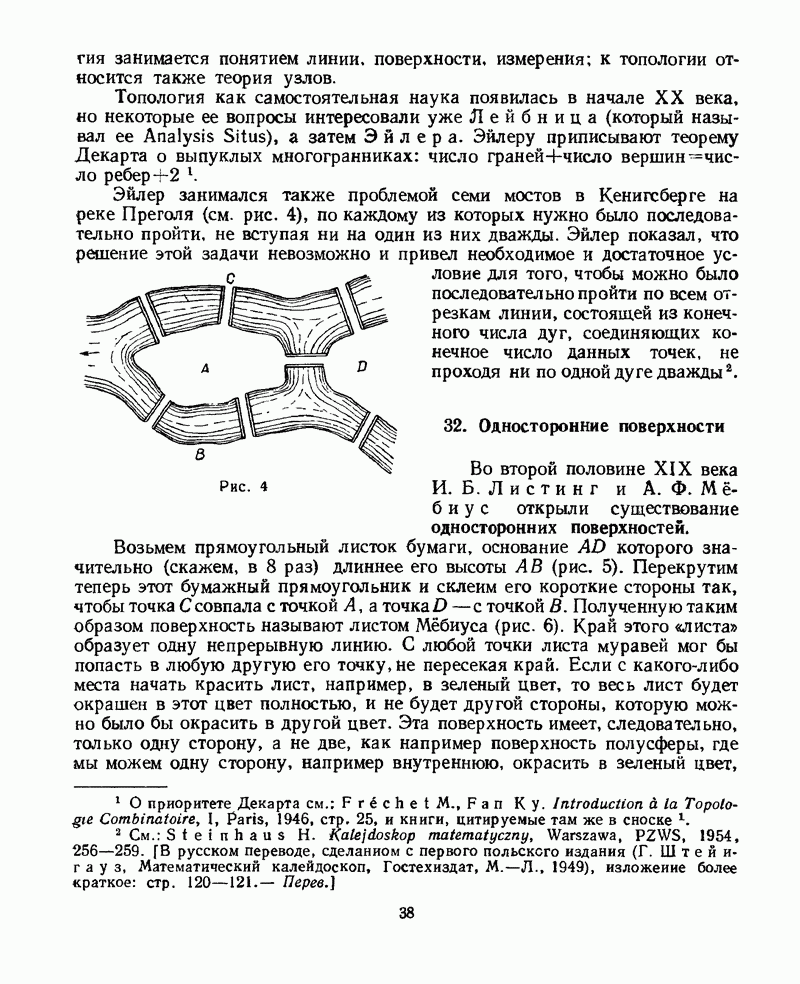
- 32. Односторонние поверхности
- 33. Проблема четырех красок
- ГЛАВА II. О КОНГРУЭНТНОСТИ МНОЖЕСТВ. КОНГРУЭНТНОСТЬ МНОЖЕСТВ ПРИ КОНЕЧНОМ РАЗБИЕНИИ
- 2. Движения множеств
- 3. Конгруэнтность множеств при конечном разбиении
- 4. Преобразования сжатия