| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.4. ИЗЛУЧЕНИЕ ИЗ АПЕРТУР
14.4.1. Линзы
Широко употребляемой антенной апертурного типа является аналог оптической линзы. Сверхвысокочастотные линзы, использовавшиеся Лоджем [288, 289] в 1889 г., были изготовлены из смолы; в настоящее время для этой цели имеется много естественных и искусственных диэлектриков с низкими потерями. В случае искусственных диэлектриков показатель преломления может быть как больше, так и меньше единицы (см. разд. 13.2).

Рис. 14. 9. Расчет профилей линз: а -  с плоской задней поверхностью; б -
с плоской задней поверхностью; б -  , направление лучей определяется законом Снеллиуса; в -
, направление лучей определяется законом Снеллиуса; в -  направление лучей определяется металлическими перегородками.
направление лучей определяется металлическими перегородками.
Поверхности линз в зависимости от требуемых свойств могут быть обе плоскими, либо одна из них или обе изогнутыми. Было проведено большое количество разработок таких сверхвысокочастотных линз [55, 57, 126, 147, 161, 210, 302, 456] и, вообще говоря, технологические допуски при их изготовлении легко выдерживаются [424].
На рис. 14.9, а показана типичная линза с показателем преломления  большим единицы. С излучающей стороны она плоская и таким образом имеет одну изогнутую преломляющую поверхность со стороны облучателя [252, 253]. Помещая точечный источник в точку
большим единицы. С излучающей стороны она плоская и таким образом имеет одну изогнутую преломляющую поверхность со стороны облучателя [252, 253]. Помещая точечный источник в точку  и обозначая фокусное расстояние через
и обозначая фокусное расстояние через  можно по геометрической оптике вычислить профиль линзы. Чтобы на поверхности
можно по геометрической оптике вычислить профиль линзы. Чтобы на поверхности  фаза была постоянна, оптическая длина луча, проходящего через произвольную точку А, должна равняться оптической длине осевого луча, т. е.
фаза была постоянна, оптическая длина луча, проходящего через произвольную точку А, должна равняться оптической длине осевого луча, т. е.

Обозначая длину  через
через  , а угол
, а угол  через
через  , получим соотношение
, получим соотношение

которое является уравнением гиперболы с фокусом в точке  и эксцентриситетом
и эксцентриситетом  Асимптоты образуют с осью угол
Асимптоты образуют с осью угол  равный
равный

На рис. 14.9, б показана линза [254, 401] с  . Ее профиль описывается уравнением
. Ее профиль описывается уравнением

которое представляет собой уравнение эллипса.
В изображенной на рис. 14.9, в решетчатой линзе лучи могут проходить через линзу лишь параллельно ее оси [320, 321], хотя профиль линзы описывается уравнением (14.22).

Рис. 14, 10. Зонирование линз. Соседние лучи изображены для наглядности несколько разнесенными; а —  показан эффект потери лучей; б -
показан эффект потери лучей; б -  , при зонировании непреломляющей поверхности потери лучей не происходит; в —
, при зонировании непреломляющей поверхности потери лучей не происходит; в —  показан эффект затенения; г -
показан эффект затенения; г -  , изгибание задней поверхности уничтожает затенение.
, изгибание задней поверхности уничтожает затенение.
Такая линза решетчатого типа может формировать луч с круговой поляризацией с помощью четвертьволновой пластины [174]. Облучатель имеет линейную поляризацию, ориентированную под углом 45°, так что между ортогональными составляющими возникает фазовый сдвиг 90°. Такое устройство по частоте является относительно узкополосным.
Толщина и вес сверхвысокочастотных линз могут быть уменьшены путем разбивки на зоны, в которых длина хода лучей отличается на целое число длин волн. На практике разности длин хода составляют около одной длины волны и таким образом физическая длина луча через линзу уменьшается на  длин волн на каждую ступеньку.
длин волн на каждую ступеньку.
На рис. 14.10, а и в изображены примеры соответственно для случаев  которые можно рассматривать как зональные пластинки с фазовой коррекцией. Максимальная толщина зонированной линзы приблизительно равна либо
которые можно рассматривать как зональные пластинки с фазовой коррекцией. Максимальная толщина зонированной линзы приблизительно равна либо  либо
либо 
смотря какой случай имеет место:  или
или  Зонирование уменьшает полосу пропускания линзы из твердого диэлектрика, но в случае металло-пластинчатой линзы может быть получено улучшение вследствие частичной компенсации зависимости
Зонирование уменьшает полосу пропускания линзы из твердого диэлектрика, но в случае металло-пластинчатой линзы может быть получено улучшение вследствие частичной компенсации зависимости  от частоты. Кроме того, зонирование приводит к потере части лучей, попадающих на боковые граничные поверхности зон, а также к появлению затенения, вследствие чего могут возникать добавочные боковые лепестки [85, 158, 257, 569]. Влияние затенения можно уменьшить, придавая линзе ступенчатую форму, как показано на рис. 14.10, б, но это приводит к неудобной форме поверхности.
от частоты. Кроме того, зонирование приводит к потере части лучей, попадающих на боковые граничные поверхности зон, а также к появлению затенения, вследствие чего могут возникать добавочные боковые лепестки [85, 158, 257, 569]. Влияние затенения можно уменьшить, придавая линзе ступенчатую форму, как показано на рис. 14.10, б, но это приводит к неудобной форме поверхности.
На рис. 14.10, г показана соответствующая модификация зонированной преломляющей поверхности [157]. Такие методы модификации формы поверхности линзы не дают идеальных результатов, поскольку при этом получаются волиы, которые распространяются параллельно ступеньке, что приводит к изменению скорости распространения для некоторых лучей.
В сверхвысокочастотных линзах, так же, как и в их оптических аналогах, имеет место отражение от поверхности. Уменьшить такие отражения как в случае твердого естественного, так и искусственного диэлектриков можно с помощью различных способов согласования, описанных в разд. 13.1. Отражения можно также уменьшить либо смещением облучателя, либо смещением в осевом направлении одной половины линзы на  относительно другой половины. В металлопластинчатых линзах из-за дисперсии в волноводе возникает хроматическая аберрация. Частотные свойства могут быть улучшены [356], если в линзе используется гребневой волновод. Требуемые свойства получаются при периодической нагрузке гребня щелями и возможно при помещении над гребнем небольшой диэлектрической пластины. Кроме того, путем «ступенчатого» изменения эффективного показателя преломления можно получить «зонированную» линзу постоянной толщины.
относительно другой половины. В металлопластинчатых линзах из-за дисперсии в волноводе возникает хроматическая аберрация. Частотные свойства могут быть улучшены [356], если в линзе используется гребневой волновод. Требуемые свойства получаются при периодической нагрузке гребня щелями и возможно при помещении над гребнем небольшой диэлектрической пластины. Кроме того, путем «ступенчатого» изменения эффективного показателя преломления можно получить «зонированную» линзу постоянной толщины.
В качестве сверхвысокочастотной линзы была рассмотрена [11, 31] диэлектрическая сфера; наличие среды с переменным показателем преломления позволило практически осуществить линзу Максвелла типа «рыбий глаз»; пример такой плоской линзы показан на рис. 14.11,а. Если зависимость показателя преломления от радиуса имеет вид

где  значение
значение  в центре линзы, то изображением точки, лежащей на ее поверхности, будет диаметрально противоположная точка. Из симметрии следует, что от половины такой линзы получится параллельный пучок. Если в металло-воздушной системе одна пластина плоская, а другая искривленная, то из уравнения
в центре линзы, то изображением точки, лежащей на ее поверхности, будет диаметрально противоположная точка. Из симметрии следует, что от половины такой линзы получится параллельный пучок. Если в металло-воздушной системе одна пластина плоская, а другая искривленная, то из уравнения
(14.23) ивыражения для показателя преломления получается следующее уравнение для профиля искривленной пластины:

где а — расстояние между пластинами.

Рис. 14. 11. Модифицированные линзы с параллельными пластинами: а — половина линзы Максвелла «рыбий глаз»; б - линза Люнеберга; в — линза с диэлектрическим диском. (См. [221, 112].)
Другая линза, которая может быть как двух-, так и трехмерной, базируется на сверхвысокочастотном аналоге теоремы Люнеберга [290], которая утверждает, что цилиндр радиуса  в котором показатель преломления изменяется по закону
в котором показатель преломления изменяется по закону

будет фокусировать параллельный пучок лучей, падающих нормально к оси цилиндра на фокальную линию, расположенную на поверхности цилиндра.
На рис.  показана металло-воздушная линза [338] из двух проводящих поверхностей; так как максимальное значение
показана металло-воздушная линза [338] из двух проводящих поверхностей; так как максимальное значение  которое достигается в центре цилиндра, не может быть больше единицы, то из уравнения (14.25) следует, что показатель преломления окружающей среды
которое достигается в центре цилиндра, не может быть больше единицы, то из уравнения (14.25) следует, что показатель преломления окружающей среды  должен быть меньше
должен быть меньше  Линзу с такими значениями показателя преломления можно выполнить в виде пары пластин, разнесенных на соответствующее расстояние; в этом случае расстояние между пластинами должно быть равно: внутри линзы
Линзу с такими значениями показателя преломления можно выполнить в виде пары пластин, разнесенных на соответствующее расстояние; в этом случае расстояние между пластинами должно быть равно: внутри линзы

в окружающей среде

Было показано [228], что линза, занимающая лишь кольцевую область  не может идеально фокусировать пучок лучей точечного источника, находящегося при
не может идеально фокусировать пучок лучей точечного источника, находящегося при  в параллельный пучок.
в параллельный пучок.
В металло-воздушных линзах, описываемых уравнениями (14.24) и (14.26), электрический вектор должен быть параллелен пластинам, что приводит к неравномерному апертурному распределению и слишком широкой диаграмме направленности в плоскости Н. Для устранения этого недостатка было предложено использовать линзу с перпендикулярной поляризацией [112], у которой показа-тель преломления изменялся за счет изменения толщины диэлектрика, расположенного между пластинами, как показано на рис. 14.11,в. Кроме того, были предложены конструкции лииз Люнеберга, у которых фокус находится внутри линзы [56, 180]. Расчет распределения поля в излучающей апертуре для контроля уровня боковых лепестков можно выполнить с помощью известного соотношения [315], связанного с диаграммой направленности облучателя. В случае неплоской [623] конструкции луч диаграммы направленности может быть ориентирован в любом направлении относительно плоскости раскрыва линзы. Двухмерную линзу можно сделать в виде структуры, несущей поверхностную волну, у которой соответствующим образом подобран закон изменения фазовой скорости поверхностной волны [705].
Линзы Люнеберга могут иметь сферическую форму [48, 126, 665 737], причем разработаны методы [227, 315] определения закона изменения показателя преломления, который необходим для получения заданной диаграммы направленности. Конструкция таких линз зависит от наличия соответствующих материалов. Так как непрерывное изменение свойств трудно осуществить, то используется ступенчатое изменение свойств [303, 341]. В этом случае сфера состоит из системы концентрических слоев, причем изменение от слоя к слою показателя преломления или диэлектрической проницаемости соответствует средним значениям среды с непрерывно изменяющимися свойствами. Диаграмма направленности в некоторой степени зависит от типа облучателя [513].
В качестве примера [341] можно указать, что  -слойная сфера диаметром 45 см при апертурном распределении, спадающем до уровня —10 дб, имеет на частоте
-слойная сфера диаметром 45 см при апертурном распределении, спадающем до уровня —10 дб, имеет на частоте  ширину луча около 4,3° и уровень боковых лепестков около
ширину луча около 4,3° и уровень боковых лепестков около  Упрощенная диэлектрическая линза состоит из внешней оболочки и внутреннего ядра у которых показатели преломления постоянны [741].
Упрощенная диэлектрическая линза состоит из внешней оболочки и внутреннего ядра у которых показатели преломления постоянны [741].
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА
- ГЛАВА 14. АНТЕННЫ
- 14.1.2. Сверхнаправленные антенны
- 14.2. АНТЕННЫ С БОКОВЫМ ИЗЛУЧЕНИЕМ
- 14.2.2. Линейные решетки
- 14.2.3. Двухмерные решетки
- 14.3. АНТЕННЫ С ПРОДОЛЬНЫМ ИЗЛУЧЕНИЕМ
- 14.3.2. Замедляющие структуры
- 14.3.3. Частотно-независимые антенны
- 14.3.4. Поверхностные излучатели
- 14.4. ИЗЛУЧЕНИЕ ИЗ АПЕРТУР
- 14.4.2. Электромагнитные рупоры
- 14.4.3. Отражающие поверхности
- 14.5. СКАНИРУЮЩИЕ СИСТЕМЫ
- 14.5.2. Методы фазирования
- 14.5.3. Широкоугольные линзы
- 14.5.4. Широкоугольные отражатели
- 14.6. ДИЭЛЕКТРИЧЕСКИЕ ОБТЕКАТЕЛИ
- 14.6.2. Практические конструкции
- 14.7. ТЕХНИКА ИЗМЕРЕНИЙ
- 14.7.1. Эквифазные контуры
- 14.7.2. Диаграмма направленности
- 14.7.3. Усиление
- ГЛАВА 15. МЕХАНИЧЕСКАЯ КОНСТРУКЦИЯ И ИЗГОТОВЛЕНИЕ
- 15.1.2. Размеры и допуски
- 15.2. МЕХАНИЧЕСКАЯ ОБРАБОТКА И СОПУТСТВУЮЩИЕ ПРОЦЕССЫ
- 15.2.2. Прессование и штамповка
- 15.2.3. Искровая обработка
- 15.3. МЕТОДЫ ИЗГОТОВЛЕНИЯ
- 15.3.1. Пайка
- 15.3.2. Сгибание и скручивание
- 15.4. ПРЕЦИЗИОННОЕ ЛИТЬЕ
- 15.4.2. Литье с удаляемыми моделями
- 15.4.3. Постоянные формы
- 15.5. МЕТОДЫ СПЕКАНИЯ И РАСПЫЛЕНИЯ
- 15.5.2. Металлизация распылением
- 15.6. ГАЛЬВАНОПЛАСТИКА
- 15.6.1. Методы гальванического покрытия
- 15.6.2. Постоянные оправки
- 15.6.3. Оправки разового применения
- 15.6.4. Изготовление деталей методом гальванопластики
- 15.7. ПРОВЕРКА И ИЗМЕРЕНИЯ
- 15.7.3. Чистота отделки поверхности
- 15.8. ПОКРЫТИЕ И УПАКОВКА
- ГЛАВА 16. ПРИЕМНИКИ
- 16.1. ПРИЕМ ПОРОГОВЫХ СИГНАЛОВ
- 16.1.2. Шумы в цепях
- 16.1.3. Шум в электронных пучках
- 16.1.4. Шумы в электронных лампах
- 16.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- 16.2.2. Детектирование сигналов с малым уровнем
- 16.2.3. Параметры смесителей
- 16.2.4. Типичные диоды и держатели кристаллов
- 16.3. СПЕЦИАЛЬНЫЕ МЕТОДЫ
- 16.3.2. Генерирование гармоник
- 16.4. МЕТОДЫ РАДИОМЕТРИИ
- 16.4.1. Энергия и шумы излучения
- 16.4.2. Форма шумового сигнала
- 16.4.3. Флюктуации усиления
- 16.4.4. Различные погрешности
- 16.5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ
- 16.5.1. Генераторы сигнала
- 16.5.2. Источники широкополосных сигналов
- 16.5.3. Газоразрядные источники шума
- 16.5.4. Шумы генераторов на электронных лампах
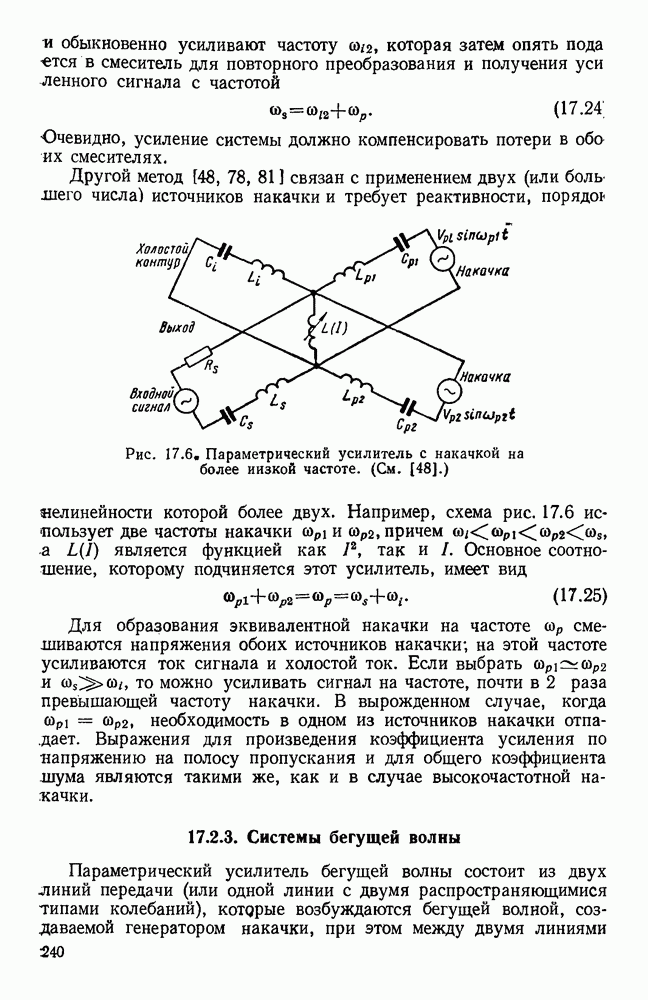
- ГЛАВА 17. МАЛОШУМЯЩИЕ УСИЛИТЕЛИ
- 17.1.2. Приборы на твердом теле
- 17.2. УСИЛЕНИЕ С ПЕРЕМЕННОЙ РЕАКТИВНОСТЬЮ
- 17.2.2. Усилители с отрицательной проводимостью
- 17.2.3. Системы бегущей волны
- 17.3. ПРАКТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ УСИЛИТЕЛИ
- 17.3.2. Волны пространственного заряда
- 17.3.3. Полупроводниковые диоды
- 17.4. КВАНТОВОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ (МАЗЕРЫ)
- 17.4.2. Материалы
- 17.5. МАЗЕРЫ С ДВУМЯ УРОВНЯМИ
- 17.5.2. Анализ во вращающихся координатах
- 17.5.3. Практические устройства
- 17.6. МАЗЕРЫ СО МНОГИМИ УРОВНЯМИ
- 17.6.2. Усилители резонаторного типа
- 17.6.3. Усилители бегущей волны
- ГЛАВА 18. АНТЕННЫЕ ПЕРЕКЛЮЧАТЕЛИ И ЭЛЕКТРОНИКА ГАЗОВОГО РАЗРЯДА
- 18.1. ПРИНЦИПЫ ПЕРЕКЛЮЧЕНИЯ АНТЕННЫ
- 18.1.2. Переключатели на твердом теле
- 18.2. ЭЛЕКТРОНИКА ГАЗОВОГО РАЗРЯДА
- 18.2.2. Свойства разряда
- 18.2.3. Процессы переноса в плазме
- 18.3. ХАРАКТЕРИСТИКИ ПЕРЕКЛЮЧАЮЩИХ ЛАМП
- 18.3.2. Поджиг разряда
- 18.3.3. Гашение разряда
- 18.4. ПРИБОРЫ С НЕСАМОСТОЯТЕЛЬНЫМ РАЗРЯДОМ
- 18.4.2. Гиромагнитные явления
- 18.4.3. Аттенюаторы
- 18.4.4. Импульсные переключатели
- 18.5. ПРИБОРЫ С САМОСТОЯТЕЛЬНЫМ РАЗРЯДОМ
- 18.5.2. Многофункциональные переключатели
- 18.6. АНТЕННЫЕ ПЕРЕКЛЮЧАТЕЛИ НА РАЗРЯДНЫХ ТРУБКАХ
- 18.6.2. Балансные схемы
- 18.6.3. Индивидуальные функции
- 18.7. ТЕХНИКА ИЗМЕРЕНИЙ
- 18.7.1. Затухание и полное сопротивление
- ГЛАВА 19. ИЗМЕРЕНИЕ И СТАБИЛИЗАЦИЯ ЧАСТОТЫ
- 19.2. СТАБИЛИЗАЦИЯ ЧАСТОТЫ
- 19.2.2. Схемы стабилизации
- 19.3. СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 19.3.2. Электронное качание частоты
- 19.4. ЭТАЛОНЫ СПЕКТРАЛЬНЫХ ЛИНИЙ
- 19.4.2. Методы излучения и образования пучка
- 19.4.3. Теории гравитации и относительности
- ГЛАВА 20. ВЫСОКОЧАСТОТНОЕ ИЗЛУЧЕНИЕ В ПРОМЫШЛЕННОСТИ, БИОЛОГИИ И МЕДИЦИНЕ
- 20.1.2. Методы парамагнитного резонанса
- 20.2. ПРОМЫШЛЕННЫЕ МЕТОДЫ ВЫСОКОЧАСТОТНОГО НАГРЕВА
- 20.3. ОБЛУЧЕНИЕ В ИНТЕНСИВНОМ ПОЛЕ
- 20.4. ОПАСНОСТЬ ПРИ РАБОТЕ ДЛЯ ТЕХНИЧЕСКОГО ПЕРСОНАЛА
- ГЛАВА 21. ПРИМЕНЕНИЕ ВЫСОКИХ ЧАСТОТ В УСКОРИТЕЛЯХ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- 21.1.2. Низкочастотные ускорители
- 21.2. ЛИНЕИНЫЕ УСКОРИТЕЛИ С РЕЗОНАТОРАМИ
- 21.2.2. Многорезонаторные системы
- 21.3. ЛИНЕЙНЫЕ УСКОРИТЕЛИ С БЕГУЩЕЙ ВОЛНОЙ
- 21.3.2. Некоторые методы конструирования ускорителей
- 21.4. ОРБИТАЛЬНЫЕ ИЛИ ЦИКЛИЧЕСКИЕ УСКОРИТЕЛИ С ПОСТОЯННЫМ ПОЛЕМ
- 21.4.2. Фазотрон (синхроциклотрон)
- 21.4.3. Электронные циклотроны
- 21.5. ИНДУКЦИОННЫЕ ЦИКЛИЧЕСКИЕ УСКОРИТЕЛИ
- 21.5.2. Электронные синхротроны
- 21.5.3. Протонные синхротроны
- 21.6. ФОКУСИРОВКА СО ЗНАКОПЕРЕМЕННЫМ ГРАДИЕНТОМ
- ГЛАВА 22. СВЯЗЬ ПО ЛИНИЯМ ПЕРЕДАЧИ
- 22.1.2. Модуляция несущей
- 22.1.3. Системы памяти
- 22.2. МЕТОДЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
- 22.2.2. Требования к линиям передачи
- 22.3. ВОЛНОВОДЫ С КРУГОВЫМИ ЭЛЕКТРИЧЕСКИМИ ПОЛЯМИ
- 22.3.2. Потери, вызванные явлением преобразования видов волн
- 22.4. ПРАКТИЧЕСКИЕ ВОЛНОВОДЫ ДЛЯ ПЕРЕДАЧИ ЭНЕРГИИ НА БОЛЬШИЕ РАССТОЯНИЯ
- 22.4.2. Узлы и методы
- ГЛАВА 23. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
- 23.1.2. Область дифракции
- 23.1.3. Поверхностное рассеяние
- 23.2. АТМОСФЕРНЫЕ ЯВЛЕНИЯ
- 23.2.2. Потери при распространении
- 23.2.3. Рассеяние осадками
- 23.3. РАСПРОСТРАНЕНИЕ РАДИОВОЛН ПРИ РАССЕЯНИИ
- 23.3.2. Ионизация северным сиянием и метеоритами
- ГЛАВА 24. РАДИОРЕЛЕЙНЫЕ ЛИНИИ СВЯЗИ
- 24.1.2. Узлы и электронные лампы
- 24.2. РАБОЧИЕ УСЛОВИЯ
- 24.2.1. Выбор пути распространения
- 24.2.2. Разнесенный прием
- 24.3. ПРАКТИЧЕСКИЕ СИСТЕМЫ
- 24.3.1. Линии связи в пределах прямой видимости
- 24.3.2. Радиорелейные линии связи, работающие при отсутствии прямой видимости
- 24.4. КОСМИЧЕСКАЯ СВЯЗЬ
- 24.4.1. Радиорелейные станции на спутниках для наземной связи
- 24.4.2. Межпланетные радиорелейные линии
- ГЛАВА 25. РАДИОЛОКАЦИОННЫЕ СИСТЕМЫ
- 25.1.2. Методы непрерывного излучения
- 25.1.3. Импульсные методы
- 25.1.4. Вероятность обнаружения сигналов
- 25.2. АППАРАТУРА И МЕТОДЫ
- 25.2.1. Блоки высокой частоты
- 25.2.2. Индикация и обработка данных
- 25.2.3. Работа при наличии пассивных помех
- 25.2.4. Средства испытаний
- 25.3. НАБЛЮДЕНИЕ И ПОИСК
- 25.3.2. Морская навигация
- 25.3.3. Системы вторичной радиолокации
- 25.4, ВОЗДУШНАЯ НАВИГАЦИЯ
- 25.4.2. Панорамные радиолокаторы и другие автономные радиолокационные системы
- 25.4.3. Комбинированные системы
- 25.5. СИСТЕМЫ ЗАХОДА НА ПОСАДКУ И ПОСАДКИ САМОЛЕТОВ
- 25.5.2. Инструментальная посадка
- 25.6. ОБНАРУЖЕНИЕ ЦЕЛЕЙ НА ЗЕМНОЙ ПОВЕРХНОСТИ И НАБЛЮДЕНИЕ ЗА ИХ ДВИЖЕНИЕМ
- 25.6.2. Измерение скорости
- 25.7. СИСТЕМЫ НАВЕДЕНИЯ И СЛЕЖЕНИЯ
- 25.7.2. Управление запуском
- 25.7.3. Наведение ракет
- 25.7.4. Управление на больших дальностях
- ГЛАВА 26. ТЕХНИКА РАДИО- И РАДИОЛОКАЦИОННОЙ АСТРОНОМИИ
- 26.1.2. Приемные системы
- 26.2. РАДИОТЕЛЕСКОПЫ
- 26.2.2. Двухволновые интерферометры
- 26.2.3. Многоэлементные интерферометры
- 26.2.4. Поляриметры
- 26.3. СОЛНЕЧНАЯ СИСТЕМА
- 26.3.1. Солнечная атмосфера
- 26.3.2. Излучение Солнца
- 26.3.3. Излучение планет
- 26.4. РАДИОВОЛНЫ КОСМИЧЕСКОГО ПРОИСХОЖДЕНИЯ
- 26.4.2. Спектральные линии
- 26.5. РАДИОЛОКАЦИОННАЯ АСТРОНОМИЯ