22.3. ВОЛНОВОДЫ С КРУГОВЫМИ ЭЛЕКТРИЧЕСКИМИ ПОЛЯМИ

22.3.1. Затухание и дисперсия

Из рассмотренных выражений для полей различных видов следует, что для обеспечения малого уровня потерь, имеющих место при малых токах проводимости, необходимо, чтобы направление вектора напряженности магнитного поля было бы параллельным стенкам. Из этого заключаем, что соответствующее поперечное поле должно быть радиальным по отношению к продольному обратному пути. Хотя рассматривались [183] волноводы типа Н, однако, как линии с малыми потерями наибольшее внимание привлекли круглые волноводы, в которых возбуждены волны вида Распределение поля в круглых волноводах таково, что величина затухания при увеличении частоты уменьшается постепенно.

Большое внимание привлекает возможность использования в линиях передачи значительной длины круглых волноводов, в которых возбуждается волна первого порядка или [5, 10, 30, 77, 78, 80, 135, 138]. Коэффициент затухания, обусловленный наличием активных потерь, определяется выражением

где равно Индексы относятся соответственно к диэлектрической среде внутри волновода и к металлическим стенкам. Из выражения (22.12) следует, что для обеспечения малого значения а требуется: а) большая величина т. е. малая величина малая величина т. е. большая величина большая величина что означает необходимость отказа от применения твердого диэлектрика.

Случай, когда величина близка к исследован в работе [163]. В более нужном случае, когда выражение для

коэффициента затухания в децибелах на километр при величине выраженной в сантиметрах имеет вид

Величина второго члена в квадратных скобках значительно меньше единицы, в результате чего значение а уменьшается значительно быстрее при увеличении чем при возрастании

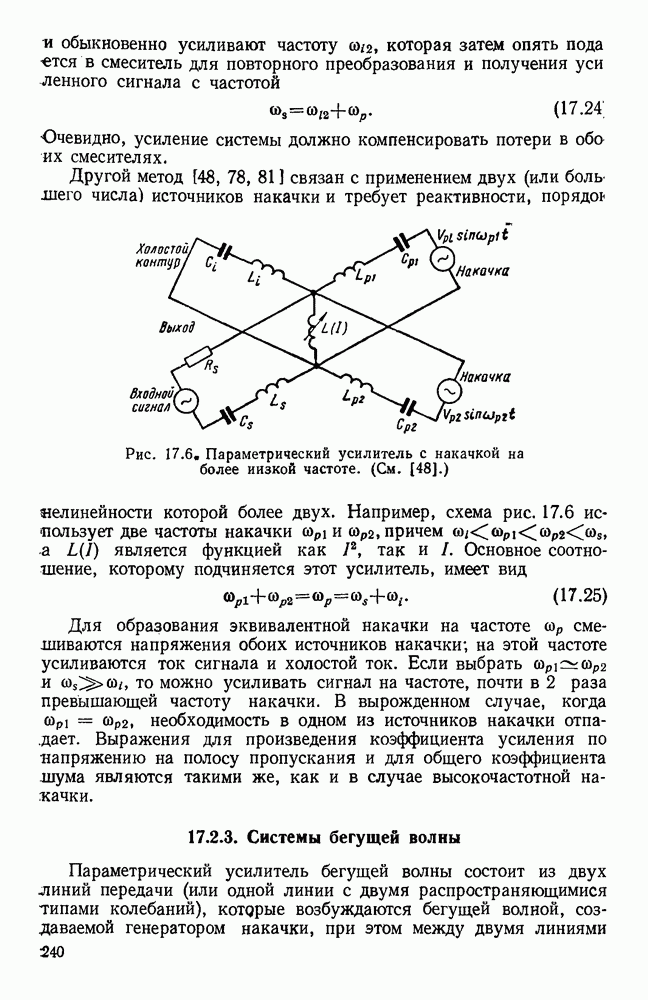
Рис. 22.5. Волноводы для связи на большие расстояния. Числа около кривых указывают на количество возможных в данном волноводе видов воли. Величины диаметров, указанные на оси ординат, относятся к следующим коэффициентам затухания: . (См [123].)

Была вычислена степень увеличения потерь, обусловленных наличием тонкой пленки диэлёктрика на стенках волновода [88, 89, 186, 229,303,304].

Из уравнения (22.13) следует, что величина а зависит от частоты, что приводит к некоторым амплитудным искажениям при передаче сигнала, спектр которого занимает полосу частот Величина изменения затухания определяется выражением

Например, если см, о для меди равна то при Для выбора размеров волновода в зависимости от требуемой величины затухания можно пользоваться графиком [123] рис. 22.5. Здесь приведена кривая зависимости диаметра волновода от рабочей частоты при коэффициентах затухания, равных 1,25 и Например, при требуемый диаметр волновода равен соответственно 17,8 и 5,08 см (7 и 2 дюйма).

Волновод представляет собой дисперсную среду, и при большой длине пути распространения радиоволн появляются искажения [44, 75, 79] сигнала, так как при увеличении частоты групповая задержка сигнала уменьшается. Время групповой задержки определяется выражением

После дифференцирования получим

Разность фаз в 180° между отдельными гармоническими составляющими в пределах полосы спектра, появляющаяся на конце линии, считается верхним граничным пределом. При подстановке этого предела в выражение для разности задержек выражение для допустимой полосы частот спектра имеет вид [123]

если I выражено в километрах.

Для примера с сигналом частотой рассмотренного выше, предел допустимых фазовых искажений достигается при длине, равной В случаях более длинных линий потребуется восстановление сигнала или выравнивание задержки на разных частотах [103]. На рис. 22.6 представлена зависимость допустимой полосы пропускания от рабочей частоты для линии длиной в при постоянном коэффициенте затухания. Из рис. 22.6 видно, что волновод диаметром 5 см, работающий на частоте обладает полосой пропускания при длине, равной На более низких частотах, если удлинять волновод, оставляя потери такими же, получается более узкая полоса пропускания.

При использовании наносекундных импульсов [14, 23, 266, 267] и длинных линий передачи влияние эффекта дисперсии в волноводах на переходные процессы при установлении сигнала становится значительным [34, 51, 131, 146, 147, 149, 159, 224, 227, 230, 235, 244, 248, 259, 263]. Если величину а оставлять постоянной, а величину поддерживать кратной частоте со, то сигнал будет передаваться без искажений [76]. Все компоненты вносят равные затухания и задержки сигналов.

Однако вообще величина а не остается постоянной, а величина меняется с частотой не по линейному закону. В последнем случае разложение в ряд фазовой характеристики при определенном значении частоты дает обычно член определяющий величину групповой задержки, и сумму членов второго и более высокого порядка, наличие которых приводит к искажению сигнала.

Рассмотрение таких членов более высокого порядка позволяет получить функциональную зависимость между максимальной полосой пропускания и длиной волновода.

Рис. 22.6. Полоса пропускания волноводов, предназначенных для дальней связи. Полоса пропускания относится к волноводу длиной а числа около кривых означают диаметр волновода в сантиметрах. Затухание является постоянным и равно для кривой а - 1,25 дб/км и кривой б - 8,2 дб/км, (См. [123].)