| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
Произвольный источник информации создает выход, который является случайным, то выход источника характеризуется статистически. Действительно, если выход источника известен точно, то нет нужды его передавать. В этом разделе мы рассмотрим дискретные аналоговые источники информации и сформулируем математические модели для каждого типа источника.
Простейший
тип дискретного источника – это такой, который выдаёт последовательность букв
(символов), выбираемых из определенного алфавита. Например, двоичный
источник выдает двоичную последовательность вида 100101110...,
причём алфавит состоит из двух символов {0, 1}. В более общем случае источник
дискретен информации с алфавитом из ![]() символов, скажем
символов, скажем ![]() , выдает последовательность
букв, выбираемых из этого алфавита.
, выдает последовательность
букв, выбираемых из этого алфавита.
Чтобы
конструировать математическую модель для дискретного источника предположим, что
каждый символ алфавита ![]() имеет
заданную вероятность выбора
имеет
заданную вероятность выбора ![]() , т.е.
, т.е.
![]() ,
, ![]() ,
,
где
![]() .
.
Мы рассмотрим две математические модели для дискретных источников. В первой мы предположим, что символы выходной последовательности источника статистически независимы, т.е. выбираемый текущий символ статистически независим от всех предыдущих и последующих. Источник, выход которого удовлетворяет условиям статистической независимости символов в выбранной последовательности, называется источником без памяти. Такой источник называется дискретным источником без памяти (ДИБП).
Если
отдельные выходные символы дискретного источника статистически взаимозависимы,
как, например, в английском тексте, мы можем сконструировать математическую
модель, основанную на статической стационарности. По определению дискретный
источник называется стационарным,
если совместные вероятности двух последовательностей длины ![]() , допустим
, допустим ![]() и
и ![]() одинаковые для всех
одинаковые для всех ![]() и при всех сдвигах
и при всех сдвигах ![]() . Другими словами, совместные вероятности для
последовательностей источника произвольной длины инвариантны по отношению к
произвольному сдвигу во времени.
. Другими словами, совместные вероятности для
последовательностей источника произвольной длины инвариантны по отношению к
произвольному сдвигу во времени.
Аналоговый источник выдает сигнал ![]() , который является
реализацией случайного процесса
, который является
реализацией случайного процесса ![]() . Предположим, что
. Предположим, что ![]() - стационарный случайный
процесс с автокорреляционной функцией
- стационарный случайный
процесс с автокорреляционной функцией ![]() и спектральной плотностью мощности
и спектральной плотностью мощности ![]() . Если
. Если ![]() - частотно-ограниченный
случайный процесс, т.е.
- частотно-ограниченный
случайный процесс, т.е. ![]() для
для ![]() , можно использовать теорему отсчётов
для представления
, можно использовать теорему отсчётов
для представления ![]() в виде
в виде
 , (3.1.1)
, (3.1.1)
где ![]() - отсчёты процесса
- отсчёты процесса ![]() , взятые
со скоростью Найквиста
, взятые
со скоростью Найквиста ![]() 1/с.
Используя теорему отсчётов, мы можем преобразовать аналоговый источник в
эквивалентный источник с дискретным временем. После этого выход источника характеризуется
совместной ФПВ
1/с.
Используя теорему отсчётов, мы можем преобразовать аналоговый источник в
эквивалентный источник с дискретным временем. После этого выход источника характеризуется
совместной ФПВ ![]() для
всех
для
всех ![]() , где
, где ![]() ,
, ![]() ,
- случайные величины, соответствующие отсчётам
,
- случайные величины, соответствующие отсчётам ![]() .
.
Заметим,
что выходные отсчёты ![]() стационарного
источника обычно непрерывны, и, следовательно, их нельзя представить в цифровой
форме без потери точности представления. Например, мы можем квантовать каждый
отсчёт рядом дискретных значений, но процесс квантования вносит потери в
точность представления, и, следовательно, исходный сигнал не может быть
восстановлен точно по квантованным отсчётам. Позже мы рассмотрим искажения,
возникающие при квантовании уровней отсчётов аналогового источника.
стационарного
источника обычно непрерывны, и, следовательно, их нельзя представить в цифровой
форме без потери точности представления. Например, мы можем квантовать каждый
отсчёт рядом дискретных значений, но процесс квантования вносит потери в
точность представления, и, следовательно, исходный сигнал не может быть
восстановлен точно по квантованным отсчётам. Позже мы рассмотрим искажения,
возникающие при квантовании уровней отсчётов аналогового источника.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
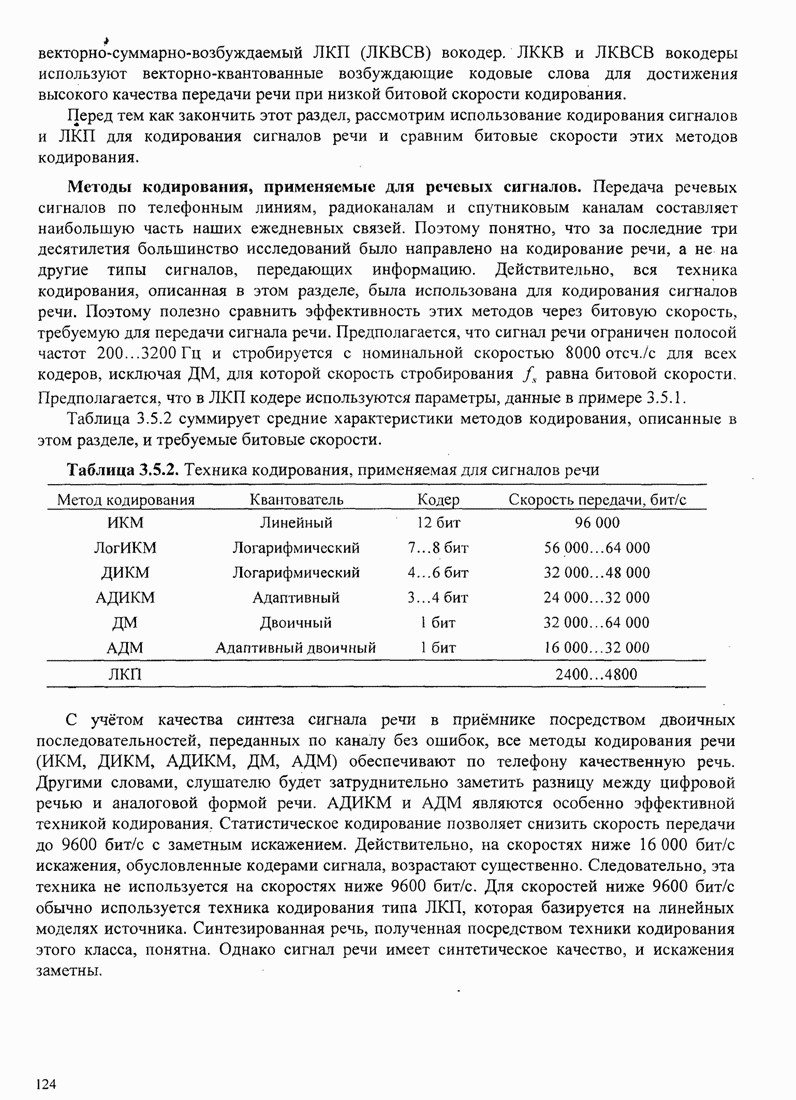
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
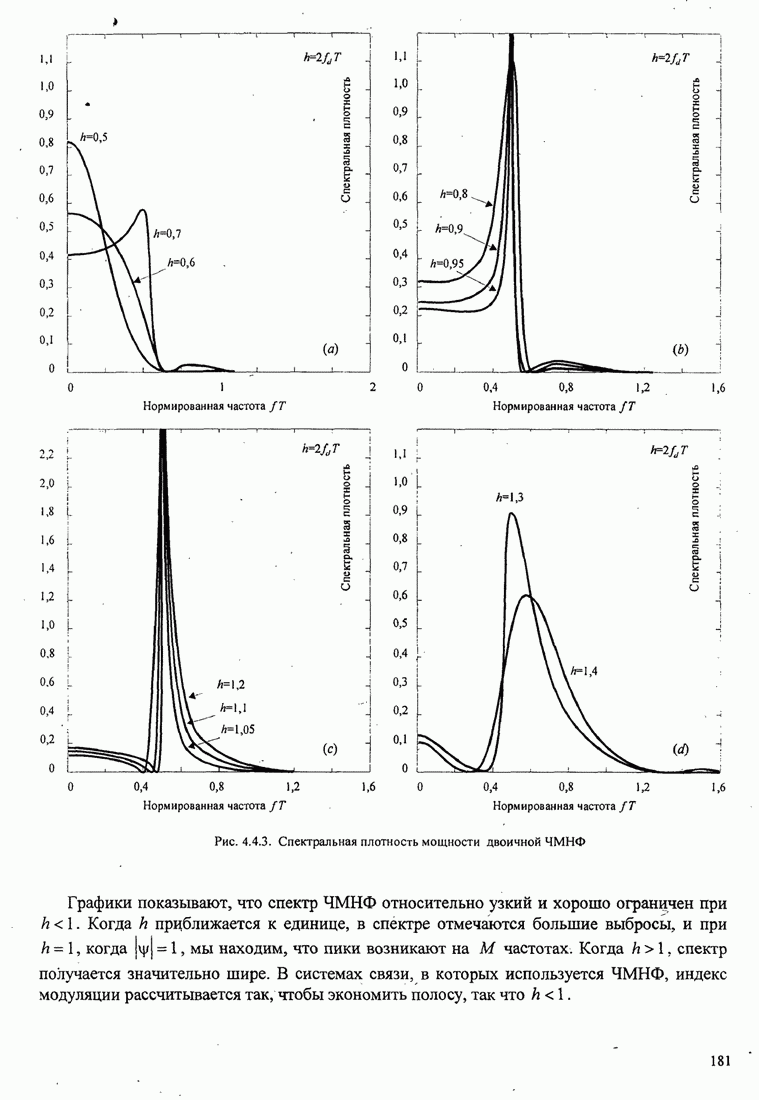
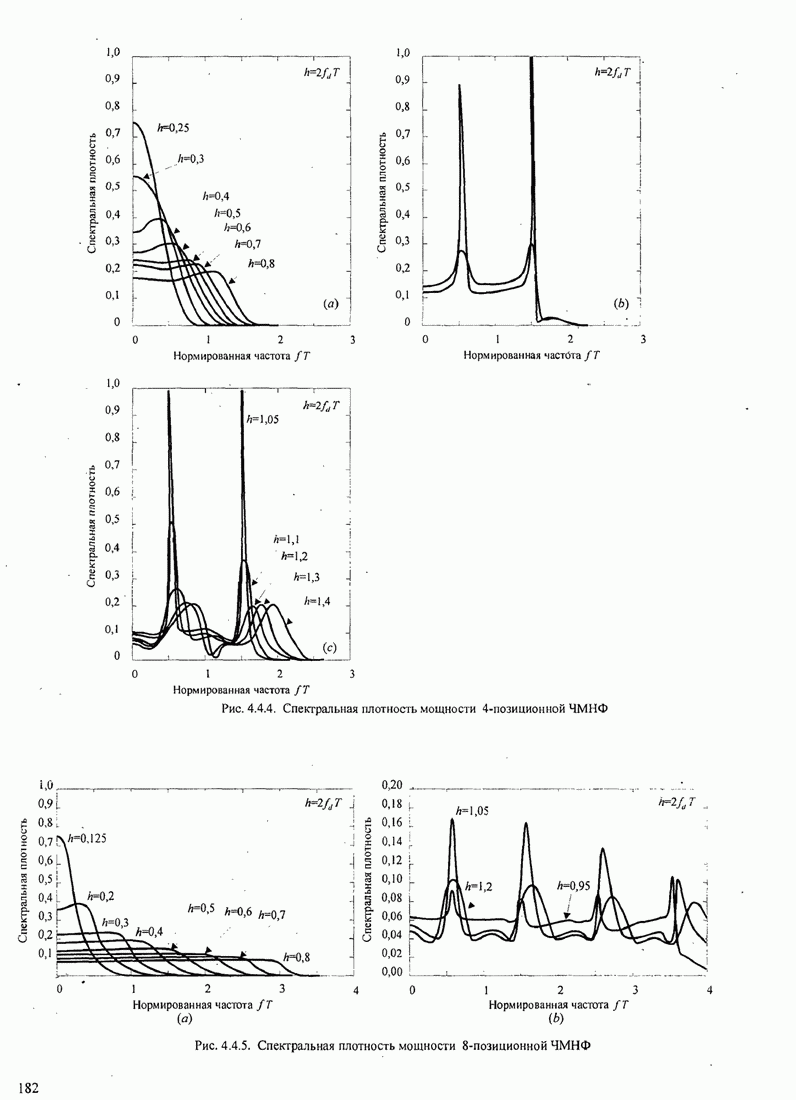
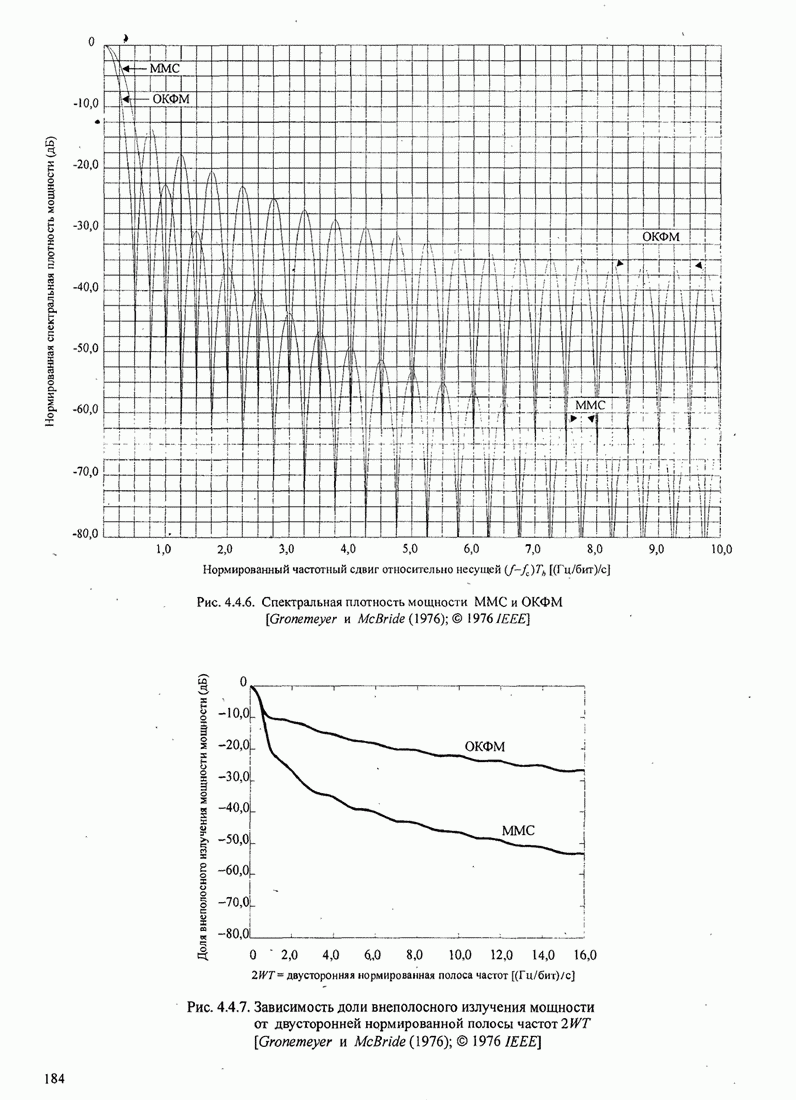
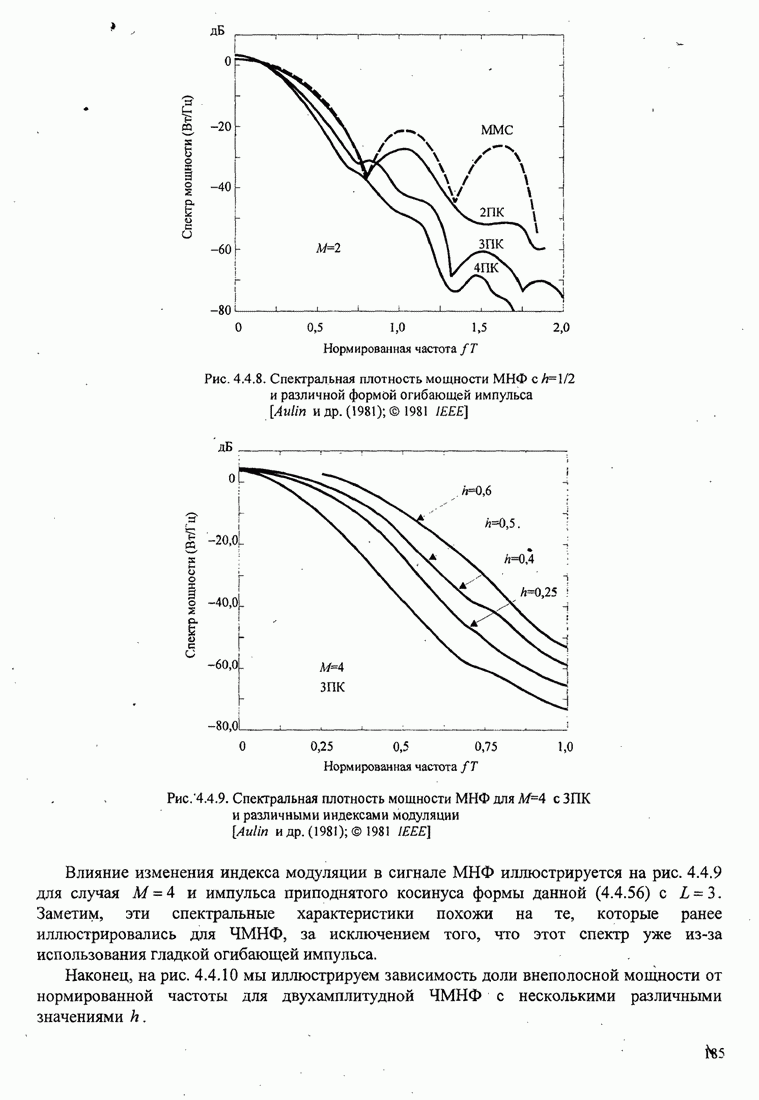
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
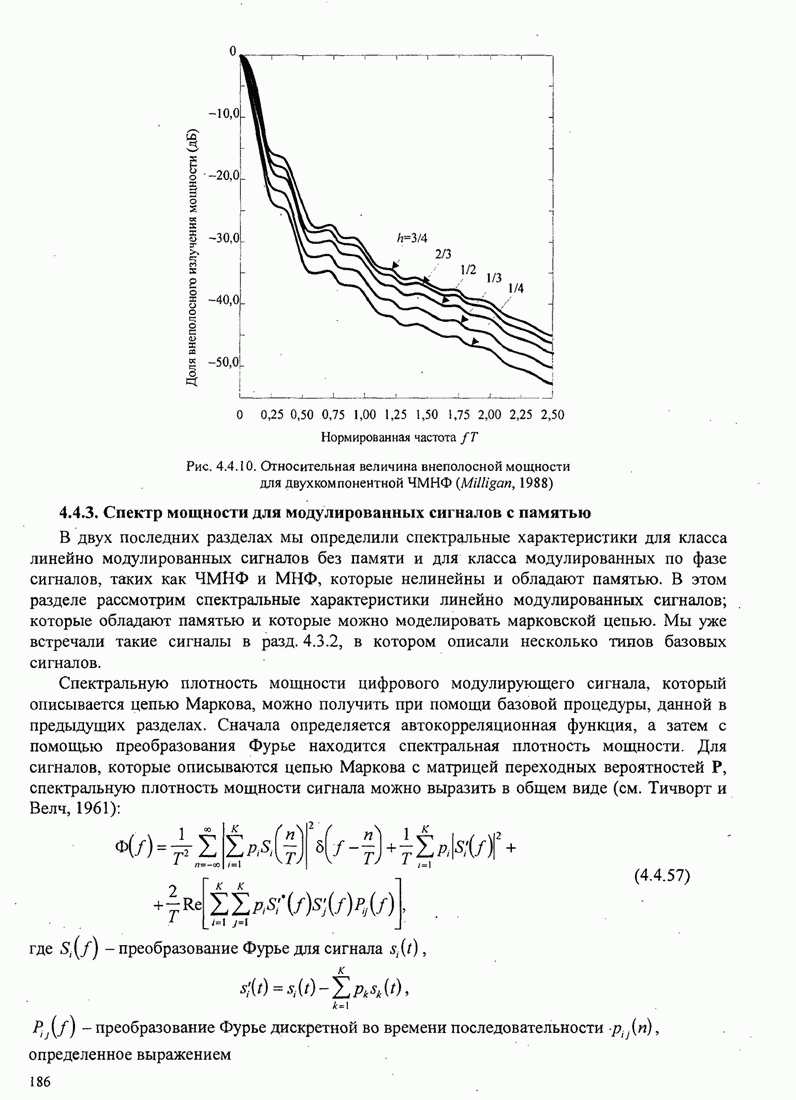
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
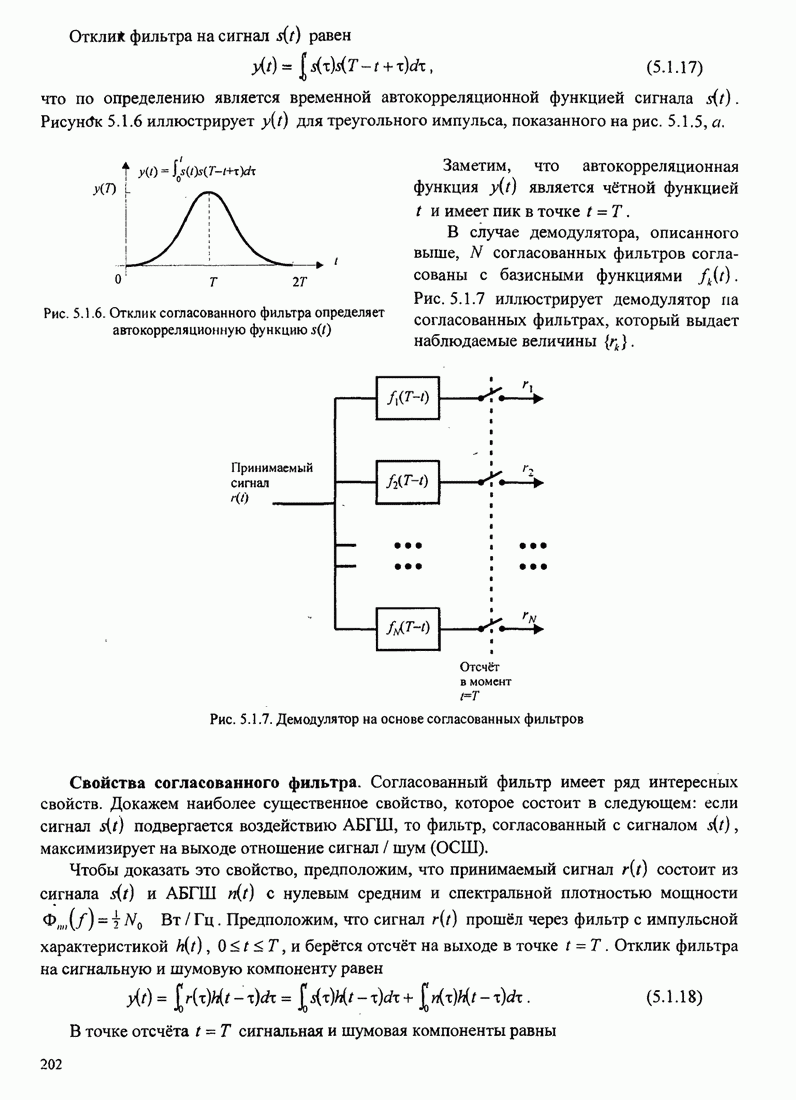
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
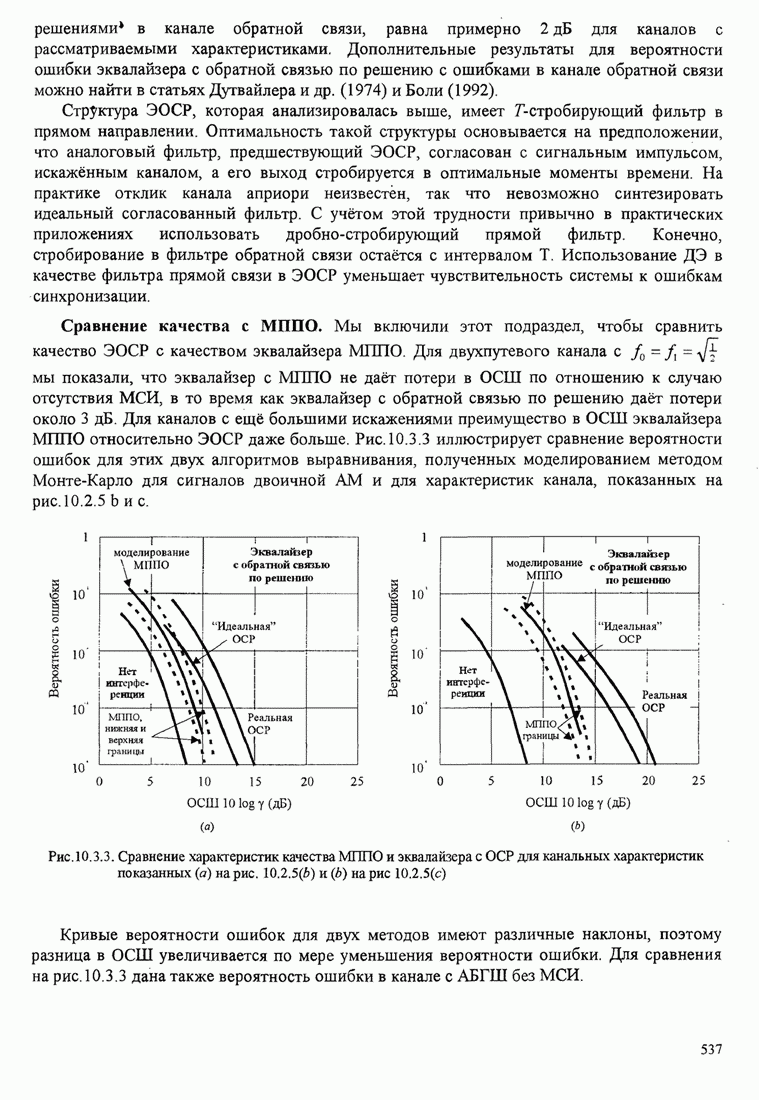
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
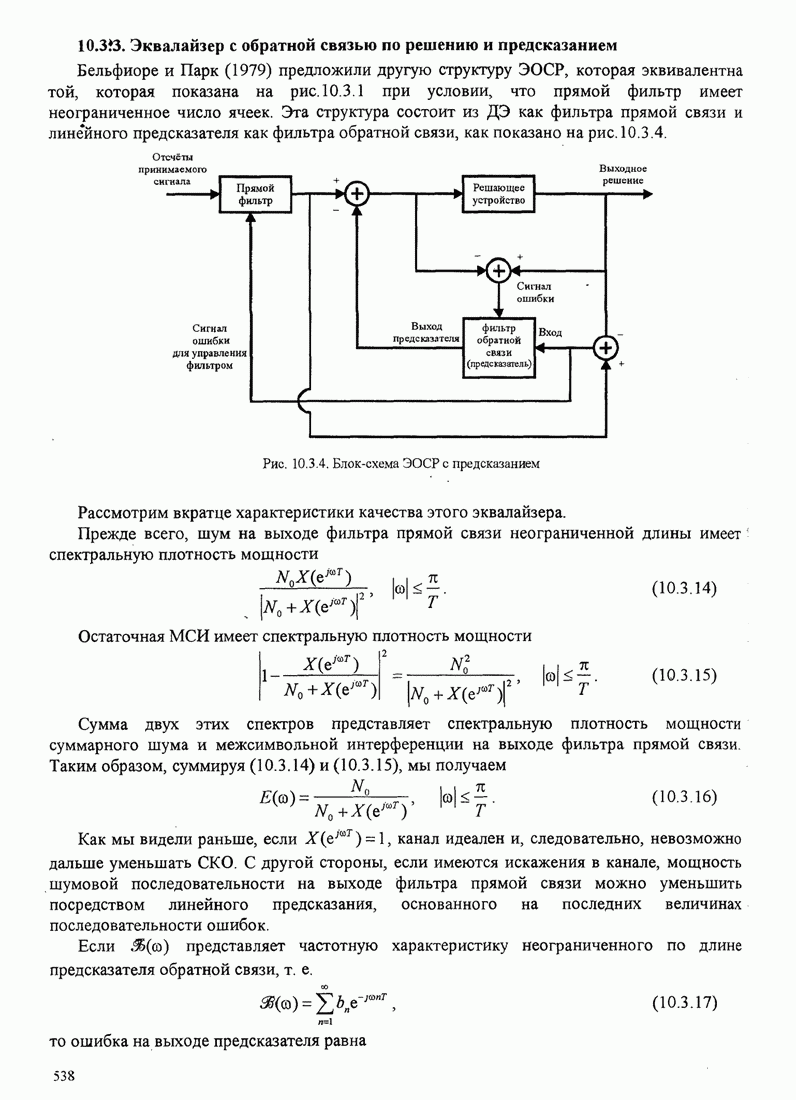
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
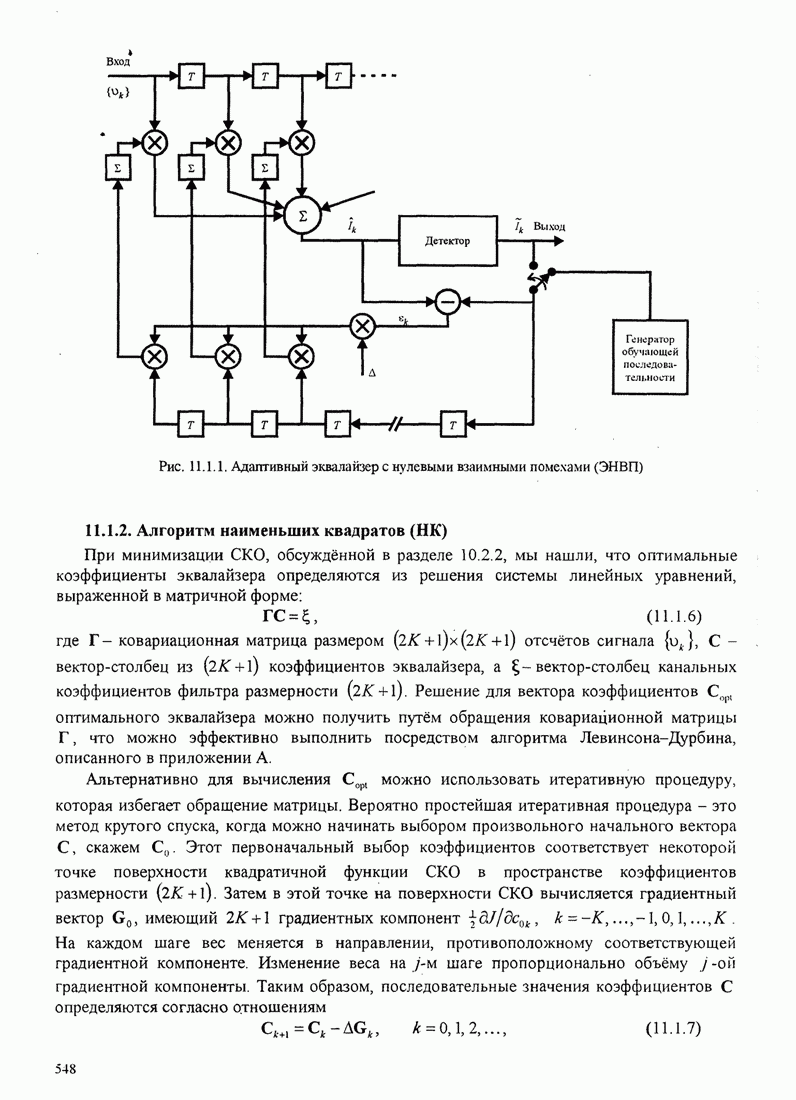
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
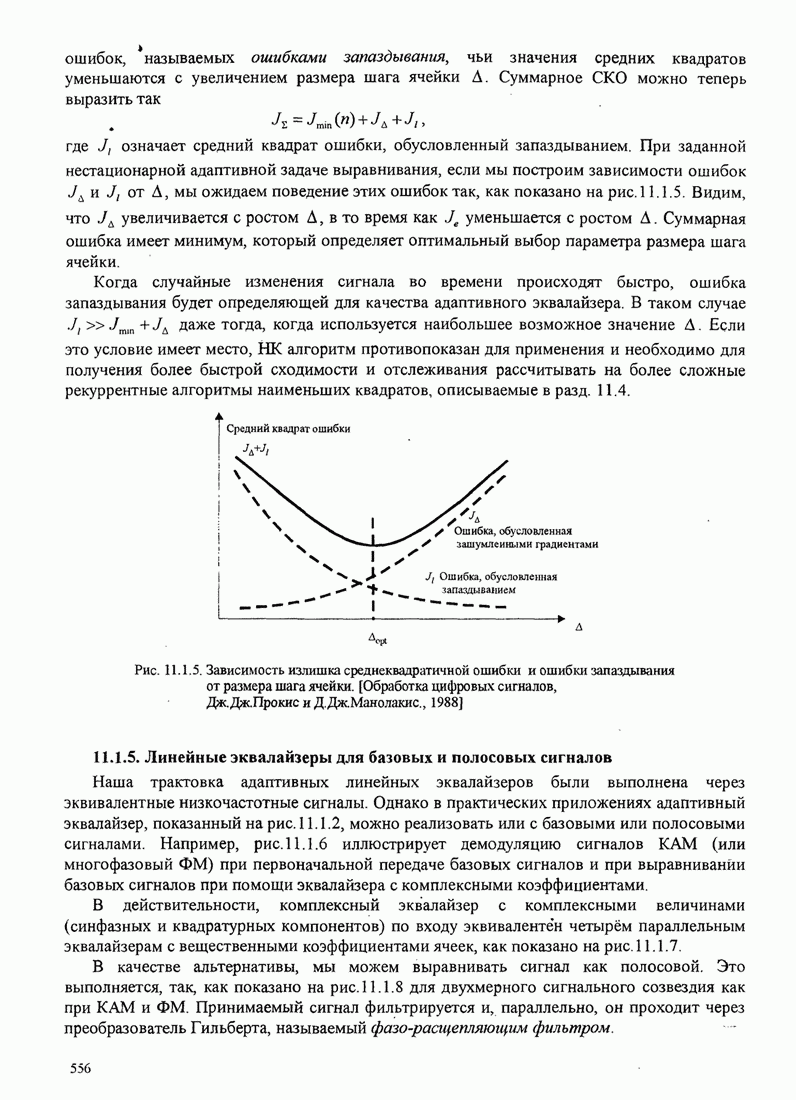
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
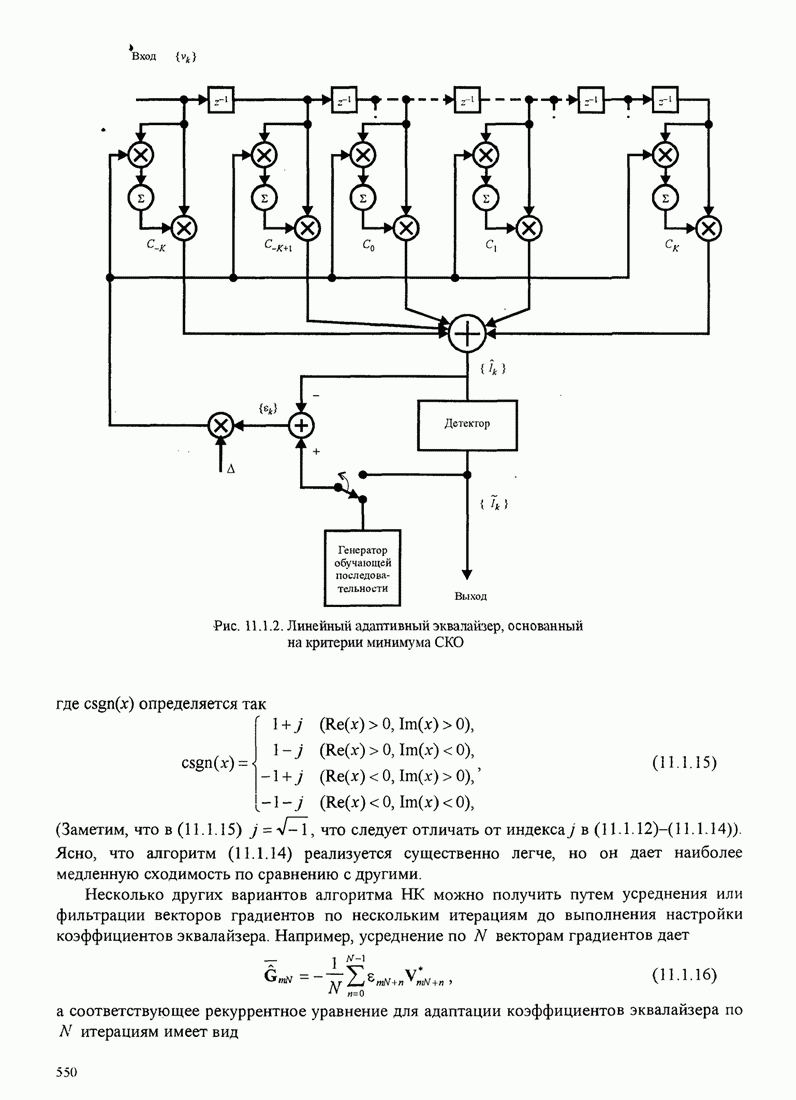
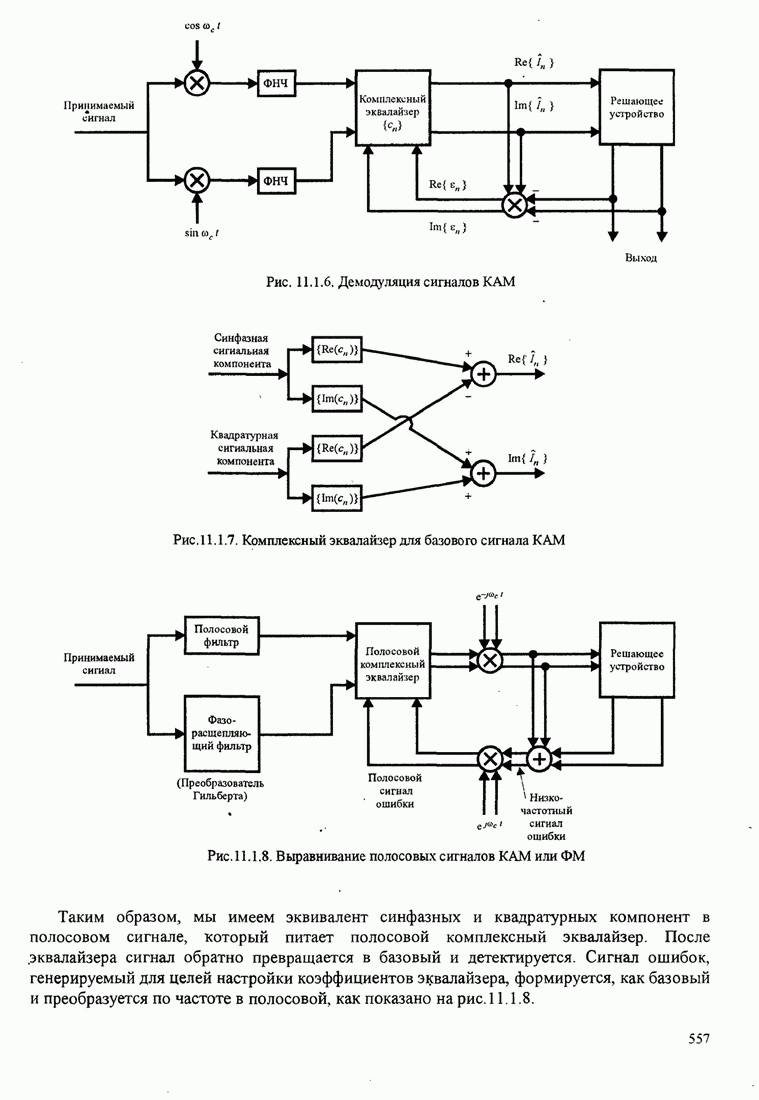
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
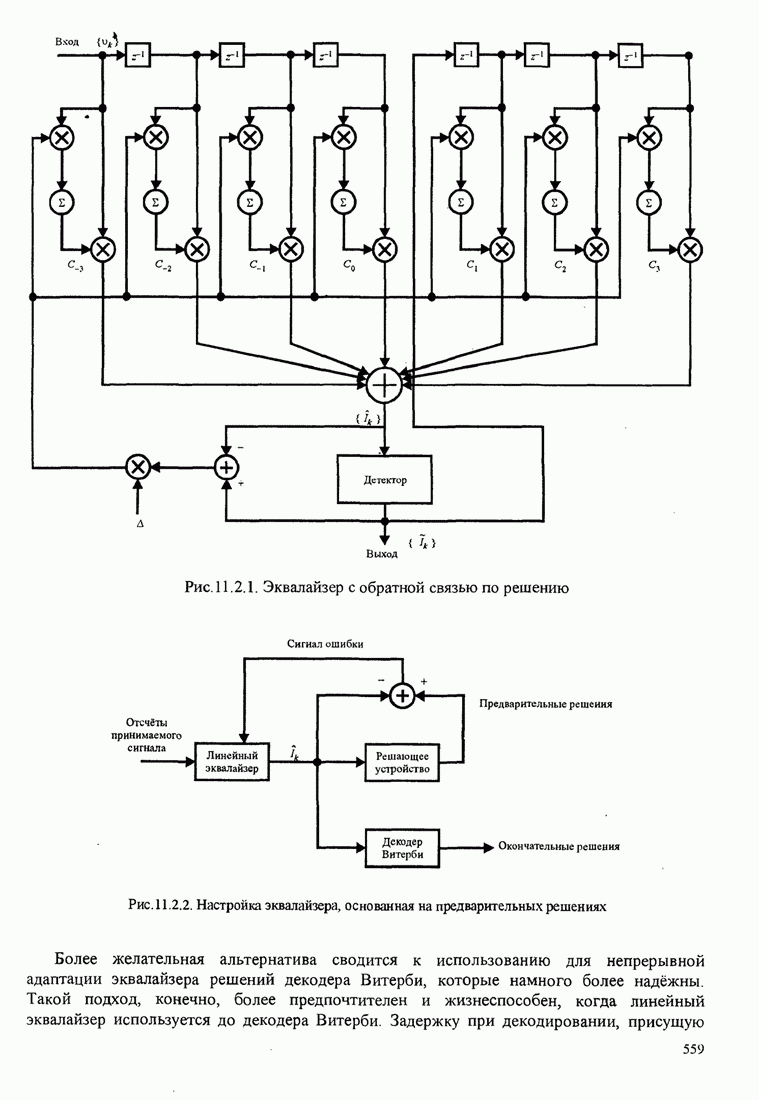
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
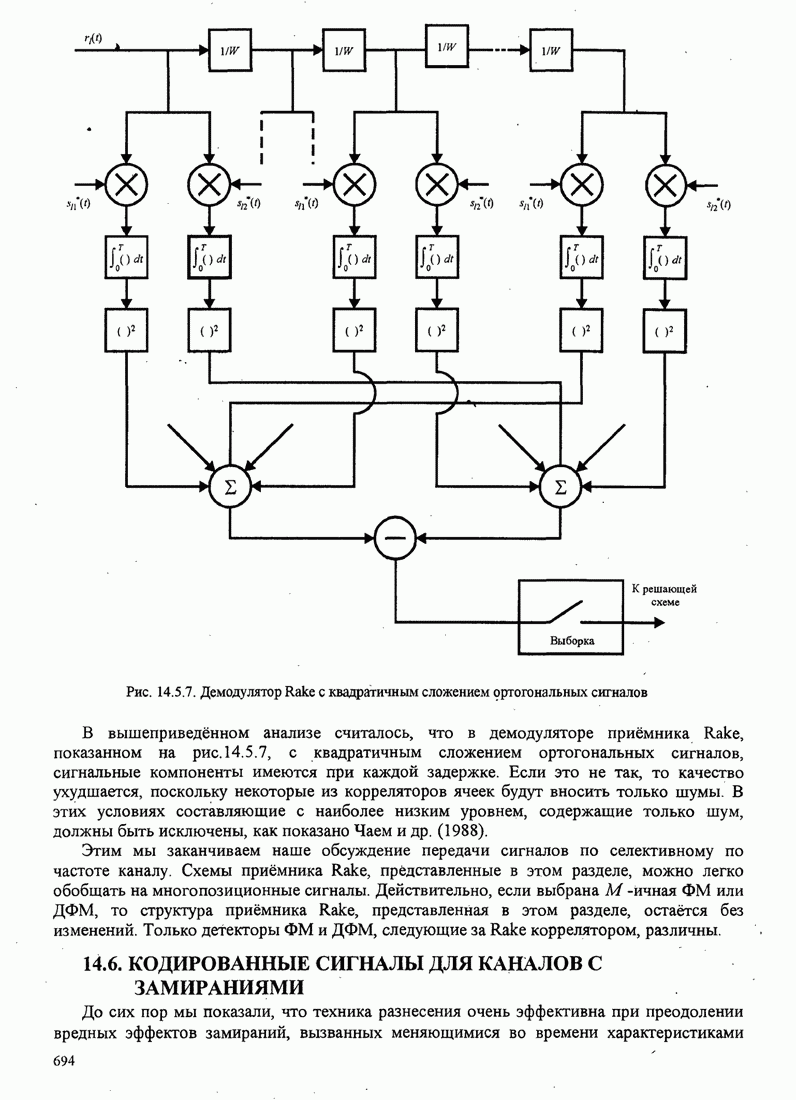
- 14.5.2. RAKE демодулятор
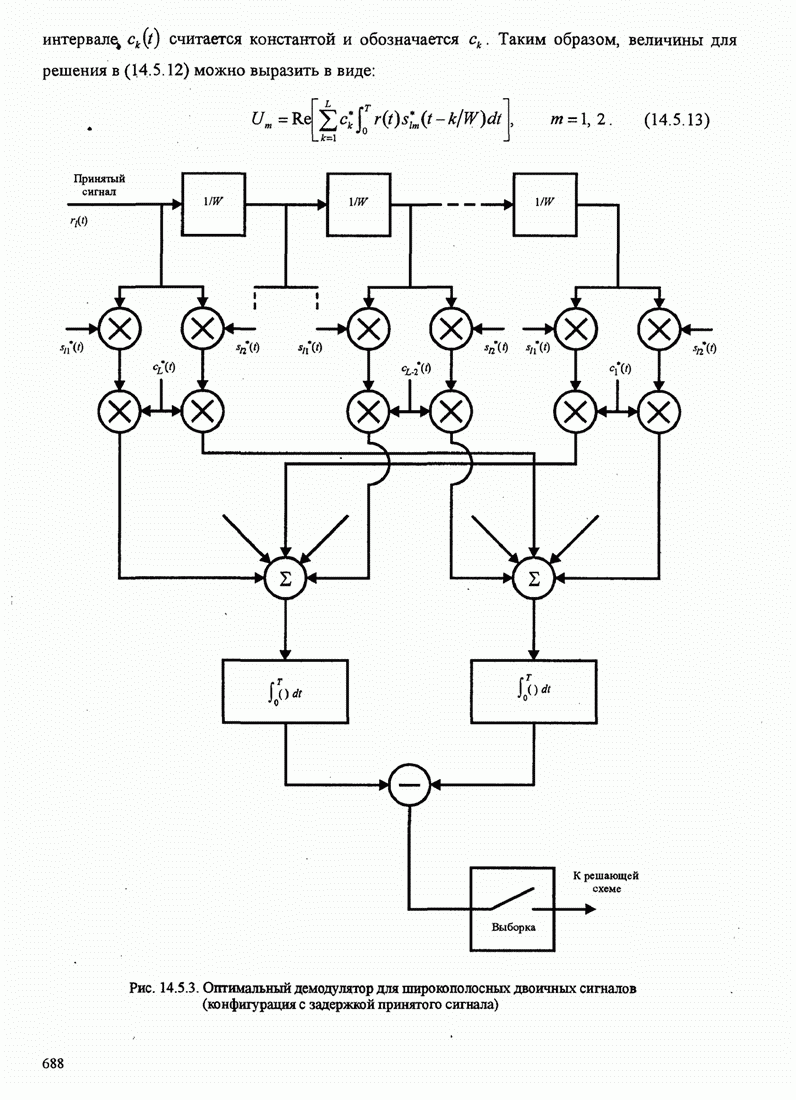
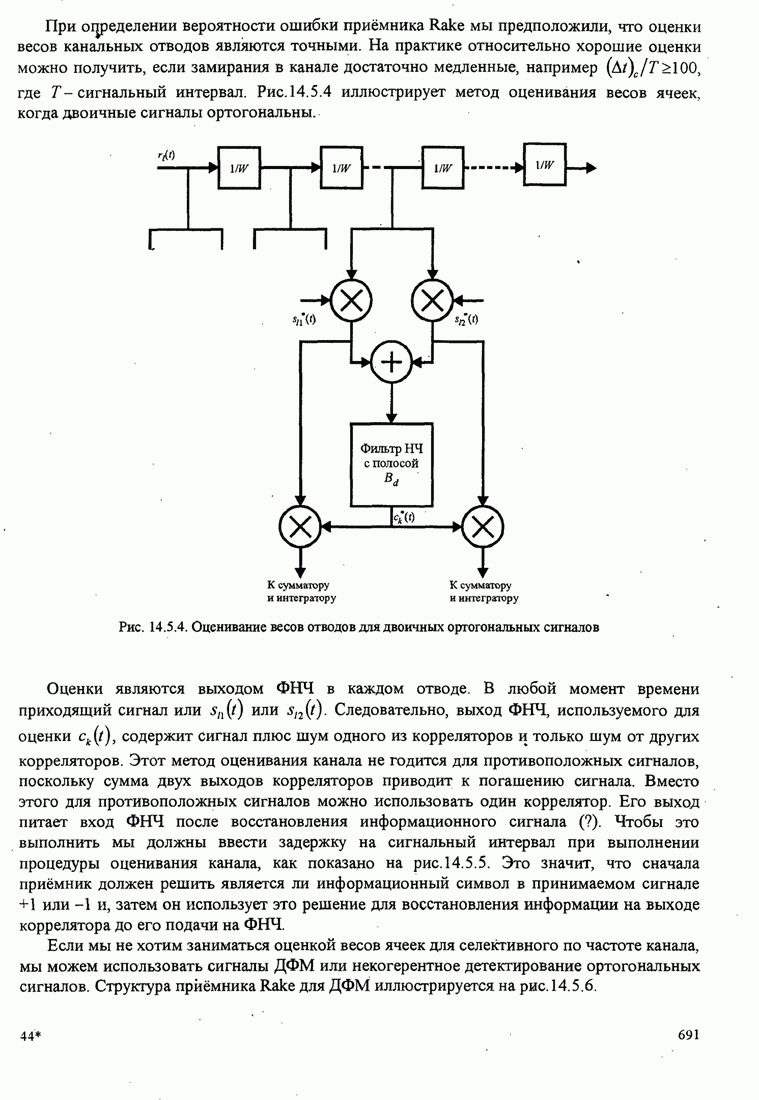
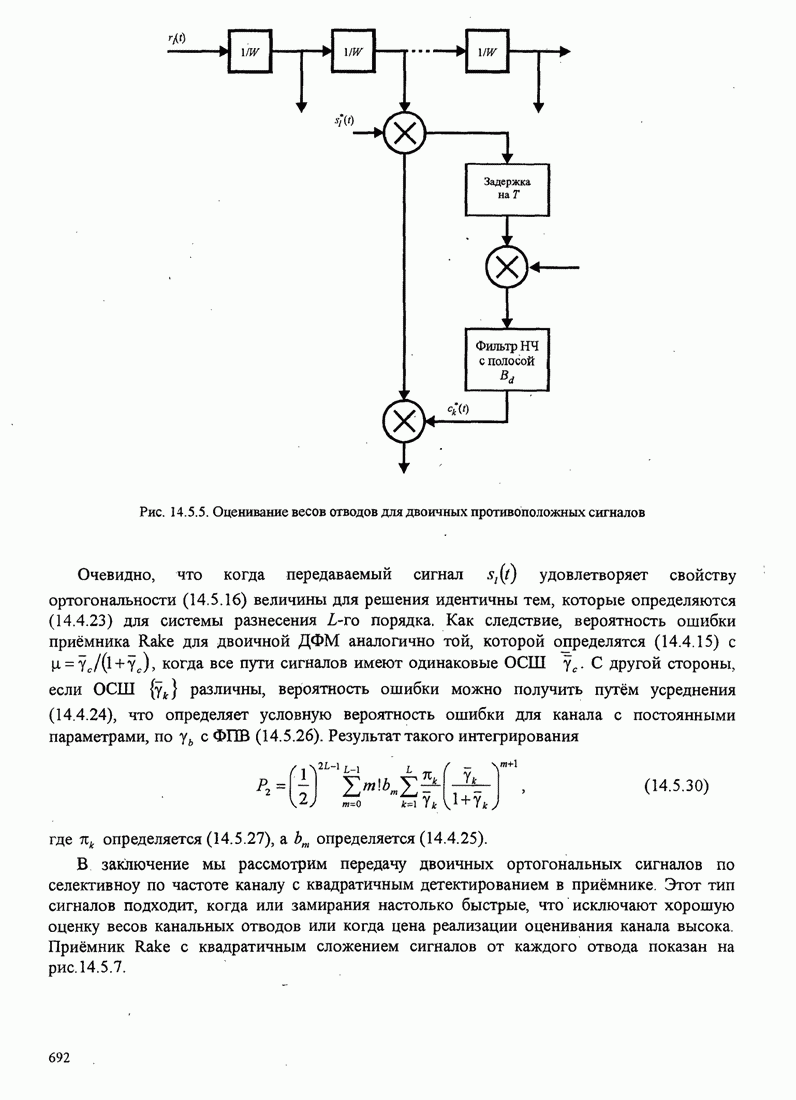
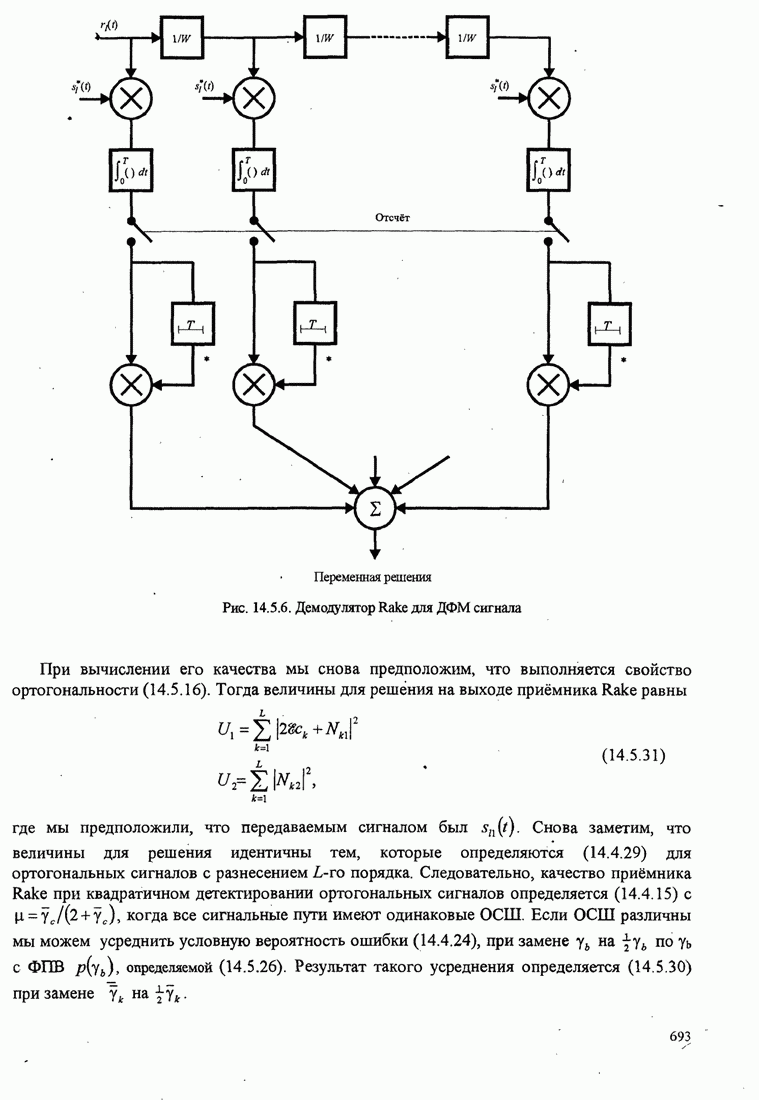
- 14.5.3. Качество RAKE приемника
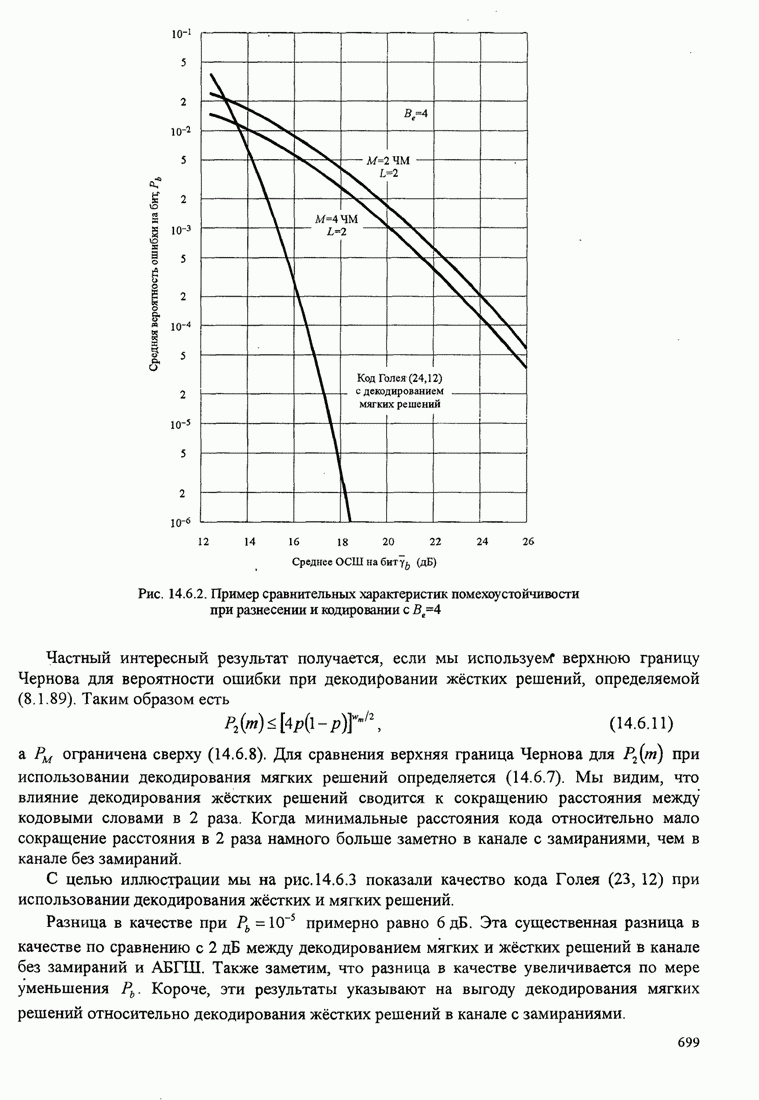
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
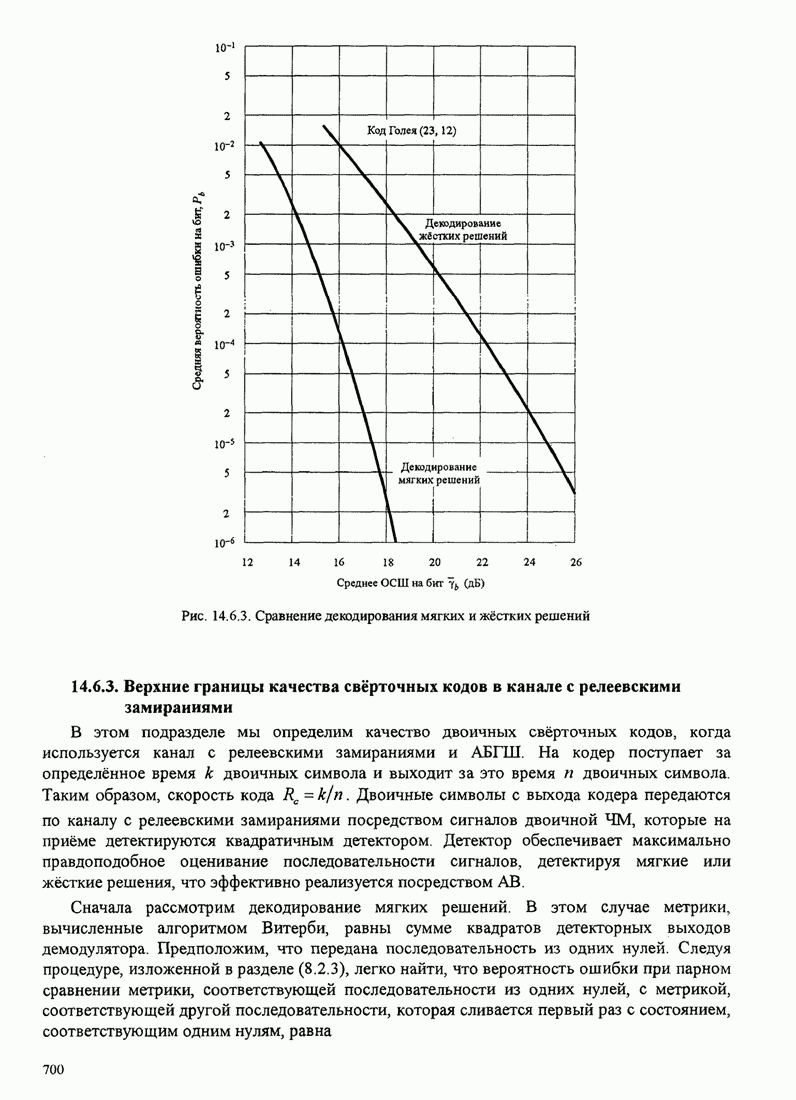
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
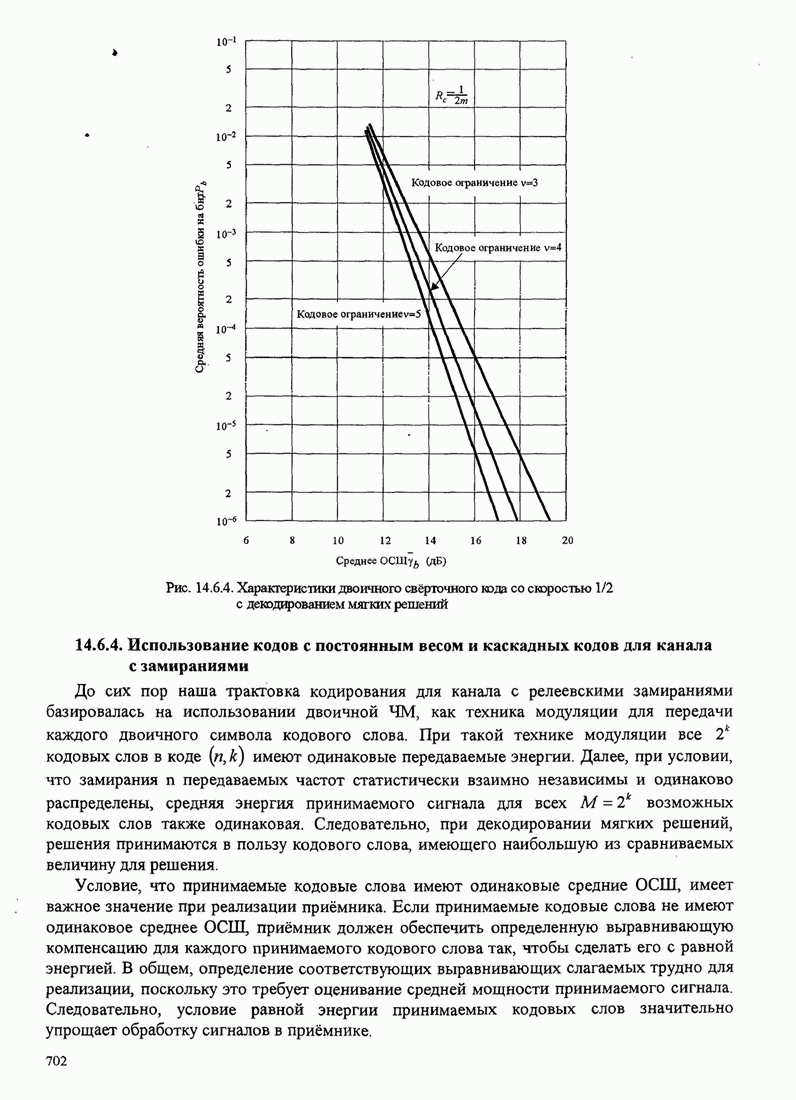
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)