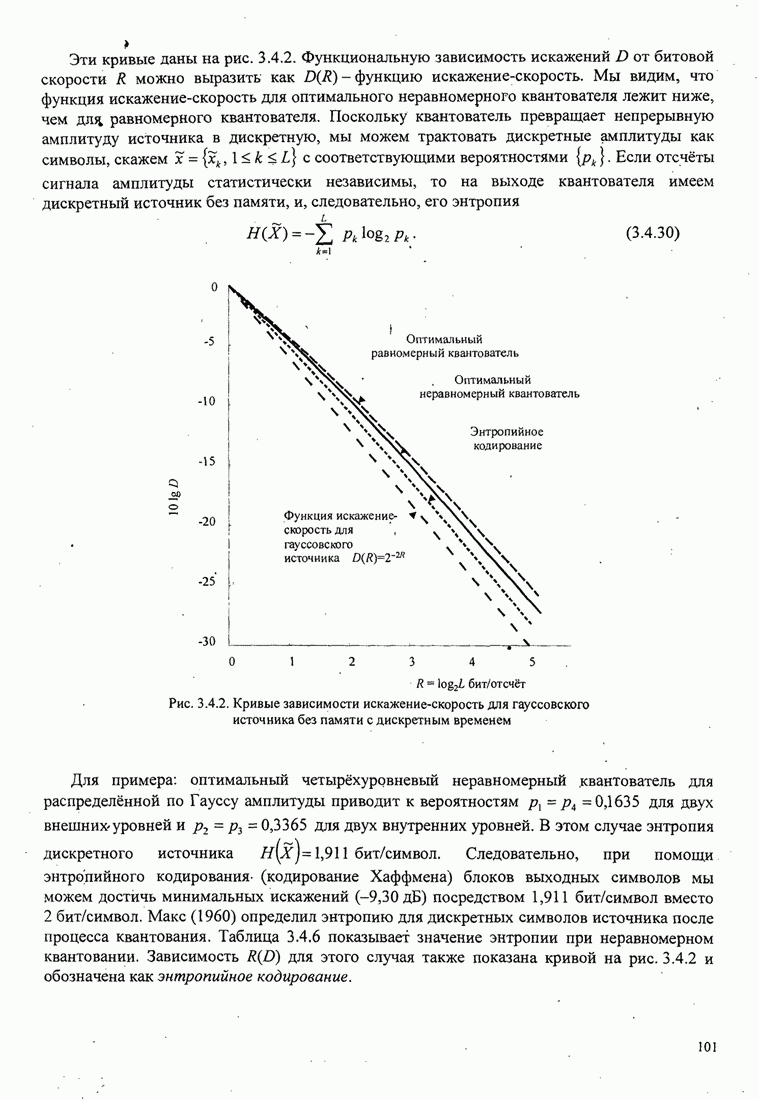
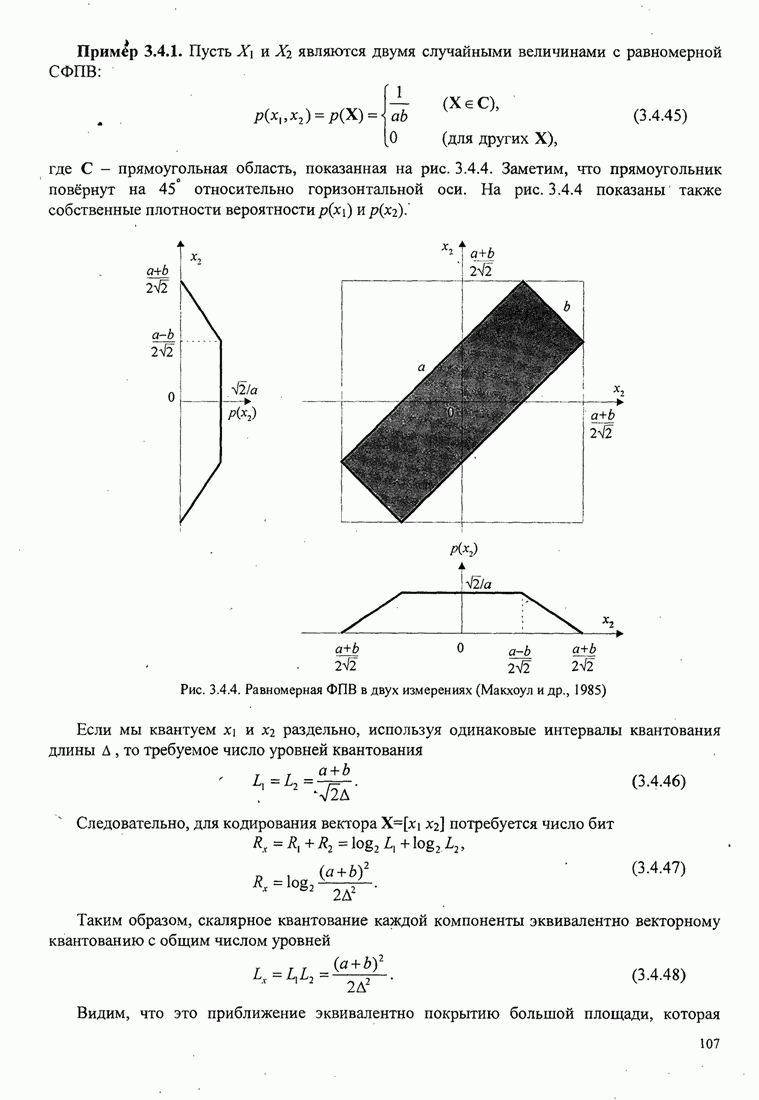
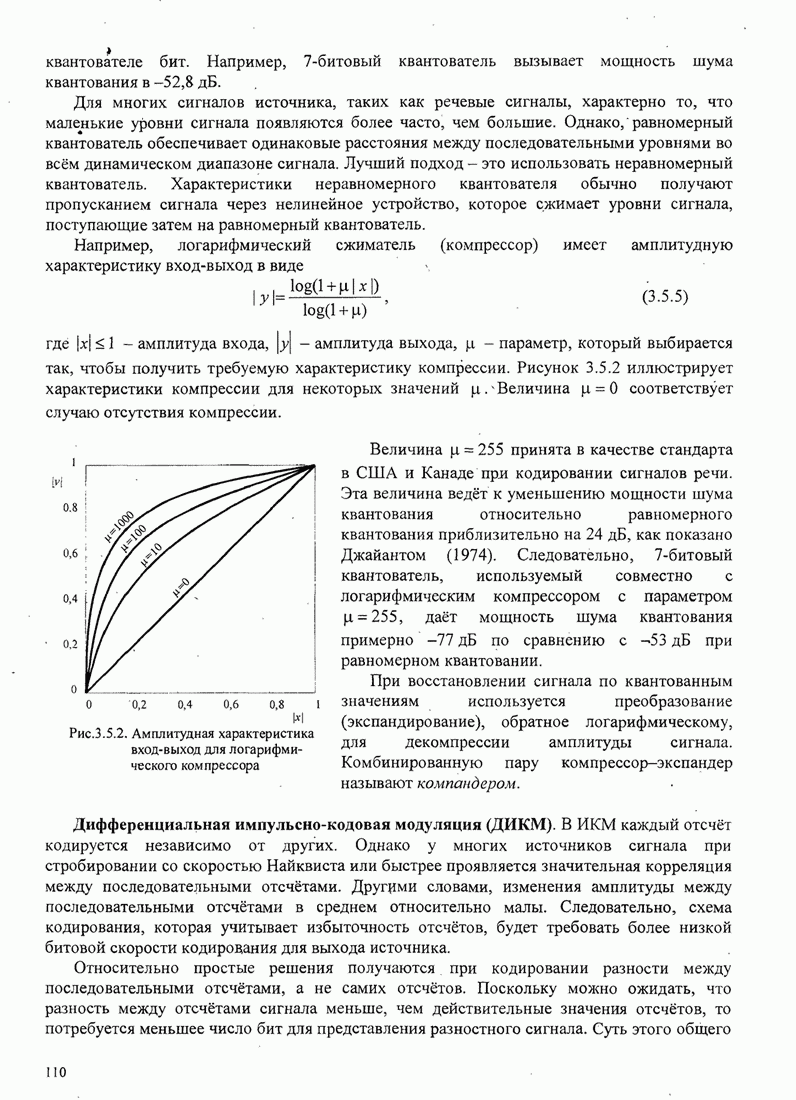
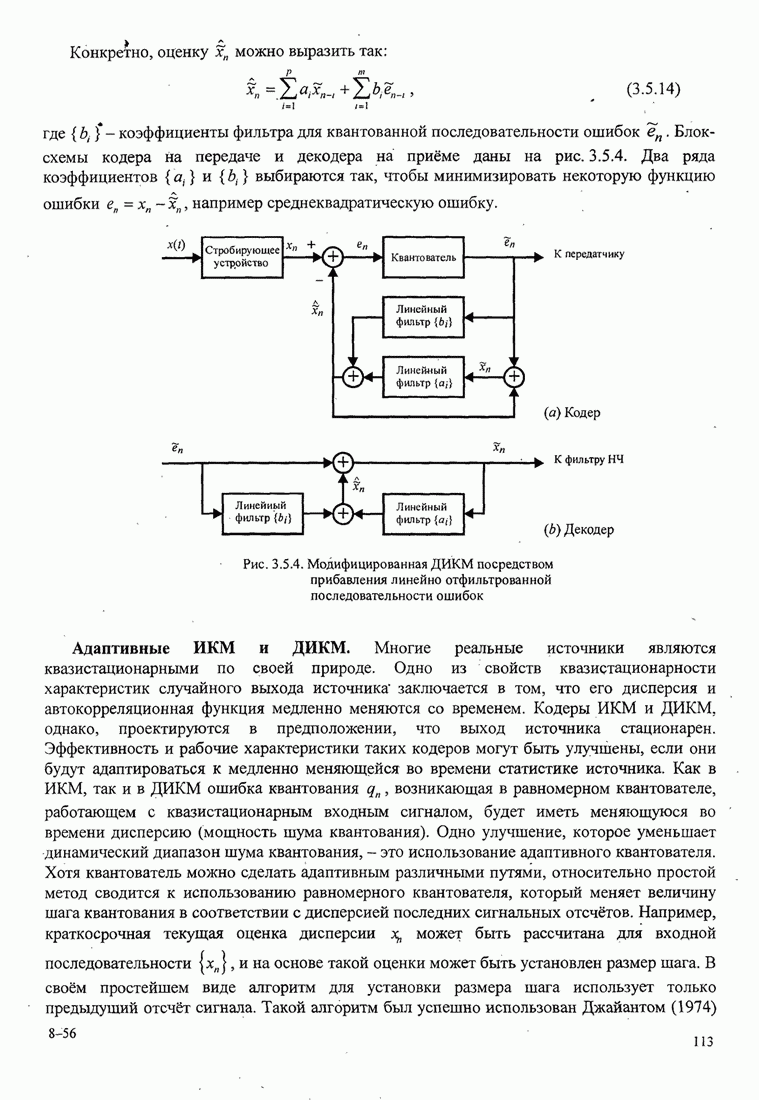
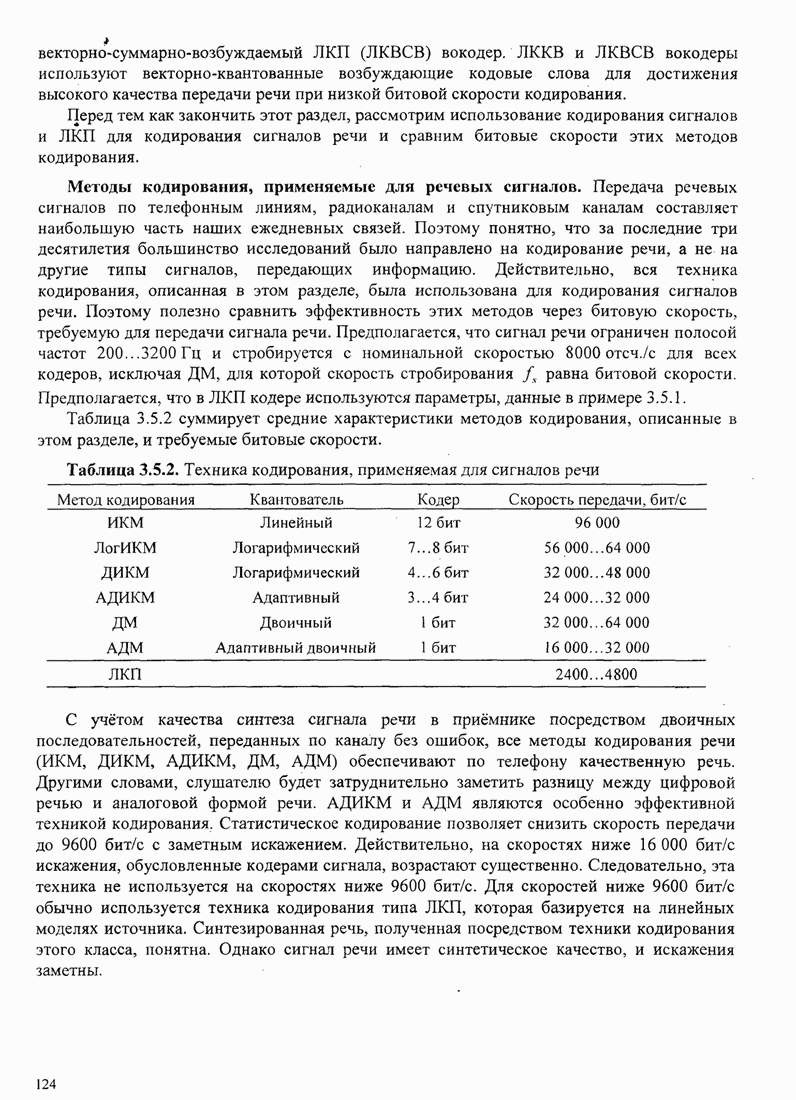
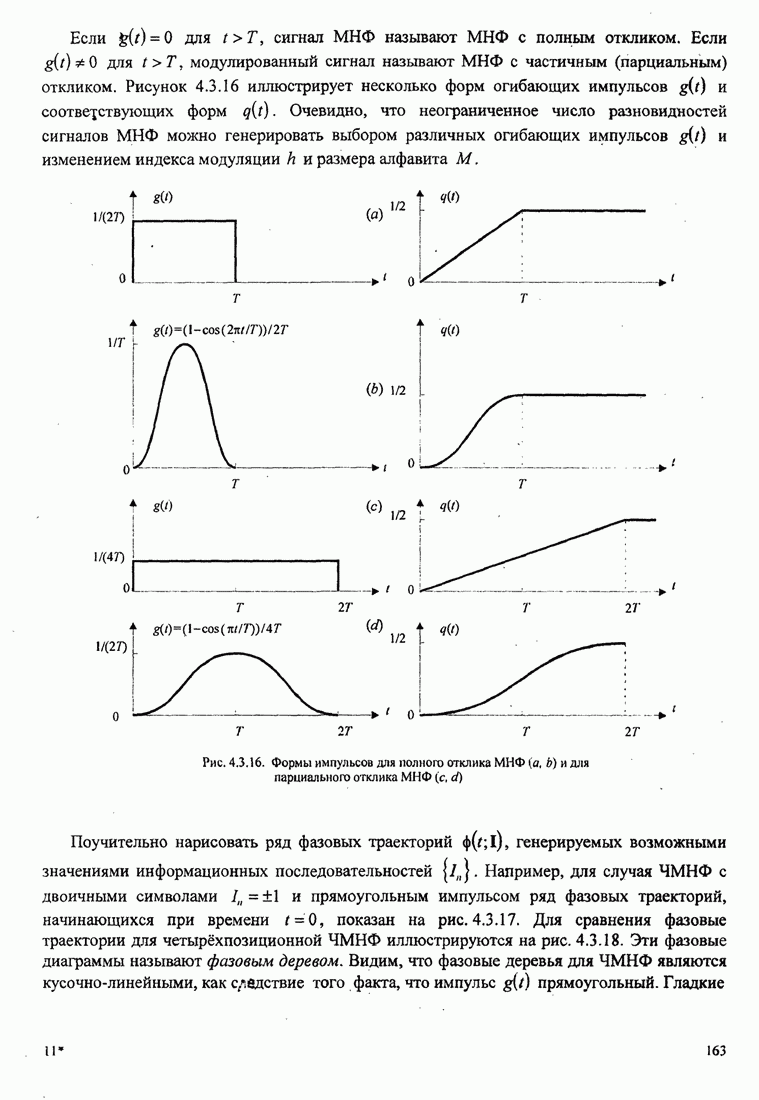
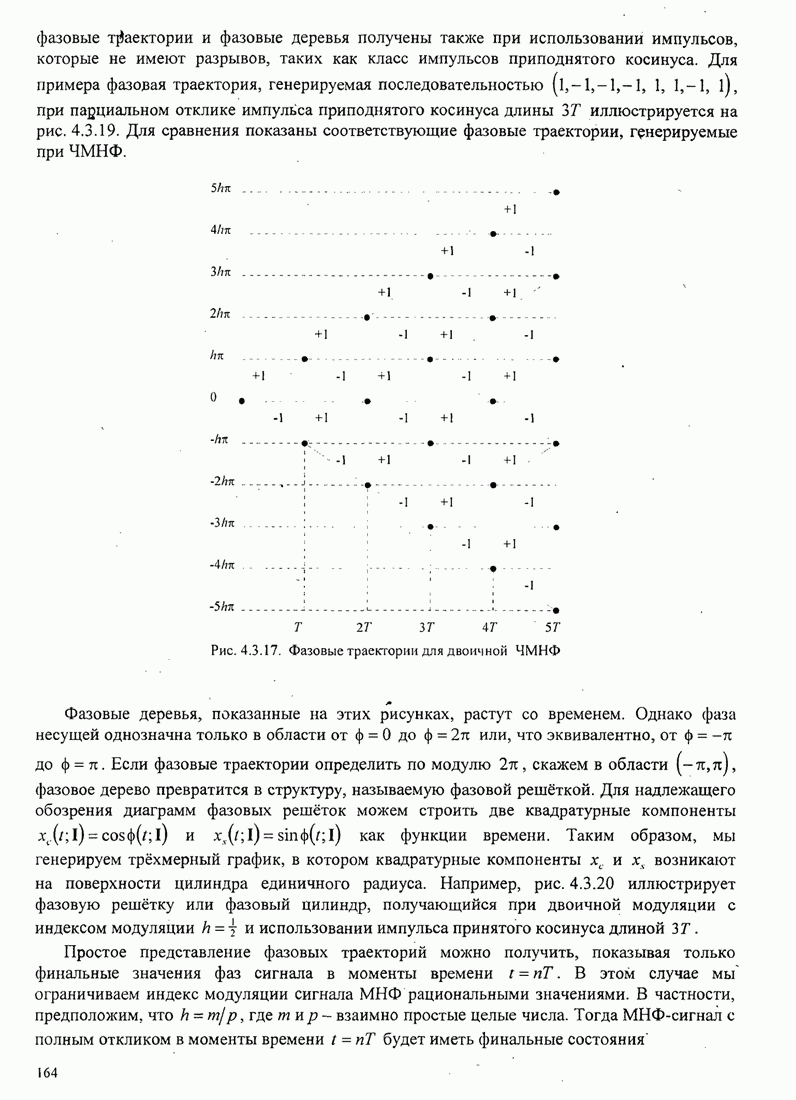
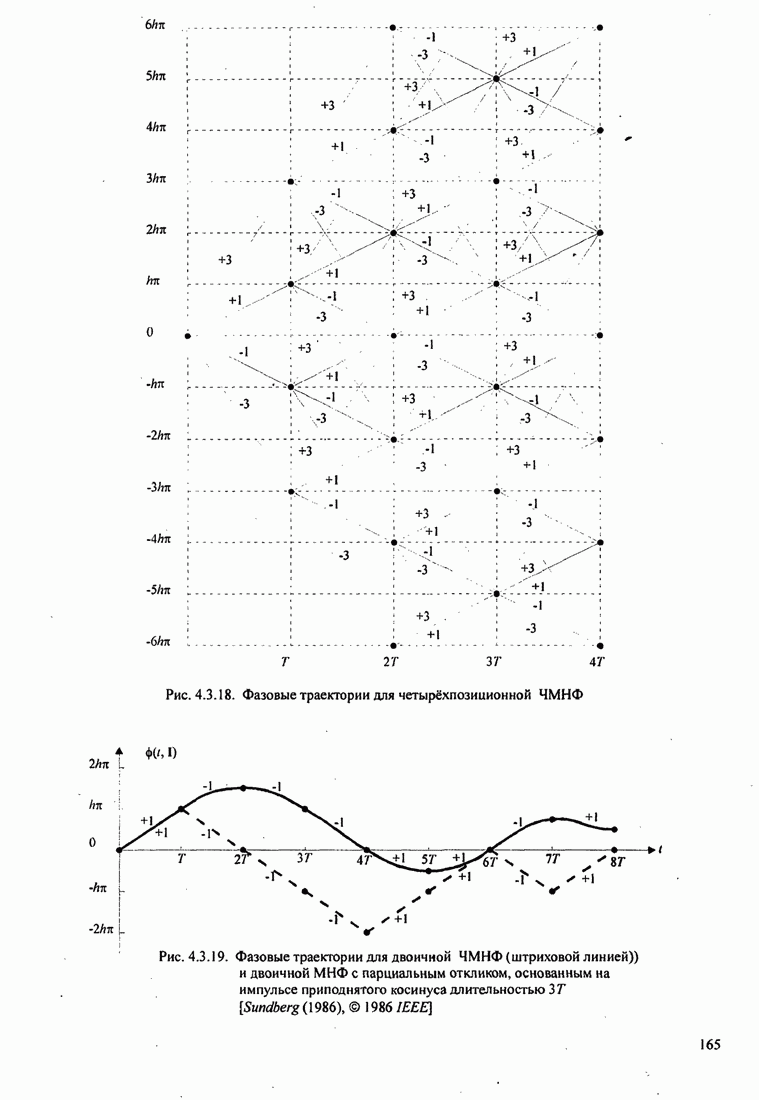
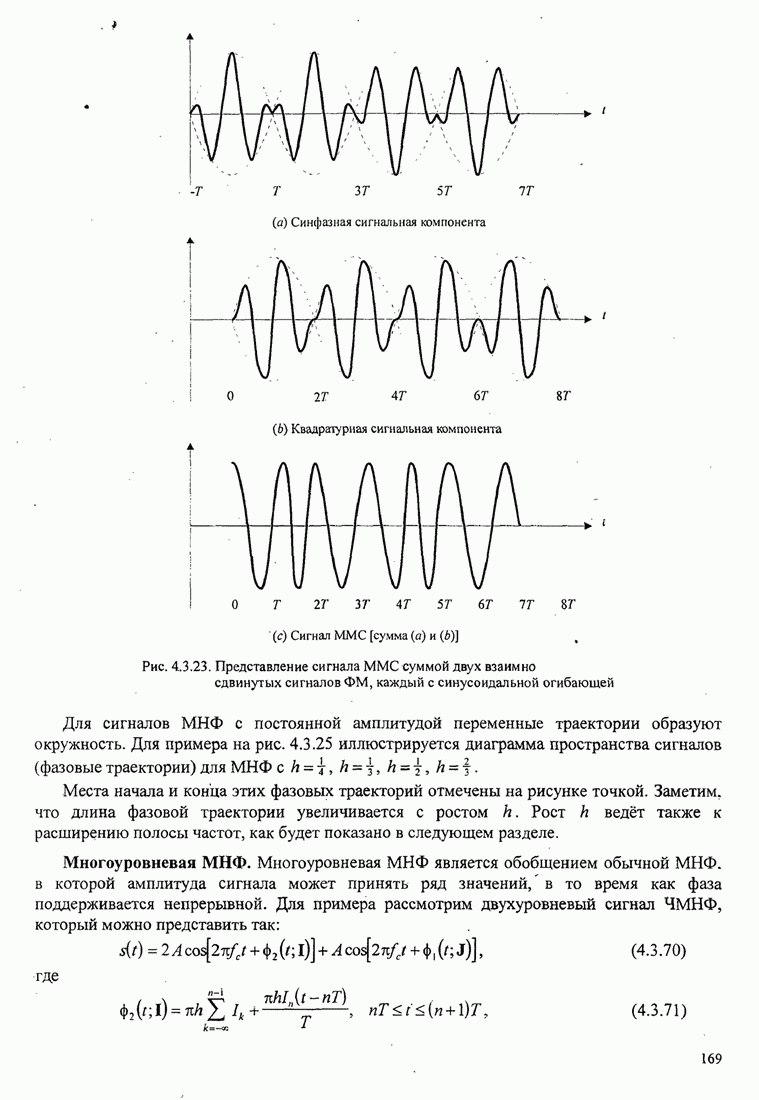
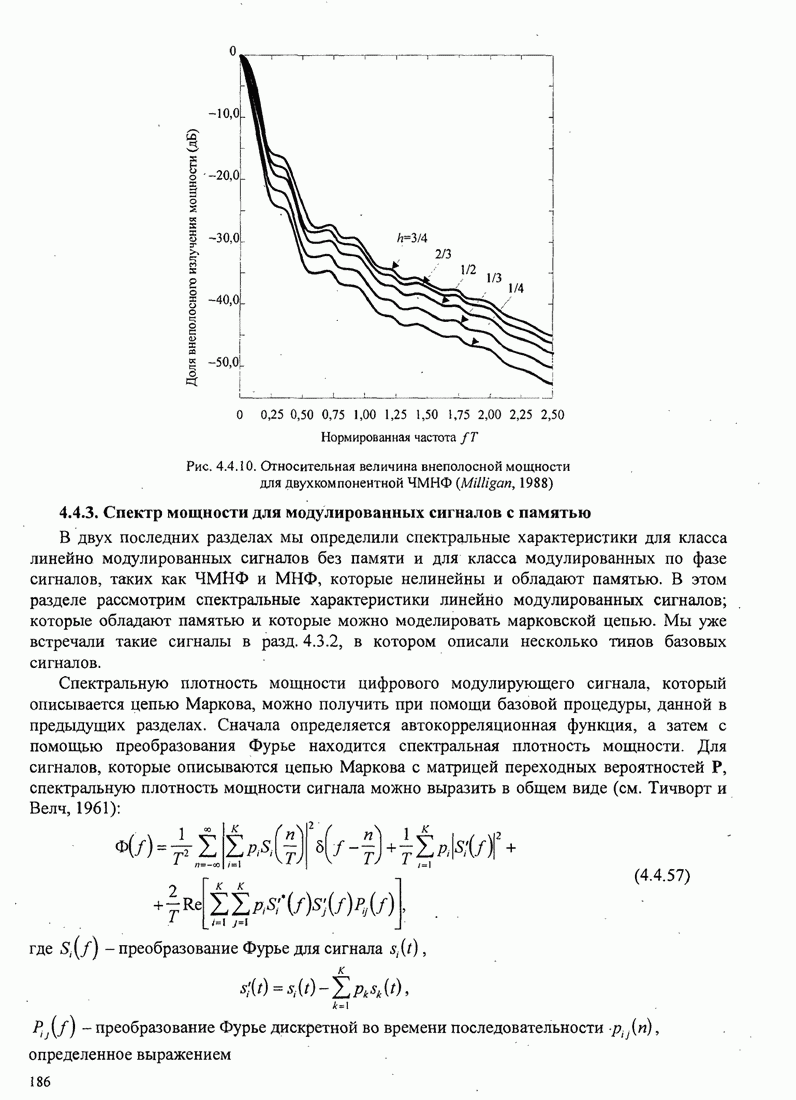
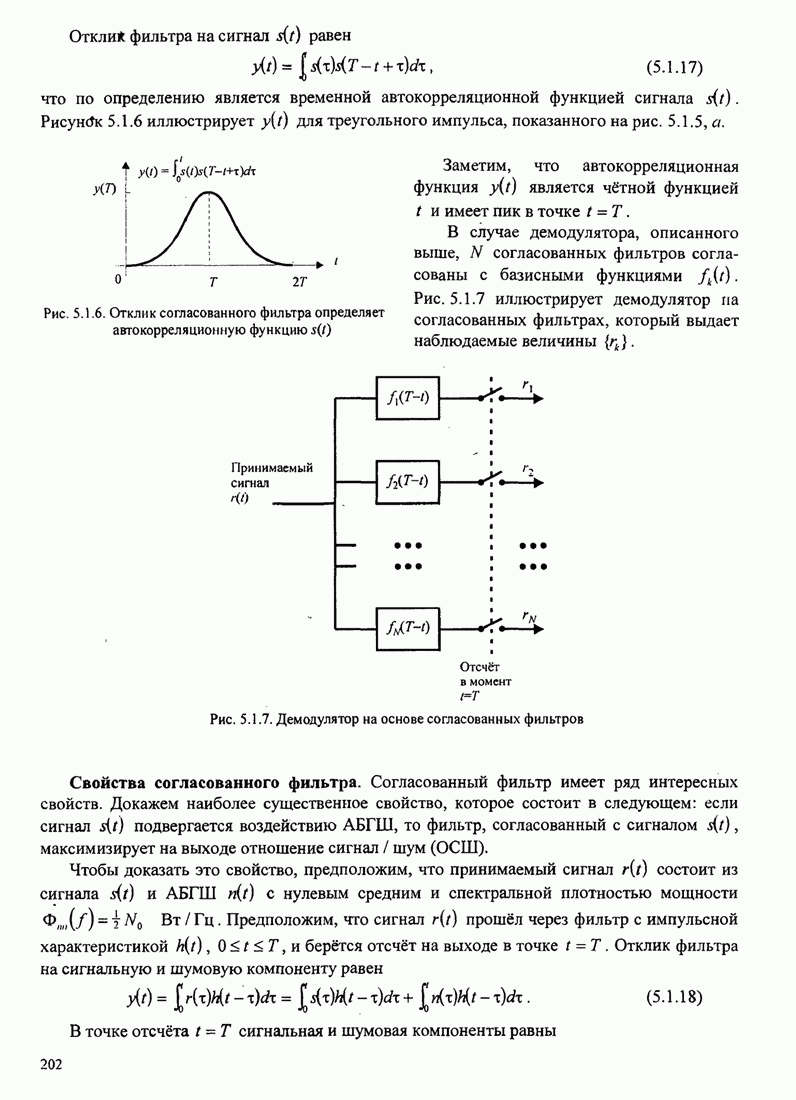
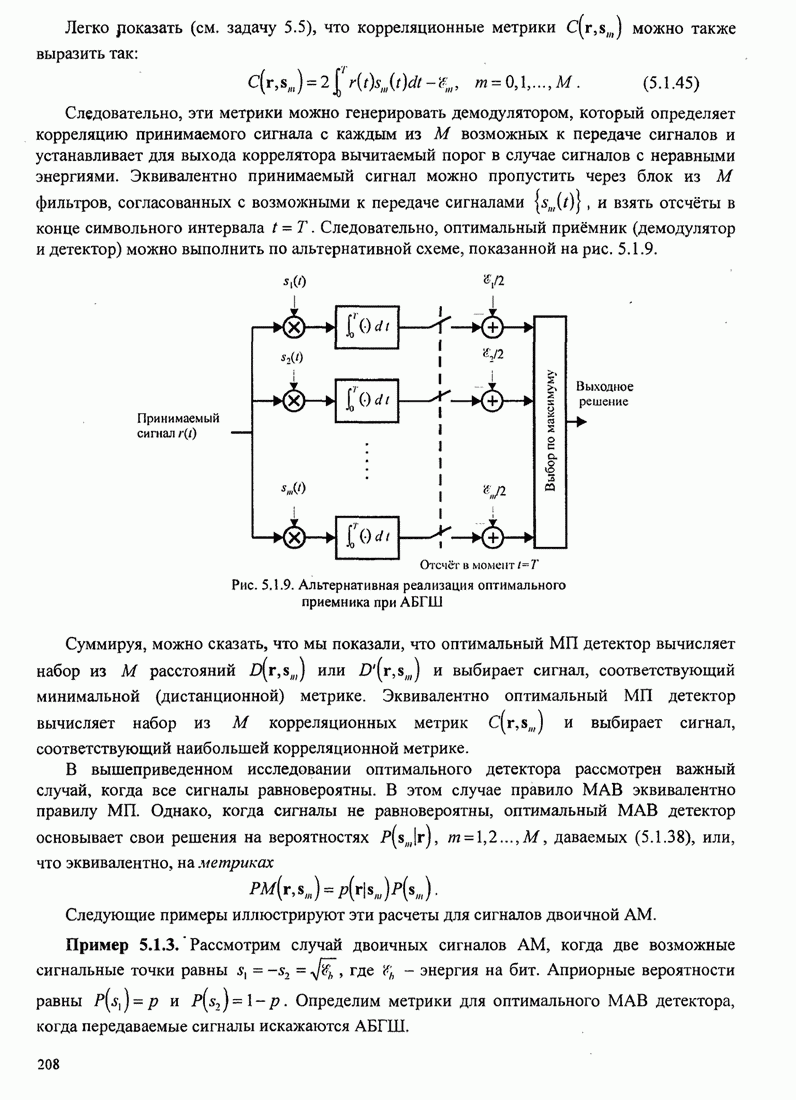
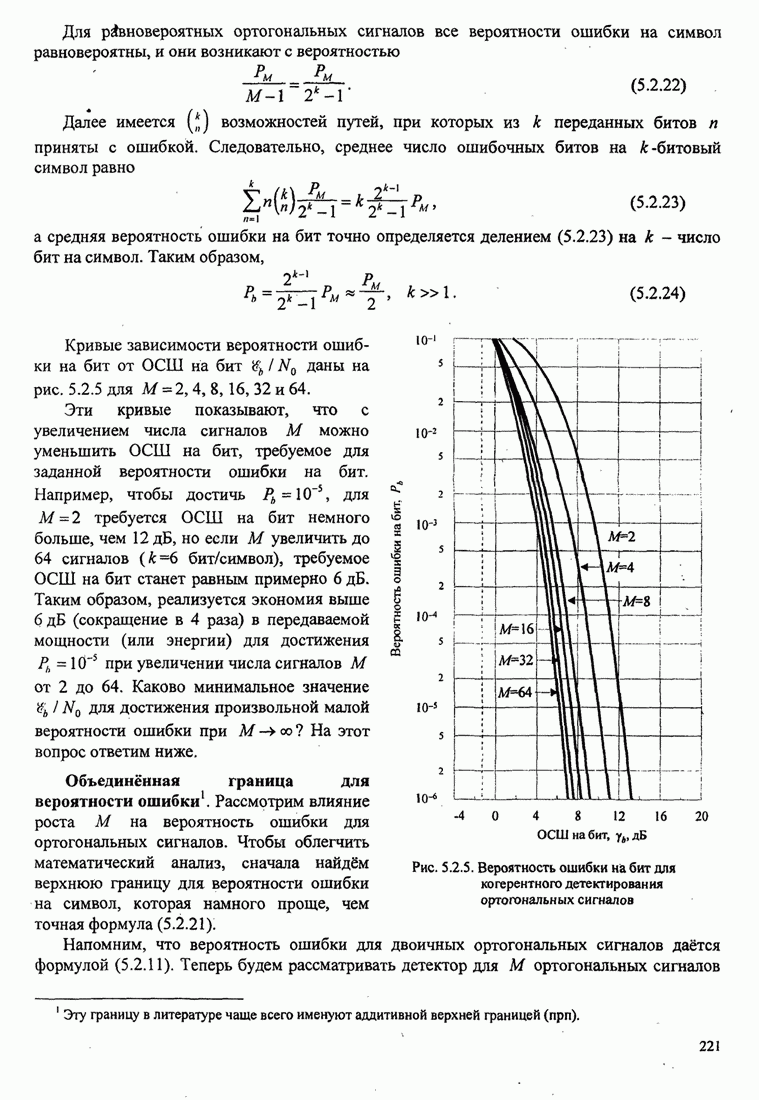
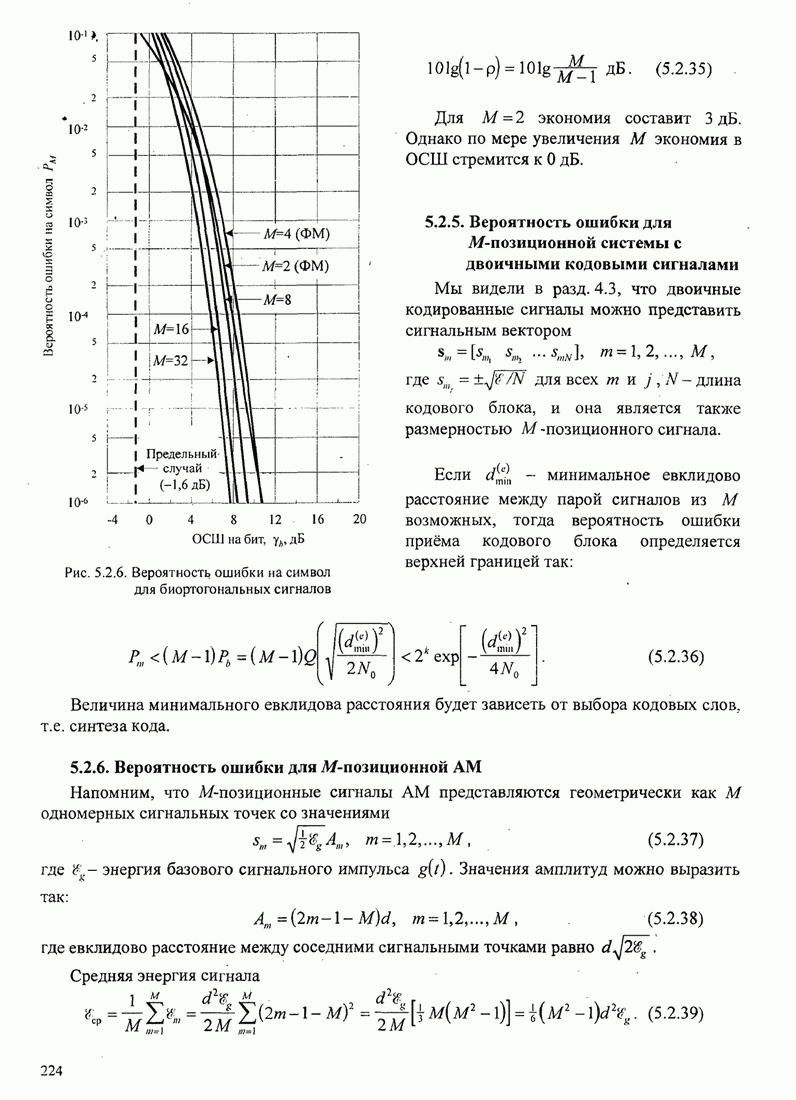
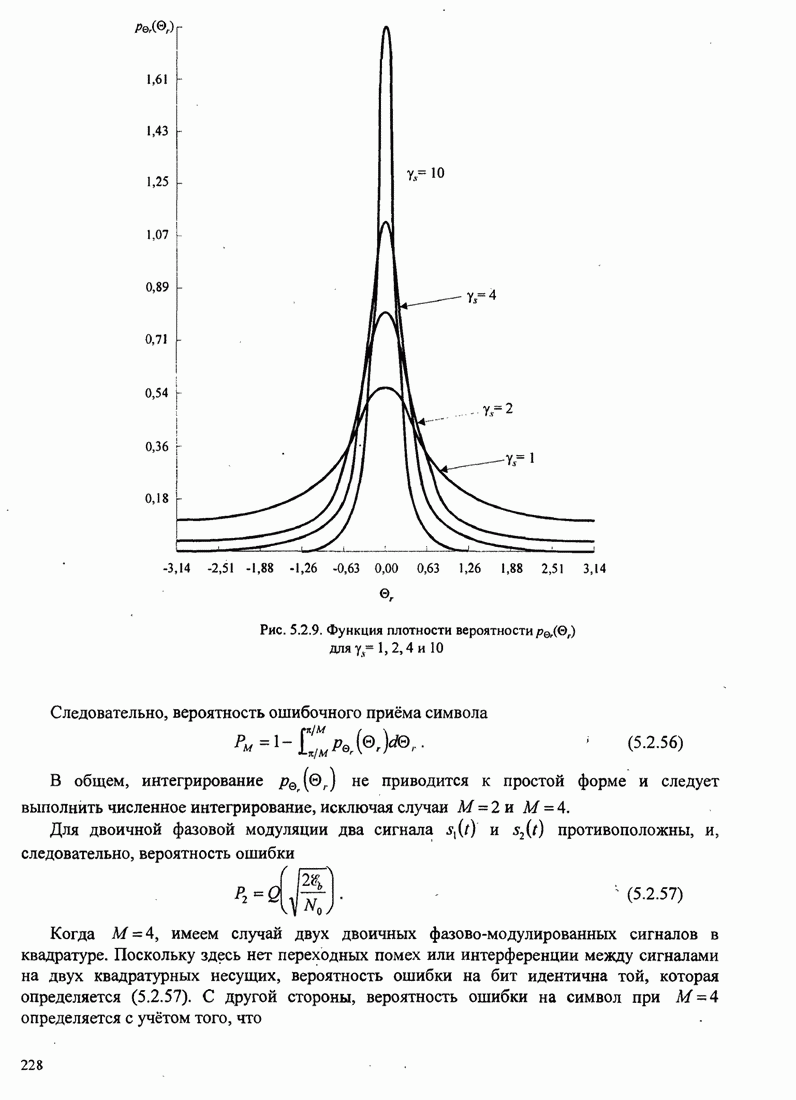
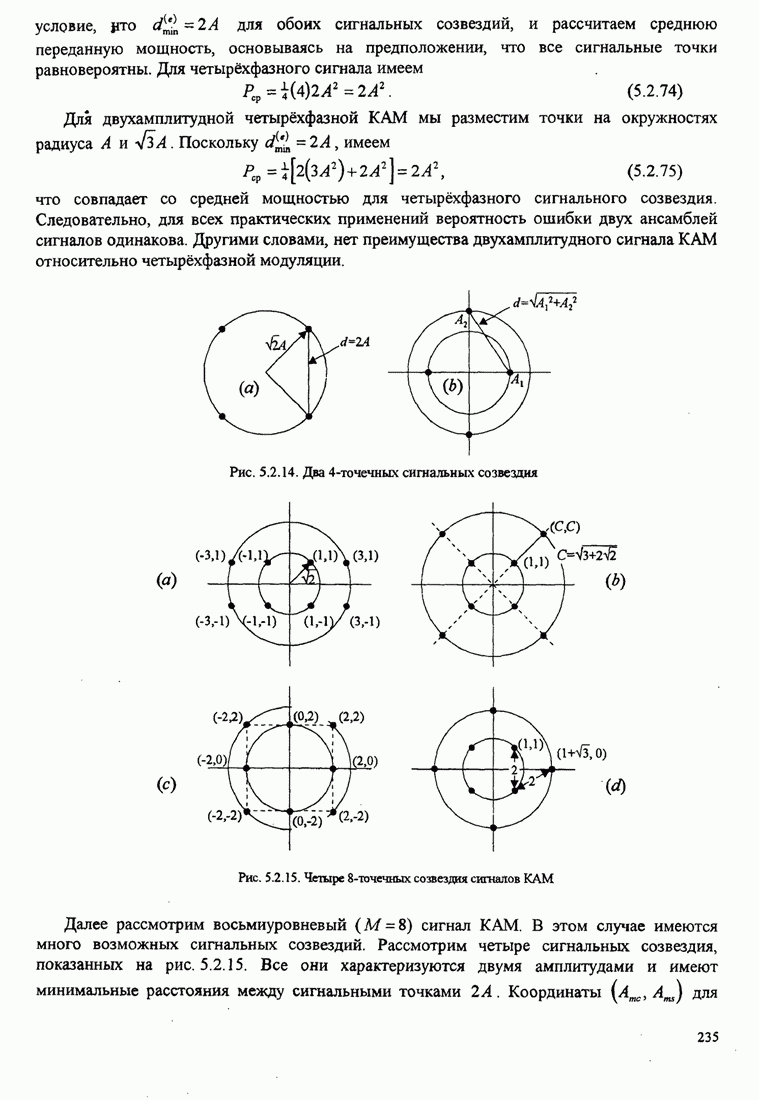
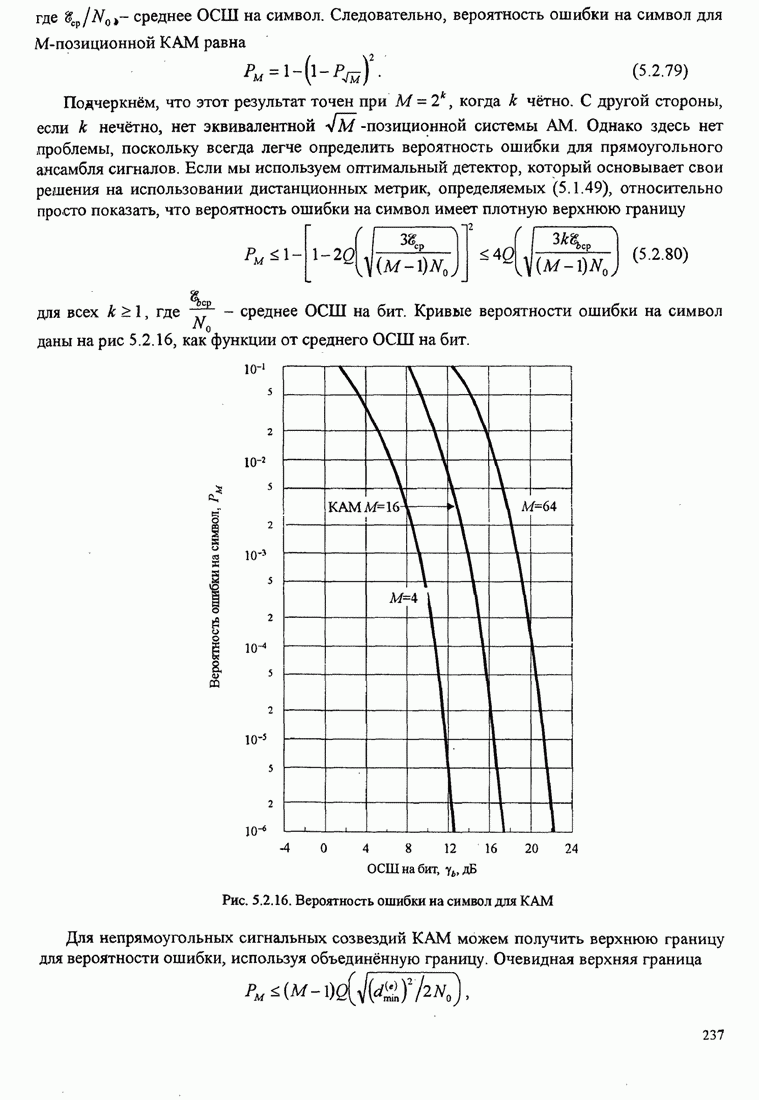
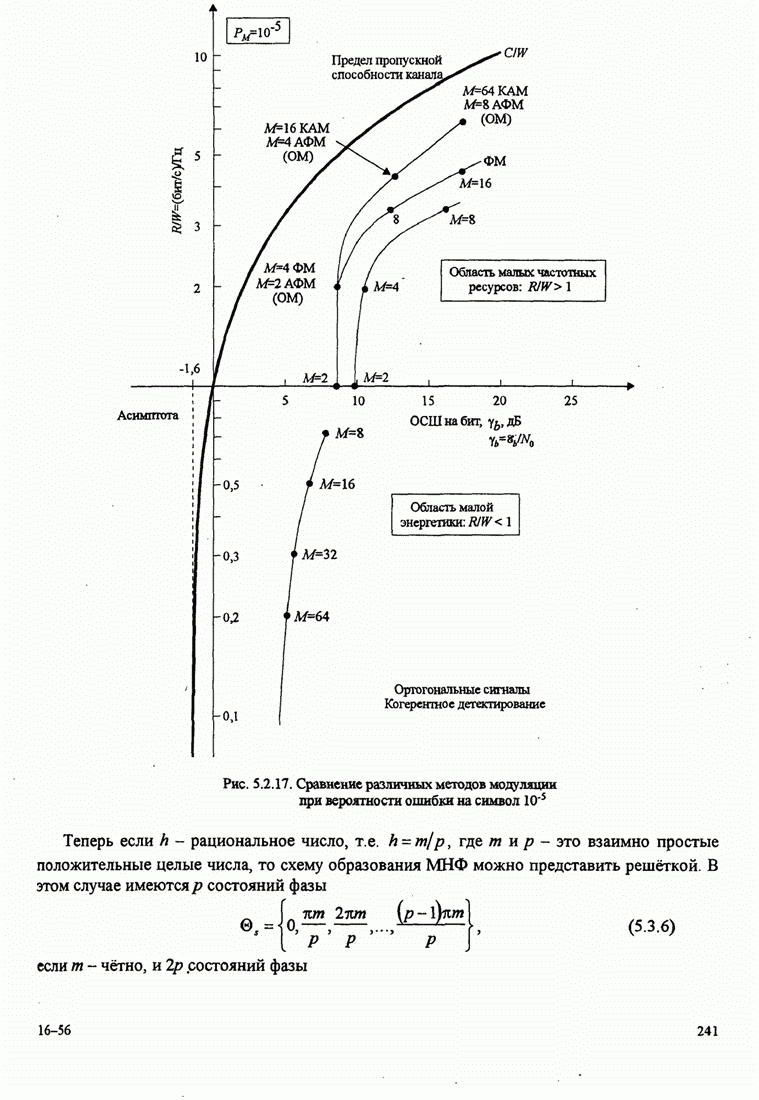
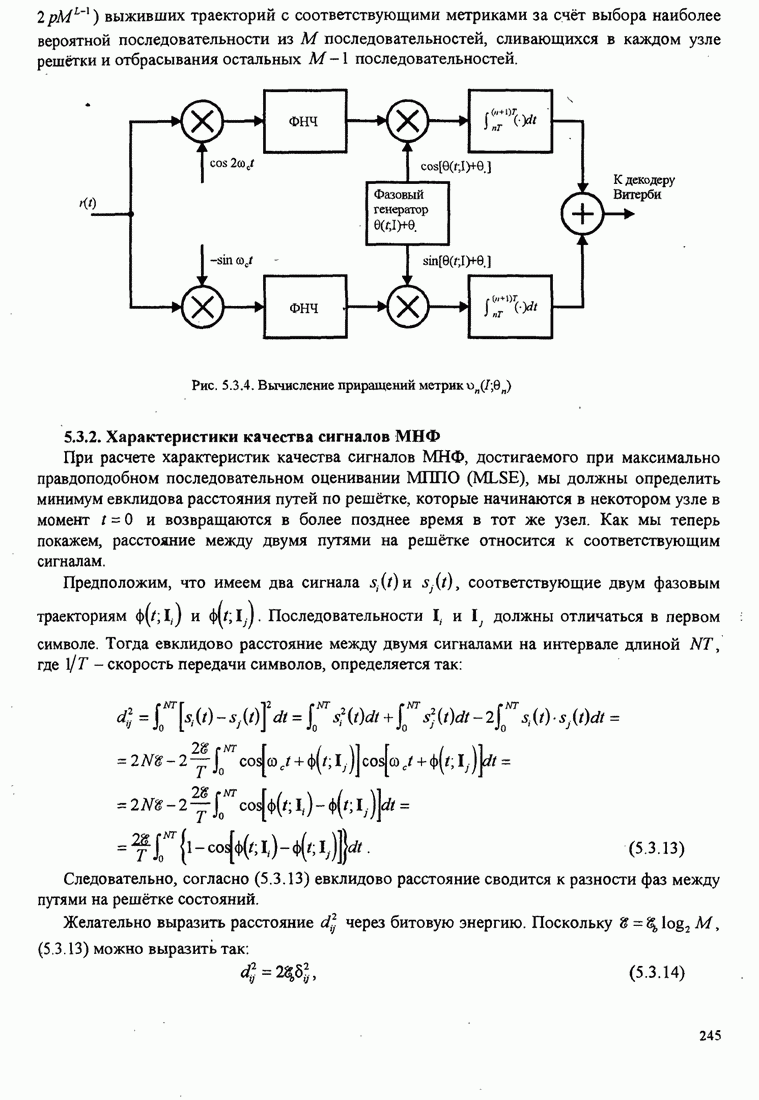
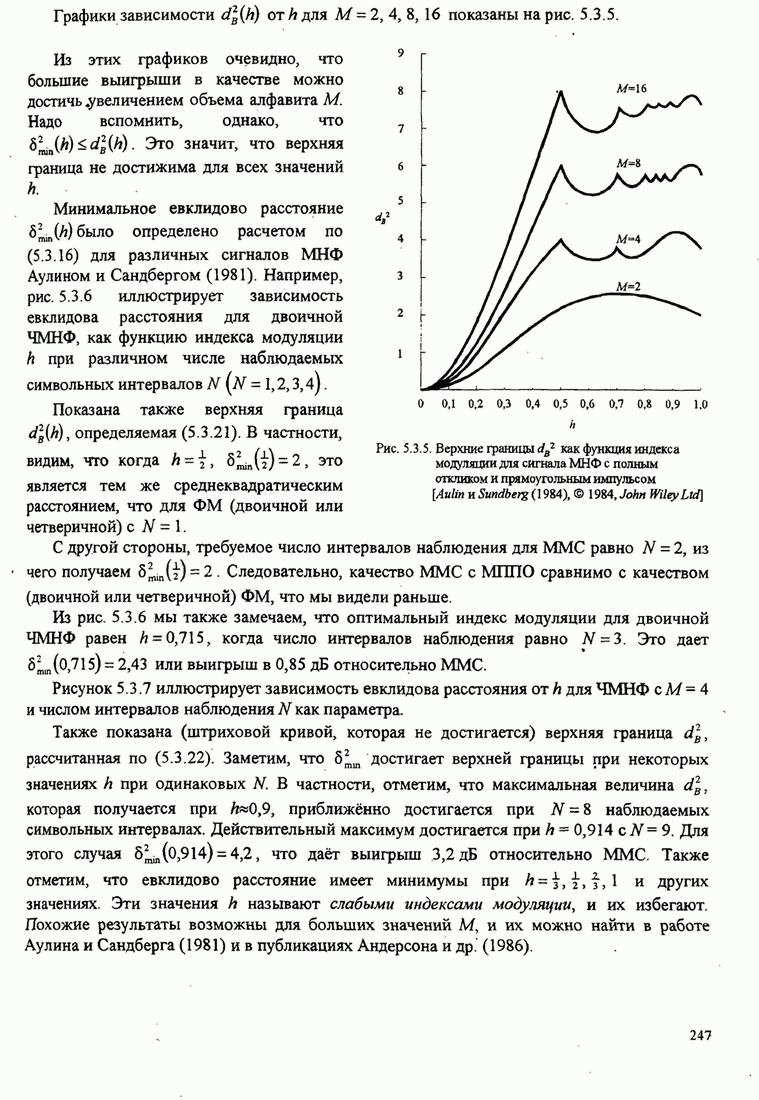
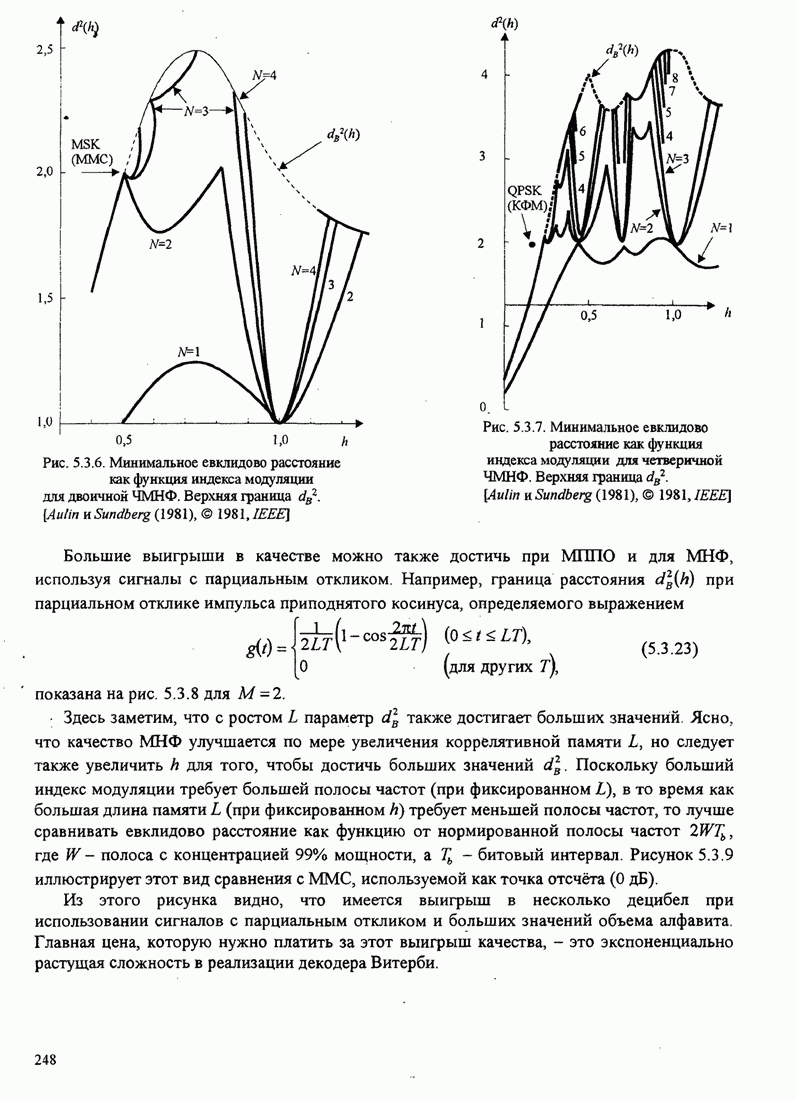
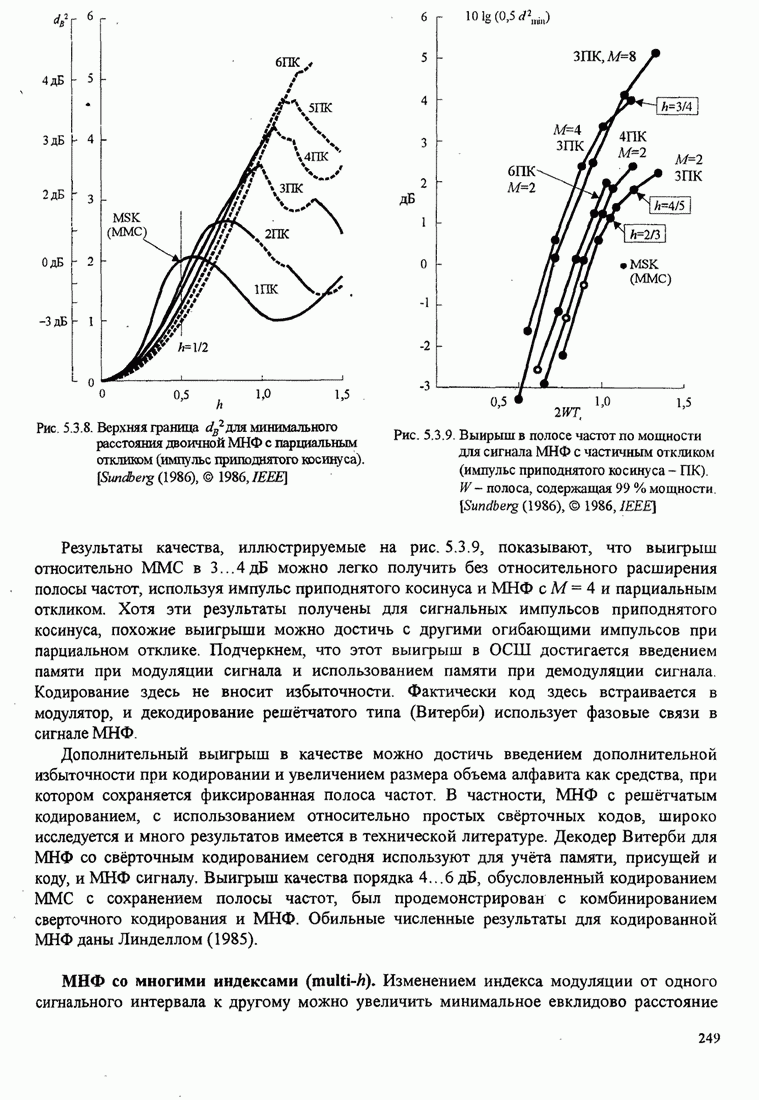
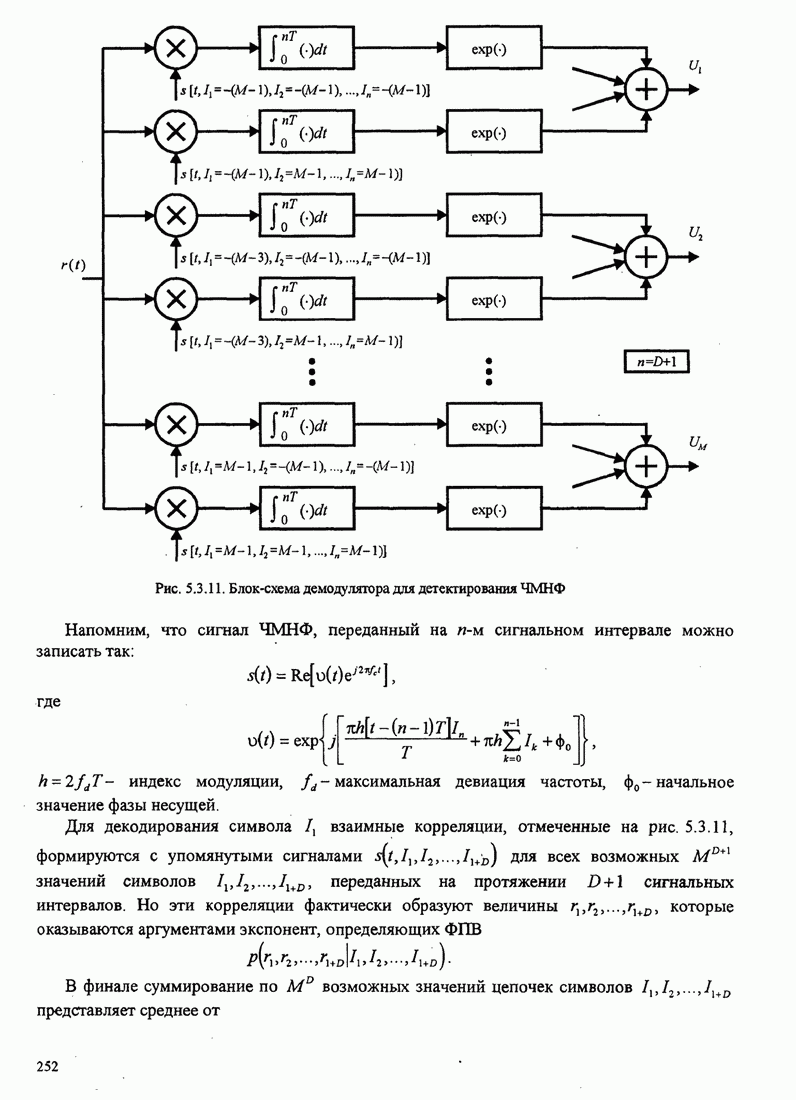
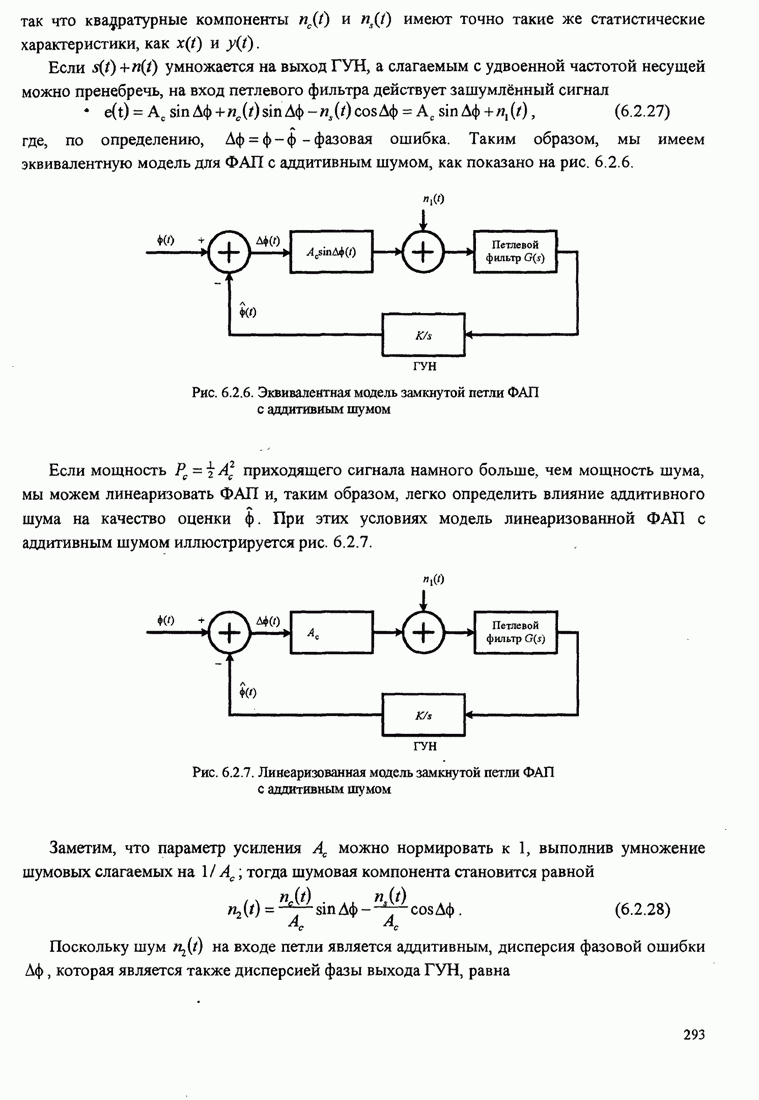
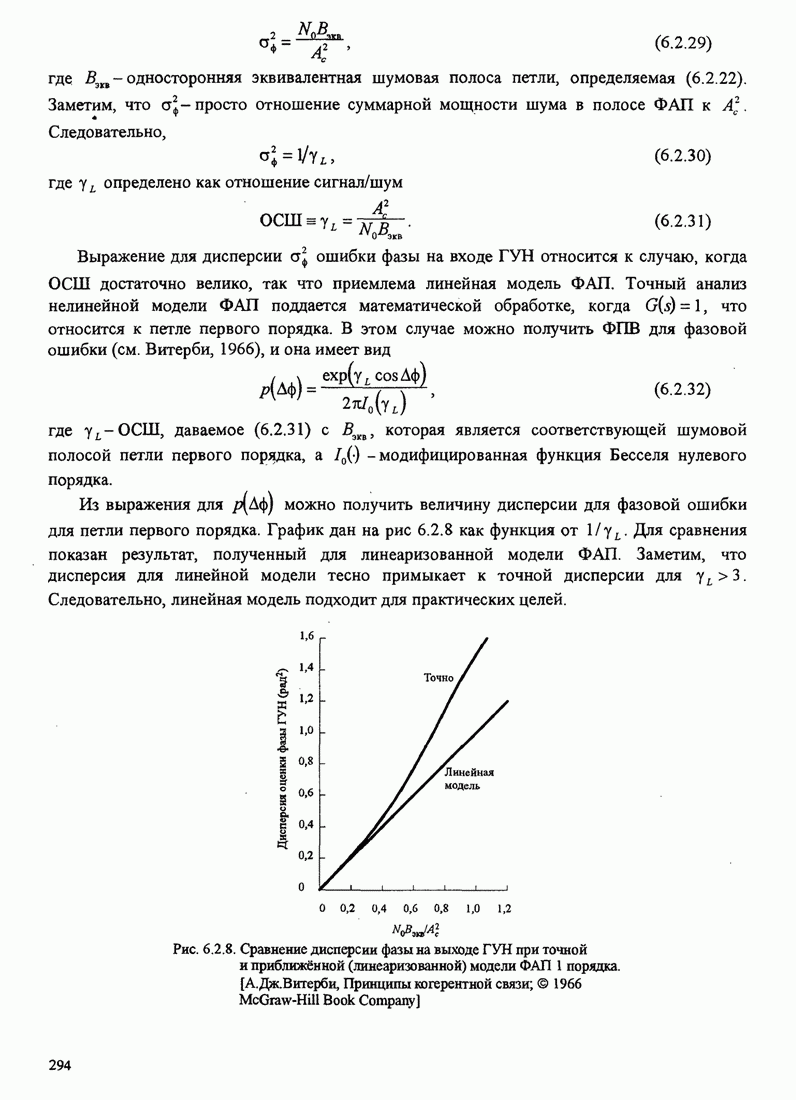
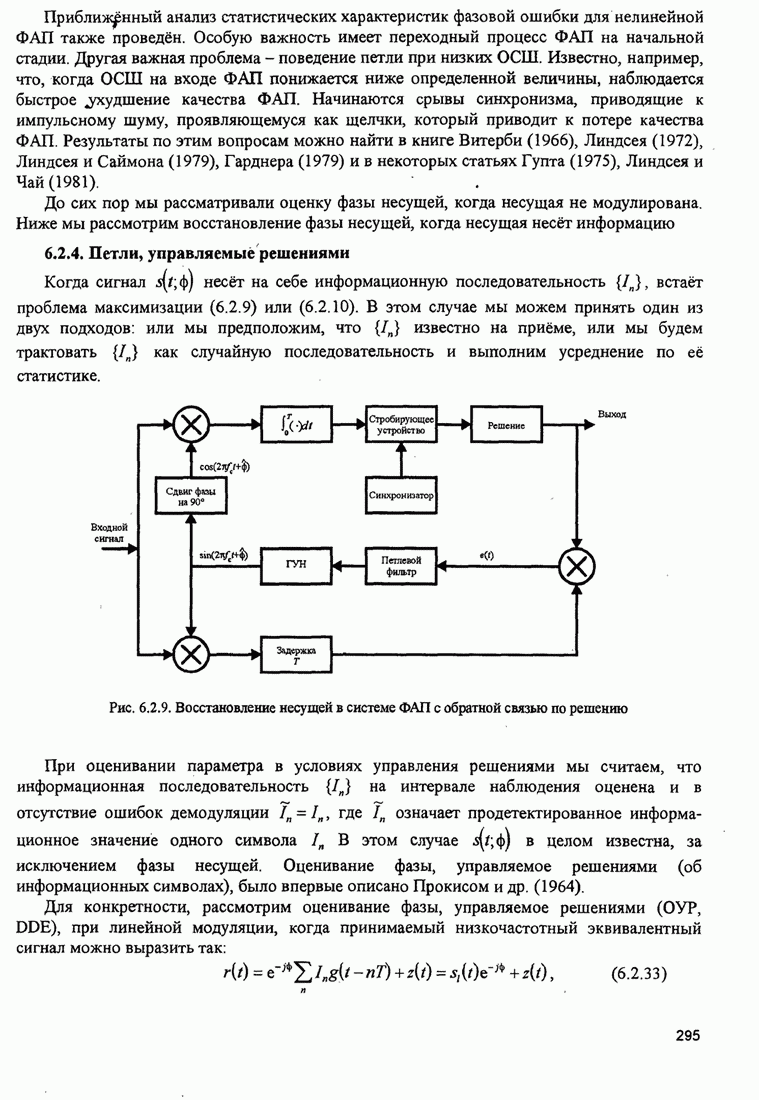
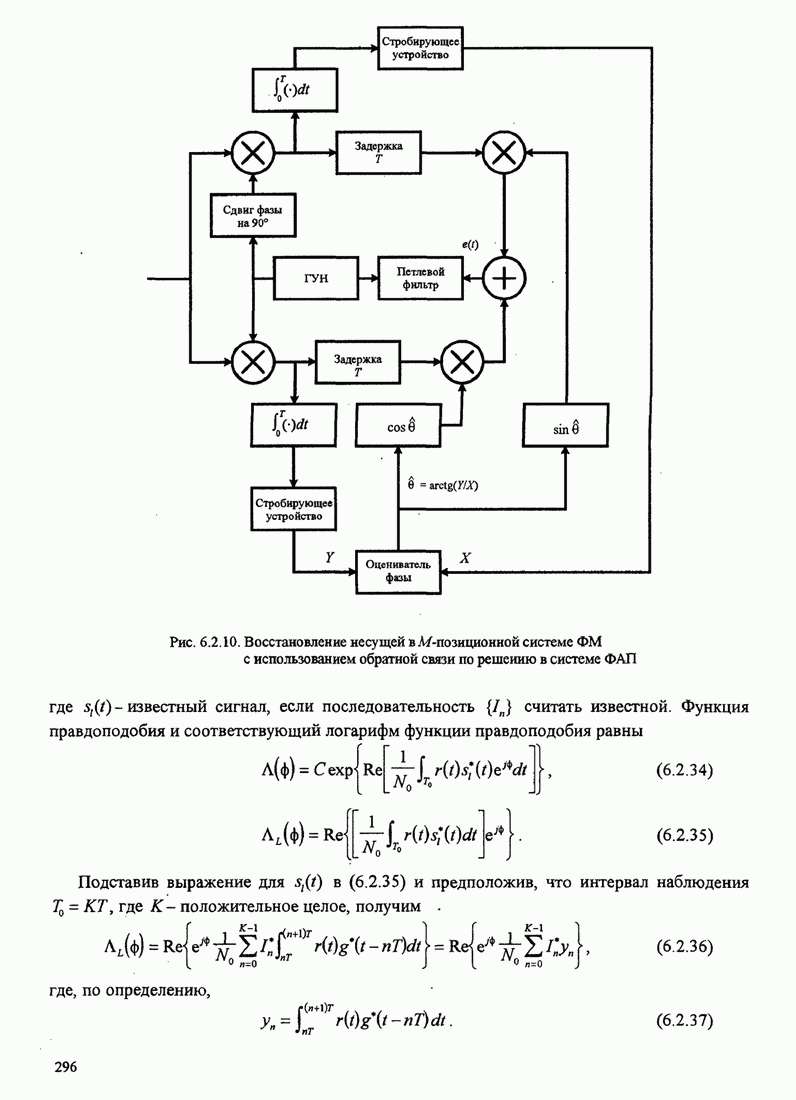
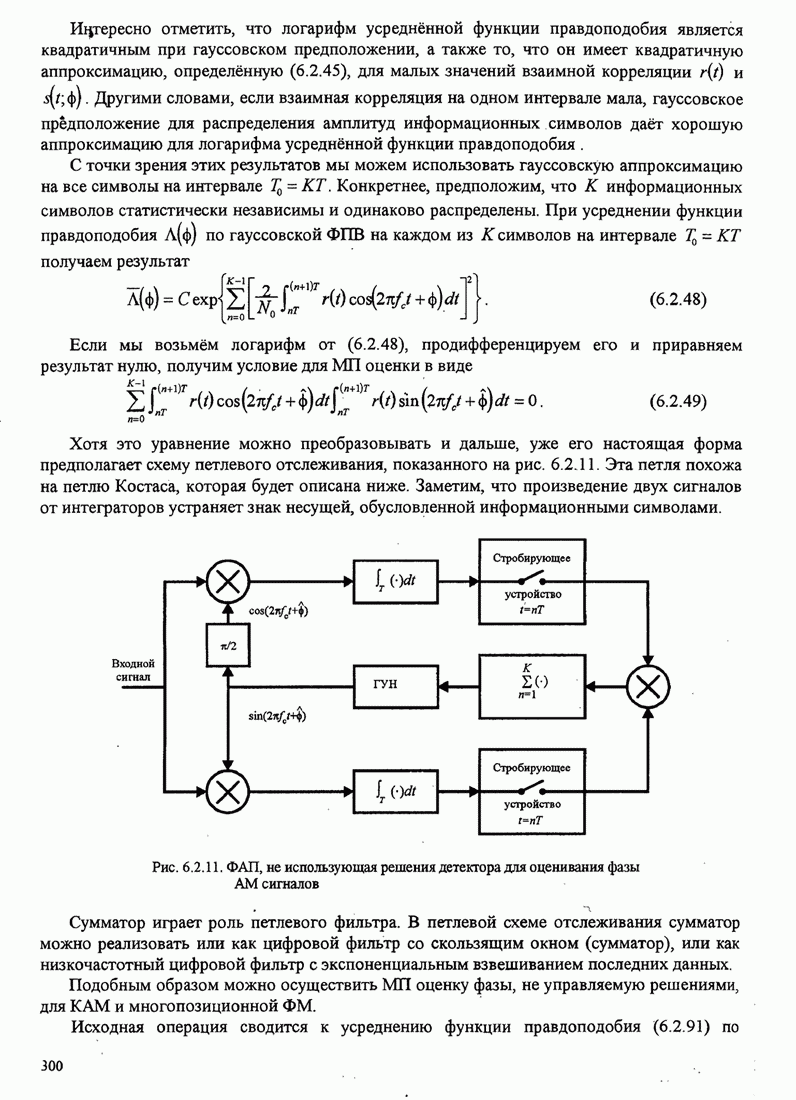
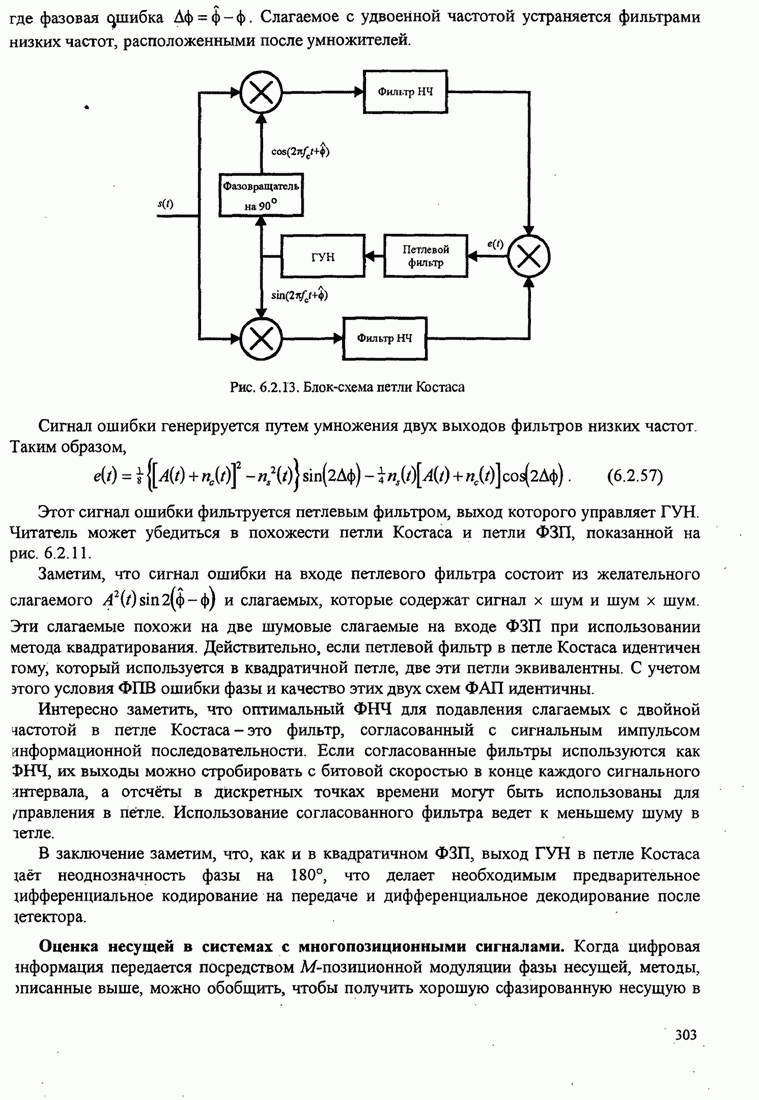
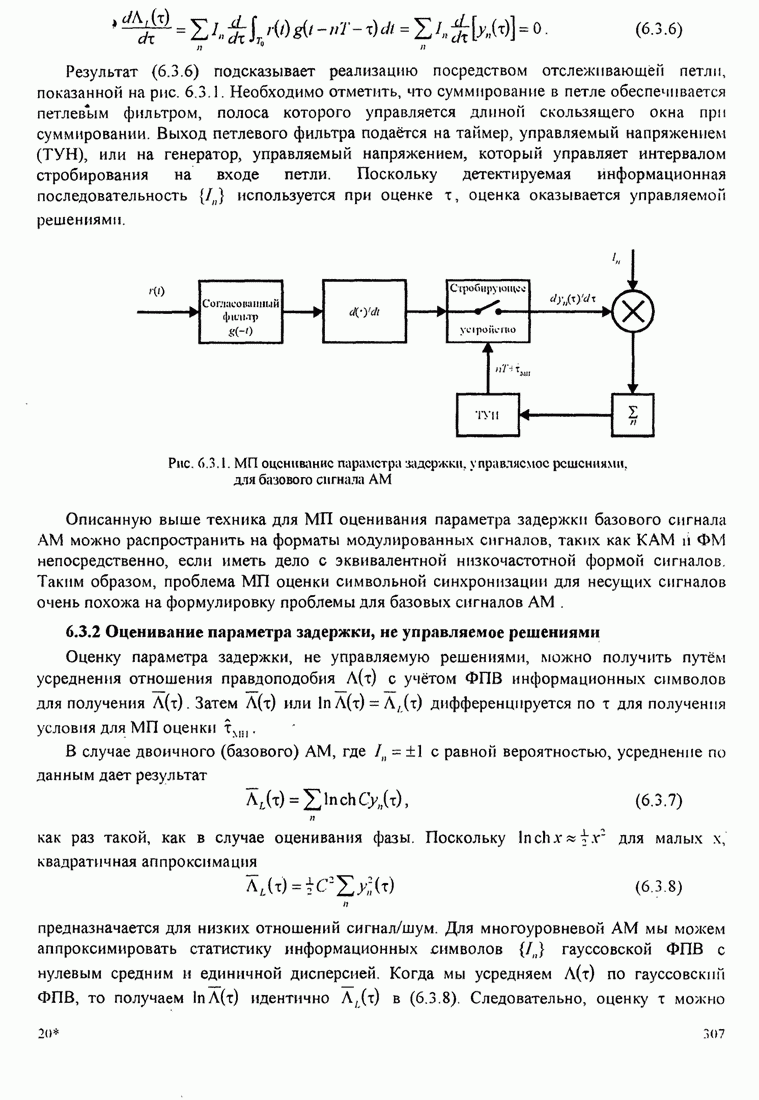
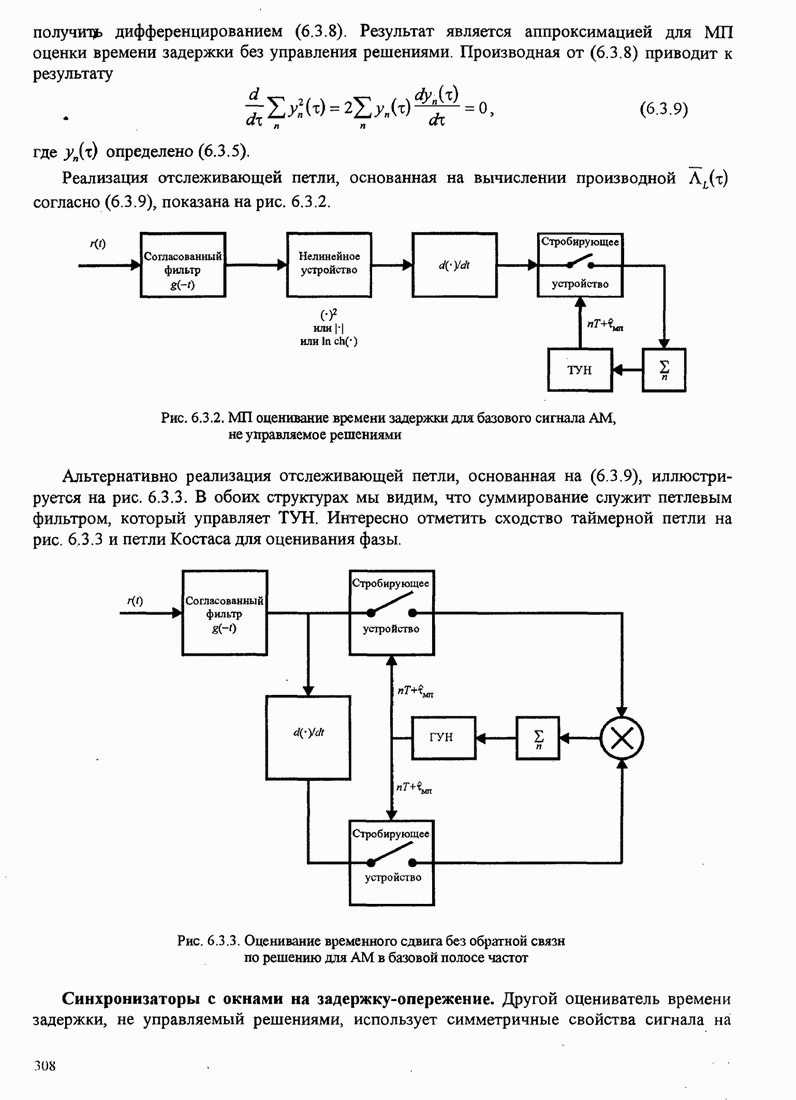
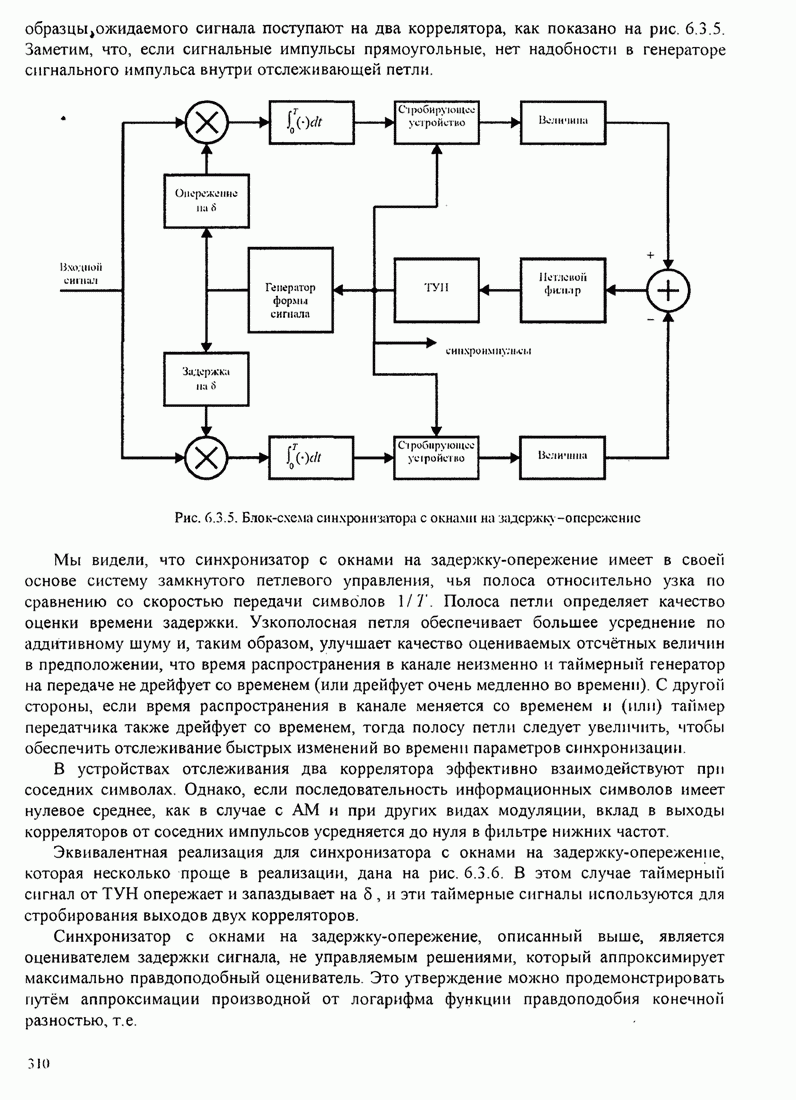
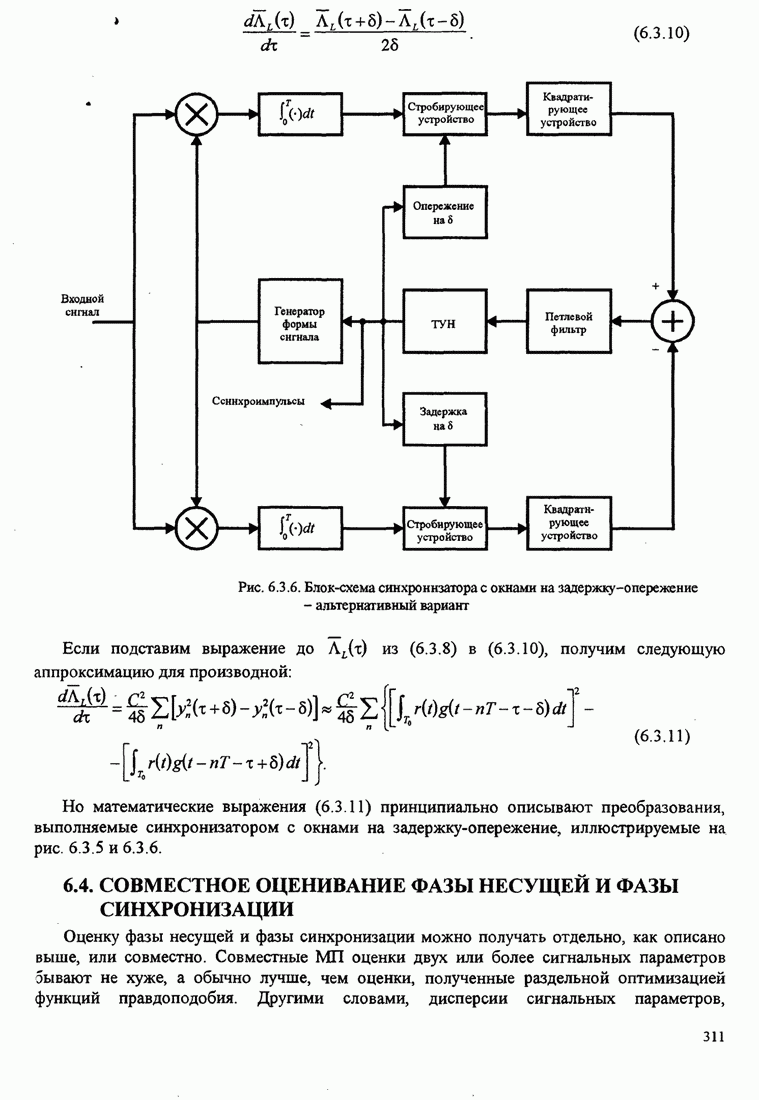
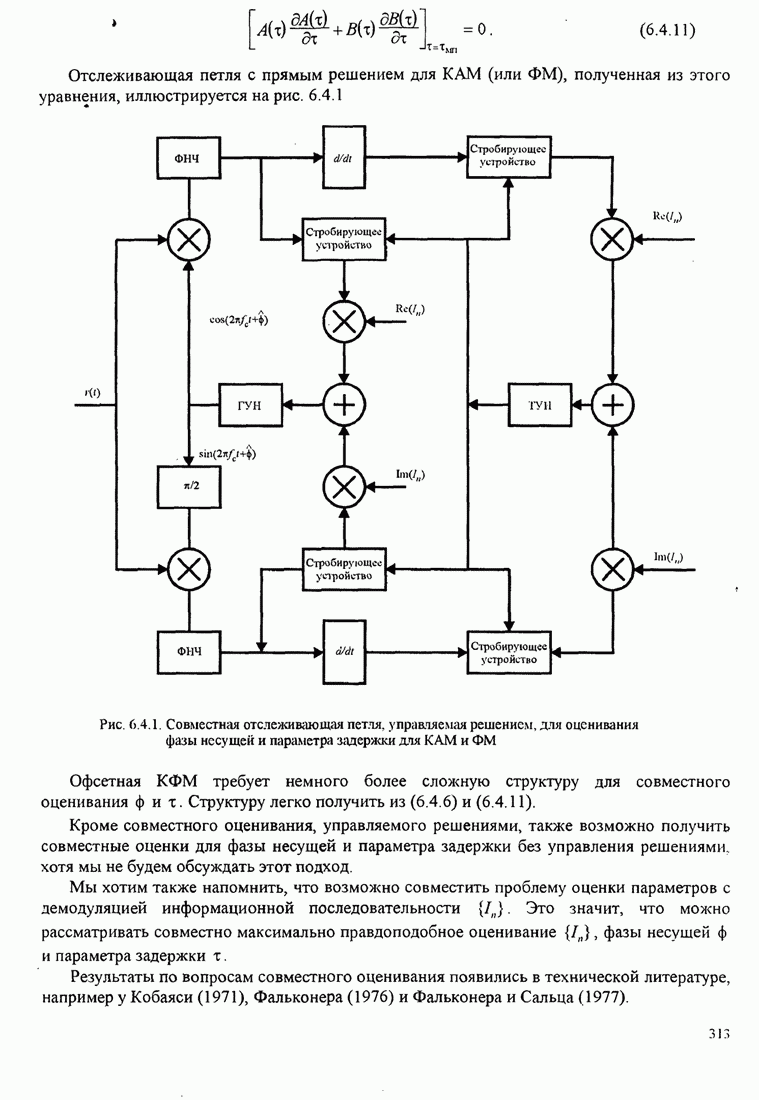
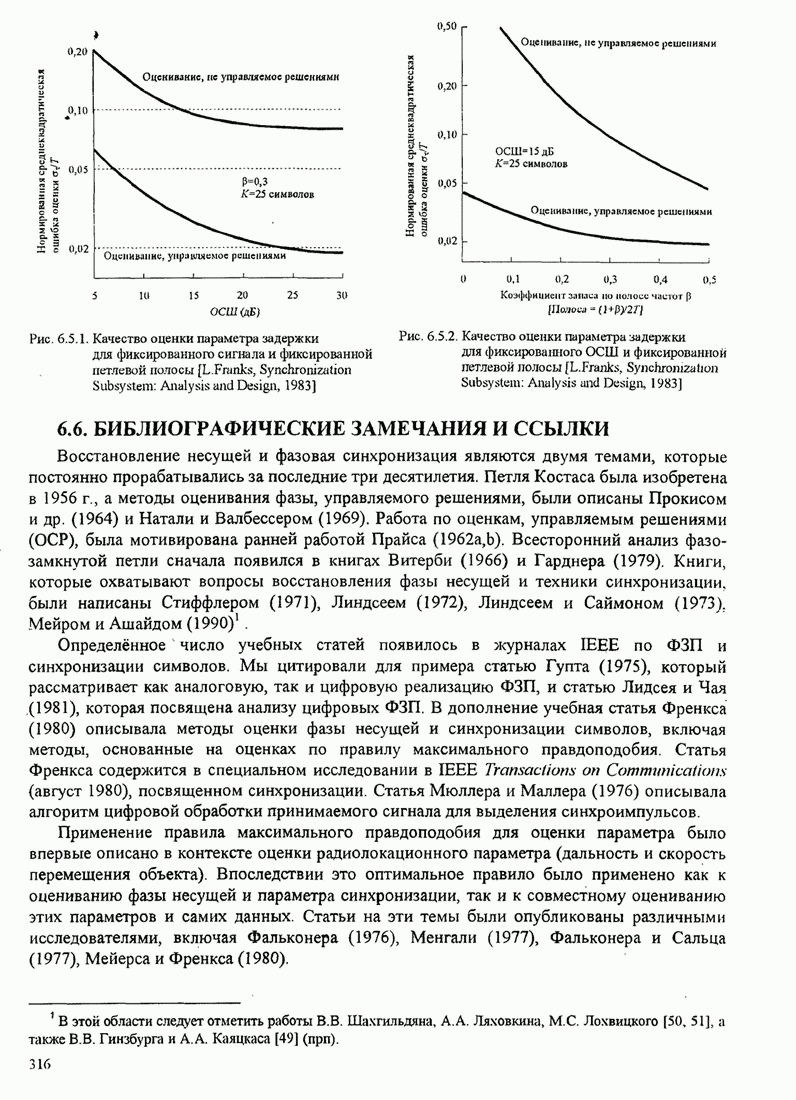
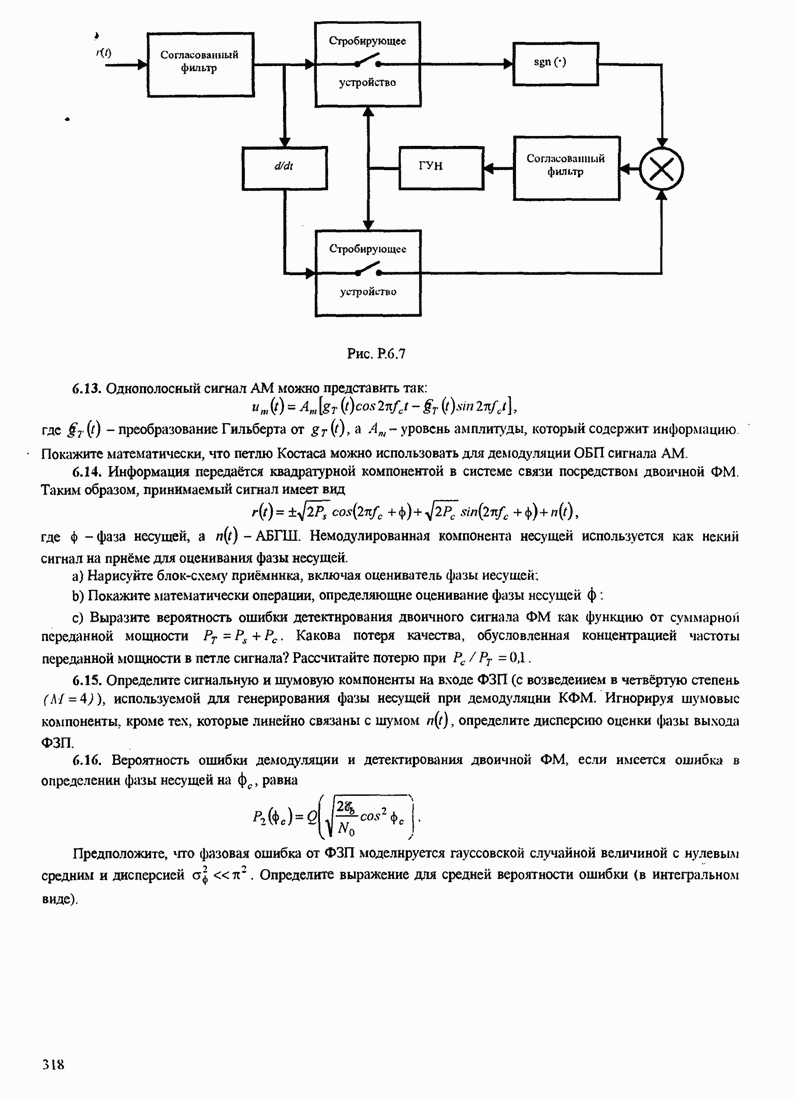
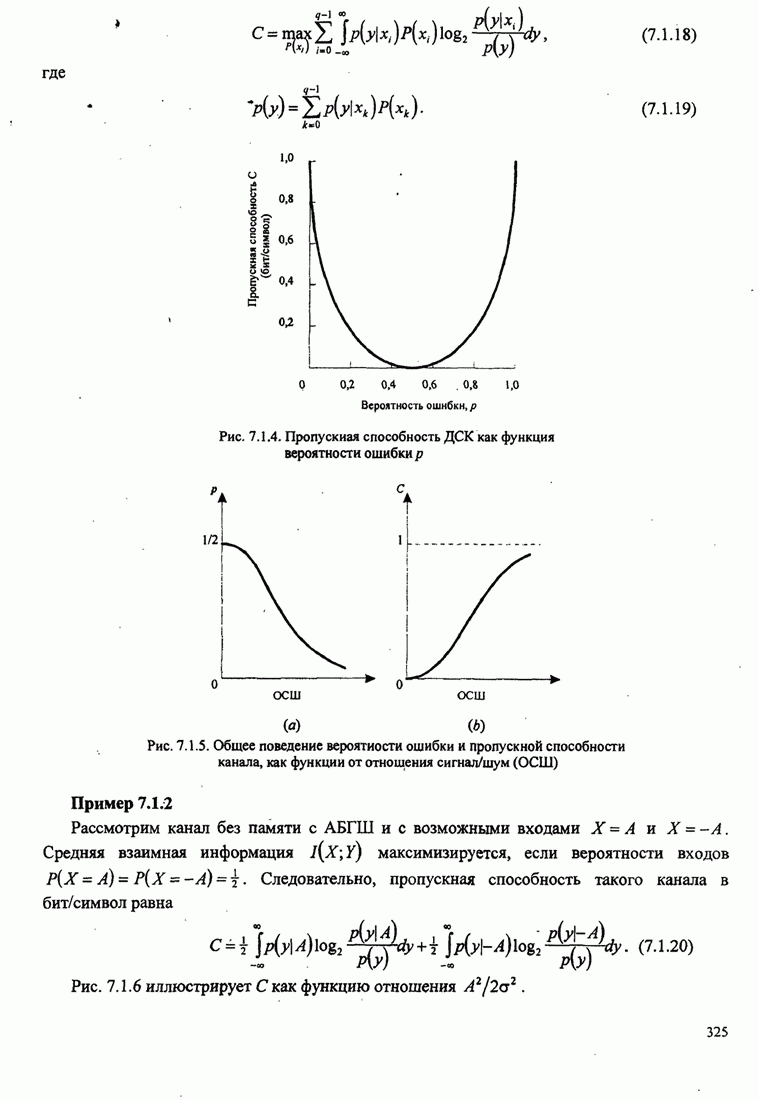
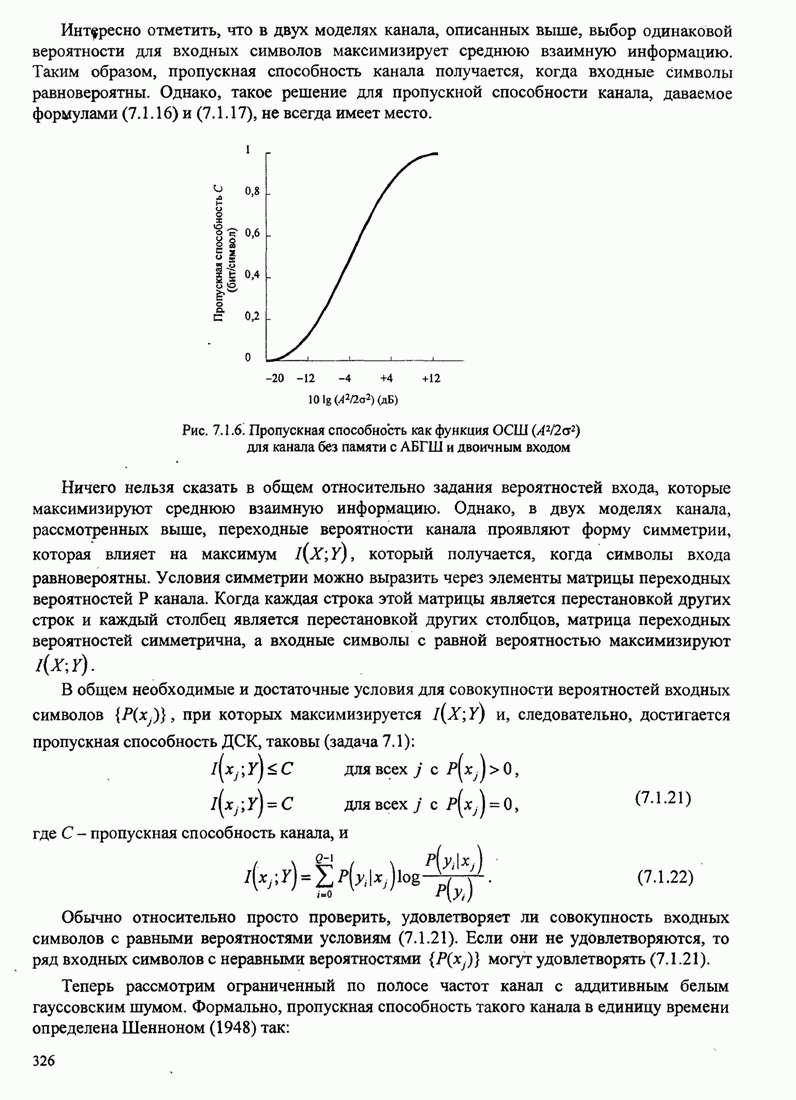
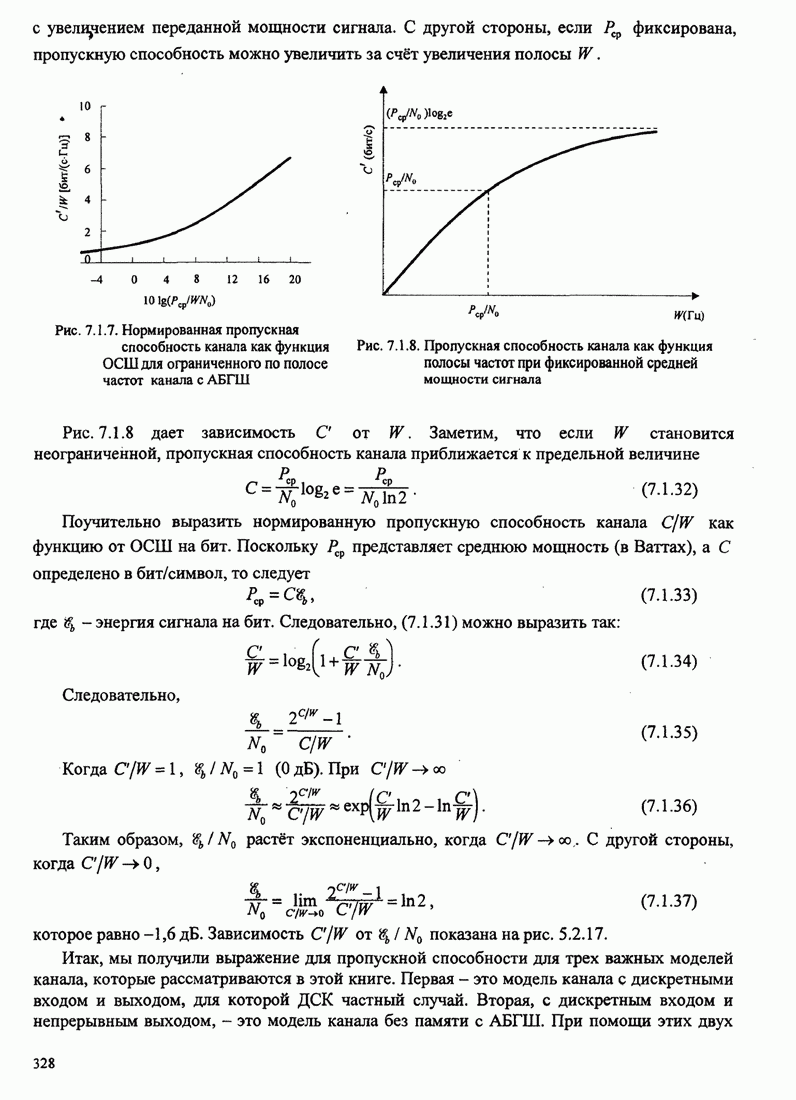
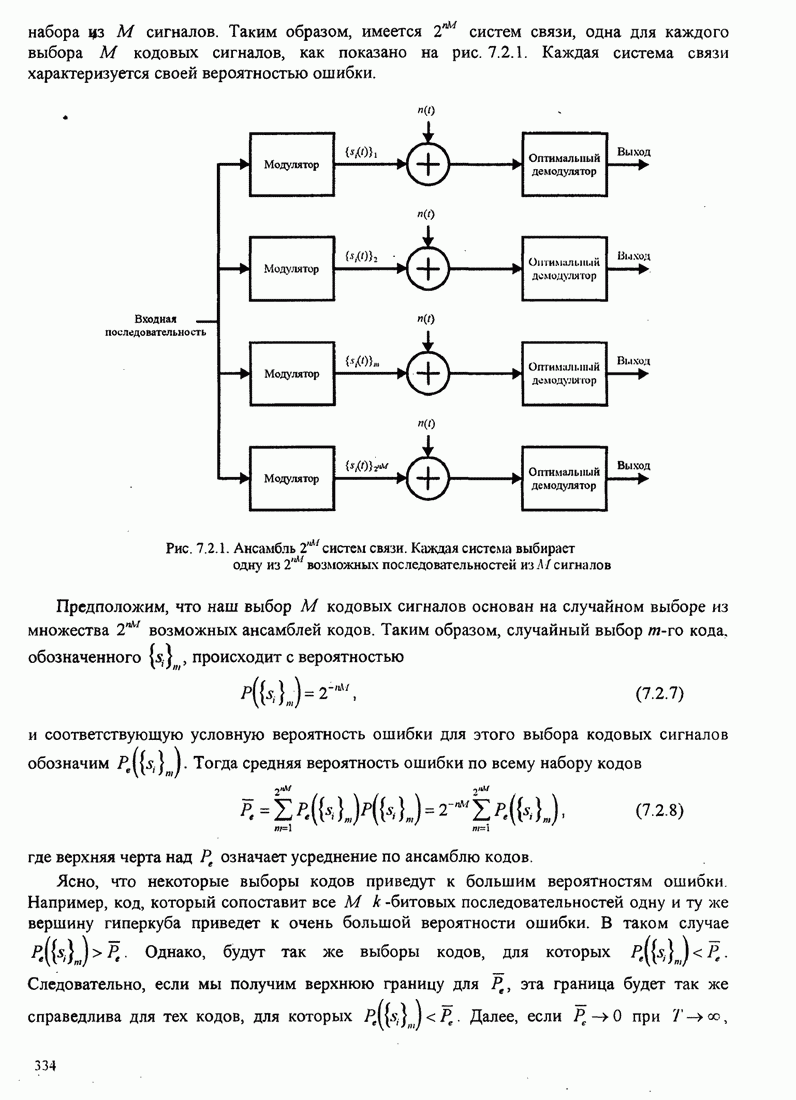
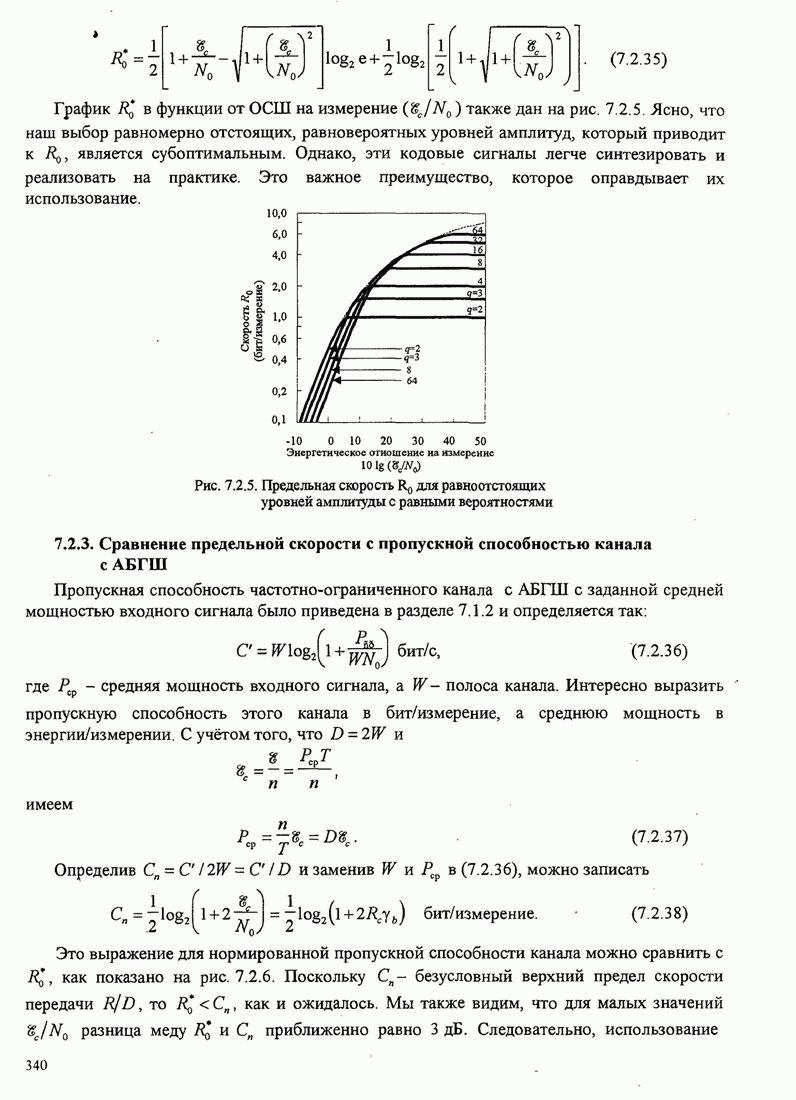
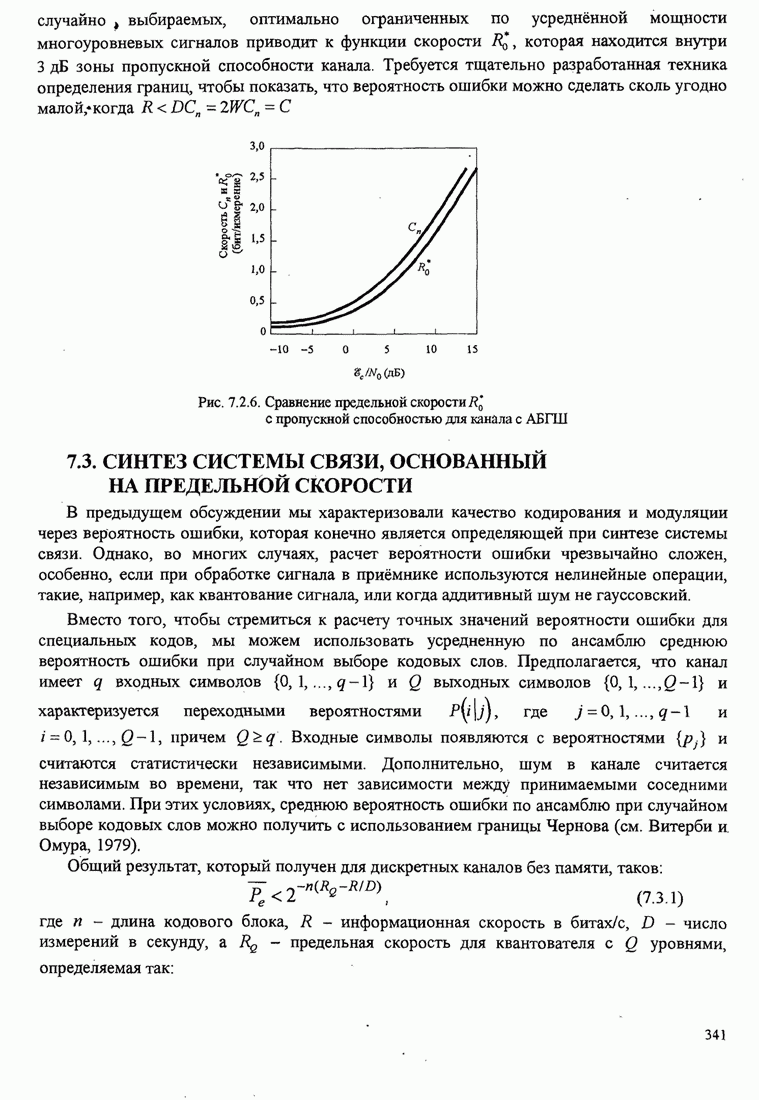
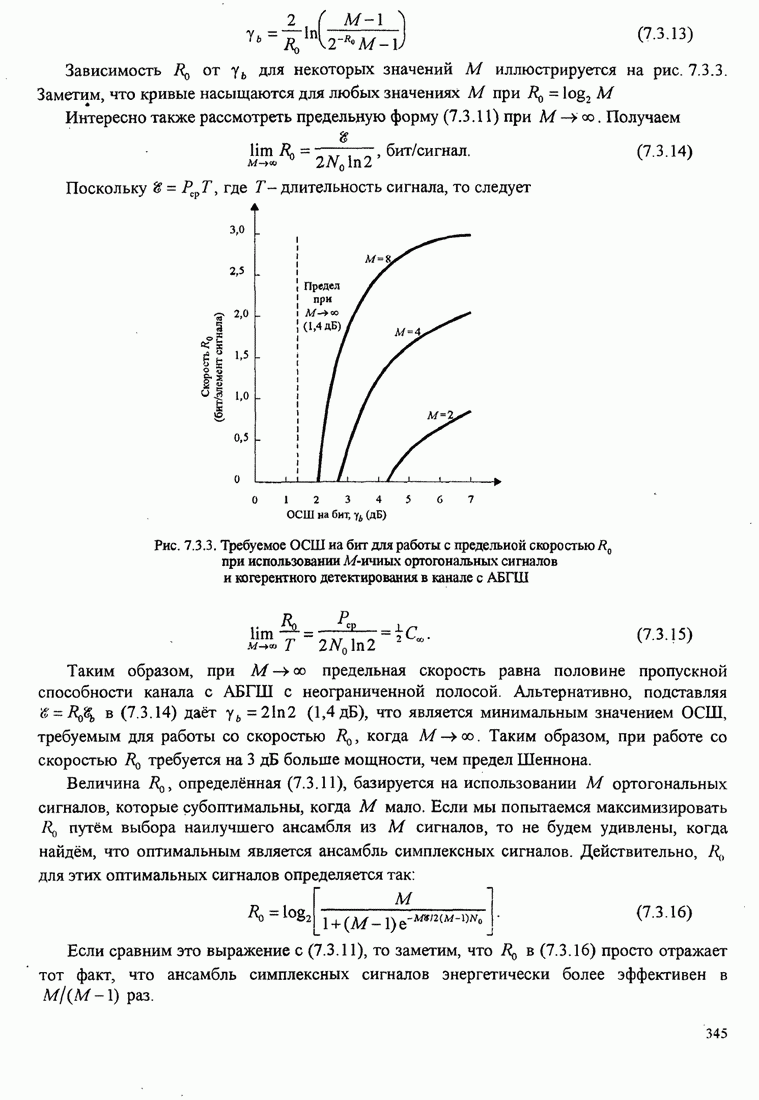
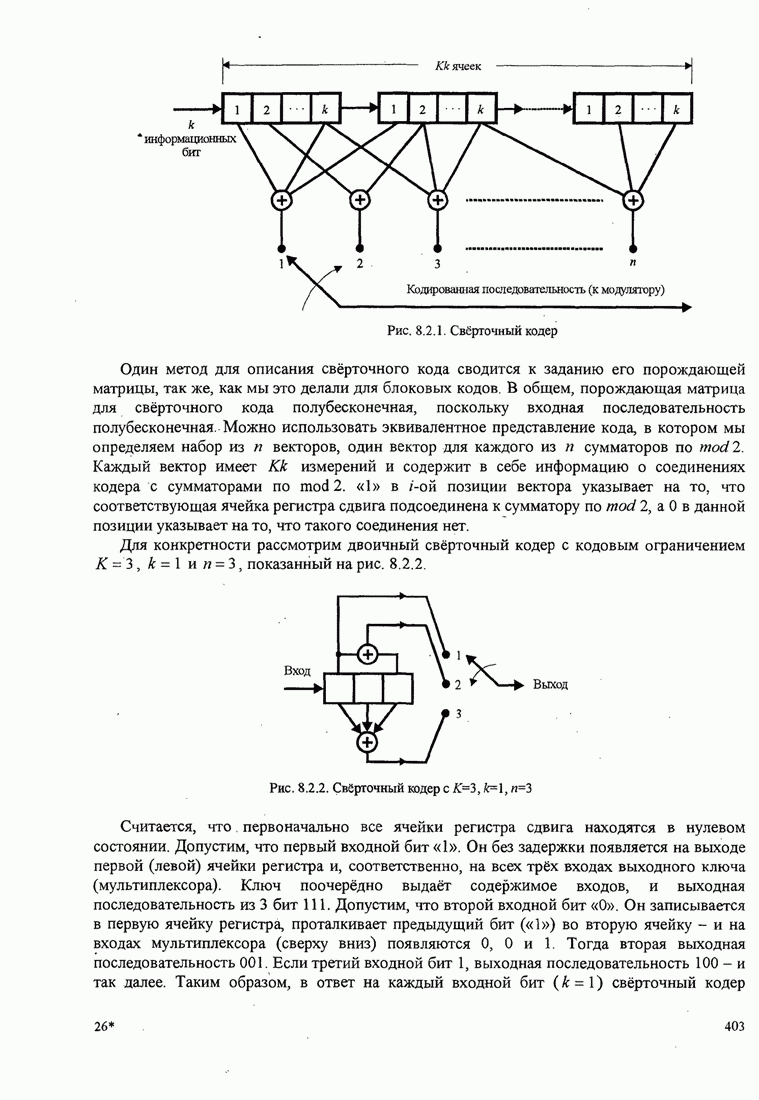
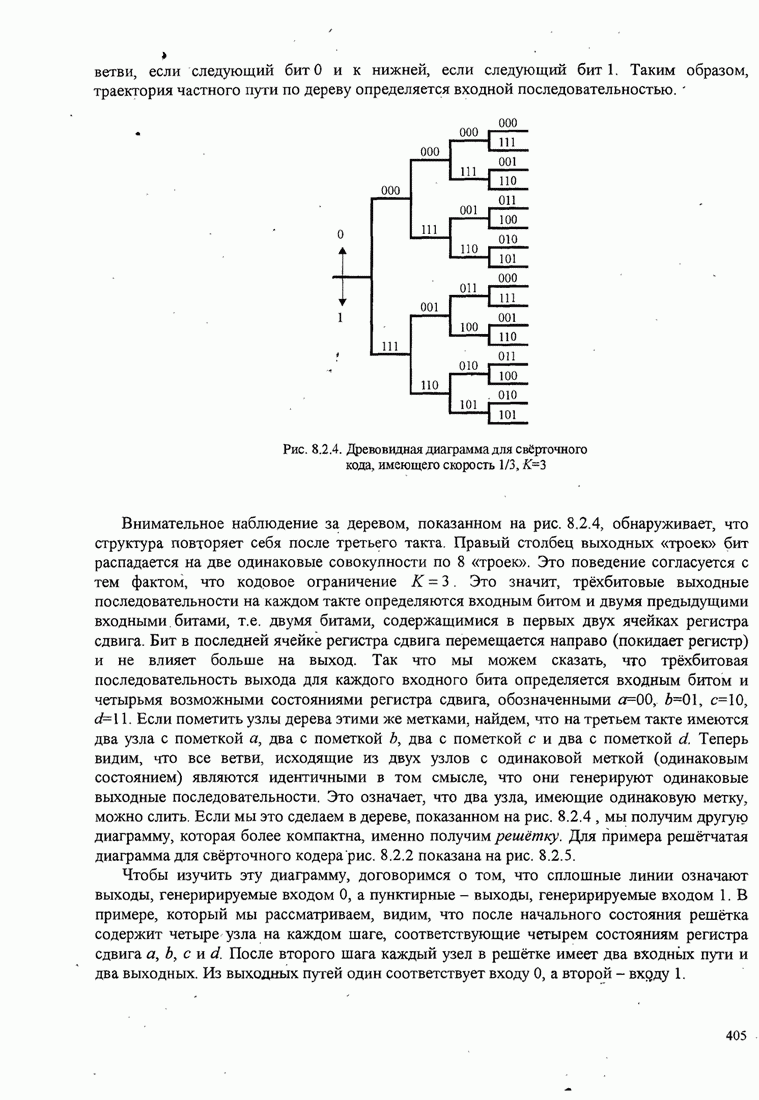
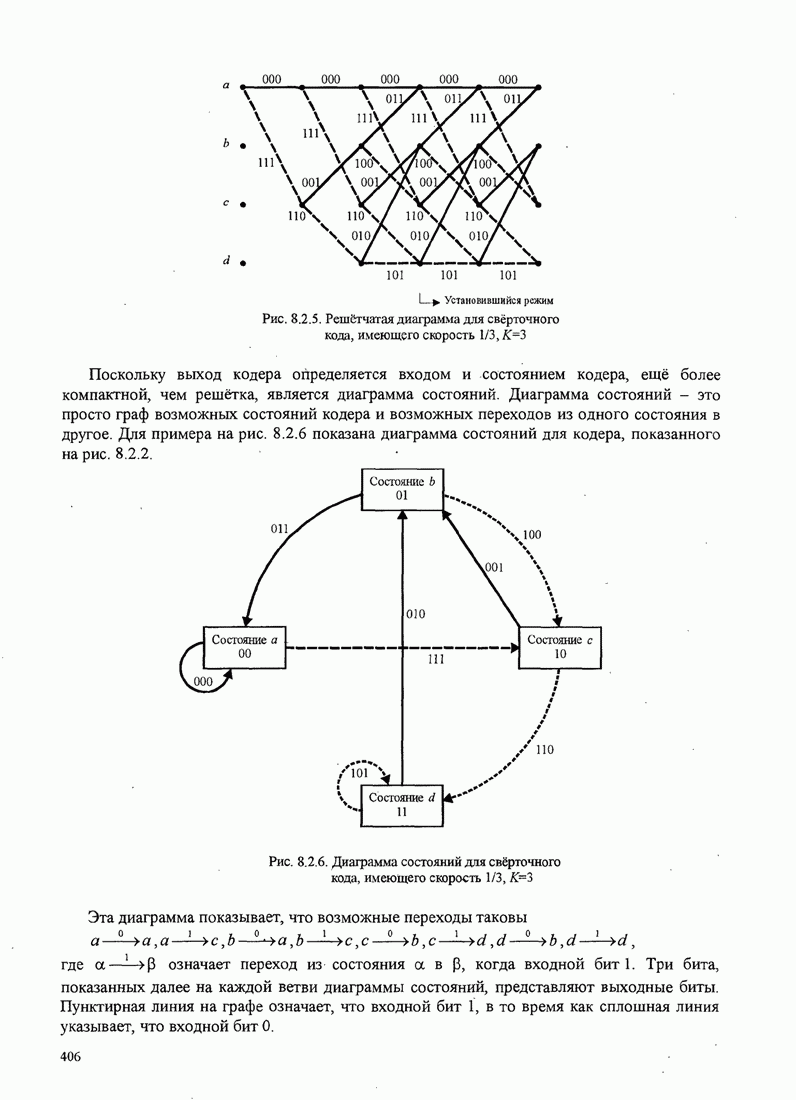
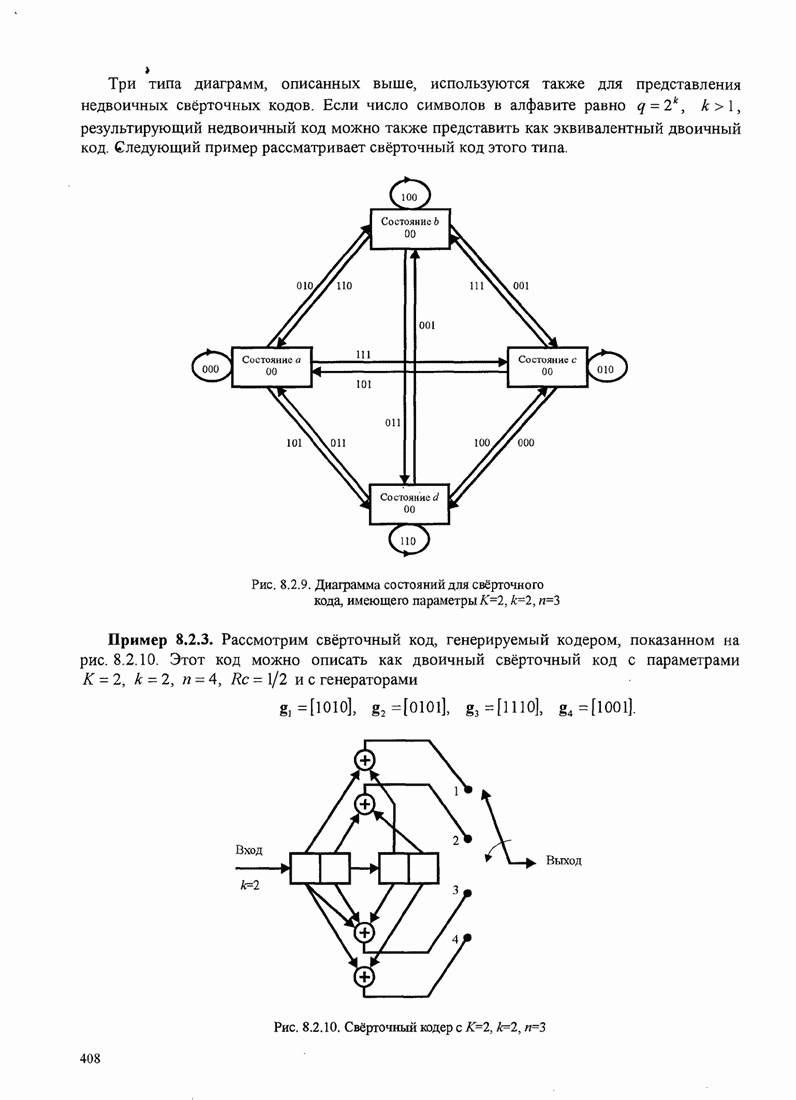
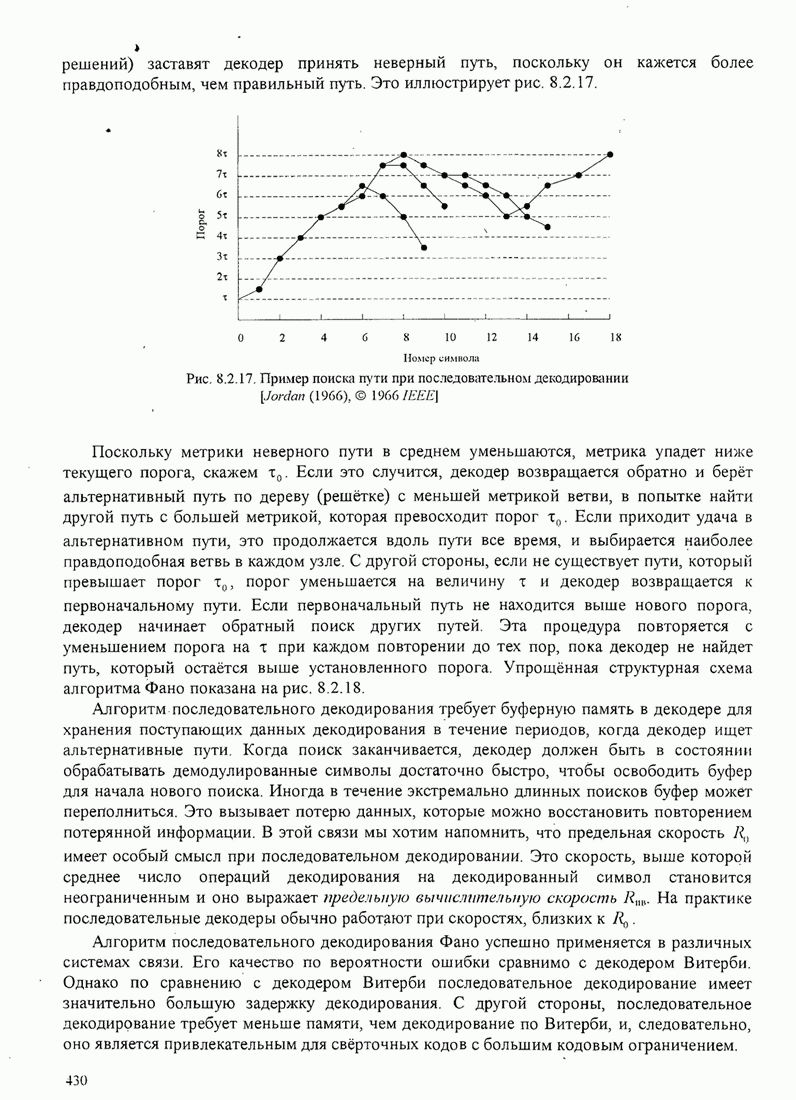
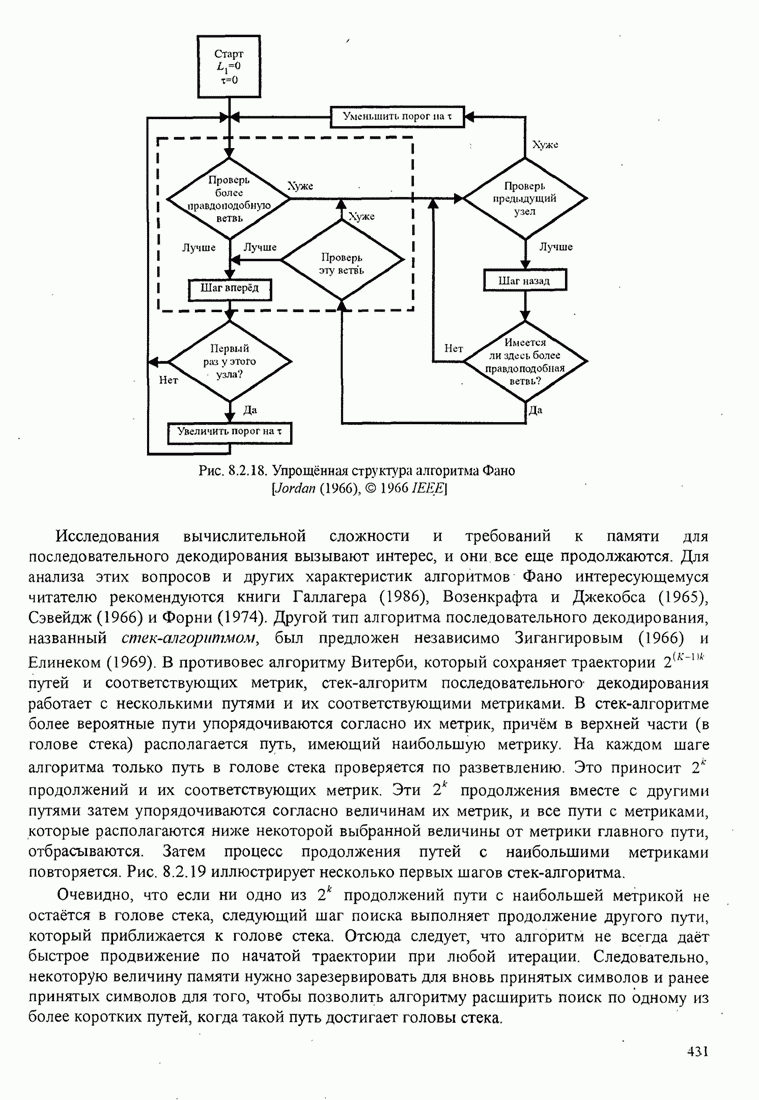
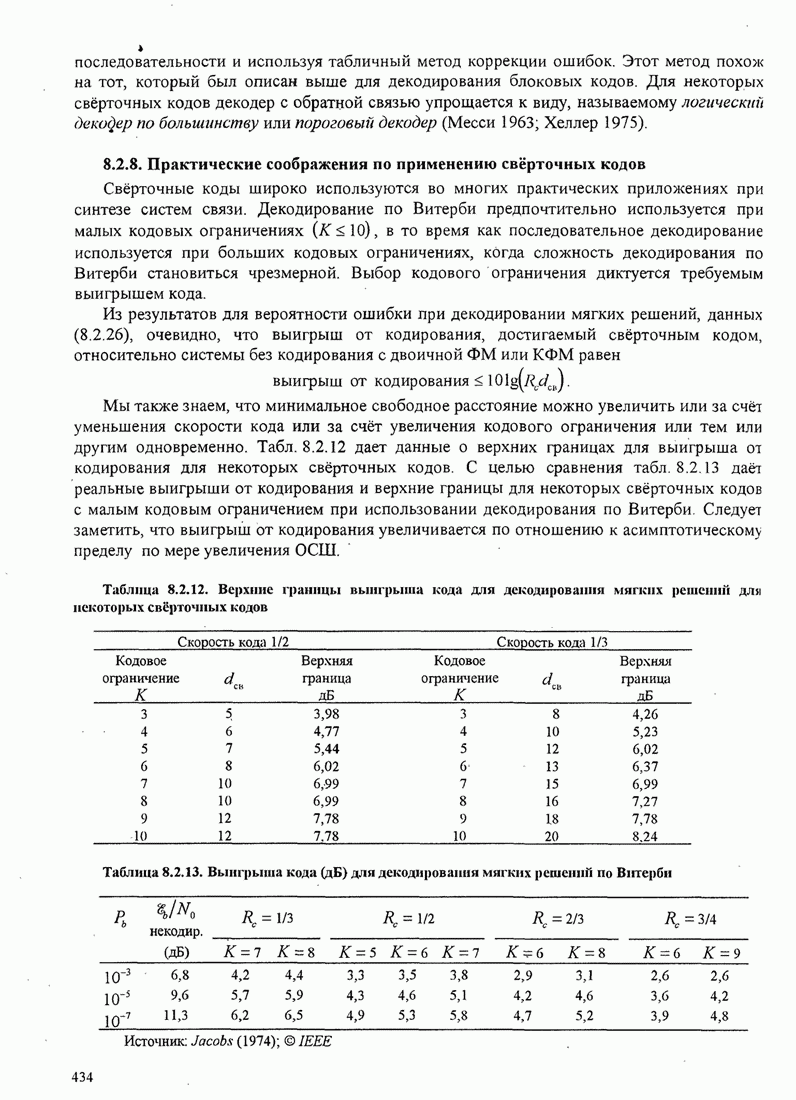
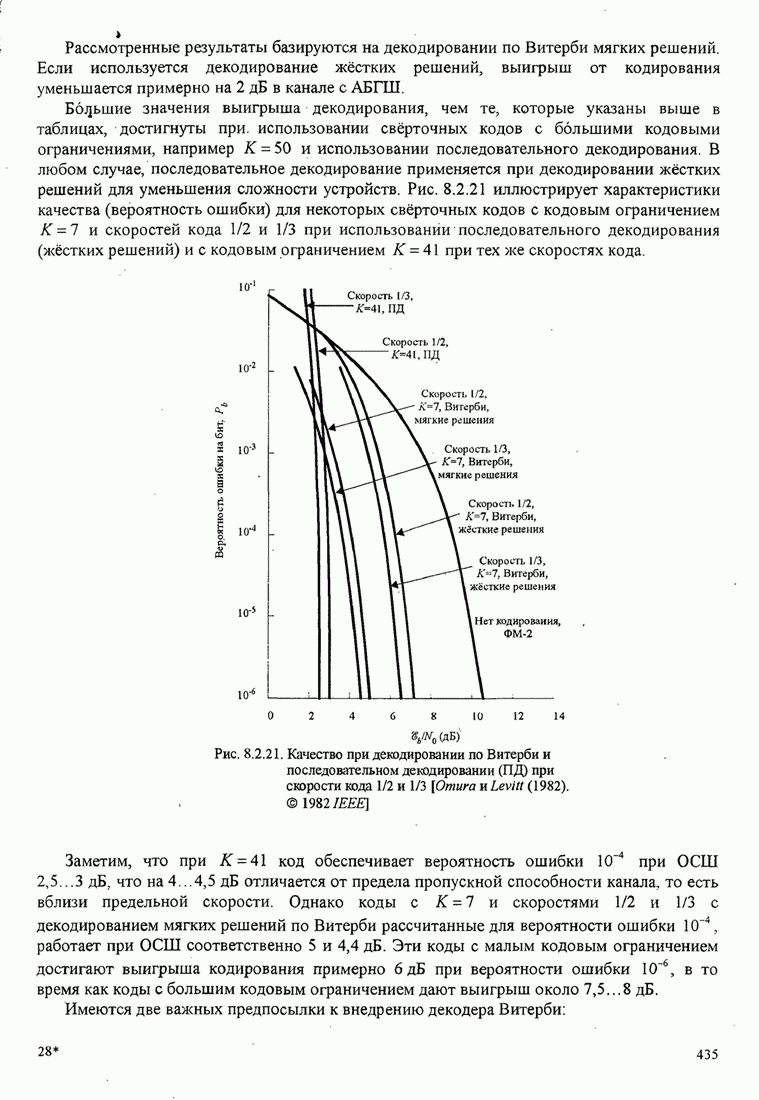
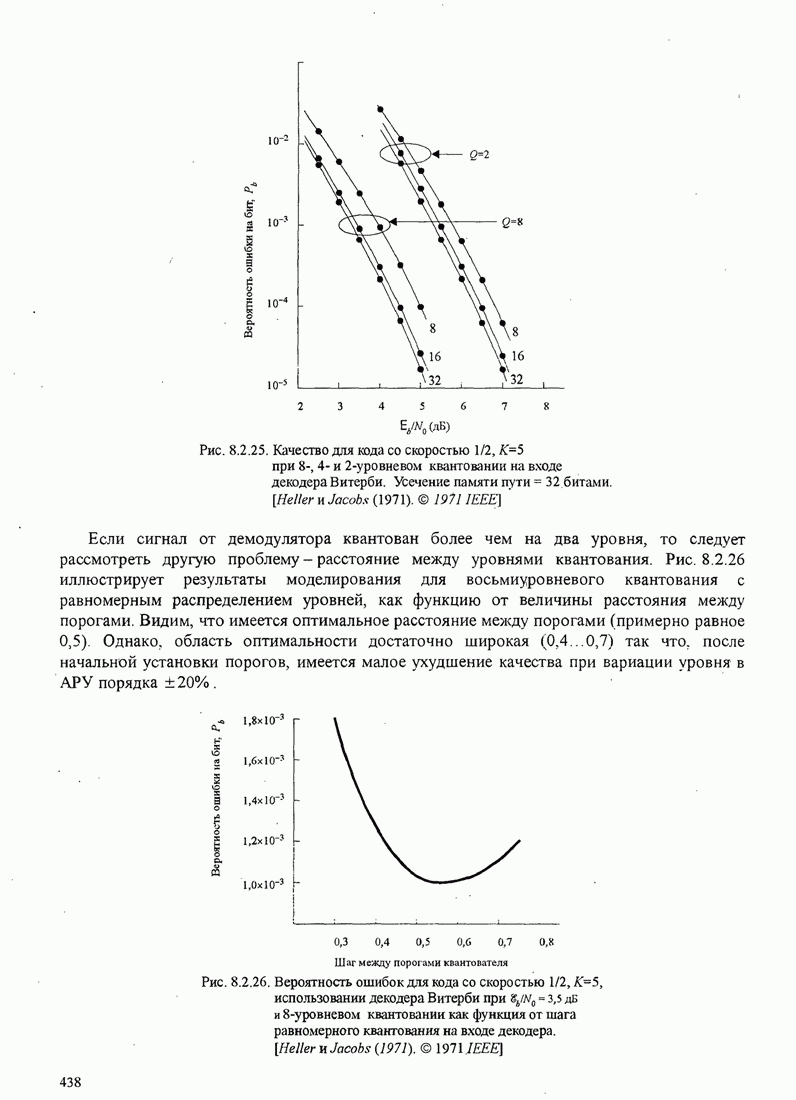
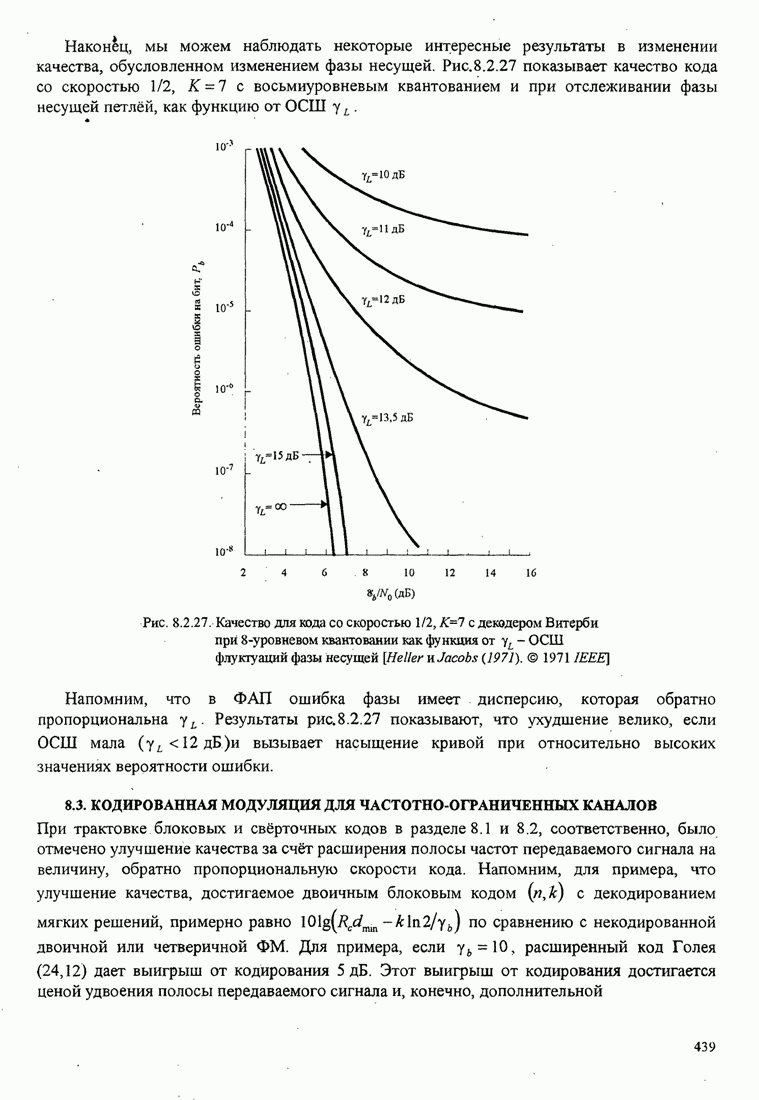
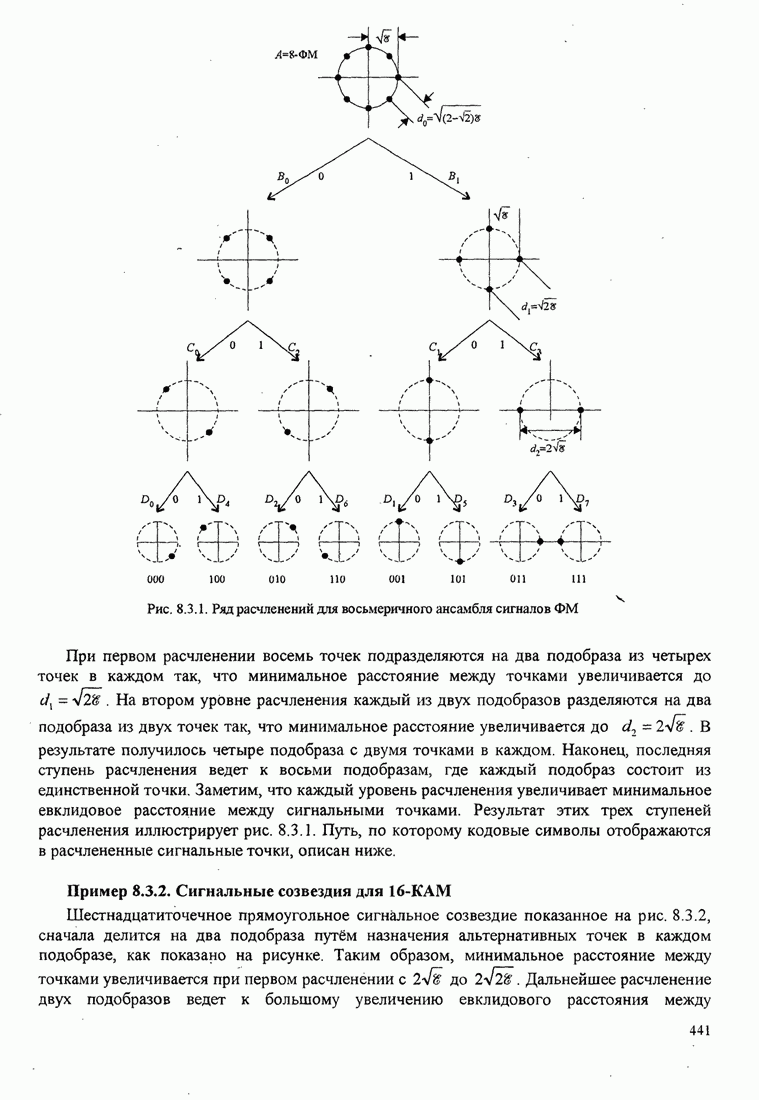
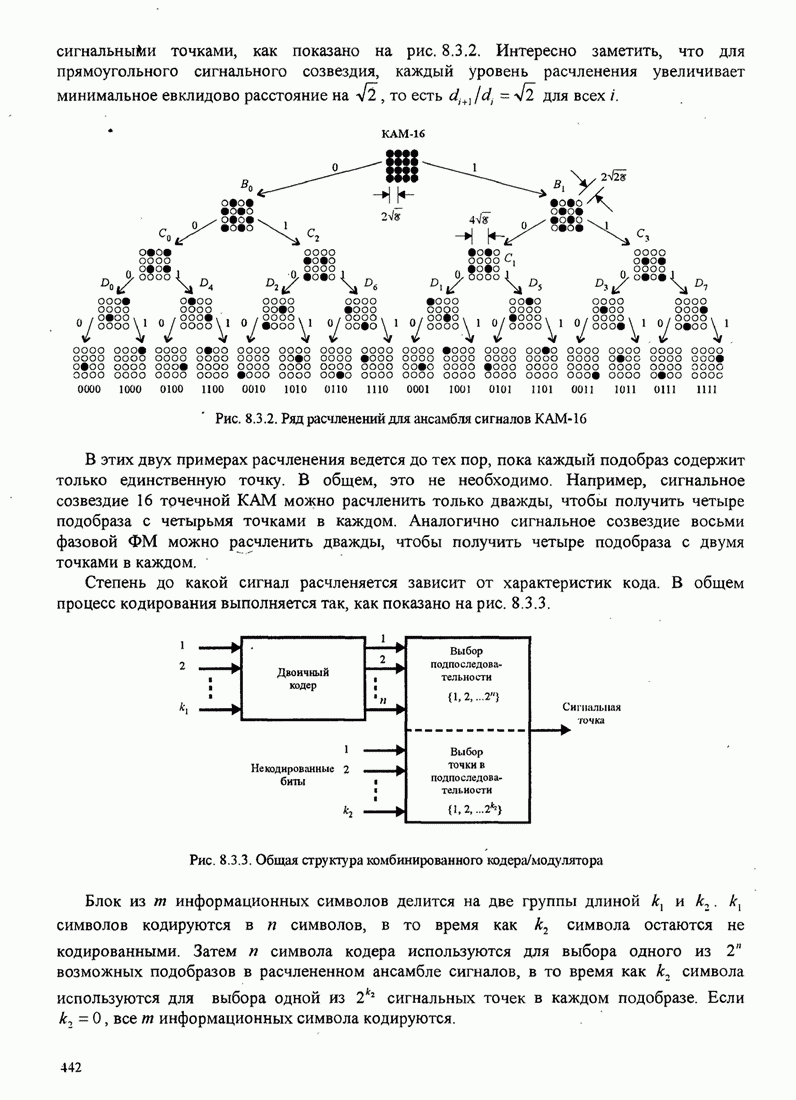
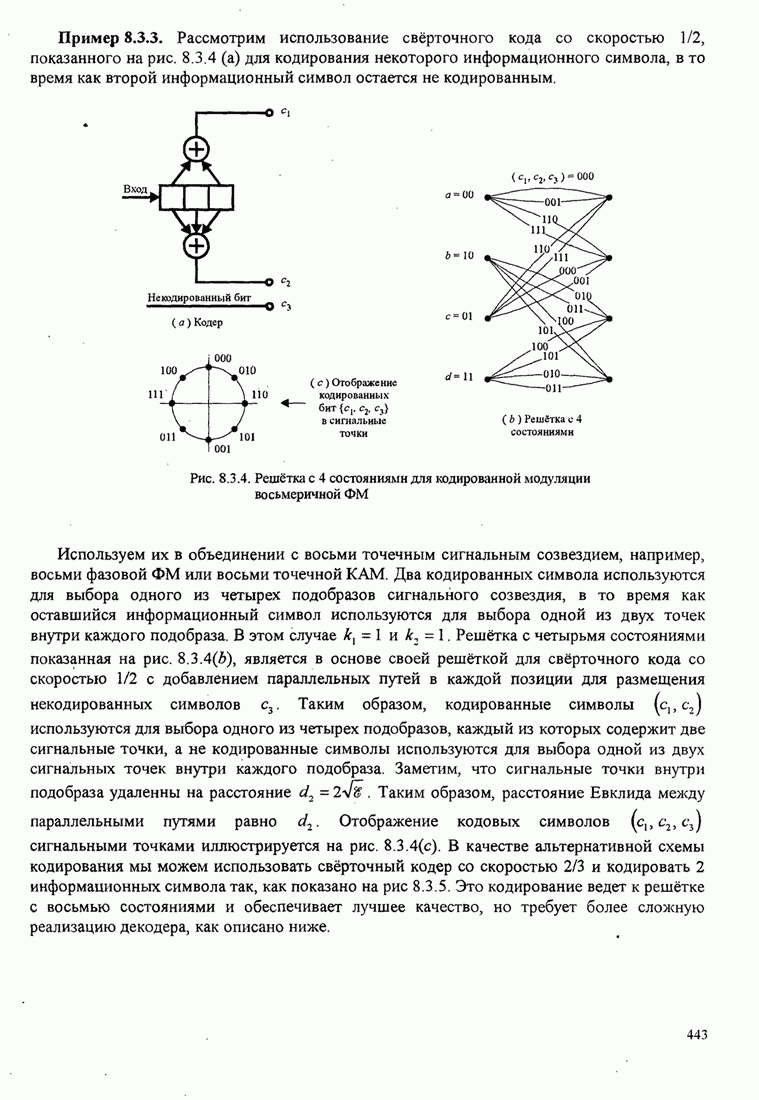
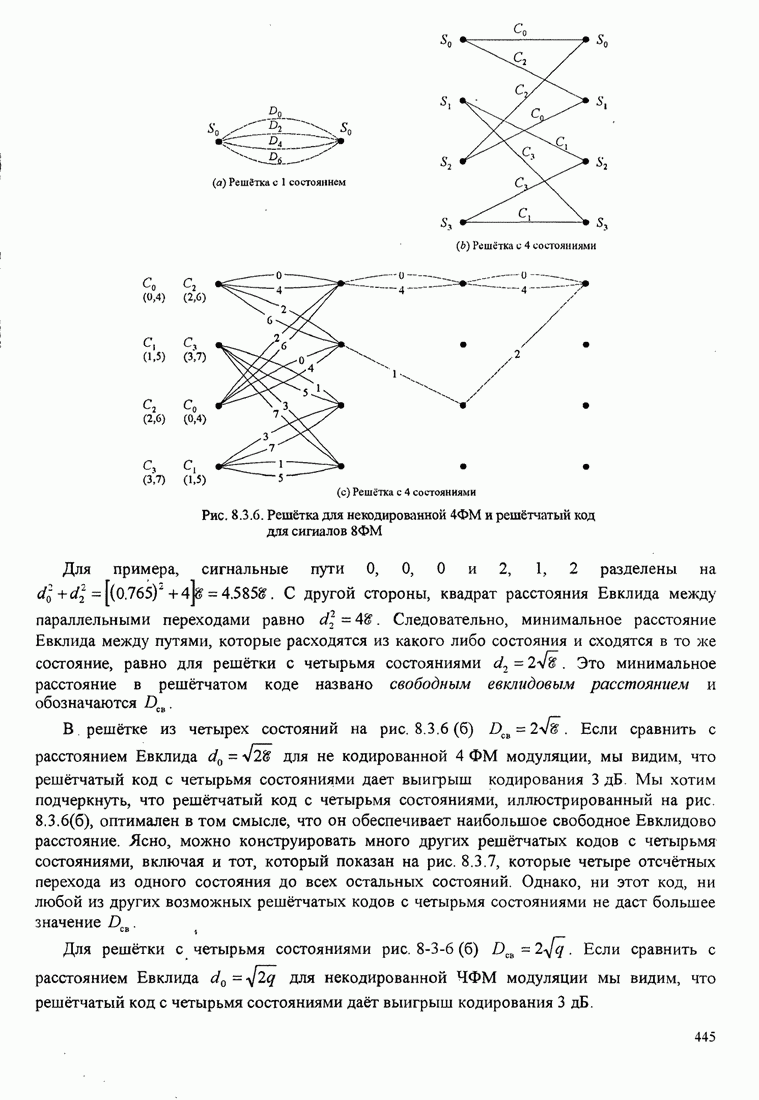
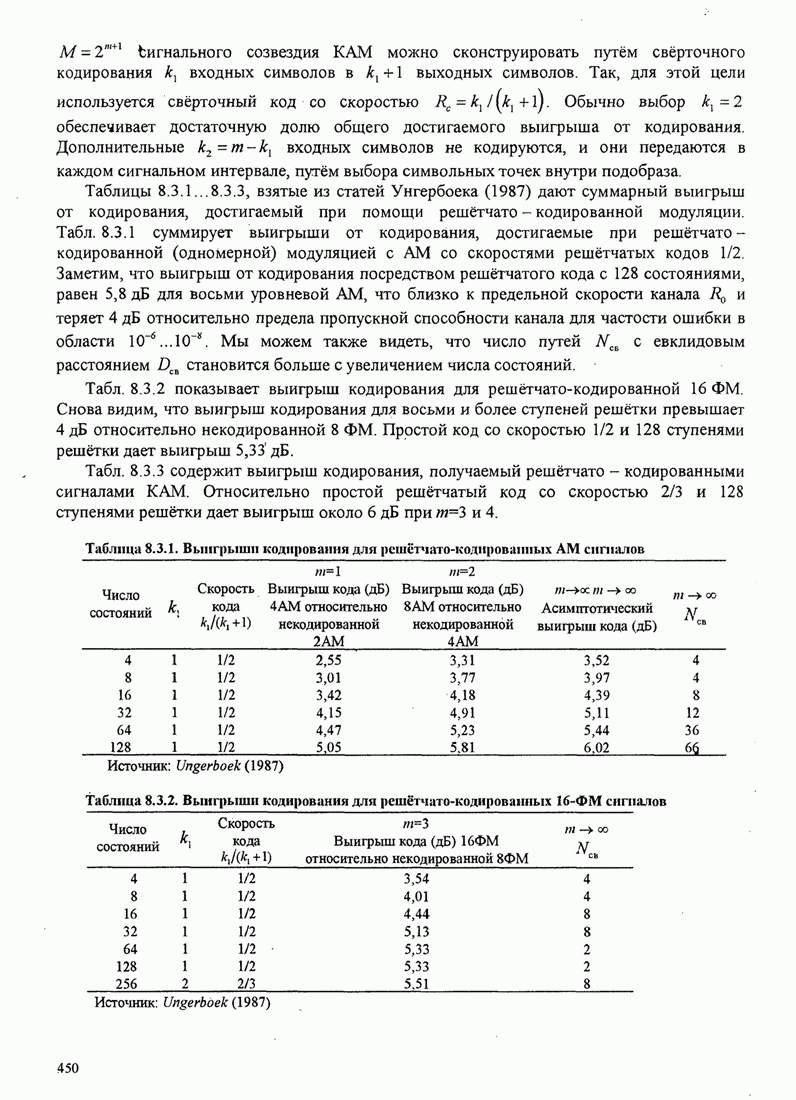
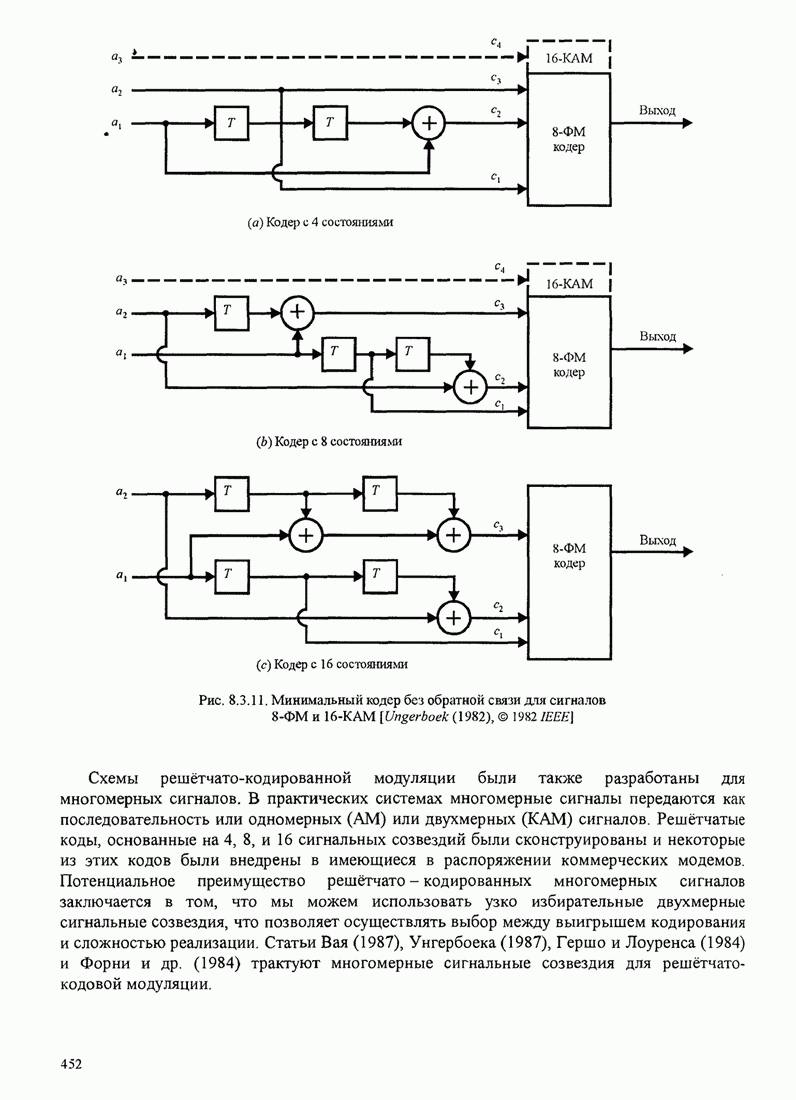
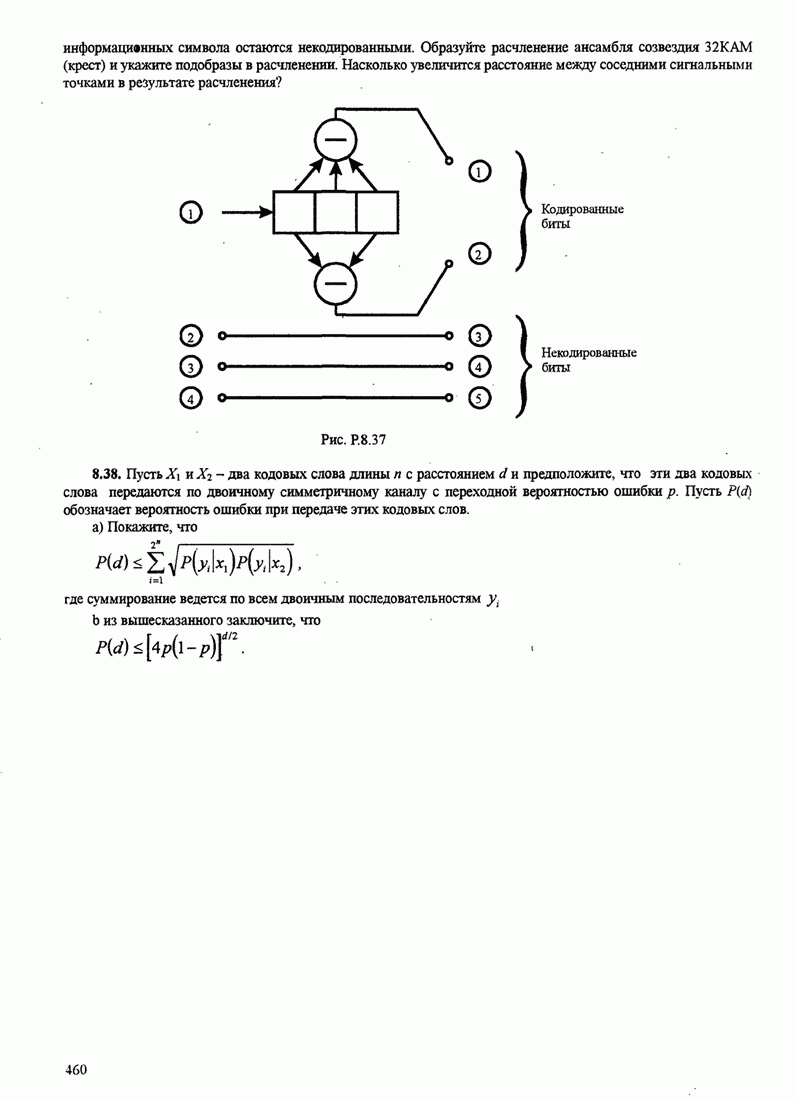
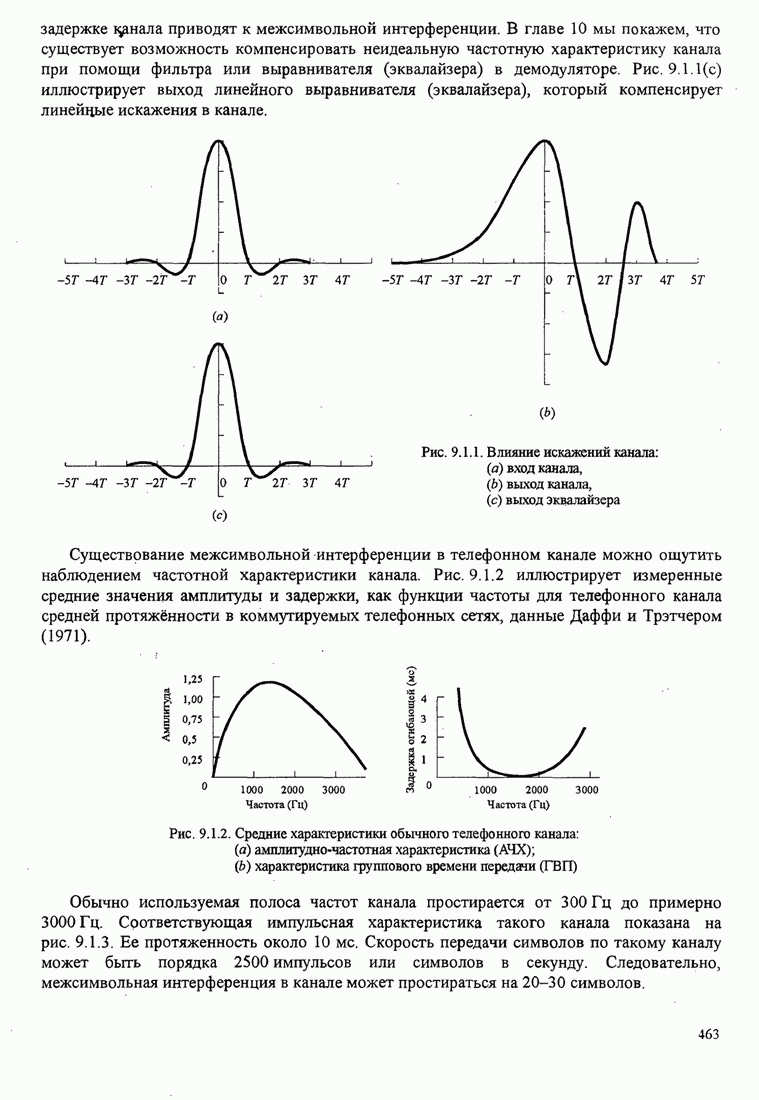
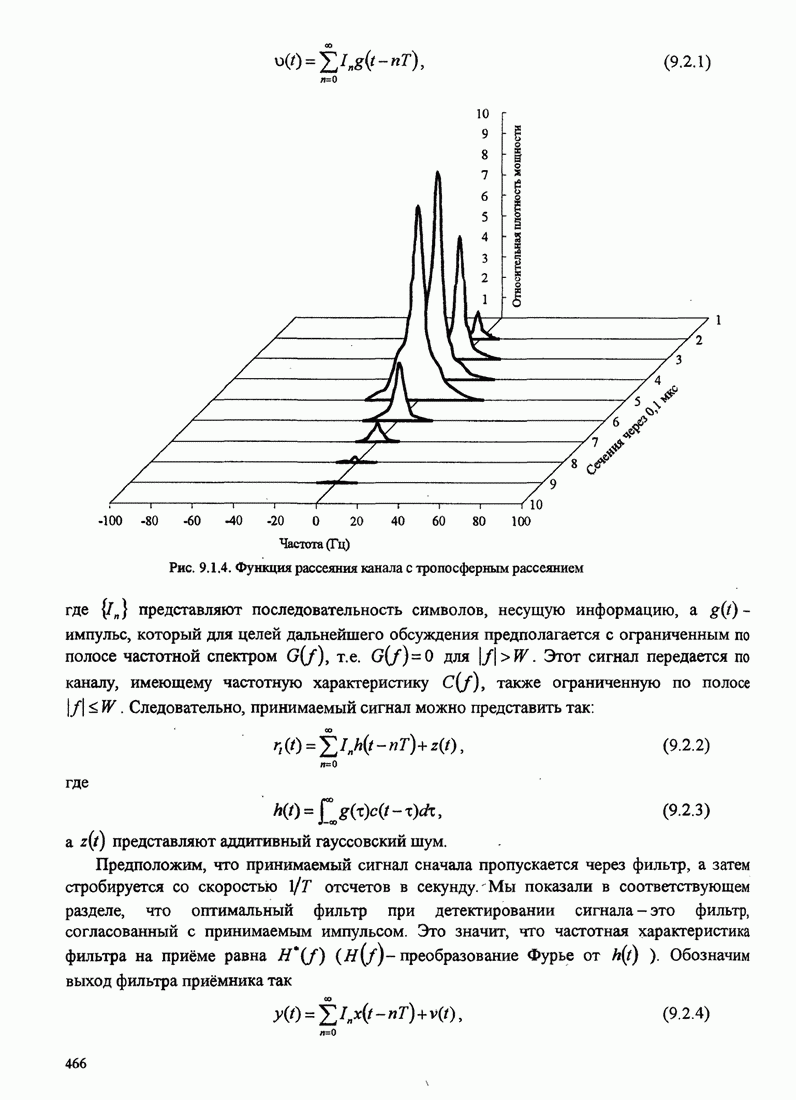
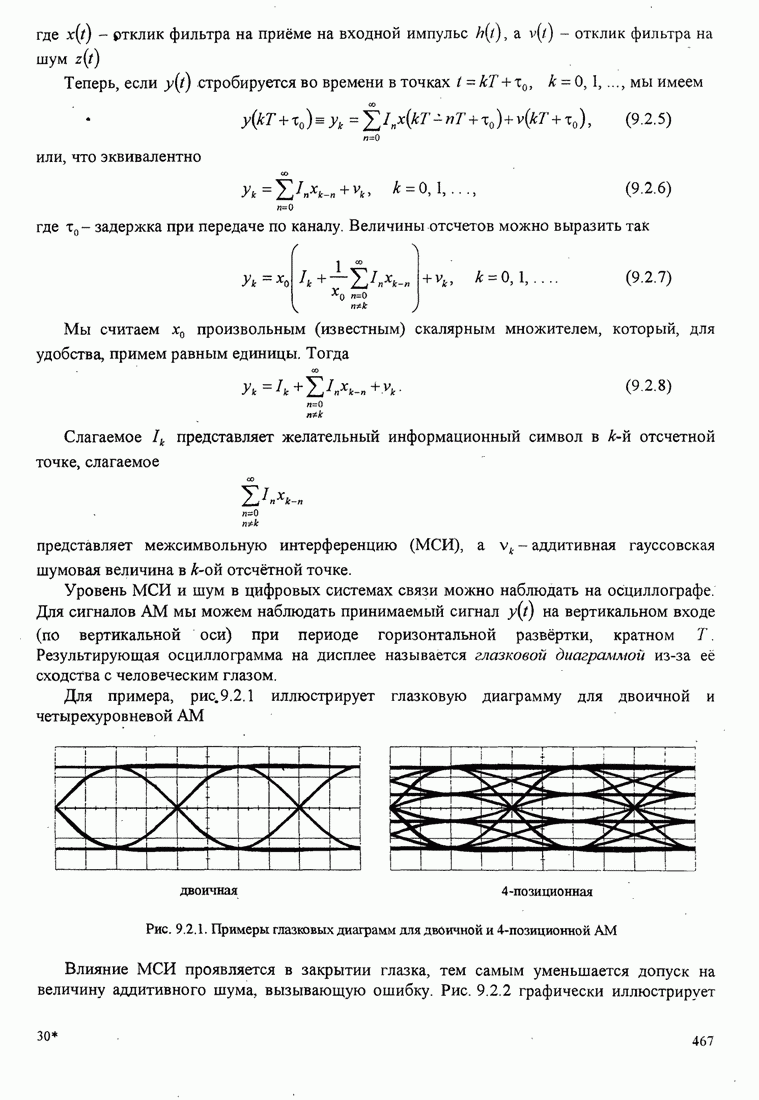
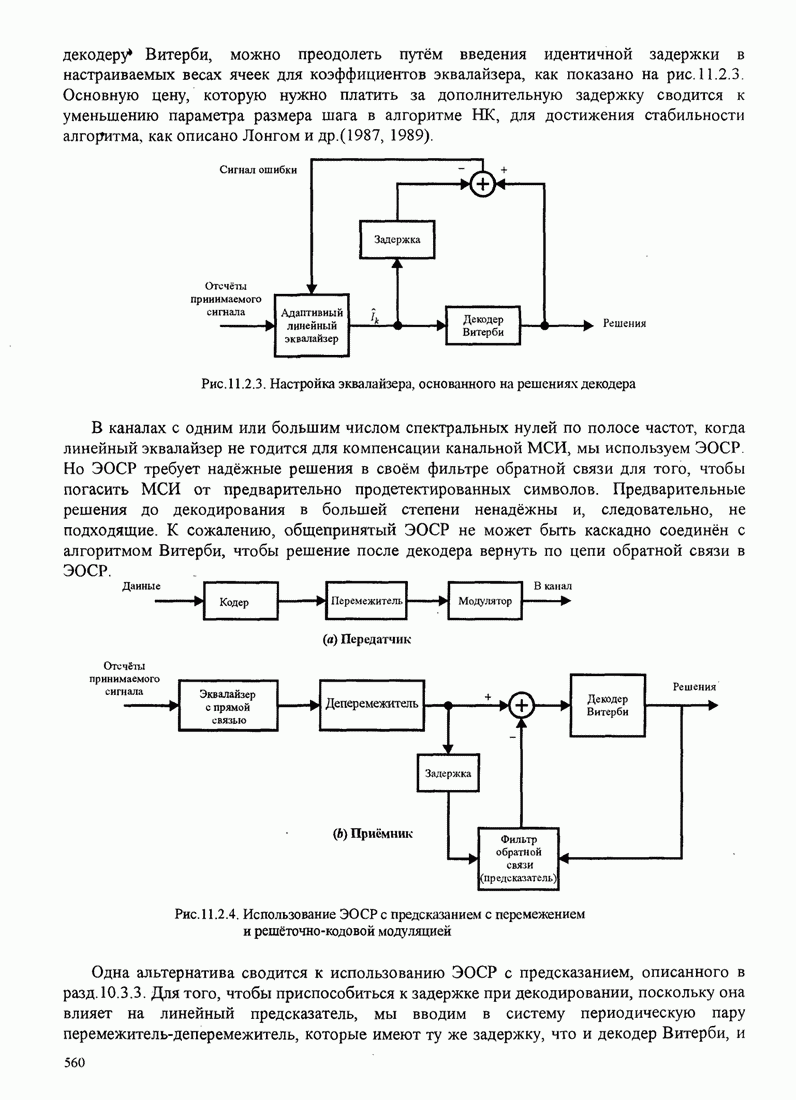
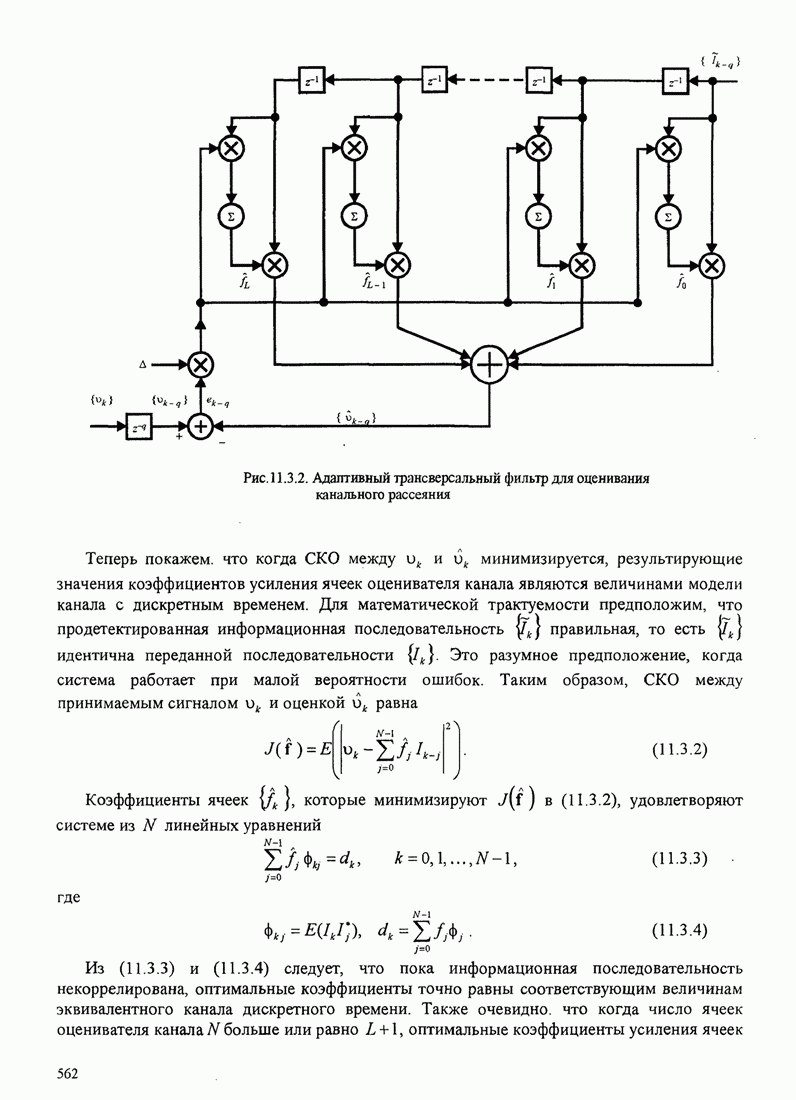
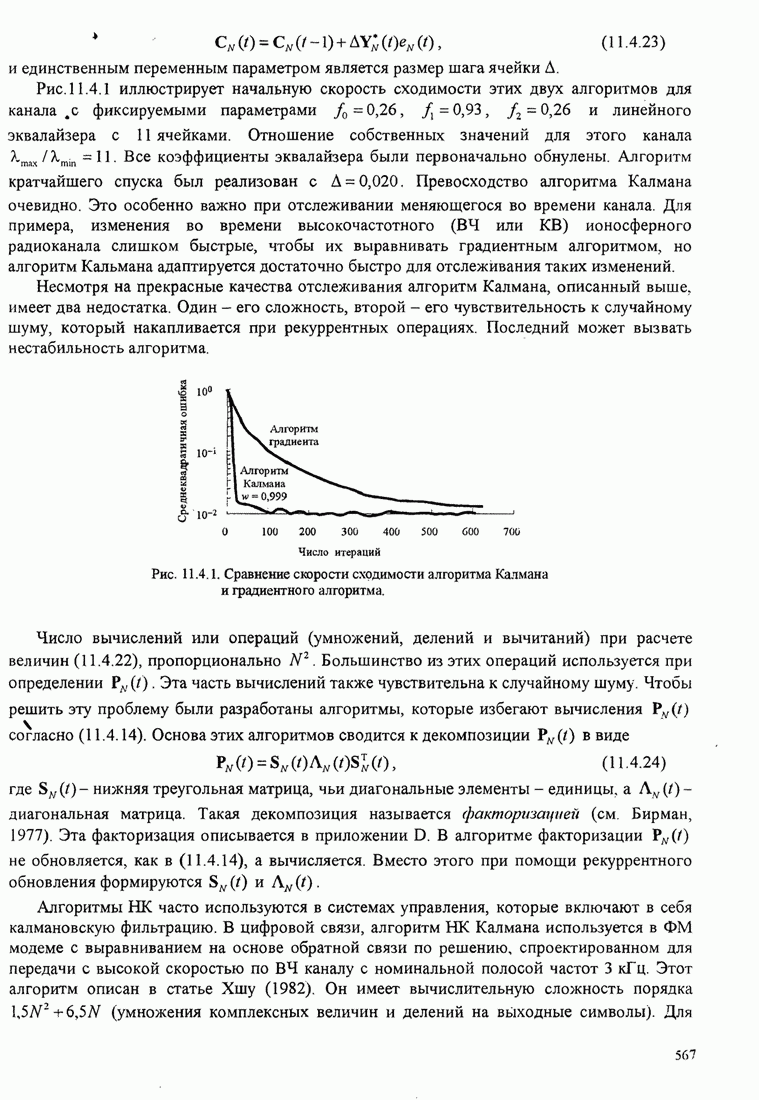
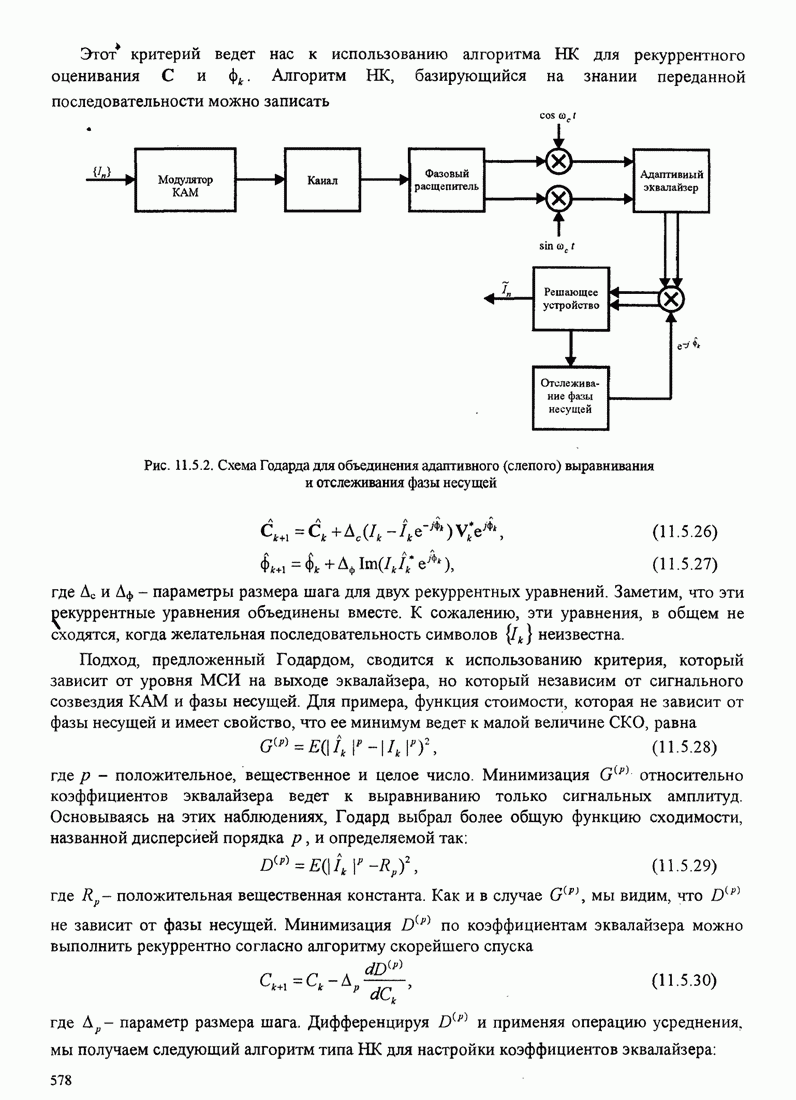
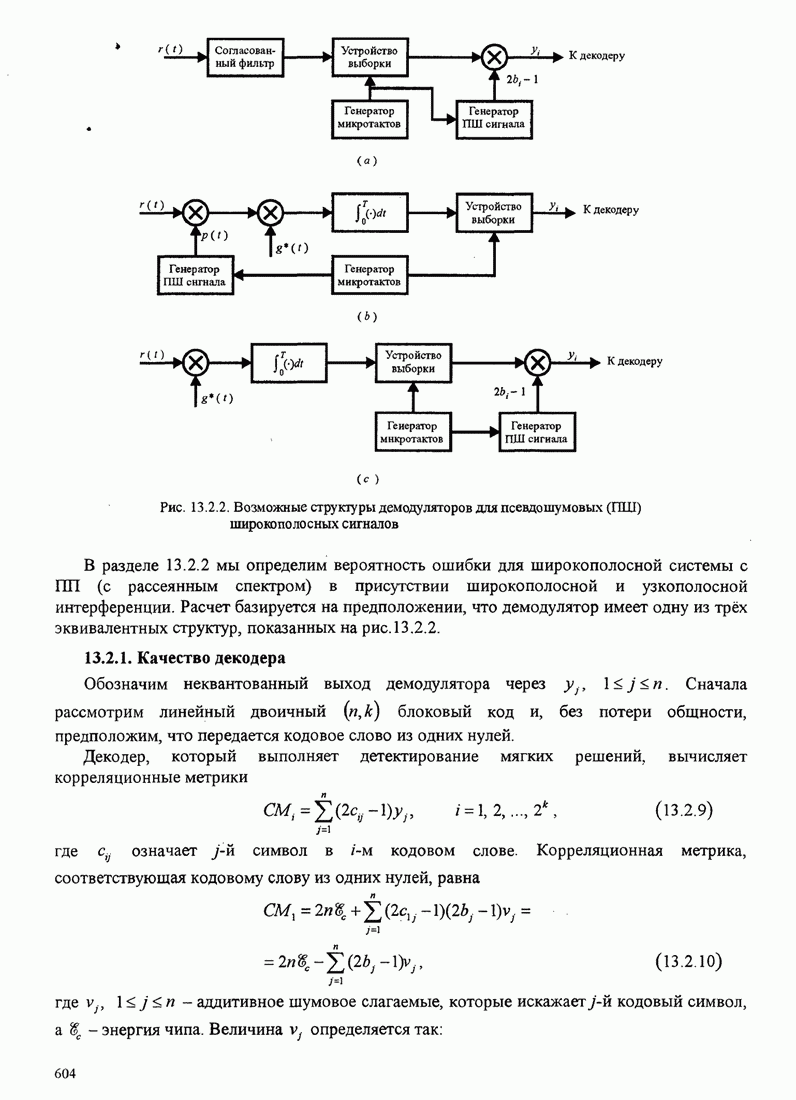
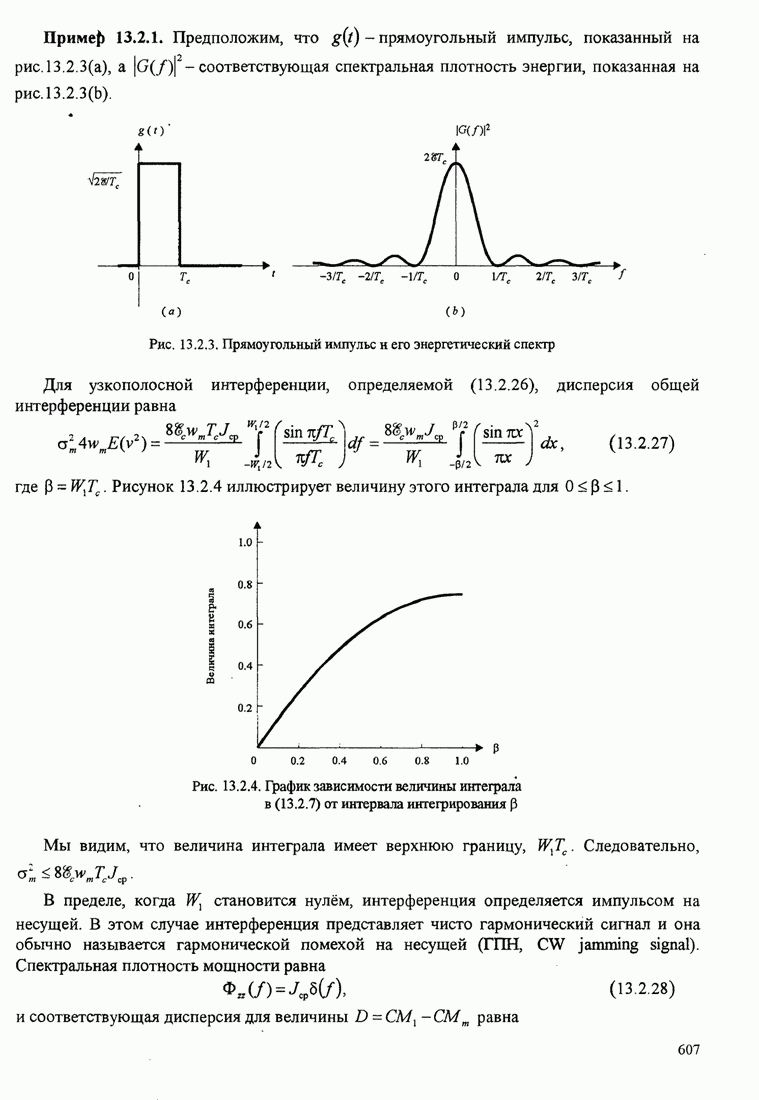
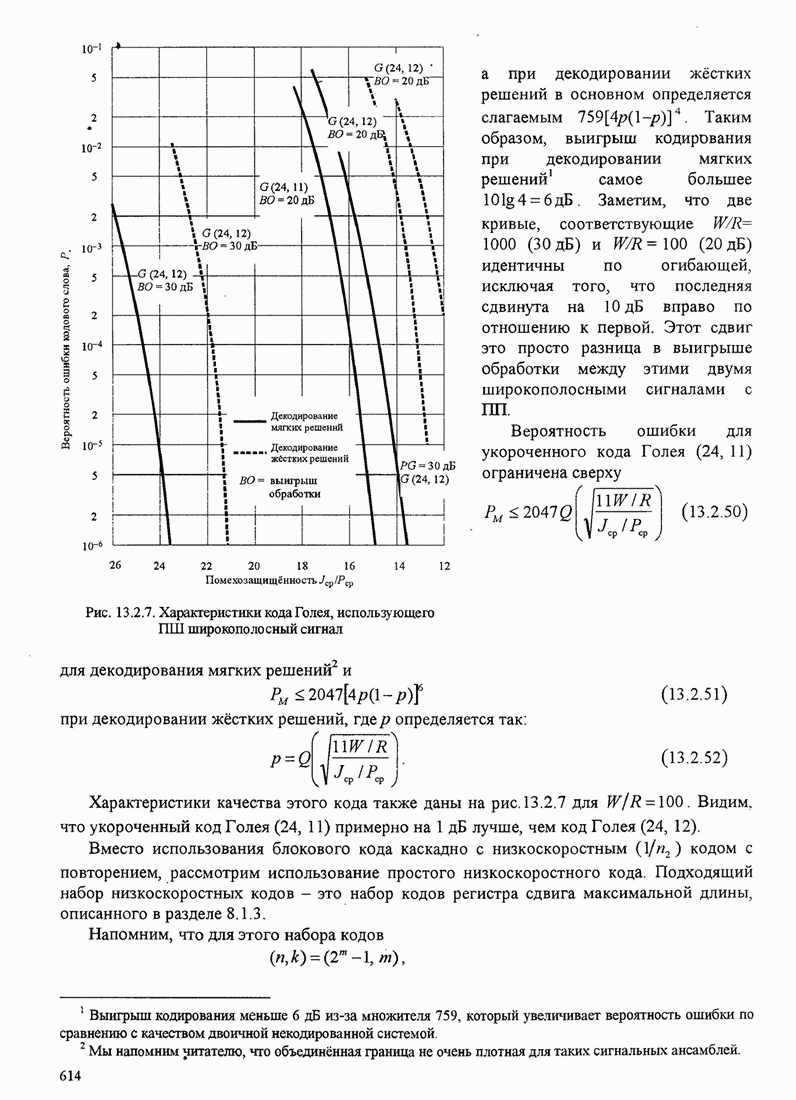
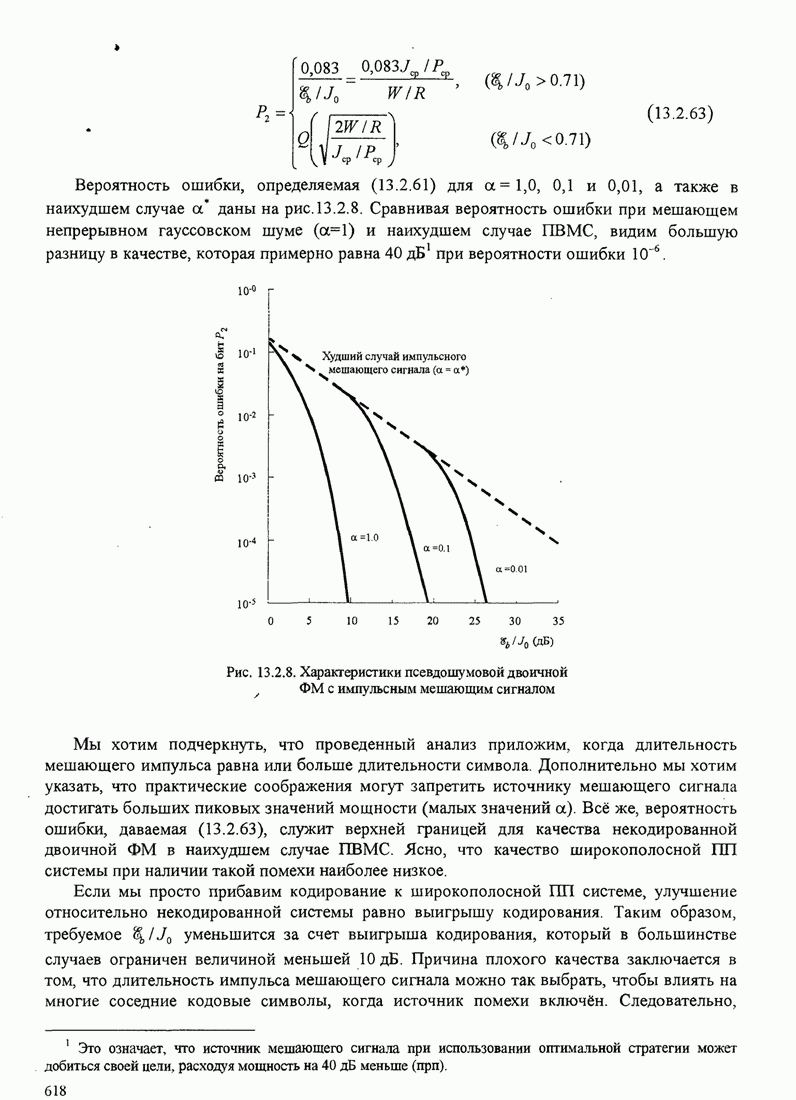
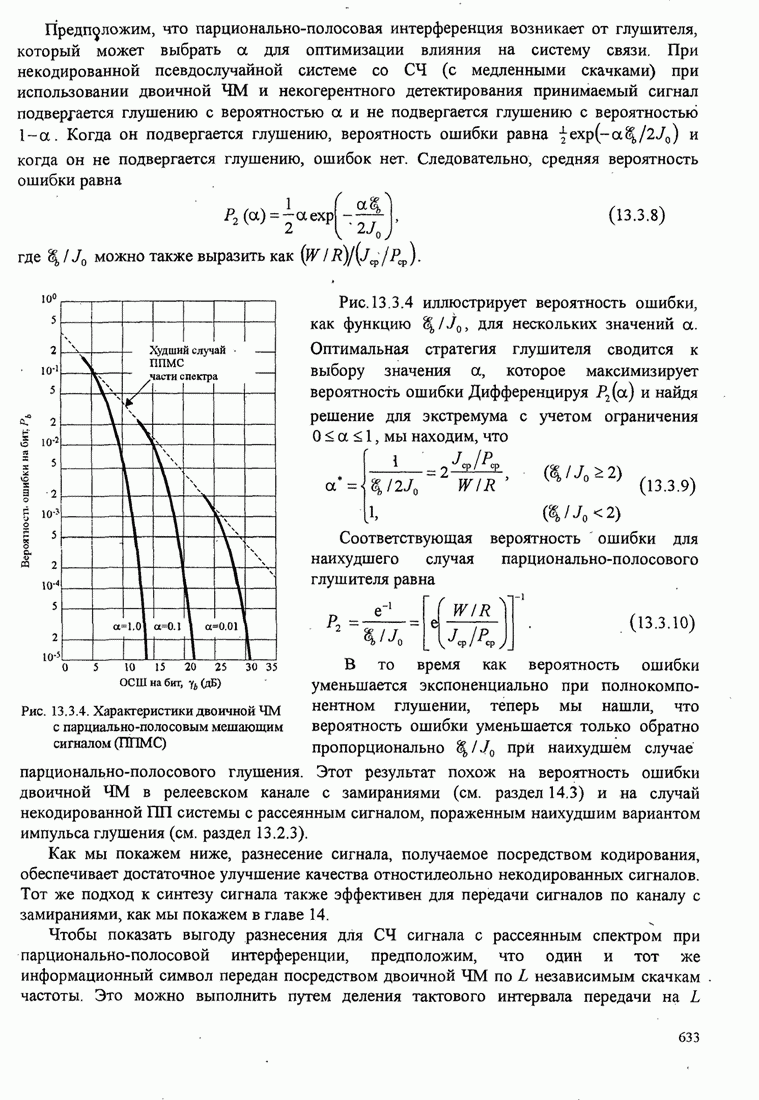
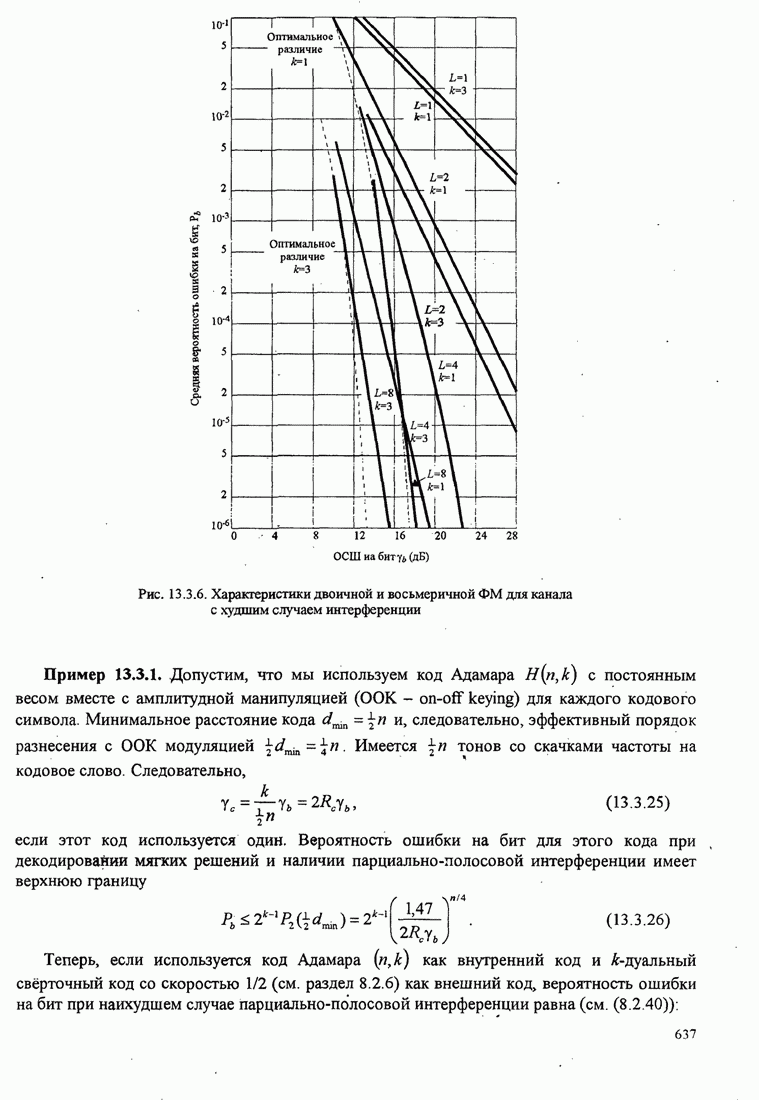
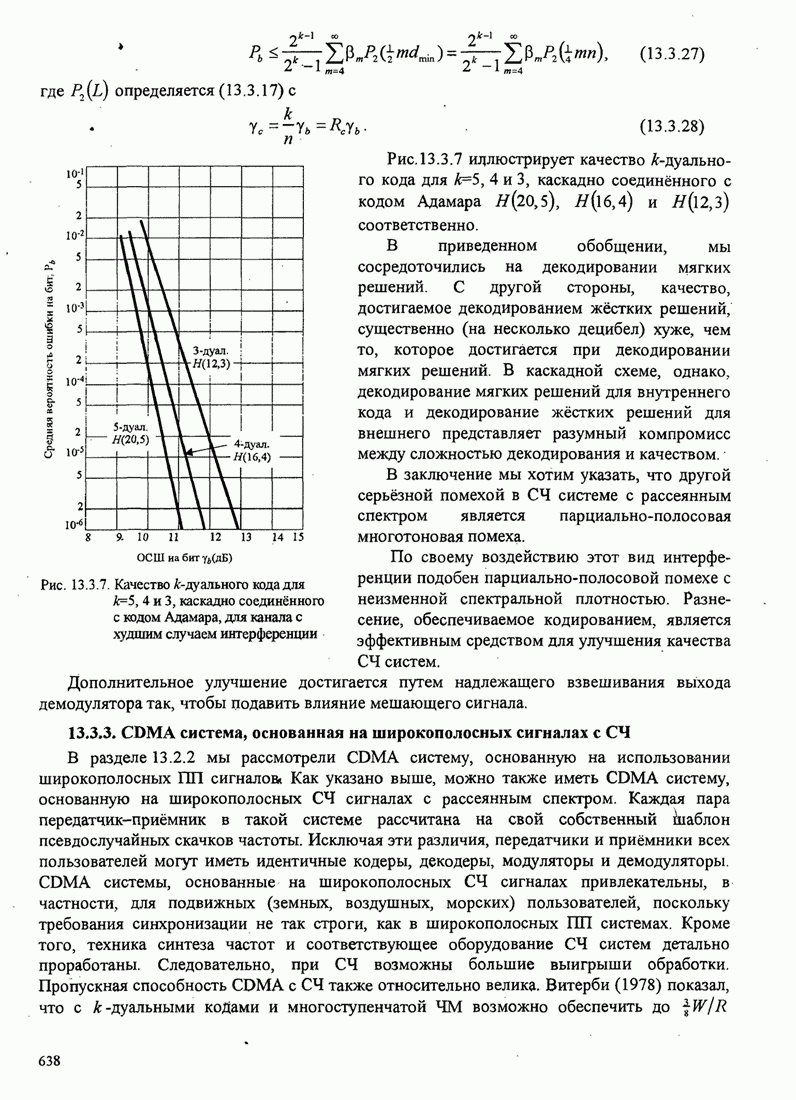
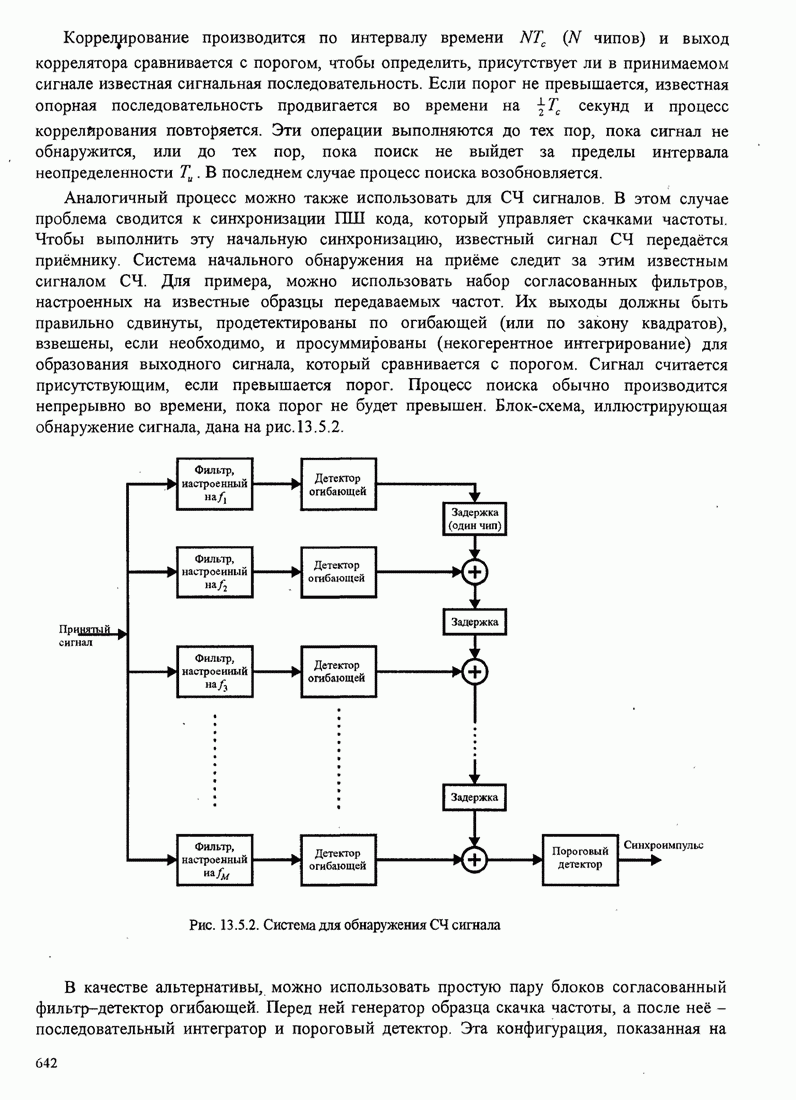
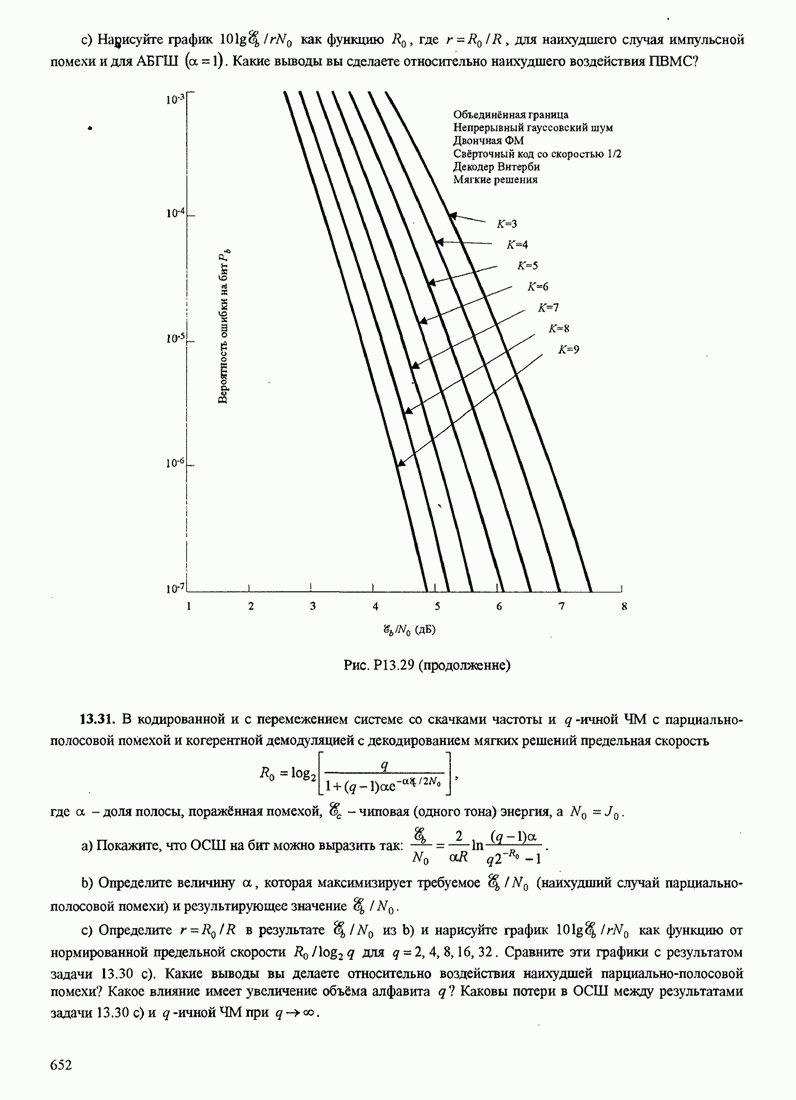
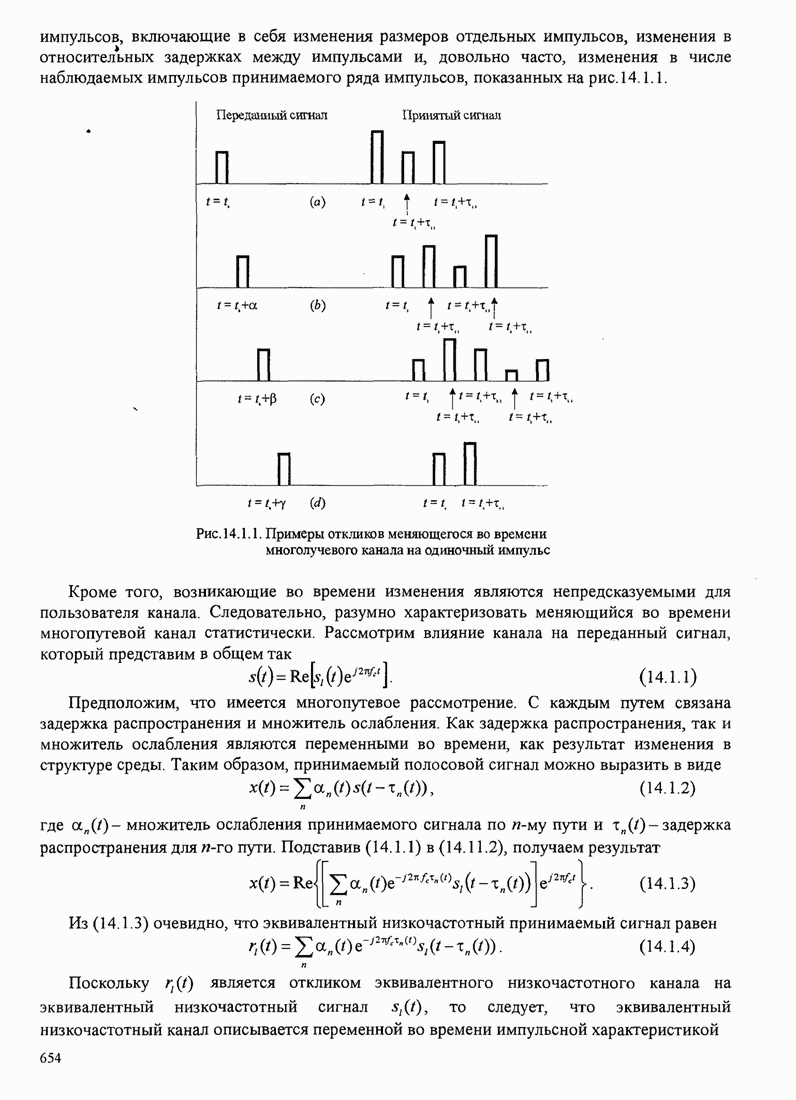
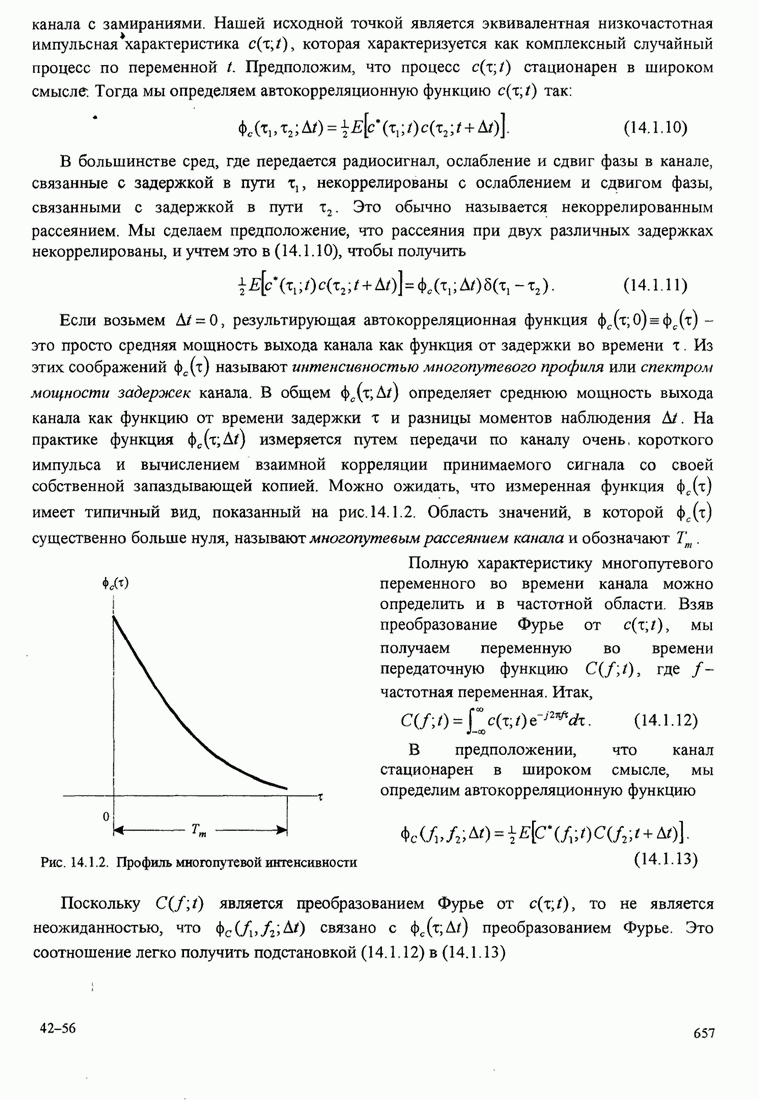
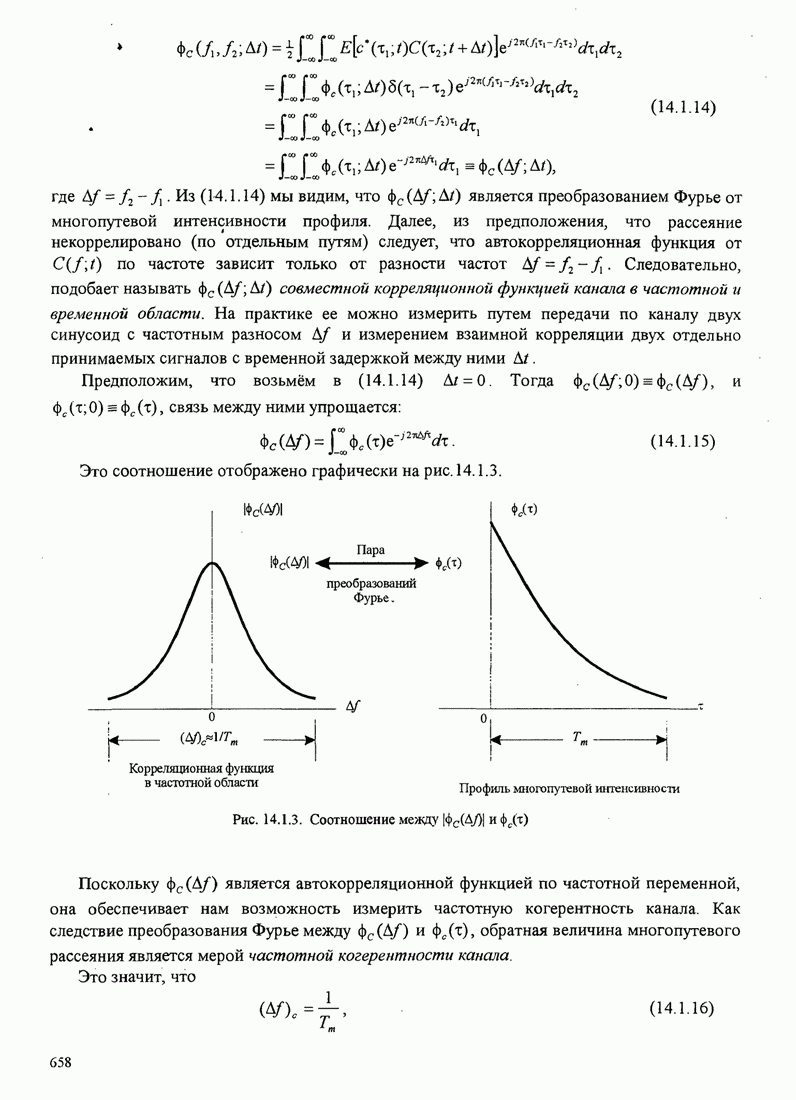
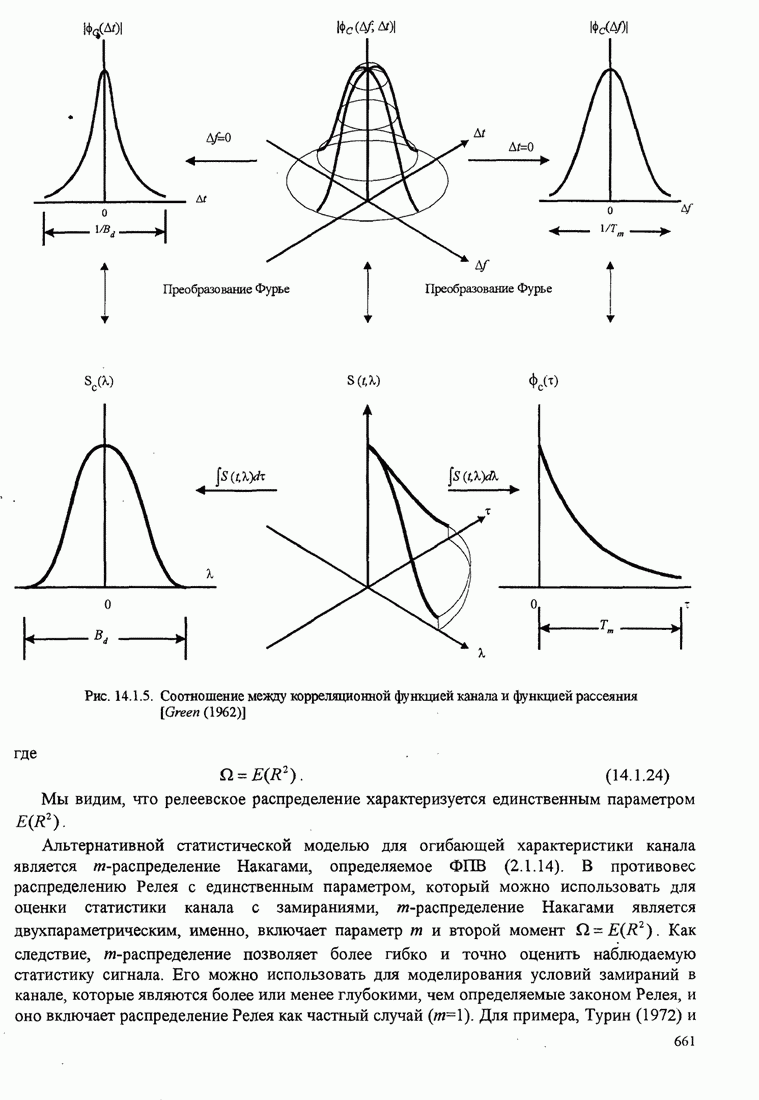
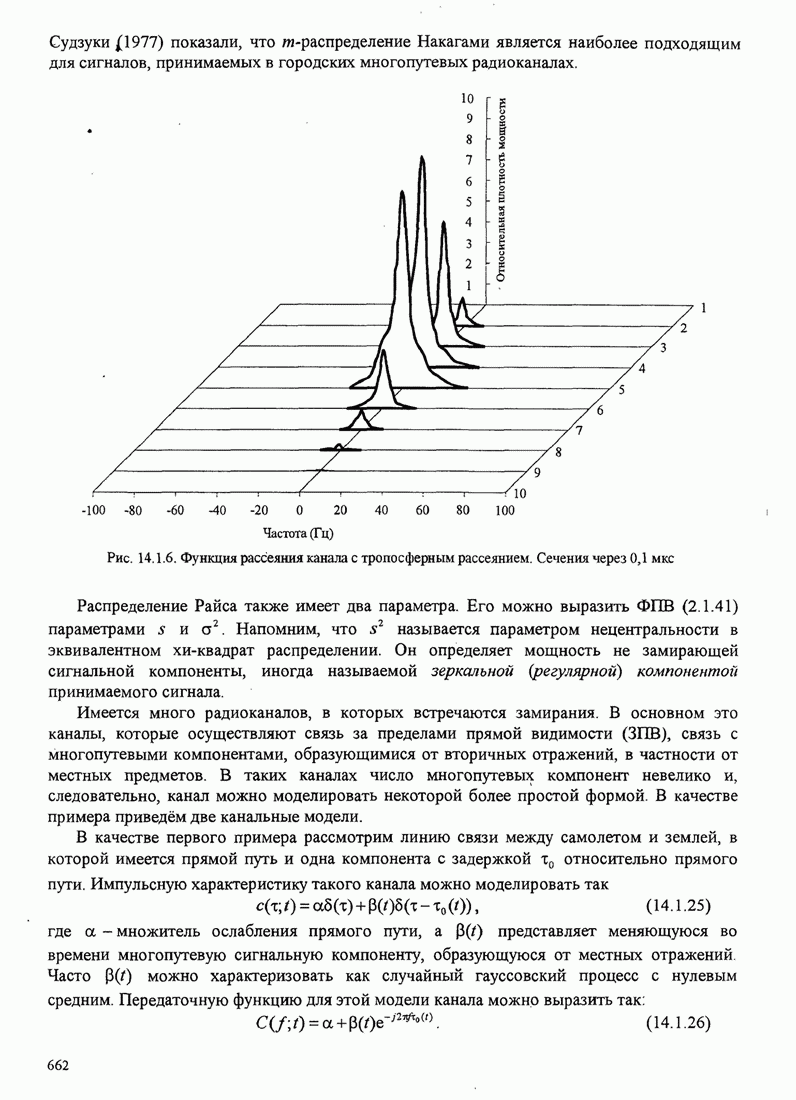
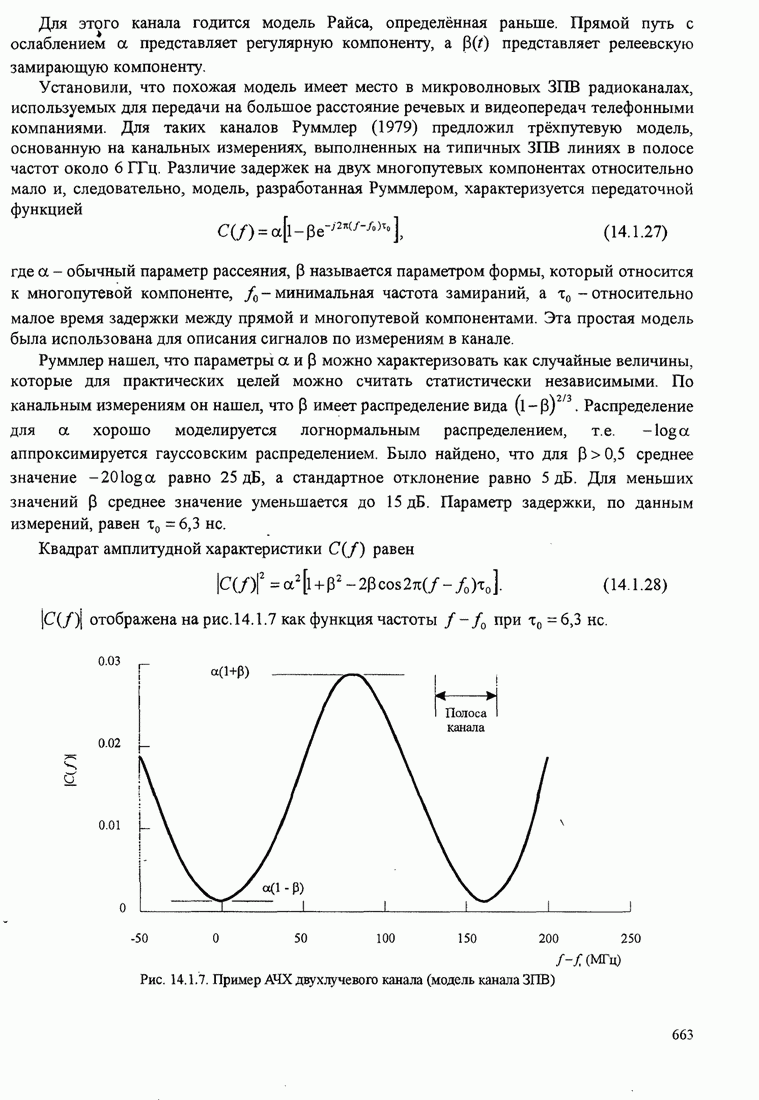
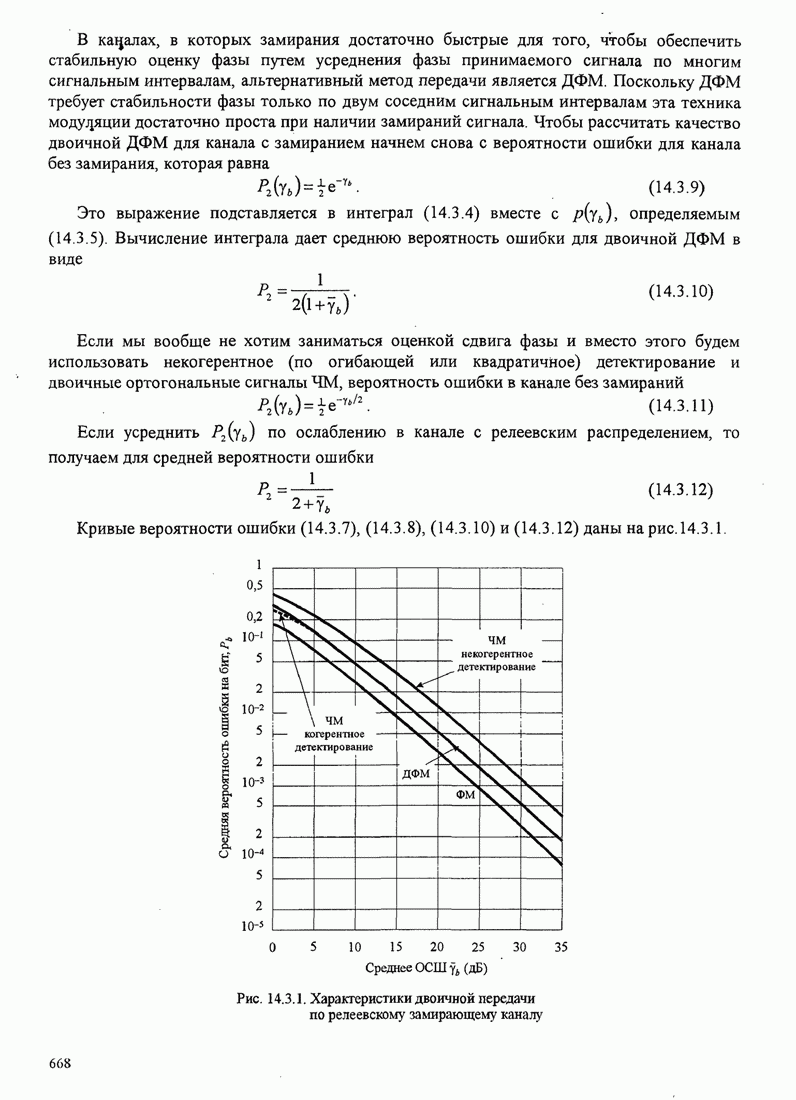
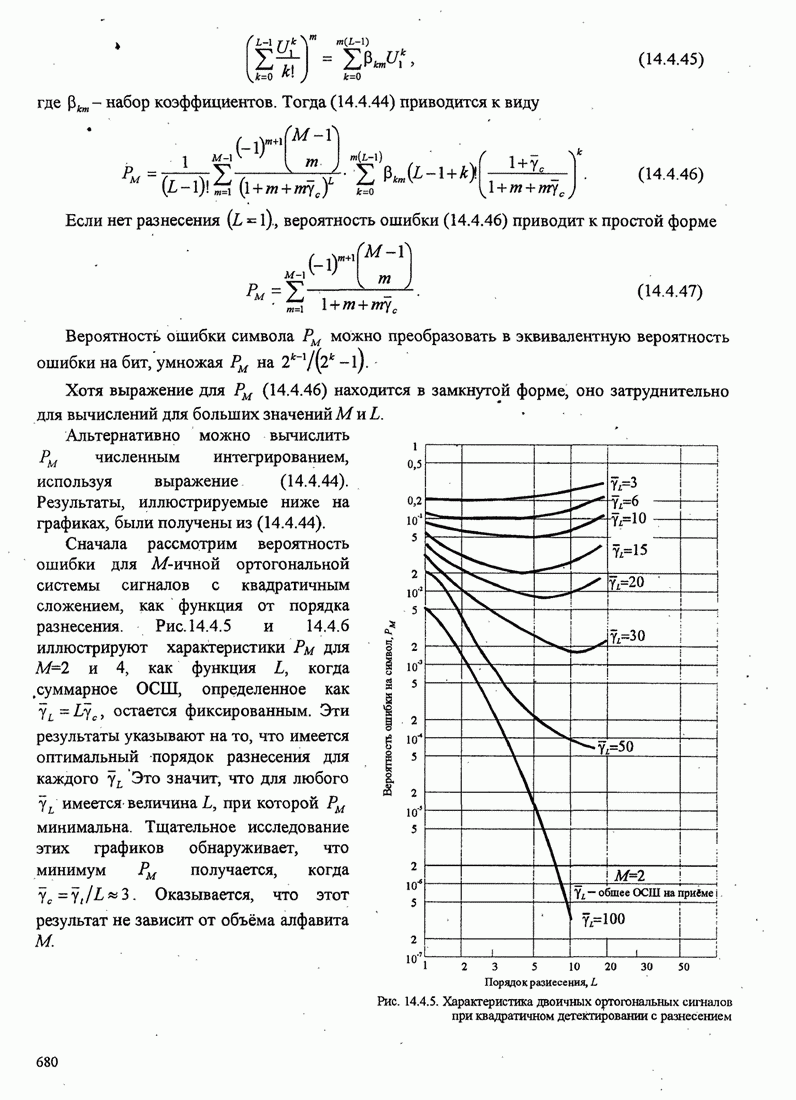
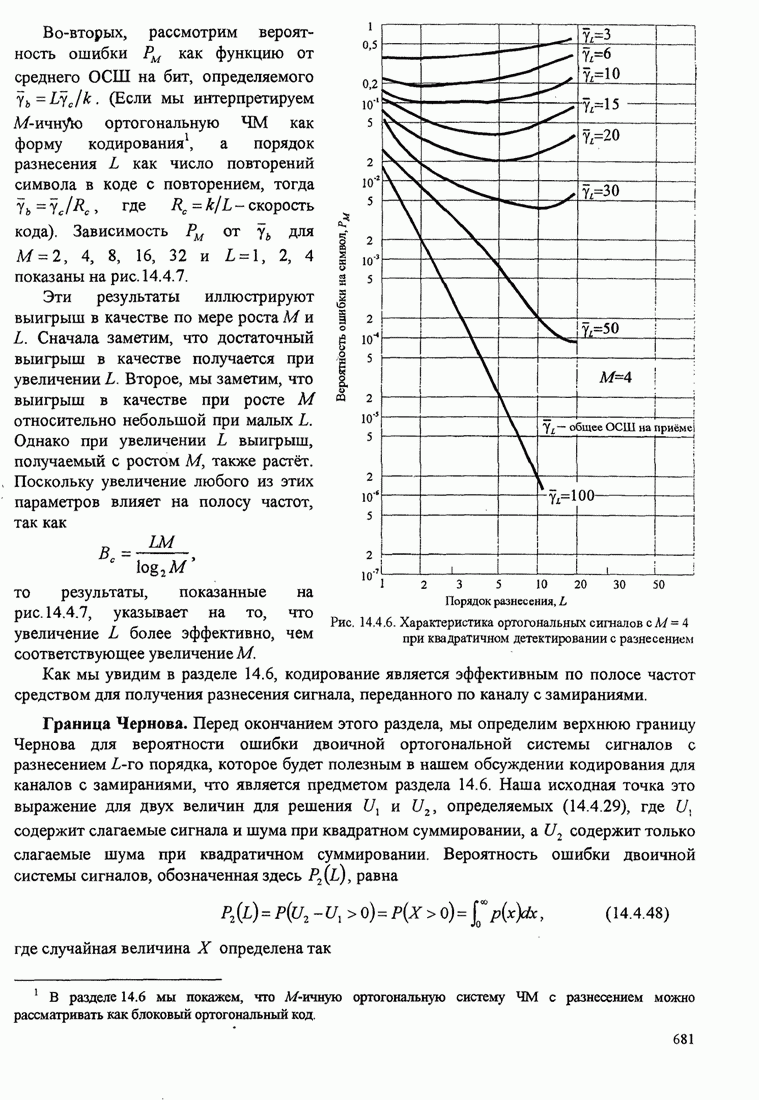
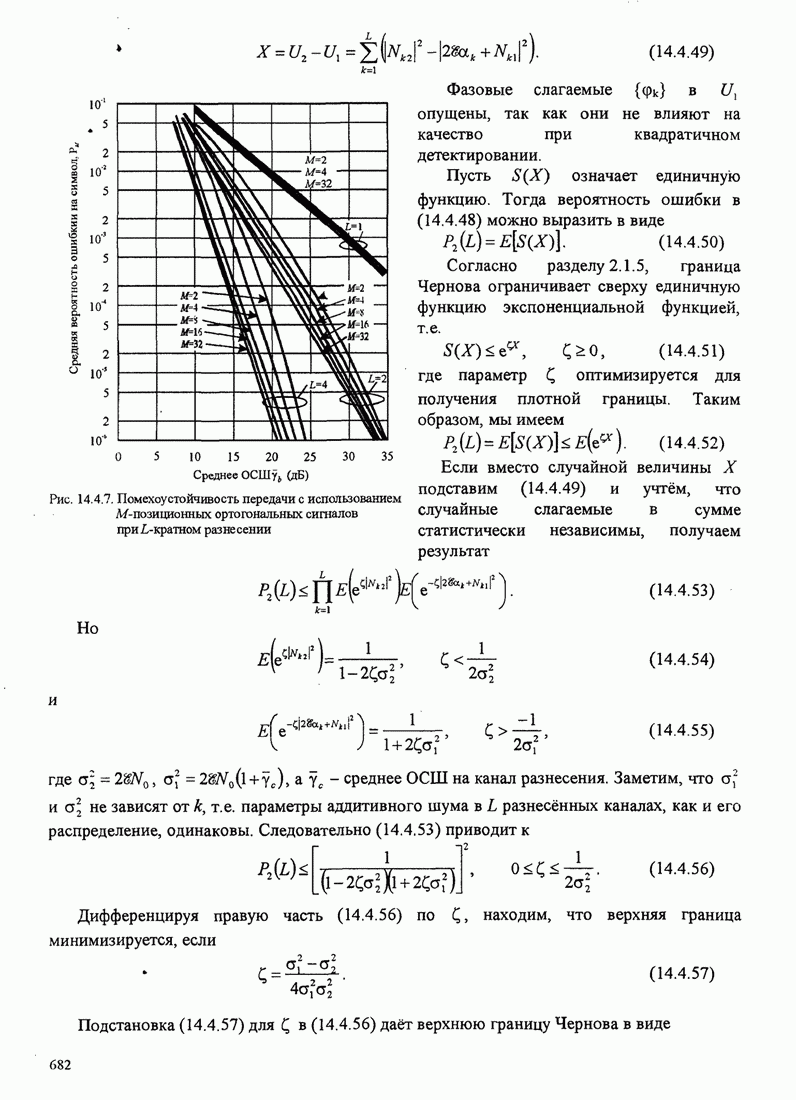
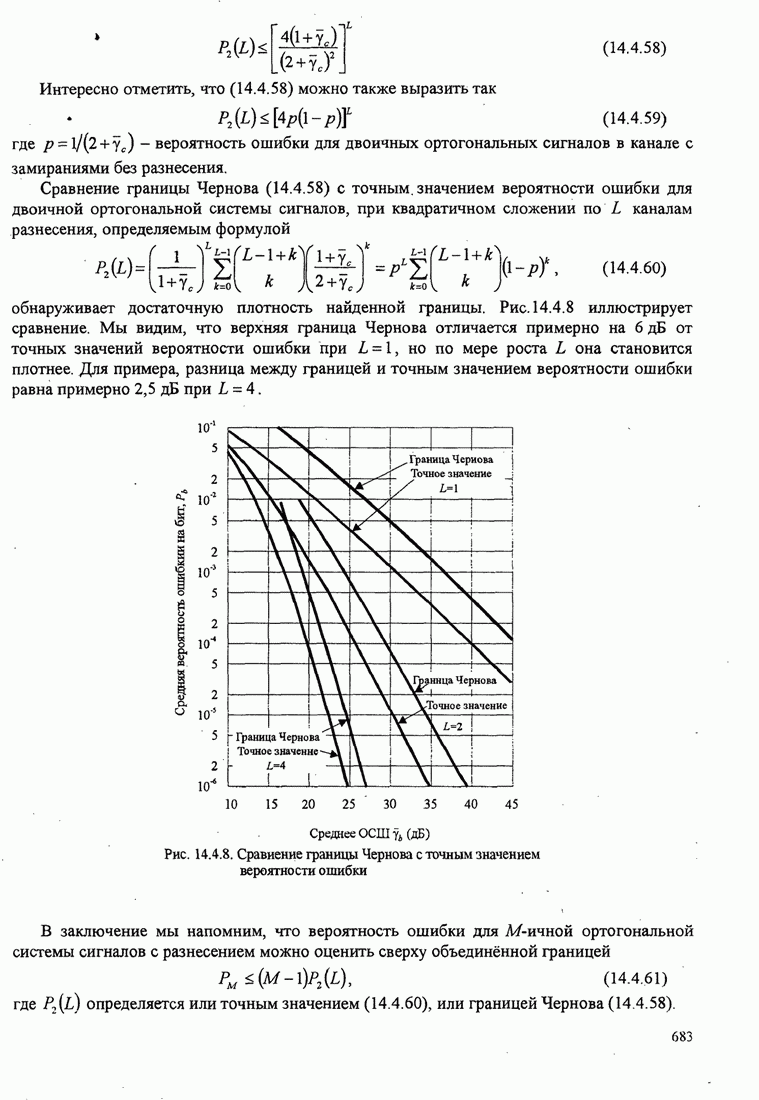
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
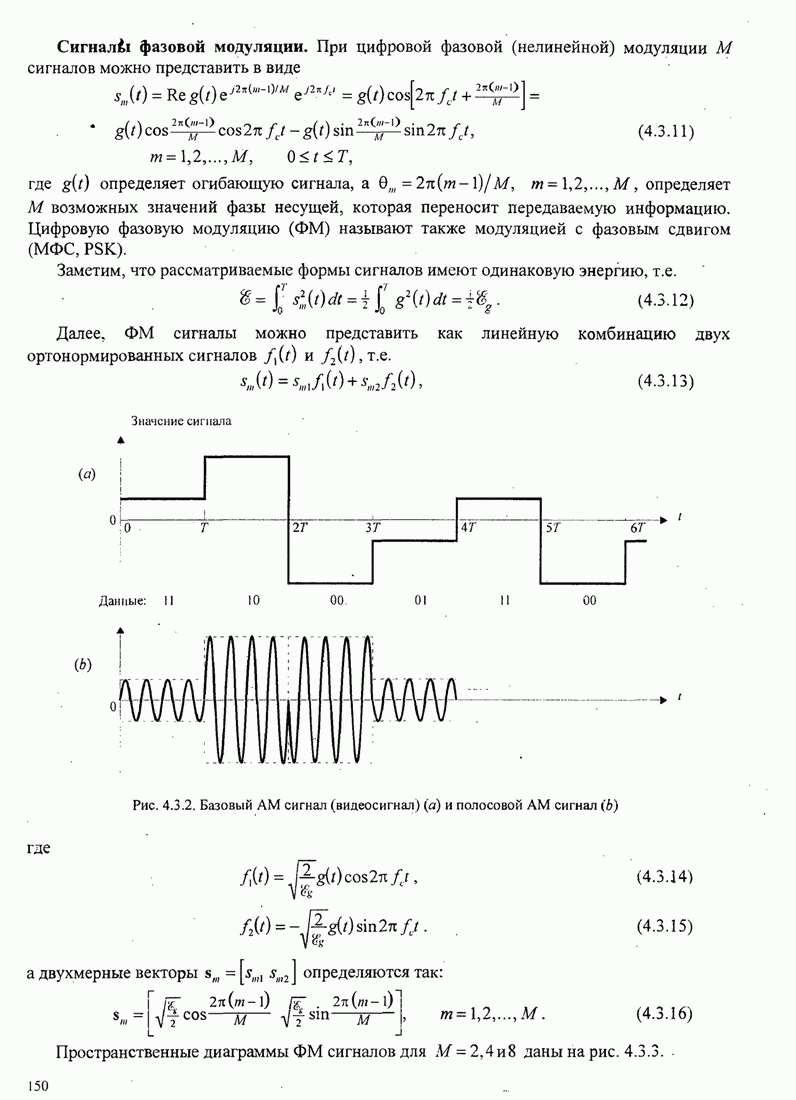
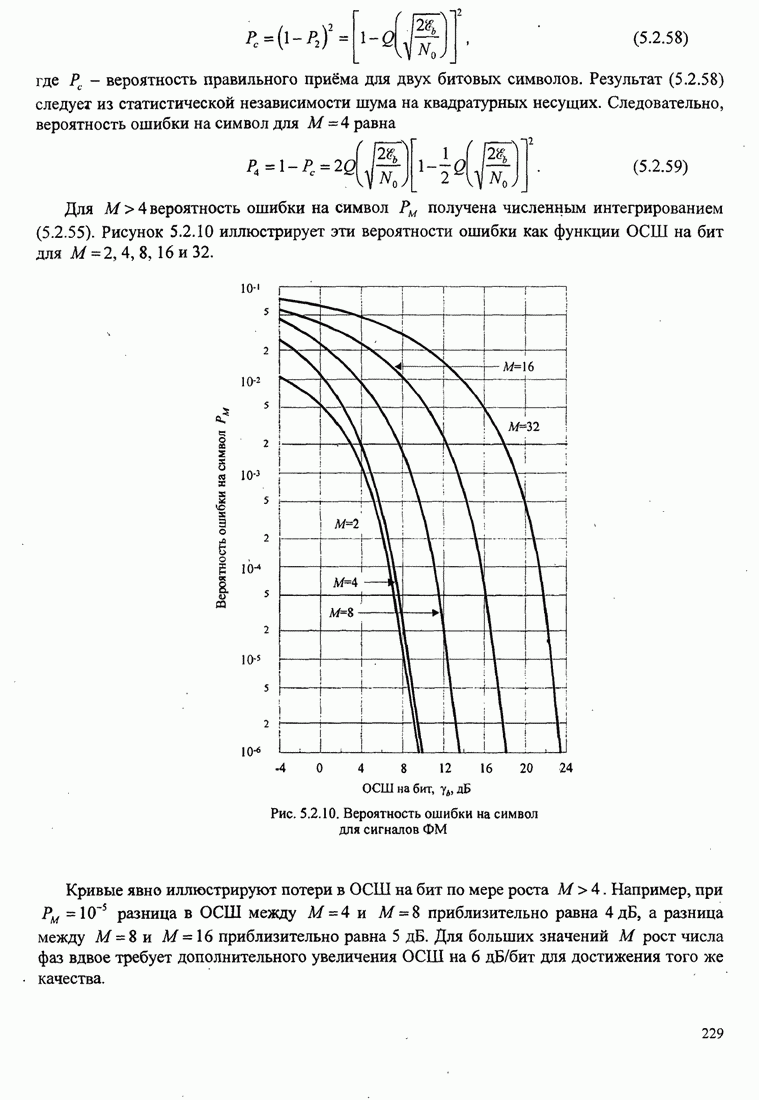
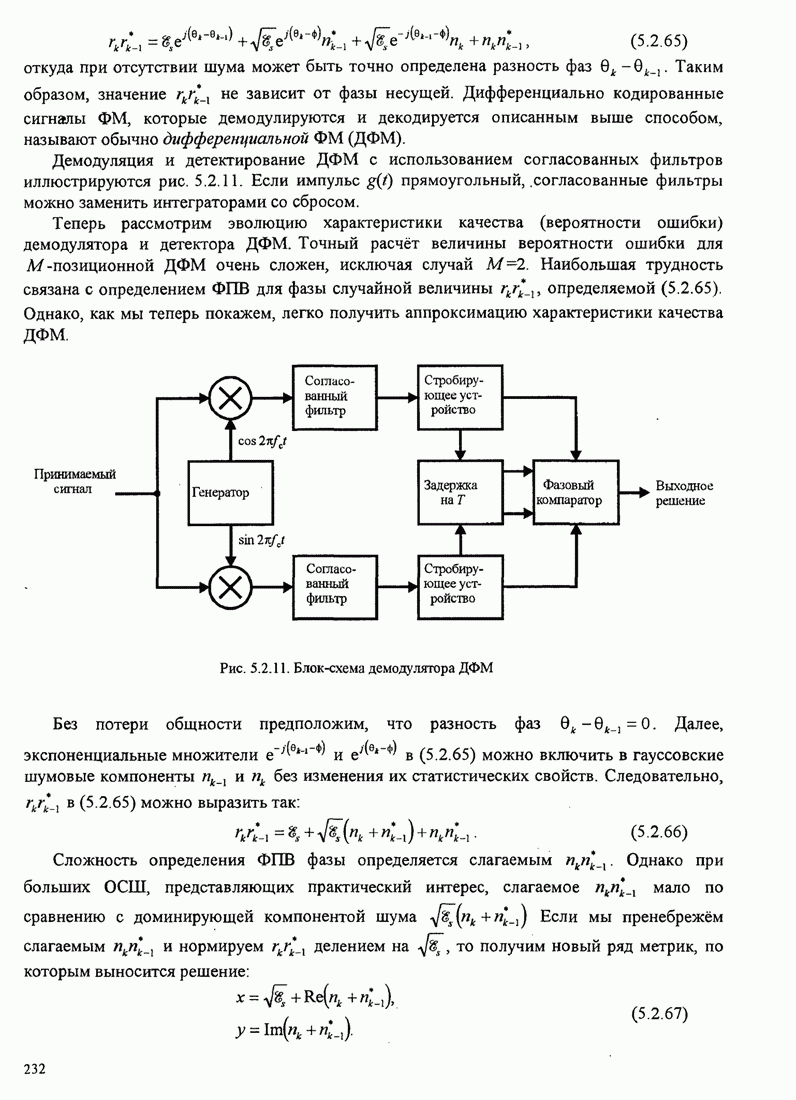
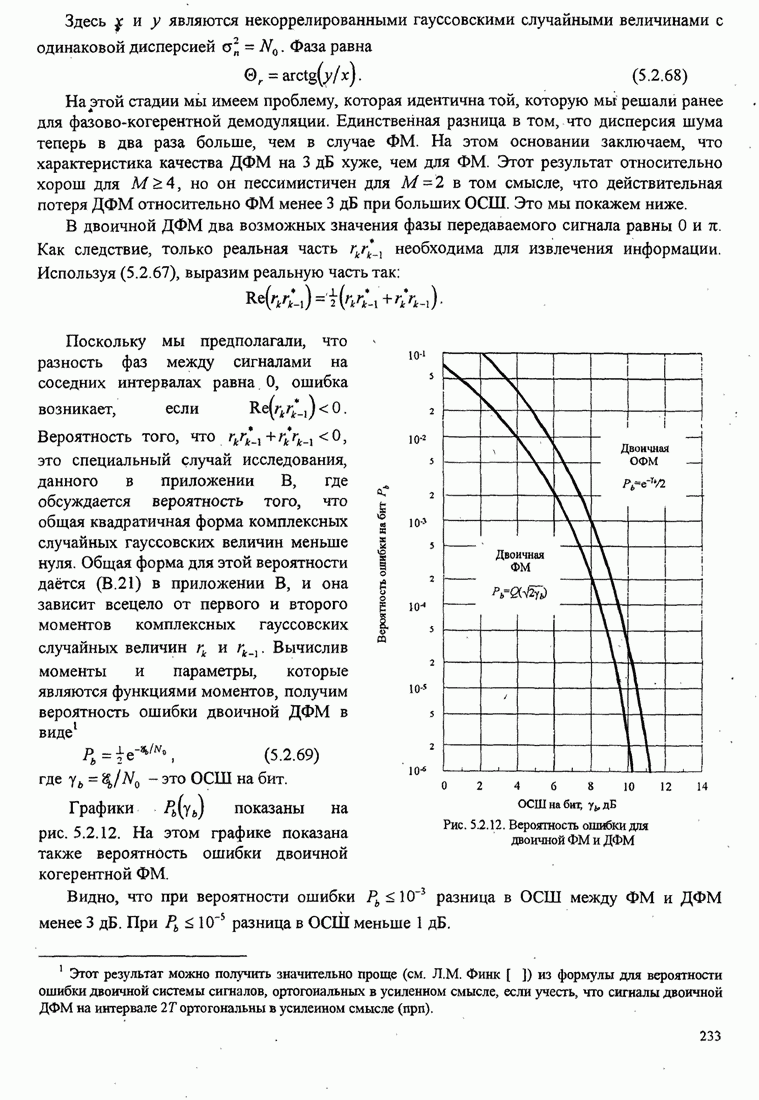
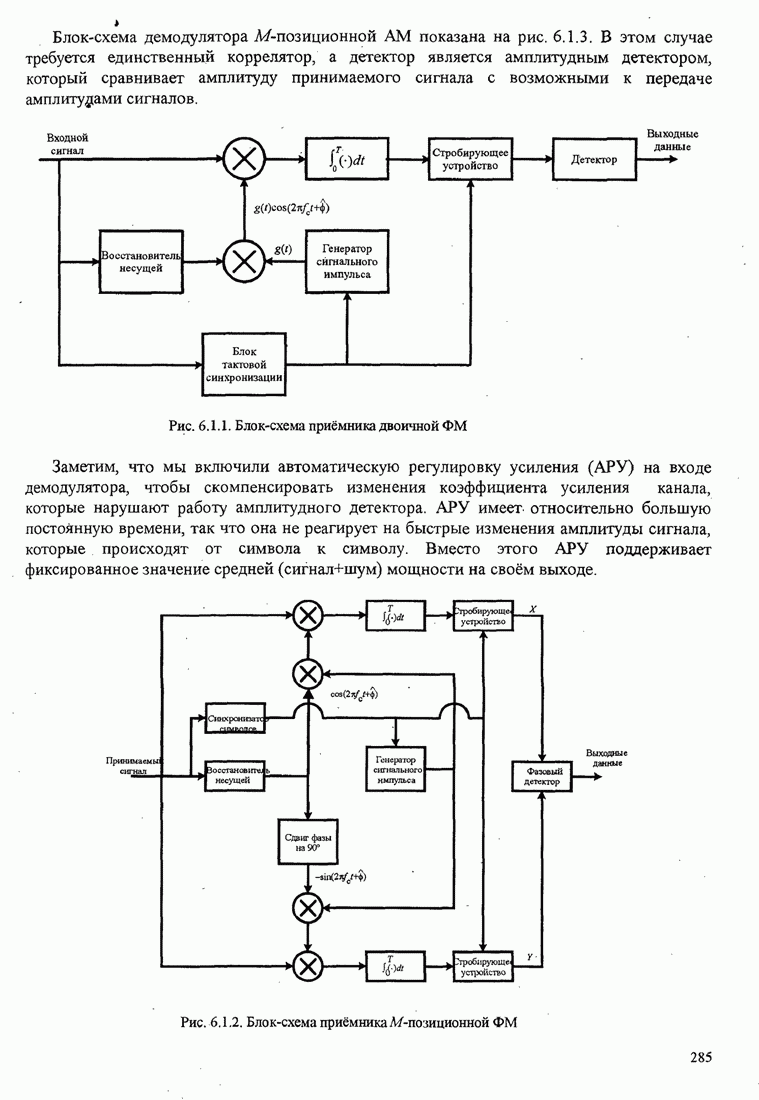
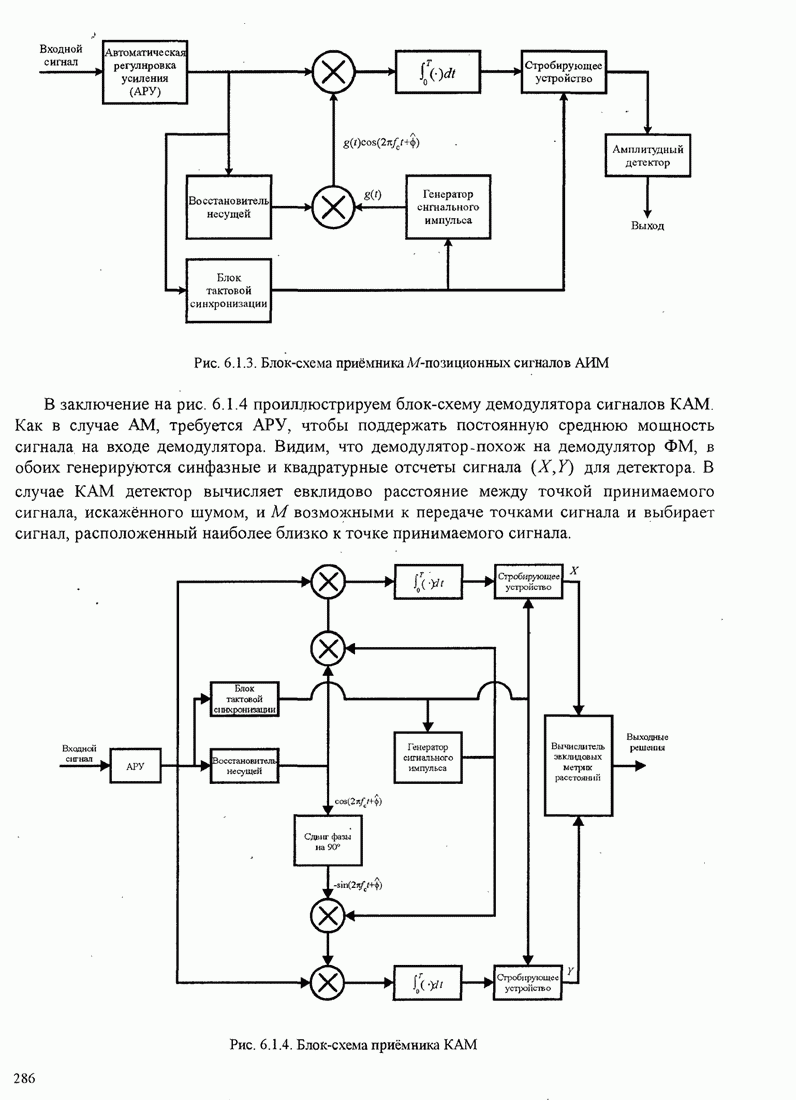
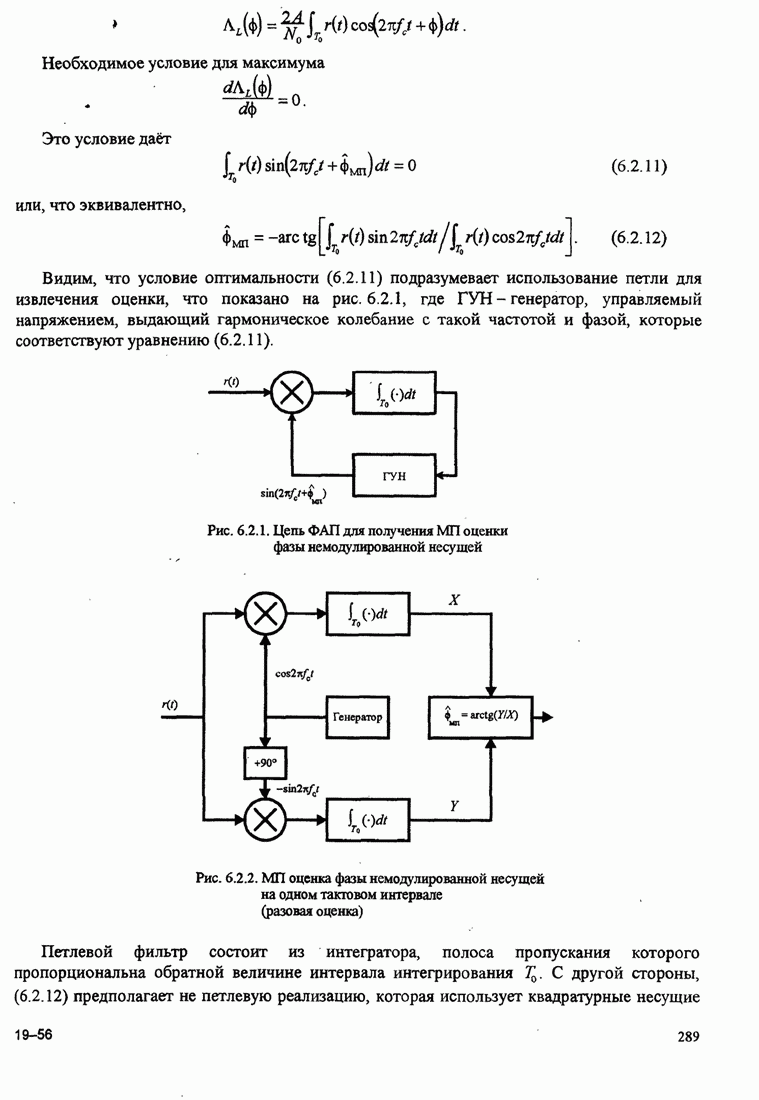
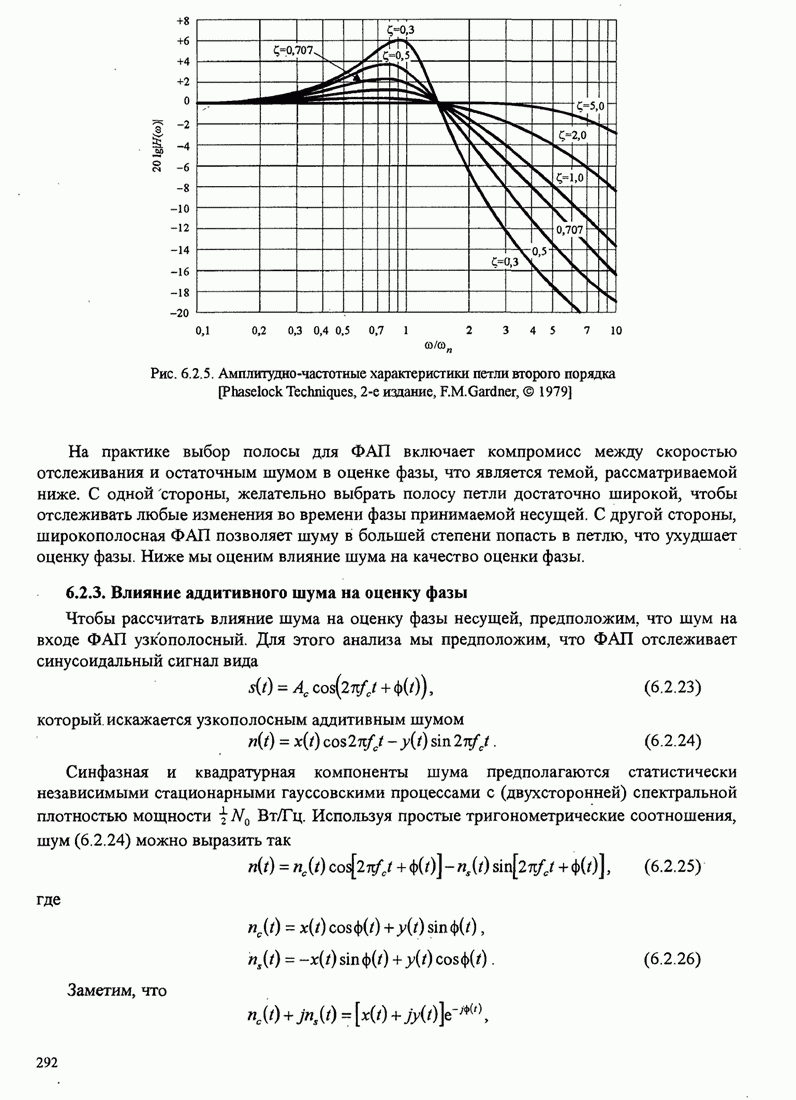
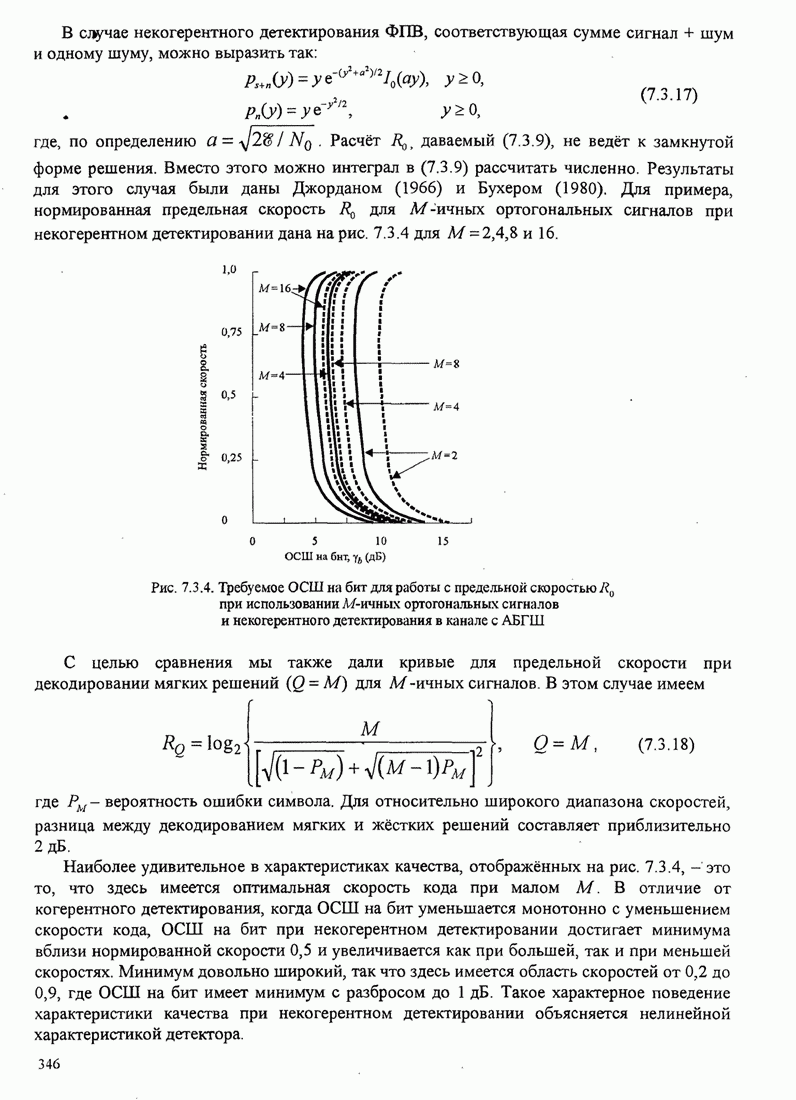
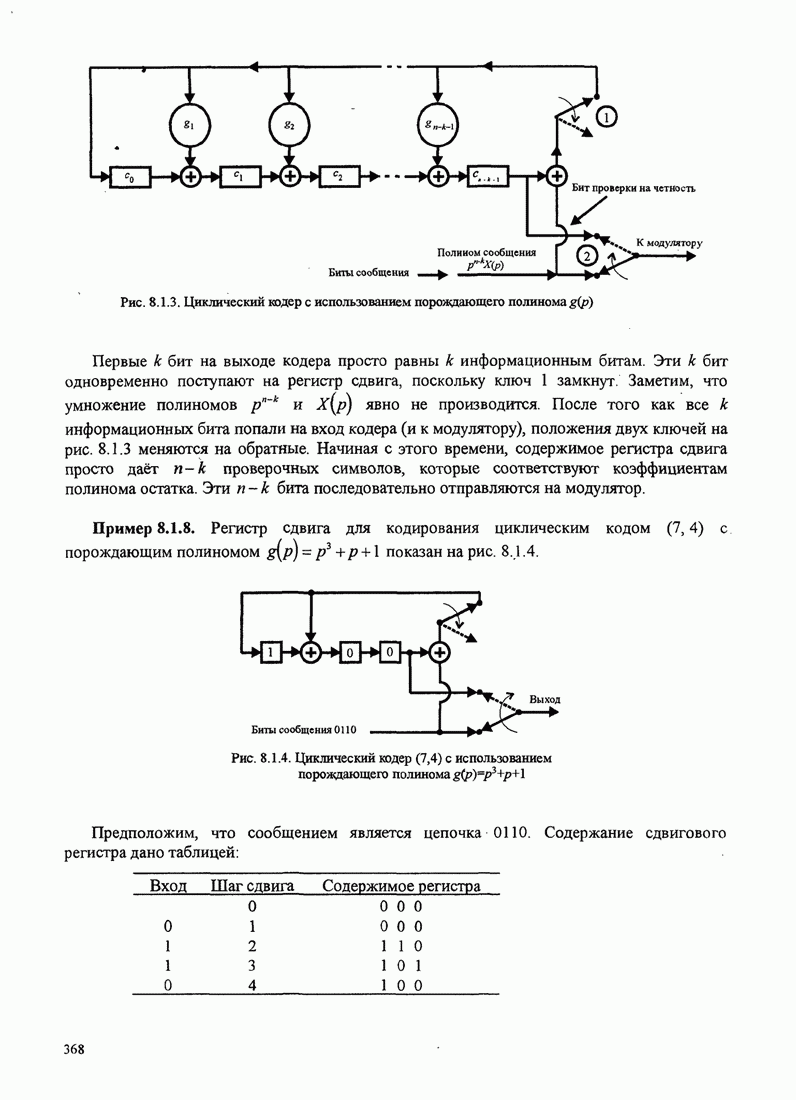
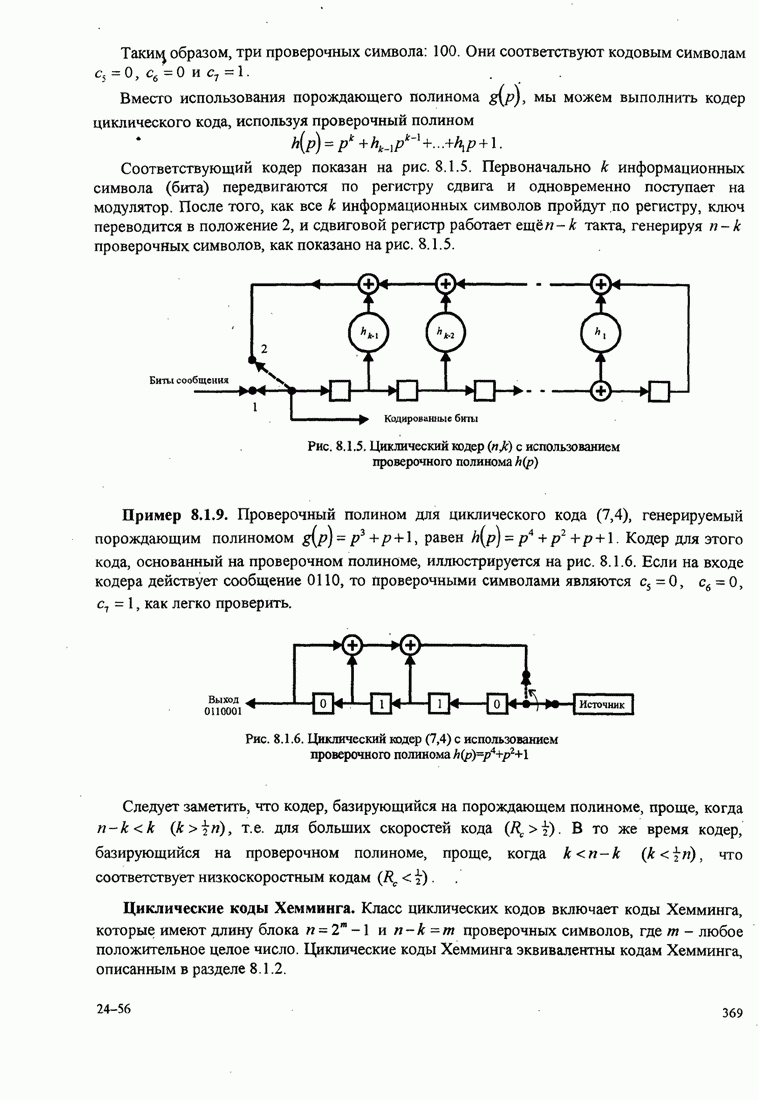
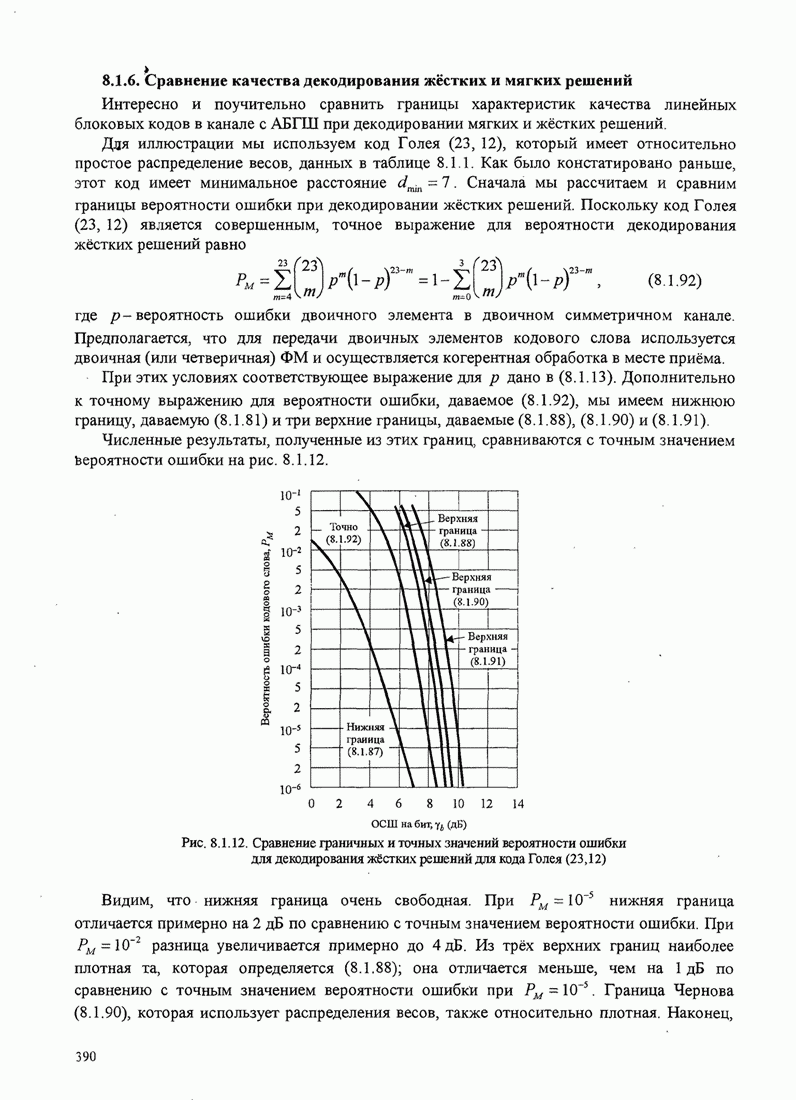
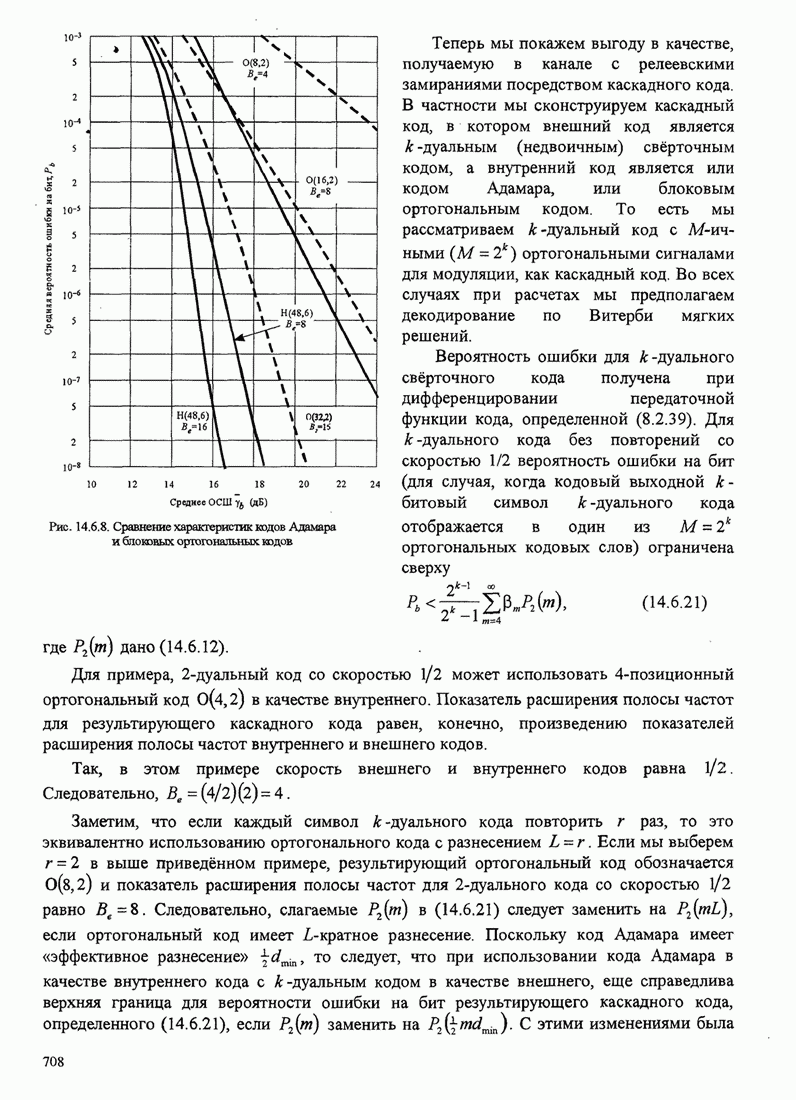
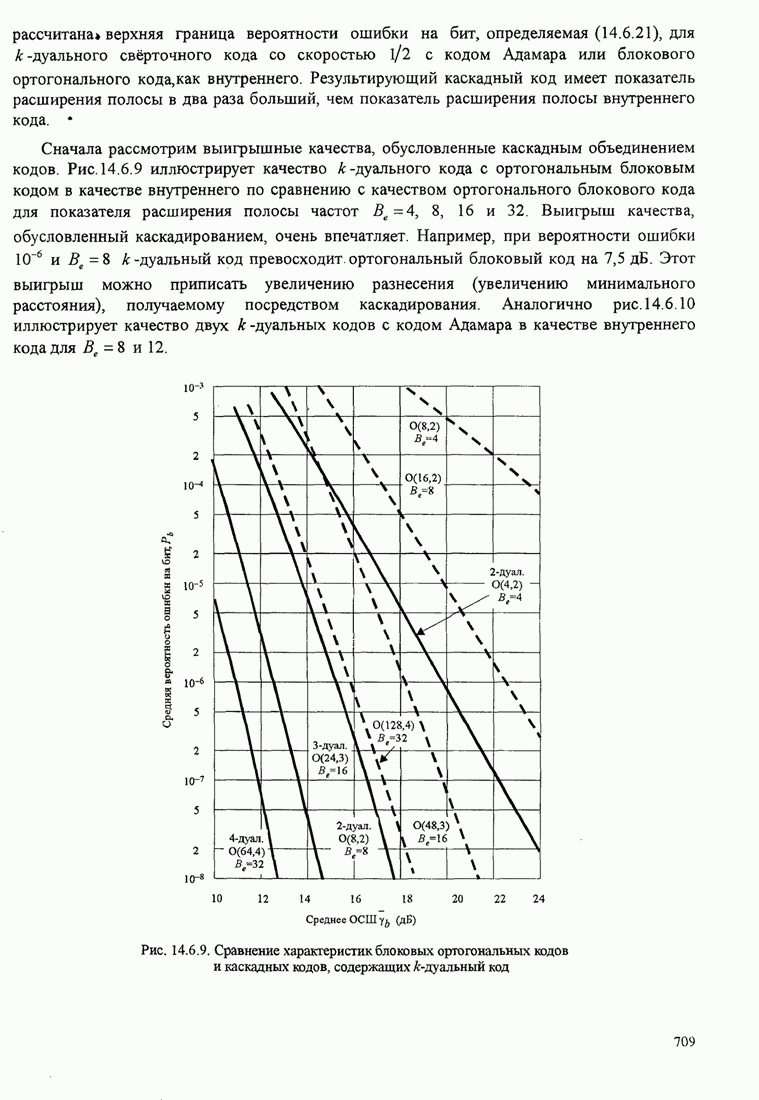
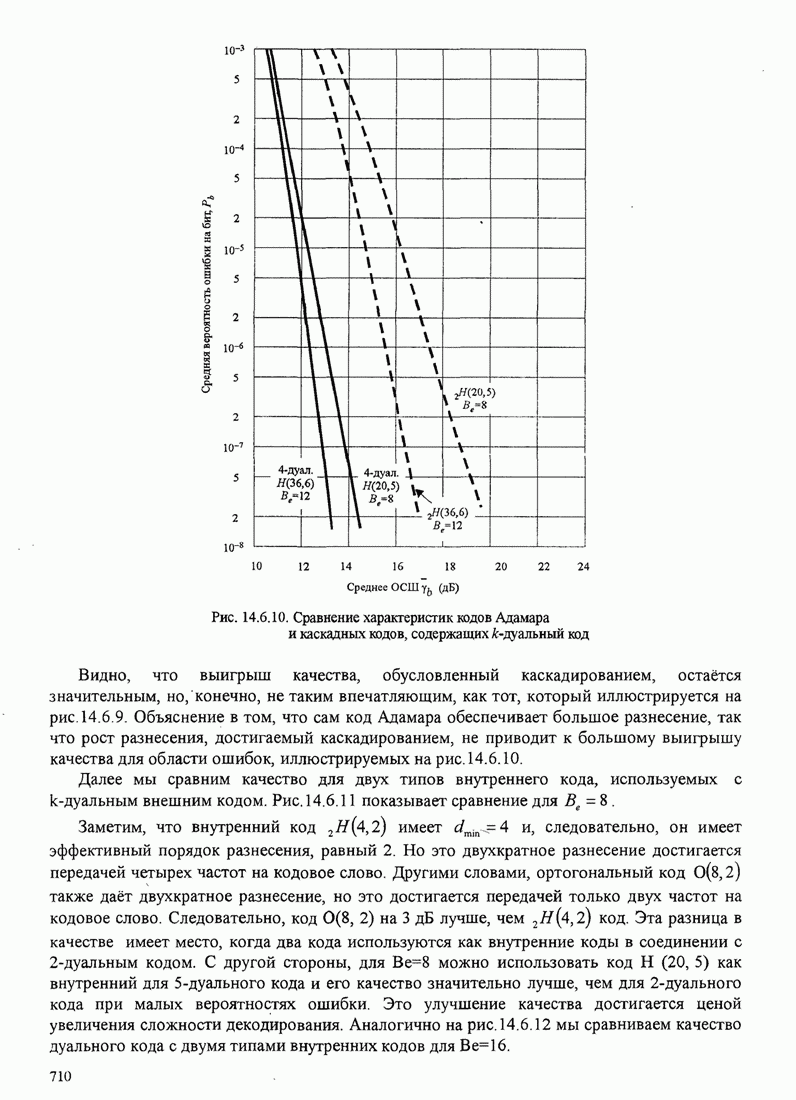
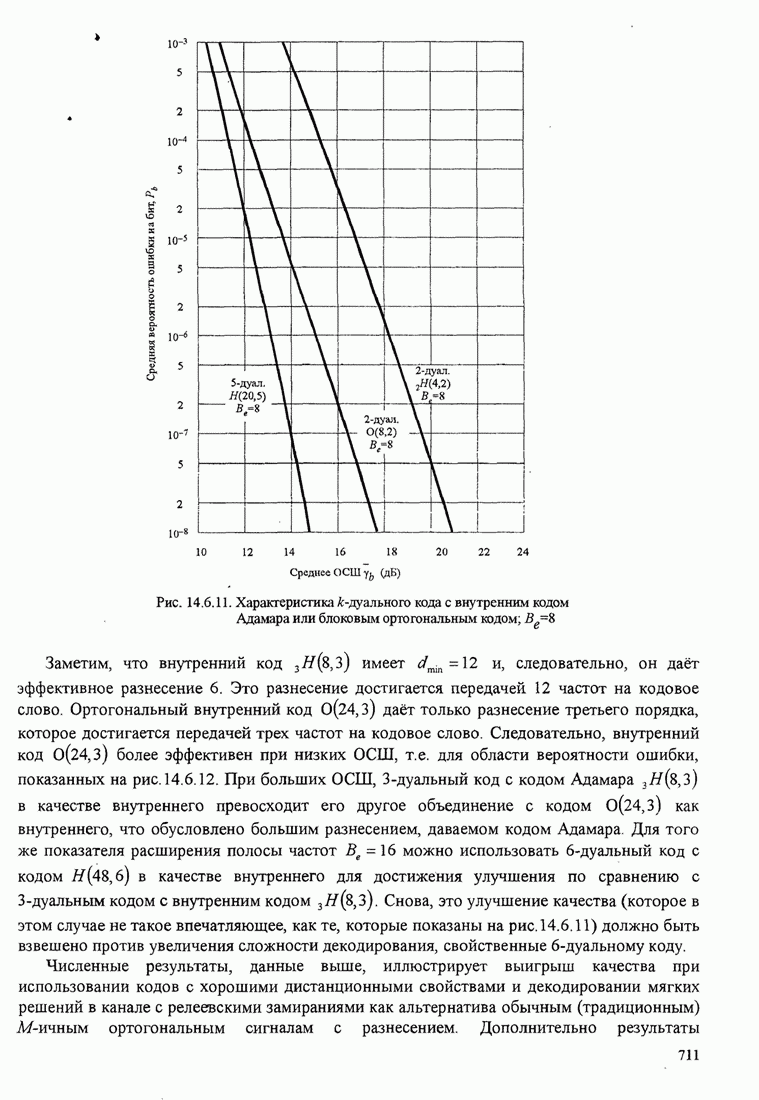
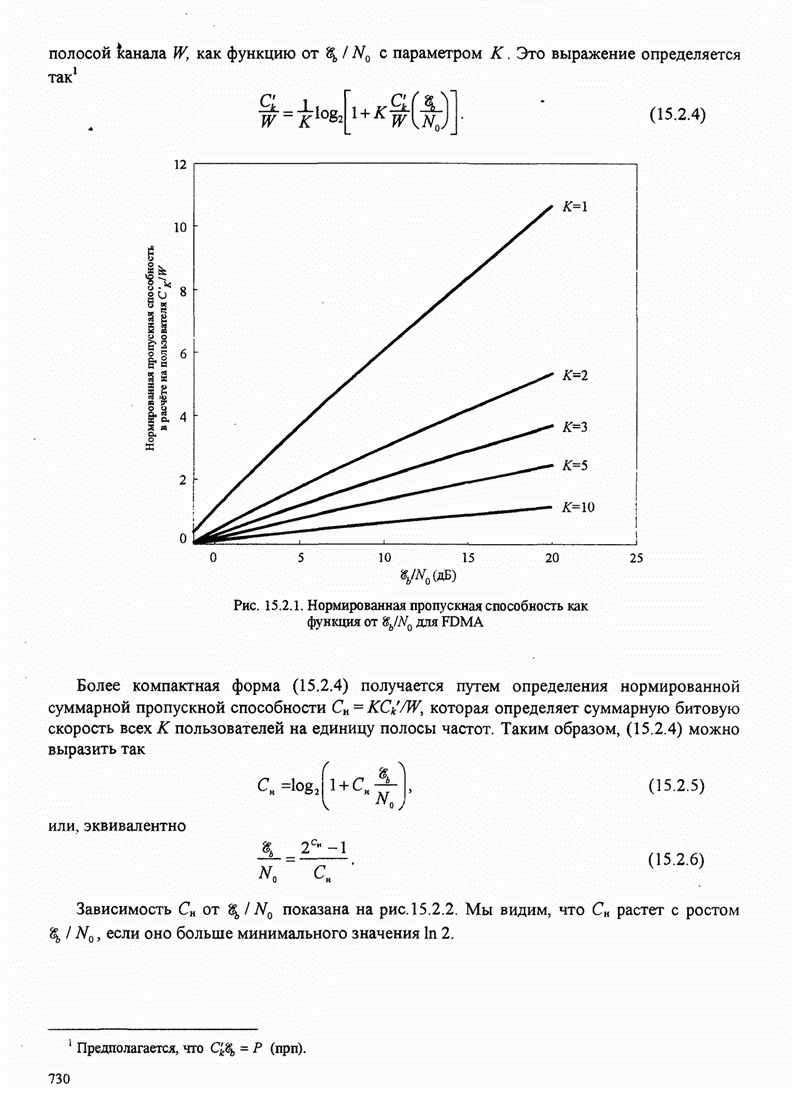
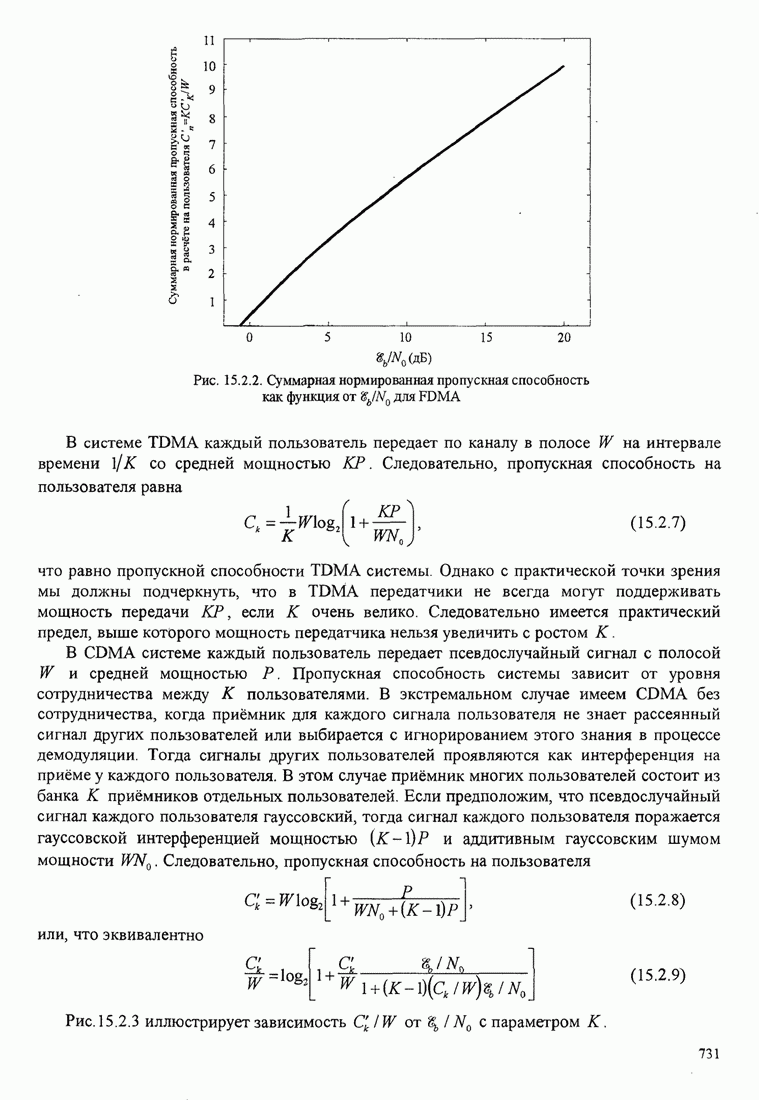
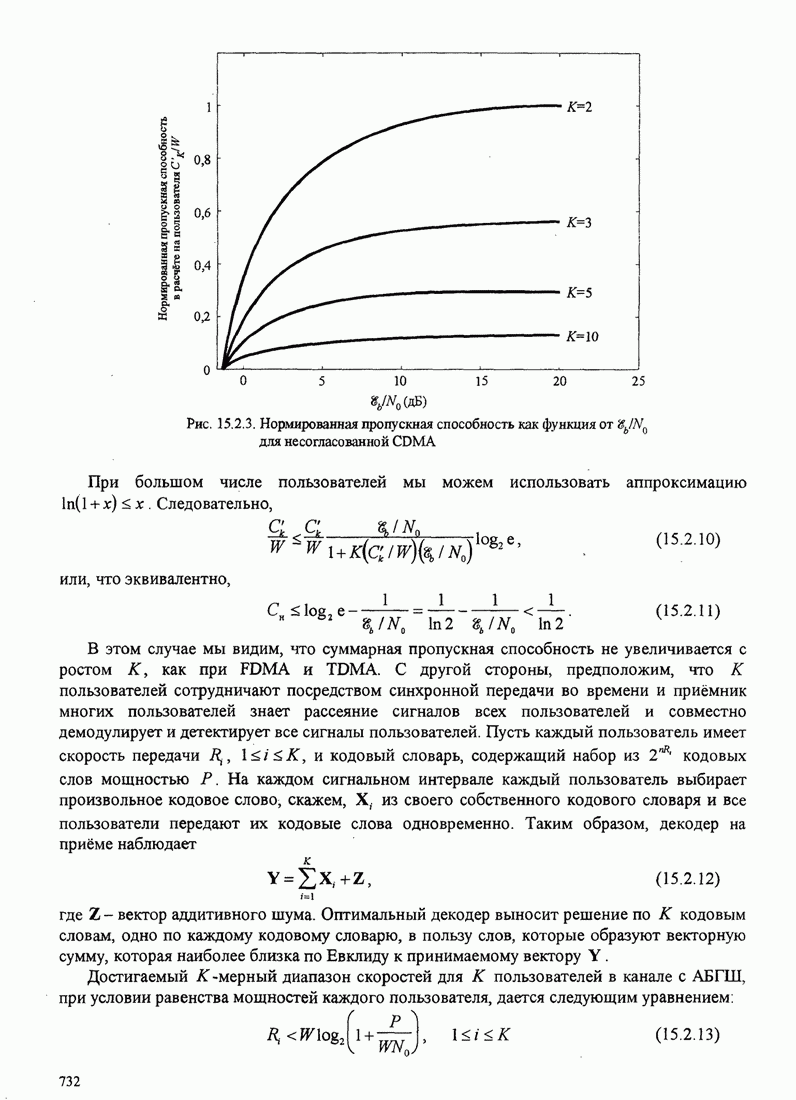
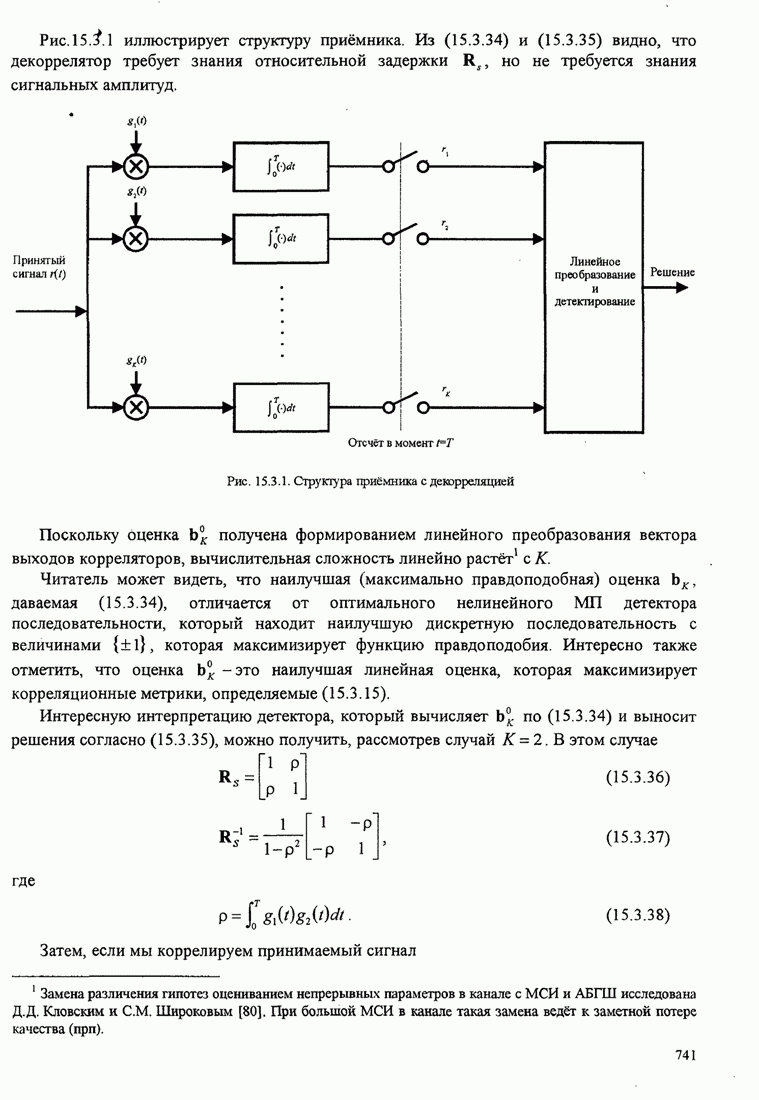
4.2.3. Ортогональное разложение сигналов
В этом разделе мы ознакомимся с векторным представлением сигналов и. таким образом продемонстрируем эквивалентность между сигналами и их векторными представлениями.
Предположим,
что ![]() является
детерминированным вещественным сигналом с ограниченной энергией
является
детерминированным вещественным сигналом с ограниченной энергией
![]() . (4.2.20)
. (4.2.20)
Далее,
предположим, что существует ансамбль функций ![]() , который ортонормирован в том смысле,
что
, который ортонормирован в том смысле,
что
 (4.2.21)
(4.2.21)
Мы
можем аппроксимировать сигнал ![]() при помощи взвешенной линейной
комбинации этих функций, т.е.
при помощи взвешенной линейной
комбинации этих функций, т.е.
![]() , (4.2.22)
, (4.2.22)
где ![]() - коэффициенты в
аппроксимации
- коэффициенты в
аппроксимации ![]() .
Ошибка аппроксимации
.
Ошибка аппроксимации
![]() . (4.2.23)
. (4.2.23)
Выберем
коэффициенты ![]() так,
чтобы минимизировать энергию
так,
чтобы минимизировать энергию ![]() ошибки аппроксимации. Имеем
ошибки аппроксимации. Имеем
 . (4.2.24)
. (4.2.24)
Оптимальные коэффициенты ![]() в представлении
в представлении ![]() рядом можно найти путём
дифференцирования (4.2.24) по каждому из коэффициентов и приравнять первые
производные нулю. В качестве альтернативы можем использовать хорошо известный
результат из теории оценок, основанный на критерии минимума среднего квадрата
ошибки оценивания, который гласит, что минимум
рядом можно найти путём
дифференцирования (4.2.24) по каждому из коэффициентов и приравнять первые
производные нулю. В качестве альтернативы можем использовать хорошо известный
результат из теории оценок, основанный на критерии минимума среднего квадрата
ошибки оценивания, который гласит, что минимум ![]() по
по ![]() достигается тогда, когда ошибка
ортогональна к каждой из функций ряда, т.е.
достигается тогда, когда ошибка
ортогональна к каждой из функций ряда, т.е.
 ,
,
![]() . (4.2.25)
. (4.2.25)
Поскольку функции ![]() ортонормированы, из 4.2.25 следует
ортонормированы, из 4.2.25 следует
![]() ,
,
![]() . (4.2.26)
. (4.2.26)
Таким образом, коэффициенты получаются как проекции
сигнала ![]() на
каждую из функций
на
каждую из функций ![]() .
Как следствие,
.
Как следствие, ![]() является
проекцией
является
проекцией ![]() в
в
![]() -мерном
пространстве сигналов, заданном функциями
-мерном
пространстве сигналов, заданном функциями ![]() . Иногда говорят, что пространство
натянуто на функции
. Иногда говорят, что пространство
натянуто на функции ![]() . Минимальное значение среднего
квадрата, ошибки аппроксимации равно
. Минимальное значение среднего
квадрата, ошибки аппроксимации равно
![]() , (4.2.27)
, (4.2.27)
и оно не отрицательно по определению.
Когда средний квадрат ошибки ![]() , то
, то
![]() . (4.2.27)
. (4.2.27)
При условии, что ![]() , сигнал
, сигнал ![]() можно выразить так:
можно выразить так:
![]() . (4.2.28)
. (4.2.28)
Равенство ![]() правой части (4.2.20) понимается в том
смысле, что ошибка представления имеет нулевую энергию.
правой части (4.2.20) понимается в том
смысле, что ошибка представления имеет нулевую энергию.
Если каждый сигнал с ограниченной энергией можно
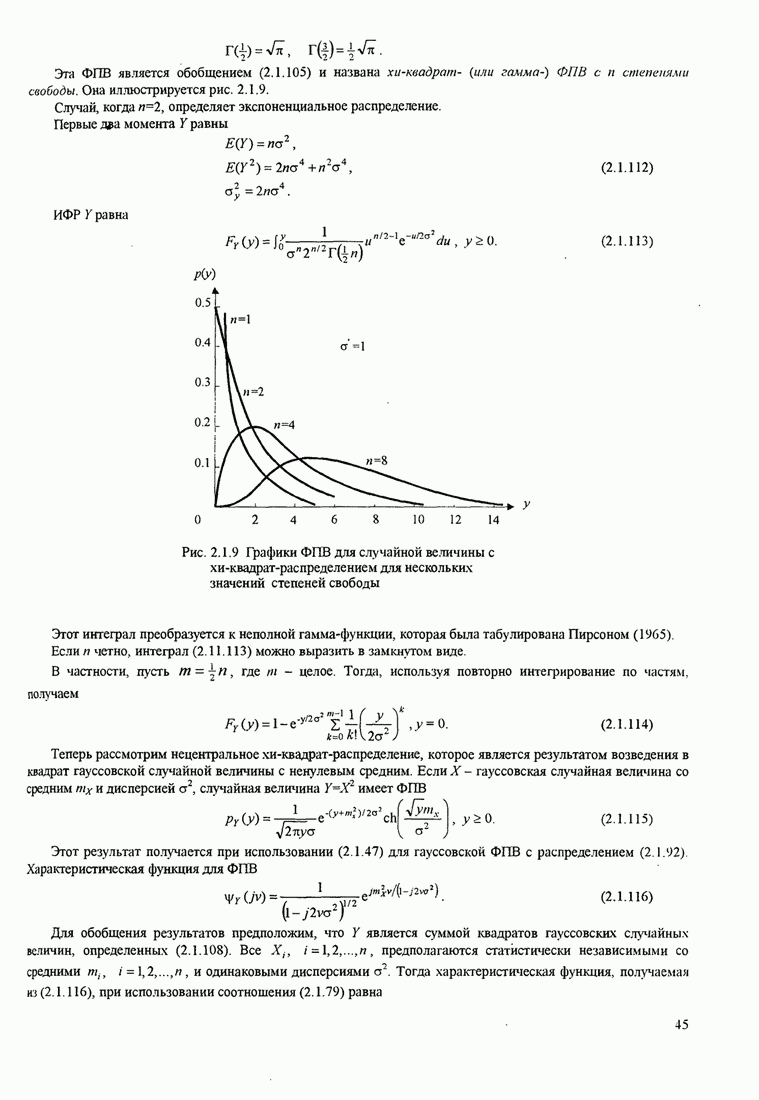
представить рядом (4.2.29) при ![]() , совокупность ортонормированных
функций
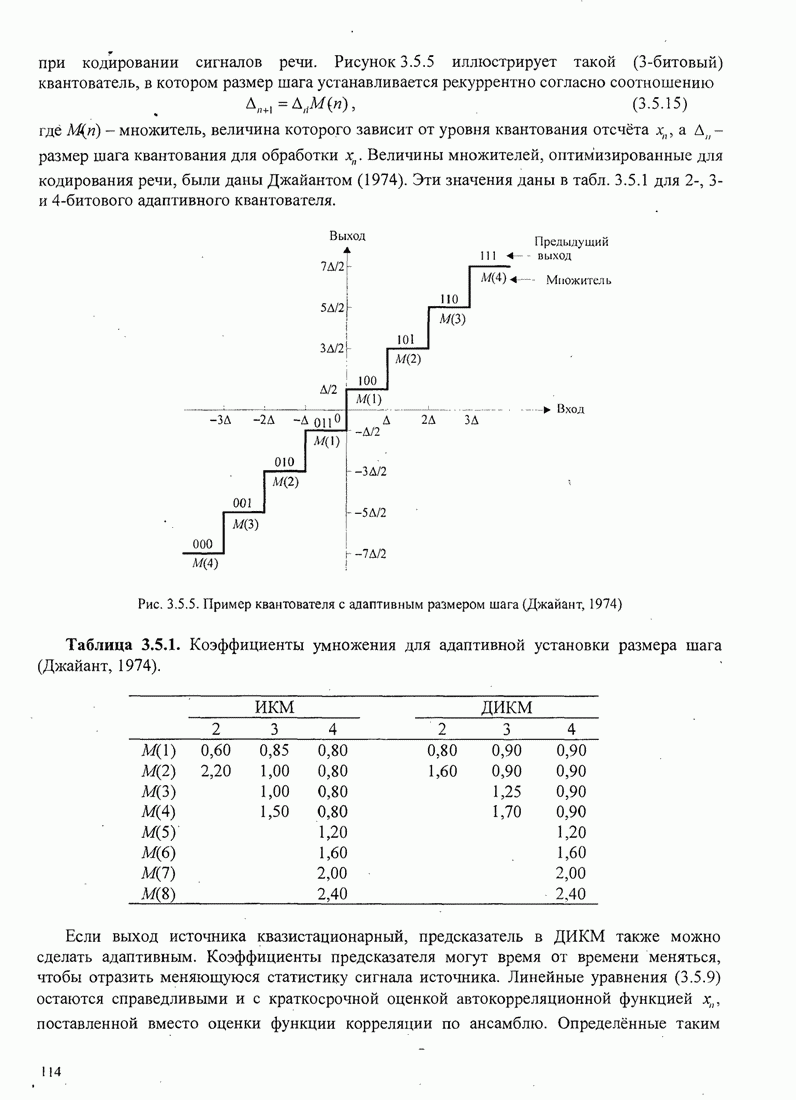
, совокупность ортонормированных
функций ![]() называют
полной.
называют
полной.
Пример 4.2.1.
Тригонометрический ряд Фурье. Сигнал ![]() с ограниченной энергией,
который равен нулю везде, кроме области
с ограниченной энергией,
который равен нулю везде, кроме области ![]() , и имеет ограниченное число
разрывов на этом интервале, может быть представлен рядом Фурье:
, и имеет ограниченное число
разрывов на этом интервале, может быть представлен рядом Фурье:
![]() , (4.2.30)
, (4.2.30)
где коэффициенты ![]() , которые минимизируют средний квадрат
ошибки, определяются выражениями
, которые минимизируют средний квадрат
ошибки, определяются выражениями
![]() ,
,
![]() . (4.2.31)
. (4.2.31)
Ансамбль ортонормированных тригонометрических функций
![]()
является полным, и, следовательно, ряд (4.2.30) обеспечивает нулевой средний квадрат ошибки. Эти свойства легко устанавливаются из проведённого выше рассмотрения.
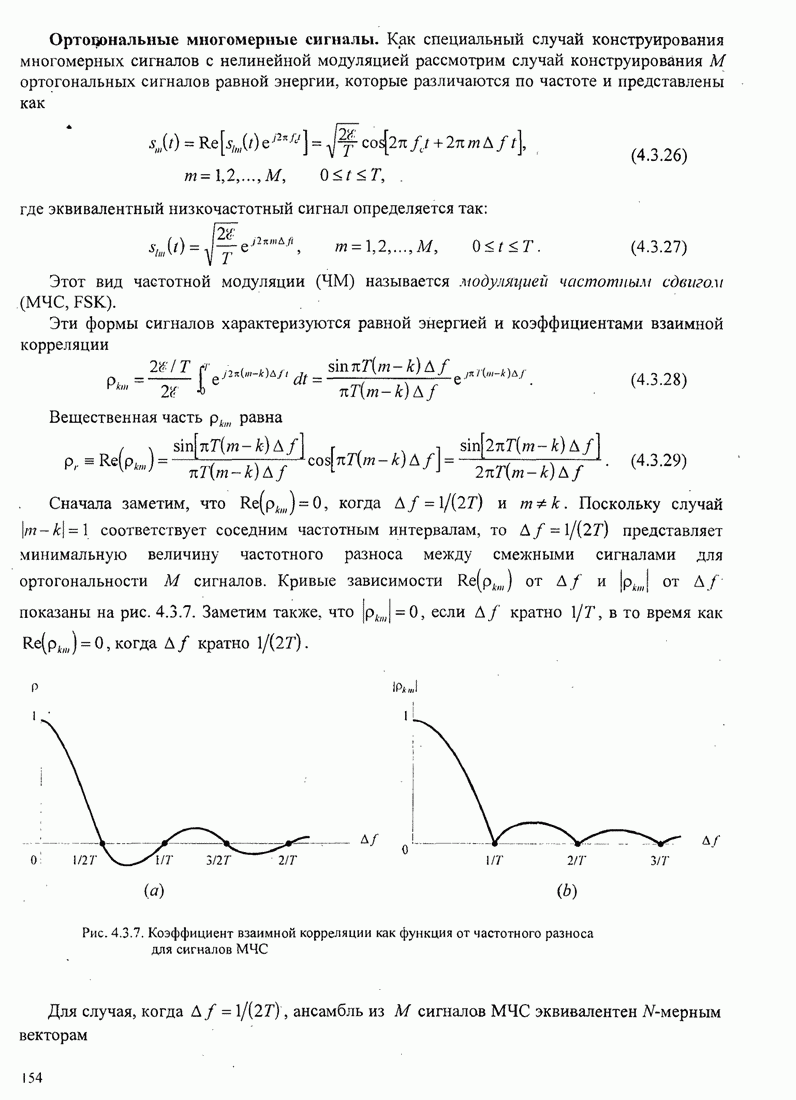
Процедура Грама-Шмидта. Теперь предположим, что мы имеем ансамбль сигналов с
ограниченной энергией ![]() , и хотим сконструировать ансамбль
ортонормированных сигналов. Процедура ортонормирования Грама-Шмидта позволяет
нам сконструировать такой ансамбль. Начнем с первого сигнала
, и хотим сконструировать ансамбль
ортонормированных сигналов. Процедура ортонормирования Грама-Шмидта позволяет
нам сконструировать такой ансамбль. Начнем с первого сигнала ![]() , причём
предполагается, что он имеет энергию
, причём
предполагается, что он имеет энергию ![]() . Первый сигнал ортонормированного
ансамбля конструируется легко:
. Первый сигнал ортонормированного
ансамбля конструируется легко:
 . (4.2.32)
. (4.2.32)
Таким образом, сигнал ![]() имеет форму
имеет форму ![]() но нормирован к единичной
энергии. Второй сигнал конструируется из
но нормирован к единичной
энергии. Второй сигнал конструируется из ![]() , причём сначала вычисляется проекция
, причём сначала вычисляется проекция ![]() на
на ![]() :
:
![]() . (4.2.33)
. (4.2.33)
Затем ![]() вычитается из
вычитается из ![]() для получения
для получения
![]() . (4.2.34)
. (4.2.34)
Этот сигнал ортогонален ![]() , но не имеет
единичной энергии. Если
, но не имеет
единичной энергии. Если ![]() означает энергию для
означает энергию для ![]() , то нормированный
сигнал, который ортогонален к
, то нормированный
сигнал, который ортогонален к ![]() , равен
, равен
 . (4.2.35)
. (4.2.35)
В общем, ортогонализация ![]() -й функции ведёт к
-й функции ведёт к
 , (4.2.36)
, (4.2.36)
где
![]() (4.2.37)
(4.2.37)
и
![]() ,
, ![]() . (4.2.38)
. (4.2.38)
Таким образом, процесс ортогонализации продолжается,
пока все ![]() сигналов
не исчерпаны и не образованы
сигналов
не исчерпаны и не образованы ![]() ортонормированных сигналов.
Размерность
ортонормированных сигналов.
Размерность ![]() -сигнального
пространства равна
-сигнального
пространства равна ![]() , если исходные сигналы ансамбля
линейно независимы, т.е. ни один из сигналов не является линейной комбинацией
других сигналов.
, если исходные сигналы ансамбля
линейно независимы, т.е. ни один из сигналов не является линейной комбинацией
других сигналов.
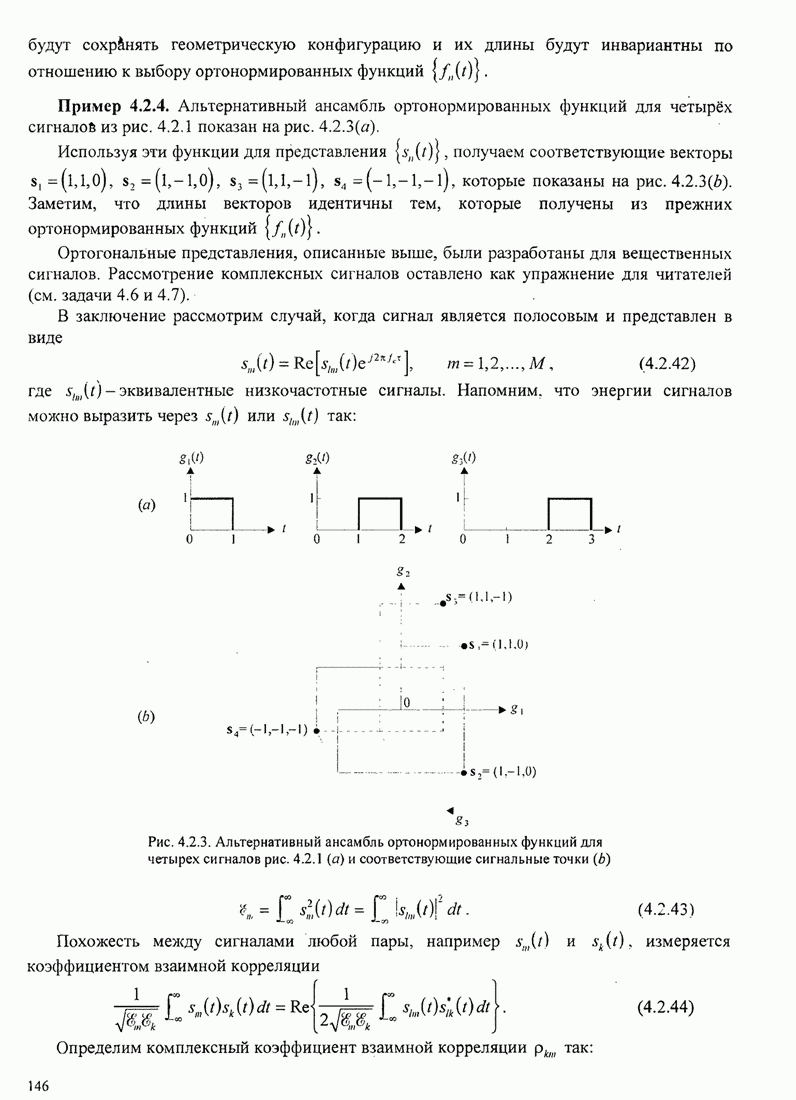
Пример 4.2.2. Применим процедуру Грама-Шмидта к ансамблю четырёх сигналов,
показанных на рис. 4.2.1(a). Сигнал ![]() имеет энергию
имеет энергию ![]() , так что
, так что ![]() . Далее мы видим,
что
. Далее мы видим,
что ![]() ;
следовательно,
;
следовательно, ![]() и
и
![]() ортогональны.
Как следствие,
ортогональны.
Как следствие, ![]() .
Чтобы получить
.
Чтобы получить ![]() ,
вычислим
,
вычислим ![]() и
и
![]() , которые
равны
, которые
равны ![]() и
и ![]() .
.
Таким образом,

Поскольку ![]() имеет единичную энергию, то следует,
что
имеет единичную энергию, то следует,
что ![]() . Для
определения
. Для
определения ![]() находим,
что
находим,
что ![]() ,
, ![]() и
и ![]() . Поэтому
. Поэтому
![]() .
.
Как следствие, ![]() является линейной комбинацией
является линейной комбинацией ![]() и
и ![]() и поэтому
и поэтому ![]() .
.
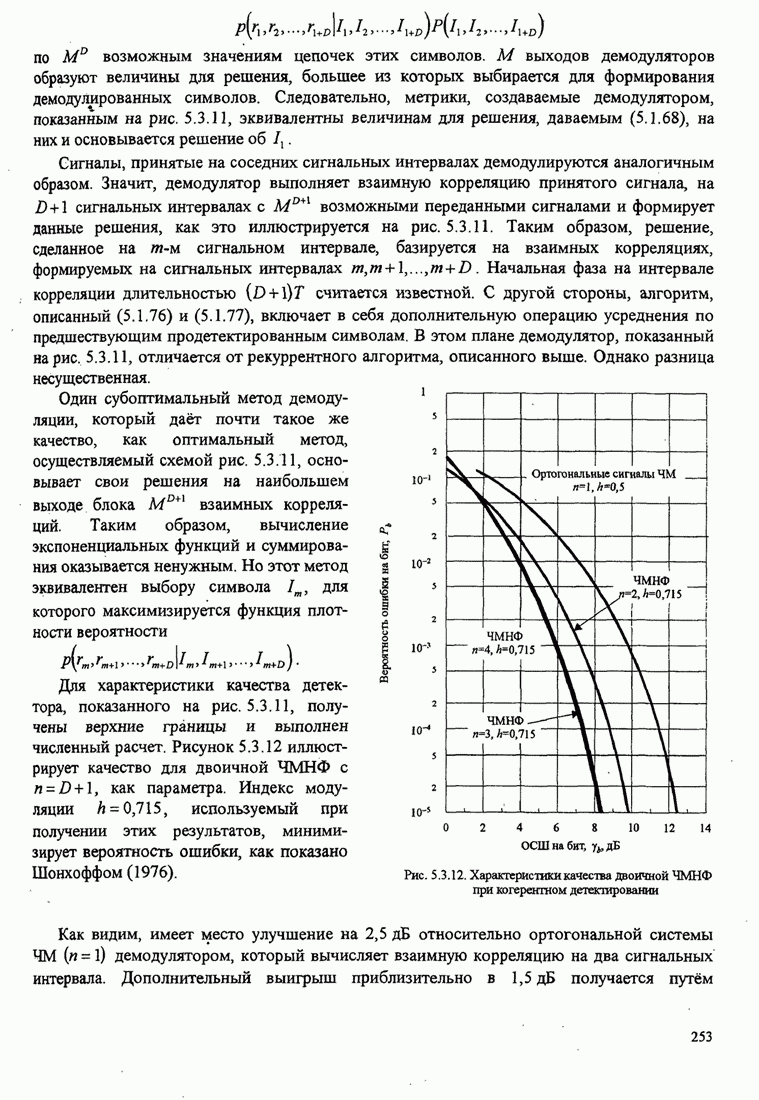
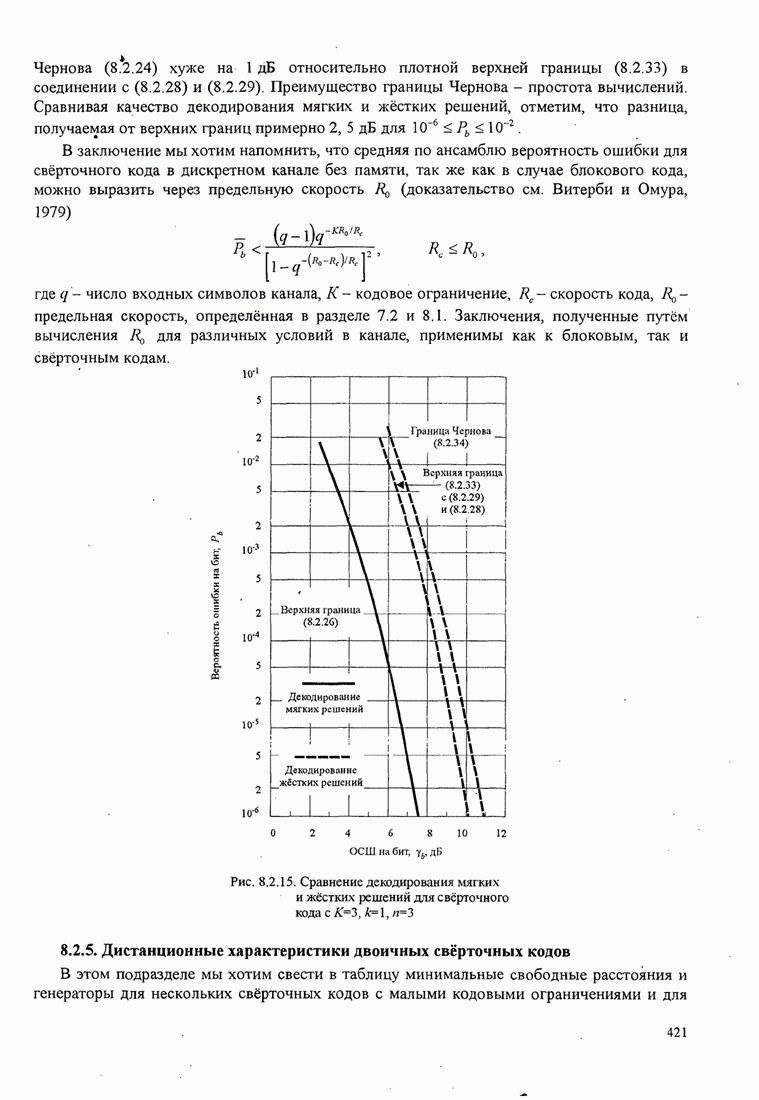
Три ортонормированные функции показаны на рис. 4.2.1(b).

Рис. 4.2.1. Ортогонализация Грамма-Шмидта для сигналов
![]() (а) и
соответствующие ортогональные сигналы (b)
(а) и
соответствующие ортогональные сигналы (b)
Поскольку мы сконструировали ансамбль
ортонормированных сигналов ![]() , можем выразить
, можем выразить ![]() сигналов
сигналов ![]() как линейную комбинацию от
как линейную комбинацию от ![]() .
.
Таким образом, можно написать

Рис. 4.2.1. Ортогонализация Грама-Шмидта для сигналов ![]() (a)
и соответствует ортогональные сигналы (b)
(a)
и соответствует ортогональные сигналы (b)
![]() , (4.2.39)
, (4.2.39)
и
 . (4.2.40)
. (4.2.40)
Основываясь на выражении (4.2.39), каждый сигнал можно представить вектором
![]() , (4.2.41)
, (4.2.41)
или,
что эквивалентно, точкой в ![]() -мерном пространстве сигналов с
координатами
-мерном пространстве сигналов с
координатами ![]() .
Энергия
.
Энергия ![]() -го
сигнала равна квадрату длины вектора или, что эквивалентно, квадрату евклидова
расстояния от начала координат к точке
-го
сигнала равна квадрату длины вектора или, что эквивалентно, квадрату евклидова
расстояния от начала координат к точке ![]() -мерного пространства. Таким образом,
любой сигнал можно представить геометрически как точку в пространстве сигналов,
заданном ортонормированными функциями.
-мерного пространства. Таким образом,
любой сигнал можно представить геометрически как точку в пространстве сигналов,
заданном ортонормированными функциями.
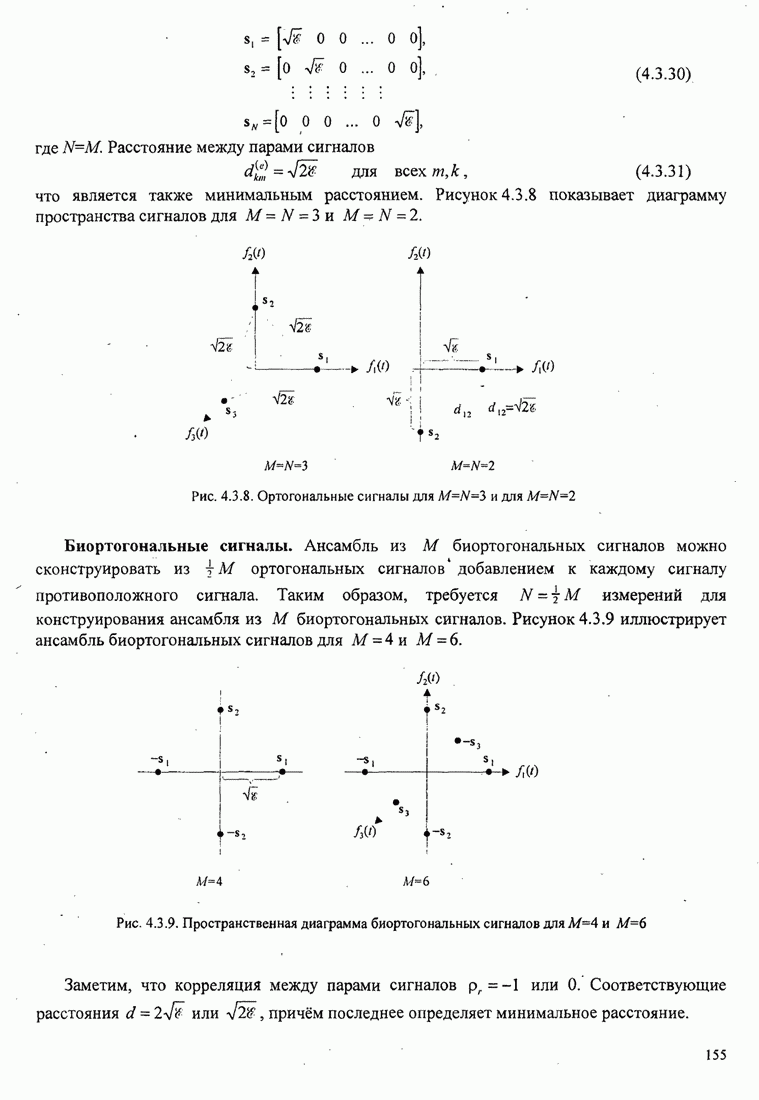
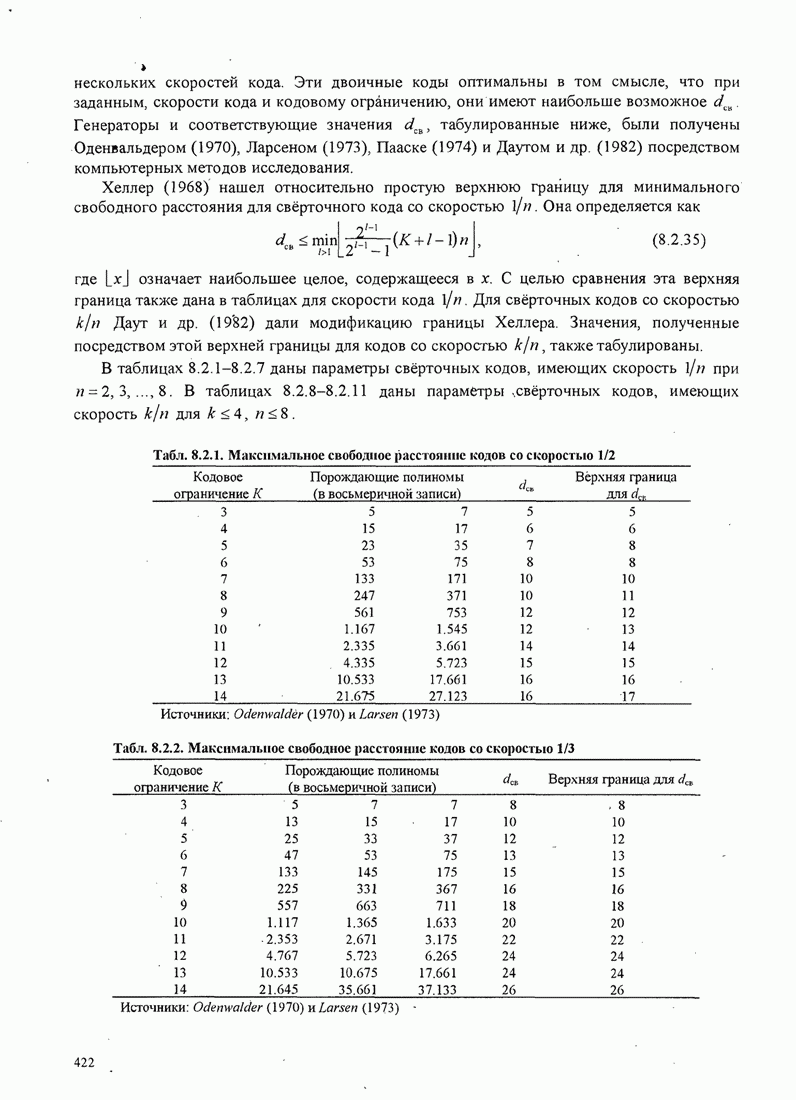
Пример 4.2.3. Получим векторное представление четырех сигналов, показанных на рис. 4.2.1(a), используя ортонормальный ансамбль функций из рис. 4.2.1(b).
Поскольку
размерность пространства сигналов ![]() , каждый сигнал описывается тремя
компонентами. Сигнал
, каждый сигнал описывается тремя
компонентами. Сигнал ![]() характеризуется вектором
характеризуется вектором ![]() . Аналогично сигналы
. Аналогично сигналы
![]() характеризуются
соответственно векторами
характеризуются
соответственно векторами ![]() ,
, ![]() ,
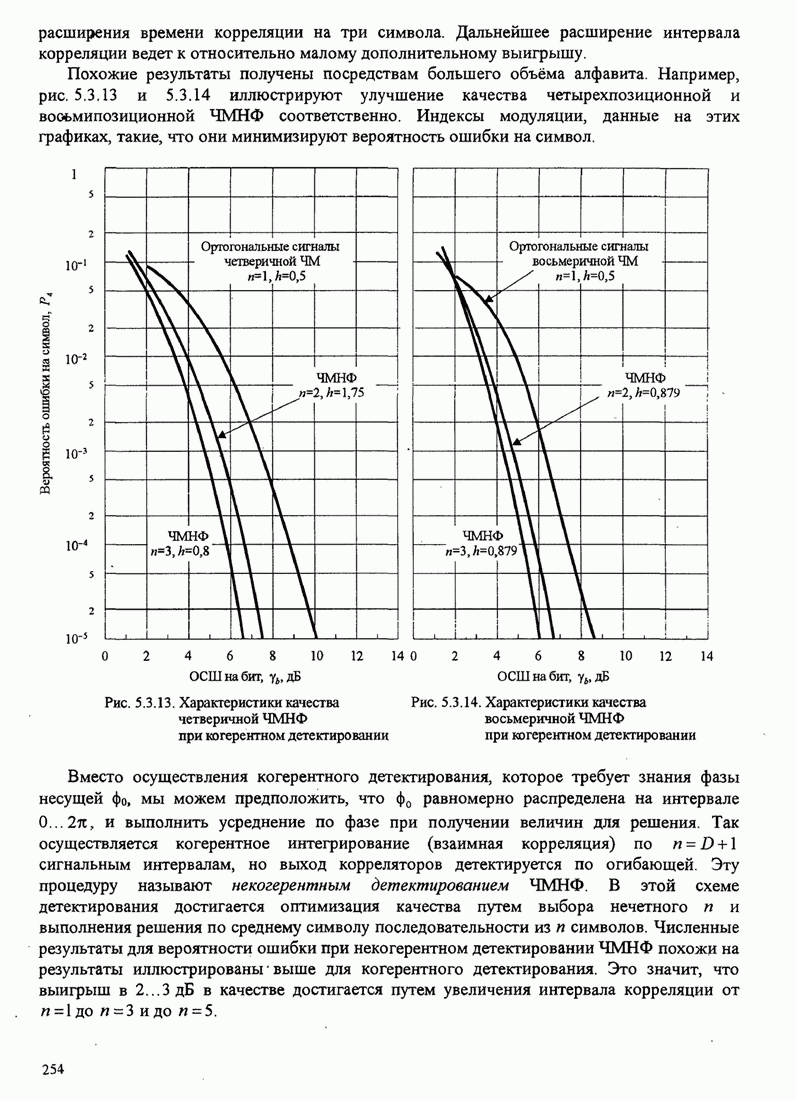
, ![]() . Эти векторы показаны на рис. 4.2.2.
Их длины равны
. Эти векторы показаны на рис. 4.2.2.
Их длины равны ![]() ,
,
![]() ,
, ![]() ,
, ![]() , а соответствующие
энергии сигналов
, а соответствующие
энергии сигналов ![]() ,
,
![]() .
.

Рис. 4.2.2. Четыре сигнальных вектора, представленных в виде точек в трехмерном функциональном пространстве
Мы
показали, что ансамбль ![]() сигналов с ограниченной энергией можно
представить взвешенной линейной комбинацией ортонормированных функций
сигналов с ограниченной энергией можно
представить взвешенной линейной комбинацией ортонормированных функций ![]() размерностью
размерностью ![]() . Функции
. Функции ![]() получены
применением процедуры ортонормализации Грама-Шмидта из
получены
применением процедуры ортонормализации Грама-Шмидта из ![]() . Следует подчеркнуть, что
функции
. Следует подчеркнуть, что
функции ![]() ,
полученные преобразованием Грама-Шмидта, не являются уникальными
(единственными). Если мы изменим порядок формирования ортонормированных
сигналов из
,
полученные преобразованием Грама-Шмидта, не являются уникальными
(единственными). Если мы изменим порядок формирования ортонормированных
сигналов из ![]() ,
получим другой ортонормированный ансамбль и соответствующее векторное
представление сигналов
,
получим другой ортонормированный ансамбль и соответствующее векторное
представление сигналов ![]() будет зависеть от выбора
ортонормальных функций
будет зависеть от выбора
ортонормальных функций ![]() . Все же, вектора
. Все же, вектора ![]() будут сохранять
геометрическую конфигурацию и их длины будут инвариантны по отношению к выбору
ортонормированных функций
будут сохранять
геометрическую конфигурацию и их длины будут инвариантны по отношению к выбору
ортонормированных функций ![]() .
.
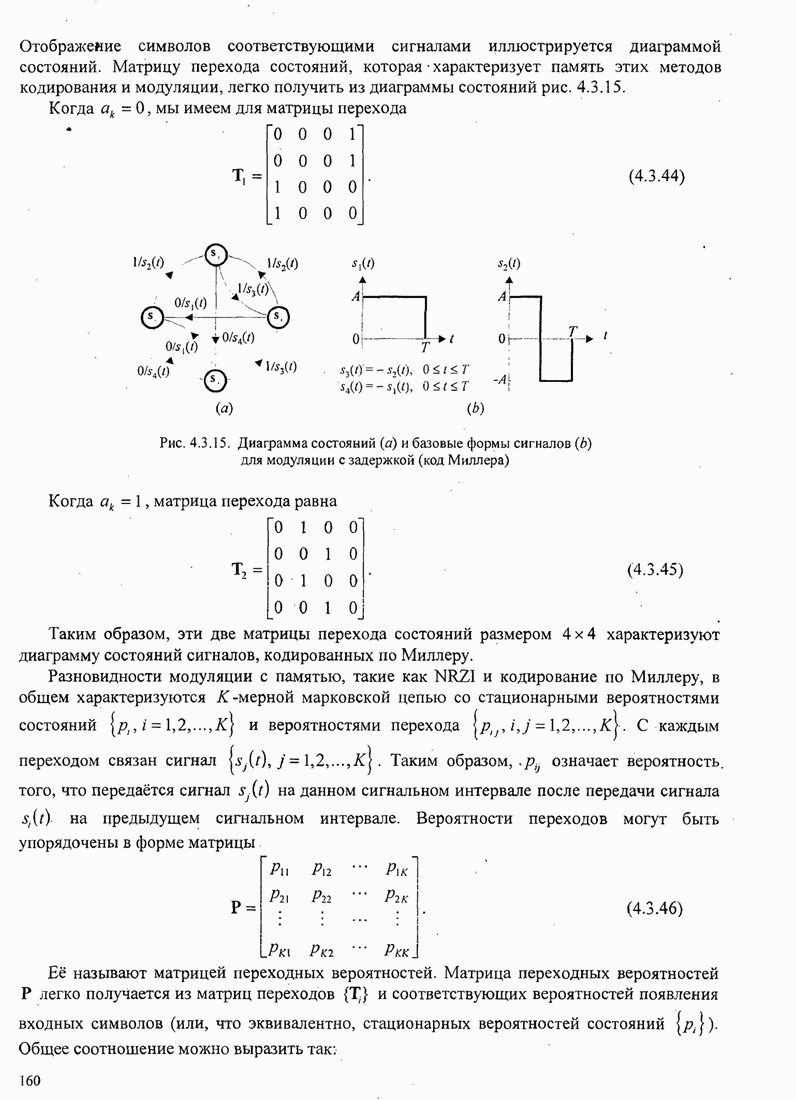
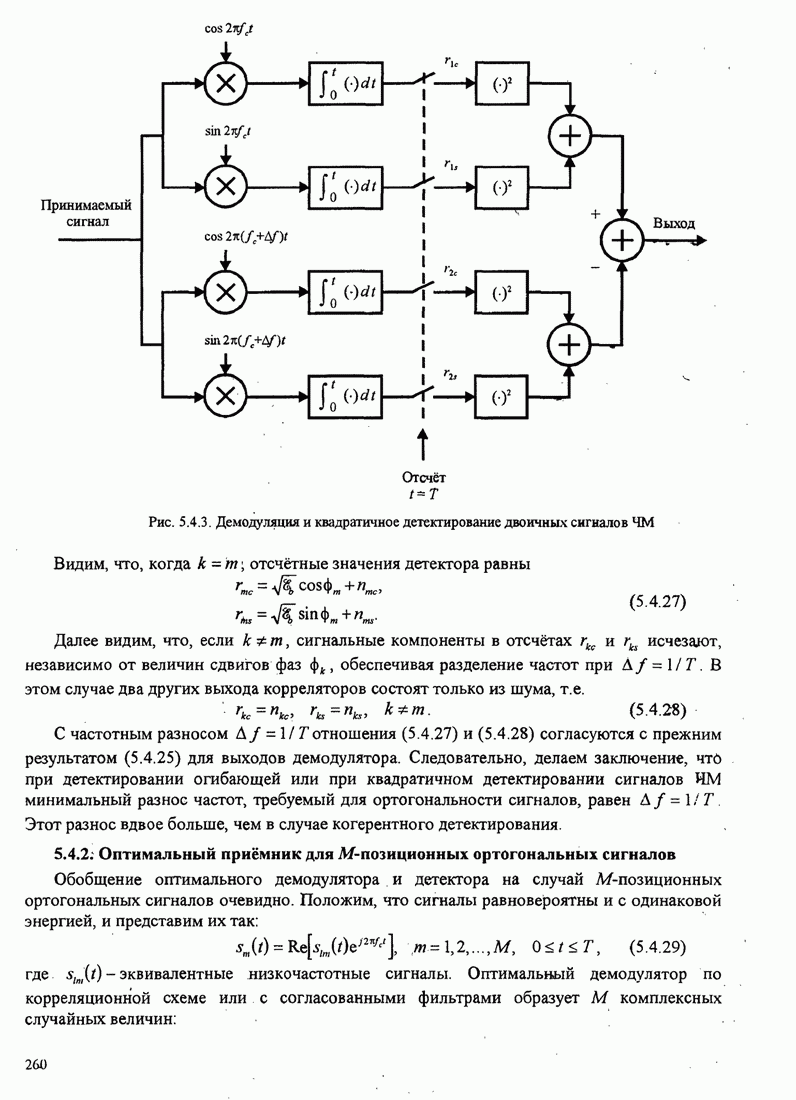
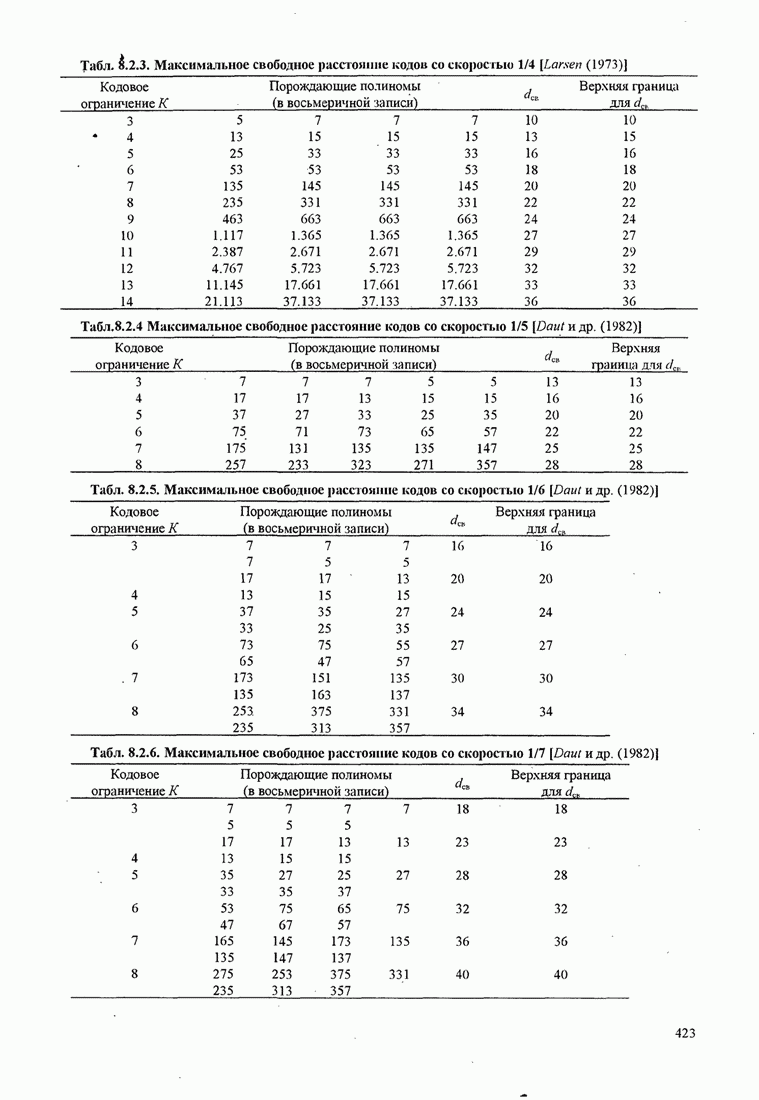
Пример 4.2.4. Альтернативный ансамбль ортонормированных функций для четырёх сигналов из рис. 4.2.1 показан на рис. 4.2.3(д).

Рис. 4.2.3. Альтернативный ансамбль ортонормированных функций для четырех сигналов рис. 4.2.1 (а) и соответствующие сигнальные точки (b)
Используя
эти функции для представления ![]() , получаем соответствующие векторы
, получаем соответствующие векторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() , которые показаны
на рис. 4.2.3(b). Заметим, что длины векторов
идентичны тем, которые получены из прежних ортонормированных функций
, которые показаны
на рис. 4.2.3(b). Заметим, что длины векторов
идентичны тем, которые получены из прежних ортонормированных функций ![]() .
.
Ортогональные представления, описанные выше, были разработаны для вещественных сигналов. Рассмотрение комплексных сигналов оставлено как упражнение для читателей (см. задачи 4.6 и 4.7).
В заключение рассмотрим случай, когда сигнал является полосовым и представлен в виде
![]() , (4.2.42)
, (4.2.42)
где
![]() -
эквивалентные низкочастотные сигналы. Напомним, что энергии сигналов можно
выразить через
-
эквивалентные низкочастотные сигналы. Напомним, что энергии сигналов можно
выразить через ![]() или
или
![]() так:
так:
 . (4.2.43)
. (4.2.43)
Похожесть
между сигналами любой пары, например ![]() и
и ![]() , измеряется коэффициентом взаимной
корреляции
, измеряется коэффициентом взаимной
корреляции
 . (4.2.44)
. (4.2.44)
Определим
комплексный коэффициент взаимной корреляции ![]() так:
так:
 . (4.2.45)
. (4.2.45)
Тогда
 , (4.2.46)
, (4.2.46)
или, что эквивалентно,
![]() . (4.2.47)
. (4.2.47)
Коэффициенты
взаимной корреляции между парами сигналов или сигнальных векторов определяют
совокупность параметров, характеризующих похожесть ансамбля сигналов. Другой
родственный параметр - расстояние Евклида ![]() между парой сигналов - определяется
так:
между парой сигналов - определяется
так:
 . (4.2.48)
. (4.2.48)
Когда
![]() для всех
для всех ![]() и
и ![]() , это выражение
упрощается:
, это выражение
упрощается:
![]() . (4.2.49)
. (4.2.49)
Итак, расстояние Евклида является альтернативной мерой похожести (или несходства) совокупности сигналов или соответствующих сигнальных векторов.
В следующем разделе мы опишем сигналы цифровой модуляции и используем пространство сигналов для их представления. Можно заметить, что сигналы цифровой модуляции удобно представить через две ортонормированные базисные функции вида
 (4.2.50)
(4.2.50)
Если
![]() выразить
как
выразить
как ![]() , то
следует, что
, то
следует, что ![]() в
(4.2.42) можно выразить так:
в
(4.2.42) можно выразить так:
![]() , (4.2.51)
, (4.2.51)
где
![]() и
и ![]() представляют
модулирующие сигналы.
представляют
модулирующие сигналы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
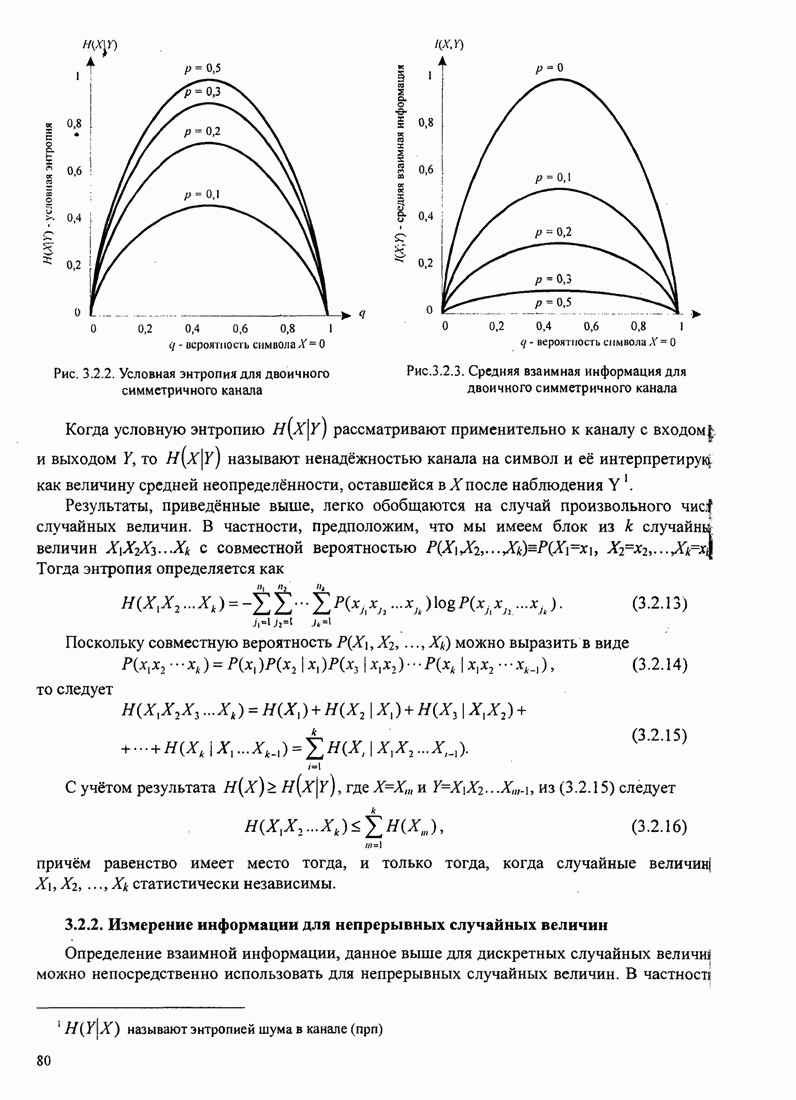
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
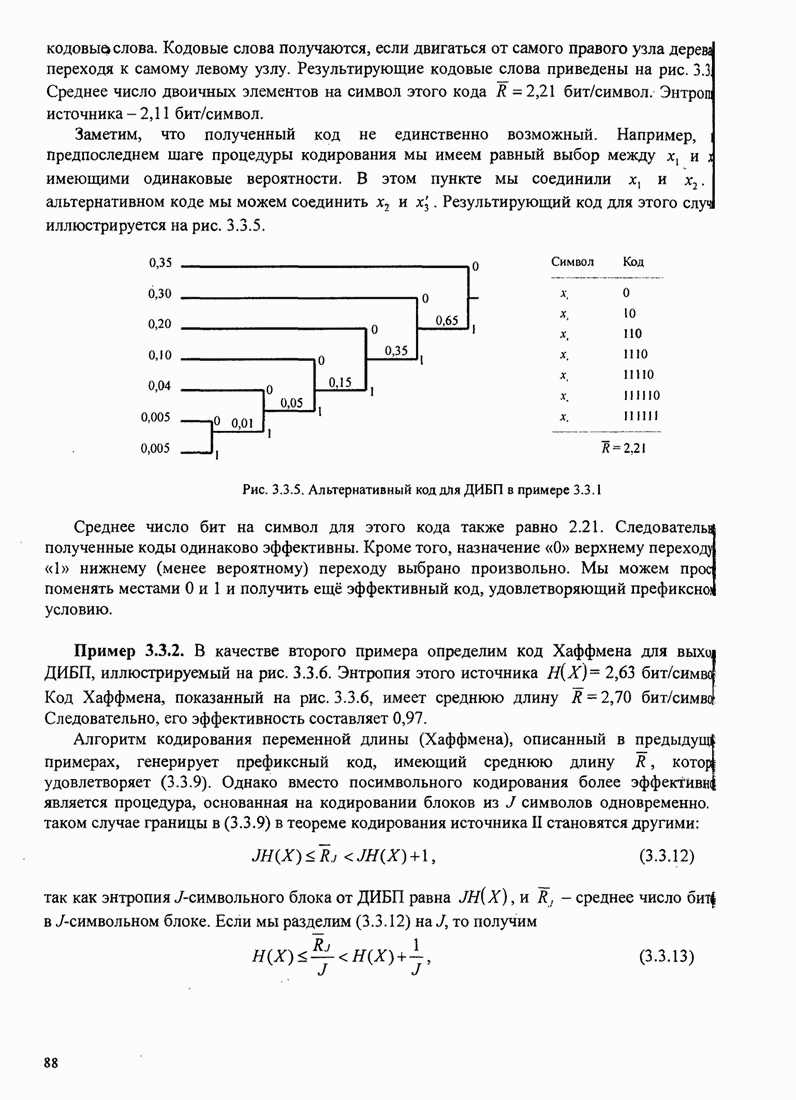
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
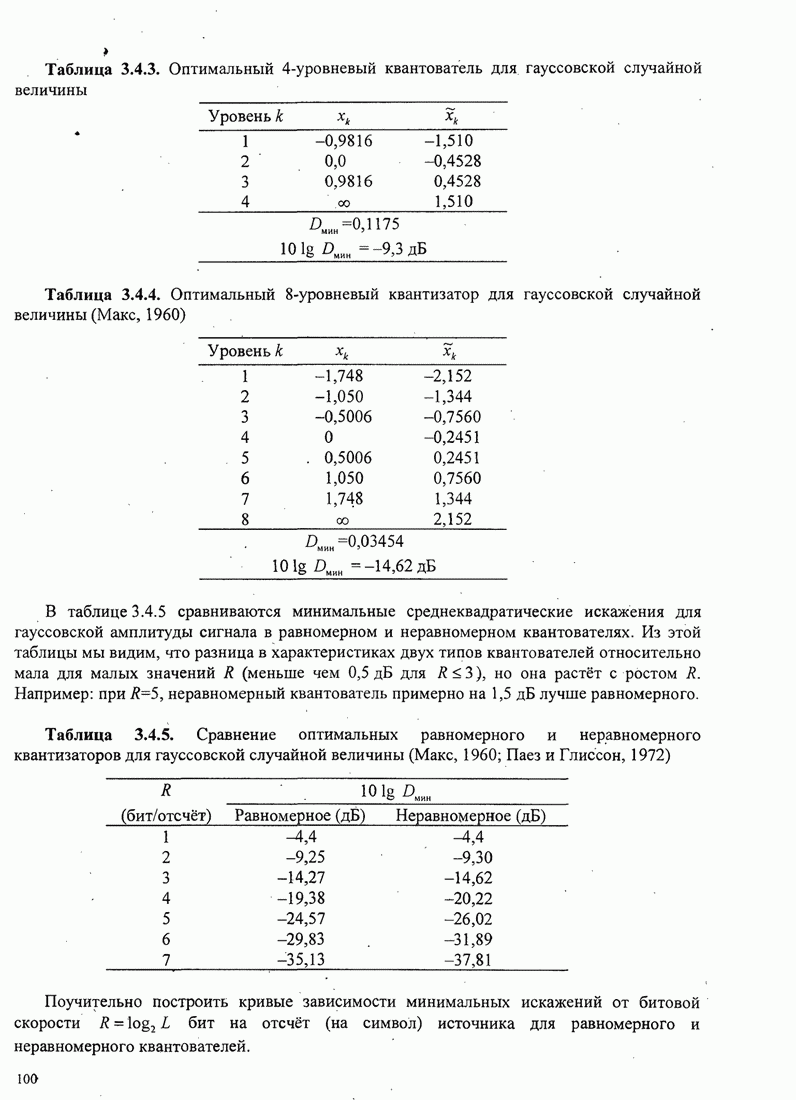
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
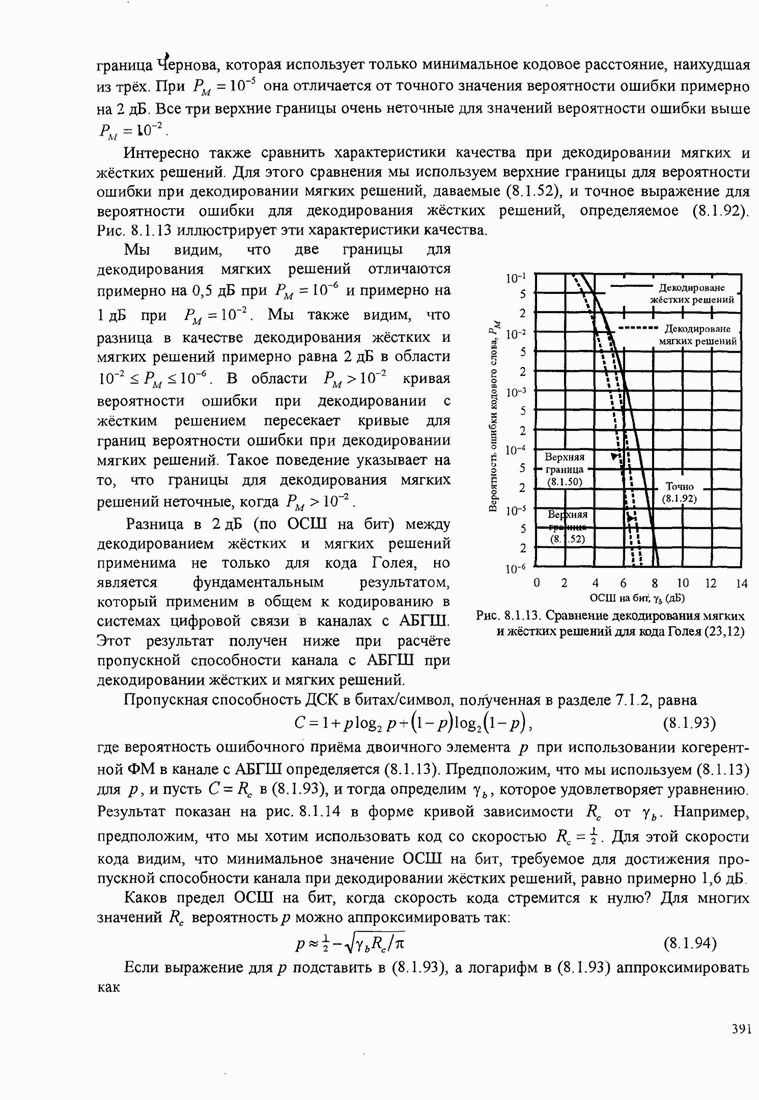
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
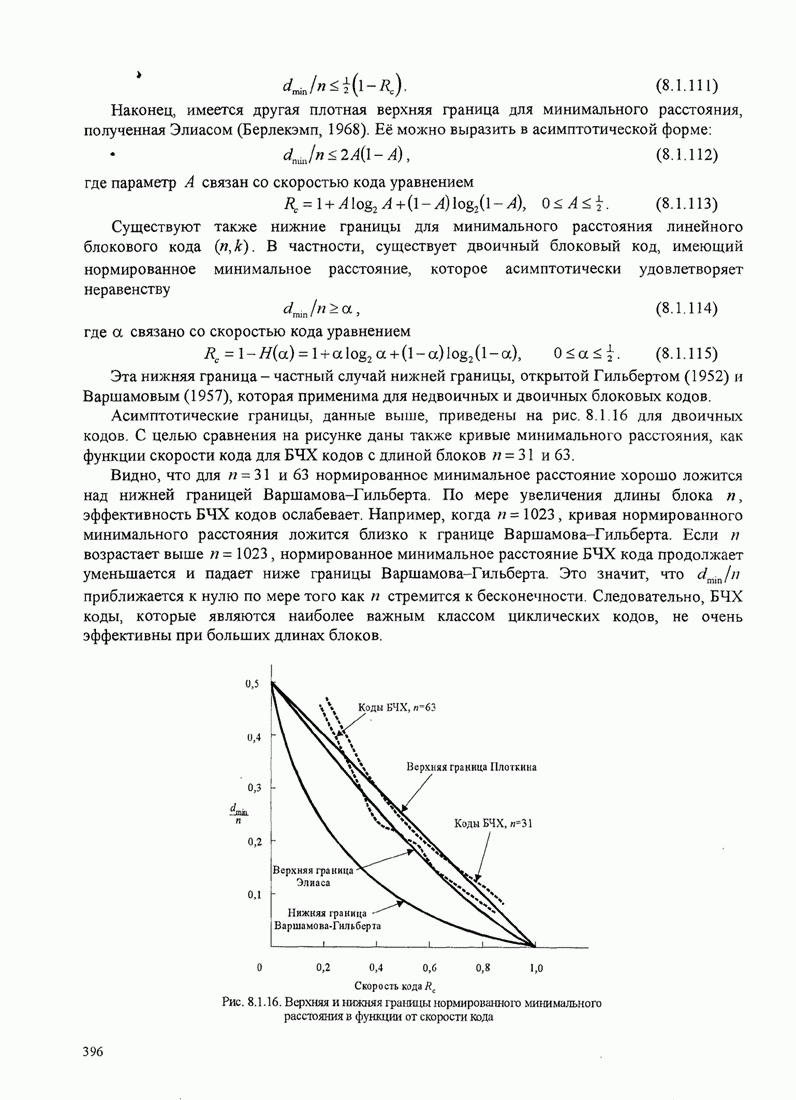
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
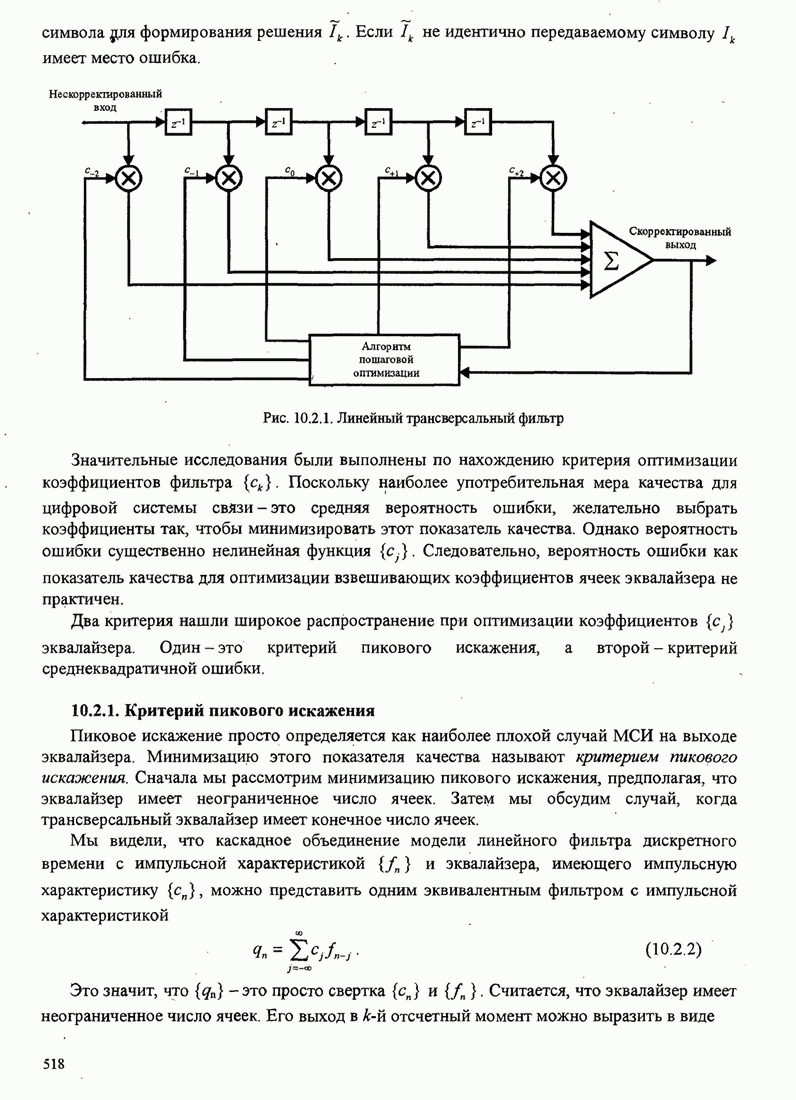
- 10.2.1. Критерий пикового скажения
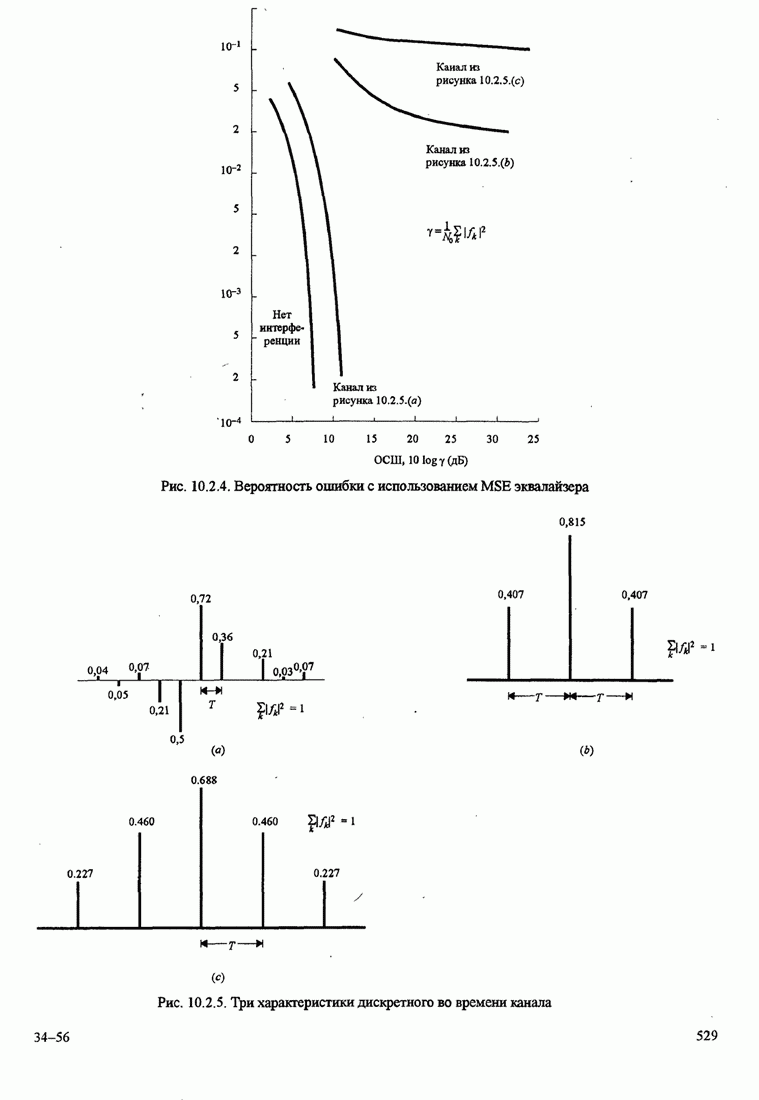
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
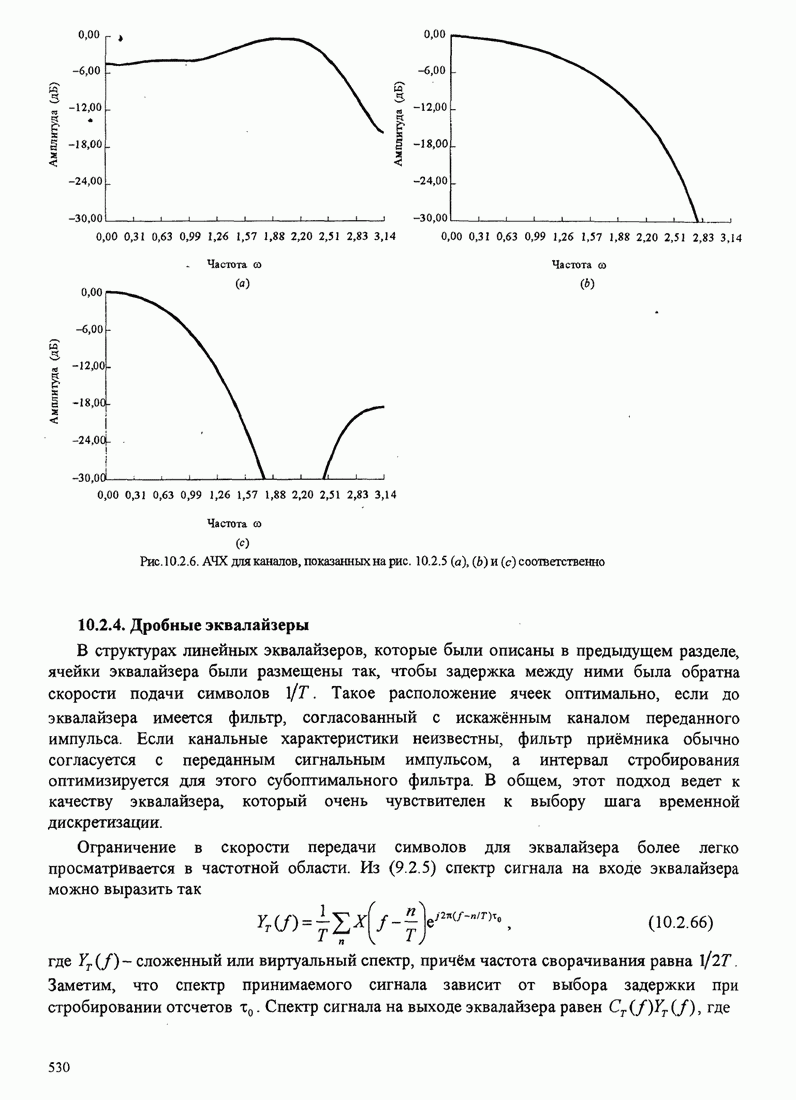
- 10.2.4. Дробные эквалайзеры
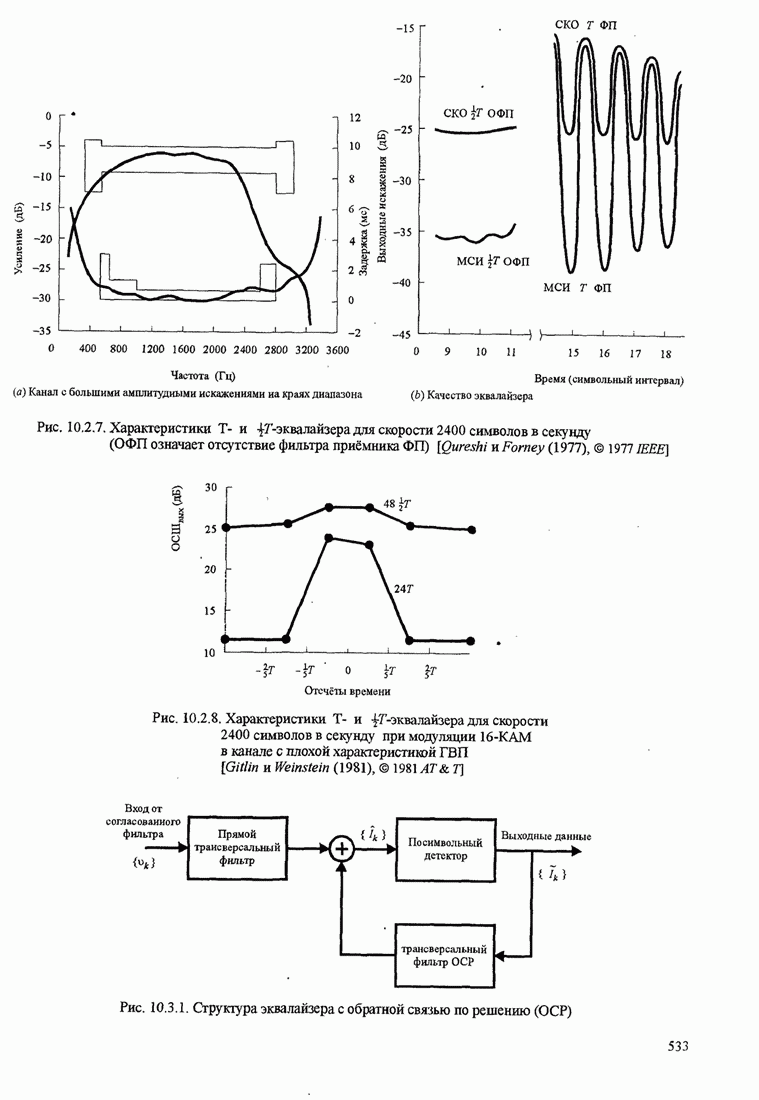
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
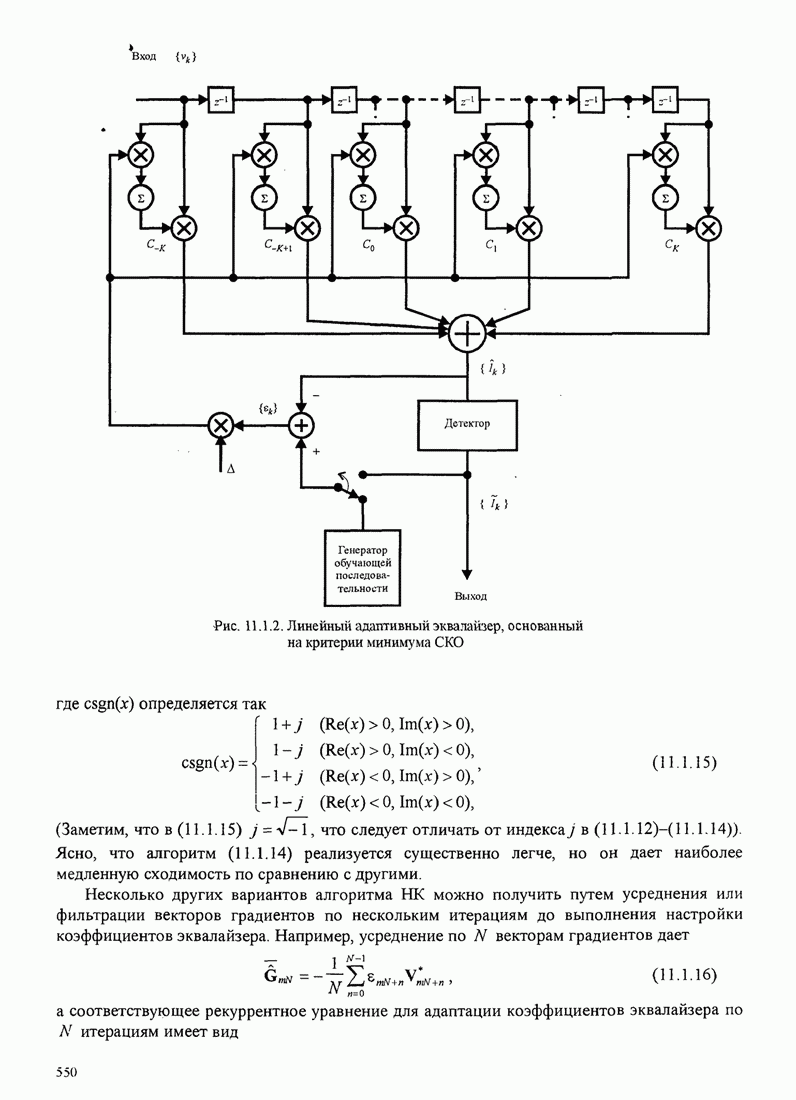
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
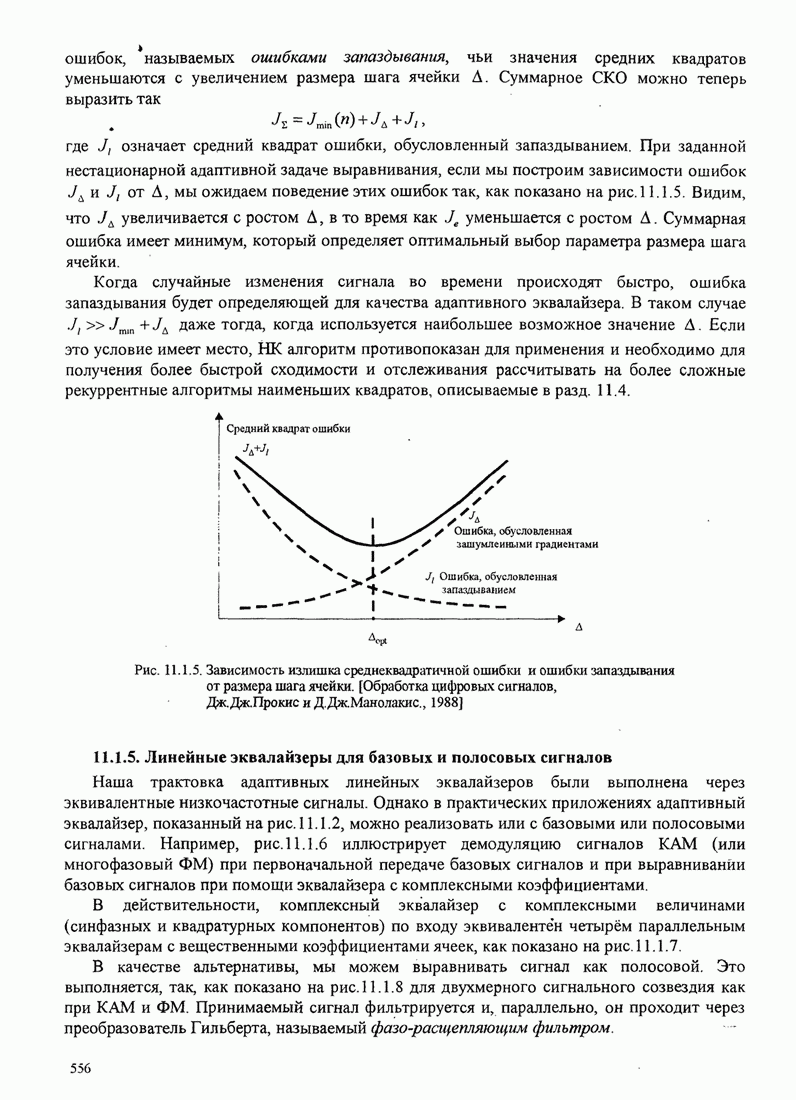
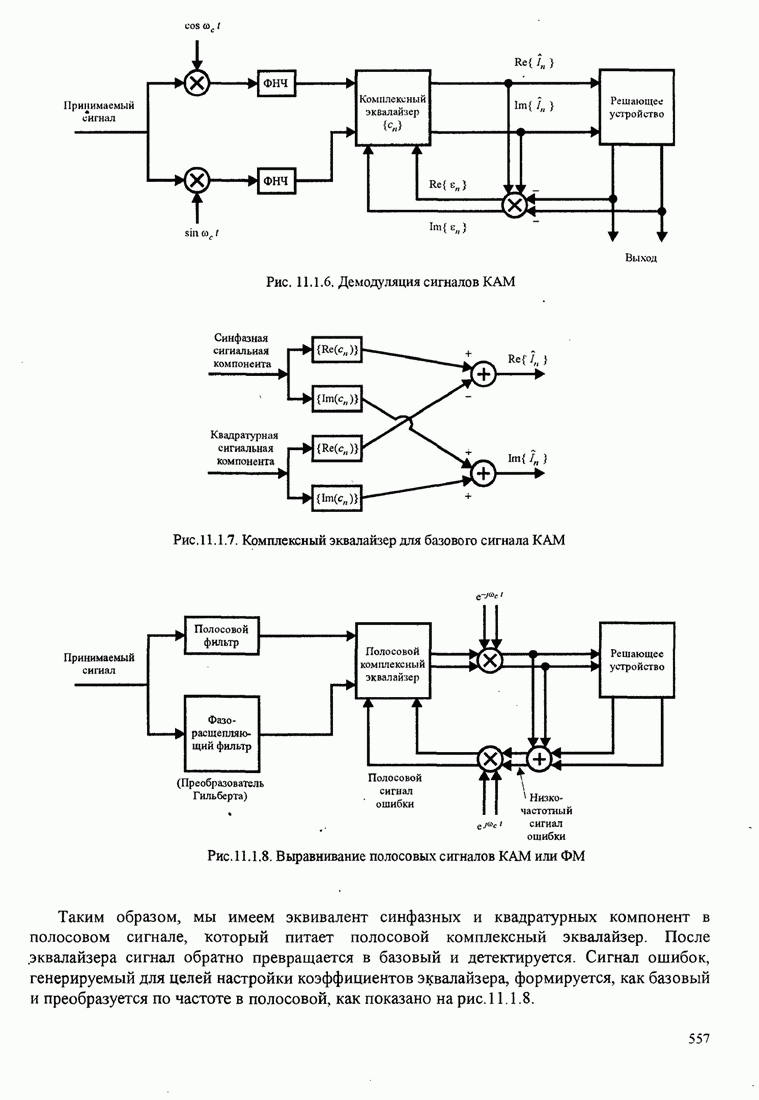
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
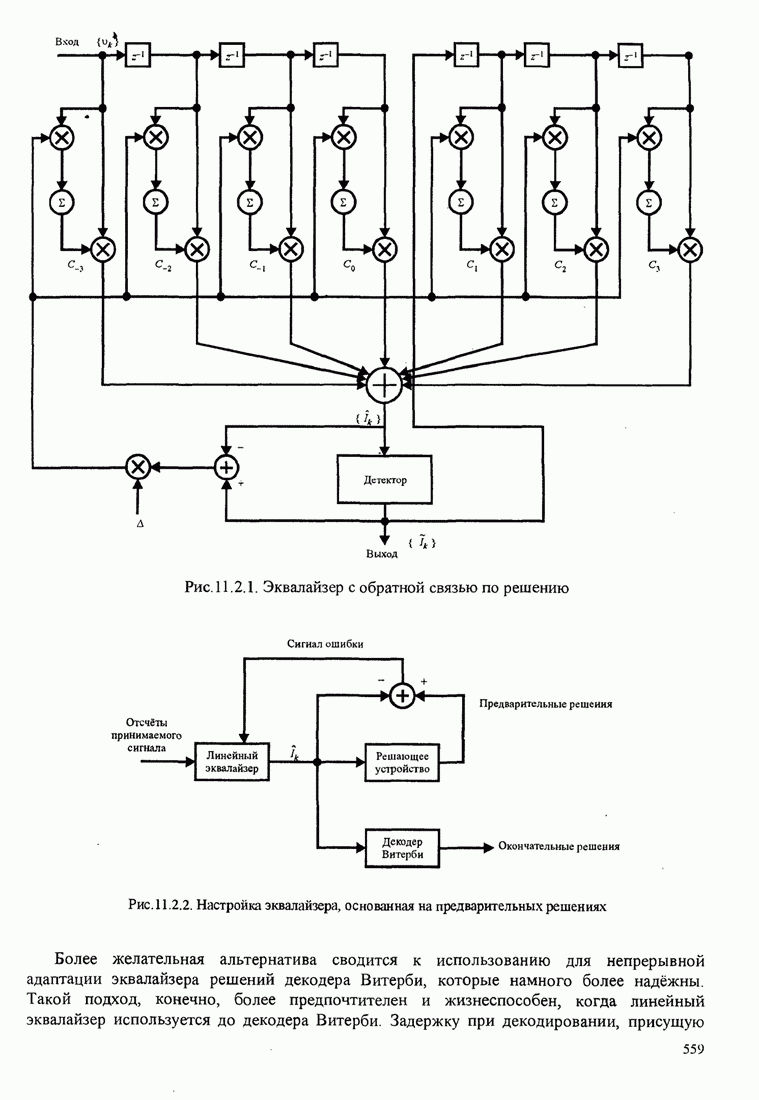
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
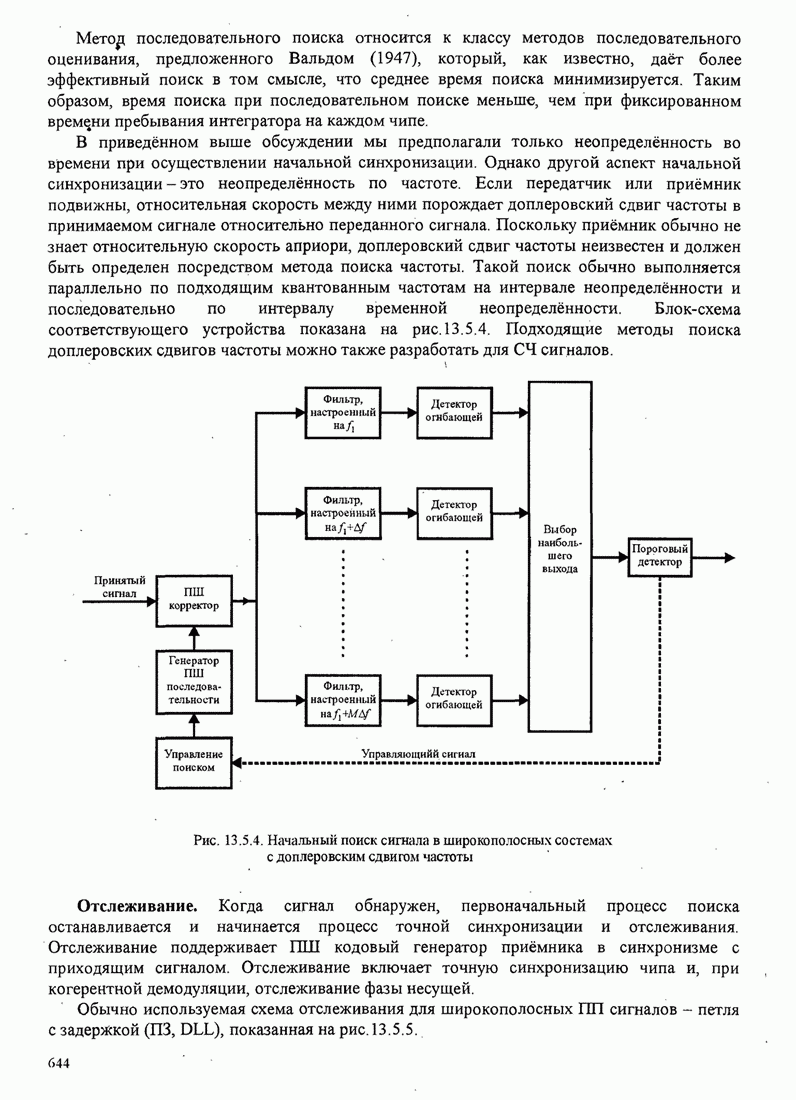
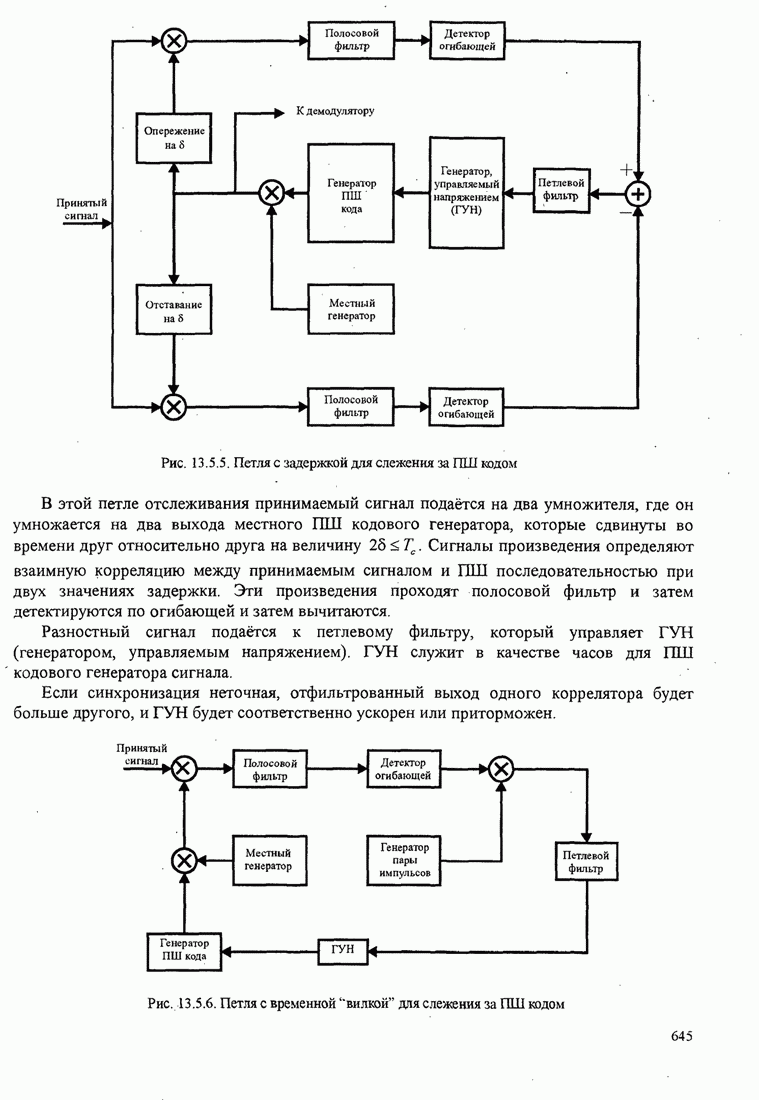
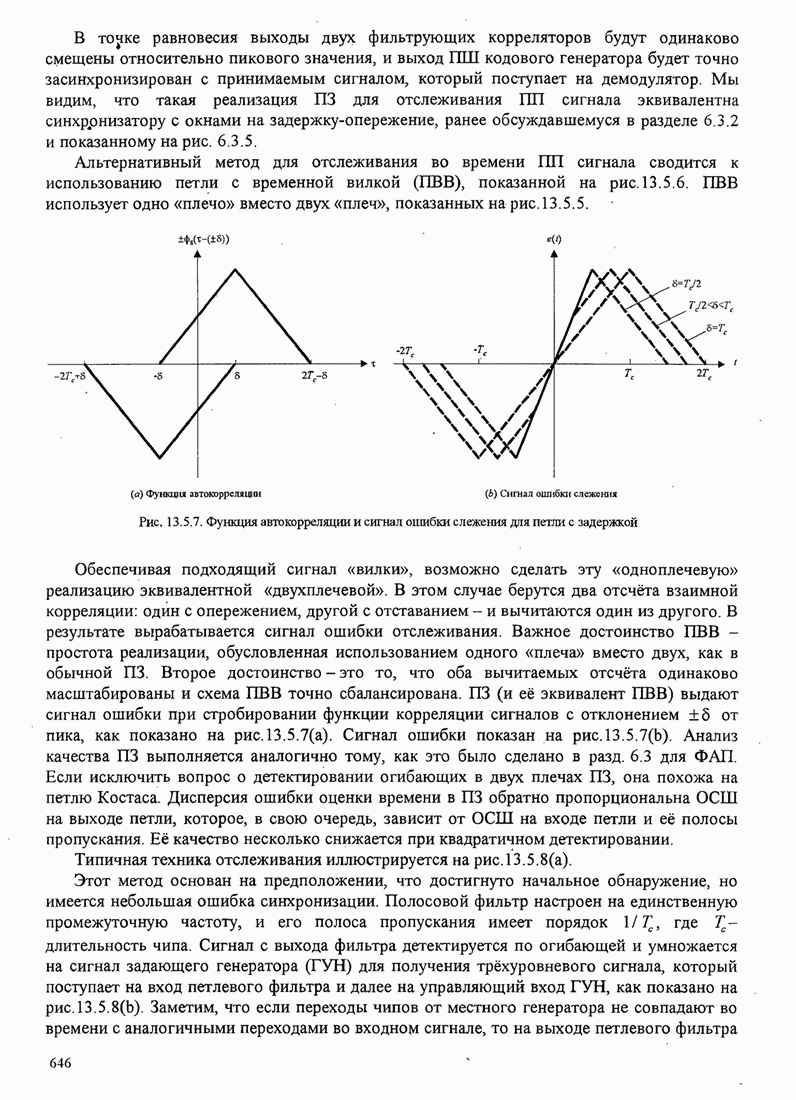
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
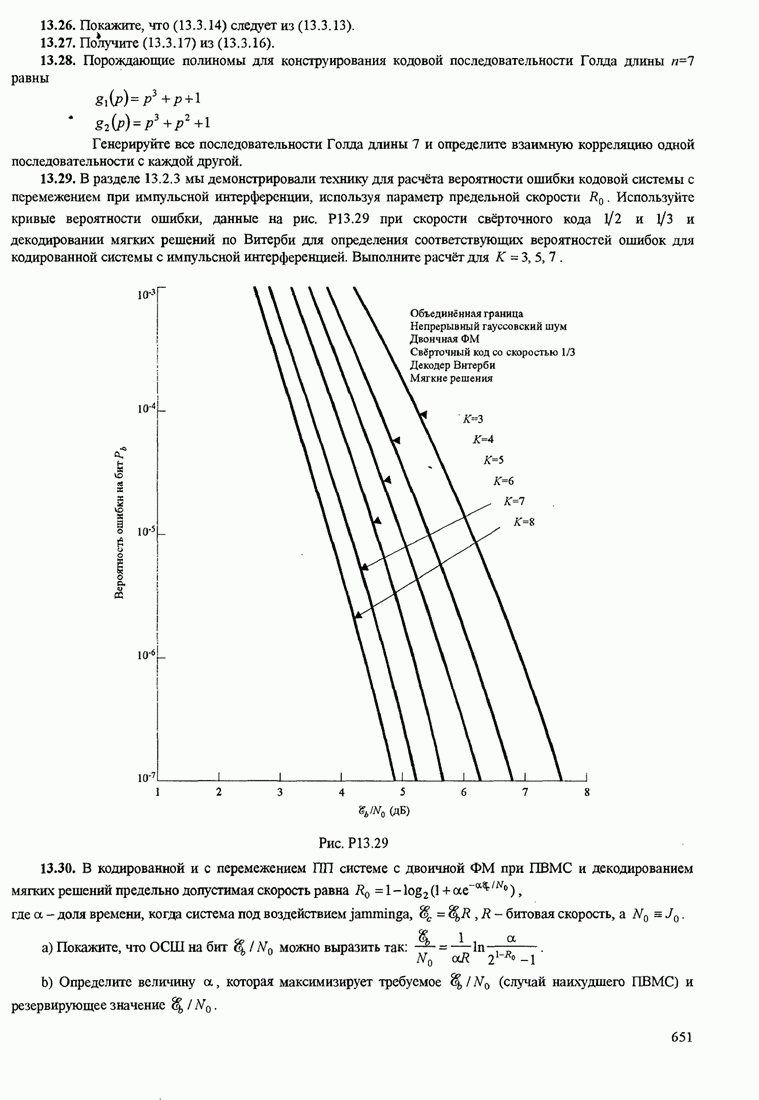
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
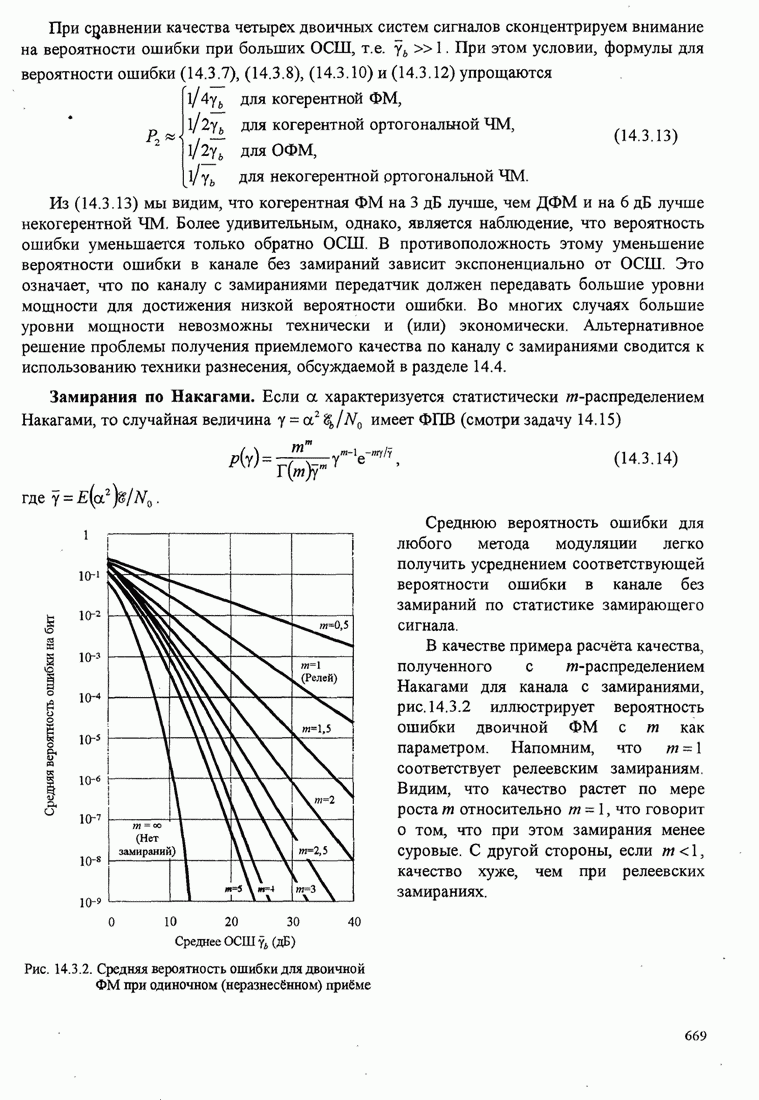
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
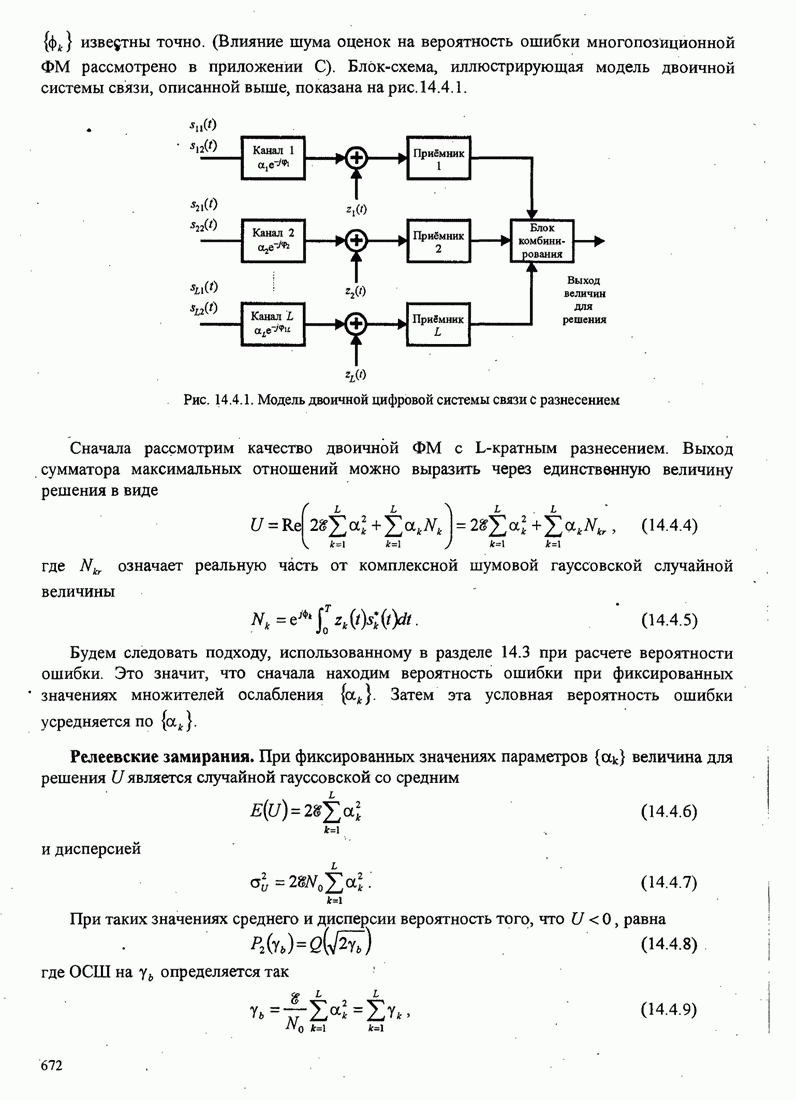
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
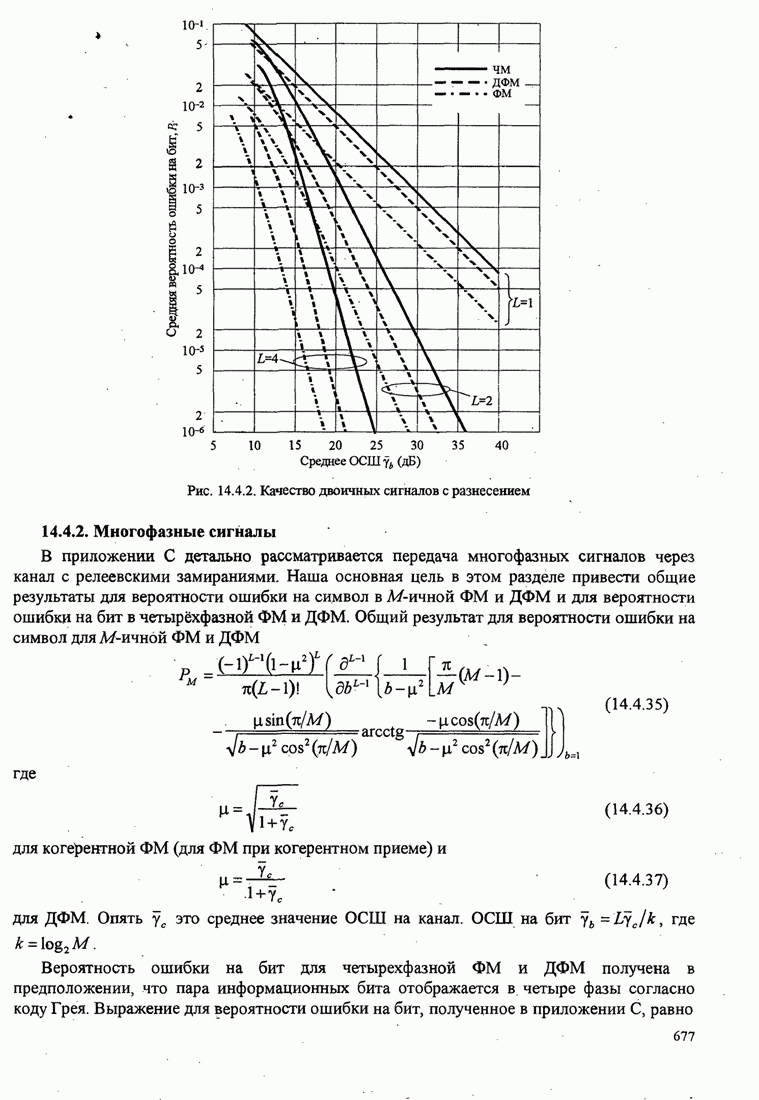
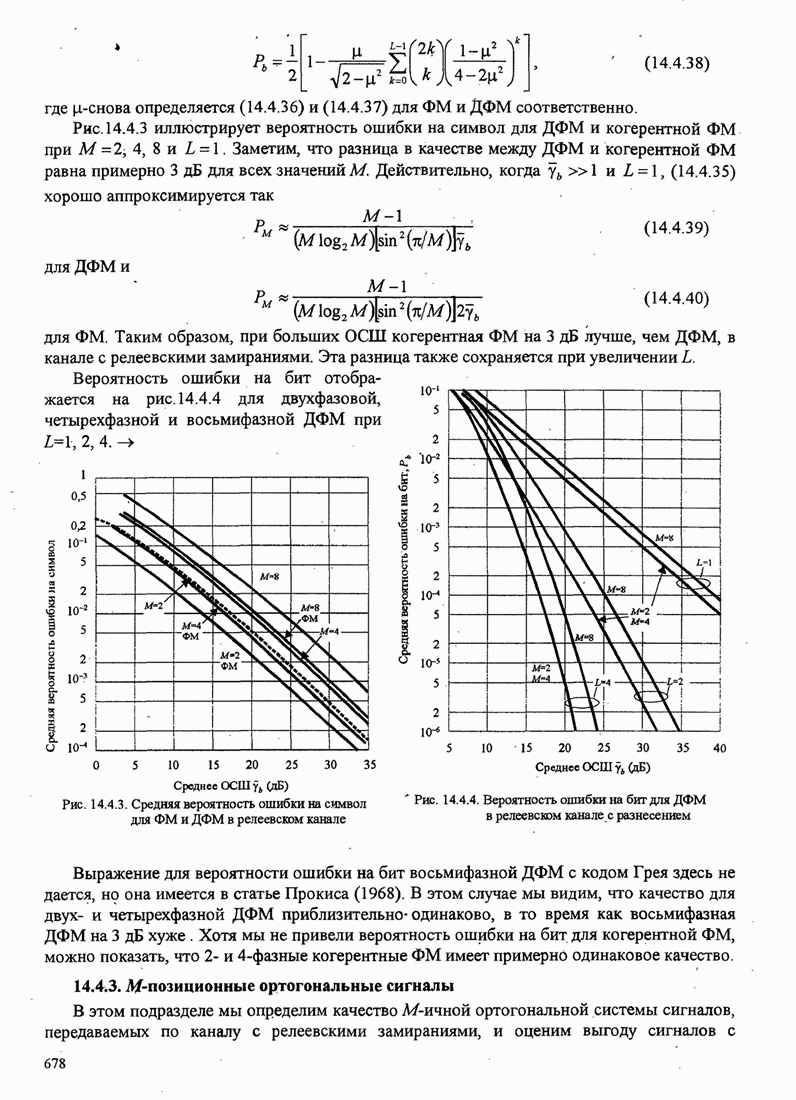
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
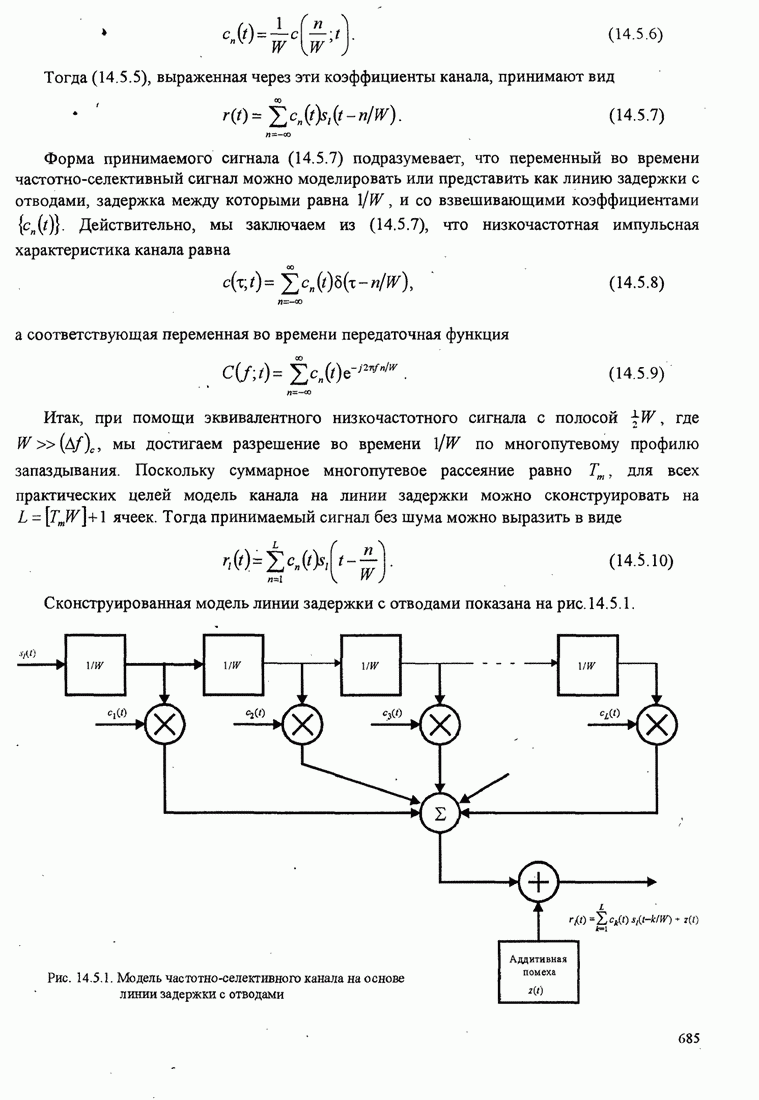
- 14.5.1. Модель канала в виде линии задержки с отводами
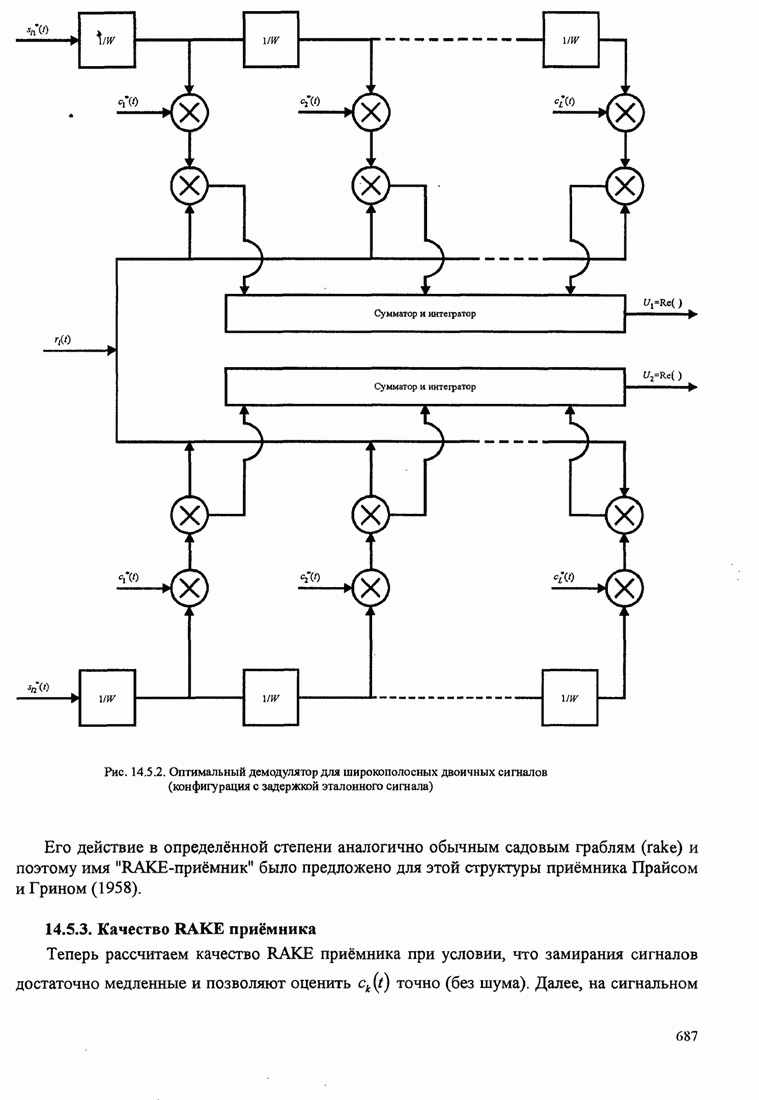
- 14.5.2. RAKE демодулятор
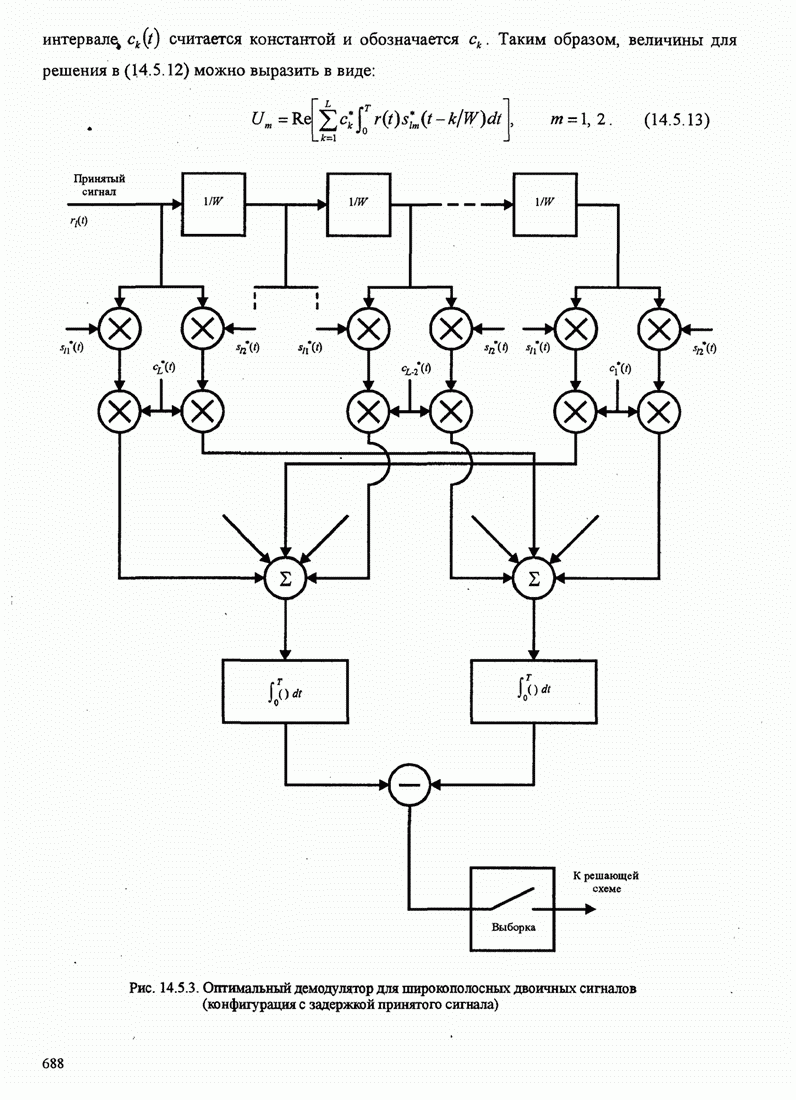
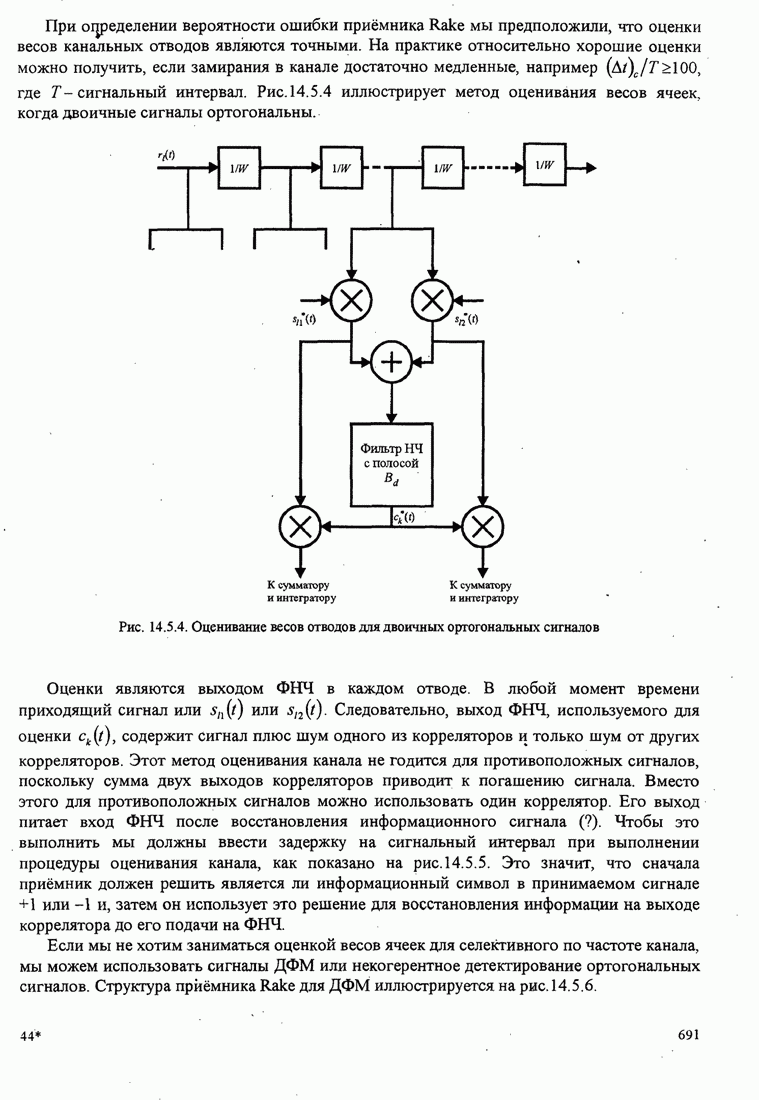
- 14.5.3. Качество RAKE приемника
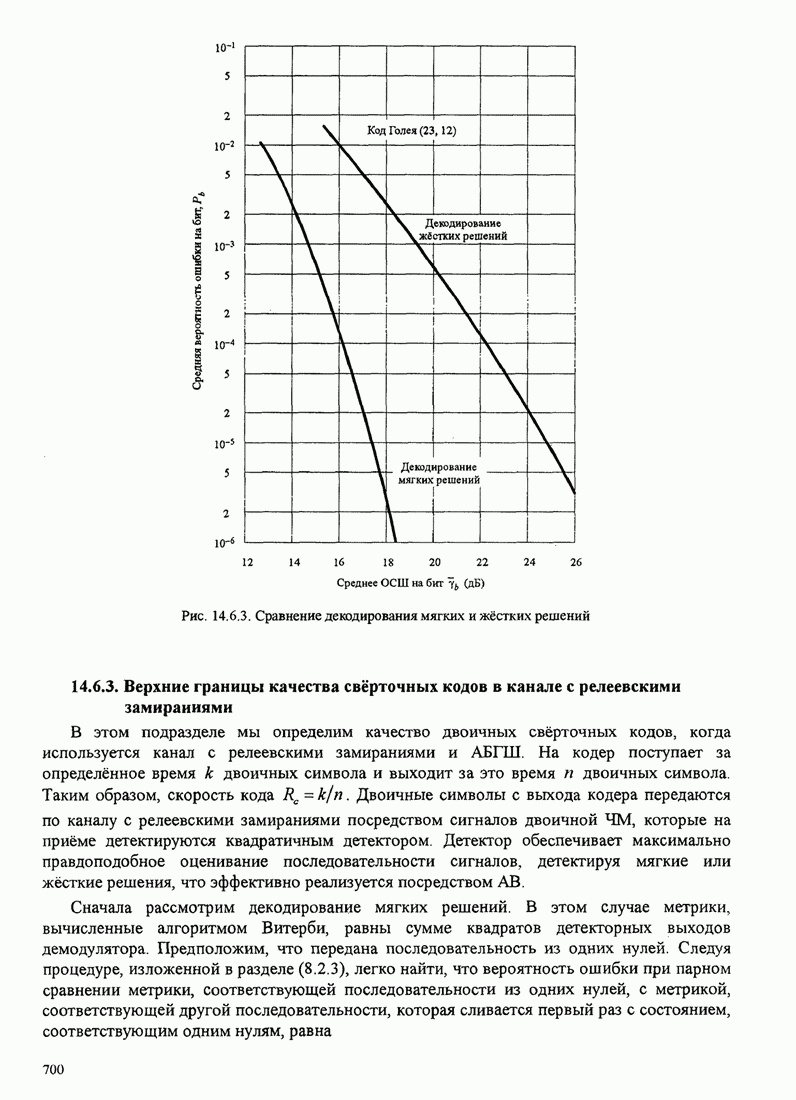
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
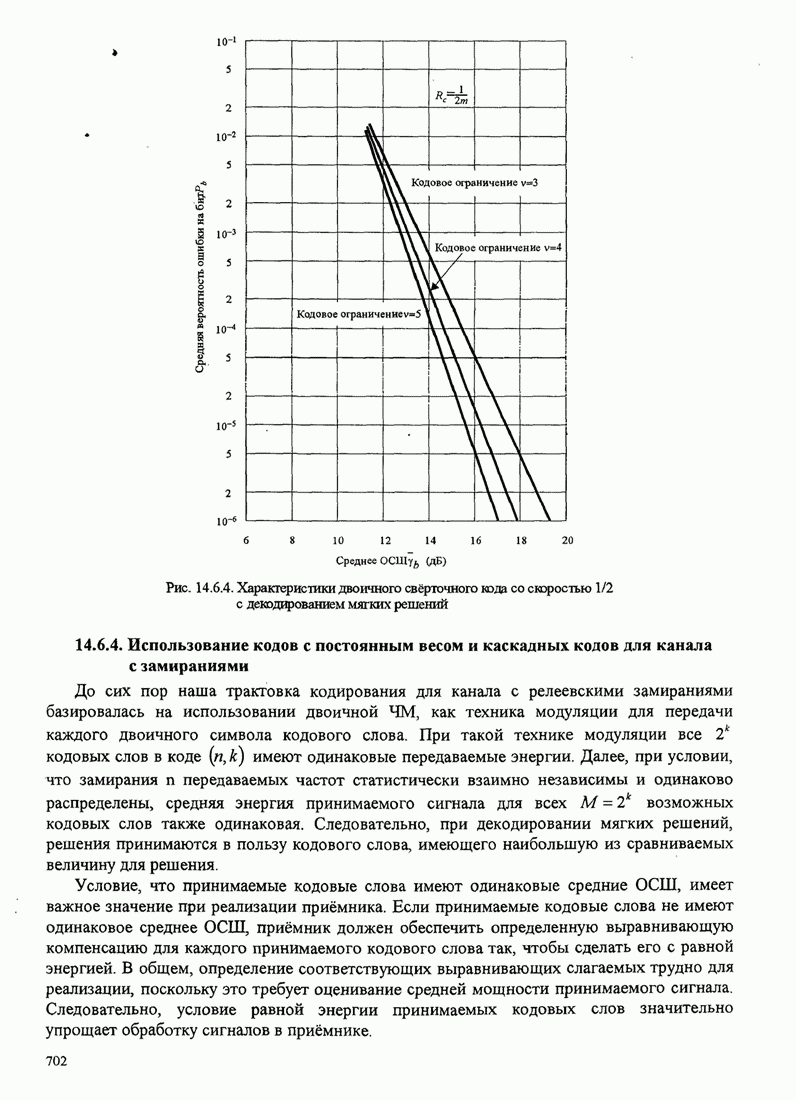
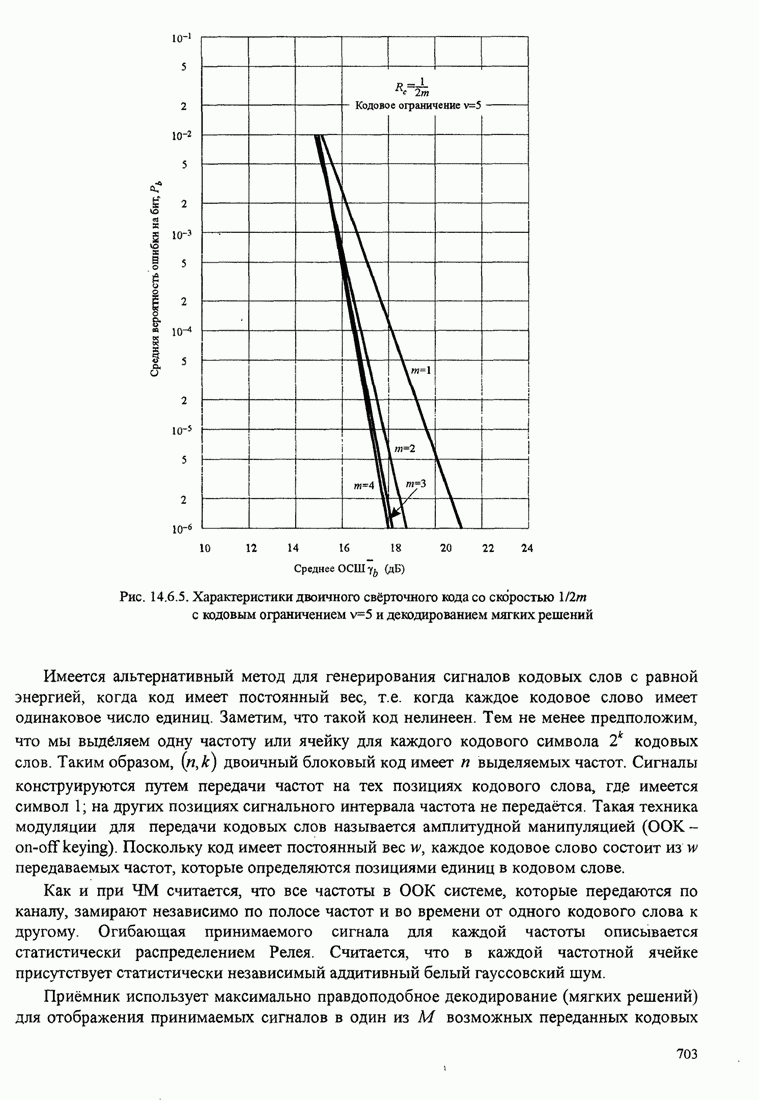
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
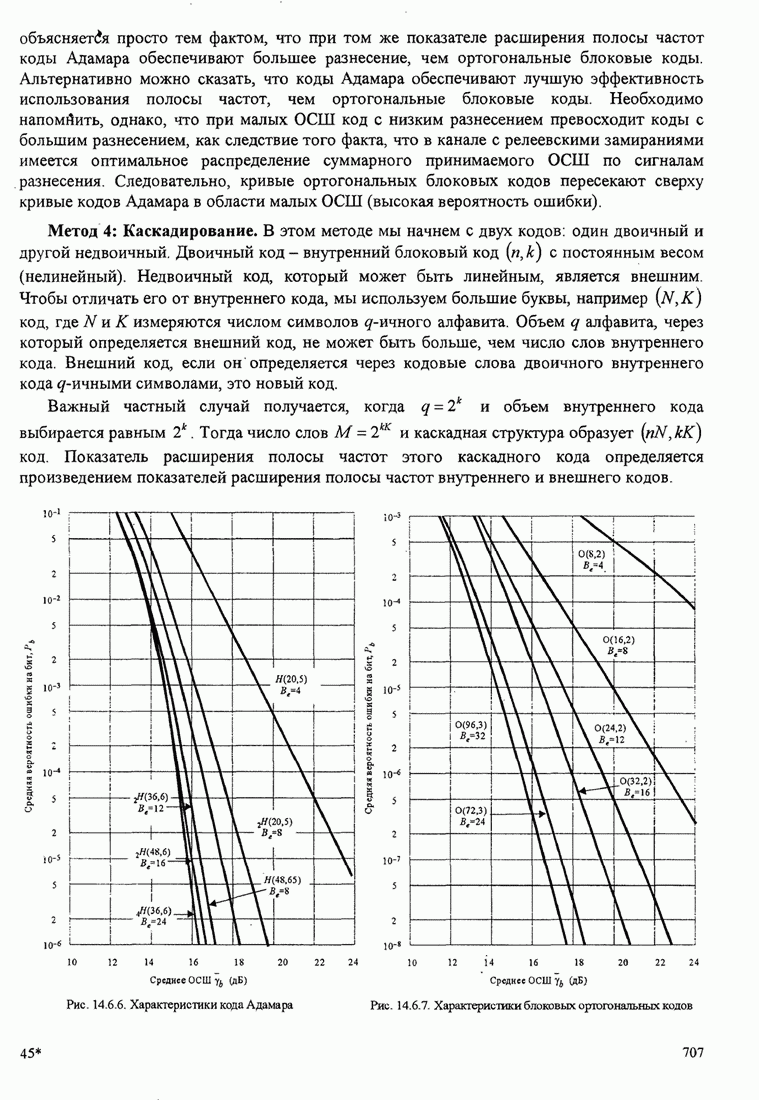
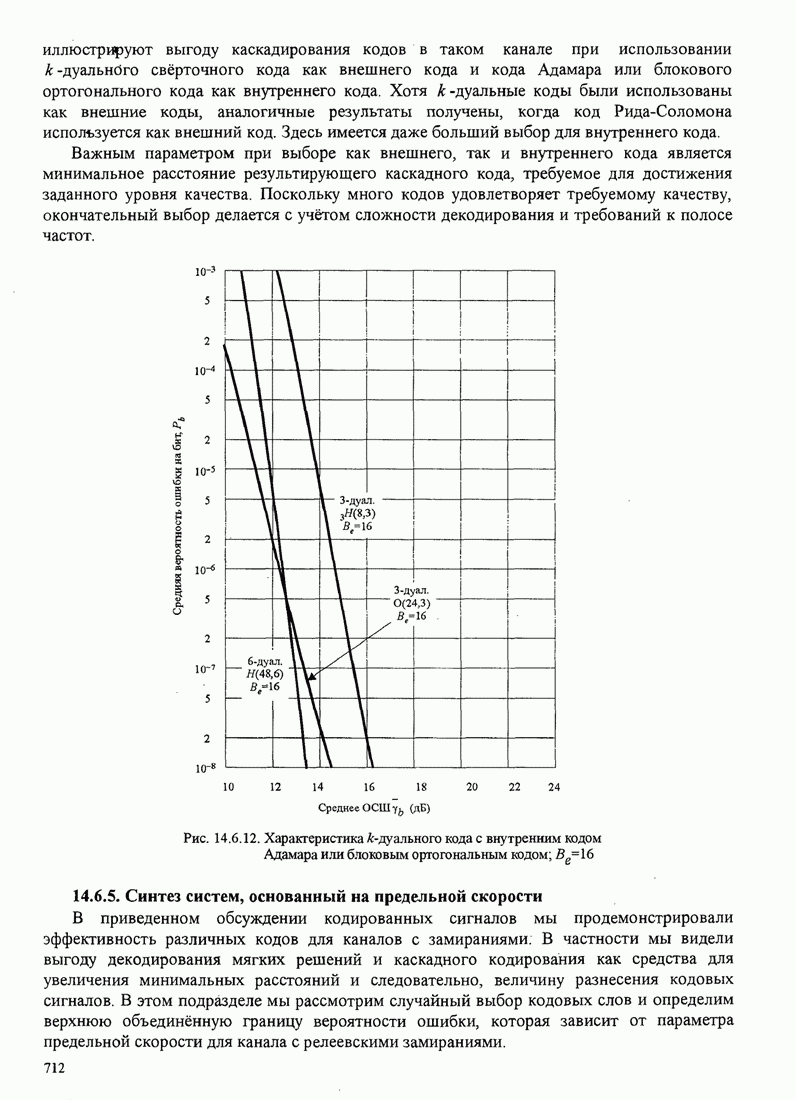
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
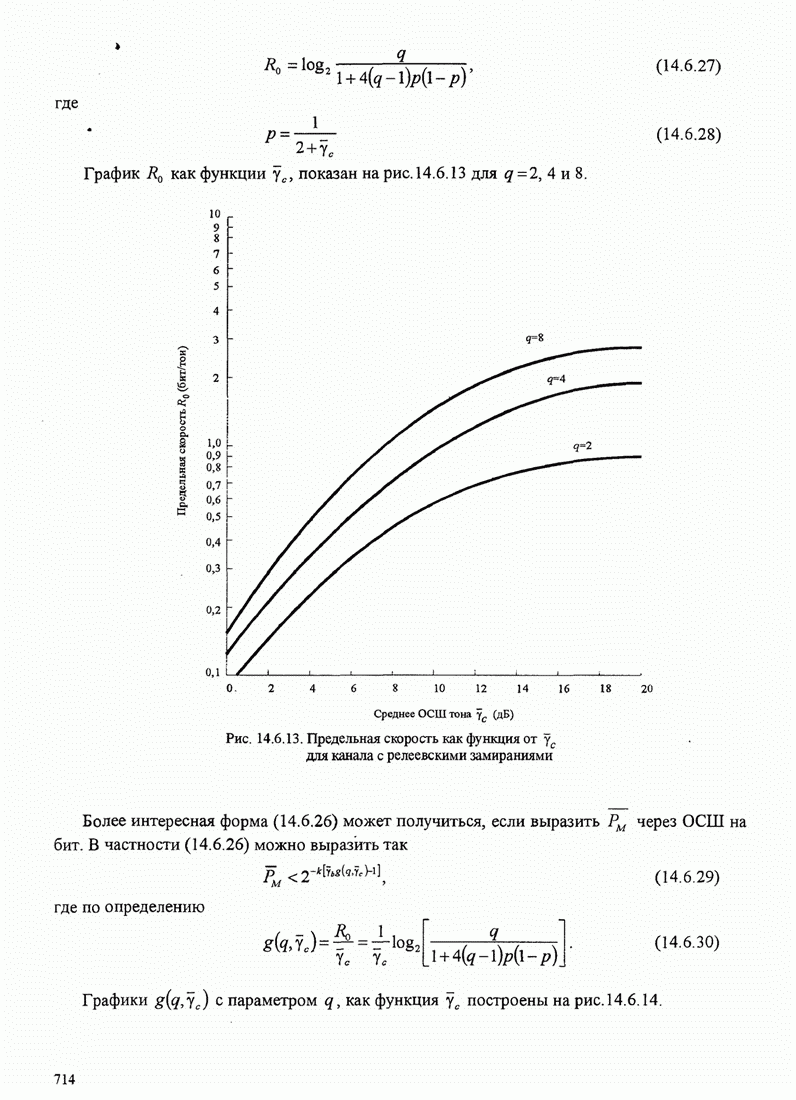
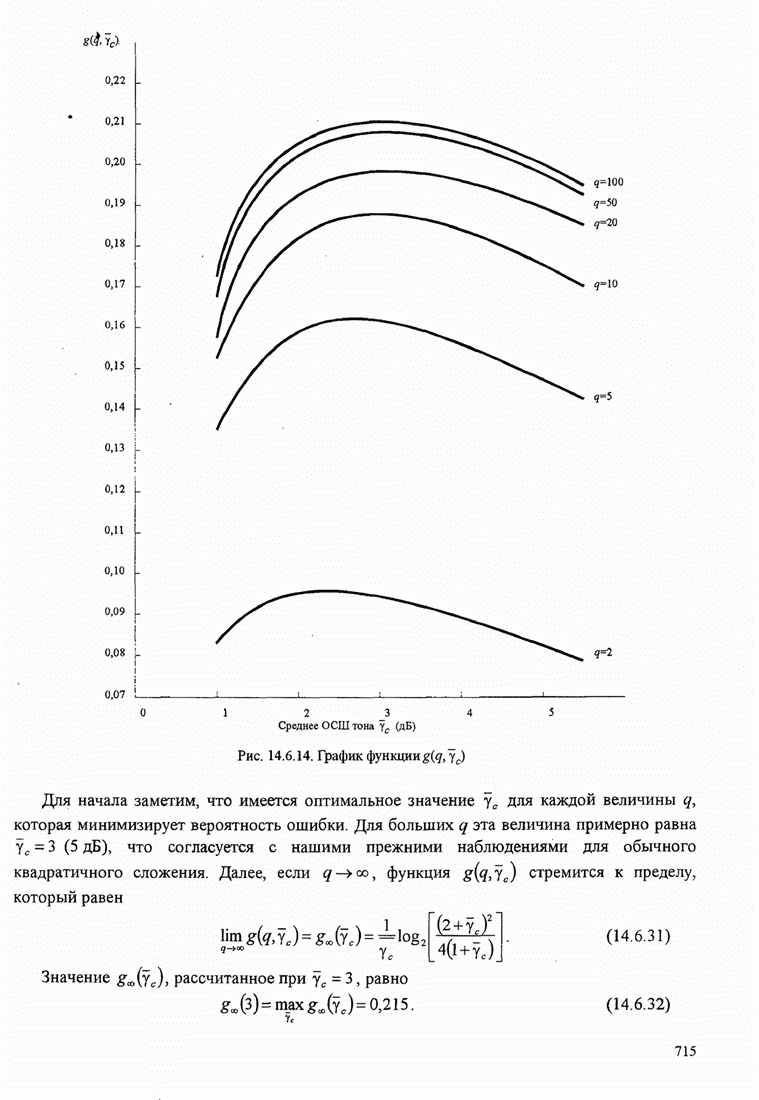
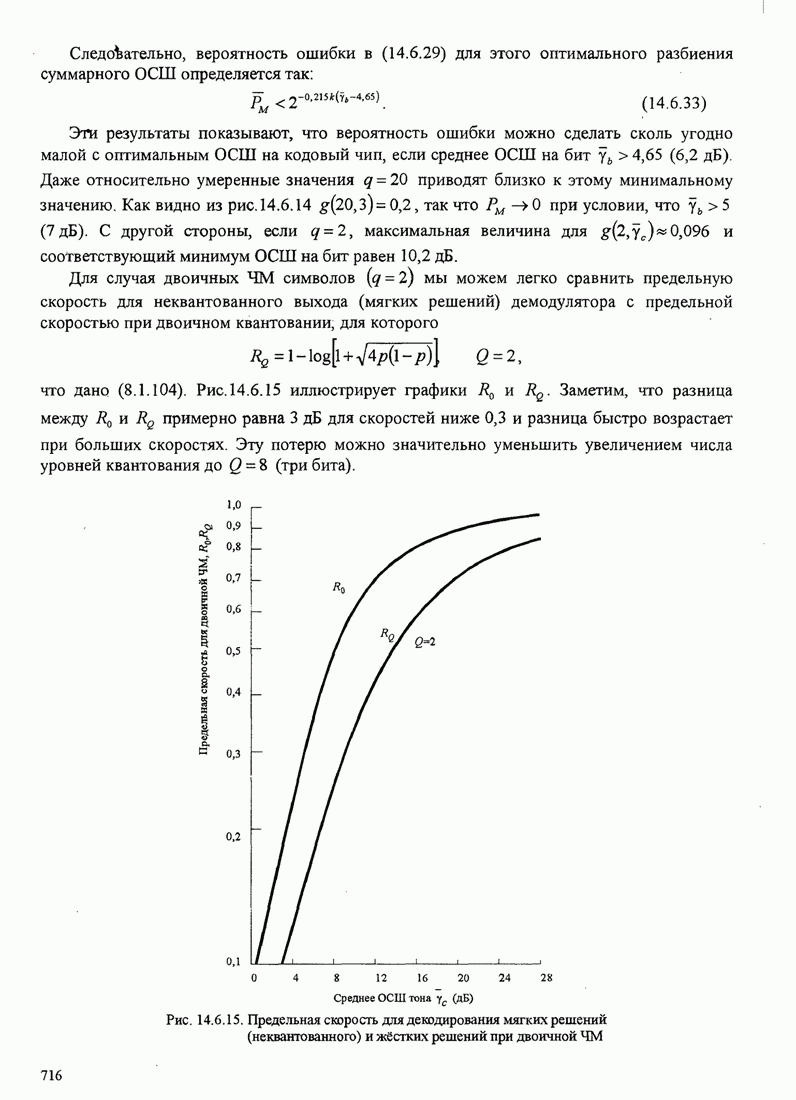
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
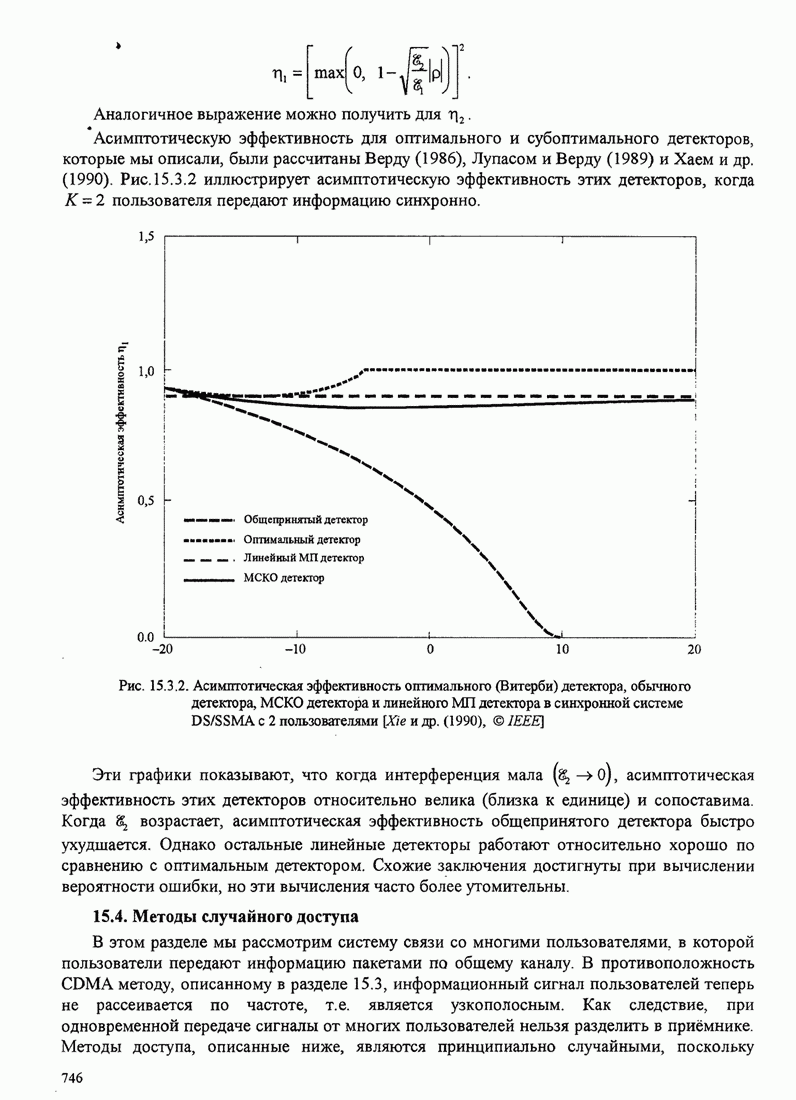
- 15.3.4. Характеристики качества детекторов
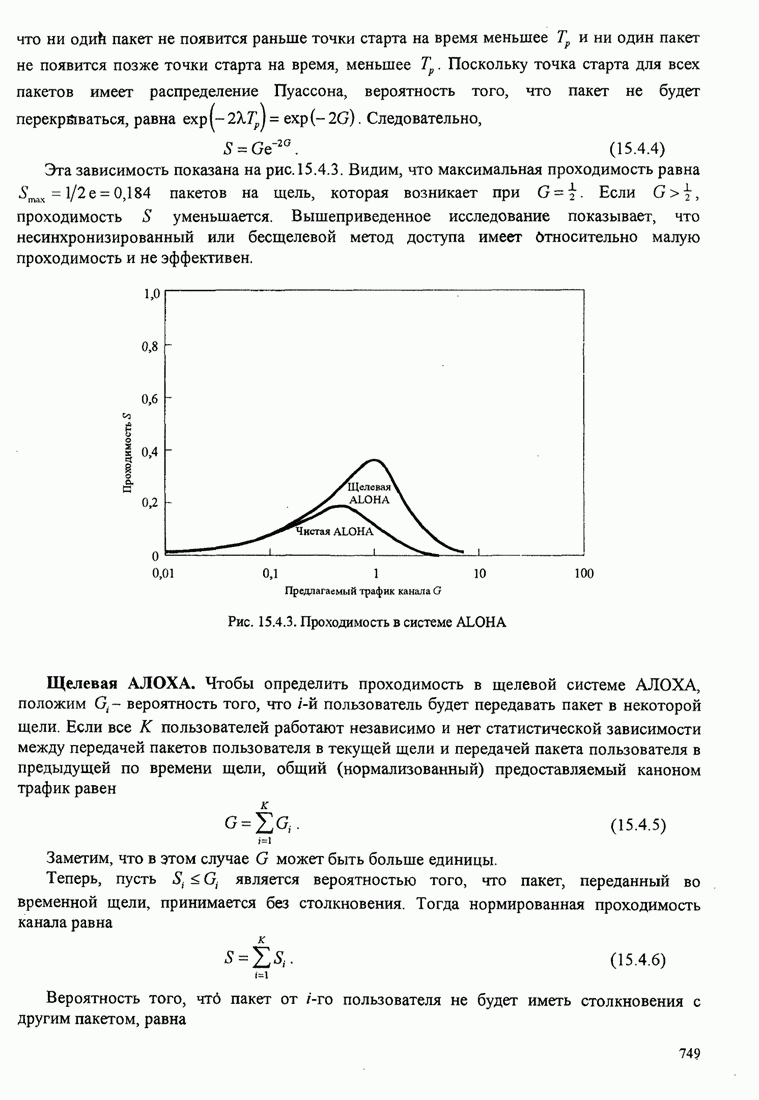
- 15.4. Методы случайного доступа
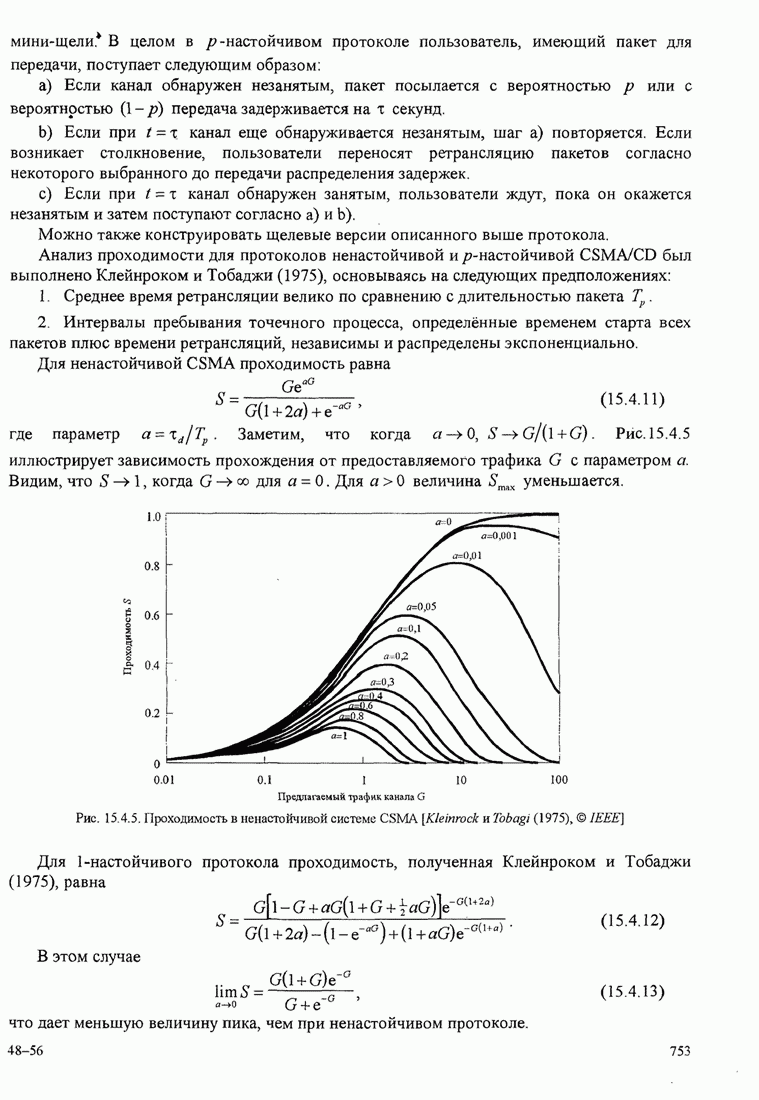
- 15.4.1. АЛОХА. Системы и протоколы
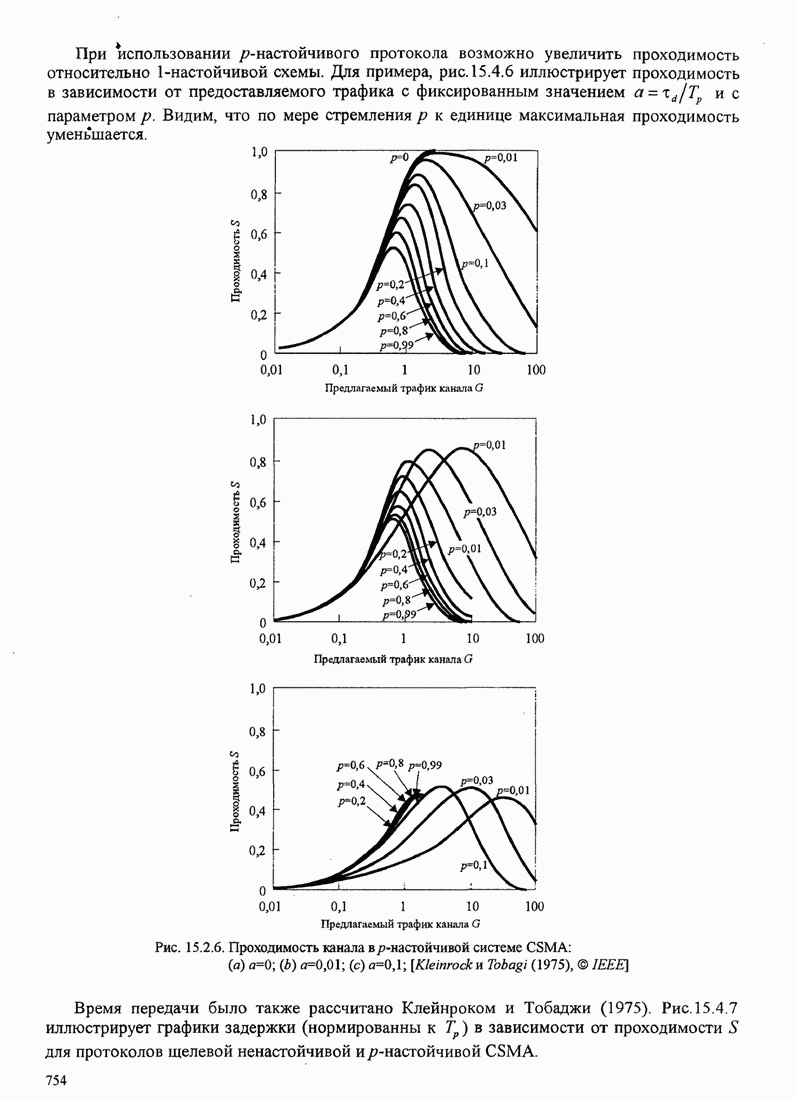
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)