| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Пространства и инвариантная контактная структура
Перейдем теперь к общему случаю произвольного пространства-времени  Мы увидим, что идеи теории твисторов плодотворны и в этом случае.
Мы увидим, что идеи теории твисторов плодотворны и в этом случае.
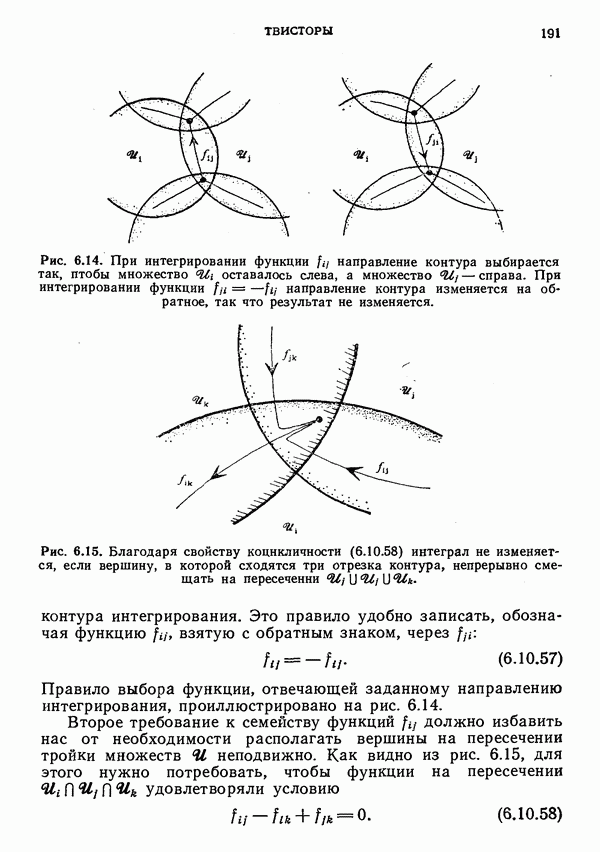
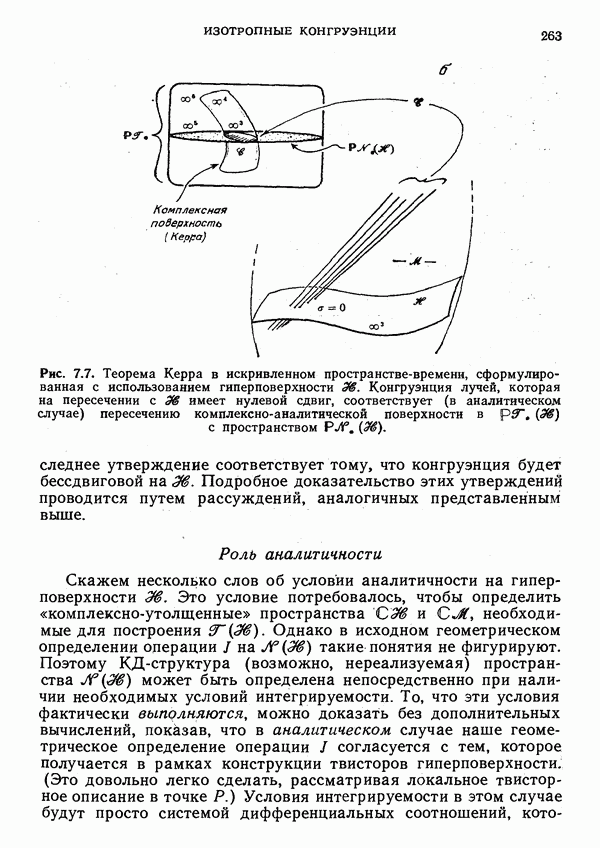
В § 1 мы показали, что, хотя изопараметричность некоего луча соседнему лучу  определяется локально, в действительности она является глобальным свойством: если она имеется в одной точке луча
определяется локально, в действительности она является глобальным свойством: если она имеется в одной точке луча  то она имеется и во всех других его точках. В § 2 мы показали, что то же справедливо для условия отсутствия вращения пучков лучей, близких к лучу
то она имеется и во всех других его точках. В § 2 мы показали, что то же справедливо для условия отсутствия вращения пучков лучей, близких к лучу  и изопараметрических ему. Следовательно, эти два свойства отвечают некоторой инвариантной структуре в пространстве
и изопараметрических ему. Следовательно, эти два свойства отвечают некоторой инвариантной структуре в пространстве  каждая точка которого изображает определенный луч в
каждая точка которого изображает определенный луч в 
Обозначение  аналогично тому, которое использовалось в гл. 6, § 10 и гл. 9, § 3, где (см. с. 370) через
аналогично тому, которое использовалось в гл. 6, § 10 и гл. 9, § 3, где (см. с. 370) через  обозначено пространство проективных изотропных твисторов в (VI. Элементы пространства
обозначено пространство проективных изотропных твисторов в (VI. Элементы пространства  изотропные твисторы, заданные с точностью до множителя, а поэтому (если не считать, что
изотропные твисторы, заданные с точностью до множителя, а поэтому (если не считать, что  содержит еще и «бесконечно удаленные лучи», см. гл. 9, § 3)
содержит еще и «бесконечно удаленные лучи», см. гл. 9, § 3)  можно рассматривать как пространство лучей в М. Но определение непроективного пространства
можно рассматривать как пространство лучей в М. Но определение непроективного пространства  изотропных твисторов содержит дополнительные требования к спинору
изотропных твисторов содержит дополнительные требования к спинору  в каждой точке луча: его флагшток должен быть касательным к лучу, а весь спинор должен переноситься вдоль луча параллельно. Положив
в каждой точке луча: его флагшток должен быть касательным к лучу, а весь спинор должен переноситься вдоль луча параллельно. Положив  мы получаем определенного рода (аффинную) параметризацию (scaling) луча
мы получаем определенного рода (аффинную) параметризацию (scaling) луча  и базовое полотнище флага, которые применялись ранее в данной главе. Строго говоря, спинор
и базовое полотнище флага, которые применялись ранее в данной главе. Строго говоря, спинор  относится к пространству
относится к пространству  (или
(или  изотропных
изотропных  -твисторов. Нештрихованный же спинор
-твисторов. Нештрихованный же спинор  относится к пространству
относится к пространству  (или
(или  ) изотропных
) изотропных  -твисторов, комплексно-сопряженному с пространством
-твисторов, комплексно-сопряженному с пространством  (Проективные образы этих пространств
(Проективные образы этих пространств  и
и  по существу одинаковы.) По аналогии с точками пространства
по существу одинаковы.) По аналогии с точками пространства  мы определим теперь точку
мы определим теперь точку
пространства  как пару: луч в
как пару: луч в  и спинор
и спинор  , флагшток которого касателен к лучу и который переносится вдоль луча параллельно. Пространство
, флагшток которого касателен к лучу и который переносится вдоль луча параллельно. Пространство  определяется аналогично, однако роль спинора
определяется аналогично, однако роль спинора  играет штрихованный спинор
играет штрихованный спинор  . Здесь мы будем иметь дело почти исключительно с пространствами
. Здесь мы будем иметь дело почти исключительно с пространствами  а потому ради простоты примем для них упрощенные обозначения
а потому ради простоты примем для них упрощенные обозначения  в тех случаях, когда не требуется подчеркнуть их отличие от
в тех случаях, когда не требуется подчеркнуть их отличие от 
Одно из преимуществ пространства  перед
перед  в том, что оно допускает интерпретацию меры неизопараметричности
в том, что оно допускает интерпретацию меры неизопараметричности

[формулы (7.1.39), (7.1.43)], а не только условия  . В силу формул (7.1.65), (7.1.66), (7.4.27) имеем представление
. В силу формул (7.1.65), (7.1.66), (7.4.27) имеем представление

для твистора  и вскоре мы покажем, что аналогичная формула справедлива в
и вскоре мы покажем, что аналогичная формула справедлива в  если использовать формализм локальных твисторов (гл. 6, § 9) в некоторой точке рассматриваемого луча. Аналогично мера вращения, т. е. либо
если использовать формализм локальных твисторов (гл. 6, § 9) в некоторой точке рассматриваемого луча. Аналогично мера вращения, т. е. либо  [где L — яркостный параметр, а t - вращение, см. формулы (7.1.51), (7.1.48), (7.2.16)], либо более общая характеристика — симплектический инвариант
[где L — яркостный параметр, а t - вращение, см. формулы (7.1.51), (7.1.48), (7.2.16)], либо более общая характеристика — симплектический инвариант  , определенный в формуле (7.2.18), также допускает в
, определенный в формуле (7.2.18), также допускает в  прямую интерпретацию.
прямую интерпретацию.
Чтобы найти выражение для величины  , рассмотрим луч
, рассмотрим луч  в пространстве М, а также два соседних с ним луча
в пространстве М, а также два соседних с ним луча  и
и 
Представим  твисторами
твисторами  . Выбирая начало координат в точке
. Выбирая начало координат в точке  имеем [здесь
имеем [здесь  см. формулы (7.1.62) — (7.1.64)]
см. формулы (7.1.62) — (7.1.64)]

Далее, опуская слагаемые третьего порядка, находим

[с учетом условий  см. формулу (7.1.29)].
см. формулу (7.1.29)].
Предпоследняя строка в формуле (7.4.30) может быть переписана в виде

а это в силу изложенного в § 1 есть произведение мнимой единицы на квадрат яркостного параметра и на вращение, когда лучи  и
и  изопараметричны лучу
изопараметричны лучу  . В случае неизопараметрических лучей дополнительная информация, содержащаяся в величине (7.4.31), состоит лишь в том, как изменяется масштаб
. В случае неизопараметрических лучей дополнительная информация, содержащаяся в величине (7.4.31), состоит лишь в том, как изменяется масштаб  задаваемый вектором
задаваемый вектором  при переходе от луча к лучу. В частности, выражение (7.4.31) равно нулю при всех значениях векторов
при переходе от луча к лучу. В частности, выражение (7.4.31) равно нулю при всех значениях векторов  в том (и только в том) случае, если поле
в том (и только в том) случае, если поле  есть поле некоего градиента
есть поле некоего градиента  ; см. формулу (7.1.57)], а не всего лишь пропорционально градиенту
; см. формулу (7.1.57)], а не всего лишь пропорционально градиенту  см. формулу (7.1.58)], что мы имеем, если выражение (7.4.31) обращается в нуль только для изопараметрических лучей (когда
см. формулу (7.1.58)], что мы имеем, если выражение (7.4.31) обращается в нуль только для изопараметрических лучей (когда  Отметим, что здесь автоматически выполняется равенство
Отметим, что здесь автоматически выполняется равенство 
Пусть теперь лучи принадлежат искривленному пространству-времени  Воспользуемся локальным твисторным описанием в точке Р и представим лучи
Воспользуемся локальным твисторным описанием в точке Р и представим лучи  и
и  с помощью локальных твисторов, которые редуцируются к виду
с помощью локальных твисторов, которые редуцируются к виду  при смещении от точки Р на
при смещении от точки Р на  соответственно. Пренебрегая слагаемыми второго порядка по
соответственно. Пренебрегая слагаемыми второго порядка по  находим, что выражения для твисторов
находим, что выражения для твисторов  заданных соотношениями (7.4.29), действительно обладают требуемым свойством, как это прямо следует из (6.9.14). Таким образом, выражение
заданных соотношениями (7.4.29), действительно обладают требуемым свойством, как это прямо следует из (6.9.14). Таким образом, выражение

определено в  в смысле локальных твисторов в точке Р. Более того, оно справедливо в каждой точке луча
в смысле локальных твисторов в точке Р. Более того, оно справедливо в каждой точке луча  так как величина
так как величина  постоянна [см. текст после формулы (7.2.18)] вдоль
постоянна [см. текст после формулы (7.2.18)] вдоль  хотя локальное твисторное описание каждого луча
хотя локальное твисторное описание каждого луча  вообще говоря, не является постоянным вдоль
вообще говоря, не является постоянным вдоль  (в смысле локальных твисторов). Аналогичное замечание справедливо в отношении величины (7.4.28).
(в смысле локальных твисторов). Аналогичное замечание справедливо в отношении величины (7.4.28).
Структура, индуцированная в пространстве  величинами
величинами  и
и  , наиболее естественно описывается с помощью дифференциальних форм. (гл. 4, § 3). Имеем 1-форму
, наиболее естественно описывается с помощью дифференциальних форм. (гл. 4, § 3). Имеем 1-форму

и 2-форму

которые канонически определены в  причем правая часть в каждом случае понимается в смысле локальных твисторов по аналогии с выражениями (7.4.28) и (7.4.32) соответственно. Величины
причем правая часть в каждом случае понимается в смысле локальных твисторов по аналогии с выражениями (7.4.28) и (7.4.32) соответственно. Величины  и Е получаются как значения форм
и Е получаются как значения форм  и
и  на векторах
на векторах  Это утверждение легко проверить (в любой точке Р луча
Это утверждение легко проверить (в любой точке Р луча  Строго говоря, векторы
Строго говоря, векторы  следует рассматривать как поля Якоби, заданные вдоль всего луча
следует рассматривать как поля Якоби, заданные вдоль всего луча  текст после формулы (7.2.2)], поскольку именно полем Якоби определяется касательный вектор в точке пространства
текст после формулы (7.2.2)], поскольку именно полем Якоби определяется касательный вектор в точке пространства  е. смещение от одного луча в целом к соседнему).
е. смещение от одного луча в целом к соседнему).
Отметим также важное соотношение

Справедливость этого соотношения более или менее очевидна из формул (7.4.33) и (7.4.34), но нужна осторожность при формальном вычислении действия операции  на величину (7.4.33), так как твисторы
на величину (7.4.33), так как твисторы  не являются независимыми, а связаны между собой в
не являются независимыми, а связаны между собой в  соотношением
соотношением

Правда, не составляет труда избавиться (локально) от этого ограничения, рассматривая  как часть (действительно-восьмимерного) многообразия
как часть (действительно-восьмимерного) многообразия  для которого условие (7.4.36) не обязательно. В этом случае равенством (7.4.36) выделяется подмножество
для которого условие (7.4.36) не обязательно. В этом случае равенством (7.4.36) выделяется подмножество  Формы
Формы  и
и  не продолжаются на
не продолжаются на  канонически, однако эта неопределенность не влияет на соотношение (7.4.35). Соответствующий произвол сводится к добавлению слагаемого вида
канонически, однако эта неопределенность не влияет на соотношение (7.4.35). Соответствующий произвол сводится к добавлению слагаемого вида  умноженного на гладкую форму, которое не дает вклада во внешнюю производную на
умноженного на гладкую форму, которое не дает вклада во внешнюю производную на  поскольку
поскольку

а это выражение равно нулю на  в силу равенства (7.4.33).
в силу равенства (7.4.33).
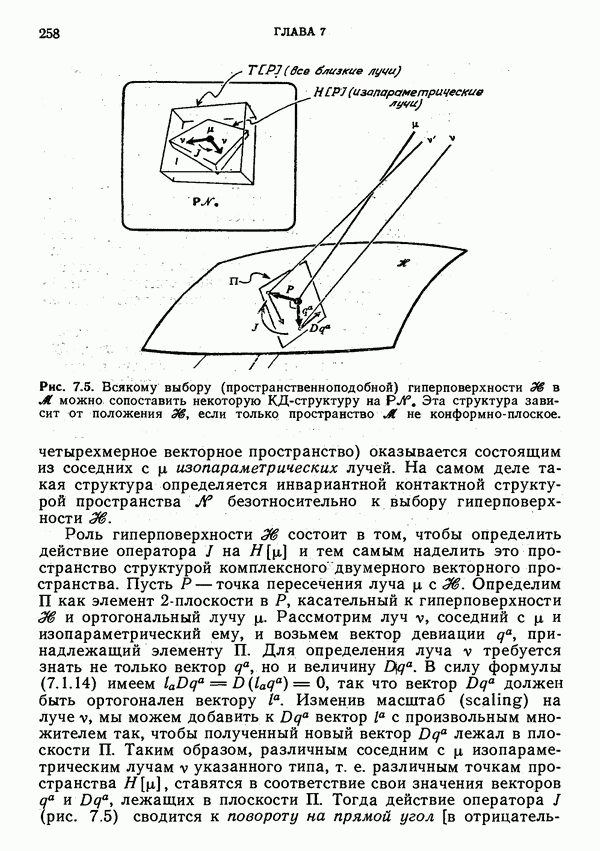
Выше мы допустили некоторую вольность, рассматривая

Рис. 7.4. В пространстве  можно ввести локальные координаты, сшив область
можно ввести локальные координаты, сшив область  искривленного пространства
искривленного пространства  с плоским пространством У (с помощью соответствующей переходной области).
с плоским пространством У (с помощью соответствующей переходной области).
локальные твисторы  с абстрактными индексами так, как если бы они были обычными функциями координат на
с абстрактными индексами так, как если бы они были обычными функциями координат на  и
и  Но наши рассуждения нетрудно изменить, чтобы они стали более строгими. Например, можно считать, что рассматриваемая область
Но наши рассуждения нетрудно изменить, чтобы они стали более строгими. Например, можно считать, что рассматриваемая область  (которая предполагается достаточно малой) гладко продолжается в другое многообразие пространства-времени
(которая предполагается достаточно малой) гладко продолжается в другое многообразие пространства-времени  которое является плоским в некоем открытом подмножестве Т, содержащем часть продолжения рассматриваемого луча
которое является плоским в некоем открытом подмножестве Т, содержащем часть продолжения рассматриваемого луча  на
на  (рис. 7.4). Многообразие
(рис. 7.4). Многообразие  не обязано удовлетворять каким-либо полевым уравнениям, так что это продолжение можно осуществить разными способами. Выберем одно такое продолжение и введем стандартный координатный базис
не обязано удовлетворять каким-либо полевым уравнениям, так что это продолжение можно осуществить разными способами. Выберем одно такое продолжение и введем стандартный координатный базис  в
в  [формулы (6.1.17), 6.1.34]. Все лучи, лежащие вблизи
[формулы (6.1.17), 6.1.34]. Все лучи, лежащие вблизи  продолжаются в
продолжаются в  , следовательно, им можно сопоставить стандартные (изотропные) твисторные компоненты, взятые по отношению к базису
, следовательно, им можно сопоставить стандартные (изотропные) твисторные компоненты, взятые по отношению к базису  Вычисляя компоненты форм
Вычисляя компоненты форм  и
и  постоянных вдоль
постоянных вдоль  в этом базисе, получаем просто координатные представления выражений (7.4.33), (7.4.34), а следовательно, и (7.4.35). Отметим, что указанная процедура позволяет ввести координатную окрестность на многообразии
в этом базисе, получаем просто координатные представления выражений (7.4.33), (7.4.34), а следовательно, и (7.4.35). Отметим, что указанная процедура позволяет ввести координатную окрестность на многообразии  в которой формы
в которой формы  представимы с помощью этих стандартных выражений. Очевидно, что в таком построении (взятом из
представимы с помощью этих стандартных выражений. Очевидно, что в таком построении (взятом из
работы [246]) имеется широкий произвол. Проведенное построение одновременно показывает, что формы  и
и  на
на  не содержат локальной информации о кривизне
не содержат локальной информации о кривизне  поскольку они эквивалентны соответствующим формам в плоской области Т.
поскольку они эквивалентны соответствующим формам в плоской области Т.
Структуру, связанную с формами  на
на  иногда называют контактной структурой [3]. Мы будем называть ее инвариантной контактной структурой на
иногда называют контактной структурой [3]. Мы будем называть ее инвариантной контактной структурой на  Форма 2, будучи невырожденной и замкнутой:
Форма 2, будучи невырожденной и замкнутой:

индуцирует в пространстве  определенном неканонически, симплектическую структуру [3, 377]. Более того, форму 2 можно рассматривать как симплектическую структуру на действительном шестимерном пространстве
определенном неканонически, симплектическую структуру [3, 377]. Более того, форму 2 можно рассматривать как симплектическую структуру на действительном шестимерном пространстве  полученном из
полученном из  факторизацией по фазовым преобразованиям:
факторизацией по фазовым преобразованиям:

(Симплектические структуры существуют только на четномерных многообразиях.) Стало быть, симплектическое многообразие  есть пространство аффинно-параметризованных (scaled) лучей в
есть пространство аффинно-параметризованных (scaled) лучей в  Что касается 1-формы
Что касается 1-формы  то она тоже хорошо определена на
то она тоже хорошо определена на  и связана с 2 соотношением (7.4.35) (подробнее см. в работах [246, 61]).
и связана с 2 соотношением (7.4.35) (подробнее см. в работах [246, 61]).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
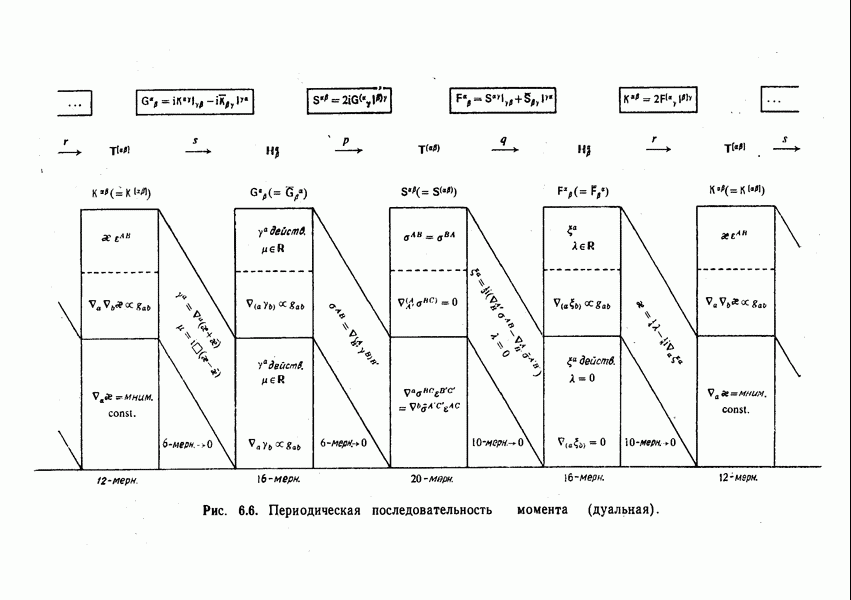
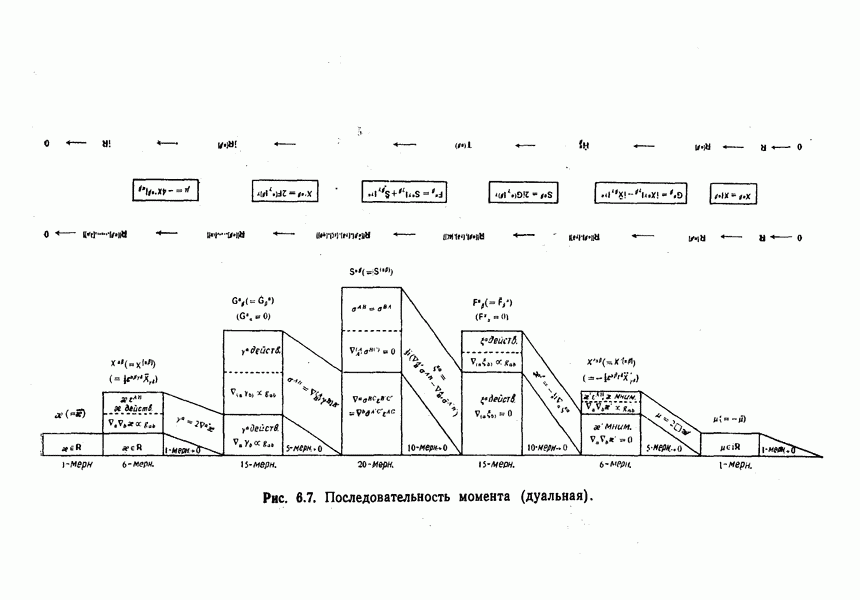
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
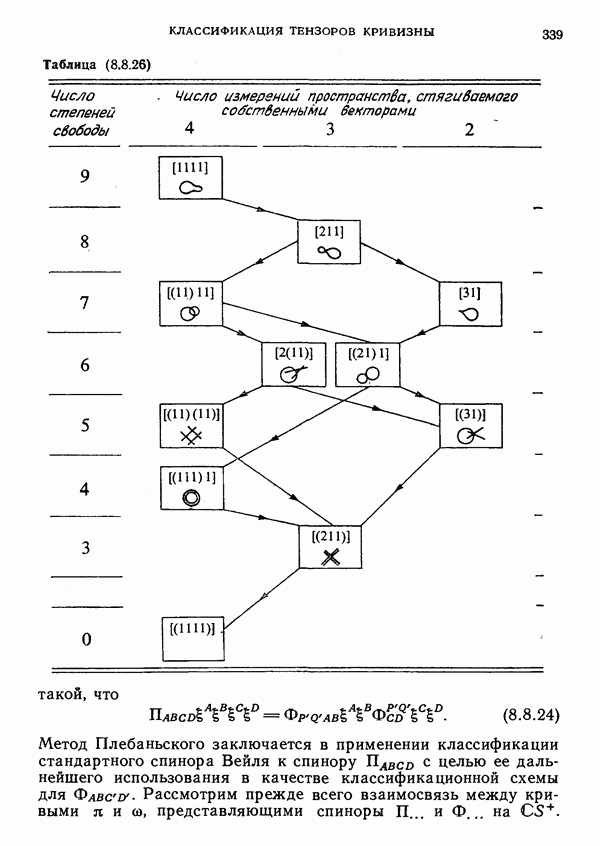
- 8. Классификация тензоров кривизны
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
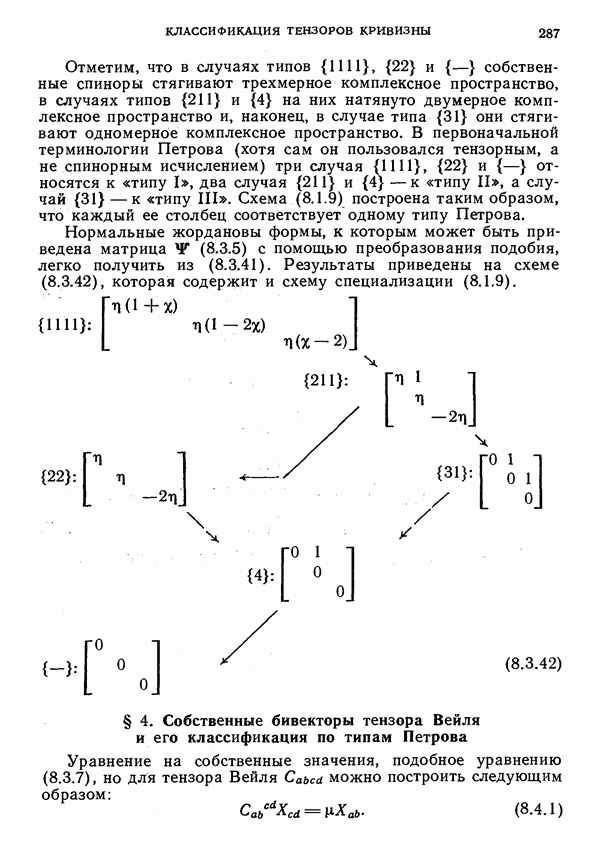
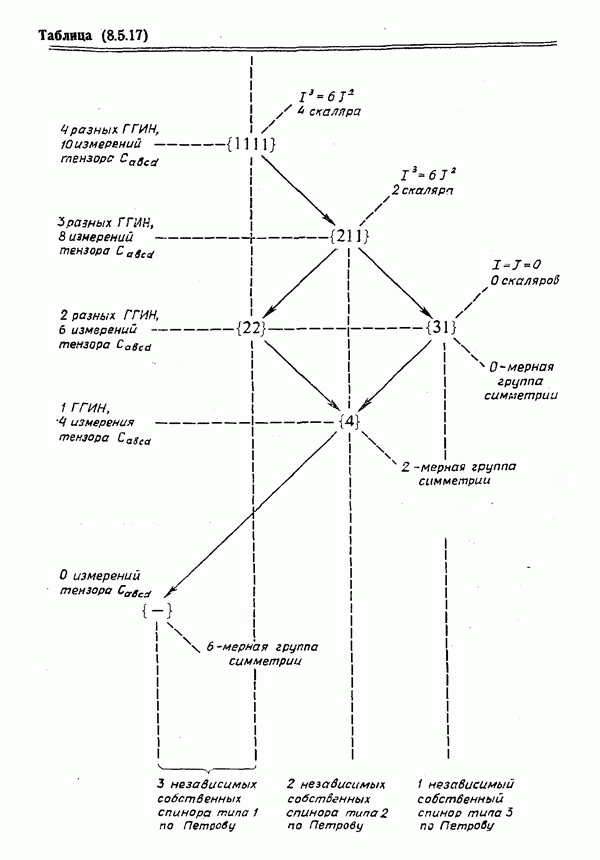
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
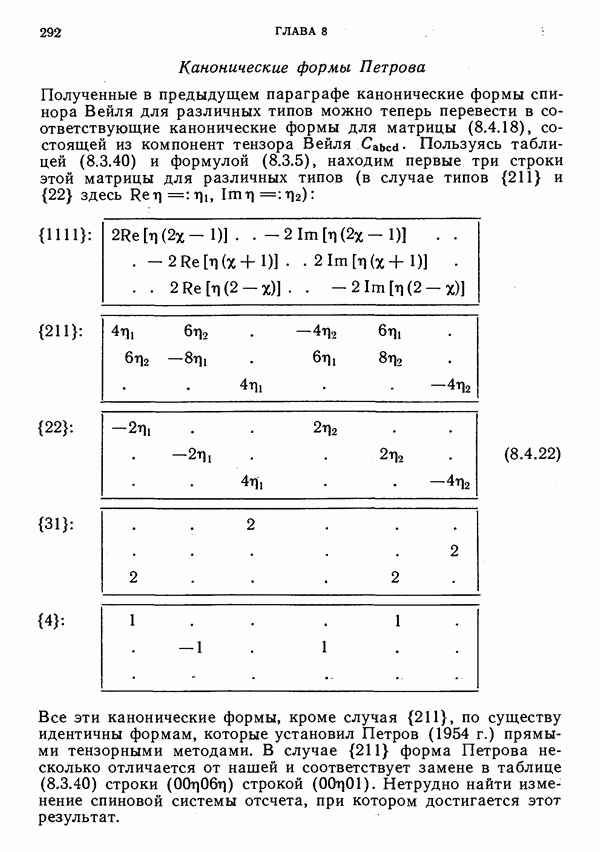
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
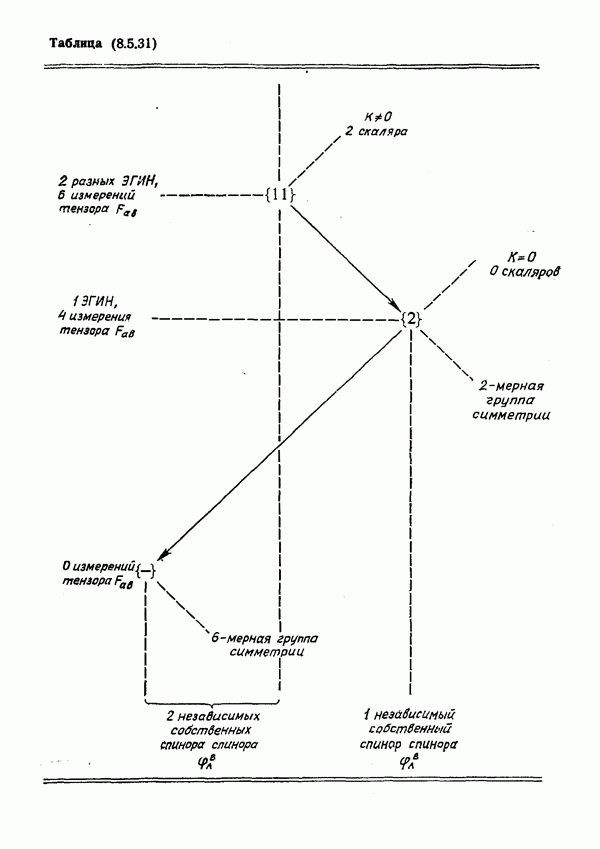
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
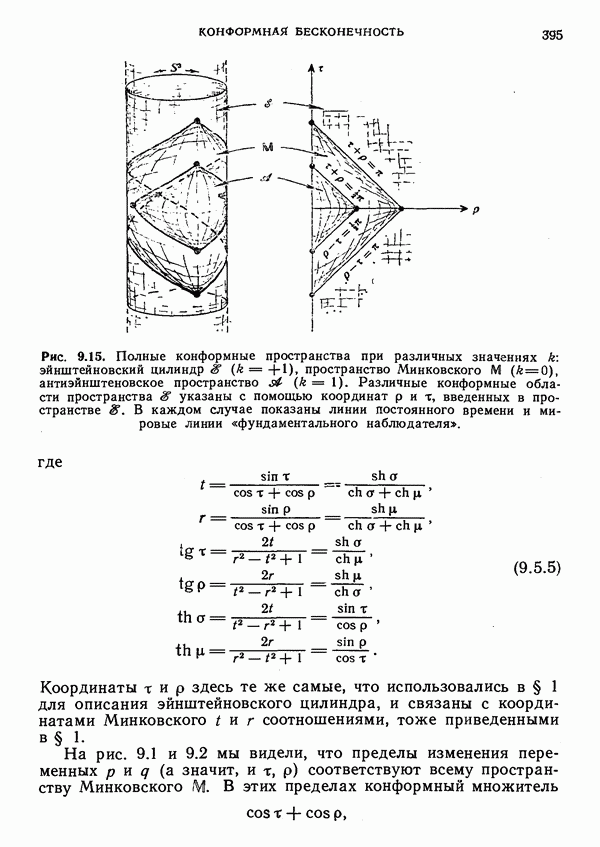
- 9. Конформная бесконечность
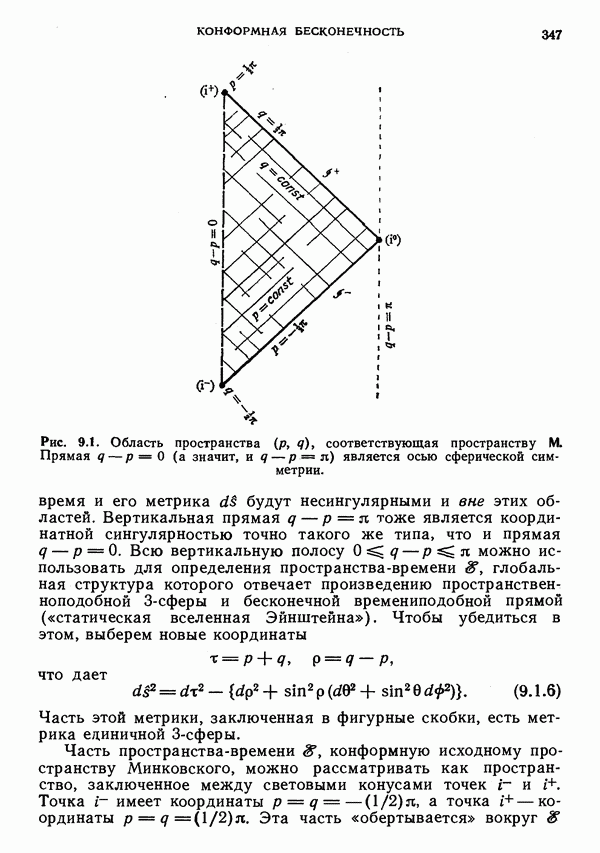
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
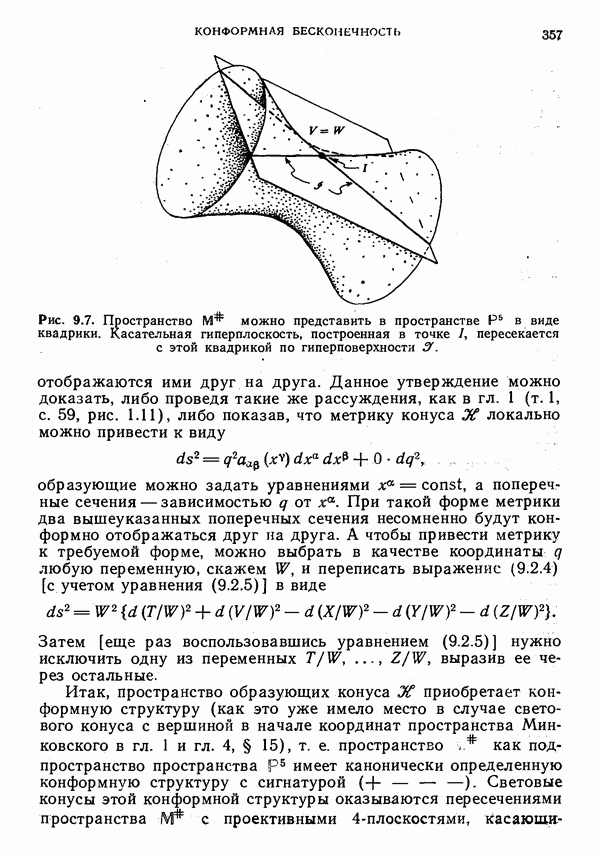
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
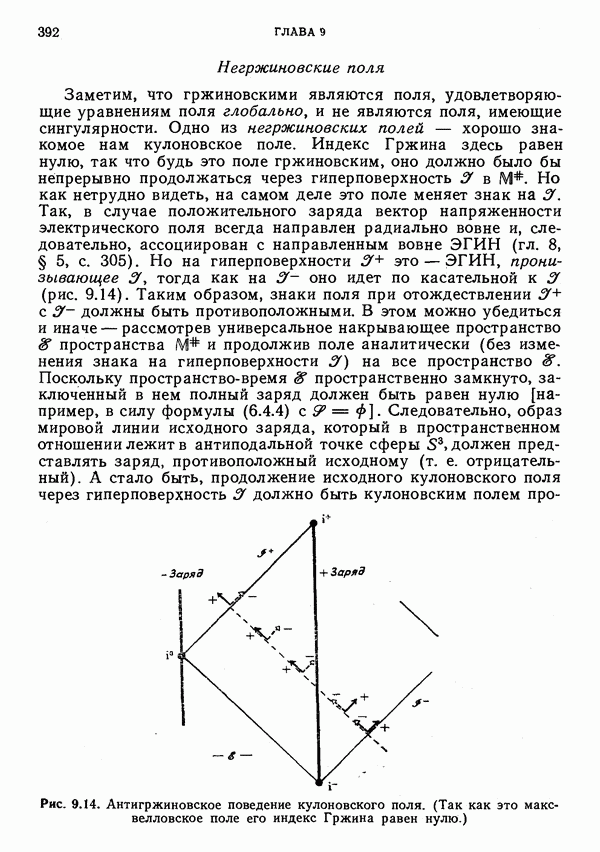
- Негржиновские поля
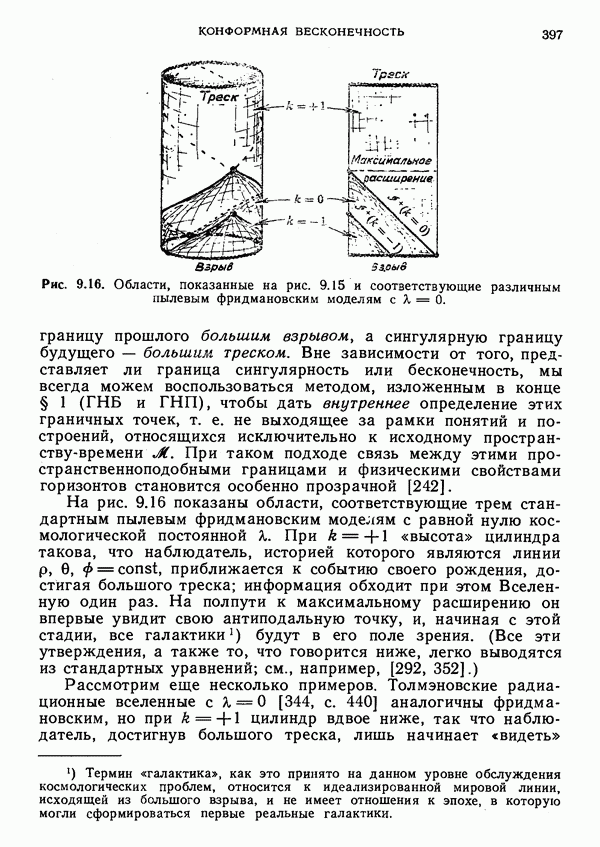
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература