| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Интерпретация величин; изопараметричность лучей
В отличие от  коэффициенты
коэффициенты  характеризуются определенными бустовыми весами, а именно при масштабном преобразовании (7.1.21) имеем
характеризуются определенными бустовыми весами, а именно при масштабном преобразовании (7.1.21) имеем

т. е. [формула (4.12.13) при  и а — величины типа
и а — величины типа  соответственно. Таким образом, их нельзя свести к нулю за счет масштабного преобразования и, как мы видели, они не зависят от выбора
соответственно. Таким образом, их нельзя свести к нулю за счет масштабного преобразования и, как мы видели, они не зависят от выбора  в случае геодезической конгруэнцни
в случае геодезической конгруэнцни  Исходя из определения этих величин, можно показать (см., например, [294]), что при
Исходя из определения этих величин, можно показать (см., например, [294]), что при 

Следовательно, можно утверждать (и мы это покажем), что условие равенства нулю коэффициента  или о связано с каким-то геометрическим свойством геодезической конгруэнции
или о связано с каким-то геометрическим свойством геодезической конгруэнции  . В случае негеодезической конгруэнции § любую из величин
. В случае негеодезической конгруэнции § любую из величин  , в можно свести к нулю за счет выбора спинора
, в можно свести к нулю за счет выбора спинора  , не изменяя масштаба. В самом деле, поскольку в этом случае
, не изменяя масштаба. В самом деле, поскольку в этом случае  , например, величина
, например, величина  не пропорциональна спинору
не пропорциональна спинору  достаточно выбрать
достаточно выбрать  чтобы коэффициент
чтобы коэффициент  обратился в нуль:
обратился в нуль:  Аналогично можно добиться того, чтобы были равны нулю коэффициенты а и е.
Аналогично можно добиться того, чтобы были равны нулю коэффициенты а и е.
Исследуем теперь взаимное расположение близких друг к другу линий конгруэнции  Для этого введем понятие вектора девиации
Для этого введем понятие вектора девиации  он направлен из точки Р луча
он направлен из точки Р луча  в точку Р соседнего луча
в точку Р соседнего луча  отвечающую тому же, что и Р, значению параметра
отвечающую тому же, что и Р, значению параметра  . (Векторы такого типа образуют векторное поле вдоль
. (Векторы такого типа образуют векторное поле вдоль
фиксированного луча  Математически это можно выразить как равенство нулю производной Ли вектора
Математически это можно выразить как равенство нулю производной Ли вектора  в направлении
в направлении  , поскольку векторы
, поскольку векторы  переносятся параллельно вдоль векторного поля
переносятся параллельно вдоль векторного поля  [формула (4.3.3)]:
[формула (4.3.3)]:

на  (При этом достаточно определить поле
(При этом достаточно определить поле  только на луче
только на луче  ). Кроме того, не обязательно считать, что поле
). Кроме того, не обязательно считать, что поле  образовано изотропными векторами, но мы примем это условие.) Можно очень просто доказать эту формулу, используя представление (7.1.3), (7.1.4) конгруэнции
образовано изотропными векторами, но мы примем это условие.) Можно очень просто доказать эту формулу, используя представление (7.1.3), (7.1.4) конгруэнции  , в котором
, в котором

Имеем очевидное равенство

Умножая обе его части на константу  и сворачивая по
и сворачивая по  получаем соотношение
получаем соотношение

которое эквивалентно второму равенству (7.1.29), так как в силу инвариантности операции (4.3.2) относительно выбора (симметричного) оператора связности V скобка Ли не изменяется при переходе от координатной производной к ковариантной.
Нас в первую очередь интересуют такие свойства конгруэнции  которые «не слишком сильно» зависят от выбора масштаба; фактически для нас важны «масштабно-ковариантные» величины, которые при изменении масштаба просто приобретают числовой множитель, например
которые «не слишком сильно» зависят от выбора масштаба; фактически для нас важны «масштабно-ковариантные» величины, которые при изменении масштаба просто приобретают числовой множитель, например  или
или  . В тензор
. В тензор  описывающий перенос векторного поля
описывающий перенос векторного поля  вдоль луча в соответствии с формулой (7.1.29), входят величины, преобразующиеся ковариантно, и другие величины, не обладающие таким свойством. Мы увидим, что можно отобрать только масштабно-ковариантные величины (или величины, им комплексно-сопряженные), которые, поскольку они обладают такими простыми трансформационными свойствами, принадлежат к модифицированному формализму спиновых коэффициентов, если ввести вектор
вдоль луча в соответствии с формулой (7.1.29), входят величины, преобразующиеся ковариантно, и другие величины, не обладающие таким свойством. Мы увидим, что можно отобрать только масштабно-ковариантные величины (или величины, им комплексно-сопряженные), которые, поскольку они обладают такими простыми трансформационными свойствами, принадлежат к модифицированному формализму спиновых коэффициентов, если ввести вектор

с масштабными свойствами

Этот же вектор можно получить из  следующим образом:
следующим образом:

а также записать в форме, в которой он лишь кажется зависящим от  :
:

Компоненты  тензора
тензора  являются масштабно-ковариантными, а величина
являются масштабно-ковариантными, а величина  —_нет. Величины первой группы могут быть выражены через
—_нет. Величины первой группы могут быть выражены через  Следовательно, скаляр
Следовательно, скаляр  будет масштабно-ковариантной частью тензора
будет масштабно-ковариантной частью тензора  если мы перемещаемся в направлении
если мы перемещаемся в направлении  Поскольку диадными компонентами вектора
Поскольку диадными компонентами вектора  будут как раз спиновые коэффициенты
будут как раз спиновые коэффициенты 

мы заключаем, что величины  грубо говоря, показывают, как изменяется направление вектора
грубо говоря, показывают, как изменяется направление вектора  при смещении вдоль
при смещении вдоль  соответственно. Однако вектор
соответственно. Однако вектор  является «более инвариантным» носителем этой информации, нежели набор спиновых коэффициентов, поскольку он не зависит от произвола в выборе спинора И.
является «более инвариантным» носителем этой информации, нежели набор спиновых коэффициентов, поскольку он не зависит от произвола в выборе спинора И.
Роль вектора 5а в уравнении переноса (7.1.29) можно выяснить, свернув это уравнение со спинором 

Более точная информация о геометрическом смысле коэффициентов  содержится в уравнении (7.1.36) неявно. Чтобы извлечь ее, удобно выбрать спиноры
содержится в уравнении (7.1.36) неявно. Чтобы извлечь ее, удобно выбрать спиноры  параллельными вдоль
параллельными вдоль  т. е. так, чтобы выполнялось равенство
т. е. так, чтобы выполнялось равенство  эквивалентное равенству
эквивалентное равенству  [формула (7.1.22)]. При таком выборе компоненты уравнения (7.1.36) записываются в виде
[формула (7.1.22)]. При таком выборе компоненты уравнения (7.1.36) записываются в виде

причем  ; входят в разложение вектора
; входят в разложение вектора  следующим образом:
следующим образом:

Уравнение переноса для  менее интересно с геометрической точки зрения, поскольку оно не является масштабно-ковариантной частью уравнения (7.1.29). Оно получается как результат свертки уравнения (7.1.29) с
менее интересно с геометрической точки зрения, поскольку оно не является масштабно-ковариантной частью уравнения (7.1.29). Оно получается как результат свертки уравнения (7.1.29) с  Для полноты напишем здесь соответствующий результат:
Для полноты напишем здесь соответствующий результат:

[формулы (4.5.21), (4.5.29)]. Напишем также закон преобразования величин  индуцированный общим допустимым преобразованием спинора
индуцированный общим допустимым преобразованием спинора  а именно преобразованием
а именно преобразованием 

Уравнения (7.1.37) и (7.1.38) допускают матричную форму записи, которая иногда оказывается полезной:

Как мы увидим, уравнение (7.1.38) позволяет дать ясную геометрическую интерпретацию величин  и а при условии, что
и а при условии, что  Правда, из соотношения (7.1.37) следует, что если
Правда, из соотношения (7.1.37) следует, что если  то величина
то величина  не может быть равна нулю вдоль всего луча
не может быть равна нулю вдоль всего луча  Но, как мы видели, коэффициенты
Но, как мы видели, коэффициенты  и о не зависят от
и о не зависят от  только при
только при  так что четкая интерпретация этих величин возможна лишь при этом условии. Однако это и есть наиболее интересный случай.
так что четкая интерпретация этих величин возможна лишь при этом условии. Однако это и есть наиболее интересный случай.
Рассмотрим теперь изотропную геодезическую конгруэнцию Ч? и предположим, что диада переносится параллельно вдоль каждого ее луча [4-е и 5-е соотношения (7.1.22)]

В этом случае уравнение (7.1.37) принимает вид

что эквивалентно уравнению

Будем называть два соседних луча изопараметрическими  если для них выполняется условие
если для них выполняется условие

т. е. h = 0. В том, что это свойство не зависит от выбора параметризации (очевидно, что оно также не зависит от выбора
спинора И), можно убедиться, выполнив подстановку

оставляющую условие (7.1.45) без изменения.
Если представить себе конгруэнцию наглядно в виде облака фотонов, то два изопараметрических луча будут соответствовать траекториям двух соседних фотонов, таких, которые в данный (а следовательно, во всякий) момент времени в локальном 3-пространстве наблюдателя лежат на 2-плоскости, перпендикулярной их траекториям (т. е. движутся «голова в голову» — abreast).
Более того, всякие два локальных наблюдателя увидят фотоны на одном и том же расстоянии друг от друга, если соответствующие лучи изопараметричны (и только при этом условии)  Действительно, если считать заданным лишь направление вектора
Действительно, если считать заданным лишь направление вектора  , а остальные векторы тетрады па, та, та выбирать произвольно по модулю требуемой нормировки, то всегда можно ввести тетраду Минковского наблюдателя, движущегося с произвольной скоростью. Его локальное 2-пространство натянуто на векторы та, та,
, а остальные векторы тетрады па, та, та выбирать произвольно по модулю требуемой нормировки, то всегда можно ввести тетраду Минковского наблюдателя, движущегося с произвольной скоростью. Его локальное 2-пространство натянуто на векторы та, та,  [формула (3.1.20), рис. 1.17]. Лучи в соответствующем 3-пространстве расположены в направлении
[формула (3.1.20), рис. 1.17]. Лучи в соответствующем 3-пространстве расположены в направлении  а векторы та, та лежат в ортогональной 2-плоскости. Путем репараметризации (7.1.46) можно добиться, чтобы выполнялось условие
а векторы та, та лежат в ортогональной 2-плоскости. Путем репараметризации (7.1.46) можно добиться, чтобы выполнялось условие  и тогда из (7.1.39) находим, что вектор девиации лежит в той же 2-плоскости, а его (инвариантная) длина
и тогда из (7.1.39) находим, что вектор девиации лежит в той же 2-плоскости, а его (инвариантная) длина  отвечает расстоянию между фотонами. Переход к новому наблюдателю отвечает выбору нового спинора
отвечает расстоянию между фотонами. Переход к новому наблюдателю отвечает выбору нового спинора  а в формуле (7.1.40) мы видели, что величина
а в формуле (7.1.40) мы видели, что величина  при этом не изменяется в том и только в том случае, если
при этом не изменяется в том и только в том случае, если  Этим и завершается доказательство нашего утверждения.
Этим и завершается доказательство нашего утверждения.
Отметим, что инвариантность расстояния между изопараметрическими фотонами, о которой говорилось выше, тесно связана с «ненаблюдаемостью лоренцевого сокращения»: все фотографии данного события, выполненные в параллельных лучах по-разному движущимися наблюдателями, выглядят одинаково (см. работы [334, 293], а также том 1, с. 44).
Напомним, что коэффициент  может служить мерой изменения вектора
может служить мерой изменения вектора  в направлении
в направлении  . Однако при исследовании свойств конгруэнции лучей данная величина оказывается не столь удобной, как
. Однако при исследовании свойств конгруэнции лучей данная величина оказывается не столь удобной, как  и
и  . Это объясняется главным образом тем, что она зависит от выбора И. Только в том случае, когда оба коэффициента
. Это объясняется главным образом тем, что она зависит от выбора И. Только в том случае, когда оба коэффициента  равны нулю, такая зависимость отсутствует. Это можно проиллюстрировать трансформационными свойствами коэффициента
равны нулю, такая зависимость отсутствует. Это можно проиллюстрировать трансформационными свойствами коэффициента  при замене
при замене  (полагая
(полагая 


Рис. 7.1. Два изопараметрических соседних луча. Мерой их относительного положения, изменяющегося во времени, служит вектор девиации  (координата на плоскости Арганда, если смотреть в направлении, противоположном направлению распространения луча).
(координата на плоскости Арганда, если смотреть в направлении, противоположном направлению распространения луча).
Как это следует из соотношения (7.1.38), в случае неизопараметрических лучей при  коэффициентом
коэффициентом  (умноженным на константу
(умноженным на константу  — «степень неизопараметричности») определяется перенос величины
— «степень неизопараметричности») определяется перенос величины 
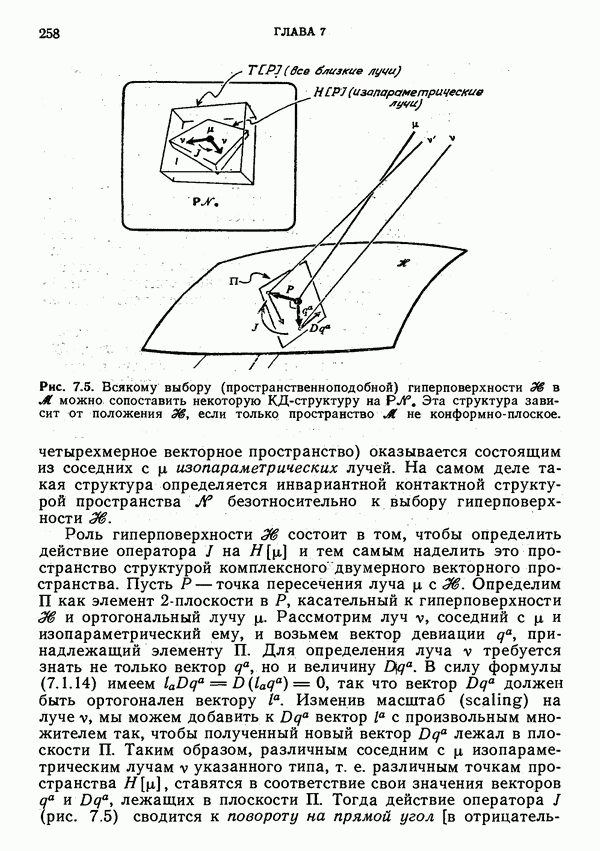
Нас будет в основном интересовать связь луча  с изопараметрическими ему соседними лучами. Мы будем рассматривать деформации пересечения пучка лучей с 2-плоскостью П, натянутой на векторы та и та, которая ортогональна лучу
с изопараметрическими ему соседними лучами. Мы будем рассматривать деформации пересечения пучка лучей с 2-плоскостью П, натянутой на векторы та и та, которая ортогональна лучу  и переносится вдоль него параллельно. Поскольку поперечные расстояния от
и переносится вдоль него параллельно. Поскольку поперечные расстояния от  до соседних лучей одинаковы для всех наблюдателей, сжатие, сдвиг и вращение указанного пересечения имеют прямой физический смысл.
до соседних лучей одинаковы для всех наблюдателей, сжатие, сдвиг и вращение указанного пересечения имеют прямой физический смысл.
Поскольку  условие изопараметричности (7.1.38) сводится к равенству
условие изопараметричности (7.1.38) сводится к равенству

Это уравнение описывает движение точки пересечения плоскости П с лучом  близким к
близким к  (которому отвечает значение
(которому отвечает значение  (рис. 7.1). Для более детальной интерпретации величин
(рис. 7.1). Для более детальной интерпретации величин  удобнее рассматривать раздельно роль величин
удобнее рассматривать раздельно роль величин  и
и  . Напишем
. Напишем

где  — действительные величины и
— действительные величины и  . Полагая
. Полагая  в (7.1.47), получаем
в (7.1.47), получаем


Рис. 7.2. Геометрическая интерпретация коэффициентов  и а как характеризующих деформацию пучка лучей в
и а как характеризующих деформацию пучка лучей в  -плоскости. Фотоны распространяются от читателя.
-плоскости. Фотоны распространяются от читателя.
откуда следует, что  есть мера сжатия однородного пучка лучей, т. е. конвергенция конгруэнции
есть мера сжатия однородного пучка лучей, т. е. конвергенция конгруэнции  Полагая
Полагая  находим соотношение
находим соотношение

которое показывает, что  есть мера вращения
есть мера вращения  Аналогично при
Аналогично при  имеем
имеем

так что производная  пропорциональна
пропорциональна  при
при  или
или  в первых двух случаях получаем сжатие по направлению к центру, а в двух других случаях — растяжение. Следовательно,
в первых двух случаях получаем сжатие по направлению к центру, а в двух других случаях — растяжение. Следовательно,  есть мера сдвига (дисторсии) пучка лучей, а величина
есть мера сдвига (дисторсии) пучка лучей, а величина  дает угол между направлением максимального сжатия и направлением полотнища флага спинора
дает угол между направлением максимального сжатия и направлением полотнища флага спинора  (рис. 7.2).
(рис. 7.2).
Рассматривая изменение вдоль площади

малого треугольника с вершинами в точках  на П, мы находим, используя (7.1.47), что всякий элемент площади
на П, мы находим, используя (7.1.47), что всякий элемент площади  удовлетворяет уравнению переноса
удовлетворяет уравнению переноса

Отсюда видно, что величина  может служить мерой конвергенции, а также, что деформации, связанные с
может служить мерой конвергенции, а также, что деформации, связанные с  и а, не изменяют площадь.
и а, не изменяют площадь.
Иногда удобно пользоваться «яркостным параметром»  для конгруэнции лучей, определяемым так, что
для конгруэнции лучей, определяемым так, что  Из соотношения (7.1.50) немедленно следует, что
Из соотношения (7.1.50) немедленно следует, что

Сравнение с (7.1.47) показывает, что в отсутствие дисторсии (и только в этом случае)

так что  изменяется пропорционально длине вектора девиации, соединяющего изопараметрические лучи.
изменяется пропорционально длине вектора девиации, соединяющего изопараметрические лучи.
Отметим и другую формулу для  справедливую при
справедливую при 

где использовано соотношение, вытекающее из формул (2.5.54),

Аналогично в случае  находим
находим

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
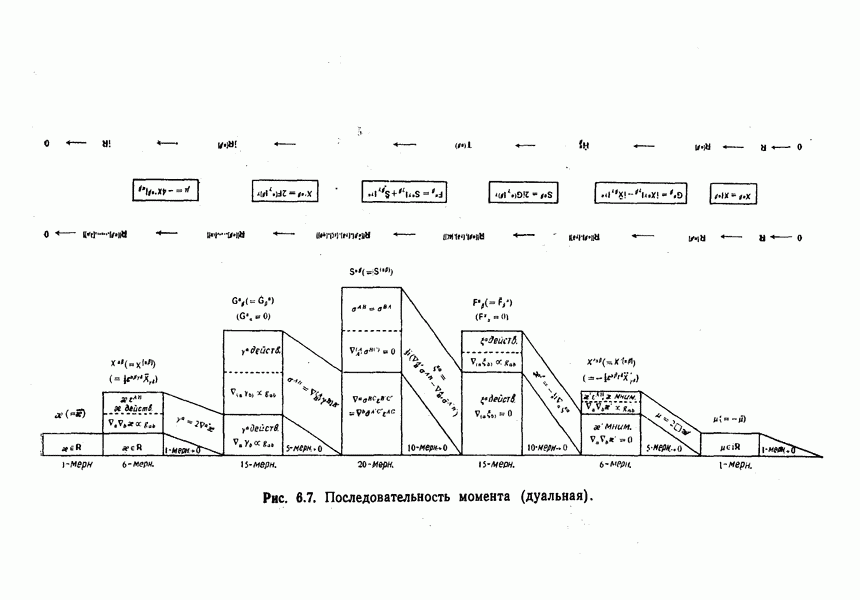
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
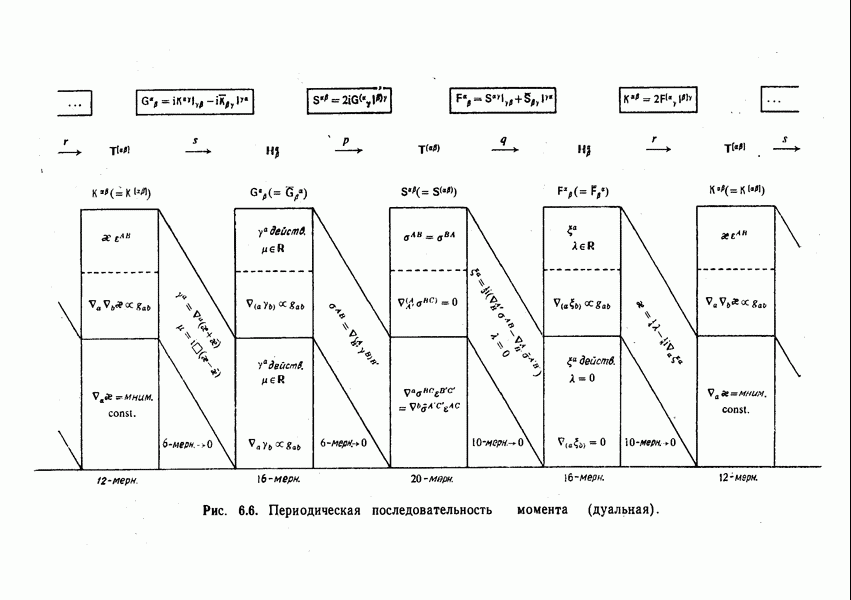
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
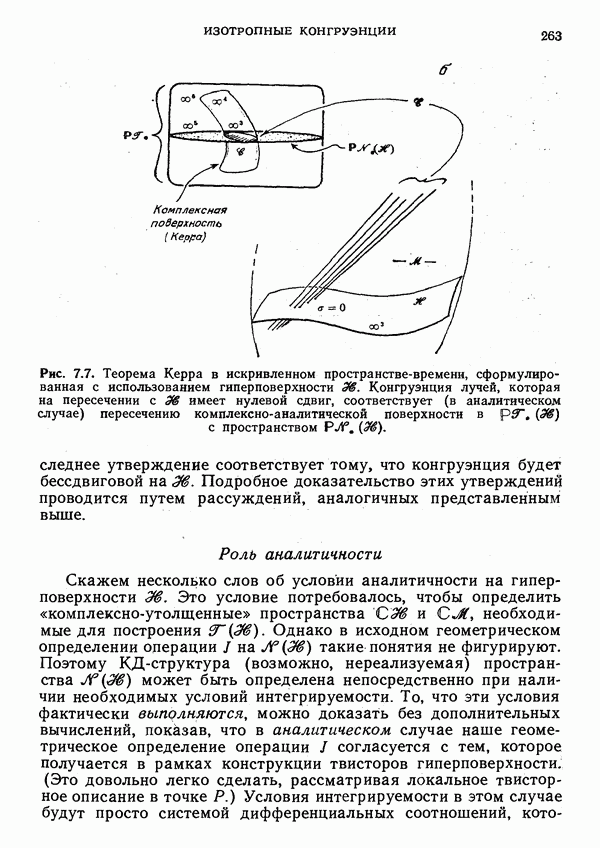
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
- 8. Классификация тензоров кривизны
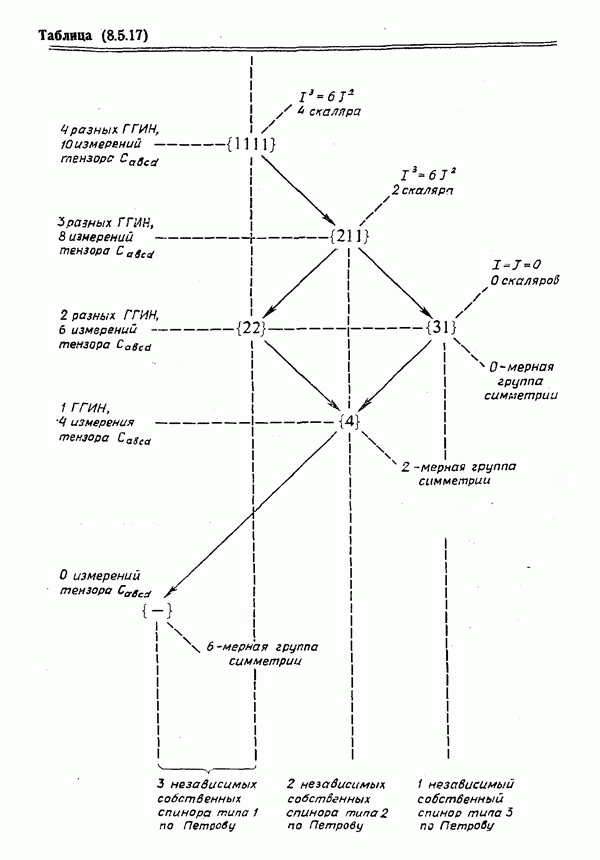
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
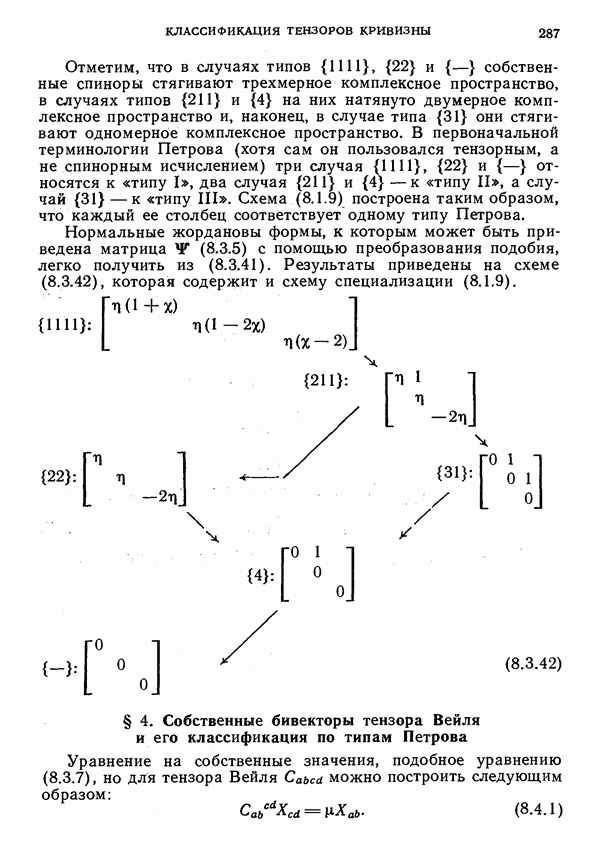
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
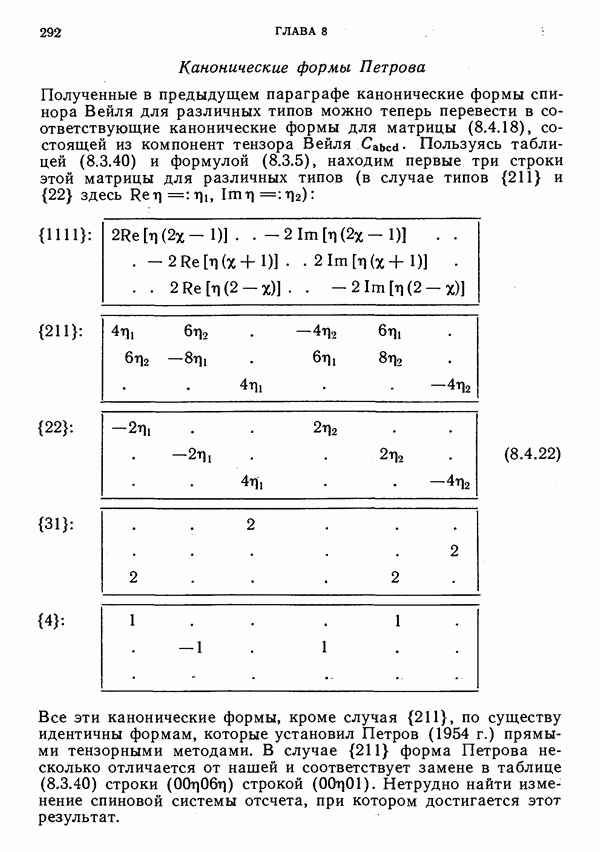
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
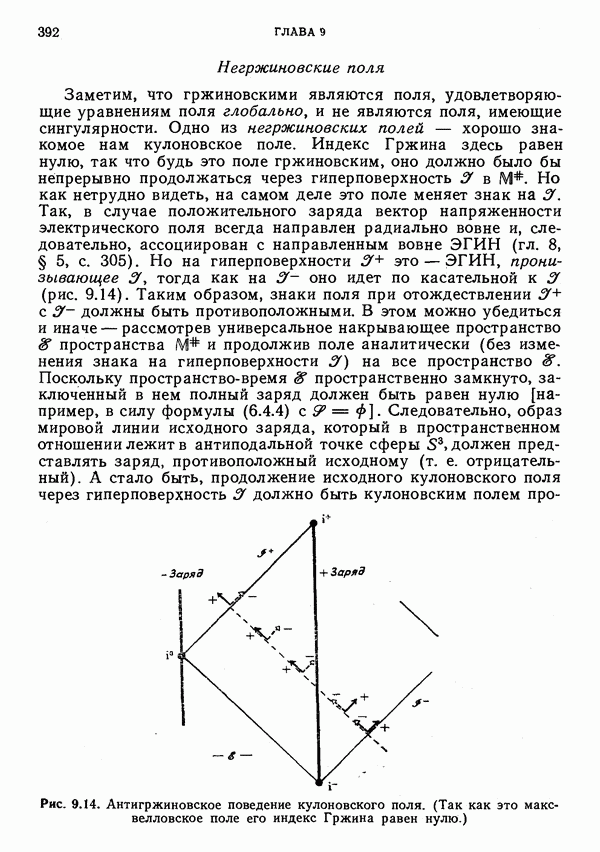
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература