| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.3. Векторное квантование
В предыдущих разделах мы рассмотрели квантование выходного сигнала непрерывного источника для случая, когда квантование выполняется последовательно по отдельным отсчётам, т.е. скалярное квантование. В этом разделе мы рассмотрим совместное квантование блока символьных отсчётов или блока сигнальных параметров. Этот вид квантования называется блоковым или векторным квантованием. Оно широко используется при кодировании речи в цифровых сотовых системах связи.
Фундаментальный результат теории искажения заключается в том, что лучшую характеристику можно достичь векторным, а не скалярным квантованием, даже если непрерывный источник без памяти. Если, кроме того, отсчёты сигнала или параметры сигнала статистически зависимы, мы можем использовать зависимость посредством совместного квантования блоков отсчётов или параметров и таким образом достичь большей эффективности (более низкой битовой скорости) по сравнению с той, которая достигается скалярным квантованием.
Проблему
векторного квантования можно сформулировать так. Имеем ![]() -мерный вектор
-мерный вектор ![]() с
с ![]() вещественными,
непрерывными амплитудами компонент
вещественными,
непрерывными амплитудами компонент ![]() , которые описываются СФПВ
, которые описываются СФПВ ![]() . Путём квантования
вектор
. Путём квантования
вектор ![]() превращается
в другой
превращается
в другой ![]() -мерный
вектор
-мерный
вектор ![]() с
компонентами
с
компонентами ![]() .
Выразим операции квантования оператором
.
Выразим операции квантования оператором ![]() , так что
, так что
![]() , (3.4.31)
, (3.4.31)
где
![]() - выход
квантователя, когда на вход поступает вектор
- выход
квантователя, когда на вход поступает вектор ![]() .
.
В
принципе векторное квантование блоков данных можно рассматривать как проблему
распознавания образов, включающую в себя классификацию блоков данных через
дискретное количество категорий или ячеек в соответствии с некоторым критерием
точности, таким, например, как среднеквадратическая погрешность. Для примера
рассмотрим квантование двумерных векторов ![]() . Двумерное пространство разделяют на
ячейки, как показано на рис. 3.4.3, где мы имеем произвольно выбранные
шестиугольные ячейки
. Двумерное пространство разделяют на
ячейки, как показано на рис. 3.4.3, где мы имеем произвольно выбранные
шестиугольные ячейки ![]() . Все входные векторы, которые попадают
в ячейку
. Все входные векторы, которые попадают
в ячейку ![]() ,
квантуются в вектор
,
квантуются в вектор ![]() , который на рис. 3.4.3 отмечен как
центр шестиугольника. В нашем примере иллюстрируются
, который на рис. 3.4.3 отмечен как
центр шестиугольника. В нашем примере иллюстрируются ![]() векторов, один для каждой из
37 ячеек, на которые разбито двумерное пространство. Обозначим ряд возможных
выходных векторов как
векторов, один для каждой из
37 ячеек, на которые разбито двумерное пространство. Обозначим ряд возможных
выходных векторов как ![]() .
.

Рис. 3.4.3. Пример квантания в двухмерном пространстве
В
общем, квантование ![]() -мерного вектора
-мерного вектора ![]() в
в ![]() -мерный вектор
-мерный вектор ![]() ведёт к ошибке
квантования или искажению
ведёт к ошибке
квантования или искажению ![]() . Среднее искажение по ряду входных
векторов
. Среднее искажение по ряду входных
векторов ![]() равно
равно
![]() , (3.4.32)
, (3.4.32)
где
![]() -
вероятность того, что вектор
-
вероятность того, что вектор ![]() попадёт в ячейку
попадёт в ячейку ![]() , а
, а ![]() - СФПВ
- СФПВ ![]() случайных величин. Как и в
случае скалярного квантования, мы можем минимизировать
случайных величин. Как и в
случае скалярного квантования, мы можем минимизировать ![]() путём выбора ячеек
путём выбора ячеек ![]() при заданной ФПВ
при заданной ФПВ ![]() . Обычно
используемая мера искажений - среднеквадратическая ошибка (
. Обычно
используемая мера искажений - среднеквадратическая ошибка (![]() - норма) определяется как
- норма) определяется как
![]() (3.4.33)
(3.4.33)
или, в более общем виде, взвешенная среднеквадратическая ошибка
![]() , (3.4.34)
, (3.4.34)
где
![]() -
положительно определённая взвешивающая матрица. Обычно мера
-
положительно определённая взвешивающая матрица. Обычно мера ![]() выбирается как обратная по
отношению к матрице ковариаций входных данных
выбирается как обратная по
отношению к матрице ковариаций входных данных ![]() .
.
Другая
мера искажений, которая иногда используется, является частным случаем ![]() нормы и
определяется как
нормы и
определяется как
![]() . (3.4.35)
. (3.4.35)
Частный
случай, когда ![]() ,
часто используется как альтернатива случаю
,
часто используется как альтернатива случаю ![]() .
.
Векторное
квантование не ограничивается квантованием блока сигнальных отсчётов источника
сигнала. Его можно использовать для квантования ряда параметров, извлечённых из
данных. Например, при линейном кодировании с предсказанием (ЛКП), описанном в
разделе 3.5.3, параметры, извлечённые из сигнала, являются коэффициентами
предсказания, которые являются коэффициентами для всеполюсной фильтровой модели
источника, который генерирует наблюдаемые данные. Эти параметры можно
рассматривать как блок и квантовать как блок символов, используя некоторую
подходящую меру искажений. В случае кодирования речи подходящей мерой
искажений, которую предложили Итакура и Саити (1986, 1975), является взвешенная
среднеквадратическая ошибка, где взвешивающая матрица ![]() выбрана как нормированная
матрица автоковариации
выбрана как нормированная
матрица автоковариации ![]() наблюдаемых данных.
наблюдаемых данных.
При
кодировании речи альтернативным рядом параметров, которые могут быть квантованы
как блок и переданы к приёмнику, могут быть коэффициенты отражения (см. ниже) ![]() .
.
Еще
один ряд параметров, которые иногда используются для векторного квантования при
линейном кодировании с предсказанием речи, содержит логарифмические отношения ![]() , которые выражаются
через коэффициенты отражения
, которые выражаются
через коэффициенты отражения
![]() ,
, ![]() . (3.4.36)
. (3.4.36)
Теперь
вернемся к математической формулировке векторного квантования и рассмотрим
разбиение ![]() -мерного
пространства на
-мерного
пространства на ![]() ячеек
ячеек
![]() с точки
зрения минимизации среднего искажения по всем
с точки
зрения минимизации среднего искажения по всем ![]() -уровневым квантователям. Имеется два
условия для минимизации. Первое заключается в том, что оптимальный квантователь
использует селекцию по правилу ближайшего соседа, которое можно выразить
математически как
-уровневым квантователям. Имеется два
условия для минимизации. Первое заключается в том, что оптимальный квантователь
использует селекцию по правилу ближайшего соседа, которое можно выразить
математически как
![]() ,
,
если, и только если
![]() ,
, ![]() ,
, ![]() . (3.4.37)
. (3.4.37)
Второе
условие, необходимое для оптимизации, заключается в том, что каждый выходной
вектор ![]() выбирается
так, чтобы минимизировать среднее искажение в ячейке
выбирается
так, чтобы минимизировать среднее искажение в ячейке ![]() . Другими словами,
. Другими словами, ![]() - это вектор в
- это вектор в ![]() , который
минимизирует
, который
минимизирует
![]() . (3.4.38)
. (3.4.38)
Вектор
![]() , который
минимизирует
, который
минимизирует ![]() ,
назван центроидом ячейки.
,
назван центроидом ячейки.
Таким
образом, эти условия оптимизации определяют разбиение ![]() -мерного пространства на ячейки
-мерного пространства на ячейки ![]() , когда СФПВ
, когда СФПВ ![]() известна. Ясно, что указанные два условия обобщают задачу оптимального
квантования скалярной величины оптимизации на случай квантования
известна. Ясно, что указанные два условия обобщают задачу оптимального
квантования скалярной величины оптимизации на случай квантования ![]() -мерного вектора. В общем, мы ожидаем, что кодовые векторы более тесно
группируются в областях, где СФПВ
-мерного вектора. В общем, мы ожидаем, что кодовые векторы более тесно
группируются в областях, где СФПВ ![]() велика, и, наоборот, разрежены в областях, где
велика, и, наоборот, разрежены в областях, где ![]() мала.
мала.
В качестве верхней границы искажений векторного
квантования мы можем использовать величину искажений оптимального скалярного
квантователя, и эту границу можно применить для каждой компоненты вектора, как
было описано в предыдущем разделе. С другой стороны, наилучшие характеристики,
которые могут быть достигнуты оптимальным векторным квантователем, определяются
функцией скорость-искажение или, что эквивалентно, функцией искажение-скорость.
Функция искажение-скорость, которая была введена в предыдущем разделе, может
быть определена в контексте векторного квантования следующим образом.
Предположим, мы формируем вектор ![]() размерности
размерности ![]() из
из ![]() последовательных отсчётов
последовательных отсчётов ![]() . Вектор
. Вектор ![]() квантуется в форму
квантуется в форму ![]() , где
, где ![]() - образованный
рядом
- образованный
рядом ![]() .
Как было описано выше, среднее искажение
.
Как было описано выше, среднее искажение ![]() , получаемое при представлении
, получаемое при представлении ![]() через
через ![]() , равно
, равно ![]() , где
, где ![]() - это искажение на
одно измерение. Например,
- это искажение на
одно измерение. Например,
![]() .
.
Минимально достижимая средняя битовая скорость, с
которой могут быть переданы векторы ![]() , равна
, равна
![]() бит/отсчет, (3.4.39)
бит/отсчет, (3.4.39)
где ![]() - энтропия квантованного выхода
источника, определяемая как
- энтропия квантованного выхода
источника, определяемая как
![]() . (3.4.40)
. (3.4.40)
Для данной средней скорости ![]() минимально достижимое
искажение
минимально достижимое
искажение
![]() , (3.4.41)
, (3.4.41)
где ![]() и минимум в (3.4.41) берётся по всем
возможным отображениям
и минимум в (3.4.41) берётся по всем
возможным отображениям ![]() . В пределе, когда размерность
. В пределе, когда размерность ![]() стремится к
бесконечности, получаем
стремится к
бесконечности, получаем
![]() , (3.4.42)
, (3.4.42)
где ![]() - это функция искажение-скорость,
которая была введена в предыдущем разделе. Из этого изложения очевидно, что
функция искажение-скорость может быть как угодно приближена к пределу путём
увеличения размерности
- это функция искажение-скорость,
которая была введена в предыдущем разделе. Из этого изложения очевидно, что
функция искажение-скорость может быть как угодно приближена к пределу путём
увеличения размерности ![]() векторов.
векторов.
Изложенный выше подход приемлем в предположении, что
СФПВ ![]() вектора
данных известна. Однако на практике СФПВ
вектора
данных известна. Однако на практике СФПВ ![]() данных может быть неизвестна. В этом
случае, возможно адаптивно выбрать квантованные выходные векторы с
использованием ряда обучающих векторов
данных может быть неизвестна. В этом
случае, возможно адаптивно выбрать квантованные выходные векторы с
использованием ряда обучающих векторов ![]() . Конкретнее, предположим, что мы имеем
ряд из
. Конкретнее, предположим, что мы имеем
ряд из ![]() векторов, причём
векторов, причём ![]() намного больше, чем
намного больше, чем ![]()
![]() . Итеративный групповой
алгоритм, названный алгоритмом
. Итеративный групповой
алгоритм, названный алгоритмом ![]() средних, где в нашем случае
средних, где в нашем случае
![]() , может
быть применён к обучающим векторам. Этот алгоритм итеративно делит
, может
быть применён к обучающим векторам. Этот алгоритм итеративно делит ![]() обучающих векторов
на
обучающих векторов
на ![]() групп
так, что два необходимых условия оптимальности выполняются. Алгоритм
групп
так, что два необходимых условия оптимальности выполняются. Алгоритм ![]() средних может быть
описан так, как дано ниже [Макхоул и др. (1985)].
средних может быть
описан так, как дано ниже [Макхоул и др. (1985)].
Алгоритм K средних
Шаг 1.
Инициализируется начальный номер итерации ![]() . Выбирается ряд выходных векторов
. Выбирается ряд выходных векторов ![]() ,
, ![]() .
.
Шаг 2.
Обучающие векторы ![]() классифицируются в группы
классифицируются в группы ![]() посредством правила
ближайшего соседа:
посредством правила
ближайшего соседа:
![]() если
если
![]() для всех
для всех
![]() .
.
Шаг 3.
Пересчитываются (для ![]() -го шага) выходные векторы каждой
группы путём вычисления центроида
-го шага) выходные векторы каждой
группы путём вычисления центроида
![]() ,
, ![]() ,
,
для обучающих векторов, которые попадают в каждую группу.
Кроме того, рассчитывается результирующее искажение ![]() на
на ![]() -й итерации.
-й итерации.
Шаг 4.
Заканчивается тестирование, если ![]() относительно мало. В противном случае
следует идти к шагу 2.
относительно мало. В противном случае
следует идти к шагу 2.
Алгоритм ![]() средних приводит к локальному минимуму
(см. Андерберг, 1973; Линде и др., 1980). Начиная этот алгоритм различными
рядами начальных выходных векторов
средних приводит к локальному минимуму
(см. Андерберг, 1973; Линде и др., 1980). Начиная этот алгоритм различными
рядами начальных выходных векторов ![]() и каждый раз выполняя оптимизацию,
описанную алгоритмом
и каждый раз выполняя оптимизацию,
описанную алгоритмом ![]() средних, можно найти глобальный
оптимум. Однако вычислительные затраты этой поисковой процедуры могут
ограничить поиск немногими инициализациями.
средних, можно найти глобальный
оптимум. Однако вычислительные затраты этой поисковой процедуры могут
ограничить поиск немногими инициализациями.
Если мы один раз выбрали выходные векторы ![]() , каждый сигнальный
вектор
, каждый сигнальный
вектор ![]() квантуется
в выходной вектор, который является ближайшим к нему с точки зрения выбранной
меры искажения. Если вычисление включает в себя оценку расстояния между
квантуется
в выходной вектор, который является ближайшим к нему с точки зрения выбранной
меры искажения. Если вычисление включает в себя оценку расстояния между ![]() и каждым из
и каждым из ![]() возможных выходных
векторов
возможных выходных
векторов ![]() ,
процедура образует полный поиск. Если предположим, что
каждое вычисление требует
,
процедура образует полный поиск. Если предположим, что
каждое вычисление требует ![]() умножений и сложений, то общее
требуемое число вычислений для полного поиска равно
умножений и сложений, то общее
требуемое число вычислений для полного поиска равно
![]() (3.4.43)
(3.4.43)
умножений и сложений на входной вектор.
Если мы выбрали ![]() как степень 2, то
как степень 2, то ![]() определяет число бит,
требуемых для представления каждого вектора. Теперь, если
определяет число бит,
требуемых для представления каждого вектора. Теперь, если ![]() обозначает битовую скорость
на отсчёт [на компоненту или на измерение
обозначает битовую скорость
на отсчёт [на компоненту или на измерение ![]() ], имеем
], имеем ![]() и, следовательно, вычислительные
затраты
и, следовательно, вычислительные
затраты
![]() . (3.4.44)
. (3.4.44)
Заметим, что число вычислений растёт экспоненциально с
параметром размерности п и битовой скорости ![]() на измерение. Вследствие этого
экспоненциального роста вычислительных затрат векторное квантование применяется
в низкобитовых кодерах источника, таких как кодирование коэффициентов отражения
или логарифмических отношений в линейном кодировании речи с предсказанием.
на измерение. Вследствие этого
экспоненциального роста вычислительных затрат векторное квантование применяется
в низкобитовых кодерах источника, таких как кодирование коэффициентов отражения
или логарифмических отношений в линейном кодировании речи с предсказанием.
Вычислительные затраты, связанные с полным поиском, можно уменьшить при помощи изящного субоптимального алгоритма (см. Чанг и др., 1984; Гершо, 1982).
Чтобы продемонстрировать пользу векторного квантования по сравнению со скалярным квантованием, мы представим следующий пример, взятый у Макхоула и др. (1985).
Пример 3.4.1. Пусть ![]() и
и
![]() являются
двумя случайными величинами с равномерной СФПВ:
являются
двумя случайными величинами с равномерной СФПВ:
 (3.4.45)
(3.4.45)
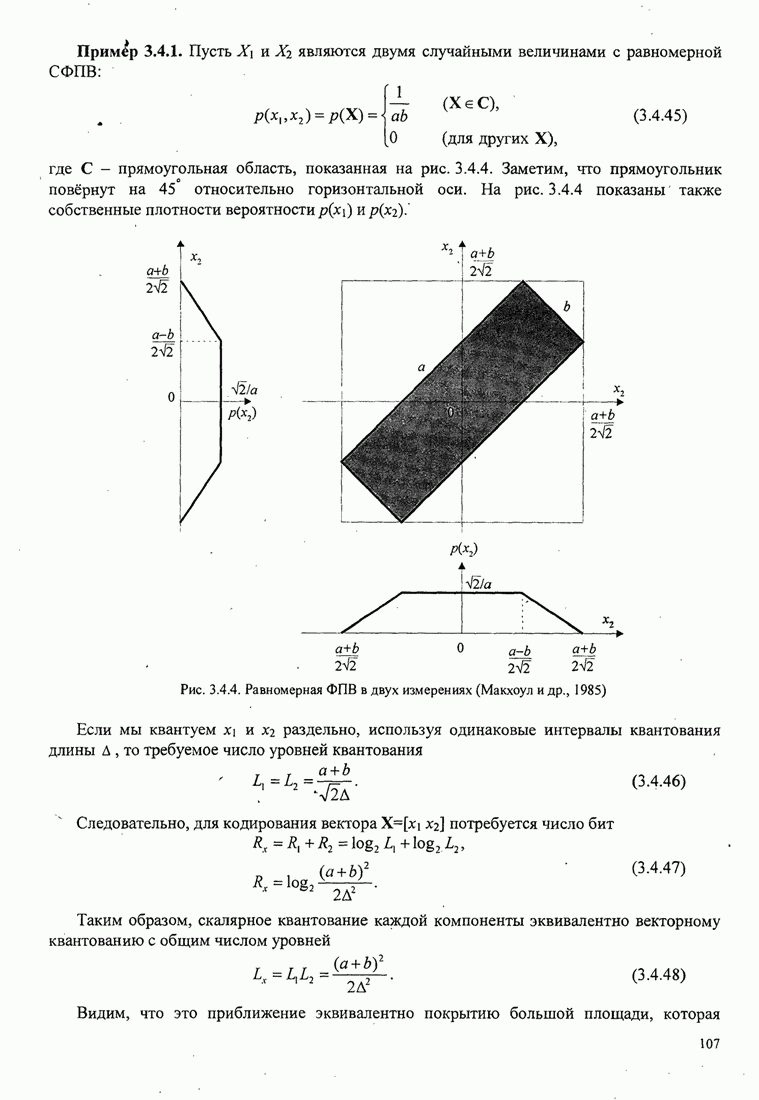
где ![]() - прямоугольная
область, показанная на рис. 3.4.4. Заметим, что прямоугольник повёрнут на 45º
относительно горизонтальной оси. На рис. 3.4.4 показаны также собственные
плотности вероятности
- прямоугольная
область, показанная на рис. 3.4.4. Заметим, что прямоугольник повёрнут на 45º
относительно горизонтальной оси. На рис. 3.4.4 показаны также собственные
плотности вероятности ![]() и
и ![]() .
.

Рис. 3.4.4. Равномерная ФПВ в двух измерениях (Макхоул и др., 1985)
Если
мы квантуем ![]() и
и
![]() раздельно,
используя одинаковые интервалы квантования длины
раздельно,
используя одинаковые интервалы квантования длины ![]() , то требуемое число уровней
квантования
, то требуемое число уровней
квантования
![]() . (3.4.46)
. (3.4.46)
Следовательно,
для кодирования вектора ![]() потребуется число бит
потребуется число бит
![]() ,
,
![]() . (3.4.47)
. (3.4.47)
Таким образом, скалярное квантование каждой компоненты эквивалентно векторному квантованию с общим числом уровней
![]() . (3.4.48)
. (3.4.48)
Видим,
что это приближение эквивалентно покрытию большой площади, которая охватывает прямоугольник посредством квадратных ячеек, причём каждая
ячейка представляет одну из ![]() областей квантования. Поскольку
областей квантования. Поскольку ![]() , за исключением
, за исключением ![]() , такое кодирование
является расточительным и приводит к увеличению битовой скорости.
, такое кодирование
является расточительным и приводит к увеличению битовой скорости.
Если же мы покроем только область, где ![]() , квадратиками,
имеющими площадь
, квадратиками,
имеющими площадь ![]() ,
то общее число уровней, которые образуются, определяется площадью
прямоугольника, делённой на
,
то общее число уровней, которые образуются, определяется площадью
прямоугольника, делённой на ![]() , т.е.
, т.е.
![]() . (3.4.49)
. (3.4.49)
Следовательно, разница в битовой скорости при скалярном и векторном методах квантования равна
![]() . (3.4.50)
. (3.4.50)
Для случая, когда ![]() , разница в битовой скорости
, разница в битовой скорости
![]() бит/вектор.
бит/вектор.
Следовательно, векторное квантование на 0,82 бит/отсчёт лучше, чем скалярное, при тех же искажениях.
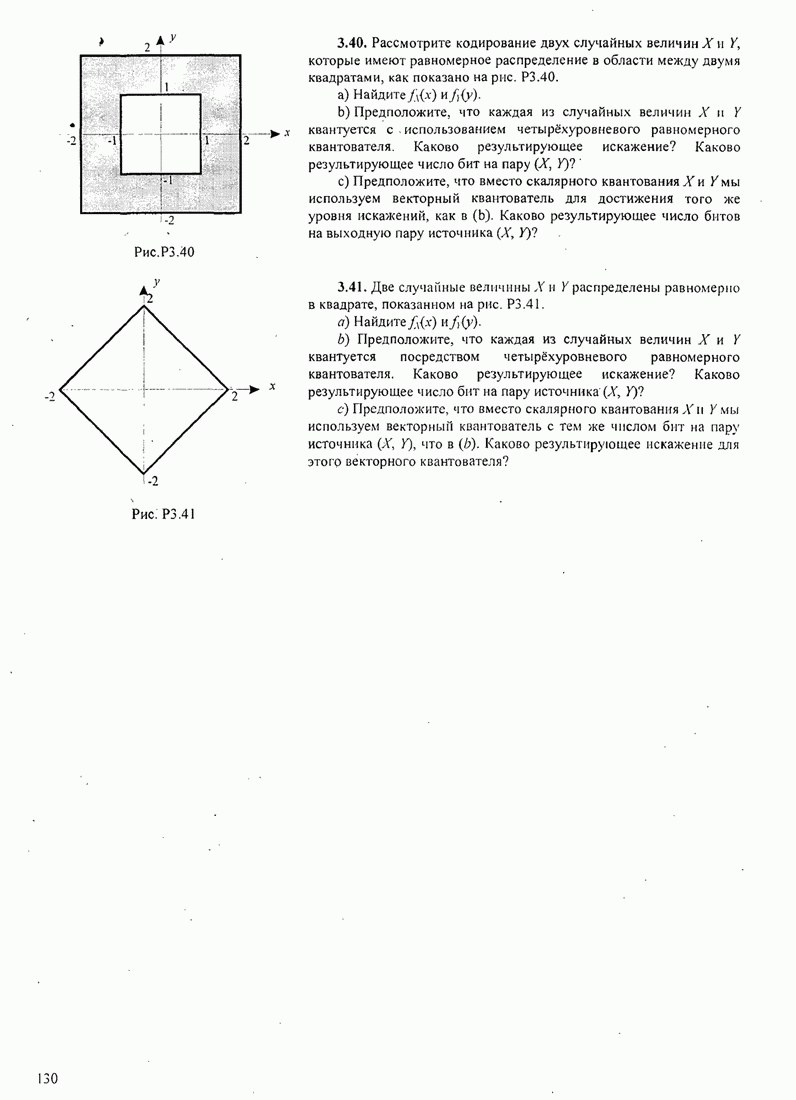
Интересно заметить, что линейное преобразование
(поворот на 45º) декоррелирует ![]() и
и ![]() и делает две случайные величины
статистически независимыми. Тогда скалярное квантование и векторное квантование
достигают одинаковой эффективности. Хотя линейное преобразование может
декоррелировать вектор случайных величин, оно не приводит к статистически
независимым случайным величинам в общем случае. Следовательно,
Векторное квантование будет всегда равняться или превосходить по
характеристикам скалярный квантователь (см. задачу 3.40).
и делает две случайные величины
статистически независимыми. Тогда скалярное квантование и векторное квантование
достигают одинаковой эффективности. Хотя линейное преобразование может
декоррелировать вектор случайных величин, оно не приводит к статистически
независимым случайным величинам в общем случае. Следовательно,
Векторное квантование будет всегда равняться или превосходить по
характеристикам скалярный квантователь (см. задачу 3.40).
Векторное квантование применяется при различных
методах кодирования речи, включая сигнальные методы и методы базовых моделей,
которые рассматриваются в разд. 3.5. В методах, основанных на базовых моделях,
таких как линейное кодирование с предсказанием, векторное квантование делает
возможным кодирование речи на скоростях ниже 1000 бит/с (см. Бузо и др., 1980;
Роукос и др., 1982; Пауль, 1983). Если использовать методы кодирования
сигналов, возможно получить хорошее качество речи на скоростях передачи 16 000
бит/с, что эквивалентно скорости кодирования ![]() бит/отсчёт. За счёт дополнительных
вычислительных усложнений в будущем станет возможным использовать сигнальные
кодеры, обеспечивающие хорошее качество речи при скорости кодирования
бит/отсчёт. За счёт дополнительных
вычислительных усложнений в будущем станет возможным использовать сигнальные
кодеры, обеспечивающие хорошее качество речи при скорости кодирования ![]() бит/отсчёт.
бит/отсчёт.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
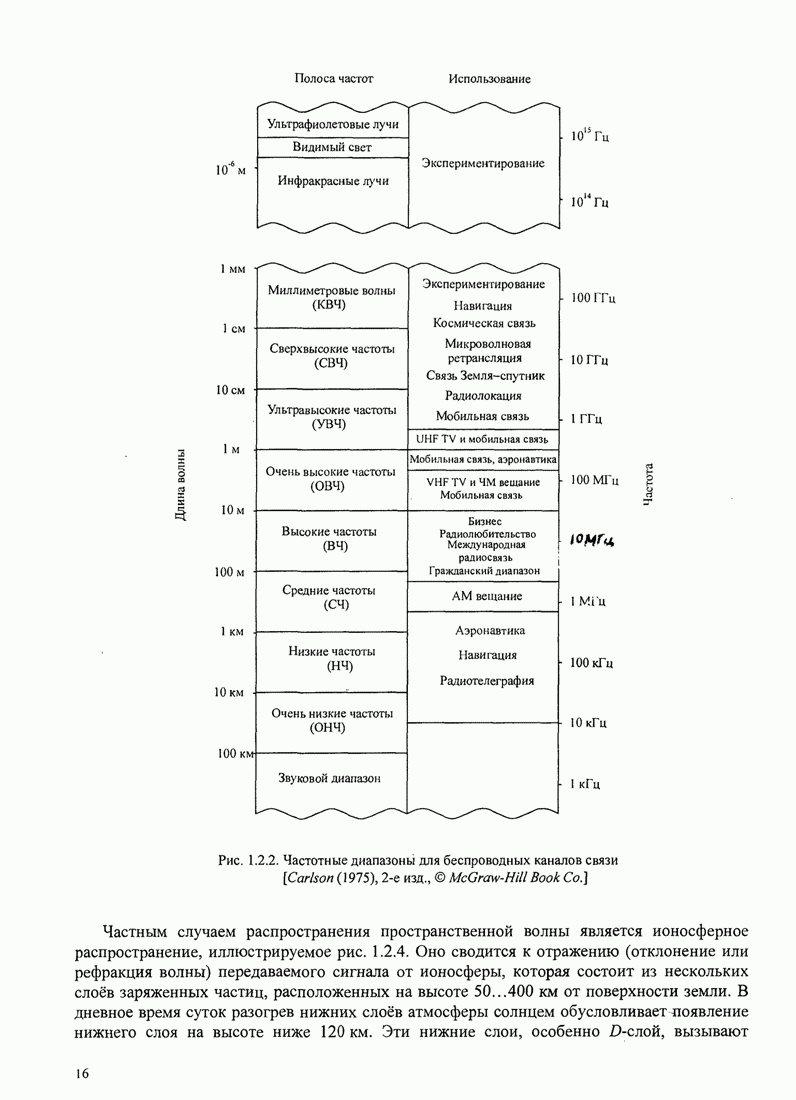
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
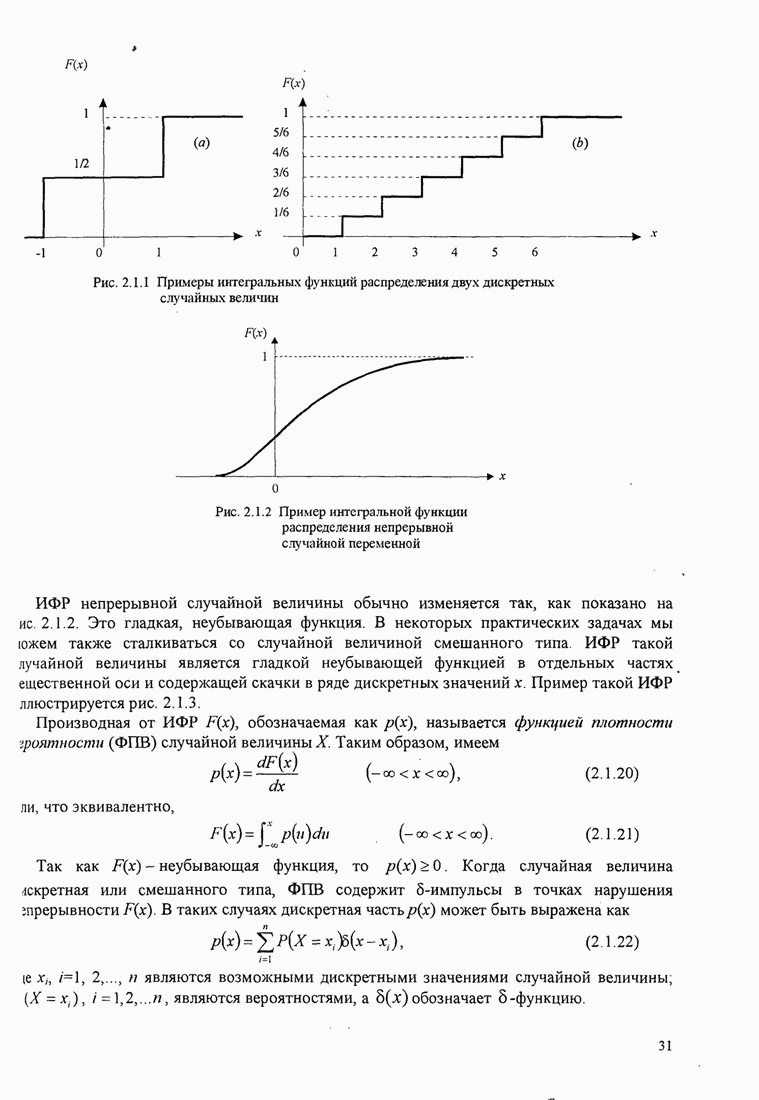
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
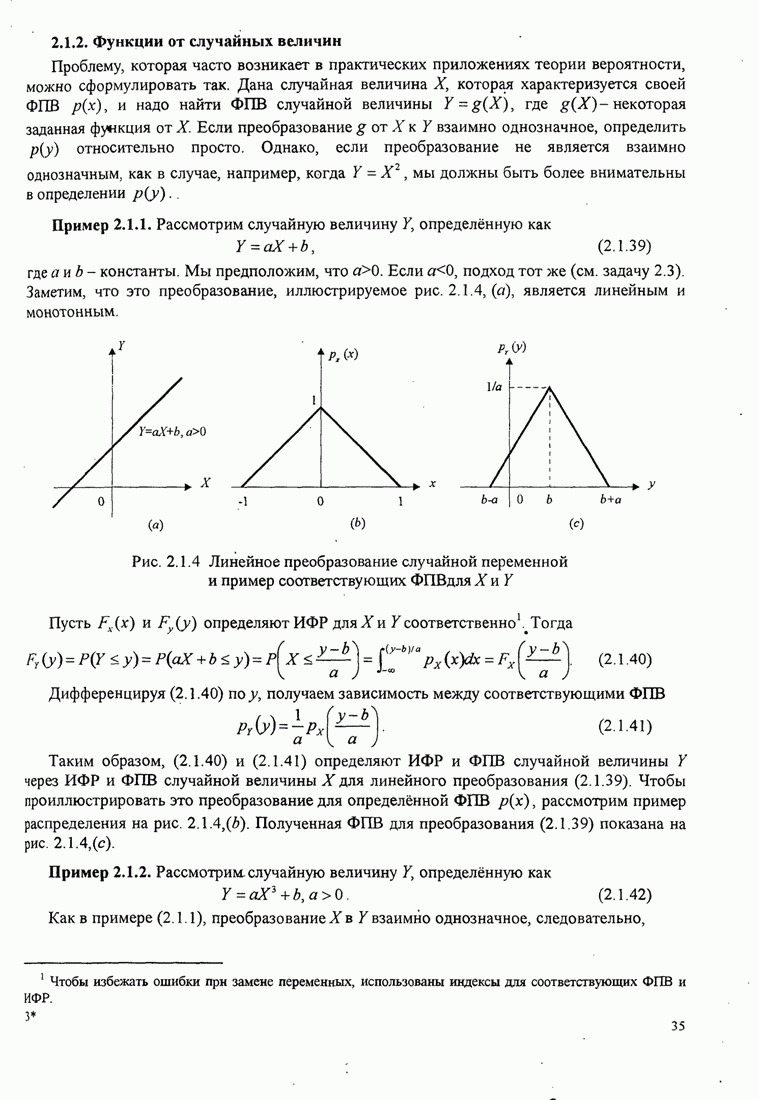
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
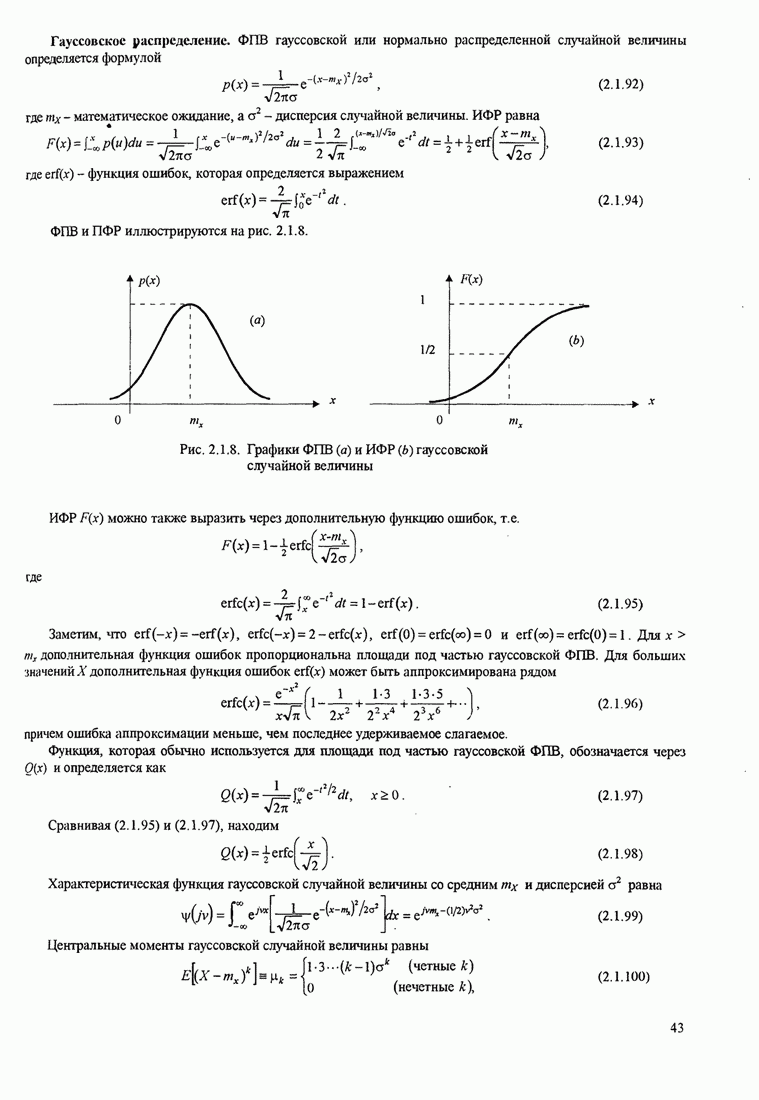
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
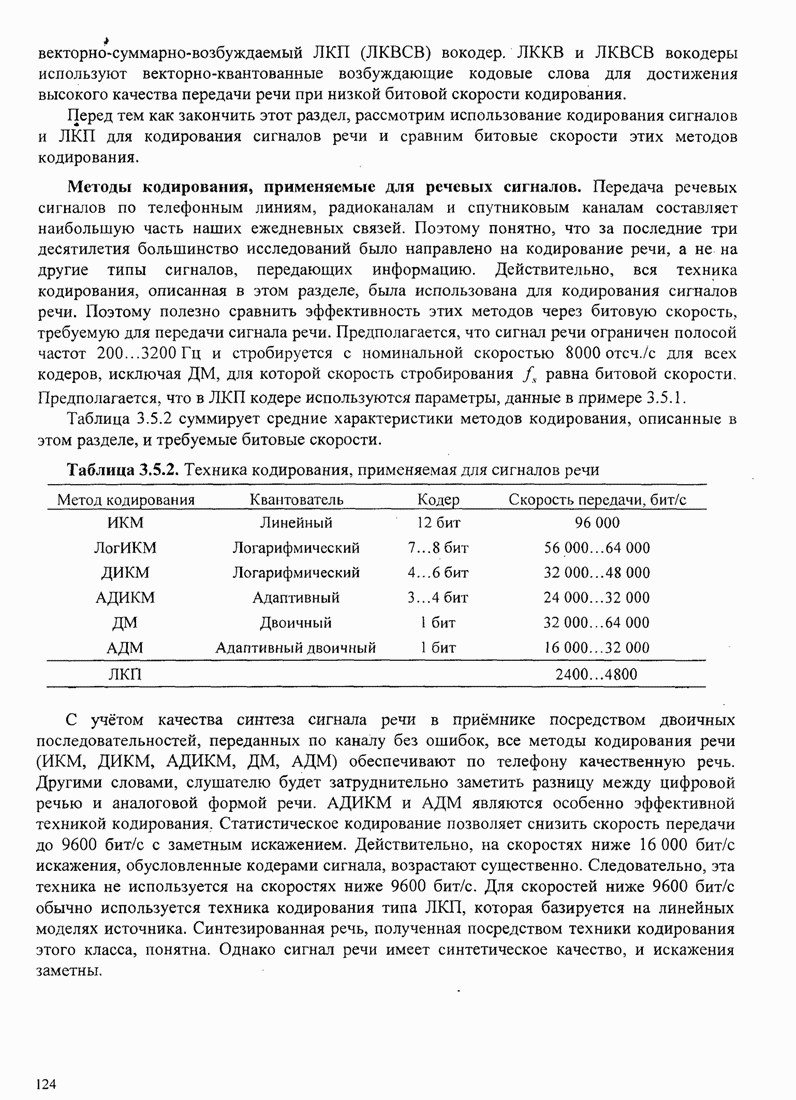
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
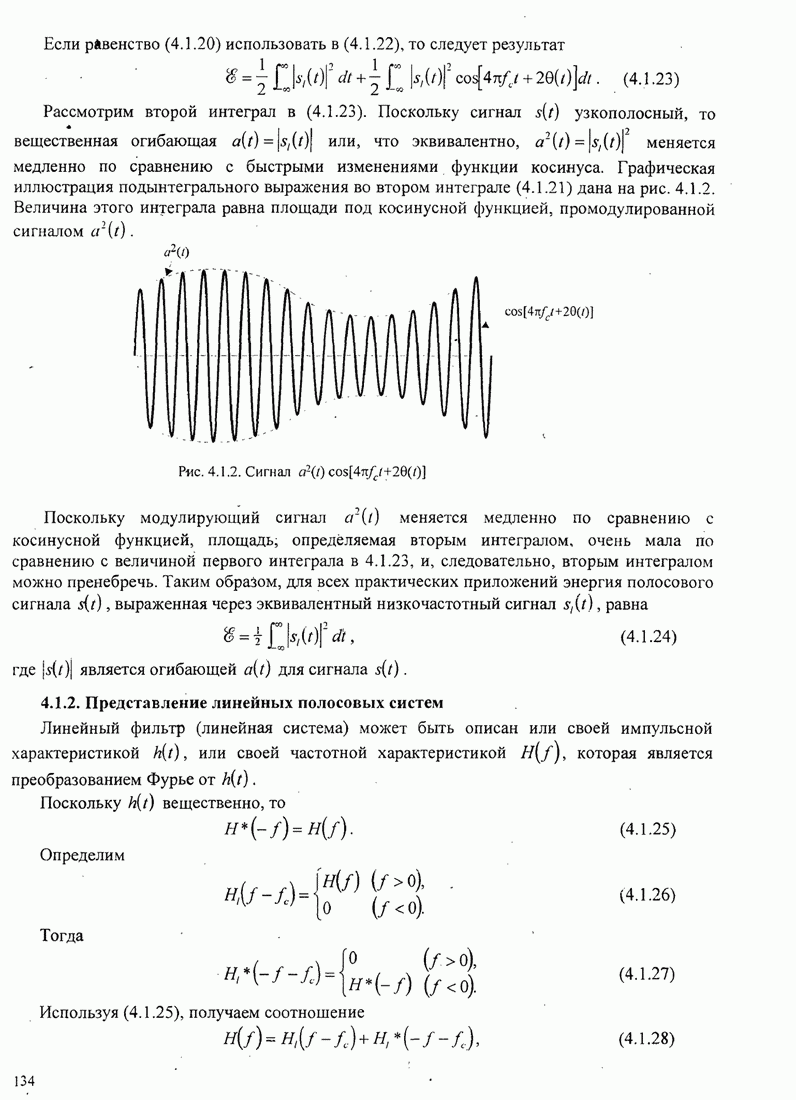
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
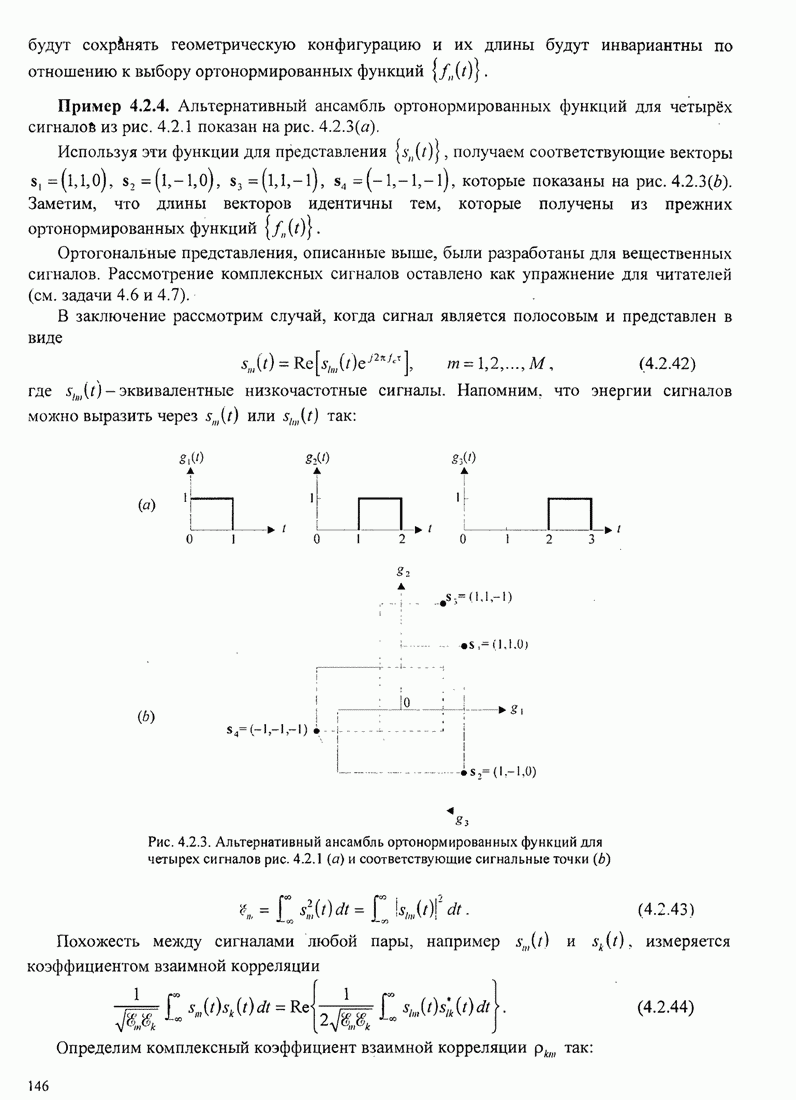
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
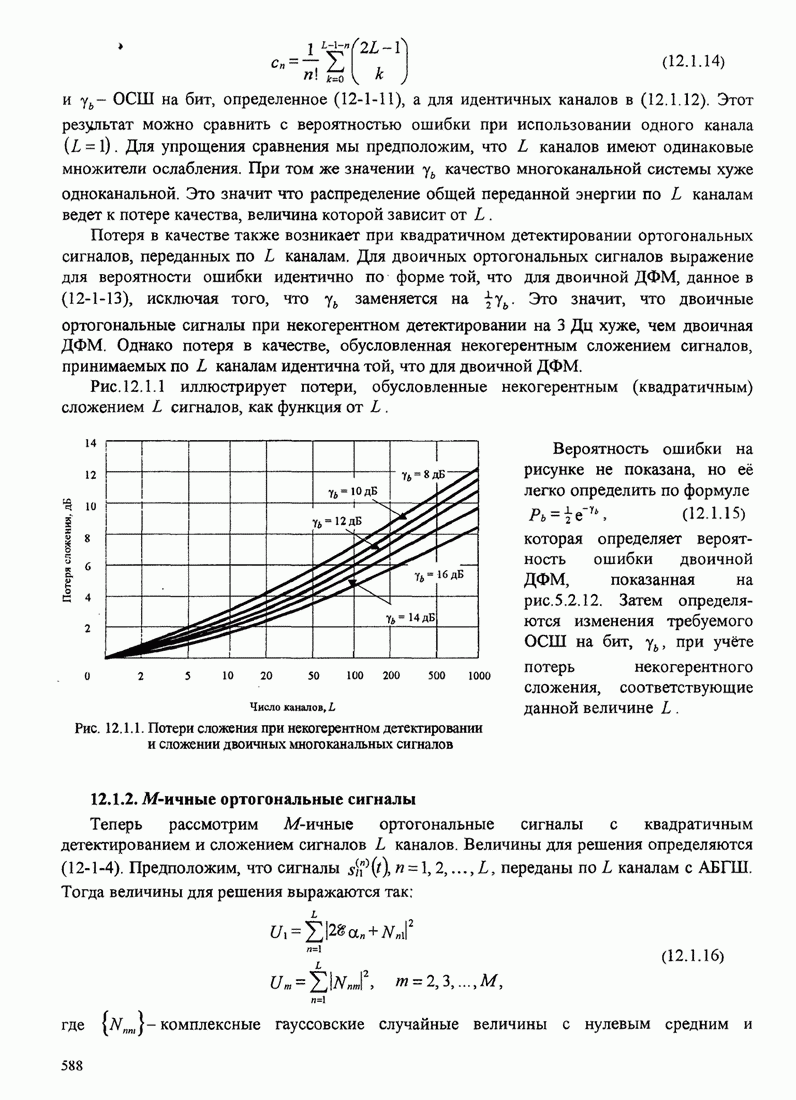
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
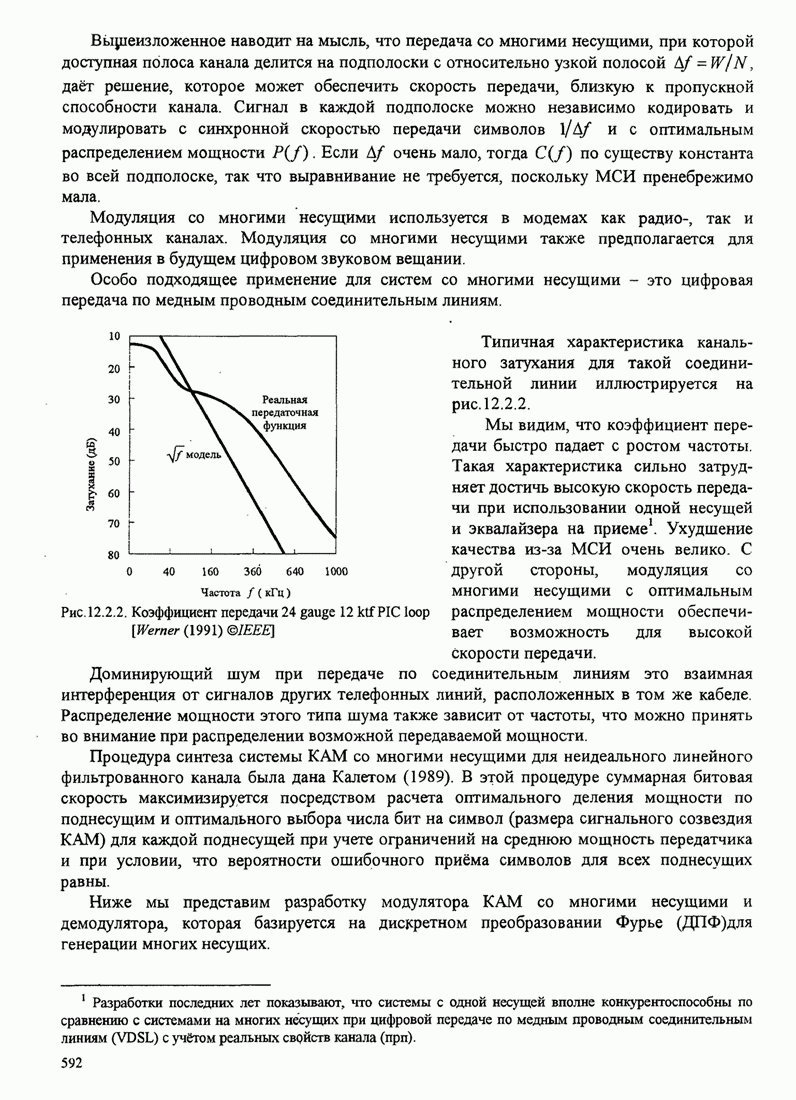
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
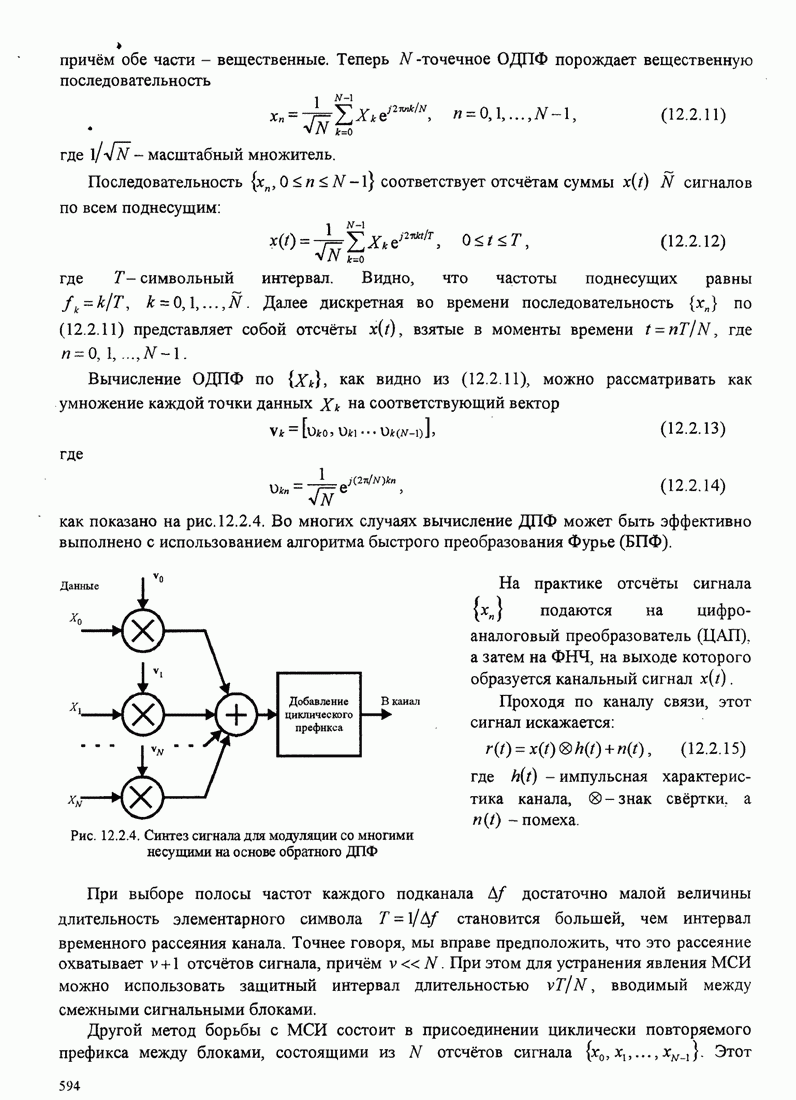
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
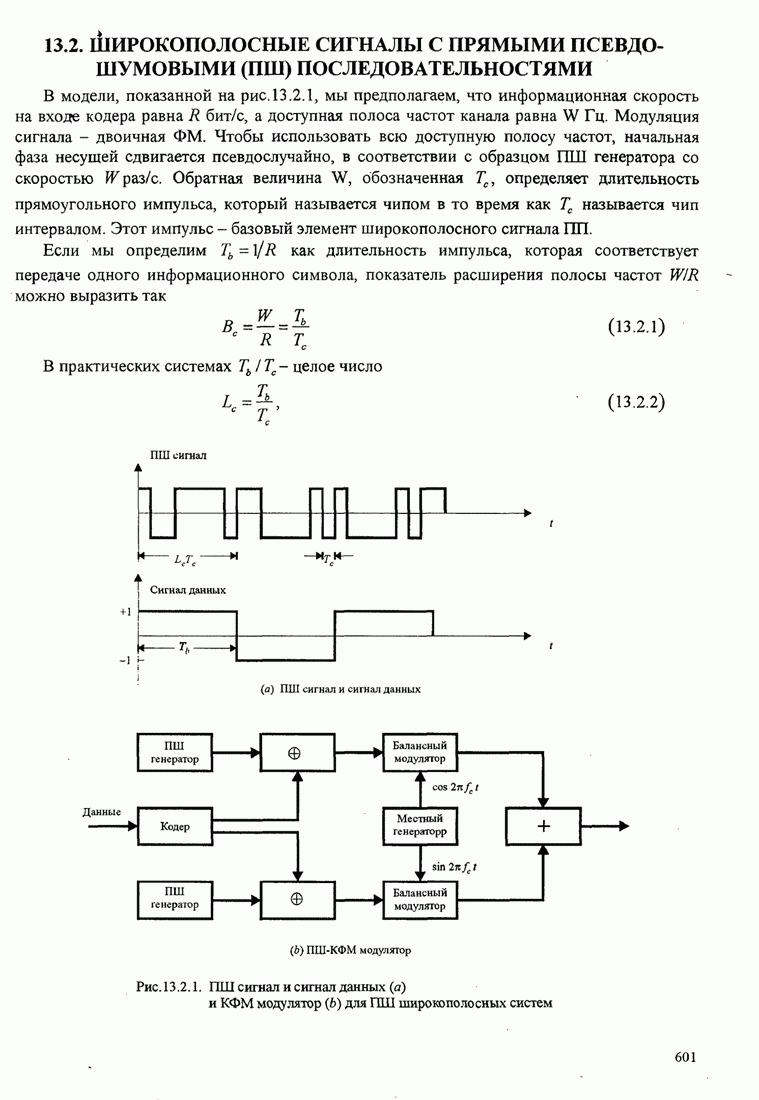
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
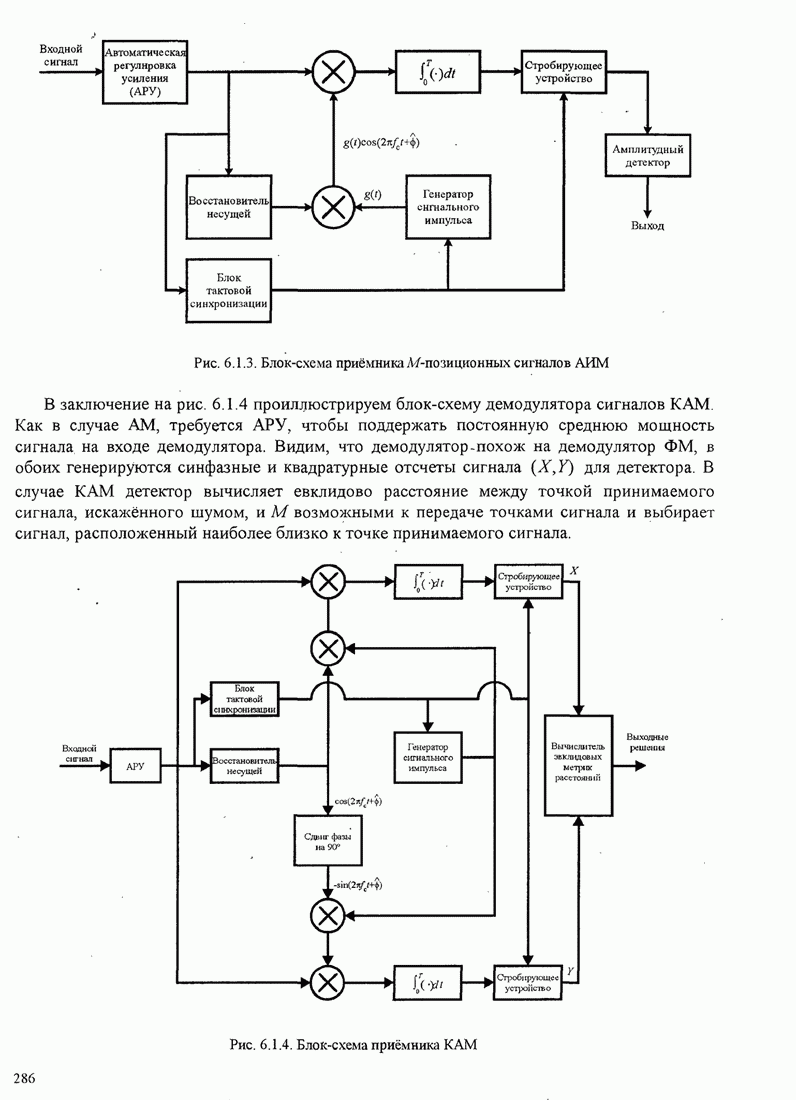
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
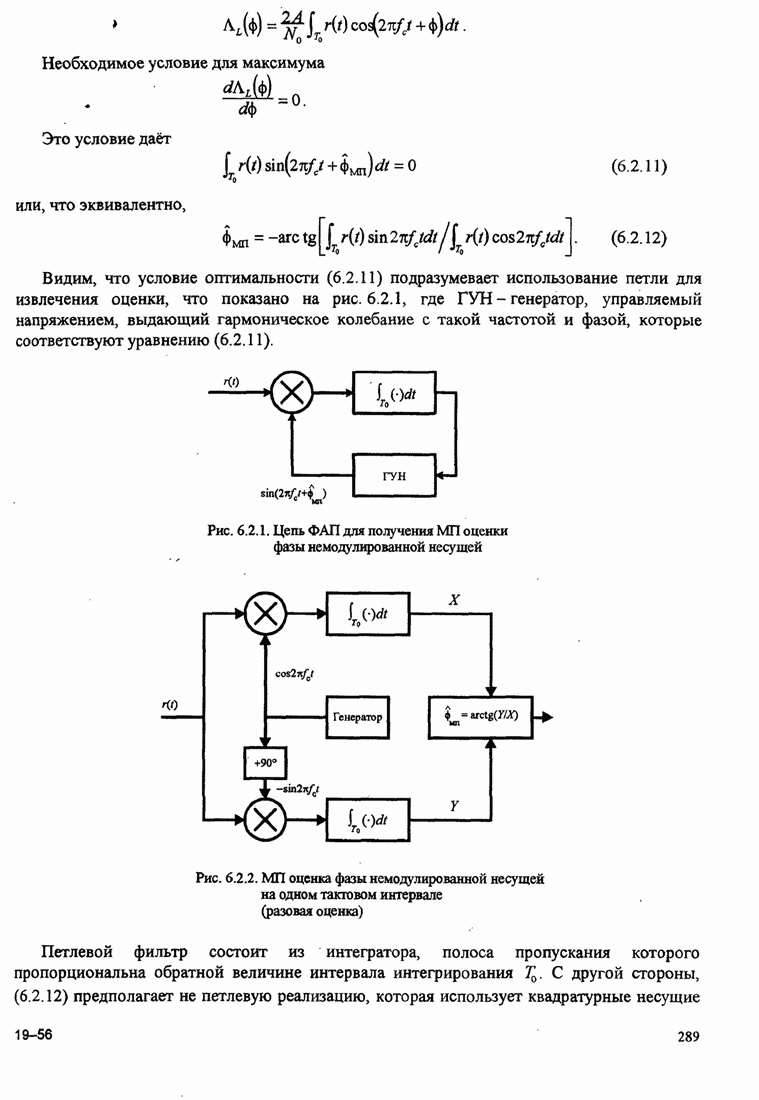
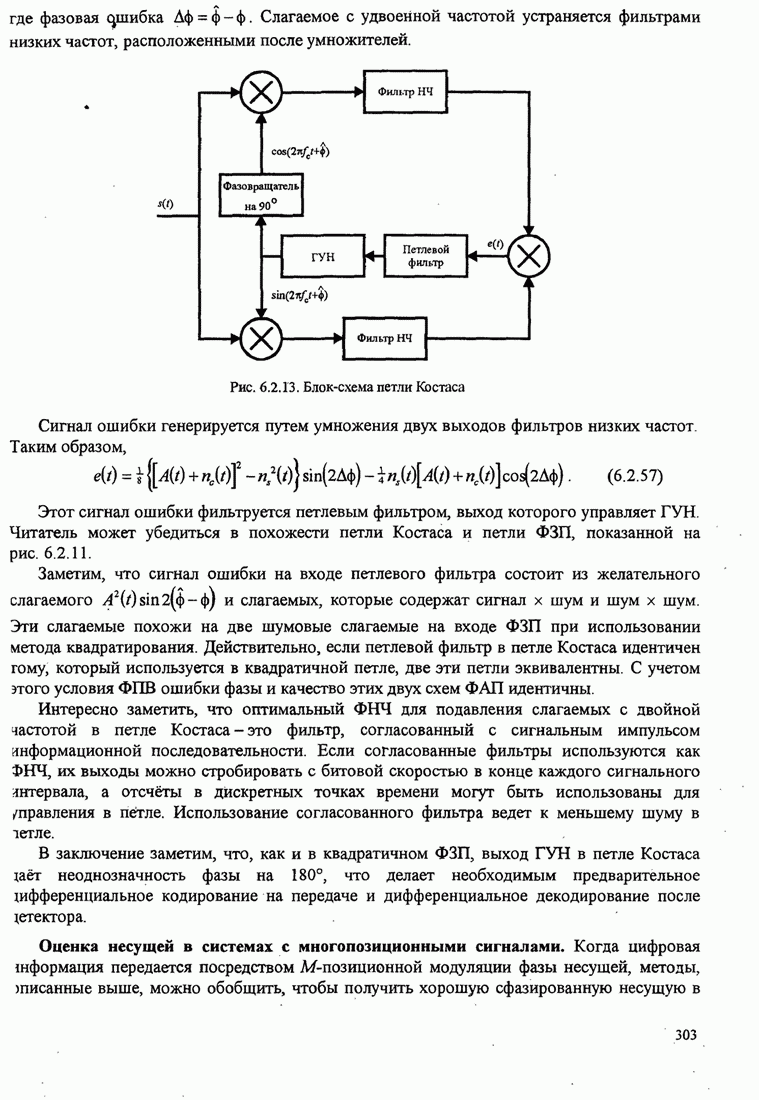
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
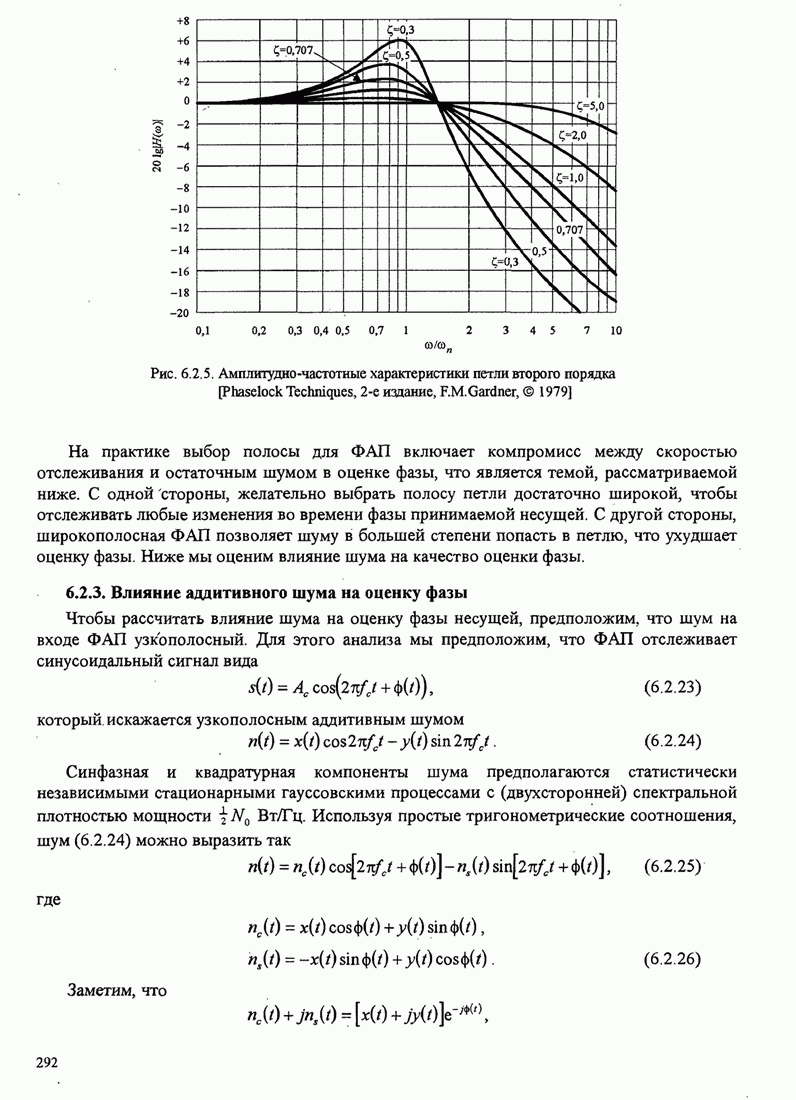
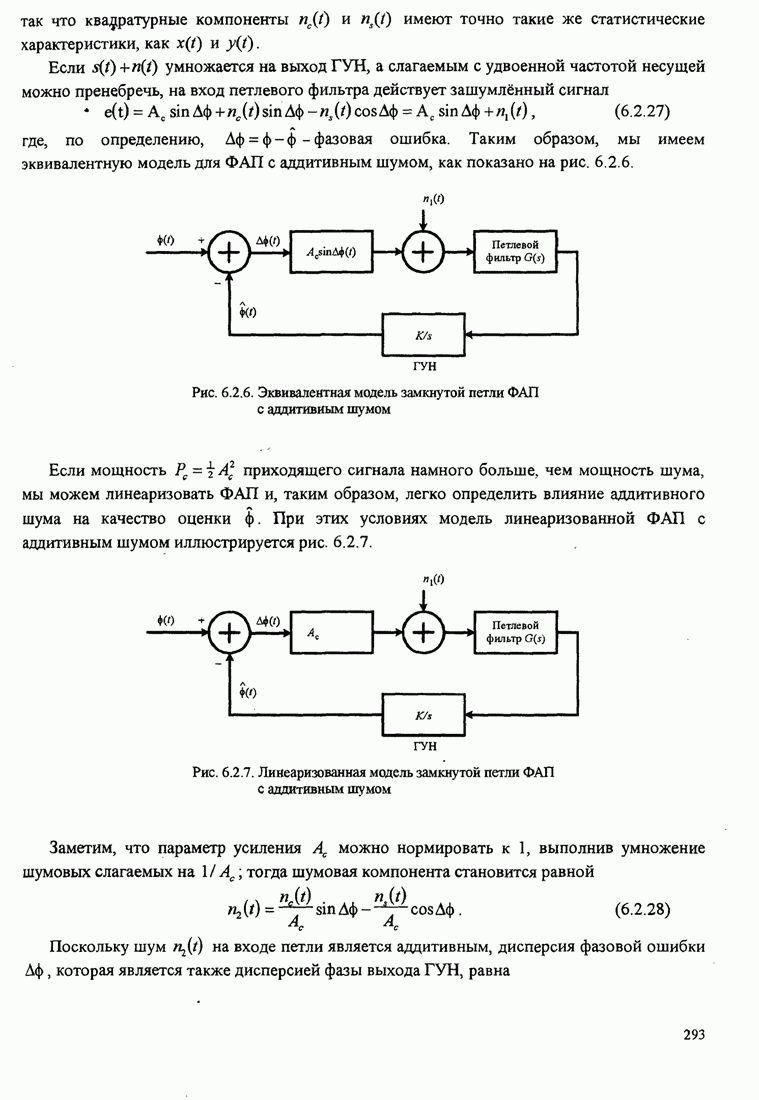
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
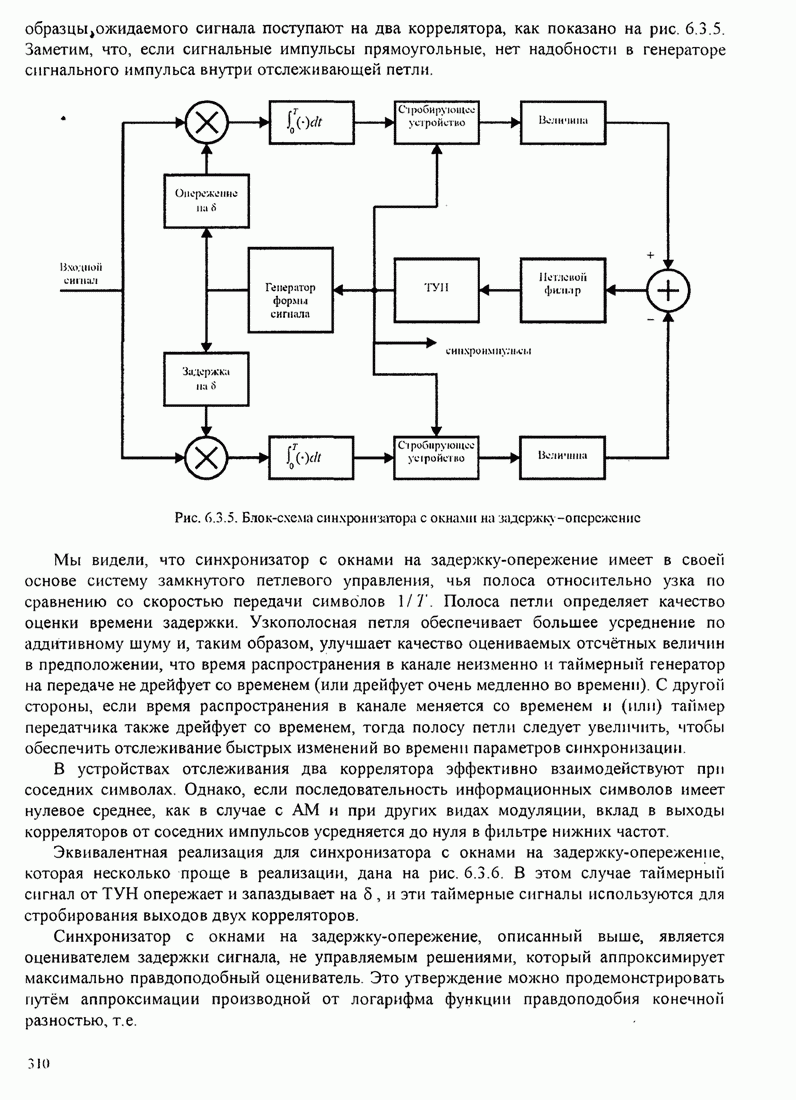
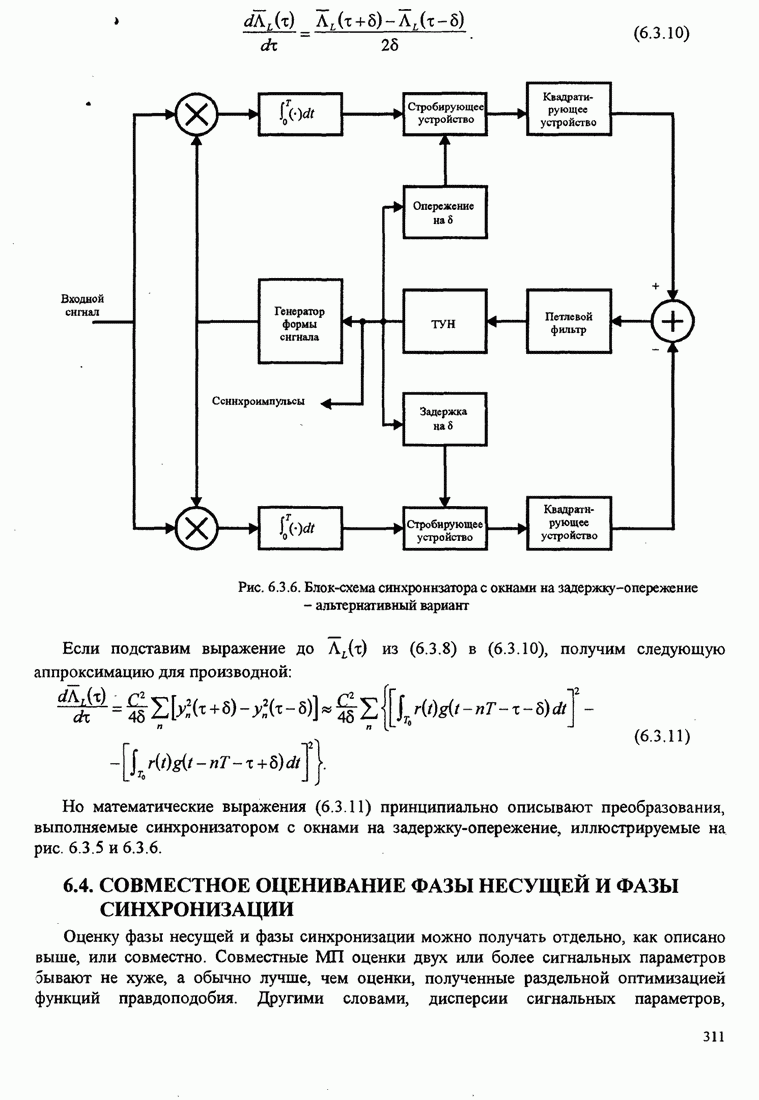
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
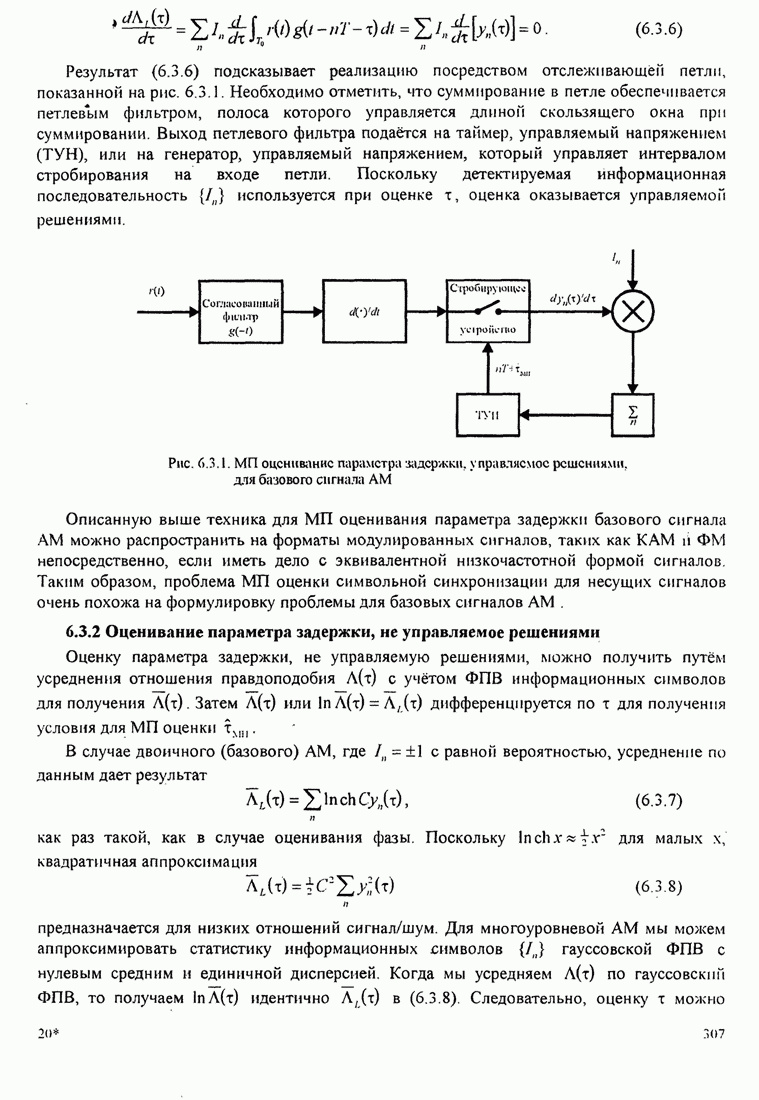
- 6.3.1. Максимально правдоподобная оценка параметра задержки
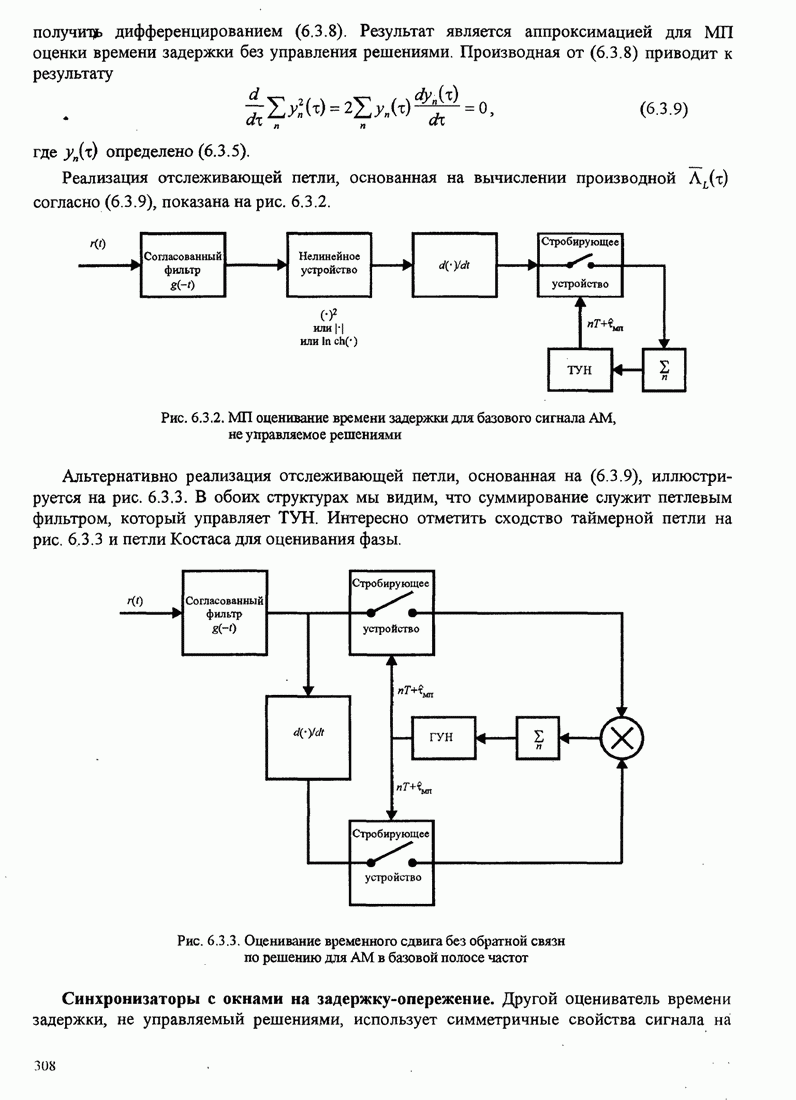
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
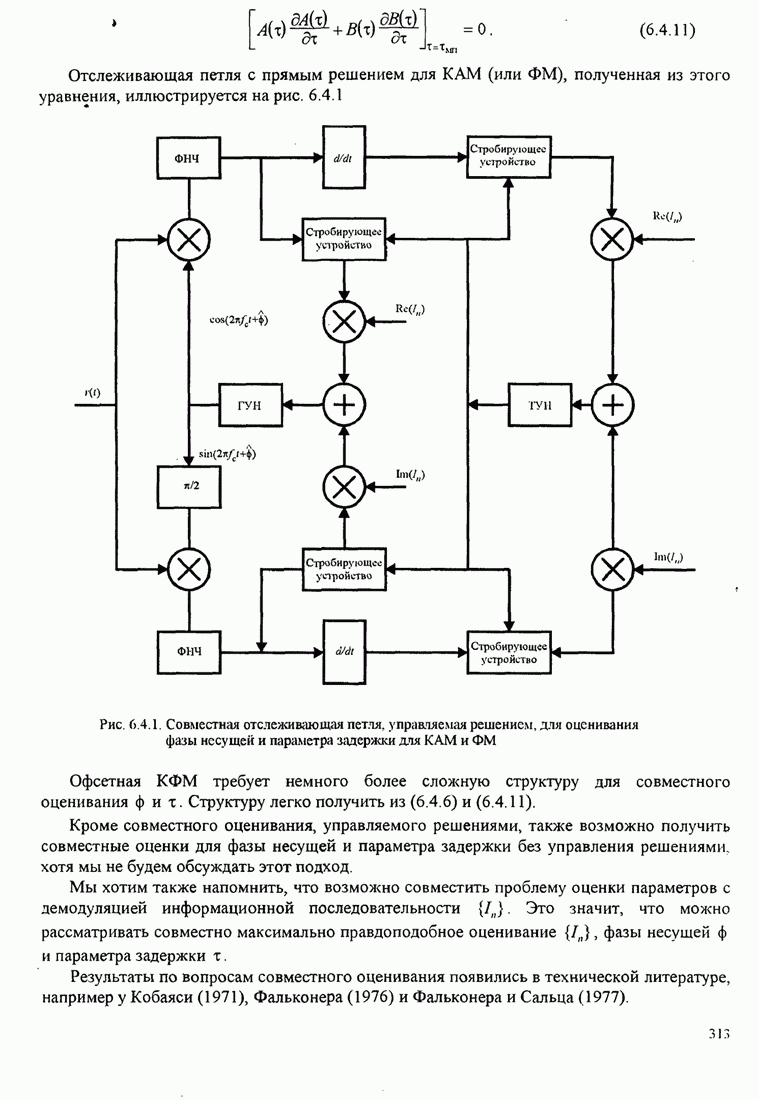
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
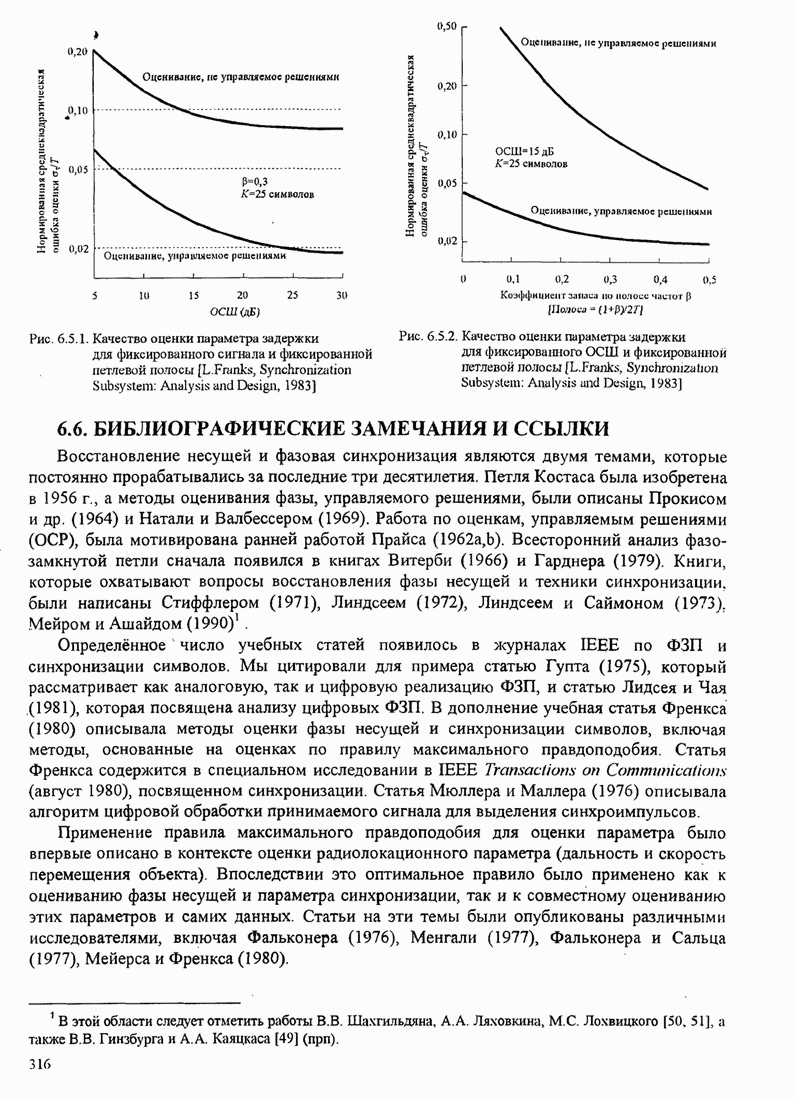
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
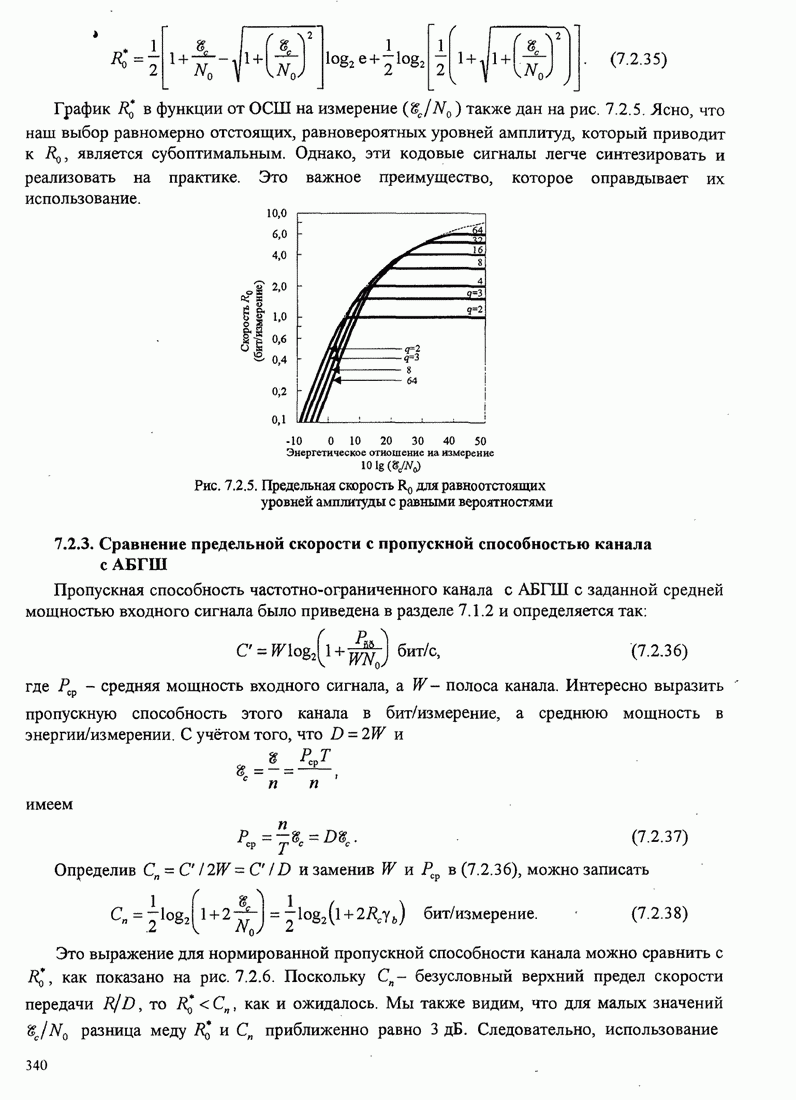
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
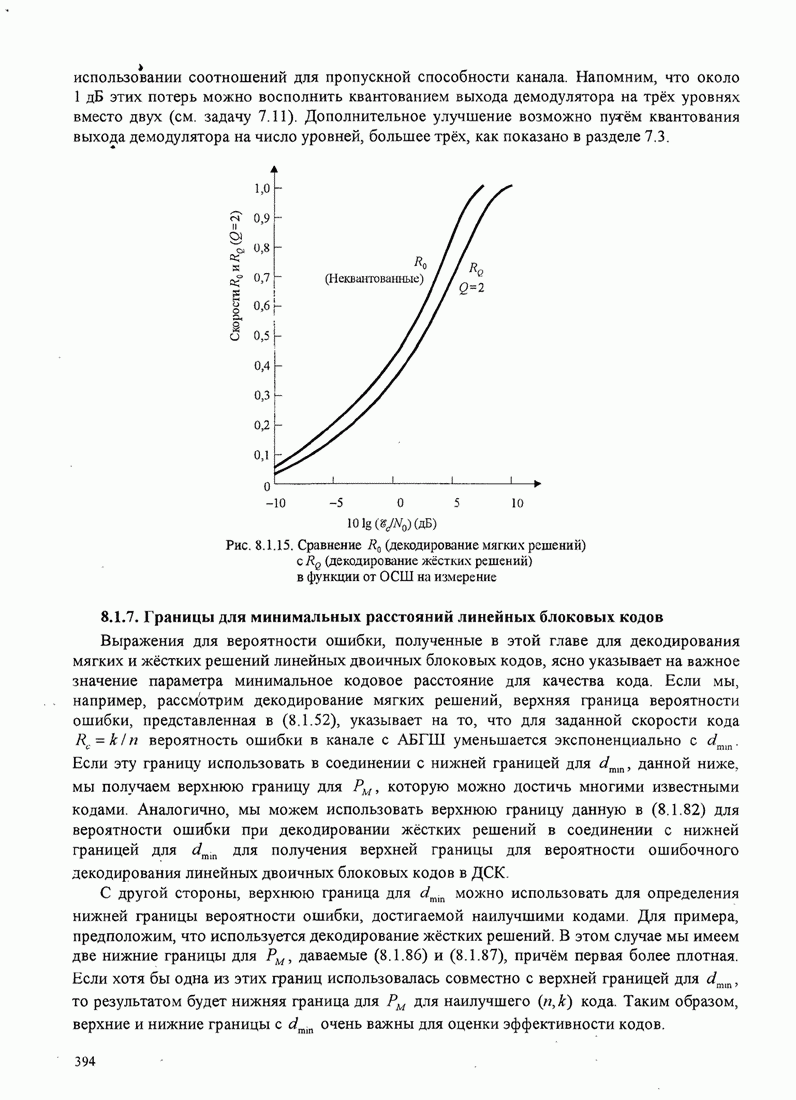
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
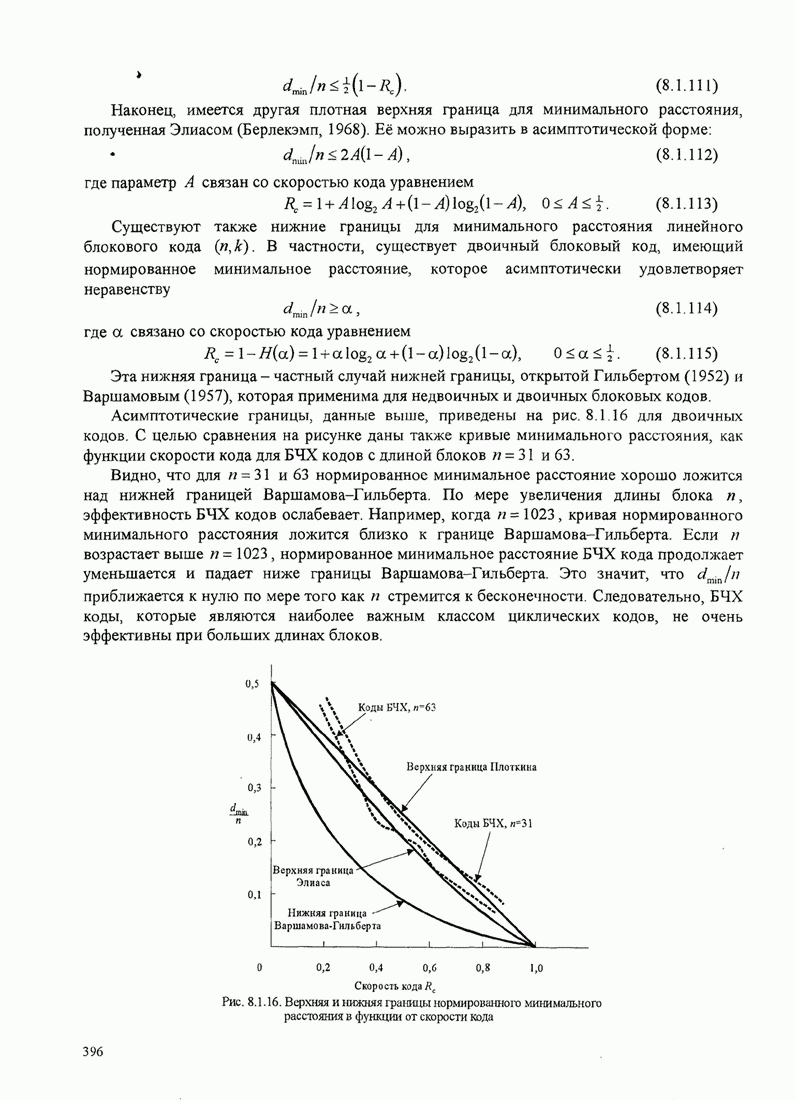
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
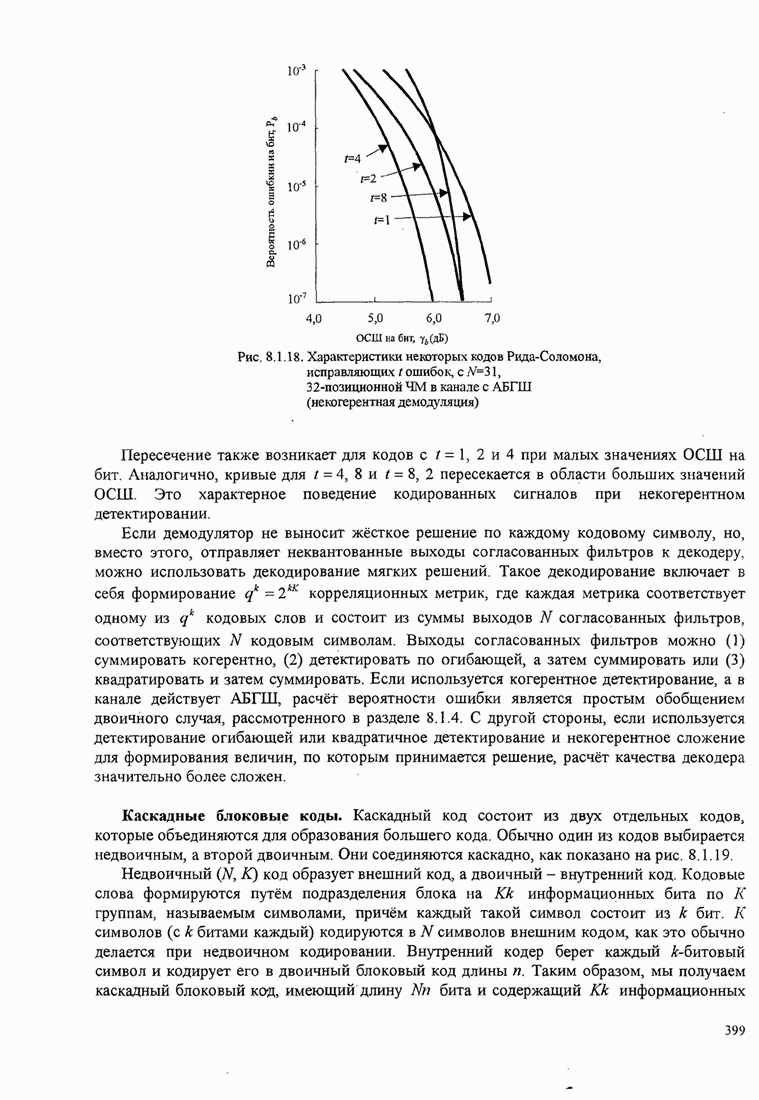
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
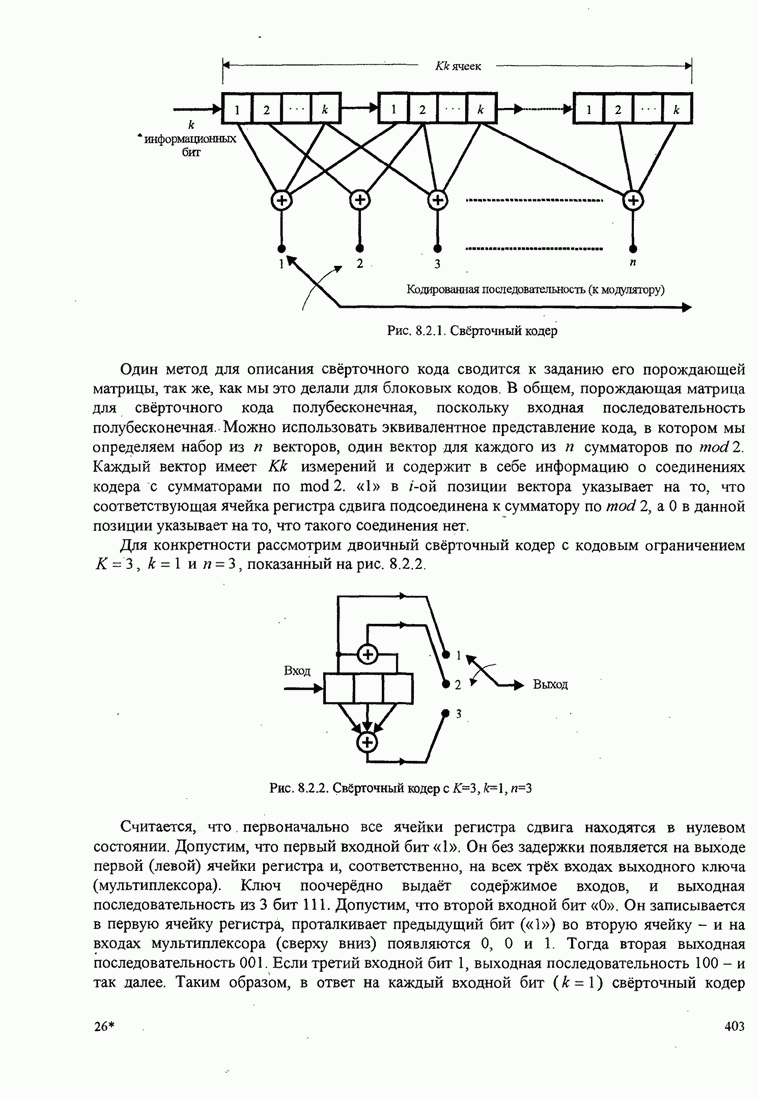
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
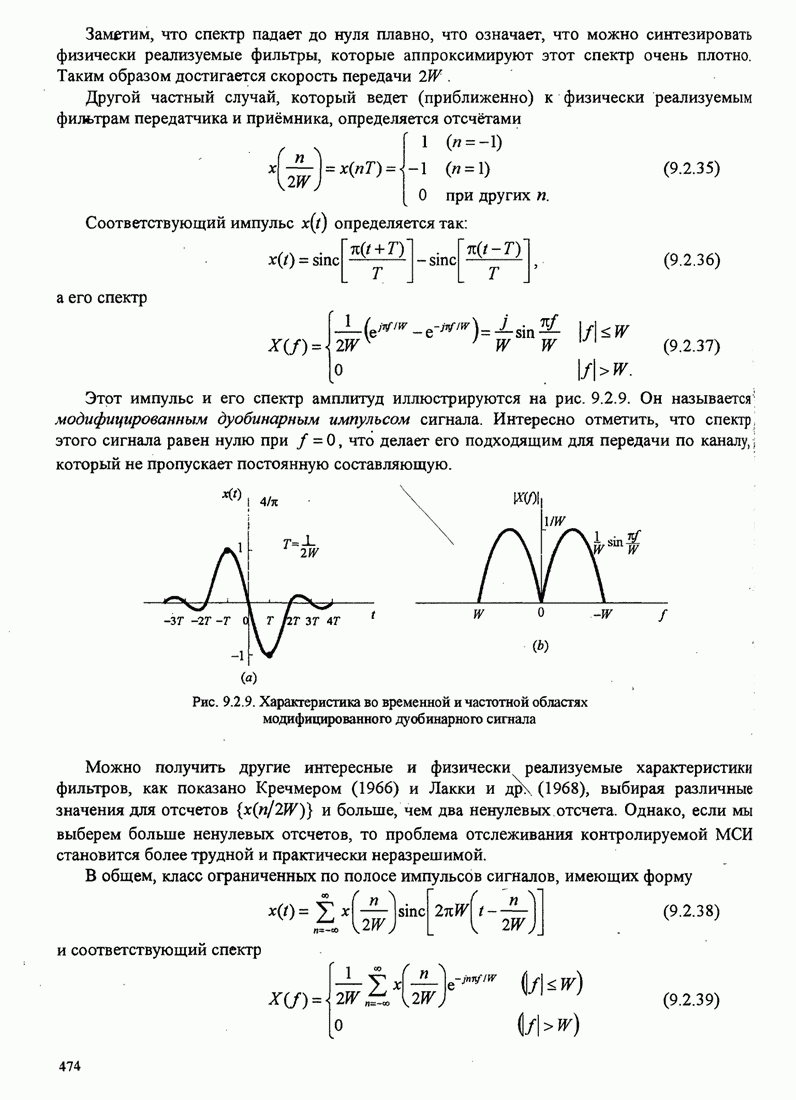
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
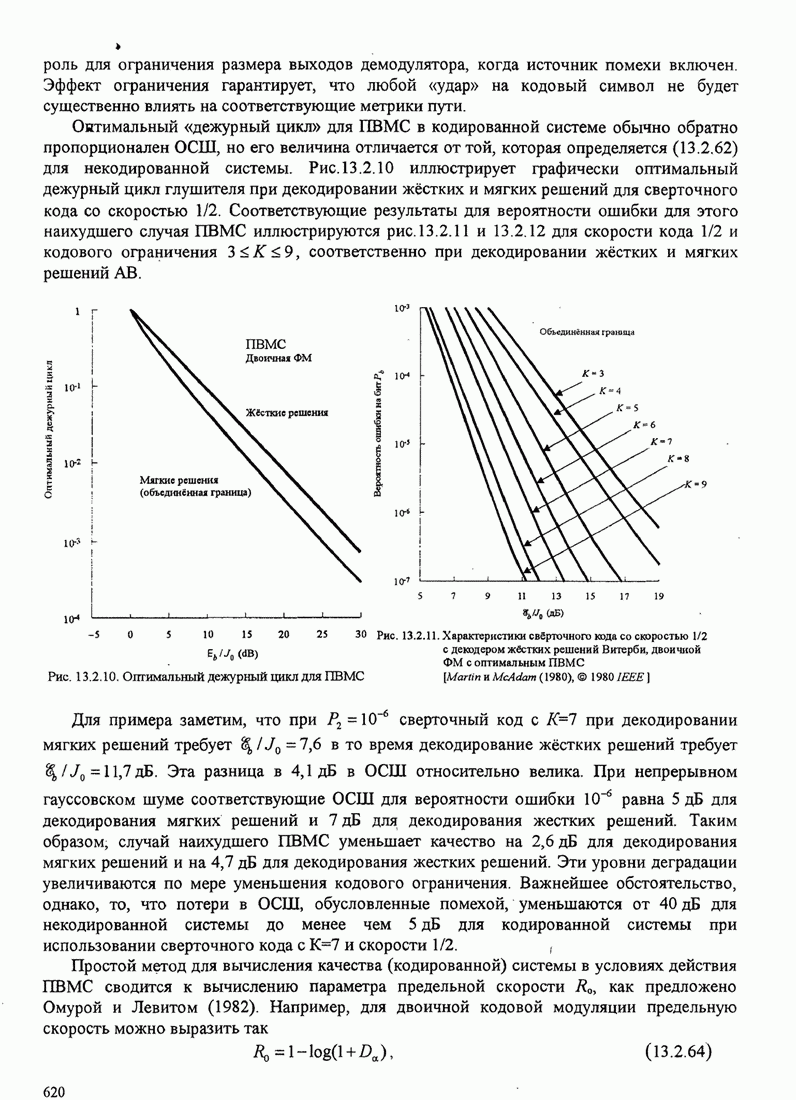
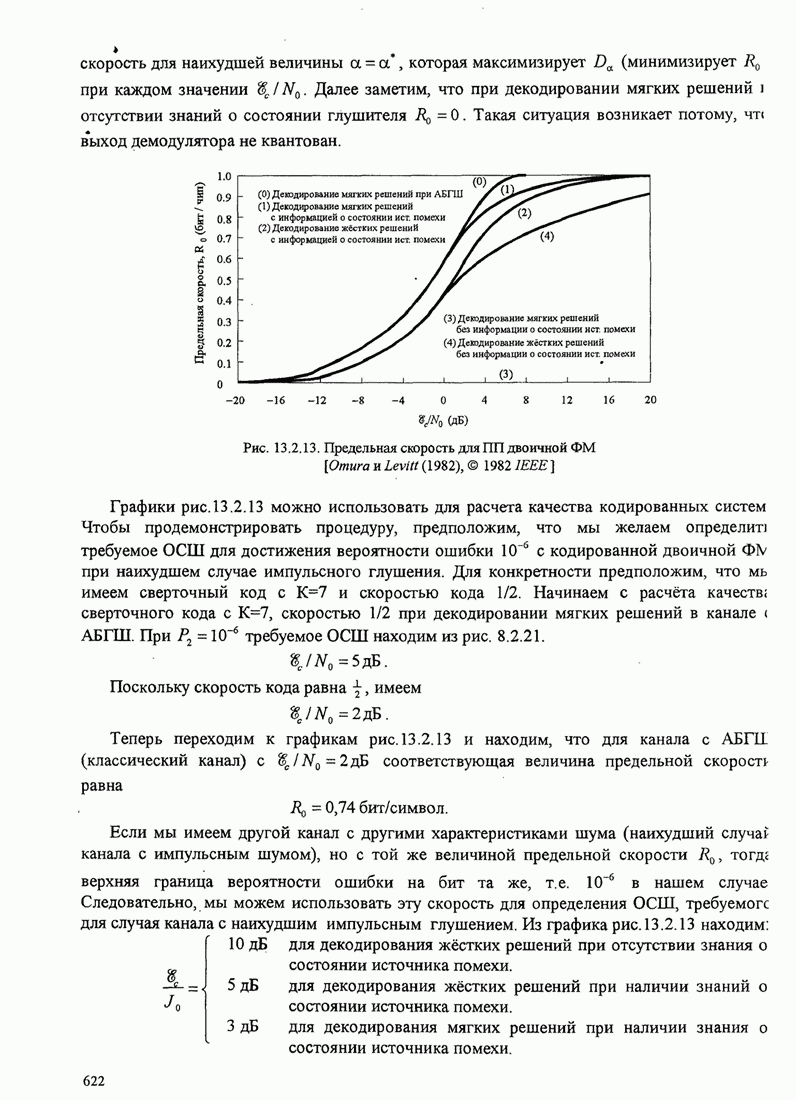
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
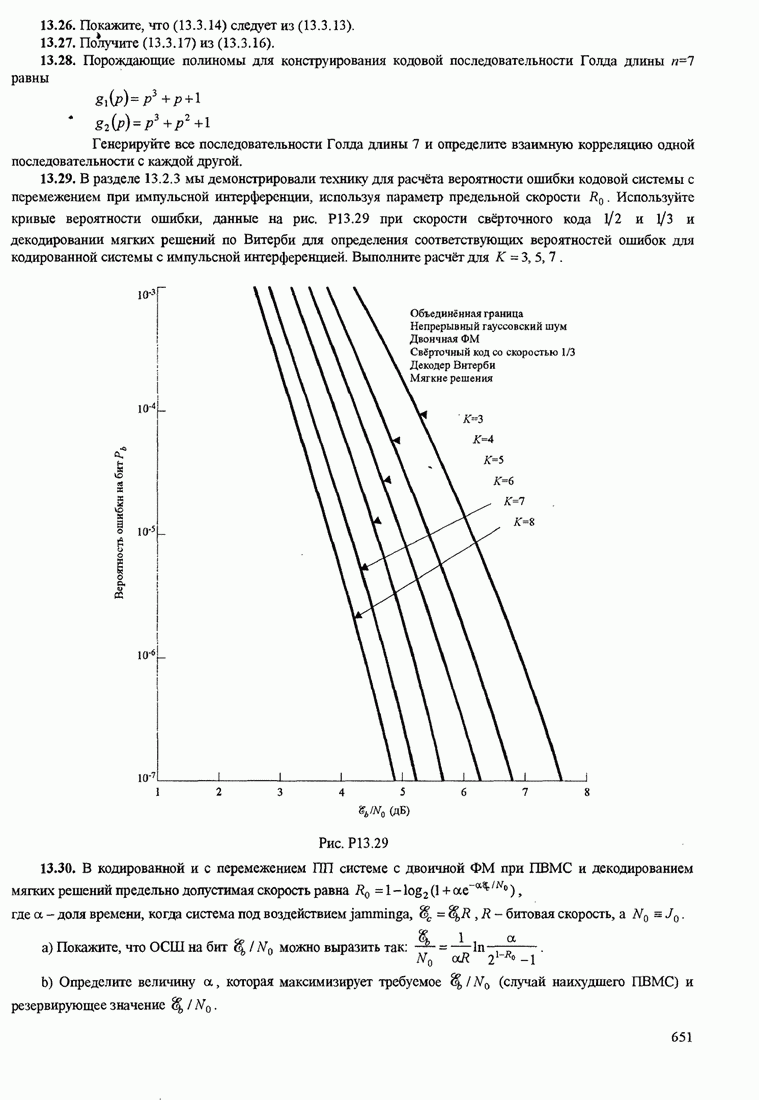
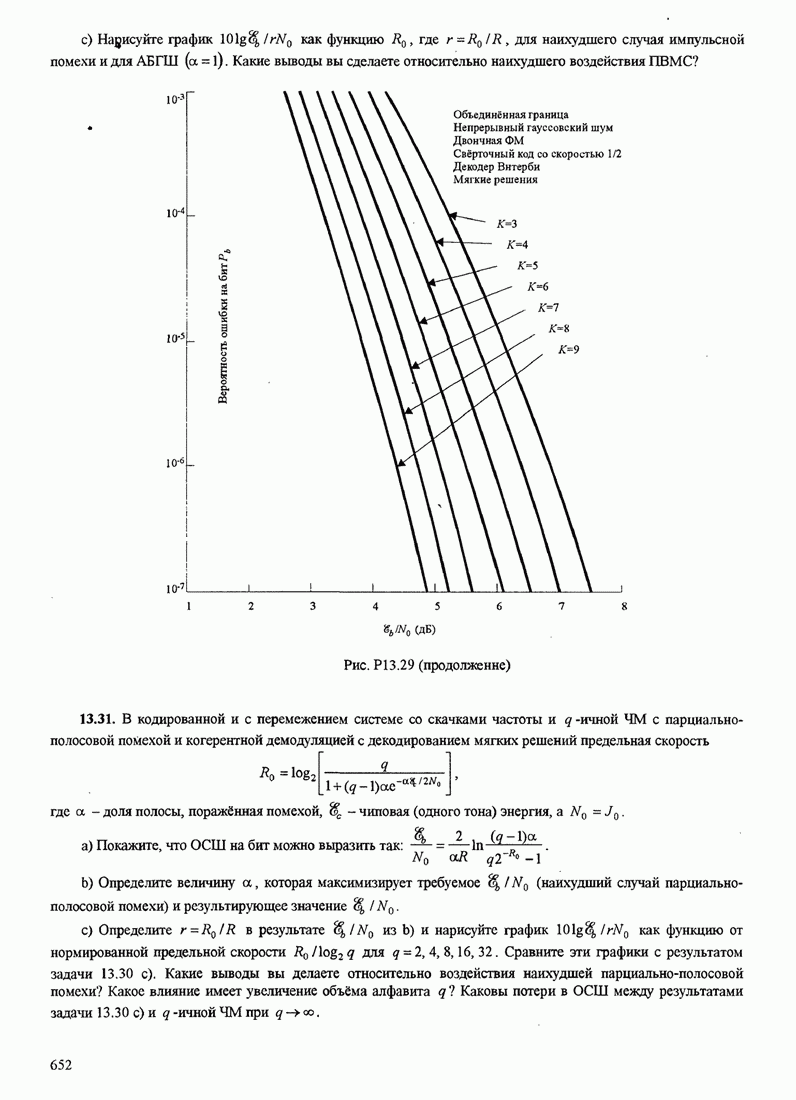
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
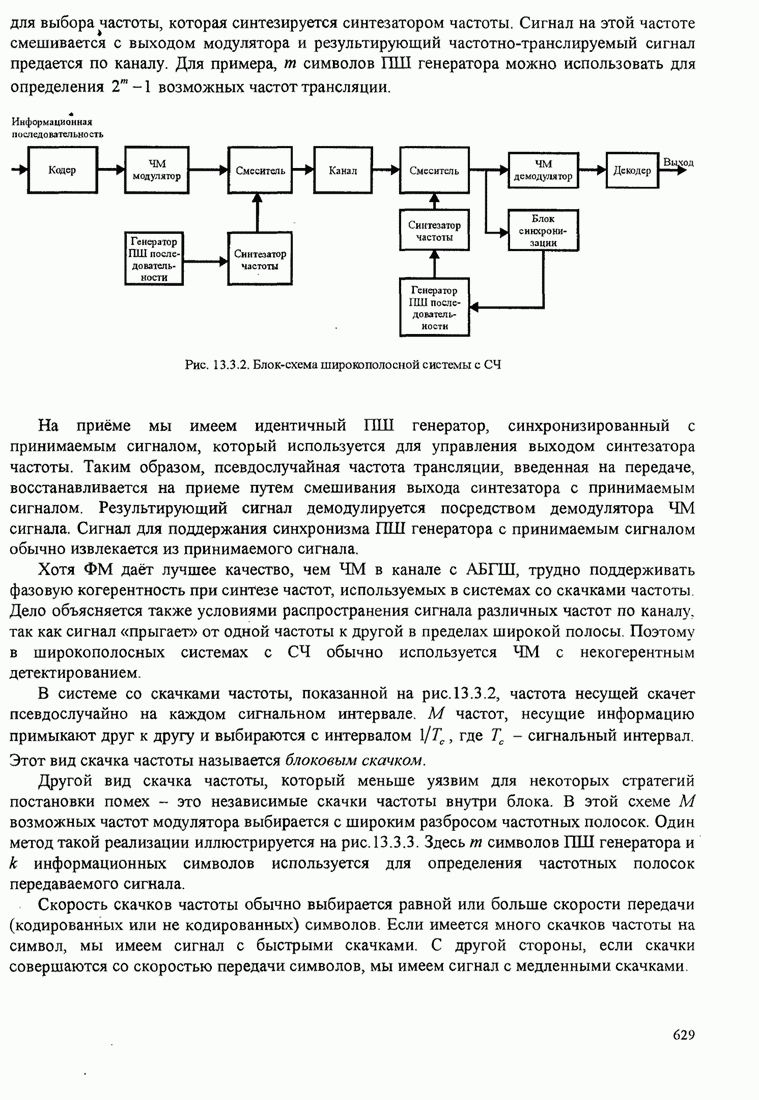
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
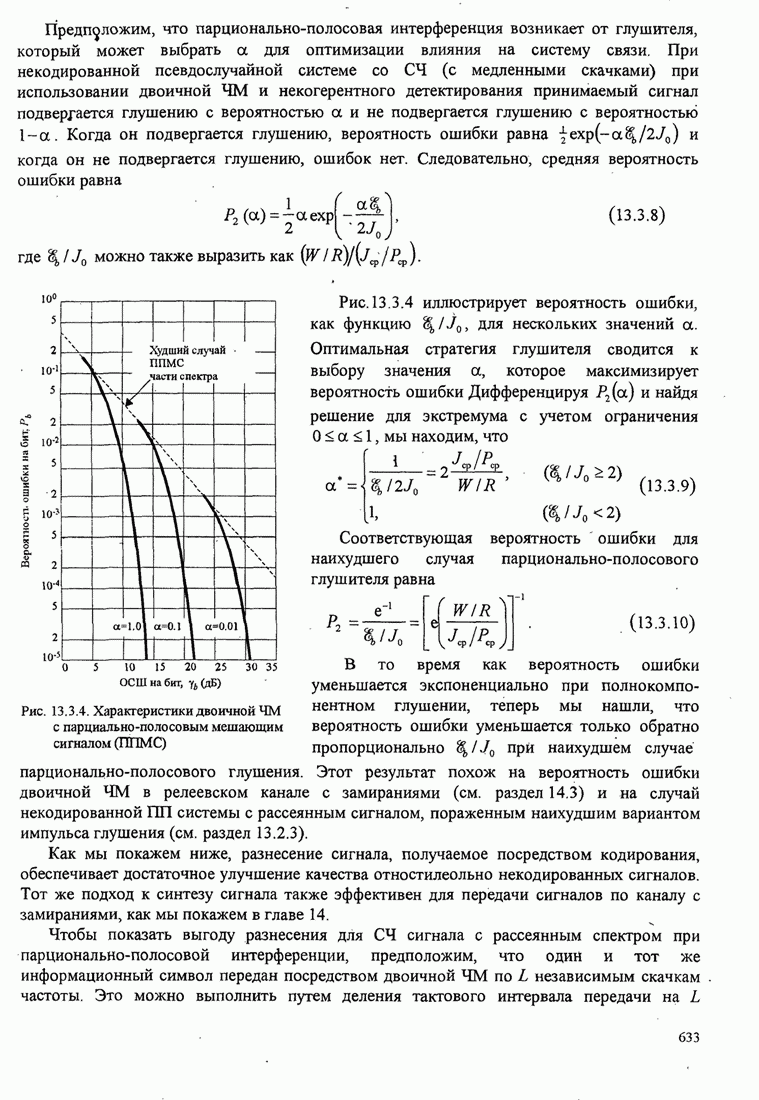
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
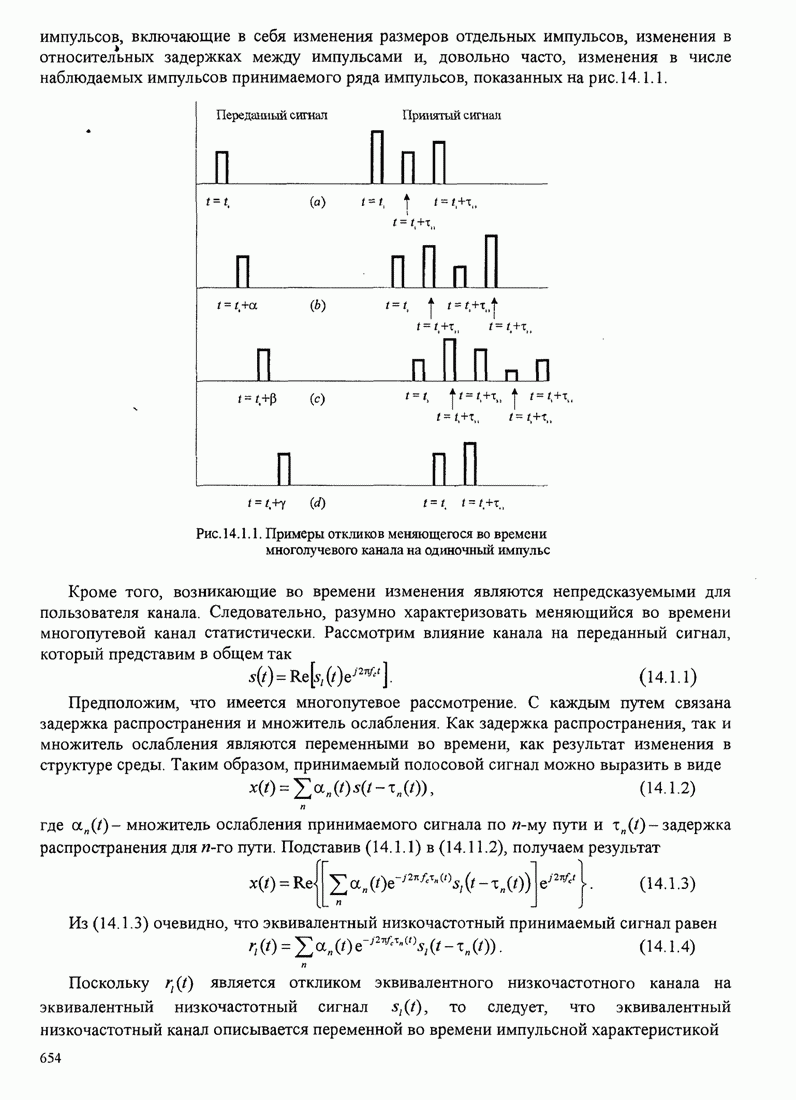
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
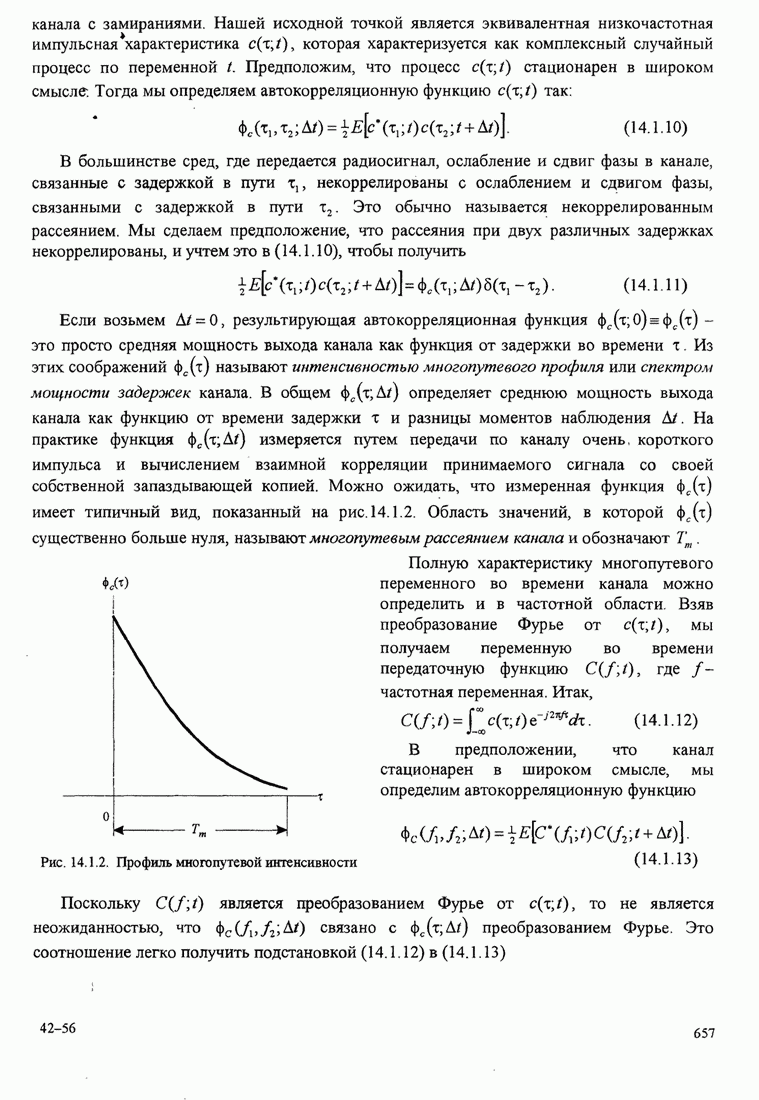
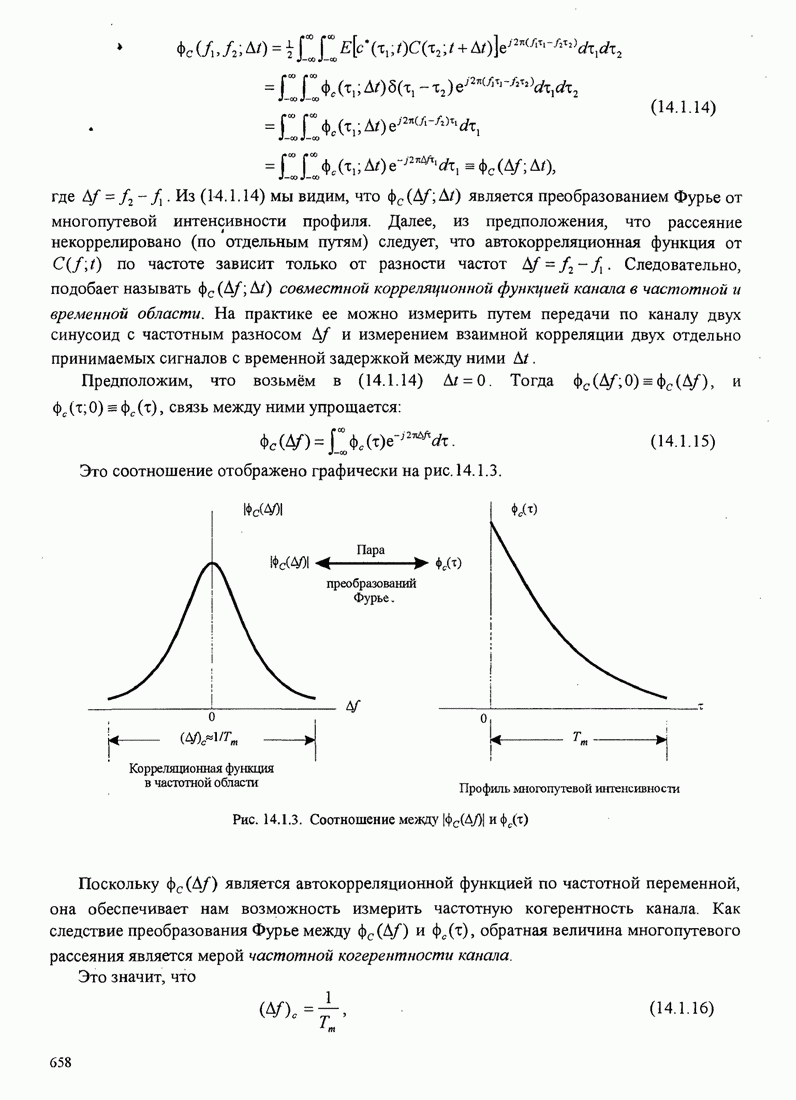
- 14.1.1. Корреляционная функция канала и спектр мощности
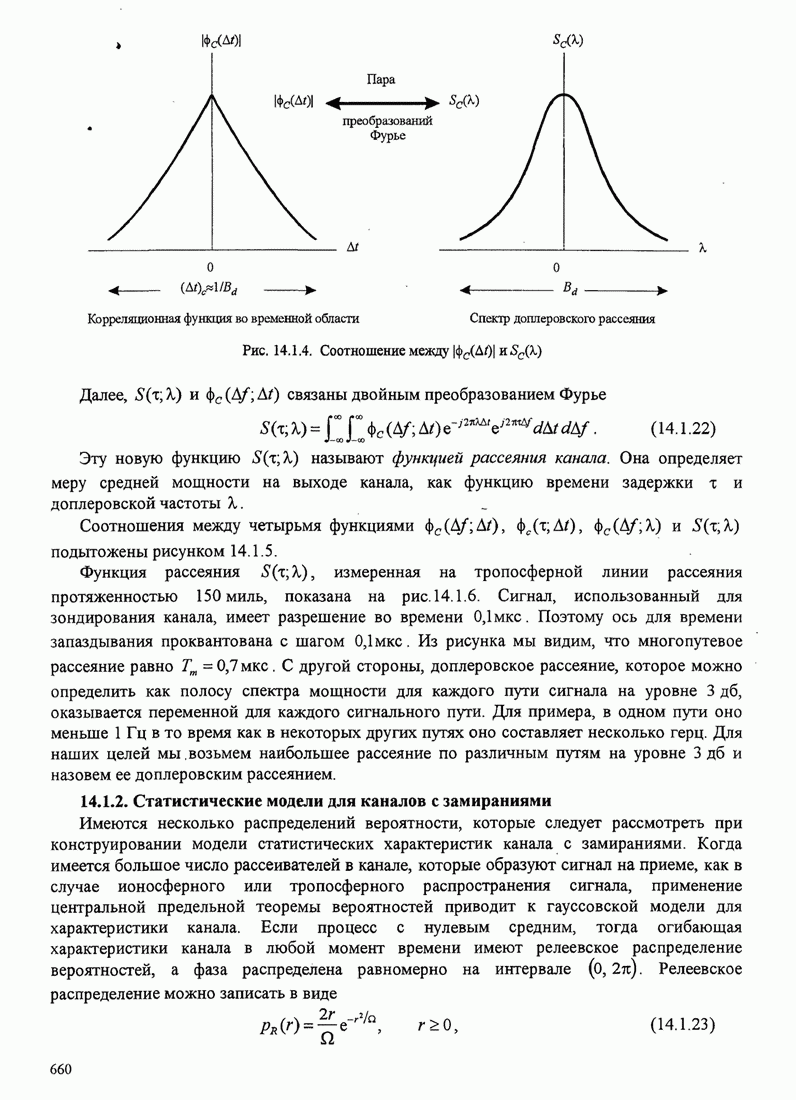
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)