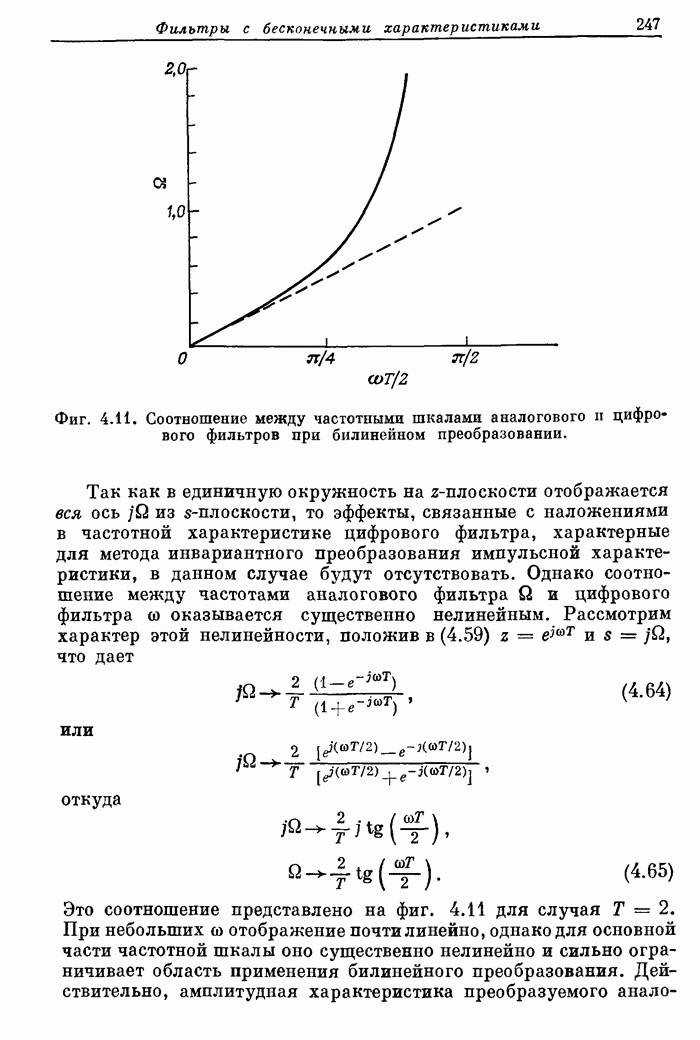
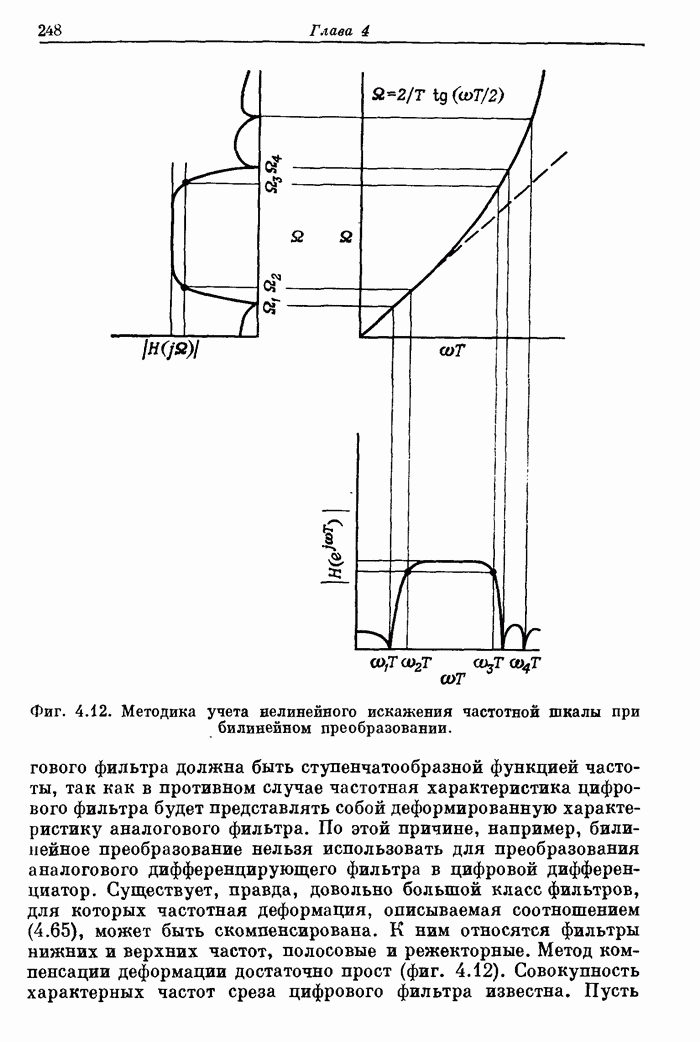
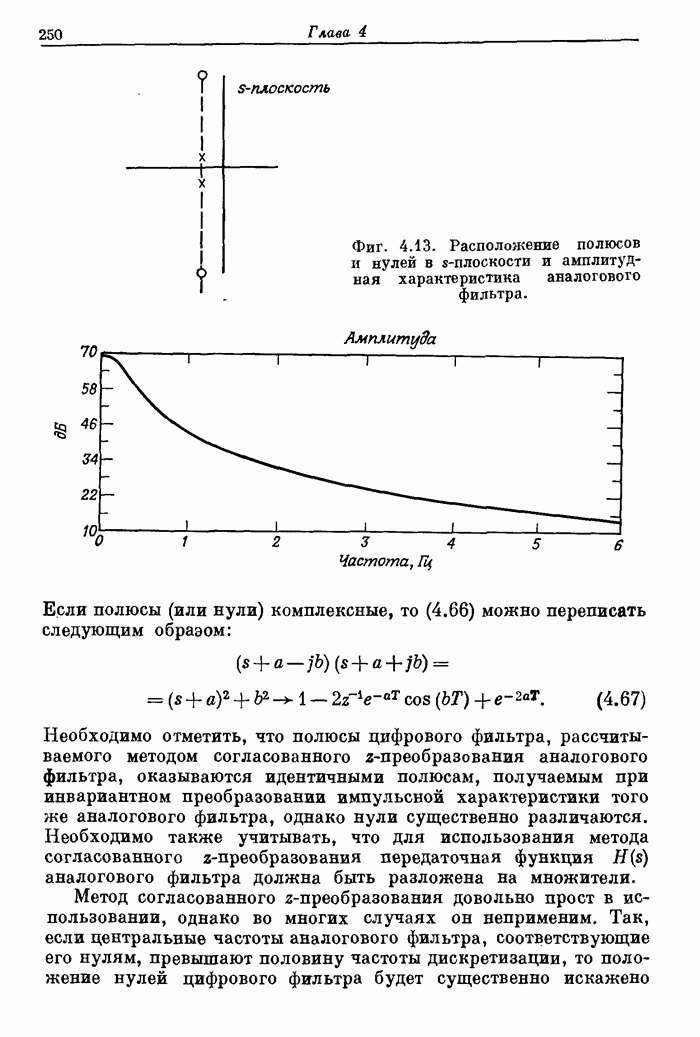
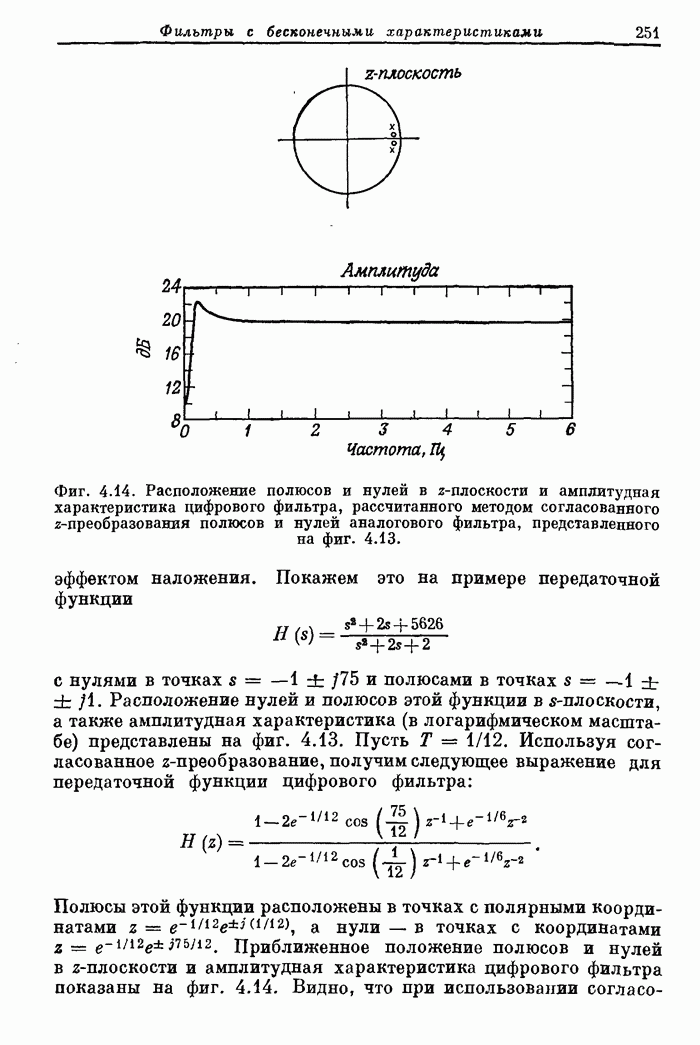
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.18. Энергетический спектр случайных сигналов
При спектральных измерениях случайных последовательностей встречается ряд трудностей. Во-первых, обычно интерес представляет энергетический спектр (определение энергетического спектра еще не было дано). Во-вторых, измерения должны быть статистически устойчивыми в том смысле, что, какая бы оценка ни рассматривалась, при увеличении интервала измерения она должна сходиться к вполне конкретной величине.
Простое и удобное условие сходимости сводится к тому, чтобы дисперсия оценки стремилась к нулю при увеличении интервала измерения. Известно, что при работе с энергетическим спектром весьма удобно пользоваться корреляционной функцией сигнала. В связи с этим в данном разделе будут кратко рассмотрены понятия корреляционной функции и энергетического спектра и связывающие их соотношения. Затем будут проанализированы с точки зрения эффективности вычислений два хорошо известных метода расчета энергетического спектра случайных сигналов.
До сих пор использовалось довольно общее определение спектра. Он определялся как значение z-преобразования в одной или ряде точек в z-плоскости. В связи с этим возникает следующий вопрос: можно ли энергетический спектр сигнала определить в таком же общем виде? По-видимому, разумным подходом является следующий: если задана спектральная плотность мощности на некоторой кривой в z-плоскости (не обязательно на единичной окружности), то, интегрируя эту плотность вдоль кривой, можно получить общую мощность сигнала. Используя теорему Парсеваля, можно убедиться в том, что такой подход возможен. Так, для ограниченной случайной последовательности  , состоящей из N отсчетов, теорема Парсеваля записывается следующим образом:
, состоящей из N отсчетов, теорема Парсеваля записывается следующим образом:

Соотношение (6.75) является упрощенным вариантом теоремы о комплексной свертке. Если последовательность имеет конечную длину, то интегрирование может проводиться по любому контуру, охватывающему начало координат, поэтому спектральную плотность мощности  можно определить как величину, пропорциональную произведению
можно определить как величину, пропорциональную произведению  на этом произвольном контуре, т. е.
на этом произвольном контуре, т. е.

Из этого соотношения следует, что для определения спектральной плотности мощности в точке  плоскости z необходимо вычислять значения z-преобразования заданного сигнала
плоскости z необходимо вычислять значения z-преобразования заданного сигнала  при
при  и при
и при  Например, если требуется измерить спектральную плотность на окружности радиуса
Например, если требуется измерить спектральную плотность на окружности радиуса  , необходимо вычислить значения z-преобразования последовательности и на этой окружности, и на окружности радиуса
, необходимо вычислить значения z-преобразования последовательности и на этой окружности, и на окружности радиуса  . При
. При  оба эти значения
оба эти значения  -преобразования становятся комплексно сопряженными, так что по существу в качестве спектральной плотности мощности измеряется величина
-преобразования становятся комплексно сопряженными, так что по существу в качестве спектральной плотности мощности измеряется величина  .
.
Чтобы определить коэффициент пропорциональности в соотношении (6.76), воспользуемся статистическим методом. Запишем

Найдем среднее значение от этого выражения

Рассмотрим простейший пример анализа «белого» шума, для которого среднее значение произведения  равно нулю всегда,
равно нулю всегда,  исключением случая
исключением случая  когда оно равно, предположим, К. Таким образом,
когда оно равно, предположим, К. Таким образом,

Поскольку желательно, чтобы среднее значение сходилось к постоянной величине при увеличении N, спектральную плотность следует определить следующим образом:

Например, при N = 5, согласно формуле (6.80), имеем

Объединяя члены с одинаковыми степенями z, получаем

Из выражений (6.81) и (6.82) легко получить формулу для произвольного N:

где

 . Выражение (6.84) определяет автокорреляционную функцию последовательности конечной длины
. Выражение (6.84) определяет автокорреляционную функцию последовательности конечной длины  .
.
Из формулы (6.83) следует, что спектральная плотность мощности равна z-преобразованию автокорреляционной функции сигнала  . Хотя выше предполагалось, что случайный сигнал имеет конечную длительность, как правило, последовательность
. Хотя выше предполагалось, что случайный сигнал имеет конечную длительность, как правило, последовательность  не ограничена. В этих случаях основная формула для вычисления автокорреляционной функции имеет вид
не ограничена. В этих случаях основная формула для вычисления автокорреляционной функции имеет вид

На практике спектральная плотность мощности чаще всего вычисляется на единичной окружности. В этом случае формула (6.83) принимает вид

т.е.  равно преобразованию Фурье от
равно преобразованию Фурье от  . Соответственно
. Соответственно  может быть получена обратным преобразованием Фурье от
может быть получена обратным преобразованием Фурье от  , т. е.
, т. е.

Соотношения (6.86) и (6.87) можно обобщить на случай, когда желательно измерить взаимный энергетический спектр или функцию взаимной корреляции двух случайных колебаний  и
и  :
:
 (6.88)
(6.88)

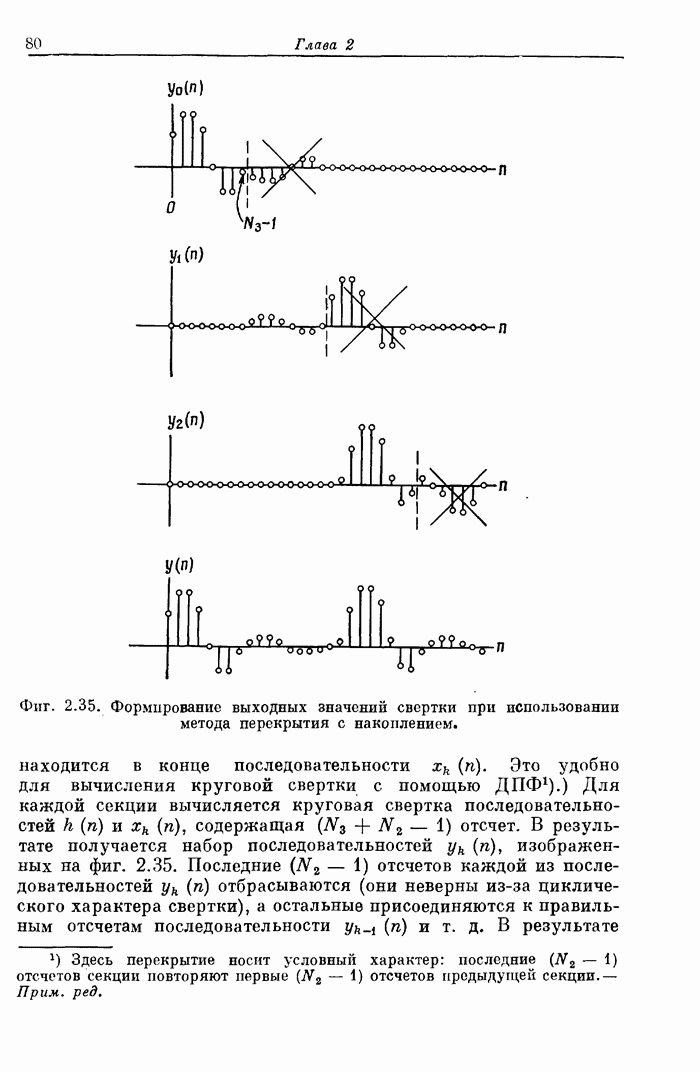
Фиг. 6.30. Два метода выполнения спектрального анализа.
Функцию взаимной корреляции измеряют в случаях, когда последовательности  связаны операциями фильтрации и задержки. Например, в радиолокационной системе
связаны операциями фильтрации и задержки. Например, в радиолокационной системе  может представлять собой отфильтрованный, зашумленный и задержанный зондирующий сигнал
может представлять собой отфильтрованный, зашумленный и задержанный зондирующий сигнал  . В таких случаях положение максимума взаимной корреляционной функции дает величину задержки входного сигнала.
. В таких случаях положение максимума взаимной корреляционной функции дает величину задержки входного сигнала.
Итак, выше было дано определение спектральной плотности мощности, установлена взаимосвязь между спектральной плотностью мощности и автокорреляционной функцией и показано, что средние значения этих оценок сходятся при больших  к некоторому определенному постоянному числу, по крайней мере в случае белого шума. Однако хорошо известно, что дисперсия оценки
к некоторому определенному постоянному числу, по крайней мере в случае белого шума. Однако хорошо известно, что дисперсия оценки  будет сходиться к нулю лишь при выполнении дальнейшего усреднения. Существуют два хорошо известных метода измерения спектральной плотности шума с использованием БПФ, для которых удовлетворяются условия сходимости дисперсии к нулю. Первый метод основан на вычислении корреляционной функции с помощью алгоритма БПФ, а второй состоит в усреднении последовательности непосредственных измерений спектральной плотности. На фиг. 6.30 иллюстрируются все этапы выполнения спектрального анализа этими методами.
будет сходиться к нулю лишь при выполнении дальнейшего усреднения. Существуют два хорошо известных метода измерения спектральной плотности шума с использованием БПФ, для которых удовлетворяются условия сходимости дисперсии к нулю. Первый метод основан на вычислении корреляционной функции с помощью алгоритма БПФ, а второй состоит в усреднении последовательности непосредственных измерений спектральной плотности. На фиг. 6.30 иллюстрируются все этапы выполнения спектрального анализа этими методами.
В методе 1 БПФ используется непосредственно для вычисления оценок взаимной корреляционной функции  при L задержках, где 2L — размер БПФ.
при L задержках, где 2L — размер БПФ.
При вычислении по значениям  спектральной плотности мощности
спектральной плотности мощности  для конечного числа частот необходимо применять сглаживающее окно
для конечного числа частот необходимо применять сглаживающее окно  , чтобы уменьшить нежелательные эффекты, связанные с конечной длиной выборки, поскольку вместо бесконечной корреляционной последовательности используются только L ее значений. С помощью L-точечного БПФ можно вычислить значения спектральной плотности мощности на L равноотстоящих частотах на единичной окружности.
, чтобы уменьшить нежелательные эффекты, связанные с конечной длиной выборки, поскольку вместо бесконечной корреляционной последовательности используются только L ее значений. С помощью L-точечного БПФ можно вычислить значения спектральной плотности мощности на L равноотстоящих частотах на единичной окружности.
В методе 2 алгоритм БПФ используется для непосредственного вычисления спектральной плотности мощности в отличие от первого метода, в котором сначала вычисляется корреляционная функция. Поэтому каждая из последовательностей  до выполнения преобразования сглаживается с помощью окна
до выполнения преобразования сглаживается с помощью окна  . Для последующего вычисления на основе спектральной плотности мощности корреляционной функции можно использовать алгоритм обратного БПФ. Так как спектральная плотность мощности была рассчитана только на L дискретных частотах (вместо бесконечного числа частот, что требуется при теоретическом рассмотрении), после обратного БПФ будет получена корреляционная функция, искаженная эффектом наложения.
. Для последующего вычисления на основе спектральной плотности мощности корреляционной функции можно использовать алгоритм обратного БПФ. Так как спектральная плотность мощности была рассчитана только на L дискретных частотах (вместо бесконечного числа частот, что требуется при теоретическом рассмотрении), после обратного БПФ будет получена корреляционная функция, искаженная эффектом наложения.
Ниже будут рассмотрены вопросы практического применения методов 1 и 2, однако сначала покажем, как можно использовать ДПФ для выполнения корреляционного анализа. Рассмотрим периодические последовательности (с периодом в L отсчетов)  ДПФ, которых
ДПФ, которых  соответственно равны
соответственно равны
 (6.91)
(6.91)
и

Выше было показано, что умножение  на
на  соответствует свертке периодических последовательностей
соответствует свертке периодических последовательностей  , т. е.
, т. е.

Покажем теперь, что круговую свертку  можно элементарно найти следующим образом:
можно элементарно найти следующим образом:

Для проверки соотношения (6.94) покажем, что обратное ДПФ произведения  равно правой части (6.94).
равно правой части (6.94).
Используя формулы (6.91) и (6.92), получим

что и требовалось доказать. [Заметим, что во всех приведенных выкладках последовательности  считаются действительными.]
считаются действительными.]
1. Метод 1 - корреляционный.
На фиг. 6.31 иллюстрируется один из способов вычисления первых пяти отсчетов автокорреляционной функции заданной  -точечной последовательности (N = 20). Сама последовательность показана на фиг. 6.31 вверху. Первый блок чисел размером (9x5) соответствует круговой корреляции двух девятиточечных последовательностей, а именно
-точечной последовательности (N = 20). Сама последовательность показана на фиг. 6.31 вверху. Первый блок чисел размером (9x5) соответствует круговой корреляции двух девятиточечных последовательностей, а именно  . Пять из полученных отсчетов
. Пять из полученных отсчетов  являются правильными; они показаны справа. Второй блок начинается с
являются правильными; они показаны справа. Второй блок начинается с  аналогичная процедура вычисления дает отсчеты от
аналогичная процедура вычисления дает отсчеты от  до
до  . Чтобы найти результирующие значения первых пяти отсчетов автокорреляционной функции, необходимо просуммировать
. Чтобы найти результирующие значения первых пяти отсчетов автокорреляционной функции, необходимо просуммировать  по i следующим образом:
по i следующим образом:

Следующий шаг состоит в том, чтобы показать, как выполнять вычисления с использованием алгоритма БПФ.

Фиг. 6.31. Иллюстрация вычисления круговой корреляции.
Каждую из четырех круговых корреляционных функций девятиточечных последовательностей можно вычислить с помощью ДПФ по следующей схеме:
1. Вычислить

и

2. Вычислить

3. Вычислить

4. Вычислить

5. Первые пять отсчетов  являются искомым результатом и также удовлетворяют соотношению
являются искомым результатом и также удовлетворяют соотношению

Описанная процедура эффективнее, чем предварительный расчет каждой из частичных корреляционных, функций  с помощью обратного ДПФ от
с помощью обратного ДПФ от  и последующее суммирование этих частичных корреляционных функций. В первом случае для каждого из показанных на фиг. 6.31 блоков чисел размером
и последующее суммирование этих частичных корреляционных функций. В первом случае для каждого из показанных на фиг. 6.31 блоков чисел размером  рассчитываются два ДПФ, что дает
рассчитываются два ДПФ, что дает  , а одно «общее» ДПФ искомой корреляционной функции получается путем накопления частичных ДПФ. «Общая» корреляционная функция вычисляется посредством единственного обратного ДПФ от полученного путем накопления «полного» ДПФ. Следовательно, общее число выполняемых преобразований равно
, а одно «общее» ДПФ искомой корреляционной функции получается путем накопления частичных ДПФ. «Общая» корреляционная функция вычисляется посредством единственного обратного ДПФ от полученного путем накопления «полного» ДПФ. Следовательно, общее число выполняемых преобразований равно  , где К — количество обрабатываемых блоков данных. Во втором случае, когда накапливаются частичные корреляционные функции, преобразование приходится выполнять
, где К — количество обрабатываемых блоков данных. Во втором случае, когда накапливаются частичные корреляционные функции, преобразование приходится выполнять  раз.
раз.
Из описанной выше методики вычислений видно, что размер ДПФ должен приблизительно вдвое превышать требуемое число отсчетов корреляционной функции, а требуемое количество преобразований равно  (здесь
(здесь  , причем N — общее число отсчетов сигнала, а М — требуемое число отсчетов корреляционной функции). Затем, дополнив
, причем N — общее число отсчетов сигнала, а М — требуемое число отсчетов корреляционной функции). Затем, дополнив  нулями и выполнив единственное ДПФ, можно получить оценку энергетического спектра с произвольным частотным разрешением. Если
нулями и выполнив единственное ДПФ, можно получить оценку энергетического спектра с произвольным частотным разрешением. Если  является хорошей оценкой корреляционной функции с малой дисперсией, то и преобразование от
является хорошей оценкой корреляционной функции с малой дисперсией, то и преобразование от  также будет достаточно хорошей оценкой спектра.
также будет достаточно хорошей оценкой спектра.
Для дальнейшего повышения эффективности вычислений можно использовать прием, предложенный Рэйдером, который отметил, что вычисляемые на первом зтапе значения  можно выразить через
можно выразить через  . Для этого следует прежде всего несколько изменить характер показанного на фиг. 6.31 секционирования последовательности, предусмотрев, чтобы секции содержали четное число отсчетов, желательно кратное 2, и перекрытие секций в точности было равно 2:1. Эти условия вполне выполнимы, потому что для большинства алгоритмов БПФ требуется или желательно иметь секции именно такой длины, а обеспечение перекрытия, в точности равного 2:1, означает, что в данном случае размер преобразования возрастает на один отсчет, что приводит конечно, к незначительному ухудшению эффективности вычислений.
. Для этого следует прежде всего несколько изменить характер показанного на фиг. 6.31 секционирования последовательности, предусмотрев, чтобы секции содержали четное число отсчетов, желательно кратное 2, и перекрытие секций в точности было равно 2:1. Эти условия вполне выполнимы, потому что для большинства алгоритмов БПФ требуется или желательно иметь секции именно такой длины, а обеспечение перекрытия, в точности равного 2:1, означает, что в данном случае размер преобразования возрастает на один отсчет, что приводит конечно, к незначительному ухудшению эффективности вычислений.
(см. скан)
Фиг. 6.32. Секционирование при вычислении оценок автокорреляционной функции.
На фиг. 6.32 изображена 20-точечная последовательность с отсчетами от  до
до  , разделенная на пять секций, и показано, для каких секций рассчитывается круговая автокорреляция. Справа показаны эквивалентные БПФ-операции. Идея излагаемого метода, как уже было отмечено, состоит в том, что любой коэффициент ДПФ
, разделенная на пять секций, и показано, для каких секций рассчитывается круговая автокорреляция. Справа показаны эквивалентные БПФ-операции. Идея излагаемого метода, как уже было отмечено, состоит в том, что любой коэффициент ДПФ  можно представить в функции от
можно представить в функции от  . Если, например,
. Если, например,

то

так как круговой сдвиг на  при ДПФ эквивалентен умножению самого ДПФ на
при ДПФ эквивалентен умножению самого ДПФ на  Следовательно,
Следовательно,

В более общем виде

Теперь, используя пару преобразований (6.93), описанную выше процедуру спектральных измерений можно изменить следующим образом:
1. Вычислить все  от
от  до
до  , где
, где  — ДПФ последовательностей, показанных на фиг. 6.32.
— ДПФ последовательностей, показанных на фиг. 6.32.
2. Вычислить

причем

3. Вычислить

4. Вычислить

После определения  можно вычислить спектральные оценки, рассчитав ДПФ от
можно вычислить спектральные оценки, рассчитав ДПФ от  Важно отметить, что количество преобразований, которые в рассматриваемом методе составляют основу всех вычислений, удалось уменьшить до К, где К — количество секций.
Важно отметить, что количество преобразований, которые в рассматриваемом методе составляют основу всех вычислений, удалось уменьшить до К, где К — количество секций.
Для того чтобы дисперсия оценки сходилась к нулю, нужно, чтобы аргумент  функции корреляции
функции корреляции  был значительно меньше интервала измерения. В результате оценка спектра вычисляется через преобразование усеченной последовательности
был значительно меньше интервала измерения. В результате оценка спектра вычисляется через преобразование усеченной последовательности  , а, как известно, усечение во временной области может вызвать чрезмерные пульсации в частотной области; в связи с этим приходится использовать окна.
, а, как известно, усечение во временной области может вызвать чрезмерные пульсации в частотной области; в связи с этим приходится использовать окна.
Проиллюстрируем сказанное на примере. Пусть интервал измерения содержит 1024 отсчета и известно, что отсчеты  малы при
малы при  , причем требуется найти 64 спектральные оценки на 64 частотах. Процедура вычислений состоит в следующем:
, причем требуется найти 64 спектральные оценки на 64 частотах. Процедура вычислений состоит в следующем:
1. Разделить секцию из 1024 отсчетов на подсекции длиной по 32 отсчета.
2. Рассчитать 32-точечные БПФ этих подсекций с перекрытием 2:1, т. е. сдвигаясь каждый раз на 16 отсчетов.
3. Используя описанный выше метод, найти  для
для  в пределах от 0 до 16.
в пределах от 0 до 16.
4. Чтобы получить оценку спектра, умножить  на соответствующее окно
на соответствующее окно  . Затем дополнить
. Затем дополнить  нулями на интервале от
нулями на интервале от  до
до  и вычислить БПФ сформированного массива.
и вычислить БПФ сформированного массива.
В общем случае, когда требуется вычислить L отсчетов корреляционной функции по N заданным отсчетам сигнала (N L), рассматриваемый корреляционный метод спектральных измерений можно сформулировать следующим образом. Искомая функция взаимной корреляции имеет вид

Простая методика вычисления по формуле (6.97) с использованием Р-точечного БПФ (Р = 2L) представлена на фиг. 6.33. Из последовательности  образуются подпоследовательности
образуются подпоследовательности  согласно правилу
согласно правилу

а из последовательности  формируются подпоследовательности
формируются подпоследовательности  по несколько иному правилу:
по несколько иному правилу:

Для каждой пары Р-точечных подпоследовательностей  вычисляется последовательность
вычисляется последовательность  представляющая собой периодическую корреляцию
представляющая собой периодическую корреляцию  . Она может быть эаписана в виде
. Она может быть эаписана в виде


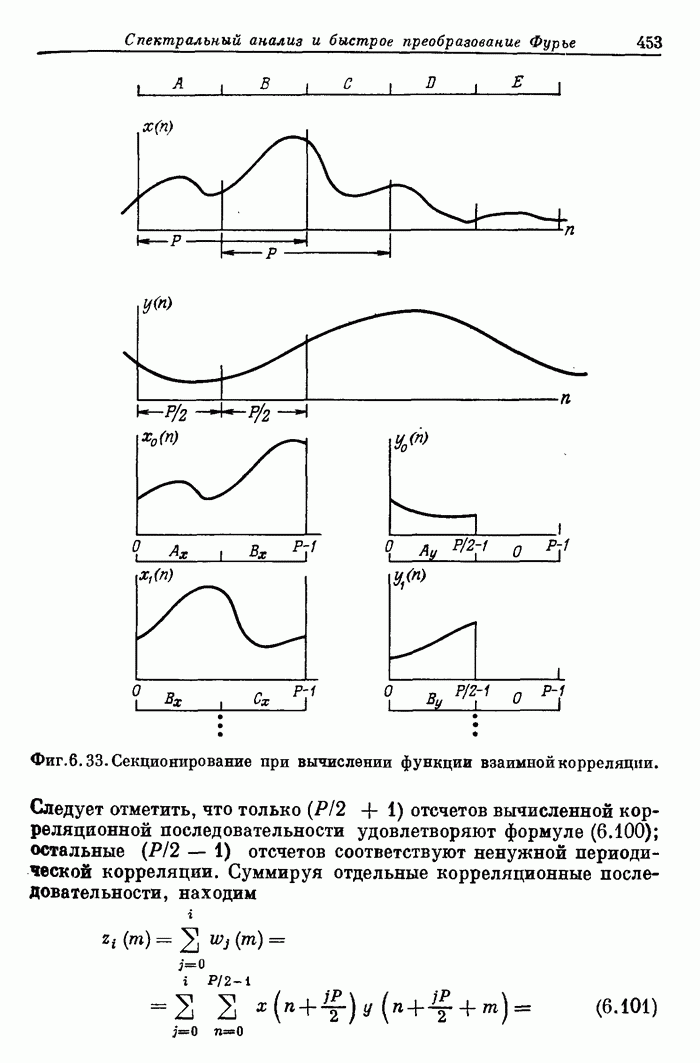
Фиг. 6.33. Секционирование при вычислении функции взаимной корреляции.
Следует отметить, что только  отсчетов вычисленной корреляционной последовательности удовлетворяют формуле (6.100); остальные
отсчетов вычисленной корреляционной последовательности удовлетворяют формуле (6.100); остальные  отсчетов соответствуют ненужной периодической корреляции. Суммируя отдельные корреляционные последовательности, находим
отсчетов соответствуют ненужной периодической корреляции. Суммируя отдельные корреляционные последовательности, находим
 (6.101)
(6.101)
 (6.102)
(6.102)
что идентично искомому результату (6.97) для  . Таким образом, корреляционные функции можно эффективно вычислять с использованием БПФ при любом числе задержек L.
. Таким образом, корреляционные функции можно эффективно вычислять с использованием БПФ при любом числе задержек L.
Как указывалось выше, при вычислении спектральной плотности мощности по корреляционной последовательности с использованием окна  могут возникнуть трудности. Если ДПФ окна не является положительным, то существует вероятность того, что вычисленная спектральная плотность мощности будет отрицательной, что весьма нежелательно. Причина этого нежелательного результата состоит в том, что вычисленная спектральная плотность мощности равна круговой свертке преобразования окна и преобразования найденной корреляционной последовательности, поэтому, если преобразование окна не является положительным на всех частотах, существует вероятность того, что из-за флуктуационных ошибок оценок корреляционной функции результирующая свертка на некоторых частотах может дать отрицательные значения спектра мощности. Существуют, однако, окна, преобразования которых положительны на всех частотах, например треугольное окно. Именно такие окна и следует применять в тех случаях, когда другие окна приводят к нежелательному результату.
могут возникнуть трудности. Если ДПФ окна не является положительным, то существует вероятность того, что вычисленная спектральная плотность мощности будет отрицательной, что весьма нежелательно. Причина этого нежелательного результата состоит в том, что вычисленная спектральная плотность мощности равна круговой свертке преобразования окна и преобразования найденной корреляционной последовательности, поэтому, если преобразование окна не является положительным на всех частотах, существует вероятность того, что из-за флуктуационных ошибок оценок корреляционной функции результирующая свертка на некоторых частотах может дать отрицательные значения спектра мощности. Существуют, однако, окна, преобразования которых положительны на всех частотах, например треугольное окно. Именно такие окна и следует применять в тех случаях, когда другие окна приводят к нежелательному результату.
Еще одна трудность применения корреляционного метода встречается при оценке взаимной спектральной плотности по функции взаимной корреляции с использованием окна. Как видно из формулы (6.100), отсчеты функции корреляции здесь измеряются только при положительных значениях  . При использовании этого метода для оценки автокорреляционной функции ее отсчеты при отрицательных
. При использовании этого метода для оценки автокорреляционной функции ее отсчеты при отрицательных  получаются автоматически благодаря симметрии автокорреляционной функции. Однако для функции взаимной корреляции эта симметрия не существует. Таким образом, неясно, как использовать окна для сглаживания взаимно корреляционной последовательности при оценке взаимной спектральной плотности. Существует несколько возможных способов сглаживания; они иллюстрируются на фиг. 6.34. Трудность заключается в том, что весьма непросто придать физический смысл значению взаимно корреляционной функции при
получаются автоматически благодаря симметрии автокорреляционной функции. Однако для функции взаимной корреляции эта симметрия не существует. Таким образом, неясно, как использовать окна для сглаживания взаимно корреляционной последовательности при оценке взаимной спектральной плотности. Существует несколько возможных способов сглаживания; они иллюстрируются на фиг. 6.34. Трудность заключается в том, что весьма непросто придать физический смысл значению взаимно корреляционной функции при  поскольку последняя зависит от задержки между
поскольку последняя зависит от задержки между  и
и  . Так, если
. Так, если  , то
, то  будет иметь пик при
будет иметь пик при  . И в этом случае можно было бы рассматривать точку
. И в этом случае можно было бы рассматривать точку  как некоторое начало координат
как некоторое начало координат  На фиг. 6.34 иллюстрируются три возможных способа взвешивания
На фиг. 6.34 иллюстрируются три возможных способа взвешивания  с использованием окна
с использованием окна  до выполнения ДПФ, позволяющих получить оценки
до выполнения ДПФ, позволяющих получить оценки  , имеющие физический смысл.
, имеющие физический смысл.

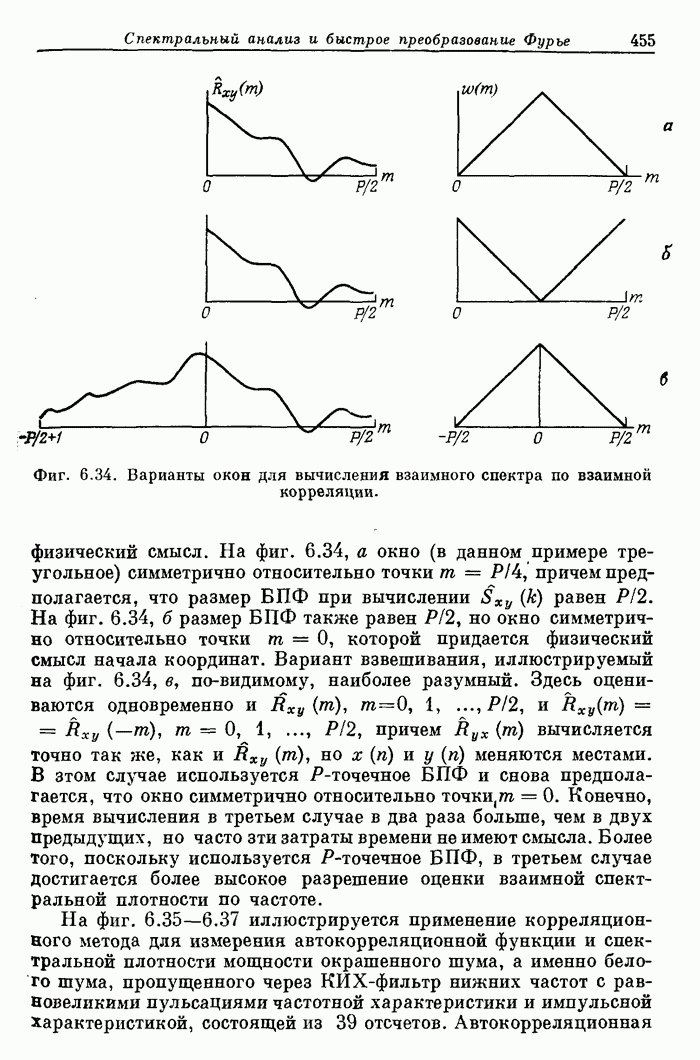
Фиг. 6.34. Варианты окон для вычисления взаимного спектра по взаимной корреляции.
На фиг. 6.34, а окно (в данном примере треугольное) симметрично относительно точки  причем предполагается, что размер БПФ при вычислении
причем предполагается, что размер БПФ при вычислении  равен
равен  На фиг. 6.34, б размер БПФ также равен
На фиг. 6.34, б размер БПФ также равен  но окно симметрично относительно точки
но окно симметрично относительно точки  , которой придается физический смысл начала координат. Вариант взвешивания, иллюстрируемый на фиг. 6.34, в, по-видимому, наиболее разумный. Здесь оцениваются одновременно и
, которой придается физический смысл начала координат. Вариант взвешивания, иллюстрируемый на фиг. 6.34, в, по-видимому, наиболее разумный. Здесь оцениваются одновременно и  причем
причем  вычисляется точно так же, как и
вычисляется точно так же, как и  но
но  меняются местами. В зтом случае используется Р-точечное БЙФ и снова предполагается, что окно симметрично относительно точки
меняются местами. В зтом случае используется Р-точечное БЙФ и снова предполагается, что окно симметрично относительно точки  . Конечно, время вычисления в третьем случае в два раза больше, чем в двух Предыдущих, но часто эти затраты времени не имеют смысла. Более того, поскольку используется Р-точечное БПФ, в третьем случае достигается более высокое разрешение оценки взаимной спектральной плотности по частоте.
. Конечно, время вычисления в третьем случае в два раза больше, чем в двух Предыдущих, но часто эти затраты времени не имеют смысла. Более того, поскольку используется Р-точечное БПФ, в третьем случае достигается более высокое разрешение оценки взаимной спектральной плотности по частоте.
На фиг. 6.35-6.37 иллюстрируется применение корреляционного метода для измерения автокорреляционной функции и спектральной плотности мощности окрашенного шума, а именно белого шума, пропущенного через КИХ-фильтр нижних частот с равновеликими пульсациями частотной характеристики и импульсной характеристикой, состоящей из 39 отсчетов.
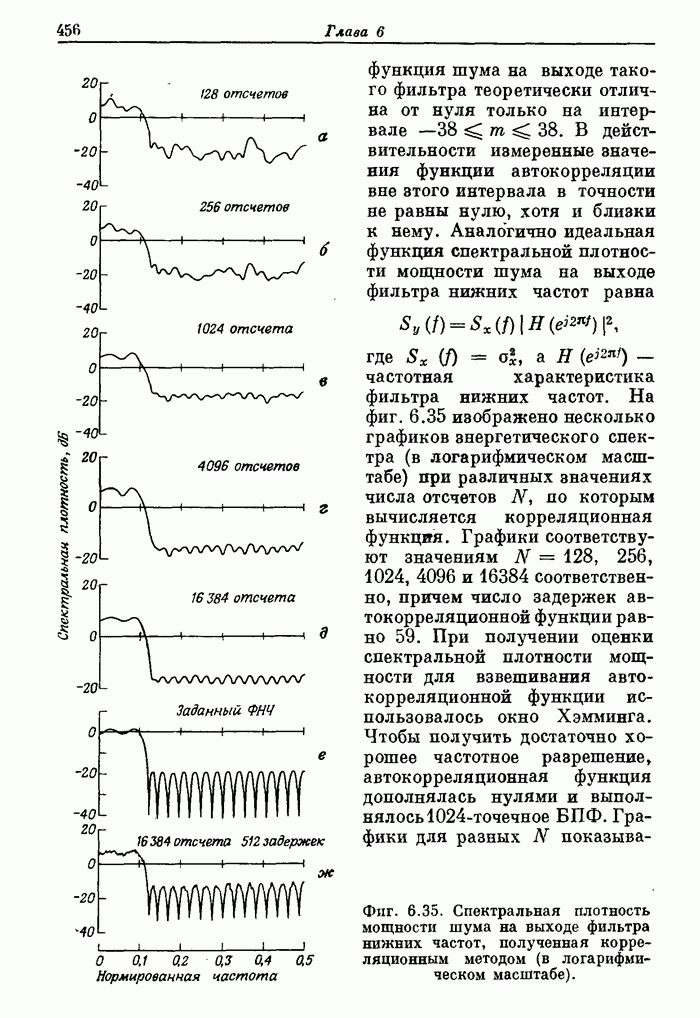
Автокорреляционная функция шума на выходе такого фильтра теоретически отлична от нуля только на интервале  . В действительности измеренные значения функции автокорреляции вне зтого интервала в точности не равны нулю, хотя и близки к нему. Аналогично идеальная функция спектральной плотности мощности шума на выходе фильтра нижних частот равна
. В действительности измеренные значения функции автокорреляции вне зтого интервала в точности не равны нулю, хотя и близки к нему. Аналогично идеальная функция спектральной плотности мощности шума на выходе фильтра нижних частот равна

где  - частотная характеристика фильтра нижних частот. На фиг. 6.35 изображено несколько графиков энергетического спектра (в логарифмическом масштабе) при различных значениях числа отсчетов N, по которым вычисляется корреляционная функция. Графики соответствуют значениям N = 128, 256, 1024, 4096 и 16384 соответственно, причем число задержек автокорреляционной функции равно 59. При получении оценки спектральной плотности мощности для взвешивания автокорреляционной функции использовалось окно Хэмминга. Чтобы получить достаточно хорошее частотное разрешение, автокорреляционная функция дополнялась нулями и выполнялось 1024-точечное БПФ. Графики для разных N показывают, что функция
- частотная характеристика фильтра нижних частот. На фиг. 6.35 изображено несколько графиков энергетического спектра (в логарифмическом масштабе) при различных значениях числа отсчетов N, по которым вычисляется корреляционная функция. Графики соответствуют значениям N = 128, 256, 1024, 4096 и 16384 соответственно, причем число задержек автокорреляционной функции равно 59. При получении оценки спектральной плотности мощности для взвешивания автокорреляционной функции использовалось окно Хэмминга. Чтобы получить достаточно хорошее частотное разрешение, автокорреляционная функция дополнялась нулями и выполнялось 1024-точечное БПФ. Графики для разных N показывают, что функция  быстро сходится к
быстро сходится к  .
.

Фиг. 6.35. Спектральная плотность мощности шума на выходе фильтра нижних частот, полученная корреляционным методом (в логарифмическом масштабе).
Для сравнения на фиг. 6.35, е показана идеальная характеристика  На фиг. 6.35, ж изображен график спектральной плотности мощности, полученный с помощью БПФ по 512 точкам автокорреляционной функции, взвешенной треугольным окном. Поскольку автокорреляционная функция при
На фиг. 6.35, ж изображен график спектральной плотности мощности, полученный с помощью БПФ по 512 точкам автокорреляционной функции, взвешенной треугольным окном. Поскольку автокорреляционная функция при  представляет собой чисто случайную шумовую последовательность, полученная функция спектральной плотности будет совпадать с идеальной характеристикой фильтра
представляет собой чисто случайную шумовую последовательность, полученная функция спектральной плотности будет совпадать с идеальной характеристикой фильтра  с наложенным на нее шумом.
с наложенным на нее шумом.

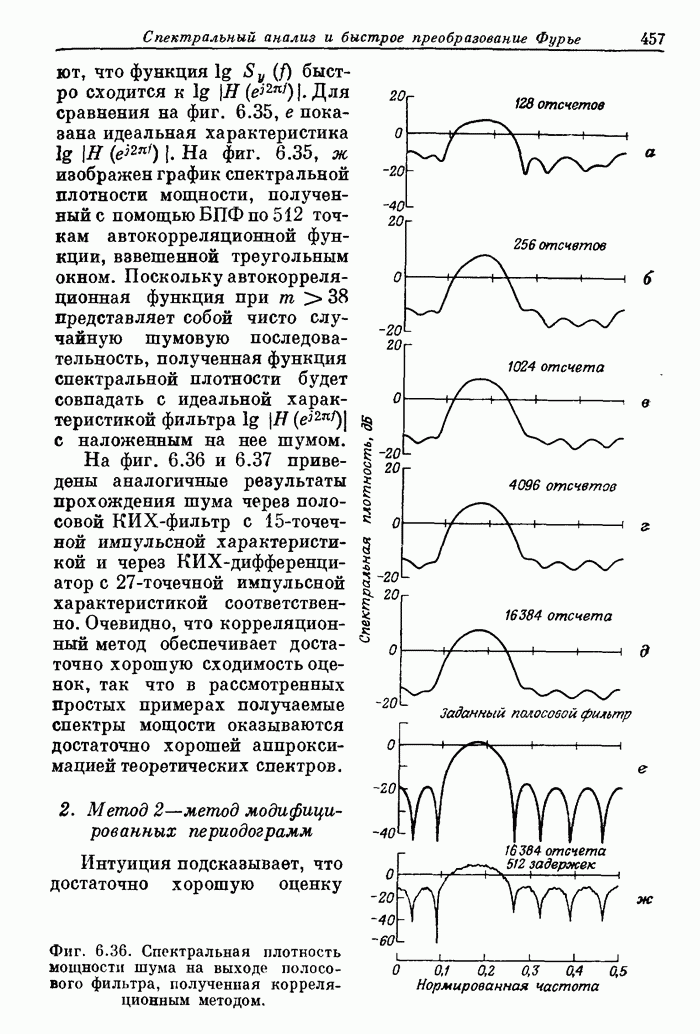
Фиг. 6.36. Спектральная плотность мощности шума на выходе полосового фильтра, полученная корреляционным методом.
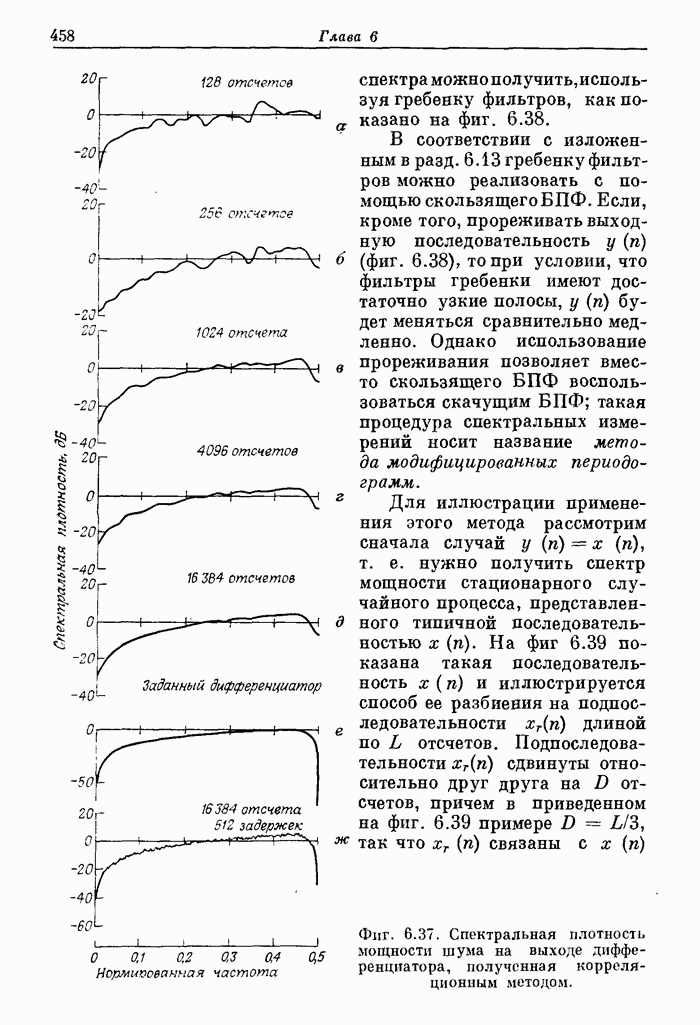
На фиг. 6.36 и 6.37 приведены аналогичные результаты прохождения шума через полосовой КИХ-фильтр с 15-точечной импульсной характеристикой и через КИХ-дифференциатор с 27-точечной импульсной характеристикой соответственно. Очевидно, что корреляционный метод обеспечивает достаточно хорошую сходимость оценок, так что в рассмотренных простых примерах получаемые спектры мощости оказываются достаточно хорошей аппроксимацией теоретических спектров.
2. Метод 2 - метод модифицированных периодограмм
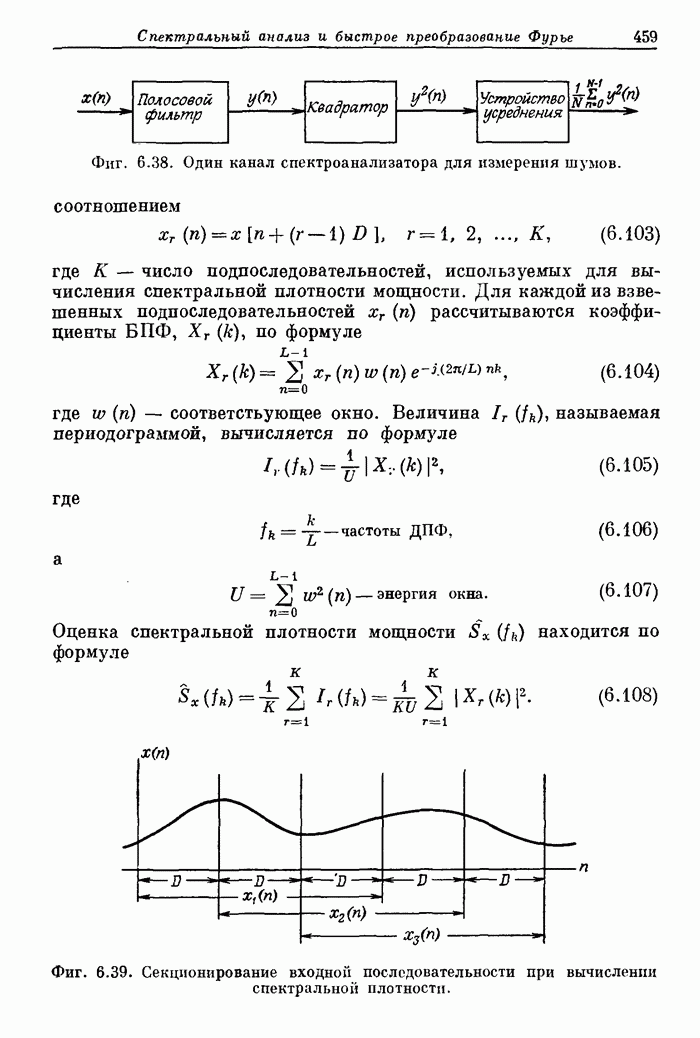
Интуиция подсказывает, что достаточно хорошую оценку спектра можно получить, используя гребенку фильтров, как показано на фиг. 6.38.
В соответствии с изложенным в разд. 6.13 гребенку фильтров можно реализовать с помощью скользящего БПФ. Если, кроме того, прореживать выходную последовательность  (фиг. 6.38), то при условии, что фильтры гребенки имеют достаточно узкие полосы,
(фиг. 6.38), то при условии, что фильтры гребенки имеют достаточно узкие полосы,  будет меняться сравнительно медленно. Однако использование прореживания позволяет вместо скользящего БПФ воспользоваться скачущим БПФ; такая процедура спектральных измерений носит название метода модифицированных периодограмм.
будет меняться сравнительно медленно. Однако использование прореживания позволяет вместо скользящего БПФ воспользоваться скачущим БПФ; такая процедура спектральных измерений носит название метода модифицированных периодограмм.
Для иллюстрации применения этого метода рассмотрим сначала случай  , т. е. нужно получить спектр мощности стационарного случайного процесса, представленного типичной последовательностью
, т. е. нужно получить спектр мощности стационарного случайного процесса, представленного типичной последовательностью  . На фиг 6.39 показана такая последовательность
. На фиг 6.39 показана такая последовательность  и иллюстрируется способ ее разбиения на подпоследовательности
и иллюстрируется способ ее разбиения на подпоследовательности  длиной по L отсчетов. Подпоследовательности
длиной по L отсчетов. Подпоследовательности  сдвинуты относительно друг друга на D отсчетов, причем в приведенном на фиг. 6.39 примере
сдвинуты относительно друг друга на D отсчетов, причем в приведенном на фиг. 6.39 примере  , так что
, так что  связаны с
связаны с  соотношением
соотношением

Фиг. 6.37. Спектральная плотность мощности шума на выходе дифференциатора, полученная корреляционным методом.

Фиг. 6.38. Один канал спектроанализатора для измерения шумов.
 (6.103)
(6.103)
где К — число подпоследовательностей, используемых для вычисления спектральной плотности мощности. Для каждой из взвешенных подпоследовательностей  рассчитываются коэффициенты БПФ,
рассчитываются коэффициенты БПФ,  , по формуле
, по формуле
 (6.104)
(6.104)
где  — соответстьующее окно. Величина
— соответстьующее окно. Величина  , называемая периодограммой, вычисляется по формуле
, называемая периодограммой, вычисляется по формуле

где

а

Оценка спектральной плотности мощности  находится по формуле
находится по формуле
 (6.108)
(6.108)

Фиг. 6.39. Секционирование входной последовательности при вычислении спектральной плотности.
Таким образом, оценка спектральной плотности мощности равна среднему значению периодограмм отдельных подпоследовательностей. Уэлч показал, что математическое ожидание этой оценки описывается формулой
 (6.109)
(6.109)
где
 (6.110)
(6.110)
а  — истинная спектральная плотность мощности анализируемого процесса с отчетами
— истинная спектральная плотность мощности анализируемого процесса с отчетами  . Из формулы (6.109) следует, что математическое ожидание искомой оценки равно свертке истинной спектральной плотности мощности с квадратом модуля фурье-преобразования от последовательности окна. Кроме того, Уэлч показал, что в случае, когда последовательность
. Из формулы (6.109) следует, что математическое ожидание искомой оценки равно свертке истинной спектральной плотности мощности с квадратом модуля фурье-преобразования от последовательности окна. Кроме того, Уэлч показал, что в случае, когда последовательность  формируется из реализации гауссовского случайного процесса, а функция
формируется из реализации гауссовского случайного процесса, а функция  является достаточно гладкой в диапазоне частот, где значения ДПФ окна достаточно велики, дисперсия оценки описывается формулой
является достаточно гладкой в диапазоне частот, где значения ДПФ окна достаточно велики, дисперсия оценки описывается формулой

где
 (6.113)
(6.113)
В качестве иллюстрации применения формулы (6.112) рассмотрим случай  , для которого
, для которого  при
при  . Для этого случая
. Для этого случая
 (6.114)
(6.114)
где  . Теперь рассмотрим случай
. Теперь рассмотрим случай  , причем считаем, что используется треугольное окно, изображенное на фиг. 6.40. Для этого случая
, причем считаем, что используется треугольное окно, изображенное на фиг. 6.40. Для этого случая  [см. формулу (6.113)] и
[см. формулу (6.113)] и  при
при  . Следовательно,
. Следовательно,
 (6.115)
(6.115)

Фиг. 6.40. Треугольное окно.
Но  , поэтому соотношение (6.115) можно переписать в виде
, поэтому соотношение (6.115) можно переписать в виде
 (6.116)
(6.116)
Итак, используя всего лишь сдвиг подпоследовательности на половину ширины окна, а не на полное окно, можно уменьшить дисперсию оценки почти в два раза (но за счет удвоения времени вычисления).
При вычислении взаимного спектра обе последовательности  разбиваются на подпоследовательности
разбиваются на подпоследовательности  , как показано на фиг. 6.39. Каждая из подпоследовательностей перед вычислением преобразований
, как показано на фиг. 6.39. Каждая из подпоследовательностей перед вычислением преобразований  взвешивается окном. Периодограмма в этом случае имеет вид
взвешивается окном. Периодограмма в этом случае имеет вид
 (6.117)
(6.117)
где U определяется согласно формуле (6.107). Оценка ваимного спектра находится по формуле


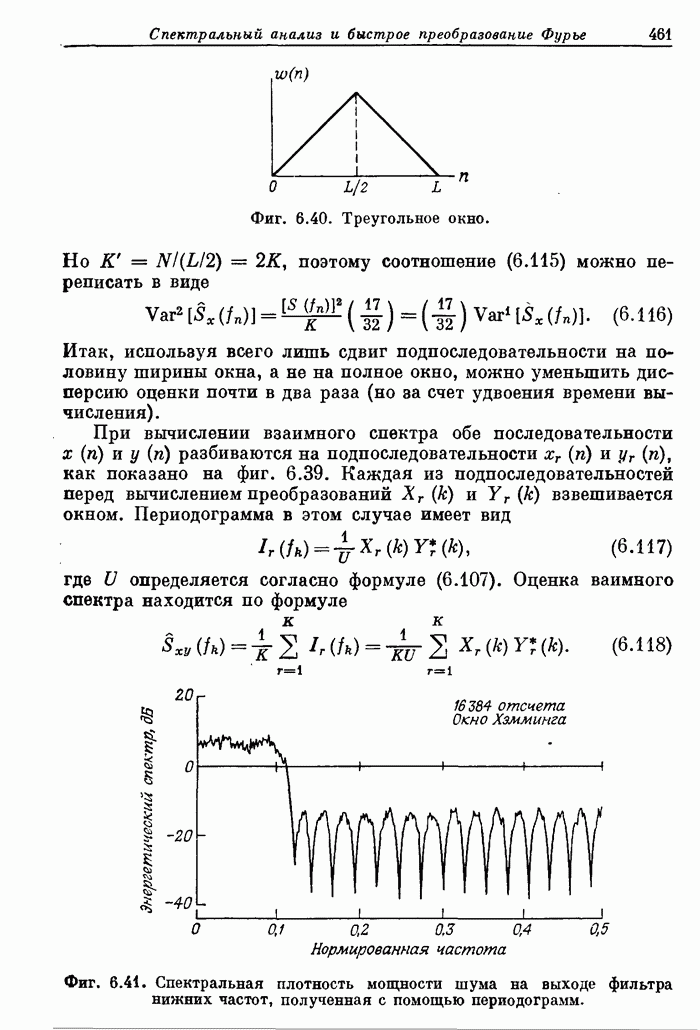
Фиг. 6.41. Спектральная плотность мощности шума на выходе фильтра нижних частот, полученная с помощью периодограмм.

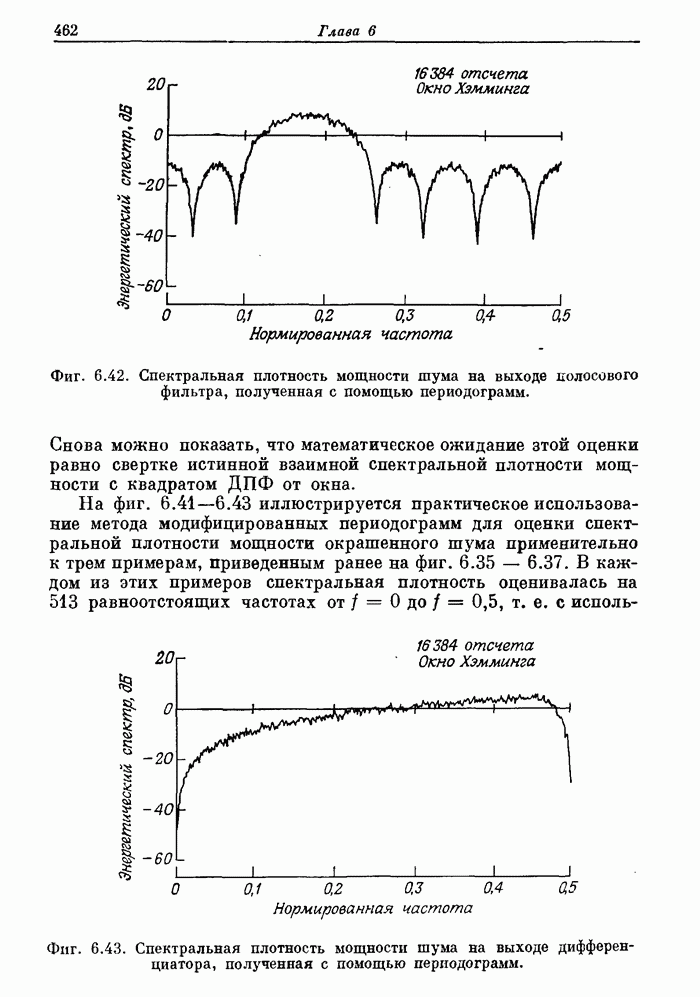
Фиг. 6.42. Спектральная плотность мощности шума на выходе колосового фильтра, полученная с помощью периодограмм.
Снова можно показать, что математическое ожидание зтой оценки равно свертке истинной взаимной спектральной плотности мощности с квадратом ДПФ от окна.
На фиг. 6.41-6.43 иллюстрируется практическое использование метода модифицированных периодограмм для оценки спектральной плотности мощности окрашенного шума применительно к трем примерам, приведенным ранее на фиг. 6.35 — 6.37. В каждом из этих примеров спектральная плотность оценивалась на 513 равноотстоящих частотах от  до
до  , т. е. с использованием L-точечного БПФ (L = 1024).
, т. е. с использованием L-точечного БПФ (L = 1024).

Фиг. 6.43. Спектральная плотность мощности шума на выходе дифференциатора, полученная с помощью периодограмм.
Для взвешивания входной последовательности применялось окно Хэмминга. С целью уменьшения дисперсии оценки при фиксированном числе входных отсчетов был использован сдвиг подпоследовательностей на D = 512 отсчетов. Общее число подпоследовательностей равно 32, т. е. всего обрабатывалось N = 16384 отсчетов. На фиг. 6.41 изображен энергетический спектр шума на выходе фильтра нижних частот (в логарифмическом масштабе), а на фиг. 6.42 и 6.43 — энергетические спектры шумовых последовательностей на выходах полосового фильтра и дифференциатора соответственно.
3. Выводы
Итак, для оценки энергетического спектра или корреляционных функций случайных процессов можно использовать два эффективных метода. В зависимости от конкретной задачи каждый из них может иметь преимущества относительно другого. Общим для обоих методов является то, что среднее значение оценки спектра сходится к определенной величине, а дисперсия оценки стремится к нулю, когда число обрабатываемых отсчетов стремится к бесконечности.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
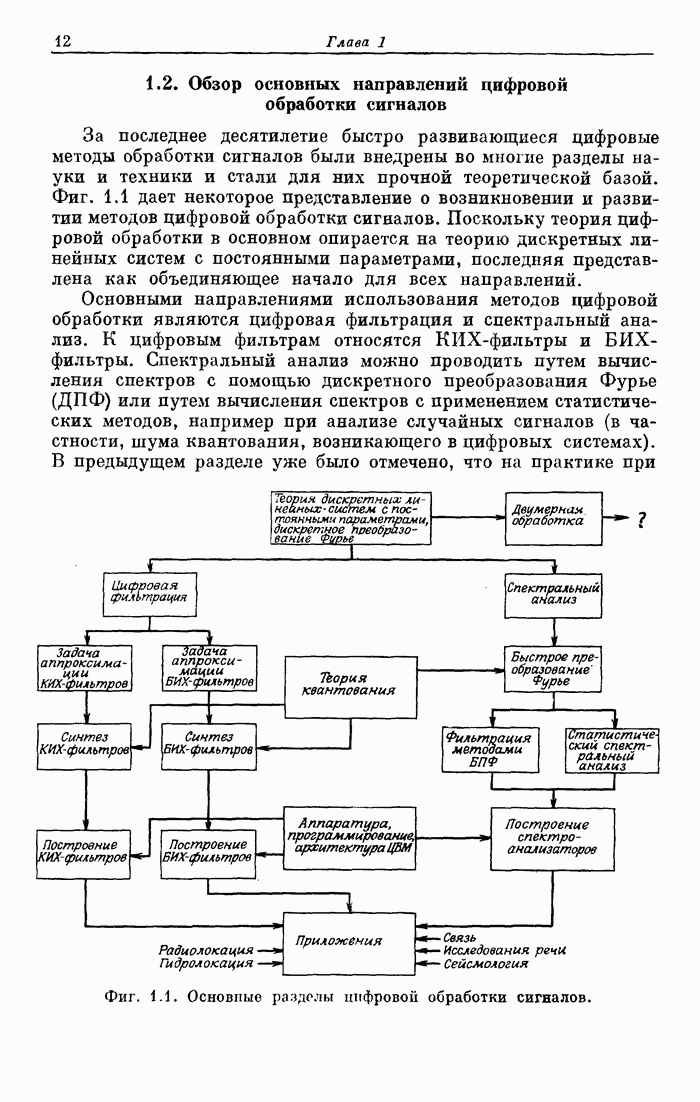
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
- 2.5. Физическая реализуемость. Устойчивость
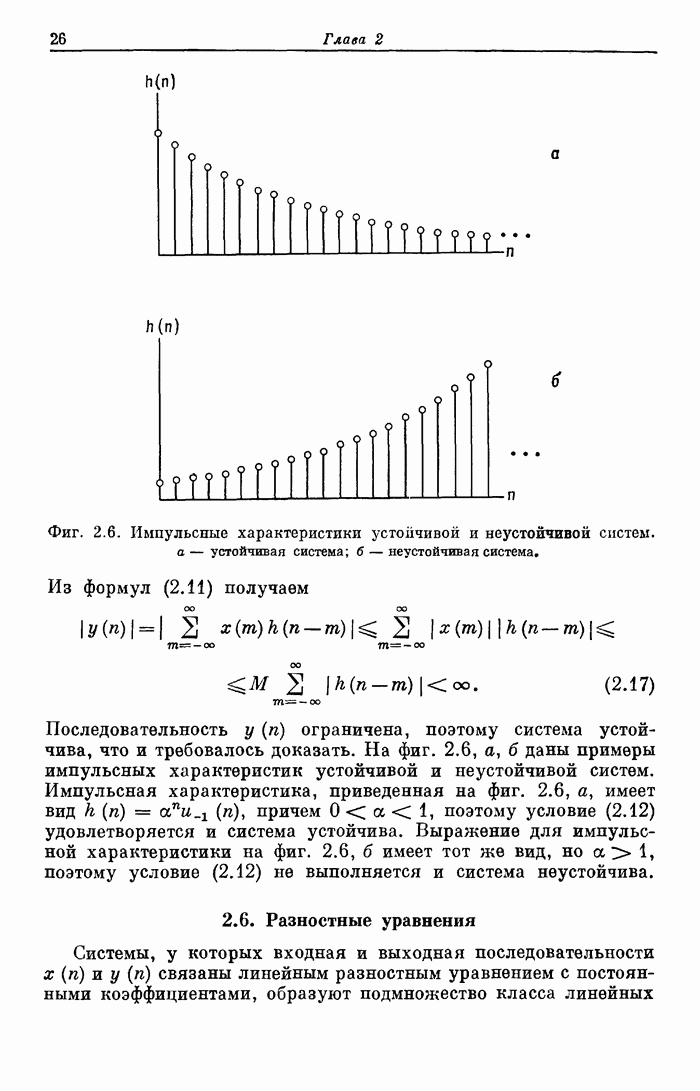
- 2.6. Разностные уравнения
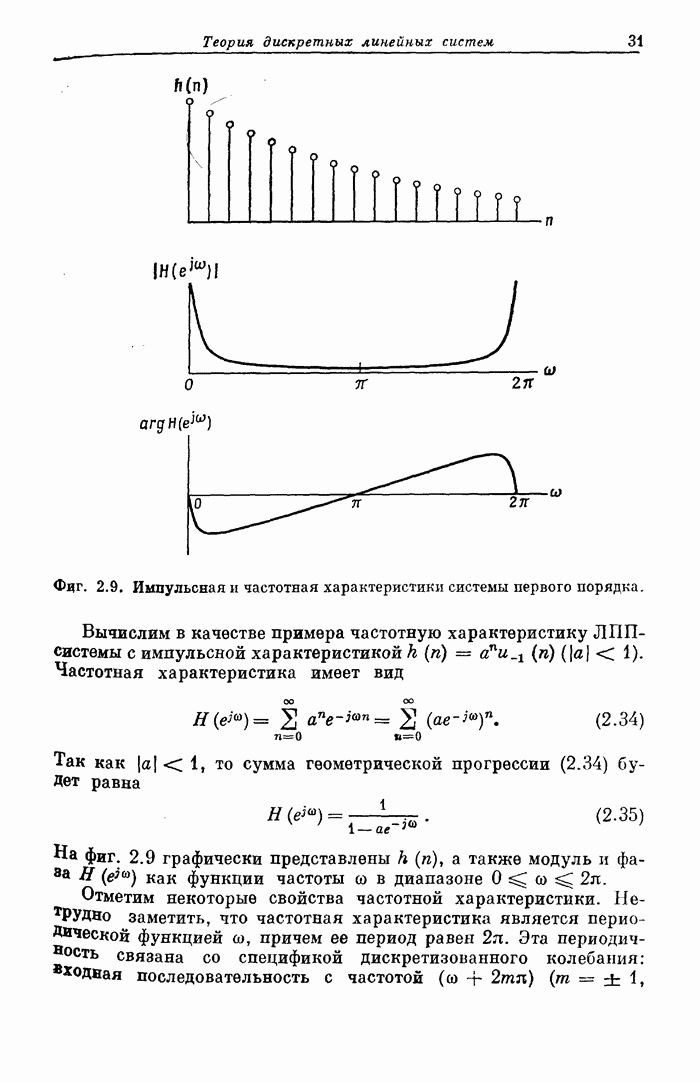
- 2.7. Частотная характеристика
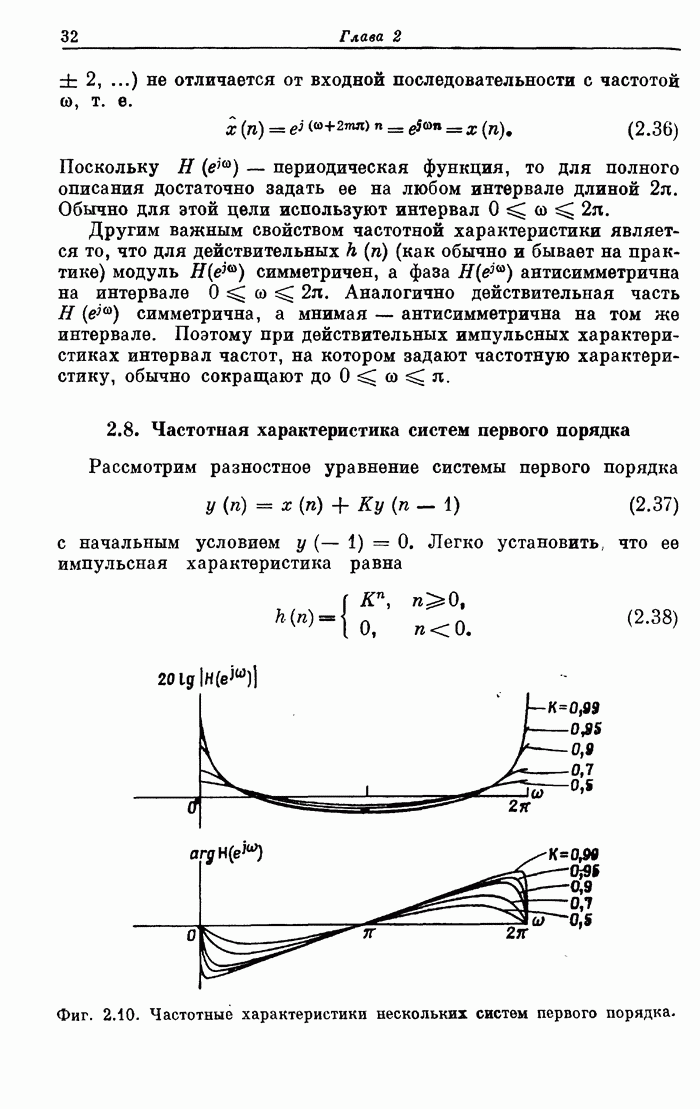
- 2.8. Частотная характеристика систем первого порядка
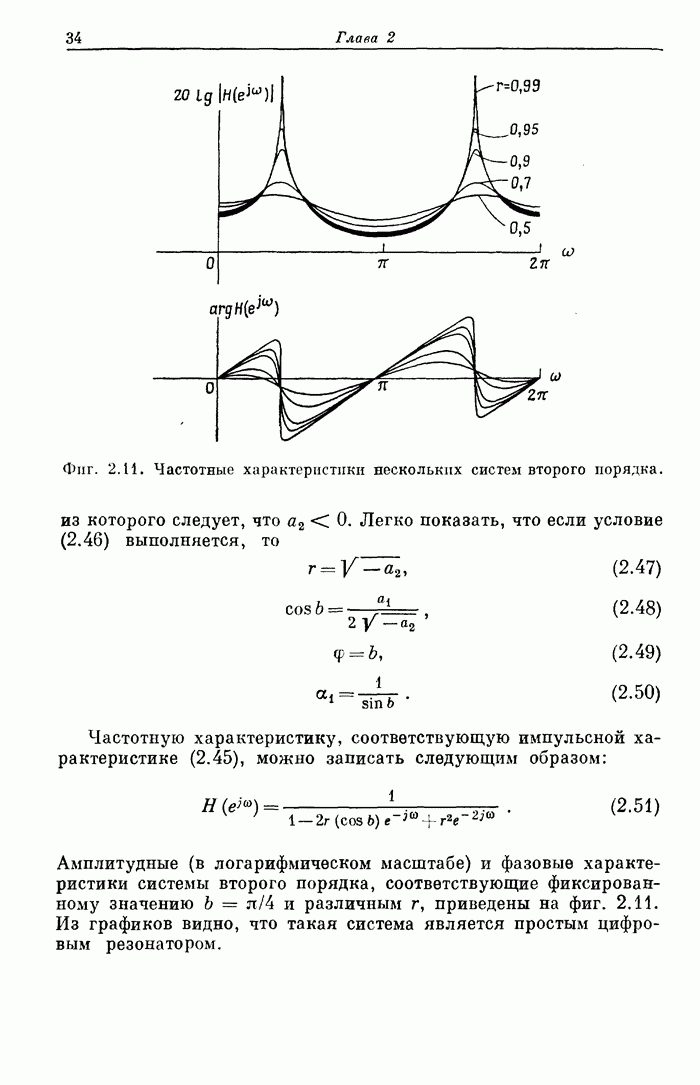
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
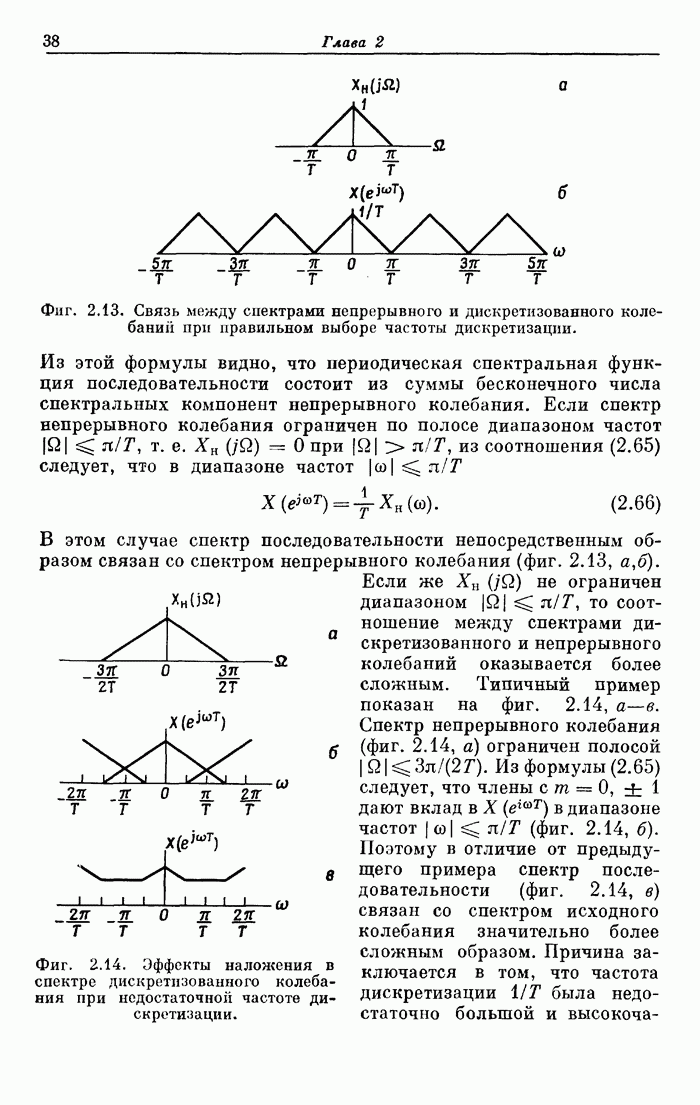
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
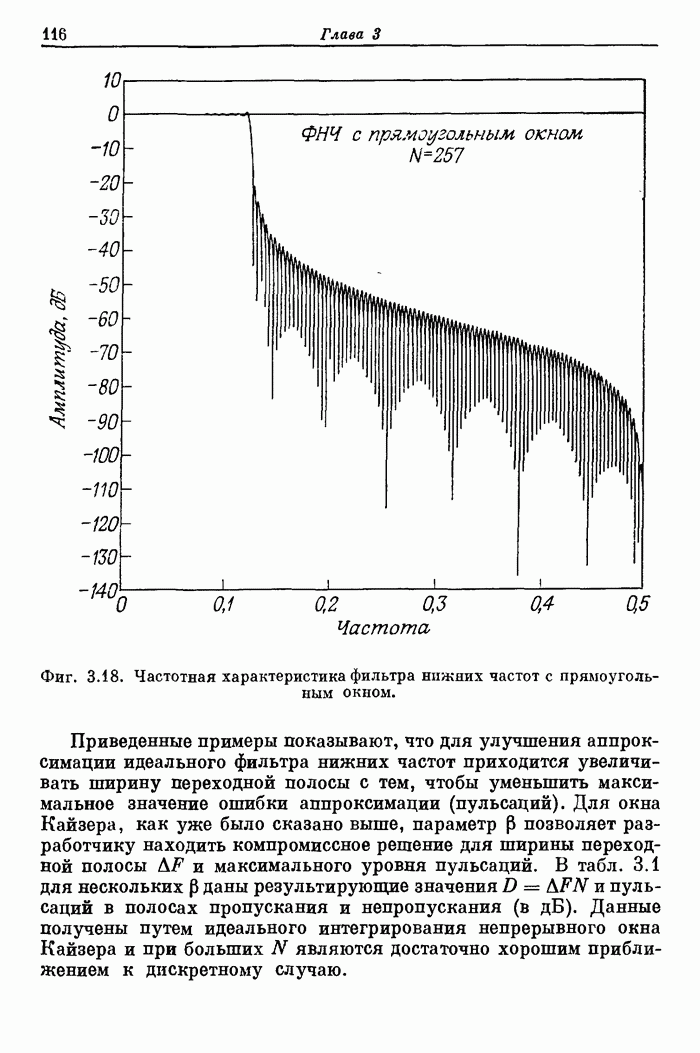
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
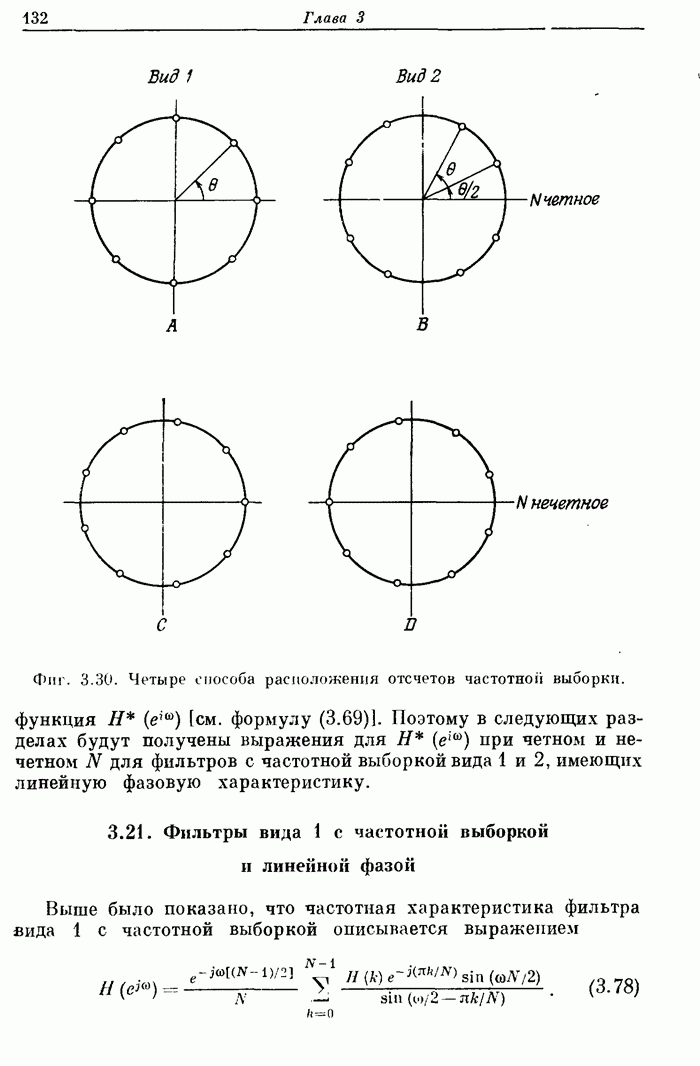
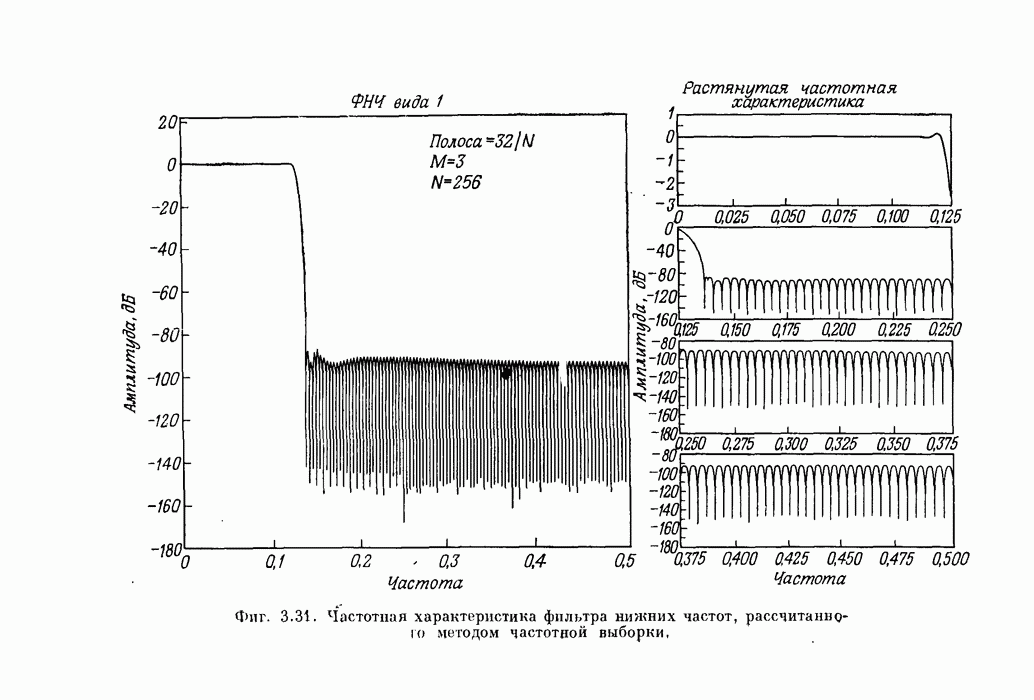
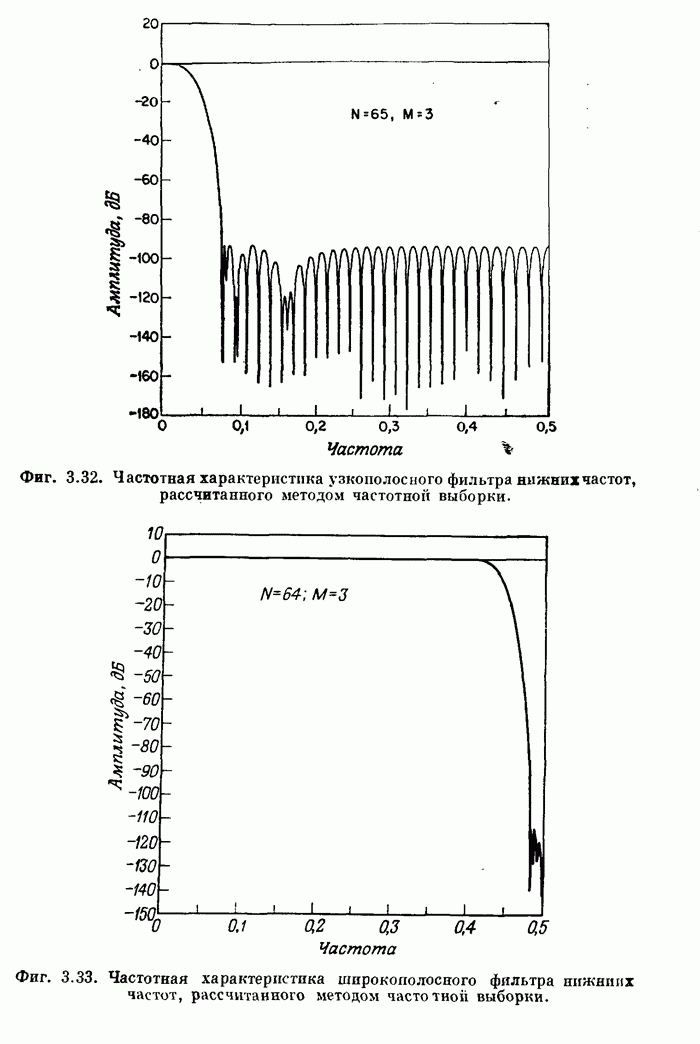
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
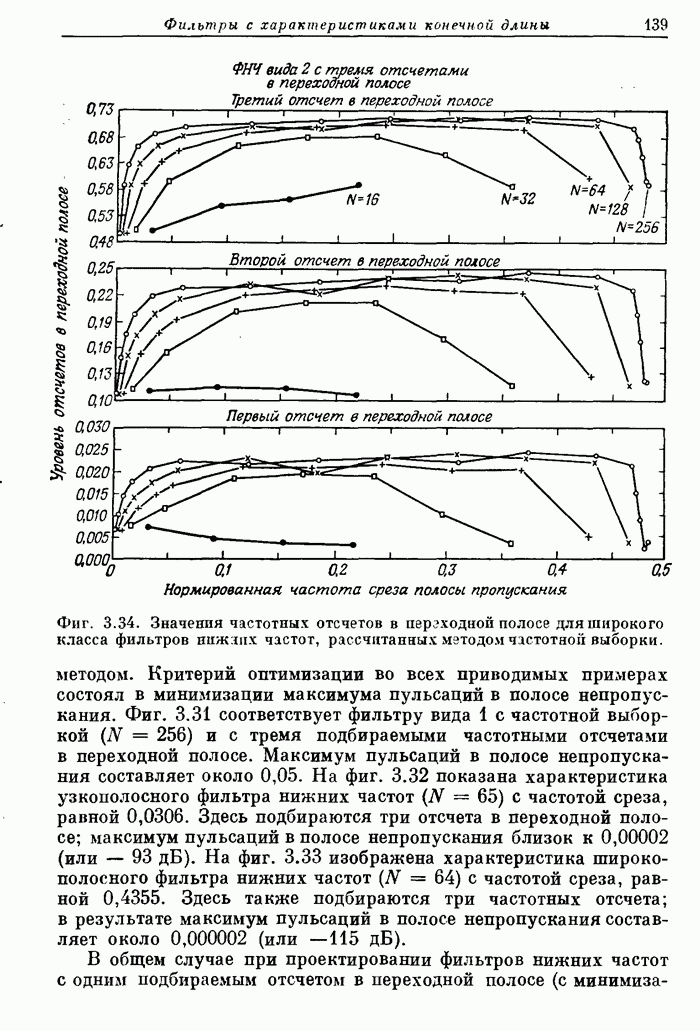
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
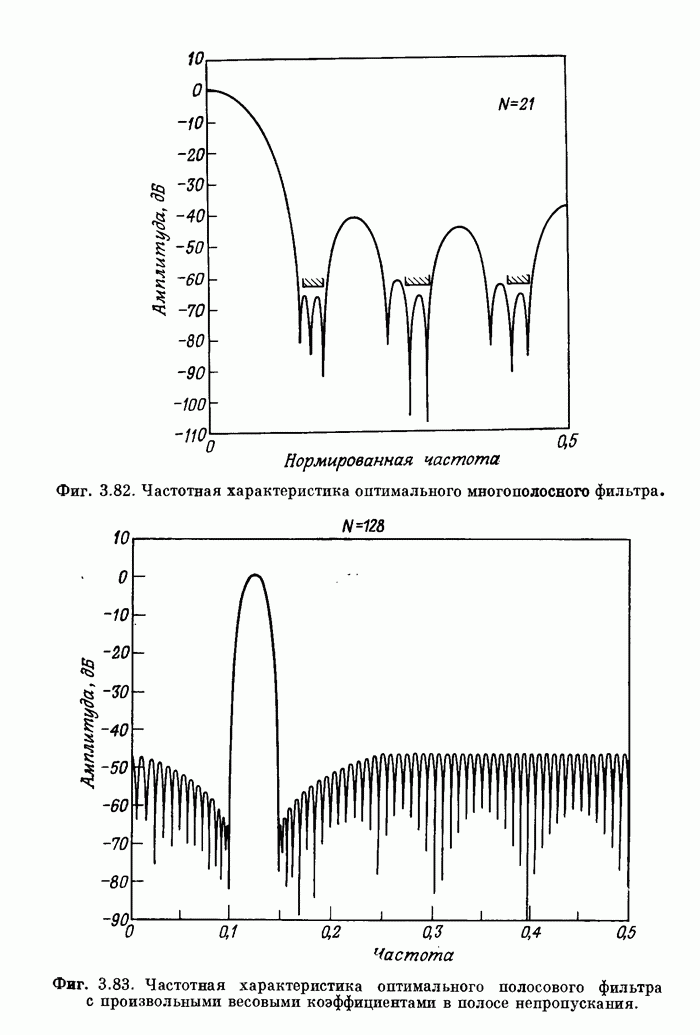
- 3.38. Многополосные оптимальные КИХ-фильтры
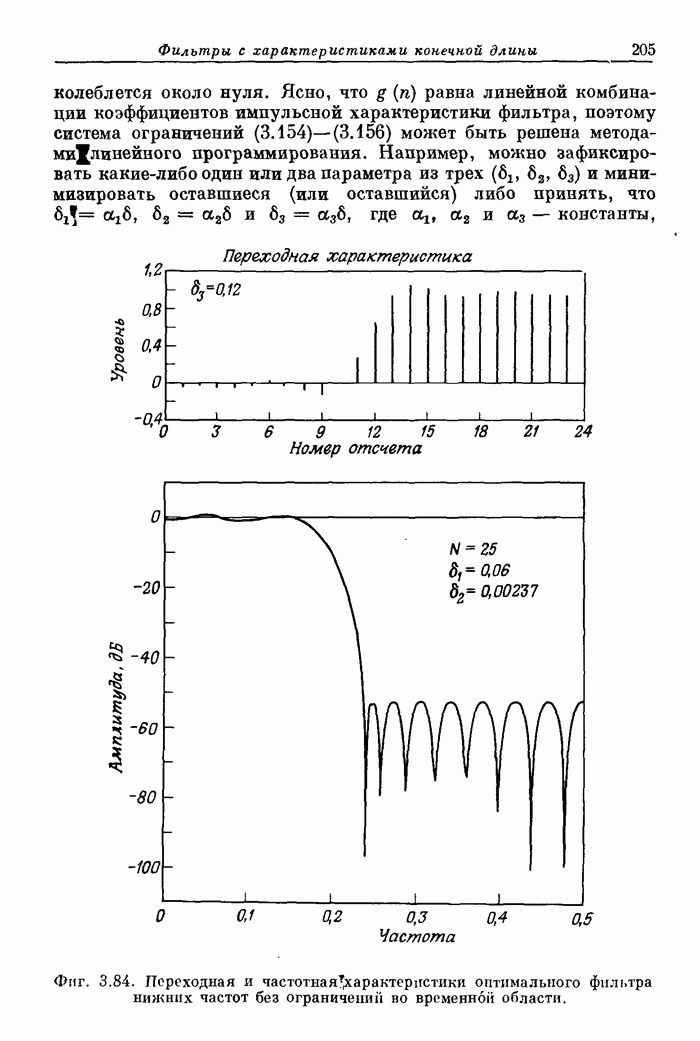
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
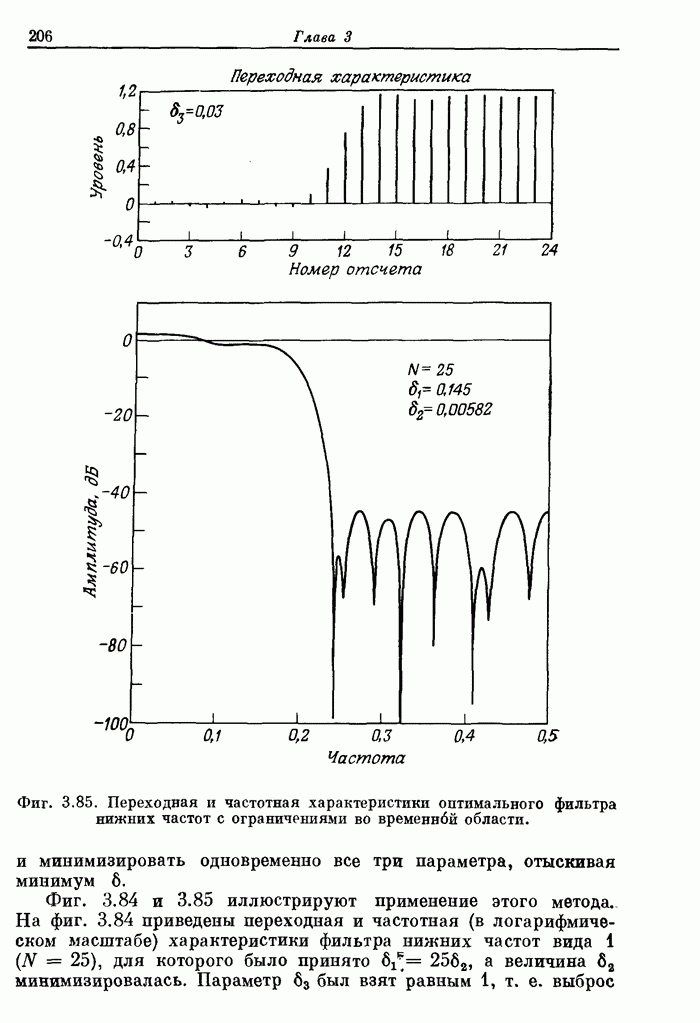
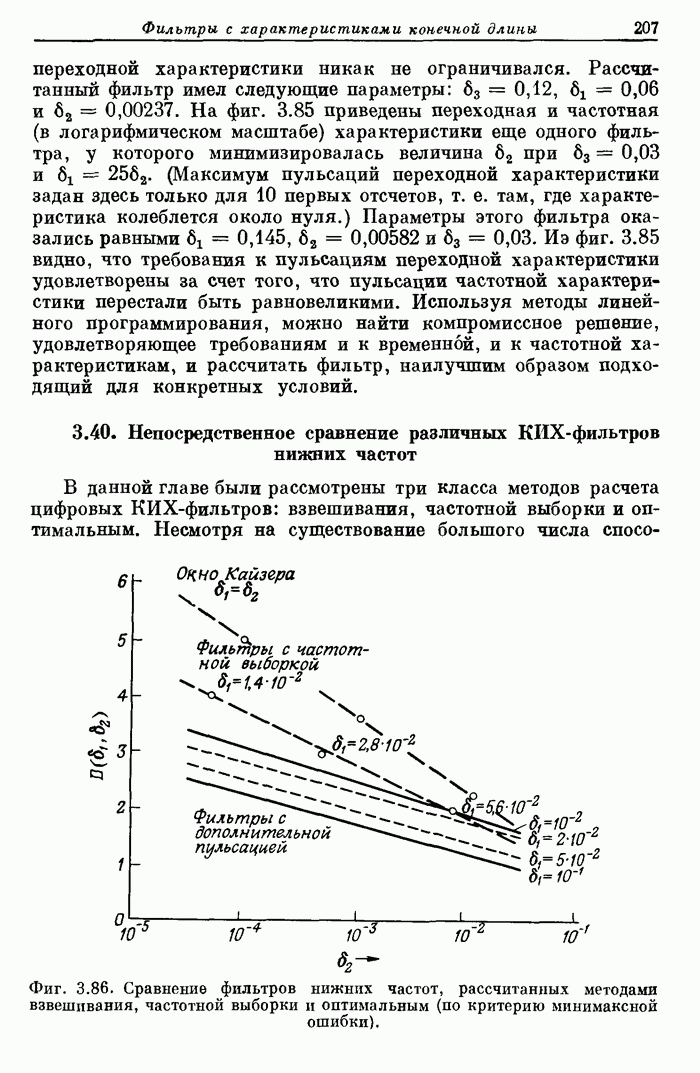
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
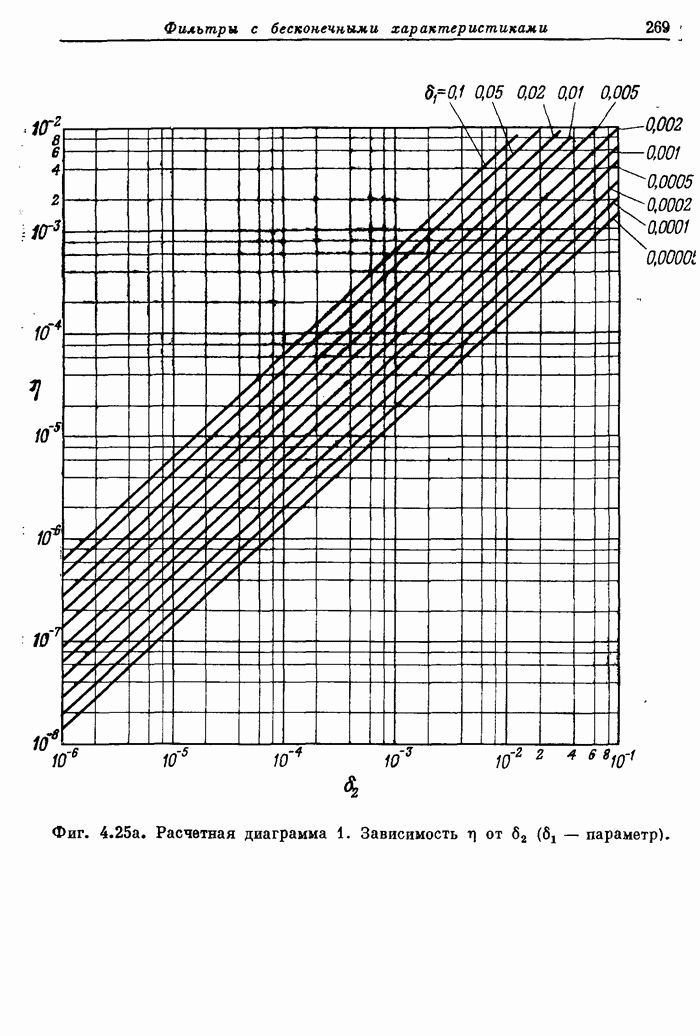
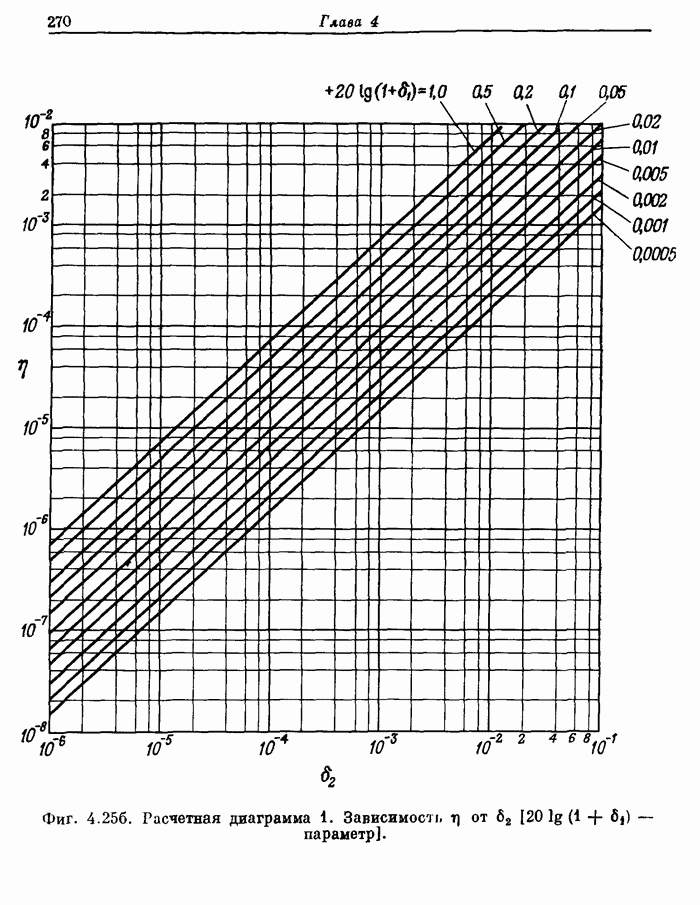
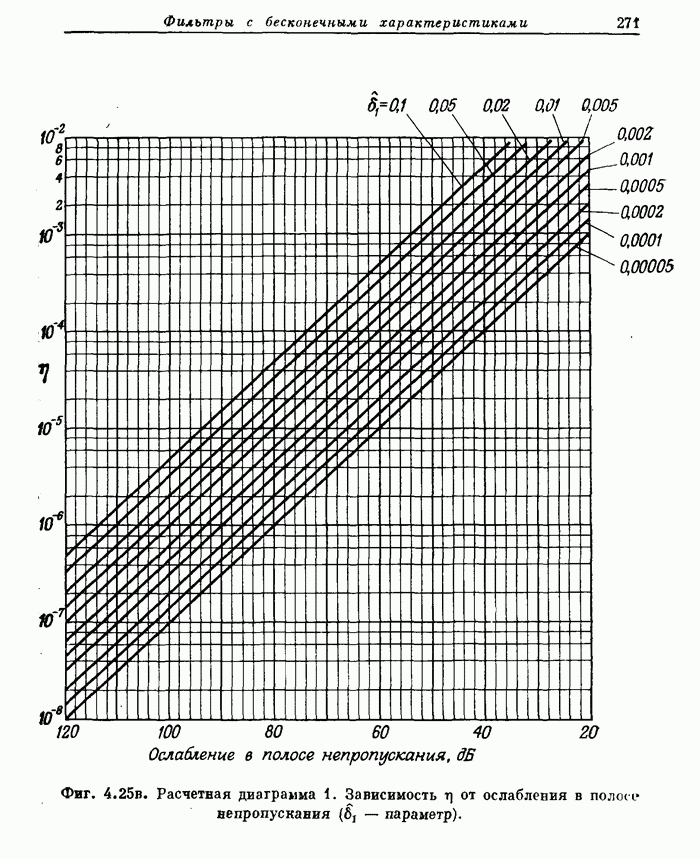
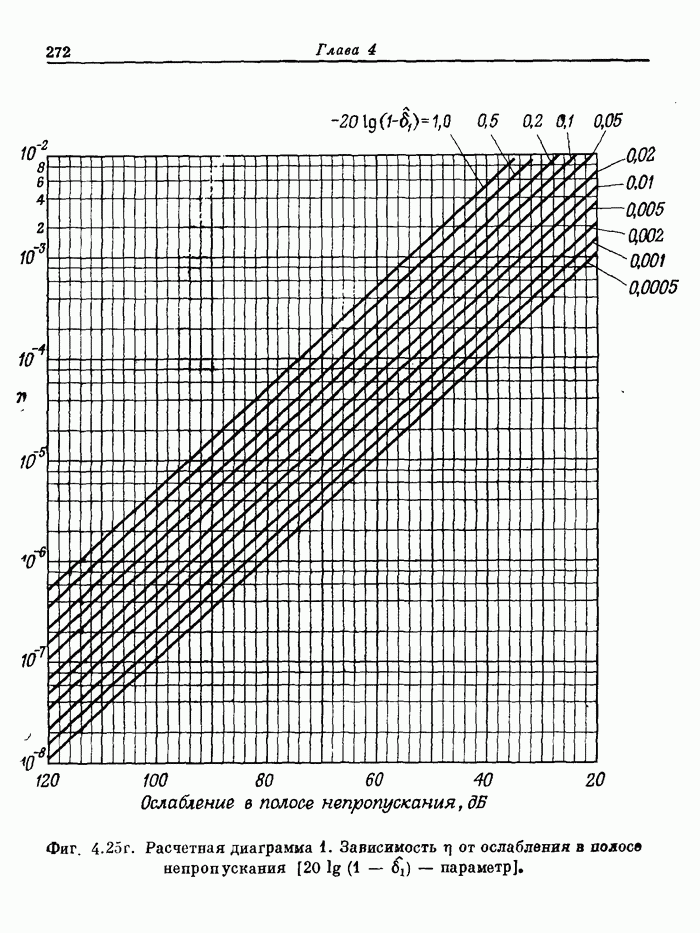
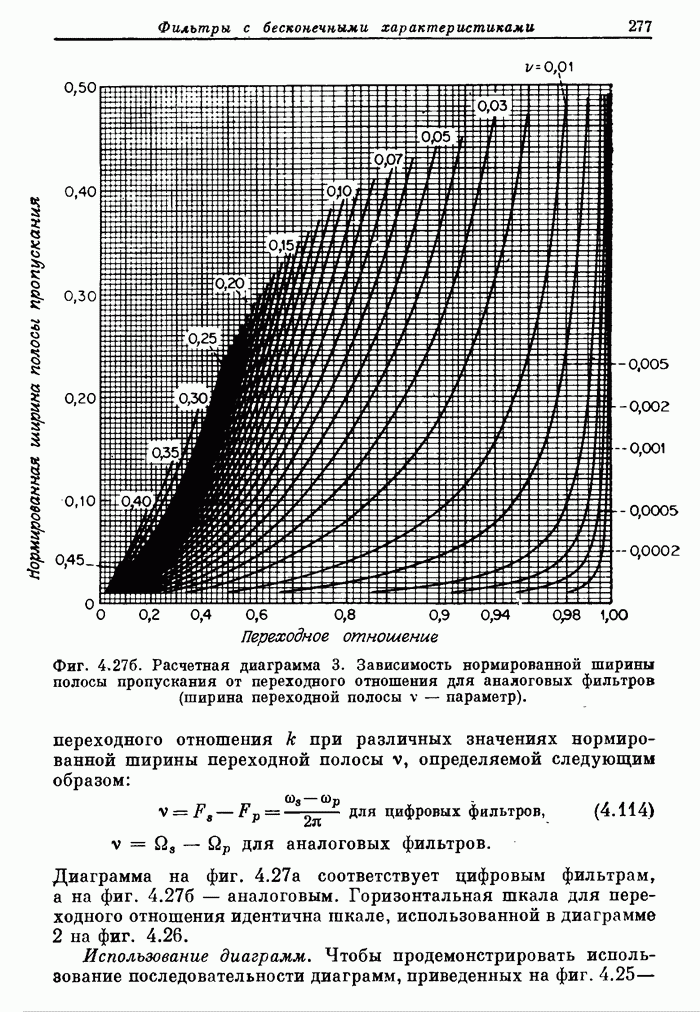
- 4.10. Расчетные диаграммы фильтров нижних частот
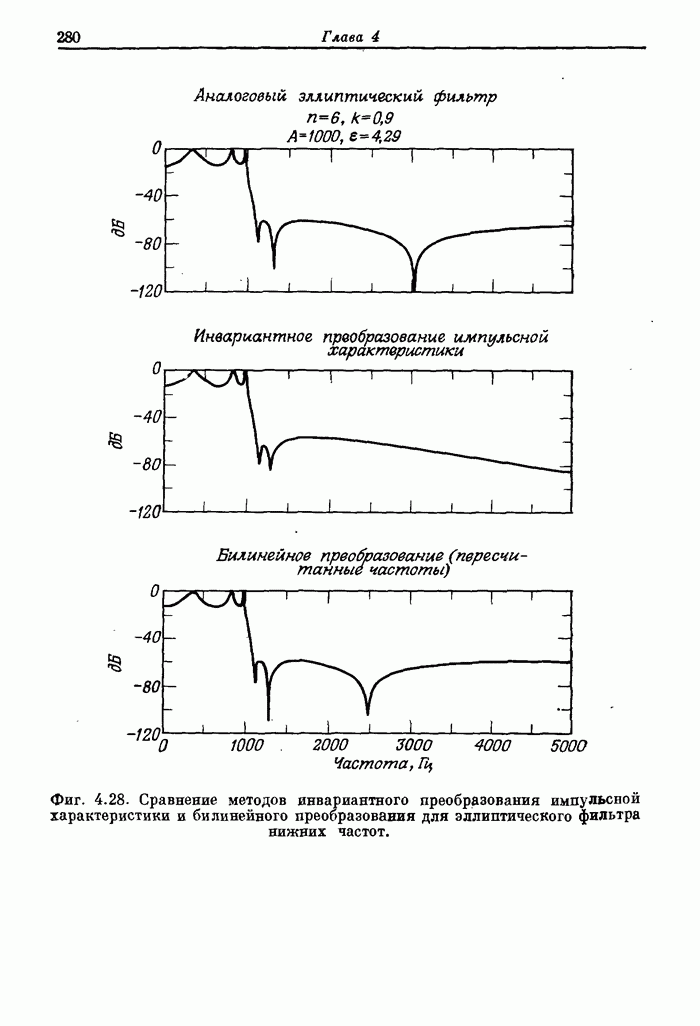
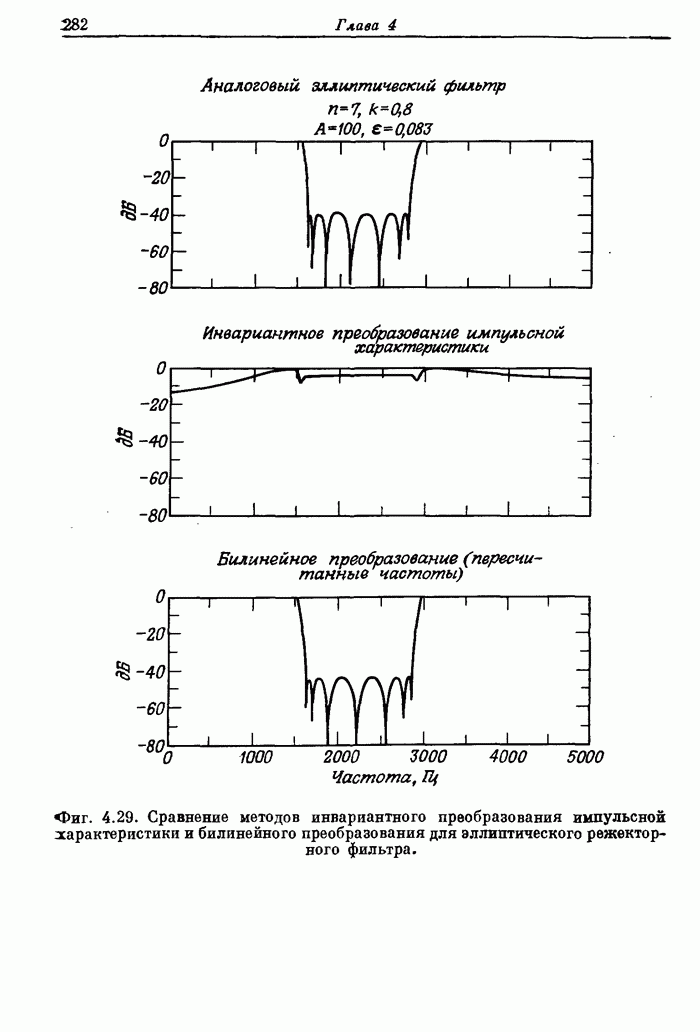
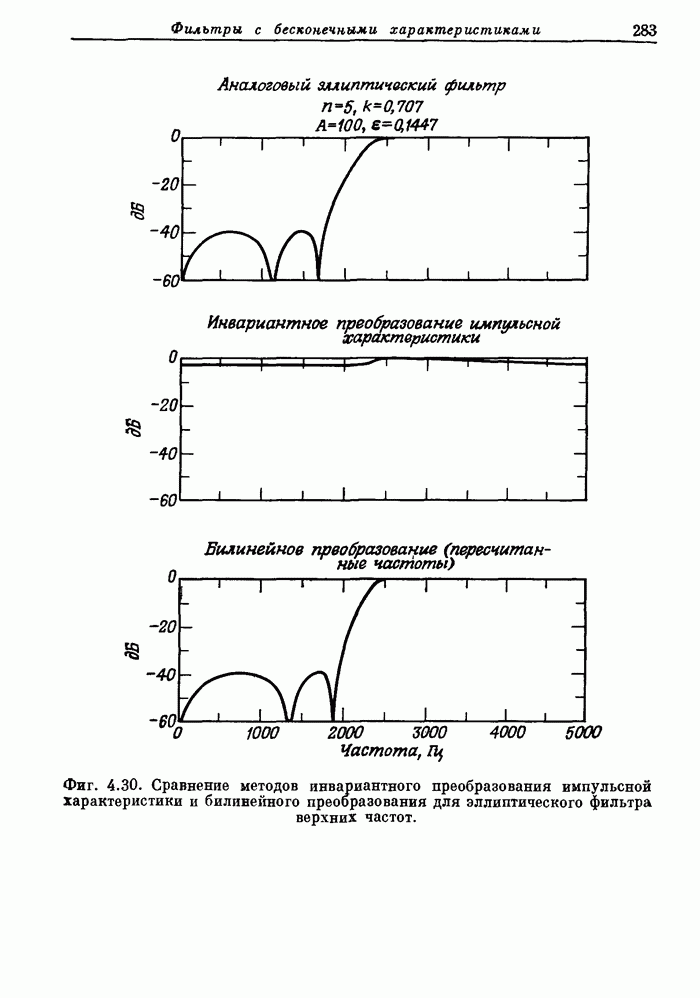
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
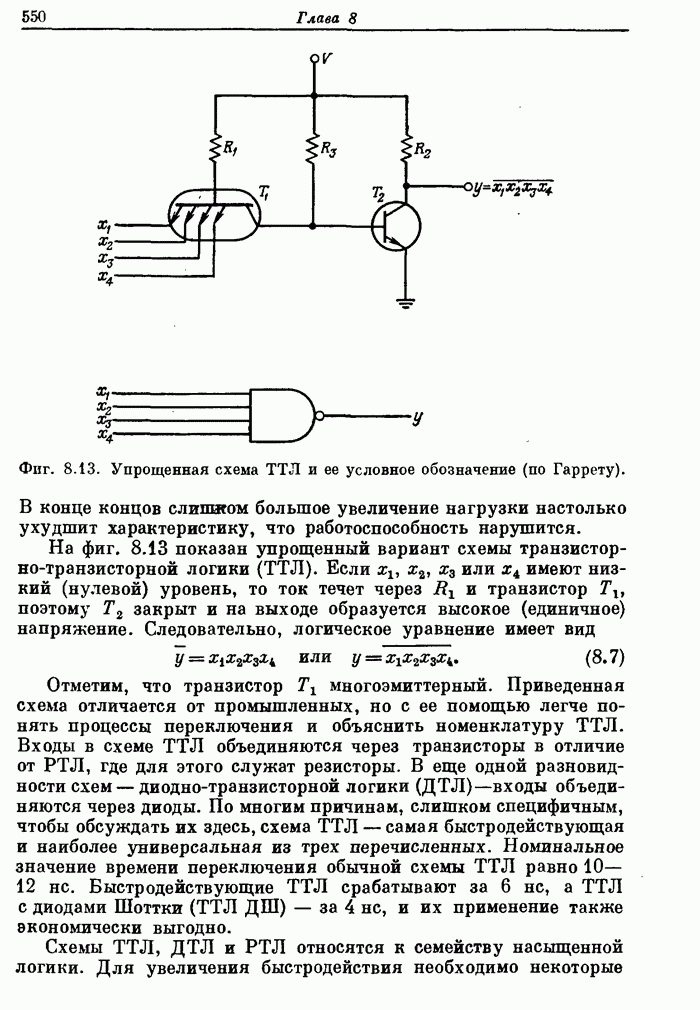
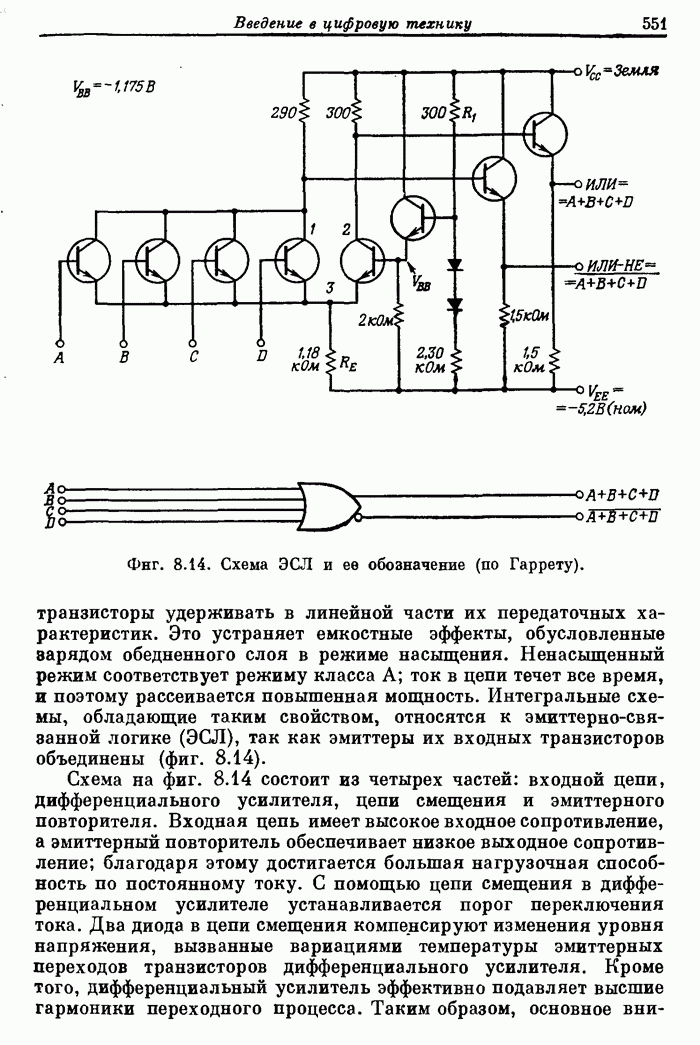
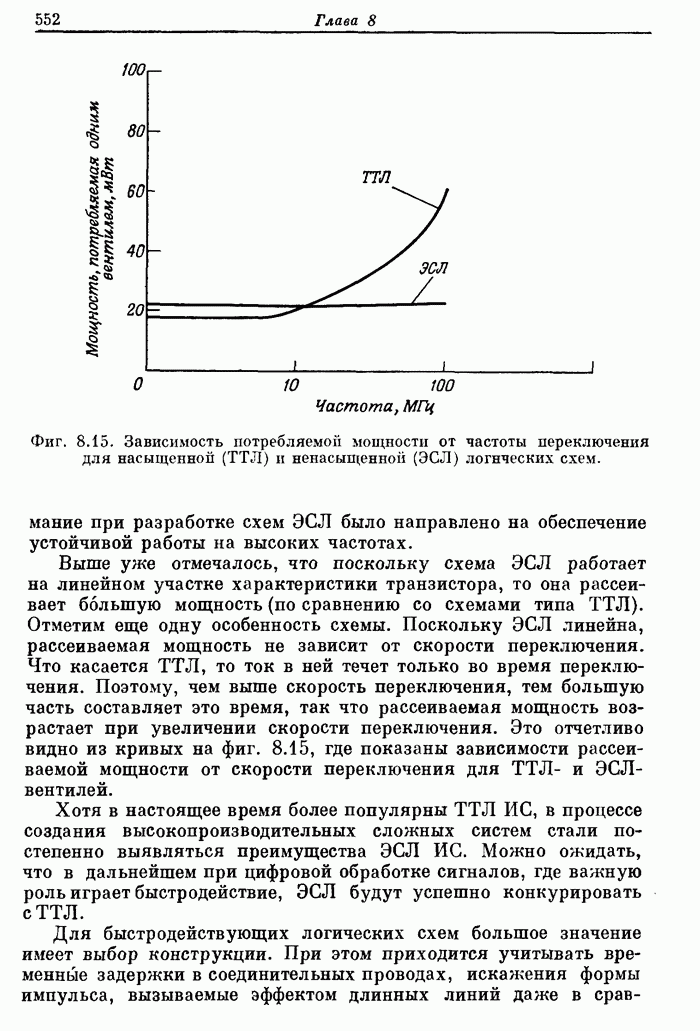
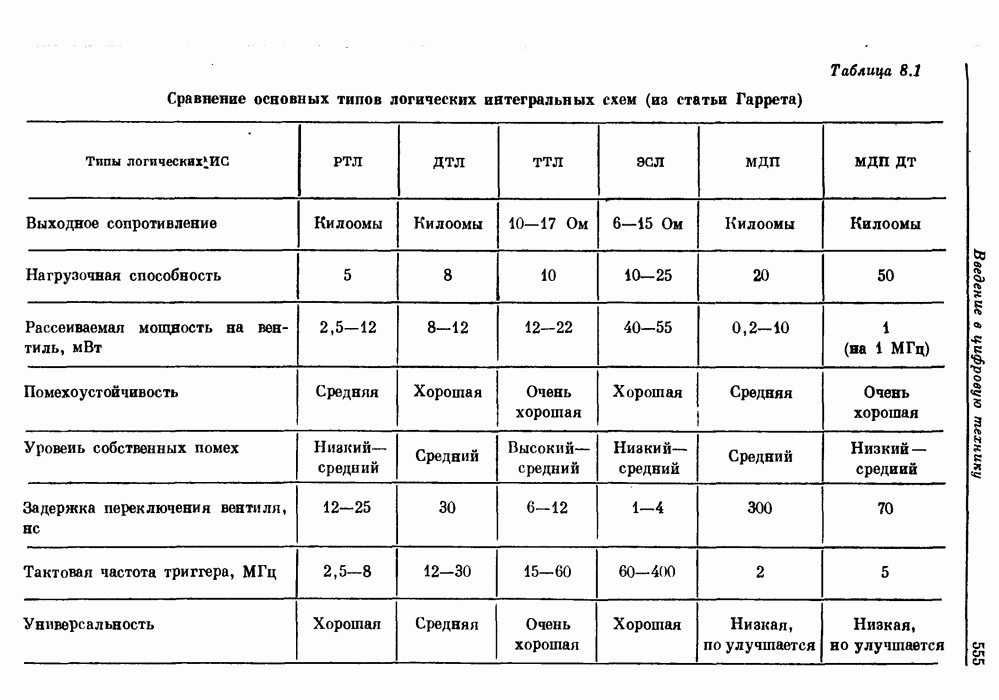
- 8.4. Основные типы интегральных логических схем
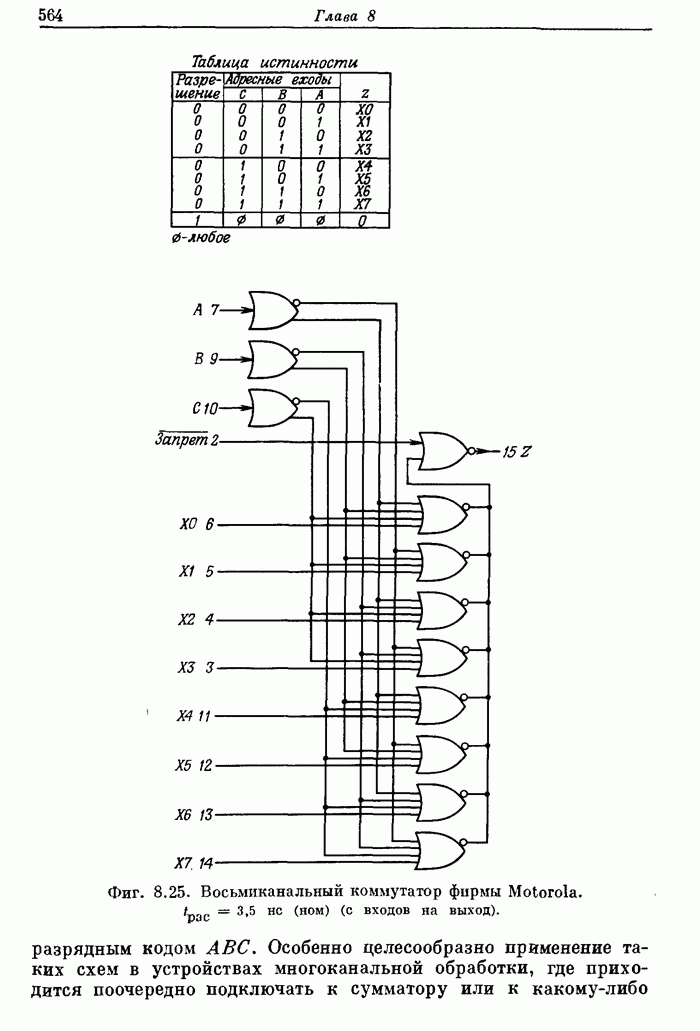
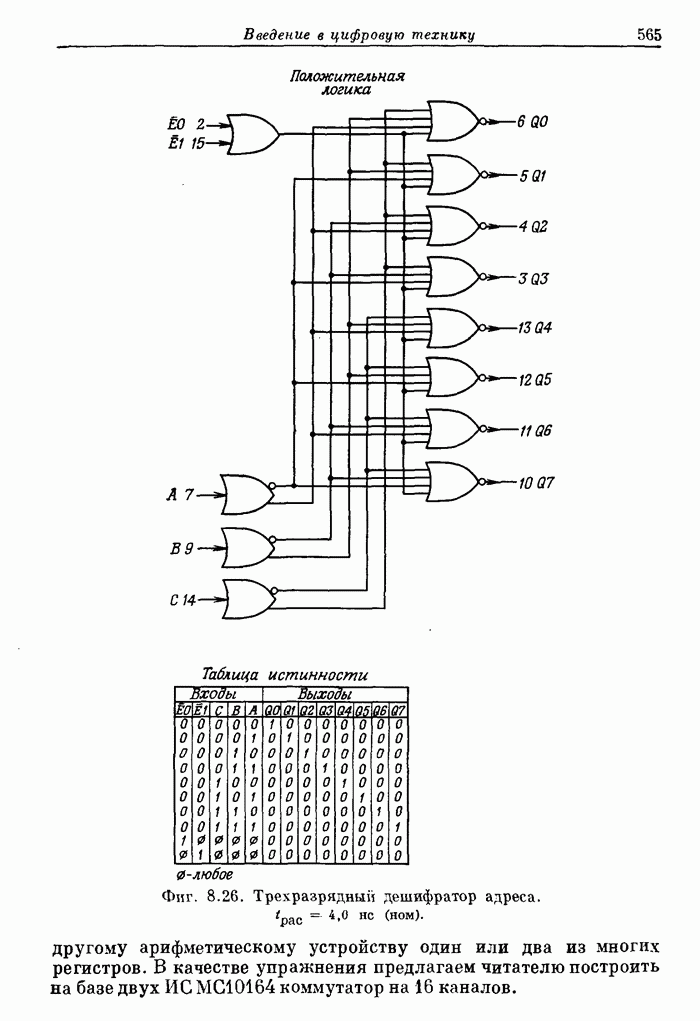
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
- 9.12. Специализированный цифровой синтезатор частот
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
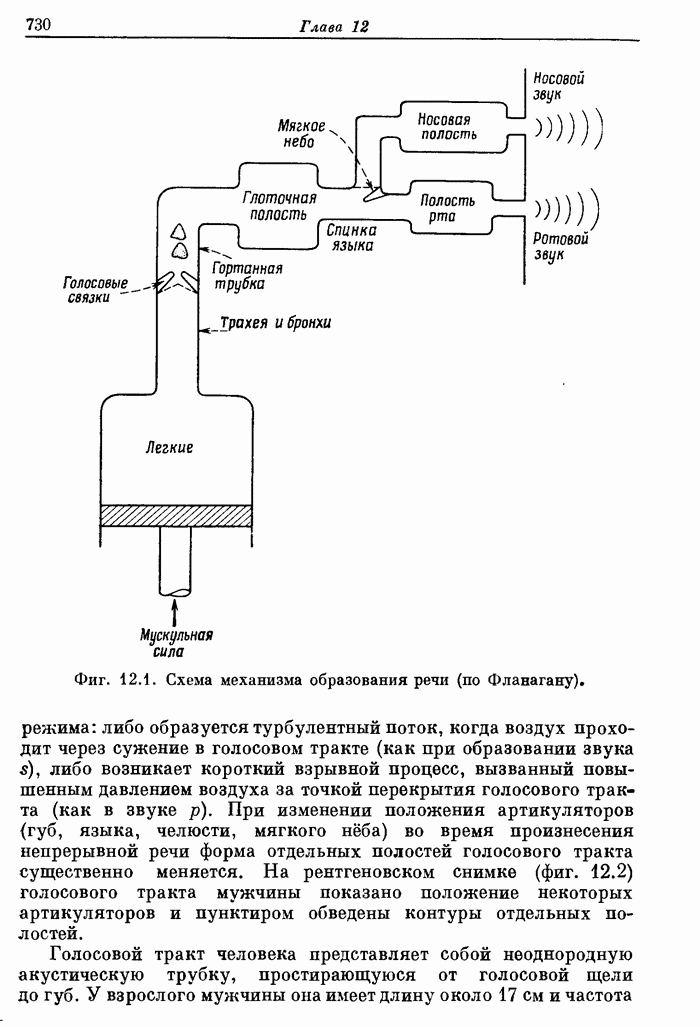
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
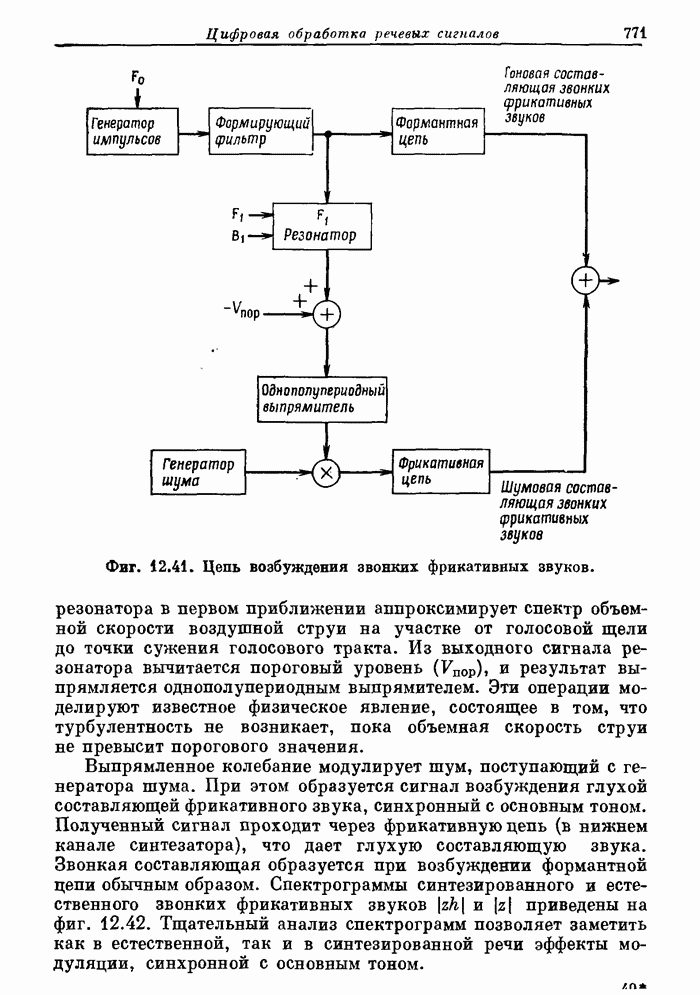
- 12.16. Цепь возбуждения звонких фрикативных звуков
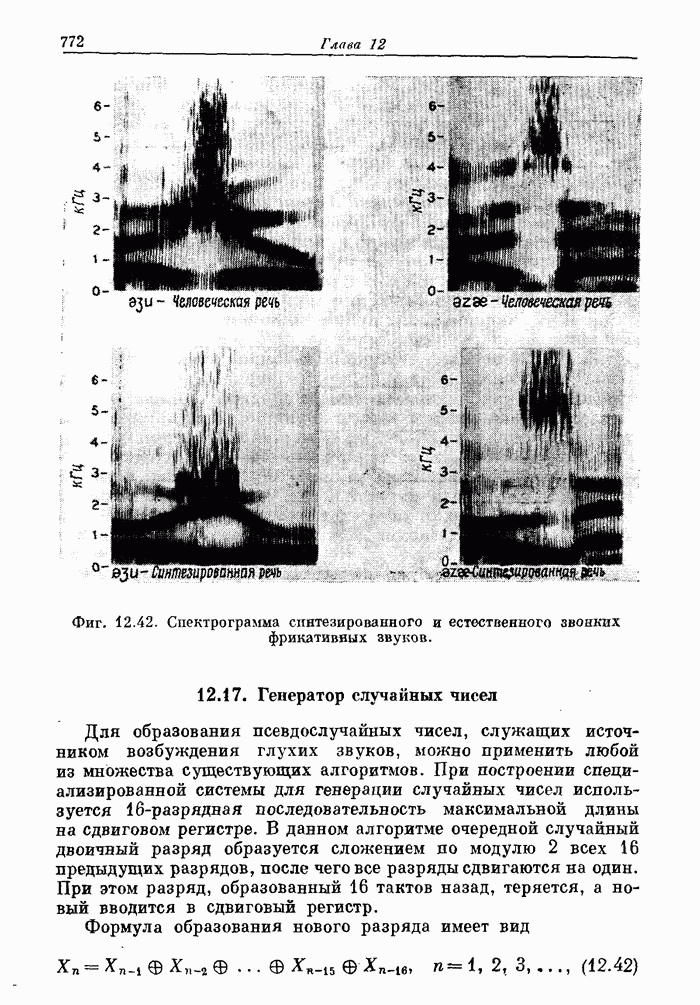
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
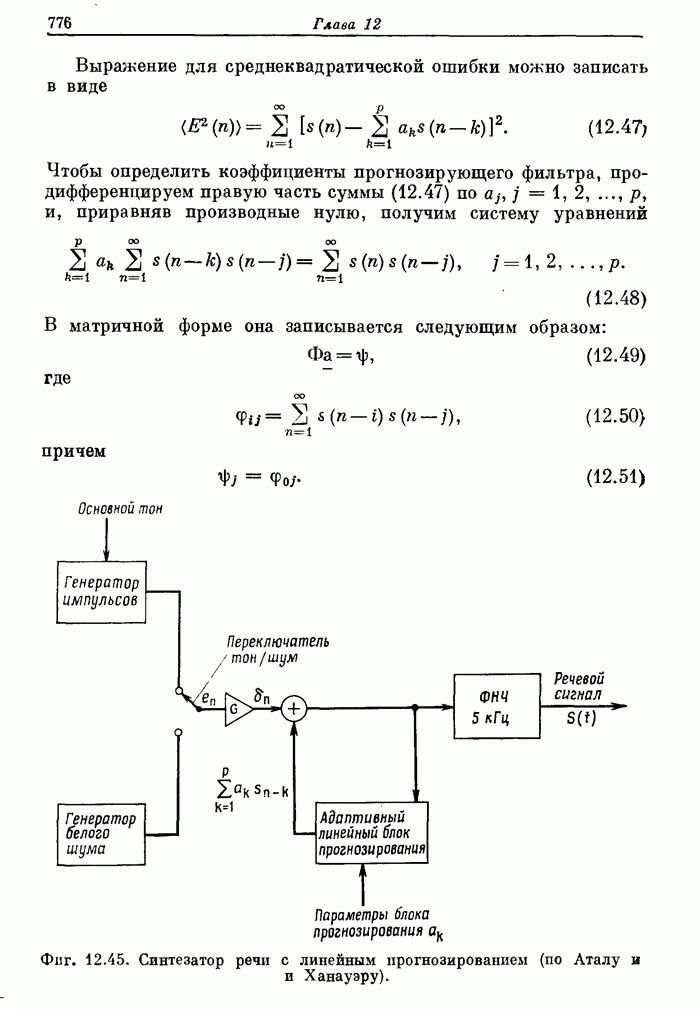
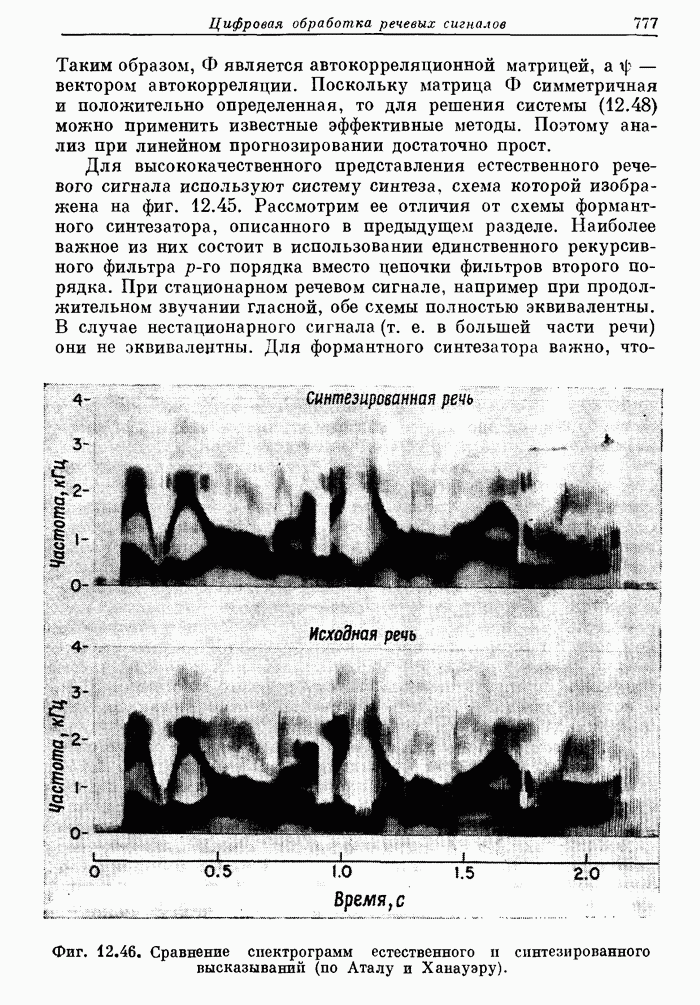
- 12.19. Линейное прогнозирование речи
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
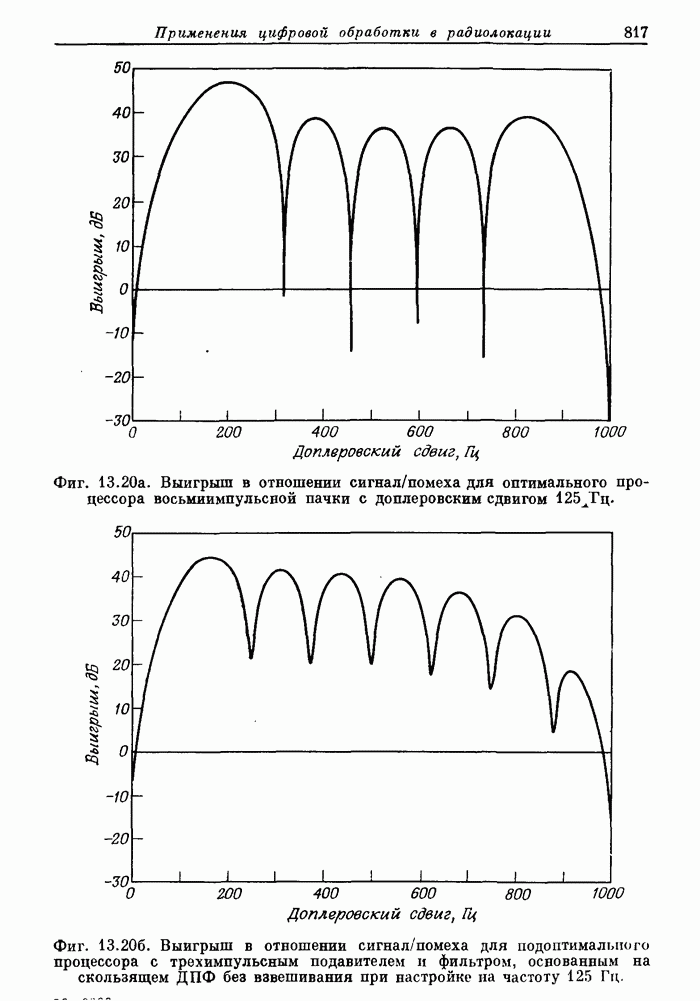
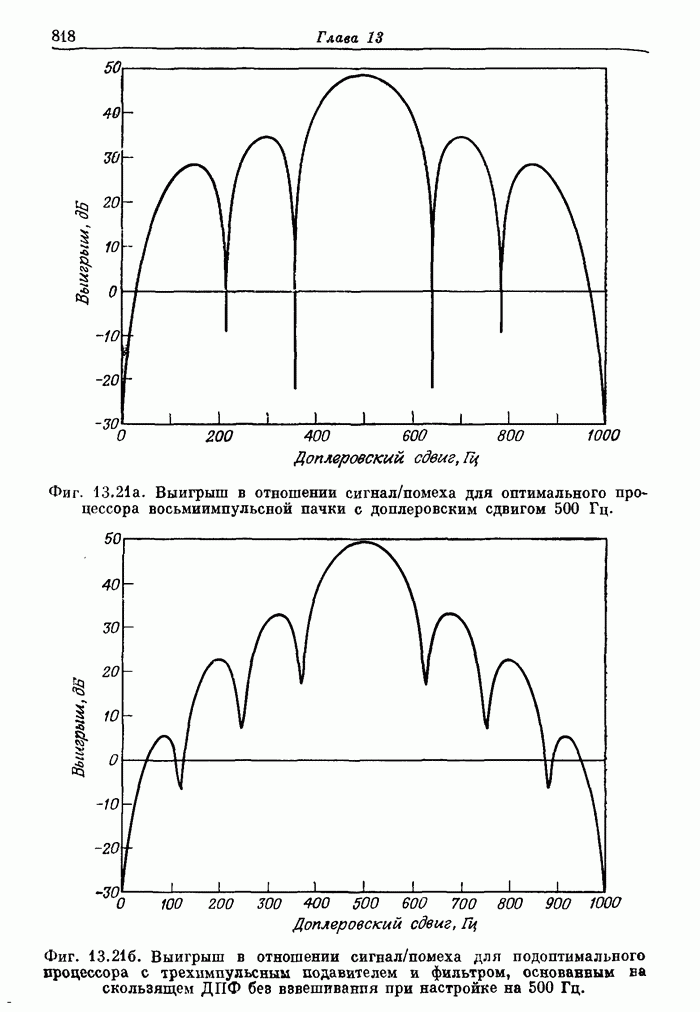
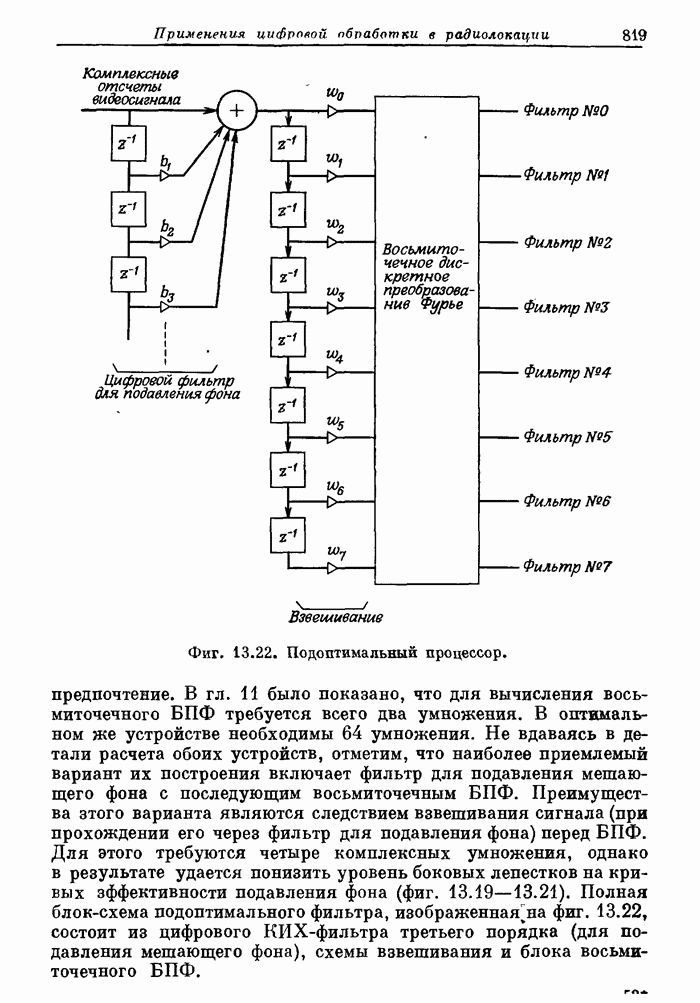
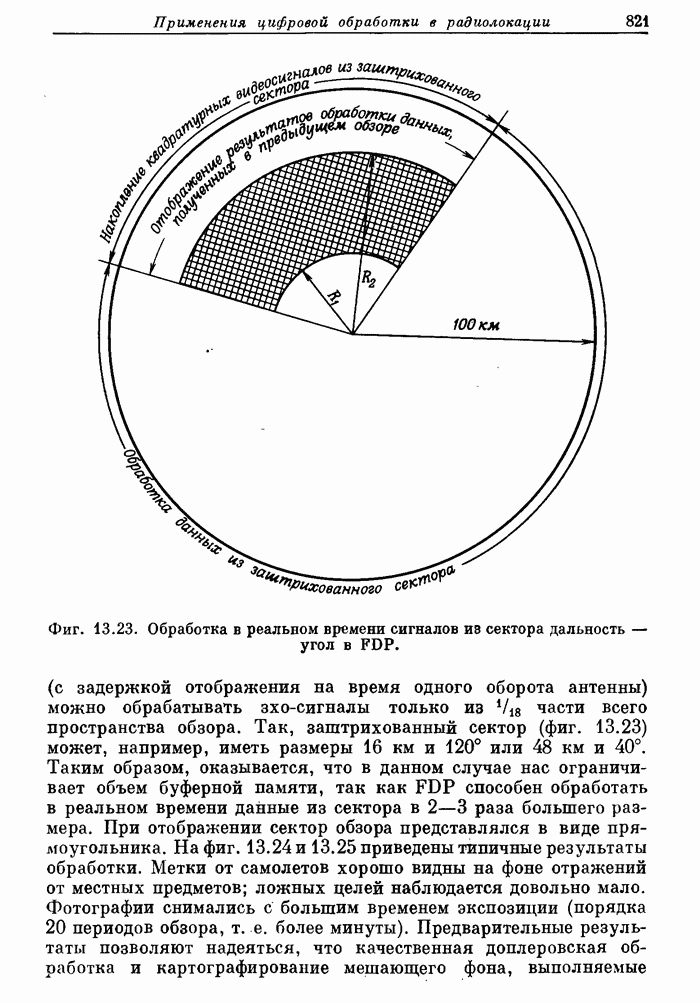
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
- 13.3. Выбор сигналов и функция неопределенности
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение