| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 142. Сегнетоэлектрики
Сегнетоэлектриками называются диэлектрики, в которых возможна самопроизвольная поляризация (§ 71). Необходимым условием существования сегнетоэлектрических свойств является отсутствие у кристалла центра симметрии, поэтому все сегнетоэлектрики обладают пьезоэлектрическими свойствами — поляризуются при деформации. Самопроизвольная поляризация сегнетоэлектриков возникает в определенных кристаллографических направлениях.

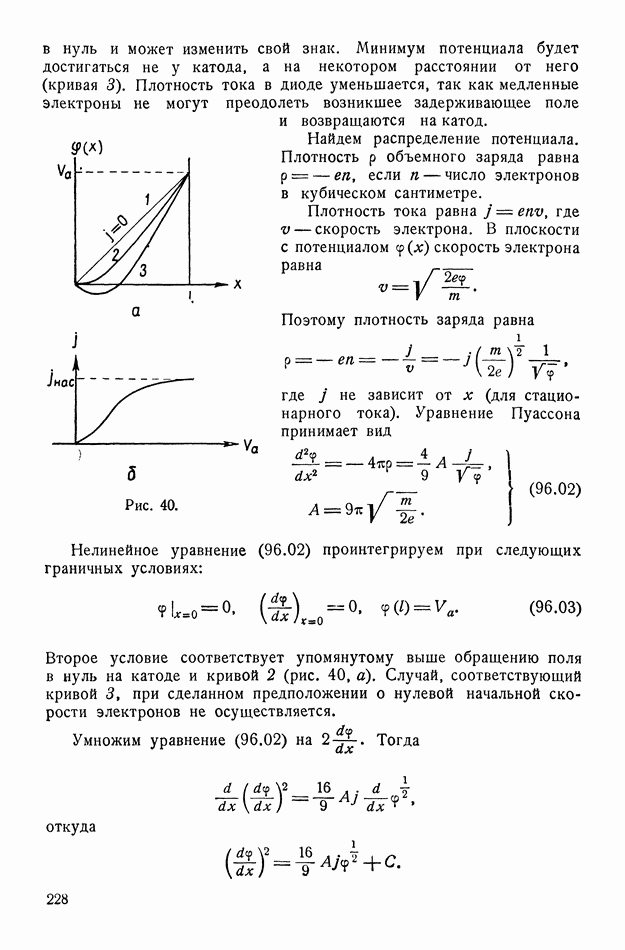
Рис. 77.
Рассмотрим объяснение сегнетоэлектрических свойств, отвлекаясь для упрощения от конкретных веществ. Возникновение сегнетоэлектрических свойств связано с действием внутреннего поля на слабо связанные ионы, смещение которых из одних равновесных положений в другие приводит к появлению электрической поляризации.
Следует иметь в виду, что ион может иметь несколько положений равновесия. Например, ион  (рис. 77) имеет шесть положений равновесия. Эти равновесия могут быть равноценными или неравноценными, то есть иметь одинаковую или различную глубину потенциальной ямы. Рассмотрим простейший случай, когда в каждой элементарной кристаллической ячейке имеется только один слабо связанный ион, имеющий два равноценных положения равновесия. Будем считать, что поле
(рис. 77) имеет шесть положений равновесия. Эти равновесия могут быть равноценными или неравноценными, то есть иметь одинаковую или различную глубину потенциальной ямы. Рассмотрим простейший случай, когда в каждой элементарной кристаллической ячейке имеется только один слабо связанный ион, имеющий два равноценных положения равновесия. Будем считать, что поле
направлено по прямой, соединяющей оба положения равновесия иона. Кроме того, пренебрегаем анизотропией и не будем учитывать пьезоэлектрических явлений.
При таких предположениях поляризация сдвига слабо связанных ионов  возникающая под влиянием действующего поля
возникающая под влиянием действующего поля  , определяется формулой (140.06)
, определяется формулой (140.06)

Рассмотрим подробнее  Полную поляризацию
Полную поляризацию  можно разложить на поляризацию
можно разложить на поляризацию  смещения слабо связанных ионов и поляризацию
смещения слабо связанных ионов и поляризацию  обусловленную смещениями электронов и всех остальных ионов решетки (§ 139). Поляризация
обусловленную смещениями электронов и всех остальных ионов решетки (§ 139). Поляризация  пропорциональна действующему полю
пропорциональна действующему полю

где  не зависящая от температуры поляризуемость единицы объема, связанная со всеми видами поляризации, кроме поляризации смещения слабо связанных ионов. Поляризация
не зависящая от температуры поляризуемость единицы объема, связанная со всеми видами поляризации, кроме поляризации смещения слабо связанных ионов. Поляризация  не направлена, поэтому вносимая ею в
не направлена, поэтому вносимая ею в  часть равна по (138.02) полю Лоренца
часть равна по (138.02) полю Лоренца  Поляризация ионного смещения
Поляризация ионного смещения  имеет направленный характер и не удовлетворяет условиям симметрии, рассмотренным в § 138. Поэтому она создает поле
имеет направленный характер и не удовлетворяет условиям симметрии, рассмотренным в § 138. Поэтому она создает поле  пропорциональное
пропорциональное  и равное
и равное

где  коэффициент, определяемый структурой элементарной ячейки, в частности числом слабо связанных ионов в ней. Теперь
коэффициент, определяемый структурой элементарной ячейки, в частности числом слабо связанных ионов в ней. Теперь

откуда

Значение  может быть определено путем измерения диэлектрического коэффициента при низких температурах, когда поляризация, обусловленная слабо связанными ионами, равна нулю (ионы «замораживаются» в своих потенциальных ямах). В таком случае, обозначая через
может быть определено путем измерения диэлектрического коэффициента при низких температурах, когда поляризация, обусловленная слабо связанными ионами, равна нулю (ионы «замораживаются» в своих потенциальных ямах). В таком случае, обозначая через  диэлектрический коэффициент при
диэлектрический коэффициент при  можно воспользоваться формулой Клаузиуса-Моссотти
можно воспользоваться формулой Клаузиуса-Моссотти

откуда

Поэтому

Полная поляризация равна

Таким образом, дипольная поляризация, измеренная любым способом (например, по кривой гистерезиса), равна дипольной поляризации слабо связанных ионов, сложенной с поляризацией электронов и остальных ионов. Она равна  Диэлектрический коэффициент равен
Диэлектрический коэффициент равен

Вернемся к (142.07). Множитель  значительно увеличивает
значительно увеличивает  . Например, для
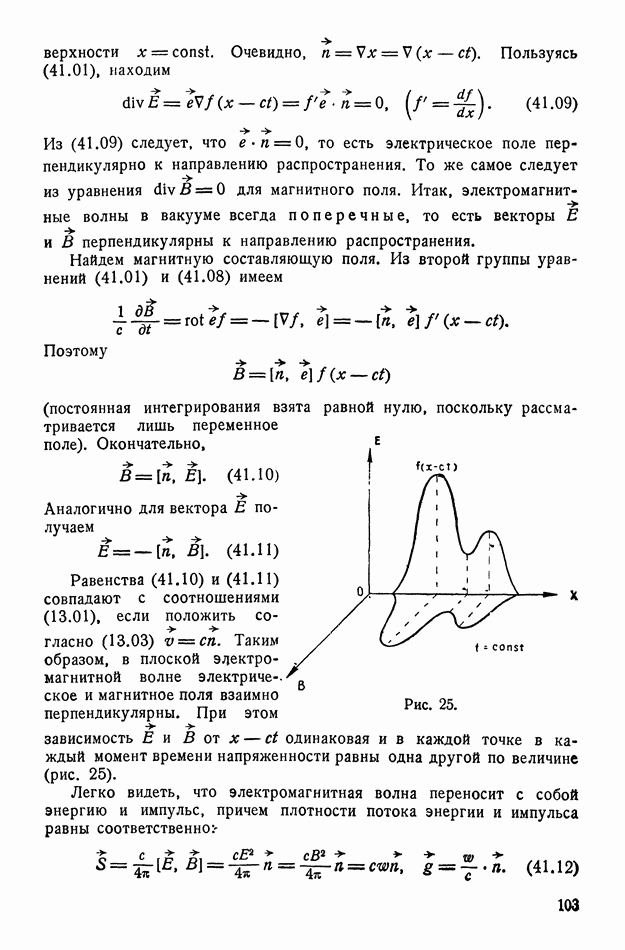
. Например, для  Поэтому для нормальных температур уже не мало по сравнению с единицей и следует ожидать значительную ионную поляризацию.
Поэтому для нормальных температур уже не мало по сравнению с единицей и следует ожидать значительную ионную поляризацию.
Легко видеть, что наблюдаемые значения поляризации насыщения объясняются смещением слабо связанных ионов. Так, для  Объем элементарного куба (рис. 77) равен
Объем элементарного куба (рис. 77) равен  поэтому дипольный момент элементарного куба равен
поэтому дипольный момент элементарного куба равен  Считая, что вся поляризация обусловлена смещением центрального иона
Считая, что вся поляризация обусловлена смещением центрального иона  (что несколько преувеличивает его роль), получим для величины смещения
(что несколько преувеличивает его роль), получим для величины смещения  см. Последнее вполне допустимо, так как составляет 5% от ребра куба.
см. Последнее вполне допустимо, так как составляет 5% от ребра куба.
Чтобы определить ионную поляризацию  при данных
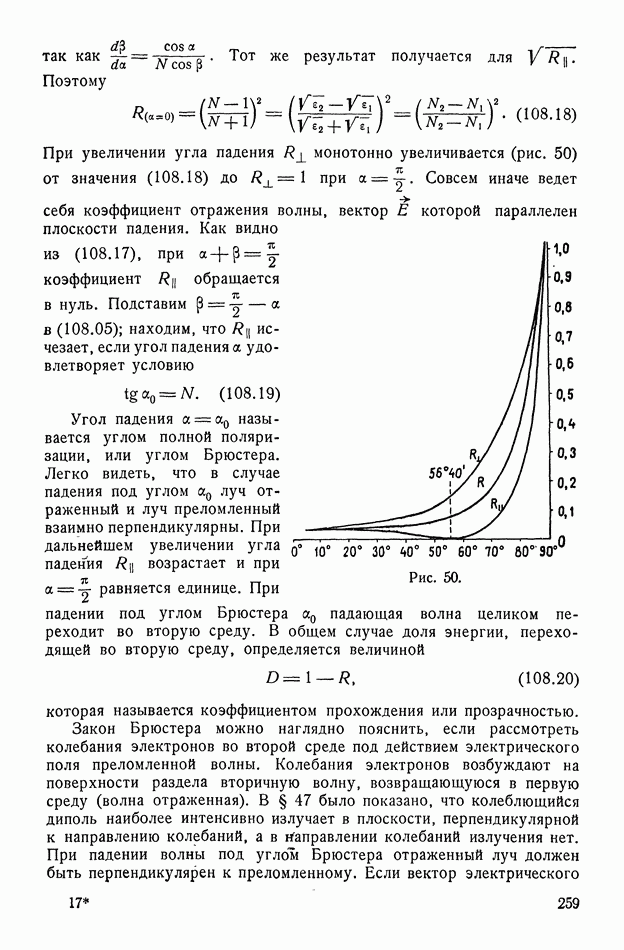
при данных  и 7, надо решить систему уравнений (142.01) и (142.07). Решение можно найти графическим методом, предложенным Вейссом в теории ферромагнетизма. Введем обозначение
и 7, надо решить систему уравнений (142.01) и (142.07). Решение можно найти графическим методом, предложенным Вейссом в теории ферромагнетизма. Введем обозначение

Тогда задача сводится к совместному решению системы

Уравнение (142.12) получено из (142.07) решением относительно  есть поляризация насыщения, поэтому
есть поляризация насыщения, поэтому  есть максимальное поле
есть максимальное поле  созданное слабо связанными ионами. Для определения поляризации
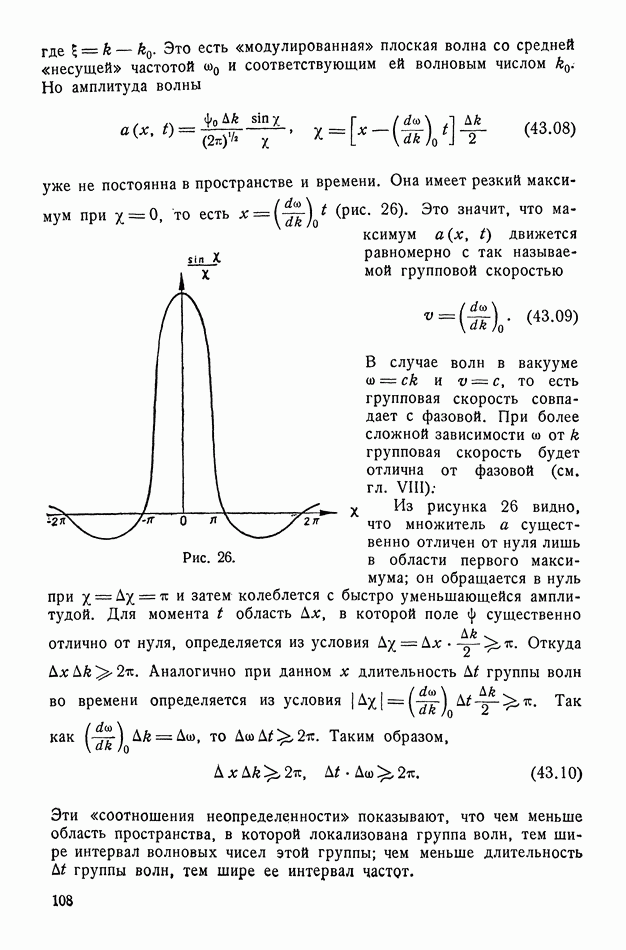
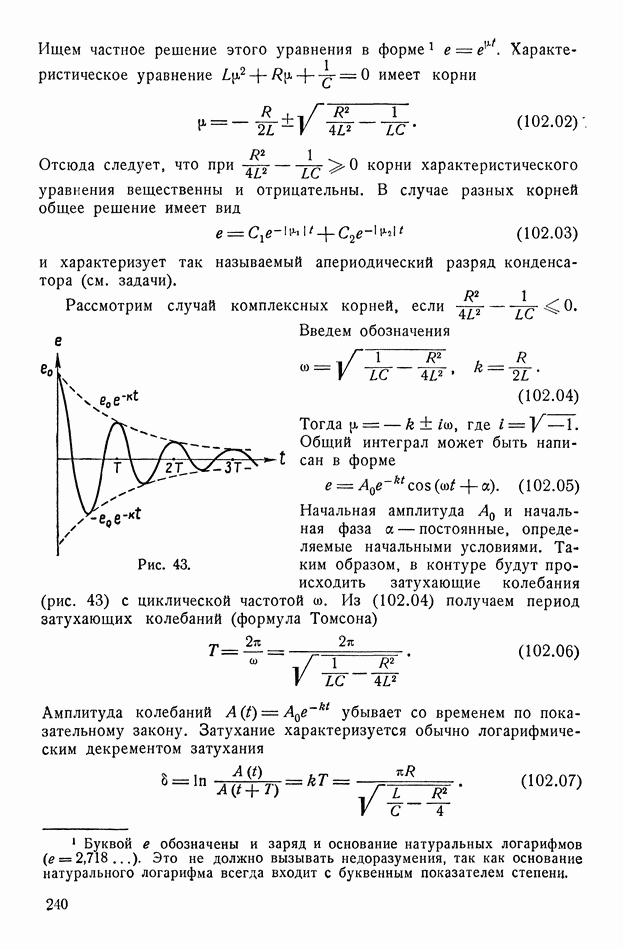
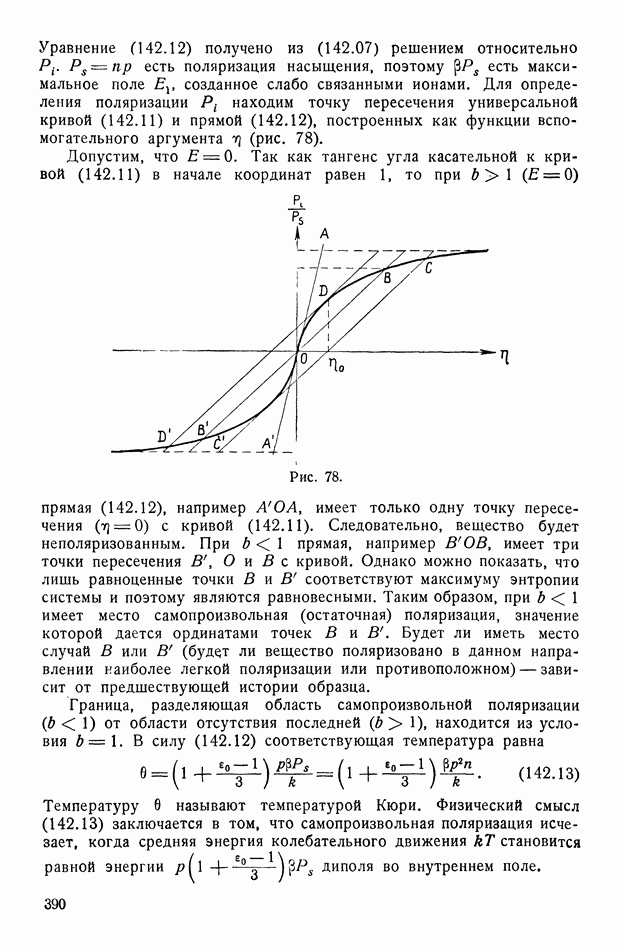
созданное слабо связанными ионами. Для определения поляризации  находим точку пересечения универсальной кривой (142.11) и прямой (142.12), построенных как функции вспомогательного аргумента
находим точку пересечения универсальной кривой (142.11) и прямой (142.12), построенных как функции вспомогательного аргумента  (рис. 78).
(рис. 78).

Рис. 78.
Допустим, что  Так как тангенс угла касательной к кривой (142.11) в начале координат равен 1, то при
Так как тангенс угла касательной к кривой (142.11) в начале координат равен 1, то при  прямая (142.12), например
прямая (142.12), например  имеет только одну точку пересечения
имеет только одну точку пересечения  с кривой (142.11). Следовательно, вещество будет неполяризованным. При
с кривой (142.11). Следовательно, вещество будет неполяризованным. При  прямая, например
прямая, например  имеет три точки пересечения
имеет три точки пересечения  с кривой. Однако можно показать, что лишь равноценные точки
с кривой. Однако можно показать, что лишь равноценные точки  соответствуют максимуму энтропии системы и поэтому являются равновесными. Таким образом, при
соответствуют максимуму энтропии системы и поэтому являются равновесными. Таким образом, при  имеет место самопроизвольная (остаточная) поляризация, значение которой дается ординатами точек
имеет место самопроизвольная (остаточная) поляризация, значение которой дается ординатами точек  Будет ли иметь место случай В или
Будет ли иметь место случай В или  (будет ли вещество поляризовано в данном направлении наиболее легкой поляризации или противоположном) — зависит от предшествующей истории образца.
(будет ли вещество поляризовано в данном направлении наиболее легкой поляризации или противоположном) — зависит от предшествующей истории образца.
Граница, разделяющая область самопроизвольной поляризации  от области отсутствия последней
от области отсутствия последней  находится из условия
находится из условия  В силу (142.12) соответствующая температура равна
В силу (142.12) соответствующая температура равна

Температуру  называют температурой Кюри. Физический смысл (142.13) заключается в том, что самопроизвольная поляризация исчезает, когда средняя энергия колебательного движения
называют температурой Кюри. Физический смысл (142.13) заключается в том, что самопроизвольная поляризация исчезает, когда средняя энергия колебательного движения  становится равной энергии диполя во внутреннем поле.
становится равной энергии диполя во внутреннем поле.
При наличии поля  прямая (142.12) проходит ниже прямой
прямая (142.12) проходит ниже прямой  (например, прямая
(например, прямая  Точка пересечения с кривой переходит в положение С и поляризация (при той же температуре) возрастает.
Точка пересечения с кривой переходит в положение С и поляризация (при той же температуре) возрастает.
Найдем зависимость остаточной поляризации от температуры. Допустим, что  близка к 0. Тогда, разлагая
близка к 0. Тогда, разлагая  в ряд, получим
в ряд, получим  Так как при
Так как при  по
по  то
то  откуда
откуда  и остаточная ионная поляризация равна
и остаточная ионная поляризация равна

По мере приближения к точке Кюри поляризация уменьшается и при  обращается в нуль, оставаясь равной нулю и при
обращается в нуль, оставаясь равной нулю и при 
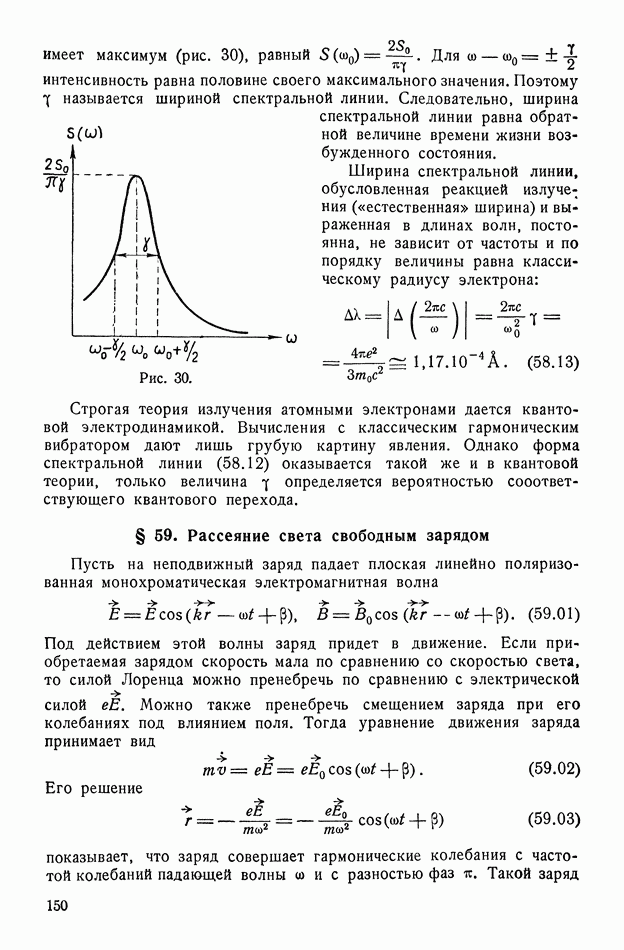
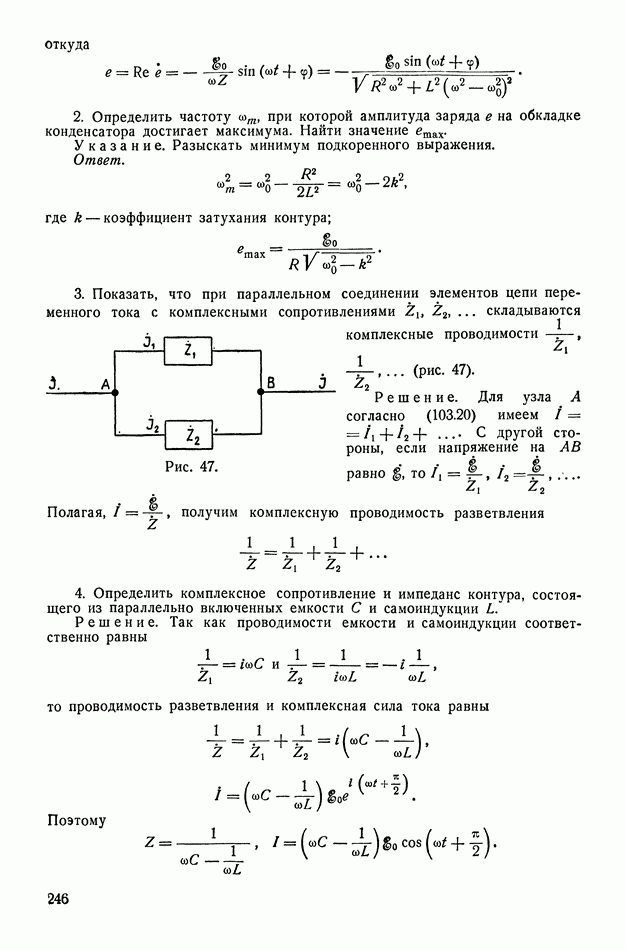
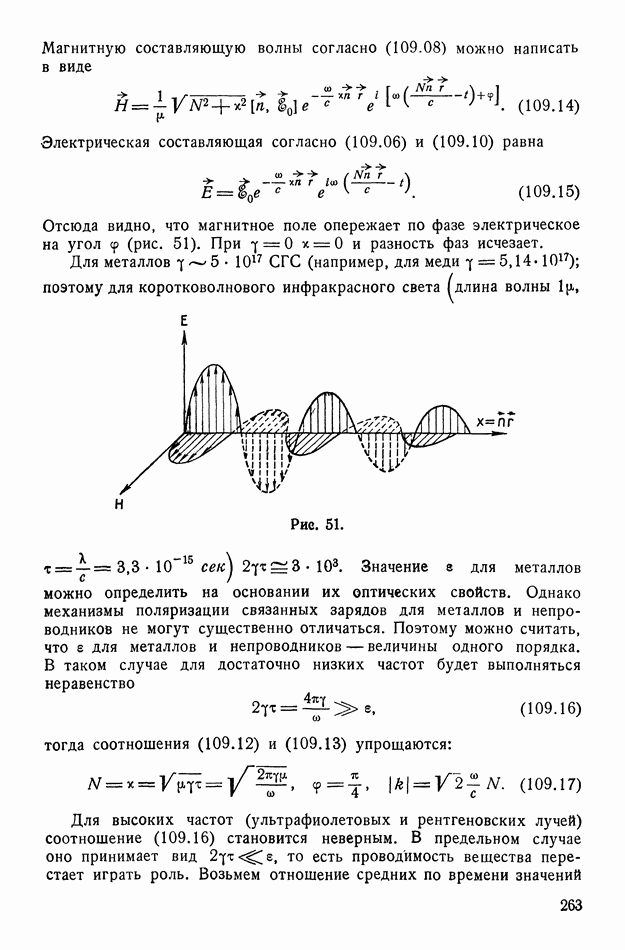
Пользуясь рисунком 78, легко объяснить явление гистерезиса и оценить коэрцитивное поле  (§ 71). При уменьшении напряженности
(§ 71). При уменьшении напряженности  поля точка пересечения прямой (142.12) с кривой скользит вдоль кривой до положения
поля точка пересечения прямой (142.12) с кривой скользит вдоль кривой до положения  а после изменения направления
а после изменения направления  до точки
до точки  (в которой прямая
(в которой прямая  касается кривой). При дальнейшем увеличении
касается кривой). При дальнейшем увеличении  остается только одна точка пересечения (левее
остается только одна точка пересечения (левее  Следовательно, поляризация скачком меняет свой знак и величину — от значения, соответствующего точке
Следовательно, поляризация скачком меняет свой знак и величину — от значения, соответствующего точке  до значения, соответствующего точке
до значения, соответствующего точке  Таким образом, получается кривая гистерезиса (рис. 79), на которой для удобства соответствующие точки обозначены теми же буквами. Эта кривая не совпадает точно с кривой на рисунке 35, так как относится к идеальному случаю.
Таким образом, получается кривая гистерезиса (рис. 79), на которой для удобства соответствующие точки обозначены теми же буквами. Эта кривая не совпадает точно с кривой на рисунке 35, так как относится к идеальному случаю.

Рис. 79.
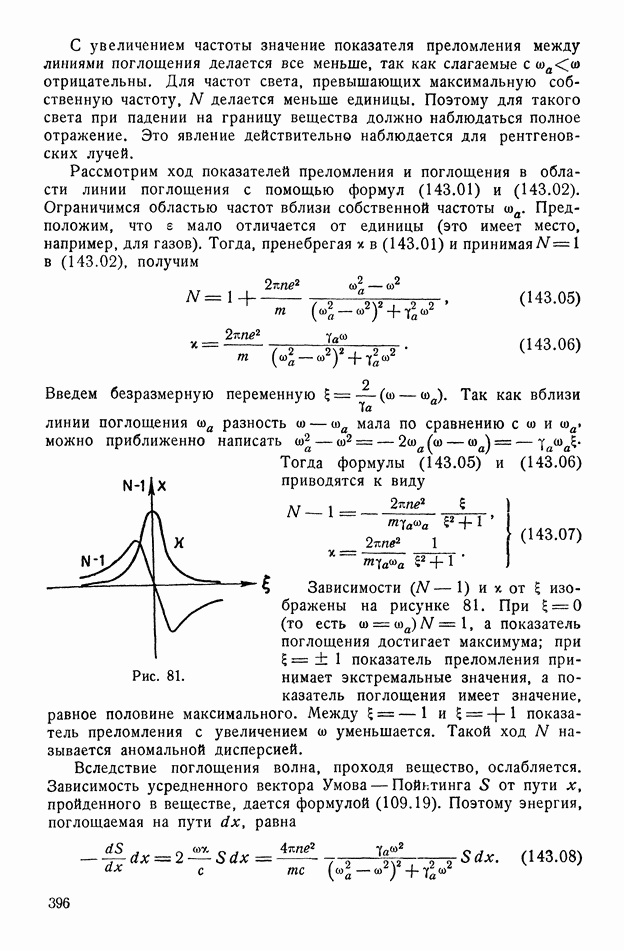
Чтобы оценить величину коэрцитивного поля  найдем координаты точки касания
найдем координаты точки касания  В точке
В точке  угловые коэффициенты кривой (142.11) и прямой (142.12) совпадают. Поэтому
угловые коэффициенты кривой (142.11) и прямой (142.12) совпадают. Поэтому  откуда
откуда  Так как
Так как  то
то  . Далее,
. Далее,  где
где  — функция, обратная гиперболическому косинусу. Для точки
— функция, обратная гиперболическому косинусу. Для точки  получаем
получаем

откуда 

Формула (142.15) дает зависимость коэрцитивного поля от температуры. Знак минус соответствует точке  Очевидно, при
Очевидно, при  коэрцитивное поле исчезает одновременно с остаточной поляризацией.
коэрцитивное поле исчезает одновременно с остаточной поляризацией.
Рассмотрим свойства сегнетоэлектрика при температурах выше температуры Кюри. В этом случае поляризация во внешнем поле мала и  Тогда
Тогда  откуда
откуда 
Ионная поляризация равна

Пользуясь (142.09), получаем диэлектрический коэффициент при 

Из последнего соотношения и (142.13) находим

Соотношения (142.18) позволяют определить коэффициент внутреннего поля  и дипольный момент ионного смещения
и дипольный момент ионного смещения  из опытных данных.
из опытных данных.
Для дигидрофосфата калия  в котором поляризация обусловлена смещением ионов
в котором поляризация обусловлена смещением ионов  при температурах, не очень близких к точке Кюри, опыт дает
при температурах, не очень близких к точке Кюри, опыт дает

Следовательно,  Это дает
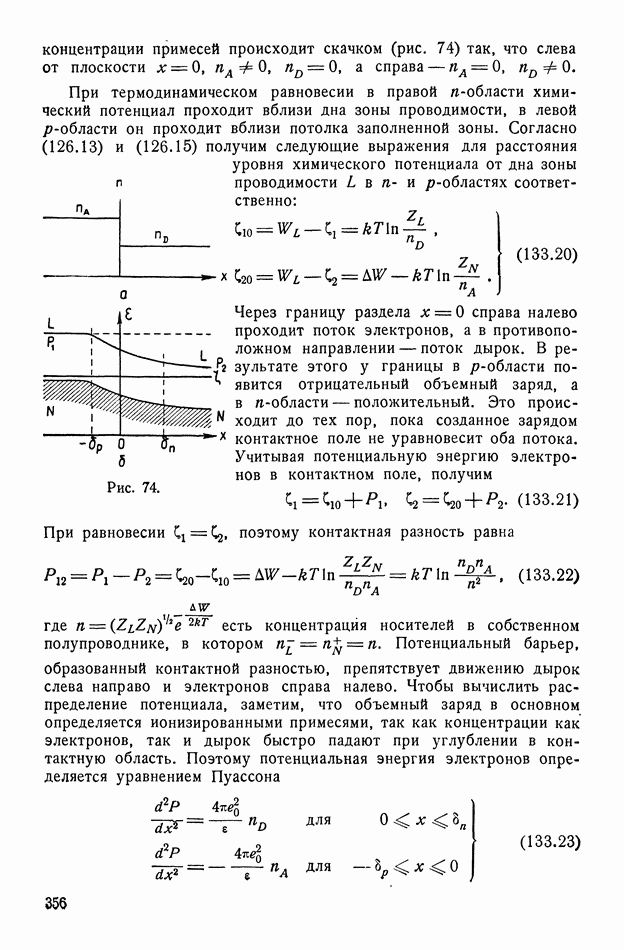
Это дает  Объем элементарной ячейки, содержащей четыре молекулы, равен
Объем элементарной ячейки, содержащей четыре молекулы, равен  Так как каждая молекула обладает двумя водородными связями, которые действуют как диполи, то
Так как каждая молекула обладает двумя водородными связями, которые действуют как диполи, то  Поэтому по (142.17) получается дипольный момент поляризации водородной связи
Поэтому по (142.17) получается дипольный момент поляризации водородной связи  Поляризация насыщения
Поляризация насыщения  Чтобы получить полную поляризацию, надо согласно (142.08) последнее умножить на
Чтобы получить полную поляризацию, надо согласно (142.08) последнее умножить на

Это дает

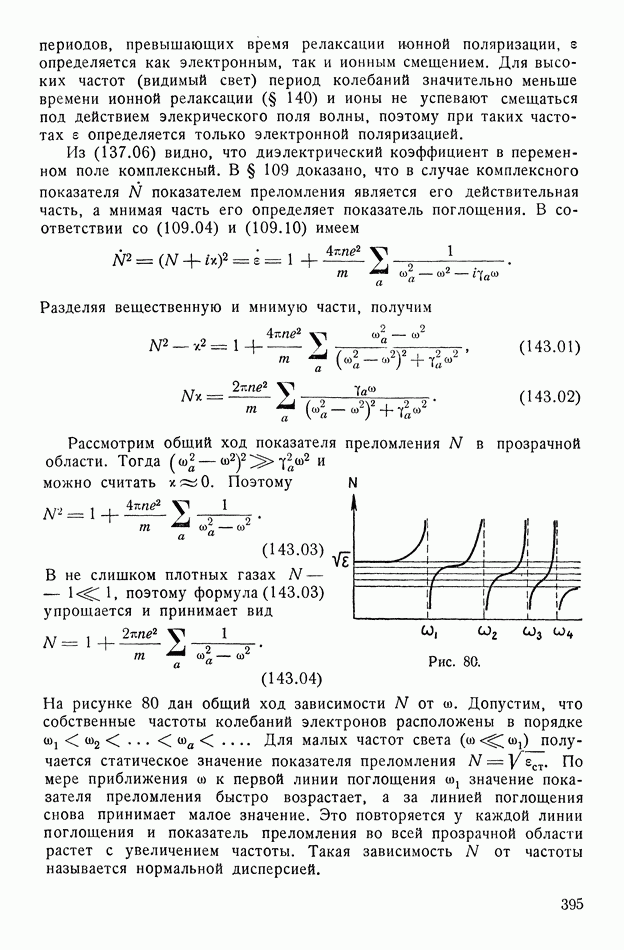
Рассмотренная теория относится к области внутри кристалла, в которой самопроизвольная поляризация имеет одно и то же направление. Такие области называются доменами. Обычно макроскопический кристалл распадается на ряд доменов, самопроизвольно поляризованных в различных направлениях, и поэтому в целом кристалл не поляризован. Однако можно вырастить кристаллы, весь объем которых занимает один домен. Переход в сегнетоэлектрическое состояние является фазовым переходом первого или второго рода. Например, кристаллы  выше точки Кюри имеют кубическую симметрию, ниже ее — тетрагональную; переход кристалла в сегяетоэлектрическое состояние является переходом первого рода, но очень близким к переходу второго рода. При охлаждении ниже точки Кюри в различных частях кристалла в тетрагональную ось превращаются различные кубические оси. Поэтому вектор самопроизвольной поляризации
выше точки Кюри имеют кубическую симметрию, ниже ее — тетрагональную; переход кристалла в сегяетоэлектрическое состояние является переходом первого рода, но очень близким к переходу второго рода. При охлаждении ниже точки Кюри в различных частях кристалла в тетрагональную ось превращаются различные кубические оси. Поэтому вектор самопроизвольной поляризации  будет располагаться в кристалле в различных направлениях в зависимости от направления тетрагональной оси. Другими словами, кристалл распадается на различно поляризованные домены. Как указали в 1930 году Я. И. Френкель и Я. Г. Дорфман, разделение на домены связано с тем обстоятельством, что при определенных размерах областей самопроизвольной поляризации сумма энергии поляризованной среды и поверхностной энергии на границах двух различно поляризованных областей достигает минимума.
будет располагаться в кристалле в различных направлениях в зависимости от направления тетрагональной оси. Другими словами, кристалл распадается на различно поляризованные домены. Как указали в 1930 году Я. И. Френкель и Я. Г. Дорфман, разделение на домены связано с тем обстоятельством, что при определенных размерах областей самопроизвольной поляризации сумма энергии поляризованной среды и поверхностной энергии на границах двух различно поляризованных областей достигает минимума.
Для кристалла, имеющего сложную доменную структуру, процесс поляризации заключается в трех процессах: 1) в увеличении поляризации каждого домена во внешнем поле, 2) в изменении направления поляризации доменов в соответствии с направлением внешнего поля и 3) в изменении объемов различных доменов — если поляризация домена ориентирована невыгодно относительно внешнего поля, то граница, разделяющая этот домен от соседнего, ориентированного более выгодно (с меньшей энергией во внешнем поле), перемещается так, что объем второго домена увеличивается за счет объема первого.
Задачи.
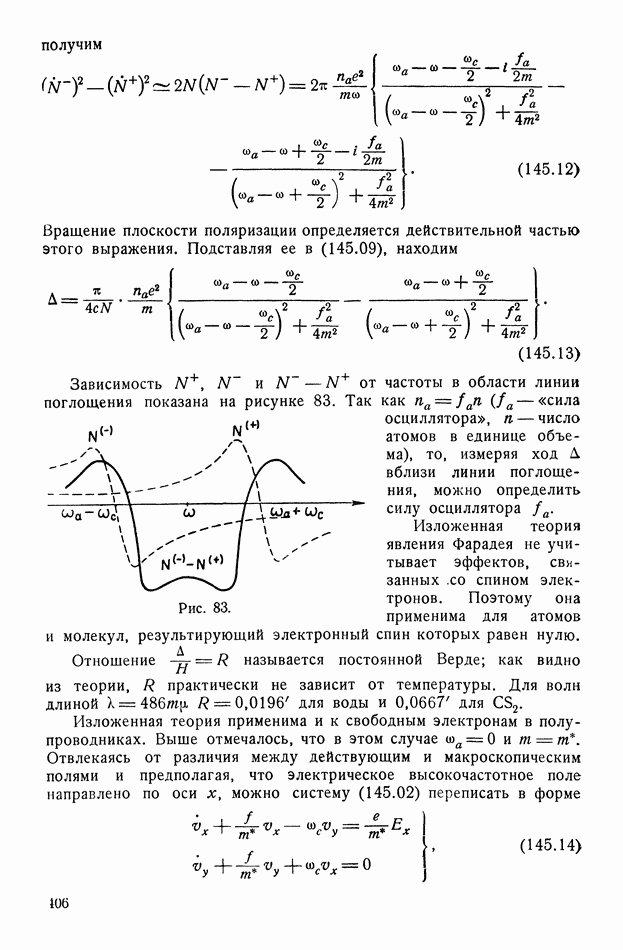
1. По данным Мерца для однодоменного кристалла  диэлектрический коэффициент при температуре выше точки Кюри удовлетворяет соотношению
диэлектрический коэффициент при температуре выше точки Кюри удовлетворяет соотношению

Определить коэффициент внутреннего поля.
Решение. В силу (142.17) имеем

2. В элементарной ячейке  ион
ион  имеет шесть положений равновесия, расположенных симметрично относительно центра (на направлениях, соединяющих ионы кислорода). Определить ионную поляризацию, если внешнее поле направлено вдоль одного из этих направлений (вдоль оси
имеет шесть положений равновесия, расположенных симметрично относительно центра (на направлениях, соединяющих ионы кислорода). Определить ионную поляризацию, если внешнее поле направлено вдоль одного из этих направлений (вдоль оси 
Решение. Обозначим через  числа ионов
числа ионов  в единице объема в шести положениях равновесия. Имеем
в единице объема в шести положениях равновесия. Имеем  Если положения 1 и 2 расположены по линии действия поля, а положения
Если положения 1 и 2 расположены по линии действия поля, а положения  перпендикулярной плоскости, то поле перебрасывает ионы из 1 в 2 или обратно, не меняя плотности ионов в положениях
перпендикулярной плоскости, то поле перебрасывает ионы из 1 в 2 или обратно, не меняя плотности ионов в положениях  Поэтому
Поэтому

Из  находим
находим  Следовательно, поляризация смещения ионов
Следовательно, поляризация смещения ионов  равна
равна

3. Показать, что температура Кюри и постоянная С в выражении для диэлектрического коэффициента  выше точки Кюри определяются формулами
выше точки Кюри определяются формулами

Указание. Воспользоваться методом, примененным для вывода (142.17), но в качестве  взять значение
взять значение  из задачи 2.
из задачи 2.
4. Определить электрический момент элементарной ячейки и поляризацию насыщения  учитывая, что число диполей в
учитывая, что число диполей в 
Решение. Пользуясь формулами задачи 3 и данными задачи 1, получаем

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
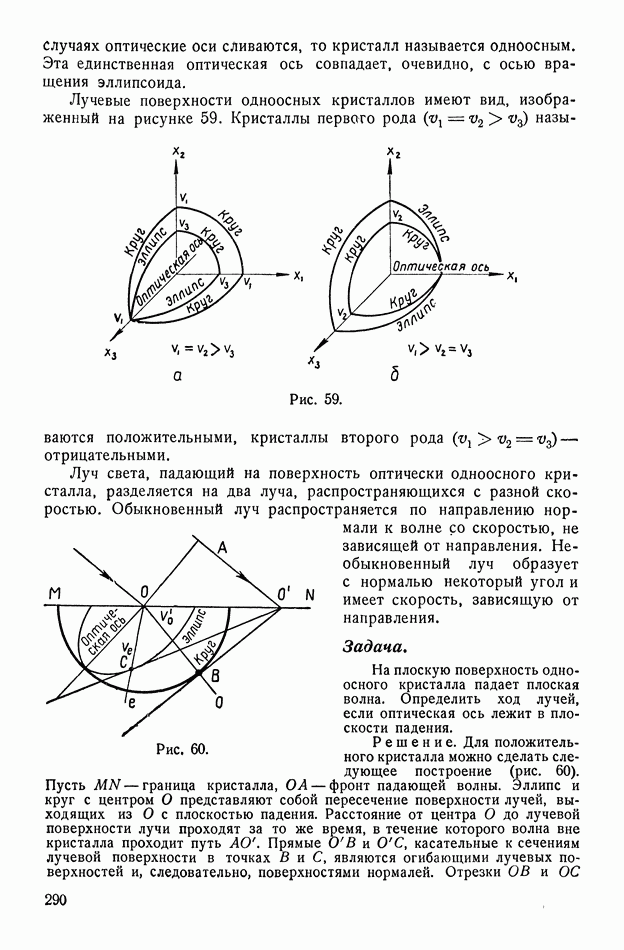
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
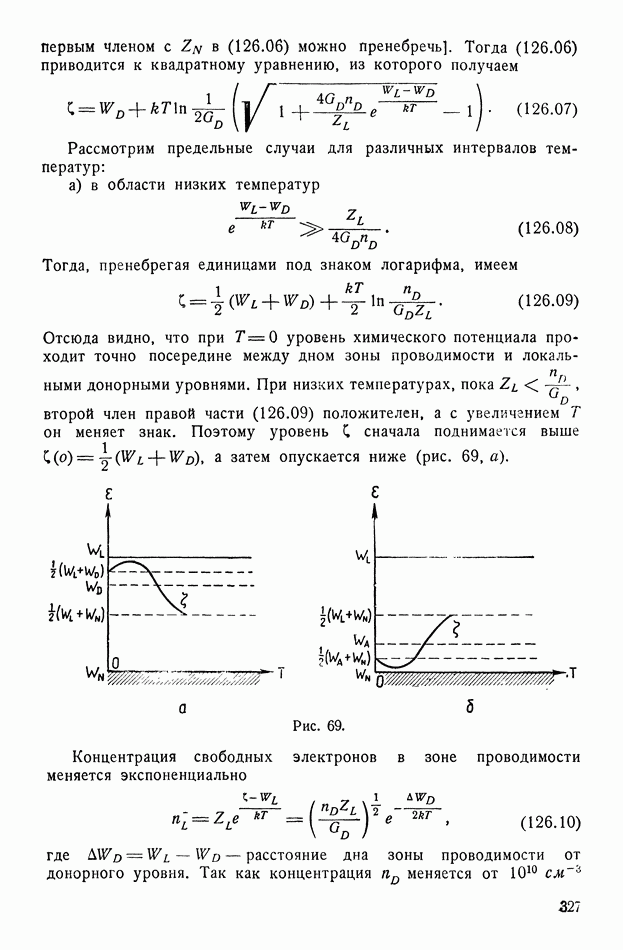
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
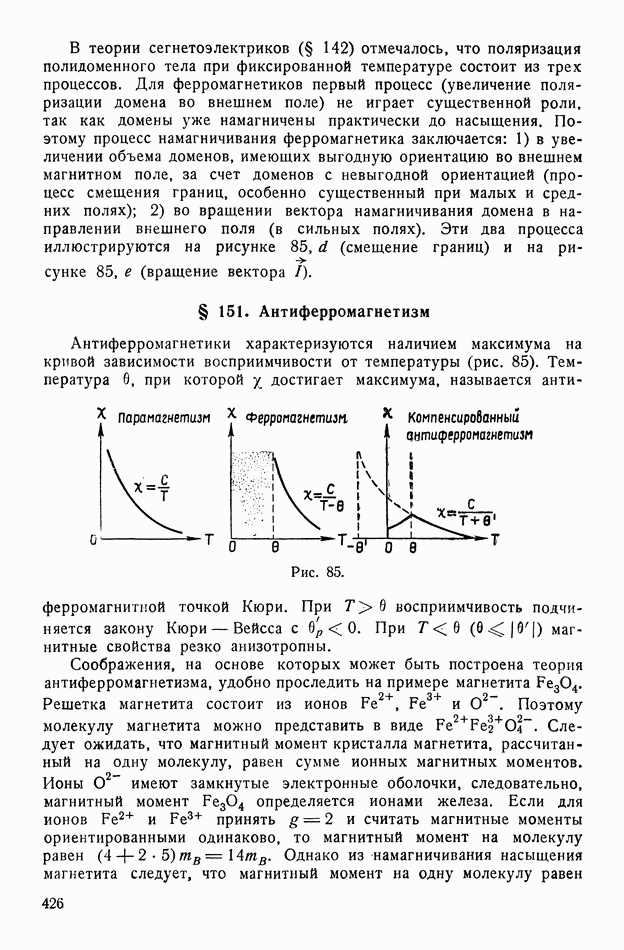
- § 151. Антиферромагнетизм
- § 152. Исторические замечания