| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 147. Парамагнетизм
В § 38 отмечалось, что полный магнитный момент атомной системы определяется равенством

Здесь  масса электрона, —
масса электрона, —  заряд электрона,
заряд электрона,  орбитальный и спиновый моменты электронной оболочки атома. Полный механический момент количества движения электронов, равный
орбитальный и спиновый моменты электронной оболочки атома. Полный механический момент количества движения электронов, равный  сохраняется. Поэтому вектор
сохраняется. Поэтому вектор  прецессирует вокруг направления У. Вследствие этого среднее значение магнитного момента атома направлено антипараллельно
прецессирует вокруг направления У. Вследствие этого среднее значение магнитного момента атома направлено антипараллельно  и равно
и равно

где  так называемый множитель Ланде или магнитомеханический фактор, возникающий при усреднении
так называемый множитель Ланде или магнитомеханический фактор, возникающий при усреднении  Теория магнитных свойств тел требует учета с самого начала квантовых свойств системы.
Теория магнитных свойств тел требует учета с самого начала квантовых свойств системы.
В квантовой теории  является оператором, собственные значения квадрата которого и проекции на произвольное направление z определяются формулами
является оператором, собственные значения квадрата которого и проекции на произвольное направление z определяются формулами

Квантовое число  характеризующее полный механический момент электронной оболочки атома, принимает или целые значения
характеризующее полный механический момент электронной оболочки атома, принимает или целые значения  (при четном числе электронов в атоме), или полуцелые значения
(при четном числе электронов в атоме), или полуцелые значения  (при нечетном числе электронов в атоме). Магнитное квантовое число
(при нечетном числе электронов в атоме). Магнитное квантовое число  принимает все значения, лежащие между
принимает все значения, лежащие между  и отличающиеся на единицу, то есть
и отличающиеся на единицу, то есть  (всего
(всего  значений).
значений).
Проекция вектора  на направление z равна
на направление z равна

где

есть магнетон Бора. Множитель Ланде  равен
равен

где I — орбитальное квантовое число (всегда целое), характеризующее полный орбитальный момент количества движения электронной оболочки,  спиновое квантовое число, характеризующее полный спин электронов оболочки.
спиновое квантовое число, характеризующее полный спин электронов оболочки.
Из (147.03) видно, что  принимают лишь дискретные значения. Так как
принимают лишь дискретные значения. Так как  где
где  угол между направлением
угол между направлением  и осью
и осью  то ориентация в пространстве механического момента (и связанного с ним магнитного) не произвольна — существует лишь дискретный ряд углов (квантование ориентации момента).
то ориентация в пространстве механического момента (и связанного с ним магнитного) не произвольна — существует лишь дискретный ряд углов (квантование ориентации момента).
Заметим, что для атомов с нечетным числом  электронов всегда
электронов всегда  Такие атомы всегда обладают собственным магнитным моментом и не могут быть диамагнитными. Для элементов первой группы периодической системы Д. И. Менделеева (щелочные элементы)
Такие атомы всегда обладают собственным магнитным моментом и не могут быть диамагнитными. Для элементов первой группы периодической системы Д. И. Менделеева (щелочные элементы)  нечетное, в основном состоянии
нечетное, в основном состоянии  -терм),
-терм),  Тогда по (147.06) и
Тогда по (147.06) и  то есть собственный момент в основном состоянии равен магнетону Бора. При четном числе электронов возможно
то есть собственный момент в основном состоянии равен магнетону Бора. При четном числе электронов возможно  (если
(если  или
или  последнее имеет место для всех благородных газов, у которых полностью заполнены электронные оболочки). В этом случае
последнее имеет место для всех благородных газов, у которых полностью заполнены электронные оболочки). В этом случае  и атом диамагнитен.
и атом диамагнитен.
Теория парамагнетизма строится так же, как теория ориентационной электрической поляризации: под действием внешнего магнитного поля магнитные дипольные моменты ориентируются по направлению поля, а тепловое движение оказывает на них дезориентирующее действие; в результате устанавливается некоторая равновесная магнитная поляризация вещества. Заметим, что тепловое движение оказывает не только дезориентирующее действие, но и помогает установлению равновесной ориентации. Действительно, магнитный момент  параллелен механическому моменту У. В магнитном поле момент обладает энергией
параллелен механическому моменту У. В магнитном поле момент обладает энергией

Следовательно, на момент действует пара сил

Под влиянием этой пары сил момент не может повернуться по полю, ибо К перпендикулярно к У и проекция — будет сохранять постоянное значение. Магнитный момент будет прецессировать вокруг направления магнитного поля, сохраняя постоянный угол  между
между  и
и  Чтобы изменилась проекция
Чтобы изменилась проекция  на направление поля, необходимо участие второго тела, которому атомная система могла бы отдать избыточное значение проекции момента
на направление поля, необходимо участие второго тела, которому атомная система могла бы отдать избыточное значение проекции момента  В газах это осуществляется путем столкновений молекул, в кристаллах — в результате взаимодействия с решеткой.
В газах это осуществляется путем столкновений молекул, в кристаллах — в результате взаимодействия с решеткой.
Магнитный момент единицы объема вещества определяется формулой

если магнитный момент частицы — атома или молекулы — свободно ориентируется в пространстве  число частиц в единице объема). Среднее значение
число частиц в единице объема). Среднее значение  вычисляется с помощью формулы Больцмана. Но в отличие от электрической ориентационной дипольной поляризации
вычисляется с помощью формулы Больцмана. Но в отличие от электрической ориентационной дипольной поляризации  и потенциальная энергия
и потенциальная энергия  принимают дискретный ряд значений. Вероятность того, что частица имеет энергию
принимают дискретный ряд значений. Вероятность того, что частица имеет энергию  (значение магнитного квантового числа
(значение магнитного квантового числа  равна
равна

Статистическая сумма  находится из условия
находится из условия  и равна
и равна

где

Вектор намагничивания равен

сумма в числителе равна  Подставляя сюда
Подставляя сюда  из (147.10), находим
из (147.10), находим

Введем аргумент

тогда

Здесь

есть функция Бриллюэна. При  (например, для щелочных атомов в нормальном состоянии)
(например, для щелочных атомов в нормальном состоянии)  При
При 

Таким образом, график функции Бриллюэна в общем случае лежит между  (рис. 76).
(рис. 76).
При  Поэтому
Поэтому  Подставляя последнее в (147.13), получаем восприимчивость в слабых полях (закон Кюри)
Подставляя последнее в (147.13), получаем восприимчивость в слабых полях (закон Кюри)

Выражение (147.15) аналогично выражению (141.10) для коэффициента поляризации дипольного диэлектрика. Однако (147.15) имеет более широкую область применимости: формула (141.10) справедлива только для газов,  и для газов, и для тех конденсированных тел, в которых магнитный момент сохраняет свободу ориентации. Ориентация электрического диполя в конденсированных телах затруднена, так как при этом поворачивается вся молекула как целое. Ориентация магнитного момента связана только с изменением направления орбитального и спинового моментов. Величина
и для газов, и для тех конденсированных тел, в которых магнитный момент сохраняет свободу ориентации. Ориентация электрического диполя в конденсированных телах затруднена, так как при этом поворачивается вся молекула как целое. Ориентация магнитного момента связана только с изменением направления орбитального и спинового моментов. Величина  в (147.15) равна
в (147.15) равна

Она дает эффективное число магнетонов Бора, а  есть эффективный магнитный момент атома (или иона).
есть эффективный магнитный момент атома (или иона).
Формула (147.15) дает правильный порядок величины восприимчивости. Действительно, полагая для твердого тела  получим
получим  Для
Для  а для
а для
 Для трехвалентных ионов редких земель сравнение данных теории и опыта
Для трехвалентных ионов редких земель сравнение данных теории и опыта  приведено в таблице.
приведено в таблице.
(см. скан)
В ионах редких земель внешние электронные оболочки  заполнены целиком и дают диамагнитный момент. Парамагнетизм этих ионов обусловлен постепенно застраивающейся
заполнены целиком и дают диамагнитный момент. Парамагнетизм этих ионов обусловлен постепенно застраивающейся  -оболочкой, расположенной глубоко в электронной оболочке иона и поэтому обладающей свободой вращения момента.
-оболочкой, расположенной глубоко в электронной оболочке иона и поэтому обладающей свободой вращения момента.
Теоретические значения  находятся в удовлетворительном согласии с опытом. Отклонение имеет место для ионов
находятся в удовлетворительном согласии с опытом. Отклонение имеет место для ионов  и
и  . Однако можно показать, что это расхождение значительно уменьшается, если учесть термы с для
. Однако можно показать, что это расхождение значительно уменьшается, если учесть термы с для  и для
и для  .
.
Рассмотрим вопрос о свободе вращения магнитных моментов ионов группы железа. Парамагнитные свойства этой группы обусловлены внешней  -оболочкой, которая постепенно заполняется электронами. Внешняя
-оболочкой, которая постепенно заполняется электронами. Внешняя  -оболочка подвержена воздействию со стороны сильных локальных полей соседних частиц кристаллической решетки. Это приводит к разрушению связи между орбитальным
-оболочка подвержена воздействию со стороны сильных локальных полей соседних частиц кристаллической решетки. Это приводит к разрушению связи между орбитальным  и спиновым
и спиновым  моментами. Поэтому орбитальный и спиновый магнитные моменты могут ориентироваться независимо друг от друга. С другой стороны, валентные
моментами. Поэтому орбитальный и спиновый магнитные моменты могут ориентироваться независимо друг от друга. С другой стороны, валентные  -электроны участвуют в образовании химических связей. Значит, пространственное распределение плотности
-электроны участвуют в образовании химических связей. Значит, пространственное распределение плотности  -электронов, а следовательно, и ориентация орбитальных моментов будут фиксированы. Поэтому надо ожидать, что свободой вращения в этих ионах будет обладать только спин и связанный
-электронов, а следовательно, и ориентация орбитальных моментов будут фиксированы. Поэтому надо ожидать, что свободой вращения в этих ионах будет обладать только спин и связанный
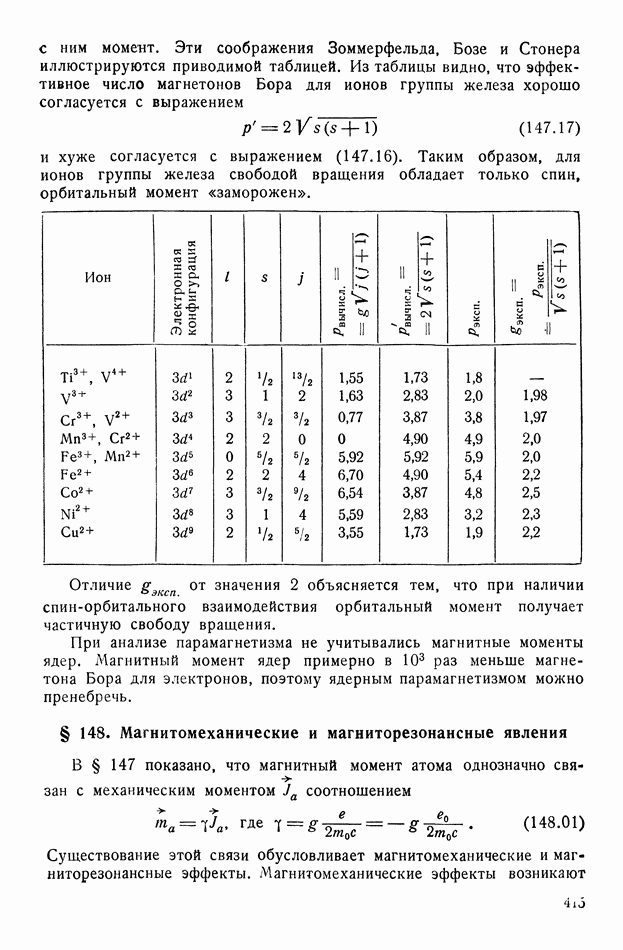
с ним момент. Эти соображения Зоммерфельда, Бозе и Стонера иллюстрируются приводимой таблицей. Из таблицы видно, что эффективное число магнетонов Бора для ионов группы железа хорошо согласуется с выражением

и хуже согласуется с выражением (147.16). Таким образом, для ионов группы железа свободой вращения обладает только спин, орбитальный момент «заморожен».
(см. скан)
Отличие  от значения 2 объясняется тем, что при наличии спин-орбитального взаимодействия орбитальный момент получает частичную свободу вращения.
от значения 2 объясняется тем, что при наличии спин-орбитального взаимодействия орбитальный момент получает частичную свободу вращения.
При анализе парамагнетизма не учитывались магнитные моменты ядер. Магнитный момент ядер примерно в 103 раз меньше магнетона Бора для электронов, поэтому ядерным парамагнетизмом можно пренебречь.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
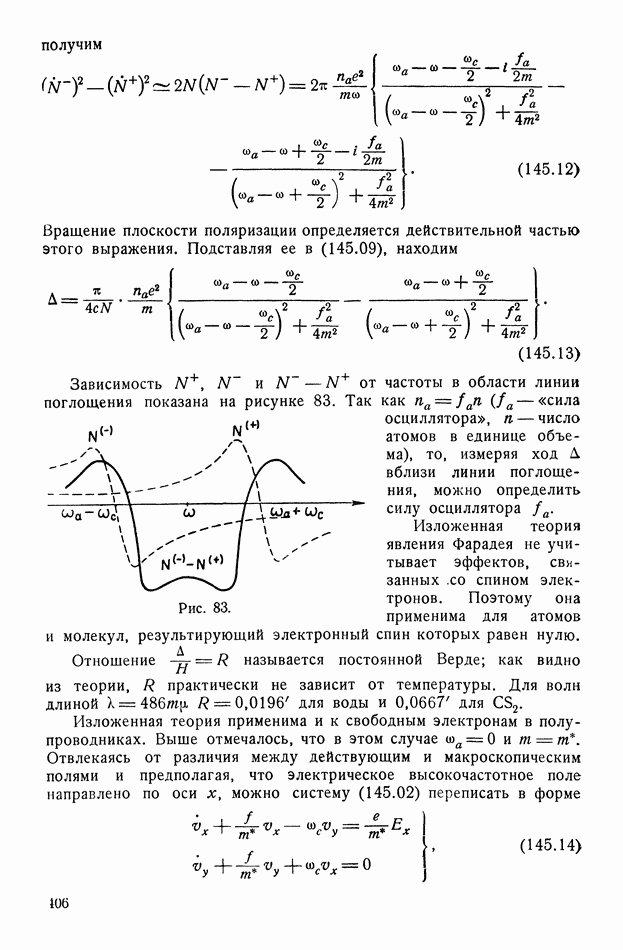
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
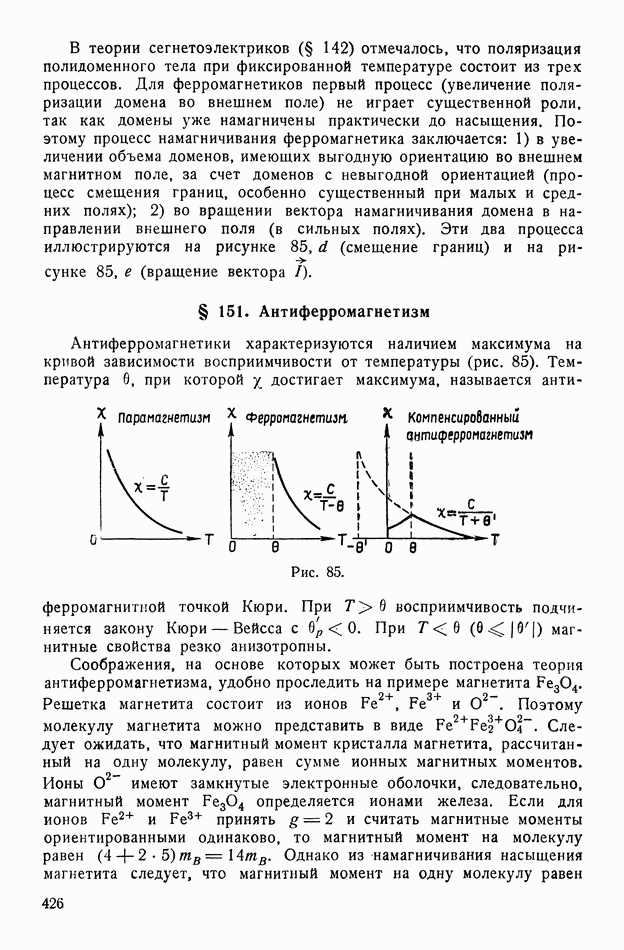
- § 151. Антиферромагнетизм
- § 152. Исторические замечания