| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
Ускоренно движущийся заряд излучает электромагнитное поле. Вследствие потери энергии на излучение кинетическая энергия заряда должна уменьшаться. Чтобы правильно учесть сохранение энергии и импульса, необходимо учесть реакцию собственного поля заряда на его движение.
Согласно (14.10) и (18.05) законы сохранения энергии и импульса частицы и ее поля можно написать в форме

где  соответственно энергия и импульс частицы,
соответственно энергия и импульс частицы,  и
и  те же величины для поля,
те же величины для поля,  внешняя сила, действующая на частицу,
внешняя сила, действующая на частицу,  ее мощность,
ее мощность,

— соответственно поток энергии и импульса поля в единицу времени. Таким образом,

есть сила реакции, с которой собственное поле заряда действует на заряд. Эта сила самодействия заряда включает силу инерции электромагнитного происхождения и реакцию излучения. Величина

есть мощность реакции поля.
Для ускоренно, но медленно движущегося заряда из (56.06) и (56.07) получим

Величину  можно рассматривать как электромагнитную силу инерции, действующую на ускоренно движущийся заряд. Тогда
можно рассматривать как электромагнитную силу инерции, действующую на ускоренно движущийся заряд. Тогда  есть работа этой силы в единицу времени.
есть работа этой силы в единицу времени.
Вычисление реакции излучения  значительно труднее. Проще всего, следуя Планку, подобрать
значительно труднее. Проще всего, следуя Планку, подобрать  так, чтобы выполнялось сохранение энергии.
так, чтобы выполнялось сохранение энергии.
Упростим уравнение сохранения энергии (57.01). Допустим, что движение частицы периодическое и для моментов  состояния движения заряда одинаковы (работа внешних сил компенсирует потерю энергии на излучение или энергией, излучаемой за период, можно пренебречь по сравнению с кинетической энергией заряда). В силу периодичности, энергии заряда
состояния движения заряда одинаковы (работа внешних сил компенсирует потерю энергии на излучение или энергией, излучаемой за период, можно пренебречь по сравнению с кинетической энергией заряда). В силу периодичности, энергии заряда  и поля
и поля  также будут одинаковыми в моменты
также будут одинаковыми в моменты  Поэтому работа, произведенная силой
Поэтому работа, произведенная силой  в течение периода
в течение периода  должна быть равна излученной за это время энергии.
должна быть равна излученной за это время энергии.
Энергия, испускаемая в единицу времени, по (50.02) равна

Поэтому

Интегрируя по частям правую часть, получим

Последнее соотношение будет удовлетворено, если допустить, что в каждый момент времени

Формула (57.07) дает искомую силу реакции излучения при периодическом движении заряда (при  которая пропорциональна производной по времени от ускорения частицы.
которая пропорциональна производной по времени от ускорения частицы.
Рассмотренный вывод (57.07) правомерен при условии, что сила реакции мала по сравнению с внешними силами. Для гармонически колеблющейся частицы это условие будет выполнено при не слишком высоких частотах. Если положить  то квазиупругая сила
то квазиупругая сила  а реакция излучения
а реакция излучения

Условие малости  дает
дает  или, вводя длину волны излучения
или, вводя длину волны излучения 

Таким образом, выражение (57.07) справедливо для волн, длина которых значительно превышает классический радиус электрона. Последнее выполняется для всех известных родов электромагнитного излучения, за исключением самых коротковолновых.
В силу (57.01) и (57.07) уравнение движения заряда под действием внешней силы  можно написать в форме
можно написать в форме

где  наблюдаемая масса, включающая в себя согласно § 56 электромагнитную массу.
наблюдаемая масса, включающая в себя согласно § 56 электромагнитную массу.
Уравнение Лоренца (57.10) применимо при условии (57.09). Но при выводе (57.10) были сделаны предположения, из-за которых это уравнение, строго говоря, не применимо ни к точечному, ни к протяженному заряду. В случае протяженного заряда исходное выражение (50.03) недостаточно — необходимо учитывать высшие члены разложения радиационного поля. Последние приведут к добавочным членам реакции излучения, содержащим высшие производные ускорения по времени. Такие члены существенно зависят от структуры заряда и вряд ли могут иметь физический смысл.
В случае точечного заряда  не зависит от размеров заряда, но электромагнитная масса
не зависит от размеров заряда, но электромагнитная масса  оказывается бесконечно большой. Поэтому необходимо предположить, что неэлектромагнитная масса
оказывается бесконечно большой. Поэтому необходимо предположить, что неэлектромагнитная масса  заряда принимает бесконечно большое отрицательное значение, чтобы
заряда принимает бесконечно большое отрицательное значение, чтобы
наблюдаемая масса  была конечной. При этом предположении уравнение (57.10) можно было бы считать точным. Однако уравнение (57.10) третьего порядка. Общий интеграл его содержит девять произвольных постоянных и, чтобы определить движение, надо задавать три начальных условия:
была конечной. При этом предположении уравнение (57.10) можно было бы считать точным. Однако уравнение (57.10) третьего порядка. Общий интеграл его содержит девять произвольных постоянных и, чтобы определить движение, надо задавать три начальных условия:  при
при  Но это, вообще говоря, противоречит механике, требующей задания только
Но это, вообще говоря, противоречит механике, требующей задания только  Противоречие с классической механикой выступает более явно, если заметить, что при отсутствии внешних сил (57.10), кроме решения, удовлетворяющего закону инерции, имеются решения, не удовлетворяющие ему. Таким образом, уравнение Лоренца имеет большее число решений, нежели это необходимо для описания движения.
Противоречие с классической механикой выступает более явно, если заметить, что при отсутствии внешних сил (57.10), кроме решения, удовлетворяющего закону инерции, имеются решения, не удовлетворяющие ему. Таким образом, уравнение Лоренца имеет большее число решений, нежели это необходимо для описания движения.
Решения уравнения (57.10) можно разделить на «физические», имеющие физический смысл, и «нефизические», не имеющие его. Формально нефизические решения можно устранить соответствующим подбором постоянных интегрирования. В качестве примера рассмотрим движение заряда вдоль оси  при отсутствии внешних сил. В этом случае решение (57.10) имеет вид
при отсутствии внешних сил. В этом случае решение (57.10) имеет вид

Если  то есть ускорение в начальный момент было отлично от нуля (например, для
то есть ускорение в начальный момент было отлично от нуля (например, для  имелась сила, которая исчезла при
имелась сила, которая исчезла при  то скорость и ускорение с течением времени будут неограниченно расти. Это противоречит закону инерции. Следовательно, физическими решениями будут лишь те, для которых
то скорость и ускорение с течением времени будут неограниченно расти. Это противоречит закону инерции. Следовательно, физическими решениями будут лишь те, для которых  Формальное устранение нефизических решений уравнения Лоренца оставляет чувство неудовлетворенности: уравнения, адекватно отражающие явления природы, не должны иметь абсурдных решений. Можно думать, что нефизические решения обусловлены бесконечной электромагнитной собственной массой точечной частицы. Конечная масса
Формальное устранение нефизических решений уравнения Лоренца оставляет чувство неудовлетворенности: уравнения, адекватно отражающие явления природы, не должны иметь абсурдных решений. Можно думать, что нефизические решения обусловлены бесконечной электромагнитной собственной массой точечной частицы. Конечная масса  получена в результате вычитания двух бесконечностей
получена в результате вычитания двух бесконечностей  и что математически не вполне корректно. Поэтому уравнение Лоренца следует применять с осторожностью.
и что математически не вполне корректно. Поэтому уравнение Лоренца следует применять с осторожностью.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
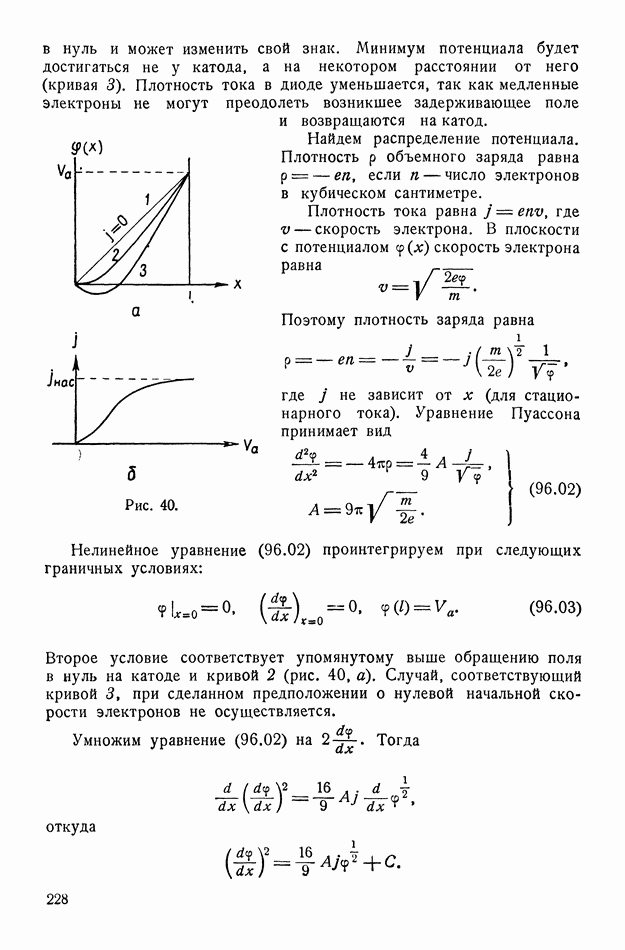
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
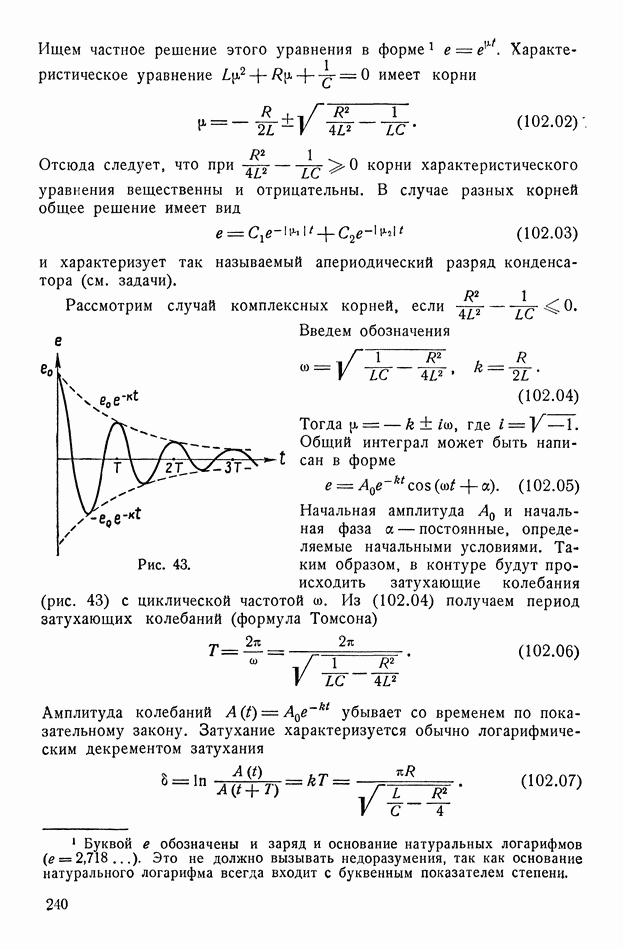
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
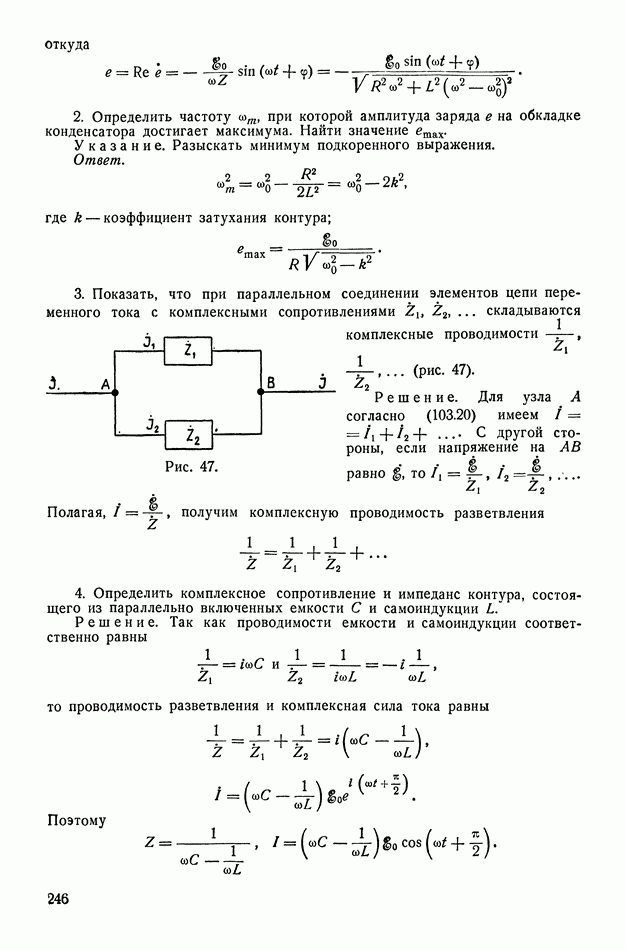
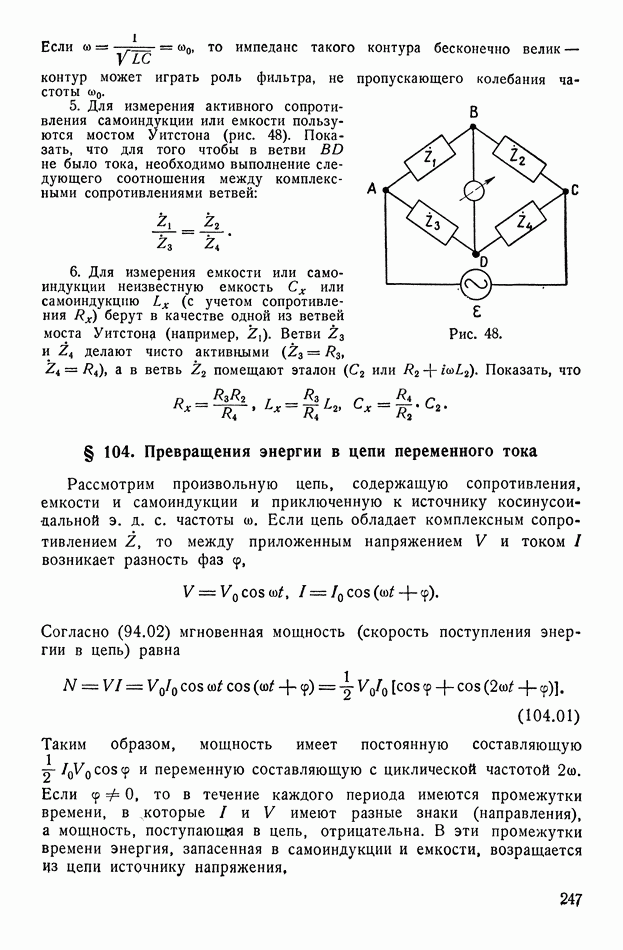
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
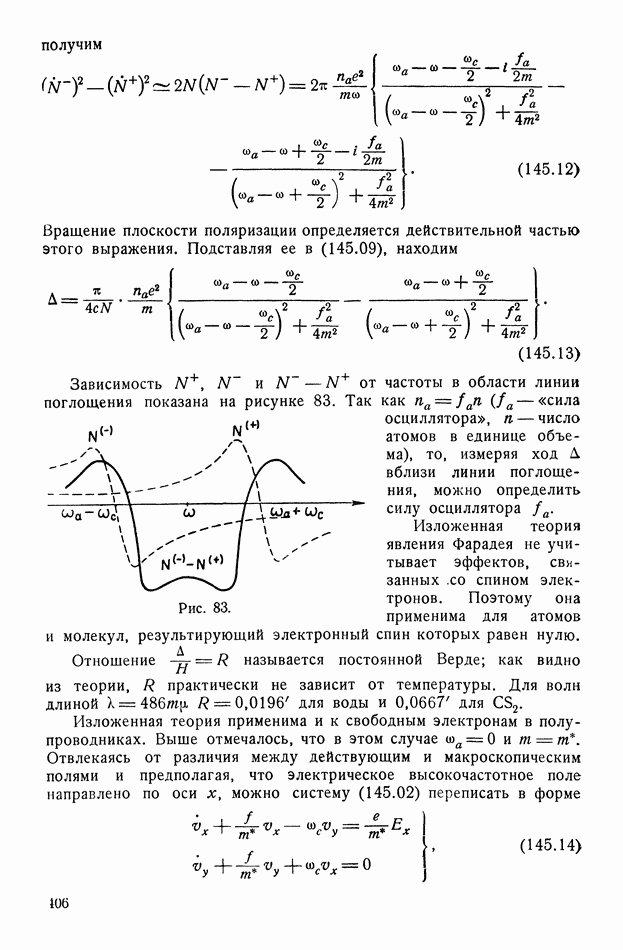
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
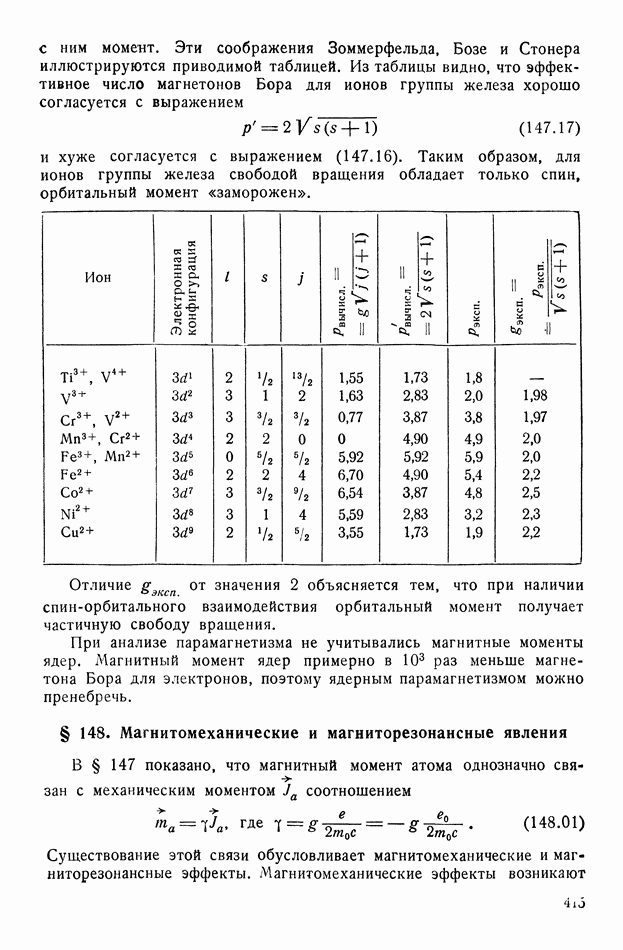
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
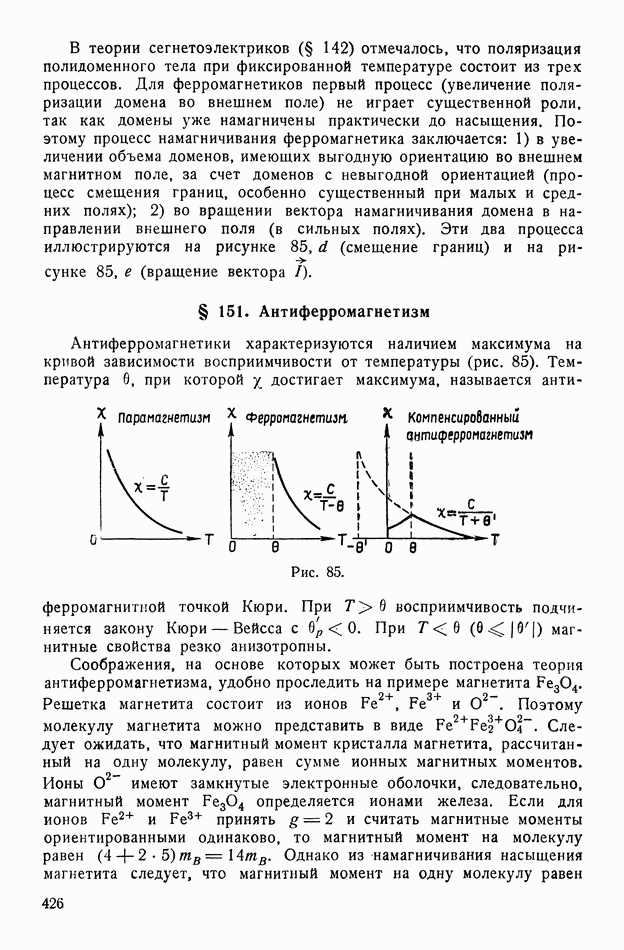
- § 151. Антиферромагнетизм
- § 152. Исторические замечания