| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 146. Диамагнетизм.
Индуцированный магнитный момент атома, обусловленный прецессией электронных орбит вокруг направления магнитного поля, согласно (55.13) равен

где  средний квадрат радиуса орбиты электрона а (суммирование производится по всем
средний квадрат радиуса орбиты электрона а (суммирование производится по всем  электронам атома). Вводя средний
электронам атома). Вводя средний
квадрат радиуса орбит всех электронов атома  получим формулу
получим формулу  Ланжевена (с учетом поправок В. Паули)
Ланжевена (с учетом поправок В. Паули)

Такой диамагнитный момент возникает в магнитном поле у всякого атома независимо от наличия у него собственного магнитного момента. Собственный магнитный момент атома (если он существует) по порядку величины равен магнетону Бора  и значительно превышает диамагнитный момент в обычных полях. Поэтому для того, чтобы вещество было диамагнитным, необходимо, чтобы атомы его не обладали собственными магнитными моментами. Диамагнитная восприимчивость на грамм-молекулу равна
и значительно превышает диамагнитный момент в обычных полях. Поэтому для того, чтобы вещество было диамагнитным, необходимо, чтобы атомы его не обладали собственными магнитными моментами. Диамагнитная восприимчивость на грамм-молекулу равна

где  число Авогадро. Для определения объемной восприимчивости надо
число Авогадро. Для определения объемной восприимчивости надо  заменить числом
заменить числом  атомов в
атомов в 
Из (146.03) видно, что задача расчета диамагнитной восприимчивости сводится к вычислению  Для этого надо знать распределение заряда электронов в данном атоме. Распределение электронного заряда может быть найдено методом квантовой механики. В приводимой таблице дается сравнение молярных диамагнитных восприимчивостей некоторых атомов (свободных) и ионов (в кристаллах), полученных экспериментально и вычисленных с помощью приближенного метода Хартри — Фока.
Для этого надо знать распределение заряда электронов в данном атоме. Распределение электронного заряда может быть найдено методом квантовой механики. В приводимой таблице дается сравнение молярных диамагнитных восприимчивостей некоторых атомов (свободных) и ионов (в кристаллах), полученных экспериментально и вычисленных с помощью приближенного метода Хартри — Фока.
(см. скан)
Из таблицы видно, что согласие теории с опытом вполне удовлетворительное, если учесть упрощения, допускаемые при квантово-механической трактовке многоэлектронных систем.
Для вычисления диамагнетизма молекул формула (146.03) оказывается, вообще говоря, не применимой, так как при выводе (146.01) неявно предполагалось, что направление внешнего магнитного поля совпадает с осью симметрии системы. Последнее выполнено для сферически симметричных атомов, но обычно не выполнено для
молекул. Ван-Флек показал, что молекула в магнитном поле наряду с диамагнитным моментом (146.01) получает добавочный парамагнитный момент, имеющий порядок величины такой же, как диамагнитный. Поэтому вещество оказывается диамагнитным или парамагнитным в зависимости от того, какой из членов — ланжевеновский или ван-флековский — преобладает. Во всех случаях восприимчивость не зависит от температуры.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
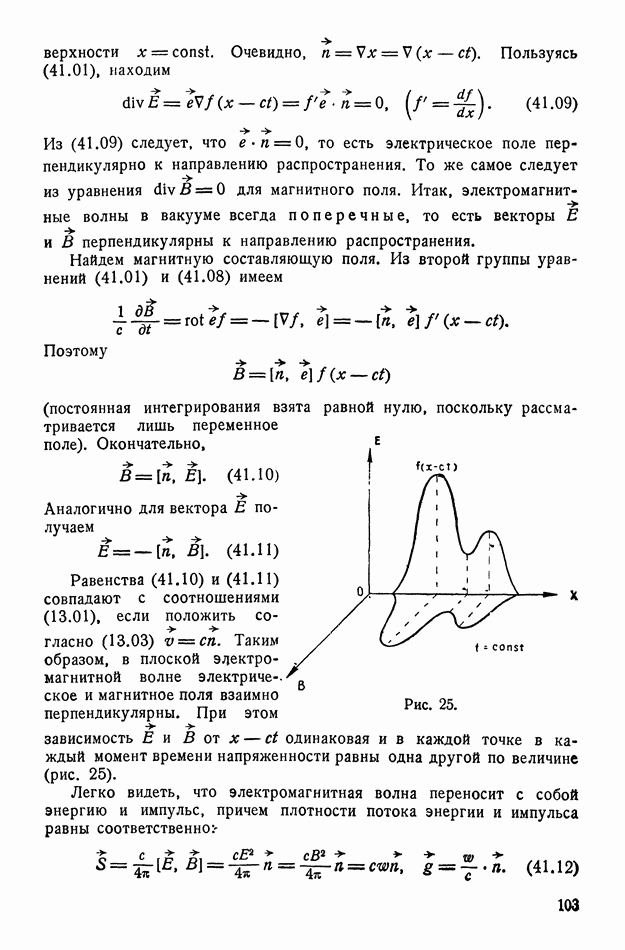
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
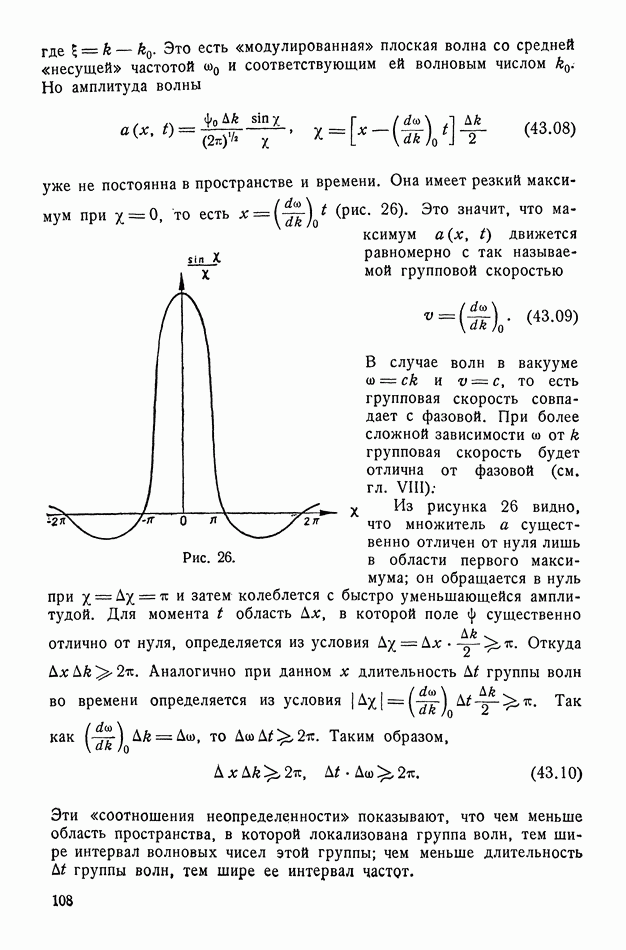
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
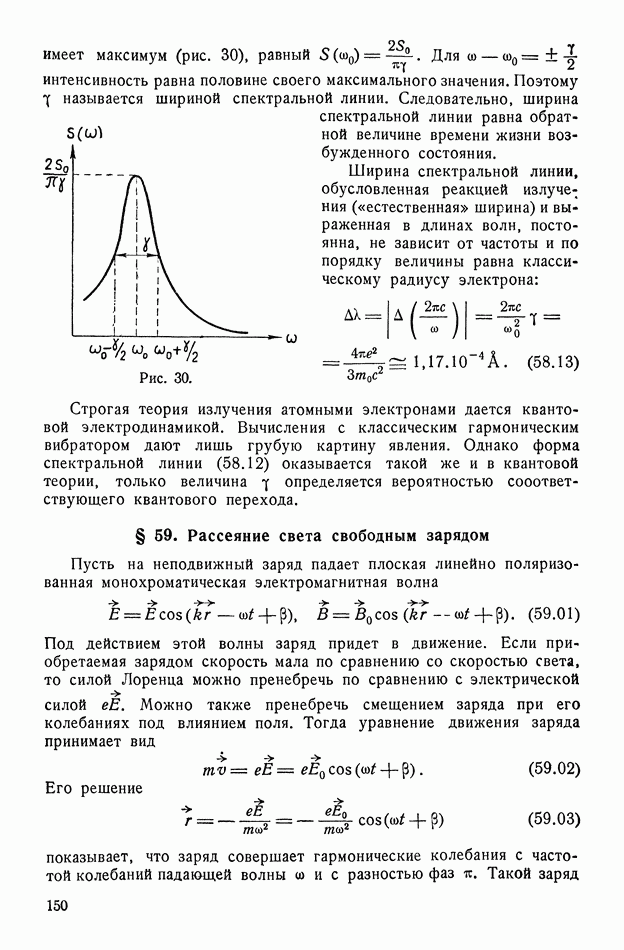
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
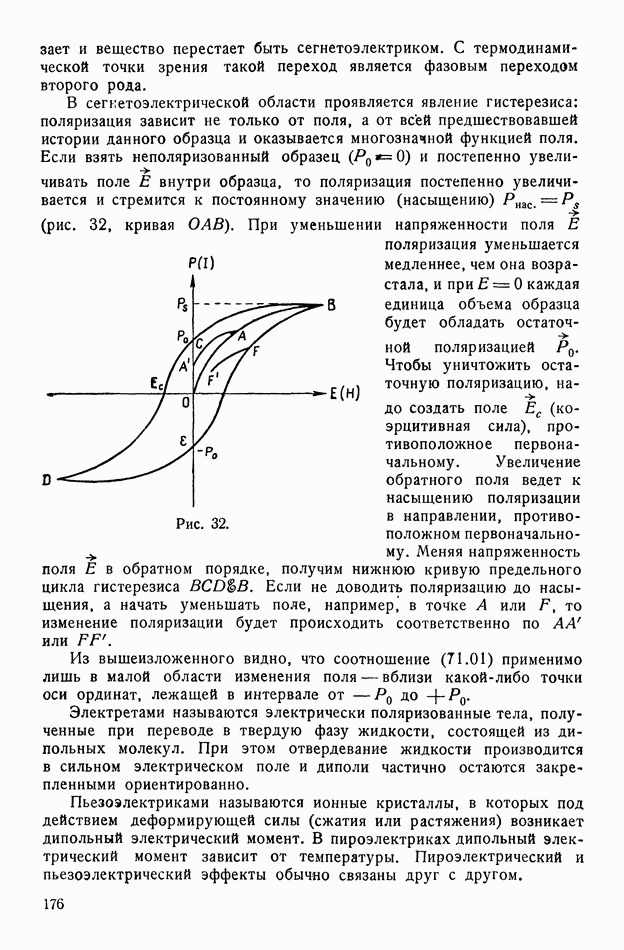
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
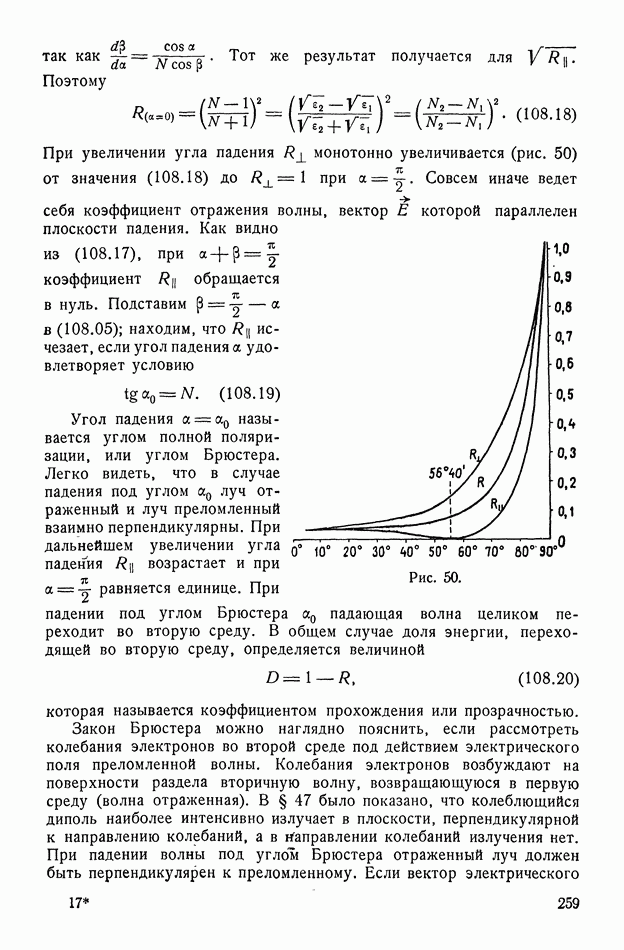
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
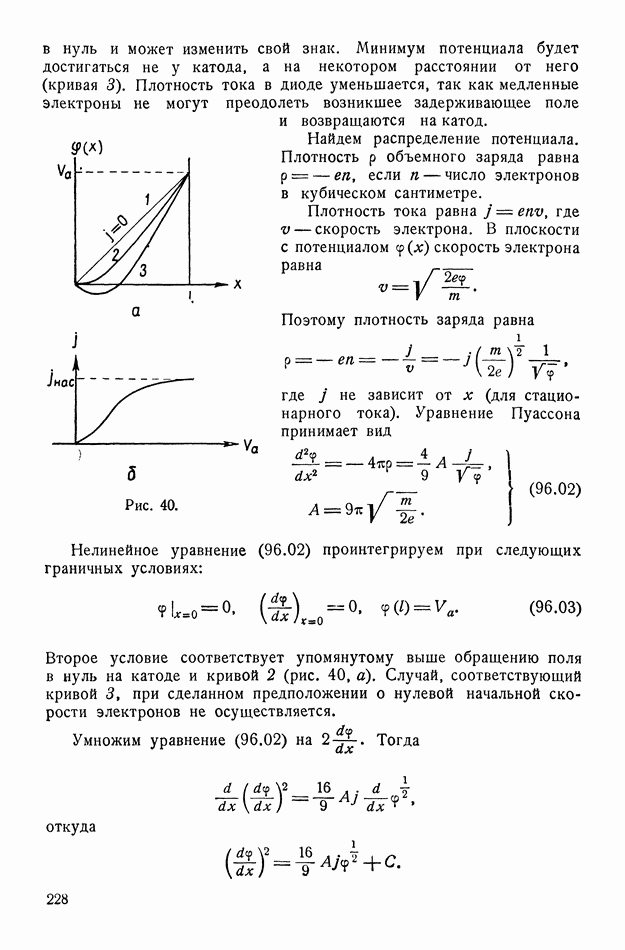
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
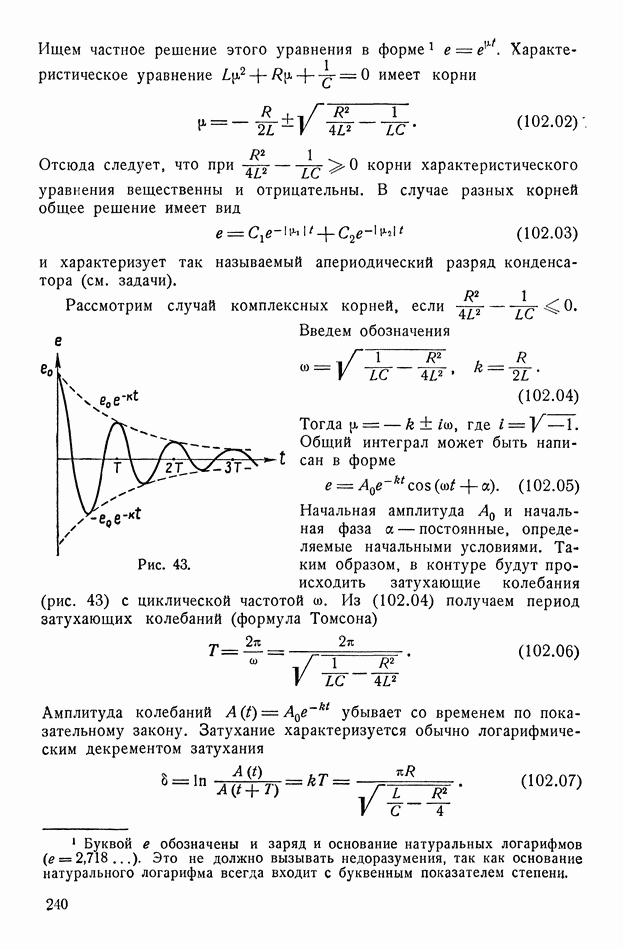
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
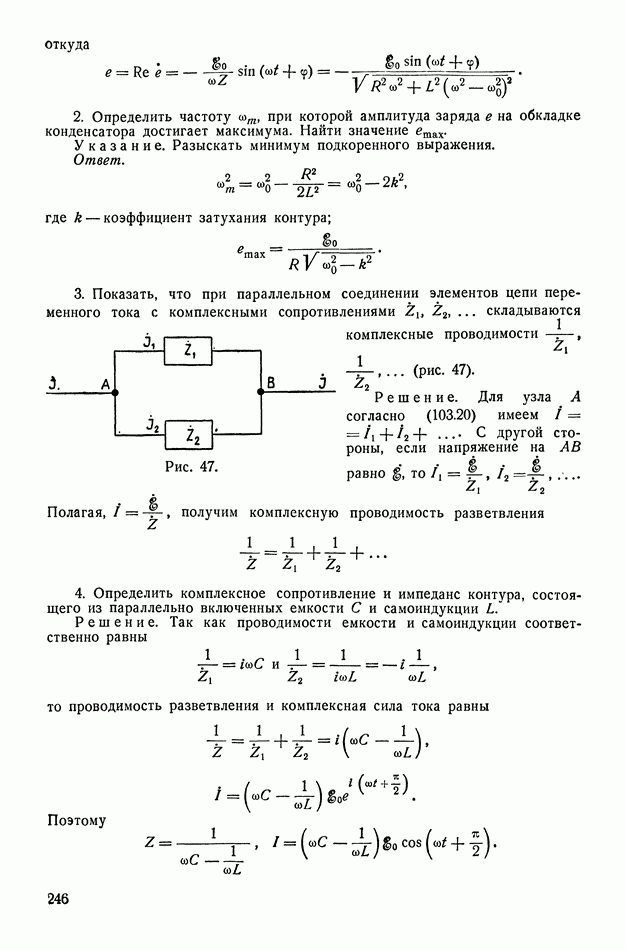
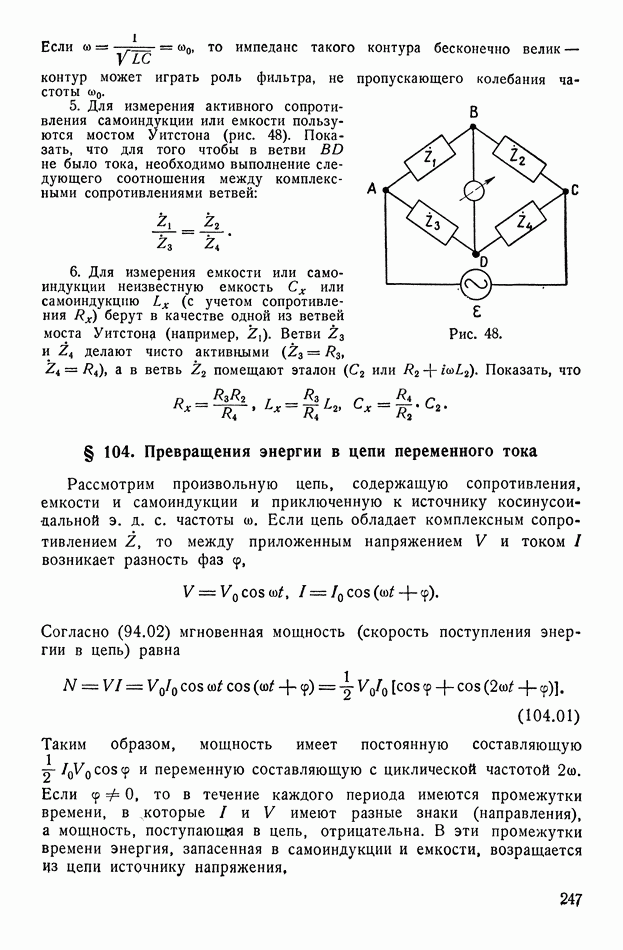
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
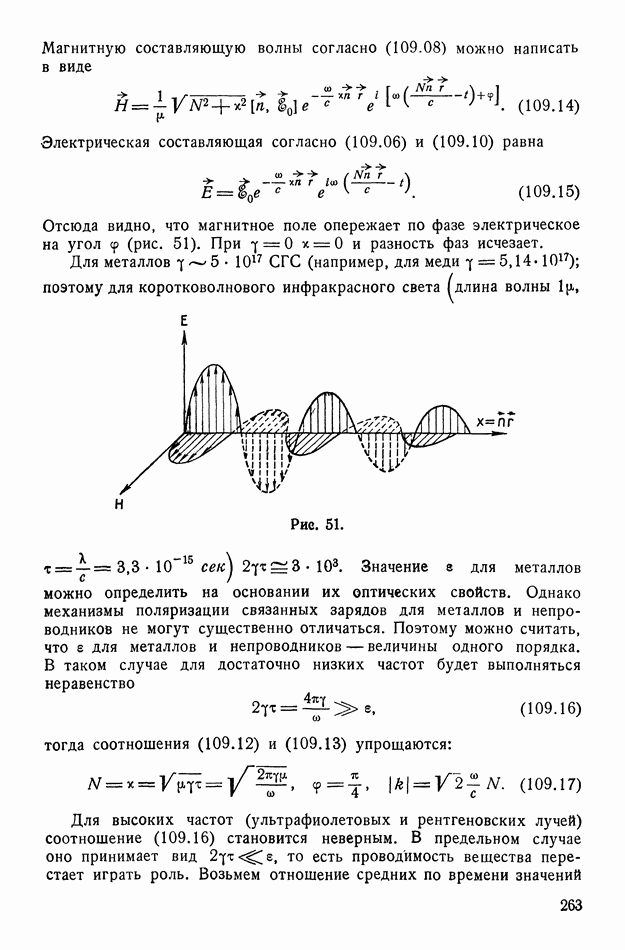
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
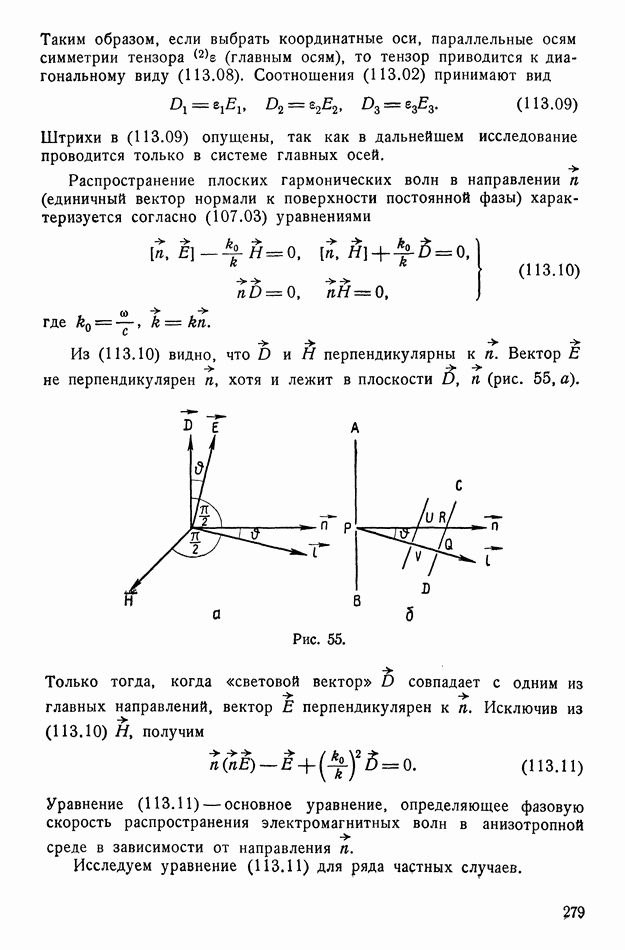
- § 113. Распространение электромагнитных волн в анизотропных телах
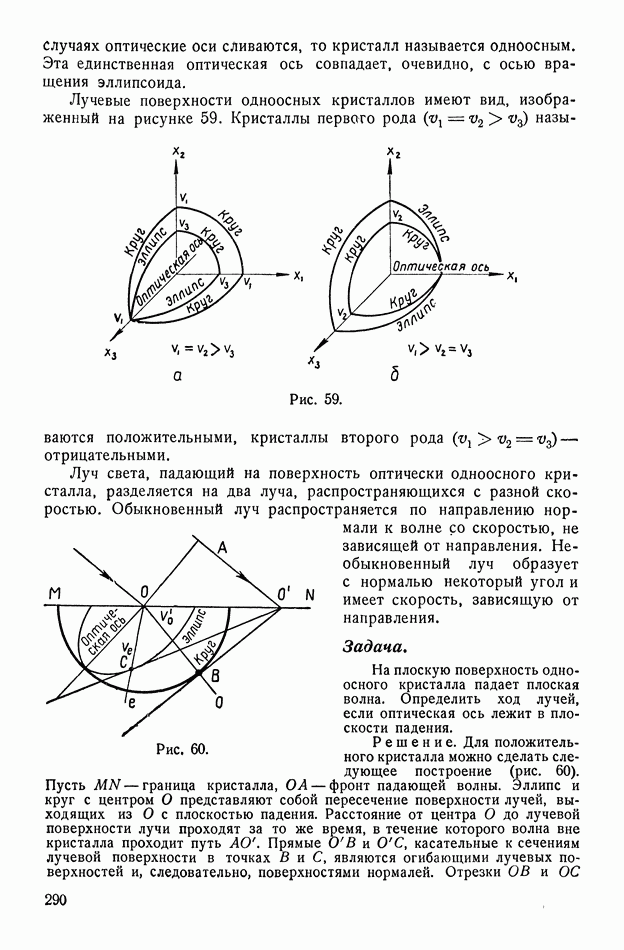
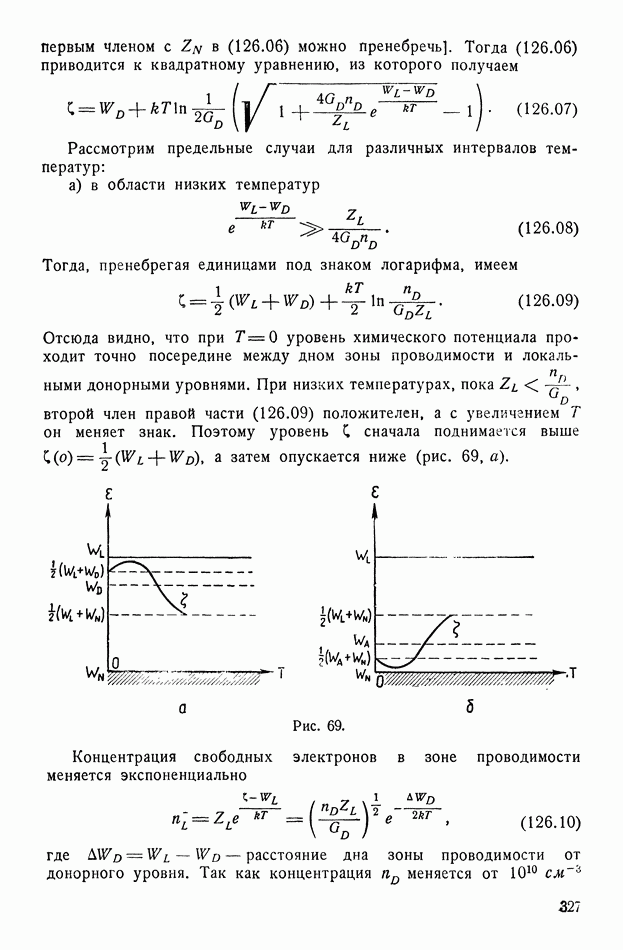
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
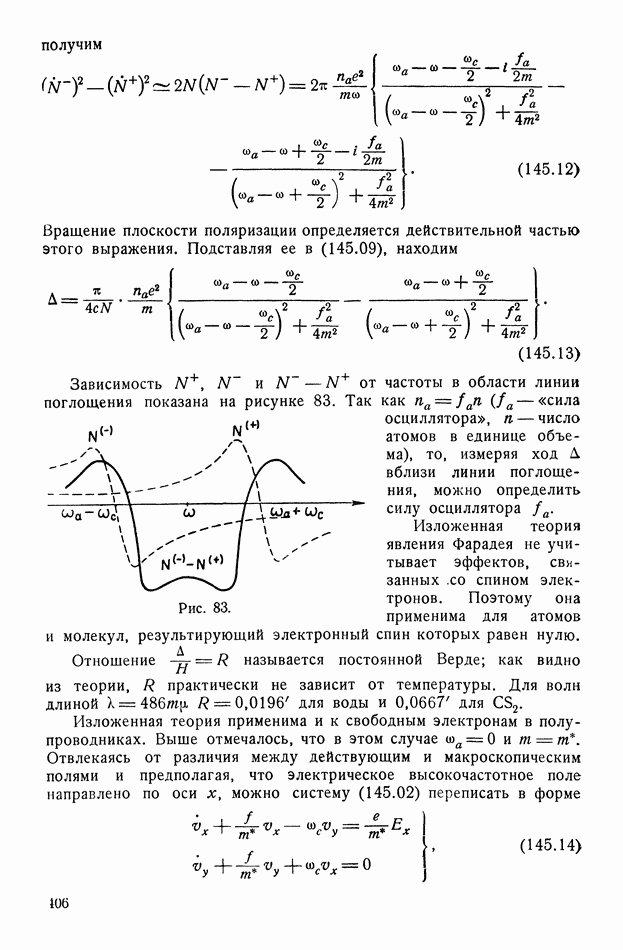
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
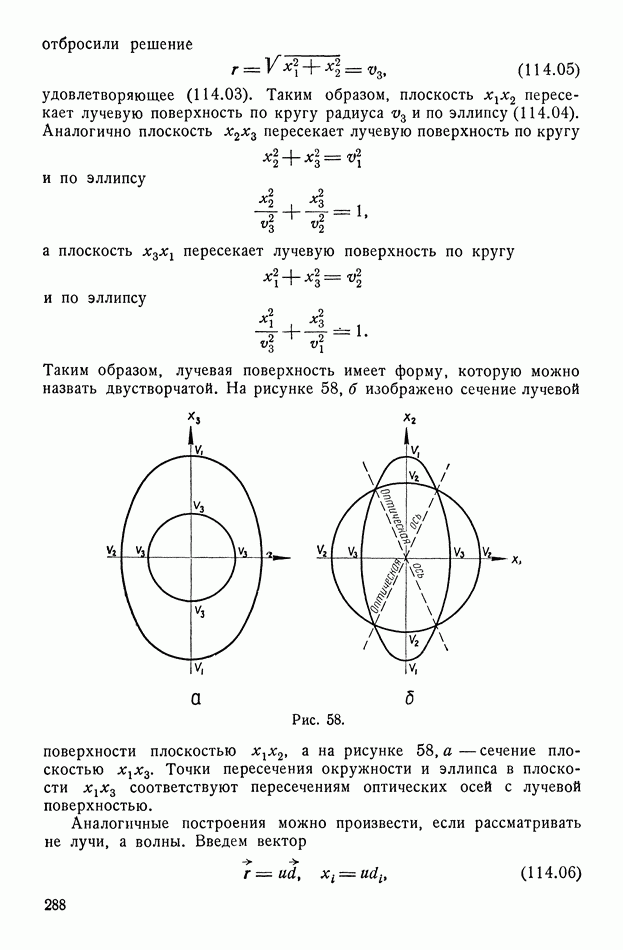
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
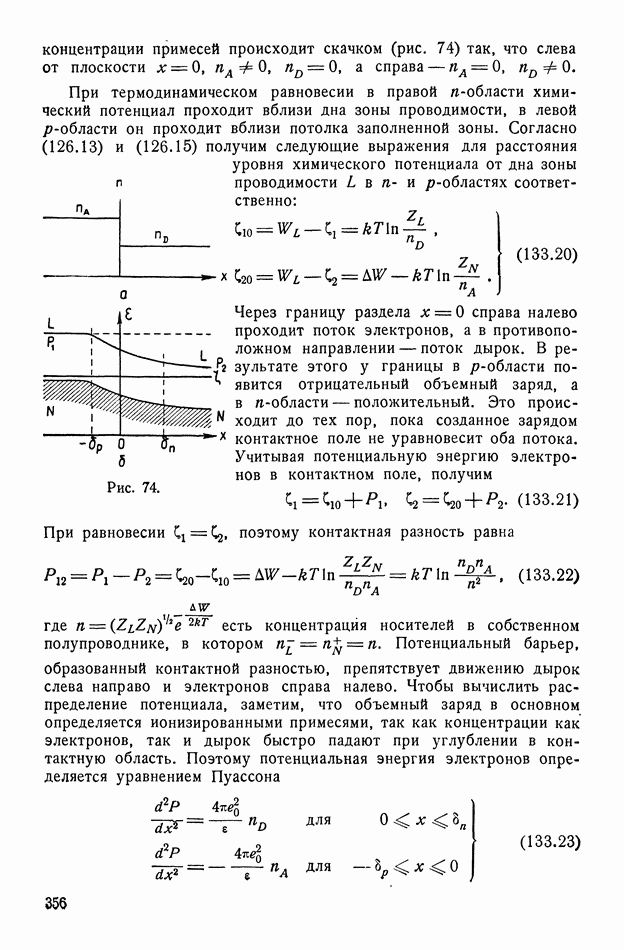
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
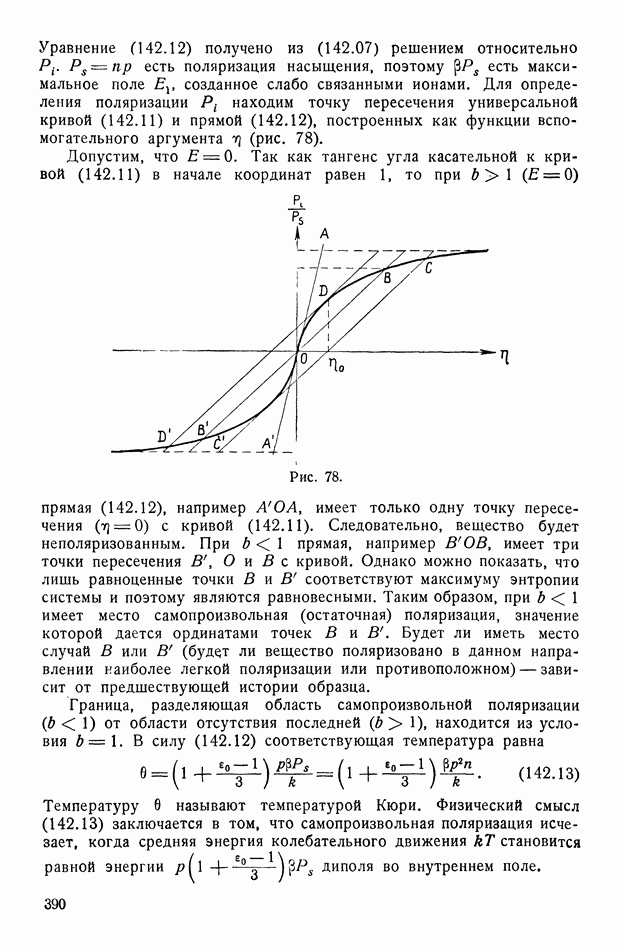
- § 142. Сегнетоэлектрики
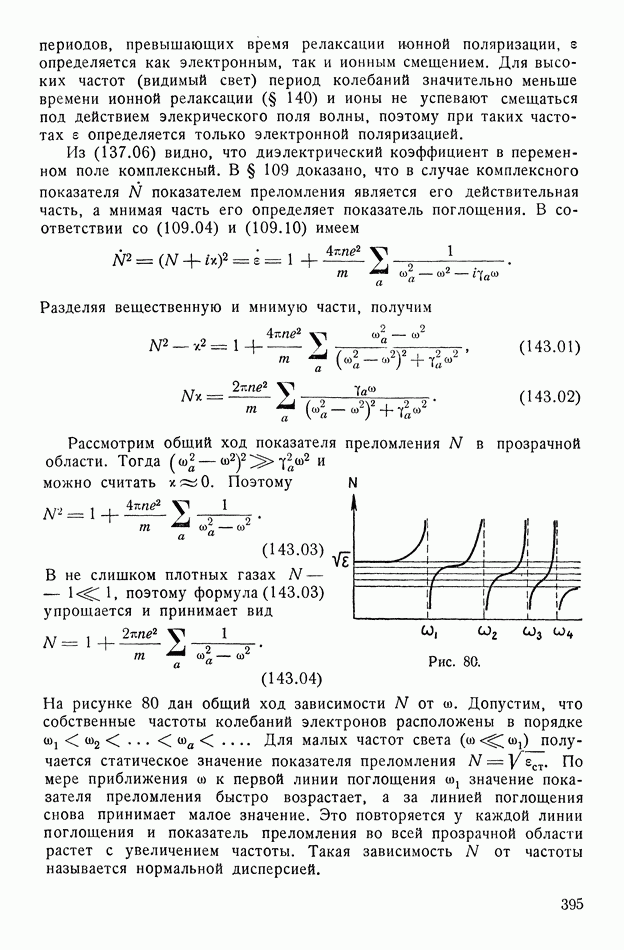
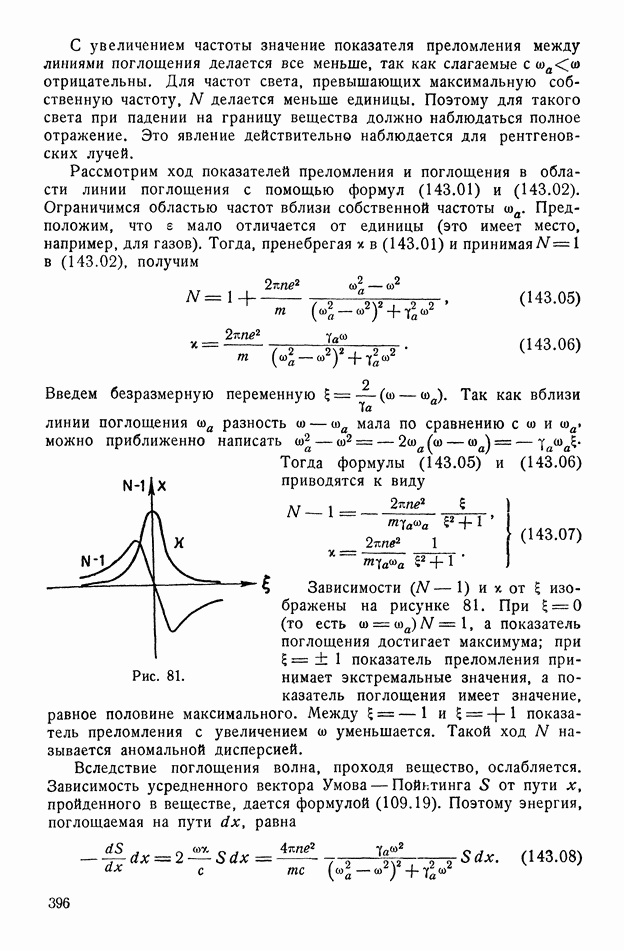
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
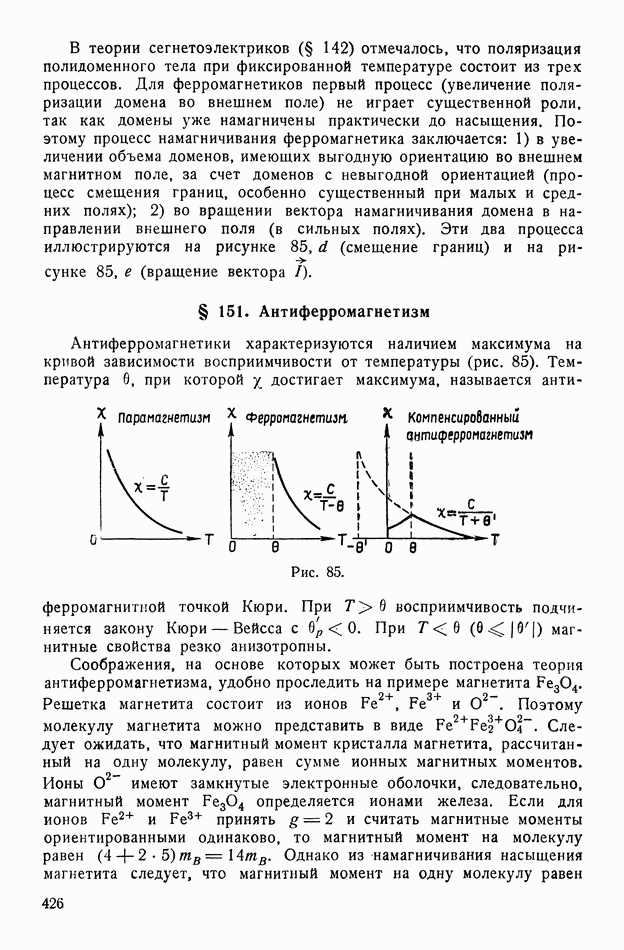
- § 151. Антиферромагнетизм
- § 152. Исторические замечания