| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ИОННЫЕ ФОРМЫ АМИНОКИСЛОТ
Аминокислоты несут по крайней мере две слабоионизируемые кислые группы, —СООН и  В растворе эти группы находятся в двух формах, заряженной и незаряженной, между которыми поддерживается протонное равновесие:
В растворе эти группы находятся в двух формах, заряженной и незаряженной, между которыми поддерживается протонное равновесие:

 и
и  здесь являются протонированными партнерами, т. е. кислотами, а
здесь являются протонированными партнерами, т. е. кислотами, а  основаниями (т.е. акцепторами протонов) соответствующих кислот. MR—СООН, и
основаниями (т.е. акцепторами протонов) соответствующих кислот. MR—СООН, и  это слабые кислоты, и все же R-СООН является в несколько тысяч раз более сильной кислотой, чем
это слабые кислоты, и все же R-СООН является в несколько тысяч раз более сильной кислотой, чем  При значениях
При значениях  характерных для плазмы крови и межклеточной жидкости (7,4 и 7,1 соответственно), карбоксильные группы находятся исключительно в форме карбоксилатных ионов,
характерных для плазмы крови и межклеточной жидкости (7,4 и 7,1 соответственно), карбоксильные группы находятся исключительно в форме карбоксилатных ионов,  При этих значениях
При этих значениях  большая часть аминогрупп находится преимущественно в ассоциированной (протонированной) форме,
большая часть аминогрупп находится преимущественно в ассоциированной (протонированной) форме,  Преобладающая ионная форма аминокислот, присутствующих в крови и в большинстве тканей, представлена на рис.
Преобладающая ионная форма аминокислот, присутствующих в крови и в большинстве тканей, представлена на рис.  Структура, изображенная на рис.
Структура, изображенная на рис.  не может существовать ни при каких
не может существовать ни при каких  При значениях
При значениях  достаточно низких для протонирования карбоксильной группы, аминогруппа, намного более слабая кислота, также будет протонирована. Примерные значения
достаточно низких для протонирования карбоксильной группы, аминогруппа, намного более слабая кислота, также будет протонирована. Примерные значения  и
и  -аминогрупп
-аминогрупп  -аминокислоты равны 2 и 10 соответственно (табл. 3.1). Кислота при
-аминокислоты равны 2 и 10 соответственно (табл. 3.1). Кислота при  ниже своего
ниже своего  будет преимущественно протонирована, причем если
будет преимущественно протонирована, причем если  будет сдвинуто на 2 единицы ниже
будет сдвинуто на 2 единицы ниже  она будет протонирована на 99%. По мере увеличения
она будет протонирована на 99%. По мере увеличения  карбоксильная группа теряет свой протон намного раньше, чем
карбоксильная группа теряет свой протон намного раньше, чем  При высоких значениях
При высоких значениях  достаточных для перехода аминогруппы преимущественно в форму незаряженного сопряженного основания, карбоксильная группа будет находиться в виде карбоксилатного иона
достаточных для перехода аминогруппы преимущественно в форму незаряженного сопряженного основания, карбоксильная группа будет находиться в виде карбоксилатного иона  Однако для удобства во многих уравнениях, когда речь не идет о протонных равновесиях, часто используется структура, изображенная на рис.
Однако для удобства во многих уравнениях, когда речь не идет о протонных равновесиях, часто используется структура, изображенная на рис. 
Относительную кислотность слабых кислот можно охарактеризовать с помощью константы диссоциации кислоты  или соответствующего ей
или соответствующего ей  отрицательного логарифма константы диссоциации:
отрицательного логарифма константы диссоциации:

В табл. 3.1 представлены кислотные группы и значения  для функциональных групп 20 аминокислот, входящих в состав белков.
для функциональных групп 20 аминокислот, входящих в состав белков.
Полный (суммарный) заряд (алгебраическая сумма всех положительных и отрицательных зарядов) аминокислоты зависит от  т.е. от концентрации протонов в окружающем растворе. Заряд аминокислоты или ее производного можно изменить, варьируя
т.е. от концентрации протонов в окружающем растворе. Заряд аминокислоты или ее производного можно изменить, варьируя  это облегчает физическое разделение аминокислот, пептидов и белков.
это облегчает физическое разделение аминокислот, пептидов и белков.
Значение  при котором суммарный заряд аминокислоты равен нулю и поэтому она не перемещается в постоянном электрическом поле, называется ее изоэлектрической точкой
при котором суммарный заряд аминокислоты равен нулю и поэтому она не перемещается в постоянном электрическом поле, называется ее изоэлектрической точкой  Для алифатических аминокислот, таких как аланин, изоэлектрическая форма имеет вид, представленный на рис. 3.3.
Для алифатических аминокислот, таких как аланин, изоэлектрическая форма имеет вид, представленный на рис. 3.3.
Изоэлектрическая точка находится посредине между ближайшими значениями  диссоциирующих групп по разные стороны от
диссоциирующих групп по разные стороны от  Для аминокислоты, имеющей только две диссоциирующие группы, никакой неоднозначности при подсчете
Для аминокислоты, имеющей только две диссоциирующие группы, никакой неоднозначности при подсчете  не возникает. Найдем, например,
не возникает. Найдем, например,  для аланина. Поскольку
для аланина. Поскольку  изоэлектрическая точка
изоэлектрическая точка  аланина равна
аланина равна

Рассчитать  для соединения, содержащего более двух диссоциирующих групп, труднее, и в этом
для соединения, содержащего более двух диссоциирующих групп, труднее, и в этом

Рис. 3.2. А. Правильная ионная структура аминокислоты при значениях  близких к физиологическим. Б. Незаряженная форма, которая не может существовать ни при каких значениях
близких к физиологическим. Б. Незаряженная форма, которая не может существовать ни при каких значениях  впрочем, такого типа формулу удобно использовать при обсуждении химии аминокислот.
впрочем, такого типа формулу удобно использовать при обсуждении химии аминокислот.
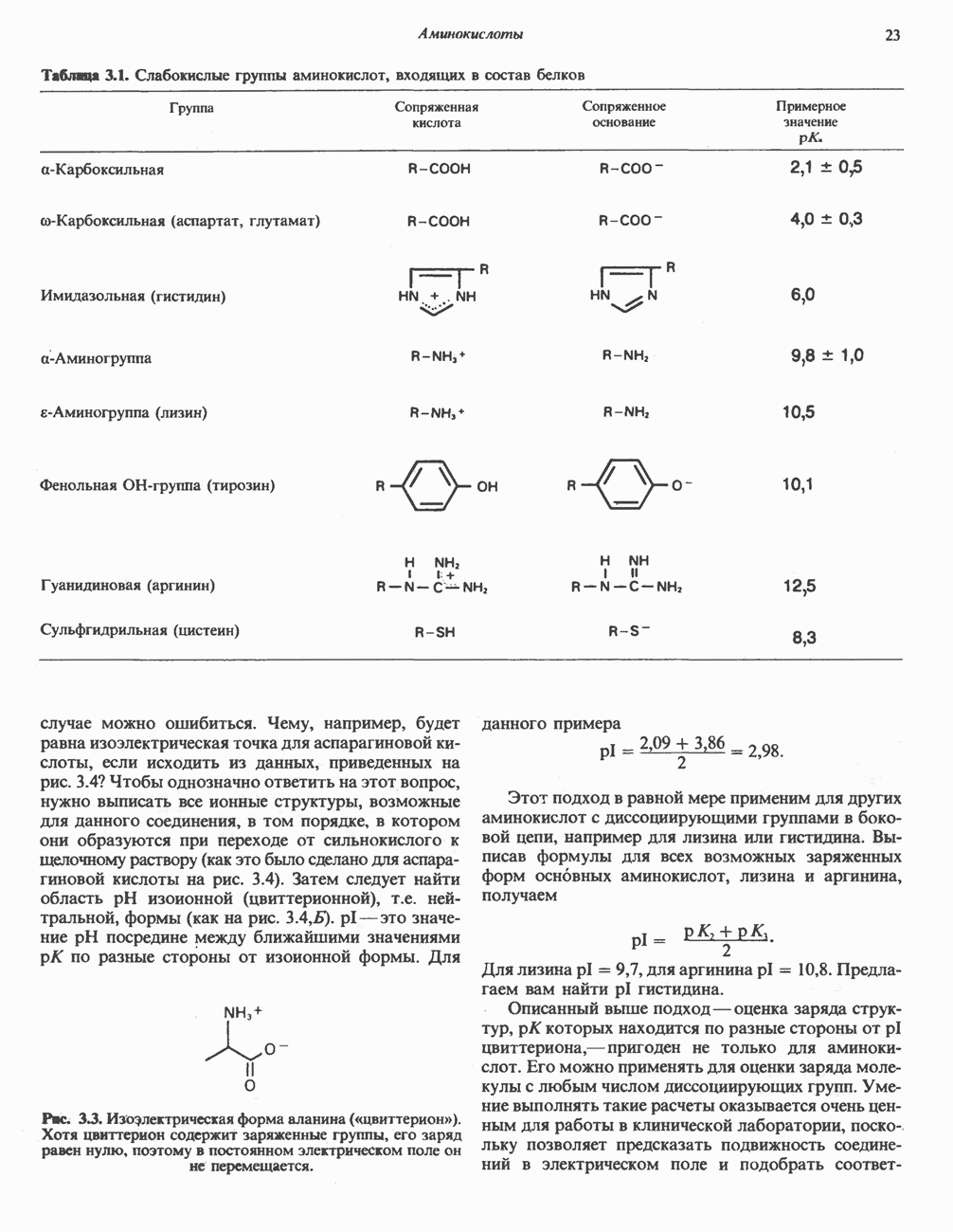
Таблица 3.1. Слабокислые группы аминокислот, входящих в состав белков

случае можно ошибиться. Чему, например, будет равна изоэлектрическая точка для аспарагиновой кислоты, если исходить из данных, приведенных на рис. 3.4? Чтобы однозначно ответить на этот вопрос, нужно выписать все ионные структуры, возможные для данного соединения, в том порядке, в котором они образуются при переходе от сильнокислого к щелочному раствору (как это было сделано для аспарагиновой кислоты на рис. 3.4). Затем следует найти область pH изоионной (цвиттерионной), т.е. нейтральной, формы (как на рис. 3.4,Б),  - это значение pH посредине между ближайшими значениями
- это значение pH посредине между ближайшими значениями  по разные стороны от изоионной формы.
по разные стороны от изоионной формы.

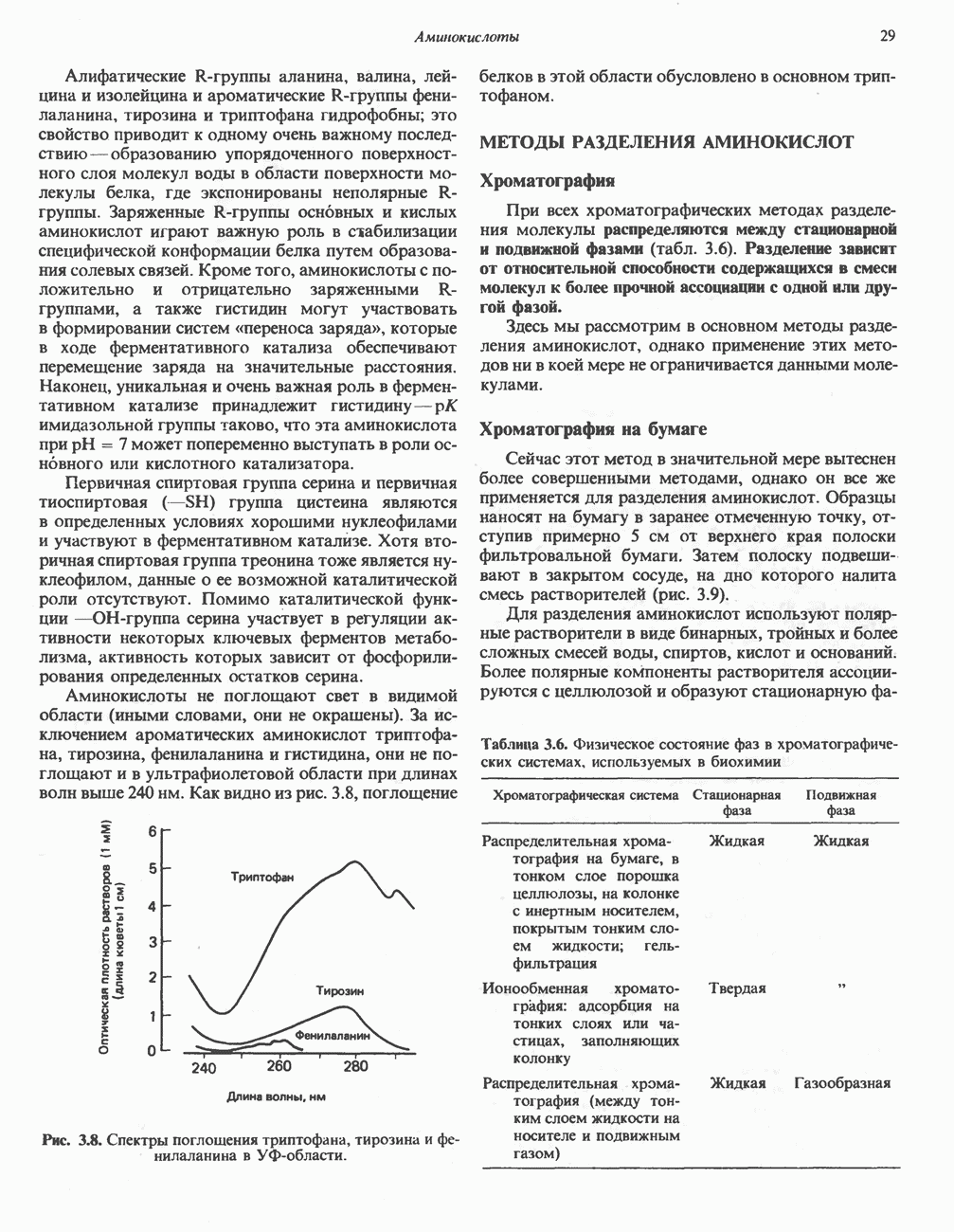
Рис. 33. Изоэлектрическая форма аланина («цвиттерион»). Хотя цвиттерион содержит заряженные группы, его заряд равен нулю, поэтому в постоянном электрическом поле он не перемещается.
Для данного примера

Этот подход в равной мере применим для других аминокислот с диссоциирующими группами в боковой цепи, например для лизина или гистидина. Выписав формулы для всех возможных заряженных форм основных аминокислот, лизина и аргинина, получаем

Для лизина  для аргинина
для аргинина  Предлагаем вам найти
Предлагаем вам найти  гистидина.
гистидина.
Описанный выше подход — оценка заряда структур,  которых находится по разные стороны от
которых находится по разные стороны от  цвиттериона, - пригоден не только для аминокислот. Его можно применять для оценки заряда молекулы с любым числом диссоциирующих групп. Умение выполнять такие расчеты оказывается очень ценным для работы в клинической лаборатории, поскольку позволяет предсказать подвижность соединений в электрическом поле и подобрать соответствующий
цвиттериона, - пригоден не только для аминокислот. Его можно применять для оценки заряда молекулы с любым числом диссоциирующих групп. Умение выполнять такие расчеты оказывается очень ценным для работы в клинической лаборатории, поскольку позволяет предсказать подвижность соединений в электрическом поле и подобрать соответствующий

Рис. 3.4. Протонное равновесие для аспарагиновой кислоты.
буфер для их разделения. Например, для разделения двух соединений со значениями  и 8 пригоден буфер с
и 8 пригоден буфер с  поскольку при этом
поскольку при этом  молекулы с
молекулы с  будут нести суммарный отрицательный заряд, а молекулы с
будут нести суммарный отрицательный заряд, а молекулы с 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- Предисловие
- Глава 1. Биохимия и медицина
- Глава 2. Биомолекулы и биохимические методы
- КЛЕТКА
- ОБЩИЙ ЭКСПЕРИМЕНТАЛЬНЫЙ ПОДХОД, ИСПОЛЬЗУЕМЫЙ В БИОХИМИИ
- ОСНОВНЫЕ ДОСТИЖЕНИЯ БИОХИМИИ
- Раздел I. Структура и функции белков и ферментов
- Глава 3. Аминокислоты
- АМИНОКИСЛОТЫ
- ИОННЫЕ ФОРМЫ АМИНОКИСЛОТ
- СТРУКТУРА АМИНОКИСЛОТ
- РАСТВОРИМОСТЬ АМИНОКИСЛОТ
- ОБЩИЕ ХИМИЧЕСКИЕ РЕАКЦИИ
- СВОЙСТВА ИНДИВИДУАЛЬНЫХ АМИНОКИСЛОТ
- МЕТОДЫ РАЗДЕЛЕНИЯ АМИНОКИСЛОТ
- Глава 4. Пептиды
- СТРУКТУРА ПЕПТИДОВ
- ИОННЫЕ ФОРМЫ ПЕПТИДОВ
- КОНФОРМАЦИЯ ПЕПТИДОВ В РАСТВОРЕ
- МЕТОДЫ РАЗДЕЛЕНИЯ ПЕПТИДОВ
- ОПРЕДЕЛЕНИЕ АМИНОКИСЛОТНОГО СОСТАВА ПЕПТИДОВ
- ОПРЕДЕЛЕНИЕ ПЕРВИЧНОЙ СТРУКТУРЫ ПОЛИПЕПТИДОВ
- АВТОМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ АМИНОКИСЛОТНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПОЛИПЕПТИДОВ МЕТОДОМ ЭДМАНА
- АВТОМАТИЧЕСКИЙ СИНТЕЗ ПЕПТИДОВ
- ЛИТЕРАТУРА
- Глава 5. Белки: структура и свойства
- КЛАССИФИКАЦИЯ БЕЛКОВ
- СВЯЗИ, ОТВЕТСТВЕННЫЕ ЗА ФОРМИРОВАНИЕ СТРУКТУРЫ БЕЛКА
- УПОРЯДОЧЕННЫЕ КОНФОРМАЦИИ ПОЛИПЕПТИДОВ
- УРОВНИ СТРУКТУРНОЙ ОРГАНИЗАЦИИ БЕЛКА
- ДЕНАТУРАЦИЯ
- МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРВИЧНОЙ СТРУКТУРЫ
- ОПРЕДЕЛЕНИЕ ВТОРИЧНОЙ И ТРЕТИЧНОЙ СТРУКТУРЫ МЕТОДОМ РЕНТГЕНОВСКОЙ КРИСТАЛЛОГРАФИИ
- ОПРЕДЕЛЕНИЕ ЧЕТВЕРТИЧНОЙ СТРУКТУРЫ
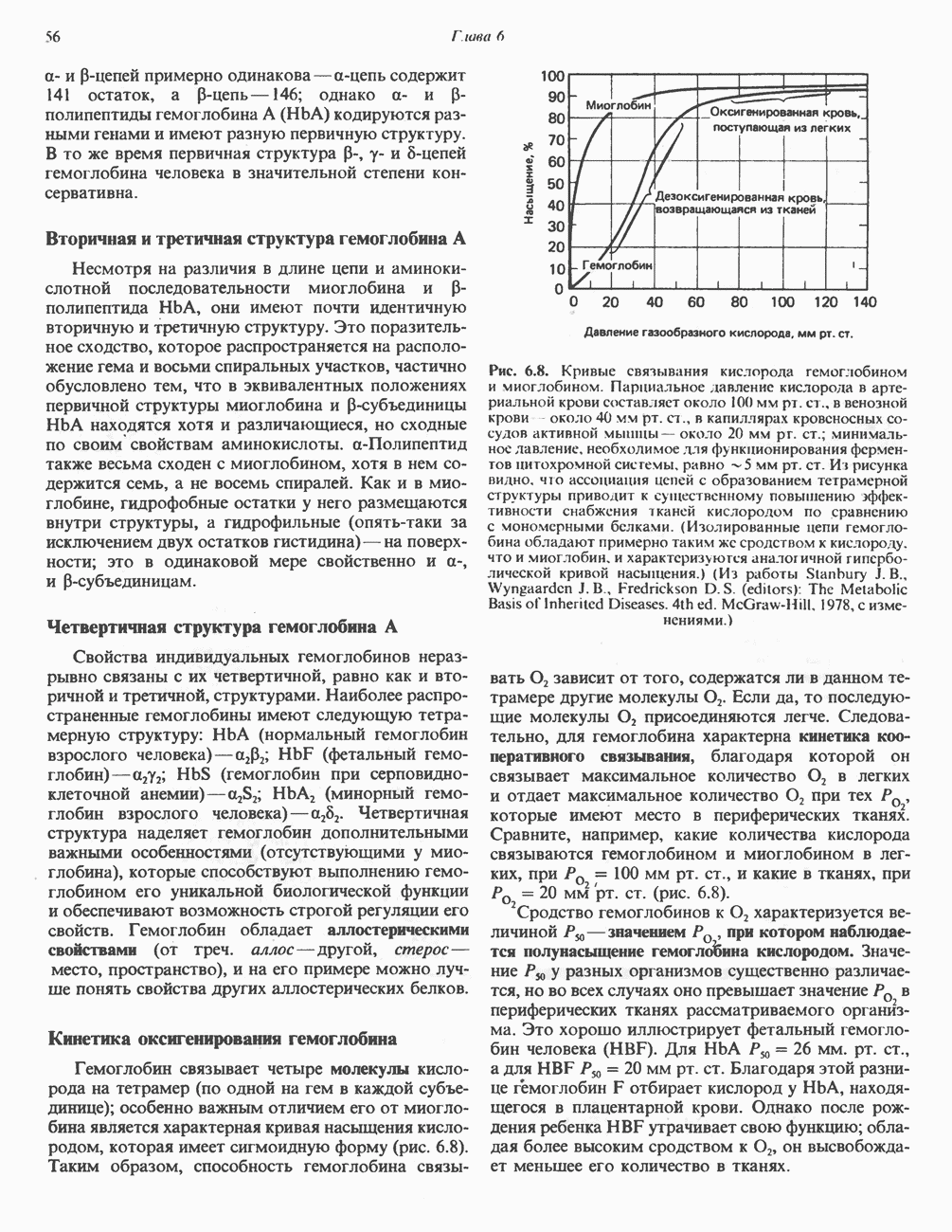
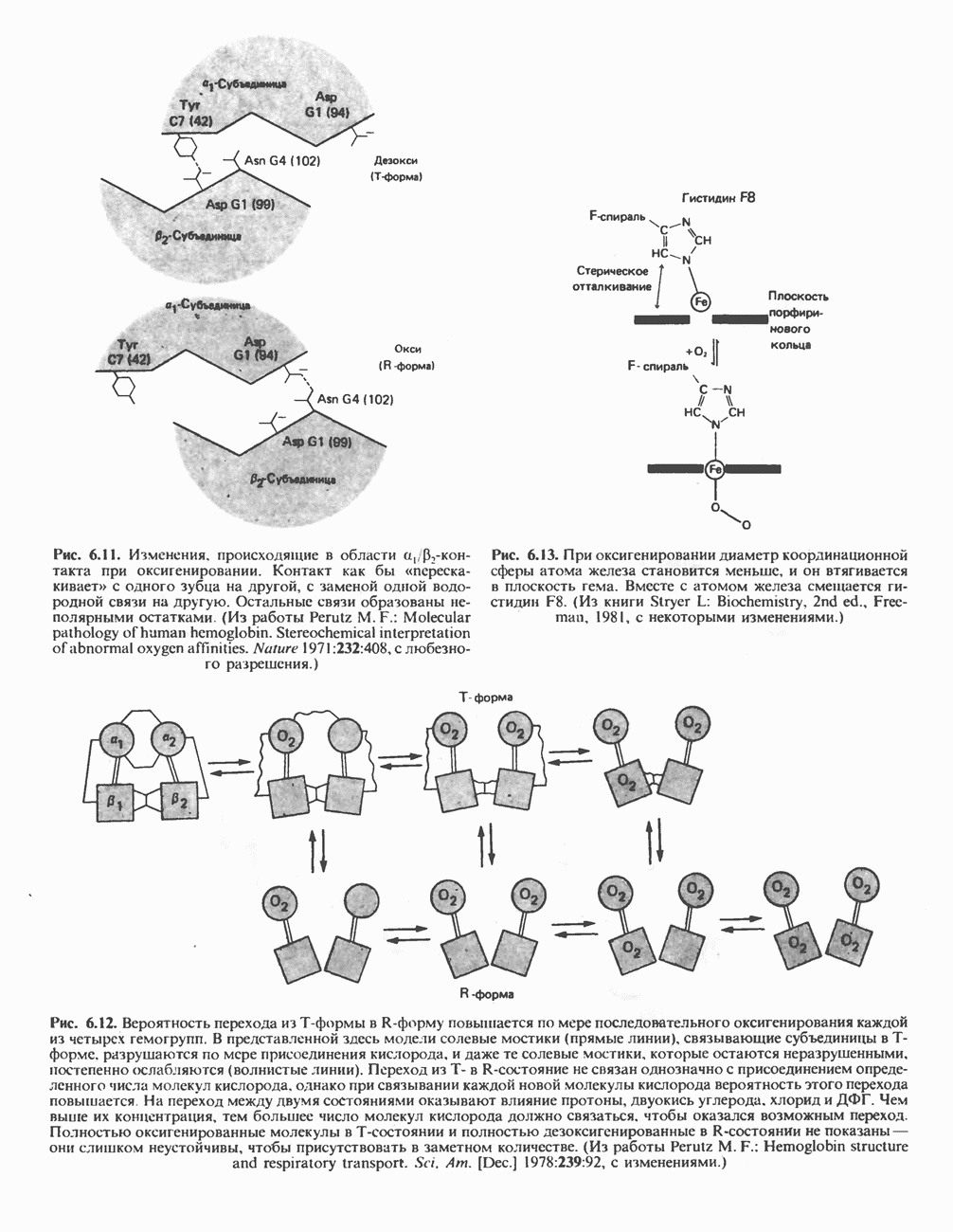
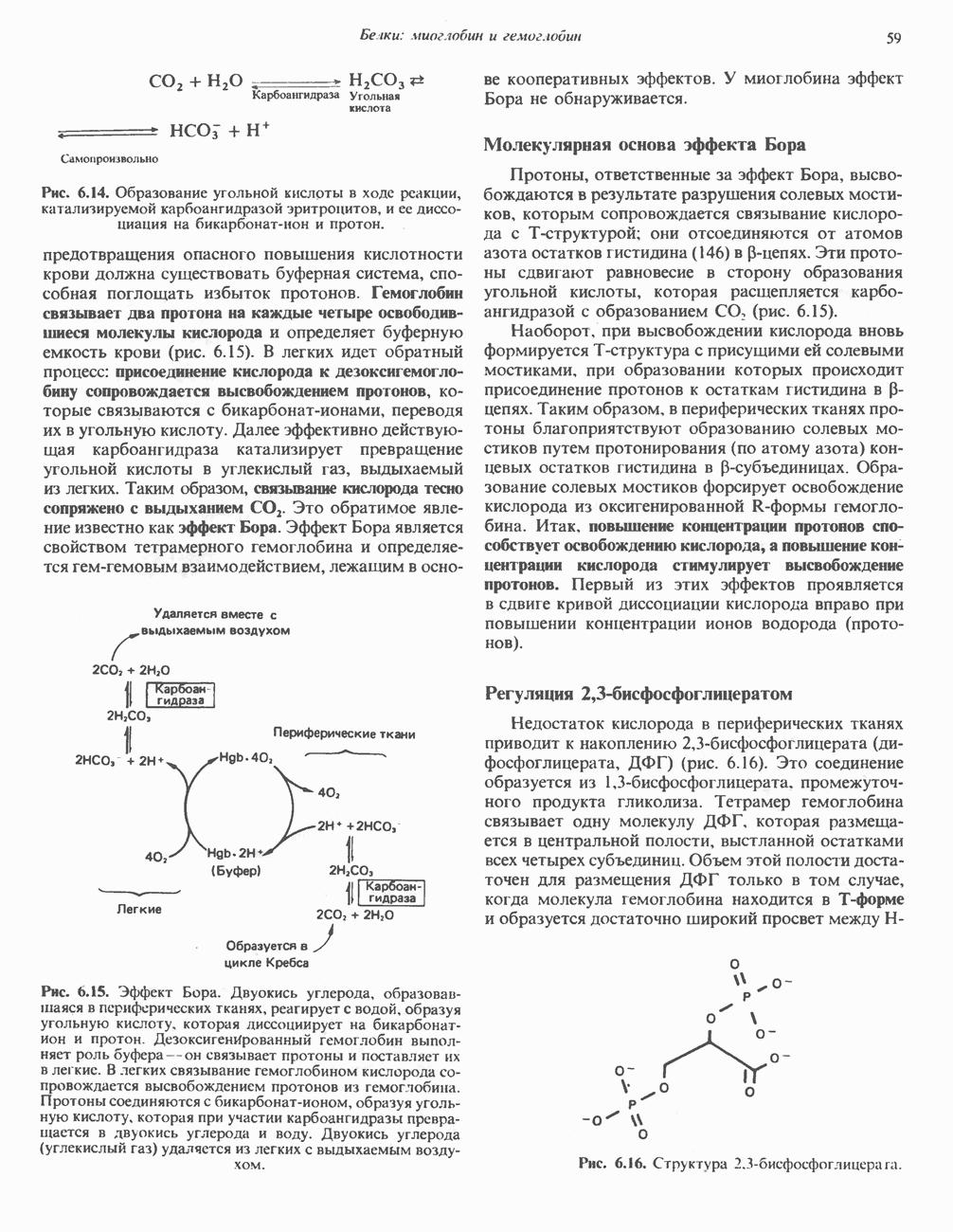
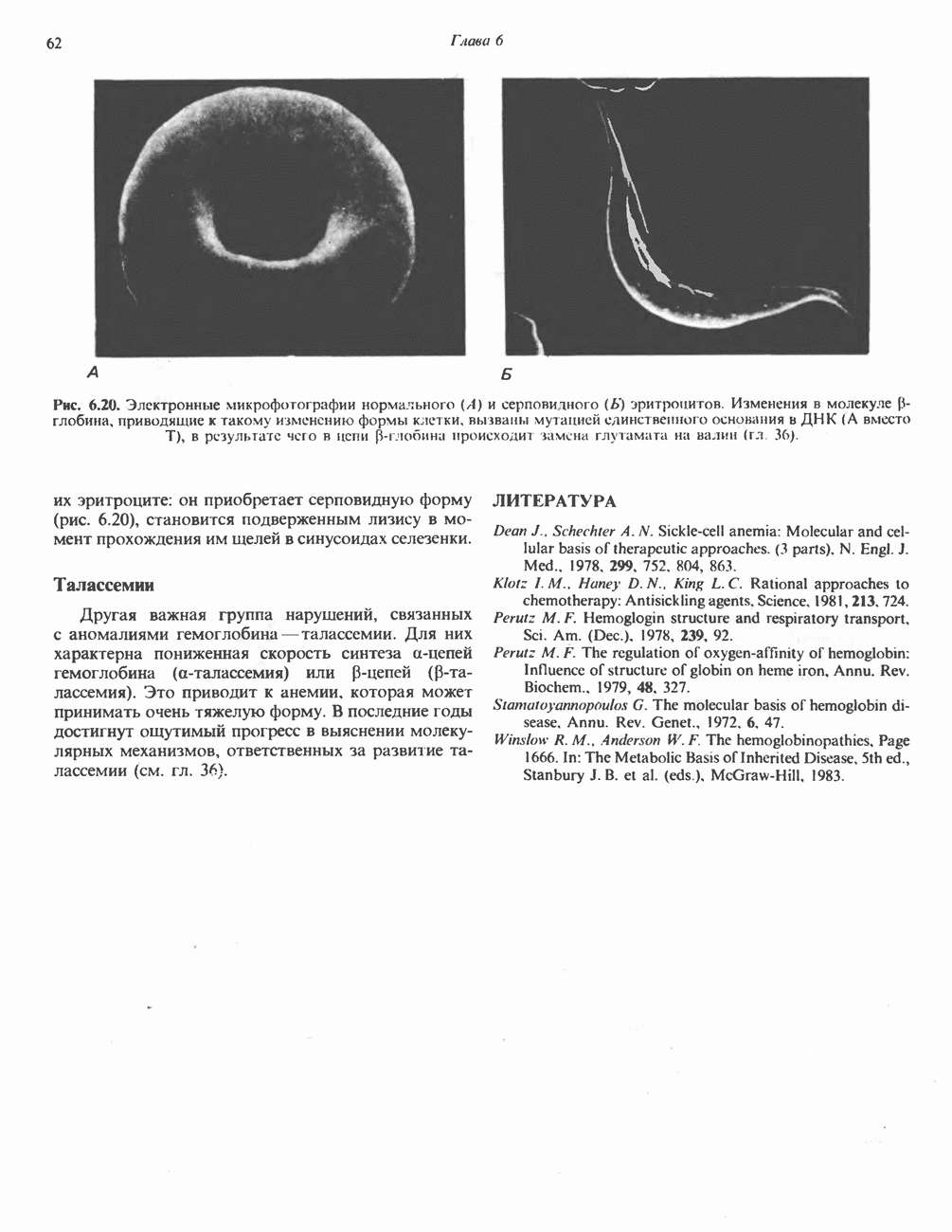
- ГЛАВА 6. Белки: миоглобин и гемоглобин
- ГЕМОПРОТЕИНЫ — МИОГЛОБИН И ГЕМОГЛОБИН
- МИОГЛОБИН
- ГЕМОГЛОБИНЫ
- Глава 7. Ферменты: общие свойства
- КОФЕРМЕНТЫ
- «ТРЕХТОЧЕЧНАЯ ФИКСАЦИЯ» СУБСТРАТОВ НА ФЕРМЕНТАХ
- СПЕЦИФИЧНОСТЬ ФЕРМЕНТОВ
- КОЛИЧЕСТВЕННОЕ ОПРЕДЕЛЕНИЕ ФЕРМЕНТАТИВНОЙ АКТИВНОСТИ
- ВЫДЕЛЕНИЕ ФЕРМЕНТОВ
- ИЗОФЕРМЕНТЫ (ИЗОЗИМЫ)
- ФЕРМЕНТЫ В КЛИНИЧЕСКОЙ ДИАГНОСТИКЕ
- ДИАГНОСТИЧЕСКОЕ И ПРОГНОСТИЧЕСКОЕ ЗНАЧЕНИЕ СПЕЦИФИЧЕСКИХ ФЕРМЕНТОВ
- ПРИМЕНЕНИЕ ЭНДОНУКЛЕАЗ РЕСТРИКЦИИ В ДИАГНОСТИКЕ
- ЛИТЕРАТУРА
- Глава 8. ФЕРМЕНТЫ: КИНЕТИКА
- ОБРАЗОВАНИЕ И РАСПАД ПЕРЕХОДНЫХ СОСТОЯНИЙ
- ИЗМЕНЕНИЯ СВОБОДНОЙ ЭНЕРГИИ, СВЯЗАННЫЕ С ОБРАЗОВАНИЕМ И РАСПАДОМ ПЕРЕХОДНЫХ СОСТОЯНИЙ
- РОЛЬ КАТАЛИЗАТОРОВ В ОБРАЗОВАНИИ ПРОДУКТИВНЫХ ПЕРЕХОДНЫХ СОСТОЯНИЙ
- ТЕОРИЯ СТОЛКНОВЕНИЙ
- РОЛЬ ФЕРМЕНТОВ В РАЗРЫВЕ И ОБРАЗОВАНИИ КОВАЛЕНТНЫХ СВЯЗЕЙ
- КАТАЛИТИЧЕСКИЙ ЦЕНТР
- ФАКТОРЫ, ВЛИЯЮЩИЕ НА АКТИВНОСТЬ ФЕРМЕНТОВ
- КОНСТАНТА РАВНОВЕСИЯ
- КОНЦЕНТРАЦИЯ ФЕРМЕНТА
- КОНЦЕНТРАЦИЯ СУБСТРАТА
- УРАВНЕНИЕ МИХАЭЛИСА—МЕНТЕН
- ОГРАНИЧЕНИЯ, ПРИСУЩИЕ УРАВНЕНИЮ МИХАЭЛИСА — МЕНТЕН
- ИНГИБИРОВАНИЕ АКТИВНОСТИ ФЕРМЕНТОВ
- МОДУЛЯТОРЫ ФЕРМЕНТАТИВНОЙ АКТИВНОСТИ
- Глава 9. Ферменты: механизм действия
- МЕХАНИЗМ КАТАЛИТИЧЕСКОГО ДЕЙСТВИЯ ХИМОТРИПСИНА
- РОЛЬ ИЗБИРАТЕЛЬНОГО ПРОТЕОЛИЗА В ФОРМИРОВАНИИ АКТИВНЫХ ЦЕНТРОВ ФЕРМЕНТОВ
- УПОРЯДОЧЕННОЕ И НЕУПОРЯДОЧЕННОЕ СВЯЗЫВАНИЕ СУБСТРАТОВ
- ФЕРМЕНТЫ КАК КАТАЛИЗАТОРЫ ОБЩЕГО КИСЛОТНОГО И ОБЩЕГО ОСНОВНОГО ТИПА
- ИОНЫ МЕТАЛЛОВ
- Глава 10. Ферменты: регуляция активности
- РЕГУЛЯЦИЯ МЕТАБОЛИЗМА
- РЕГУЛЯЦИЯ КОЛИЧЕСТВА ФЕРМЕНТА ПУТЕМ РЕГУЛЯЦИИ СКОРОСТИ ЕГО СИНТЕЗА И РАСПАДА
- РЕГУЛЯЦИЯ КАТАЛИТИЧЕСКОЙ АКТИВНОСТИ ФЕРМЕНТОВ
- АЛЛОСТЕРИЧЕСКАЯ РЕГУЛЯЦИЯ
- КОВАЛЕНТНАЯ МОДИФИКАЦИЯ ФЕРМЕНТОВ
- Раздел II. Биоэнергетика и метаболизм углеводов и липидов
- Глава 11. Биоэнергетика
- СВОБОДНАЯ ЭНЕРГИЯ И ЗАКОНЫ ТЕРМОДИНАМИКИ
- СОПРЯЖЕНИЕ ЭНДЕРГОНИЧЕСКИХ ПРОЦЕССОВ С ЭКЗЕРГОНИЧЕСКИМИ
- РОЛЬ ВЫСОКОЭНЕРГЕТИЧЕСКИХ ФОСФАТОВ В БИОЭНЕРГЕТИКЕ И В ПРОЦЕССАХ УЛАВЛИВАНИЯ ЭНЕРГИИ
- МЕТАБОЛИЗМ ПИРОФОСФАТА
- Глава 12. Биологическое окисление
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНОЕ РАВНОВЕСИЕ, ОКИСЛИТЕЛЬНОВОССТАНОВИТЕЛЬНЫЙ ПОТЕНЦИАЛ
- ФЕРМЕНТЫ И КОФЕРМЕНТЫ, УЧАСТВУЮЩИЕ В ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ ПРОЦЕССАХ
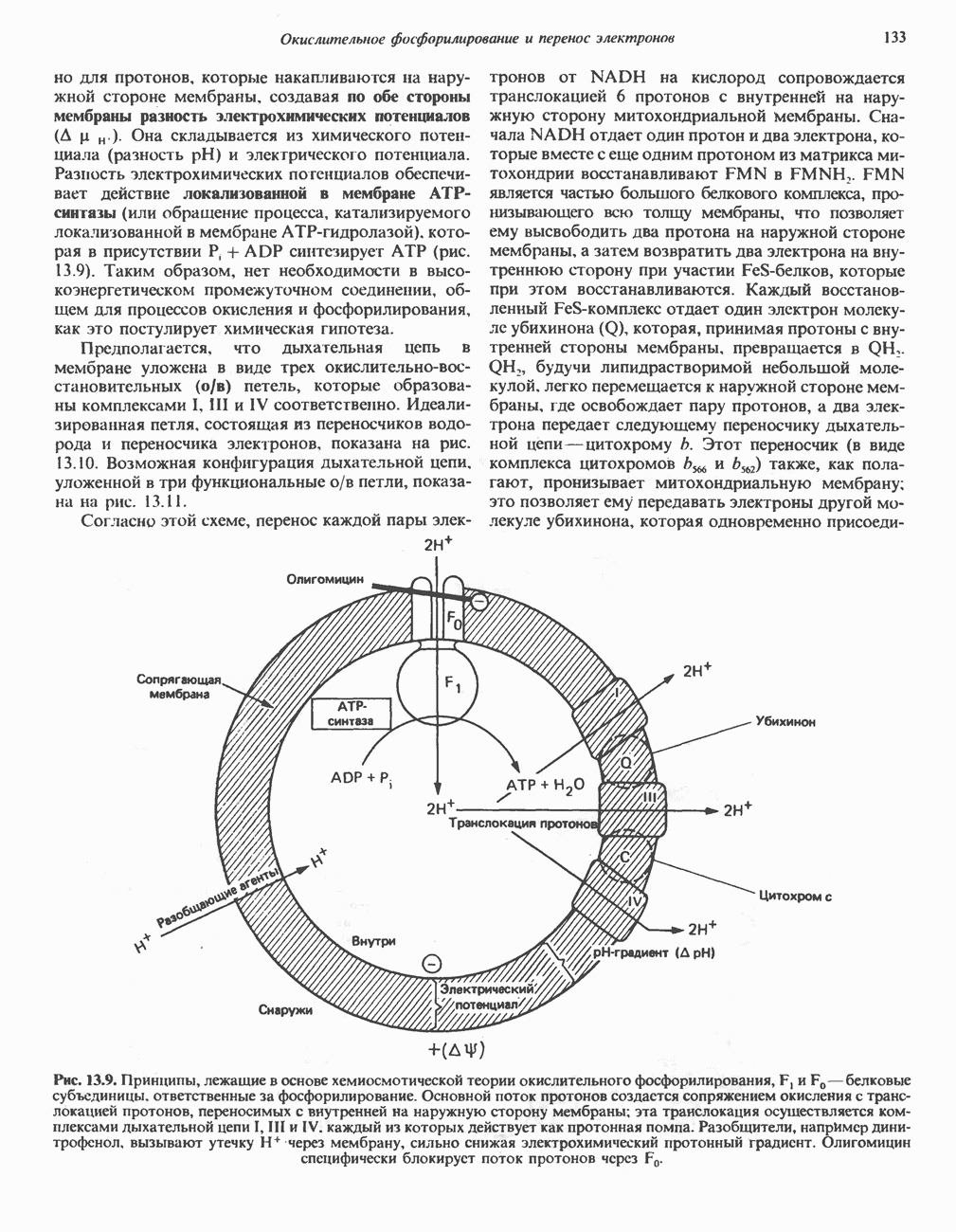
- Глава 13. Окислительное фосфорилирование и транспортные системы митохондрий
- ДЫХАТЕЛЬНАЯ ЦЕПЬ
- ОРГАНИЗАЦИЯ ДЫХАТЕЛЬНОЙ ЦЕПИ В МИТОХОНДРИЯХ
- РОЛЬ ДЫХАТЕЛЬНОЙ ЦЕПИ В УЛАВЛИВАНИИ ЭНЕРГИИ
- ДЫХАТЕЛЬНЫЙ КОНТРОЛЬ
- ИНГИБИТОРЫ ДЫХАТЕЛЬНОЙ ЦЕПИ И ОКИСЛИТЕЛЬНОГО ФОСФОРИЛИРОВАНИЯ
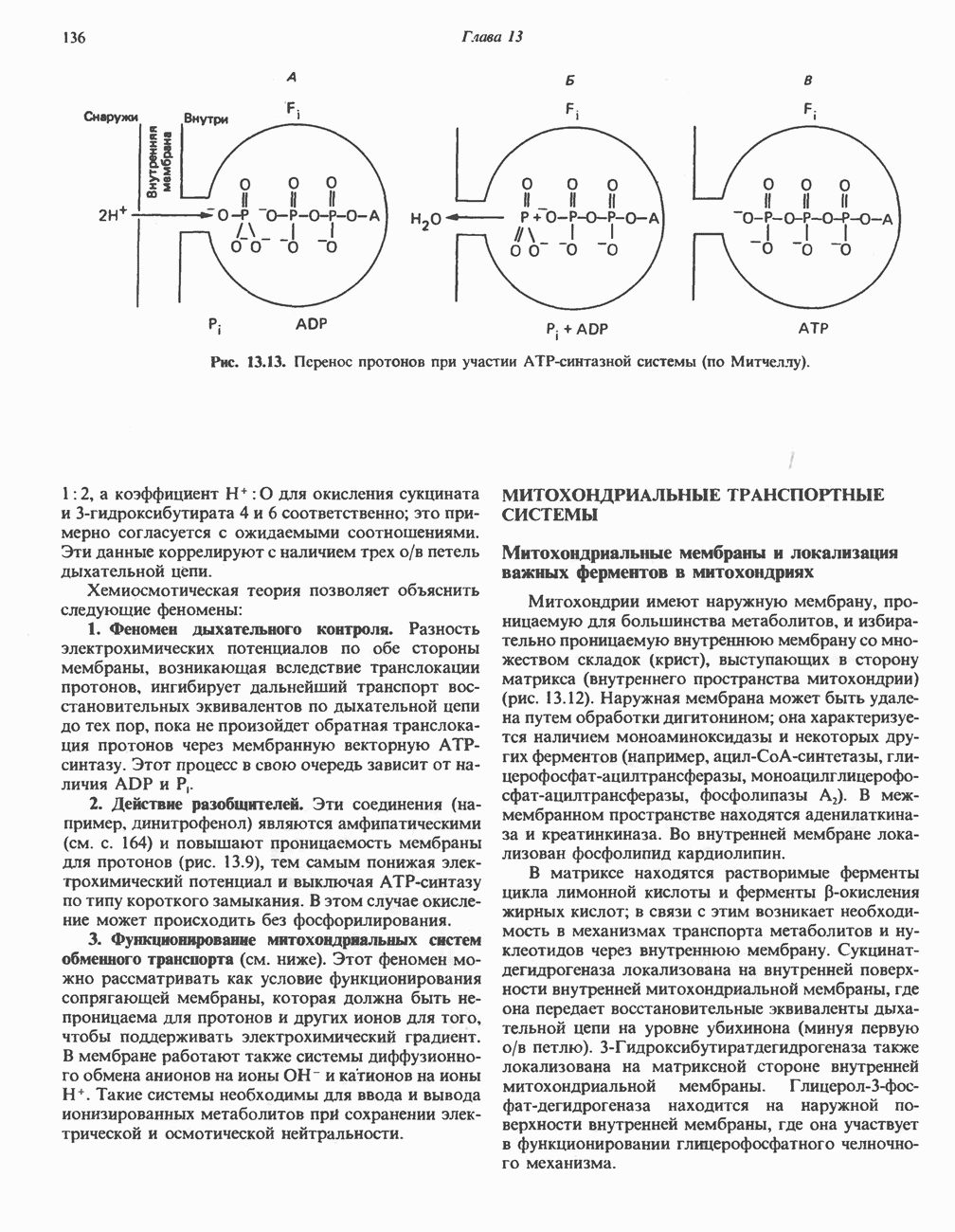
- МЕХАНИЗМ ОКИСЛИТЕЛЬНОГО ФОСФОРИЛИРОВАНИЯ
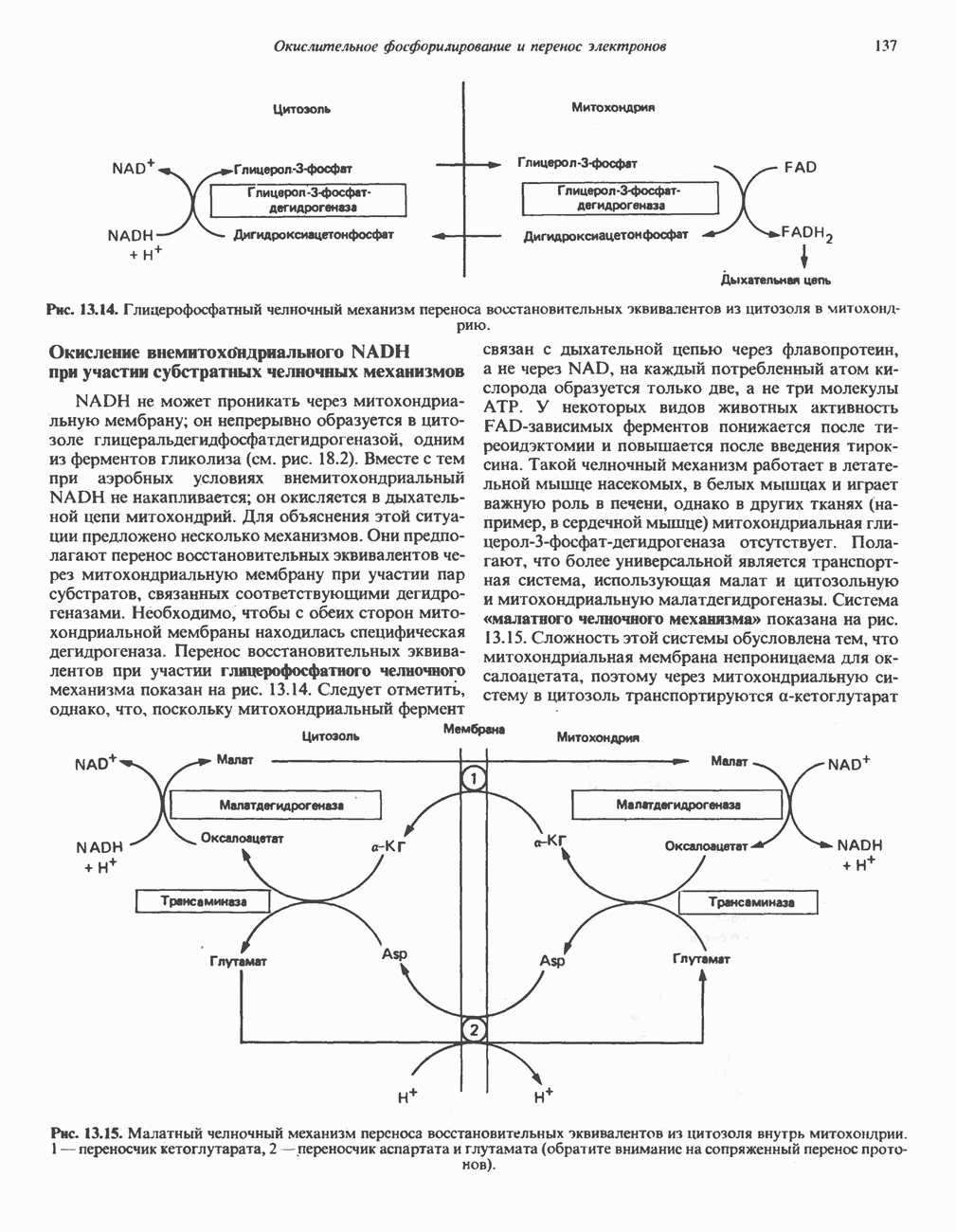
- МИТОХОНДРИАЛЬНЫЕ ТРАНСПОРТНЫЕ СИСТЕМЫ
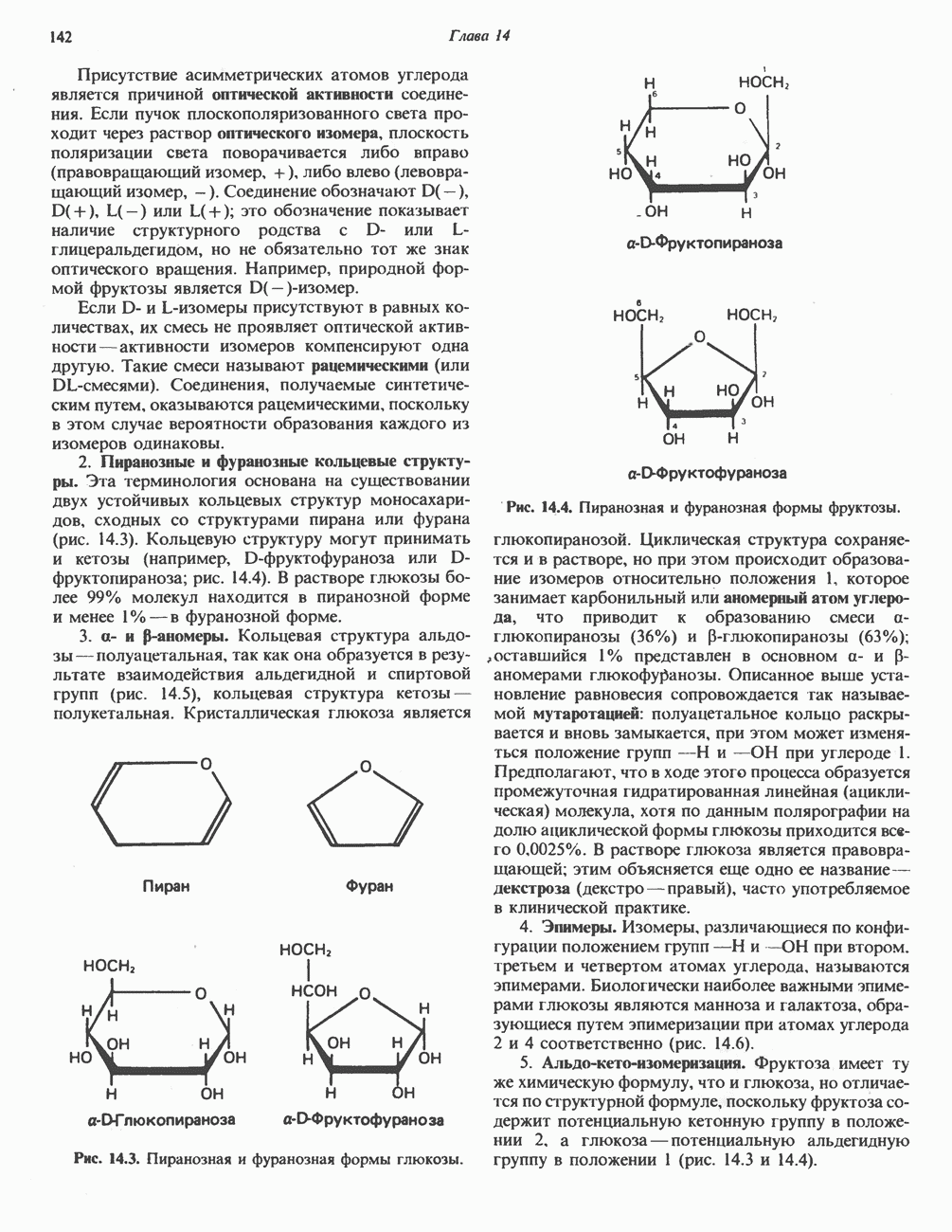
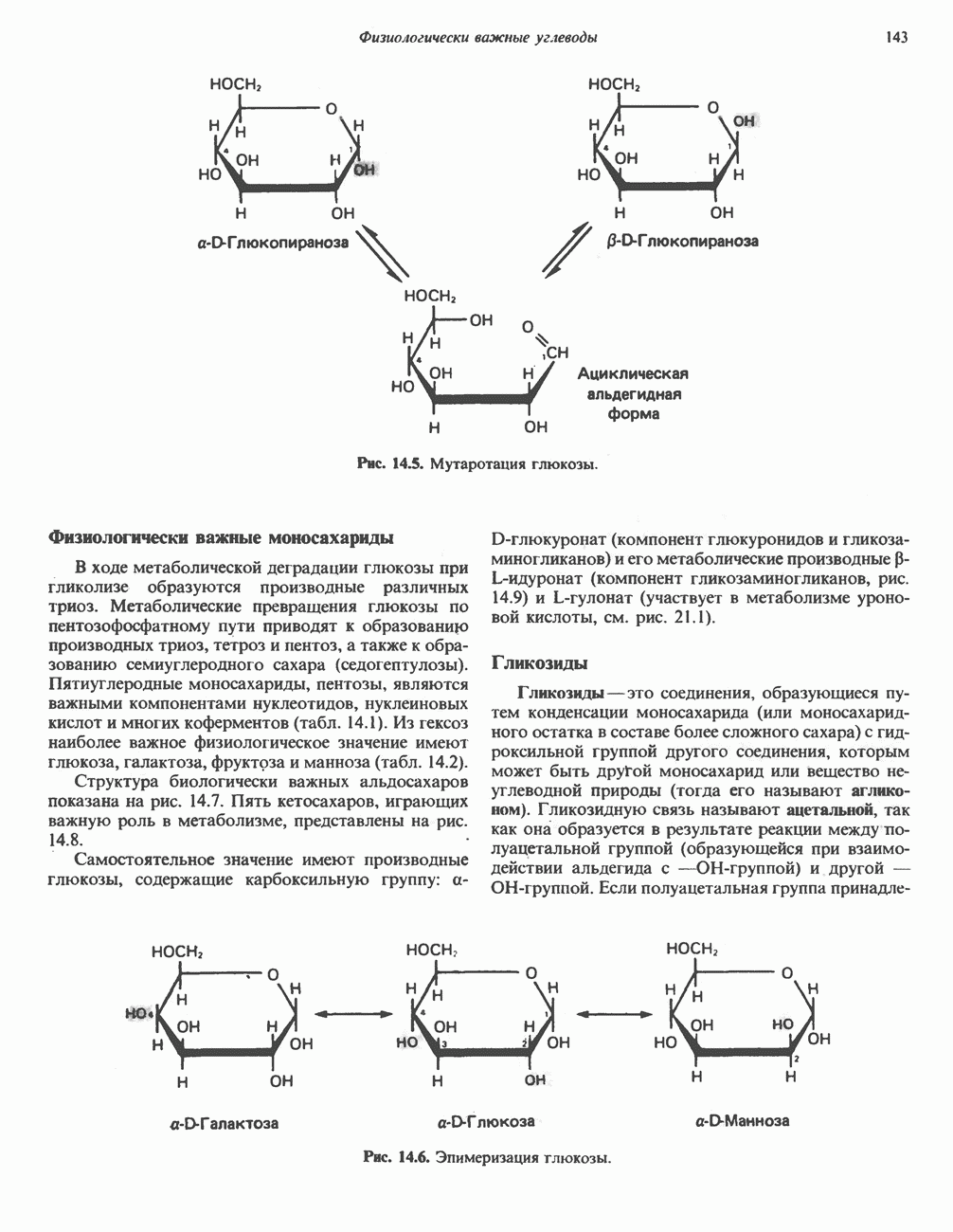
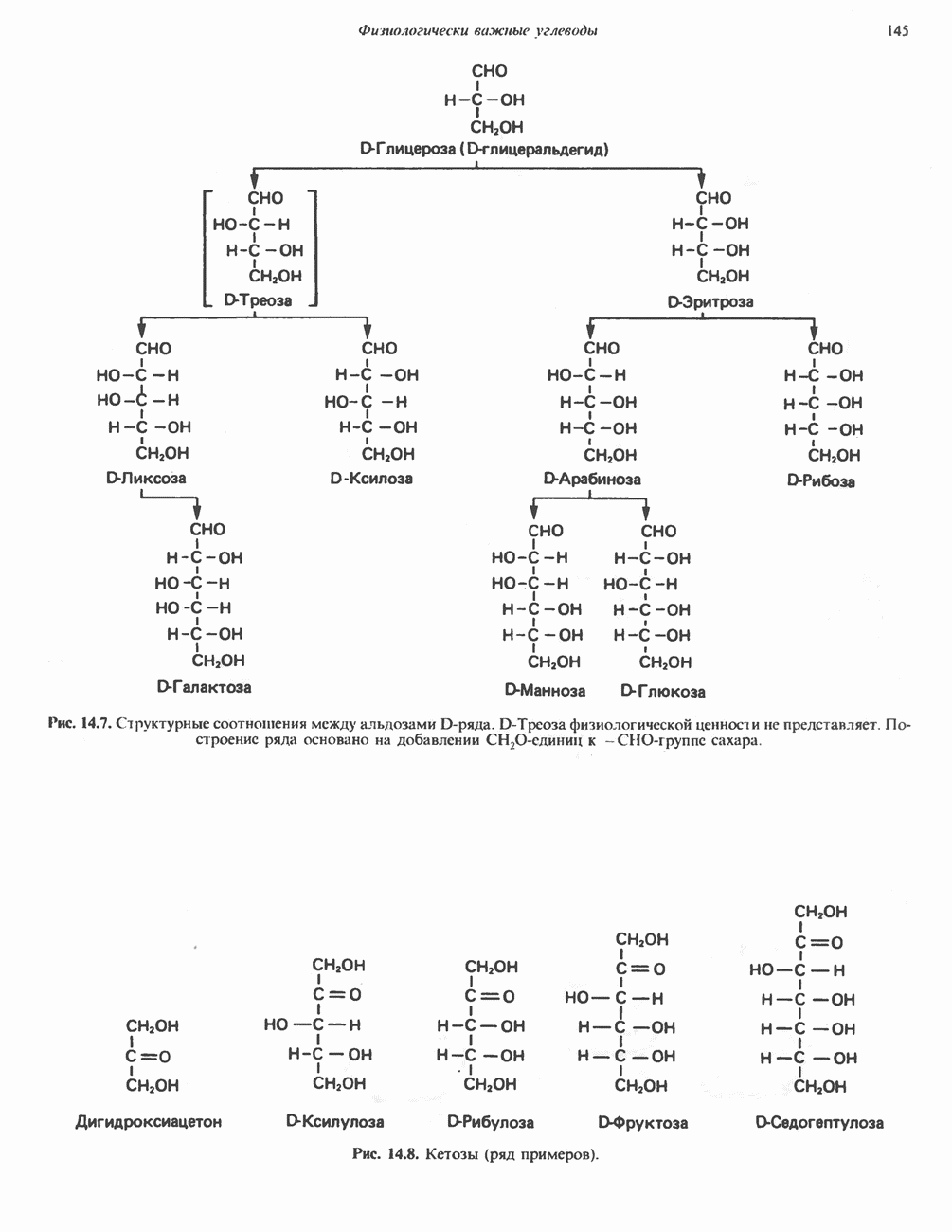
- Глава 14. Физиологически важные углеводы
- КЛАССИФИКАЦИЯ УГЛЕВОДОВ
- МОНОСАХАРИДЫ
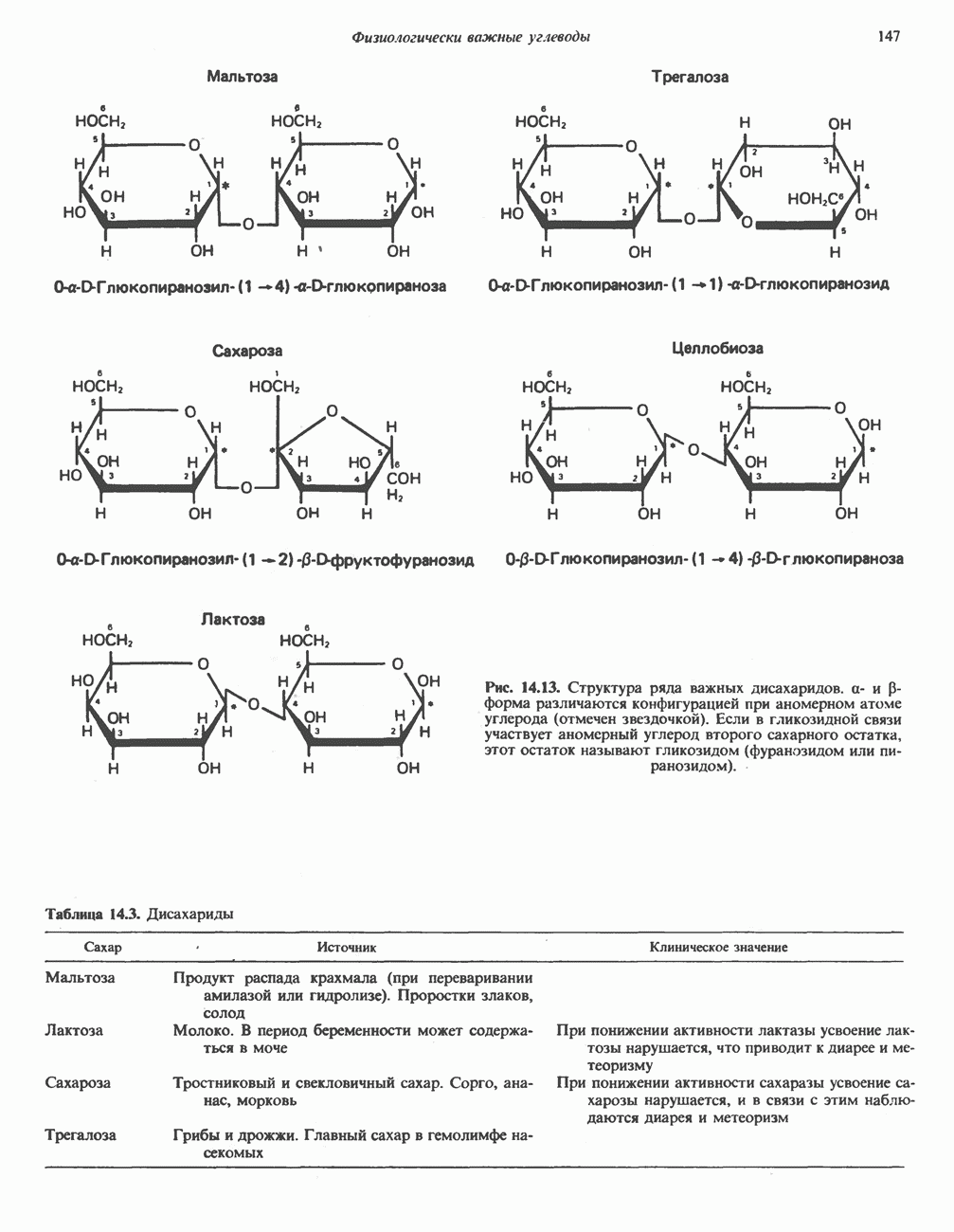
- ДИСАХАРИДЫ
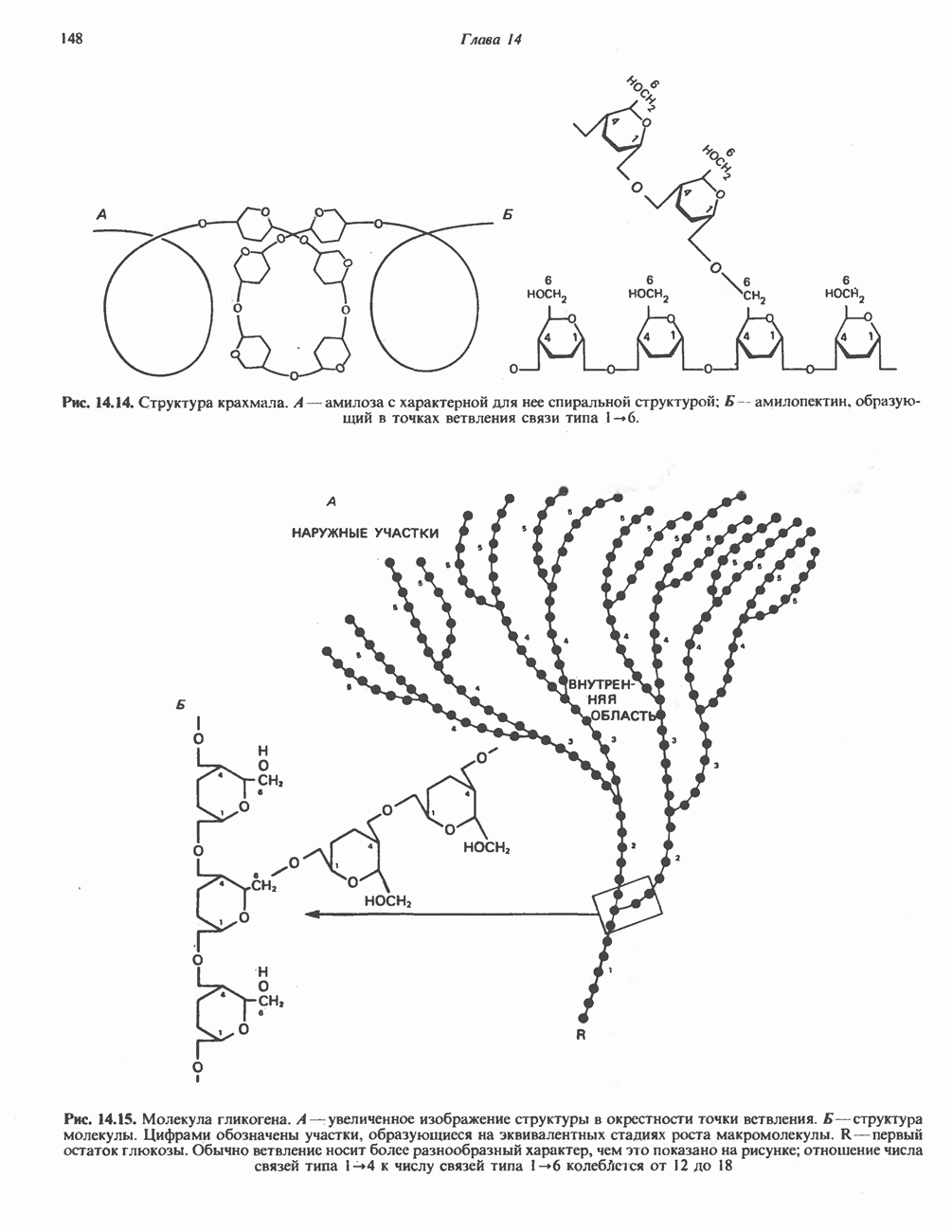
- ПОЛИСАХАРИДЫ
- УГЛЕВОДЫ КЛЕТОЧНЫХ МЕМБРАН
- Глава 15. Физиологически важные липиды
- КЛАССИФИКАЦИЯ ЛИПИДОВ
- ЖИРНЫЕ КИСЛОТЫ
- ТРИАЦИЛГЛИЦЕРОЛЫ (триглицериды)
- ФОСФОЛИПИДЫ
- ГЛИКОЛИПИДЫ (ГЛИКОСФИНГОЛИПИДЫ)
- СТЕРОИДЫ
- ПЕРЕКИСНОЕ ОКИСЛЕНИЕ ЛИПИДОВ
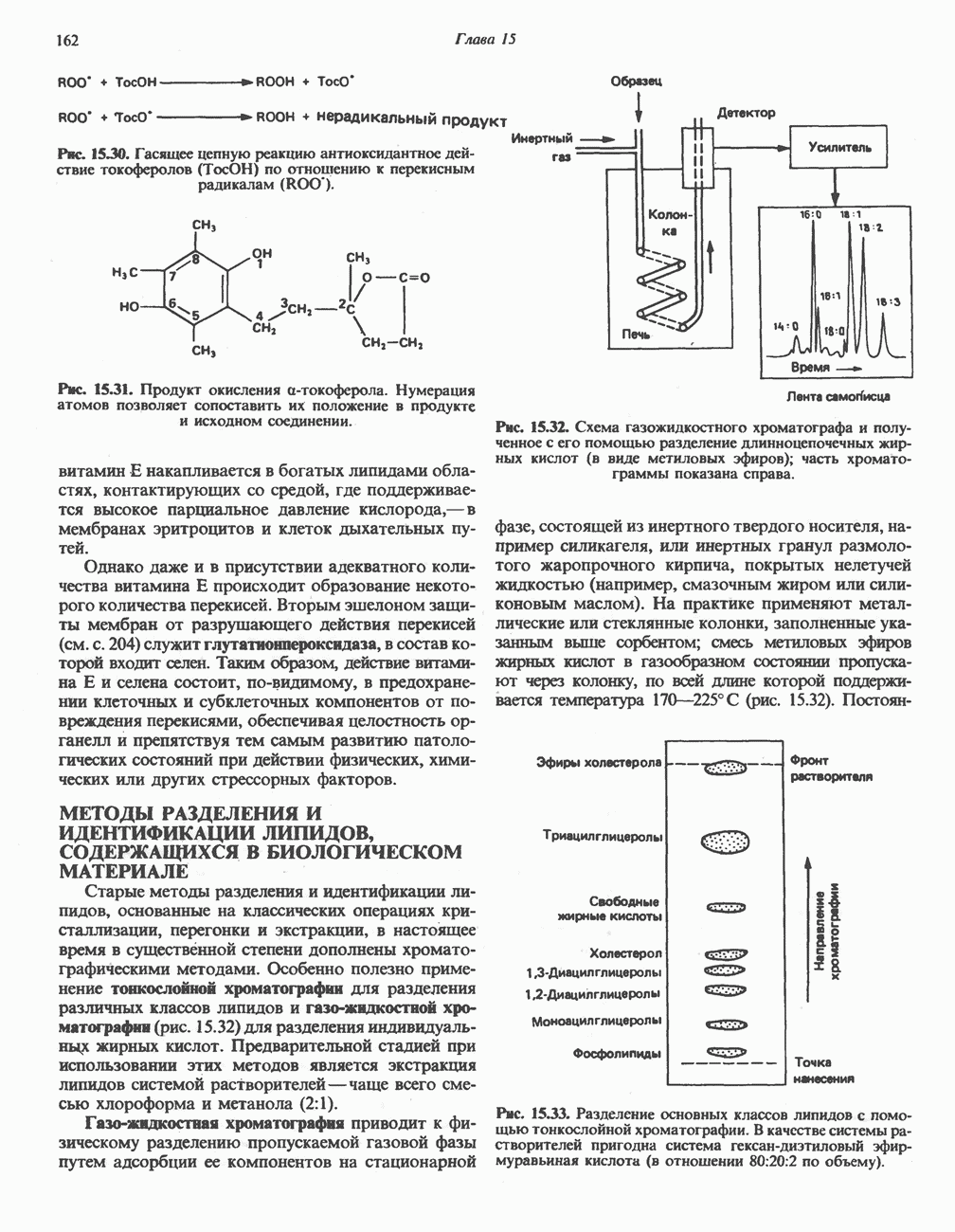
- МЕТОДЫ РАЗДЕЛЕНИЯ И ИДЕНТИФИКАЦИИ ЛИПИДОВ, СОДЕРЖАЩИХСЯ В БИОЛОГИЧЕСКОМ МАТЕРИАЛЕ
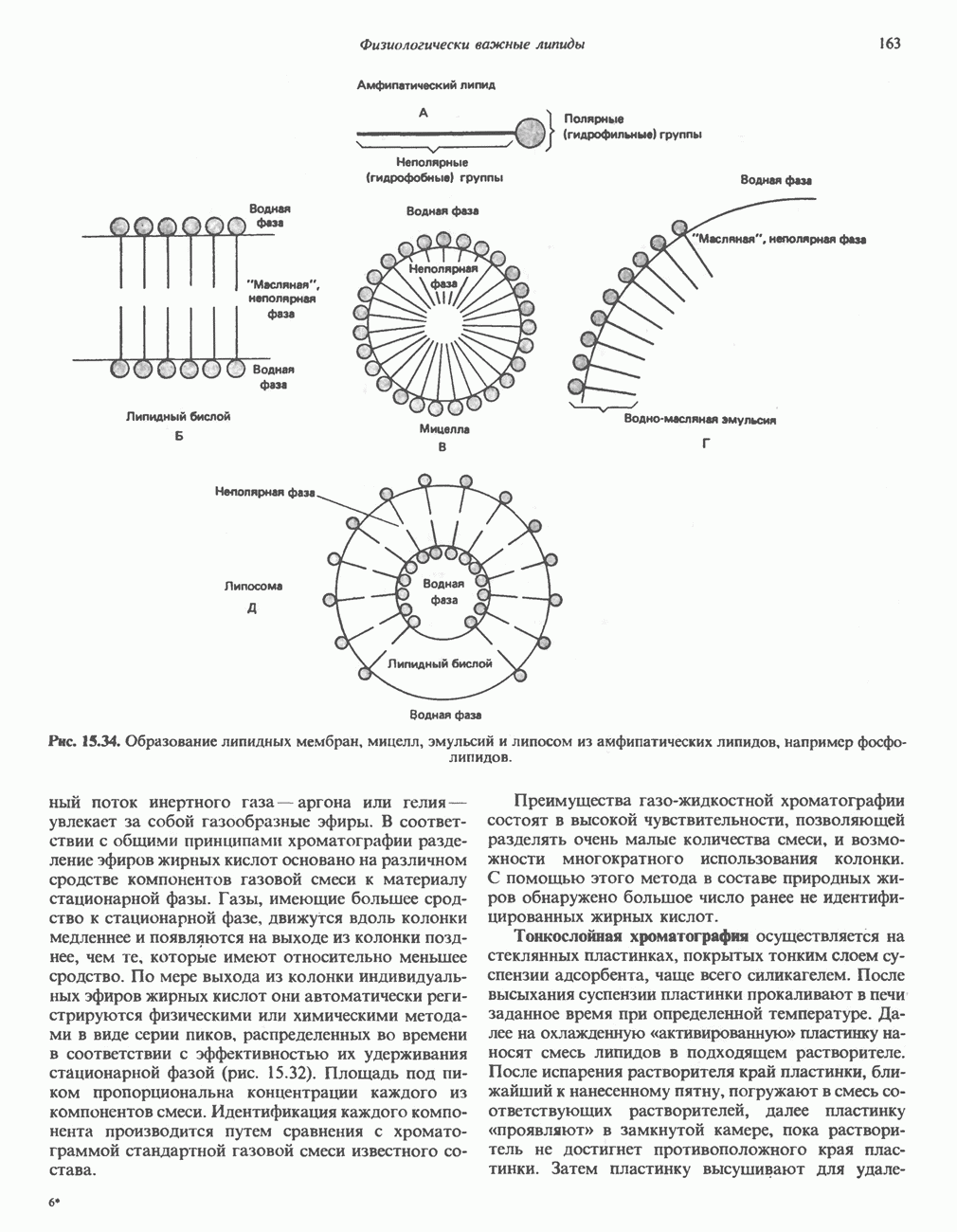
- АМФИПАТИЧЕСКИЕ ЛИПИДЫ
- Глава 16. Промежуточный обмен
- ОСНОВНЫЕ МЕТАБОЛИЧЕСКИЕ ПУТИ
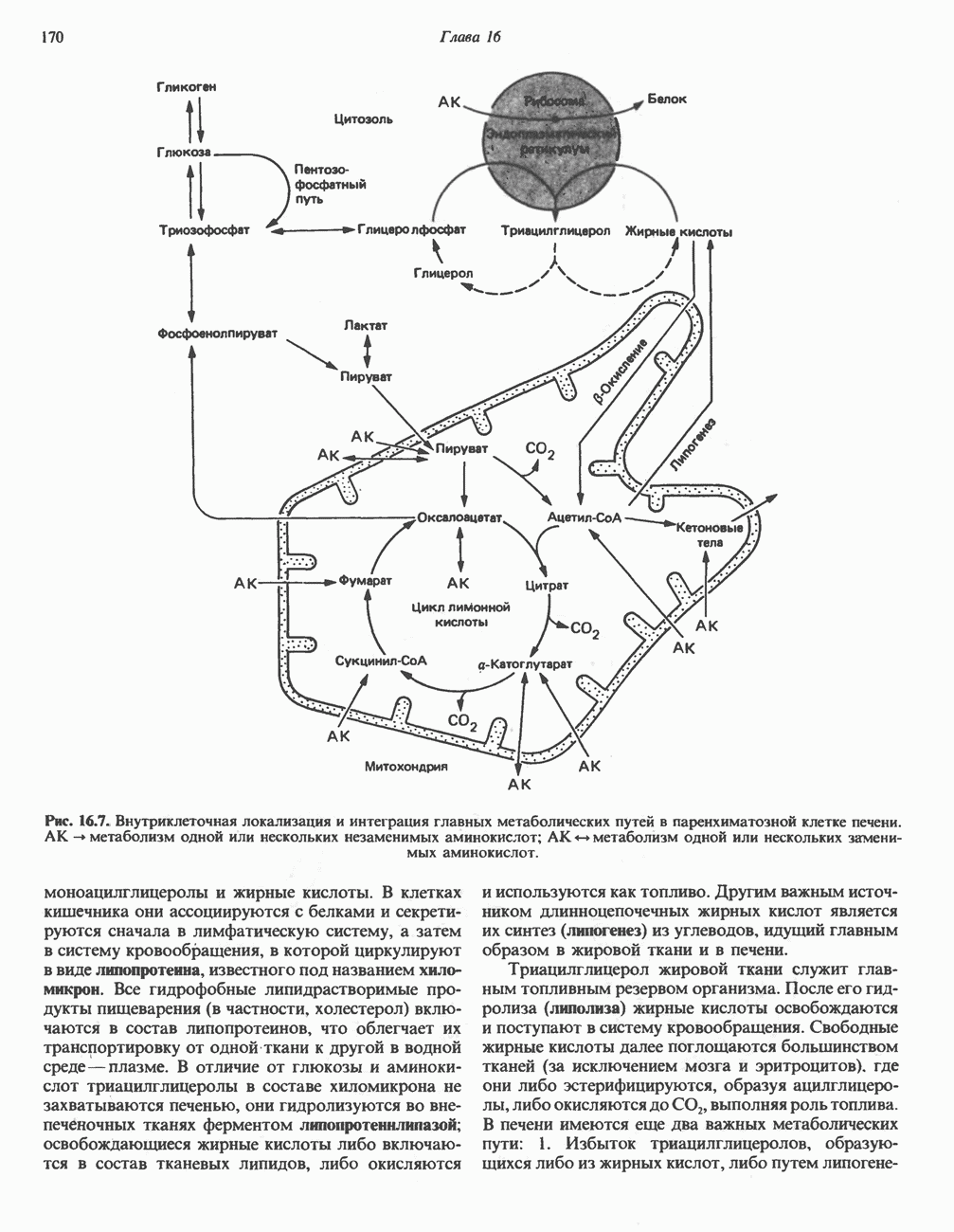
- ЛОКАЛИЗАЦИЯ МЕТАБОЛИЧЕСКИХ ПУТЕЙ
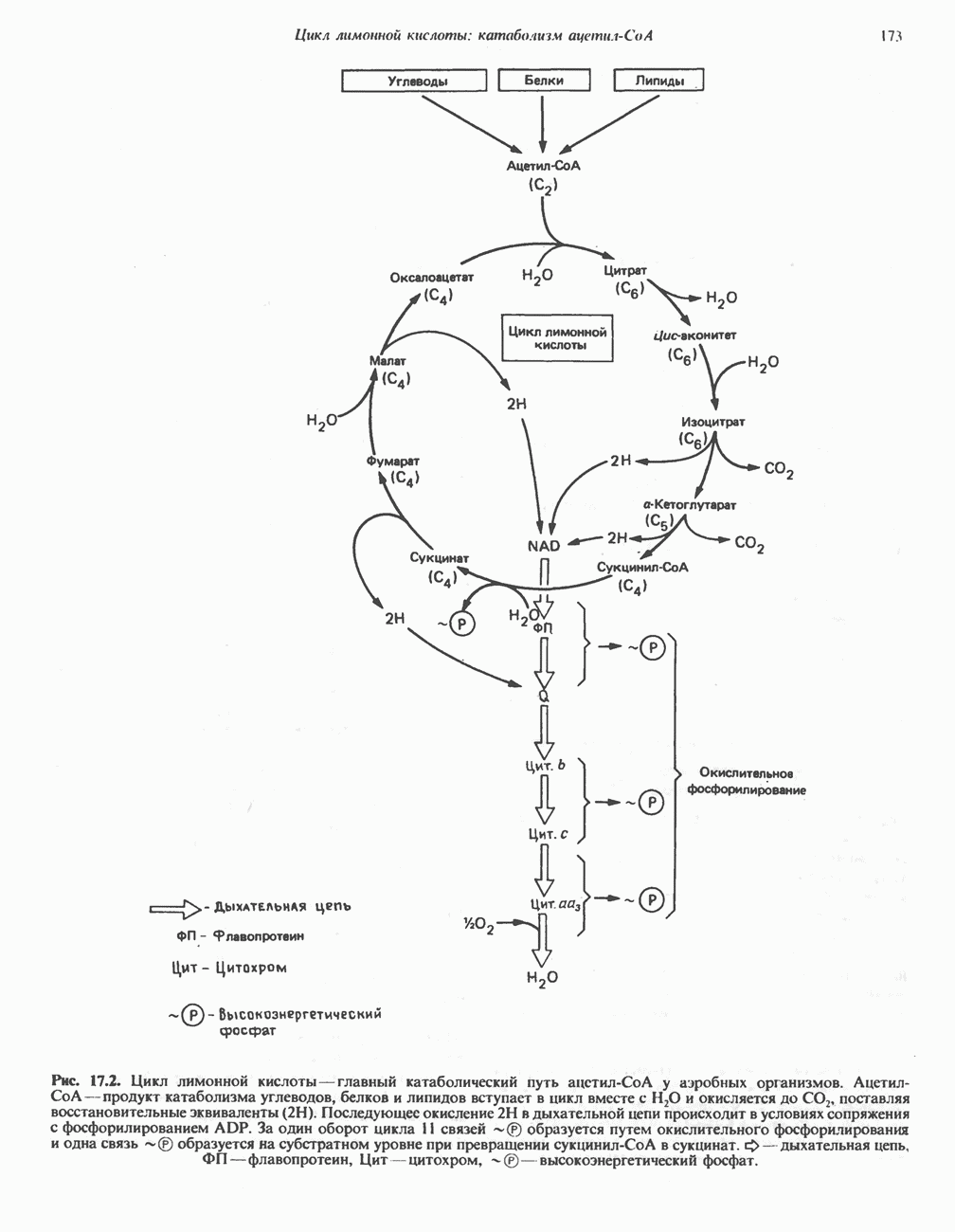
- Глава 17. Цикл лимонной кислоты: катаболизм ацетил-СоА
- КАТАБОЛИЧЕСКАЯ РОЛЬ ЦИКЛА ЛИМОННОЙ КИСЛОТЫ
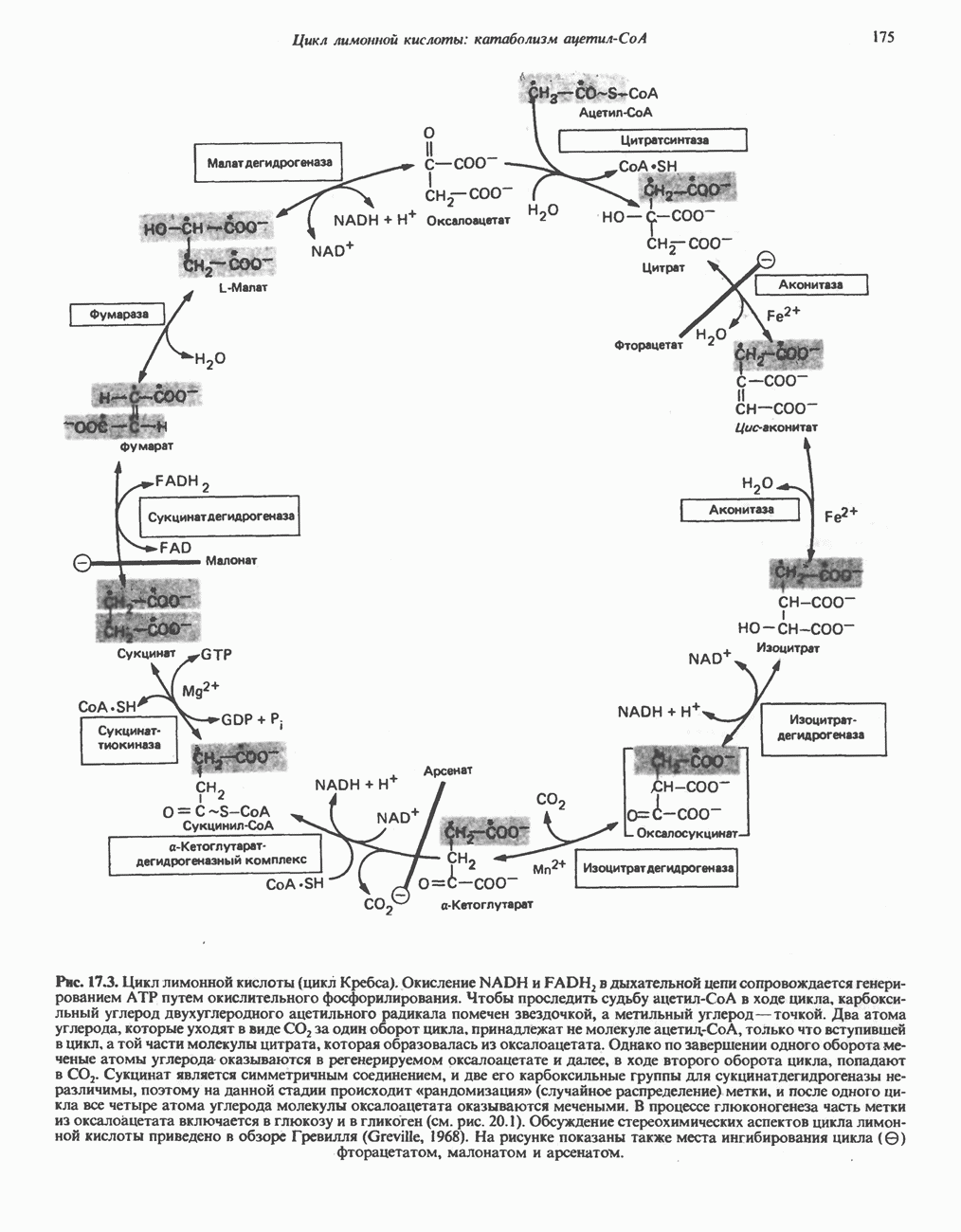
- РЕАКЦИИ ЦИКЛА ЛИМОННОЙ КИСЛОТЫ (рис. 17.3)
- ЭНЕРГЕТИКА ЦИКЛА ЛИМОННОЙ КИСЛОТЫ
- РОЛЬ ВИТАМИНОВ В ЦИКЛЕ ЛИМОННОЙ КИСЛОТЫ
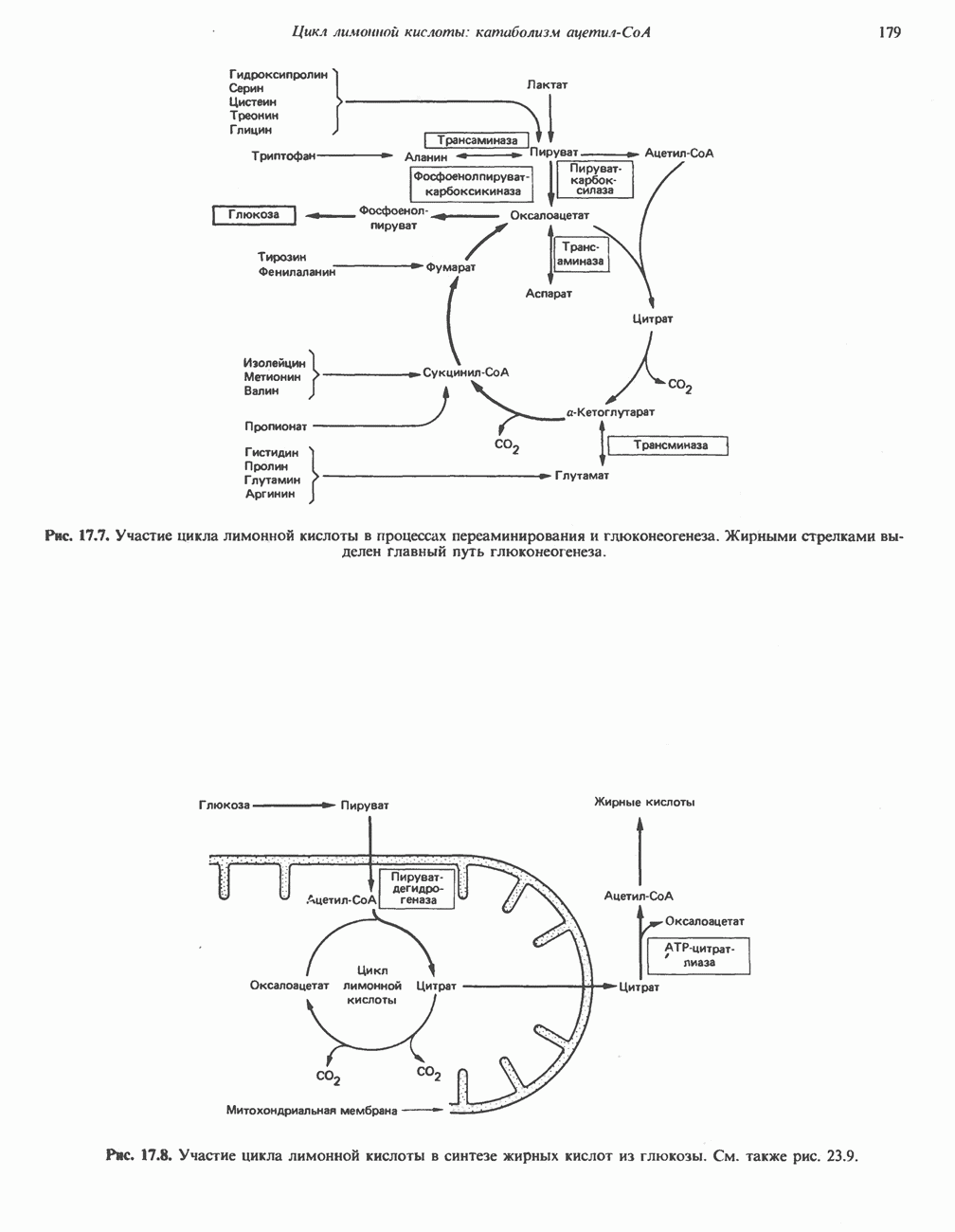
- АМФИБОЛИЧЕСКАЯ РОЛЬ ЦИКЛА ЛИМОННОЙ КИСЛОТЫ
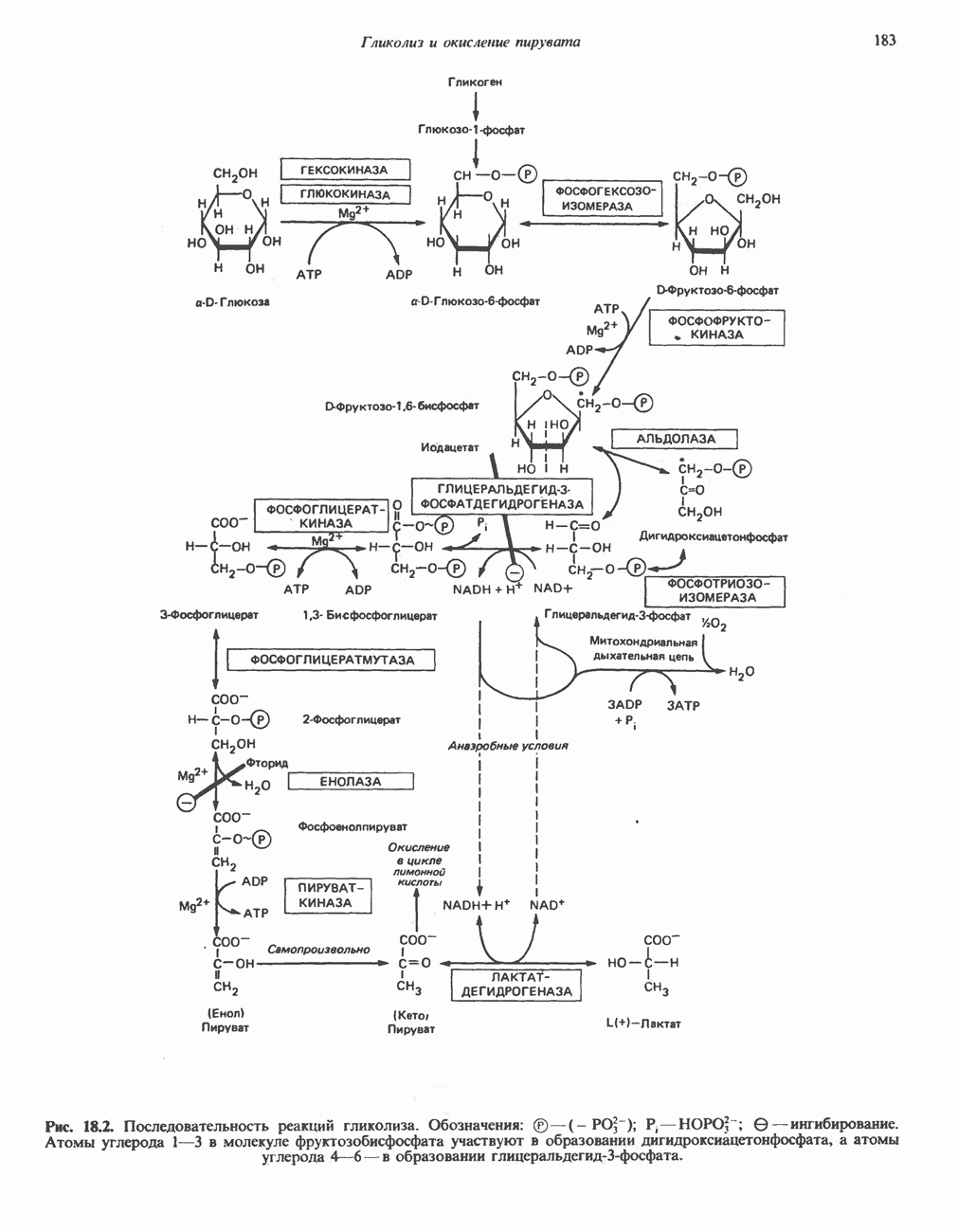
- Глава 18. Гликолиз и окисление пирувата
- ГЛИКОЛИТИЧЕСКИЙ ПУТЬ
- ПОСЛЕДОВАТЕЛЬНЫЕ СТАДИИ ГЛИКОЛИЗА
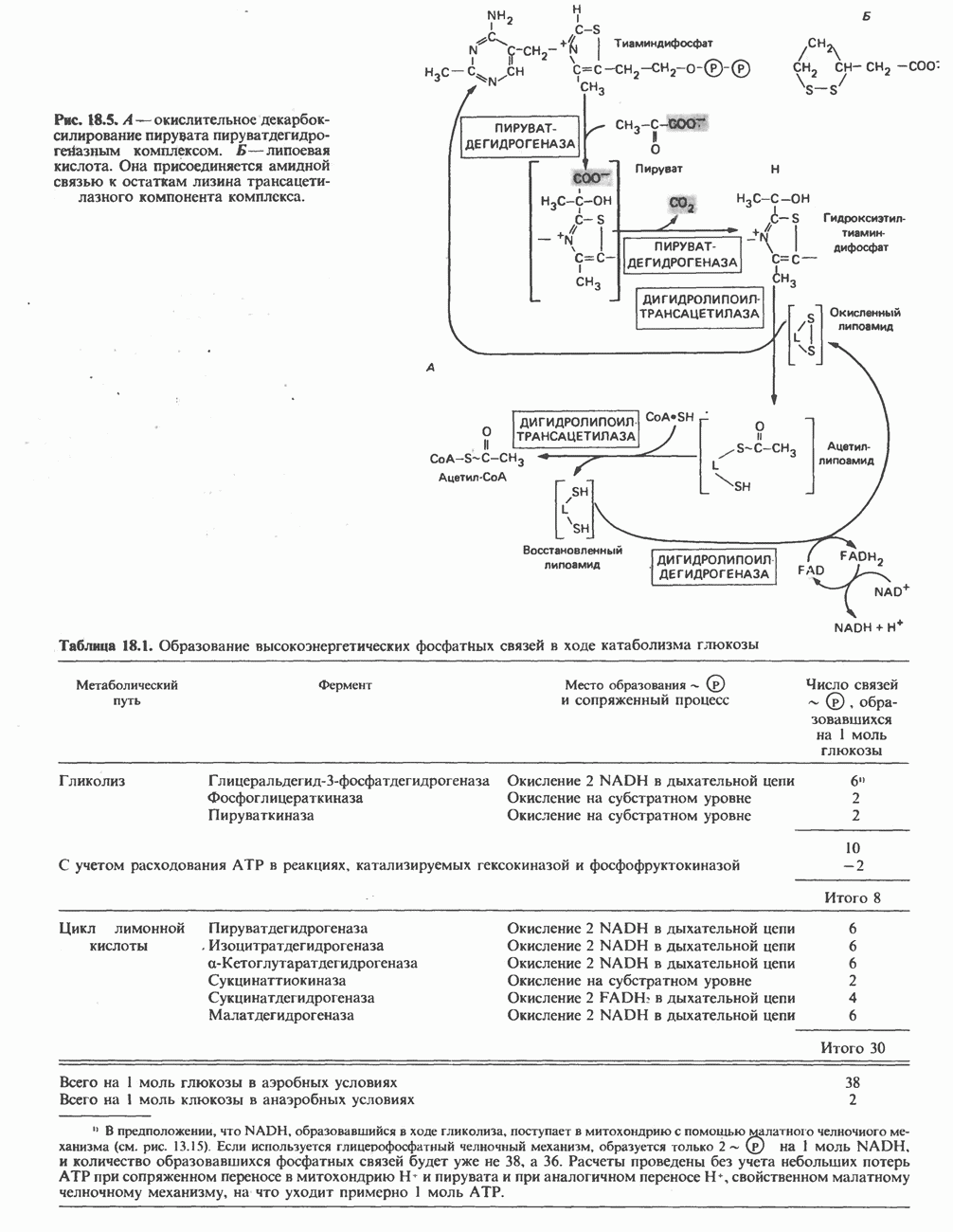
- ОКИСЛЕНИЕ ПИРУВАТА В АЦЕТИЛ-СоА
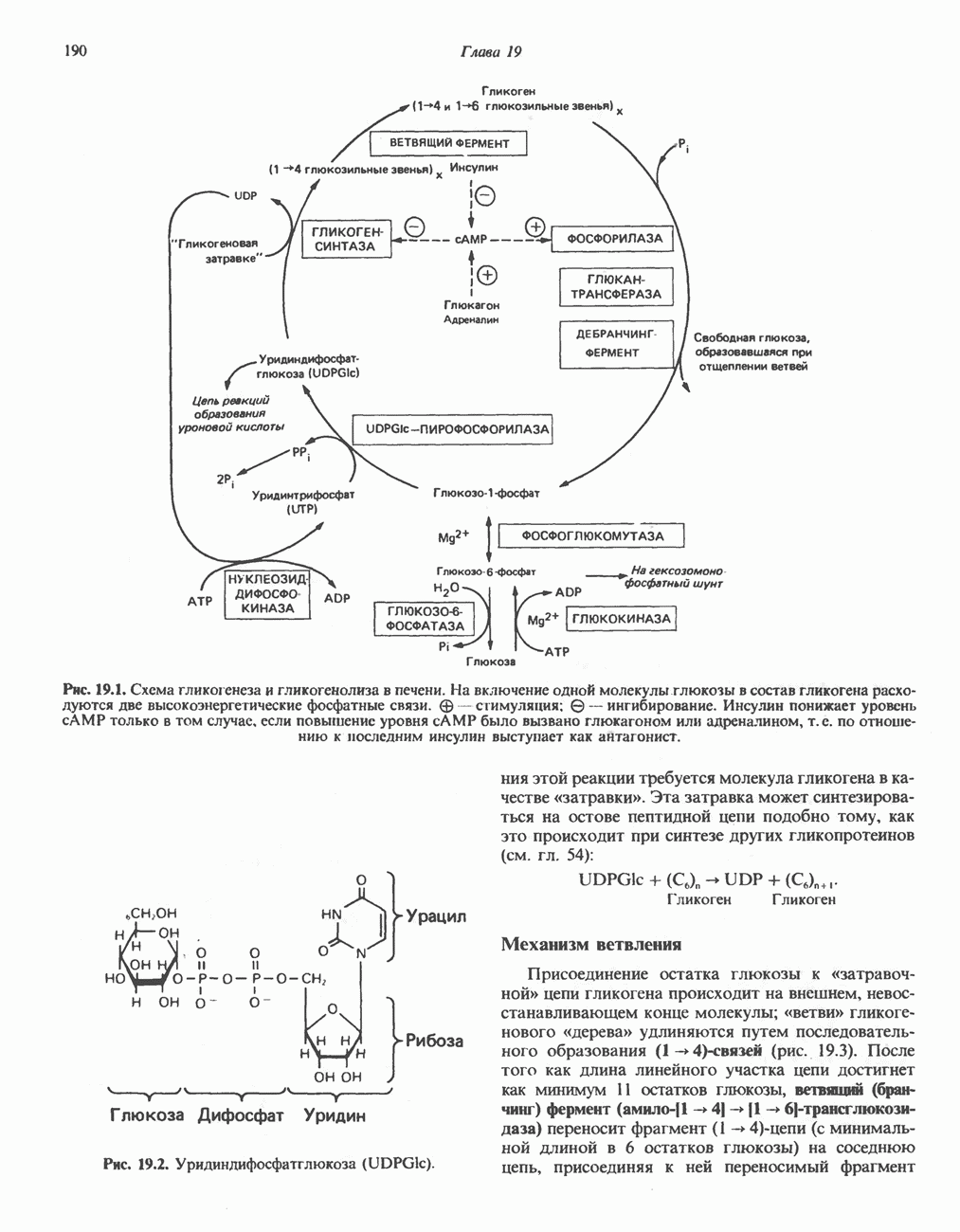
- Глава 19. Метаболизм гликогена
- ГЛИКОГЕНЕЗ
- ГЛИКОГЕНОЛИЗ
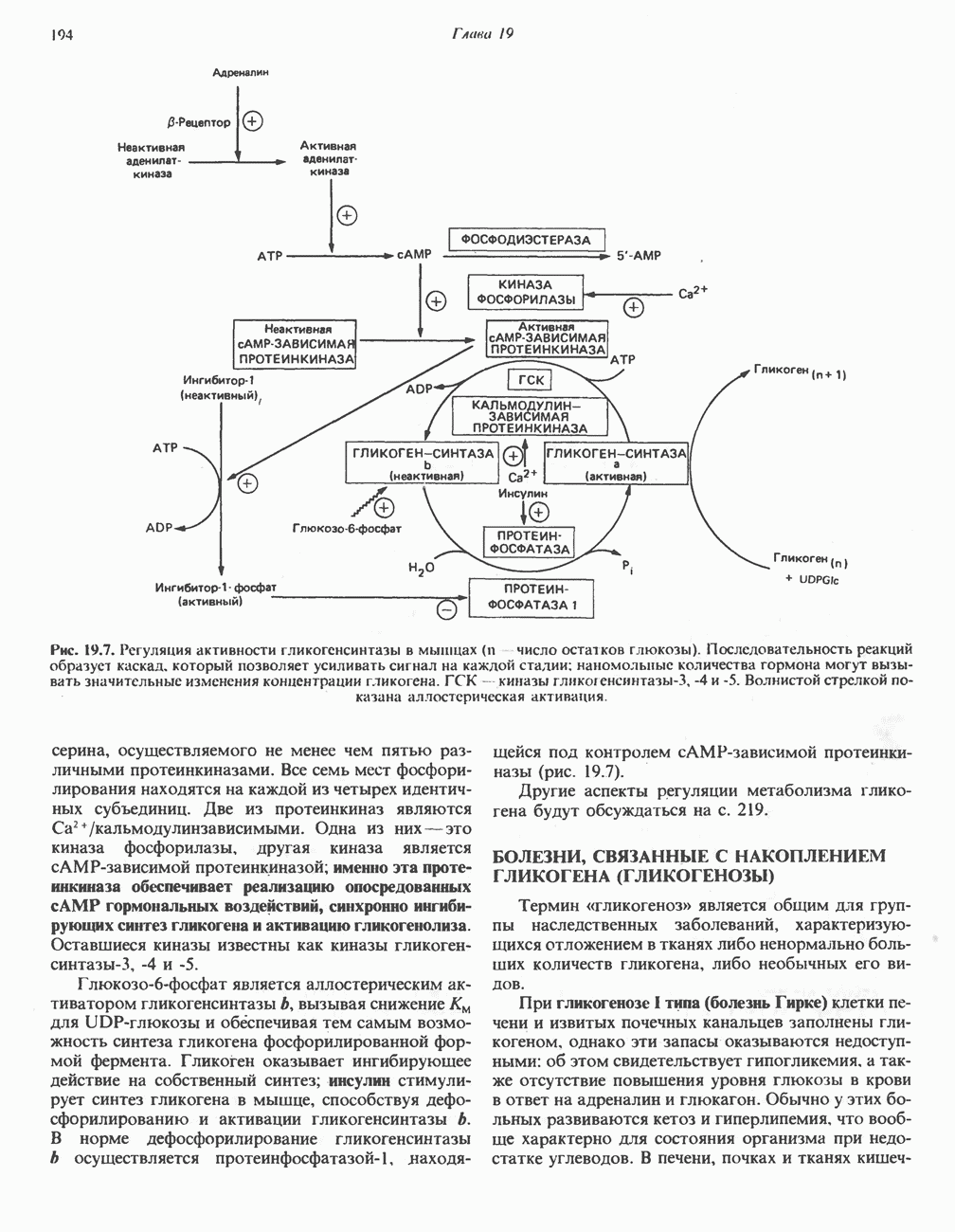
- МЕХАНИЗМЫ КОНТРОЛЯ ГЛИКОГЕНОЛИЗА И ГЛИКОГЕНЕЗА
- БОЛЕЗНИ, СВЯЗАННЫЕ С НАКОПЛЕНИЕМ ГЛИКОГЕНА (ГЛИКОГЕНОЗЫ)
- Глава 20. Глюконеогенез и пентозофосфатный путь
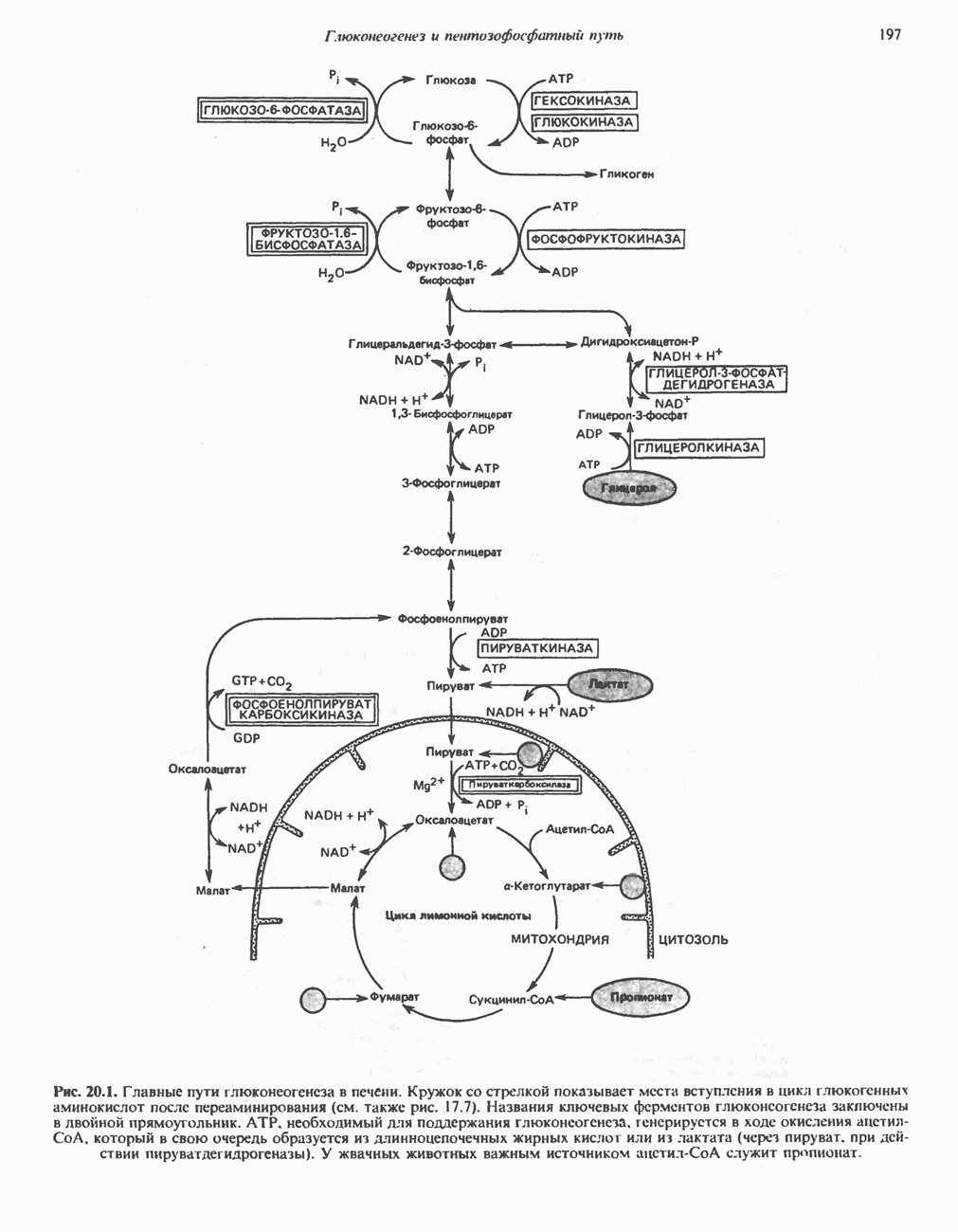
- МЕТАБОЛИЧЕСКИЕ ПУТИ, УЧАСТВУЮЩИЕ В ГЛЮКОНЕОГЕНЕЗЕ (рис. 20.1)
- ПЕНТОЗОФОСФАТНЫЙ ПУТЬ ИЛИ ГЕКСОЗОМОНОФОСФАТНЫЙ ШУНТ
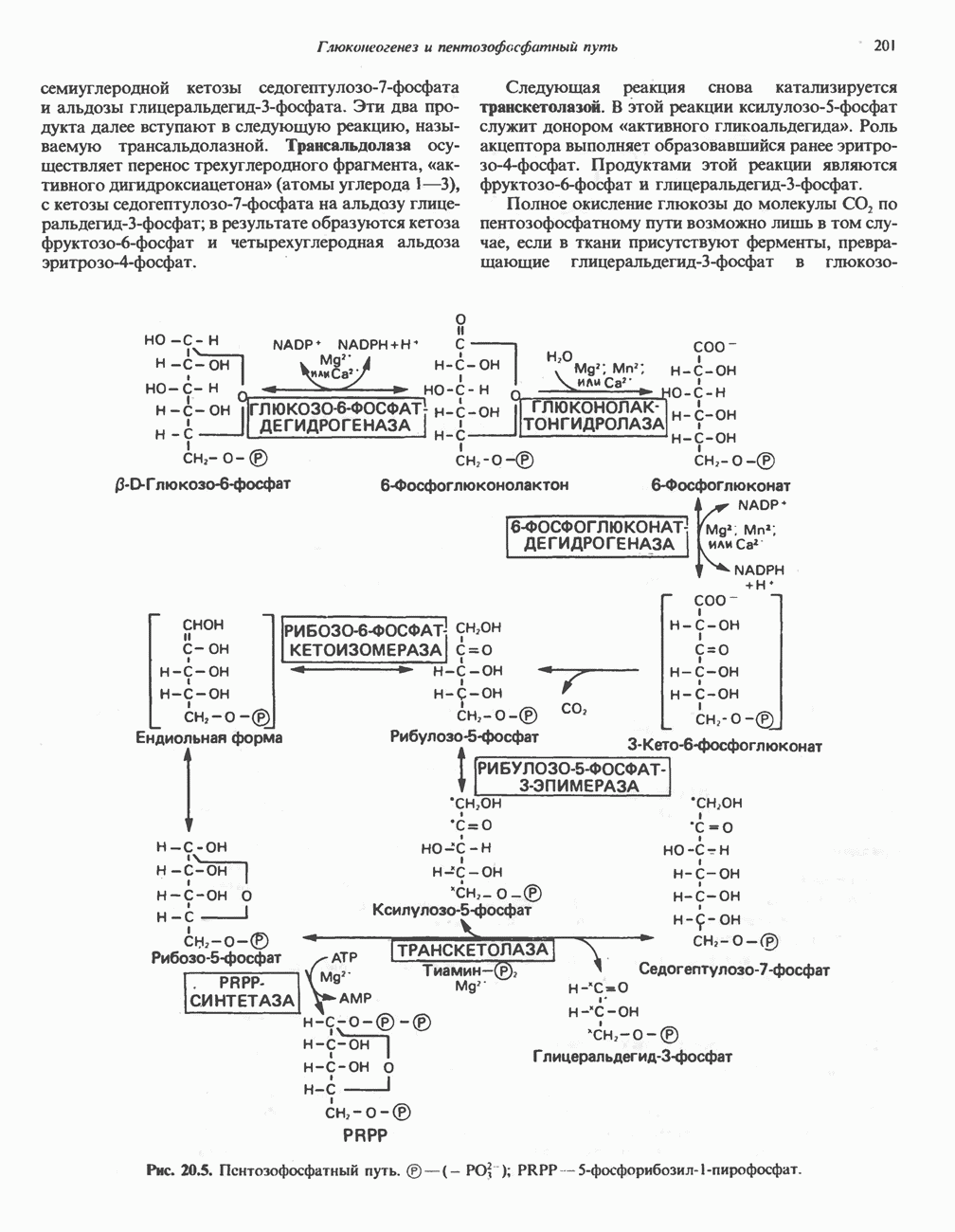
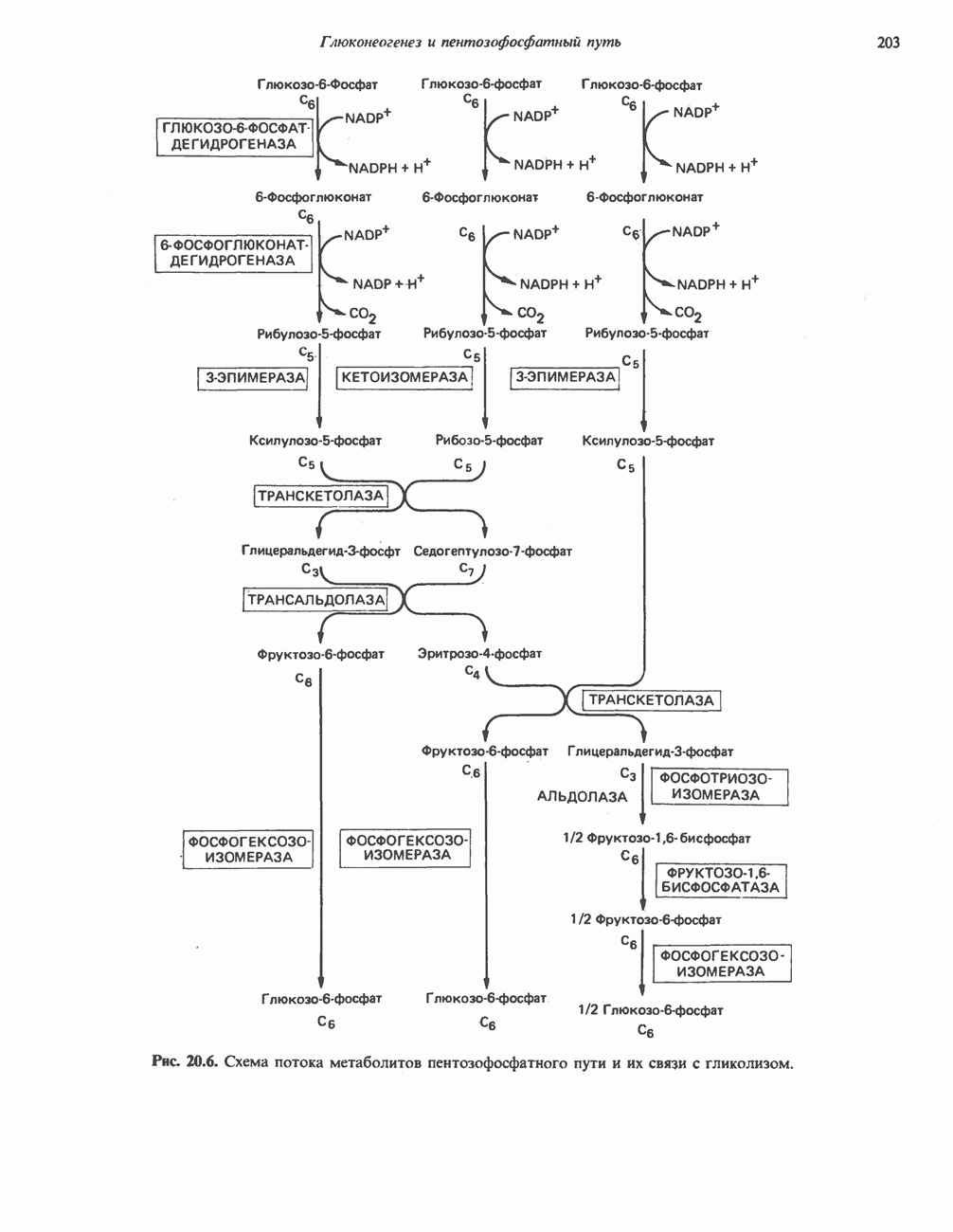
- ПОСЛЕДОВАТЕЛЬНОСТЬ РЕАКЦИЙ
- МЕТАБОЛИЧЕСКОЕ ЗНАЧЕНИЕ ПЕНТОЗОФОСФАТНОГО ПУТИ
- КЛИНИЧЕСКИЕ АСПЕКТЫ
- Глава 21. Метаболизм наиболее важных гексоз
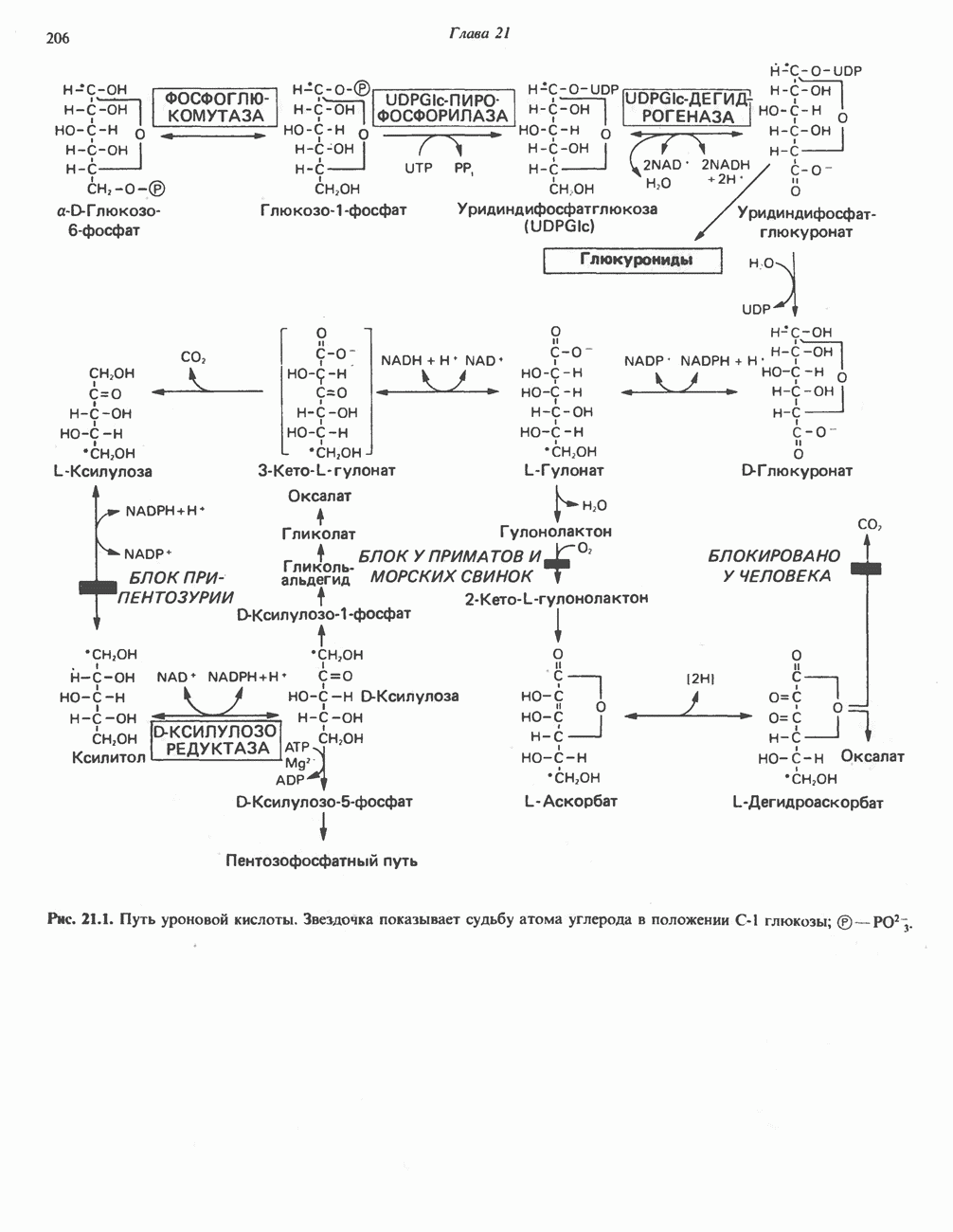
- ПУТЬ УРОНОВЫХ КИСЛОТ
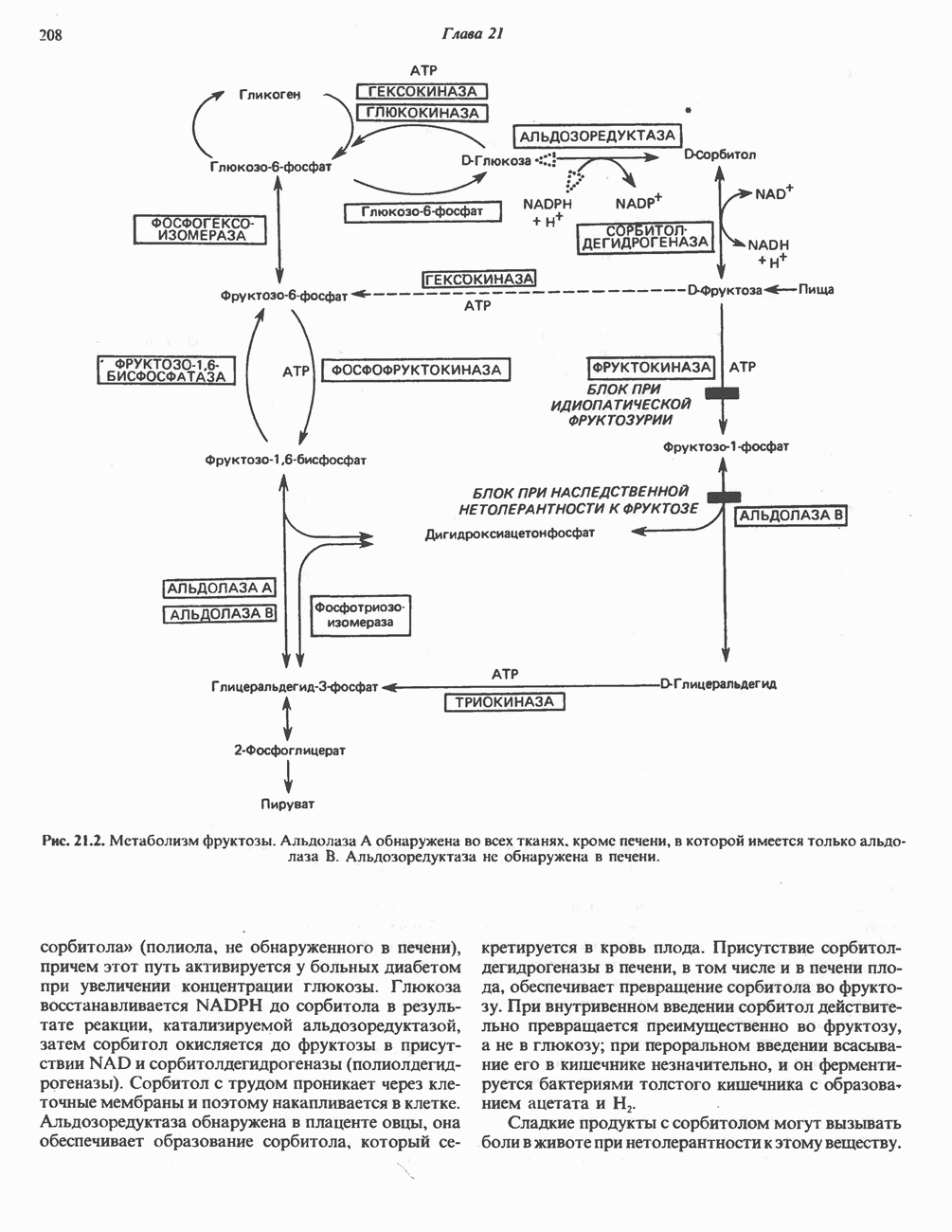
- МЕТАБОЛИЗМ ФРУКТОЗЫ
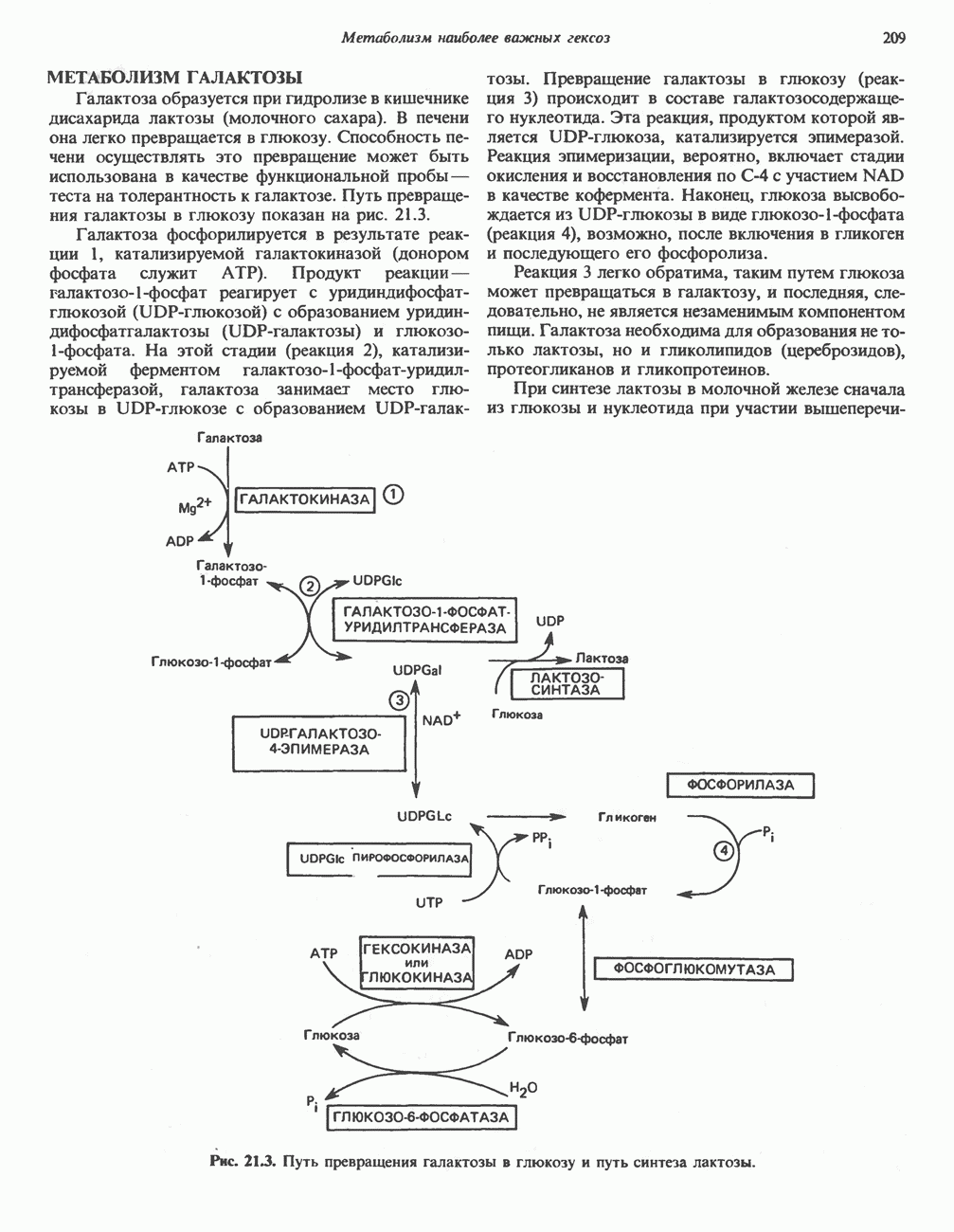
- МЕТАБОЛИЗМ ГАЛАКТОЗЫ
- Глава 22. Регуляция метаболизма углеводов
- ОБЩИЕ ПРИНЦИПЫ РЕГУЛЯЦИИ ПУТЕЙ МЕТАБОЛИЗМА
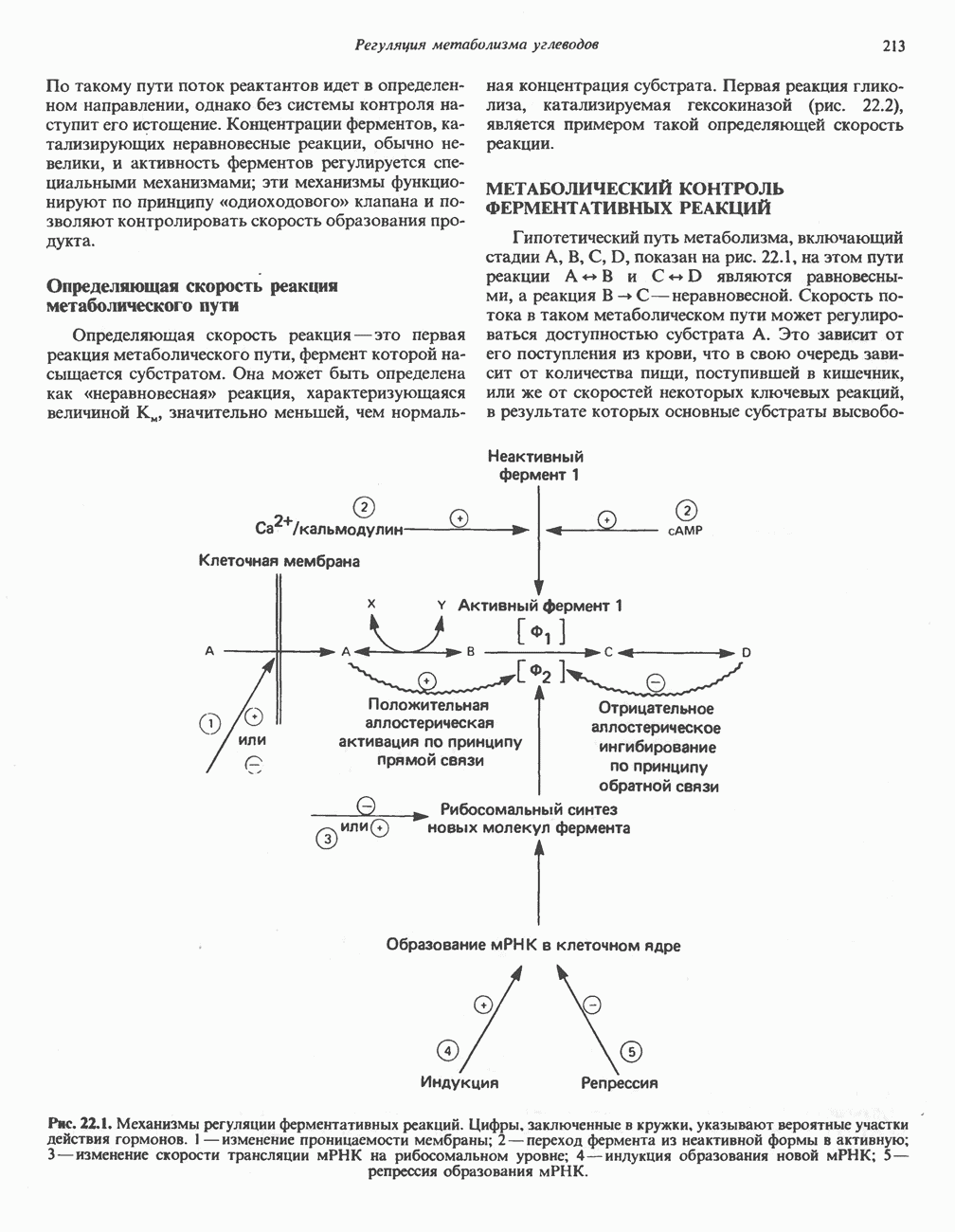
- МЕТАБОЛИЧЕСКИЙ КОНТРОЛЬ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- РЕГУЛЯЦИЯ МЕТАБОЛИЗМА УГЛЕВОДОВ НА КЛЕТОЧНОМ И ФЕРМЕНТНОМ УРОВНЕ
- РЕГУЛЯЦИЯ ГЛИКОЛИЗА, ГЛЮКОНЕОГЕНЕЗА И ПЕНТОЗОФОСФАТНОГО ПУТИ
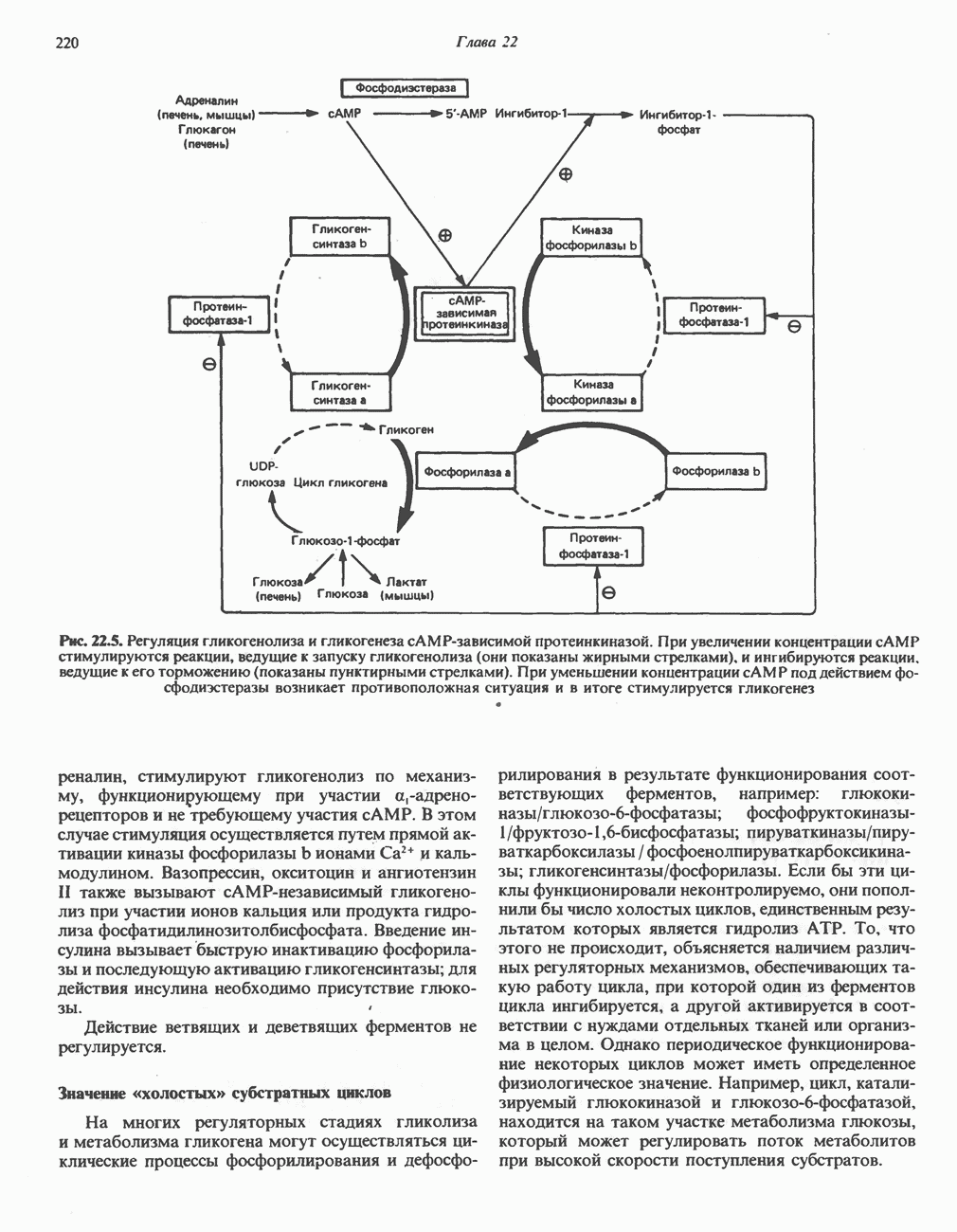
- РЕГУЛЯЦИЯ МЕТАБОЛИЗМА ГЛИКОГЕНА (РИС. 22.5)
- РЕГУЛЯЦИЯ ЦИКЛА ЛИМОННОЙ КИСЛОТЫ (СМ. РИС. 18.3)
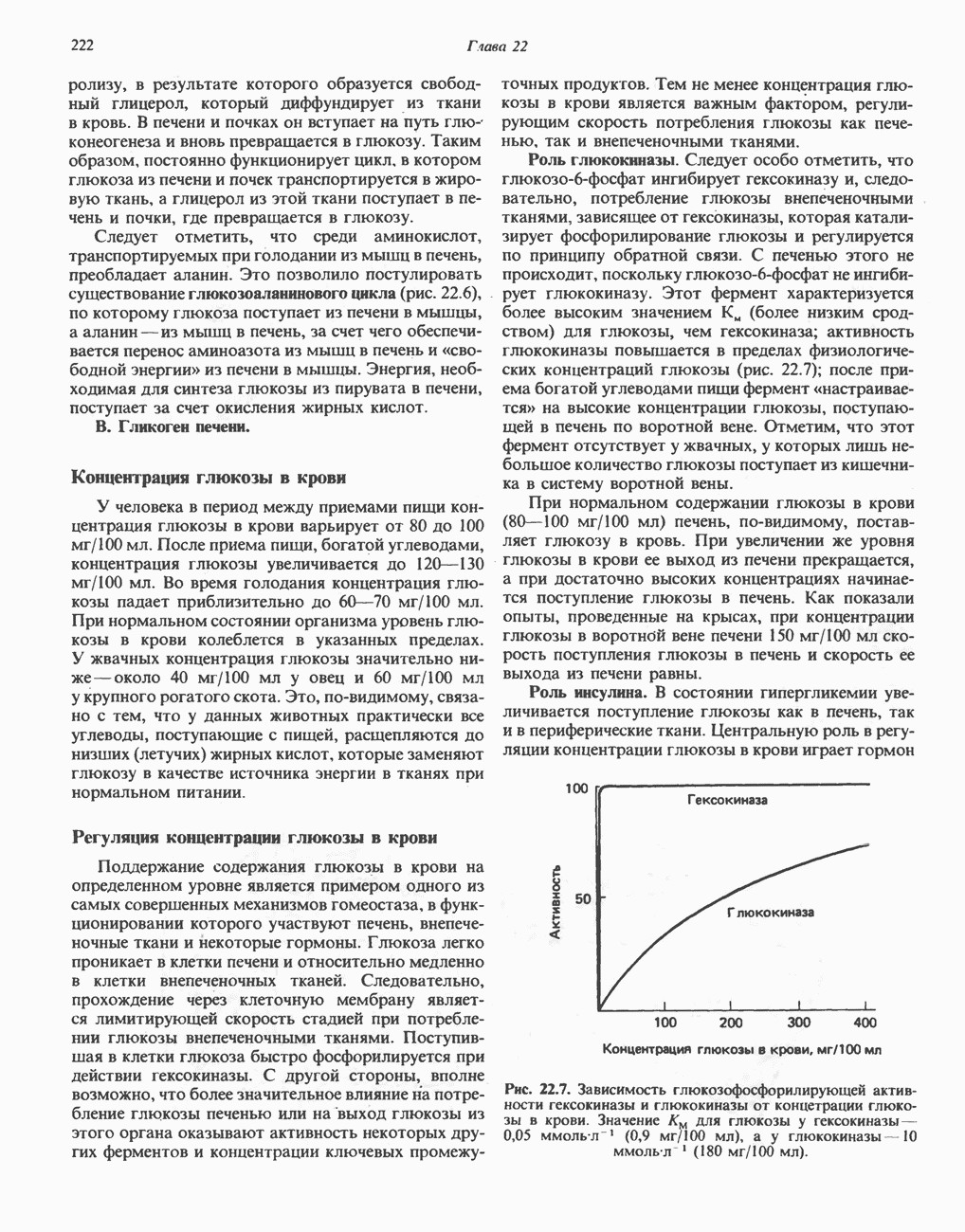
- РЕГУЛЯЦИЯ УРОВНЯ ГЛЮКОЗЫ В КРОВИ
- Глава 23. Окисление и биосинтез жирных кислот
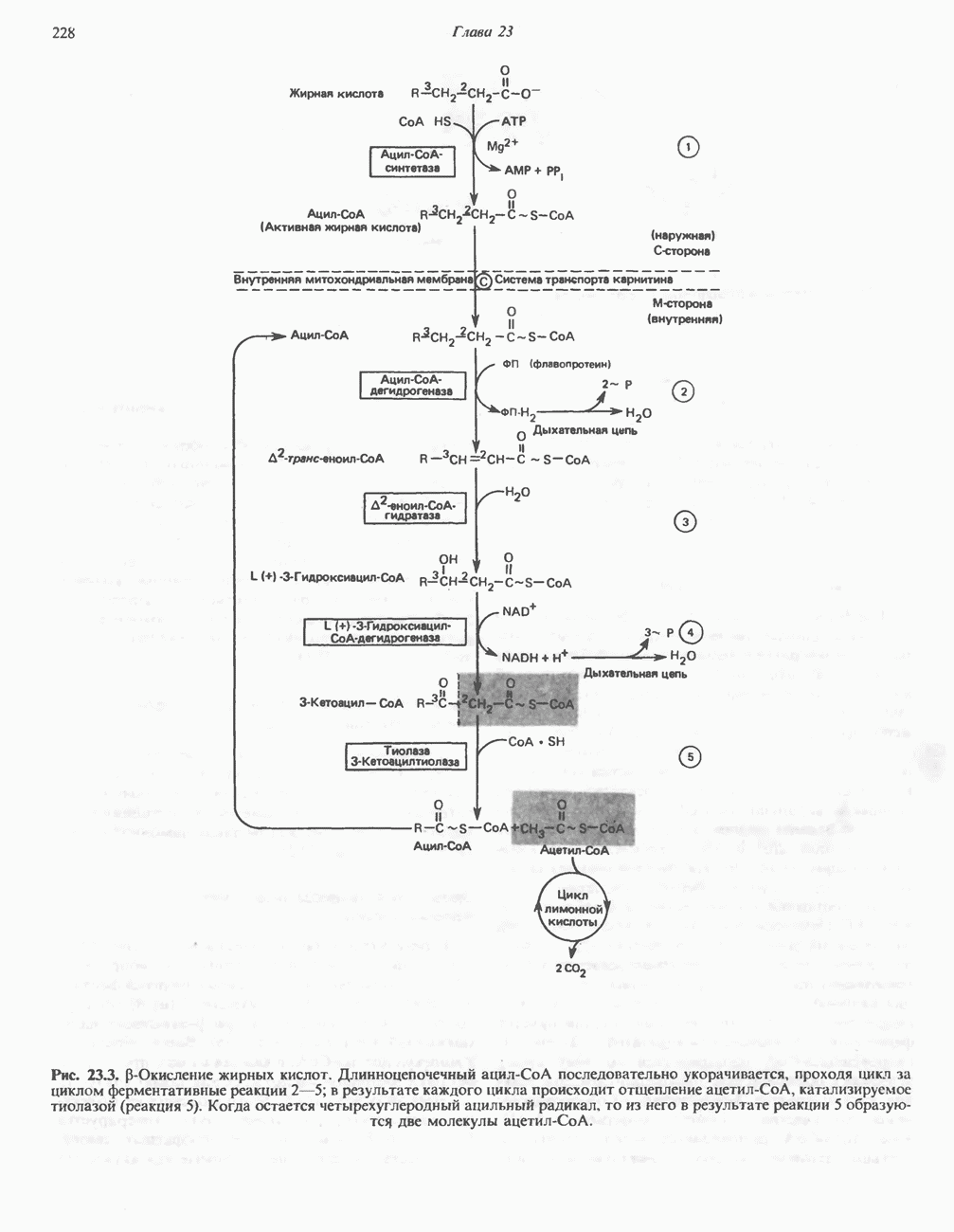
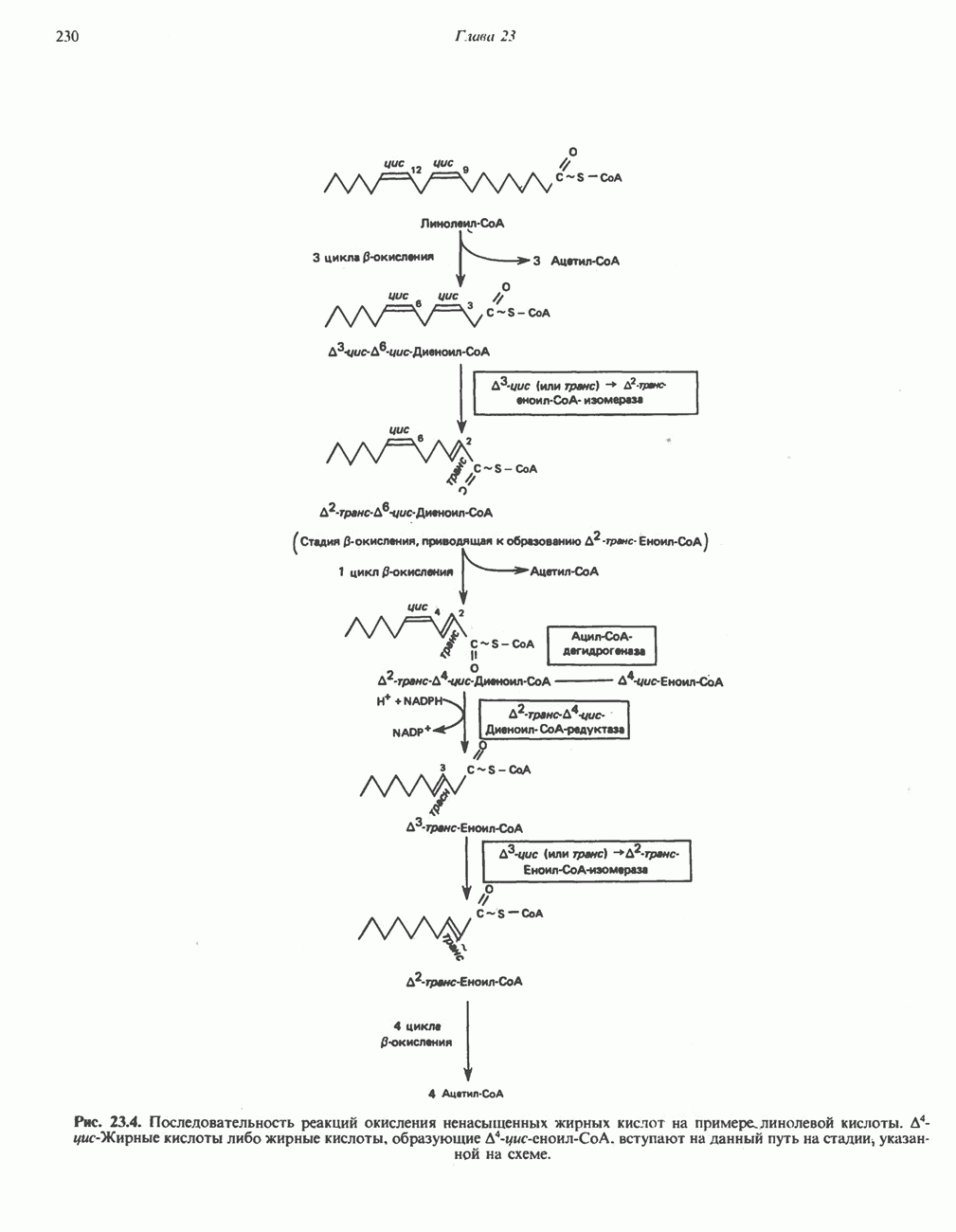
- ОКИСЛЕНИЕ ЖИРНЫХ КИСЛОТ
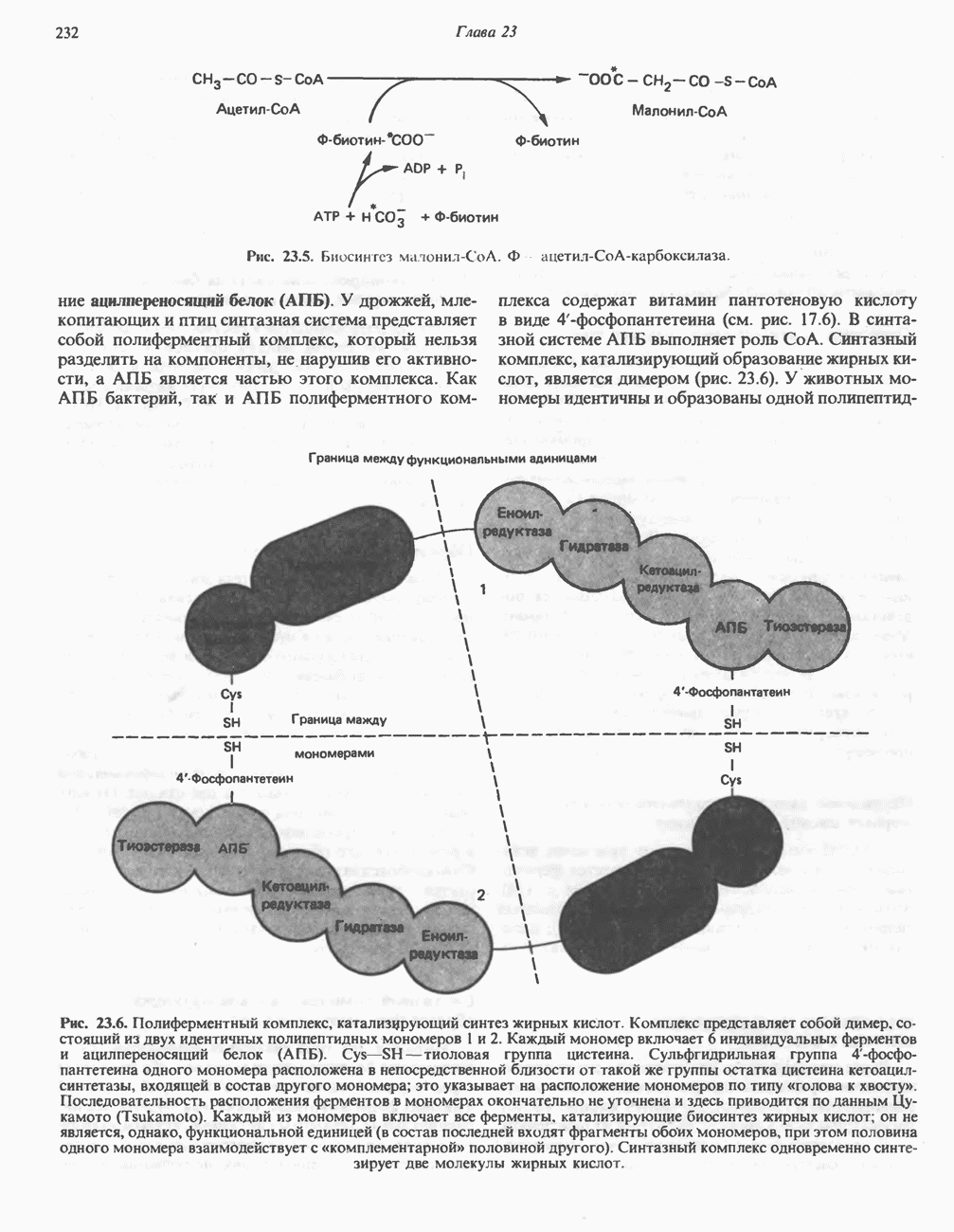
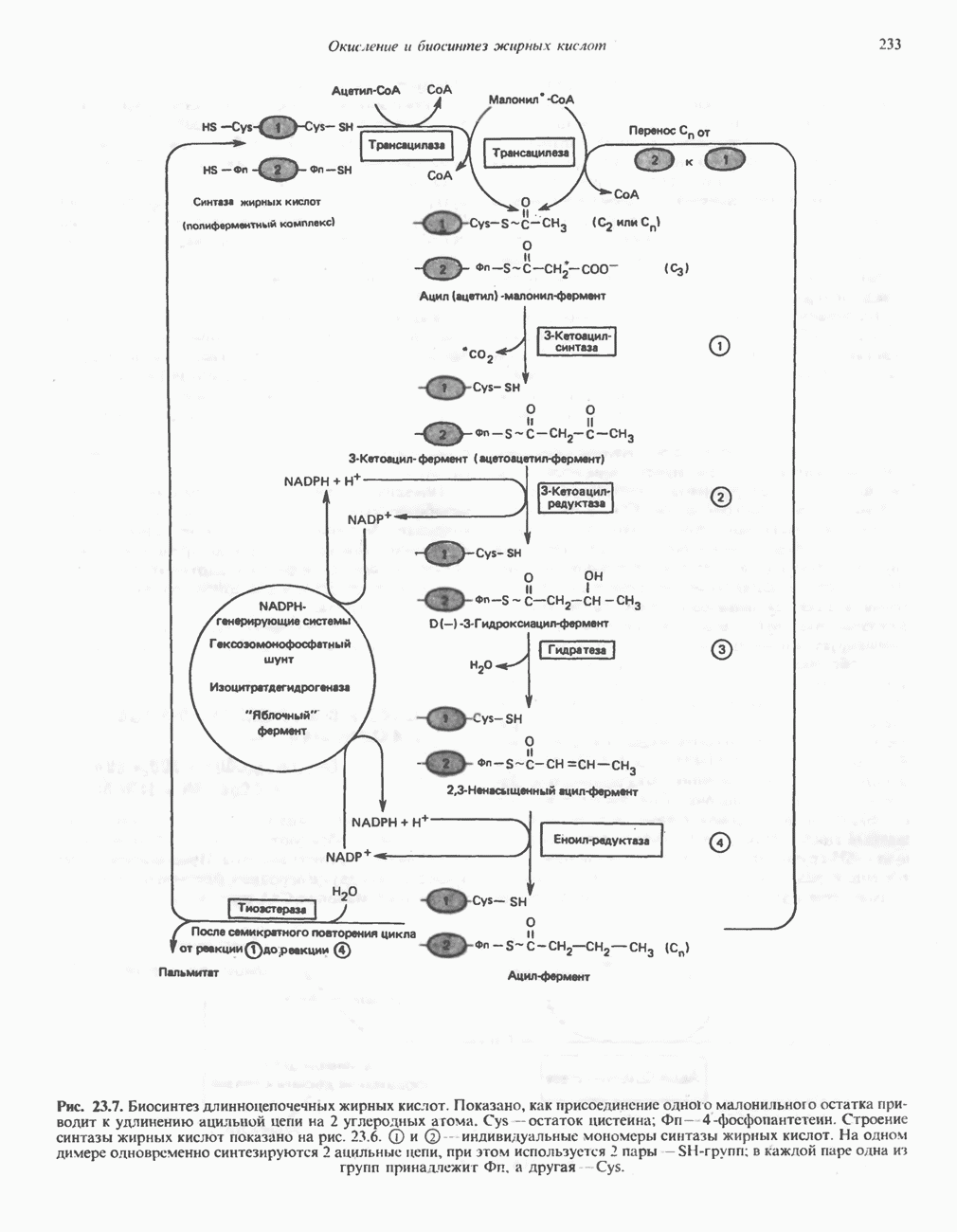
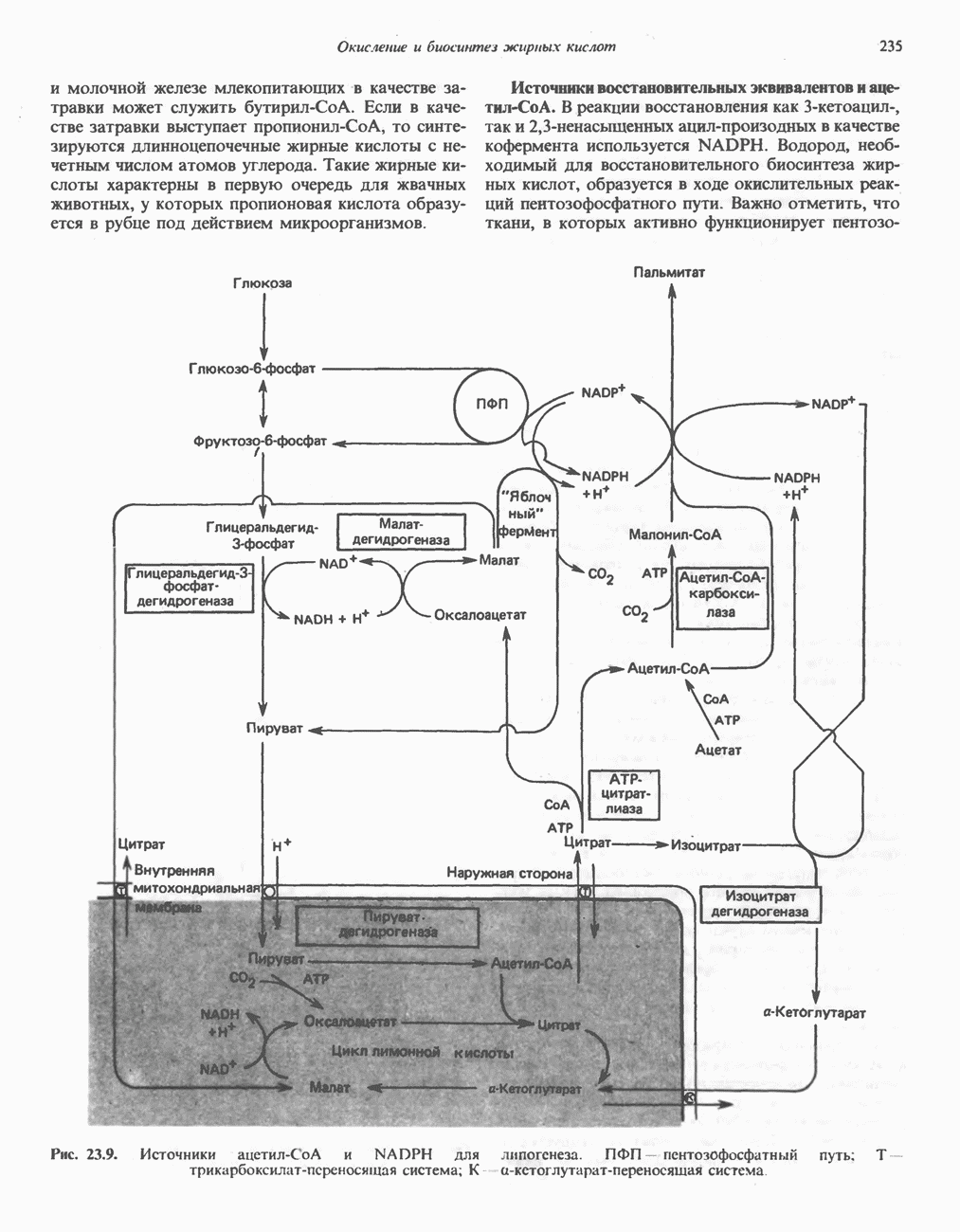
- БИОСИНТЕЗ НАСЫЩЕННЫХ ЖИРНЫХ КИСЛОТ
- Глава 24. Метаболизм ненасыщенных жирных кислот и эйкозаноидов
- МЕТАБОЛИЗМ НЕНАСЫЩЕННЫХ ЖИРНЫХ КИСЛОТ
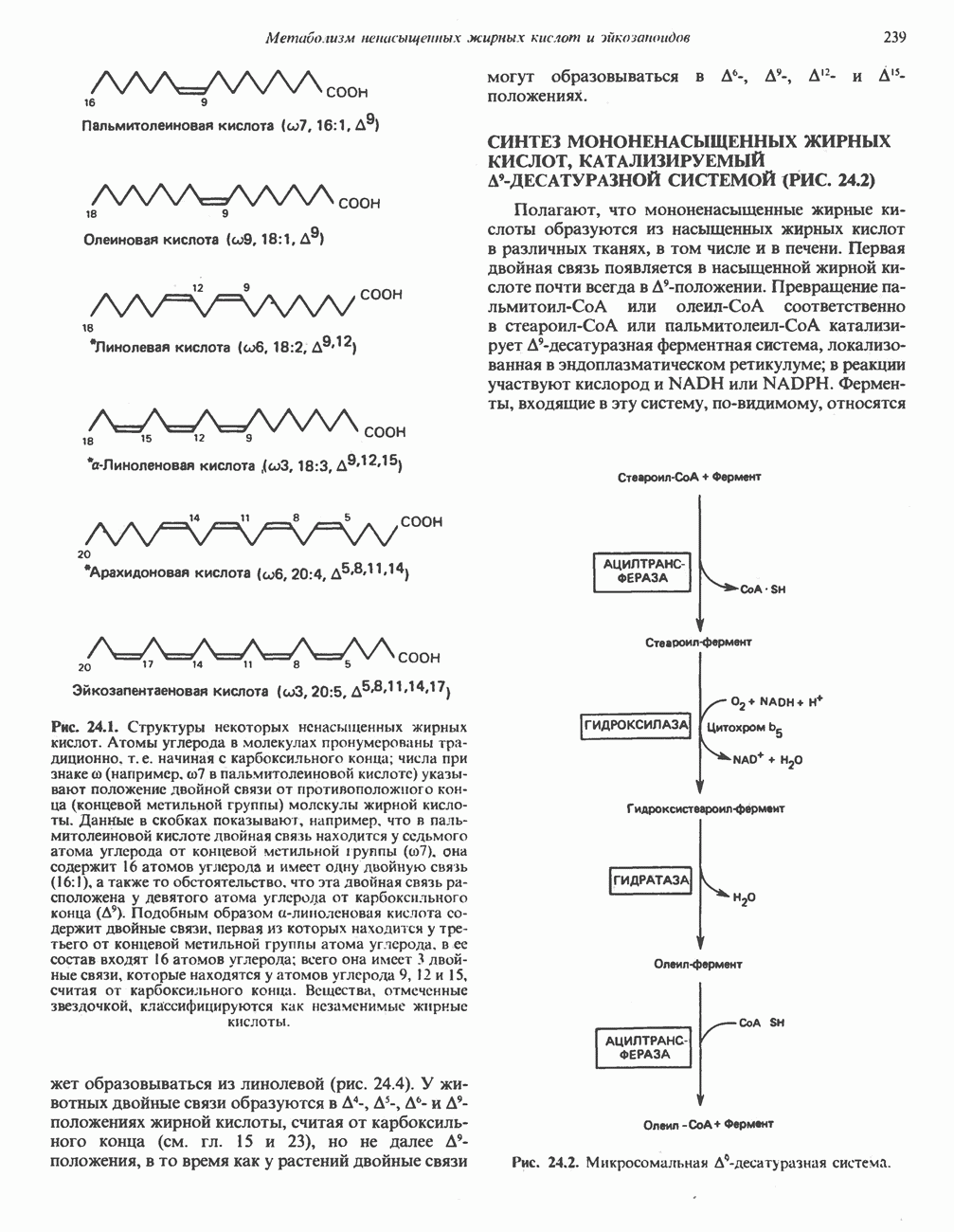
- СИНТЕЗ МОНОНЕНАСЫЩЕННЫХ ЖИРНЫХ КИСЛОТ, КАТАЛИЗИРУЕМЫЙ Д9-ДЕСАТУРАЗНОЙ СИСТЕМОЙ (РИС. 24.2)
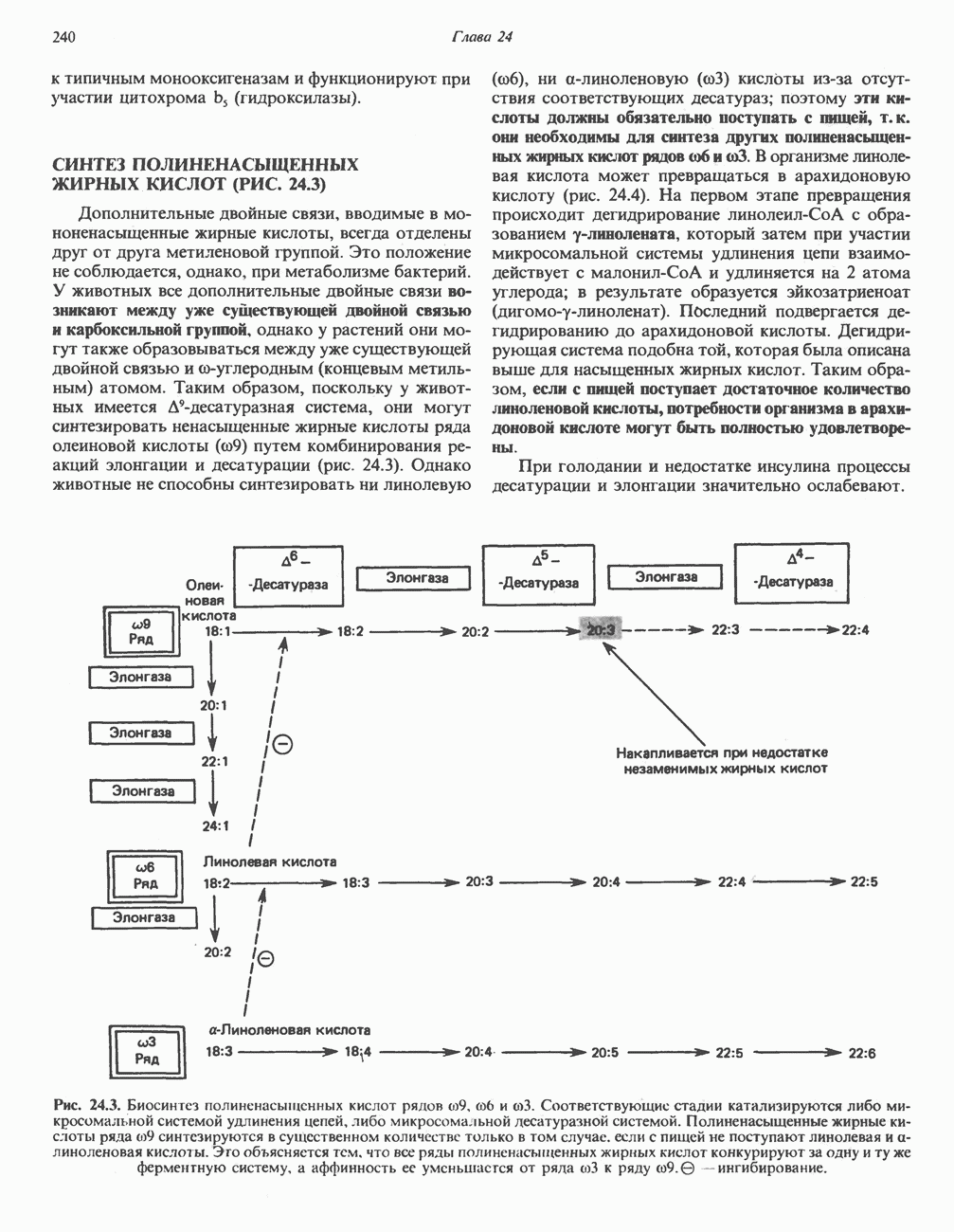
- СИНТЕЗ ПОЛИНЕНАСЫЩЕННЫХ ЖИРНЫХ КИСЛОТ (РИС. 24.3)
- НЕЗАМЕНИМЫЕ ЖИРНЫЕ КИСЛОТЫ (НЖК)
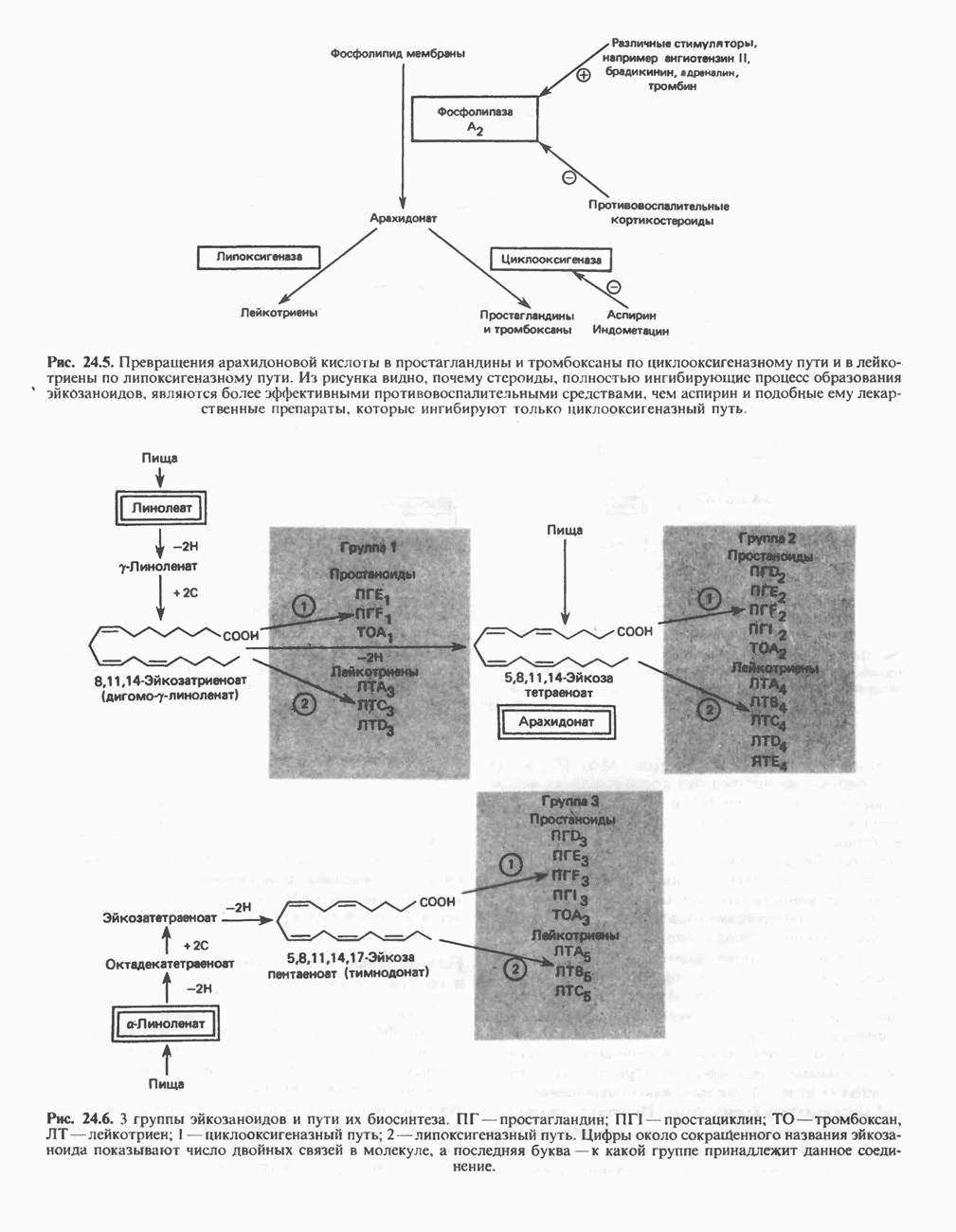
- ЭЙКОЗАНОИДЫ
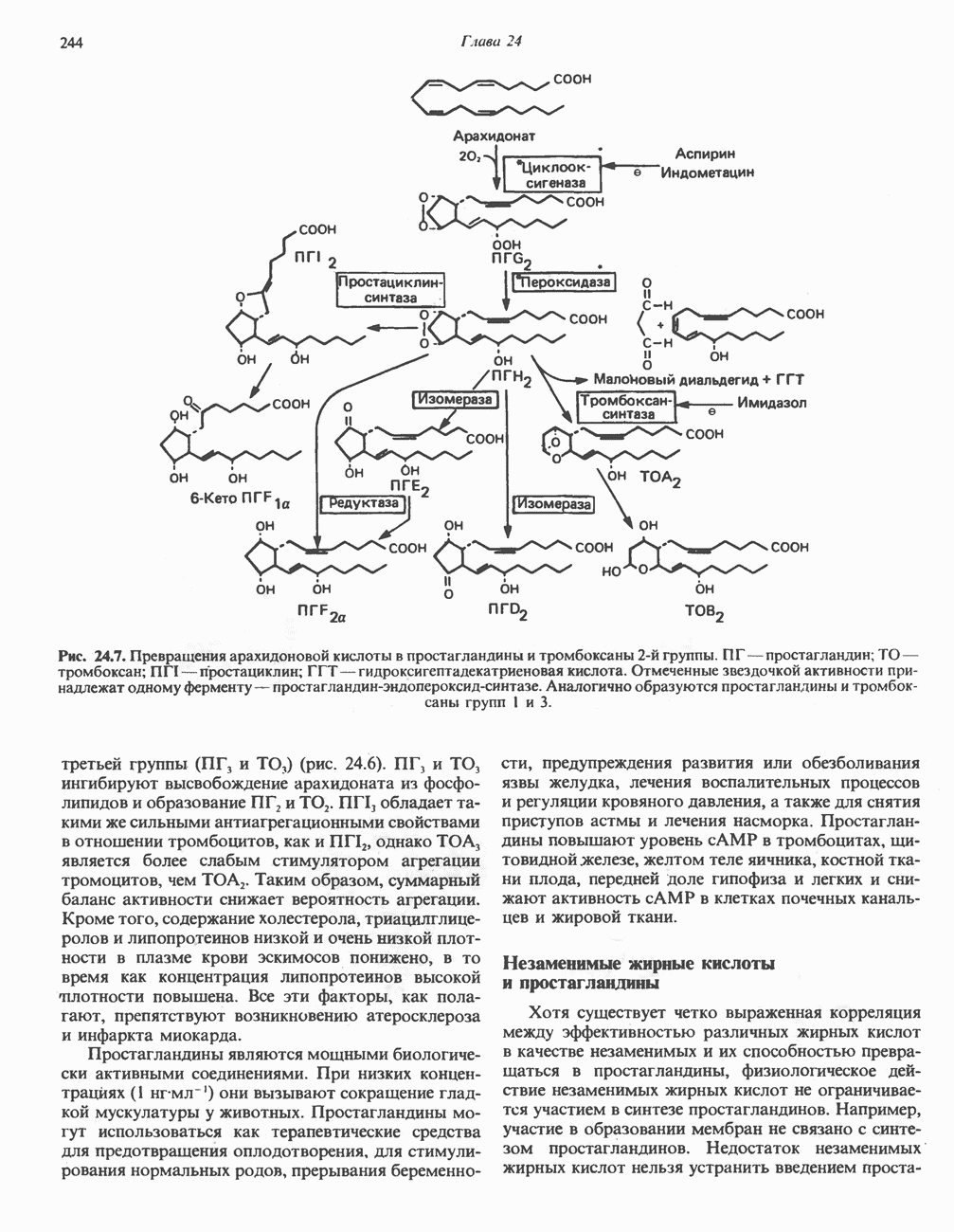
- ПРОСТАНОИДЫ
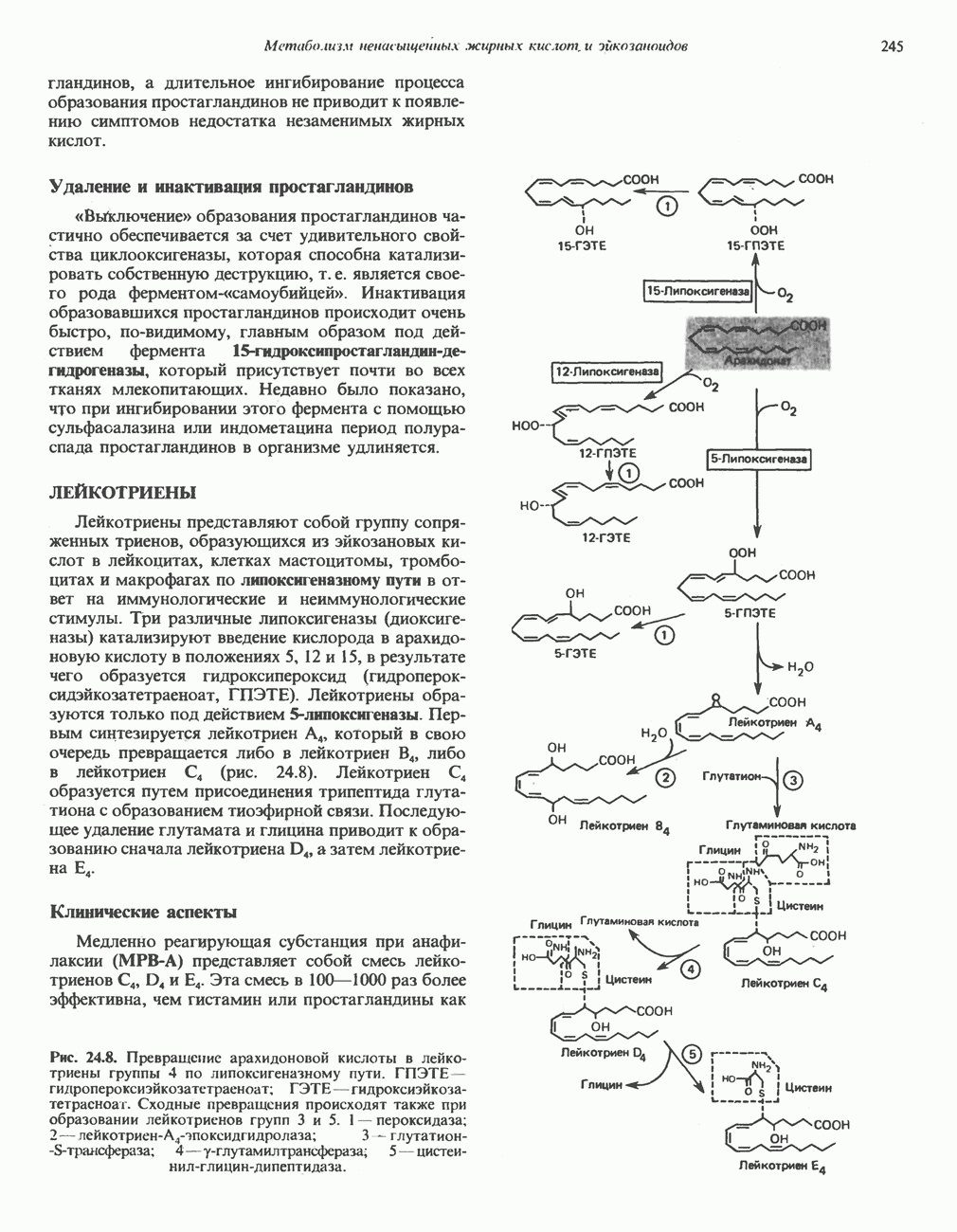
- ЛЕЙКОТРИЕНЫ
- Глава 25. Метаболизм ацилглицеролов и сфинголипидов
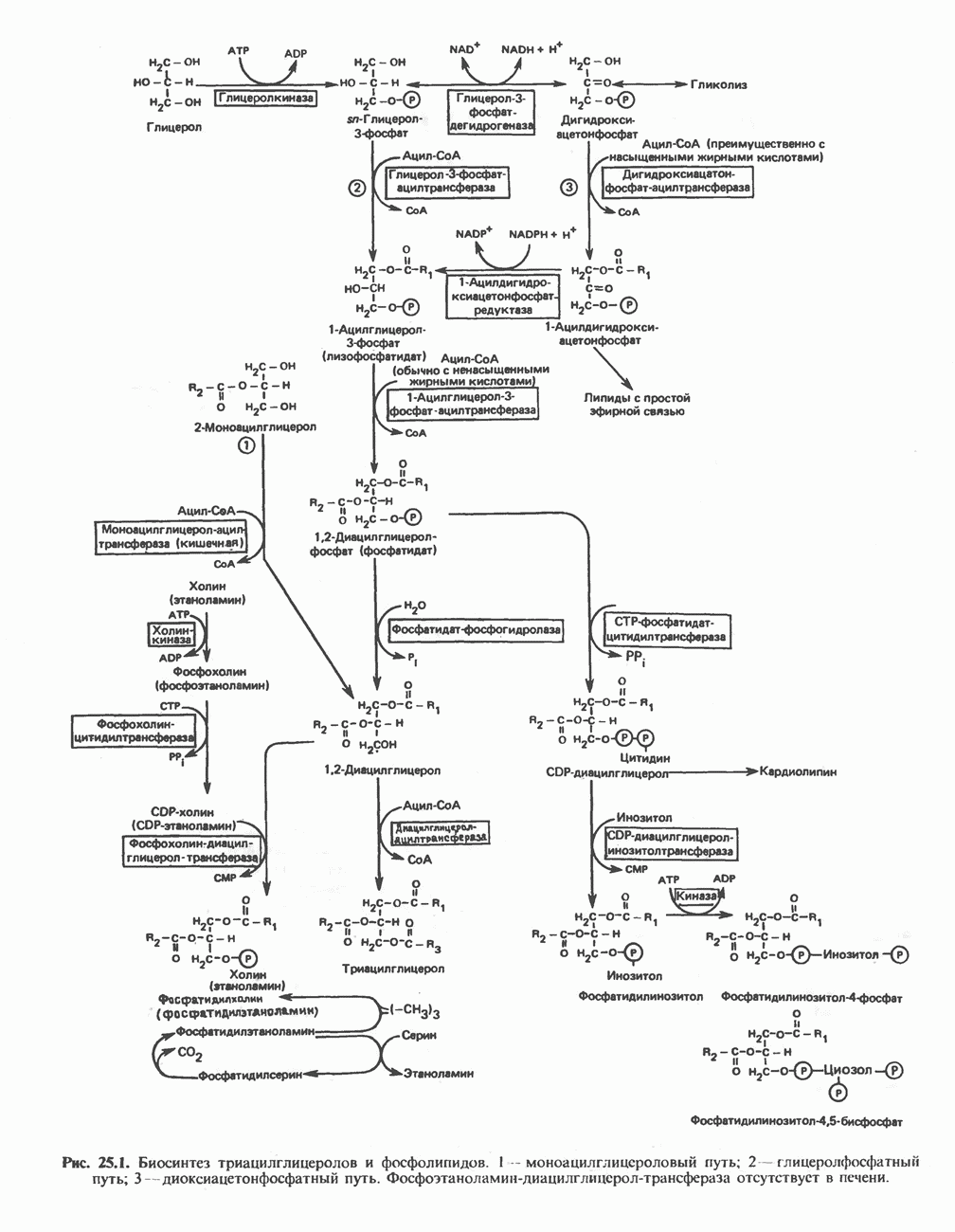
- МЕТАБОЛИЗМ АЦИЛГЛИЦЕРОЛОВ
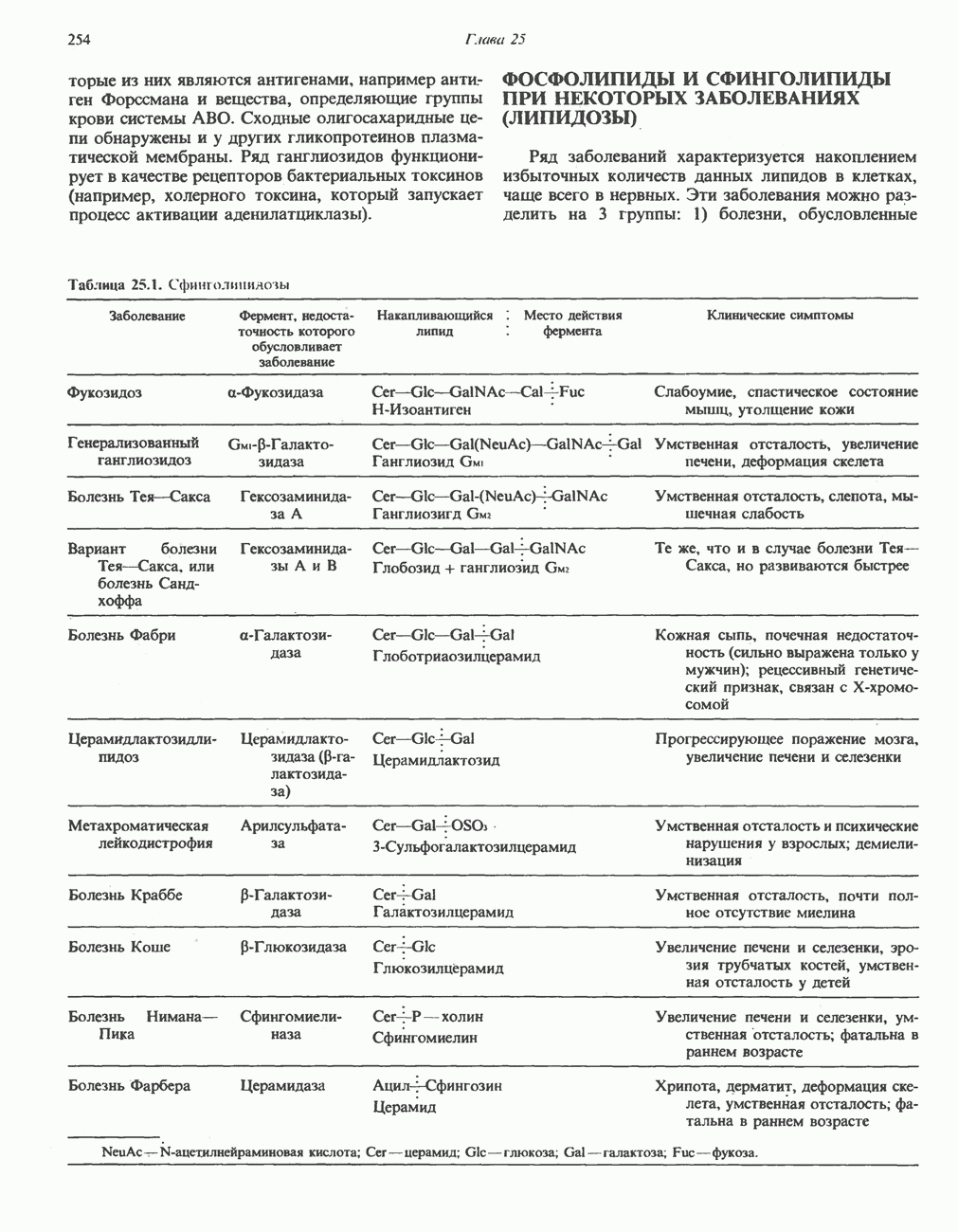
- МЕТАБОЛИЗМ СФИНГОЛИПИДОВ
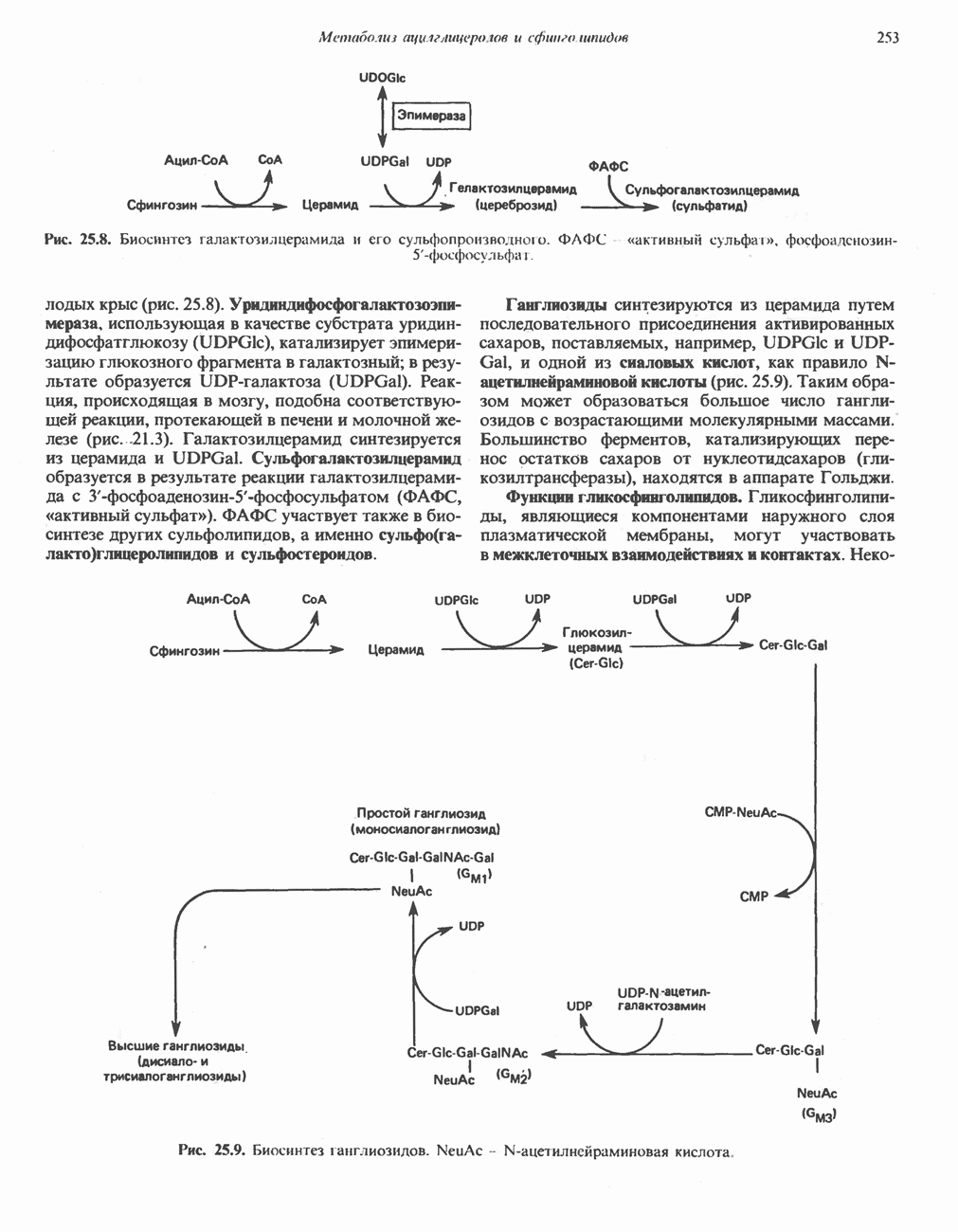
- ГЛИКОЛИПИДЫ
- ФОСФОЛИПИДЫ И СФИНГОЛИПИДЫ ПРИ НЕКОТОРЫХ ЗАБОЛЕВАНИЯХ (ЛИПИДОЗЫ)
- Глава 26. Транспорт и запасание липидов
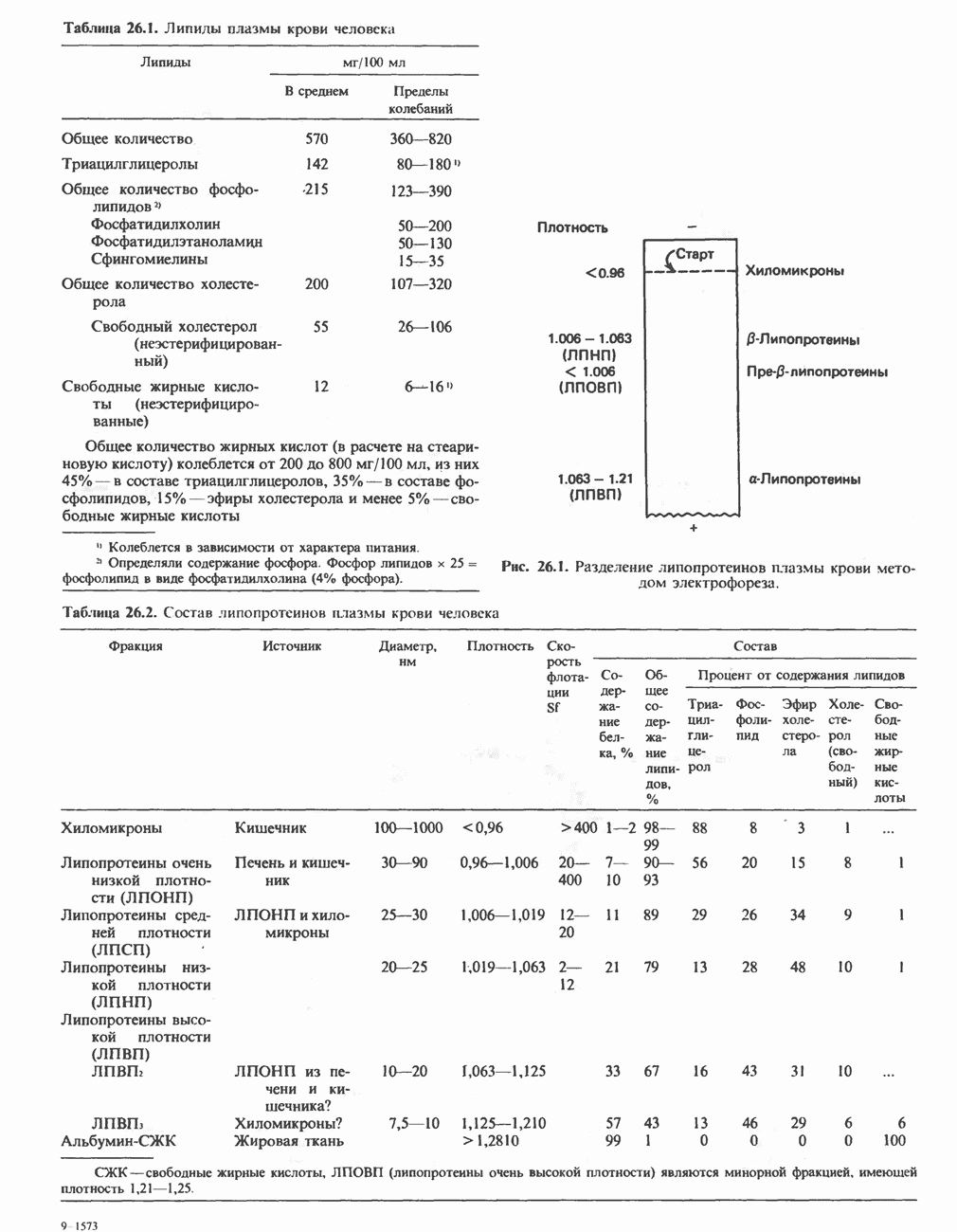
- ЛИПИДЫ ПЛАЗМЫ КРОВИ И ЛИПОПРОТЕИНЫ
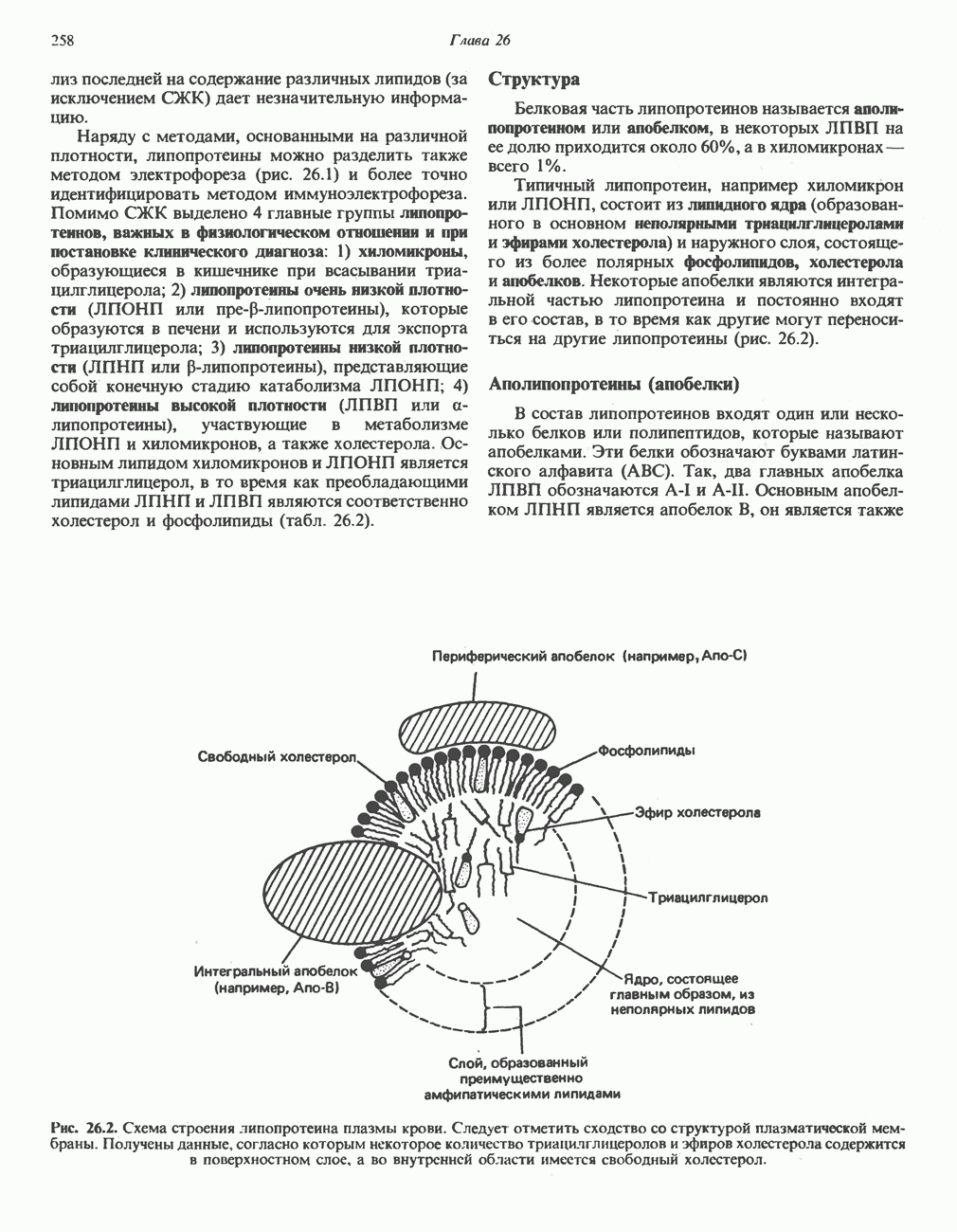
- МЕТАБОЛИЗМ ЛИПОПРОТЕИНОВ ПЛАЗМЫ КРОВИ
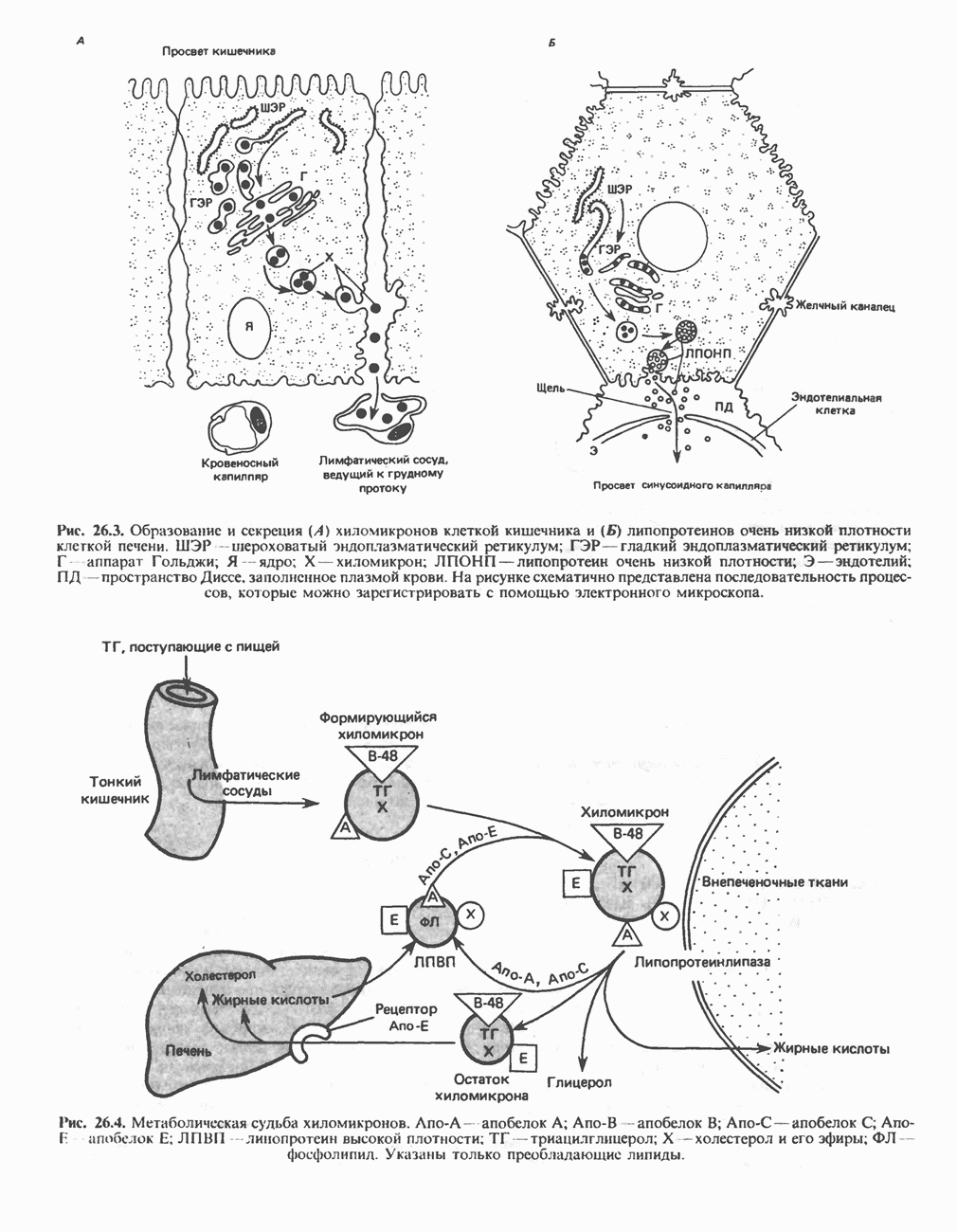
- ОБРАЗОВАНИЕ ХИЛОМИКРОНОВ И ЛИПОПРОТЕИНОВ ОЧЕНЬ НИЗКОЙ ПЛОТНОСТИ (ЛПОНП)
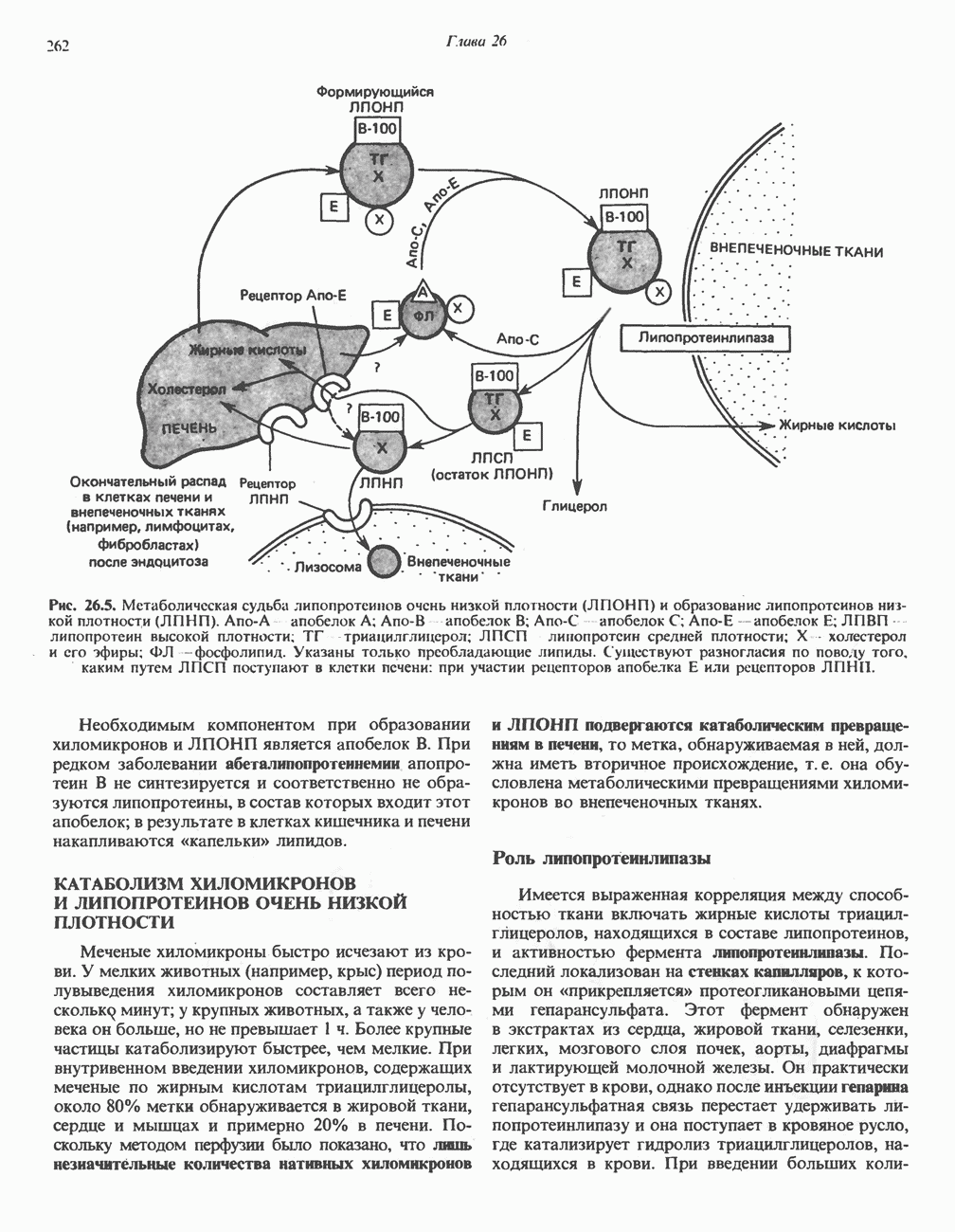
- КАТАБОЛИЗМ ХИЛОМИКРОНОВ И ЛИПОПРОТЕИНОВ ОЧЕНЬ НИЗКОЙ ПЛОТНОСТИ
- МЕТАБОЛИЗМ ЛПНП
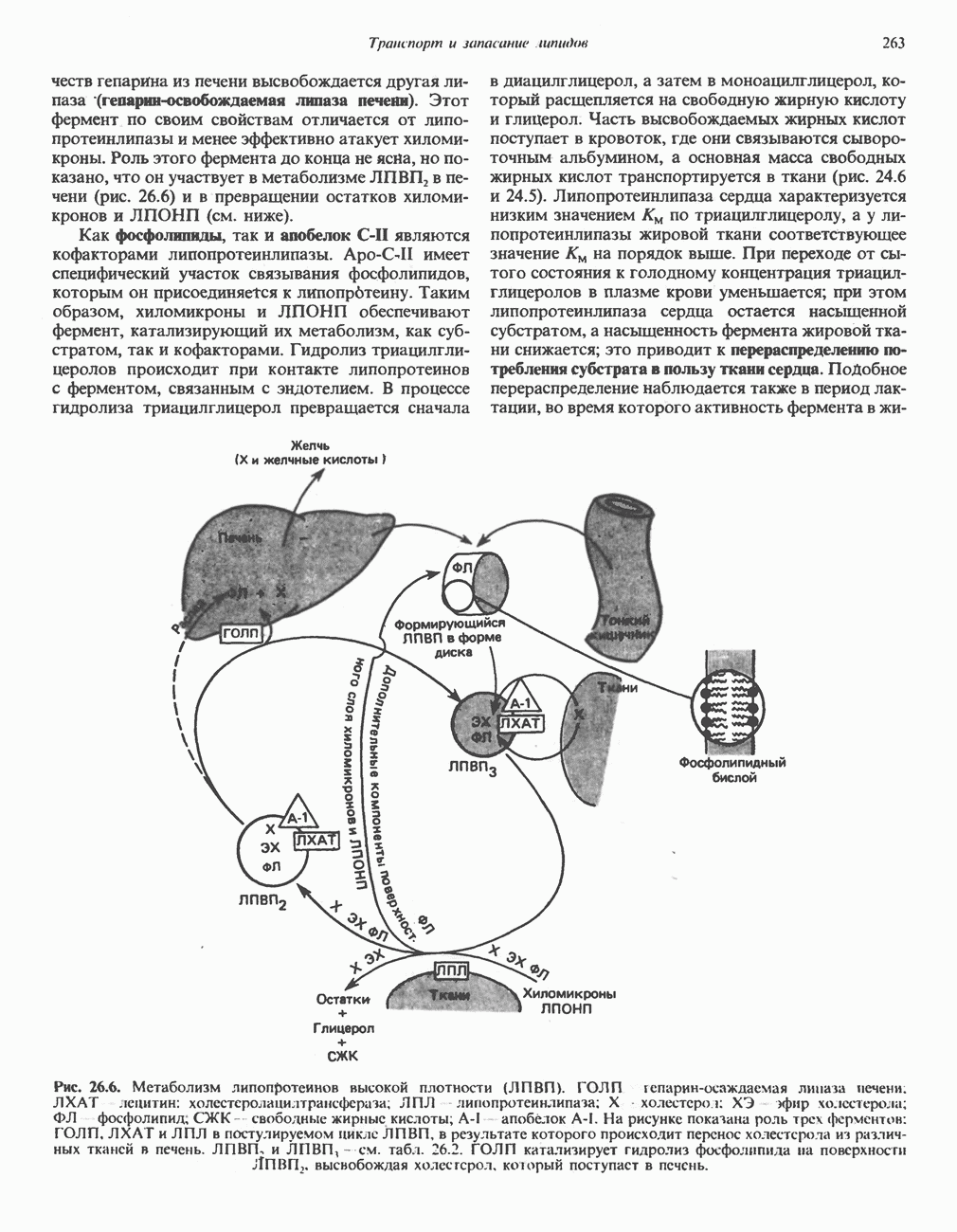
- МЕТАБОЛИЗМ ЛПВП (рис. 26.6)
- РОЛЬ ПЕЧЕНИ В ТРАНСПОРТЕ И МЕТАБОЛИЗМЕ ЛИПИДОВ
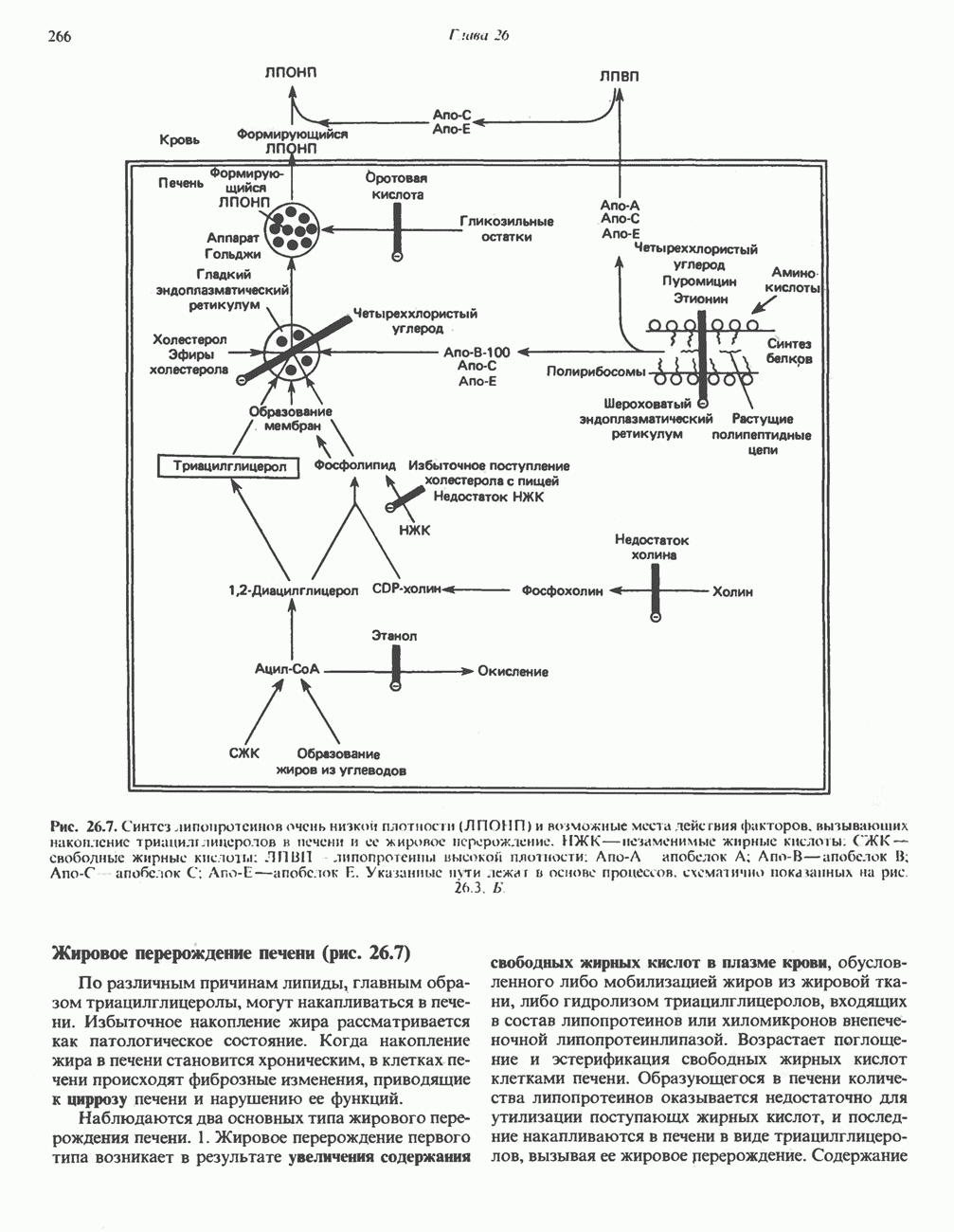
- СИНТЕЗ ТРИАЦИЛГЛИЦЕРОЛОВ И ОБРАЗОВАНИЕ ЛПОНП (рис. 26.7)
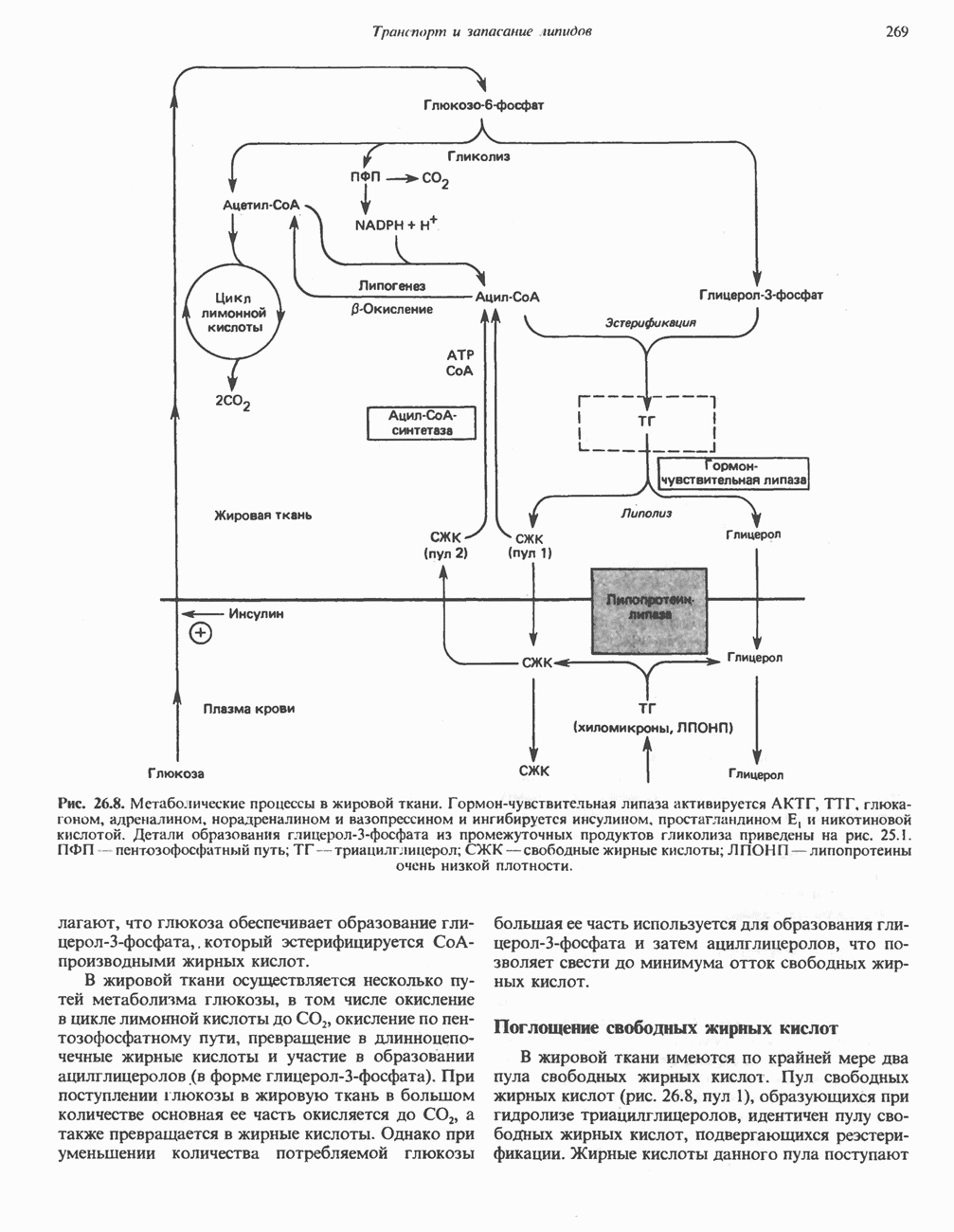
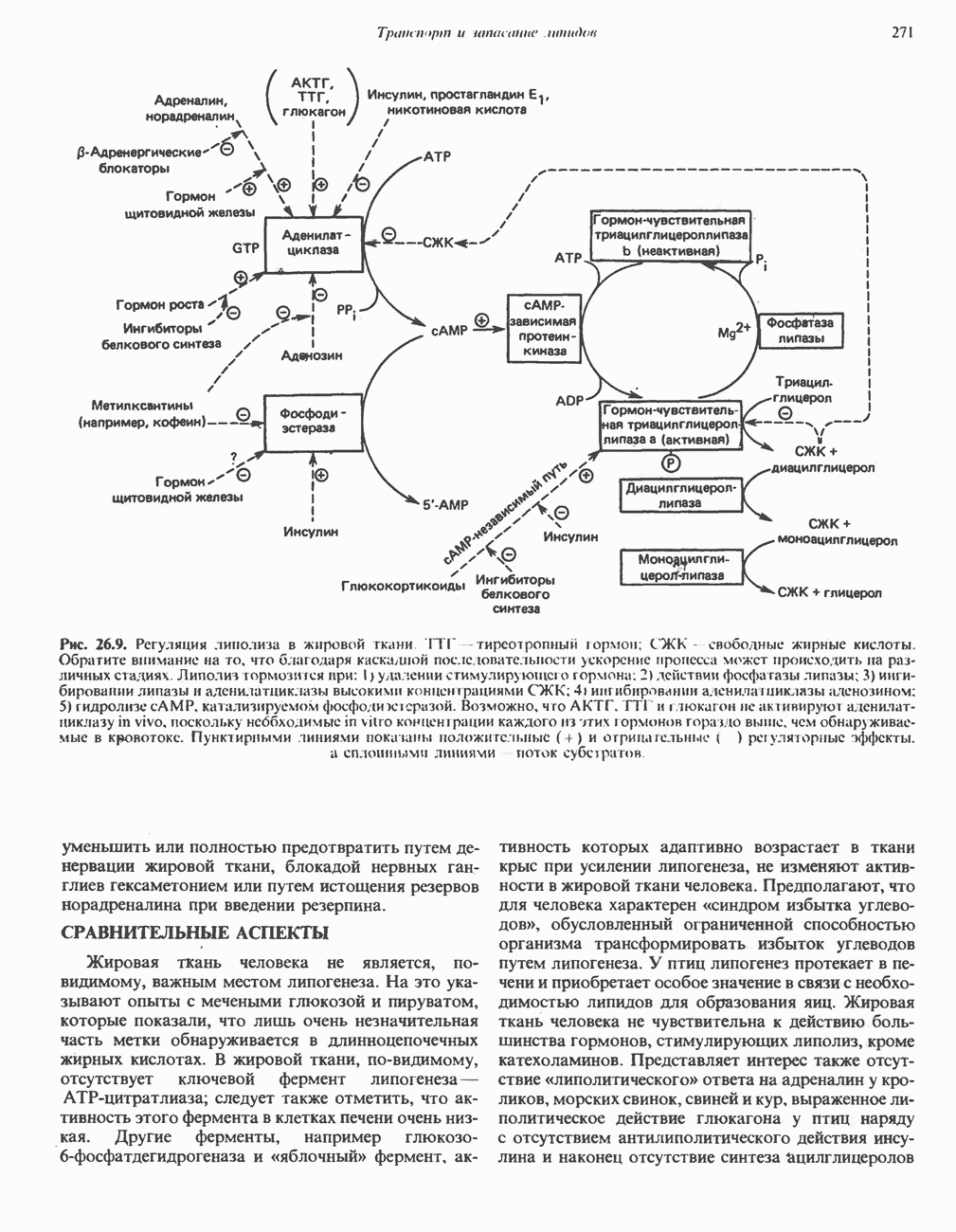
- МЕТАБОЛИЧЕСКИЕ ПРЕВРАЩЕНИЯ В ЖИРОВОЙ ТКАНИ И МОБИЛИЗАЦИЯ ЖИРОВ
- РОЛЬ ГОРМОНОВ В МОБИЛИЗАЦИИ ЖИРОВ
- СРАВНИТЕЛЬНЫЕ АСПЕКТЫ
- РОЛЬ БУРОЙ ЖИРОВОЙ ТКАНИ В ТЕРМОГЕНЕЗЕ
- Глава 27. Синтез, транспорт и экскреция холестерола
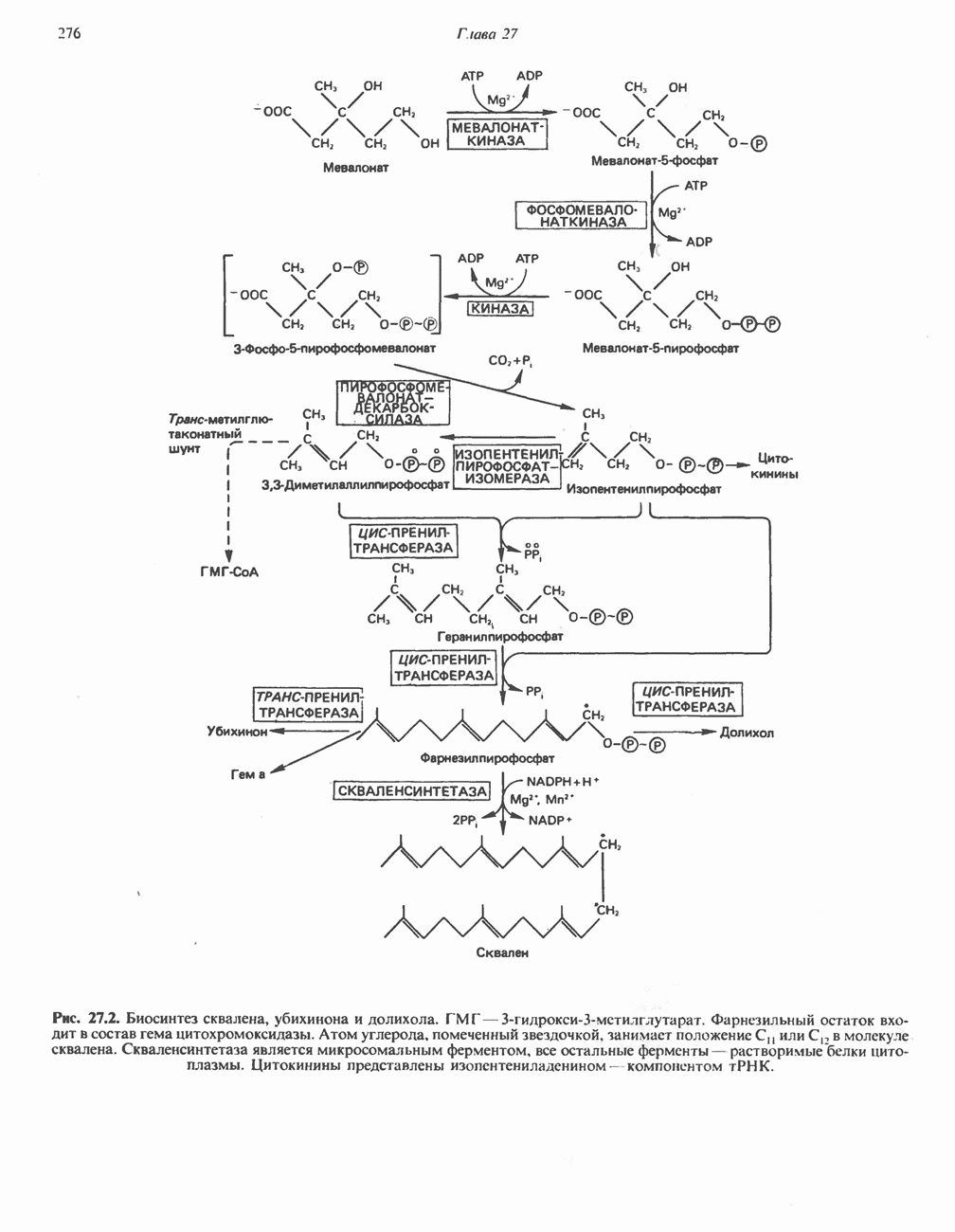
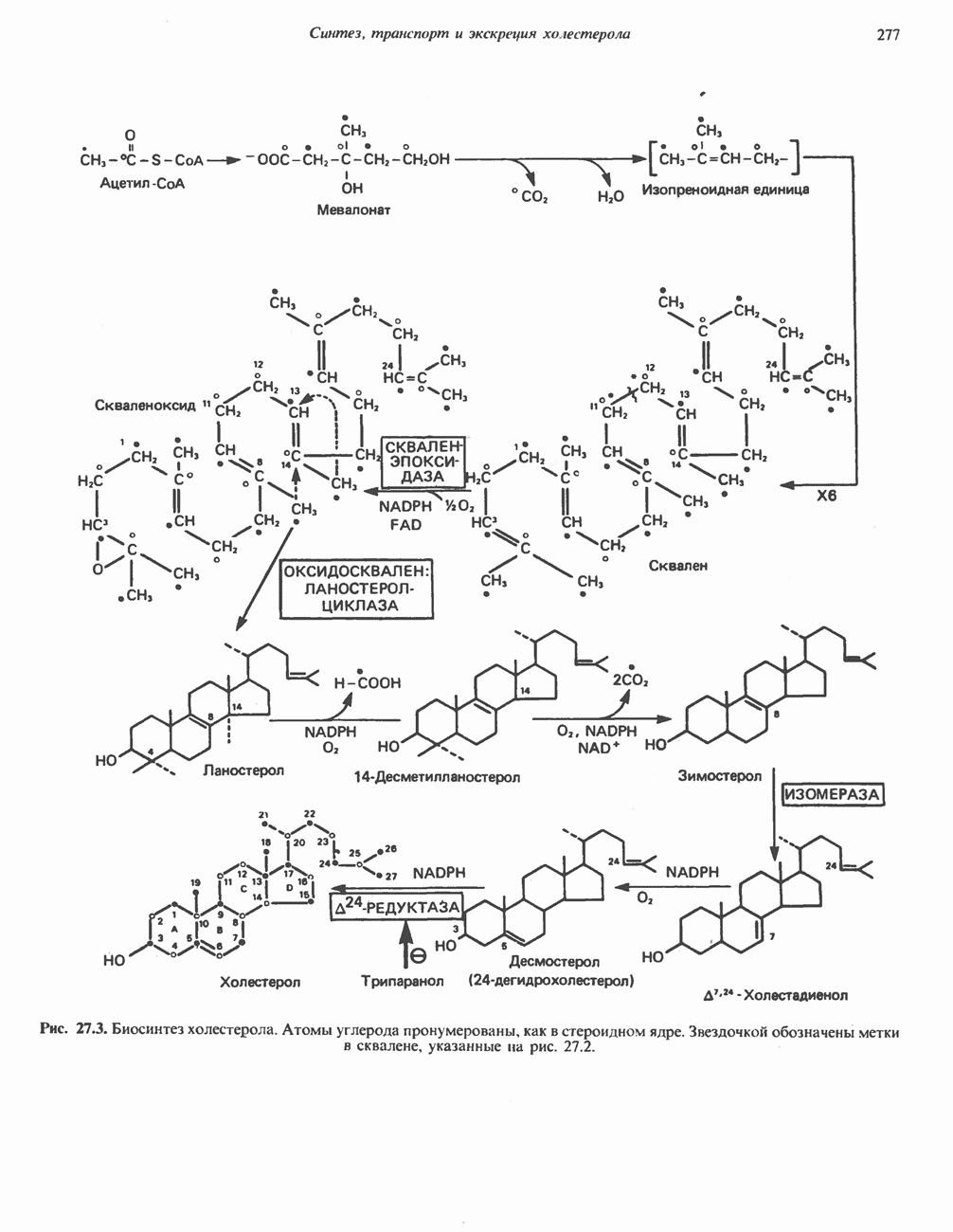
- БИОСИНТЕЗ ХОЛЕСТЕРОЛА
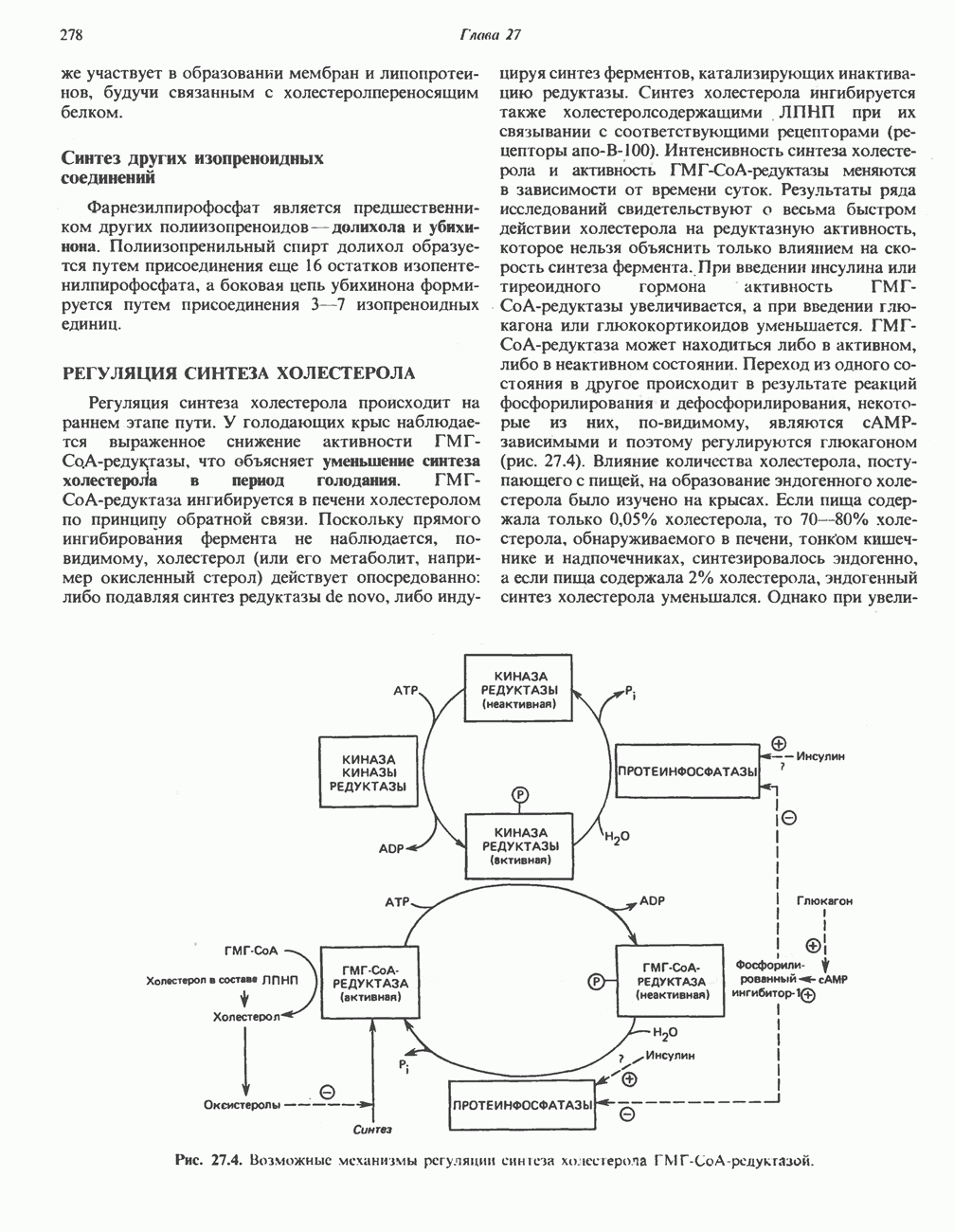
- РЕГУЛЯЦИЯ СИНТЕЗА ХОЛЕСТЕРОЛА
- ТРАНСПОРТ ХОЛЕСТЕРОЛА
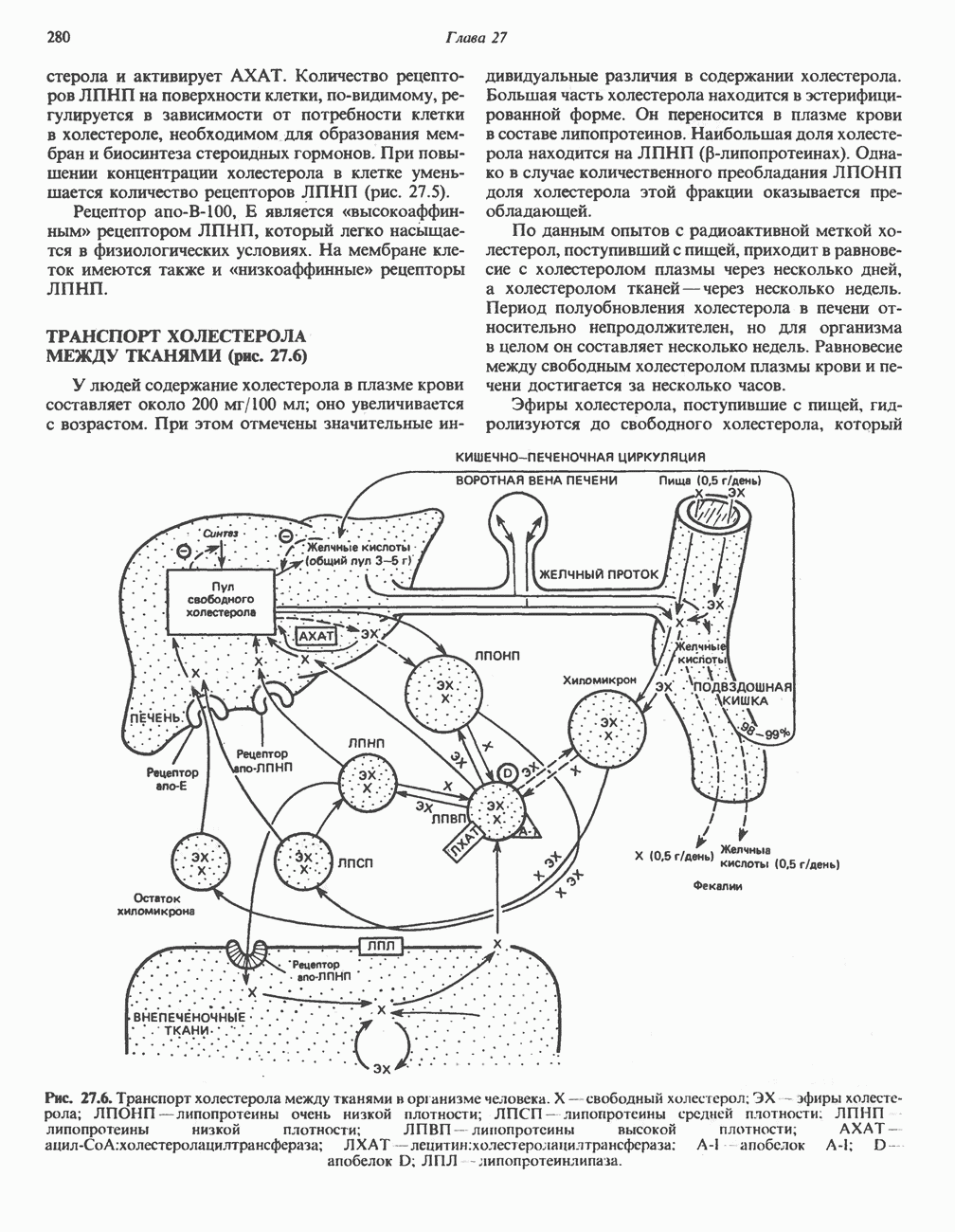
- ТРАНСПОРТ ХОЛЕСТЕРОЛА МЕЖДУ ТКАНЯМИ (рис. 27.6)
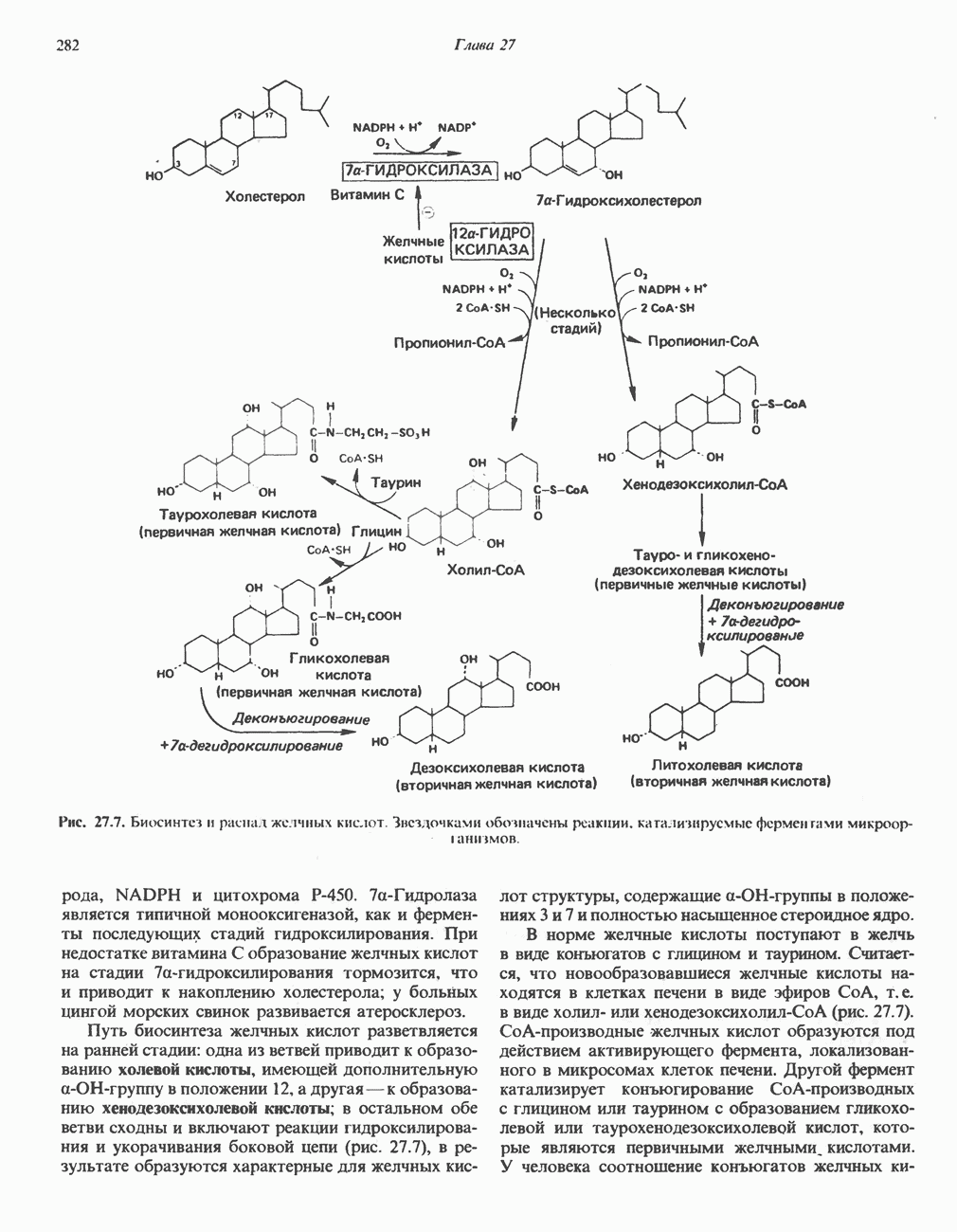
- ВЫВЕДЕНИЕ ХОЛЕСТЕРОЛА И ОБРАЗОВАНИЕ СОЛЕЙ ЖЕЛЧНЫХ КИСЛОТ
- КИШЕЧНО-ПЕЧЕНОЧНАЯ ЦИРКУЛЯЦИЯ ЖЕЛЧНЫХ КИСЛОТ
- КЛИНИЧЕСКИЕ АСПЕКТЫ
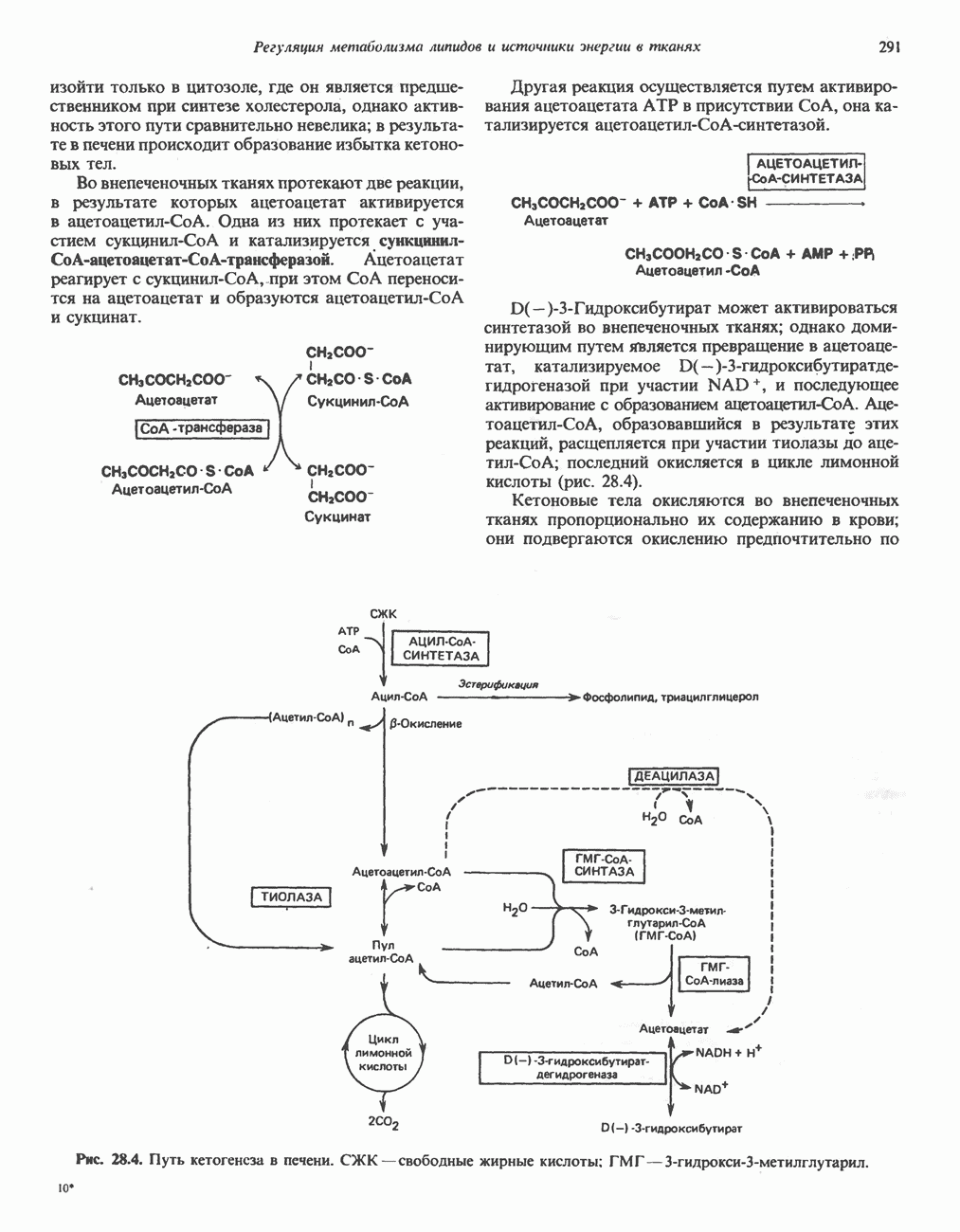
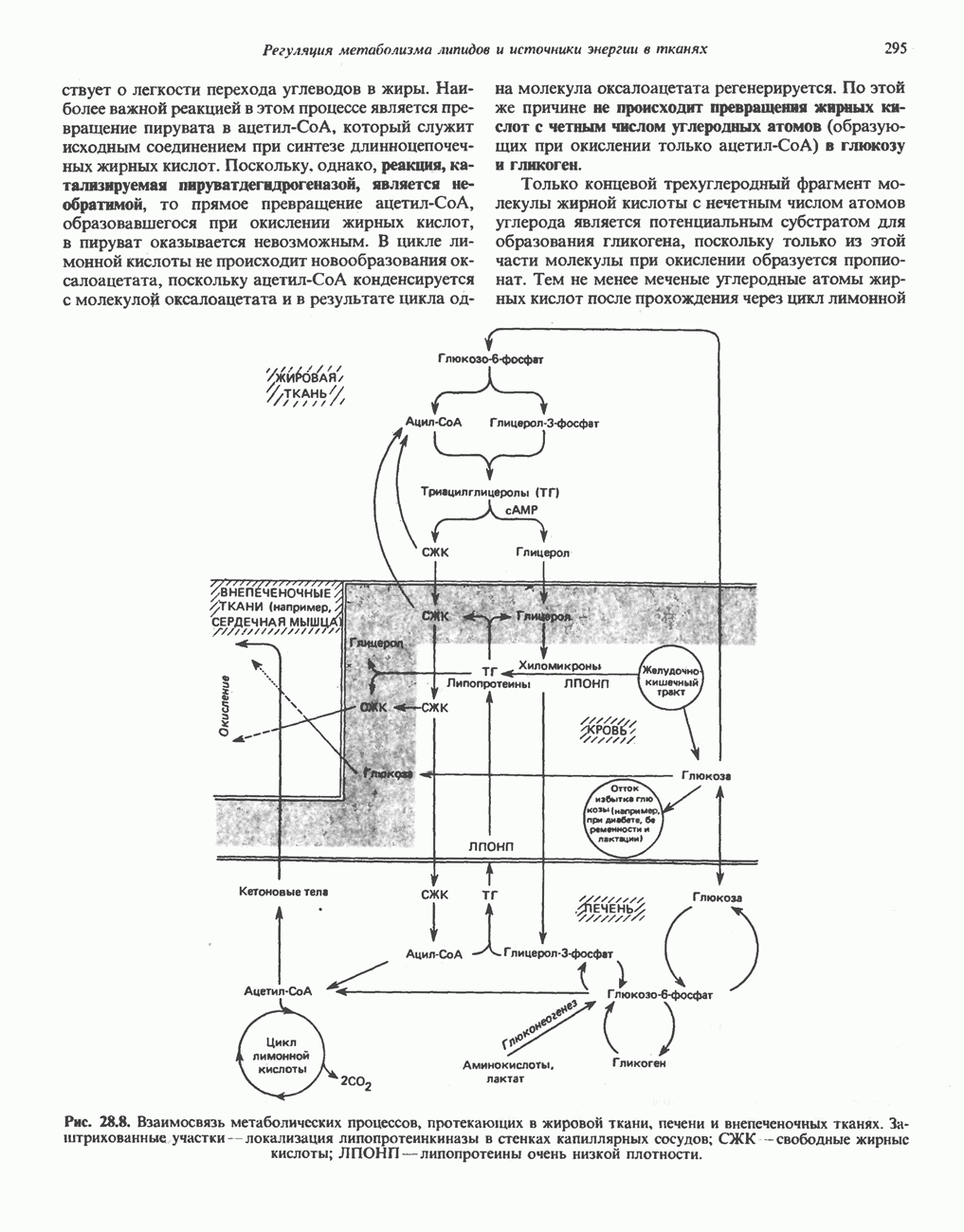
- Глава 28. Регуляция метаболизма липидов и источники энергии в тканях
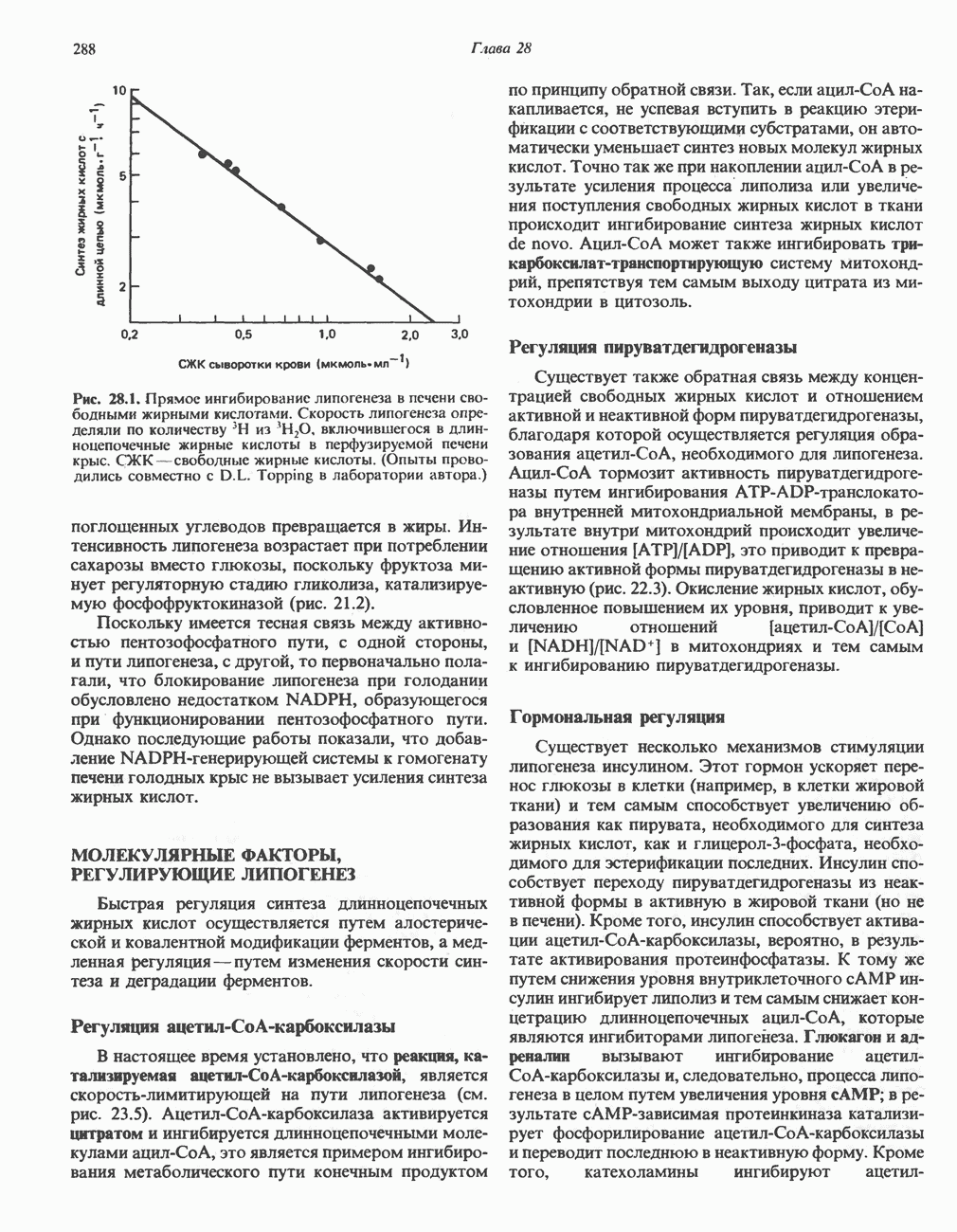
- РЕГУЛЯЦИЯ БИОСИНТЕЗА ЖИРНЫХ КИСЛОТ (ЛИПОГЕНЕЗА)
- МОЛЕКУЛЯРНЫЕ ФАКТОРЫ, РЕГУЛИРУЮЩИЕ ЛИПОГЕНЕЗ
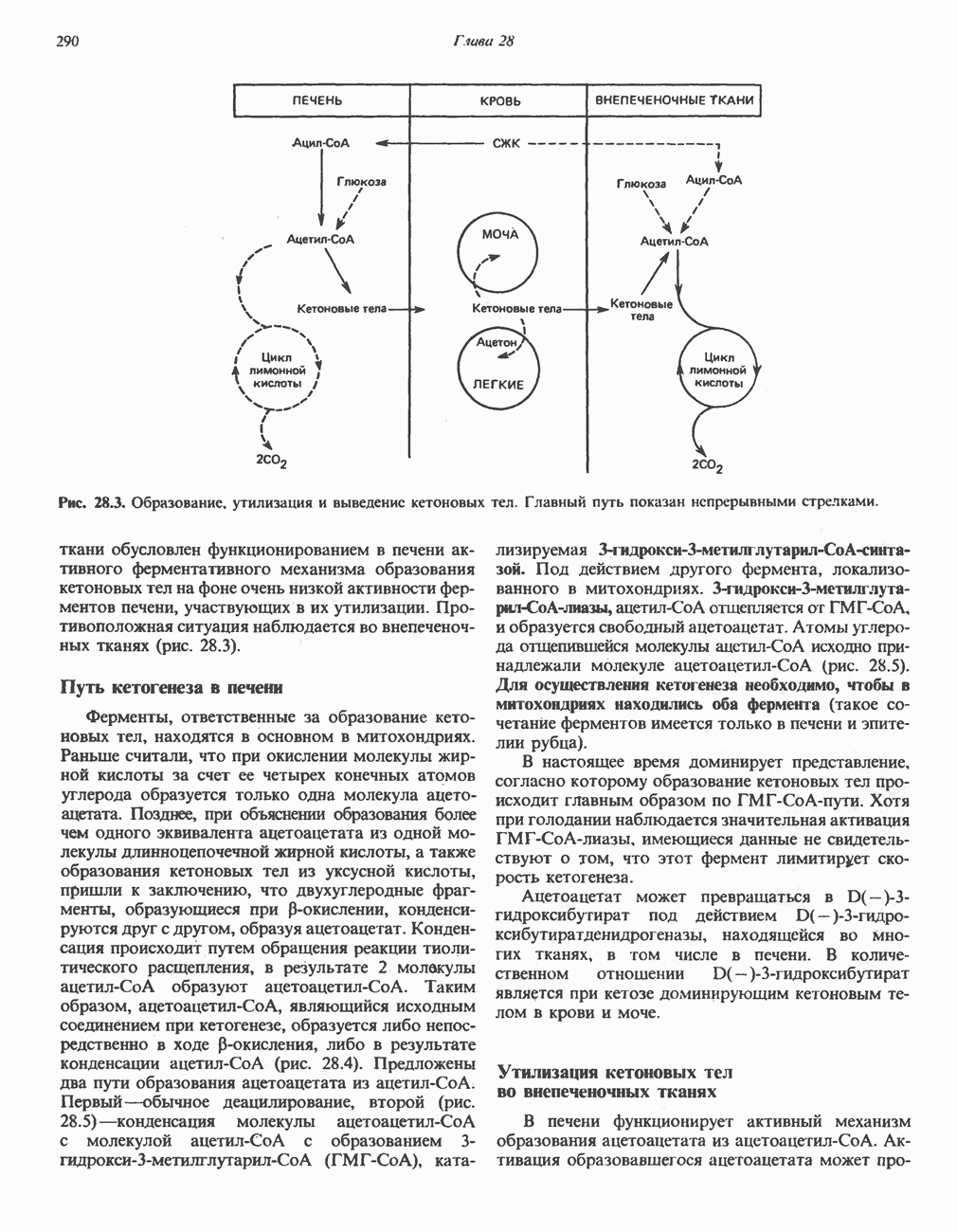
- РЕГУЛЯЦИЯ ОКИСЛЕНИЯ ЖИРНЫХ КИСЛОТ
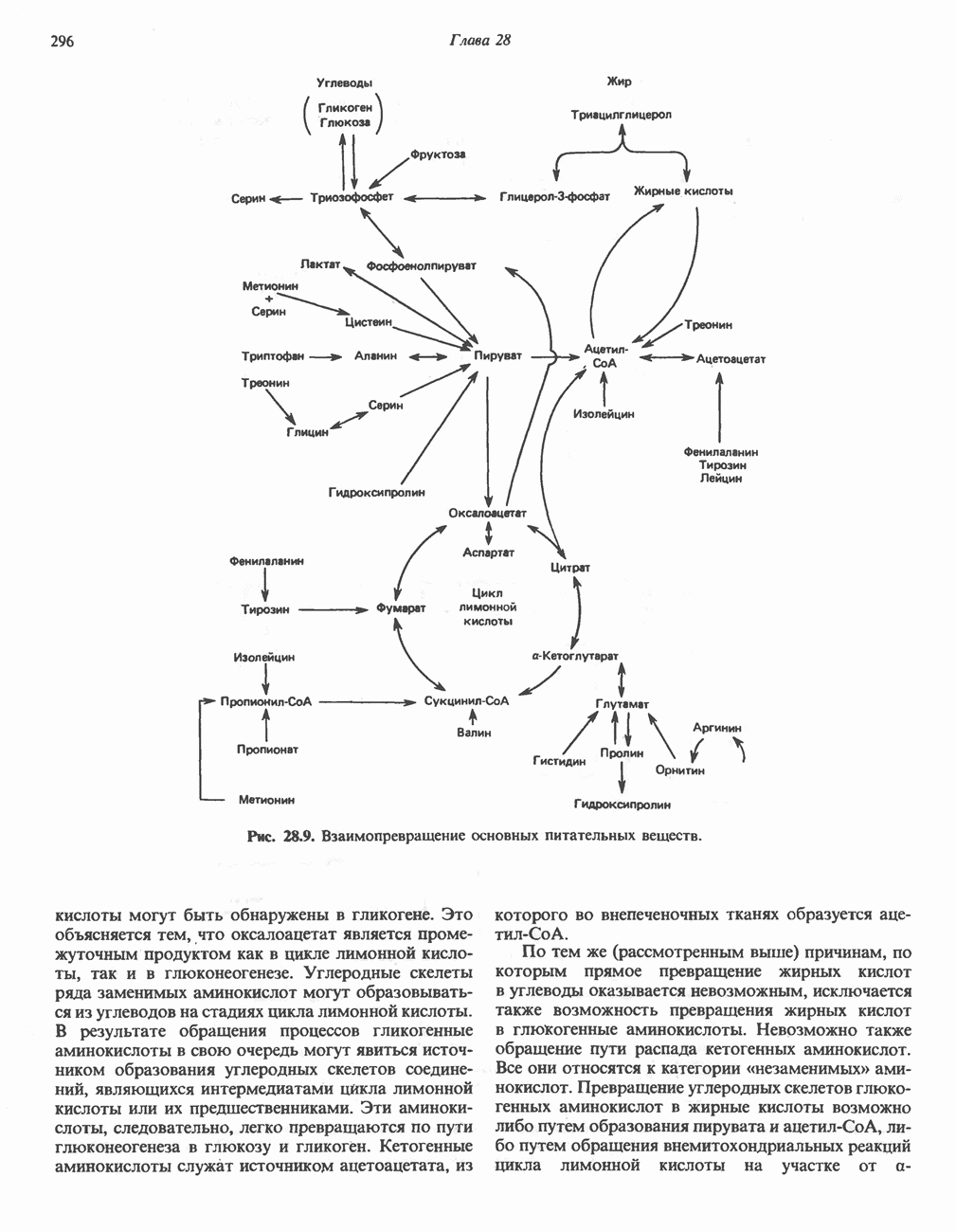
- ВЗАИМНОЕ ПРЕВРАЩЕНИЕ ОСНОВНЫХ ПИТАТЕЛЬНЫХ ВЕЩЕСТВ (рис. 28.9)
- ЭКОНОМИКА УГЛЕВОДНОГО И ЛИПИДНОГО ОБМЕНА В ОРГАНИЗМЕ
- ГОЛОДАНИЕ
- Раздел III. Метаболизм белков и аминокислот
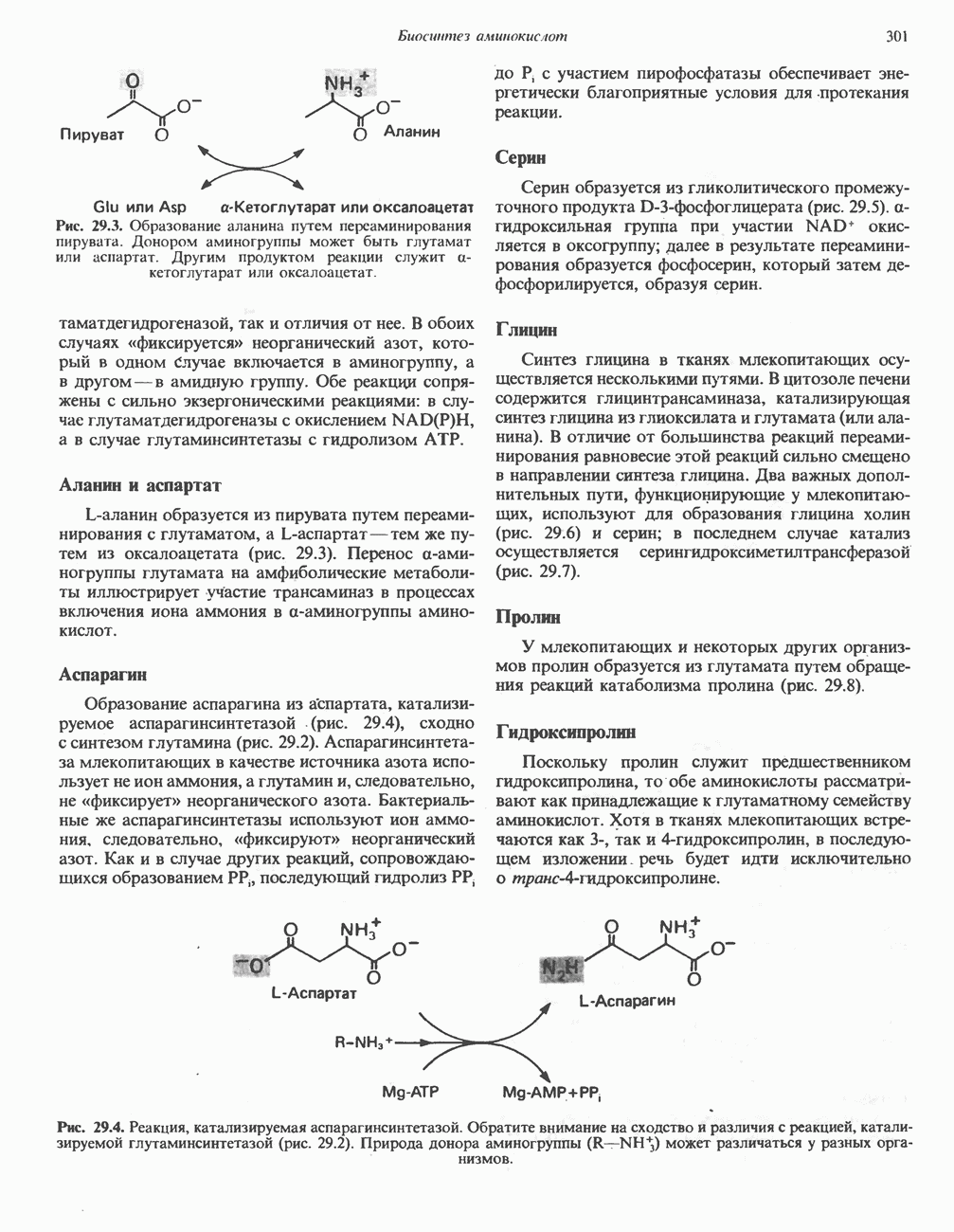
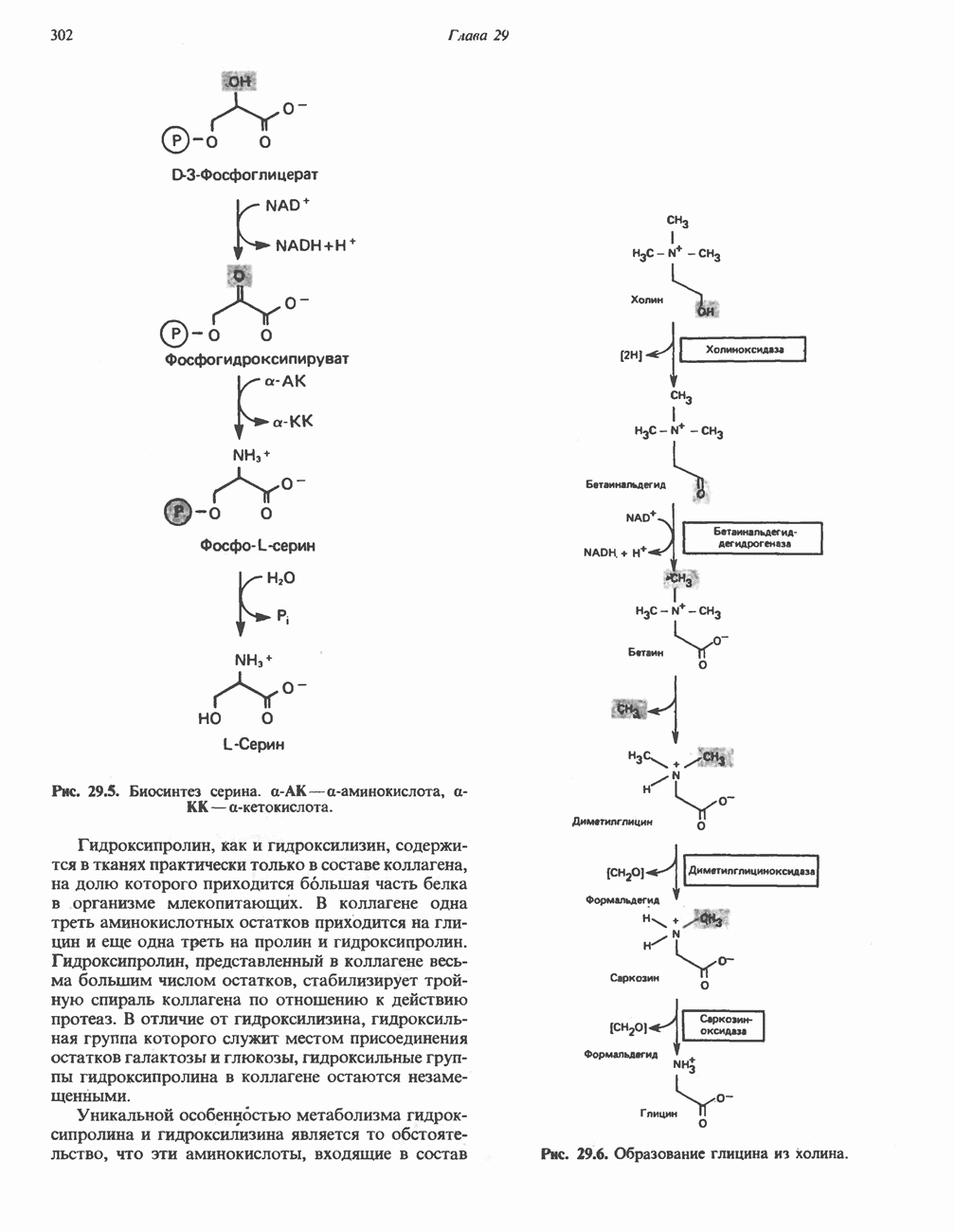
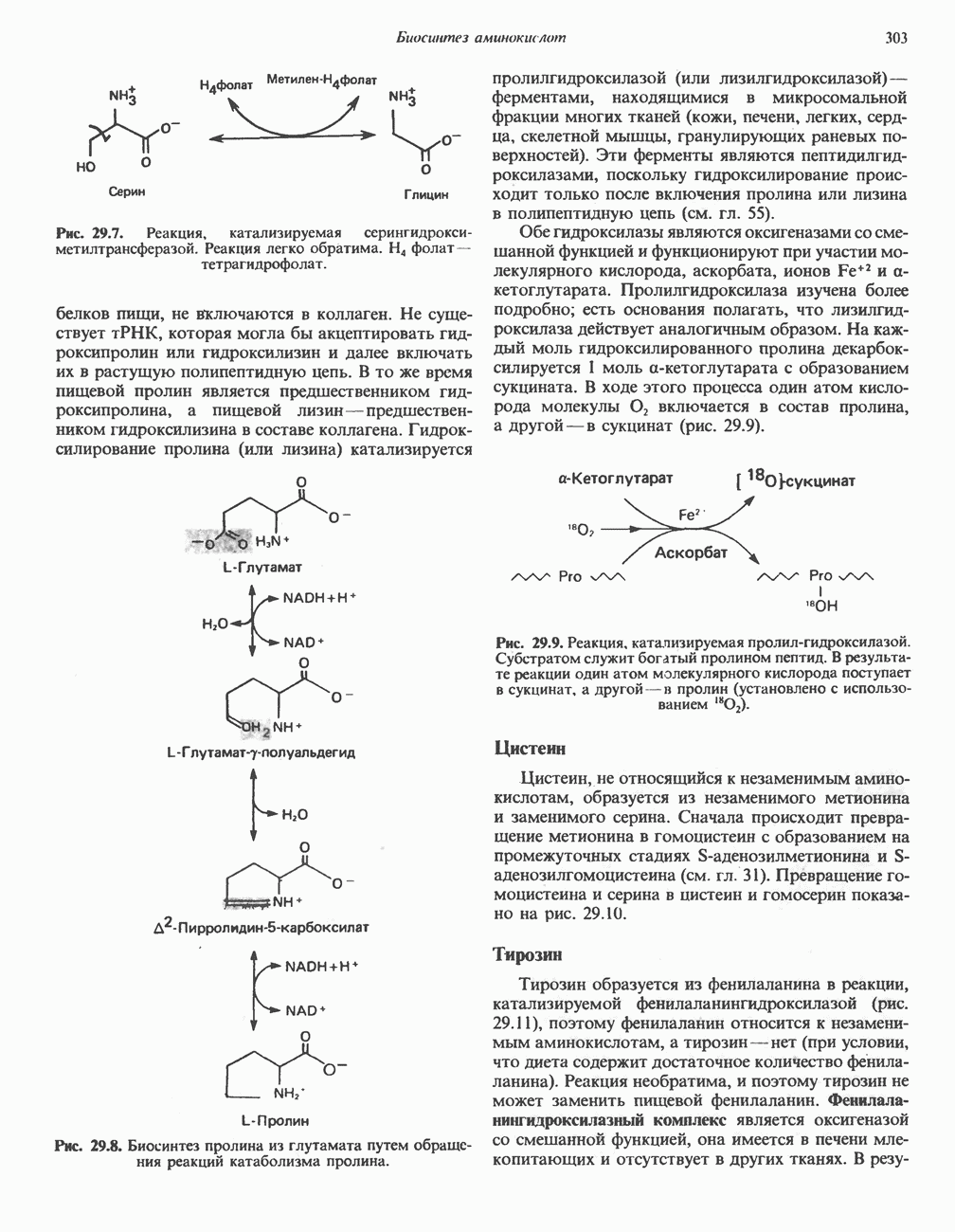
- Глава 29. Биосинтез аминокислот
- БИОСИНТЕЗ ЗАМЕНИМЫХ АМИНОКИСЛОТ
- БИОСИНТЕЗ НЕЗАМЕНИМЫХ АМИНОКИСЛОТ
- Глава 30. Катаболизм азота аминокислот
- ПЕРЕАМИНИРОВАНИЕ
- ОКИСЛИТЕЛЬНОЕ ДЕЗАМИНИРОВАНИЕ
- ОБРАЗОВАНИЕ АММИАКА
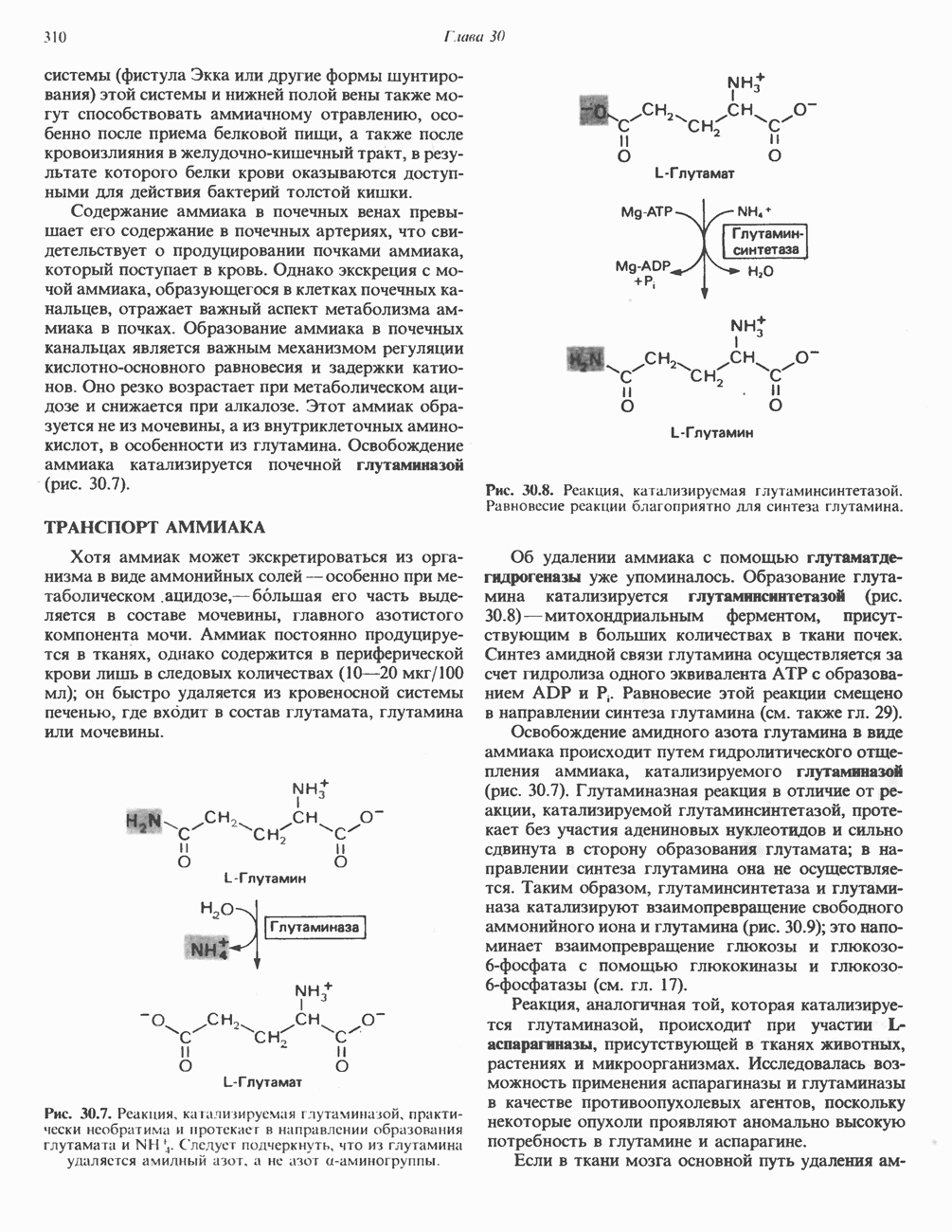
- ТРАНСПОРТ АММИАКА
- ОБМЕН АМИНОКИСЛОТАМИ МЕЖДУ ОРГАНАМИ В ПОСТАБСОРБТИВНОМ СОСТОЯНИИ
- ОБМЕН АМИНОКИСЛОТ МЕЖДУ ОРГАНАМИ ПОСЛЕ ПРИЕМА ПИЩИ
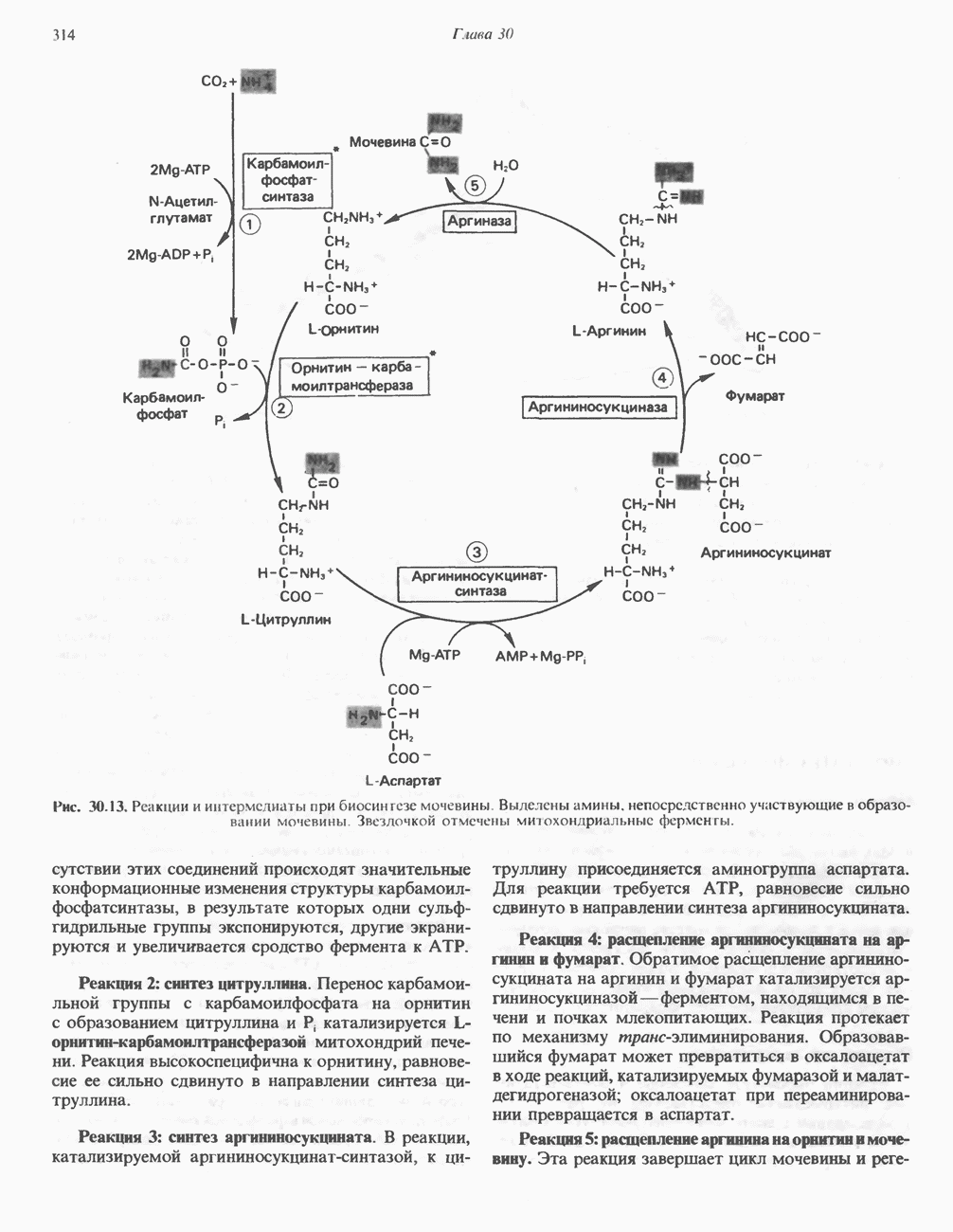
- БИОСИНТЕЗ МОЧЕВИНЫ
- РЕГУЛЯЦИЯ СИНТЕЗА МОЧЕВИНЫ
- МЕТАБОЛИЧЕСКИЕ НАРУШЕНИЯ ЦИКЛА МОЧЕВИНЫ
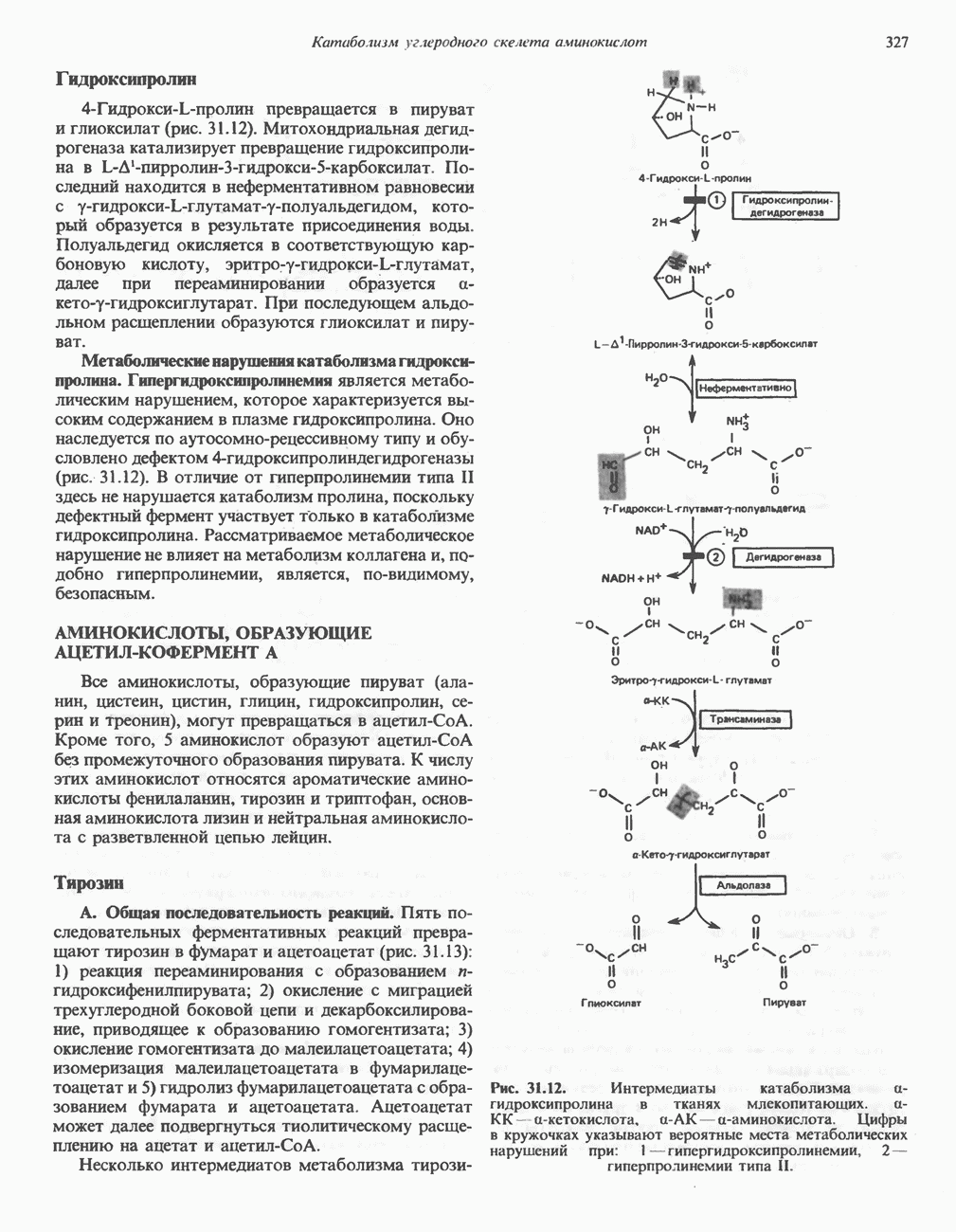
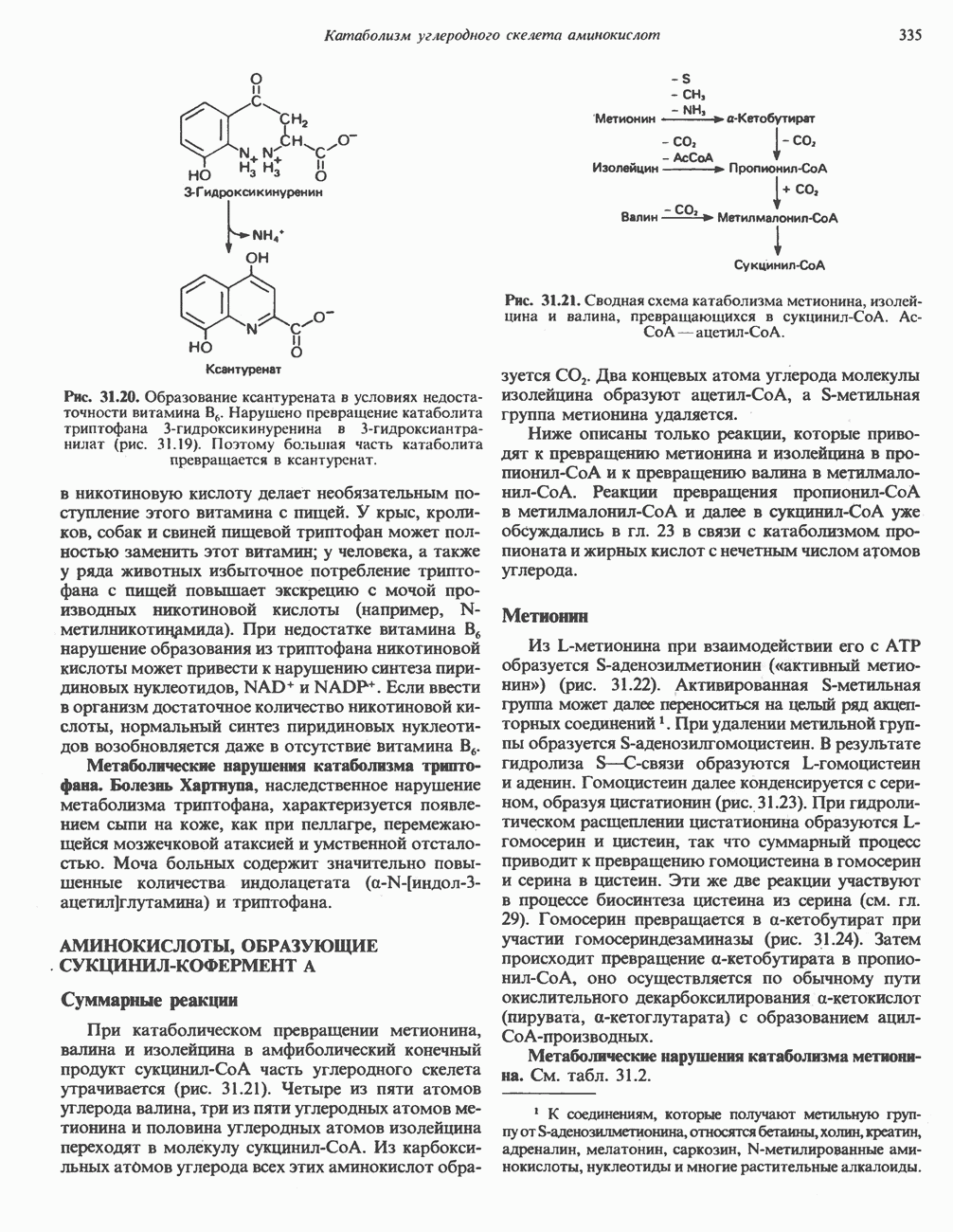
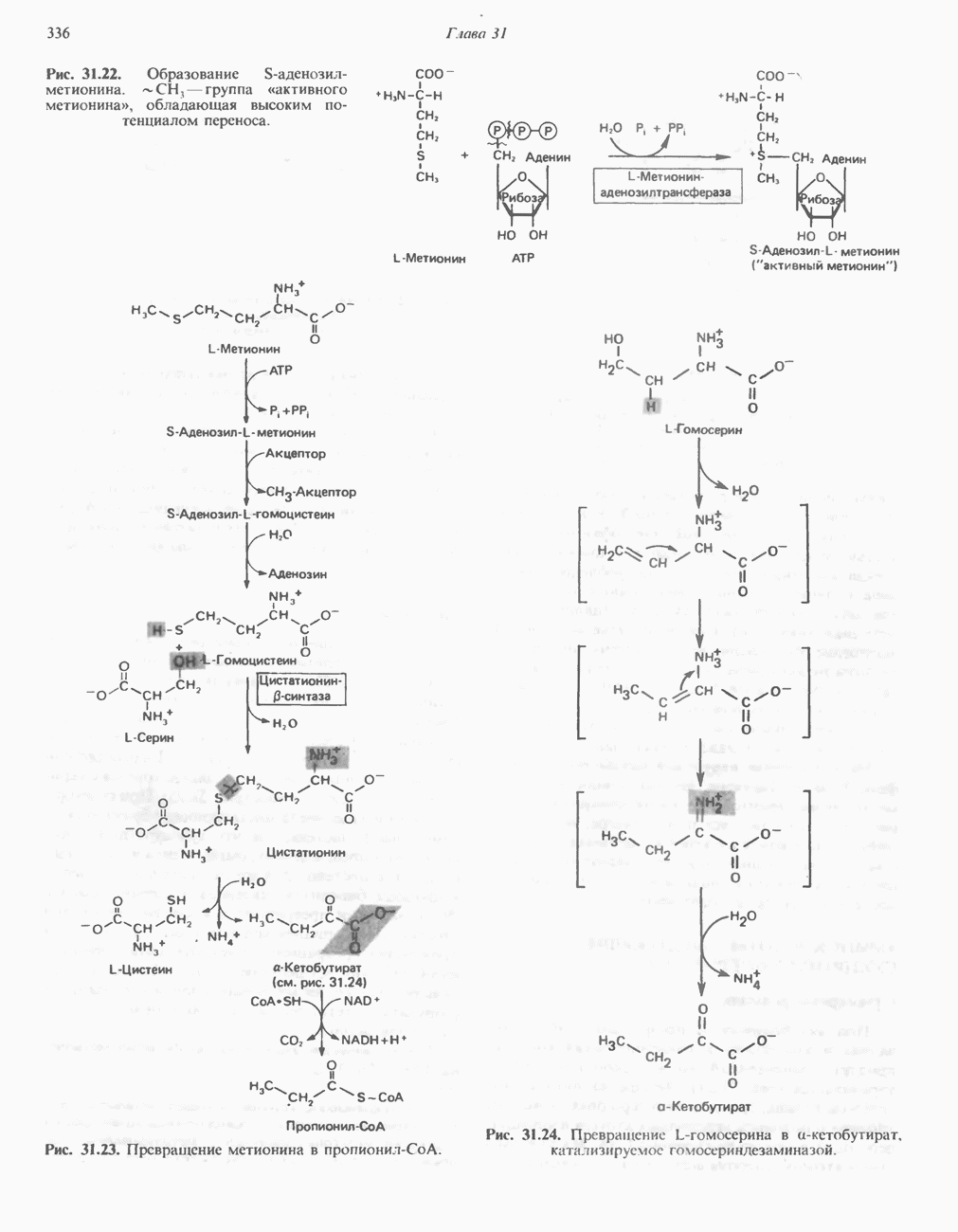
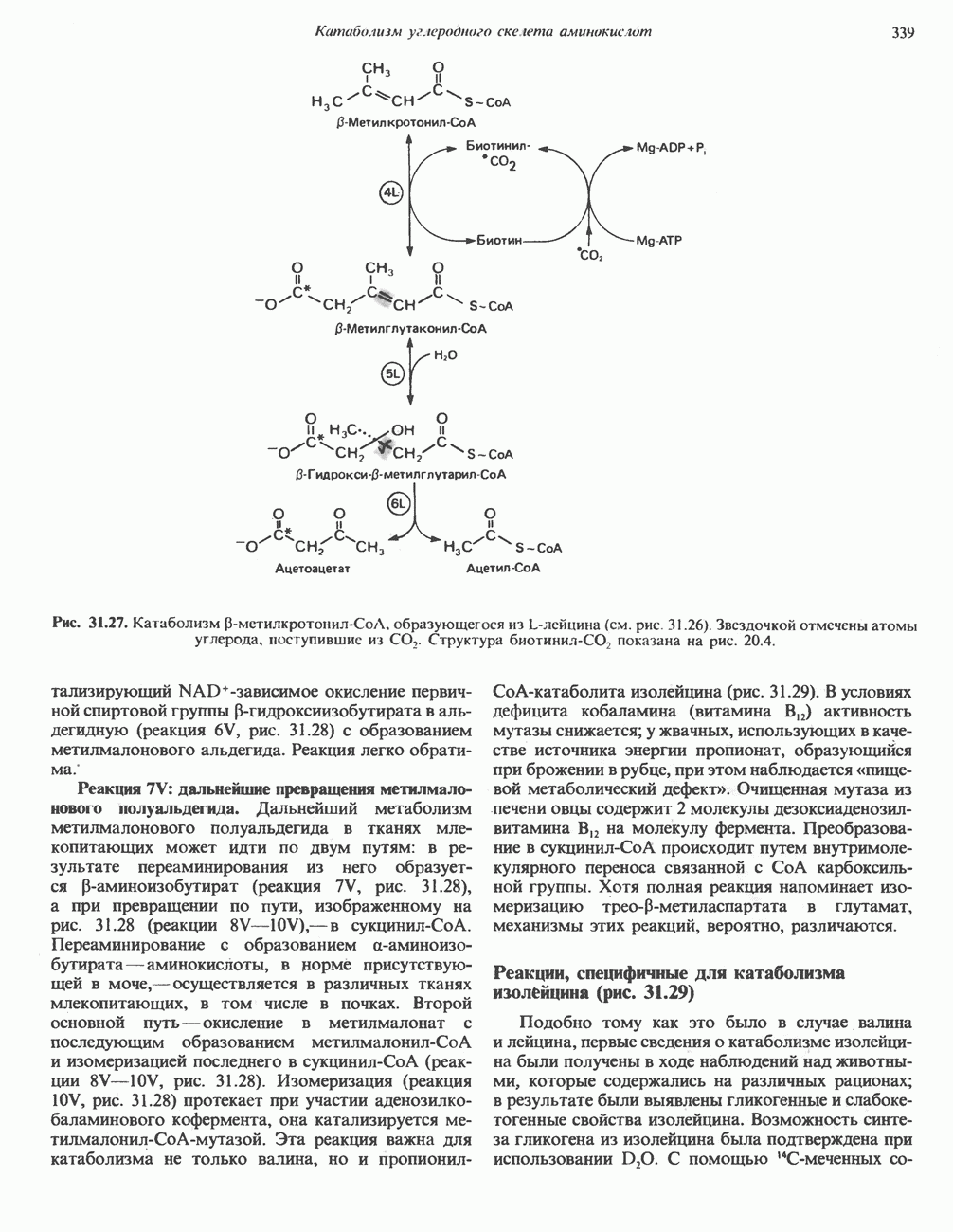
- Глава 31. Катаболизм углеродного скелета аминокислот
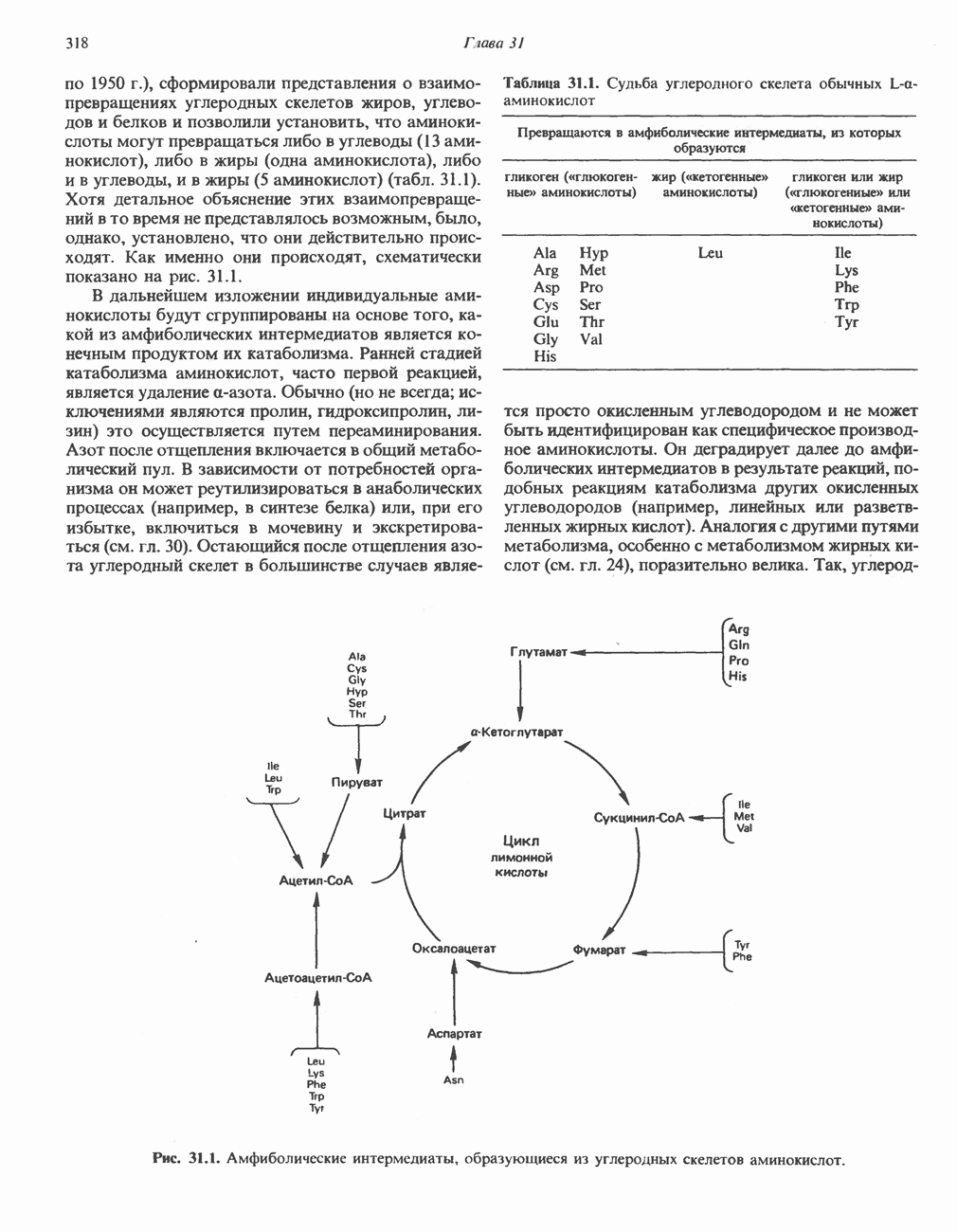
- ПРЕВРАЩЕНИЕ УГЛЕРОДНОГО СКЕЛЕТА ОБЫЧНЫХ L-a-АМИНОКИСЛОТ В АМФИБОЛИЧЕСКИЕ ИНТЕРМЕДИАТЫ
- АМИНОКИСЛОТЫ, ОБРАЗУЮЩИЕ ОКСАЛОАЦЕТАТ
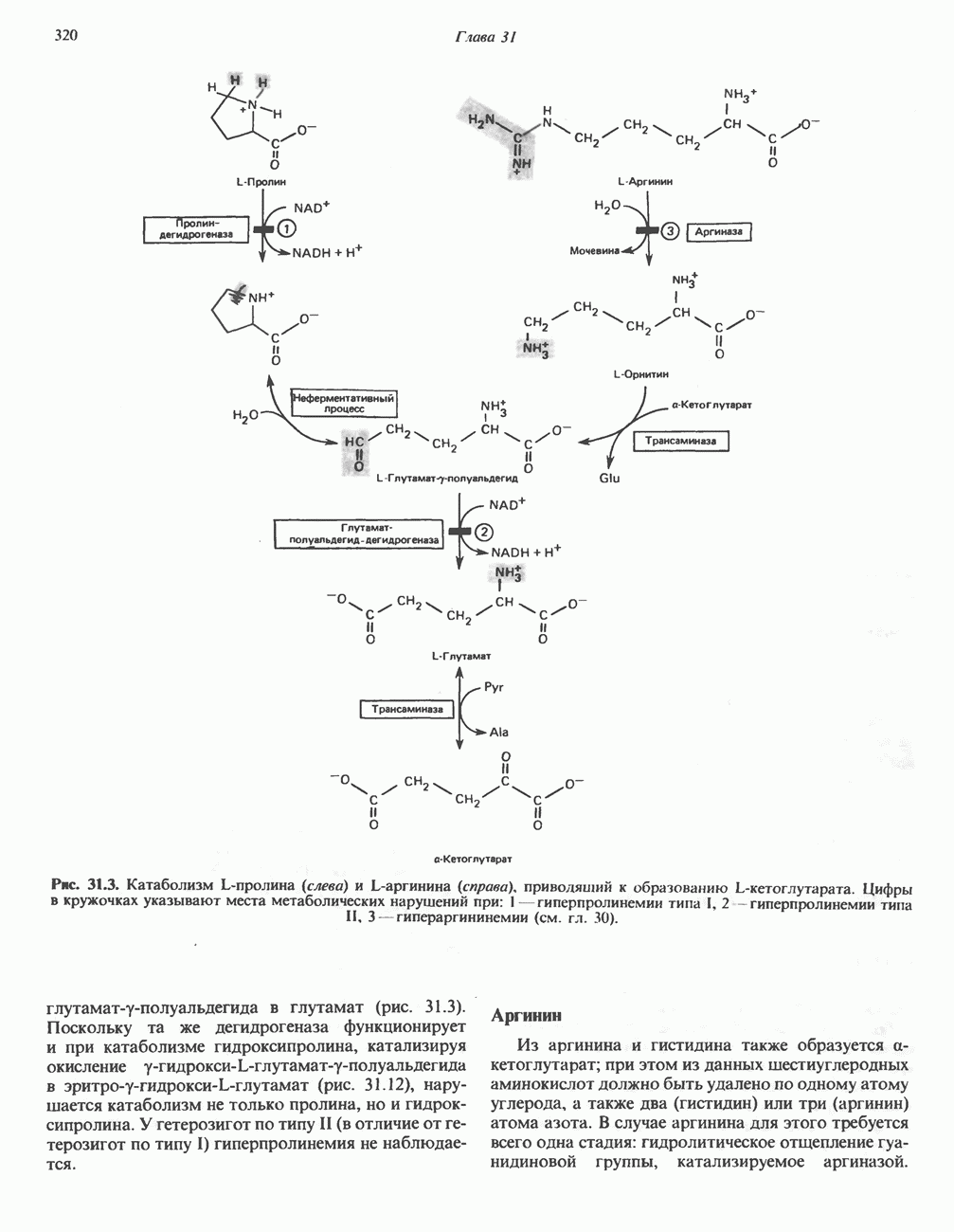
- АМИНОКИСЛОТЫ, ОБРАЗУЮЩИЕ а-КЕТОГЛУТАРАТ
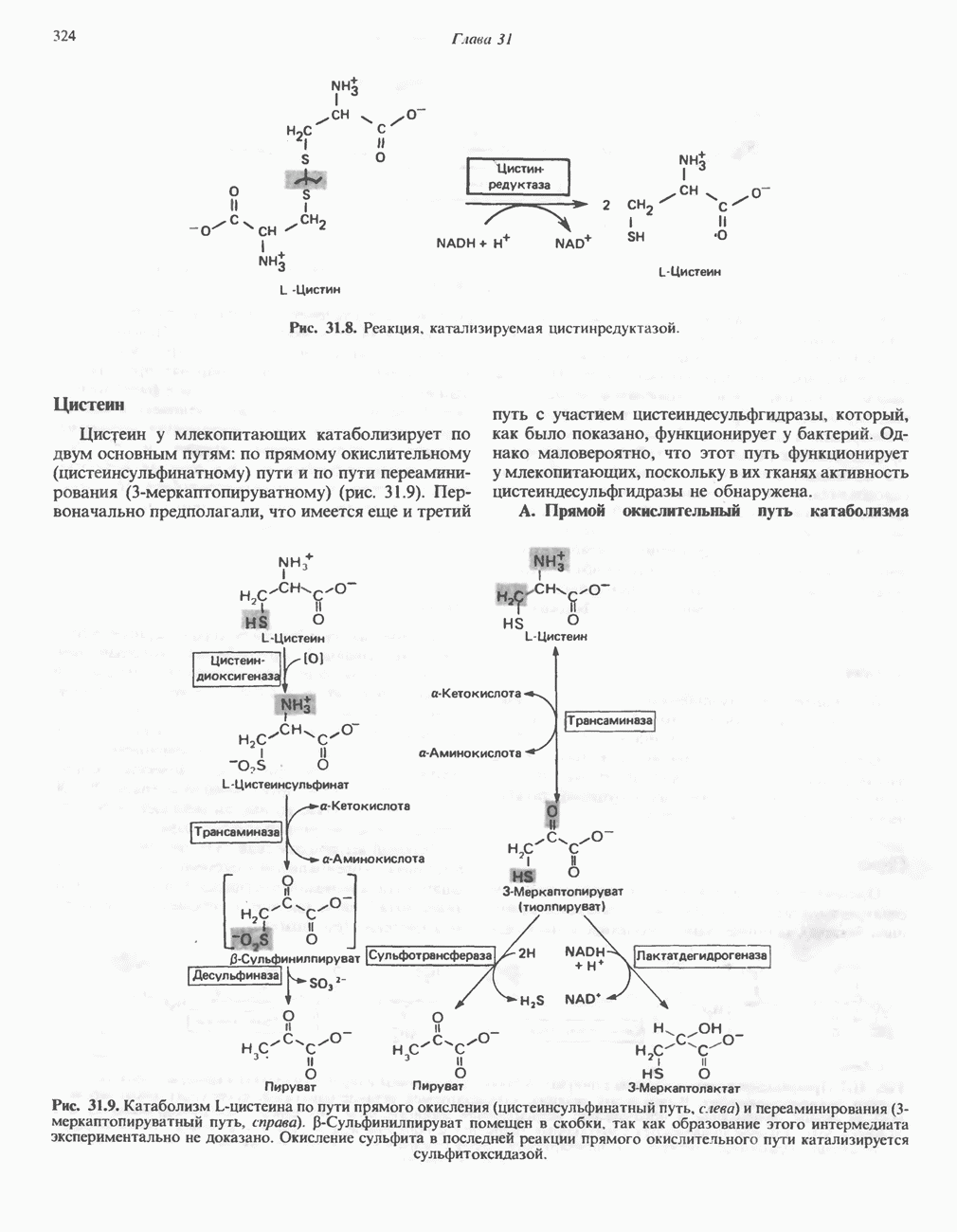
- АМИНОКИСЛОТЫ, ОБРАЗУЮЩИЕ ПИРУВАТ
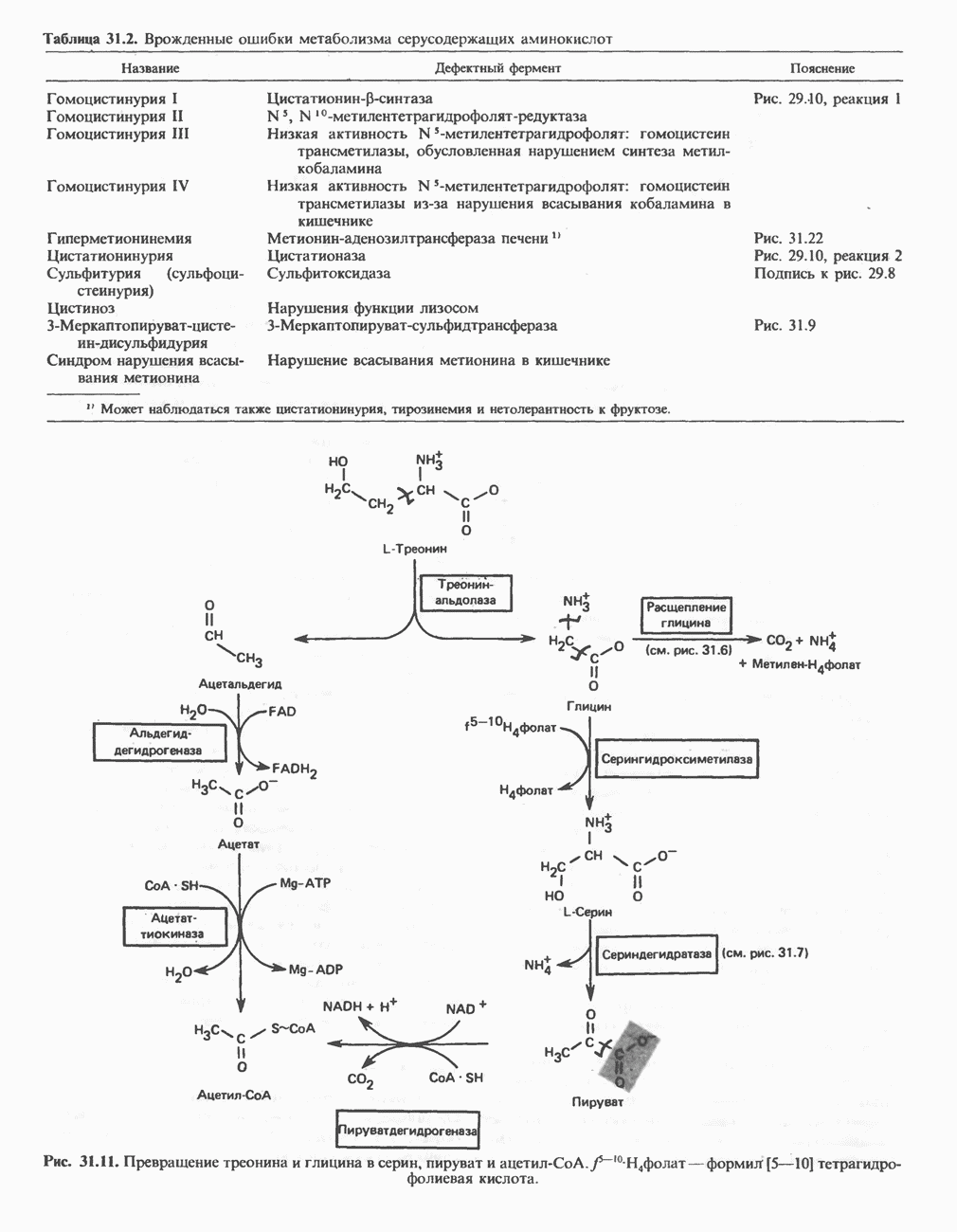
- АМИНОКИСЛОТЫ, ОБРАЗУЮЩИЕ АЦЕТИЛ-КОФЕРМЕНТ А
- АМИНОКИСЛОТЫ, ОБРАЗУЮЩИЕ СУКЦИНИЛ-КОФЕРМЕНТ А
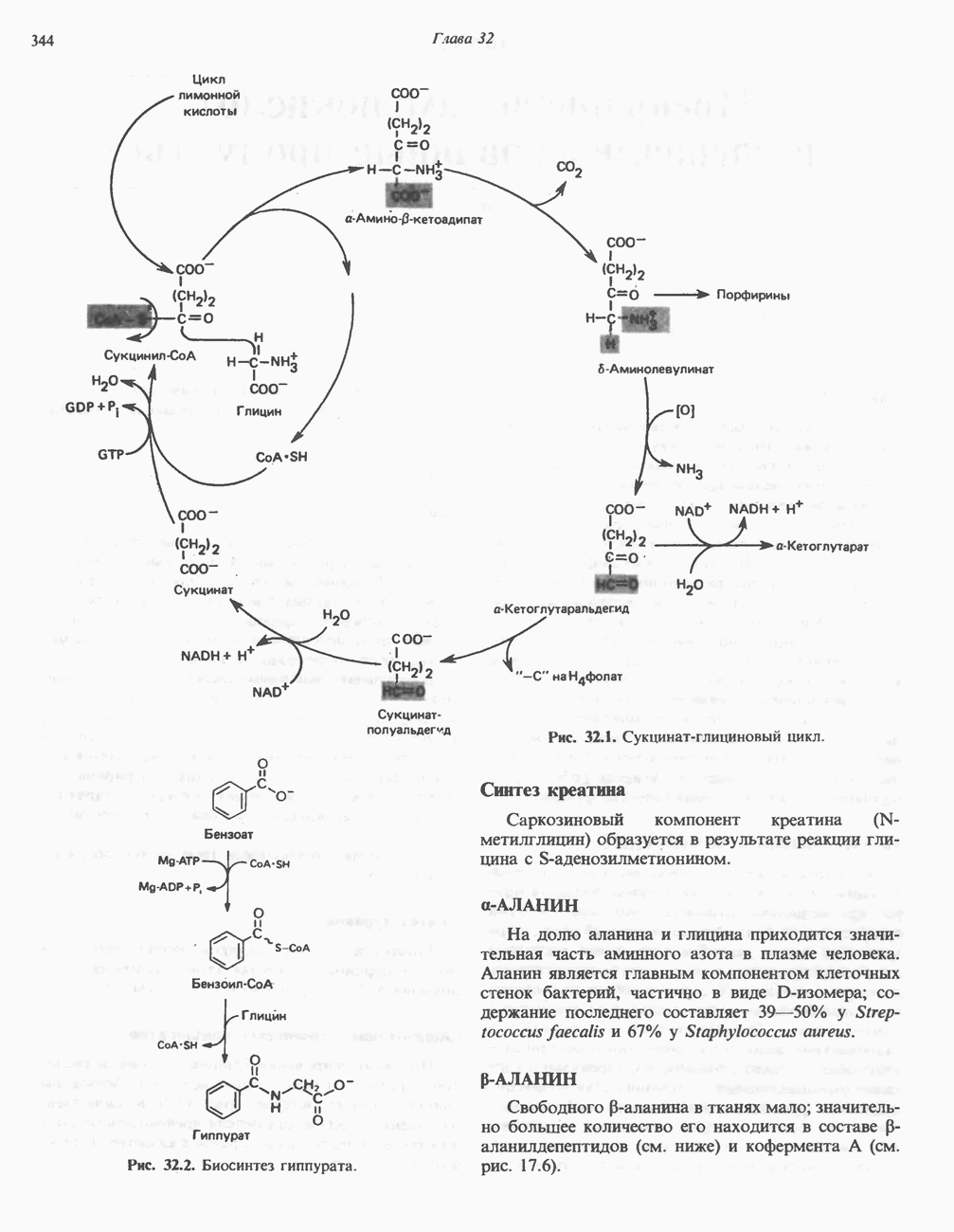
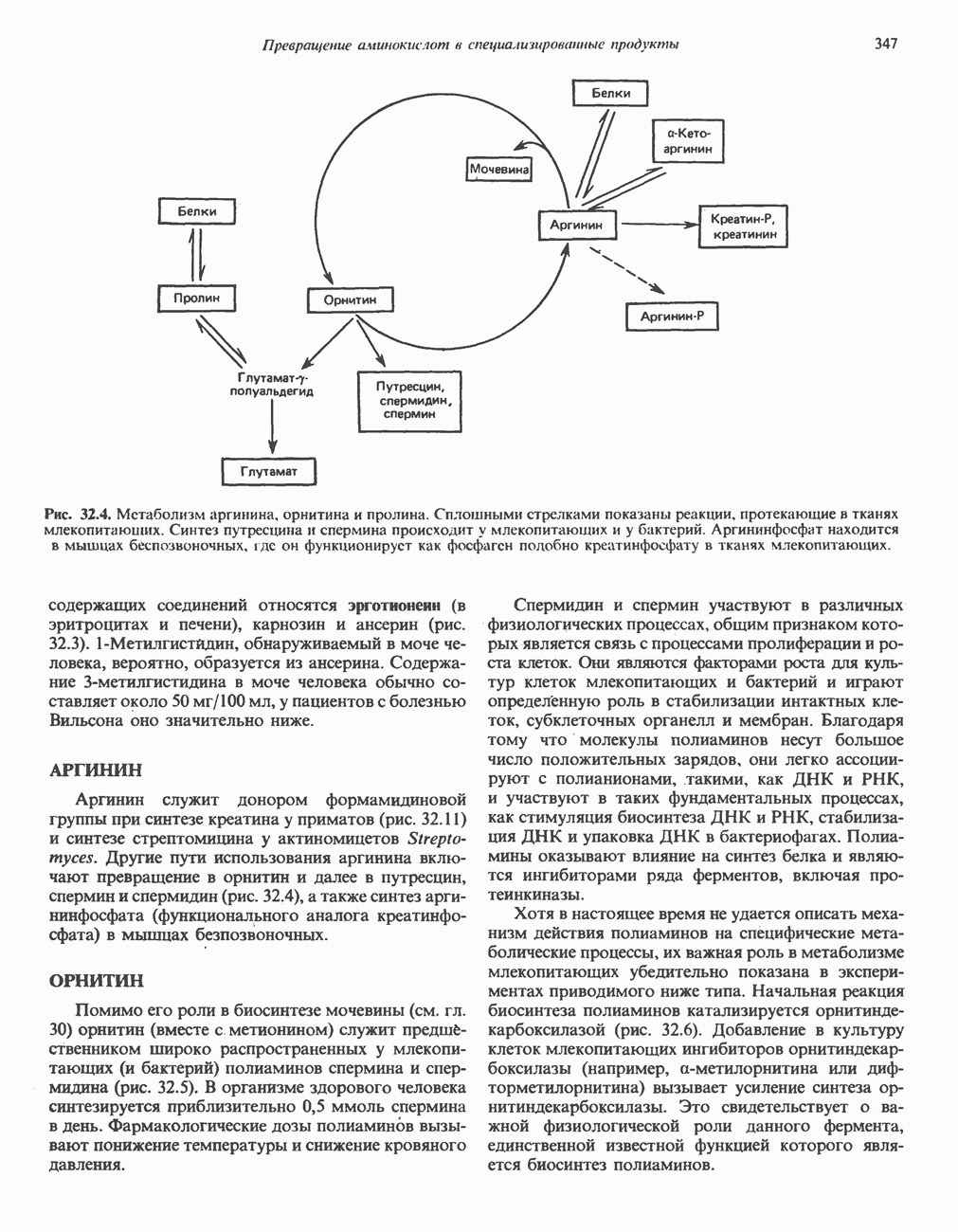
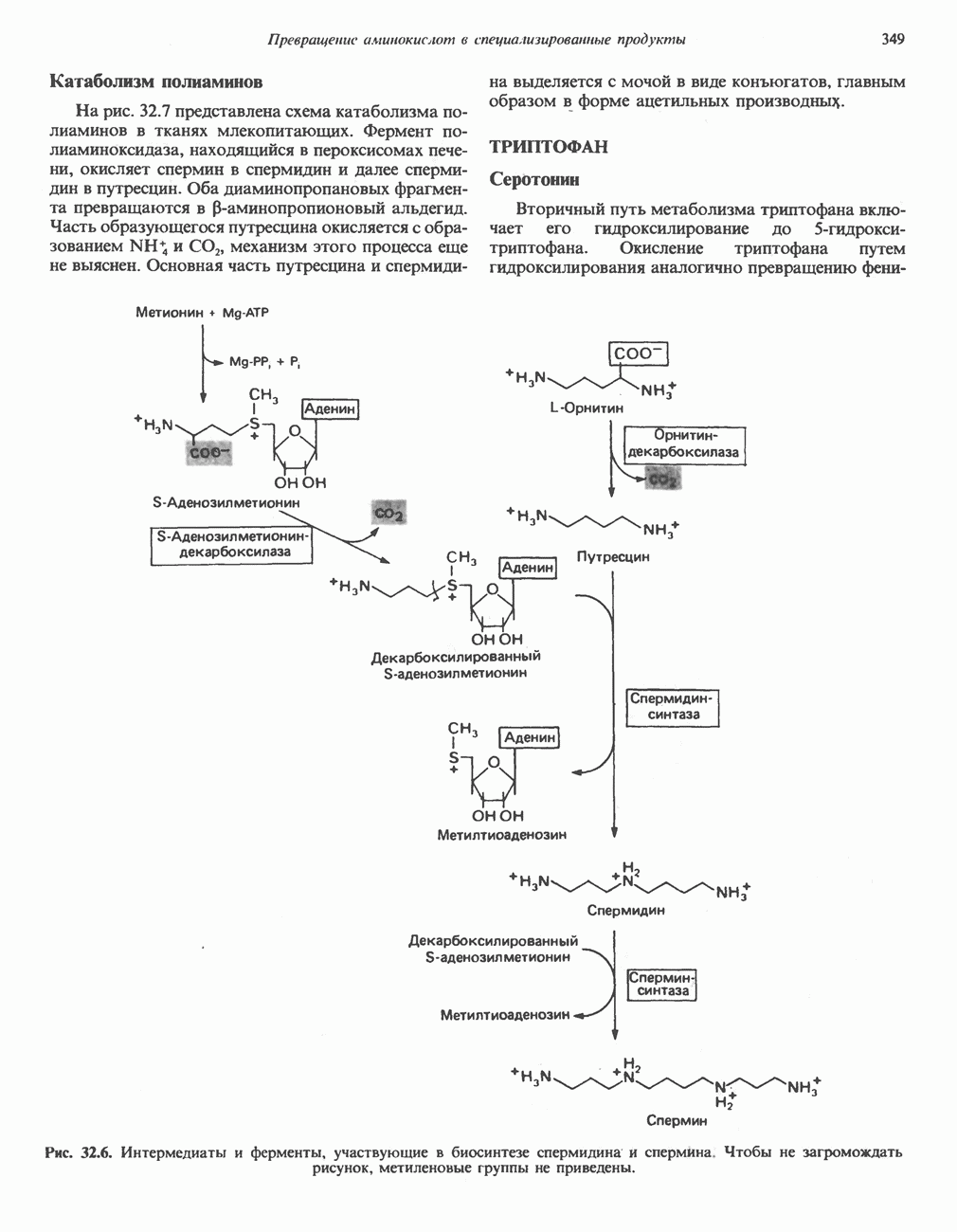
- Глава 32. Превращение аминокислот в специализированные продукты
- ГЛИЦИН
- р-АЛАНИНОВЫЕ ДИПЕПТИДЫ
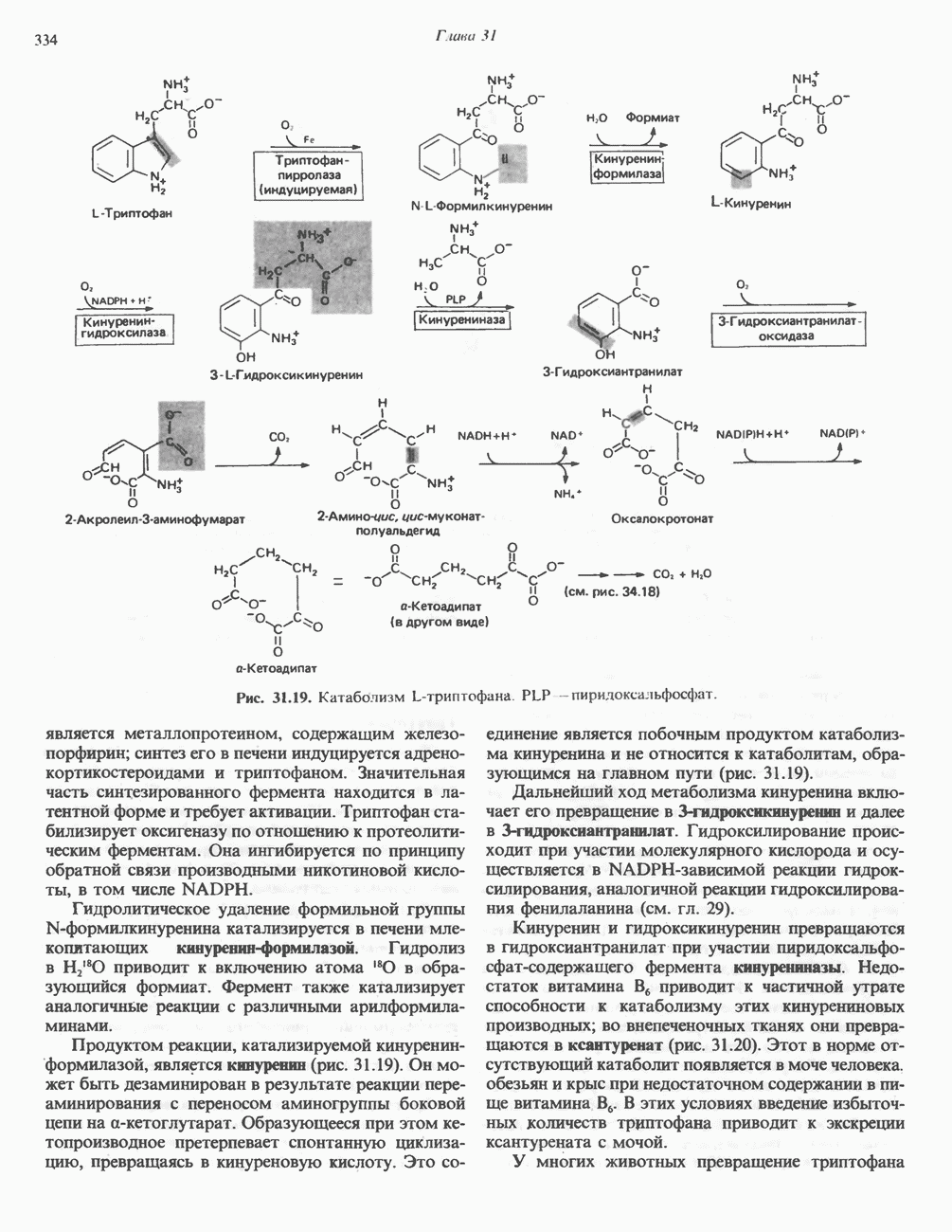
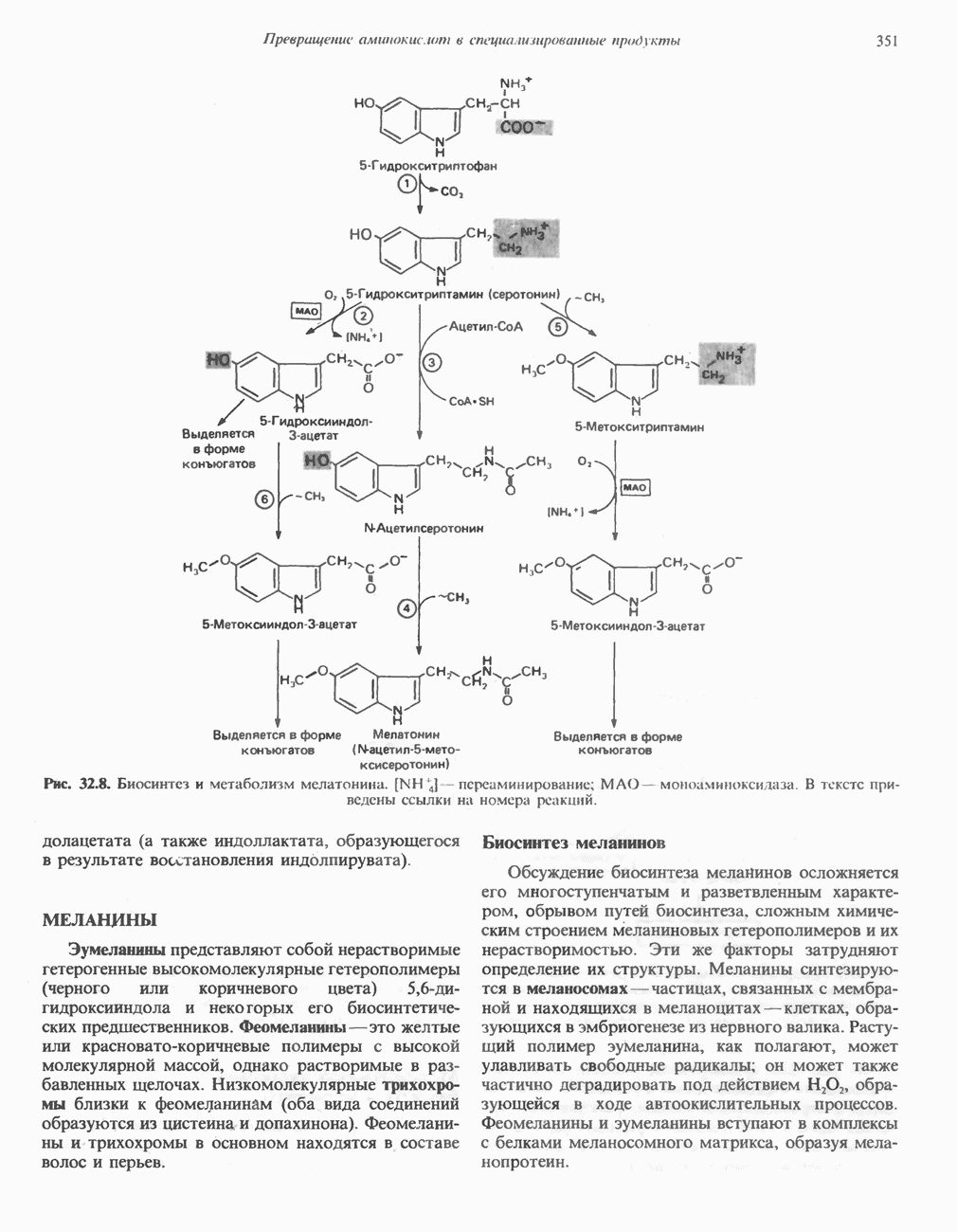
- ТРИПТОФАН
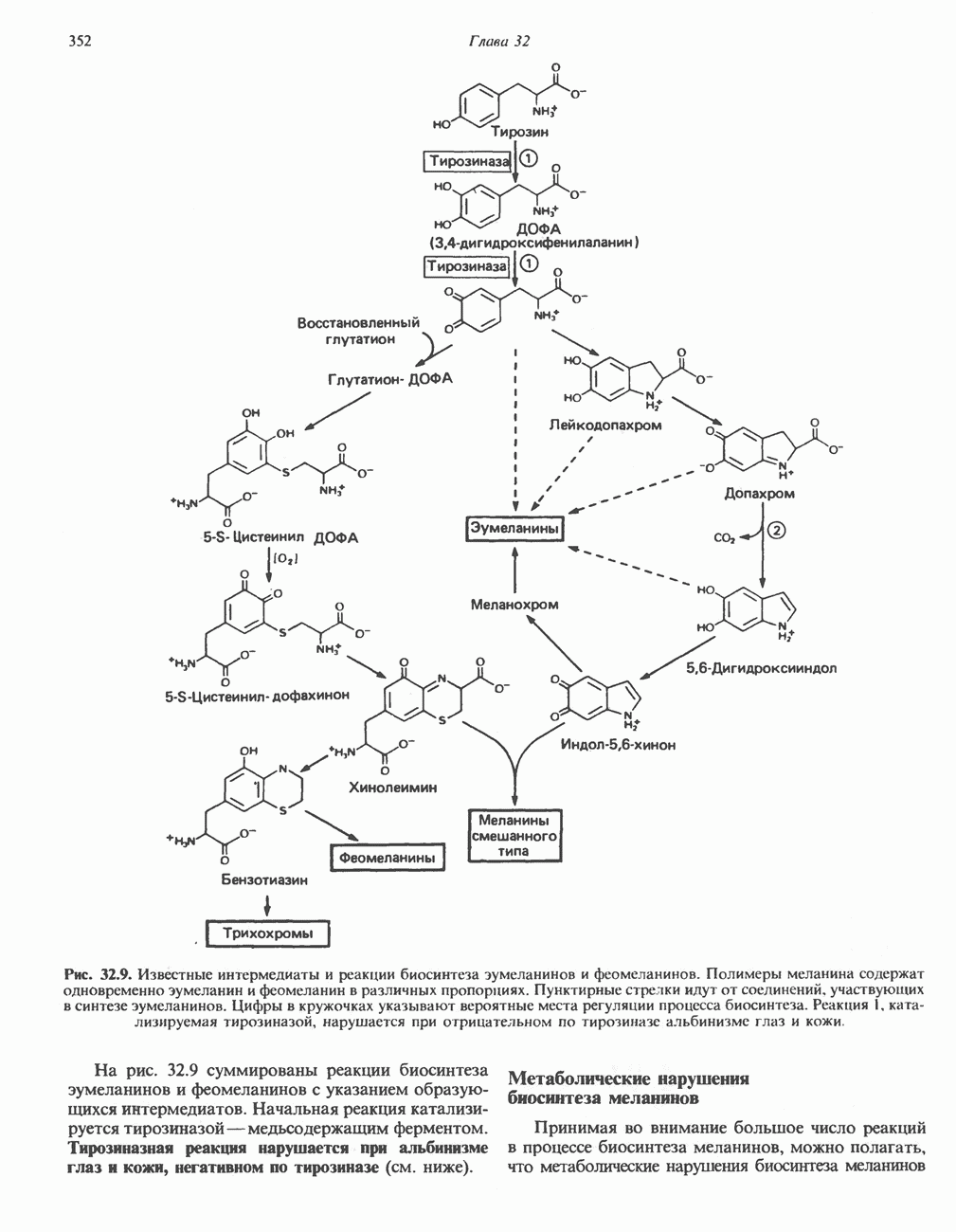
- МЕЛАНИНЫ
- ТИРОЗИН
- КРЕАТИН И КРЕАТИНИН
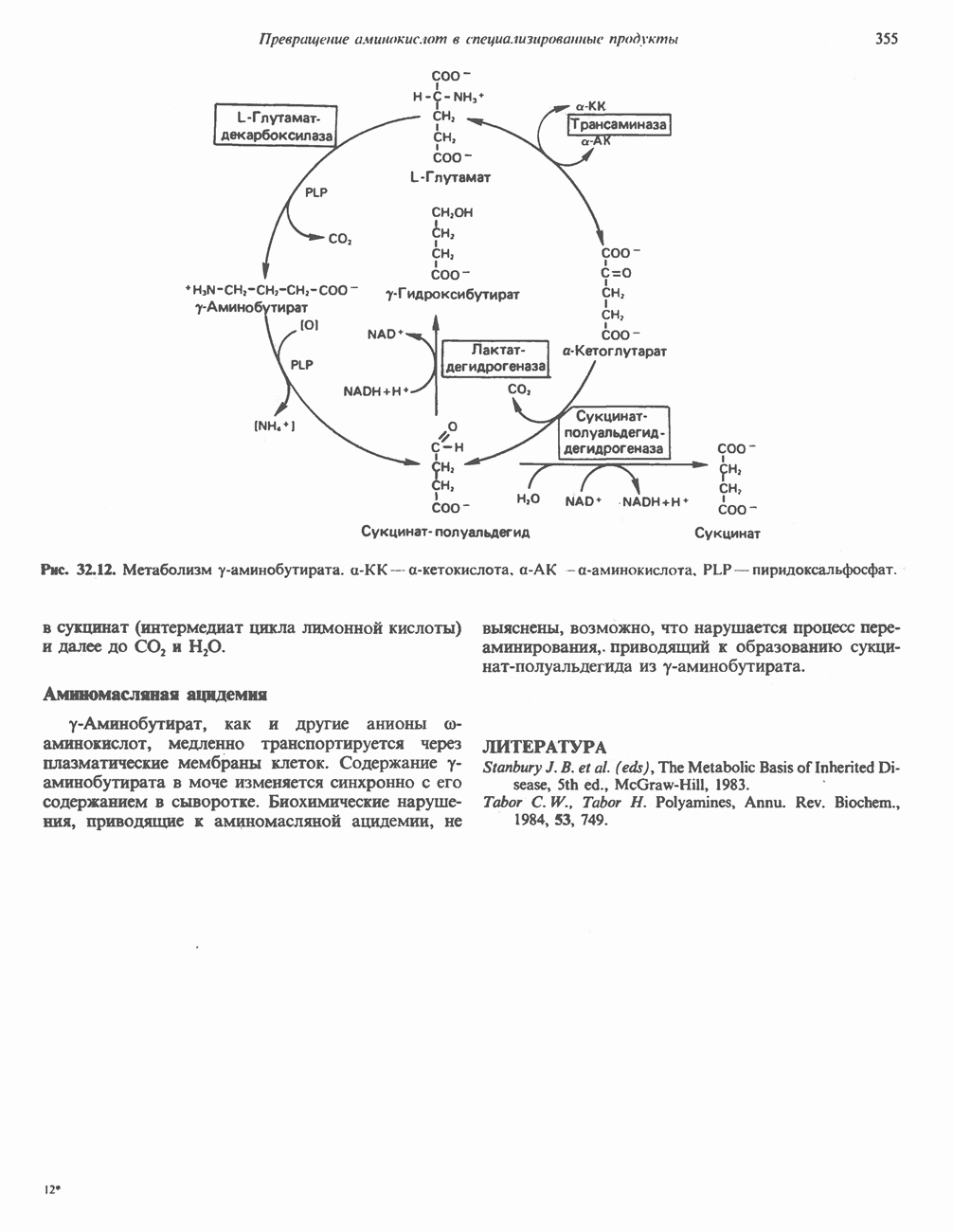
- у-АМИНОБУТИРАТ
- Глава 33. Порфирины и желчные пигменты
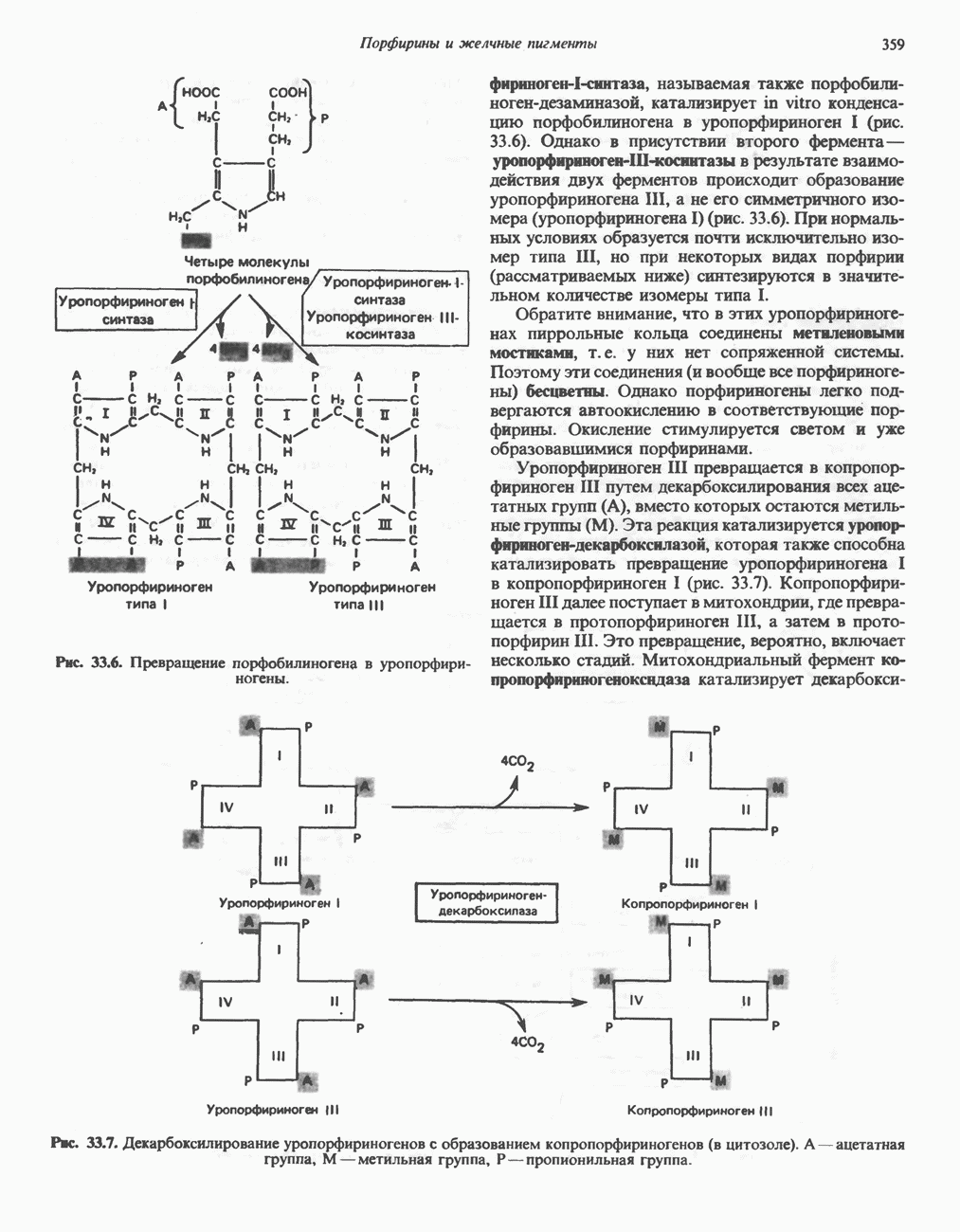
- ПОРФИРИНЫ
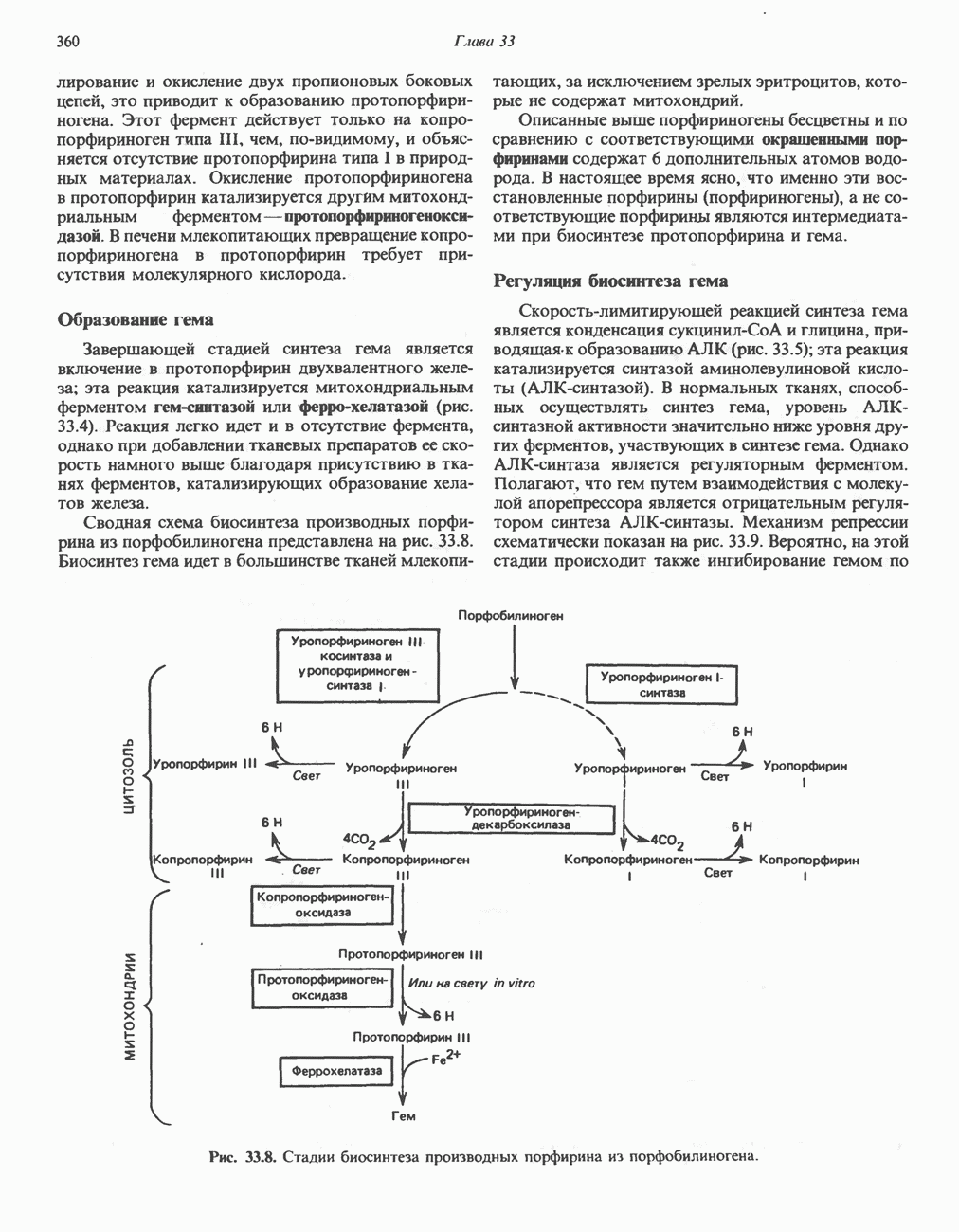
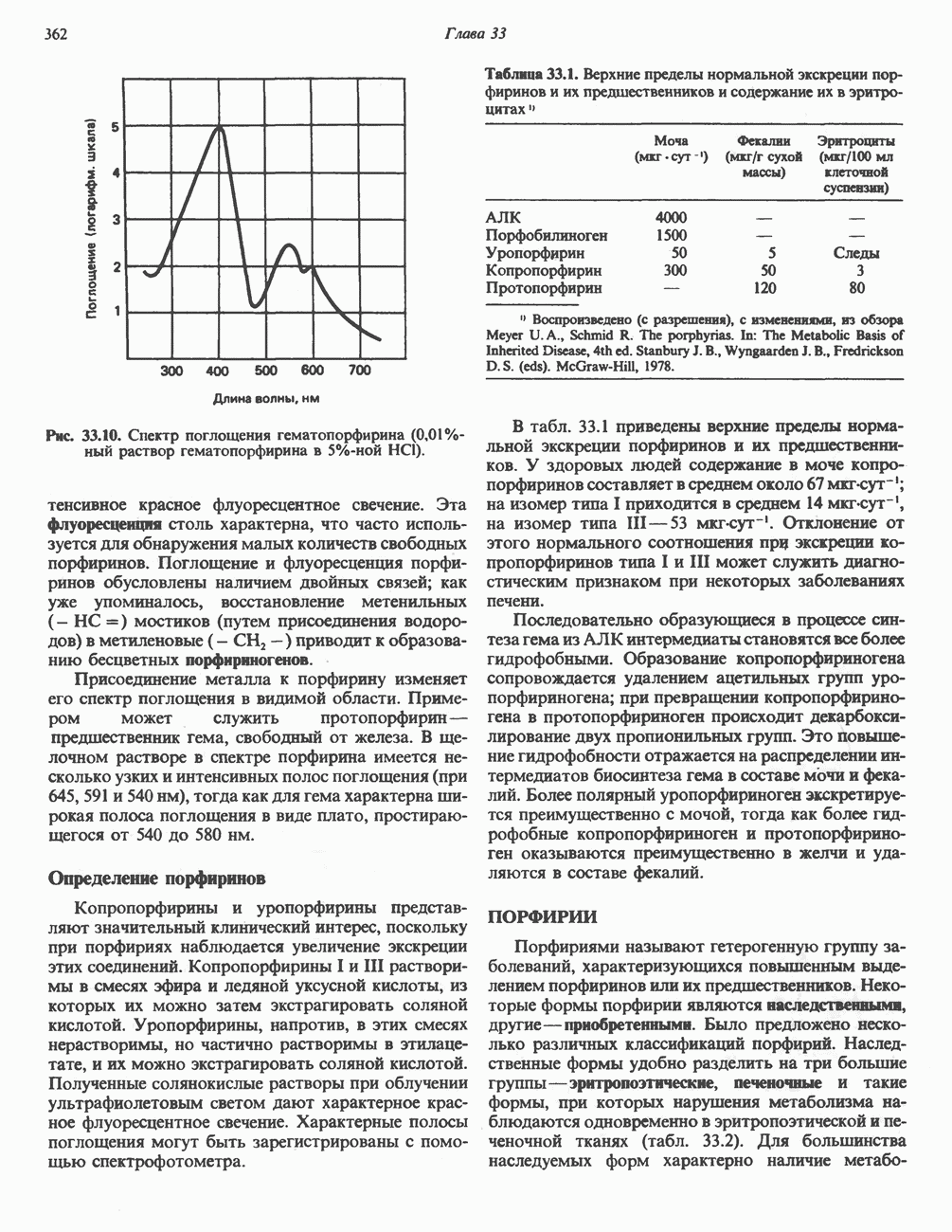
- ПОРФИРИН
- КАТАБОЛИЗМ ГЕМА: ОБРАЗОВАНИЕ ЖЕЛЧНЫХ ПИГМЕНТОВ
- МЕТАБОЛИЗМ БИЛИРУБИНА В КИШЕЧНИКЕ
- ГИПЕРБИЛИРУБИНЕМИЯ
- Список сокращений