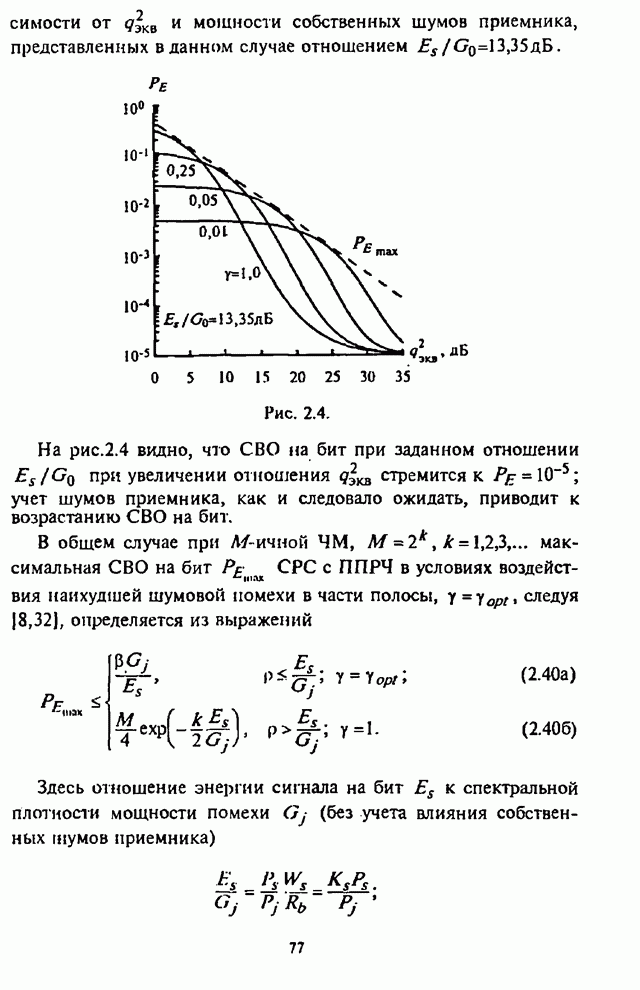
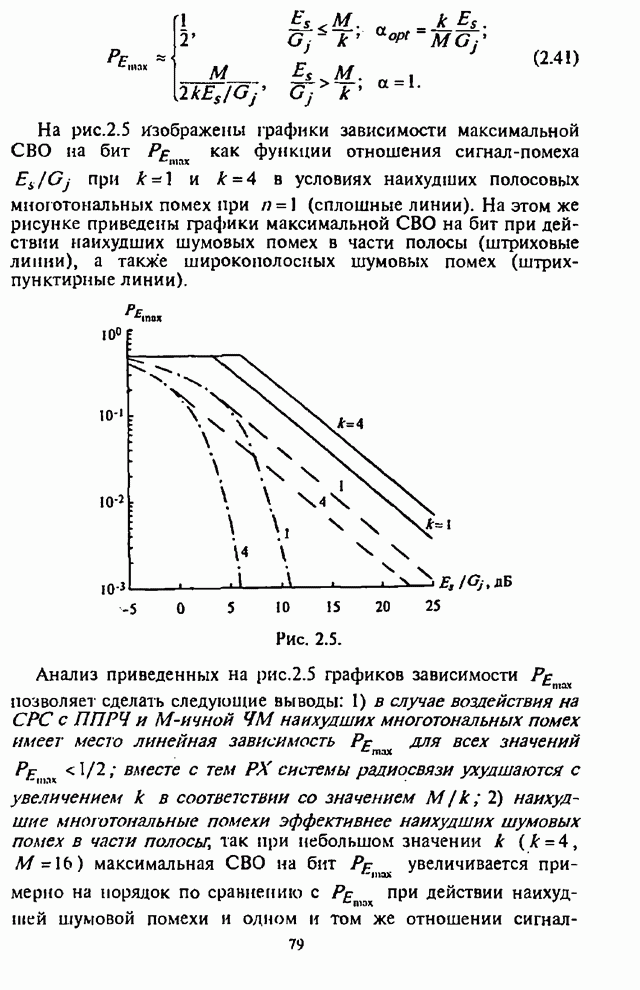
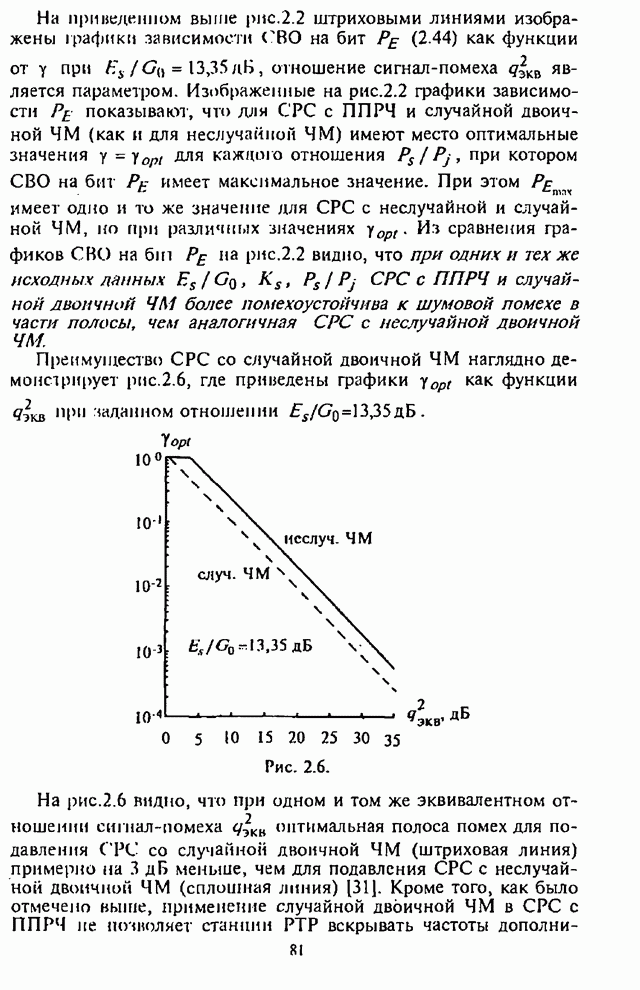
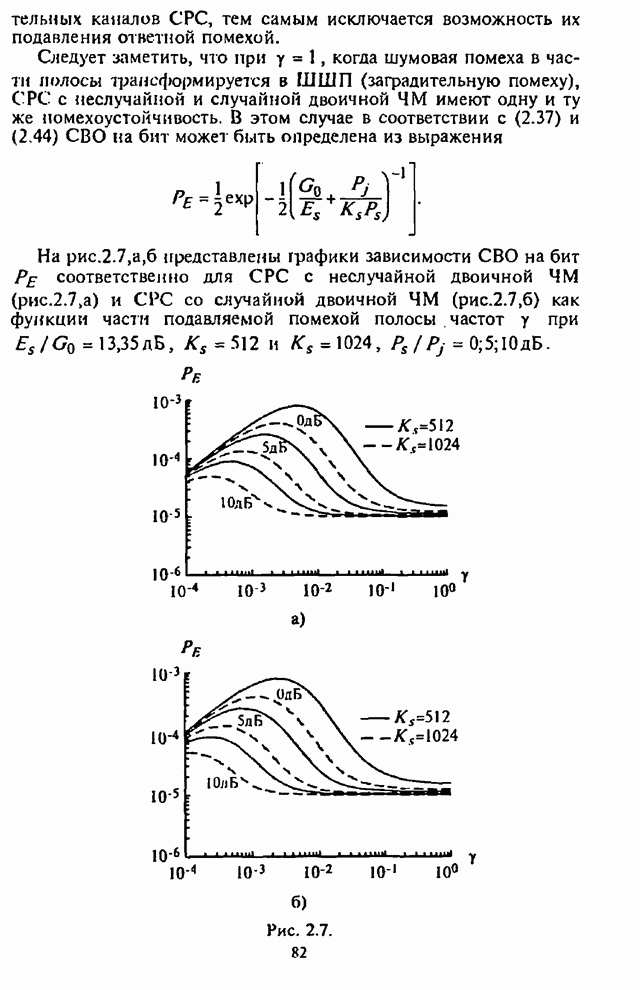
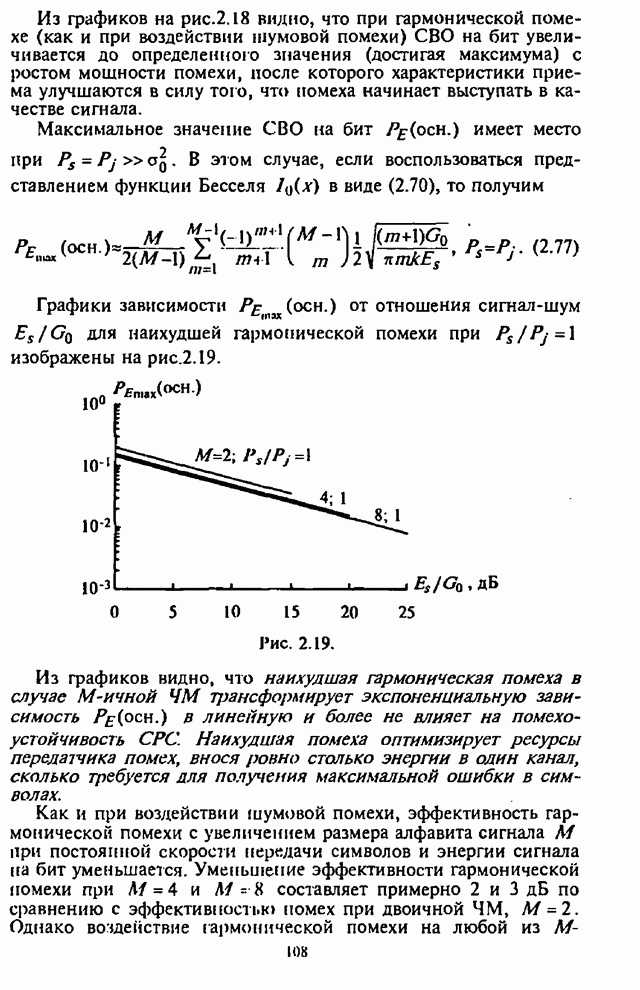
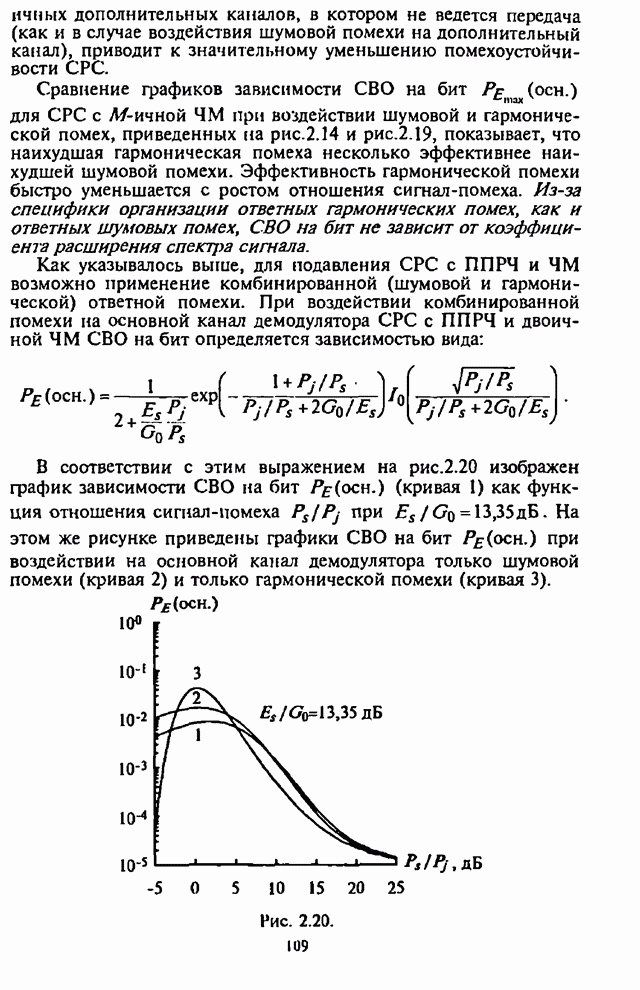
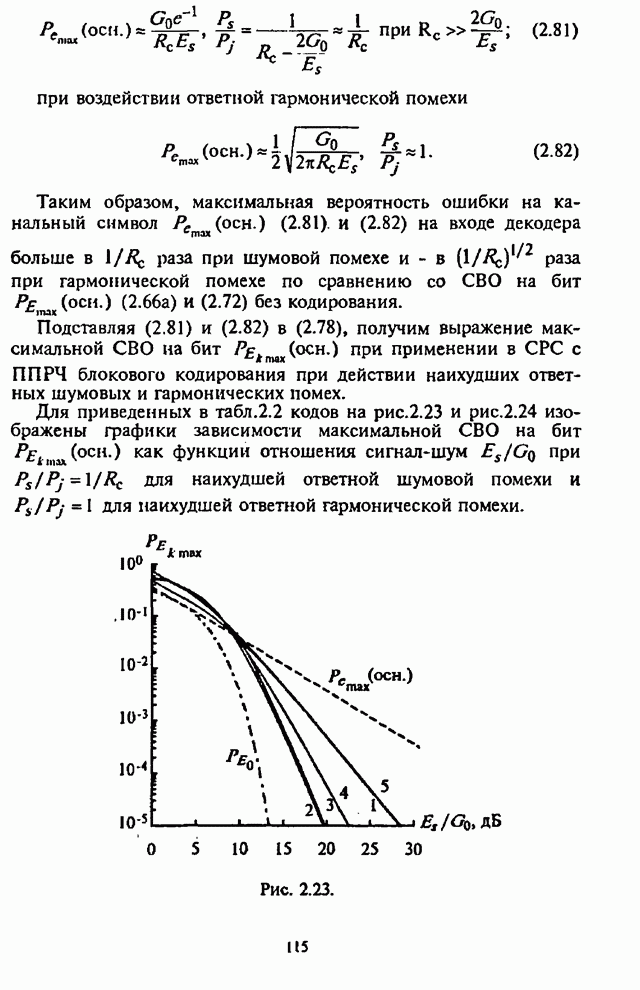
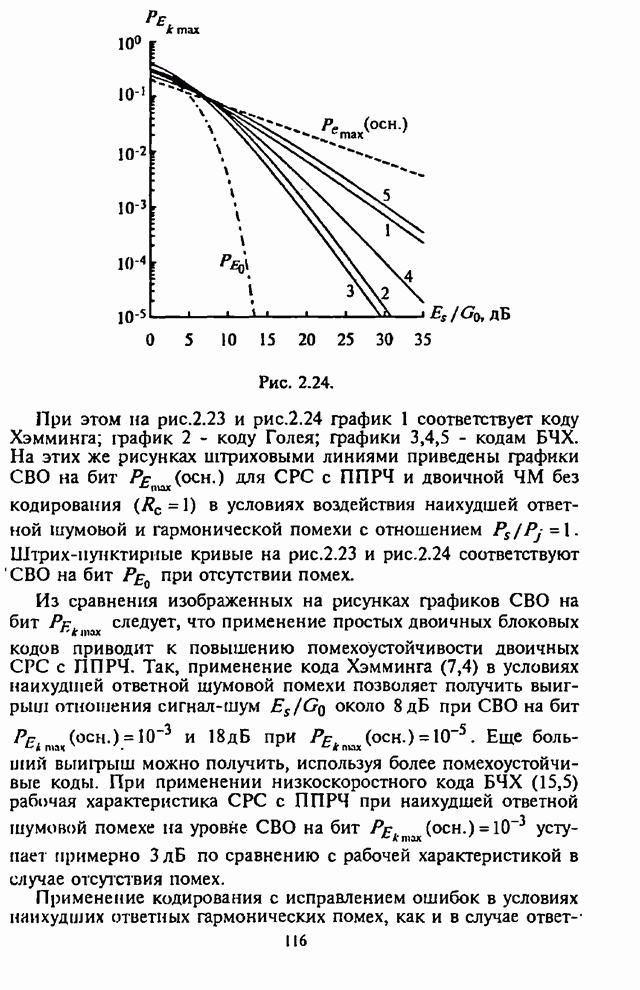
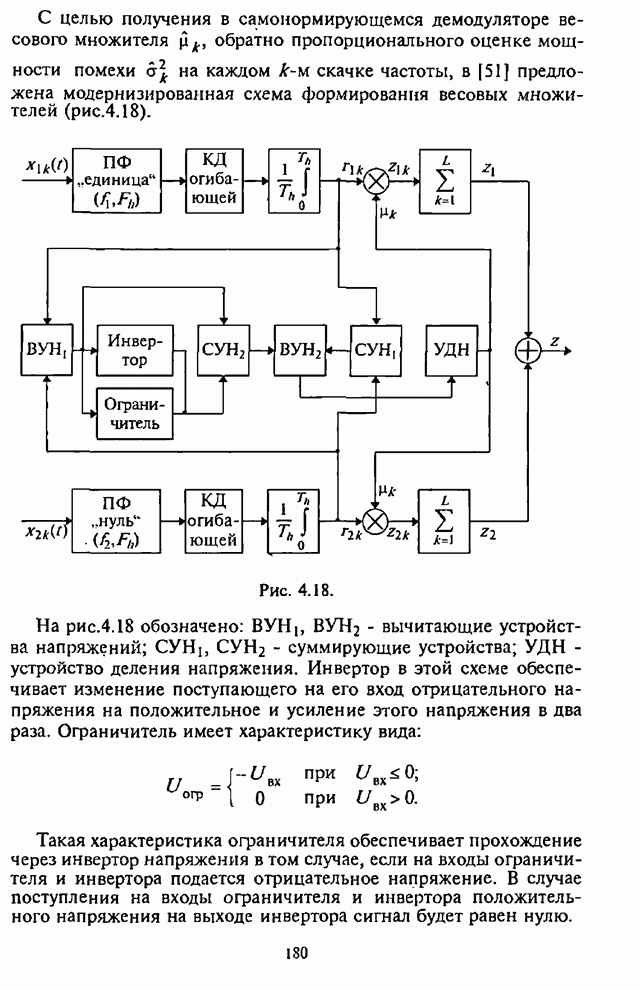
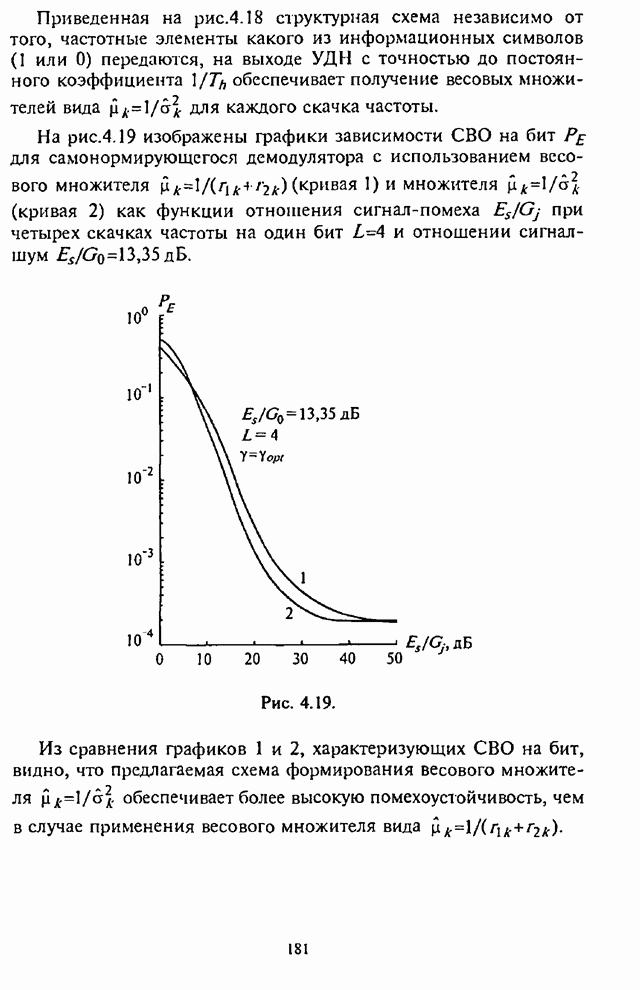
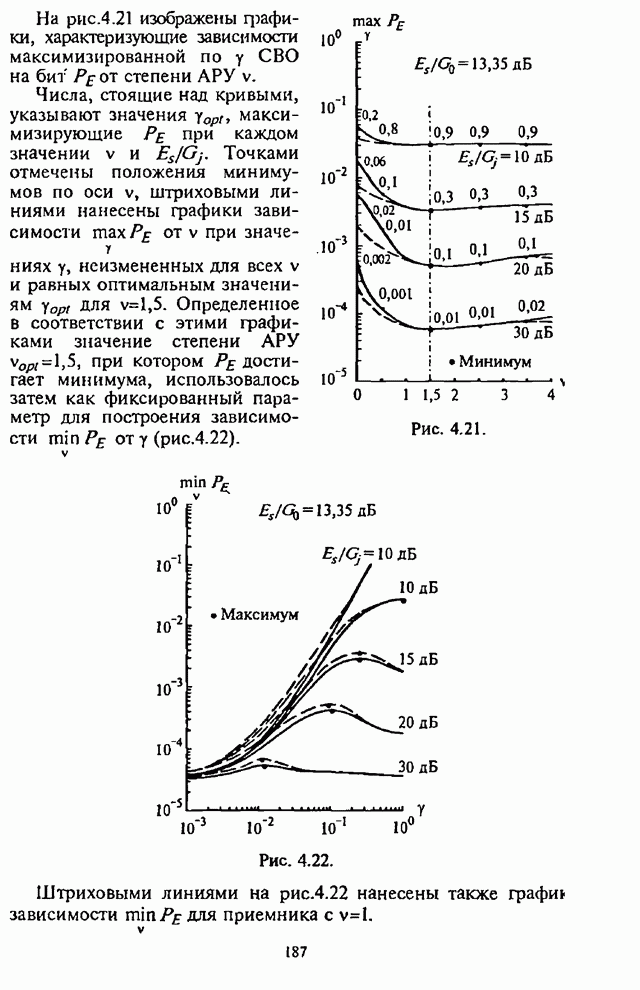
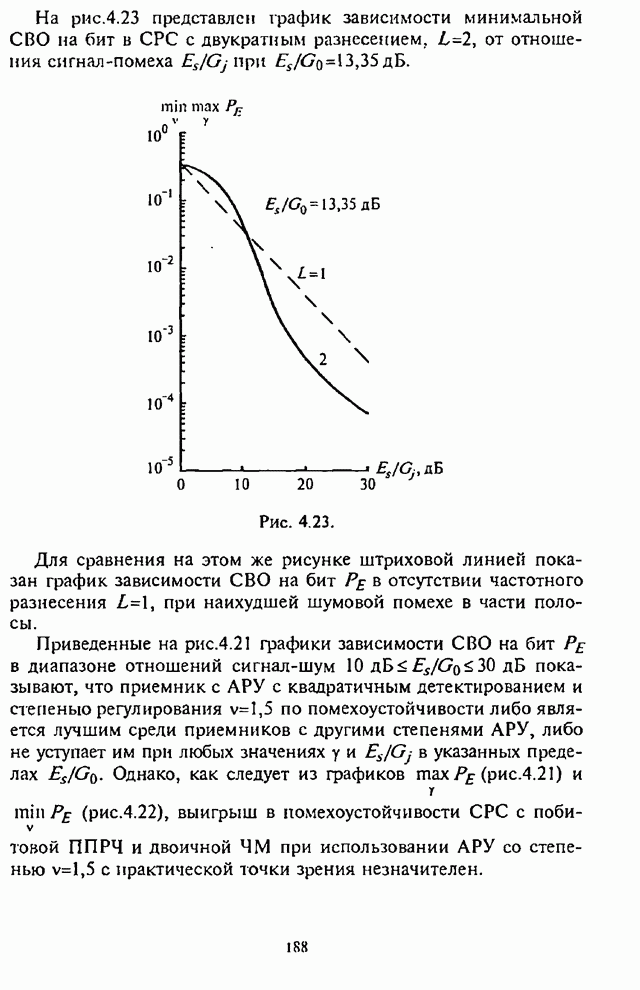
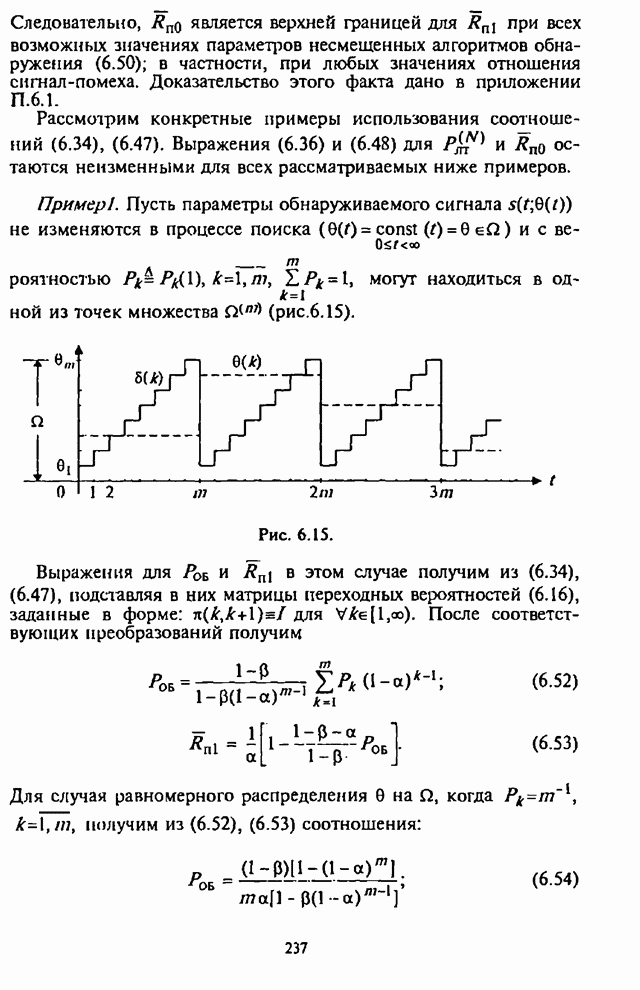
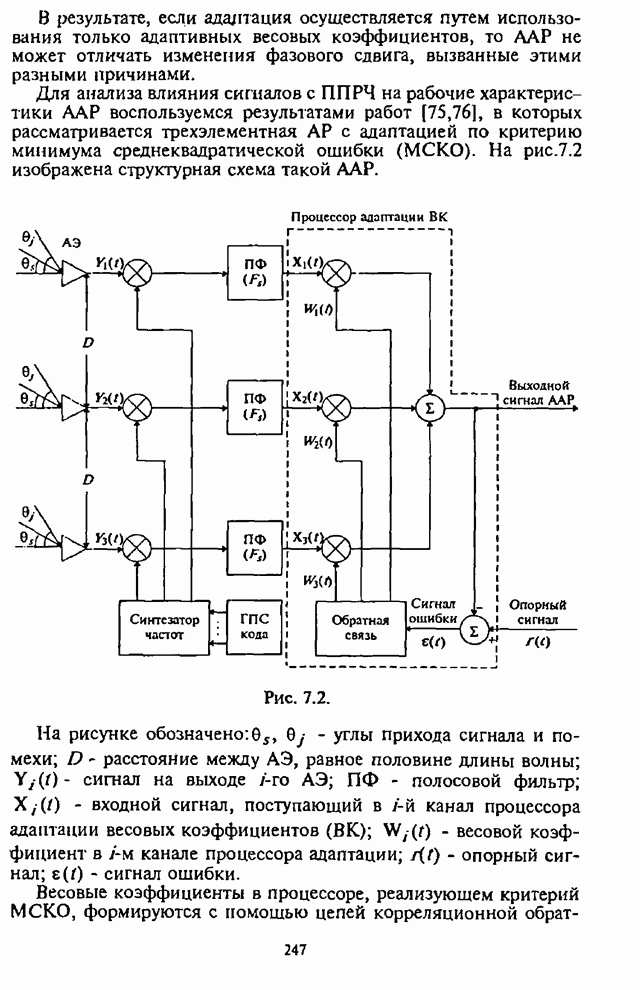
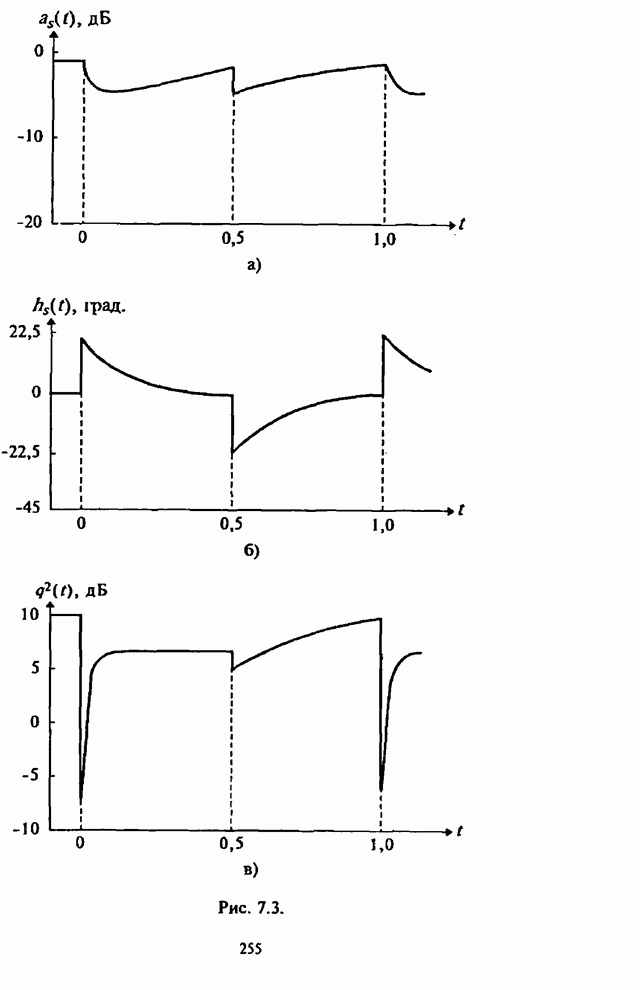
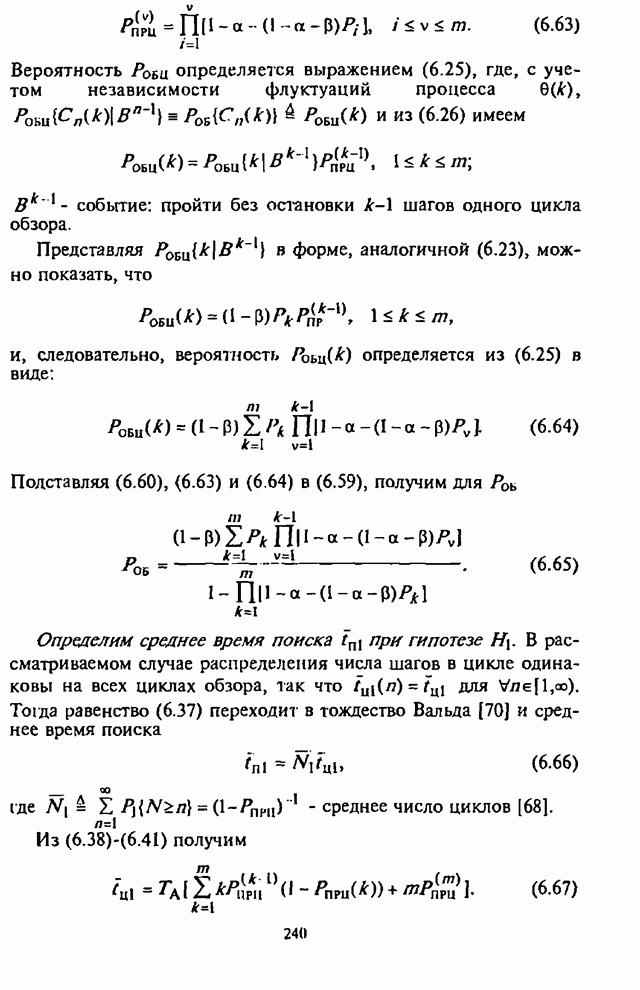| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
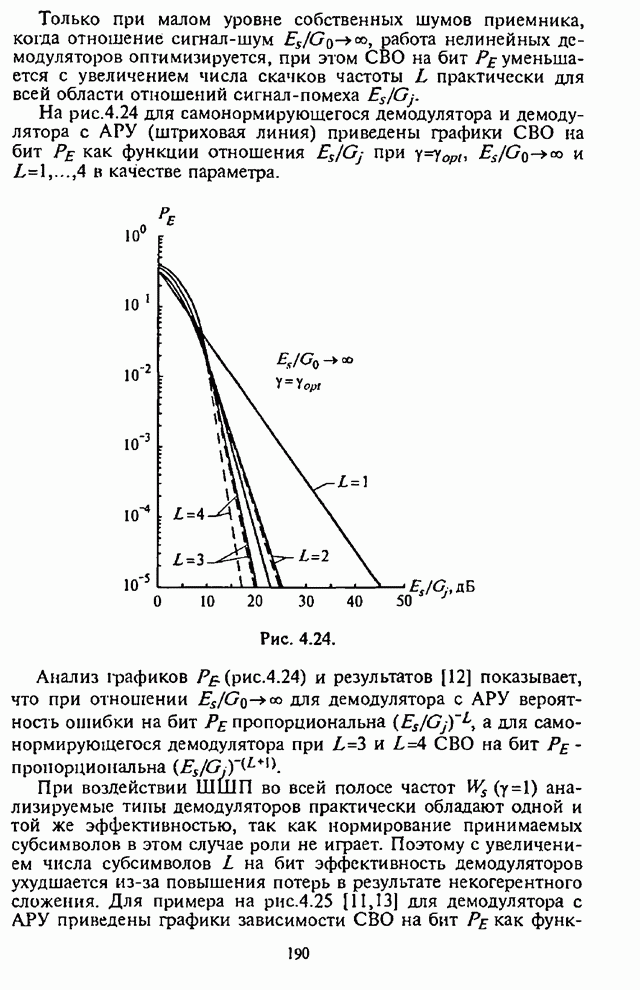
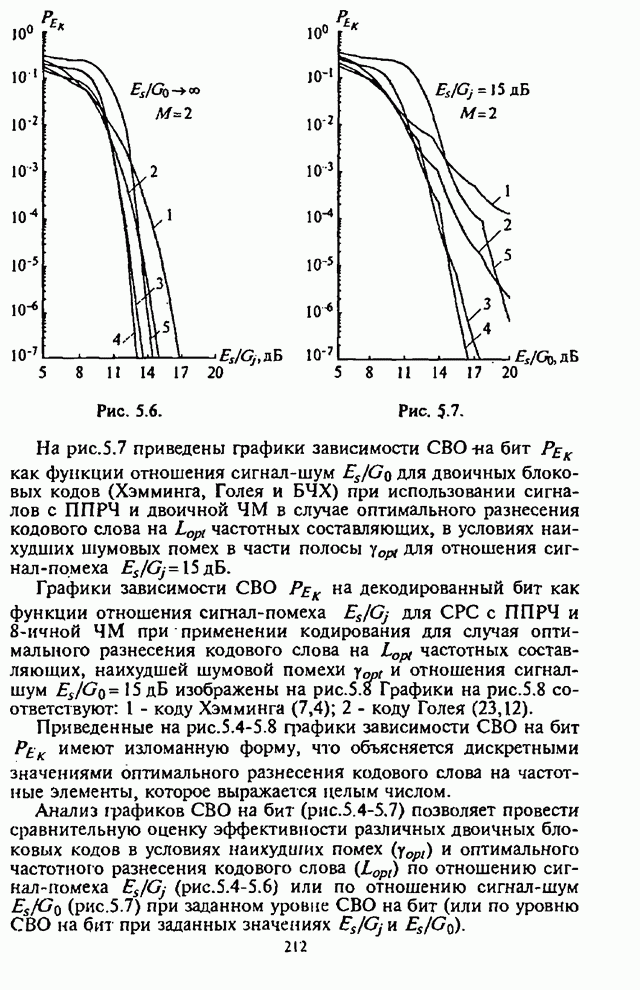
Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
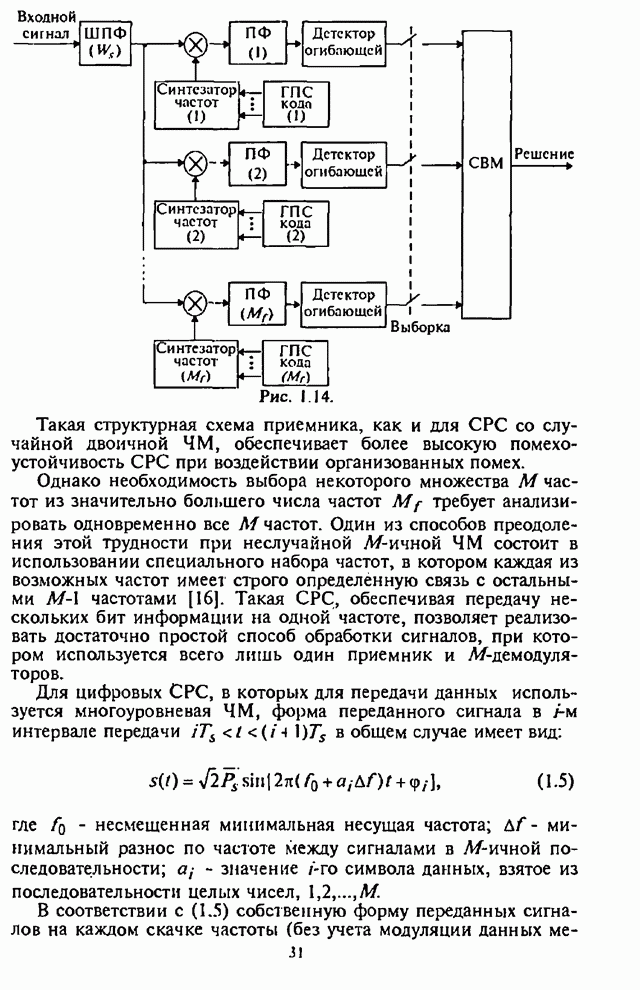
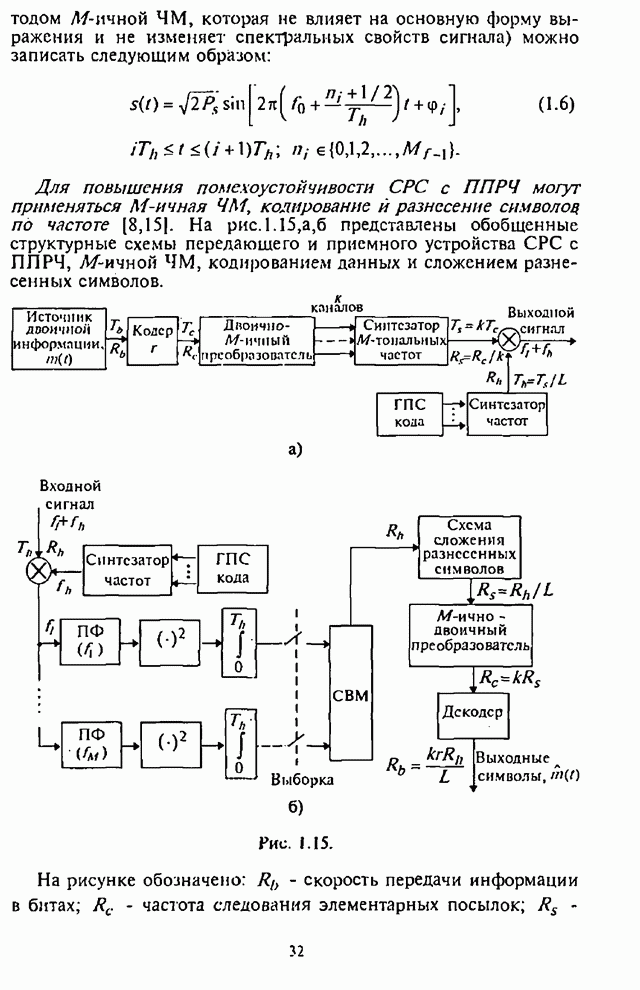
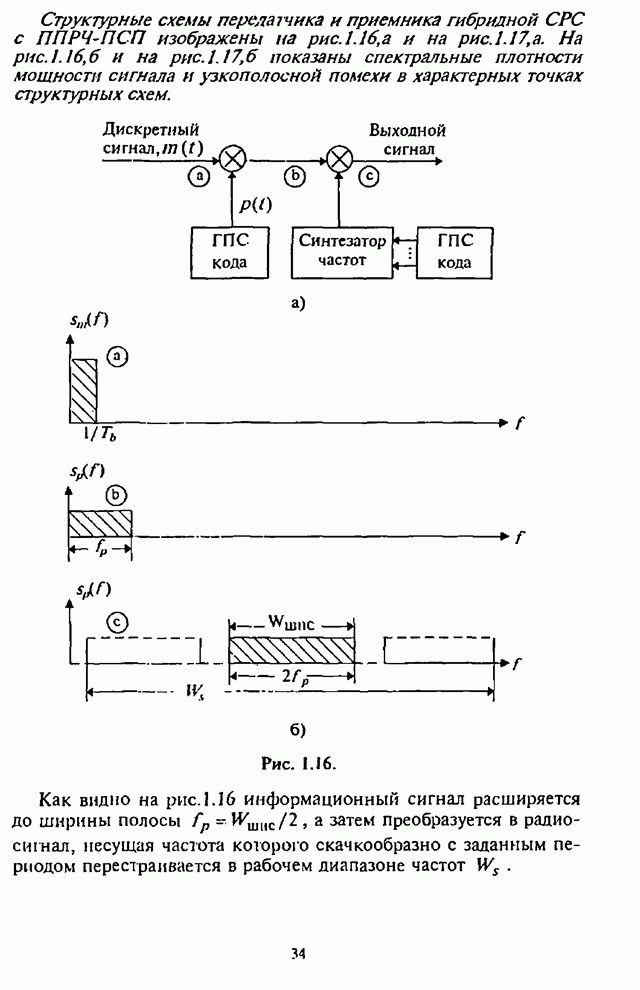
В связи с широким внедрением в СРС быстродействующей микропроцессорной техники и современной элементной базы заметно повысился научный и практический интерес к разработке и применению в СРС с ППРЧ сигналов с частотным разнесением символов. Опубликован ряд работ отечественных и зарубежных специалистов, в которых проведен анализ помехоустойчивости СРС с ППРЧ и разнесением символов по частоте, например [10-15].
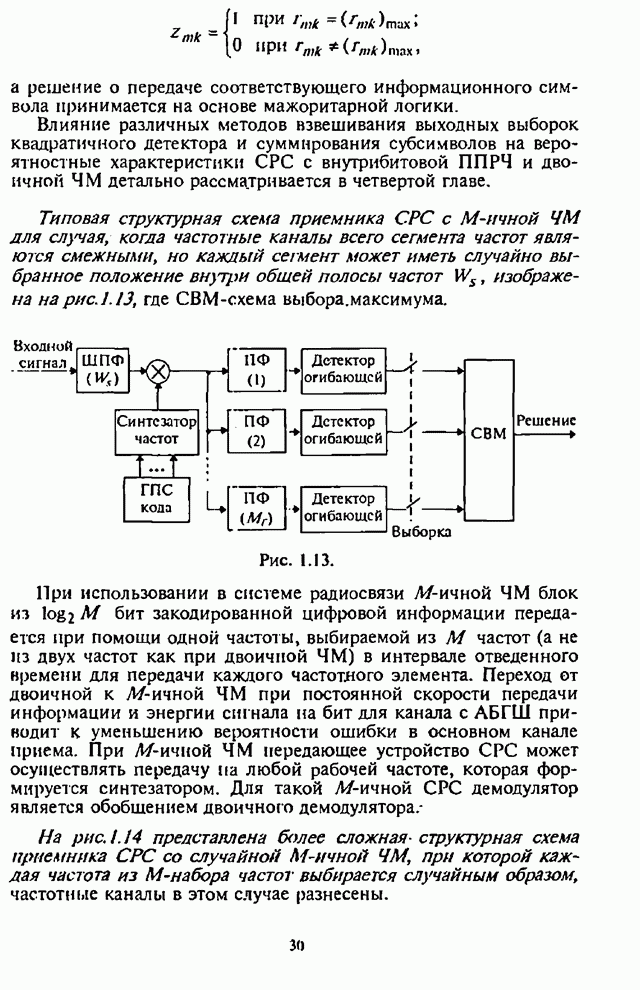
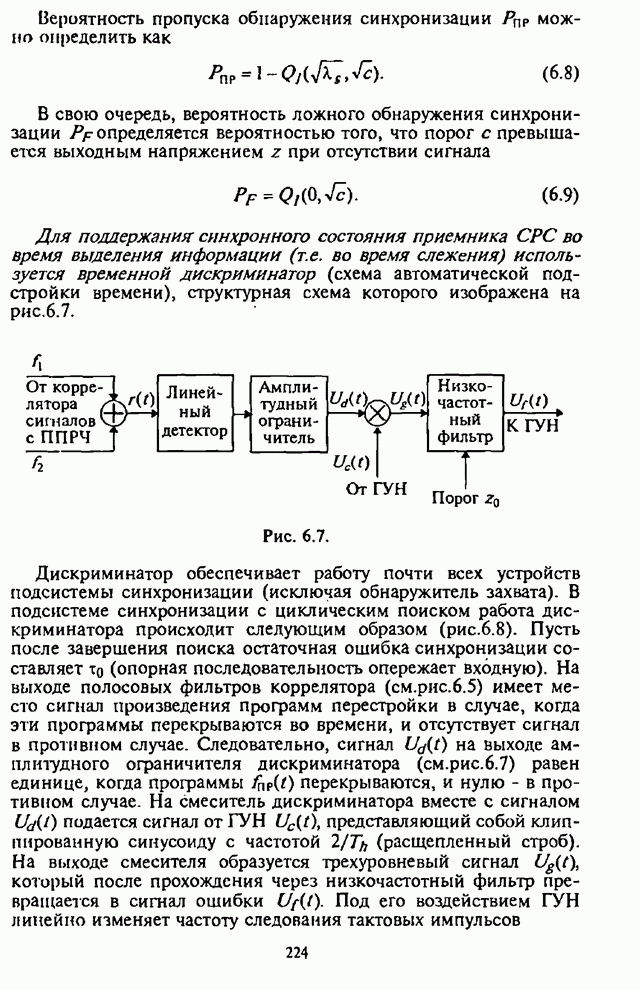
Частотное разнесение символов (также как и пространственное, временное, поляризационное разнесение сигналов) с последующей их обработкой приводит к улучшению рабочих характеристик приема сигналов. Системы радиосвязи с внутрисимвольной ППРЧ и ЧМ являются, как правило, некогерентными системами. Разнесение символов на более короткие по длительности частотные элементы (субсимволы) на передающей стороне СРС и их последующая обработка на приемной стороне СРС сопровождается некогерентными потерями, что отрицательно сказывается на помехоустойчивости таких СРС. Результат взаимодействия указанных двух противоположных с точки зрения помехоустойчивости СРС процессов, т.е. частотного разнесения символов и некогерентной обработки субсимволов, определяется структурой используемого в приемнике СРС демодулятора, типом решающего устройства, наличием дополнительной информации о «надежности» отдельных субсимволов при воздействии помех.
Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ проведем для случая воздействия на СРС шумовой помехи в части полосы и собственных шумов приемника СРС в условиях априорной неопределенности относительно дисперсии помехи и амплитуды субсимвола на каждом скачке частоты.
Для
случая, когда в качестве информационной дискретной модуляции используется M-ичная
ЧМ, математическая модель ![]() -го субсимвола может быть
записана в виде:
-го субсимвола может быть
записана в виде:
![]() (3.1)
(3.1)
где![]() - амплитуда и частотный сдвиг
- амплитуда и частотный сдвиг ![]() –го субсимвола,
–го субсимвола,
![]()
![]() - начало и окончание
- начало и окончание ![]() –го субсимвола (
–го субсимвола (![]() –го скачка несущей частоты),
–го скачка несущей частоты), ![]() ;
;![]() - число субсимволов
(частотных элементов) в символе,
- число субсимволов
(частотных элементов) в символе, ![]() ;
;![]() - длительность символа (бита)
и скачка частоты;
- длительность символа (бита)
и скачка частоты; ![]() -
начальная фаза
-
начальная фаза ![]() –го субсимвола,
–го субсимвола, ![]()
![]() - ширина полосы частот субсимвола,
- ширина полосы частот субсимвола, ![]() .
.
Результирующий
полезный сигнал, представляющий собой информационный символ 1 или 0, состоит из
![]() отрезков гармонического колебания (3.1) и имеет энергию
отрезков гармонического колебания (3.1) и имеет энергию
 (3.2)
(3.2)
где ![]() - мощность сигнала.
- мощность сигнала.
Шумовая
помеха в части полосы ![]() , как указывалось выше, может
быть представлена в виде сосредоточенного по полосе белого гауссовского шума,
мощность которого
, как указывалось выше, может
быть представлена в виде сосредоточенного по полосе белого гауссовского шума,
мощность которого ![]() ограничена и равномерно распределена в пределах полосы
ограничена и равномерно распределена в пределах полосы ![]() ,
, ![]() . При этом мощность помехи, воздействующей на каждый
субсимвол в подавляемой полосе
. При этом мощность помехи, воздействующей на каждый
субсимвол в подавляемой полосе ![]() , можно записать в виде:
, можно записать в виде:
 (3.3)
(3.3)
где ![]() - средняя спектральная плотность мощности помехи в
расширенной полосе
- средняя спектральная плотность мощности помехи в
расширенной полосе ![]() .
.
При
равномерном распределении субсимволов в полосе ![]() помехой может быть подавлено
помехой может быть подавлено ![]() из
из ![]() . субсимволов,
. субсимволов, ![]() . На остальные (
. На остальные (![]() ) субсимволы воздействуют
только собственные шумы приемника
) субсимволы воздействуют
только собственные шумы приемника ![]() которые можно описать гауссовской помехой
с нулевым средним и равномерной спектральной плотностью мощности
которые можно описать гауссовской помехой
с нулевым средним и равномерной спектральной плотностью мощности![]() .
.
Мощность
помехи и шума на входе приемника СРС на частотe ![]() -го субсимвола представим в
виде:
-го субсимвола представим в
виде:
 (3.4)
(3.4)
![]()
В соответствии с (3.4) действующую на входе приемника СРС помеху можно рассматривать как нестационарную с изменяющейся мощностью.
Для
решения задачи синтеза оптимального алгоритма адаптивного различения сигналов
с внутрисимвольной ППРЧ и ЧМ примем, что на входе приемного устройства
действует аддитивная смесь ![]() -го субсимвола
-го субсимвола ![]() шумовой помехи
шумовой помехи ![]() и собственных шумов приемника
и собственных шумов приемника ![]()
![]() ,
, ![]() , (3.5)
, (3.5)
где ![]() ,
, ![]() .
.
Задача синтеза заключается
в том,
чтобы по совокупности принятых
реализаций (3.5) определить оптимальный алгоритм различения символов
1 и 0 за время длительности
символа ![]() . Данная задача аналогична синтезу алгоритма некогерентного
приема сигналов при использовании нескольких каналов разнесения [23]. При
выбранных моделях сигнала, помехи и собственных шумов приемника наиболее
предпочтительным критерием оптимальной обработки в СРС является критерий В.А.
Котельникова (критерий идеального наблюдателя). В случае различения
. Данная задача аналогична синтезу алгоритма некогерентного
приема сигналов при использовании нескольких каналов разнесения [23]. При
выбранных моделях сигнала, помехи и собственных шумов приемника наиболее
предпочтительным критерием оптимальной обработки в СРС является критерий В.А.
Котельникова (критерий идеального наблюдателя). В случае различения ![]() детерминированных сигналов данный критерий позволяет получить
минимум вероятности ошибки на бит
детерминированных сигналов данный критерий позволяет получить
минимум вероятности ошибки на бит
 (3.6)
(3.6)
где ![]() - априорная
вероятность передачи частотных элементов символа, характеризующая среднюю частоту,
с которой субсимвол
- априорная
вероятность передачи частотных элементов символа, характеризующая среднюю частоту,
с которой субсимвол ![]() посылается
в канал, по физической сущности
посылается
в канал, по физической сущности ![]() ;
; ![]() -
условная вероятность того, что передаваемый символ принят ошибочно, т.е.
вероятность решения
-
условная вероятность того, что передаваемый символ принят ошибочно, т.е.
вероятность решения ![]() oприеме символа
oприеме символа
![]() , когда в
действительности был передан символ
, когда в
действительности был передан символ ![]() .
.
При
выбранной стратегии формирования символа можно допустить, что передача
частотных элементов сигнала ![]() , равновероятна на любой из
, равновероятна на любой из ![]() несущих частот в
диапазоне
несущих частот в
диапазоне ![]() , поэтому
, поэтому
![]() (3.7)
(3.7)
С учетом (3.7) вероятность ошибки
 (3.8)
(3.8)
Стратегия различителя, минимизирующего (3.8), сводится к использованию правила максимального правдоподобия
![]() при всеx
при всеx ![]() (3.9)
(3.9)
где ![]() - отношение правдоподобия, соответствующее
- отношение правдоподобия, соответствующее ![]() -у информационному символу.
-у информационному символу.
Из
(3.9) следует, что для нахождения оптимального алгоритма обработки сигналов с
внутрисимвольной ППРЧ и ЧМ требуется знание функционалов правдоподобия как для
отдельных субсимволов за время скачка частоты ![]() , так и сигнала с ППРЧ в целом за время
одного бита информации
, так и сигнала с ППРЧ в целом за время
одного бита информации ![]() .
.
При заданных моделях сигнала и помехи и принятой стратегии передачи субсимволов функционалы правдоподобия можно представить в виде [42,43]:
для каждого частотного элемента сигнала с ППРЧ
 (3.10)
(3.10)
для сигнала с ППРЧ в целом
 (3.11)
(3.11)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
энергия, отношение сигнал-помеха, спектральная плотность мощности помехи и
собственных шумов приемника СРС на
-
энергия, отношение сигнал-помеха, спектральная плотность мощности помехи и
собственных шумов приемника СРС на ![]() -м скачке частоты, начальная
фаза
-м скачке частоты, начальная
фаза ![]() -го субсимвола,
соответственно;
-го субсимвола,
соответственно; ![]()

Так
как начальная фаза каждого субсимвола случайна и равномерно распределена на
интервале ![]() ,
то функционал правдоподобия сигнала с ППРЧ в целом может быть получен путем
усреднения правой части выражения (3.11) по начальным фазам:
,
то функционал правдоподобия сигнала с ППРЧ в целом может быть получен путем
усреднения правой части выражения (3.11) по начальным фазам:
 (3.12)
(3.12)
Для определения функционала правдоподобия ![]() представим внутренний
интеграл в виде:
представим внутренний
интеграл в виде:
 (3.13)
(3.13)
где

![]() ;
; ![]() ,
, ![]() ; (3.14)
; (3.14)
![]() - амплитуда ортогональных сигналов; в дальнейшем можно
принять, что
- амплитуда ортогональных сигналов; в дальнейшем можно
принять, что ![]() .
.
Учитывая (3.12) и выполнив необходимые преобразования, получим
 (3.15)
(3.15)
Интеграл,
входящий в (3.15), представляет собой модифицированную функцию Бесселя
нулевого порядка ![]()
 (3.16)
(3.16)
Подставив (3.16) в (3.12) и проделав соответствующие преобразования, функционал правдоподобия (3.12) запишем в виде [43]:
 (3.17)
(3.17)
где
![]() (3.18)
(3.18)
В
соответствии с правилом максимального правдоподобия (3.9) а также, учитывая
(3.18), решение ![]() о том, что за время
о том, что за время ![]() , передавался сигнал
, передавался сигнал ![]() , соответствующий
, соответствующий ![]() -у информационному
символу, принимается в том случае, когда
-у информационному
символу, принимается в том случае, когда
 (3.19)
(3.19)
![]()
Условие (3.19) определяет
оптимальный алгоритм различения сигналов с внутрисимвольной ППРЧ и ЧМ. Построение решающей схемы, реализующей
алгоритм (3.19), существенно упрощается, если при обработке реализаций ![]() вычисляются не отношения
правдоподобия (3.9), а соответствующие им логарифмы. Прологарифмировав обе
части выражения (3.19), получим:
вычисляются не отношения
правдоподобия (3.9), а соответствующие им логарифмы. Прологарифмировав обе
части выражения (3.19), получим:
 (3.20)
(3.20)
или
![]() ;
; ![]()
где
 ;
; 
Как
следует из (3.20), оптимальный алгоритм адаптивного различения сигналов
с ППРЧ за время ![]() отличается
от оптимальных алгоритмов различения некогерентных сигналов без ППРЧ и
различения сигналов с ППРЧ для случая, когда известна амплитуда сигнала, а
спектральная плотность мощности помехи постоянна во всем частотном диапазоне
СРС.
отличается
от оптимальных алгоритмов различения некогерентных сигналов без ППРЧ и
различения сигналов с ППРЧ для случая, когда известна амплитуда сигнала, а
спектральная плотность мощности помехи постоянна во всем частотном диапазоне
СРС.
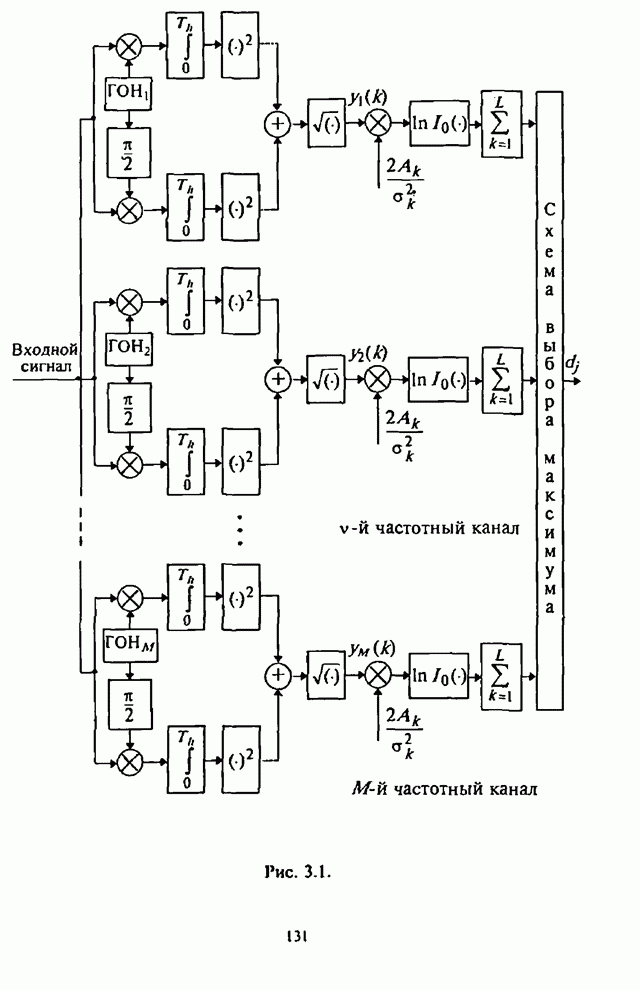
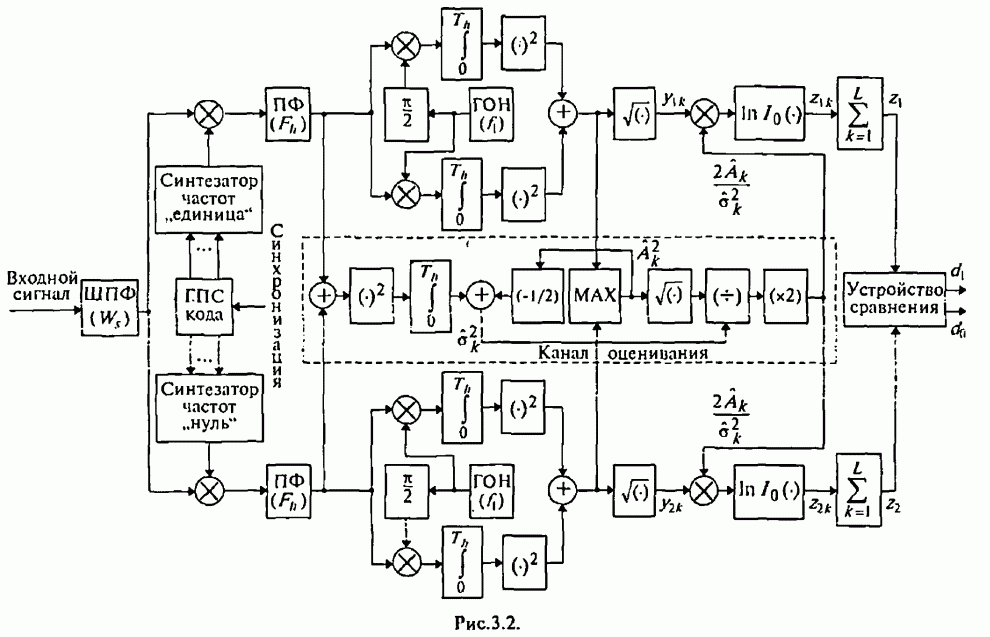
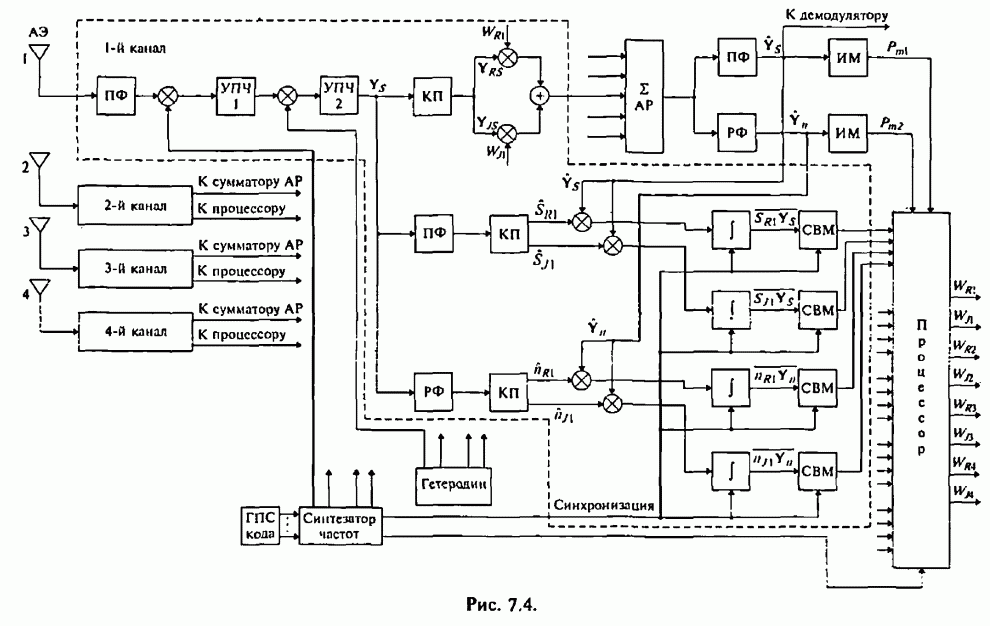
На
рис.3.1 изображена структурная схема приемника, реализующая оптимальный
алгоритм различения сигналов с внутри символьной ППРЧ и M-ичной
ЧМ [44], на рисунке обозначено: ГОН - генератор опорного напряжения; ![]() - фазовращатель
на 90°; СВМ - схема выбора максимума. Как следует из выполненною синтеза такой
приемник при
- фазовращатель
на 90°; СВМ - схема выбора максимума. Как следует из выполненною синтеза такой
приемник при ![]() должен быть приемником взаимокорреляционного типа, в
котором по принятым реализациям смеси сигнала, помехи и шума в течении
действия каждого
должен быть приемником взаимокорреляционного типа, в
котором по принятым реализациям смеси сигнала, помехи и шума в течении
действия каждого ![]() -го субсимвола
вычисляются корреляционные интегралы
-го субсимвола
вычисляются корреляционные интегралы ![]() и
и ![]() , которые затем возводятся в
квадрат, суммируются и далее находятся значения огибающей функции взаимной
корреляции между принятыми реализациями
, которые затем возводятся в
квадрат, суммируются и далее находятся значения огибающей функции взаимной
корреляции между принятыми реализациями ![]() и опорными сигналами
и опорными сигналами ![]() ,
, ![]() . Таким путем формируются статистики
(3.18), которые умножаются на весовой множитель вида:
. Таким путем формируются статистики
(3.18), которые умножаются на весовой множитель вида:
![]() (3.21)
(3.21)
Напряжения,
пропорциональные ![]() ,
подвергаются нелинейной обработке вида
,
подвергаются нелинейной обработке вида ![]() и дальнейшему суммированию в каждом
и дальнейшему суммированию в каждом ![]() -м канале.
Результирующее суммарное напряжение с выхода
-м канале.
Результирующее суммарное напряжение с выхода ![]() частотного канала подается на схему
выбора максимума, на выходе которой формируется решение
частотного канала подается на схему
выбора максимума, на выходе которой формируется решение ![]() о приеме сигнала
о приеме сигнала ![]() . Заметим, что в соответствии с (3.19)
решающая схема может быть реализована на нелинейных элементах с характеристикой
вида функции Бесселя нулевого порядка
. Заметим, что в соответствии с (3.19)
решающая схема может быть реализована на нелинейных элементах с характеристикой
вида функции Бесселя нулевого порядка ![]() и
перемножителях с характеристикой вида
и
перемножителях с характеристикой вида  .
.
Из анализа оптимальной структурной схемы обработки сигналов с внутирсимвольной ППРЧ и M-ичной ЧМ (рис.3.1) следует: 1) оптимальный приемник сигналов с внутрисимвольной ППРЧ и ЧМ состоит из двух частей: одна часть обеспечивает обработку

Рис. 3.1.
принятых реализаций ![]() как при
обычном некогерентном накоплении; вторая
- производит
весовую обработку сформированных
статистик
как при
обычном некогерентном накоплении; вторая
- производит
весовую обработку сформированных
статистик![]() ;
2) для
реализации оптимального алгоритма
различения сигналов с ППРЧ (3.20) необходимо иметь априорную информацию об амплитуде частотного
элемента сигнала
;
2) для
реализации оптимального алгоритма
различения сигналов с ППРЧ (3.20) необходимо иметь априорную информацию об амплитуде частотного
элемента сигнала ![]() и дисперсии
помехи
и дисперсии
помехи ![]() для
каждого
для
каждого ![]() скачка
частоты, тогда как на входе
приемника одновременно действуют частотный элемент сигнала, помеха и
собственный шум приемника СРС; 3) чем больше мощность помехи
скачка
частоты, тогда как на входе
приемника одновременно действуют частотный элемент сигнала, помеха и
собственный шум приемника СРС; 3) чем больше мощность помехи ![]() на частоте
на частоте ![]() частотного
элемента, тем с меньшим весом учитывается вклад помехи принятого элемента
частотного
элемента, тем с меньшим весом учитывается вклад помехи принятого элемента ![]() в результирующее
отношение сигнал-помеха на выходе сумматора
в результирующее
отношение сигнал-помеха на выходе сумматора ![]() частотного канала.
частотного канала.
В [1]
указаны трудности формирования весовых множителей вида ![]() . Преодоление этих трудностей
возможно путем нахождения способов получения статистических оценок параметров
. Преодоление этих трудностей
возможно путем нахождения способов получения статистических оценок параметров ![]() и
и ![]() . Данная задача сводится к
оценке математического ожидания и дисперсии случайного процесса по его реализации
конечной длительности.
. Данная задача сводится к
оценке математического ожидания и дисперсии случайного процесса по его реализации
конечной длительности.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
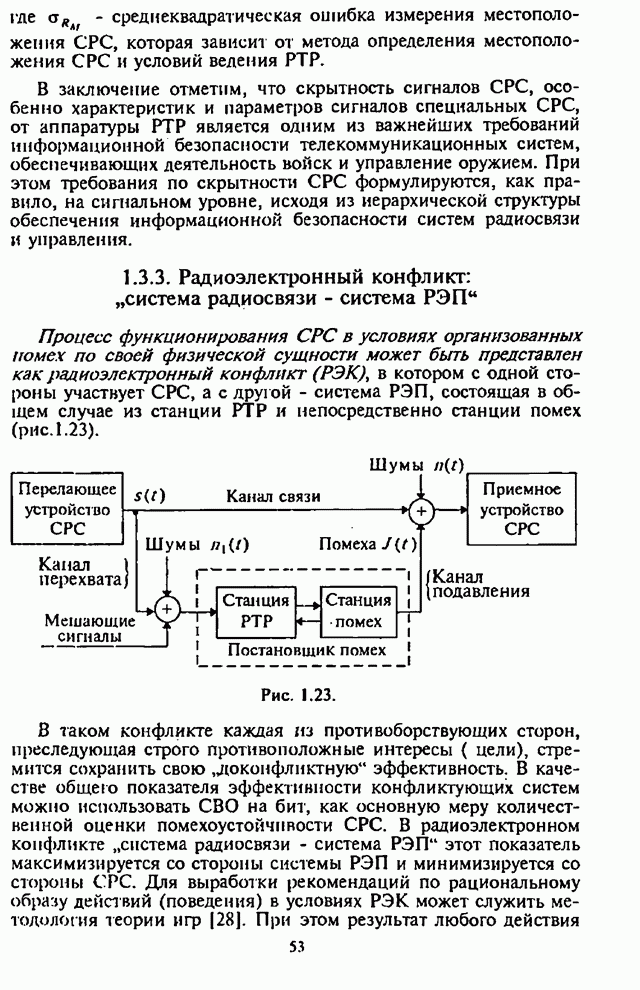
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
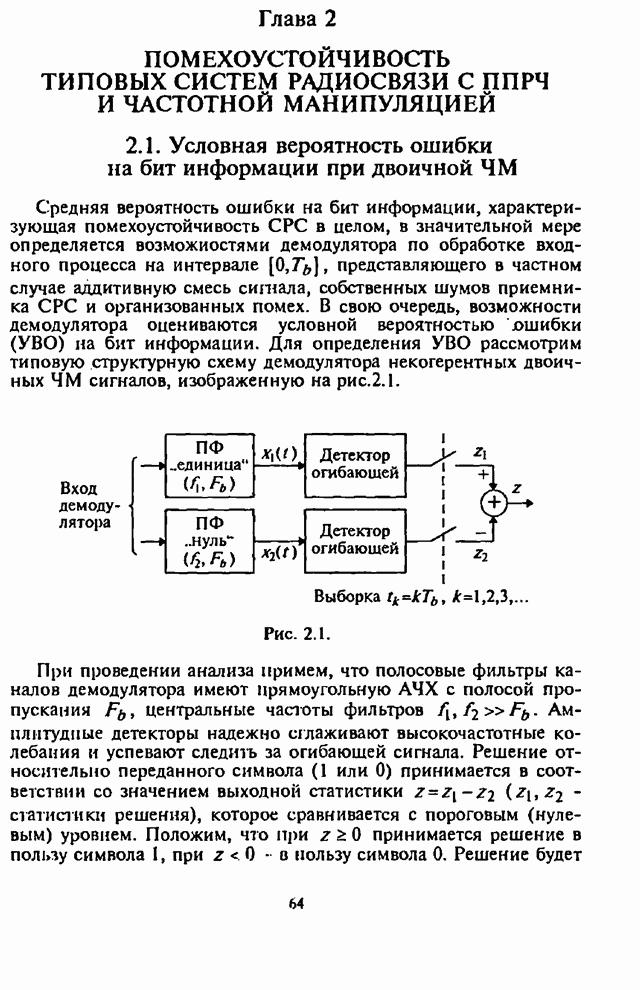
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
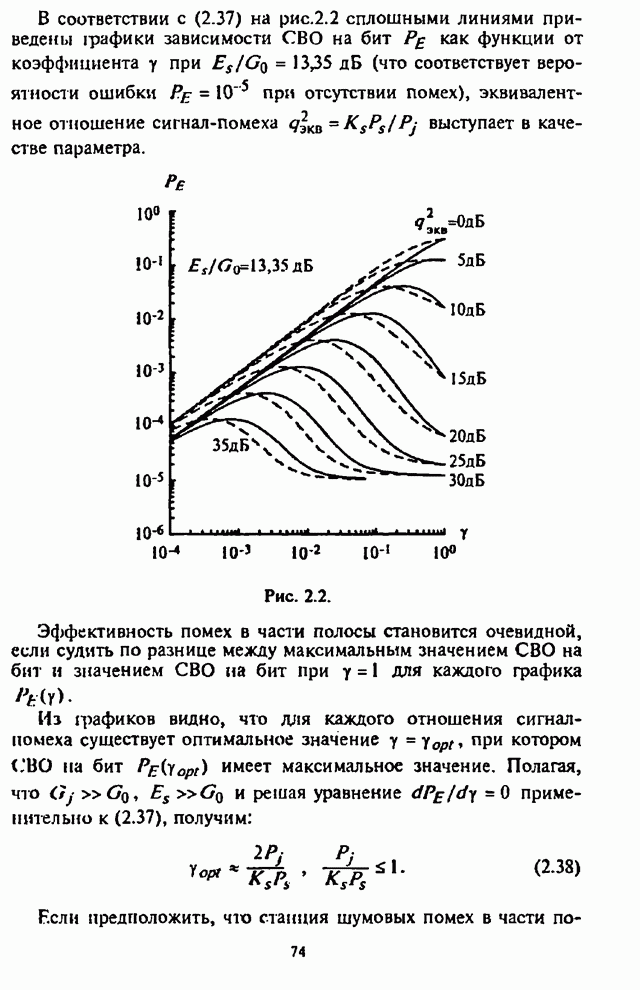
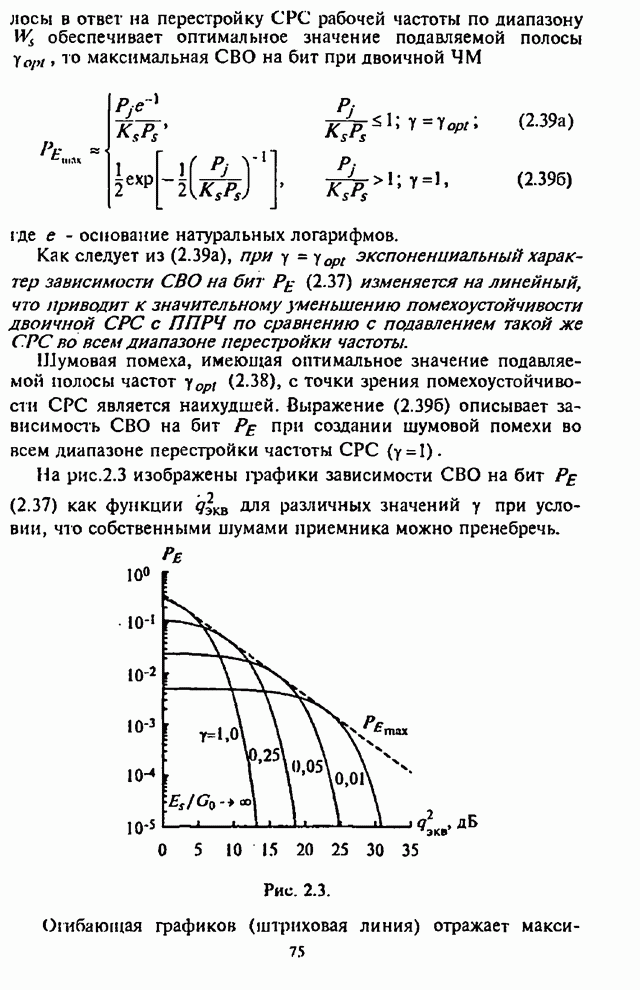
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
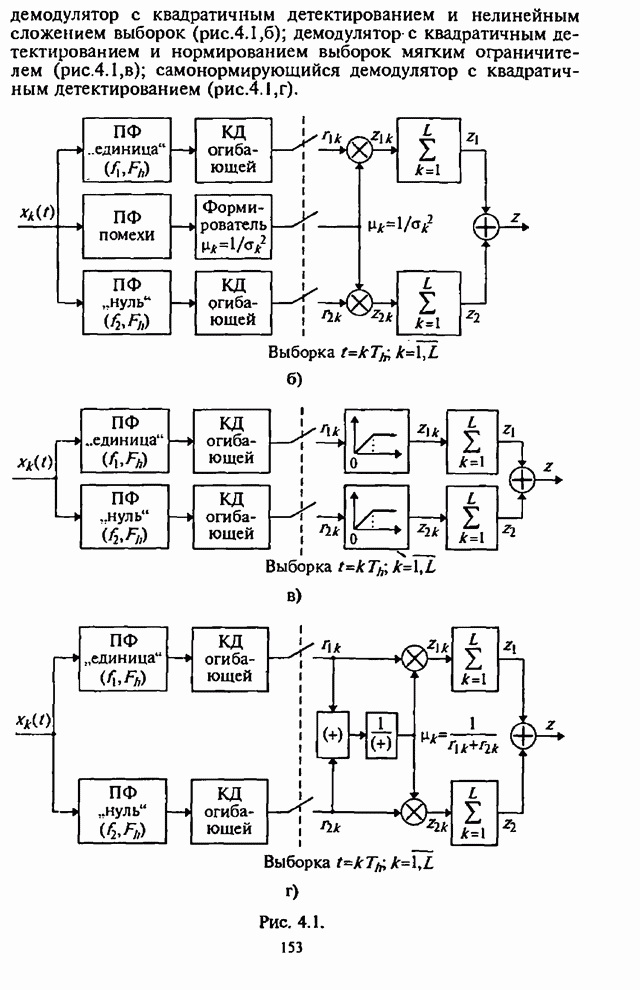
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
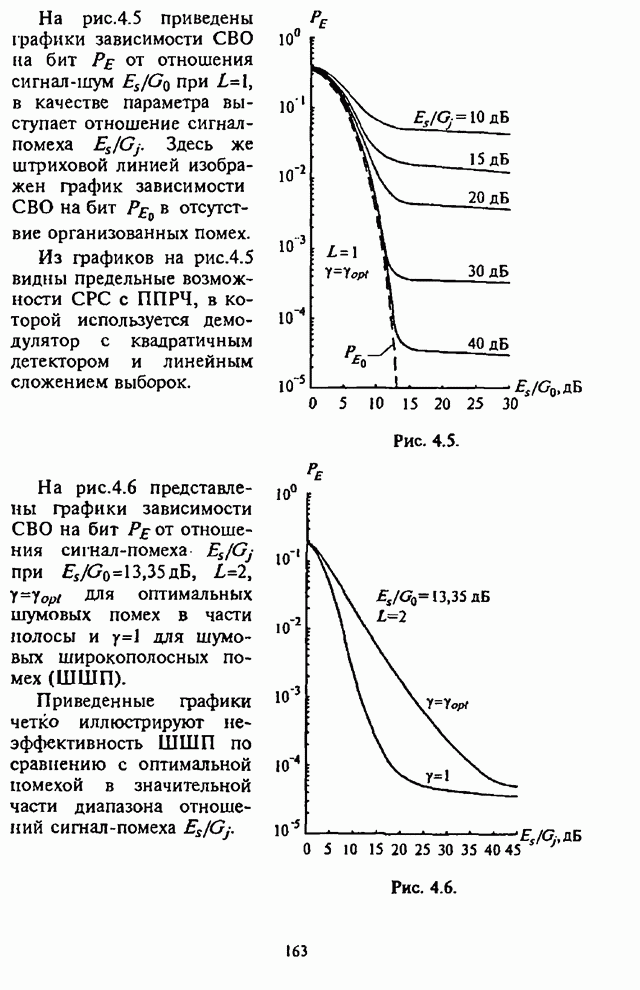
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
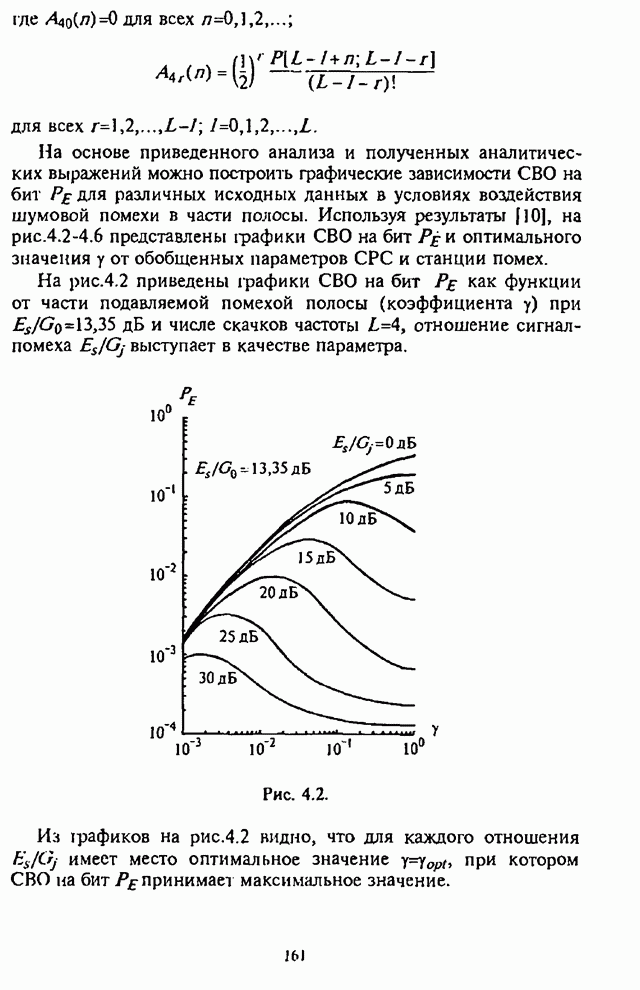
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
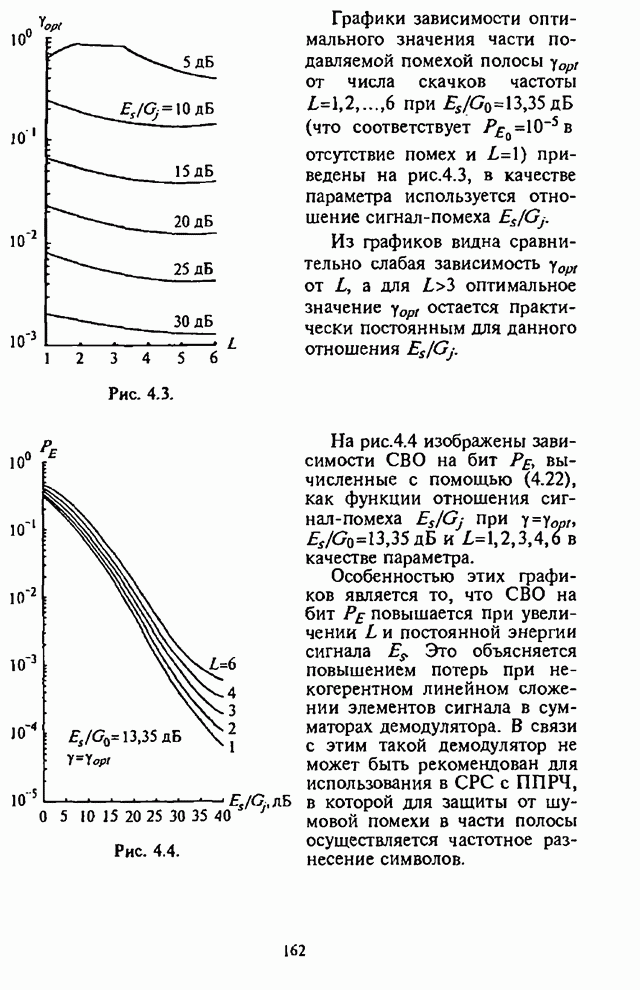
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
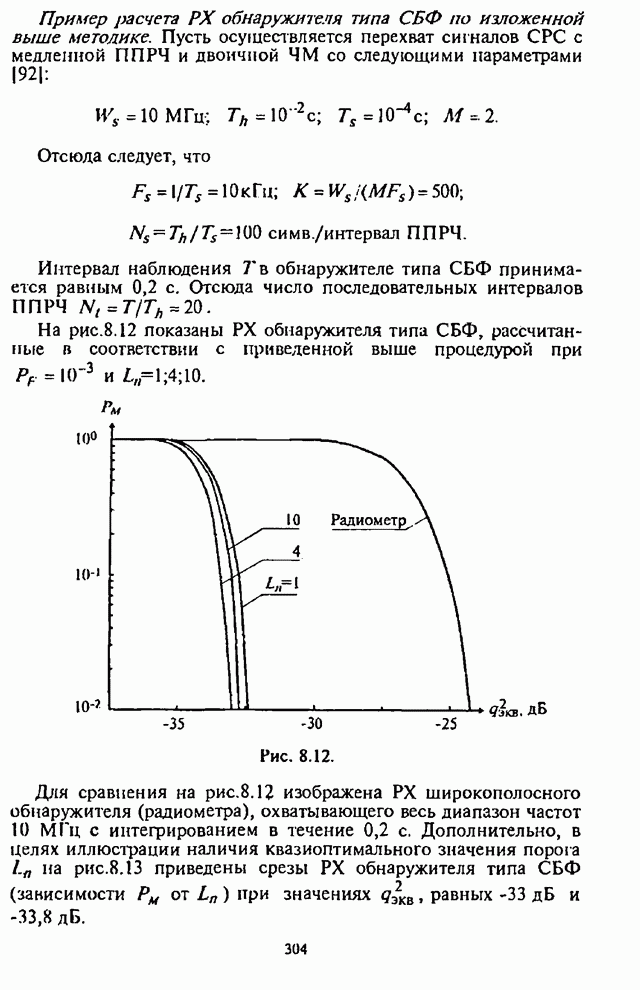
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
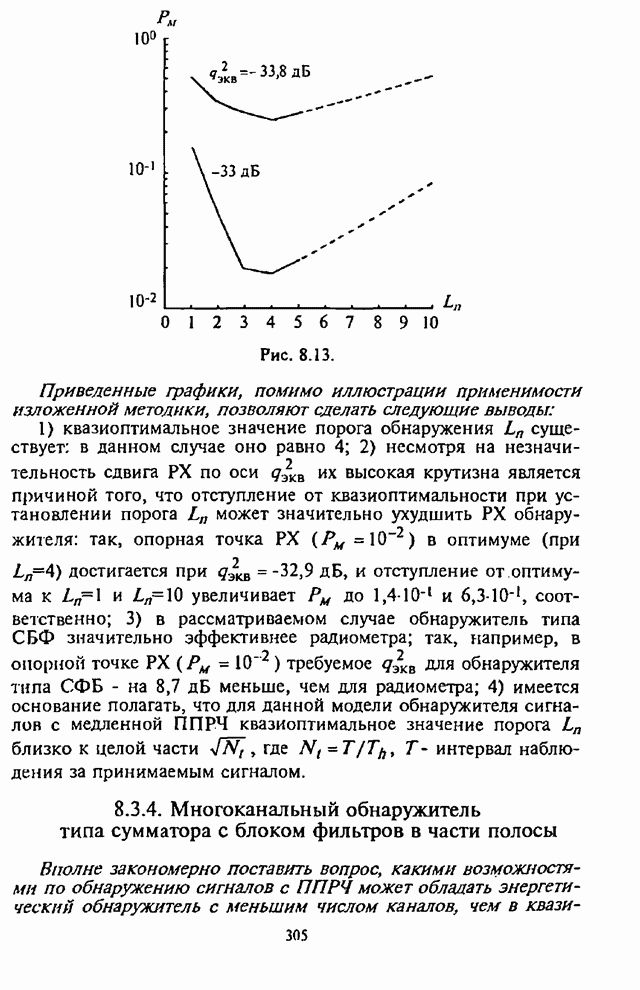
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
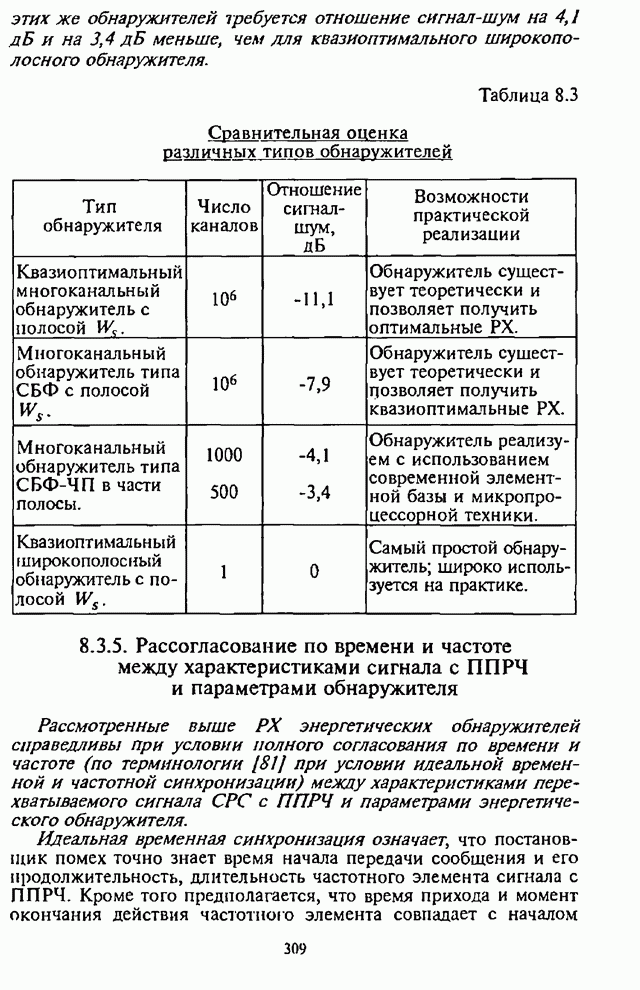
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
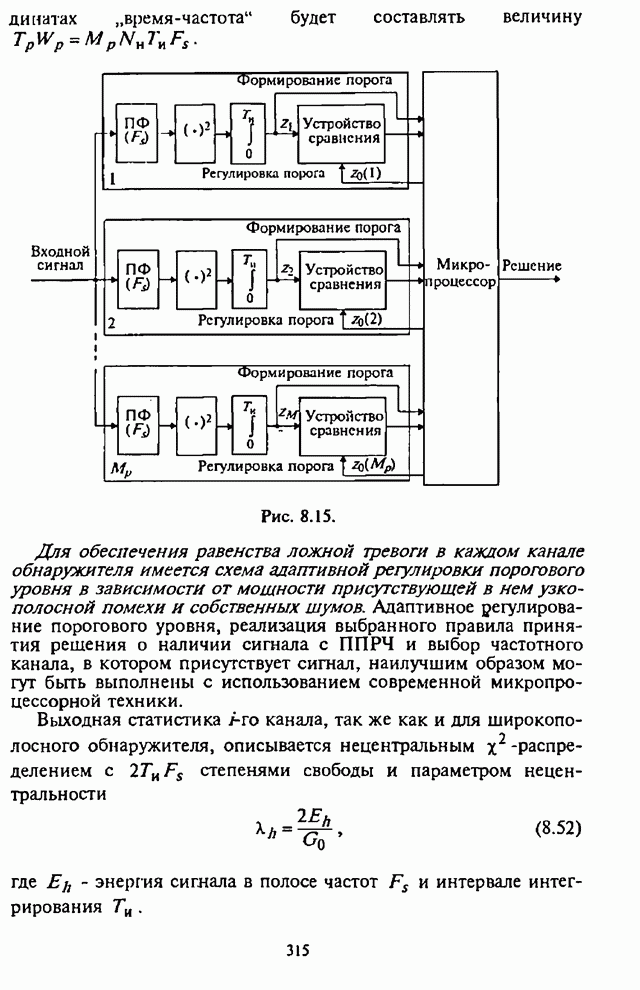
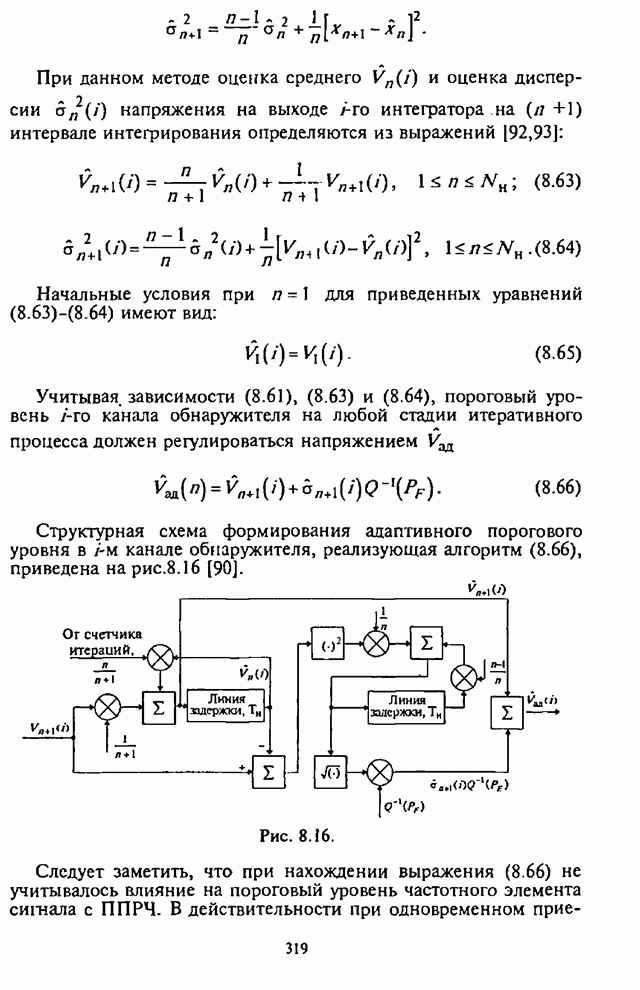
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
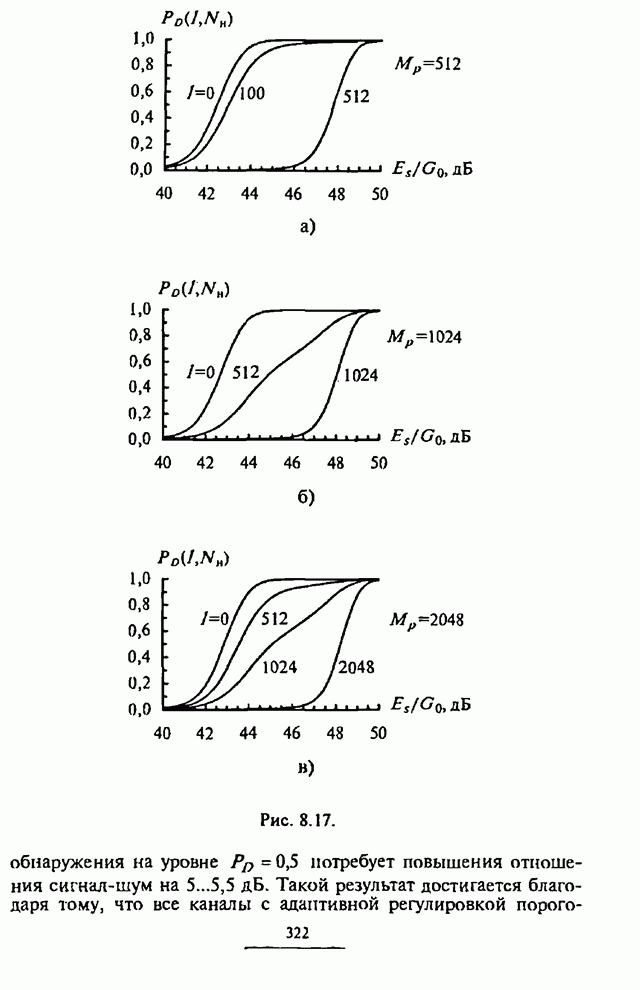
- 8.4.3. Вероятность обнаружения
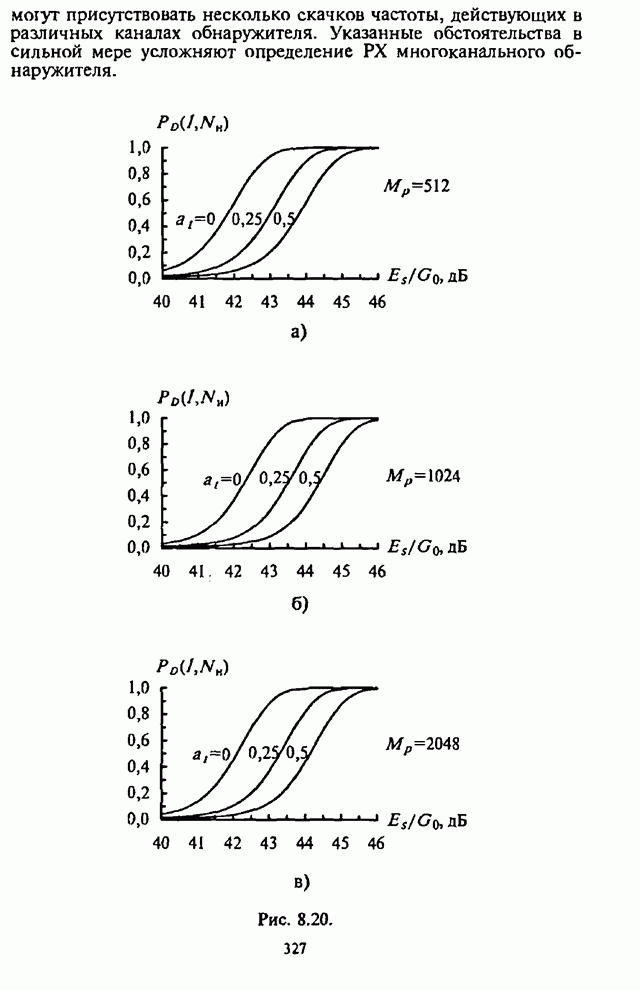
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
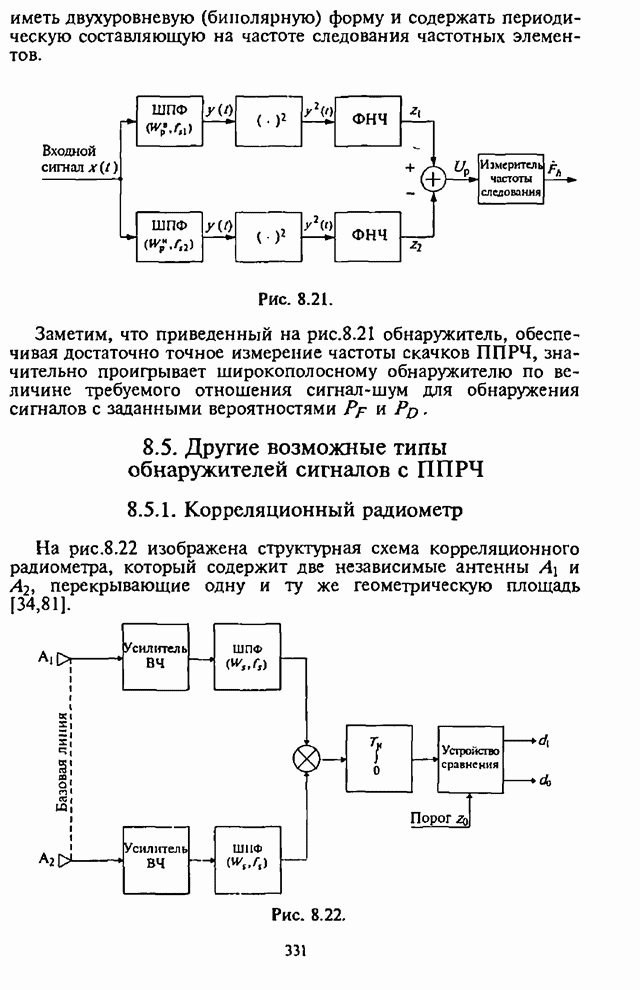
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ