| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
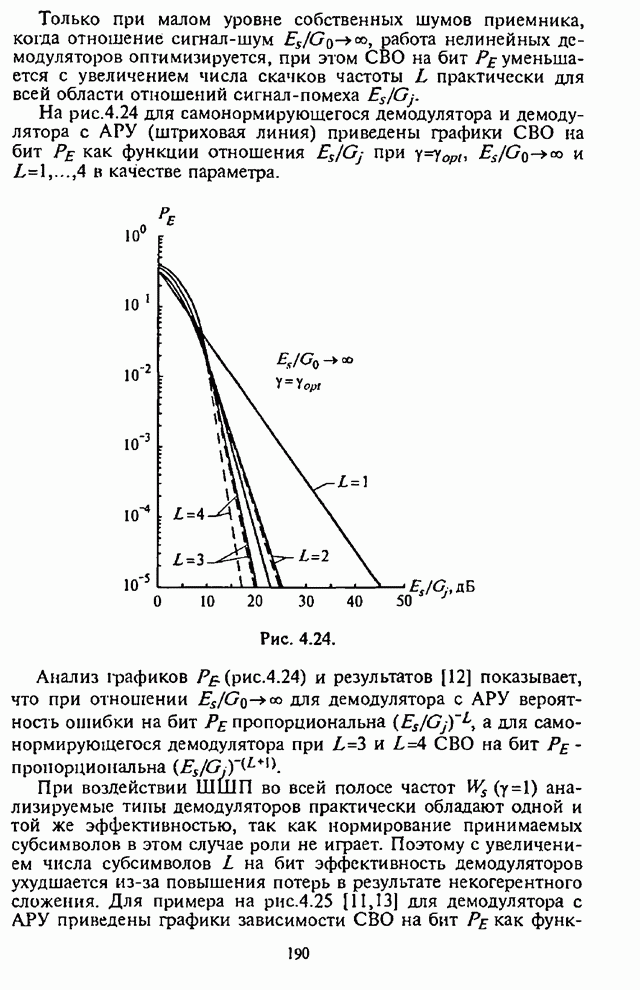
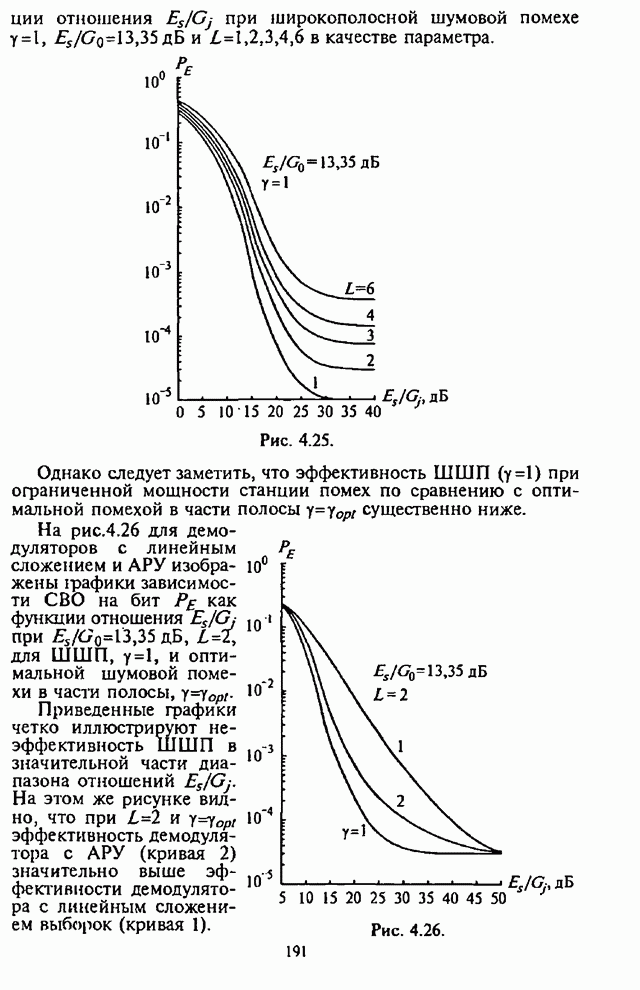
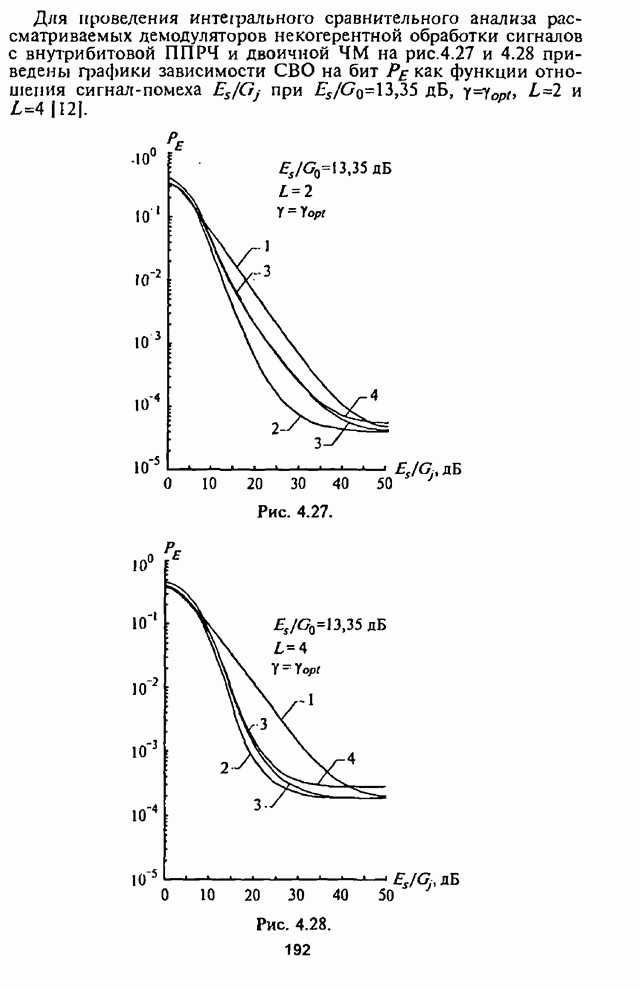
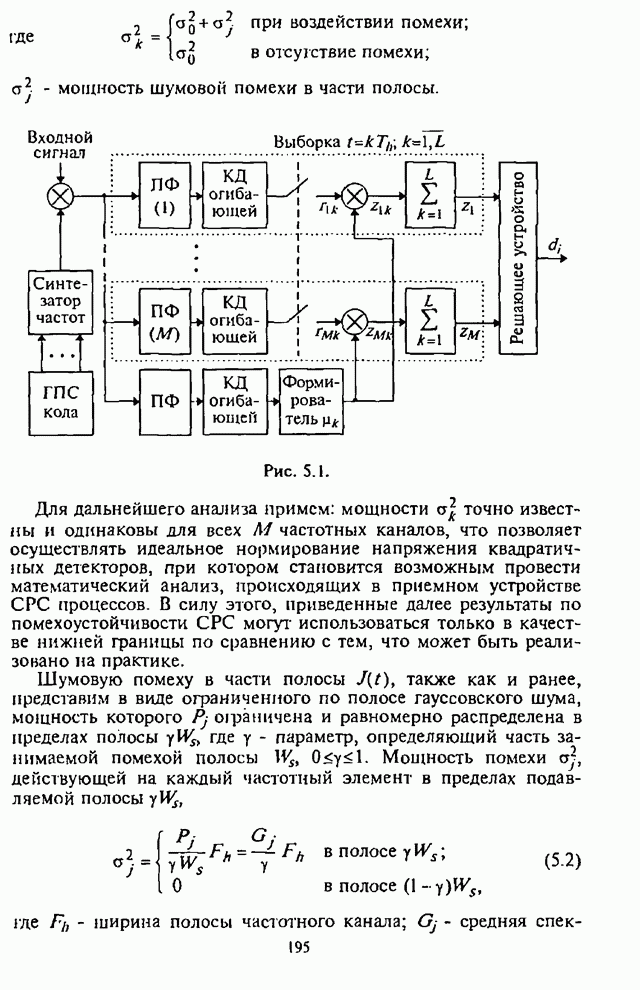
5.2.3. Анализ средней вероятности ошибки на бит информации
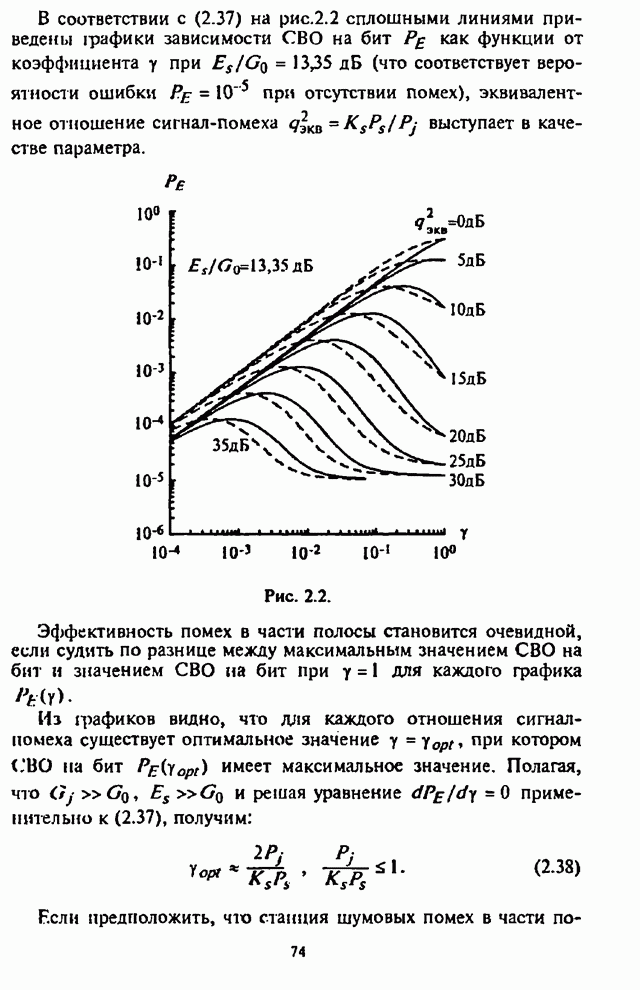
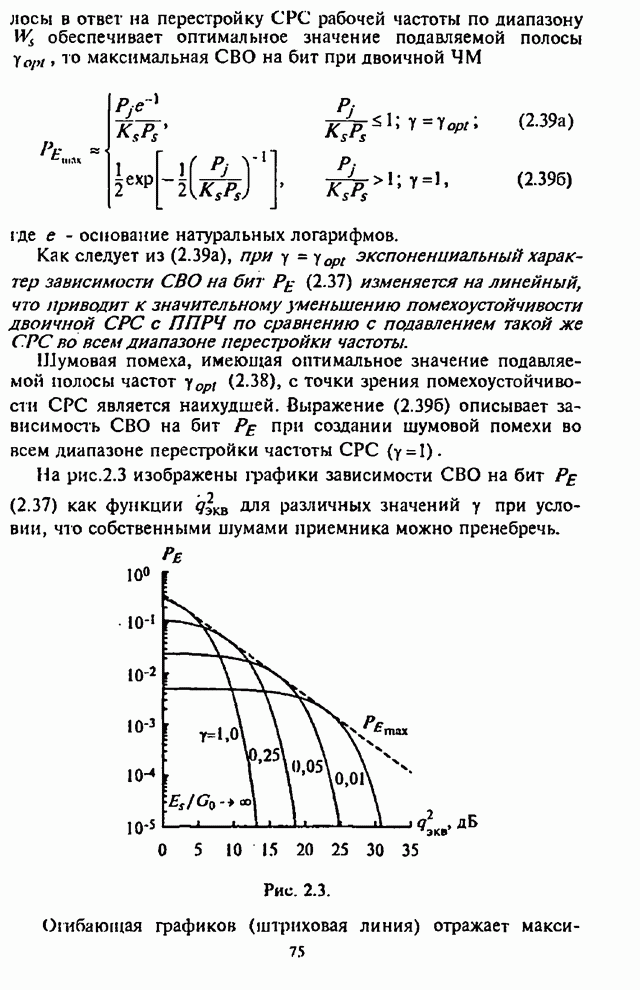
Используя выражение (5.26) и входящие в него
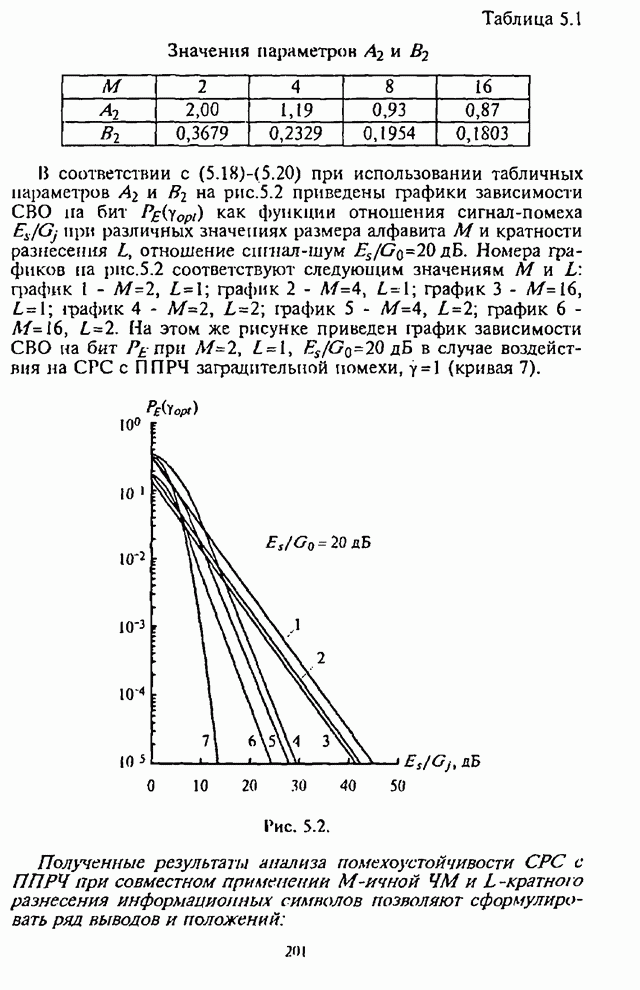
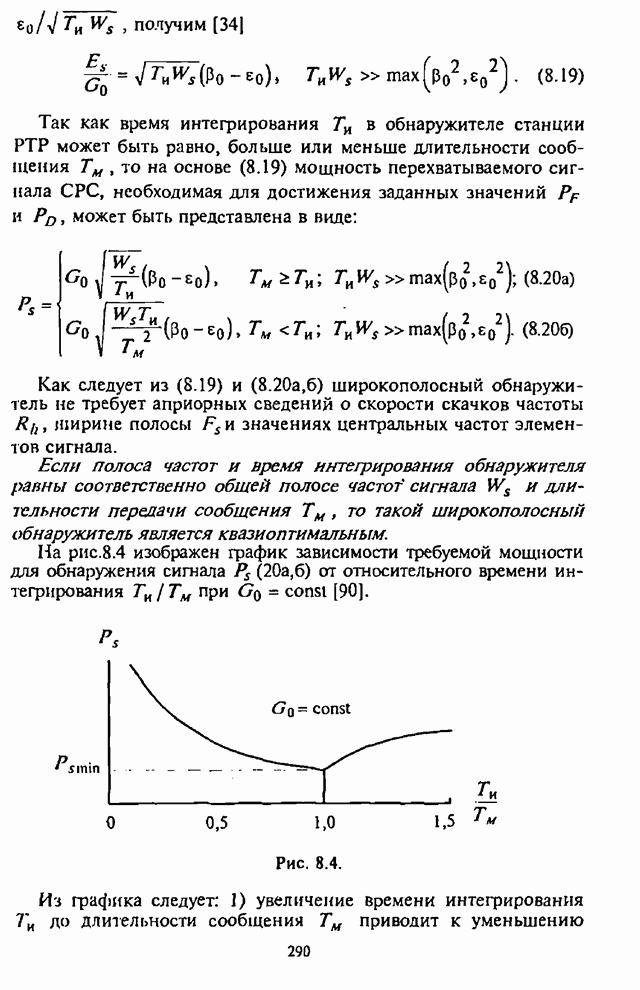
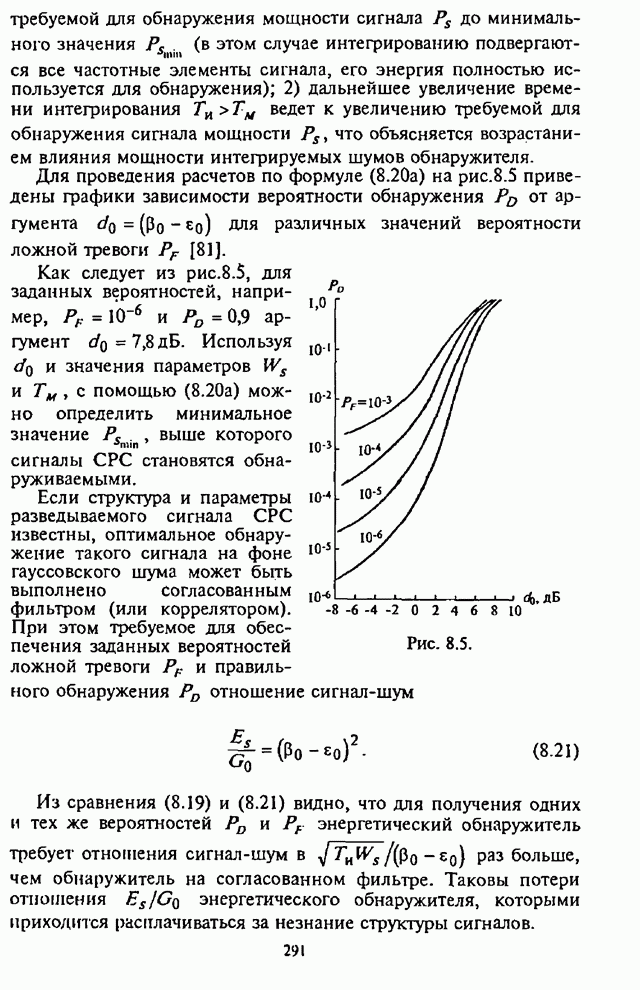
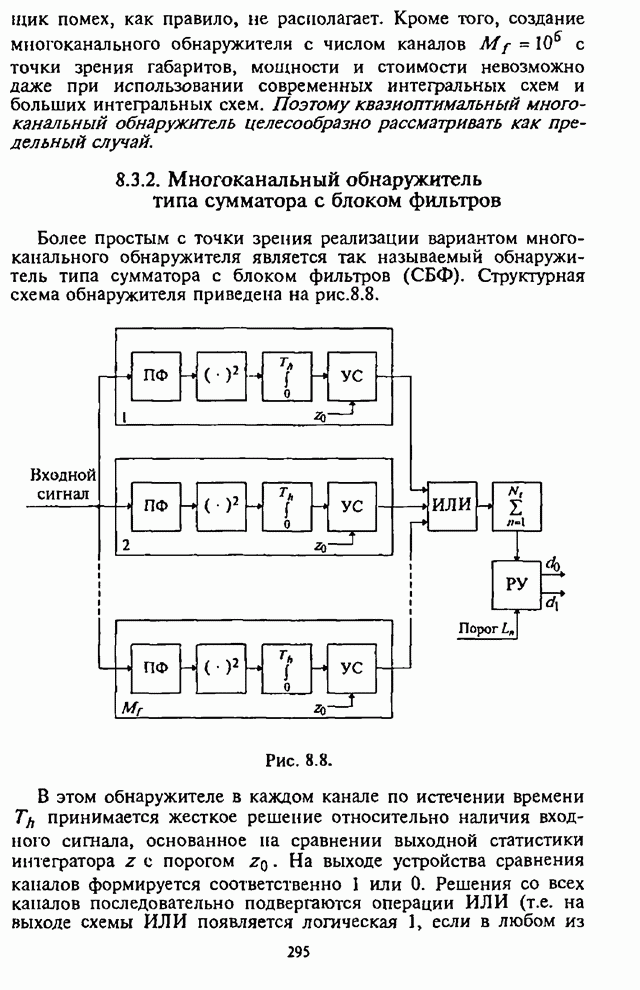
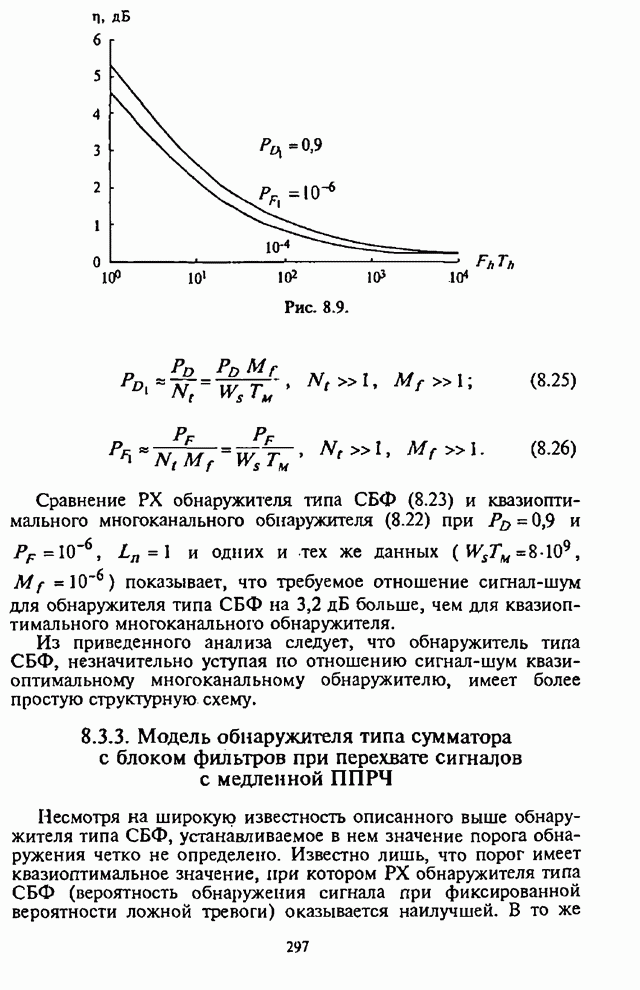
зависимости, характеризующие УВО на бит![]() , можно провести анализ СВО на бит информации
, можно провести анализ СВО на бит информации![]() . Однако применение в
СРС с ППРЧ помехоустойчивого кодирования наиболее эффективно в условиях
воздействия наихудших помех. Характеристику наихудших помех
. Однако применение в
СРС с ППРЧ помехоустойчивого кодирования наиболее эффективно в условиях
воздействия наихудших помех. Характеристику наихудших помех ![]() выбранного кода и заданных
значений
выбранного кода и заданных
значений ![]() ,
, ![]() и
и ![]() можно получить, решая
уравнение:
можно получить, решая
уравнение:
![]()
или, в крайнем случае, ![]() .
.
При этом задачу оптимизации можно решать
не только
для системы РЭП (относительно ![]() и
и
![]() ), когда определяется
функция
), когда определяется
функция ![]() , но и для СРС (относительно
, но и для СРС (относительно ![]() ). Для этого, очевидно, должны
быть найдена функция
). Для этого, очевидно, должны
быть найдена функция ![]() и соответствующие оптимальные
значения параметров
и соответствующие оптимальные
значения параметров ![]() . Из-за сложности и
многофакторности выражения (5.27) его оптимизация в явном виде затруднительна.
В этом случае задача оптимизации СВО на бит
. Из-за сложности и
многофакторности выражения (5.27) его оптимизация в явном виде затруднительна.
В этом случае задача оптимизации СВО на бит ![]() выбор параметров
выбор параметров ![]() и
и ![]() могут быть решены численным
методом. Учитывая изложенное и результаты [15], ниже приведены некоторые
количественные оценки воздействия наихудших помех на
могут быть решены численным
методом. Учитывая изложенное и результаты [15], ниже приведены некоторые
количественные оценки воздействия наихудших помех на ![]() -ичную СРС с ППРЧ, в которой
применяются блоковые коды и частотное разнесение кодовых слов.
-ичную СРС с ППРЧ, в которой
применяются блоковые коды и частотное разнесение кодовых слов.
При этом сравнение эффективности различных видов кодов производится при условии постоянной скорости передачи информации, так как применяемые в СРС коды и кратность разнесения кодового слова предназначаются для обеспечения помехоустойчивости СРС при заданной ограниченной энергии сигнала.
В табл.5.2 [15] приведены требуемые значения отношения
сигнал-помеха ![]() для СРС
с ППРЧ и двоичной ЧМ при использовании двоичных блоковых кодов, обеспечивающих
СВО на бит на уровне
для СРС
с ППРЧ и двоичной ЧМ при использовании двоичных блоковых кодов, обеспечивающих
СВО на бит на уровне ![]() , в условиях наихудшей шумовой помехи в части полосы
, в условиях наихудшей шумовой помехи в части полосы ![]() и оптимального частотного
разнесения кодового слова
и оптимального частотного
разнесения кодового слова ![]() .
.
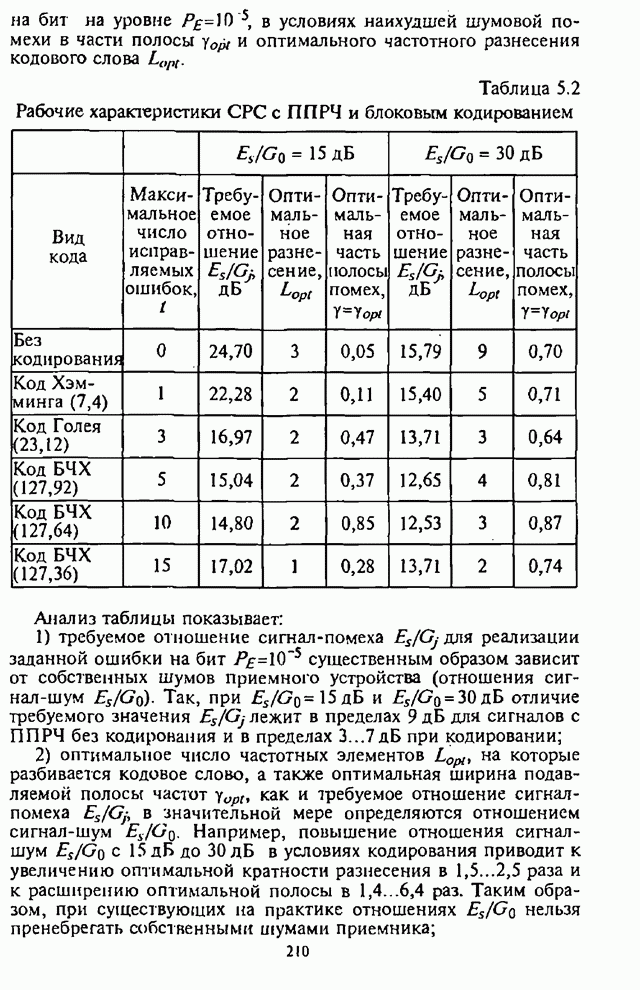
Таблица 5.2. Рабочие характеристики СРС с ППРЧ и блоковым кодированием
|
|
|
|
|
||||
|
Вид кода |
Максимальное число исправляемых ошибок, |
Требуемое отношение
дБ |
Оптимальное разнесение, |
Оптимальная часть полосы помех,
|
Требуемое отношение
дБ |
Оптимальное разнесение, |
Оптимальная часть полосы помех,
|
|
Без кодирования |
0 |
24,70 |
3 |
0,05 |
15,79 |
9 |
0,70 |
|
Код Хэм-минга (7,4) |
1 |
22,28 |
2 |
0,11 |
15,40 |
5 |
0,71 |
|
Код Голея (23,12) |
3 |
16,97 |
2 |
0,47 |
13,71 |
3 |
0,64 |
|
Код БЧХ (127,92) |
5 |
15,04 |
2 |
0,37 |
12,65 |
4 |
0,81 |
|
Код БЧХ (127,64) |
10 |
14,80 |
2 |
0,85 |
12,53 |
3 |
0,87 |
|
Код БЧХ (127,36) |
15 |
17,02 |
1 |
0,28 |
13,71 |
2 |
0,74 |
Анализ таблицы показывает:
1) требуемое отношение сигнал-помеха ![]() для реализации заданной ошибки на
бит
для реализации заданной ошибки на
бит ![]() существенным
образом зависит от собственных шумов приемного устройства (отношения сигнал-шум
существенным
образом зависит от собственных шумов приемного устройства (отношения сигнал-шум
![]() ). Так, при
). Так, при ![]() и
и ![]() отличие требуемого значения
отличие требуемого значения ![]() лежит в пределах 9 дБ для
сигналов с ППРЧ без кодирования и в пределах 3...7дБ при кодировании;
лежит в пределах 9 дБ для
сигналов с ППРЧ без кодирования и в пределах 3...7дБ при кодировании;
2) оптимальное число частотных элементов ![]() , на которые разбивается кодовое
слово, а также оптимальная ширина подавляемой полосы частот
, на которые разбивается кодовое
слово, а также оптимальная ширина подавляемой полосы частот ![]() , как и требуемое отношение
сигнал-помеха
, как и требуемое отношение
сигнал-помеха ![]() ;
в значительной мере
определяются отношением сигнал-шум
;
в значительной мере
определяются отношением сигнал-шум ![]() . Например, повышение отношения
сигнал-шум
. Например, повышение отношения
сигнал-шум ![]() с
15дБ до 30 дБ в условиях кодирования приводит к увеличению оптимальной
кратности разнесения в 1,5...2,5 раза и к расширению оптимальной полосы в
1,4...6,4 раз. Таким образом, при существующих на практике отношениях
с
15дБ до 30 дБ в условиях кодирования приводит к увеличению оптимальной
кратности разнесения в 1,5...2,5 раза и к расширению оптимальной полосы в
1,4...6,4 раз. Таким образом, при существующих на практике отношениях ![]() нельзя пренебрегать
собственными шумами приемника;
нельзя пренебрегать
собственными шумами приемника;
3) использование кодирования для СРС с ППРЧ и двоичной
ЧМ при заданной СВО на бит ![]() приводит, по сравнению с аналогичной СРС,
но без кодирования, к уменьшению требуемого отношения сигнал-помеха
приводит, по сравнению с аналогичной СРС,
но без кодирования, к уменьшению требуемого отношения сигнал-помеха ![]() . Так, использование кода БЧХ (127,64) позволяет снизить
требуемое отношение сигнал-помеха
. Так, использование кода БЧХ (127,64) позволяет снизить
требуемое отношение сигнал-помеха ![]() на 10 дБ при
на 10 дБ при ![]() и на 3,26
дБ при
и на 3,26
дБ при ![]() .
.
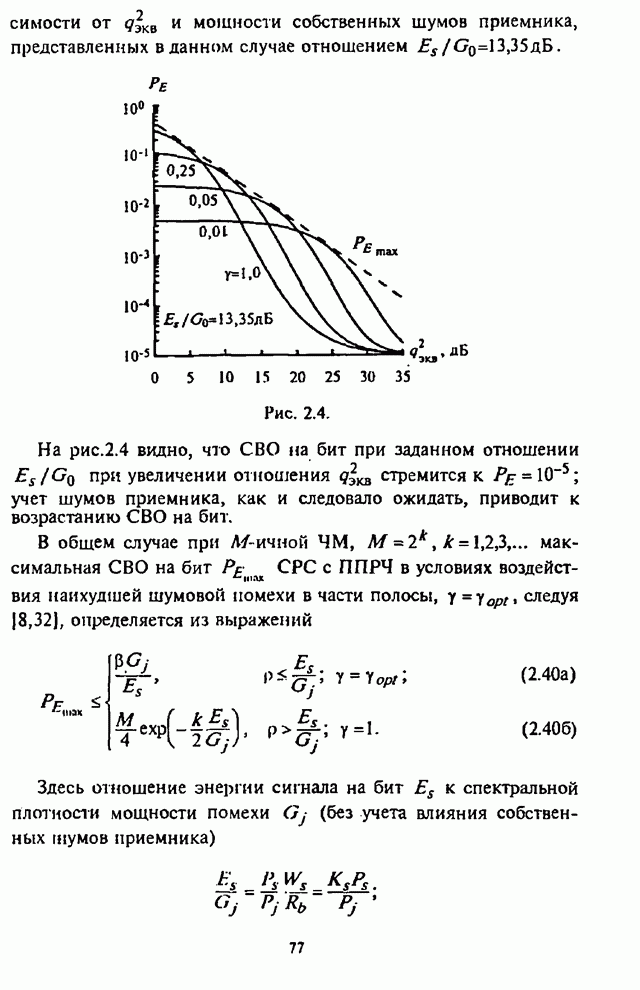
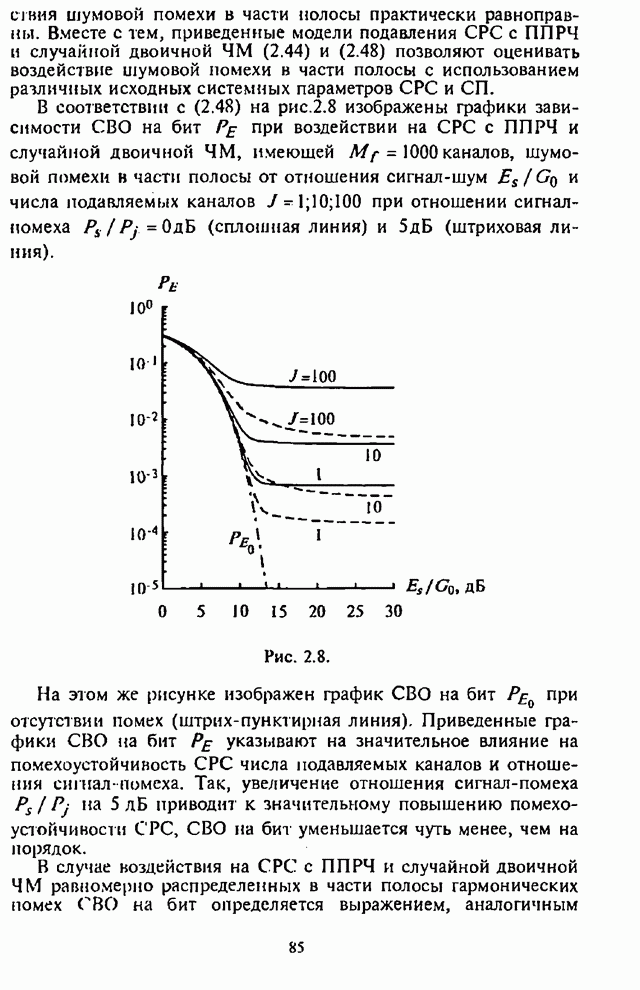
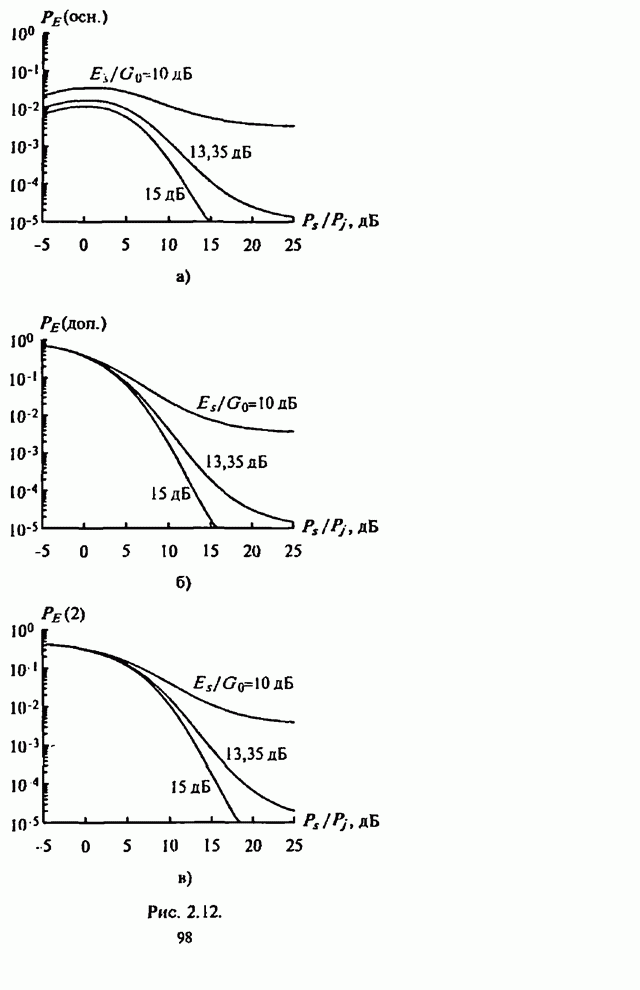
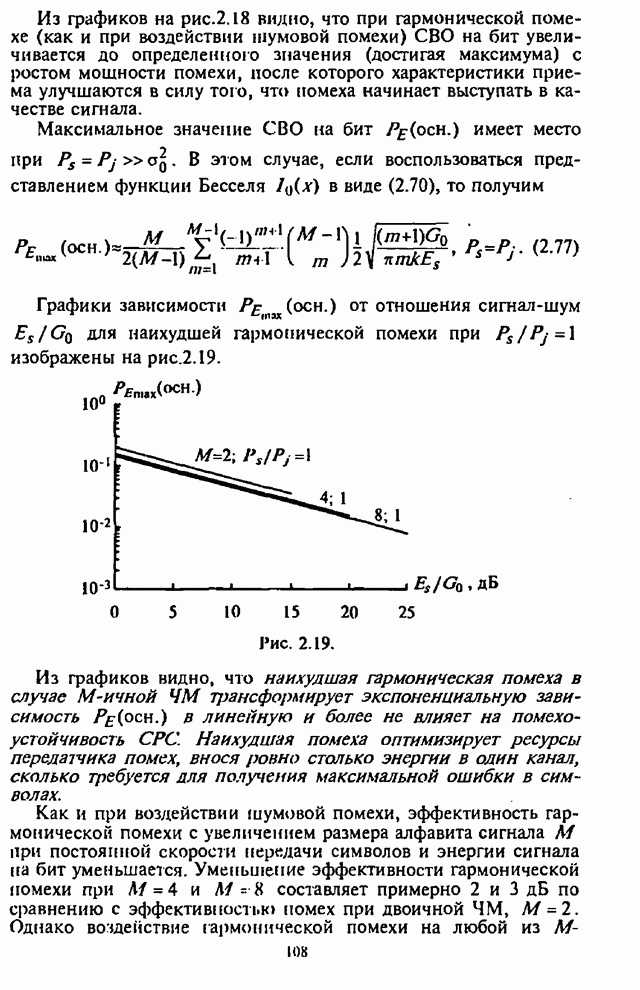
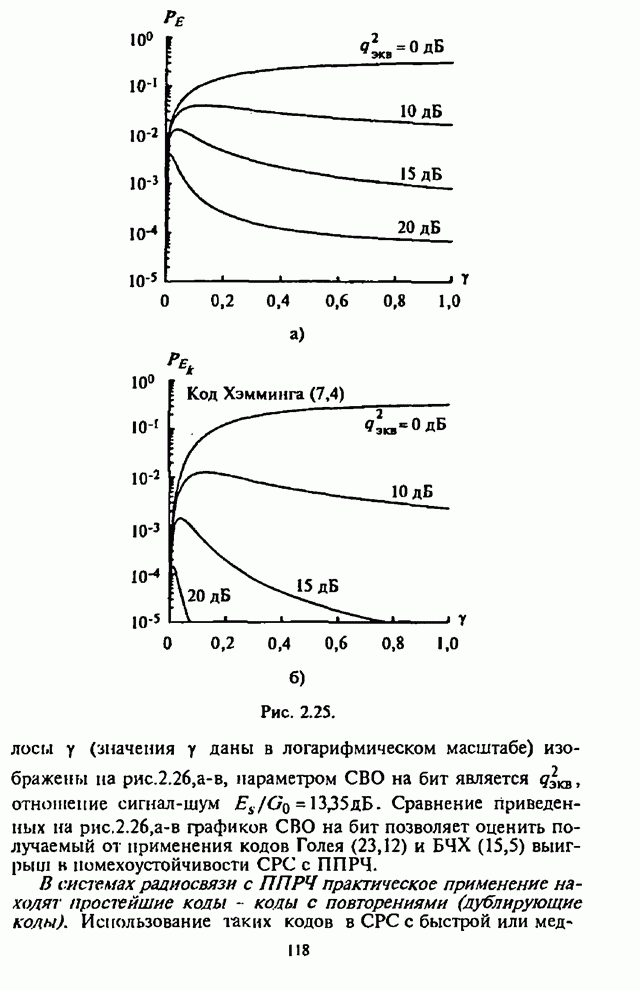
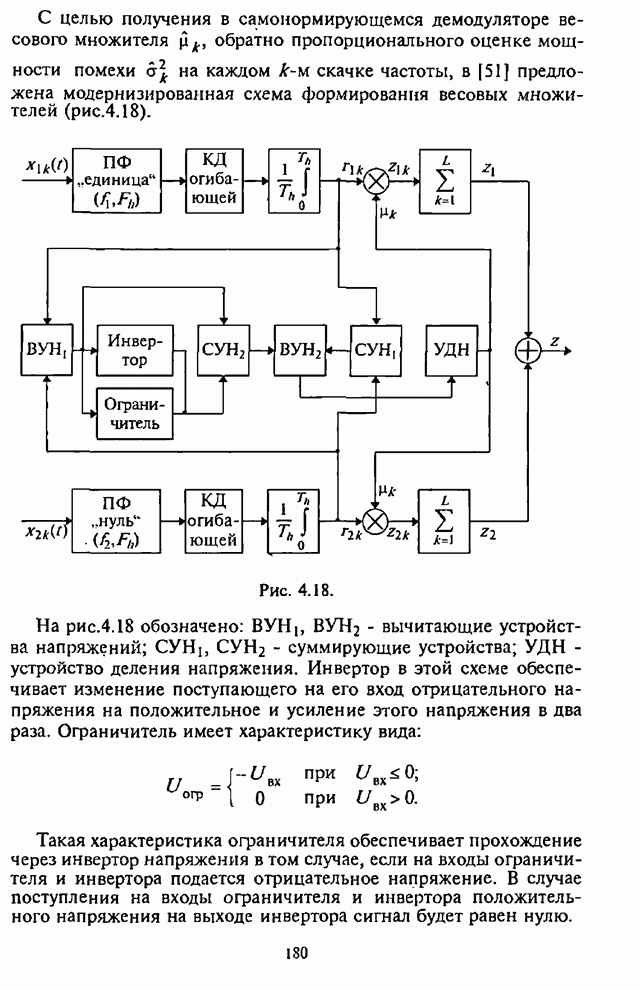
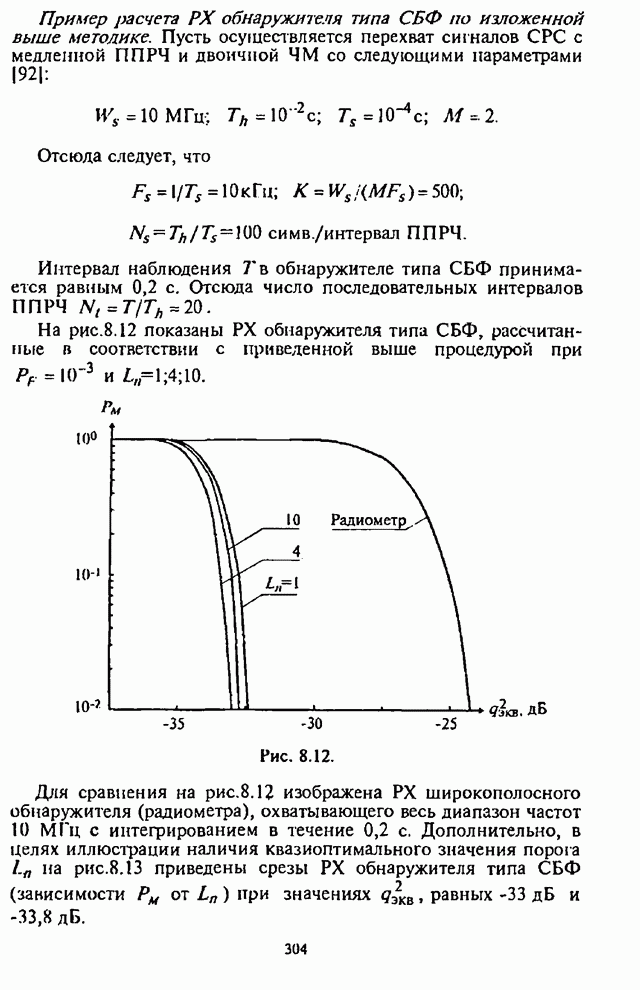
На рис.5.4-5.7, заимствованных из [15], изображены
трафики зависимости СВО на бит ![]() для СРС с ППРЧ и двоичной ЧМ в
условиях воздействия наихудших помех
для СРС с ППРЧ и двоичной ЧМ в
условиях воздействия наихудших помех ![]() при использовании блоковых
кодов с параметрами из табл.5.2 с оптимальным разнесением кодового слова на
при использовании блоковых
кодов с параметрами из табл.5.2 с оптимальным разнесением кодового слова на ![]() частотных составляющих.
частотных составляющих.

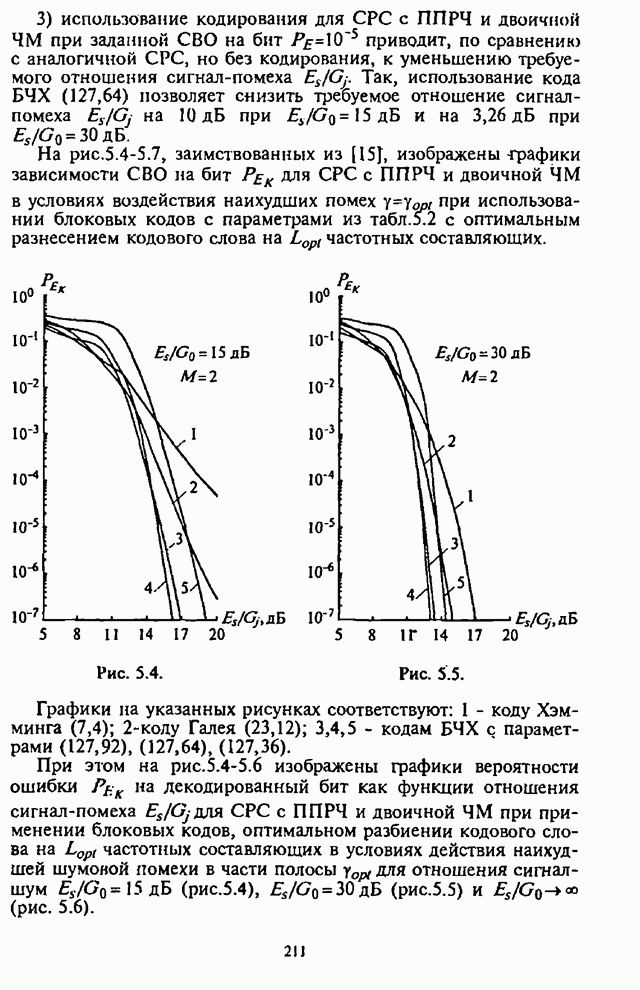
Рис. 5.4. Рис. 5.5.
Графики на указанных рисунках соответствуют: 1 - коду Хэмминга (7,4); 2 - коду Галея (23,12); 3,4,5 - кодам БЧХ с параметрами (127,92), (127,64), (127,36).
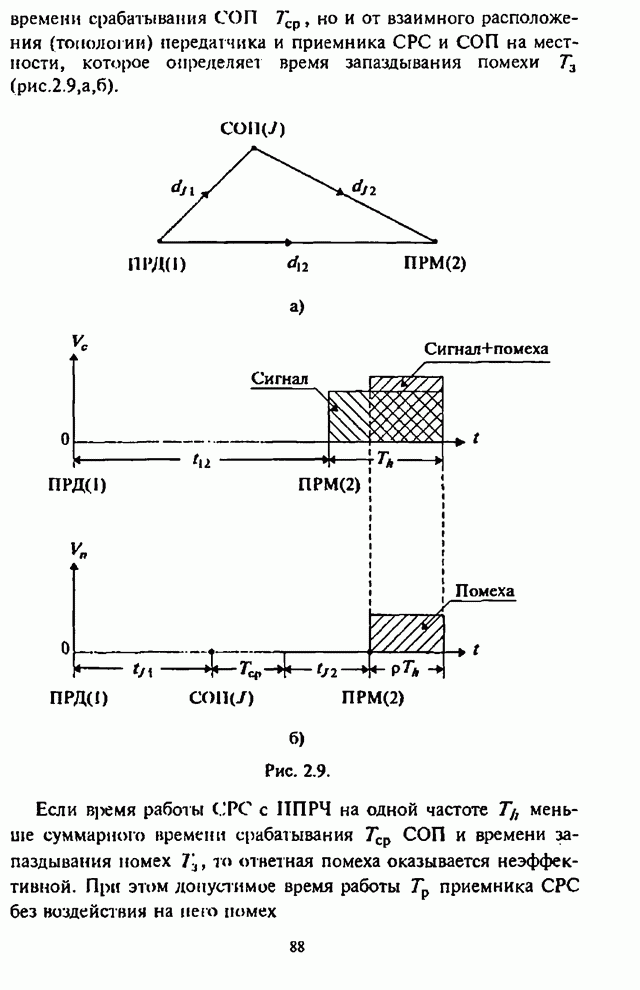
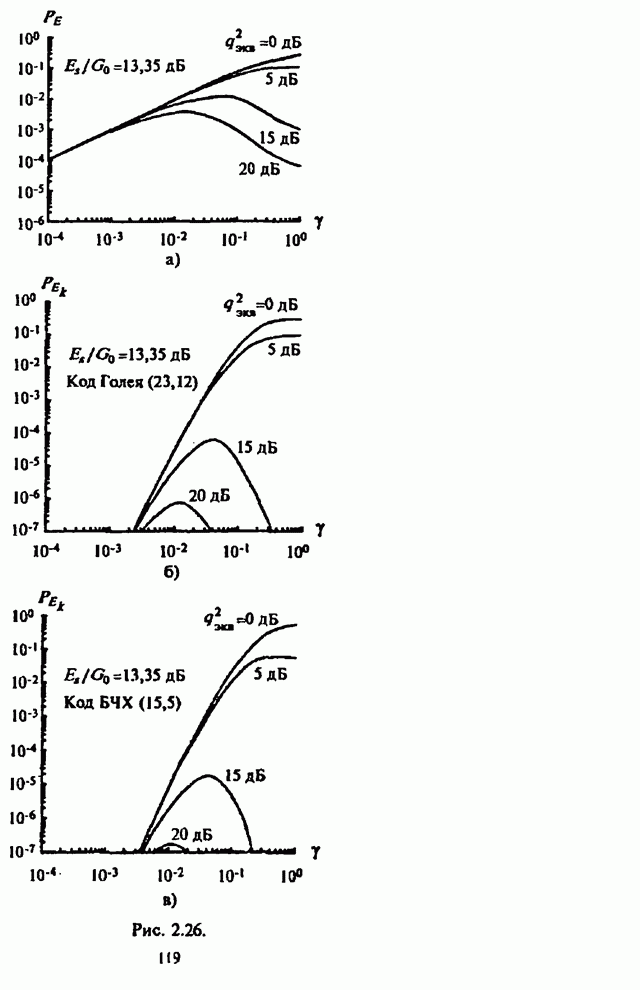
При этом на рис.5.4-5.6 изображены графики вероятности
ошибки ![]() на декодированный бит как
функции отношения сигнал-помеха
на декодированный бит как
функции отношения сигнал-помеха ![]() для СРС с ППРЧ и двоичной ЧМ при
применении блоковых кодов, оптимальном разбиении кодового слова на
для СРС с ППРЧ и двоичной ЧМ при
применении блоковых кодов, оптимальном разбиении кодового слова на ![]() частотных составляющих в
условиях действия наихудшей шумовой помехи в части полосы
частотных составляющих в
условиях действия наихудшей шумовой помехи в части полосы ![]() для отношения сигнал-шум
для отношения сигнал-шум ![]() (рис.5.4),
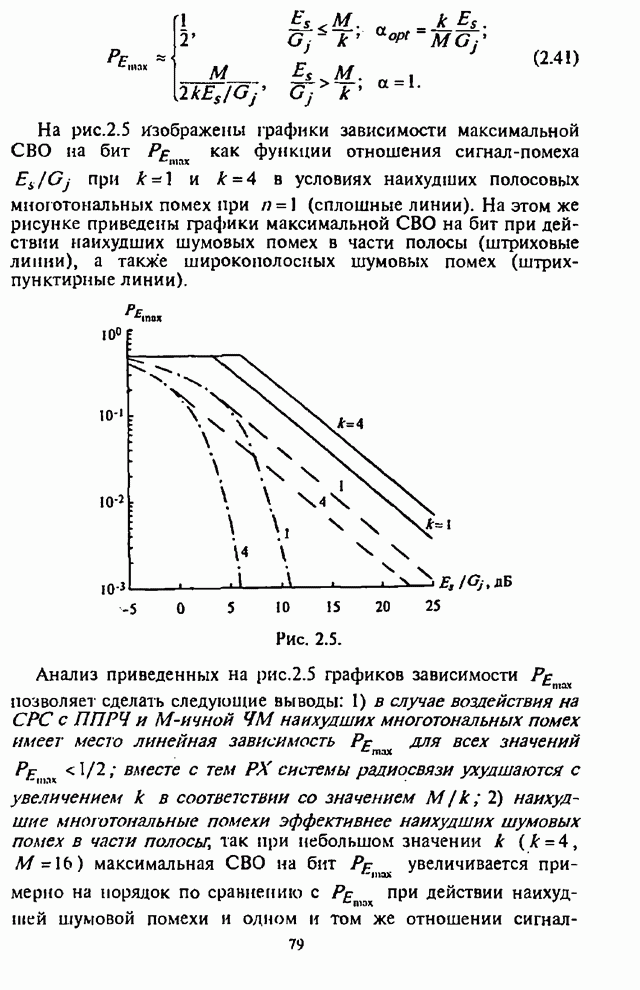
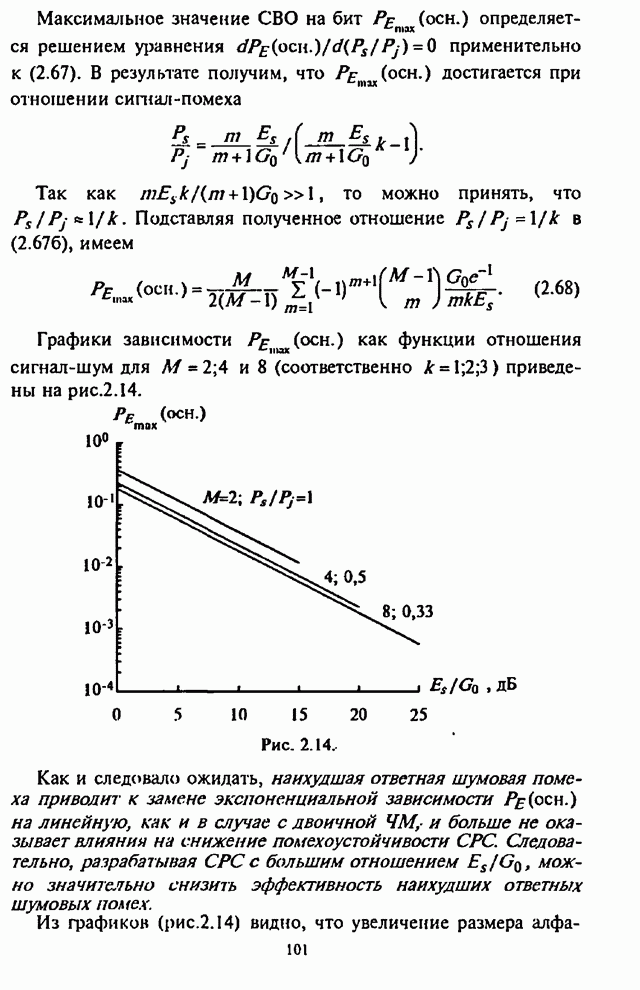
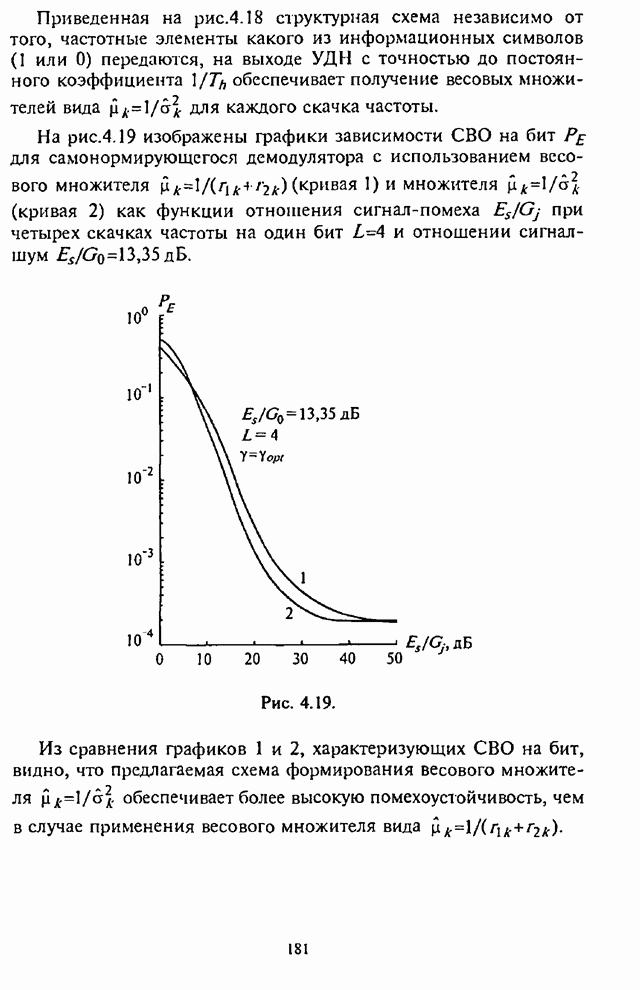
(рис.5.4), ![]() (рис.5.5) и
(рис.5.5) и ![]() (рис. 5.6).
(рис. 5.6).

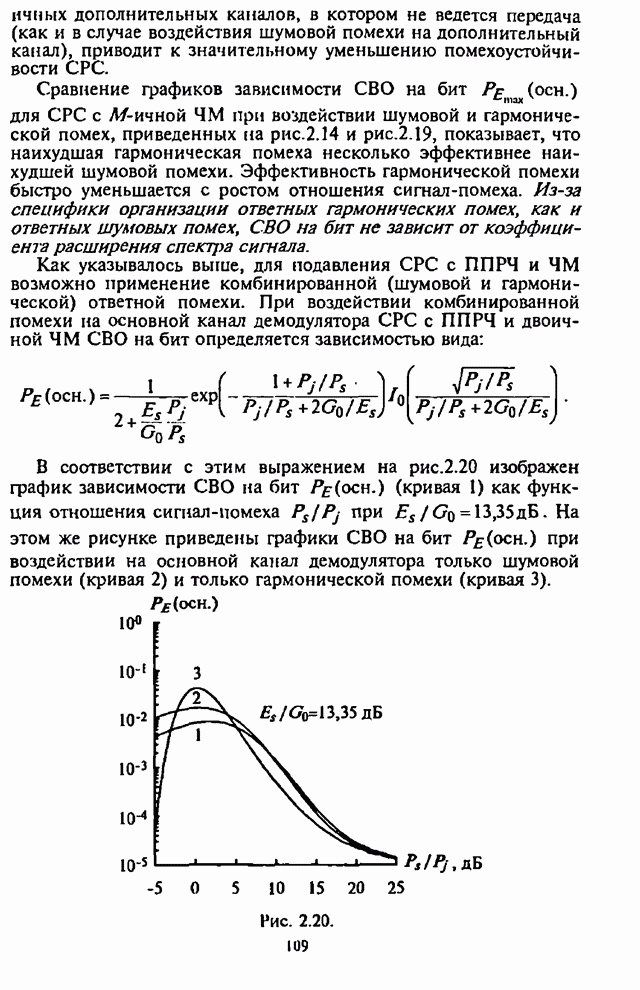
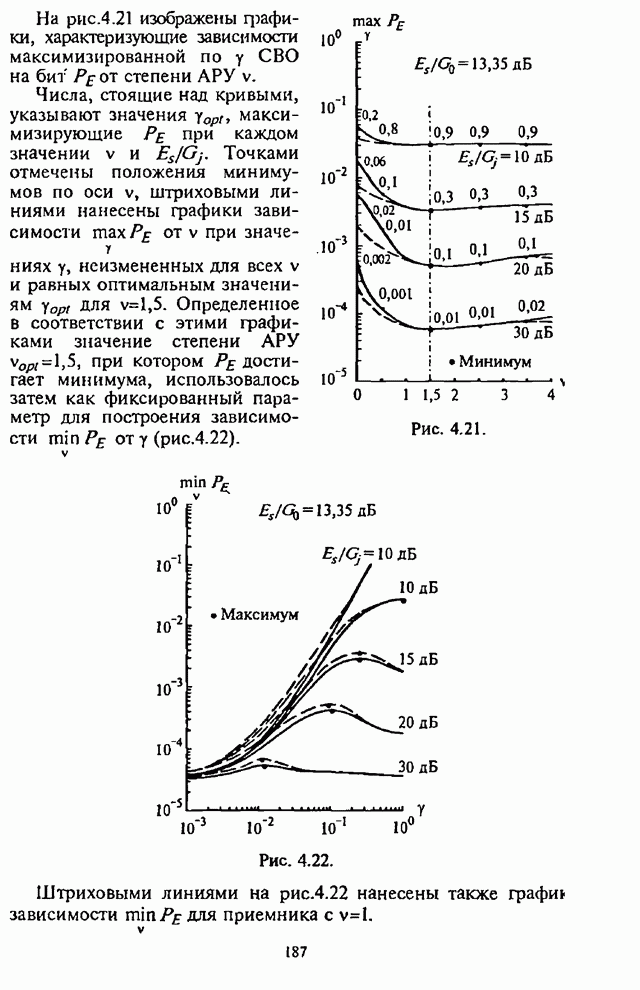
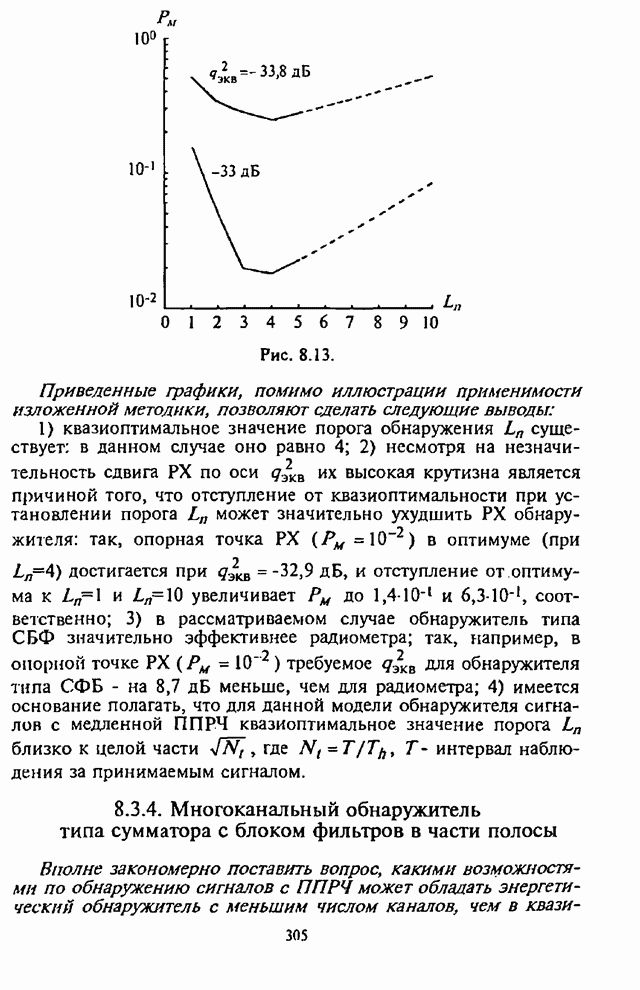
Рис. 5.6. Рис. 5.7.
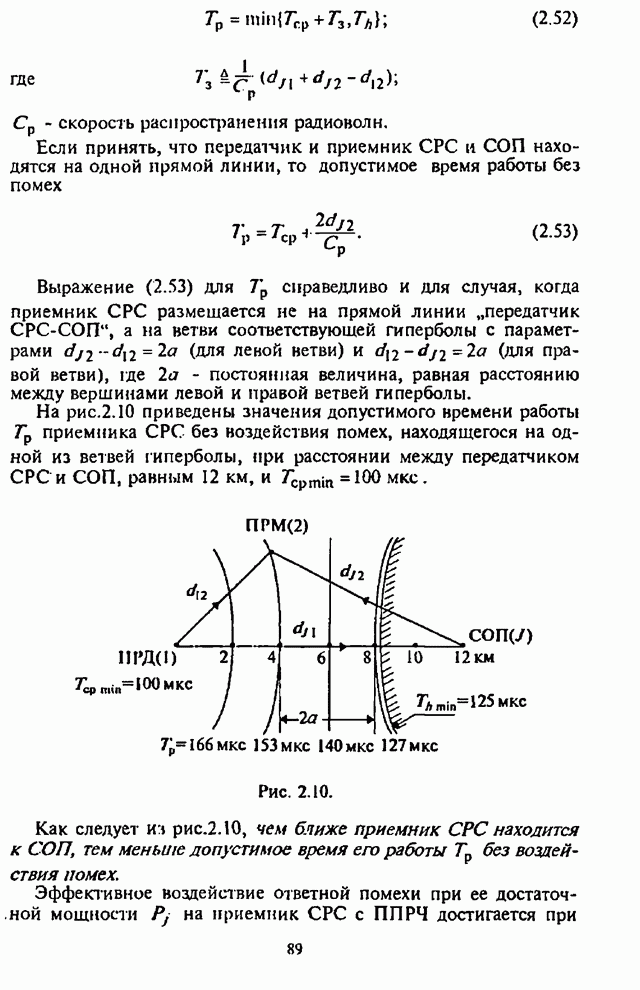
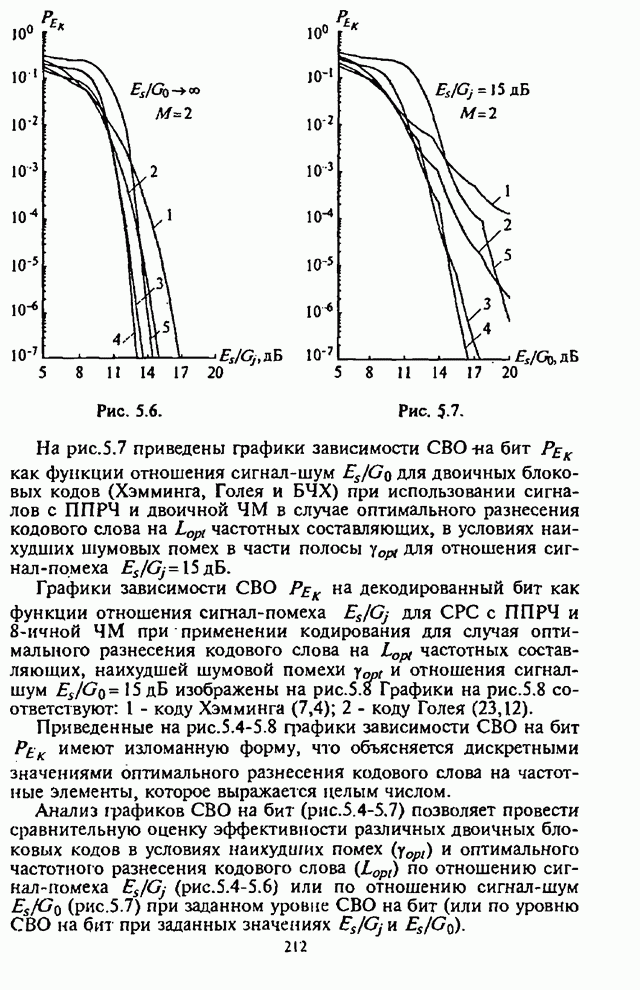
На рис.5.7 приведены графики
зависимости СВО на бит ![]() как
функции отношения сигнал-шум
как
функции отношения сигнал-шум ![]() для двоичных блоковых кодов
(Хэмминга, Голея и БЧХ) при использовании сигналов с ППРЧ и двоичной ЧМ в
случае оптимального разнесения кодового слова на
для двоичных блоковых кодов
(Хэмминга, Голея и БЧХ) при использовании сигналов с ППРЧ и двоичной ЧМ в
случае оптимального разнесения кодового слова на ![]() частотных
составляющих, в условиях наихудших шумовых помех в части полосы
частотных
составляющих, в условиях наихудших шумовых помех в части полосы ![]() для отношения сигнал-помеха
для отношения сигнал-помеха ![]() .
.
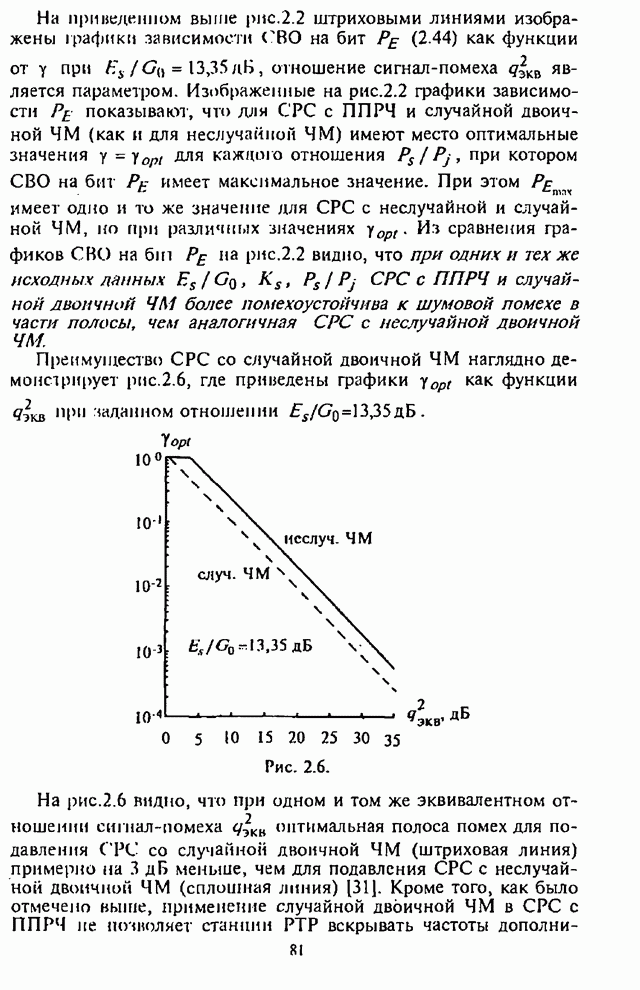
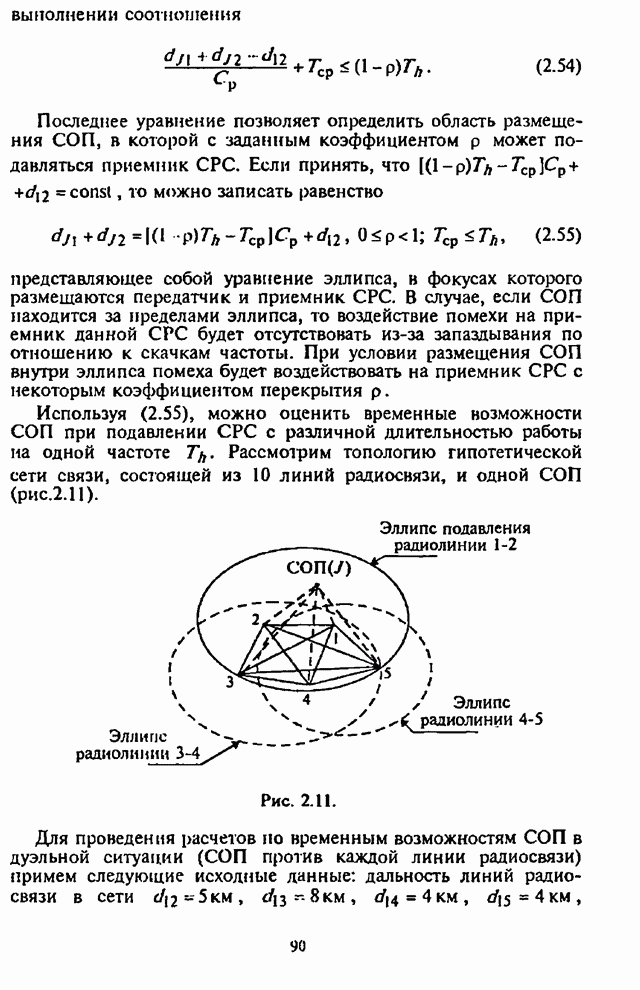
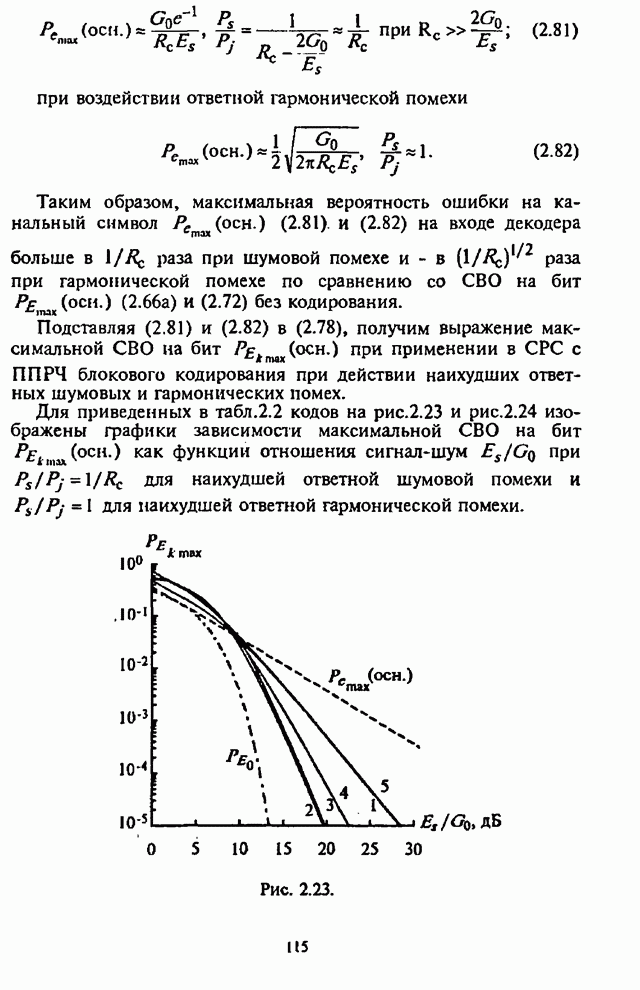
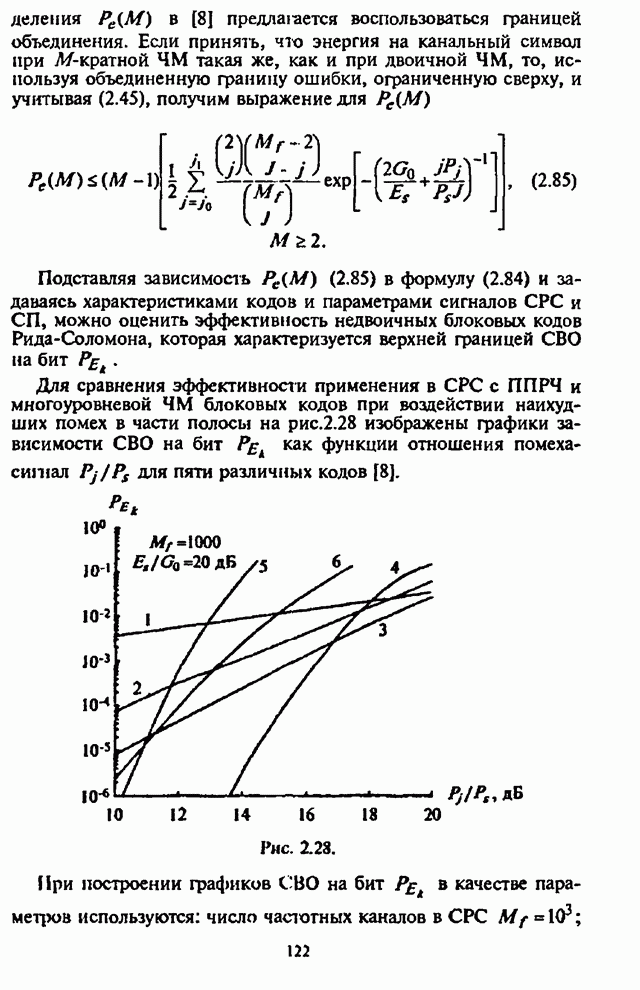
Графики зависимости СВО ![]() на декодированный бит как функции
отношения сигнал-помеха
на декодированный бит как функции
отношения сигнал-помеха ![]() для СРС с
ППРЧ и 8-ичной ЧМ при применении
кодирования для случая оптимального разнесения кодового слова на
для СРС с
ППРЧ и 8-ичной ЧМ при применении
кодирования для случая оптимального разнесения кодового слова на ![]() частотных составляющих, наихудшей
шумовой помехи
частотных составляющих, наихудшей
шумовой помехи ![]() и
отношения сигнал-шум
и
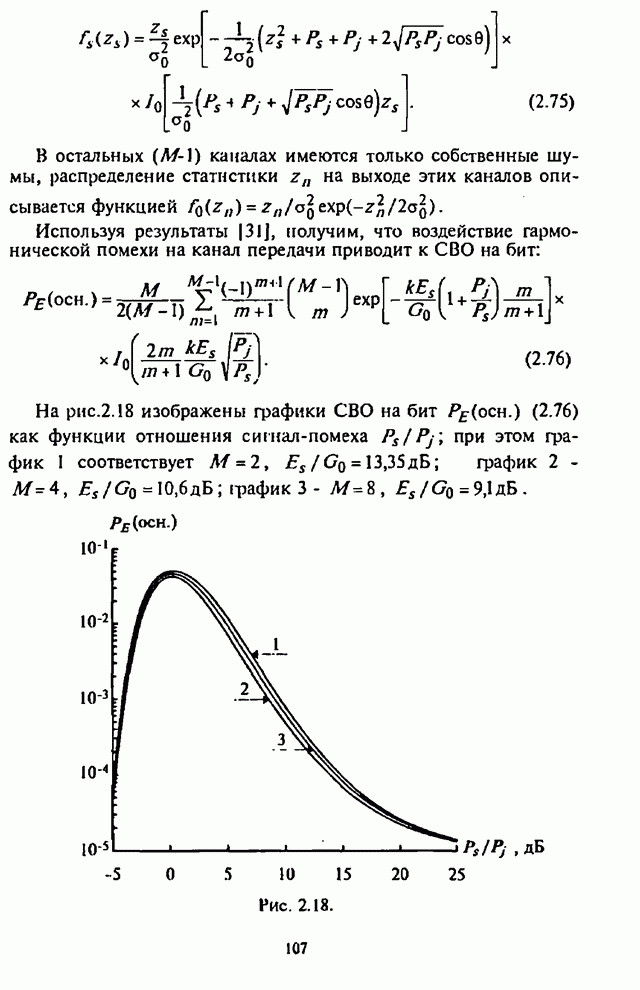
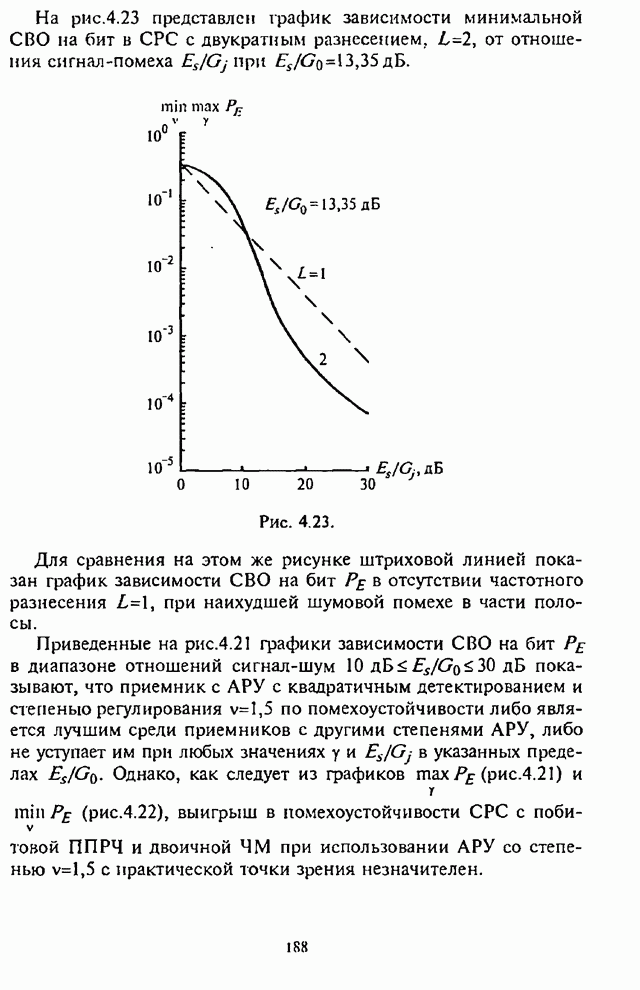
отношения сигнал-шум ![]() изображены на рис.5.8 Графики на рис.5.8
соответствуют: 1 - коду Хэмминга (7,4); 2 - коду Голея (23,12).
изображены на рис.5.8 Графики на рис.5.8
соответствуют: 1 - коду Хэмминга (7,4); 2 - коду Голея (23,12).
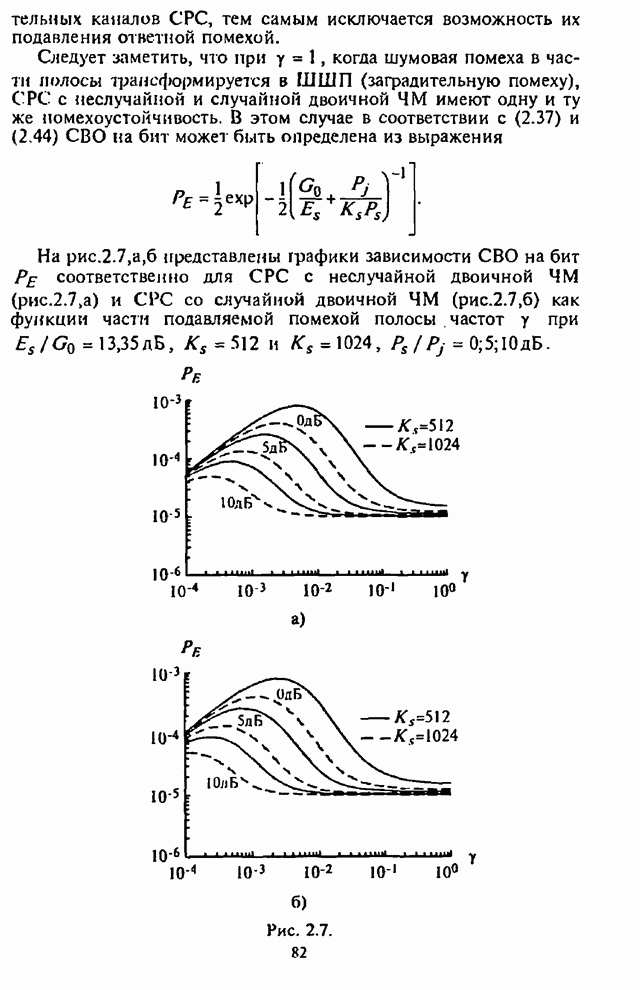
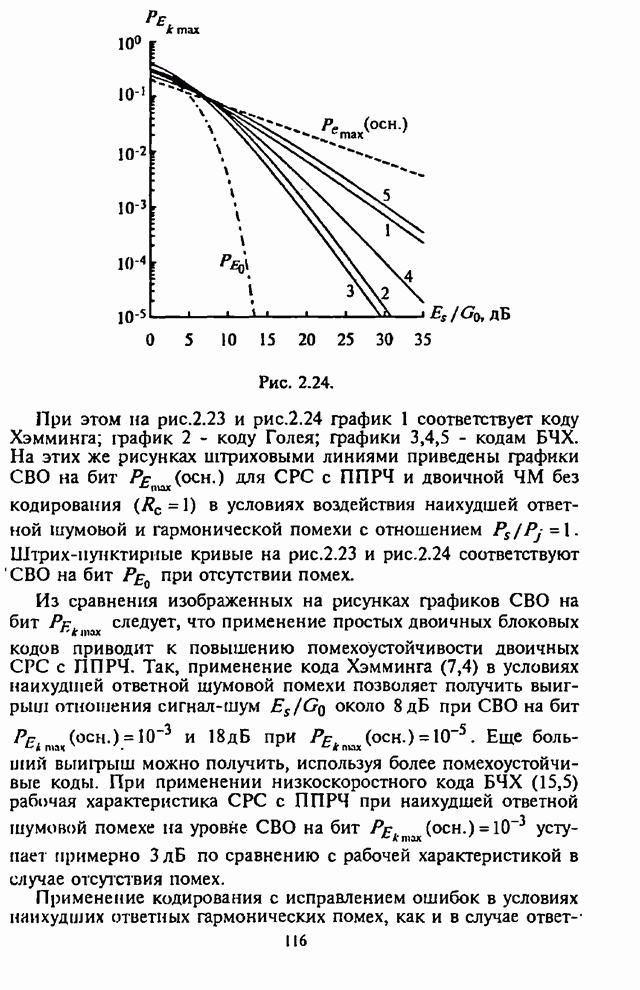
Приведенные на рис.5.4-5.8 графики
зависимости СВО на бит ![]() имеют
изломанную форму, что объясняется дискретными значениями оптимального
разнесения кодового слова на частотные элементы, которое выражается целым
числом.
имеют
изломанную форму, что объясняется дискретными значениями оптимального
разнесения кодового слова на частотные элементы, которое выражается целым
числом.
Анализ графиков СВО на бит
(рис.5.4-5.7) позволяет провести сравнительную оценку эффективности различных
двоичных блоковых кодов в условиях наихудших помех ![]() и оптимального частотного
разнесения кодового слова
и оптимального частотного
разнесения кодового слова ![]() по
отношению сигнал-помеха
по
отношению сигнал-помеха ![]() (рис.5.4-5.6)
или по отношению сигнал-шум
(рис.5.4-5.6)
или по отношению сигнал-шум ![]() (рис.5.7)
при заданном уровне СВО на бит (или по уровню СВО на бит при заданных значениях
(рис.5.7)
при заданном уровне СВО на бит (или по уровню СВО на бит при заданных значениях
![]() и
и ![]() ).
).

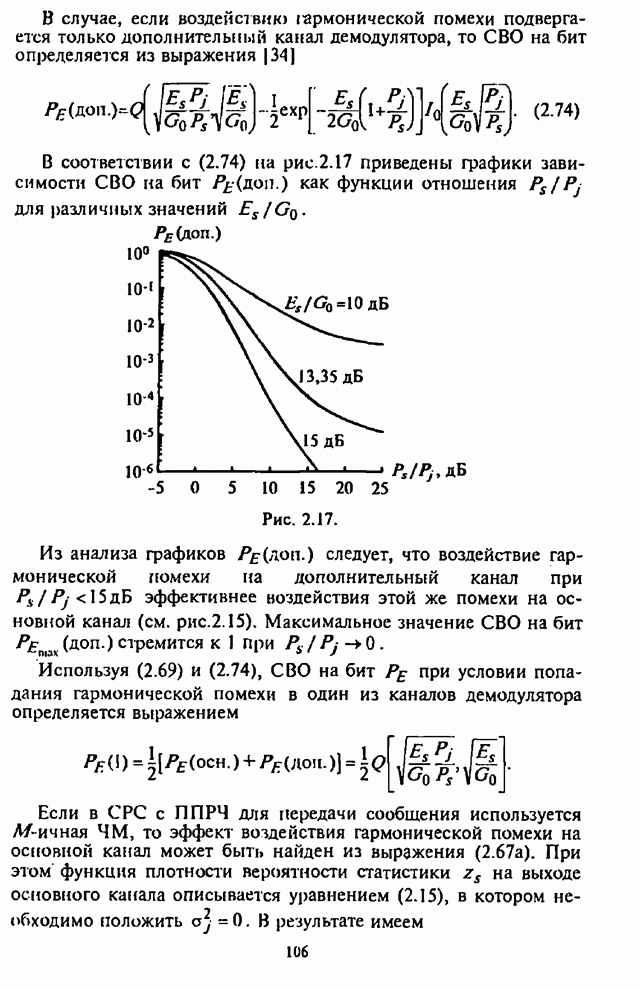
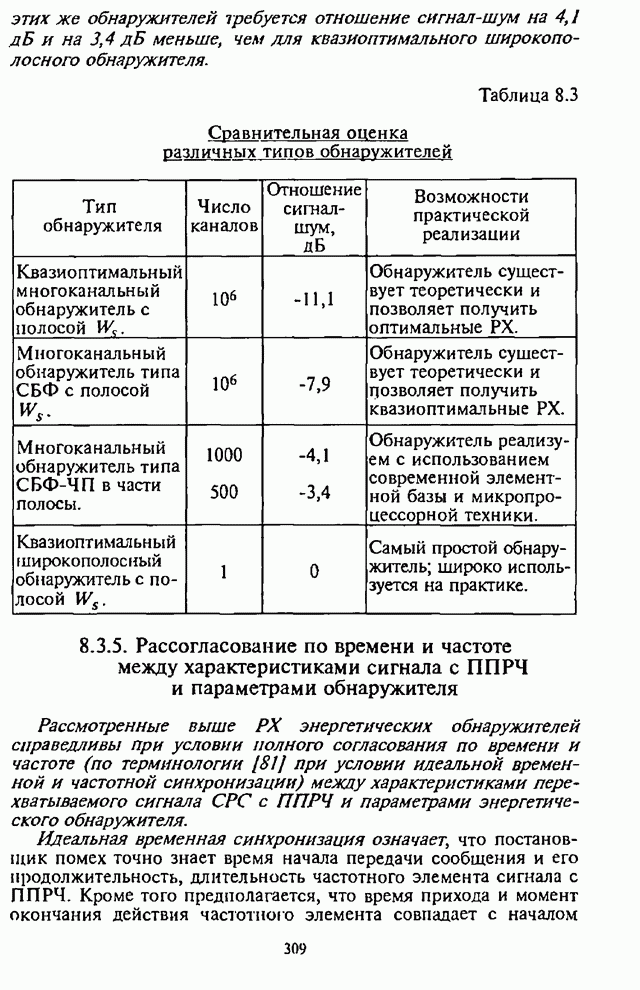
Рис. 5.8.
Графики зависимости СВО на бит на рис.5.8 показывают,
что при заданной вероятности ошибки, например, на уровне ![]() СРС с ППРЧ и 8-ичной ЧМ имеют
выигрыш по отношению сигнал-помеха
СРС с ППРЧ и 8-ичной ЧМ имеют
выигрыш по отношению сигнал-помеха ![]() примерно на 7...8 дБ по
сравнению с двоичной СРС, в то время как без кодирования выигрыш 8-ичной СРС
составляет примерно 3 дБ (см.рис.2.14).
примерно на 7...8 дБ по
сравнению с двоичной СРС, в то время как без кодирования выигрыш 8-ичной СРС
составляет примерно 3 дБ (см.рис.2.14).
Из изложенных выше материалов видно, что совместное использование в СРС
с ППРЧ
![]() -ичной ЧМ,
двоичных блоковых кодов с прямым исправлением
ошибок,
-ичной ЧМ,
двоичных блоковых кодов с прямым исправлением
ошибок, ![]() -кратного
частотного разнесения кодового слова
и нелинейного
сложения выборок сигнала является
эффективным способом повышения помехоустойчивости СРС в условиях наихудших
шумовых помех в части полосы.
-кратного
частотного разнесения кодового слова
и нелинейного
сложения выборок сигнала является
эффективным способом повышения помехоустойчивости СРС в условиях наихудших
шумовых помех в части полосы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
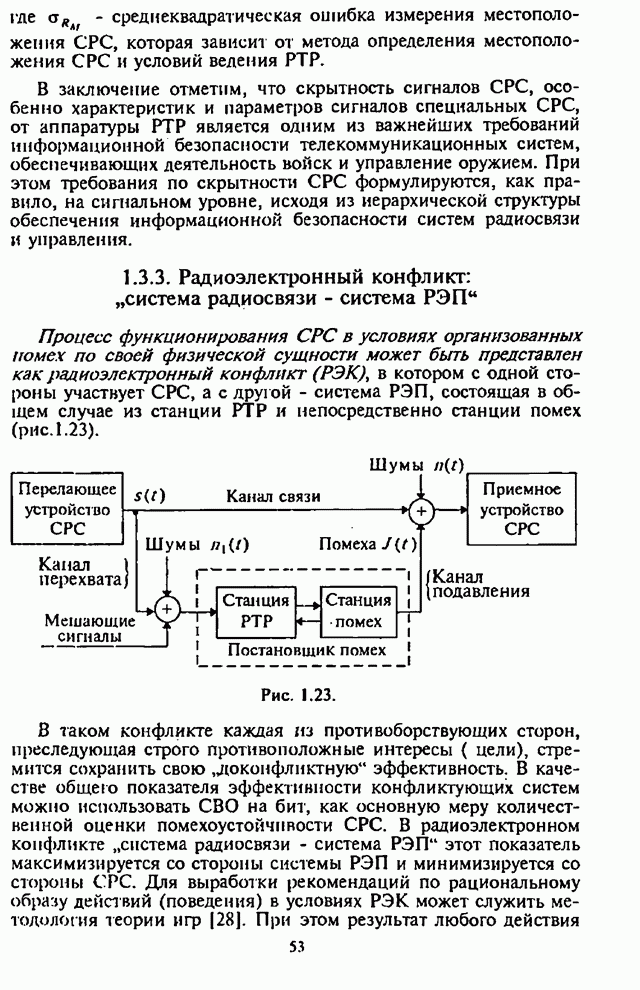
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
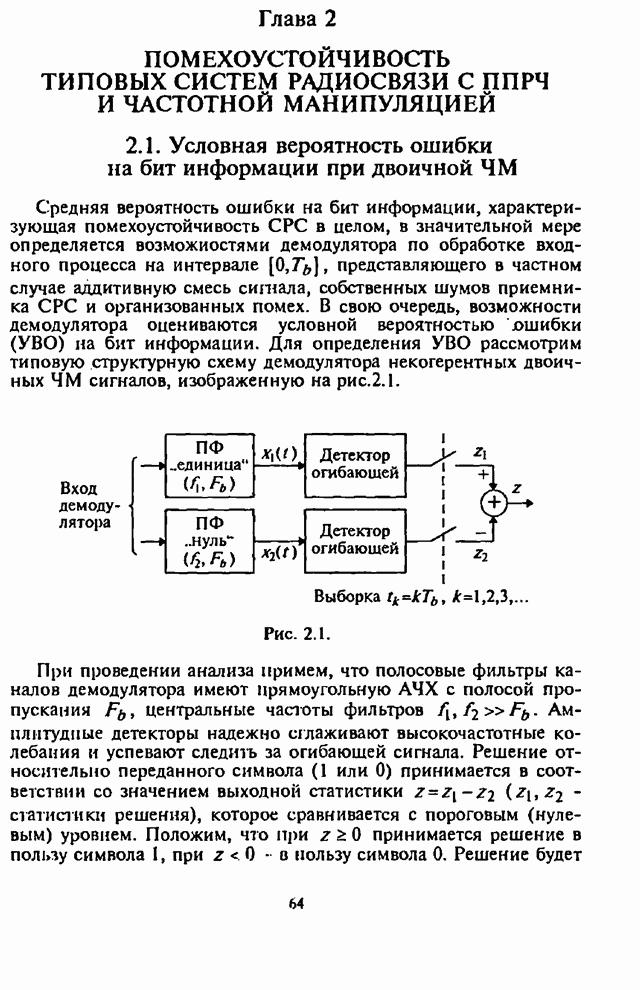
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
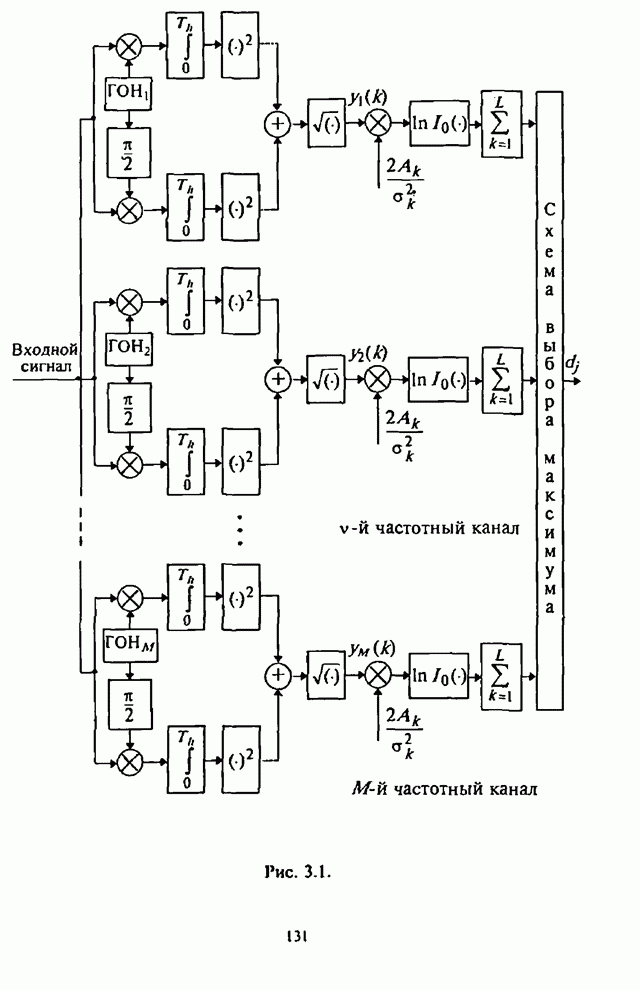
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
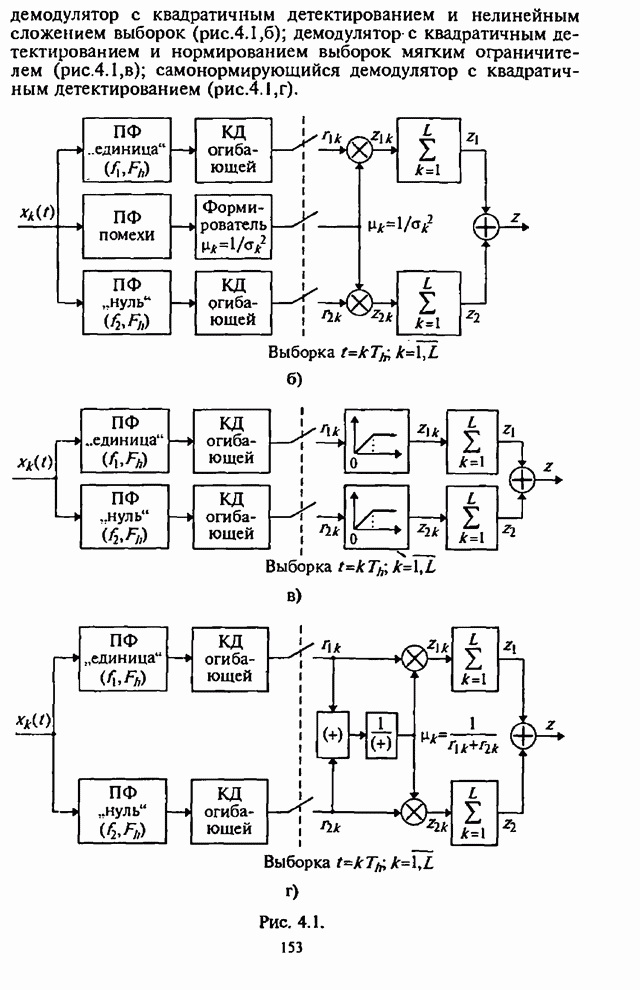
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
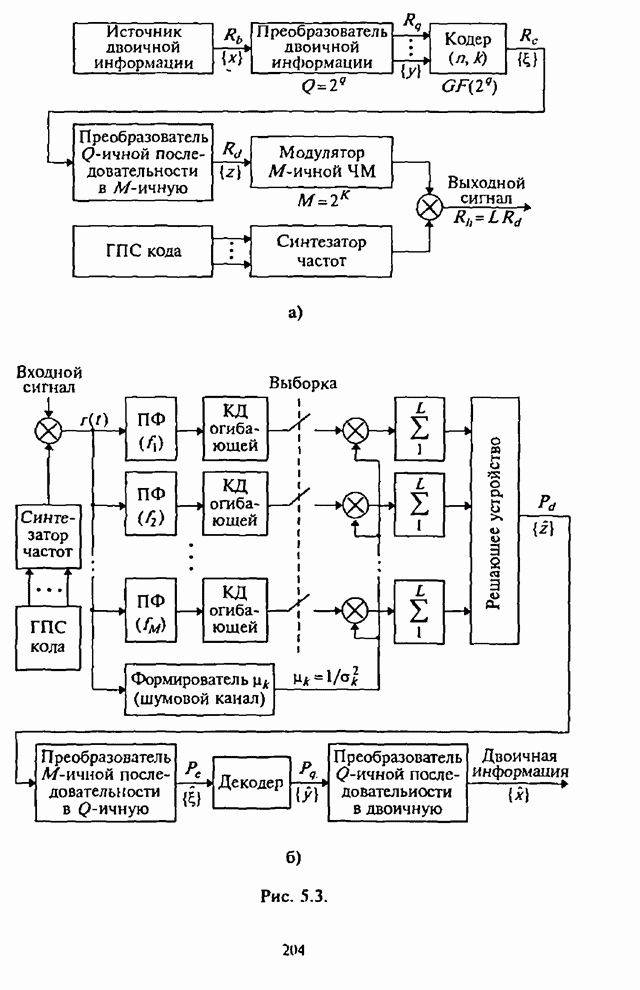
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
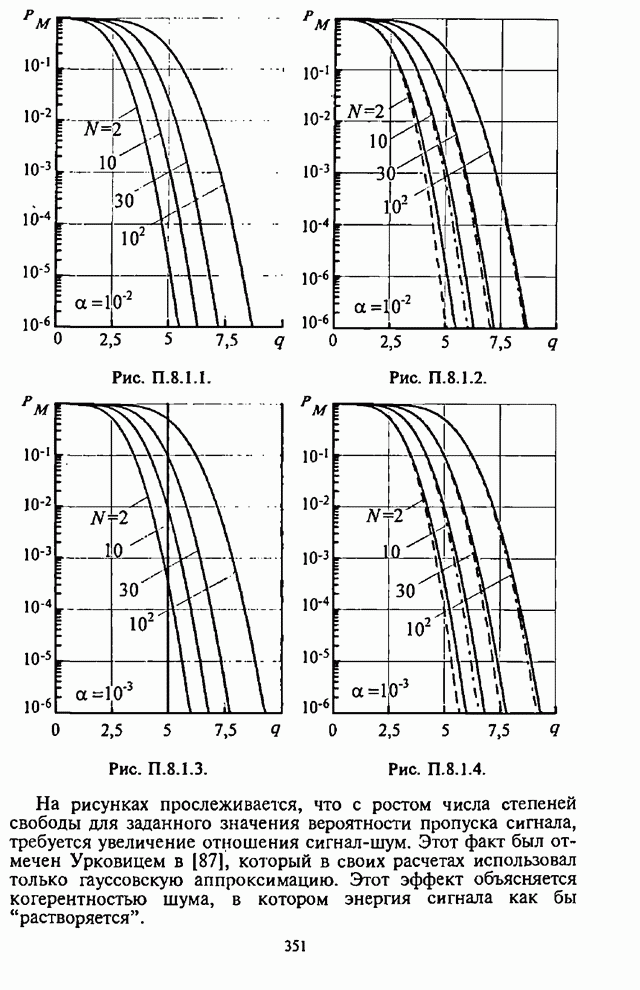
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
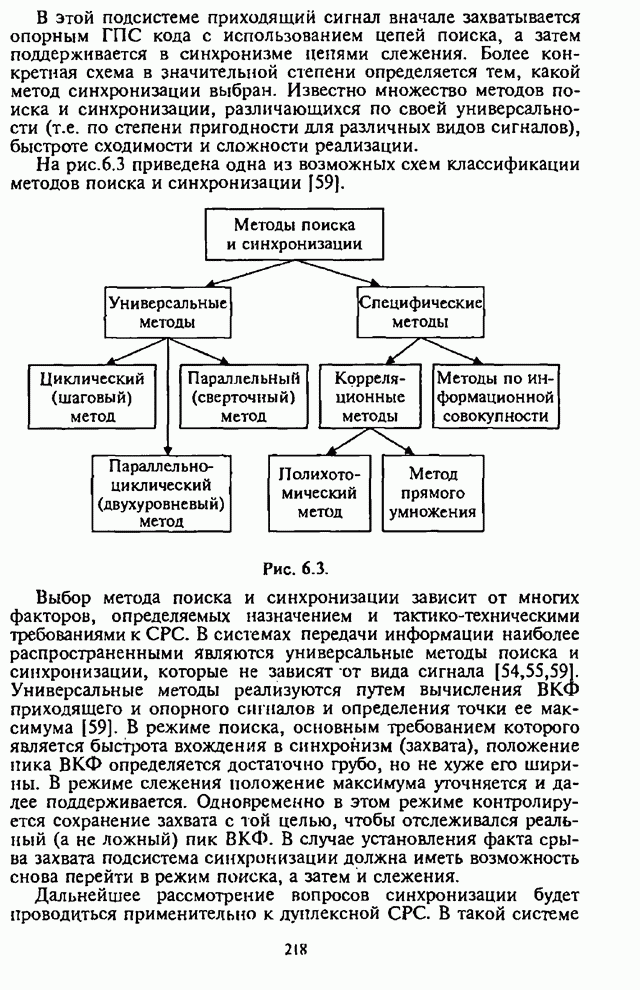
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
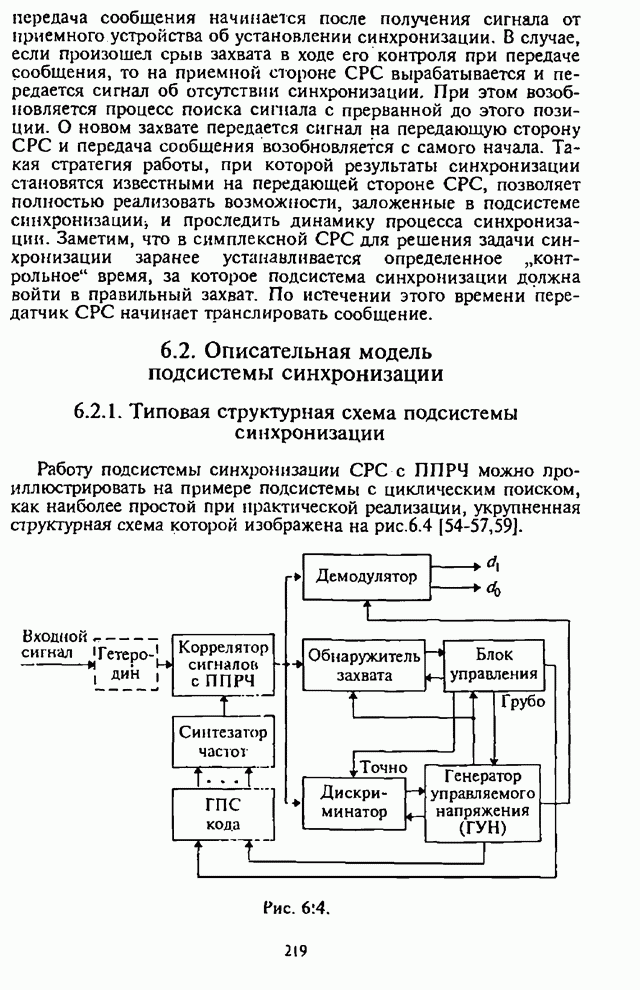
- 6.2.1. Типовая структурная схема подсистемы синхронизации
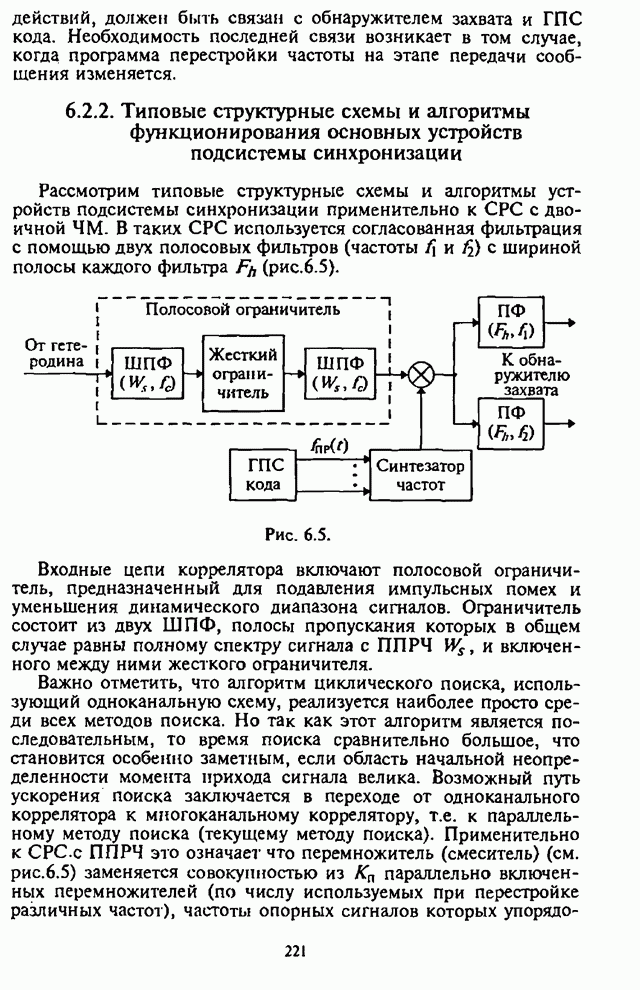
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ