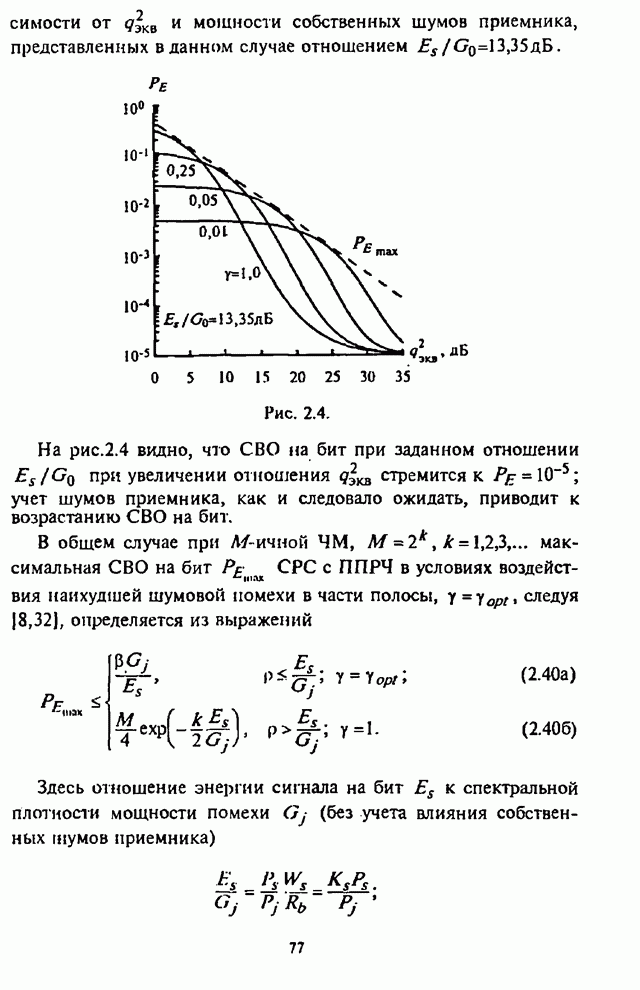
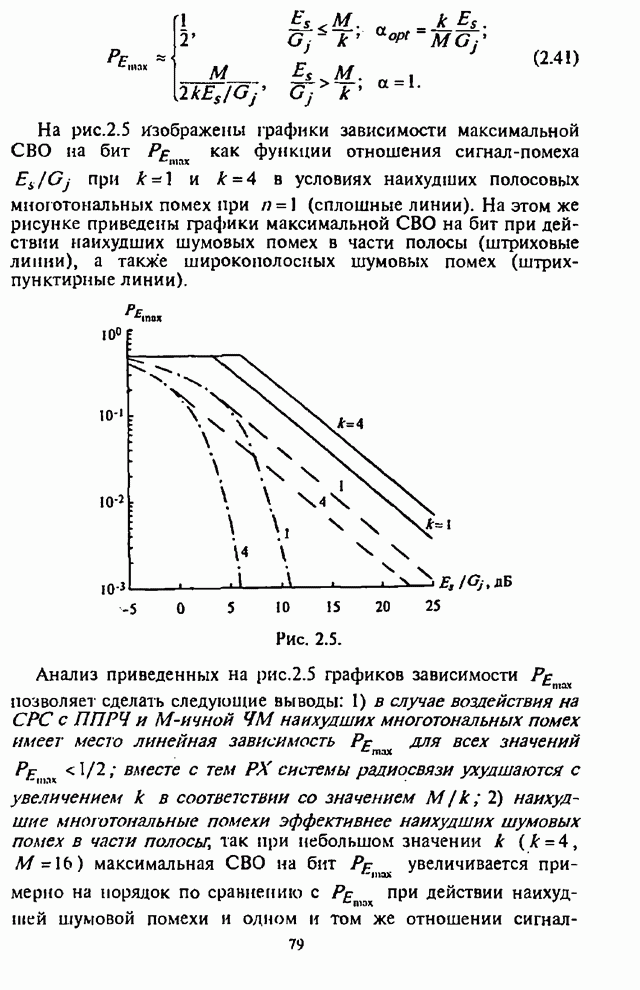
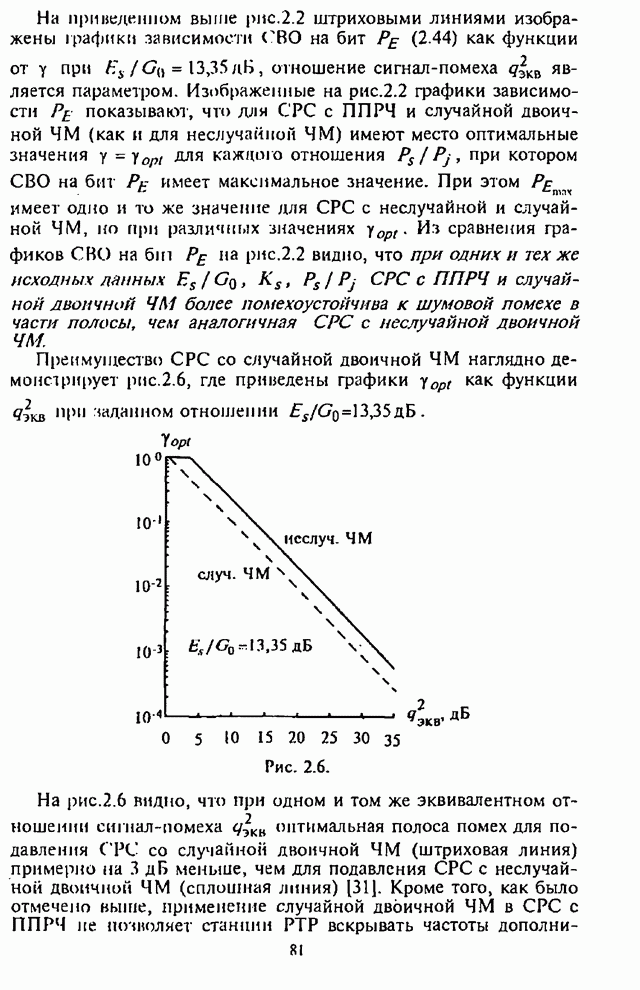
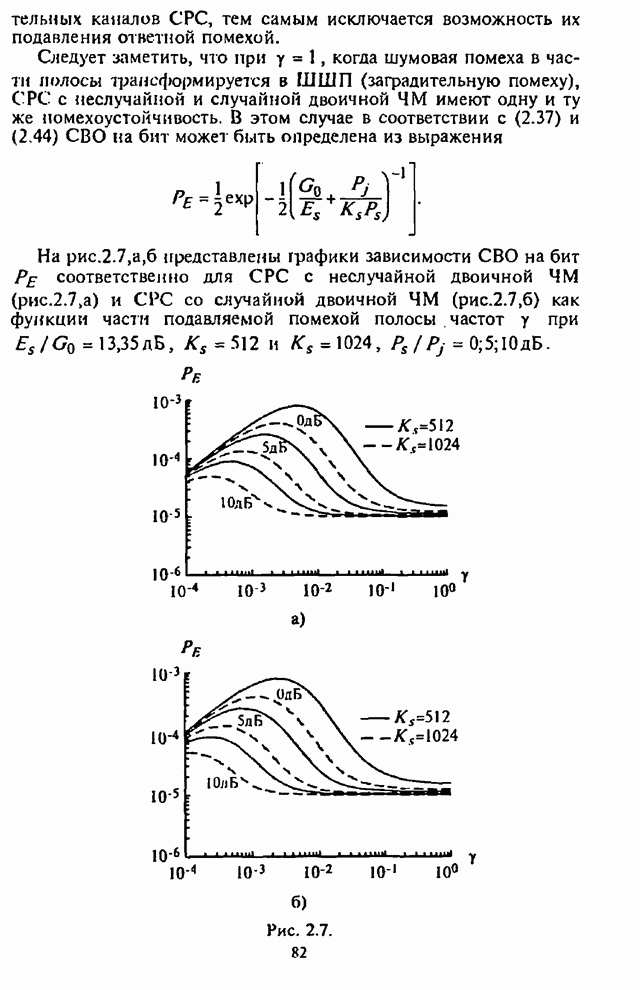
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
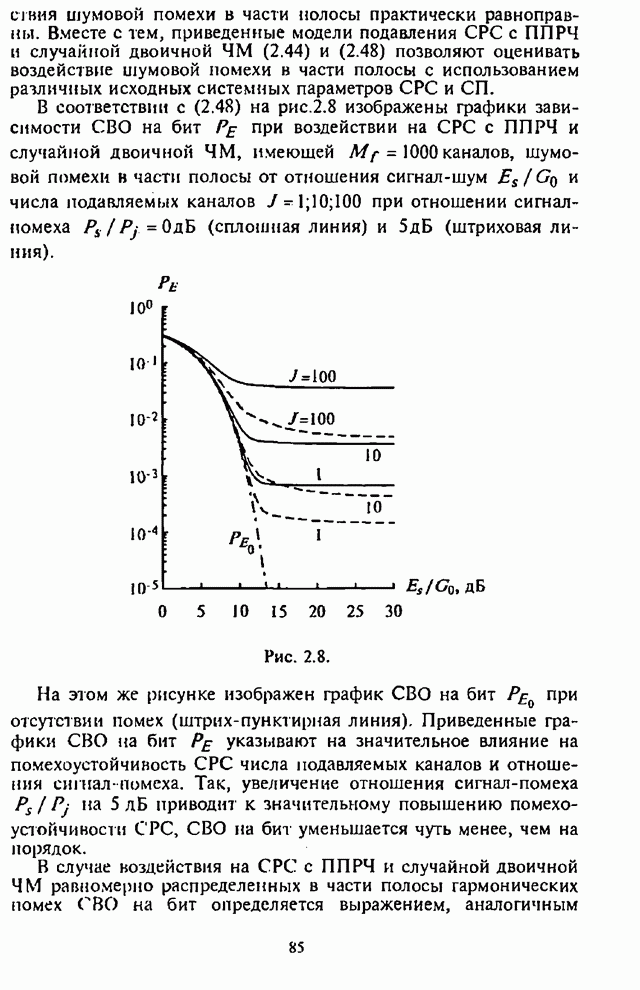
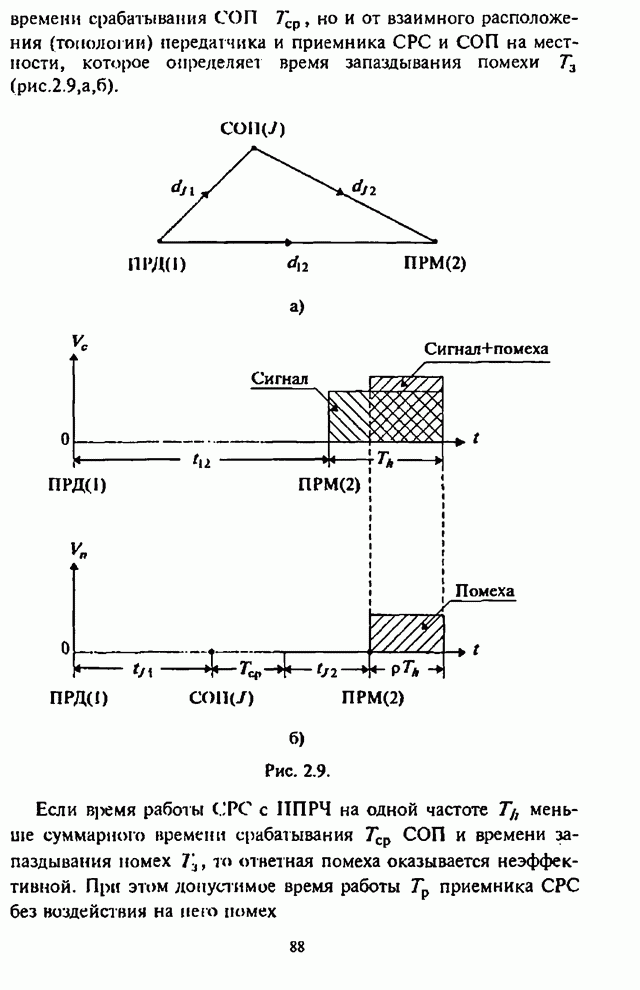
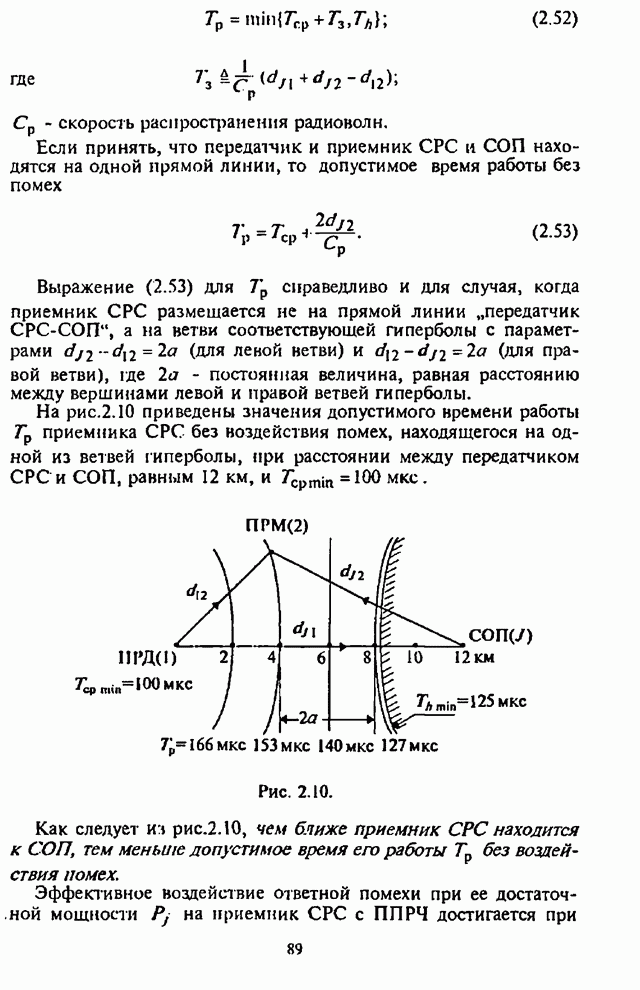
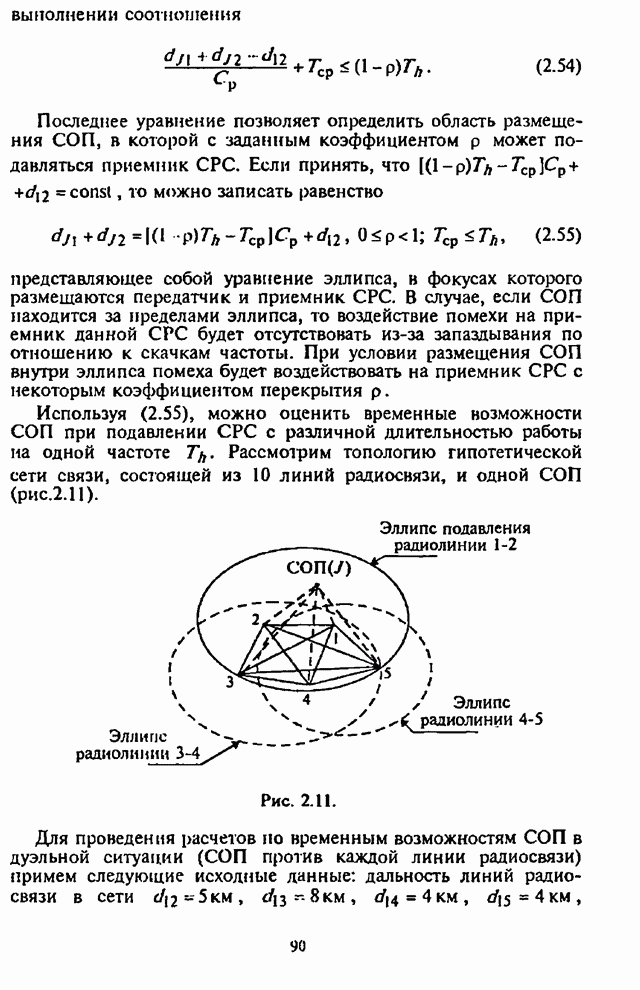
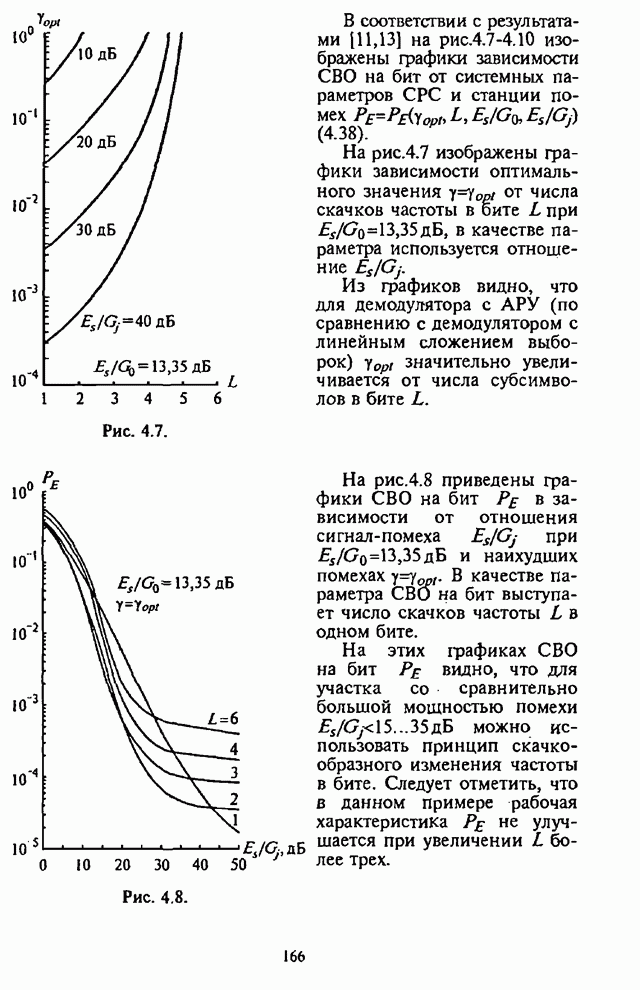
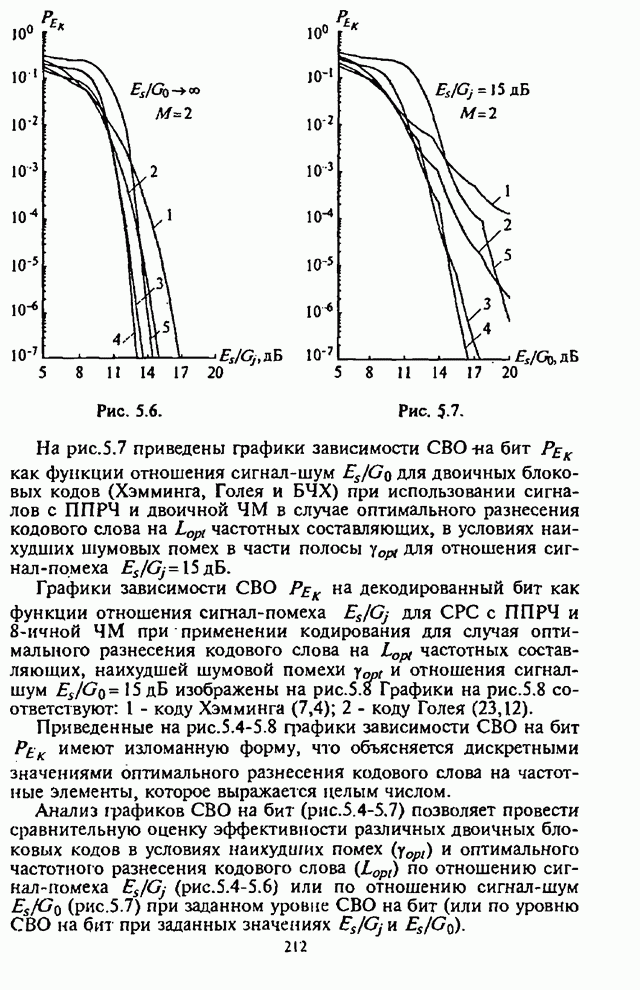
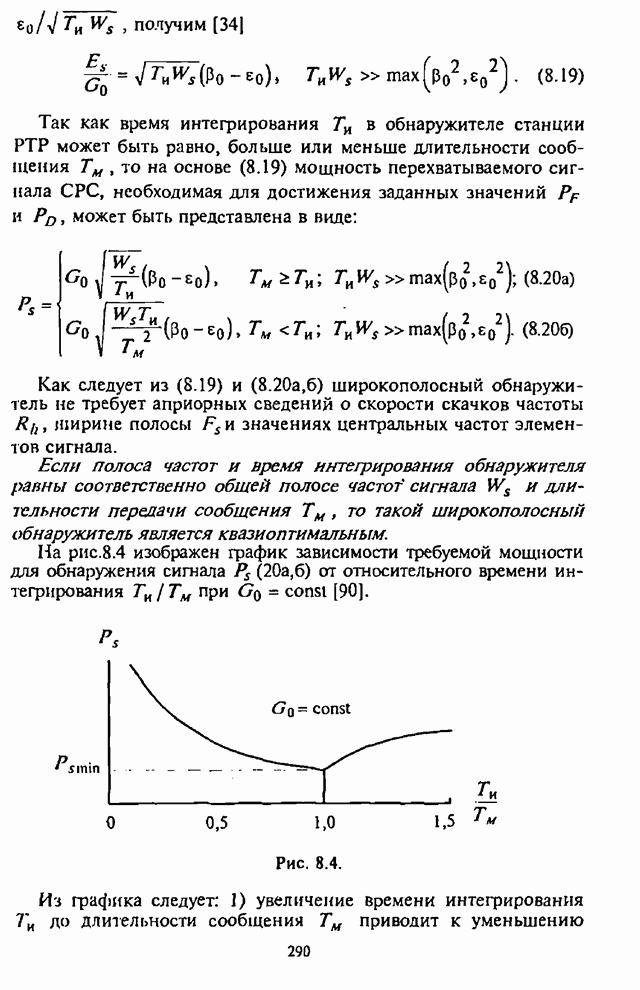
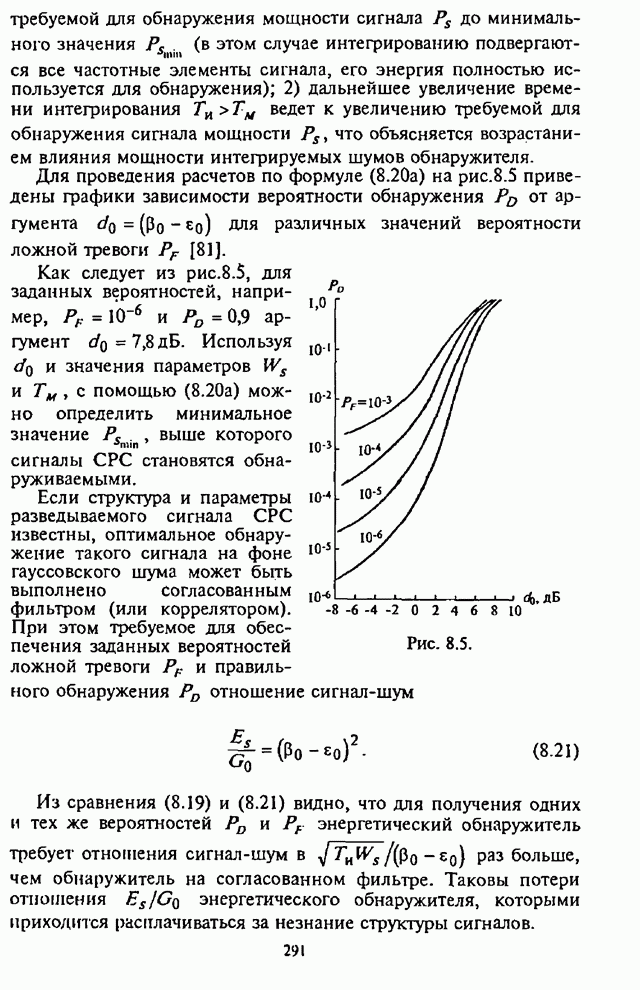
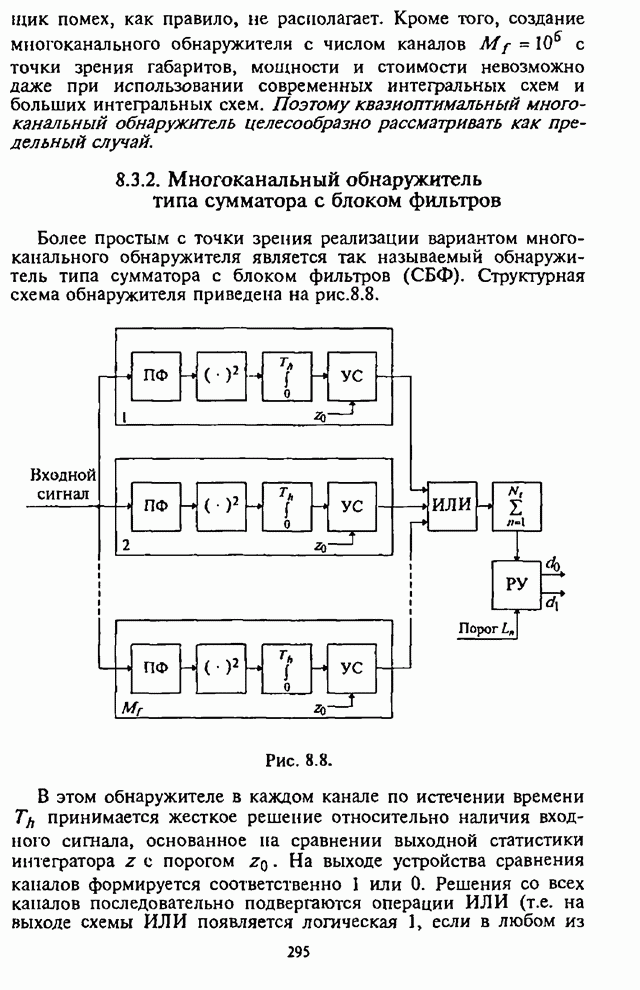
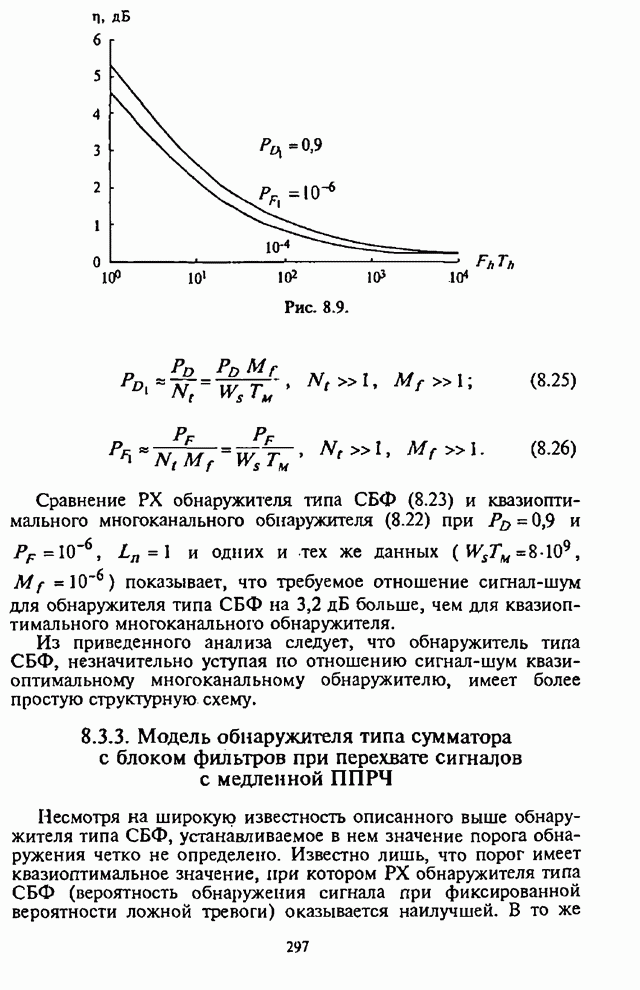
4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
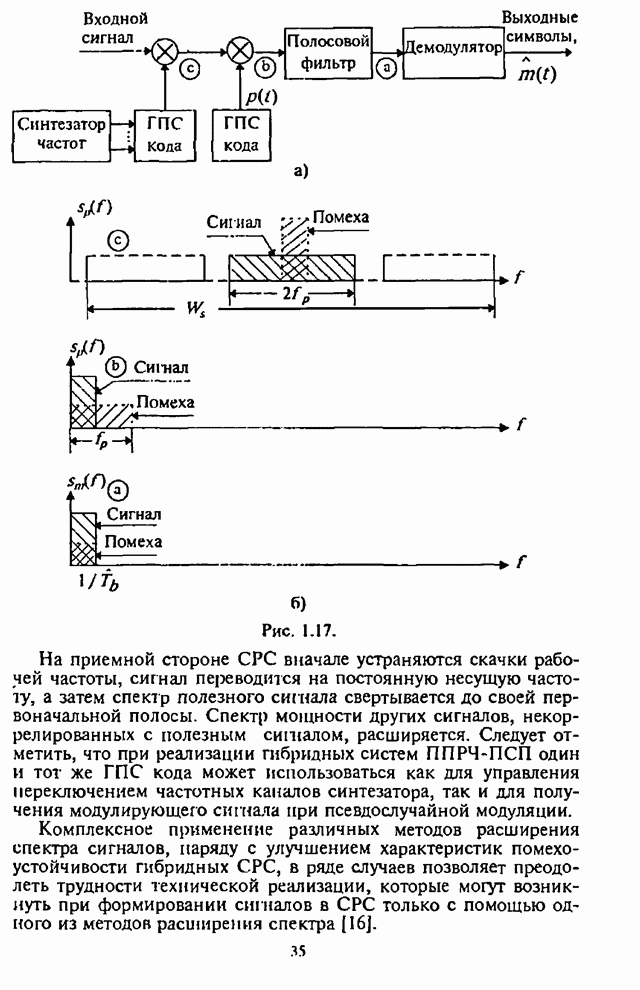
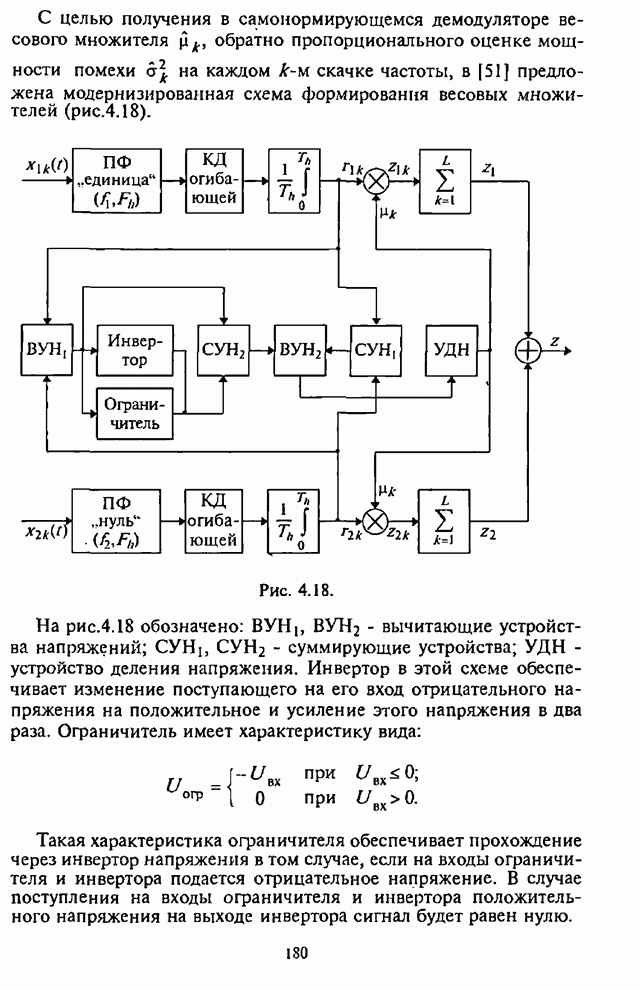
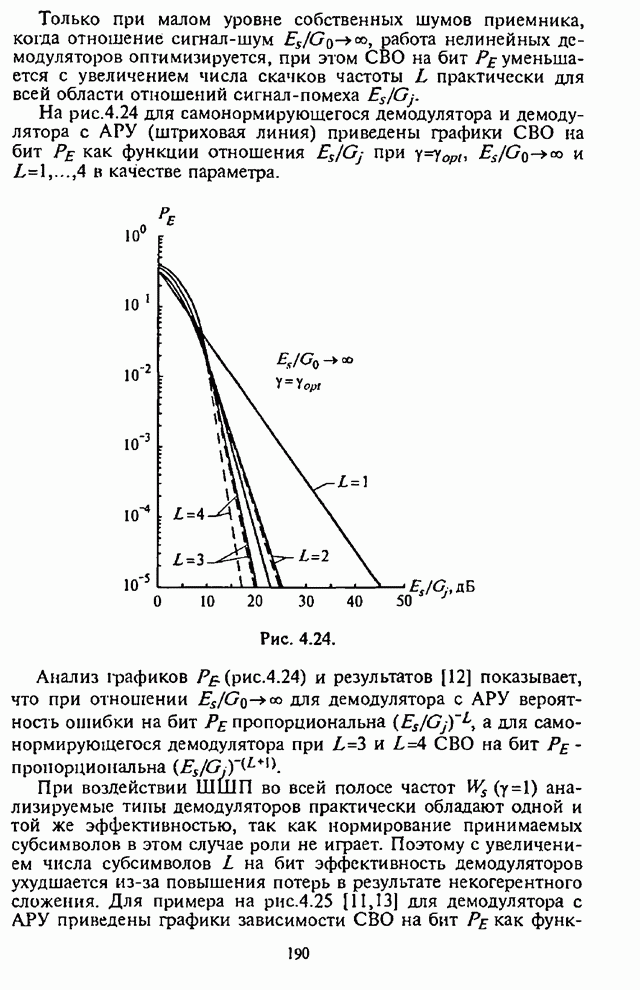
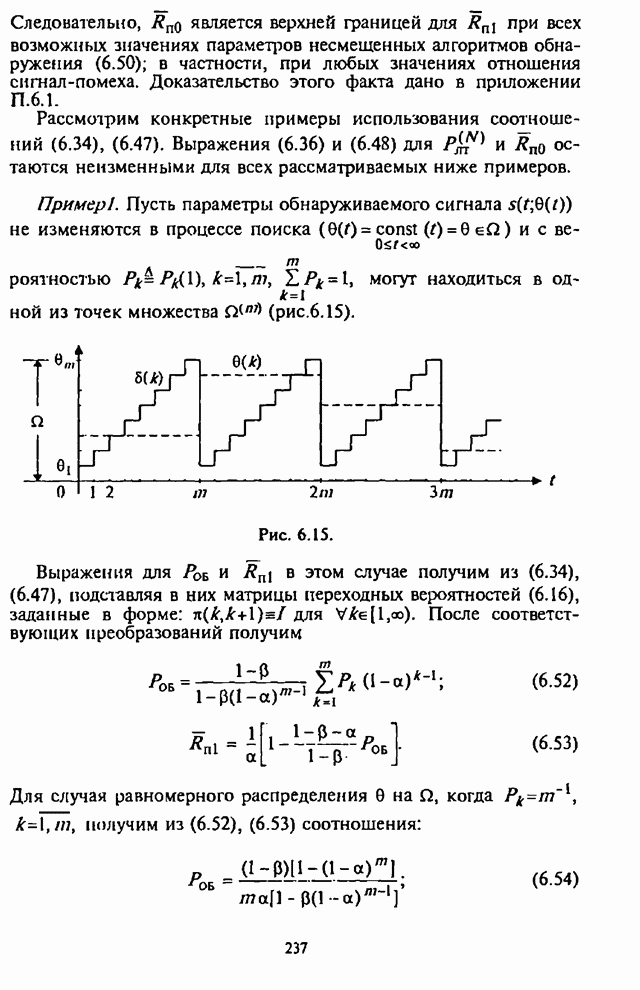
Как указывалось выше, применение в СРС сигналов с внутрибитовой ППРЧ в условиях воздействия помех может быть эффективным лишь при осуществлении в демодуляторе нормирования выборок частотных элементов. Из теории обнаружения сигналов с постоянной амплитудой следует, что адаптивное (по уровню шума) регулирование усиления (АРУ) в оптимальном приемнике должно быть таким, чтобы значение корреляционного интеграла, характеризующего уровень сигнала на выходе фильтра, изменялось обратно пропорционально спектральной плотности помехи [1-3].
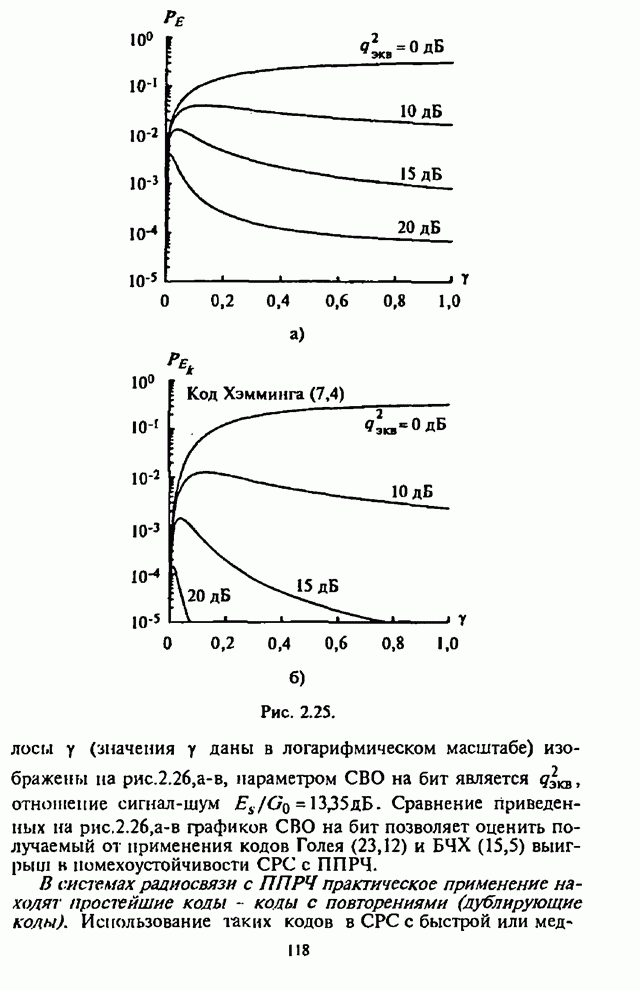
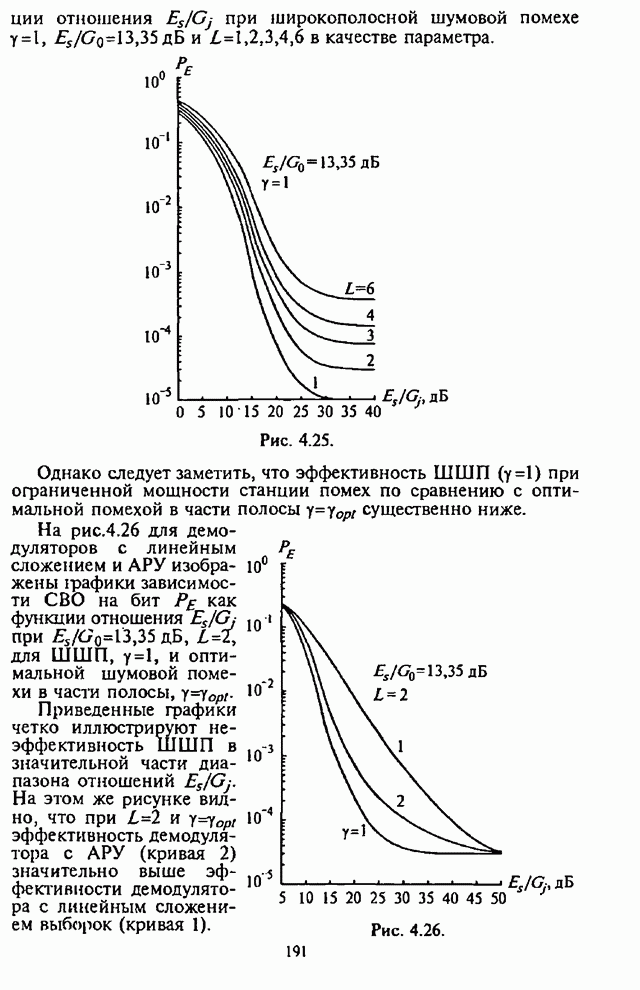
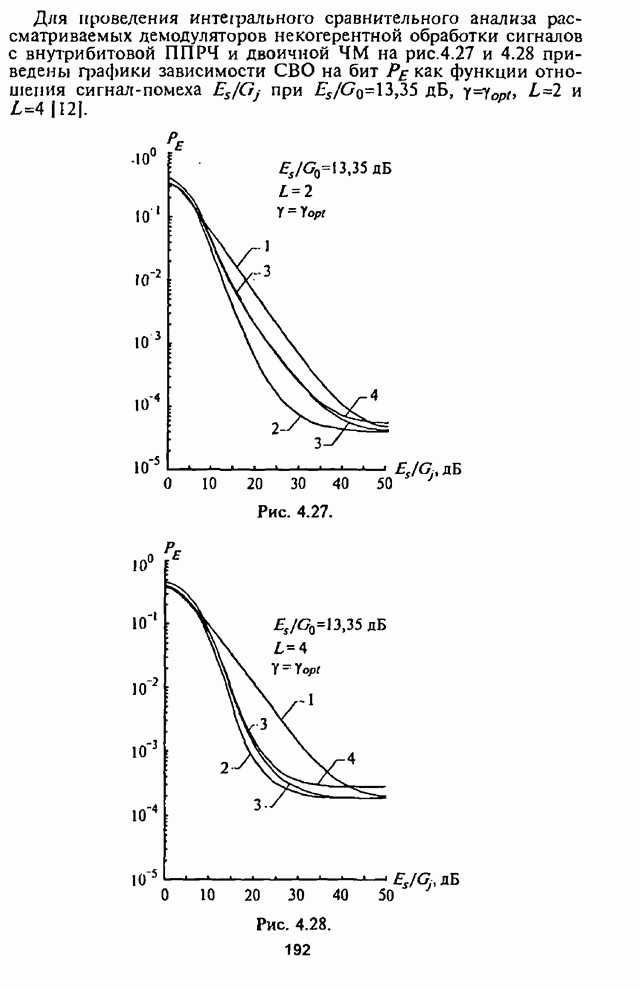
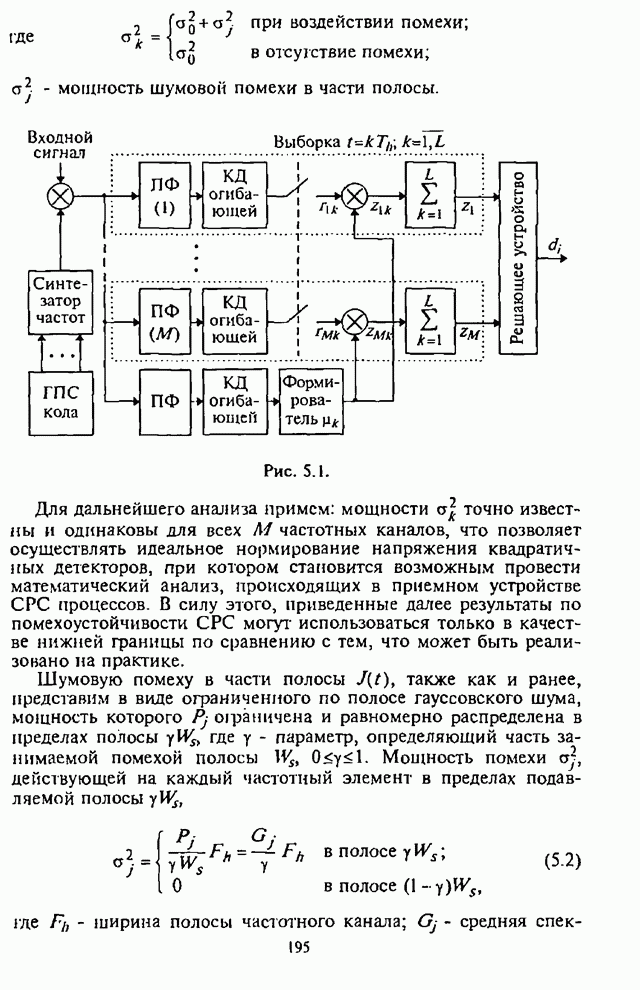
При обработке принятых сигналов с разнесением символов применяются в основном приемники с квадратичным детектированием. Следовательно, при отказе от оптимального приемника в СРС с внутрибитовой ППРЧ встает вопрос о том, какова должна быть степень АРУ для получения наибольшей помехоустойчивости. При этом ситуация усложняется наличием шумовой помехи в части полосы, постановщик которой в силу ограниченной мощности СП стремится оптимизировать основной параметр помехи - подавляемую часть полосы частот, занимаемую сигналом с ППРЧ.
Таким образом, возникает типичная теоретико-игровая задача. В [9-14] подобный вопрос не рассматривается, авторы этих работ вводят и исследуют процессы адаптивной регулировки усиления, которая изменяет значение корреляционного интеграла обратно пропорционально корню квадратному из спектральной плотности помехи.
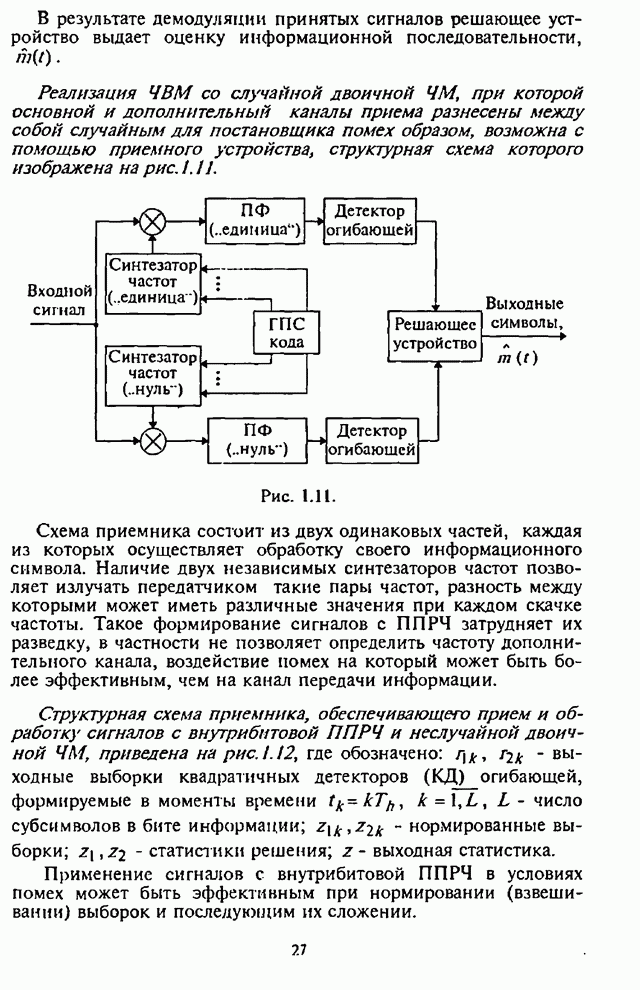
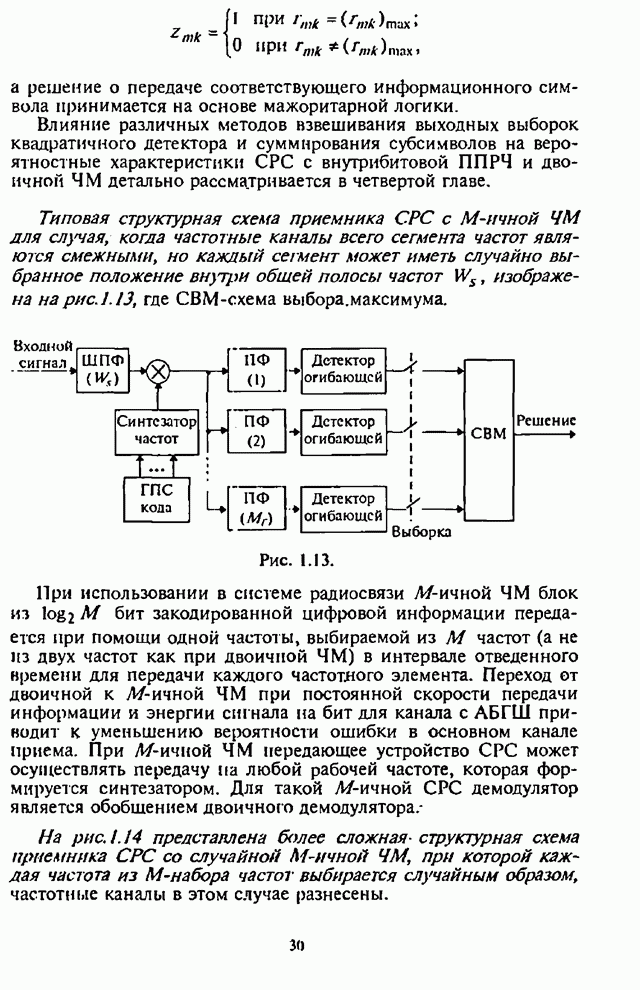
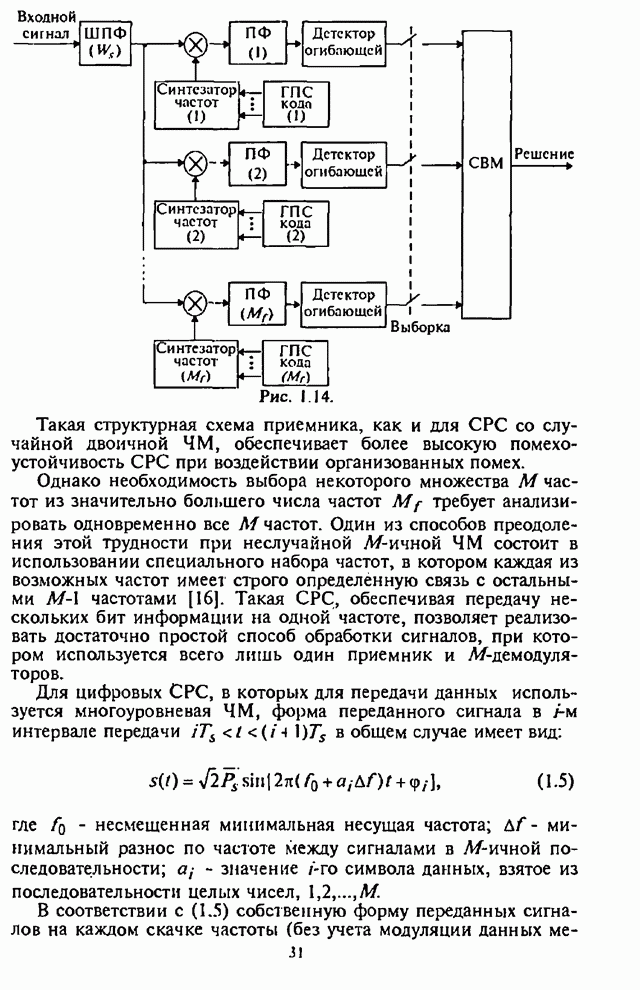
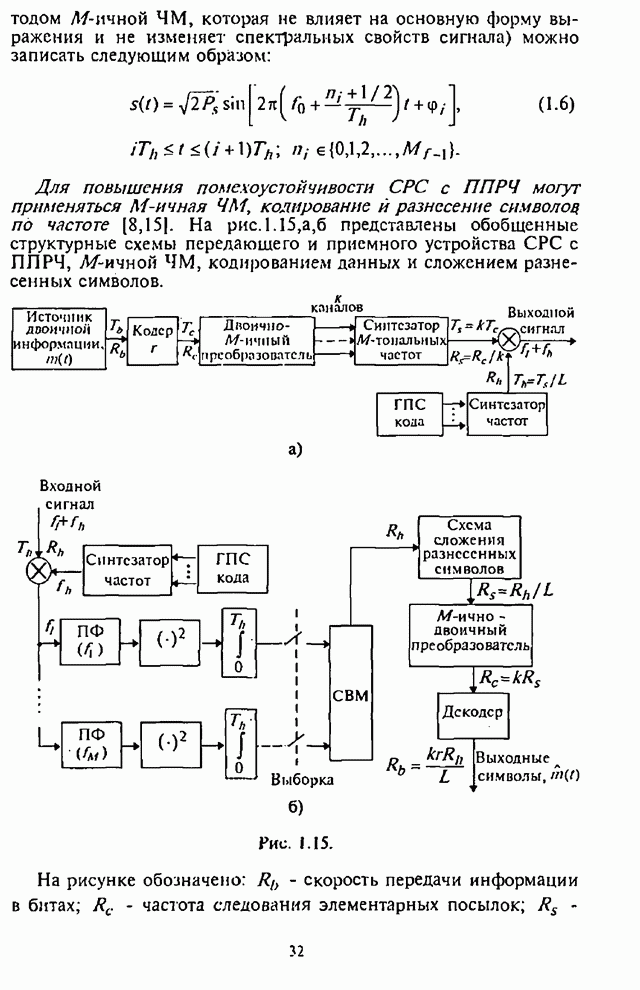
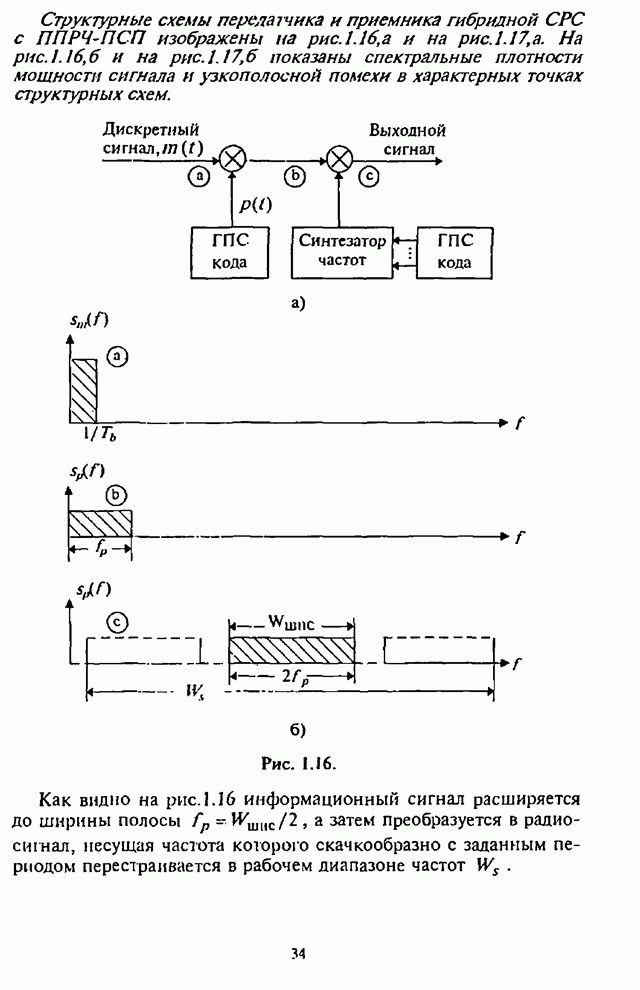
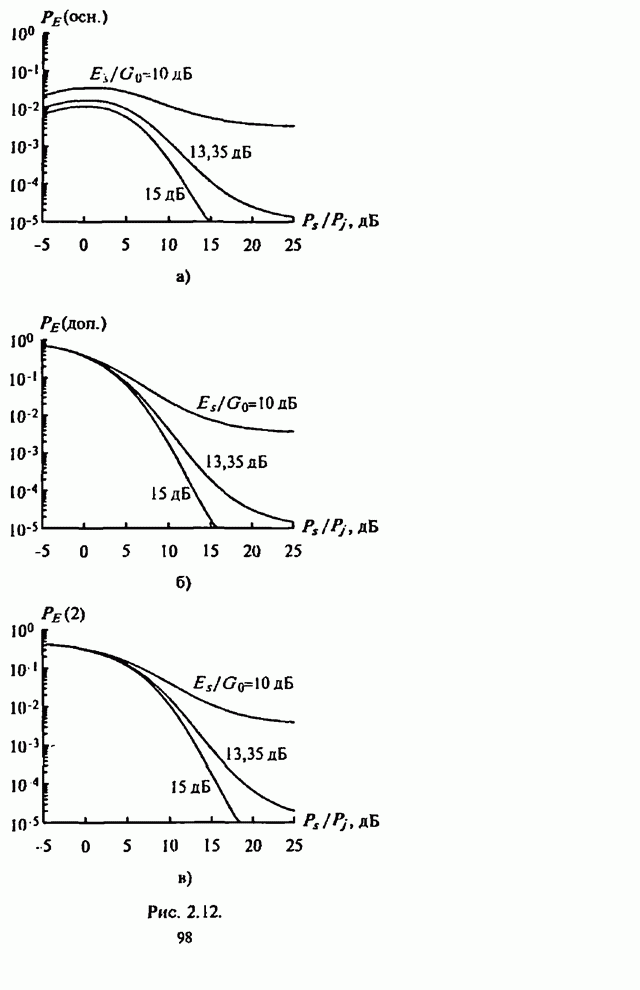
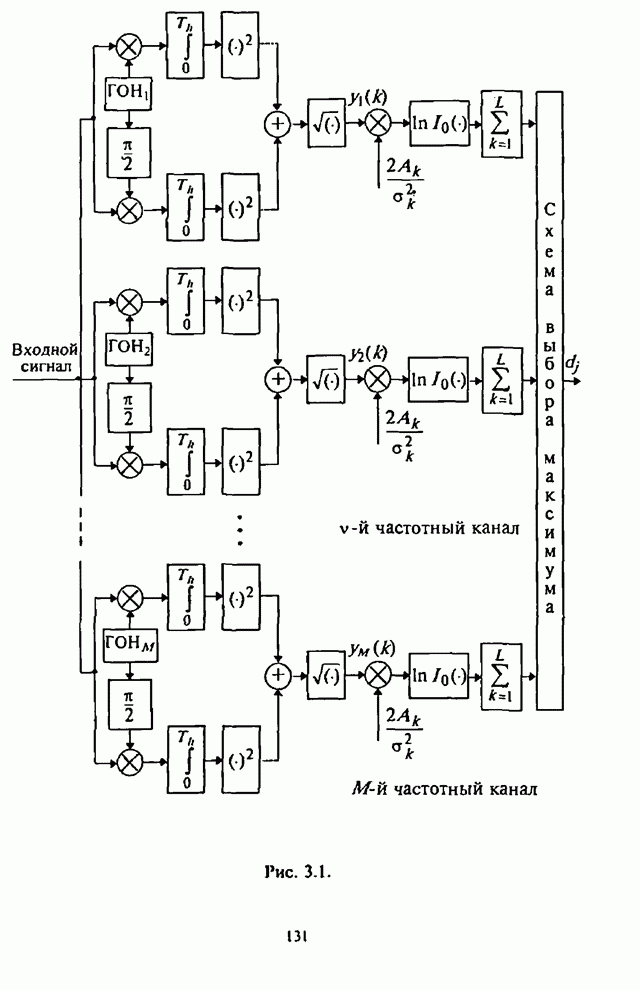
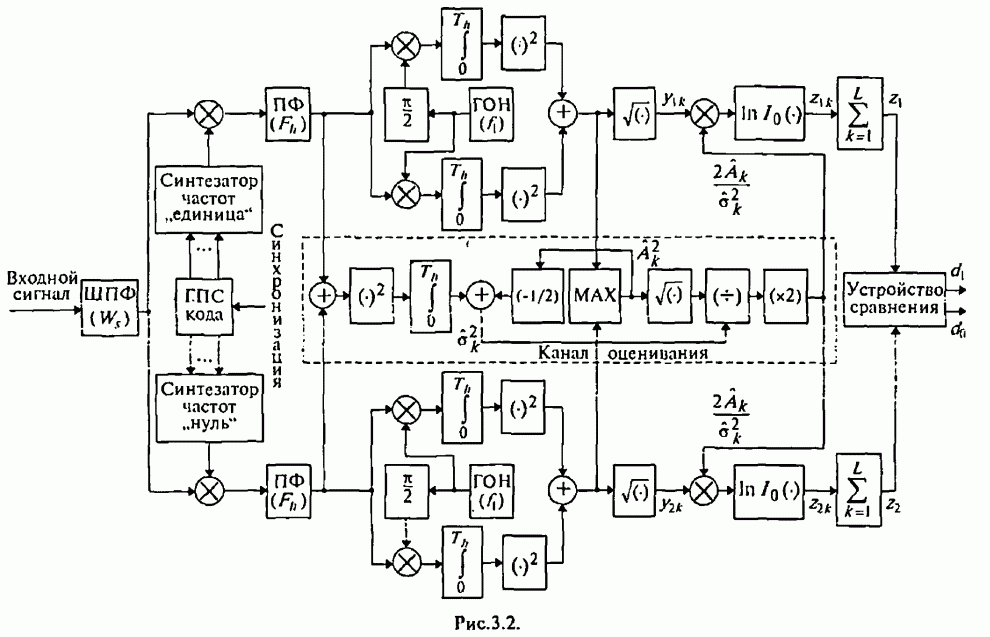
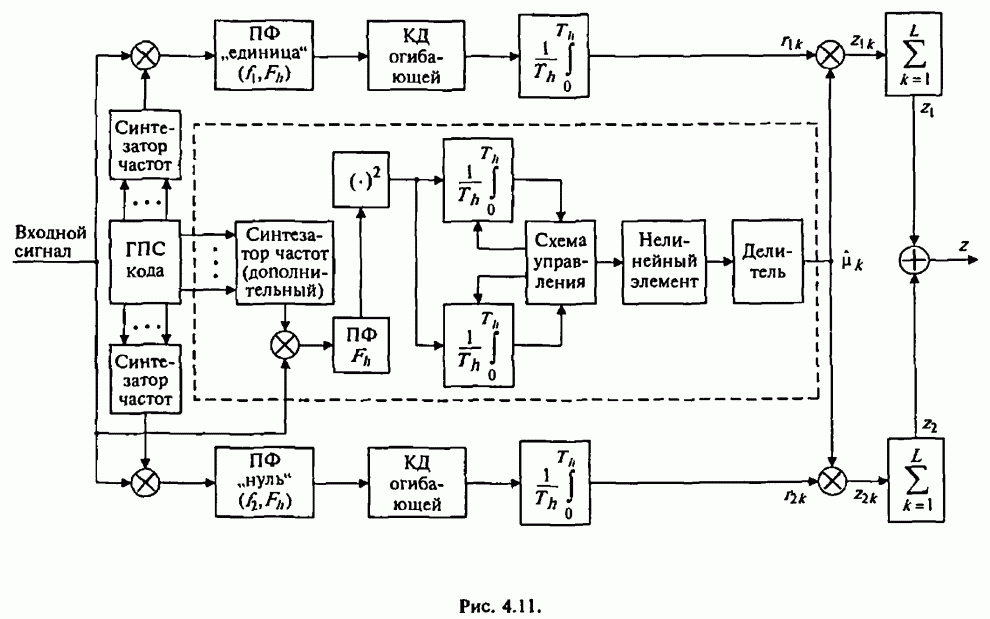
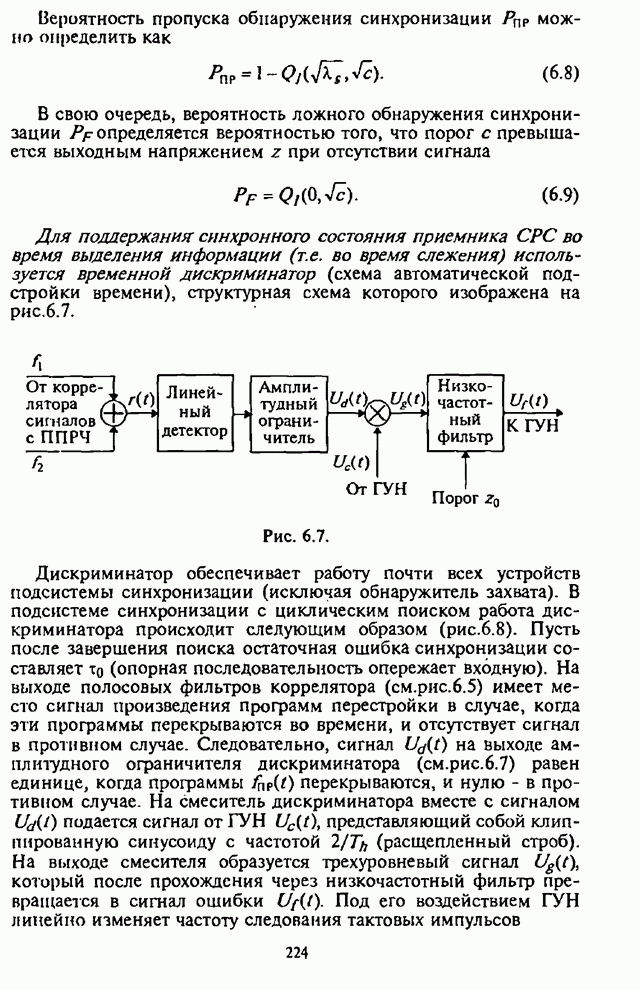
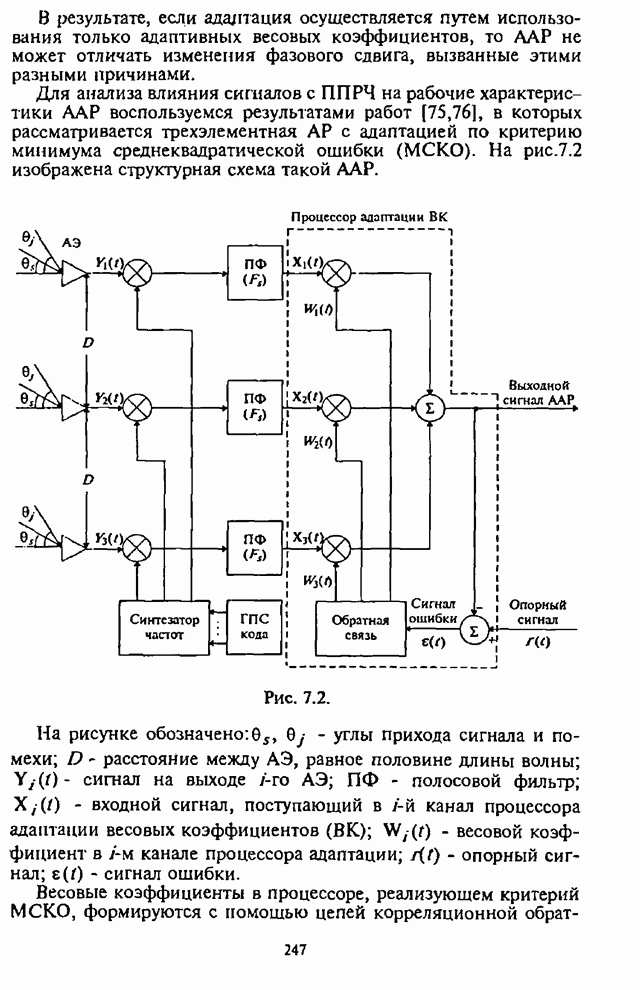
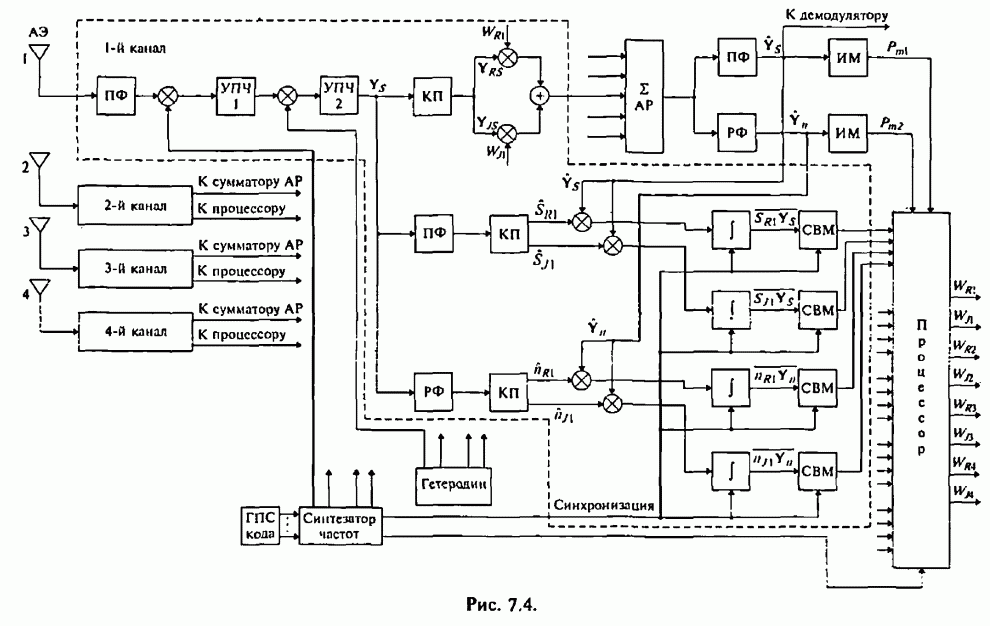
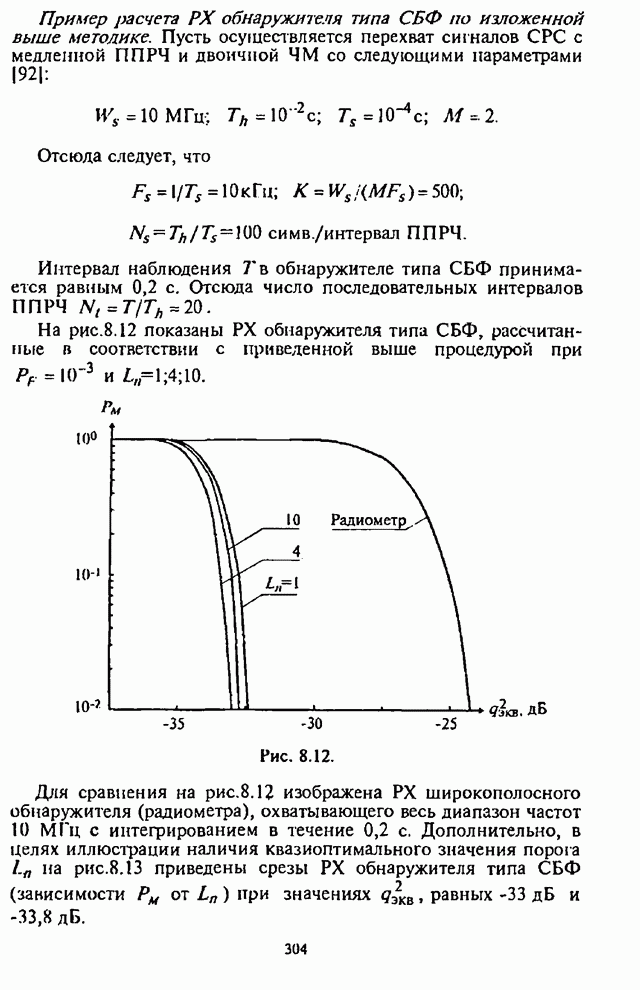
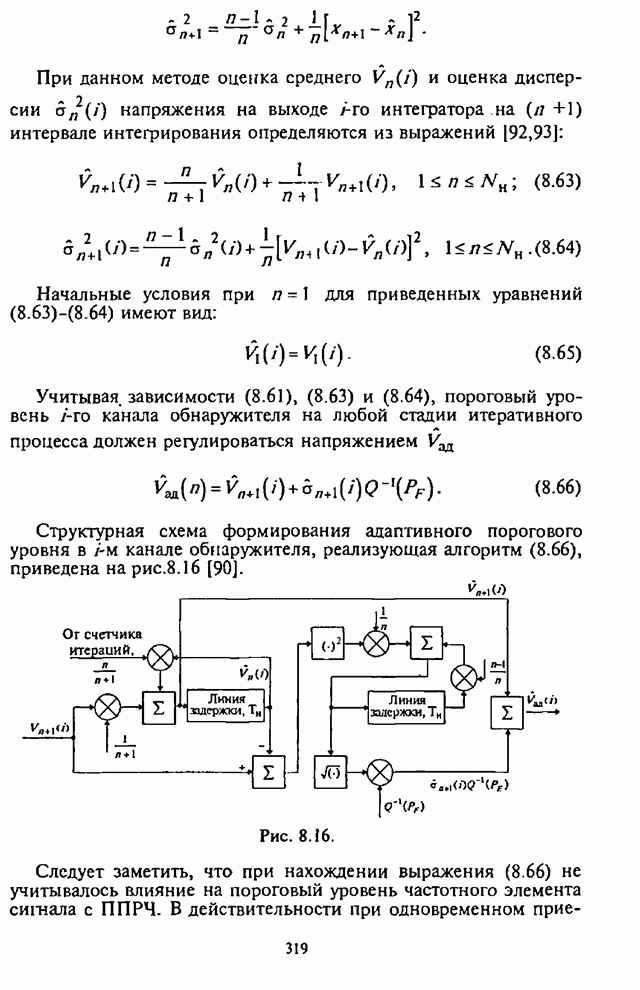
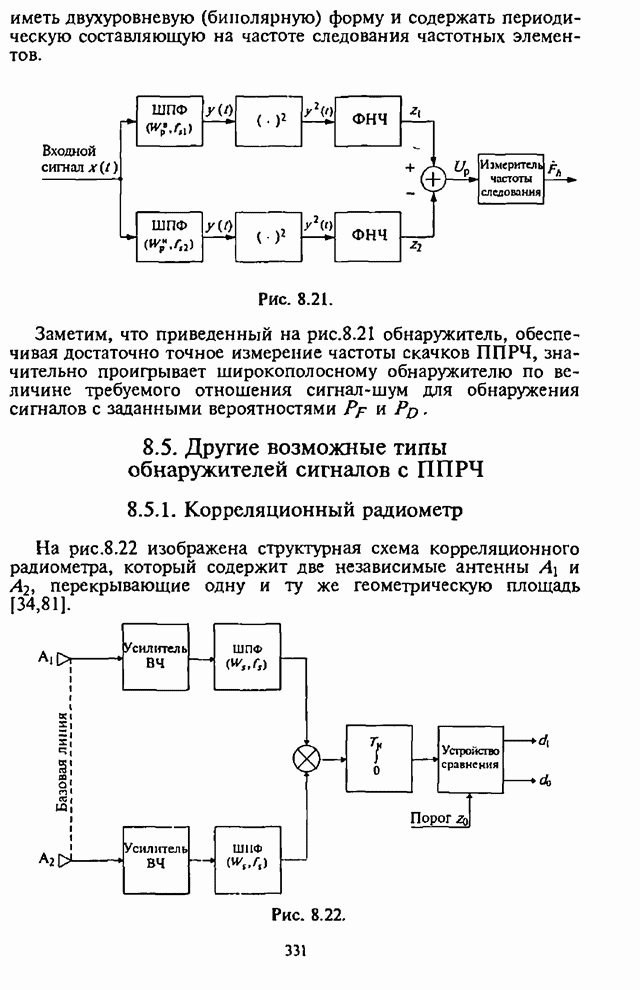
Существенная для анализа часть некогерентного приемника сигналов с внугрибитовой ППРЧ и двоичной ЧМ изображена на рис.4.20.

Рис. 4.20.
Основные обозначения элементов на этой структурной
схеме и процесс формирования статистик решения ![]() и
и ![]() и выходной статистики
и выходной статистики ![]() соответствуют описанной ранее
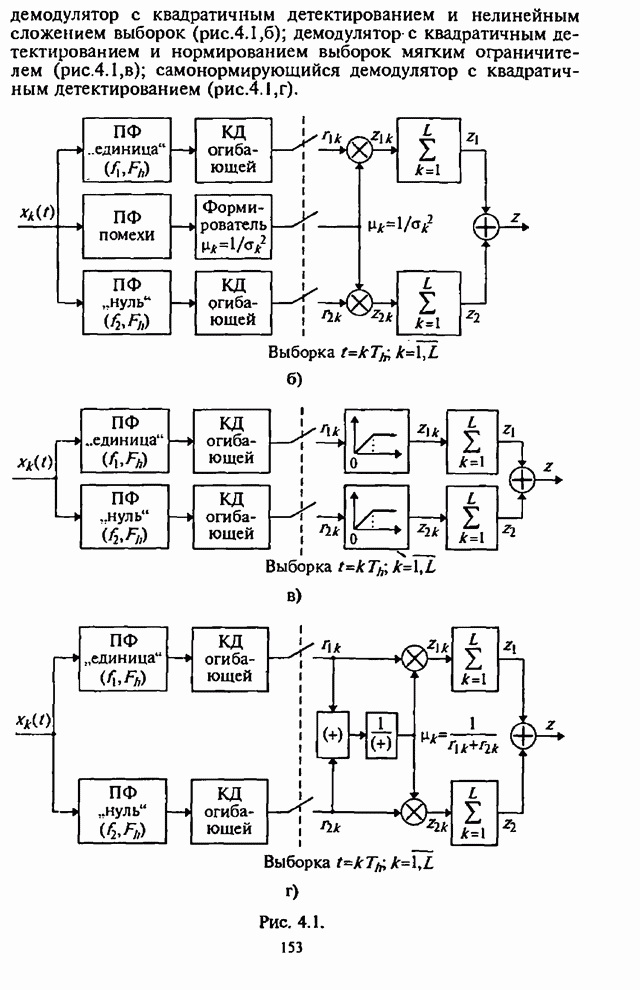
схеме демодулятора с квадратичным детектированием и нелинейным сложением субсимволов
(см. рис.4.1,б). Для измерения спектральной плотности мощности помехи
соответствуют описанной ранее
схеме демодулятора с квадратичным детектированием и нелинейным сложением субсимволов
(см. рис.4.1,б). Для измерения спектральной плотности мощности помехи ![]() на каждом скачке частоты и
формирования напряжения, регулирующего усиление каналов в соответствии с функцией
на каждом скачке частоты и
формирования напряжения, регулирующего усиление каналов в соответствии с функцией
![]() , где
, где ![]() - степень АРУ,
имеется дополнительный канал. В данном демодуляторе (рис.4.20) АРУ
осуществляется путем перемножения напряжения сигнала + помеха и напряжения, пропорционального
- степень АРУ,
имеется дополнительный канал. В данном демодуляторе (рис.4.20) АРУ
осуществляется путем перемножения напряжения сигнала + помеха и напряжения, пропорционального![]() , в каждом канале на выходе
квадратичного детектора.
, в каждом канале на выходе
квадратичного детектора.
Как уже неоднократно приводилось, СВО на бит ![]() в приемном устройстве
в приемном устройстве ![]() типа СРС с внутрибитовой ППРЧ и двоичной
ЧМ может быть представлена в виде:
типа СРС с внутрибитовой ППРЧ и двоичной
ЧМ может быть представлена в виде:
![]() (4.66)
(4.66)
где ![]() - УВО на бит при подавлении шумовой помехой в части полосы
- УВО на бит при подавлении шумовой помехой в части полосы ![]() субсимволов из
субсимволов из ![]() .
.
Выражение (4.66) является исходным для оптимизации параметрических
стратегий постановщика помех (ПП) и СРС с внугрибитовой ППРЧ. При этом цель ПП
заключается в том, чтобы сосредоточить ограниченную мощность помехи в такой
части у полосы перестройки ![]() при которой
при которой ![]() достигает максимума при любом конкретном значении
степени АРУ (
достигает максимума при любом конкретном значении
степени АРУ (![]() ).
Предполагается, следовательно, что какая бы степень АРУ ни реализовывалась в
СРС, постановщику помех это известно, и для подавления СРС им выбирается
оптимальная часть полосы
).
Предполагается, следовательно, что какая бы степень АРУ ни реализовывалась в
СРС, постановщику помех это известно, и для подавления СРС им выбирается
оптимальная часть полосы ![]() , что представляет наихудший случай для
СРС.
, что представляет наихудший случай для
СРС.
В свою очередь, разработчик СРС заинтересован в том,
чтобы получаемый постановщиком помех результат ![]() оказался наименьшим из
возможных. Это можно обеспечить путем выбора степени АРУ приемного устройства.
В этом заключается оптимизация параметрической стратегии СРС. В итоге результирующая
помехоустойчивость СРС приобретает вид
оказался наименьшим из
возможных. Это можно обеспечить путем выбора степени АРУ приемного устройства.
В этом заключается оптимизация параметрической стратегии СРС. В итоге результирующая
помехоустойчивость СРС приобретает вид
![]() ,
,
т.е. налицо типичная минимаксная задача из теории игр [28].
С целью упрощения анализа примем, что число скачков частоты
на бит ![]() . Тогда из (4.66) получаем
. Тогда из (4.66) получаем
![]() (4.67)
(4.67)
Вероятности ![]() и
и ![]() не зависят от степени АРУ, так как при
не зависят от степени АРУ, так как при ![]() и
и ![]() шумовая помеха в части
полосы проявляется как стационарная по всей длительности бита. Выбор
шумовая помеха в части
полосы проявляется как стационарная по всей длительности бита. Выбор ![]() не препятствует сравнительному анализу приемных
устройств СРС с различной степенью АРУ и имеет практическое значение. В общем
же случае кратность разнесения бита
не препятствует сравнительному анализу приемных
устройств СРС с различной степенью АРУ и имеет практическое значение. В общем
же случае кратность разнесения бита ![]() - это еще один параметр стратегии СРС и он также должен
оптимизироваться. Однако при увеличении
- это еще один параметр стратегии СРС и он также должен
оптимизироваться. Однако при увеличении ![]() , как было показано выше, выражение для
, как было показано выше, выражение для ![]() сильно усложняется.
сильно усложняется.
Таким образом, поставленная задача заключается в
нахождении ![]() при
при
![]() ;
; ![]() . Если для
определенности принять, что передавался символ
. Если для
определенности принять, что передавался символ ![]() , то в этом случае ошибка будет иметь
место при
, то в этом случае ошибка будет иметь
место при ![]() , а
УВО на бит определяется из выражения
, а
УВО на бит определяется из выражения
 (4.68)
(4.68)
где ![]() - плотность вероятности
выходной статистики
- плотность вероятности
выходной статистики ![]() в
приемном устройстве
в
приемном устройстве ![]() типа
на фоне помехи, поражающей часть полосы
типа
на фоне помехи, поражающей часть полосы ![]() , при условии подавления
, при условии подавления ![]() субсимволов. Выходную
статистику
субсимволов. Выходную
статистику
![]()
целесообразно представить в виде
![]() (4.69)
(4.69)
и, учитывая, что ![]() невелико (
невелико (![]() ), закон распределения статистики
), закон распределения статистики ![]() находить
прямым путем в соответствии с функциональным преобразованием (4.69).
находить
прямым путем в соответствии с функциональным преобразованием (4.69).
Для случая передачи символа 1 переменные ![]() и
и ![]() (квадраты огибающих), как
приводилось ранее, распределены следующим образом:
(квадраты огибающих), как
приводилось ранее, распределены следующим образом:
 (4.70)
(4.70)
где
![]() -
модифицированная функция Бесселя нулевого порядка;
-
модифицированная функция Бесселя нулевого порядка; ![]() ;
;

При нахождении распределения ![]() , т.е.
, т.е. ![]() примем, что общим случаем
является распределение
примем, что общим случаем
является распределение ![]() , относящееся к ситуации, когда мощность
помехи разная в различных субсимволах. В соответствии с (4.69) и (4.70) функция
распределения
, относящееся к ситуации, когда мощность
помехи разная в различных субсимволах. В соответствии с (4.69) и (4.70) функция
распределения ![]() при
при
![]() имеет
вид [52]:
имеет
вид [52]:

![]() (4.71)
(4.71)
где
 (4.72)
(4.72)
Подставив (4.71) в (4.68), получим выражение для СВО на
бит ![]() при
подавлении помехой одного из двух субсимволов:
при
подавлении помехой одного из двух субсимволов:
 (4.73)
(4.73)
Осуществляя предельные переходы в (4.73), можно найти, что
 (4.74)
(4.74)
Как и следовало ожидать, выражения (4.74) показывают,
что СВО в условиях стационарной помехи не зависит от степени АРУ. Заключенный в
скобки первый сомножитель в каждой из формул (4.74) характеризует увеличение ![]() и
и ![]() за счет некогерентного сложения
взвешенных выборок
за счет некогерентного сложения
взвешенных выборок ![]() .
.
Для демодулятора с ![]() [9,11-14] также требуется раскрыть
неопределенность в (4.73), поскольку при этом
[9,11-14] также требуется раскрыть
неопределенность в (4.73), поскольку при этом![]() . В результате
. В результате
 (4.75)
(4.75)
На основе (4.67) с учетом (4.73) - (4.75) выражение для
СВО на бит ![]() в некогерентном приемнике
сигналов с ППРЧ и двоичной ЧМ при
в некогерентном приемнике
сигналов с ППРЧ и двоичной ЧМ при ![]() имеет вид [52]:
имеет вид [52]:
 (4.76)
(4.76)
Выражение (4.76) позволяет оценить помехоустойчивость
некогерентного приемника сигналов с ППРЧ при ![]() и двоичной ЧМ в условиях шумовой помехи в
части полосы при произвольной степени АРУ. Используя (4.76), можно решать
задачу оптимизации
и двоичной ЧМ в условиях шумовой помехи в
части полосы при произвольной степени АРУ. Используя (4.76), можно решать
задачу оптимизации ![]() как
для ПП (по отношению к
как
для ПП (по отношению к![]() ), так и для СРС (по отношению к
), так и для СРС (по отношению к ![]() ). Для этого должны
быть найдены
). Для этого должны
быть найдены ![]() и
и
![]() с выводами об оптимальных
значениях параметров
с выводами об оптимальных
значениях параметров ![]() и
и
![]() . В виду сложности и
многофакторности выражения (4.76) его оптимизация в аналитической форме
оказывается затруднительной, поэтому задача может быть решена численным
методом.
. В виду сложности и
многофакторности выражения (4.76) его оптимизация в аналитической форме
оказывается затруднительной, поэтому задача может быть решена численным
методом.
В соответствии с (4.76) рассчитаны СВО на бит для различных
степеней АРУ (![]() )
в условиях шумовой помехи в части полосы с отношением сигнал-помеха
)
в условиях шумовой помехи в части полосы с отношением сигнал-помеха ![]() и при изменении части
подавляемой полосы в пределах
и при изменении части
подавляемой полосы в пределах ![]() . В качестве параметра использовалось
отношение сигнал-шум приемника
. В качестве параметра использовалось
отношение сигнал-шум приемника ![]() .
.

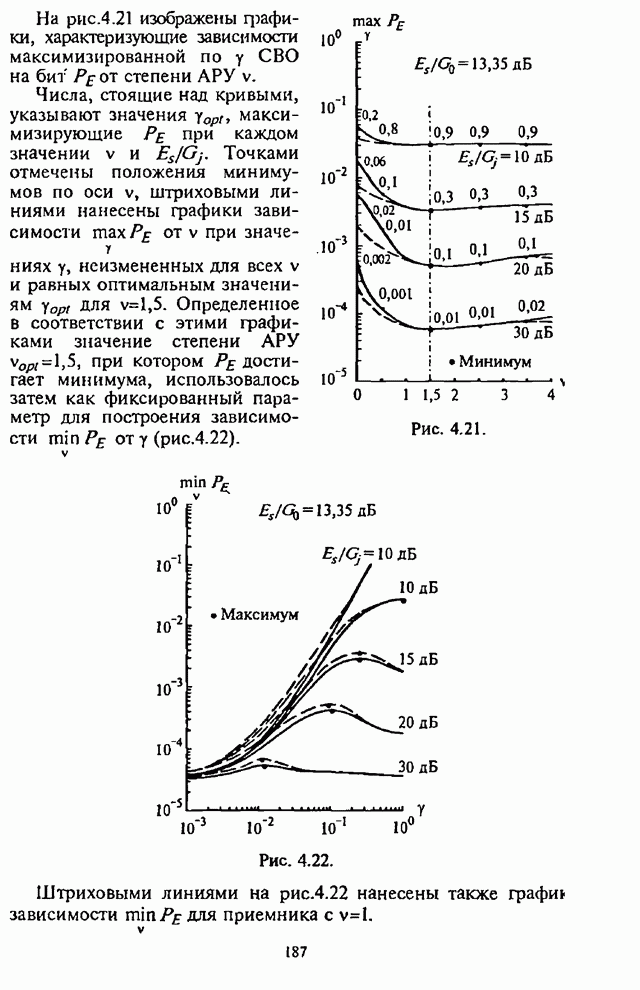
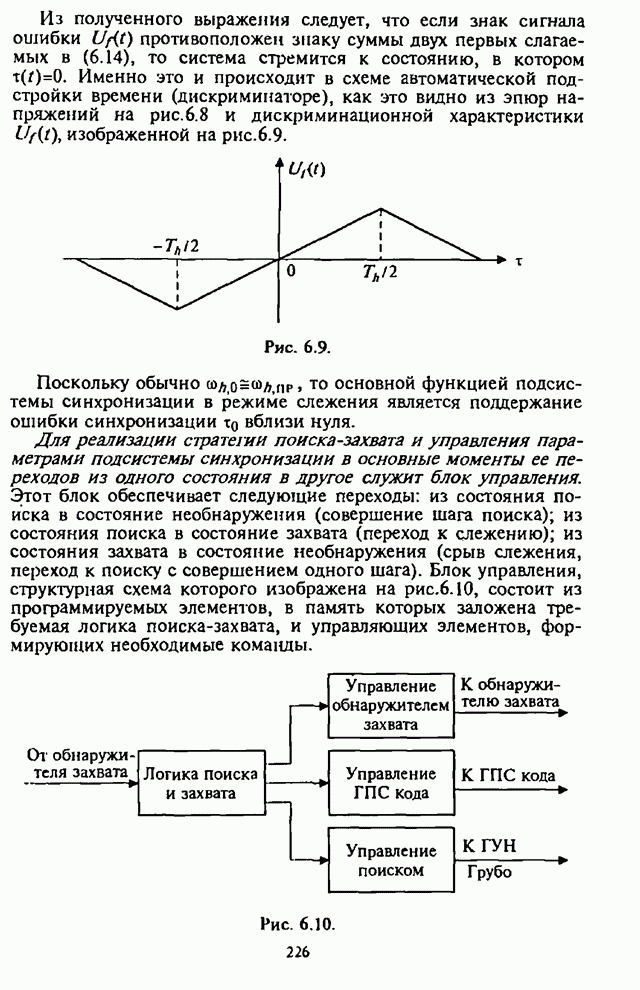
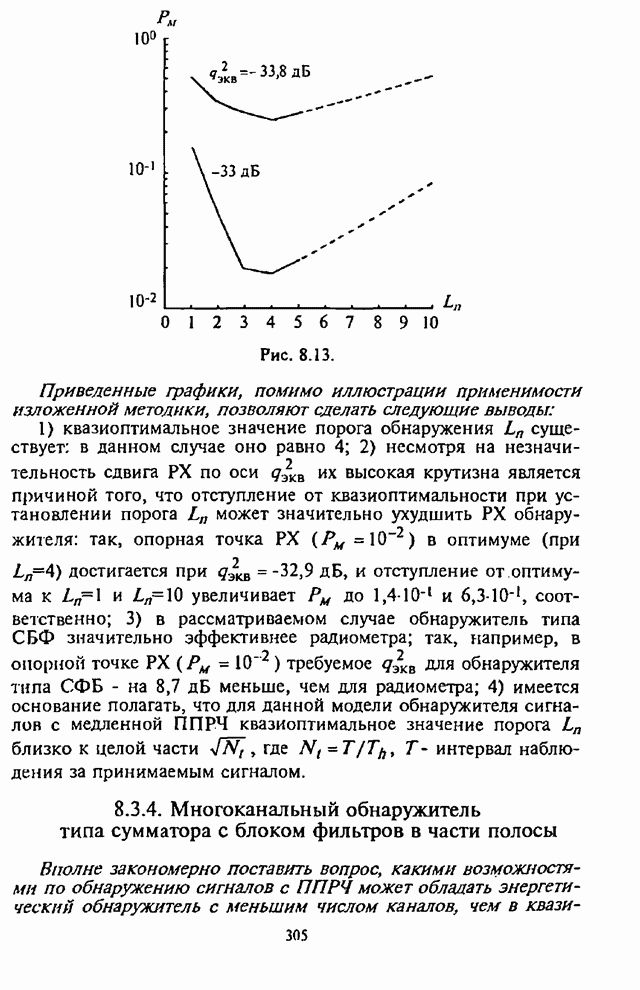
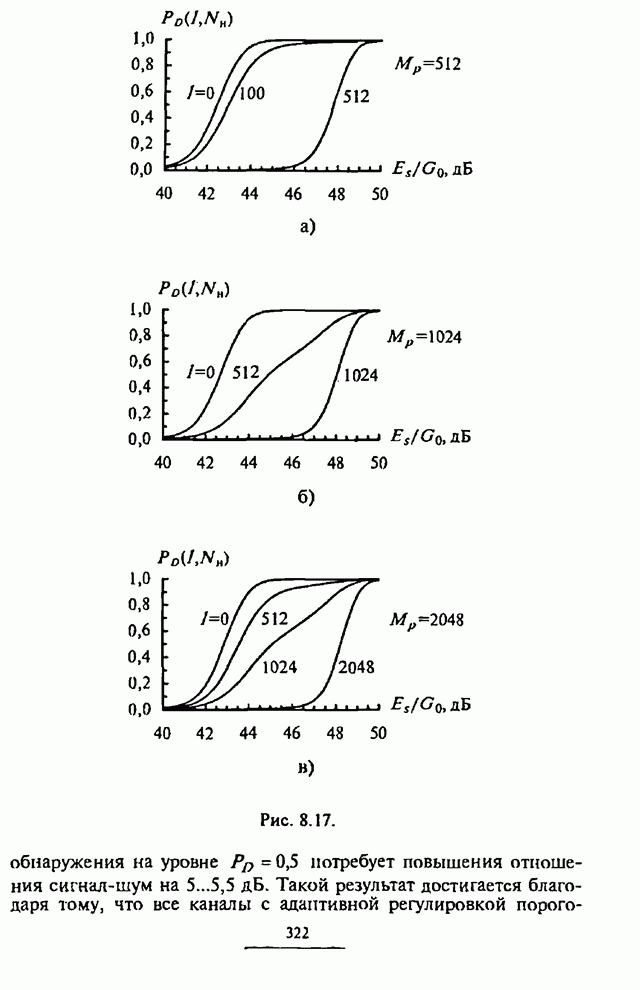
Рис. 4.21.
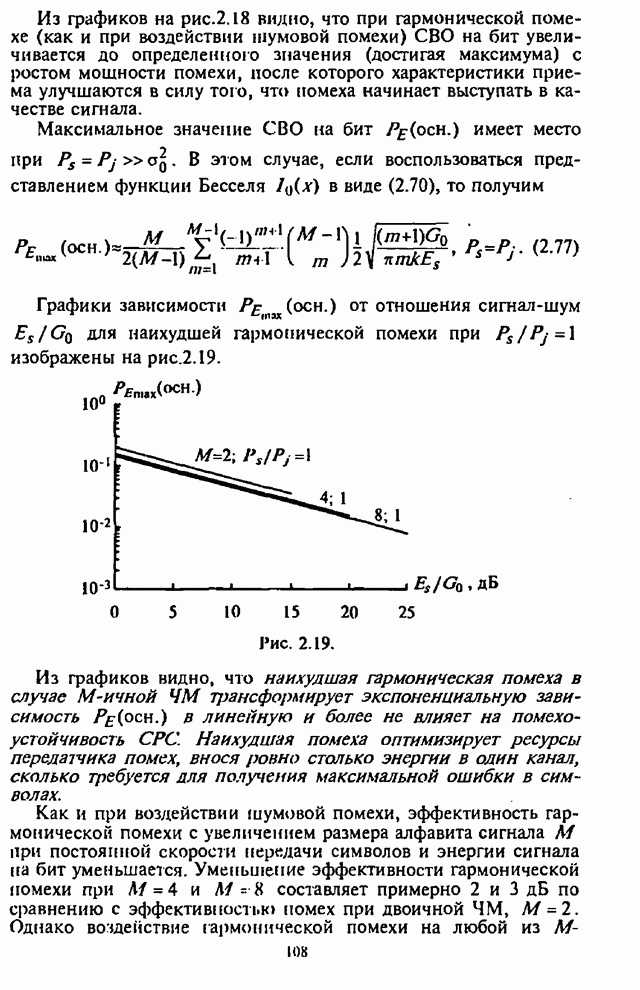
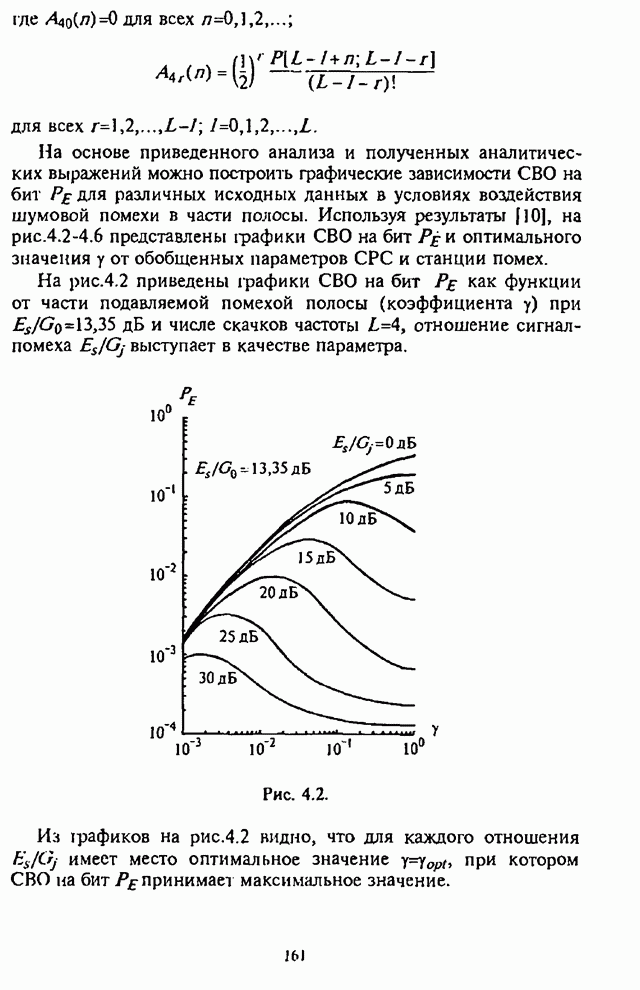
На рис.4.21 изображены графики, характеризующие
зависимости максимизированной по ![]() СВО на бит
СВО на бит ![]() от степени АРУ
от степени АРУ ![]() .
.
Числа, стоящие над кривыми, указывают значения ![]() , максимизирующие
, максимизирующие ![]() при каждом значении
при каждом значении ![]() и
и ![]() . Точками отмечены положения
минимумов по оси
. Точками отмечены положения
минимумов по оси ![]() ,
штриховыми линиями нанесены графики зависимости
,
штриховыми линиями нанесены графики зависимости ![]() от
от ![]() при значениях
при значениях ![]() , неизмененных для всех
, неизмененных для всех ![]() и равных оптимальным
значениям
и равных оптимальным
значениям ![]() для
для ![]() . Определенное в соответствии с
этими графиками значение степени АРУ
. Определенное в соответствии с
этими графиками значение степени АРУ ![]() , при котором
, при котором ![]() достигает минимума,
использовалось затем как фиксированный параметр для построения зависимости
достигает минимума,
использовалось затем как фиксированный параметр для построения зависимости ![]() от
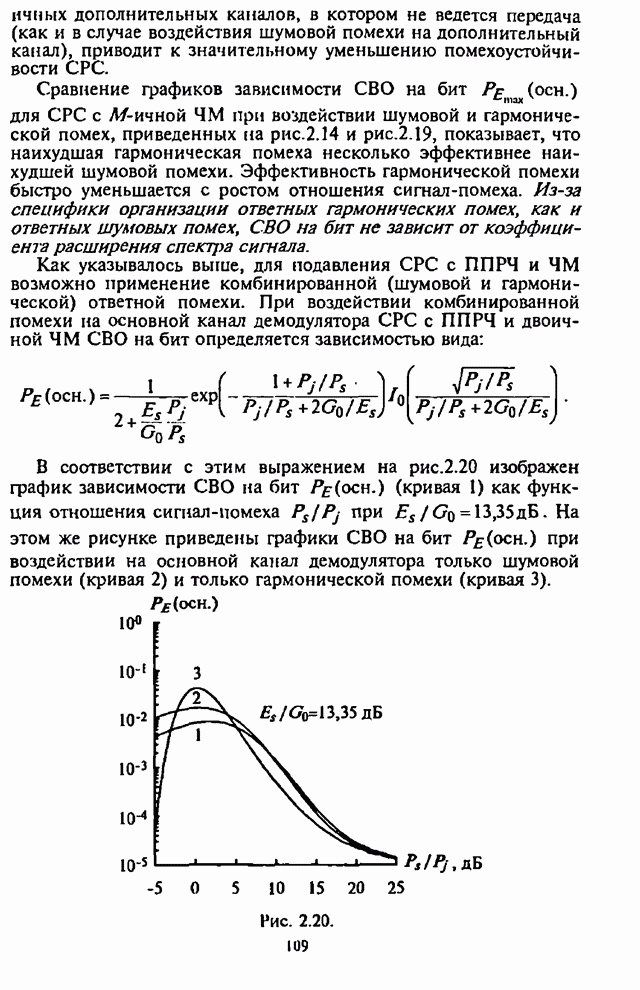
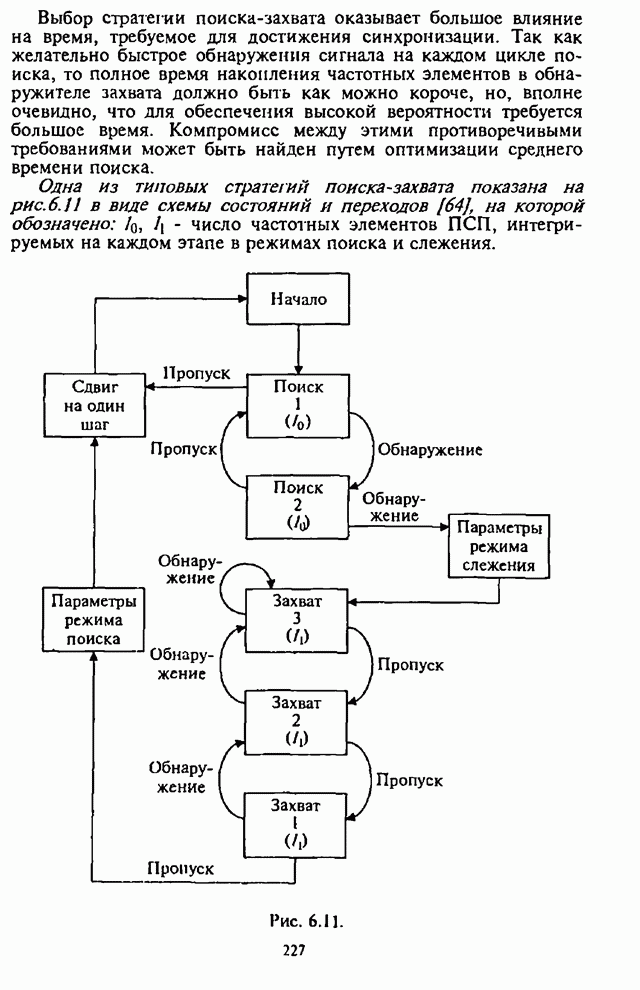
от ![]() (рис.4.22).
(рис.4.22).

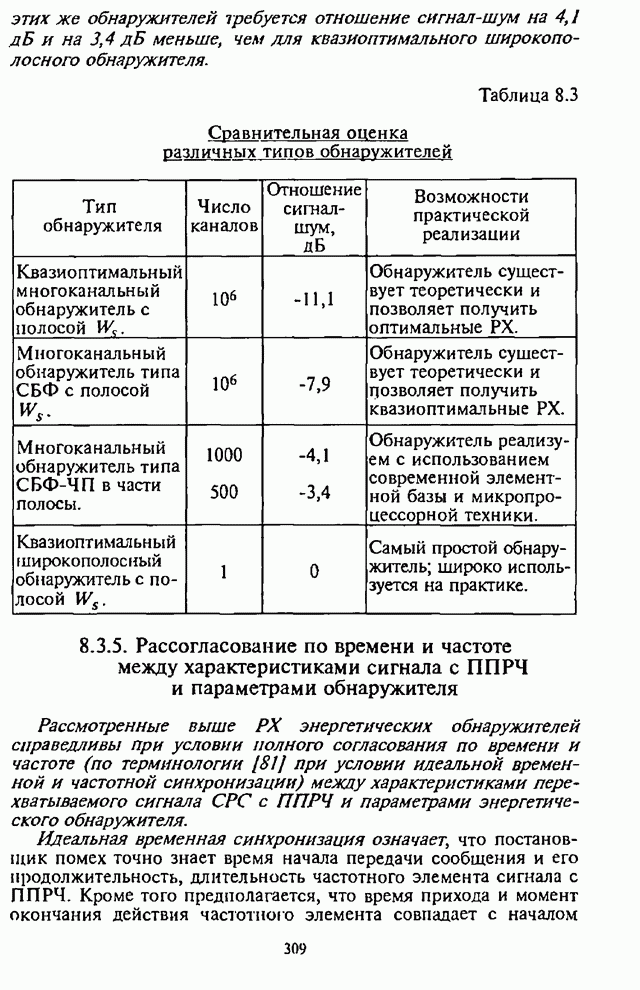
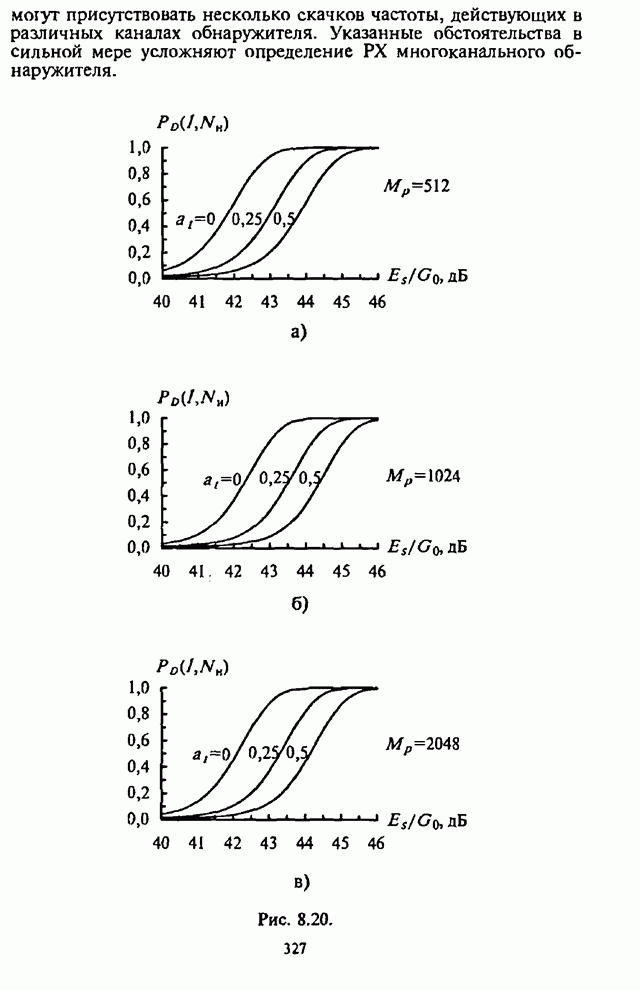
Рис. 4.22.
Штриховыми линиями на рис.4.22 нанесены также график
зависимости ![]() для приемника с
для приемника с ![]() .
.
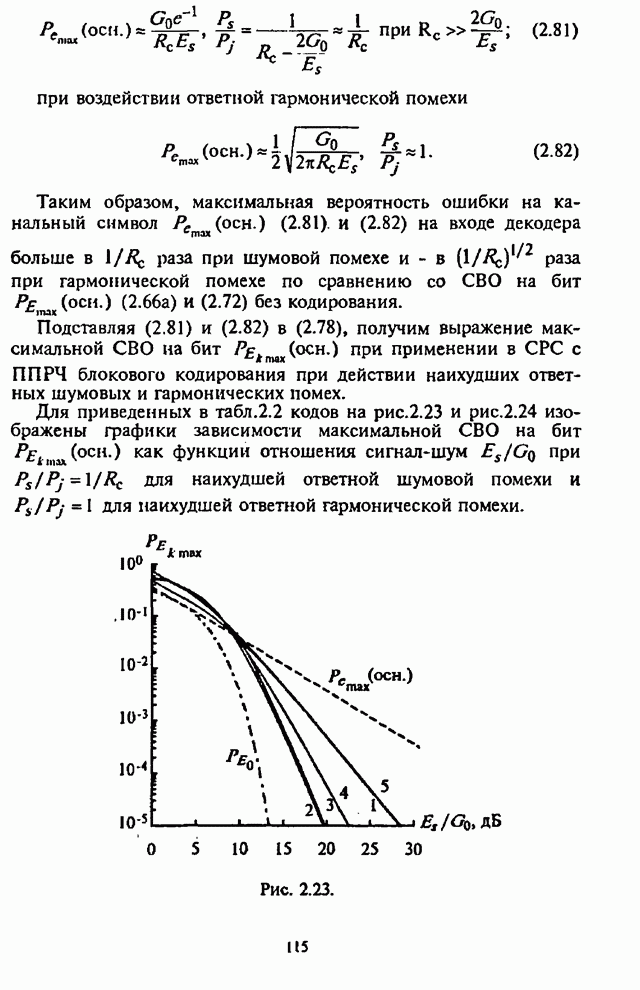
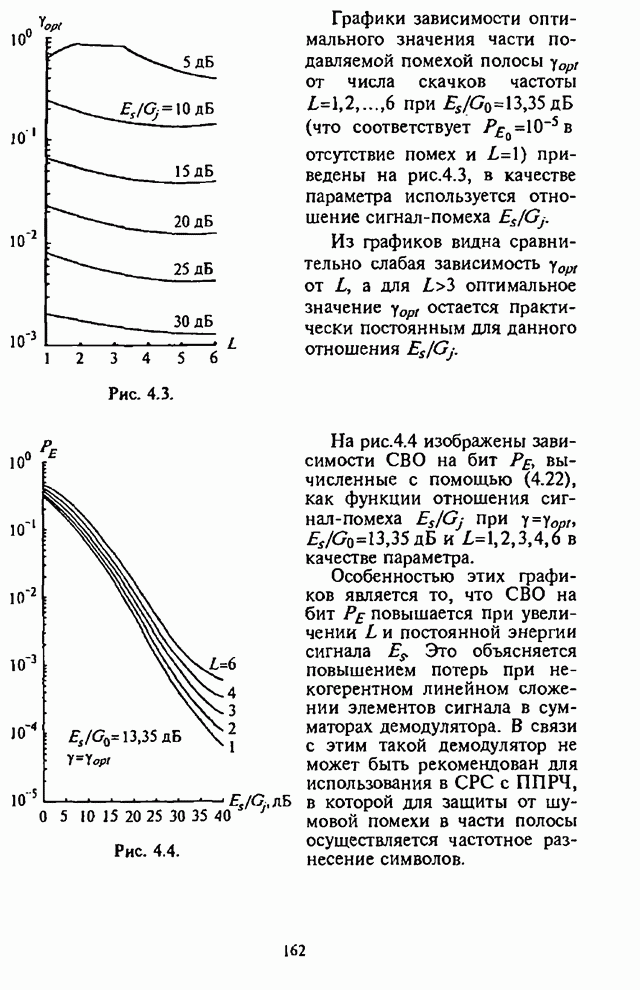
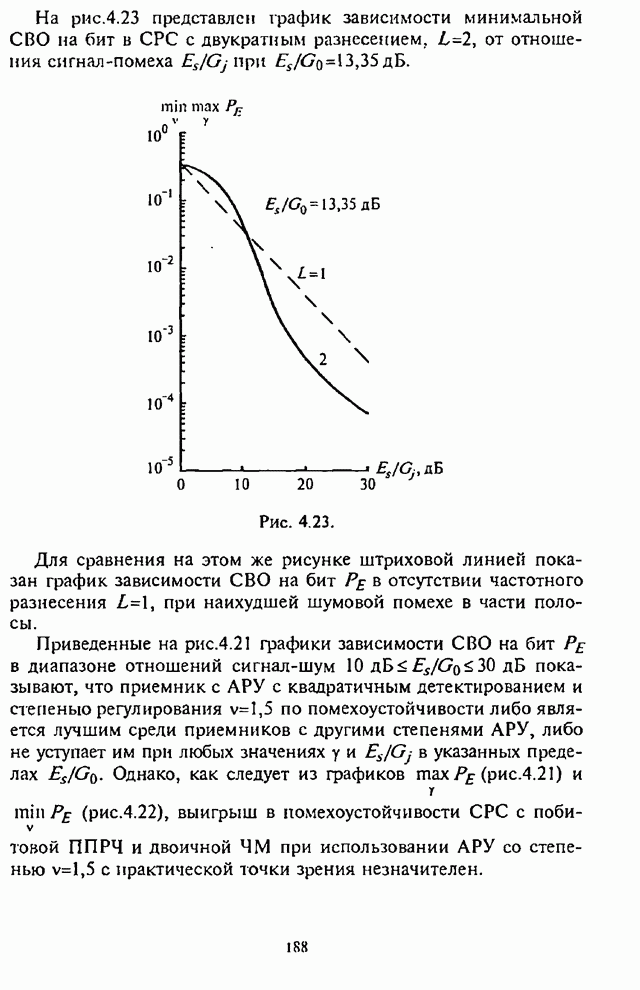
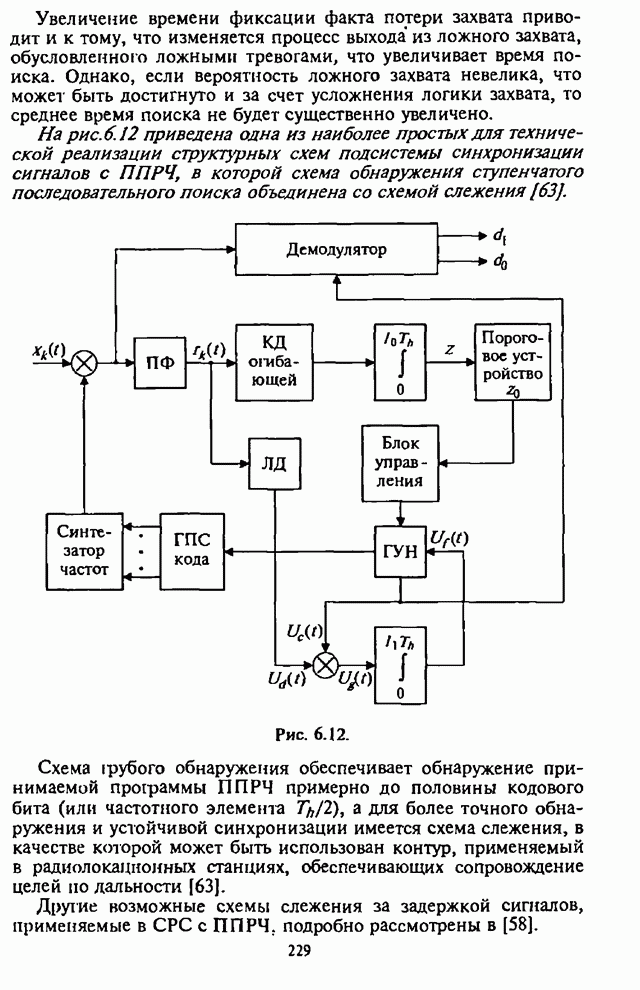
На рис.4.23 представлен график зависимости минимальной
СВО на бит в СРС с двукратным разнесением ![]() от отношения сигнал-помеха
от отношения сигнал-помеха ![]() при
при ![]() .
.

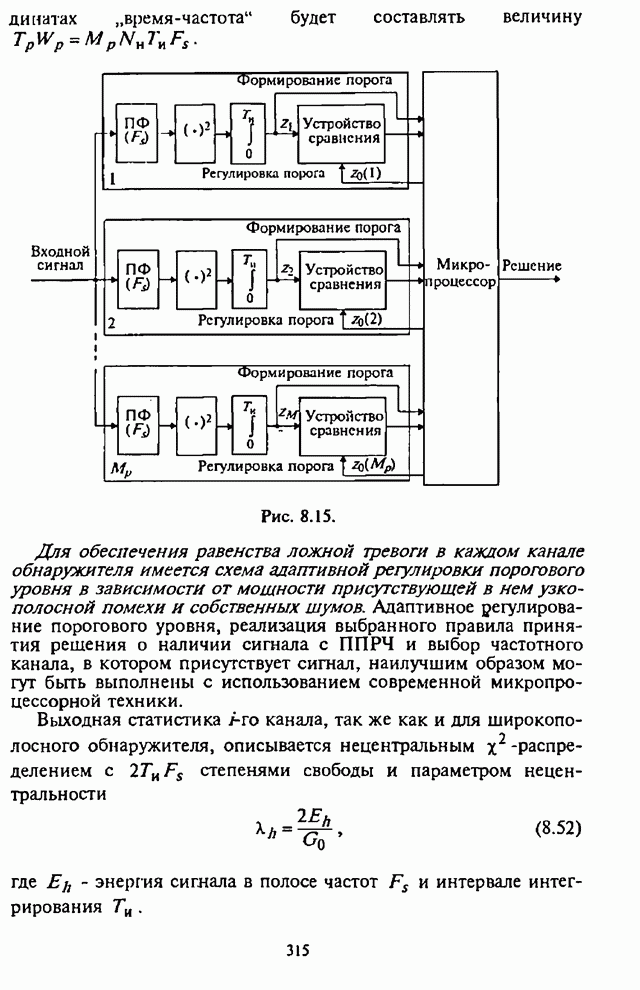
Рис. 4.23.
Для сравнения на этом же рисунке штриховой линией показан
график зависимости СВО на бит ![]() в отсутствии частотного разнесения
в отсутствии частотного разнесения ![]() , при наихудшей шумовой помехе в
части полосы.
, при наихудшей шумовой помехе в
части полосы.
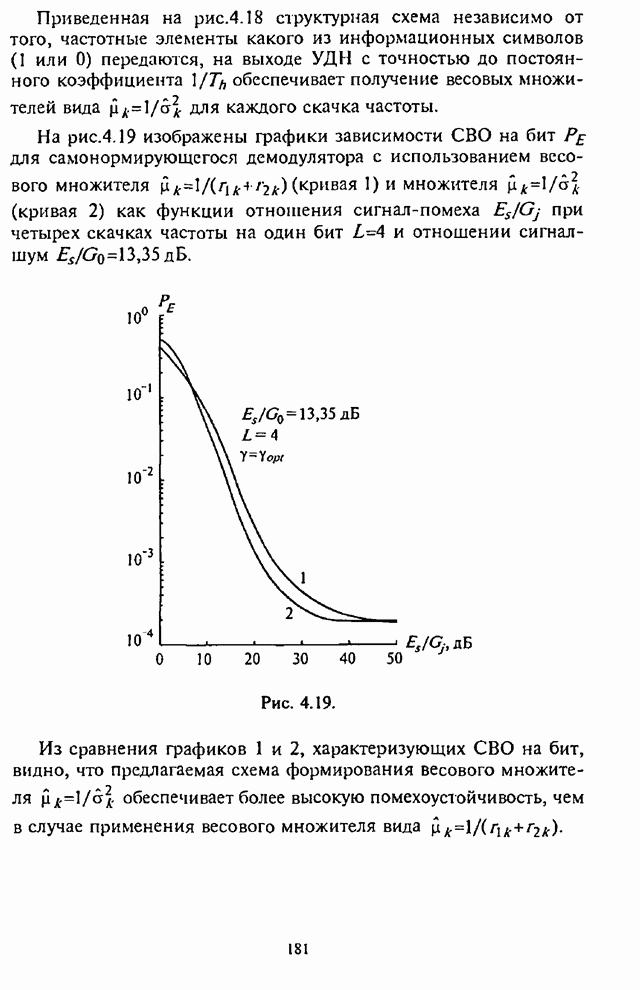
Приведенные на рис.4.21 графики зависимости СВО на бит ![]() в диапазоне отношений
сигнал-шум
в диапазоне отношений
сигнал-шум ![]() показывают, что приемник с АРУ с квадратичным
детектированием и степенью регулирования
показывают, что приемник с АРУ с квадратичным
детектированием и степенью регулирования ![]() по помехоустойчивости либо
является лучшим среди приемников с другими степенями АРУ, либо не уступает им
при любых значениях
по помехоустойчивости либо
является лучшим среди приемников с другими степенями АРУ, либо не уступает им
при любых значениях ![]() и
и
![]() в указанных пределах
в указанных пределах ![]() .
Однако,
как следует из графиков
.
Однако,
как следует из графиков ![]() (рис.4.21) и
(рис.4.21) и ![]() (рис.4.22), выигрыш в помехоустойчивости
СРС с побитовой
ППРЧ и двоичной ЧМ при использовании АРУ со степенью
(рис.4.22), выигрыш в помехоустойчивости
СРС с побитовой
ППРЧ и двоичной ЧМ при использовании АРУ со степенью ![]() с практической точки зрения
незначителен.
с практической точки зрения
незначителен.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
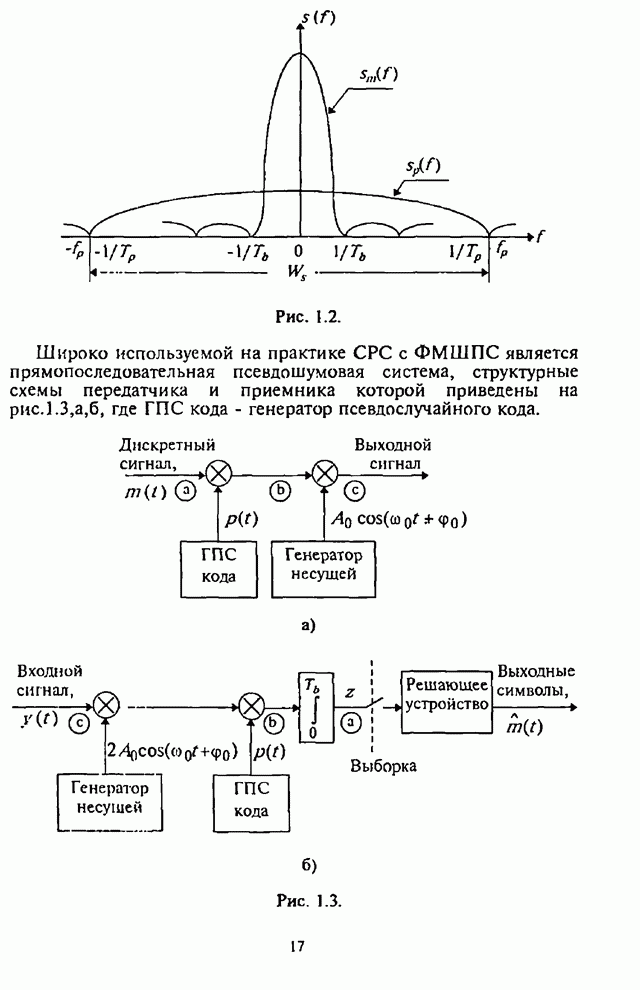
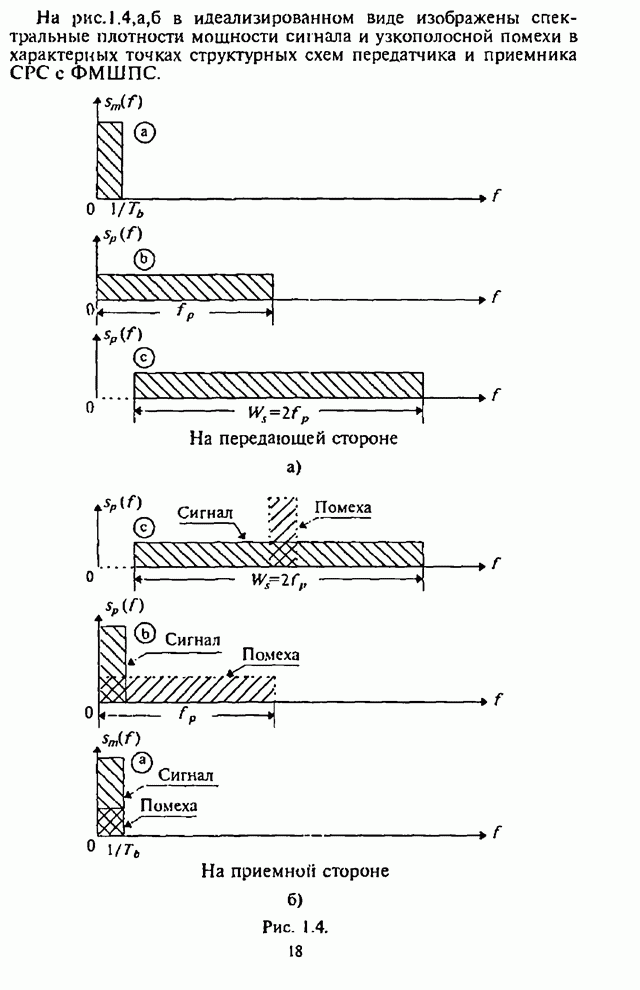
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
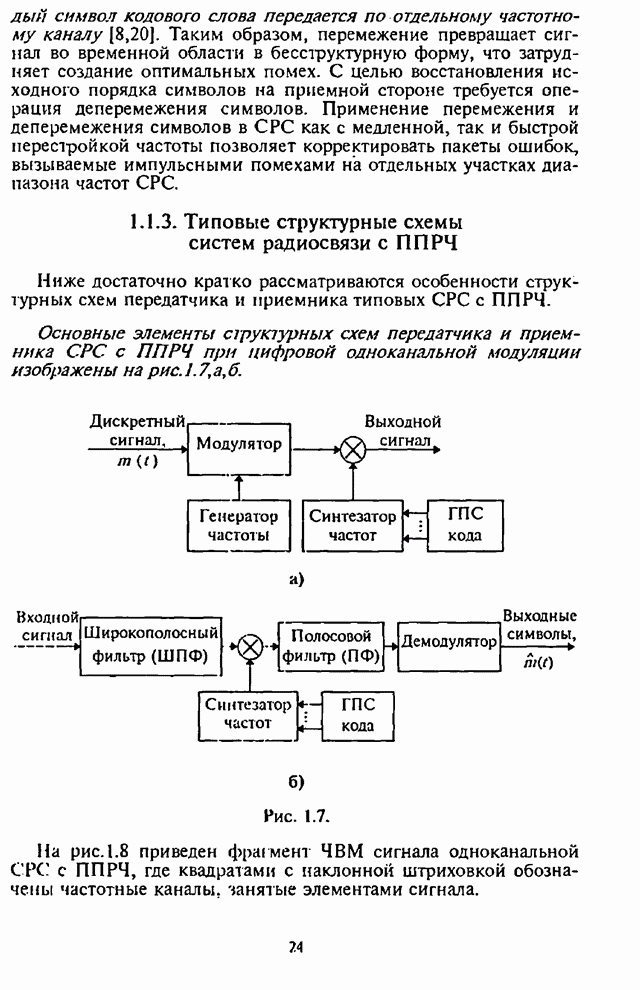
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
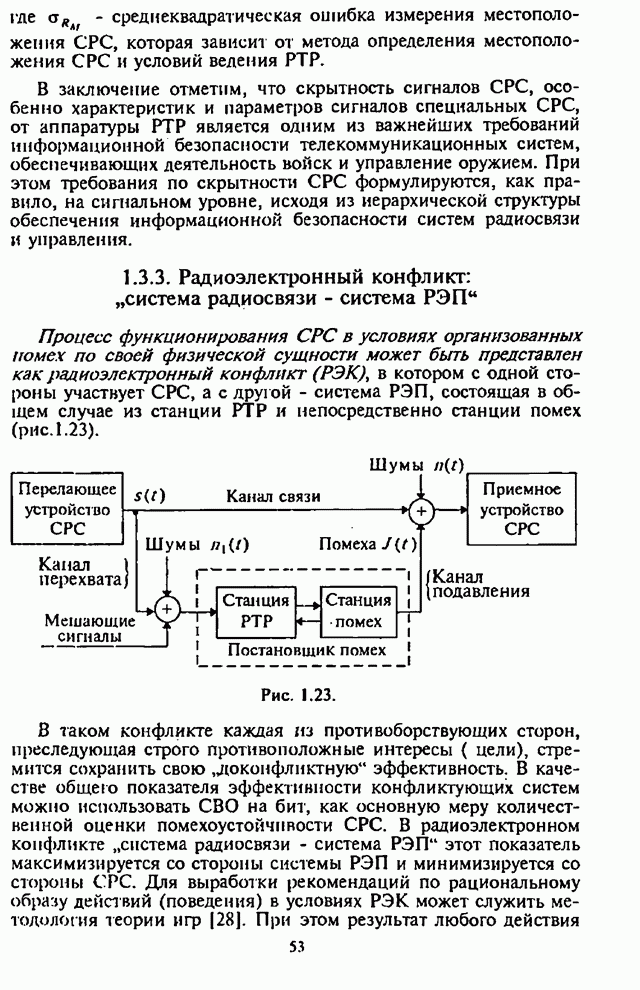
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
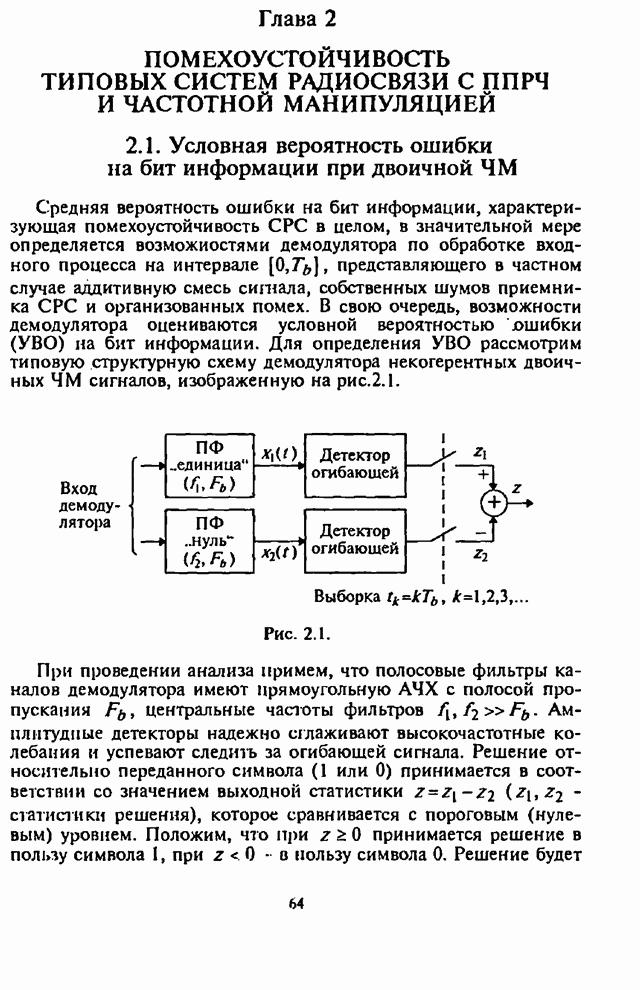
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
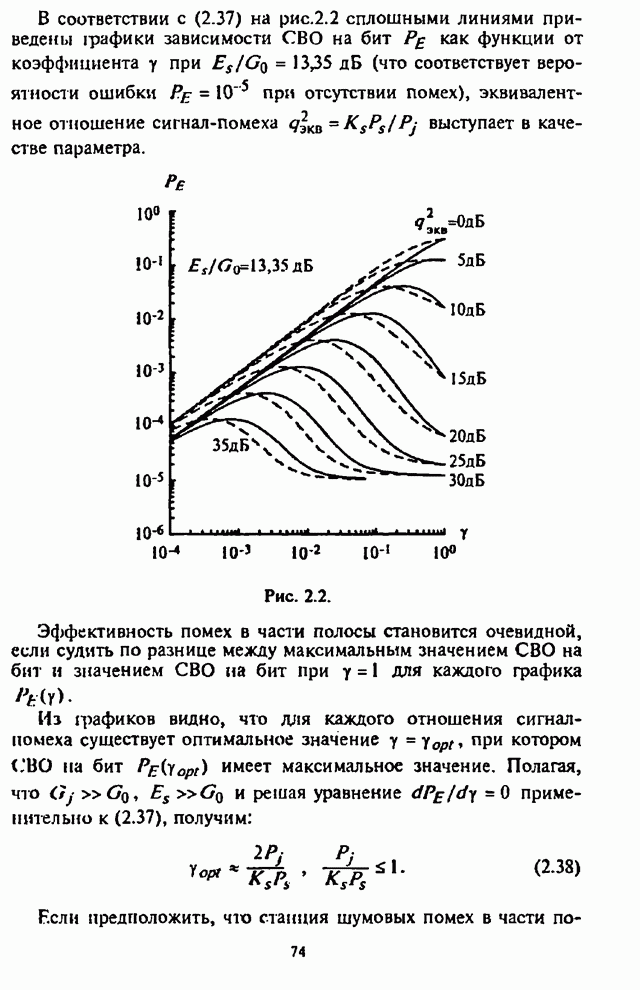
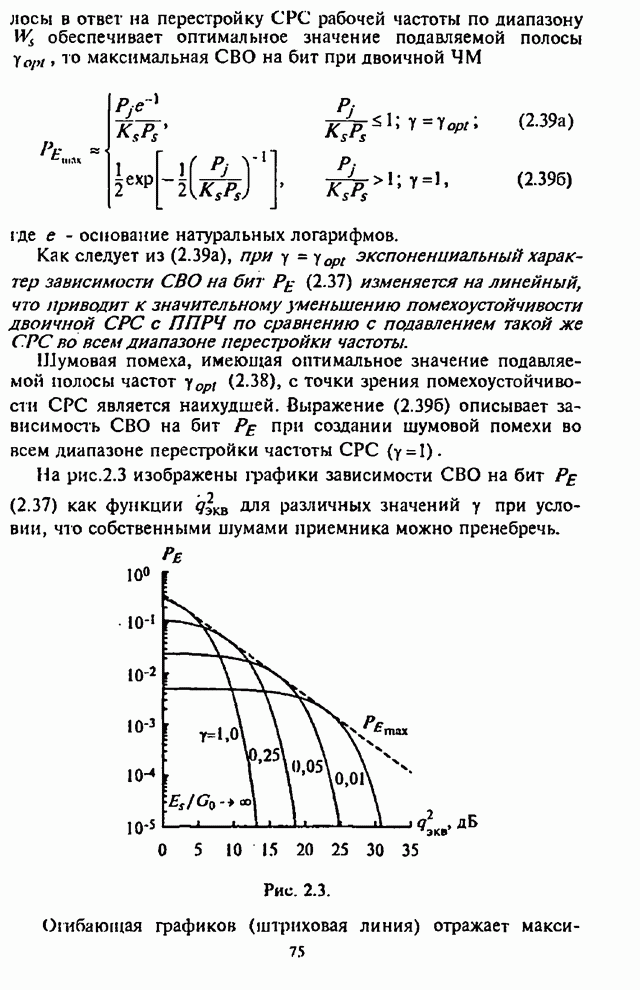
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
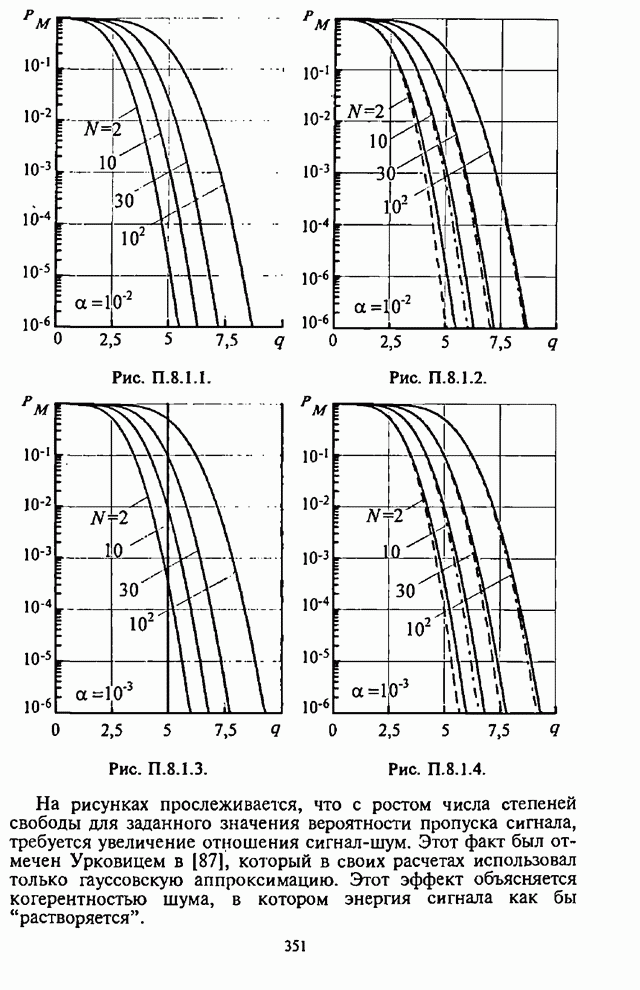
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
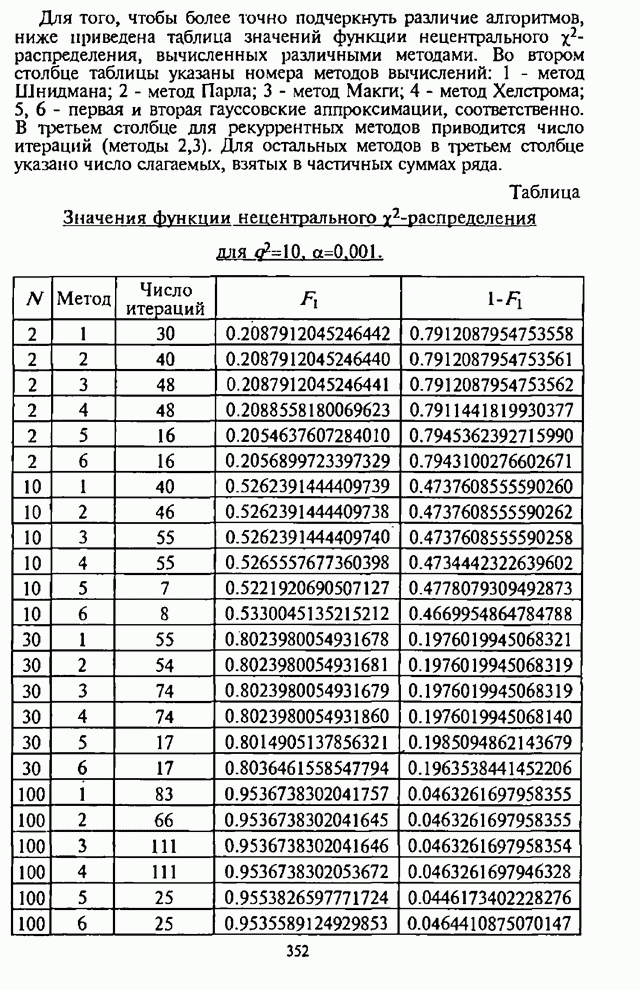
- П.8.1.6. Численные результаты
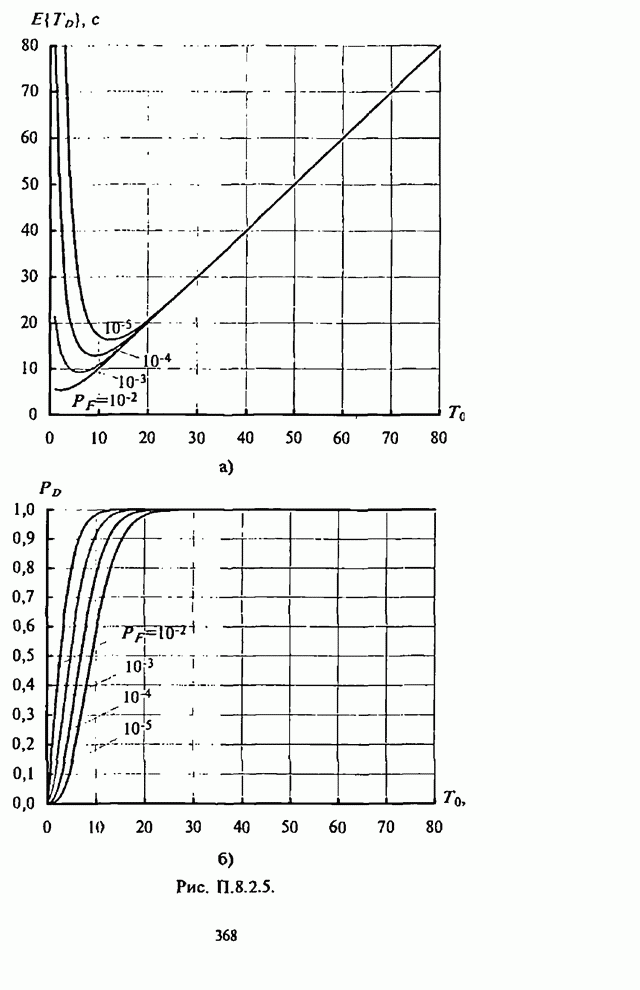
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
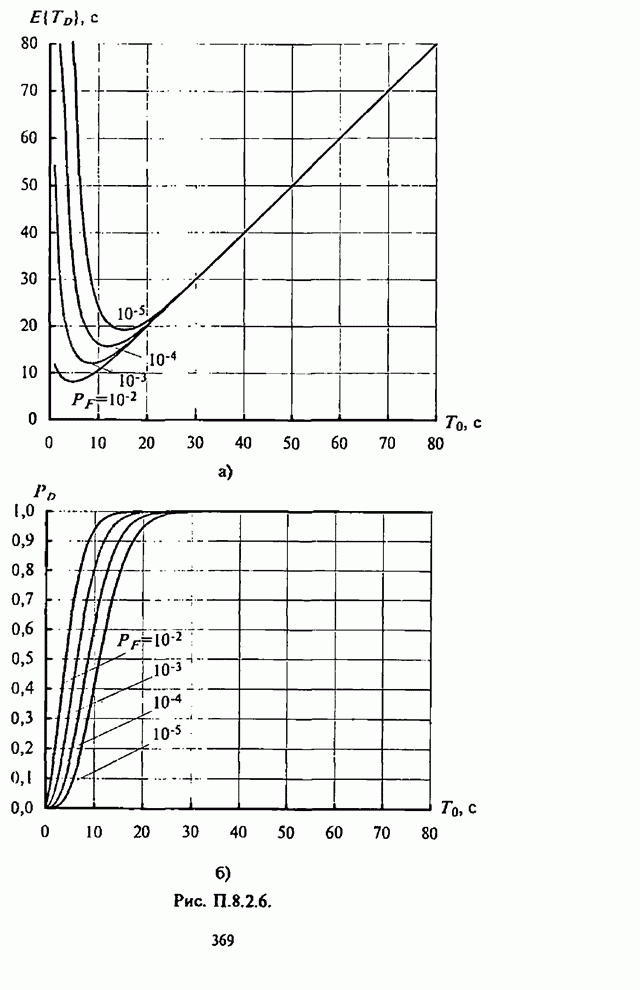
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ