| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
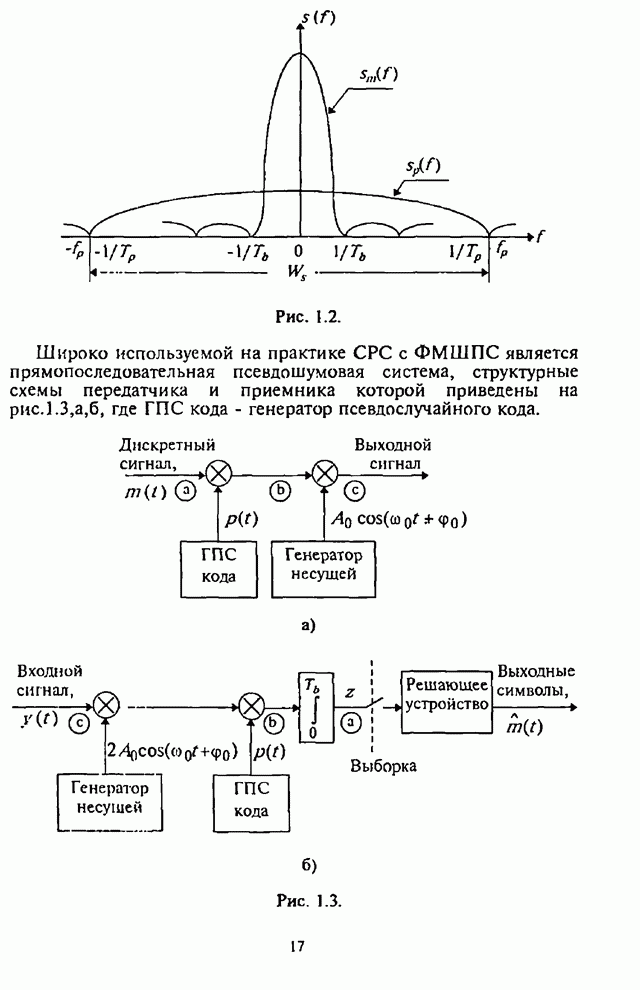
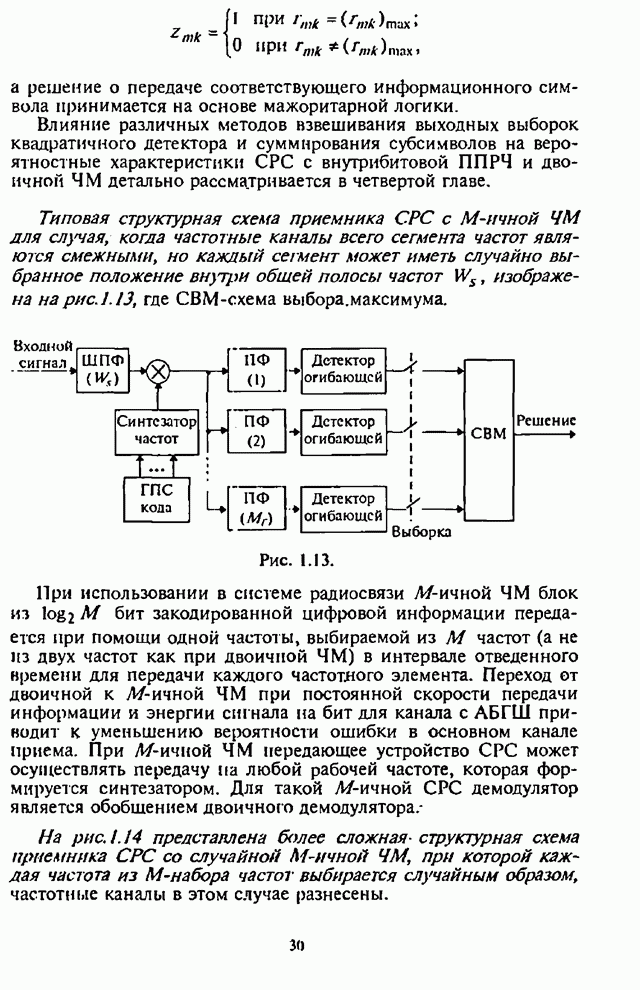
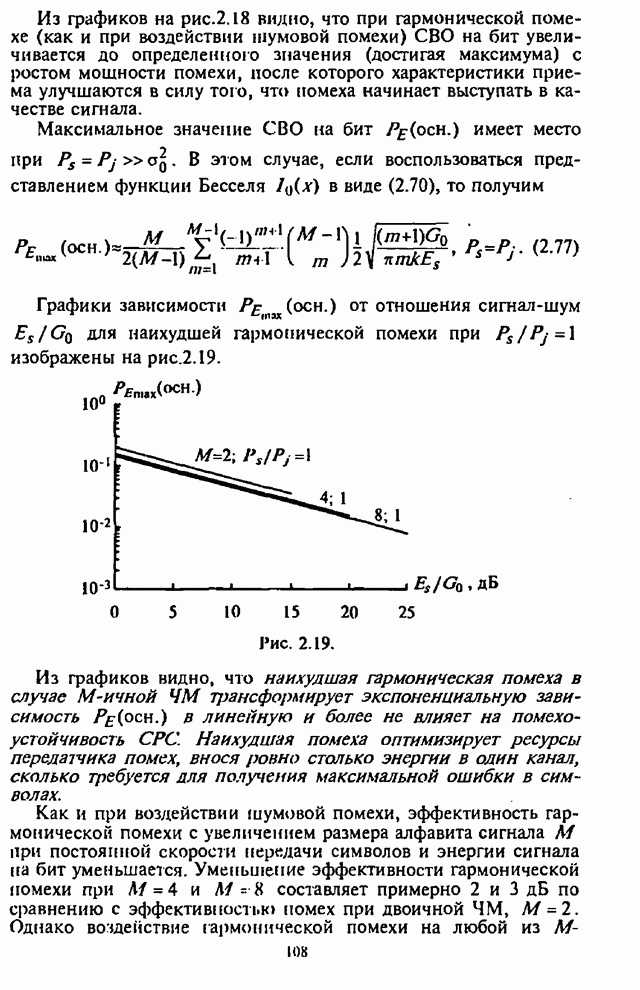
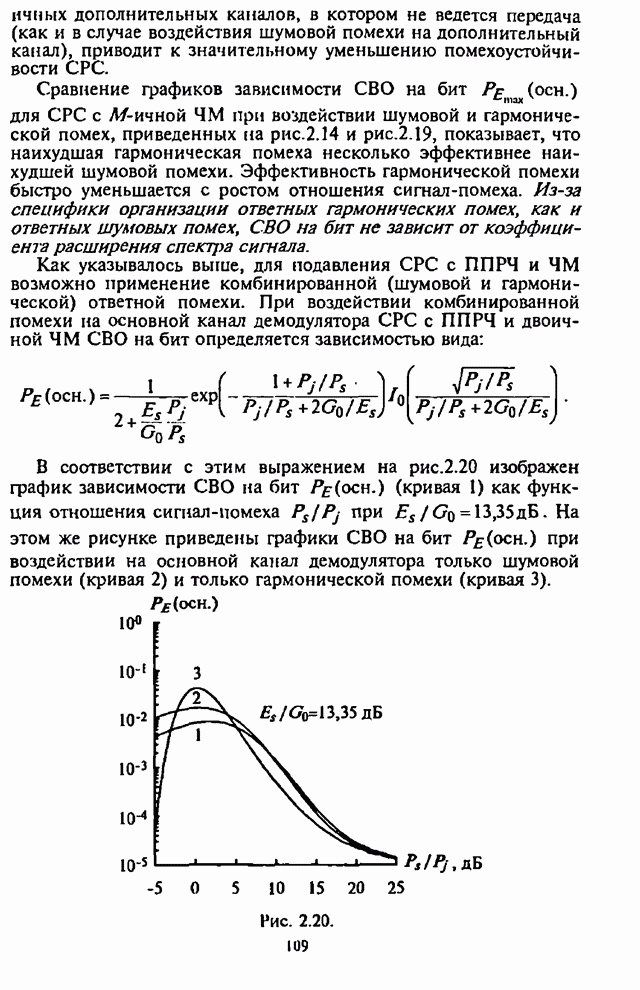
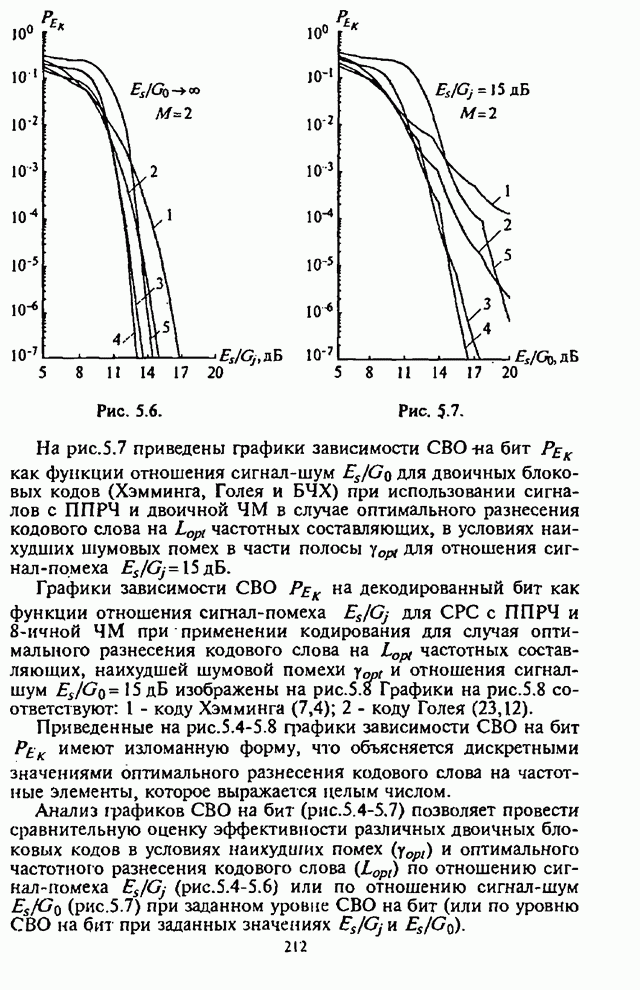
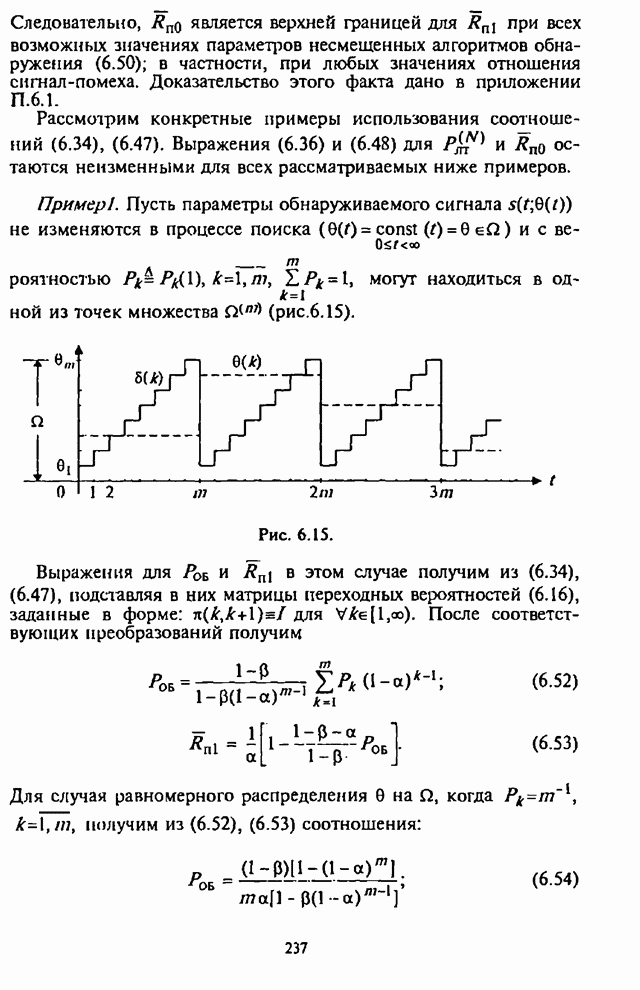
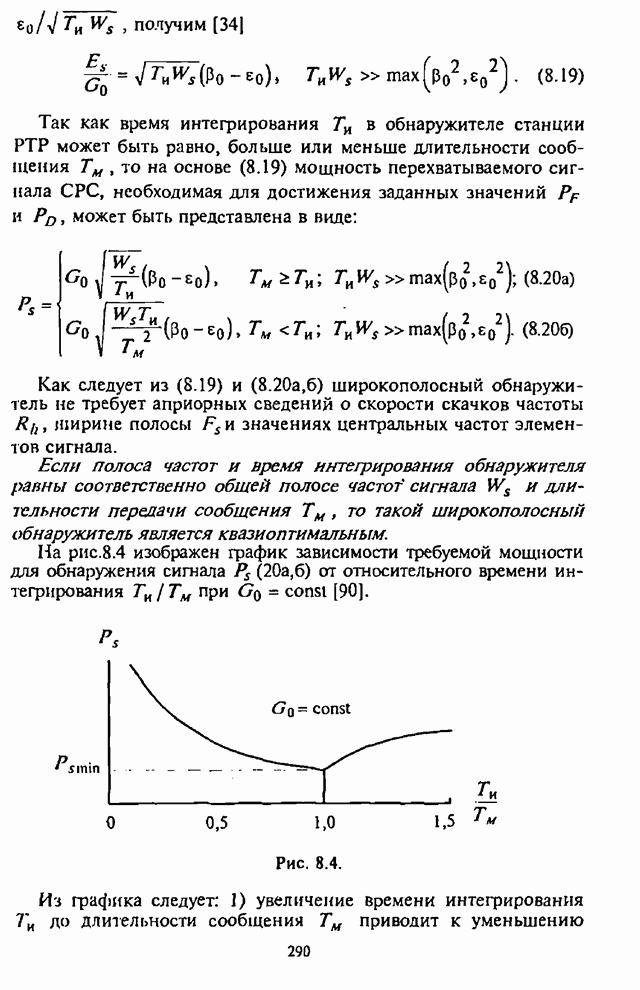
2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
Системы
радиосвязи с ППРЧ весьма чувствительны к наихудшим помехам. Так, выше было
показано, что при действии наихудшей ответной шумовой помехи на основной канал
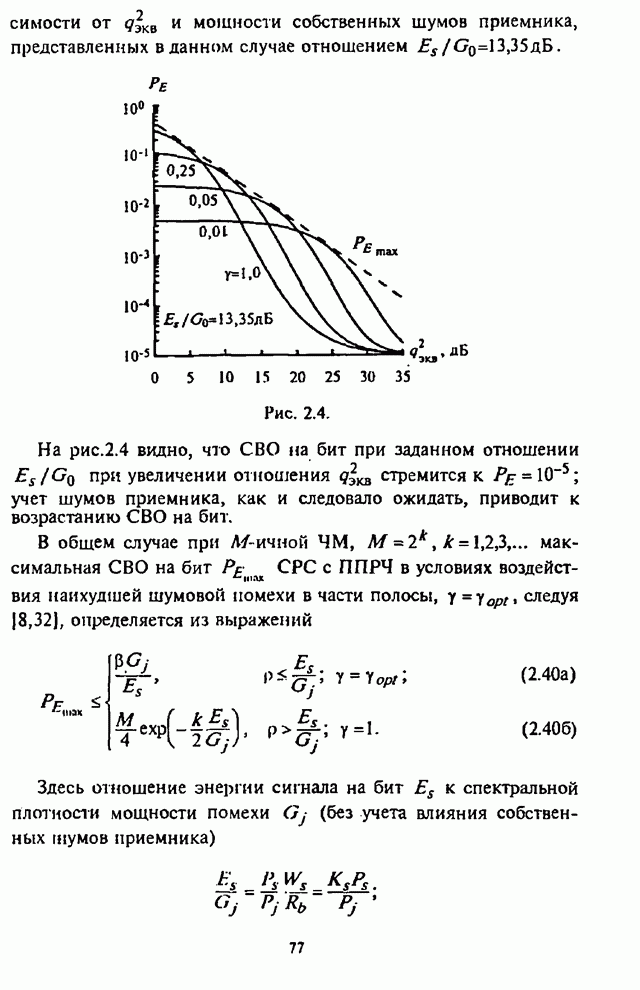
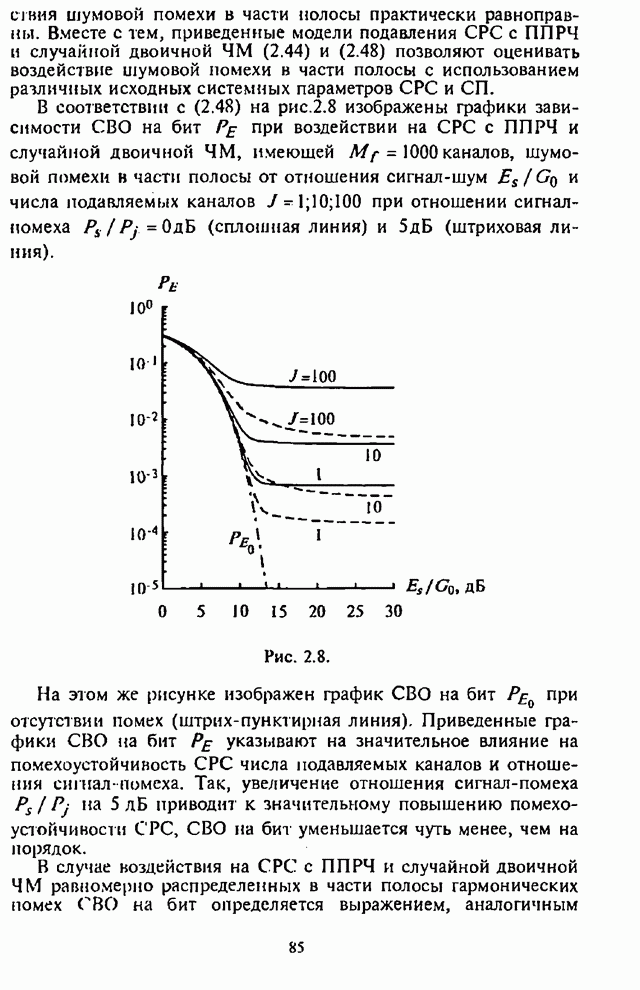
приемника максимальная СВО на бит ![]() , а при наихудшей шумовой помехе в части
полосы –
, а при наихудшей шумовой помехе в части
полосы – ![]() .
Экспоненциальный характер зависимости СВО на бит превращается в линейный, что
резко снижает помехоустойчивость СРС. Рабочие характеристики СРС с ППРЧ в
условиях таких помех могут быть значительно улучшены с помощью кодов, исправляющих
ошибки. С этой целью оценим возможности сравнительно просто реализуемых
блоковых кодов в СРС с ППРЧ и двоичной ЧМ при воздействии различных видов помех.
.
Экспоненциальный характер зависимости СВО на бит превращается в линейный, что
резко снижает помехоустойчивость СРС. Рабочие характеристики СРС с ППРЧ в
условиях таких помех могут быть значительно улучшены с помощью кодов, исправляющих
ошибки. С этой целью оценим возможности сравнительно просто реализуемых
блоковых кодов в СРС с ППРЧ и двоичной ЧМ при воздействии различных видов помех.
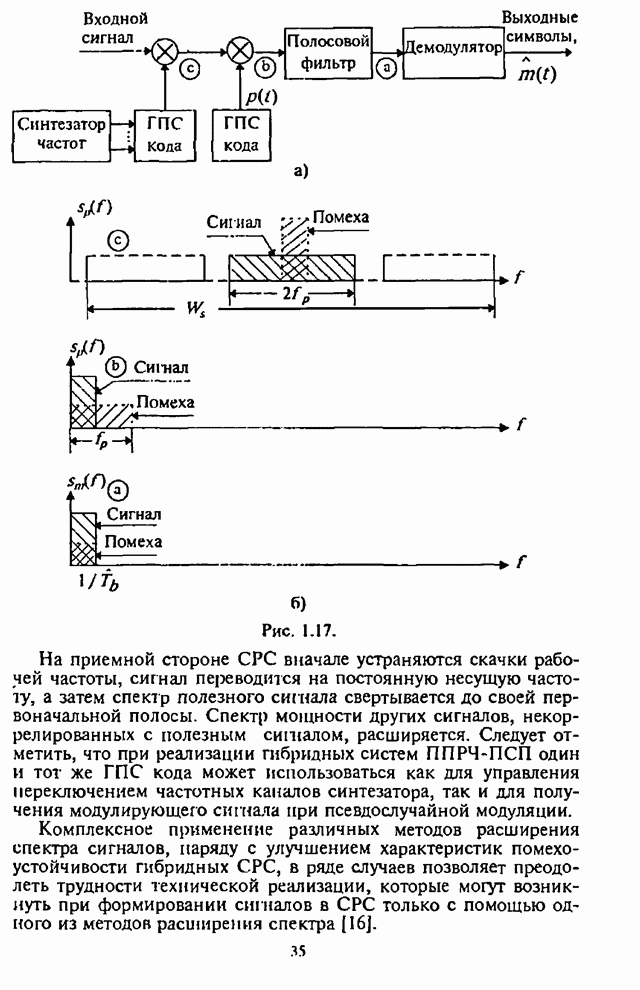
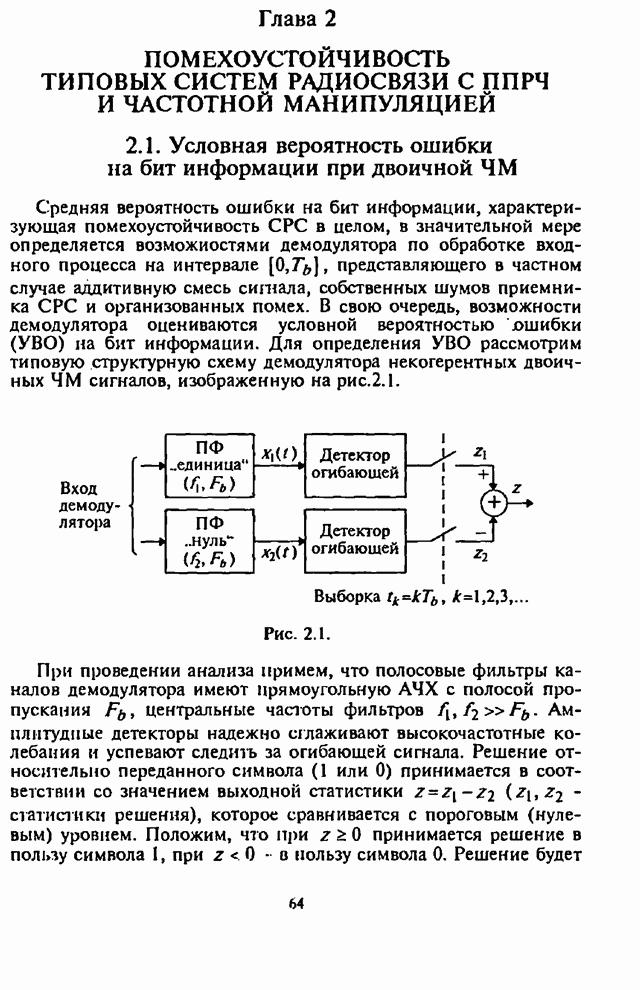
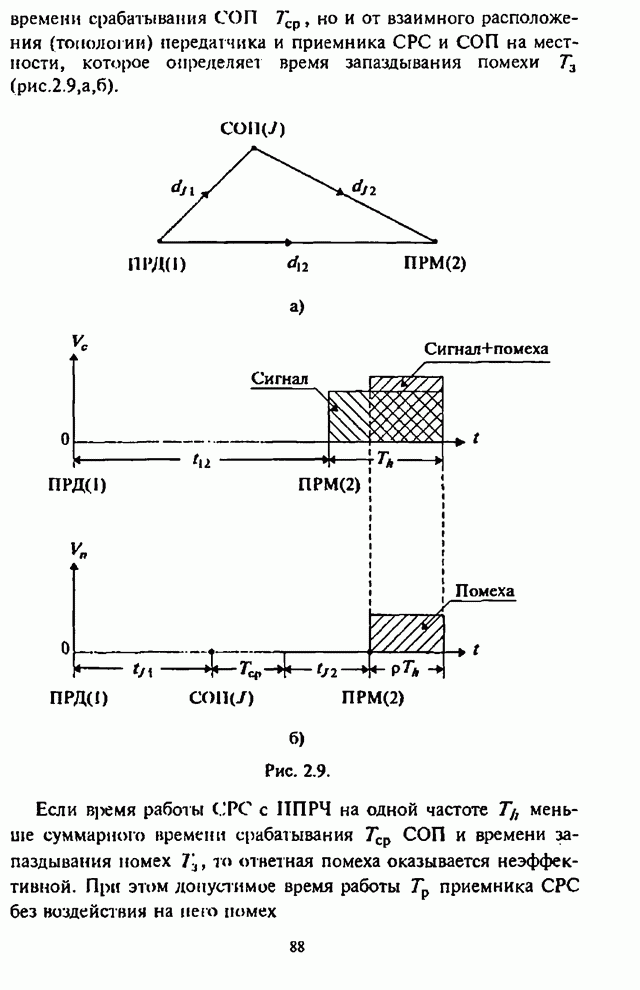
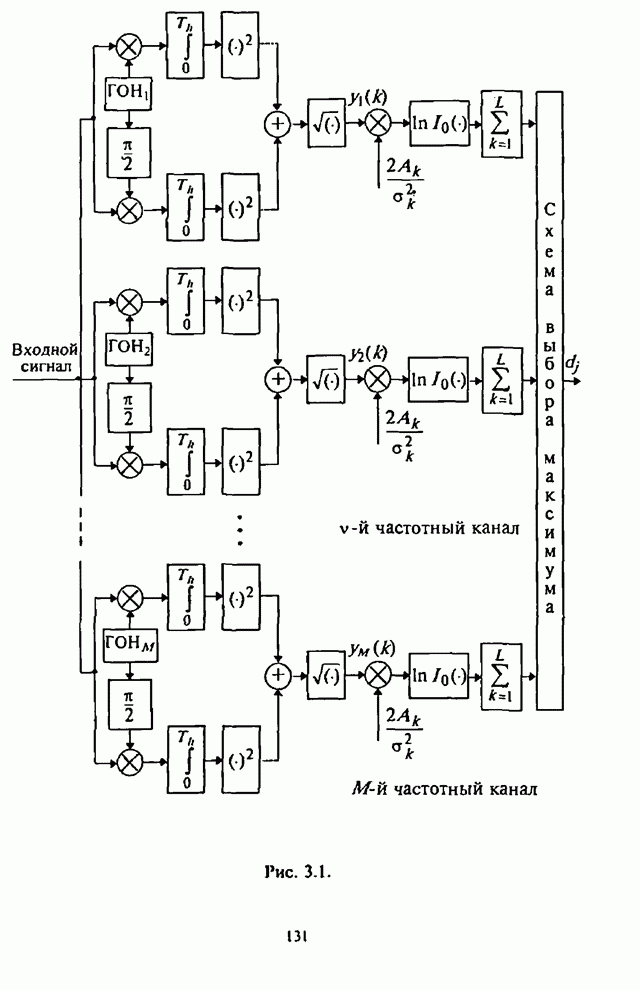
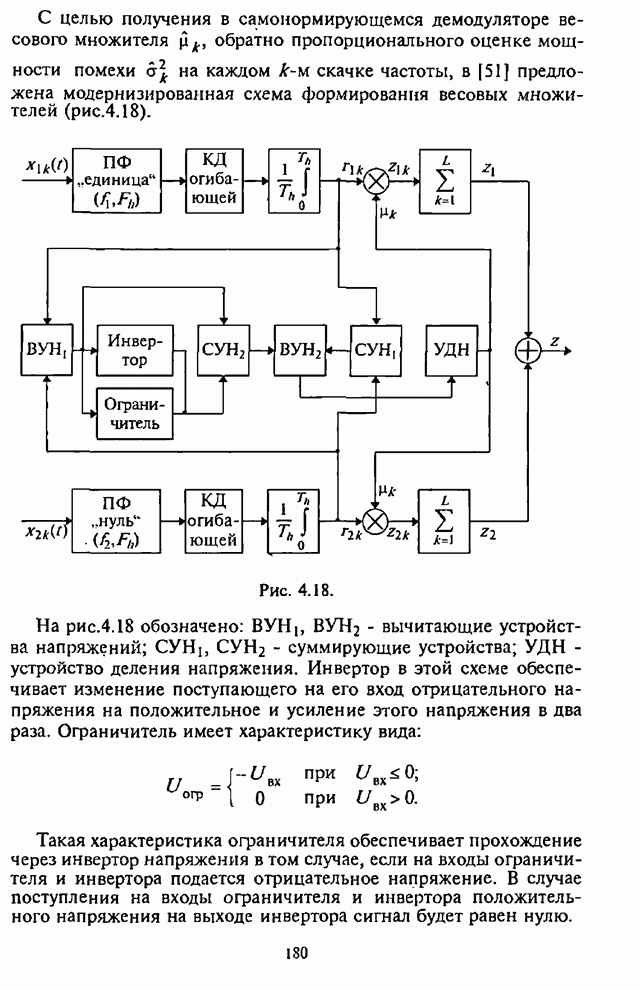
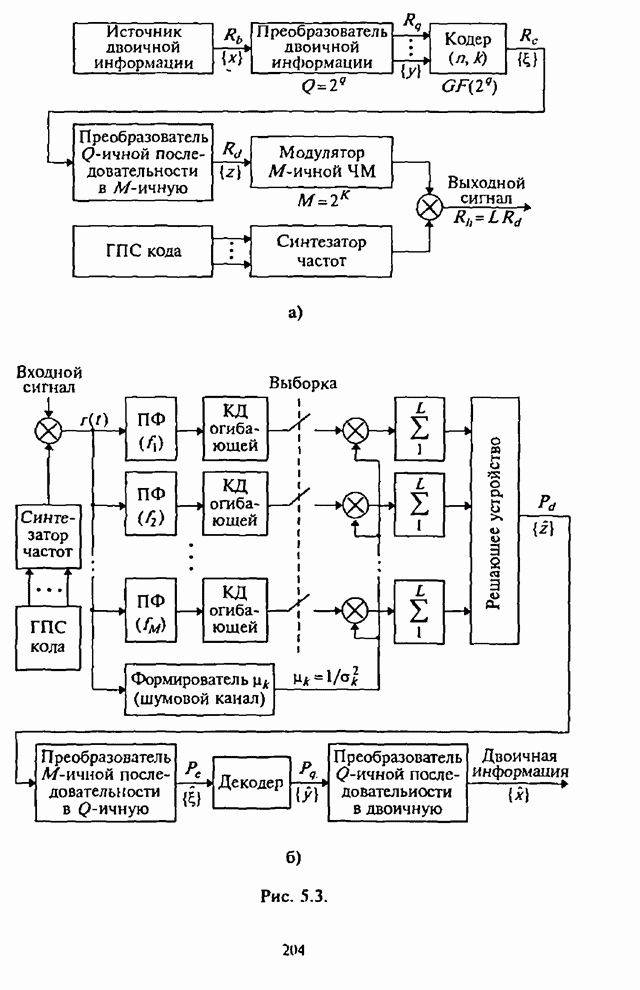
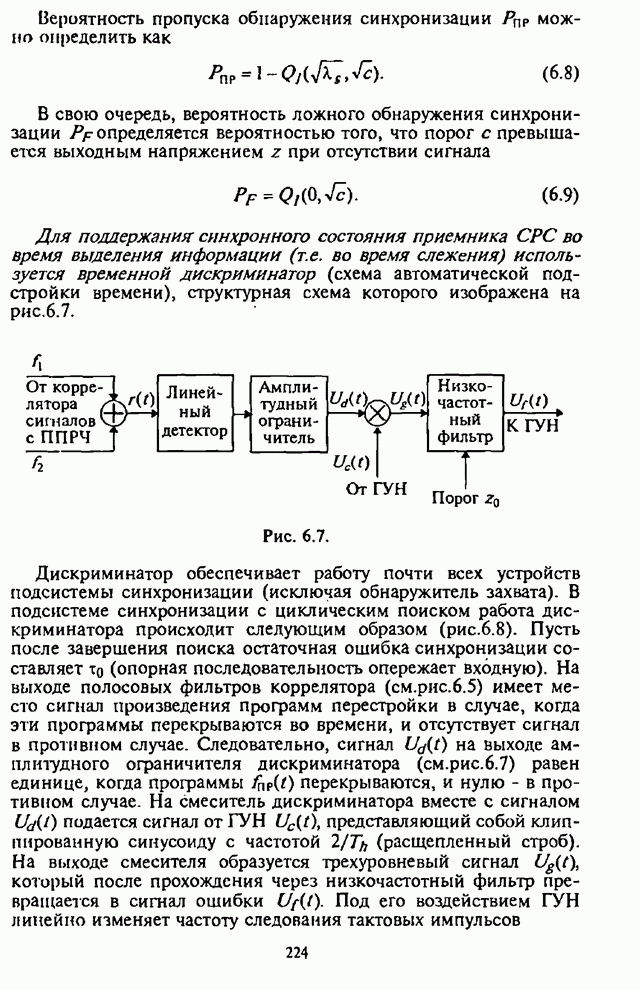
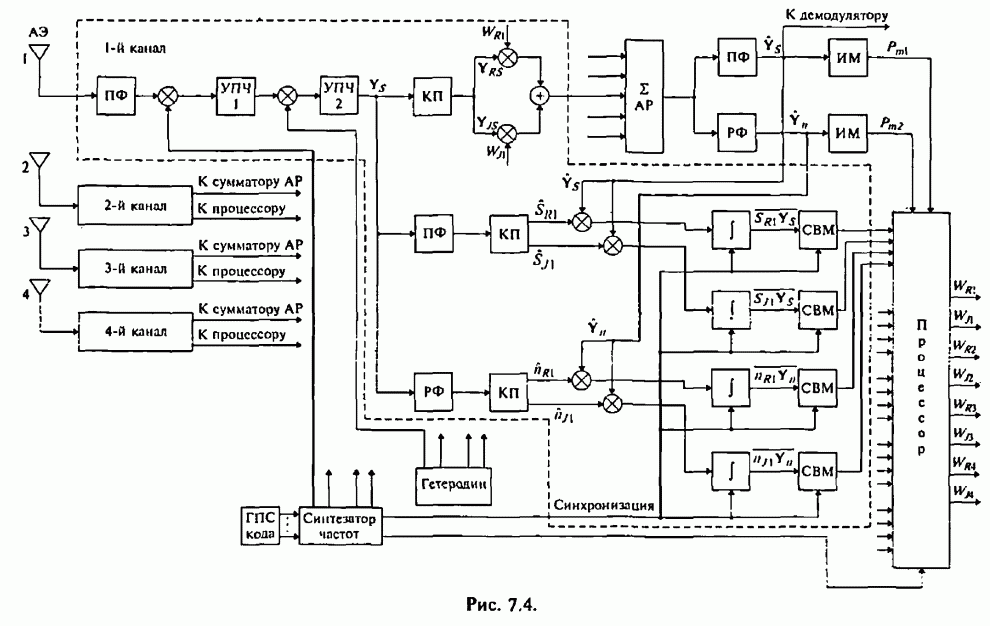
При использовании помехоустойчивого кодирования существенно, чтобы демодулятор СРС был в состоянии обнаруживать сильно зашумленные символы. Поэтому в качестве модели демодулятора ЧМ сигналов рассмотрим, как и ранее, типовой некогерентный (по огибающей) обнаружитель максимального правдоподобия, выход которого соединен со входом соответствующего декодера (рис.2.22, где обозначено: РУ - решающее устройство).

Рис. 2.22.
Положим далее, что информация о состоянии канала при обработке принятых сигналов не используется и на выходе демодулятора выносятся «жесткие» решения [8].
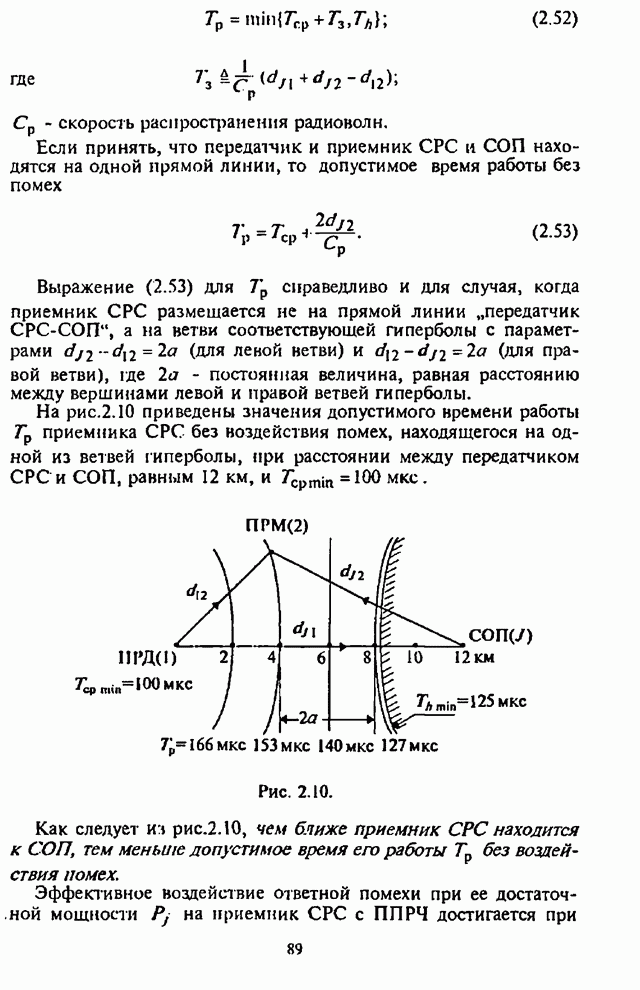
Процесс
помехоустойчивого кодирования заключается в том, что наборы из ![]() информационных
символов отображаются в кодовые последовательности (комбинации, кодовые слова),
состоящие из
информационных
символов отображаются в кодовые последовательности (комбинации, кодовые слова),
состоящие из ![]() символов,
символов,
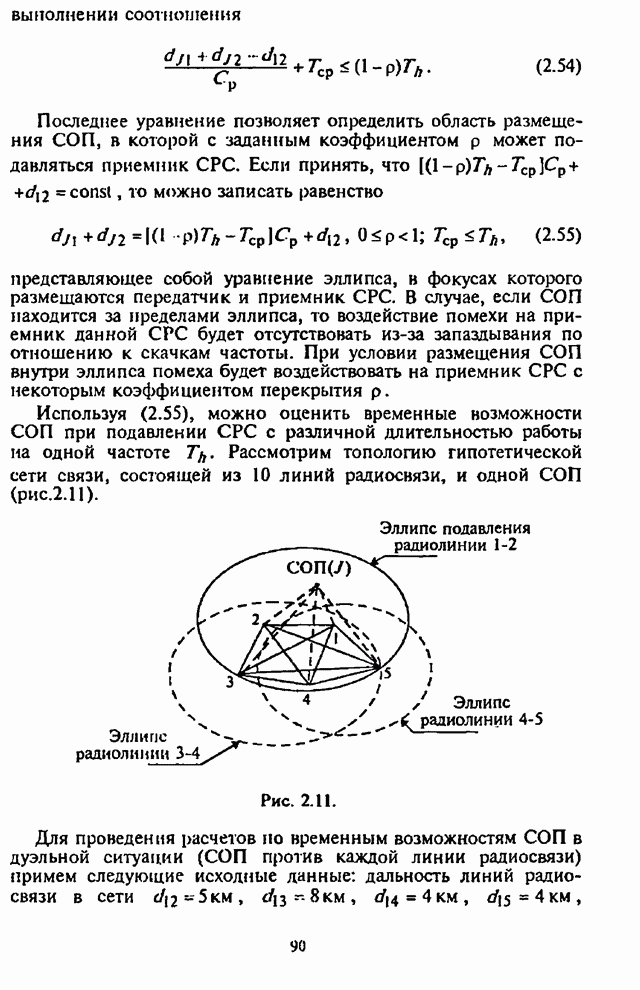
![]() . При этом
. При этом ![]() позиций заполняются
символами 1 и 0 по правилам первичного кодирования элементов (букв) алфавита
источника сообщения. Оставшиеся
позиций заполняются
символами 1 и 0 по правилам первичного кодирования элементов (букв) алфавита
источника сообщения. Оставшиеся ![]() позиций также заполняются
символами 1 и 0, но уже по соответствующим правилам кодирования. Основными параметрами
блоковых кодов являются [20]: число информационных бит
позиций также заполняются
символами 1 и 0, но уже по соответствующим правилам кодирования. Основными параметрами
блоковых кодов являются [20]: число информационных бит ![]() и полное число бит в кодовом
слове (длина кода)
и полное число бит в кодовом
слове (длина кода) ![]() ;
относительная скорость кода
;
относительная скорость кода ![]() ; минимальное кодовое расстояние
; минимальное кодовое расстояние ![]() , равное наименьшему
значению расстояния Хэмминга, представляющему собой число позиций, в которых
кодовые комбинации отличаются друг от друга (например, кодовое расстояние
между комбинациями 11100 и 11011 равно трем); максимальное число исправляемых
ошибок на длине кодового слова
, равное наименьшему
значению расстояния Хэмминга, представляющему собой число позиций, в которых
кодовые комбинации отличаются друг от друга (например, кодовое расстояние
между комбинациями 11100 и 11011 равно трем); максимальное число исправляемых
ошибок на длине кодового слова ![]() , связанное с
, связанное с ![]() зависимостью,
зависимостью,
![]() , где
, где ![]() - целая часть числа;
избыточность кода, под которой понимается параметр
- целая часть числа;
избыточность кода, под которой понимается параметр ![]() определяющий долю избыточно
передаваемых символов.
определяющий долю избыточно
передаваемых символов.
Так как при кодировании для исправления случайных ошибок (или пакетов ошибок) в форму сигнала вводятся соответствующие структуры во временной области, тот это может быть использовано системой РЭП для организации наихудших помех. Поэтому при применении кодов необходимо превращать сигнал во временной области в бесструктурную форму [8,20]. С этой целью, как указывалось ранее, целесообразно использовать псевдослучайное перемежение, при котором за счет случайных перестановок изменяется порядок передачи символов. На приемной стороне СРС после деперемежения символов поступающие в декодер ошибки в канале будут представляться случайными, облегчая тем самым устранение ошибок с помощью декодера.
В качестве примера рассмотрим простейшие двоичные блоковые коды, характеристики которых приведены в табл. 2.2.
Таблица 2.2 . Характеристики двоичных блоковых кодов
|
Вид кода |
Характеристики кода |
||||
|
|
|
|
|
|
|
|
Хэмминга |
(7,4) |
1 |
3 |
1/2 |
50 |
|
Голея |
(23,12) |
3 |
7 |
1/2 |
50 |
|
БЧХ (Боуза- |
(15,5) |
3 |
7 |
1/3 |
70 |
|
Чоудхури- |
(15,7) |
2 |
5 |
1/2 |
50 |
|
Хоквингема) |
(15,11) |
1 |
3 |
3/4 |
25 |
При
применении в СРС с ППРЧ и ЧМ двоичных блоковых кодов и демодулятора с
«жесткими» решениями СВО на бит ![]() (в случае статистической независимости
ошибок в приеме различных символов) может быть представлена выражением [8,40]
(в случае статистической независимости
ошибок в приеме различных символов) может быть представлена выражением [8,40]
![]() , (2.78)
, (2.78)
где
![]() -
вероятность ошибки на бит кодового слова (на канальный символ) на выходе
демодулятора (на входе декодера).
-
вероятность ошибки на бит кодового слова (на канальный символ) на выходе
демодулятора (на входе декодера).
Выражение
для вероятности ошибки ![]() при воздействии
ответных шумовых и гармонических помех на основной канал демодулятора можно
определить из (2.63) и (2.69), если учесть, что энергия канального символа
при воздействии
ответных шумовых и гармонических помех на основной канал демодулятора можно
определить из (2.63) и (2.69), если учесть, что энергия канального символа ![]() , где
, где ![]() -
энергия сигнала на длительности бита информации. В результате получим:
-
энергия сигнала на длительности бита информации. В результате получим:
при воздействии ответной шумовой помехи
 ; (2.79)
; (2.79)
при воздействии ответной гармонической помехи
 . (2.80)
. (2.80)
Как
следует из (2.79) и (2.80), применение кодирования приводит к увеличению
вероятности ошибки на канальный символ по сравнению с отсутствием кодирования,
когда ![]() .
Заметим также, если при применении кодирования длительность кодового слова
(или скорость передачи информации) сохраняется, то длительность передаваемого
канального символа уменьшается. Следовательно, полоса пропускания каждого
канала должна быть увеличена. Это ведет к тому, что при заданном диапазоне перестройки
частот СРС с ППРЧ число каналов
.
Заметим также, если при применении кодирования длительность кодового слова
(или скорость передачи информации) сохраняется, то длительность передаваемого
канального символа уменьшается. Следовательно, полоса пропускания каждого
канала должна быть увеличена. Это ведет к тому, что при заданном диапазоне перестройки
частот СРС с ППРЧ число каналов![]() , которое можно было иметь без
кодирования, сокращается до
, которое можно было иметь без
кодирования, сокращается до
 ,
,
а мощность шумов в каналах приемного устройства СРС увеличивается
![]() ,
,
что приводит к уменьшению помехоустойчивости СРС по отношению к шумам системы.
Эти примеры отражают известное в теории кодирования положение о негативном влиянии на помехоустойчивость СРС увеличения избыточности [8,20]: ...если при цифровой передаче вводятся избыточные символы, а скорость передачи информации и мощность сигнала сохраняются постоянными, то энергия, приходящаяся на один канальный символ, уменьшается и вероятность ошибки увеличивается. Таким образом, применение в СРС кодирования может быть эффективным при условии, если уменьшение вероятности ошибки благодаря кодированию будет достаточным для компенсации потерь, обусловленных введением избыточности.
Рассмотрим
возможности двоичных блоковых кодов (см. табл.2.2) в условиях действия
наихудших помех, при которых СВО на бит имеет максимальное значение.
Максимальная ошибка в приеме бита информации имеет место при вполне определенном
значении отношения сигнал-помеха. Применяя уравнение ![]() к
выражениям (2.79) и (2.80), имеем:
к
выражениям (2.79) и (2.80), имеем:
при воздействии ответной шумовой помехи
 ; (2.81)
; (2.81)
при воздействии ответной гармонической помехи
 (2.82)
(2.82)
Таким
образом, максимальная вероятность ошибки на канальный символ ![]() (2.81) и (2.82) на
входе декодера больше в
(2.81) и (2.82) на
входе декодера больше в ![]() раза при шумовой помехе и – в
раза при шумовой помехе и – в ![]() раза при гармонической
помехе по сравнению со СВО на бит
раза при гармонической
помехе по сравнению со СВО на бит ![]() (2.66а) и (2.72) без кодирования.
(2.66а) и (2.72) без кодирования.
Подставляя
(2.81) и (2.82) в (2.78), получим выражение максимальной СВО на бит ![]() при применении в СРС с
ППРЧ блокового кодирования при действии наихудших ответных шумовых и
гармонических помех.
при применении в СРС с
ППРЧ блокового кодирования при действии наихудших ответных шумовых и
гармонических помех.
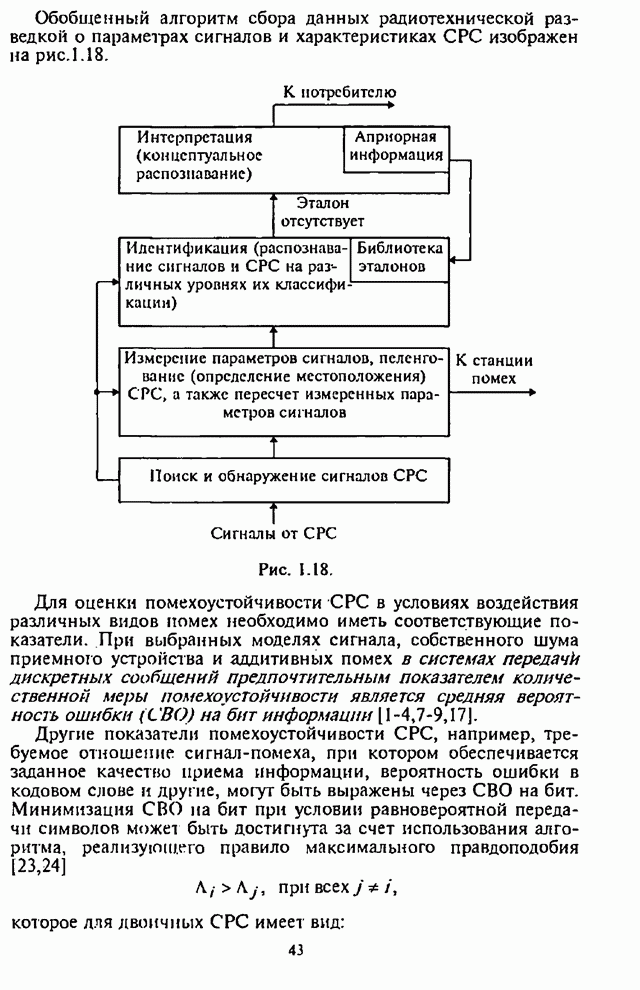
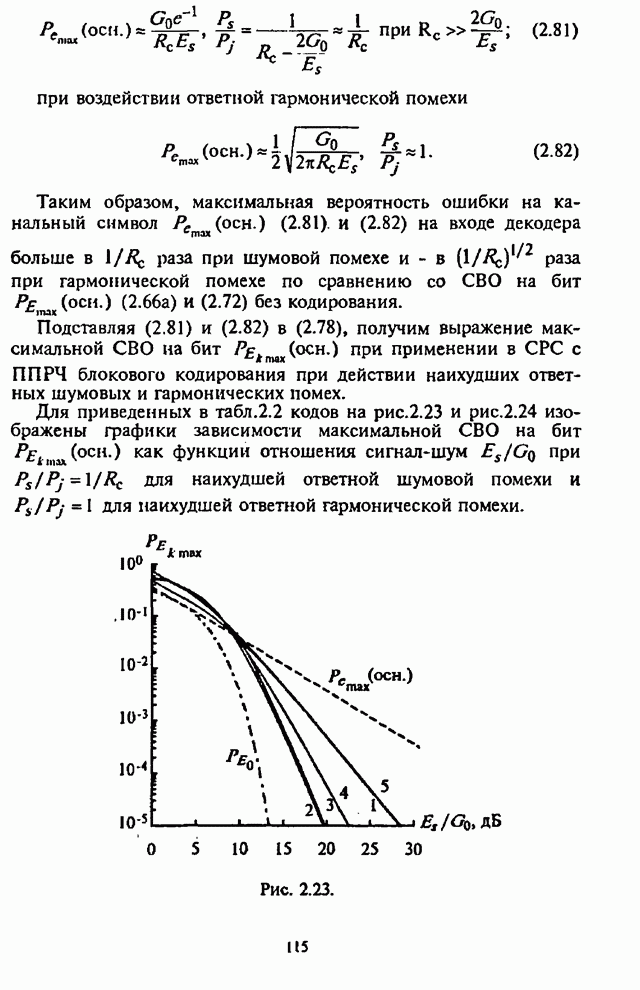
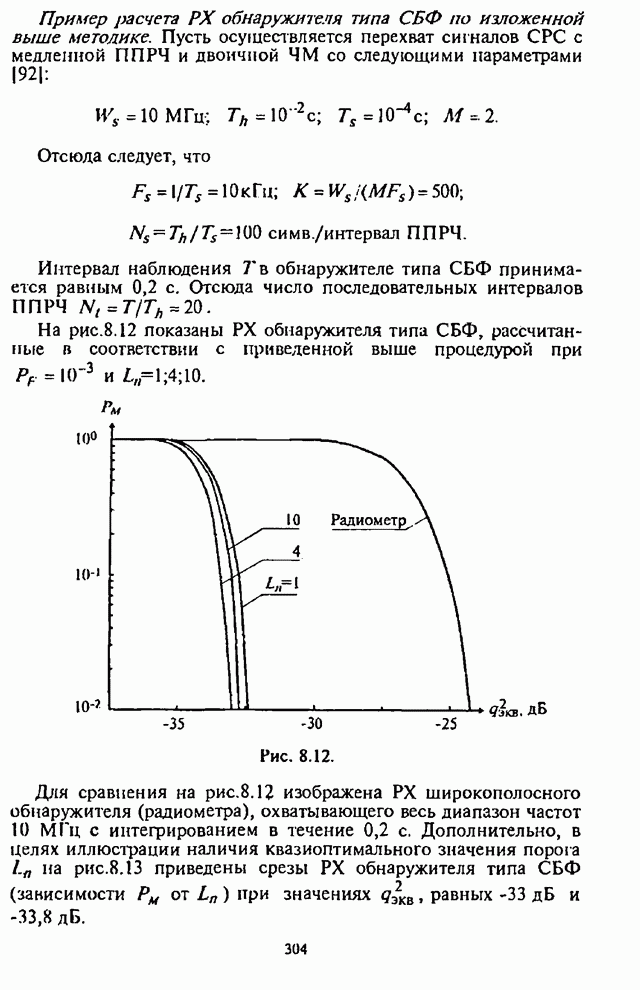
Для
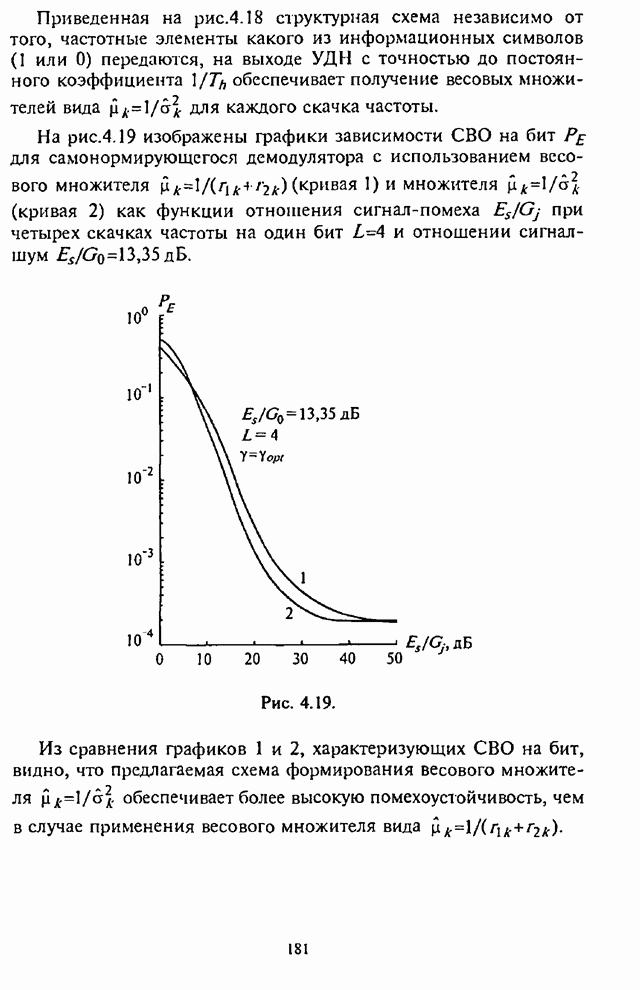
приведенных в табл.2.2 кодов на рис.2.23 и рис.2.24 изображены графики
зависимости максимальной СВО на бит ![]() как функции отношения сигнал-шум
как функции отношения сигнал-шум ![]() при
при ![]() для наихудшей ответной шумовой
помехи и
для наихудшей ответной шумовой
помехи и ![]() для
наихудшей ответной гармонической помехи.
для
наихудшей ответной гармонической помехи.

Рис. 2.23.

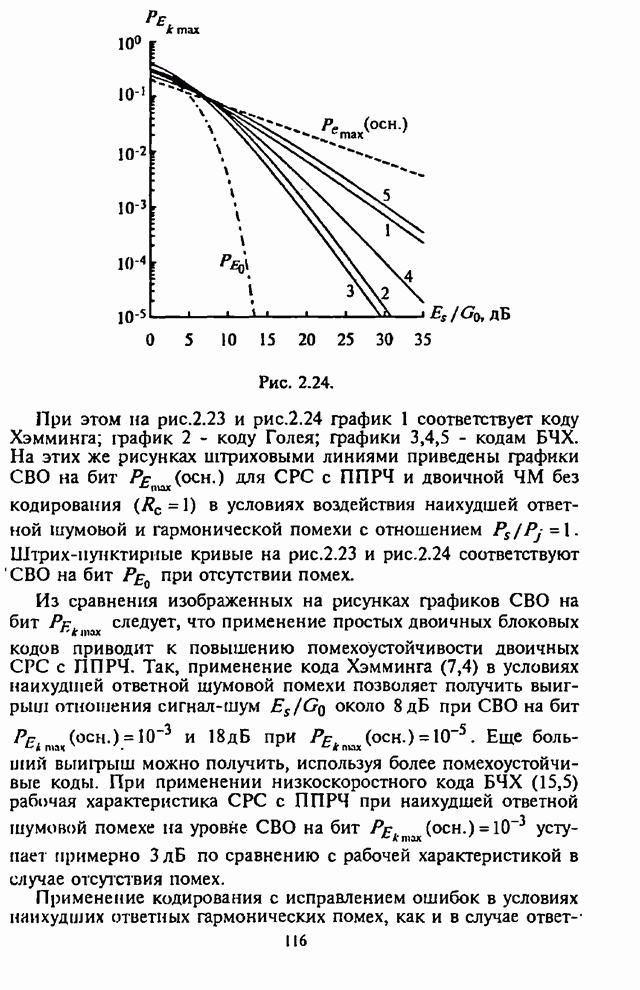
Рис. 2.24.
При
этом на рис.2.23 и рис.2.24 график 1 соответствует коду Хэмминга; график 2 -
коду Голея; графики 3,4,5 - кодам БЧХ. На этих же рисунках штриховыми линиями
приведены графики СВО на бит ![]() для СРС с ППРЧ
и двоичной ЧМ без кодирования
для СРС с ППРЧ
и двоичной ЧМ без кодирования ![]() в условиях воздействия наихудшей ответной
шумовой и гармонической помехи с отношением
в условиях воздействия наихудшей ответной
шумовой и гармонической помехи с отношением![]() . Штрих-пунктирные кривые на рис.2.23 и
рис.2.24 соответствуют СВО на бит
. Штрих-пунктирные кривые на рис.2.23 и
рис.2.24 соответствуют СВО на бит ![]() при отсутствии помех.
при отсутствии помех.
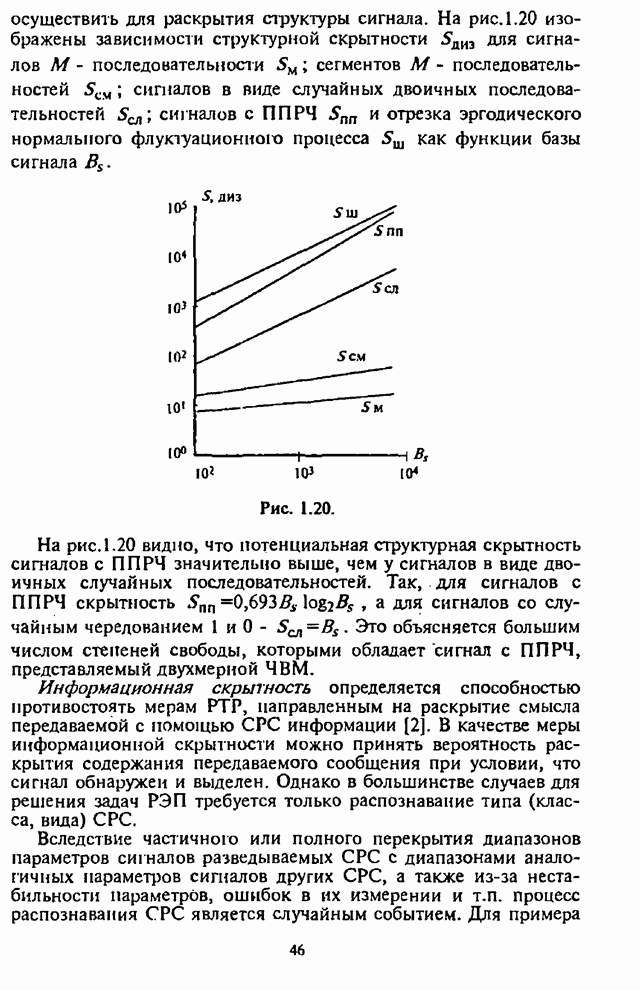
Из
сравнения изображенных на рисунках графиков СВО на бит ![]() следует,
что применение простых двоичных блоковых кодов приводит к повышению
помехоустойчивости двоичных СРС с ППРЧ. Так, применение кода Хэмминга (7,4) в
условиях наихудшей ответной шумовой помехи позволяет получить выигрыш
отношения сигнал-шум
следует,
что применение простых двоичных блоковых кодов приводит к повышению
помехоустойчивости двоичных СРС с ППРЧ. Так, применение кода Хэмминга (7,4) в
условиях наихудшей ответной шумовой помехи позволяет получить выигрыш
отношения сигнал-шум ![]() около
8 дБ при СВО на бит
около
8 дБ при СВО на бит ![]() и
18 дБ при
и
18 дБ при ![]() . Еще больший выигрыш можно
получить, используя более помехоустойчивые коды. При применении
низкоскоростного кода БЧХ (15,5) рабочая характеристика СРС с ППРЧ при
наихудшей ответной шумовой помехе на уровне СВО на бит
. Еще больший выигрыш можно
получить, используя более помехоустойчивые коды. При применении
низкоскоростного кода БЧХ (15,5) рабочая характеристика СРС с ППРЧ при
наихудшей ответной шумовой помехе на уровне СВО на бит ![]() уступает примерно 3 дБ по
сравнению с рабочей характеристикой в случае отсутствия помех.
уступает примерно 3 дБ по
сравнению с рабочей характеристикой в случае отсутствия помех.
Применение
кодирования с исправлением ошибок в условиях наихудших ответных гармонических
помех, как и в случае ответных шумовых помех, значительно улучшает рабочие
характеристики СРС с ППРЧ, повышая помехоустойчивость. Так, применение кода
Голея (23,12) обеспечивает выигрыш отношения сигнал-шум ![]() примерно
на 25 дБ при СВО на бит
примерно
на 25 дБ при СВО на бит ![]() .
.
Заметим, что полученный выигрыш в помехоустойчивости при применении кодов достигается в СРС с ППРЧ и случайной ЧМ, так как для такой СРС ответные помехи могут воздействовать только на основной канал приема.
Аналогичные
результаты приведены в [31], где показано, что использование помехоустойчивого
кодирования в СРС с медленной ППРЧ при действии наихудших ретранслированных
помех позволяет значительно снизить требования к отношению сигнал- шум. Так,
использование длинных блоковых кодов, таких как БЧХ (127,36), (127,64), в
условиях наихудшей ответной шумовой помехи и ответной гармонической помехи дает
выигрыш отношения сигнал-шум примерно на 20 дБ и 30 дБ, соответственно, по
сравнению со случаем отсутствия кодирования при СВО на бит ![]() .
.
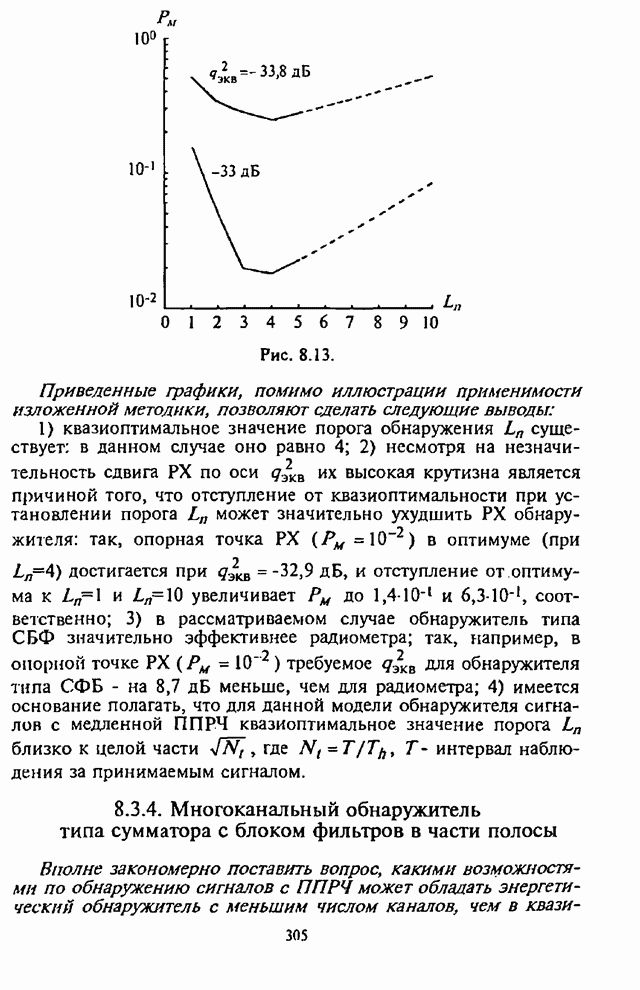
Применение
двоичных блоковых кодов существенным образом может повысить помехоустойчивость
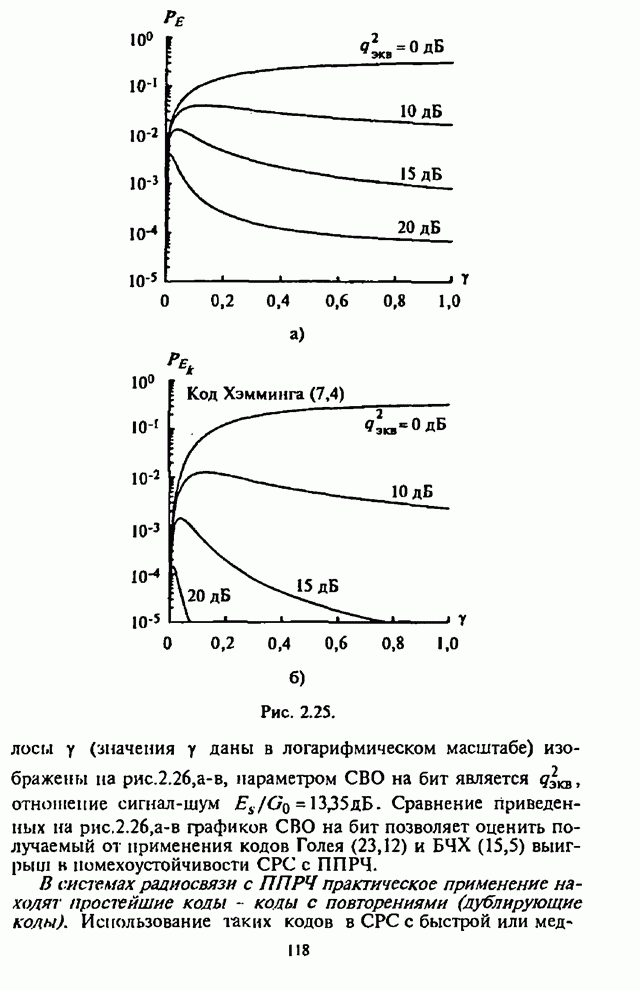
СРС с ППРЧ и при сосредоточенных в части полосы помехах. Для примера на
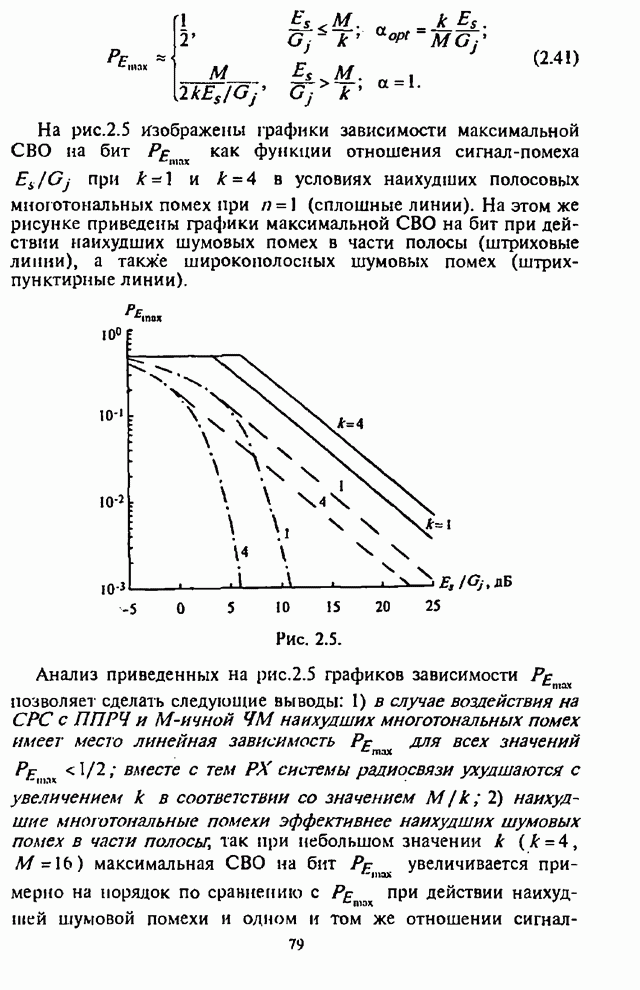
рис.2.25,а,б изображены графики зависимости СВО на бит как функции от части
занимаемой помехой полосы ![]() для некодированной двоичной СРС со
случайной ЧМ (2.44) и для кодированной двоичной СРС со случайной ЧМ и кодом
Хэмминга (7,4) (2.78) при отношении сигнал-шум
для некодированной двоичной СРС со
случайной ЧМ (2.44) и для кодированной двоичной СРС со случайной ЧМ и кодом
Хэмминга (7,4) (2.78) при отношении сигнал-шум
![]() дБ.
дБ.
На
рис.2.25,а видно, что при сравнительно большом эквивалентном отношении
сигнал-помеха ![]() дБ
и
дБ
и ![]() , близкой
к
, близкой
к ![]() ,
СВО на бит имеет значение
,
СВО на бит имеет значение ![]() для СРС без кодирования. С целью
уменьшения СВО на бит такие ошибки можно обрабатывать с использованием
помехоустойчивого кодирования. При данном значении ошибки в приеме бита
информации
для СРС без кодирования. С целью
уменьшения СВО на бит такие ошибки можно обрабатывать с использованием
помехоустойчивого кодирования. При данном значении ошибки в приеме бита
информации ![]() простейший
код Хэмминга (7,4) позволяет обеспечить СВО на бит от
простейший
код Хэмминга (7,4) позволяет обеспечить СВО на бит от ![]() до
до ![]() при
при ![]() (см. рис.2.25,б).
(см. рис.2.25,б).
Для
получения СВО на бит ![]() только
за счет увеличения отношения сигнал-помеха потребовалось бы повысить отношение
сигнал-помеха
только
за счет увеличения отношения сигнал-помеха потребовалось бы повысить отношение
сигнал-помеха ![]() с
10…15 дБ до 35…40 дБ.
с
10…15 дБ до 35…40 дБ.
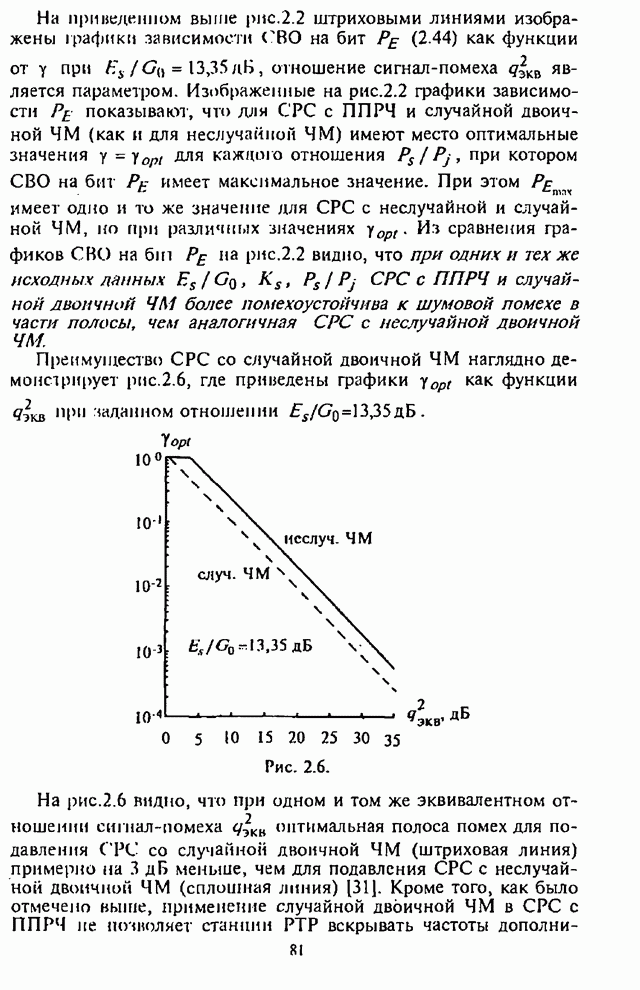
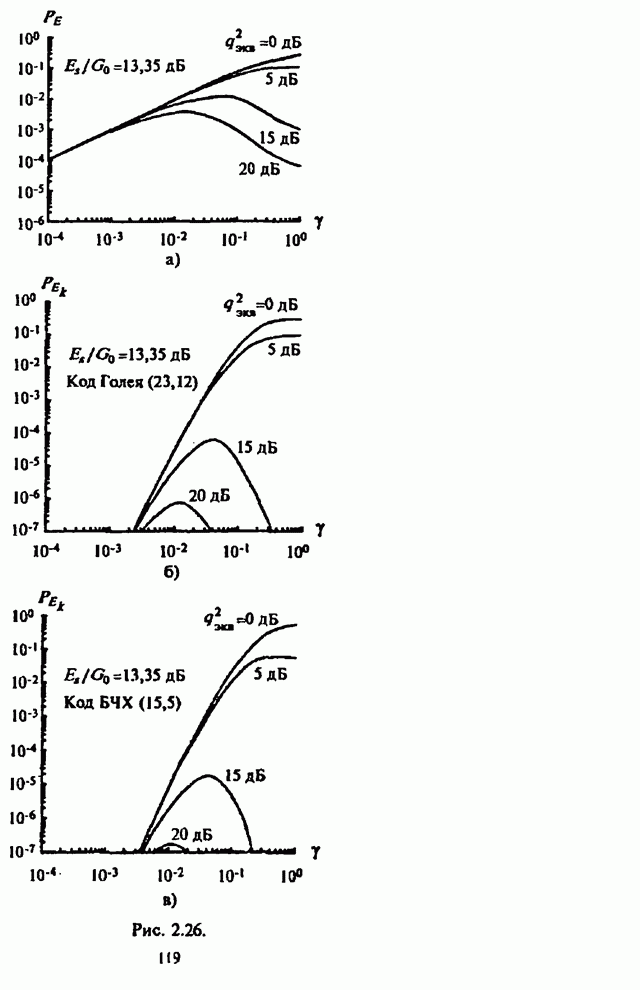
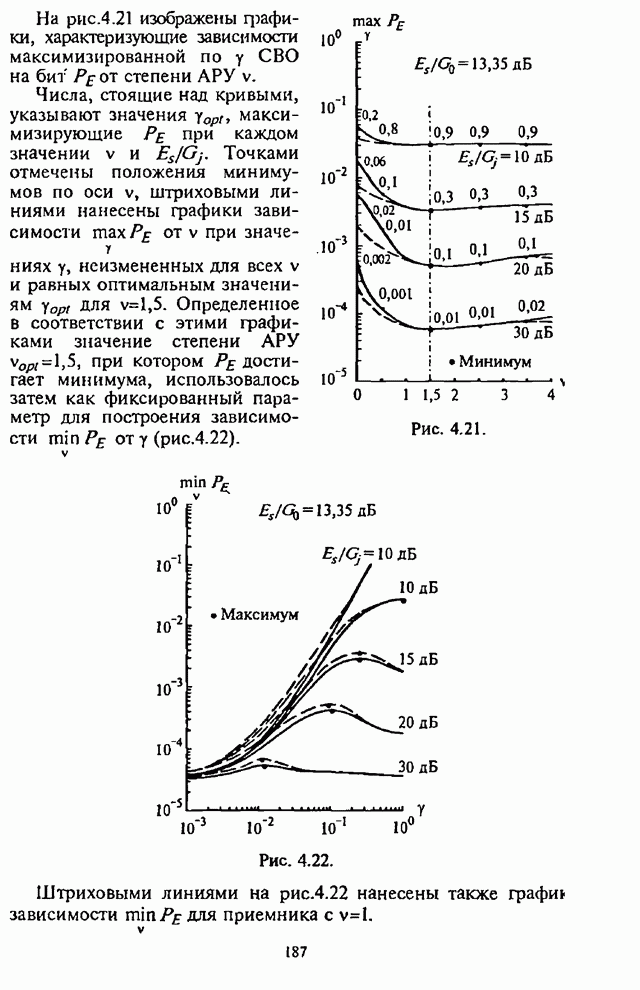
Графики
зависимости СВО на бит ![]() для не кодированной двоичной СРС
со случайной ЧМ (2.44) и двоичной СРС со случайной ЧМ и кодами Голея (23,12) и
БЧХ (15,5), рассчитанные на основе (2.78), как функции от части занимаемой
помехой полосы
для не кодированной двоичной СРС
со случайной ЧМ (2.44) и двоичной СРС со случайной ЧМ и кодами Голея (23,12) и
БЧХ (15,5), рассчитанные на основе (2.78), как функции от части занимаемой
помехой полосы ![]() (значения
(значения
![]() даны в
логарифмическом масштабе) изображены на рис.2.26,а-в, параметром СВО на бит
является отношение сигнал-шум
даны в
логарифмическом масштабе) изображены на рис.2.26,а-в, параметром СВО на бит
является отношение сигнал-шум ![]() дБ. Сравнение
приведенных на рис.2.26,а-в графиков СВО на бит позволяет оценить получаемый
от применения кодов Голея (23,12) и БЧХ (15,5) выигрыш в помехоустойчивости
СРС с ППРЧ.
дБ. Сравнение
приведенных на рис.2.26,а-в графиков СВО на бит позволяет оценить получаемый
от применения кодов Голея (23,12) и БЧХ (15,5) выигрыш в помехоустойчивости
СРС с ППРЧ.

Рис. 2.25.
В системах радиосвязи с ППРЧ практическое применение находят простейшие коды - коды с повторениями (дублирующие коды). Использование таких кодов в СРС с быстрой или медленной перестройкой частоты с перемежением по битам часто является эффективным способом повышения помехоустойчивости в условиях воздействия помех. Кодирование с повторением осуществляется путем передачи одних и тех же символов на различных частотах. На приемной стороне СРС при обработке таких сигналов применяют некогерентное накопление выборок символов, решение о приеме символа (1 или 0) принимается на основе мажоритарной логики по большинству одинаковых результатов.

Рис. 2.26
При применении в СРС с ППРЧ кодов с повторением в условиях
действия шумовой помехи в части полосы ![]() ,
, ![]() , ошибка в приеме произойдет
только в том случае, когда все
, ошибка в приеме произойдет
только в том случае, когда все ![]() символов кода будут подавлены. Вероятность
такого события определяется величиной
символов кода будут подавлены. Вероятность
такого события определяется величиной ![]() и фактически очень мала.
и фактически очень мала.
Выражение для СВО на бит при использовании кодов с повторением
может быть получено из формулы (2.78) путем подстановки в нее ![]() ,
, ![]() . Так как при дублирующих кодах (
. Так как при дублирующих кодах (![]() ,1) число повторений
,1) число повторений ![]() , как правило,
нечетное, то СВО на бит
, как правило,
нечетное, то СВО на бит
 (2.38)
(2.38)
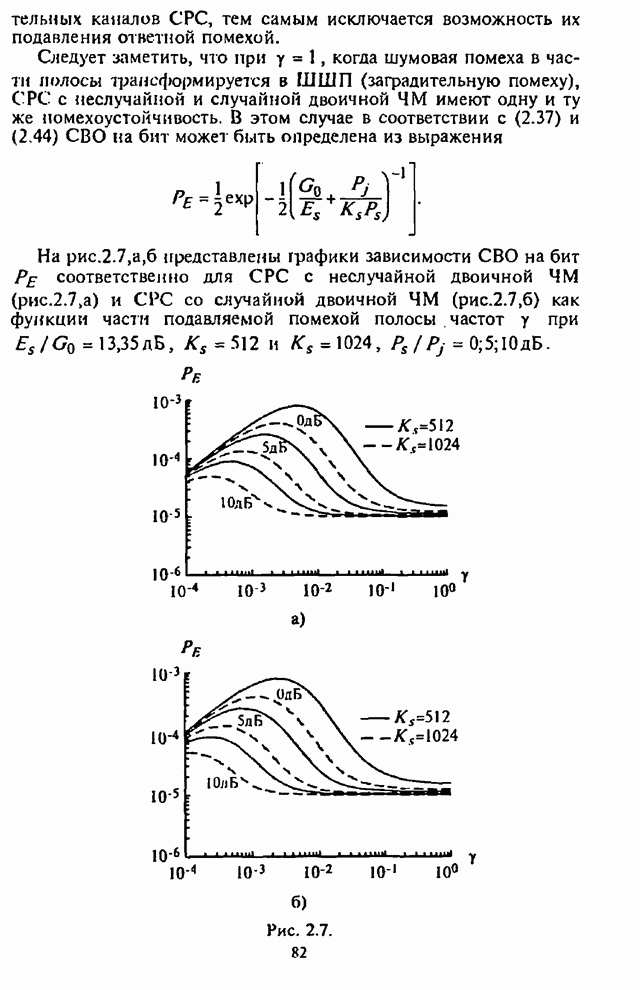
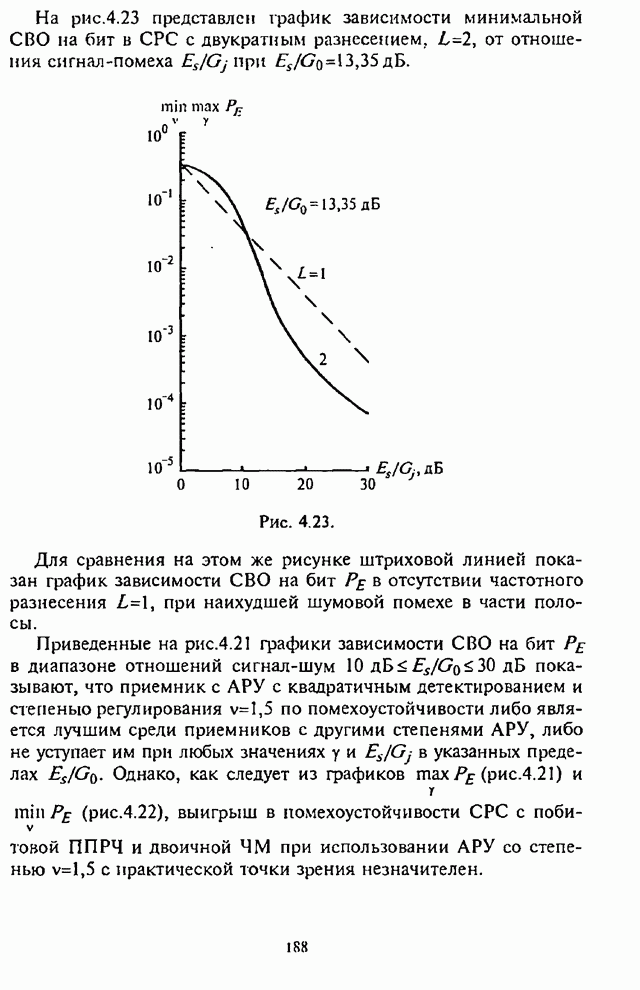
Для оценки эффективности кодов с повторением на
рис.2.27 изображены графики зависимости СВО на бит ![]() (2.83)
(2.83)
Как функции ![]() при
при ![]() для СРС с ППРЧ и неслучайной
двоичной ЧМ при действии наихудшей шумовой помехи в части полосы.
для СРС с ППРЧ и неслучайной
двоичной ЧМ при действии наихудшей шумовой помехи в части полосы.

Рис. 2.27.
Для этого случая максимальная ошибка на бит кодового
слова определяется из выражения ![]() (см. (2.39а)). Из графиков зависимости
(см. (2.39а)). Из графиков зависимости ![]() , представленных на рис.2.27,
видно, что при заданном значении отношения сигнал-помеха
, представленных на рис.2.27,
видно, что при заданном значении отношения сигнал-помеха ![]() увеличение числа повторений
увеличение числа повторений ![]() приводит
к заметному уменьшению СВО на бит. Так, например, увеличение числа повторений
с
приводит
к заметному уменьшению СВО на бит. Так, например, увеличение числа повторений
с ![]() до
до
![]() при
отношении сигнал-помеха
при
отношении сигнал-помеха ![]() приводит к уменьшению
СВО на бит примерно на два порядка (с
приводит к уменьшению
СВО на бит примерно на два порядка (с ![]() до
до ![]() ).
).
Однако повышение помехоустойчивости СРС за счет применения
кодов повторения ведет к снижению скорости передачи информации. Обеспечение
требуемой скорости передачи можно добиться путем уменьшения длительности
частотных элементов сигнала, но при этом увеличивается ширина полосы частотных
каналов и сокращается общее число частотных каналов при заданном диапазоне
частот СРС. Подчеркнем тот факт, что если мощность организованных помех
распределена равномерно по всему частотному диапазону СРС с ППРЧ ![]() , то применение
дублирующих кодов становится нецелесообразным.
, то применение
дублирующих кодов становится нецелесообразным.
При воздействии наихудших шумовых помех в части полосы сравнительно высокую помехоустойчивость СРС с ППРЧ можно обеспечить с помощью недвоичных блоковых кодов Рида-Соломона. Использование таких кодов позволяет получить СВО на бит из [8,40]:
 (2.84)
(2.84)
где ![]() - длина блока,
- длина блока, ![]() ;
; ![]() ;
; ![]() - максимальное расстояние,
- максимальное расстояние, ![]() ;
;![]() ;
;![]() - вероятность ошибки на
канальный символ на выходе
- вероятность ошибки на
канальный символ на выходе ![]() -канального демодулятора (на входе
декодера).
-канального демодулятора (на входе
декодера).
Ошибка на канальный символ ![]() имеет место, если значение
выборки огибающей в одном из каналов, в котором присутствует сигнал, не
превышает значений выборок огибающей в остальных
имеет место, если значение
выборки огибающей в одном из каналов, в котором присутствует сигнал, не
превышает значений выборок огибающей в остальных ![]() каналах, в которых сигнал
отсутствует. Из-за наличия помехи с разным уровнем мощности в каналах
приемника СРС не представляется возможным получить конструктивное выражение для
оценки вероятности ошибки
каналах, в которых сигнал
отсутствует. Из-за наличия помехи с разным уровнем мощности в каналах
приемника СРС не представляется возможным получить конструктивное выражение для
оценки вероятности ошибки ![]() . Для определения
. Для определения ![]() в [8] предлагается
воспользоваться границей объединения. Если принять, что энергия на канальный
символ при
в [8] предлагается
воспользоваться границей объединения. Если принять, что энергия на канальный
символ при ![]() -кратной
ЧМ такая же, как и при двоичной ЧМ, то, используя объединенную границу ошибки,
ограниченную сверху, и учитывая (2.45), получим выражение для
-кратной
ЧМ такая же, как и при двоичной ЧМ, то, используя объединенную границу ошибки,
ограниченную сверху, и учитывая (2.45), получим выражение для ![]()
 (2.85)
(2.85)
Подставляя зависимость ![]() (2.85) в формулу (2.84) и задаваясь
характеристиками кодов и параметрами сигналов СРС и СП, можно оценить
эффективность недвоичных блоковых кодов Рида-Соломона, которая характеризуется
верхней границей СВО на бит
(2.85) в формулу (2.84) и задаваясь
характеристиками кодов и параметрами сигналов СРС и СП, можно оценить
эффективность недвоичных блоковых кодов Рида-Соломона, которая характеризуется
верхней границей СВО на бит ![]()
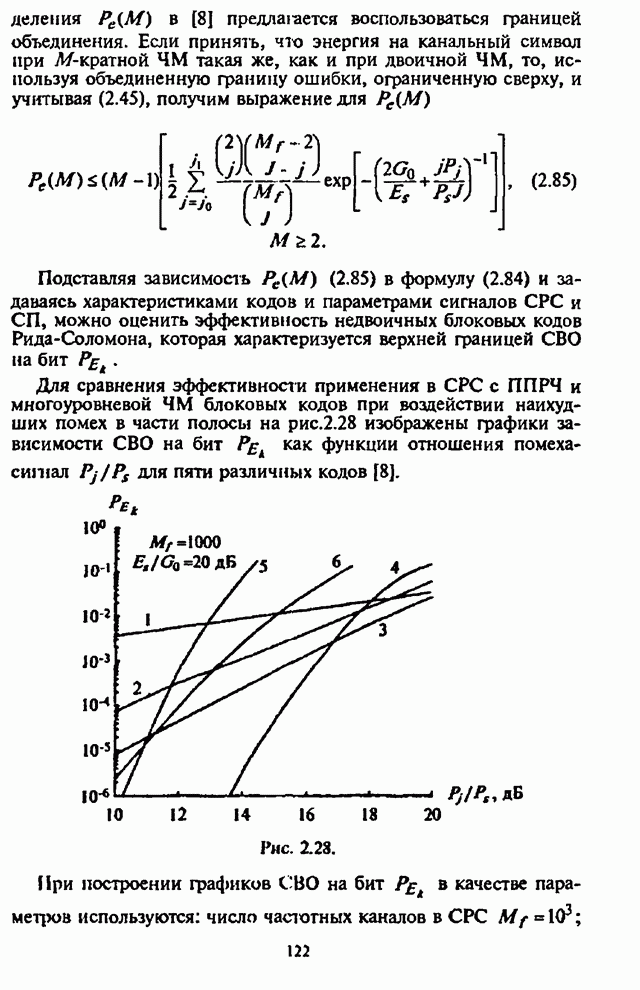
Для сравнения эффективности применения в СРС с ППРЧ и
многоуровневой ЧМ блоковых кодов при воздействии наихудших помех в части
полосы на рис.2.28 изображены графики зависимости СВО на бит ![]() как функции отношения
помеха-сигнал
как функции отношения
помеха-сигнал ![]() для пяти различных кодов [8]
для пяти различных кодов [8]

Рис. 2.28.
При построении графиков СВО на бит ![]() в качестве параметров
используются: число частотных каналов в СРС
в качестве параметров
используются: число частотных каналов в СРС ![]() ; отношение сигнал-шум для некодированной
двоичной ЧМ
; отношение сигнал-шум для некодированной
двоичной ЧМ ![]() .
На рис.2.28 график 1 соответствует зависимости СВО на бит без кодирования;
график 2 - для кода с повторением (5,1); график 3 - для кода Голея (23,12);
график 4 - для кода БЧХ (127,36); графики 5 и 6 - для недвоичных кодов
Рида-Соломона с характеристиками (63,21) и (31,15),соответственно.
.
На рис.2.28 график 1 соответствует зависимости СВО на бит без кодирования;
график 2 - для кода с повторением (5,1); график 3 - для кода Голея (23,12);
график 4 - для кода БЧХ (127,36); графики 5 и 6 - для недвоичных кодов
Рида-Соломона с характеристиками (63,21) и (31,15),соответственно.
Из сравнения графиков зависимости СВО на бит, приведенных
на рис.2.28, видно: 1) недвоичные коды Рида-Соломона наиболее предпочтительны
при относительной скорости кода ![]() и
и ![]() и небольших отношениях
помеха-сигнал
и небольших отношениях
помеха-сигнал ![]() ; ростом отношения
; ростом отношения ![]() эффективность недвоичных кодов
Рида-Соломона уменьшается, соответственно СВО на бит
эффективность недвоичных кодов
Рида-Соломона уменьшается, соответственно СВО на бит ![]() увеличивается и преимущество недвоичных кодов по сравнению с двоичными
кодами утрачивается; 2) наименее эффективными в широком диапазоне отношений
помеха-сигнал
увеличивается и преимущество недвоичных кодов по сравнению с двоичными
кодами утрачивается; 2) наименее эффективными в широком диапазоне отношений
помеха-сигнал ![]()
являются коды с повторением; 3) эффективное кодирование в СРС с ППРЧ позволяет свести до минимума преимущества наихудших помех и восстановить экспоненциальную зависимость СВО на бит.
При построении графиков зависимости СВО на бит в качестве
аргумента использовалось отношение помеха-сигнал ![]() (либо
(либо ![]() ). Этот аргумент может быть выражен через
отношение энергии сигнала на бит
). Этот аргумент может быть выражен через
отношение энергии сигнала на бит ![]() к спектральной плотности мощности
помехи
к спектральной плотности мощности
помехи ![]() и параметры СРС, в частности
через число каналов
и параметры СРС, в частности
через число каналов ![]() и произведение полосы
пропускания частотного канала
и произведение полосы
пропускания частотного канала ![]() при двоичной ЧМ без
кодирования на длительность информационного бита
при двоичной ЧМ без
кодирования на длительность информационного бита ![]() .
.
Действительно,
 (2.86)
(2.86)
или в децибелах
![]() (2.87)
(2.87)
Приведенные выше примеры показывают принципиальную возможность повышения эффективности СРС с ППРЧ в условиях РЭП за счет применения простейших блоковых кодов. С целью более значительного повышения помехоустойчивости СРС с ППРЧ в условиях воздействия различного вида наихудших помех требуются более мощные коды с высокой корректирующей способностью [20,41].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
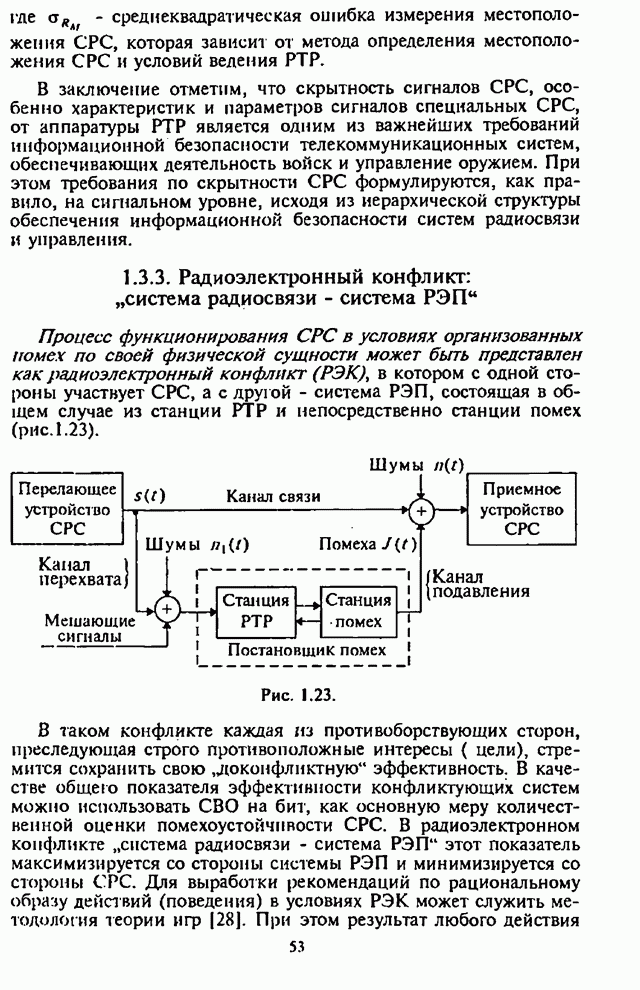
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
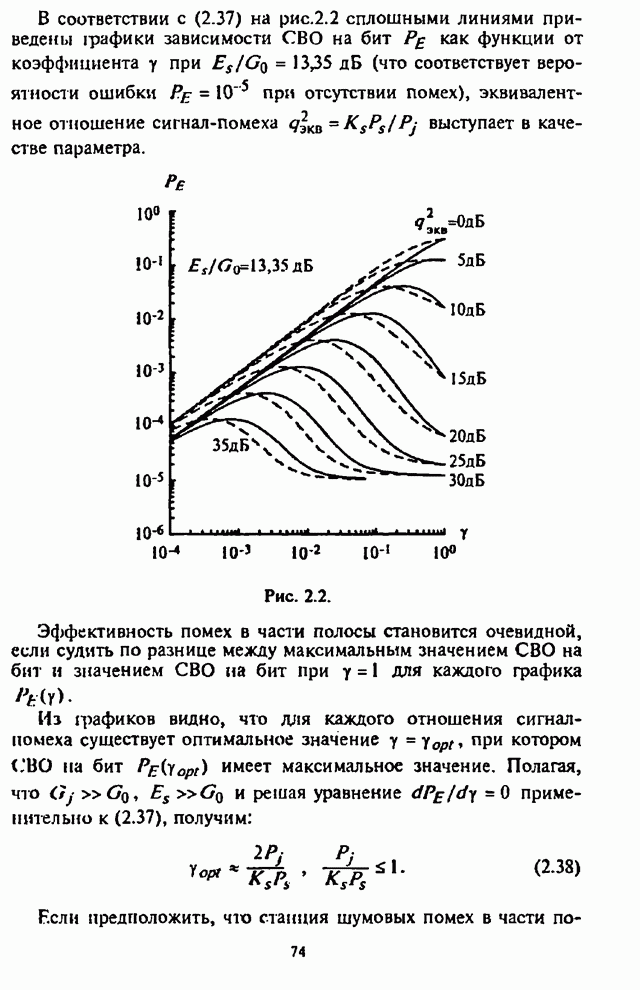
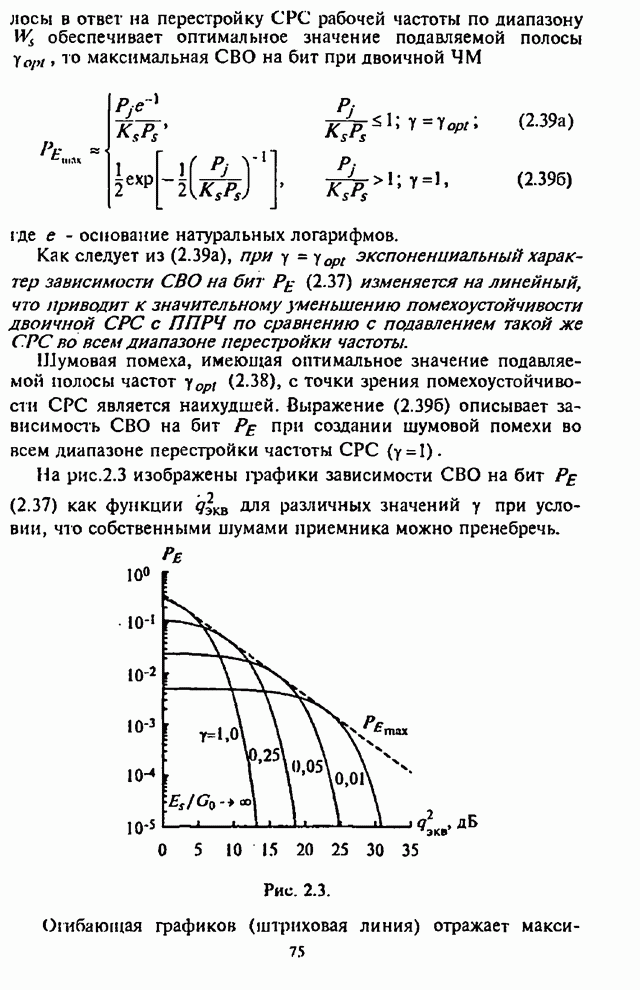
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
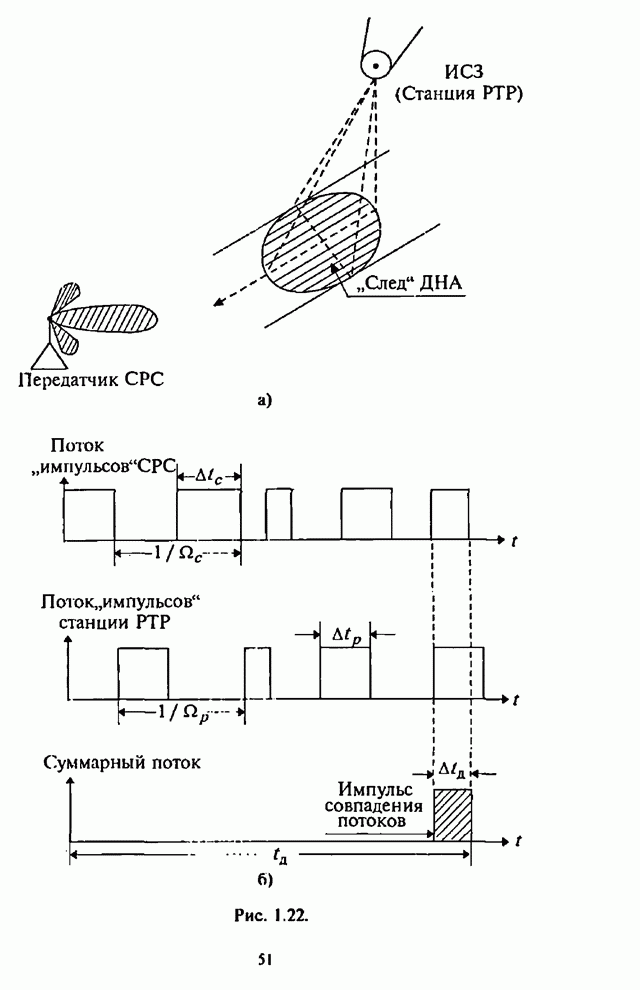
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
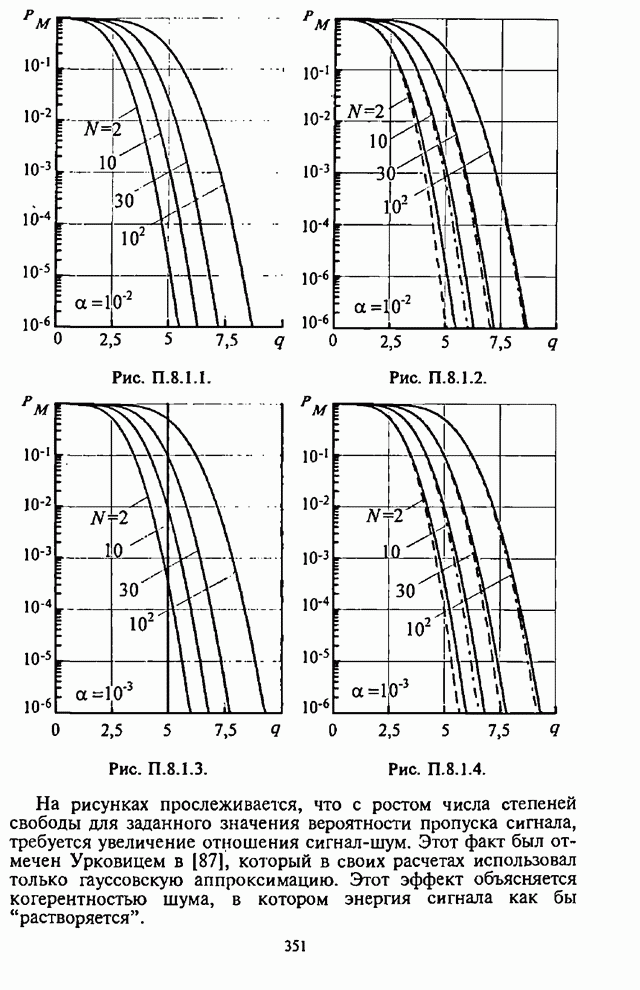
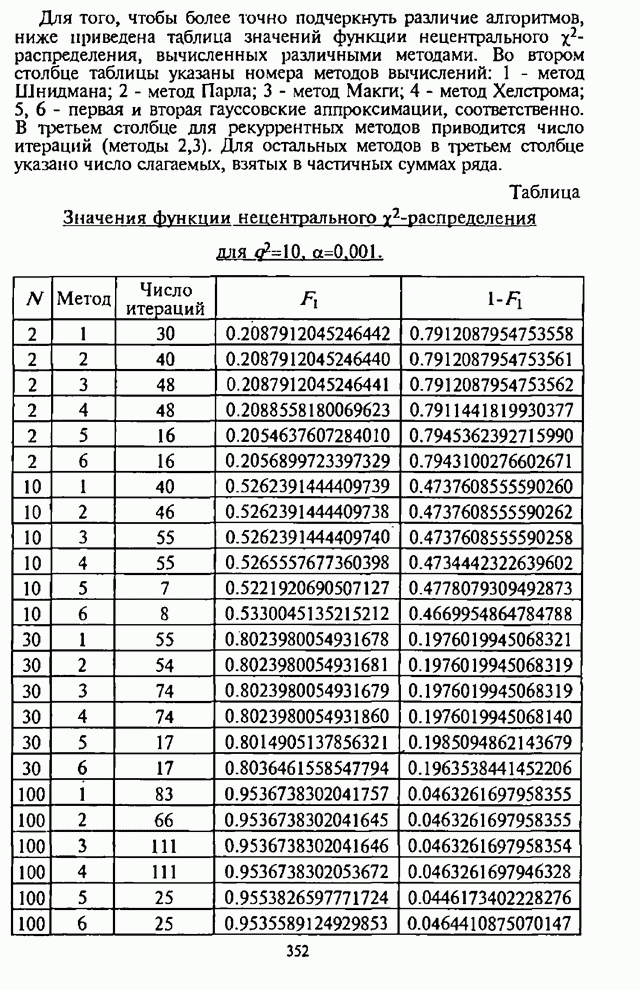
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
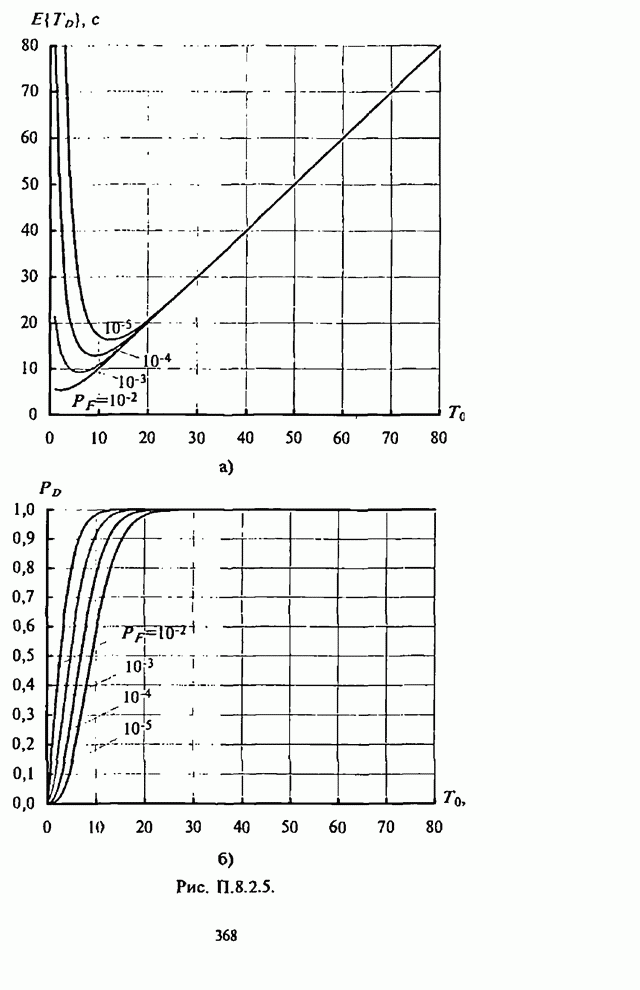
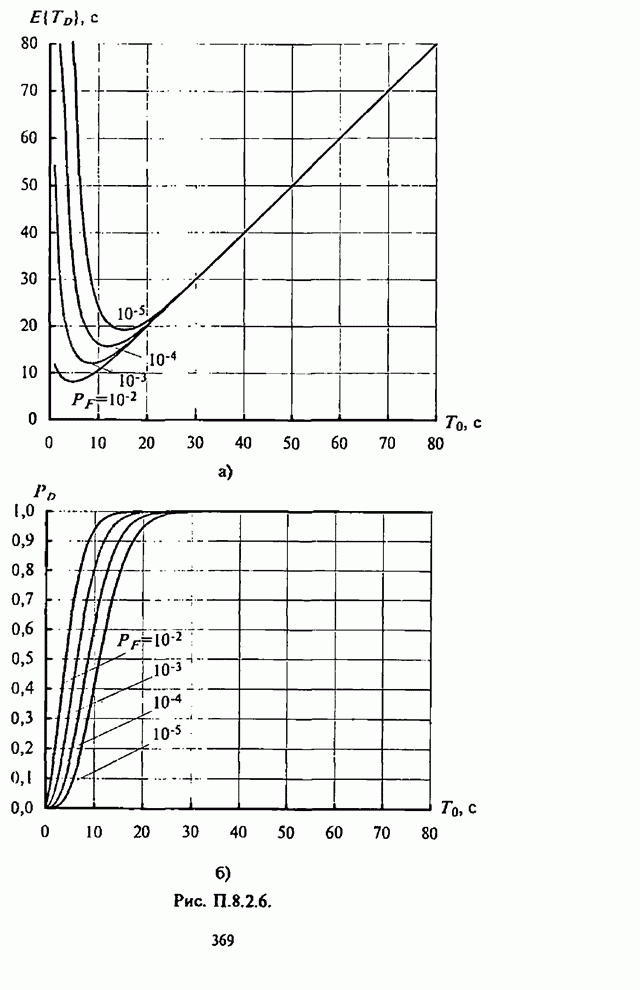
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ