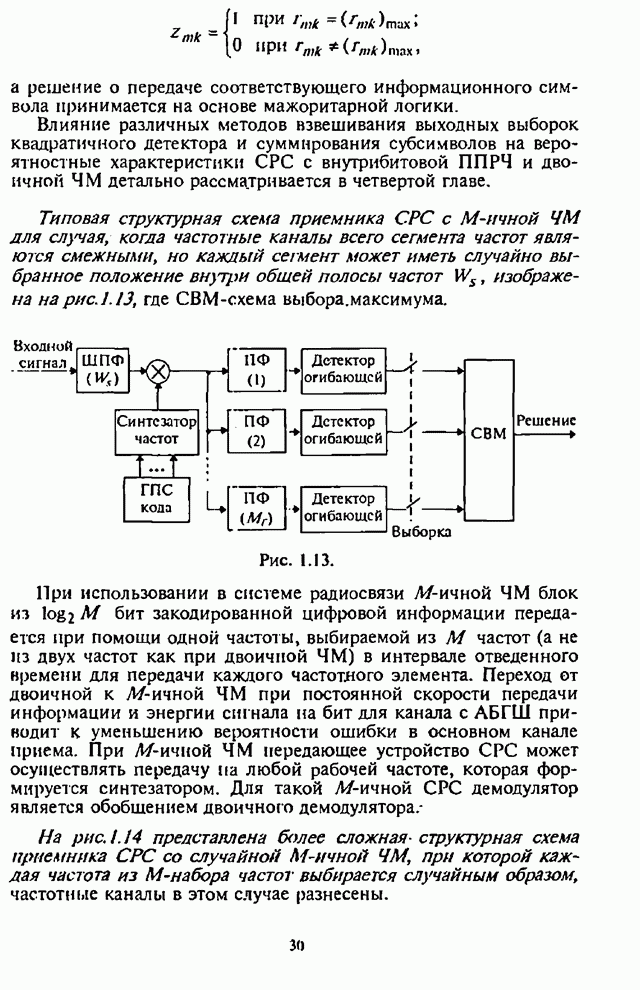
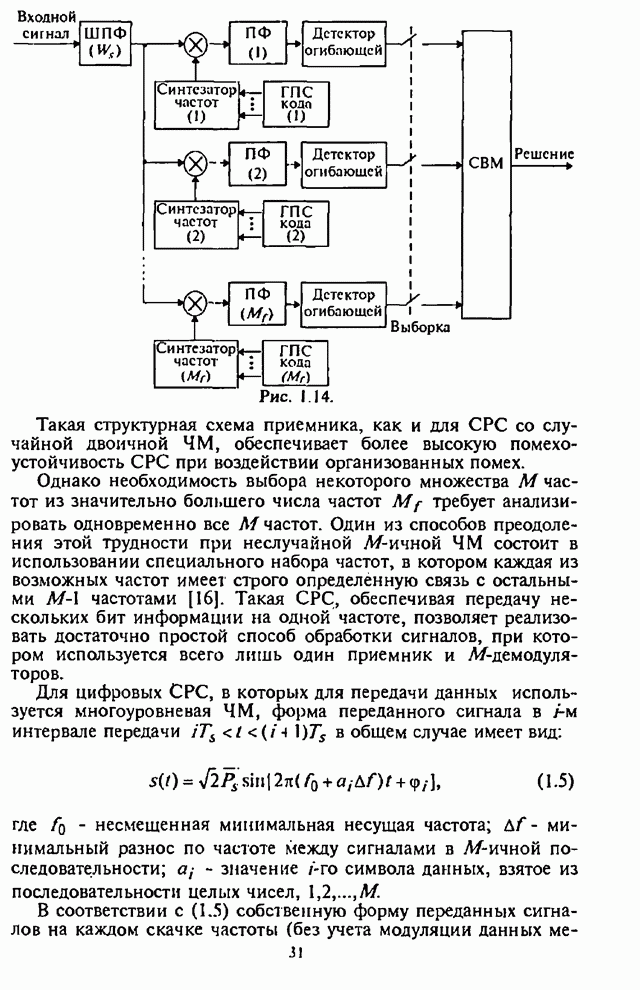
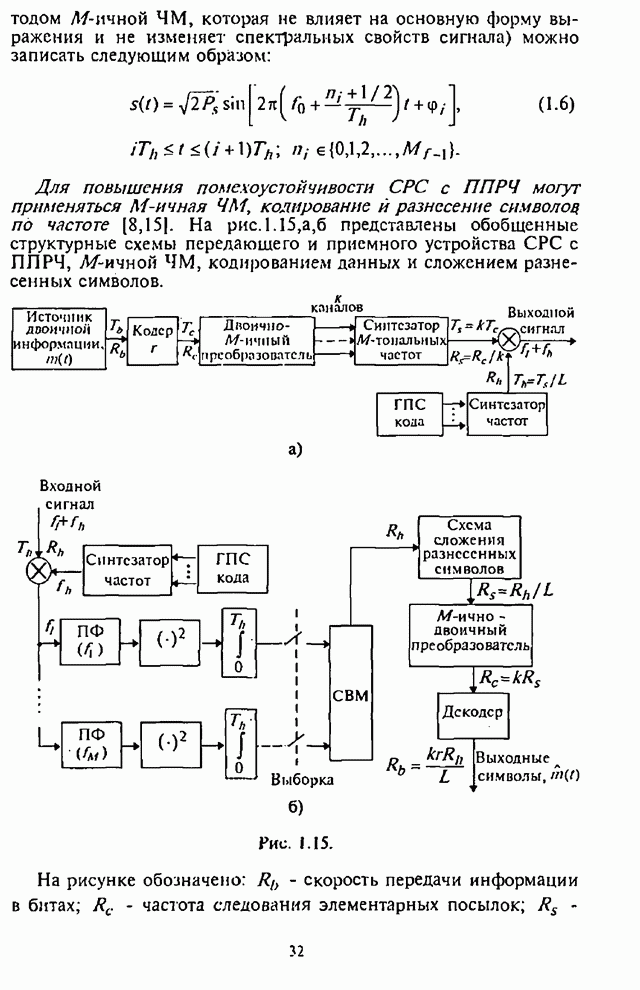
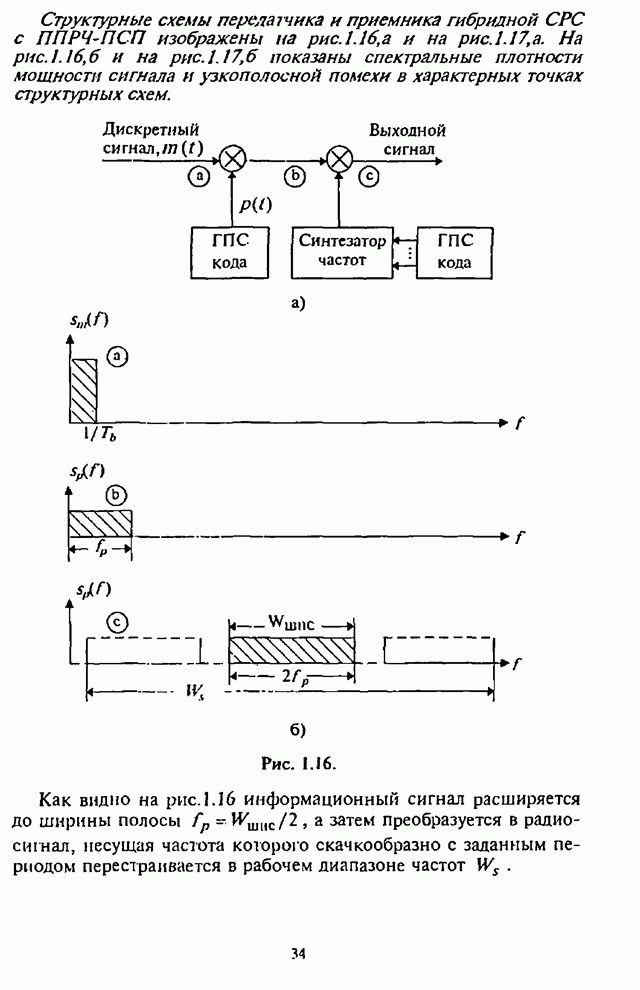
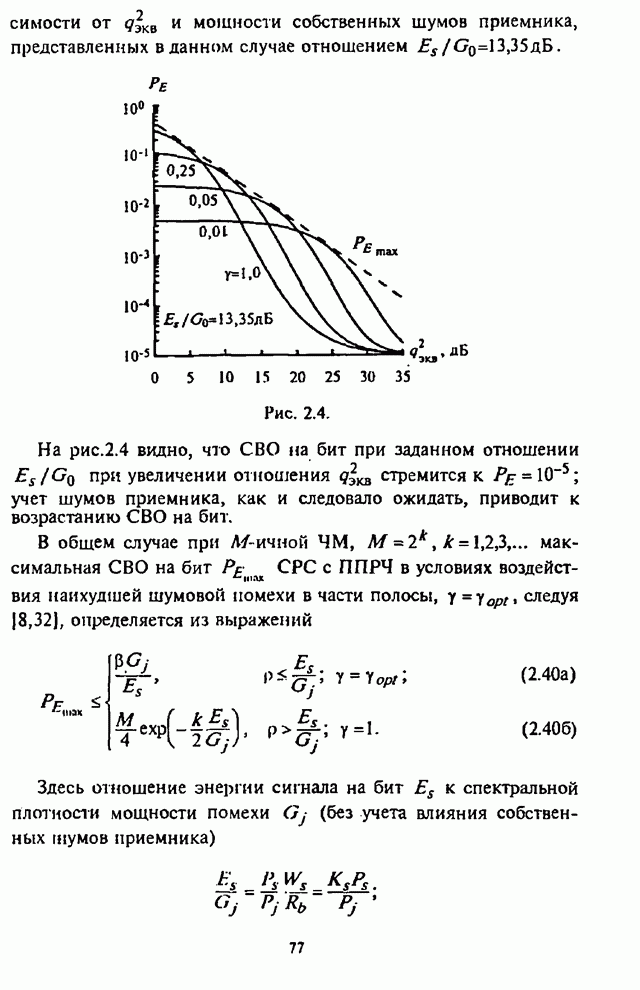
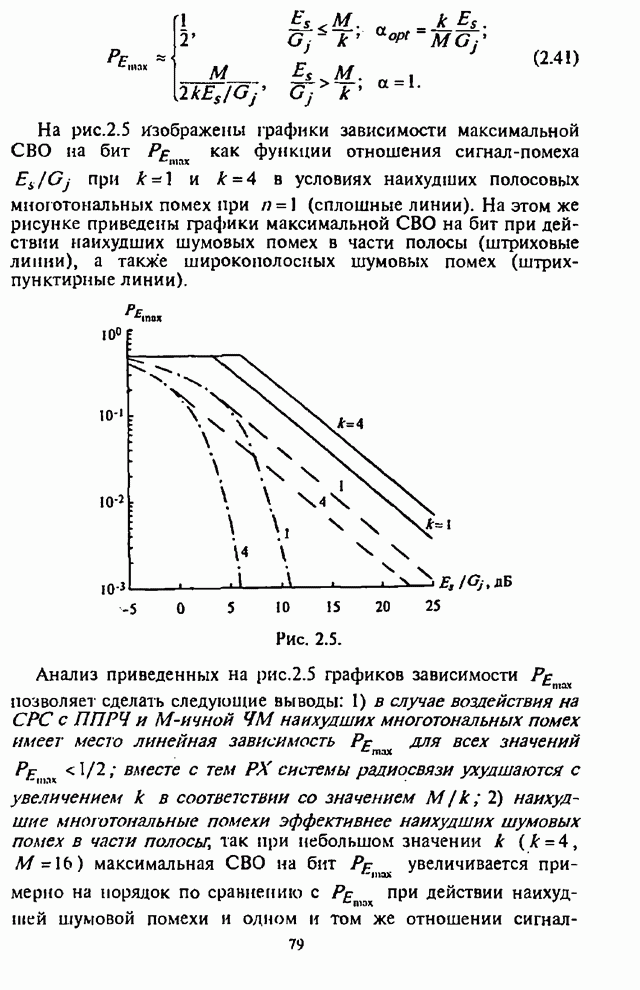
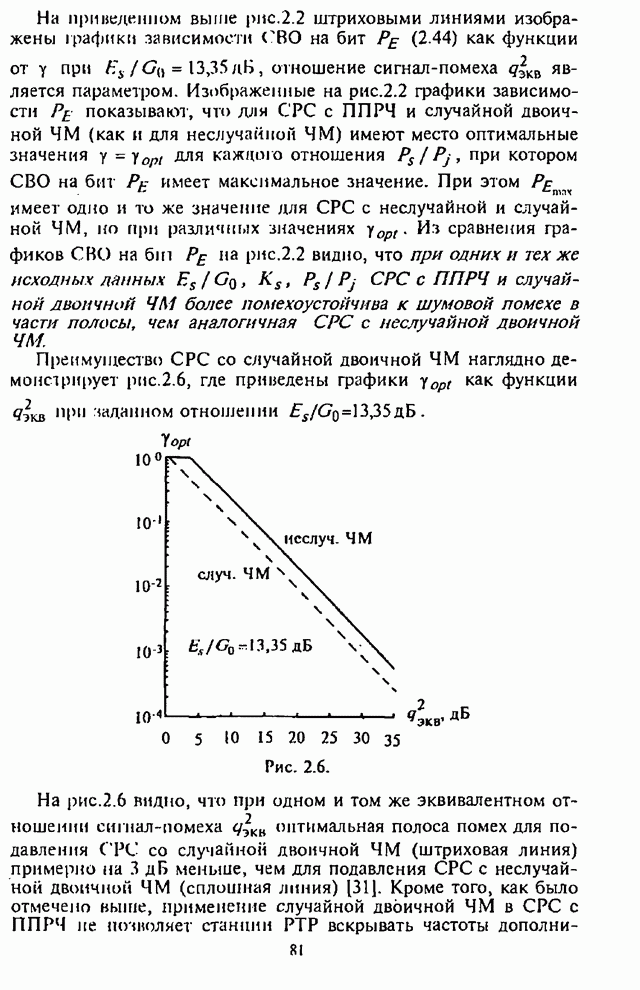
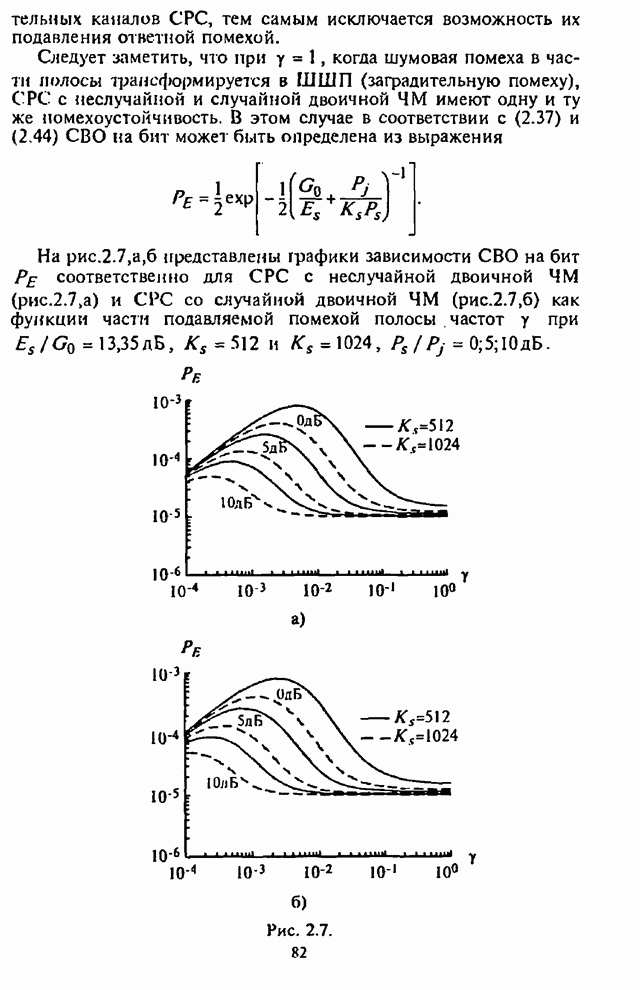
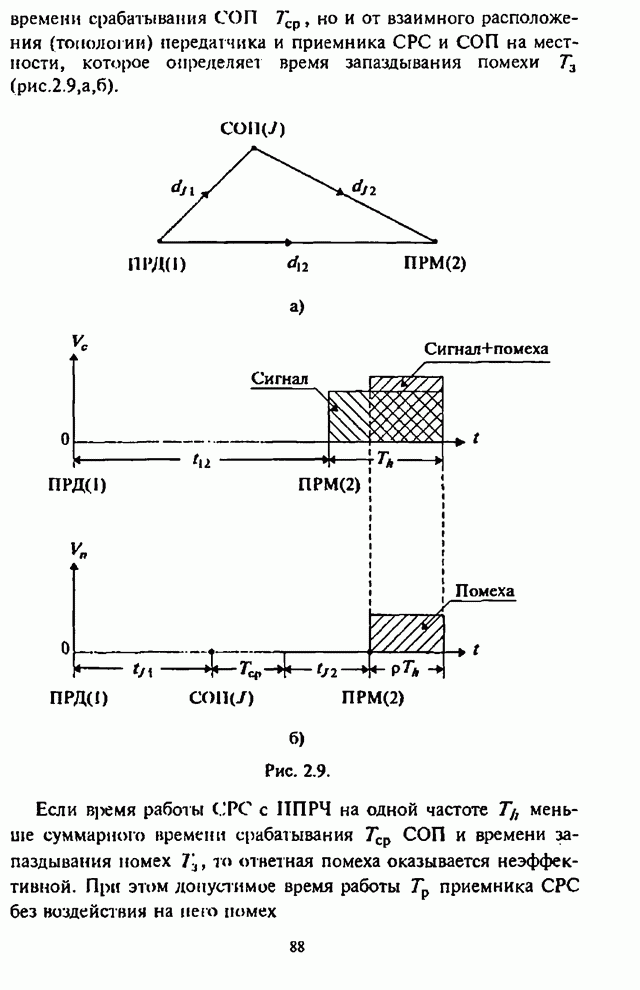
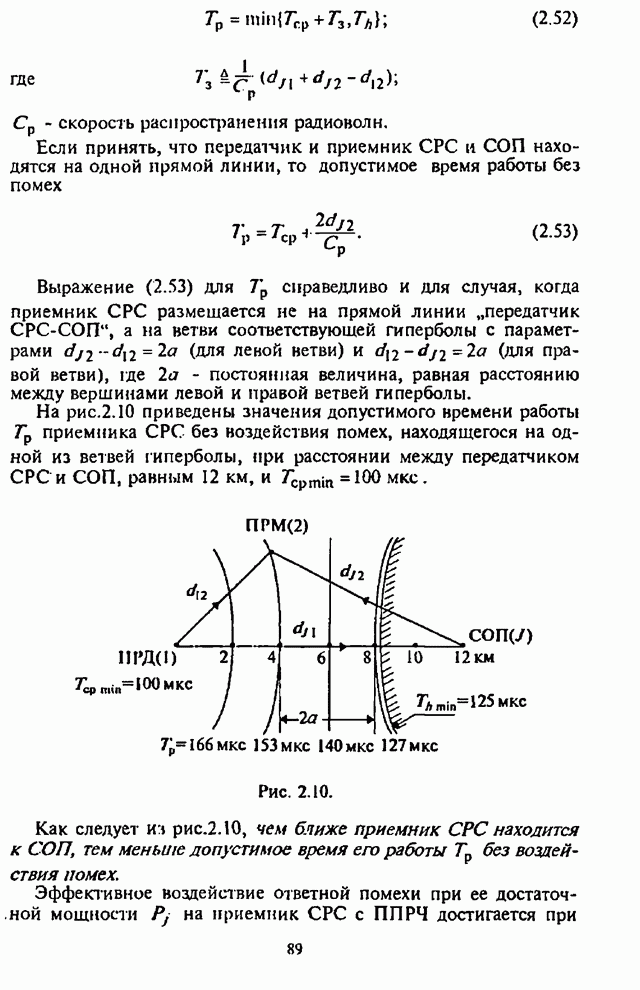
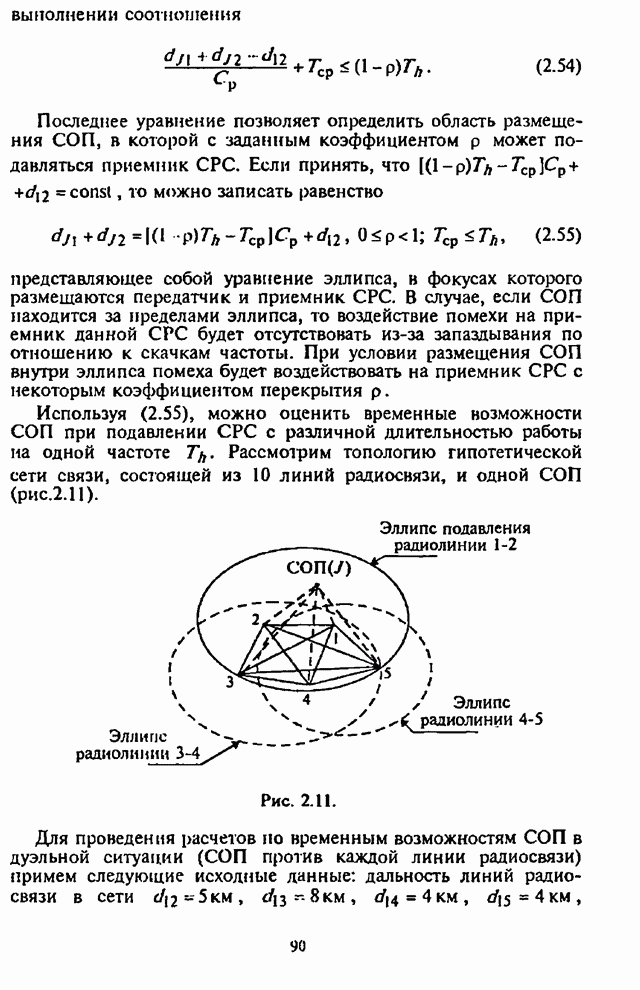
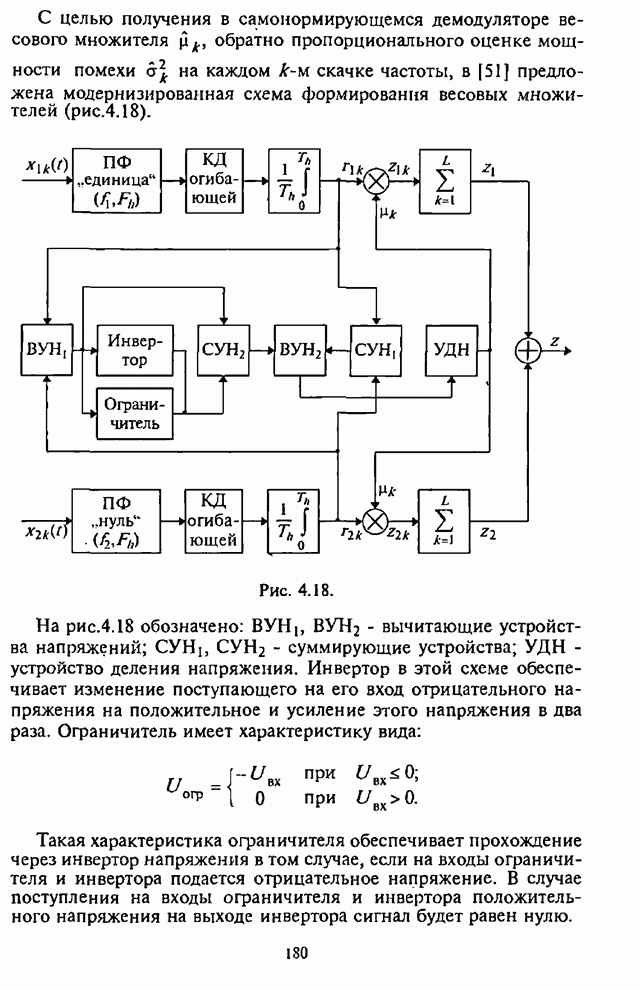
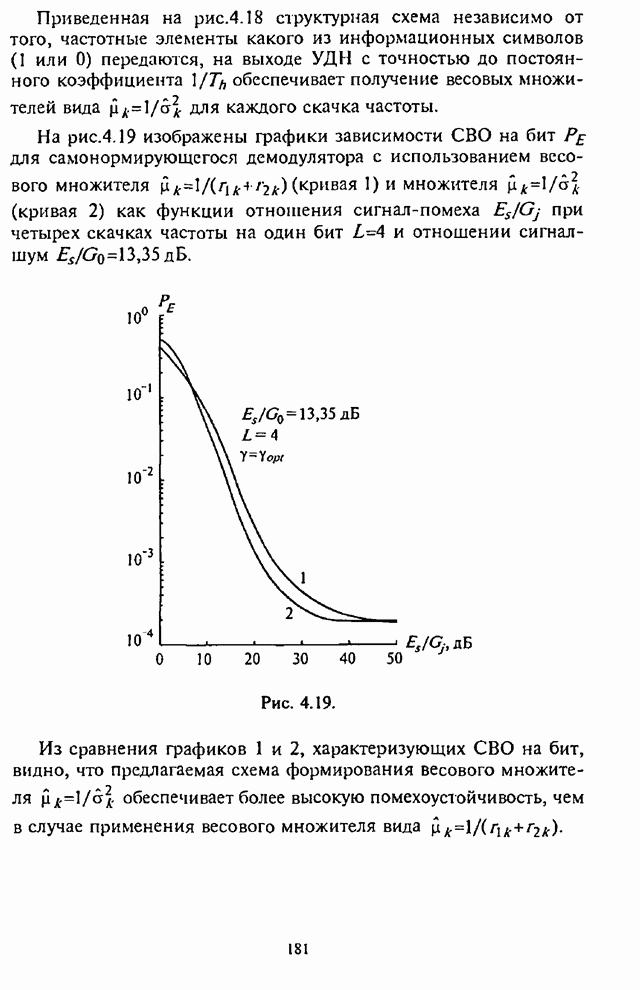
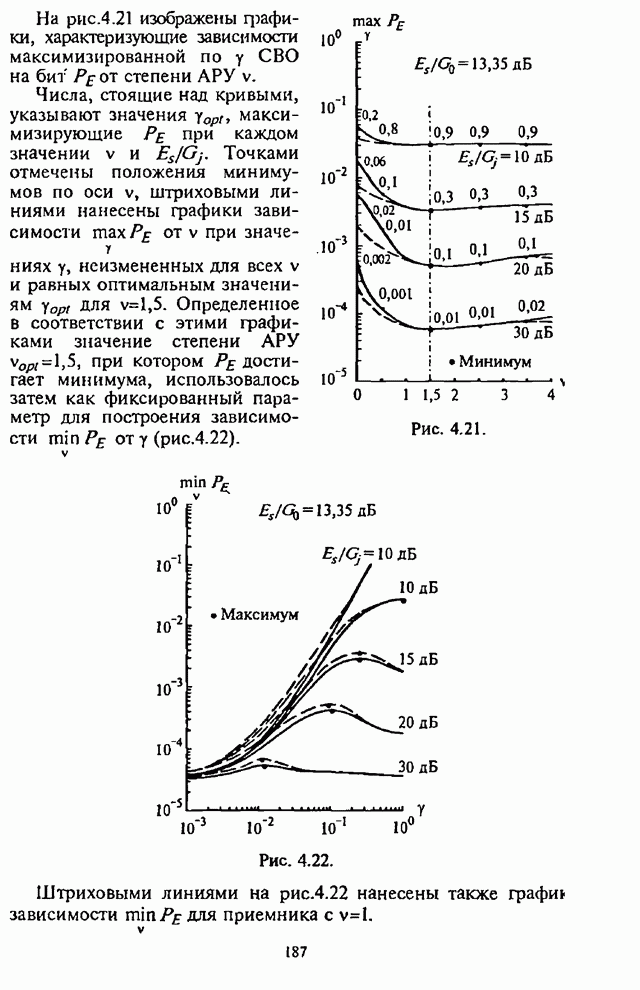
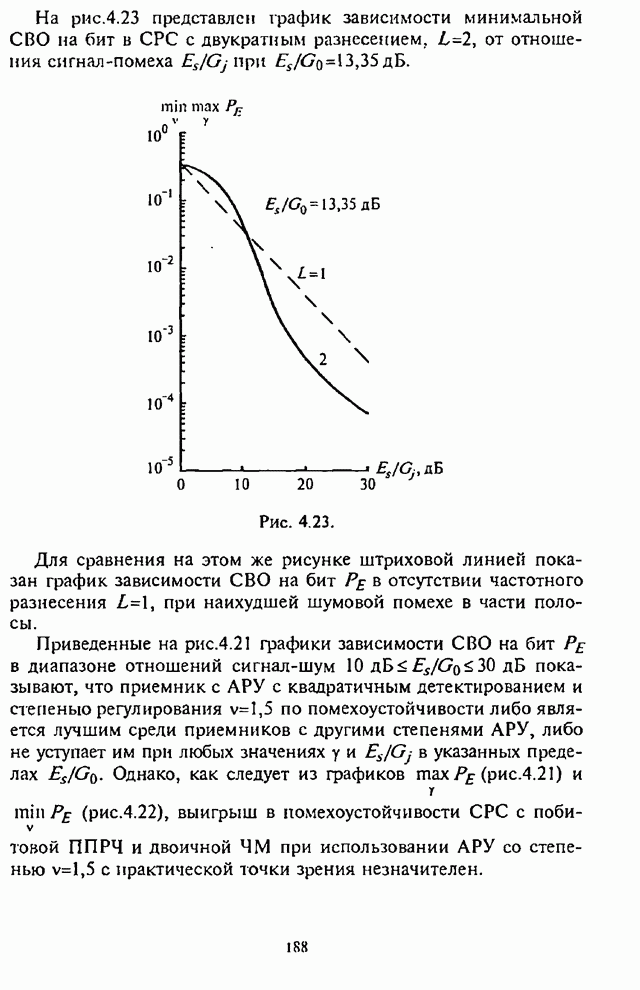
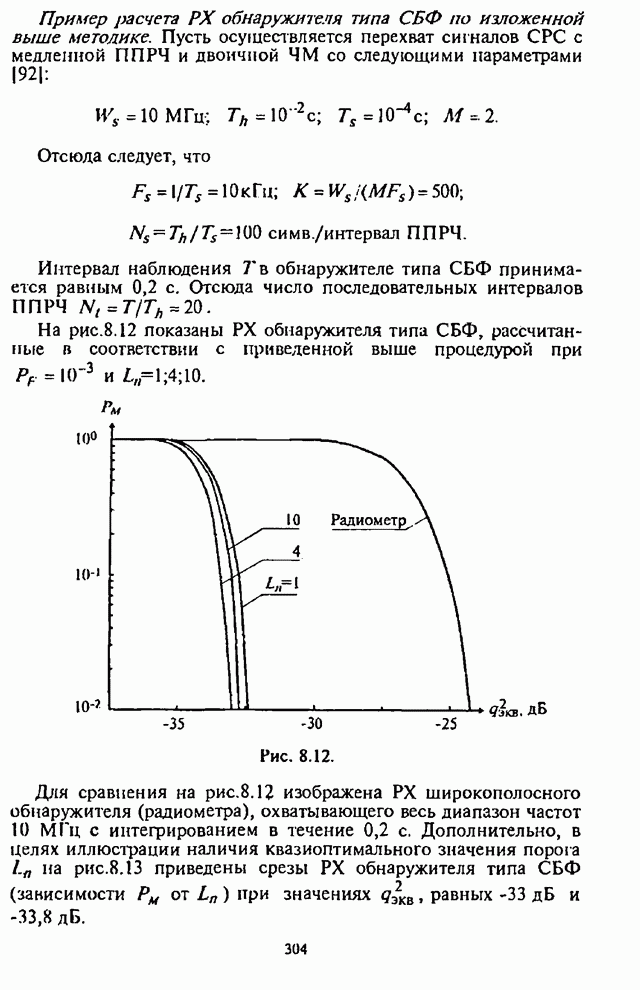
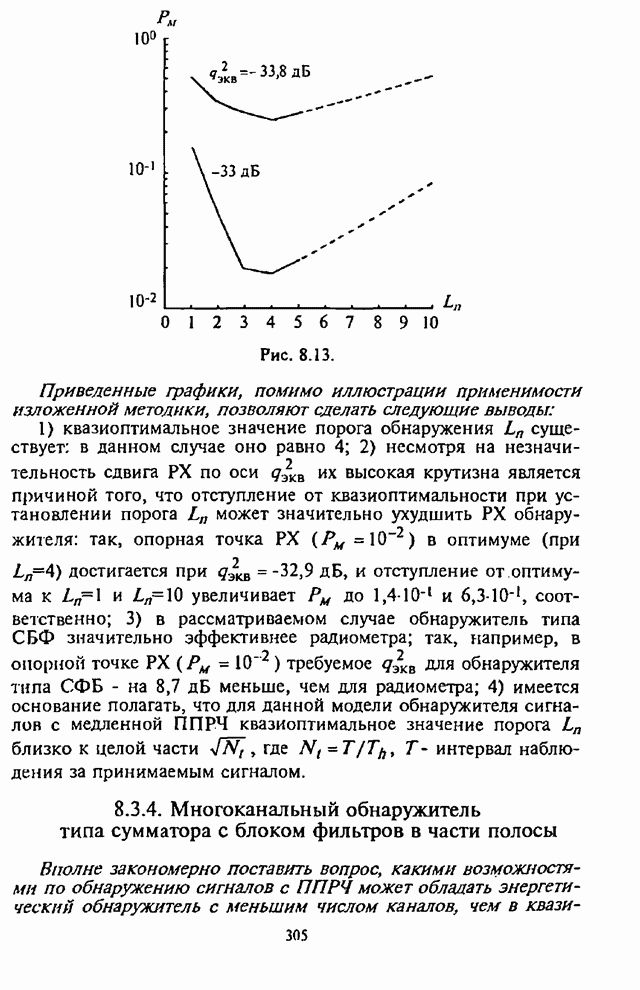
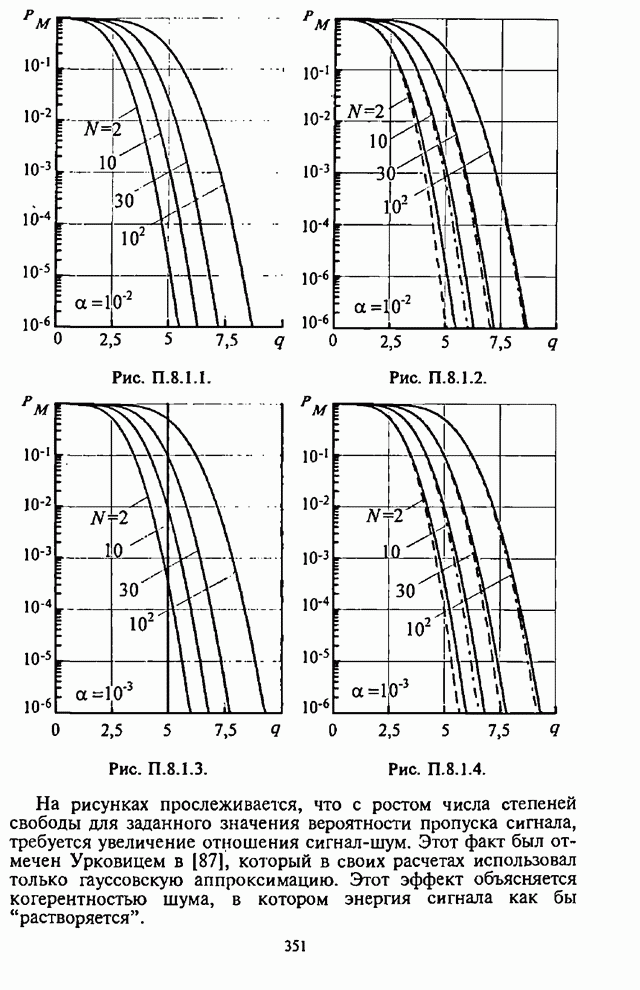
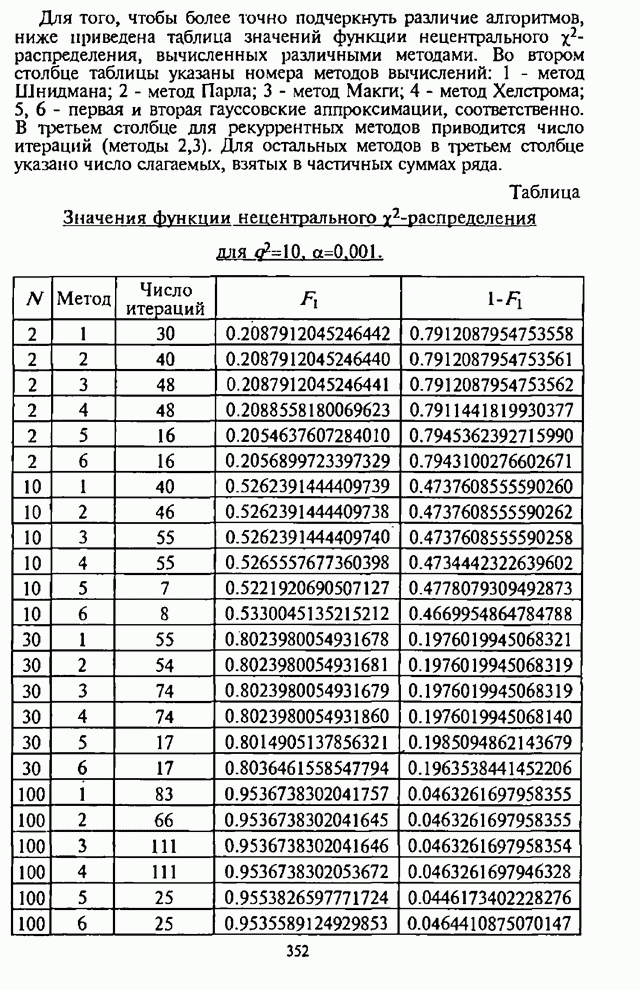
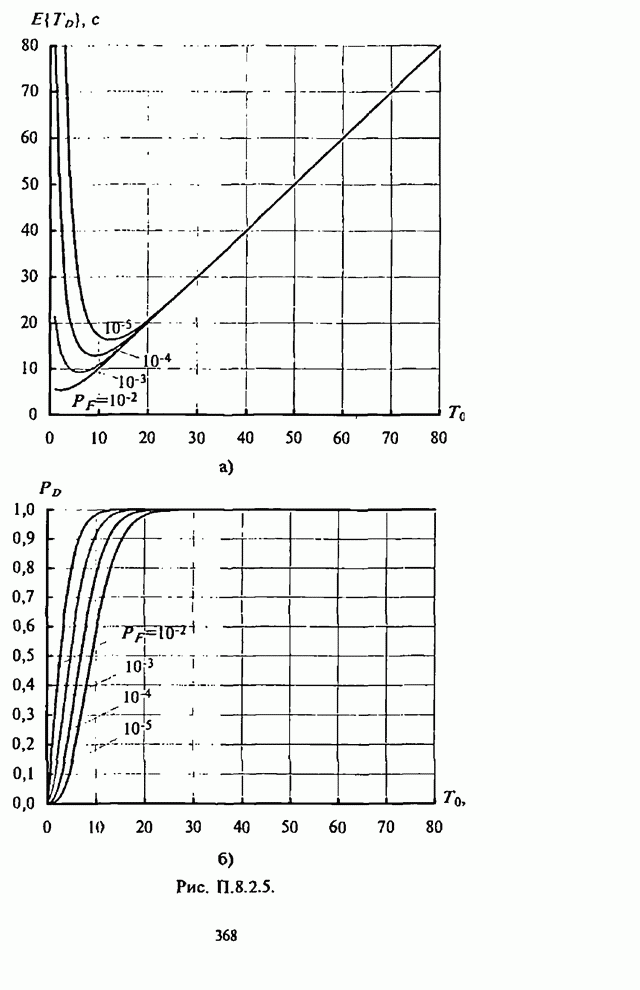
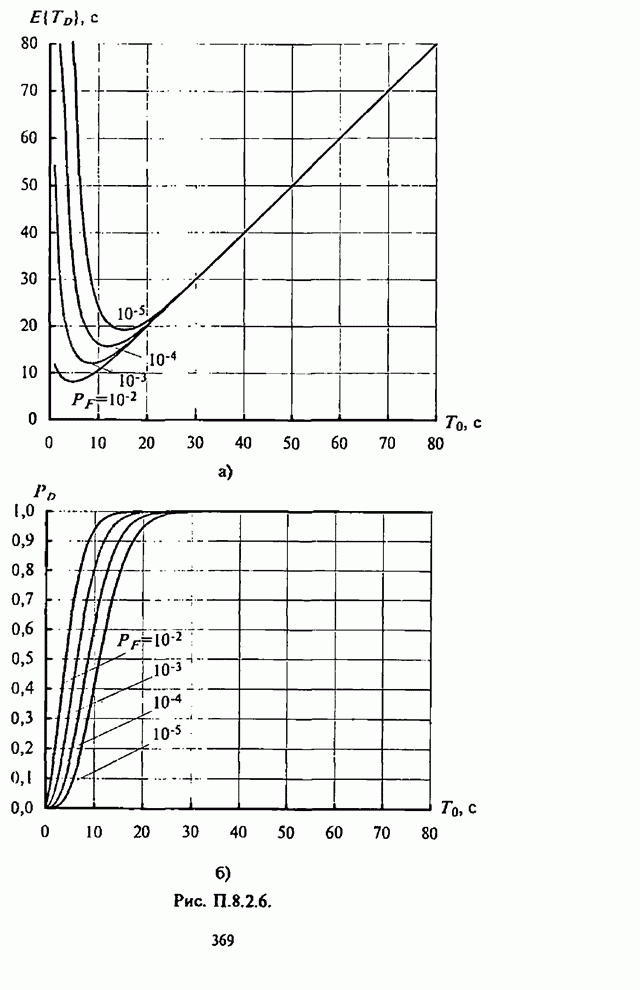
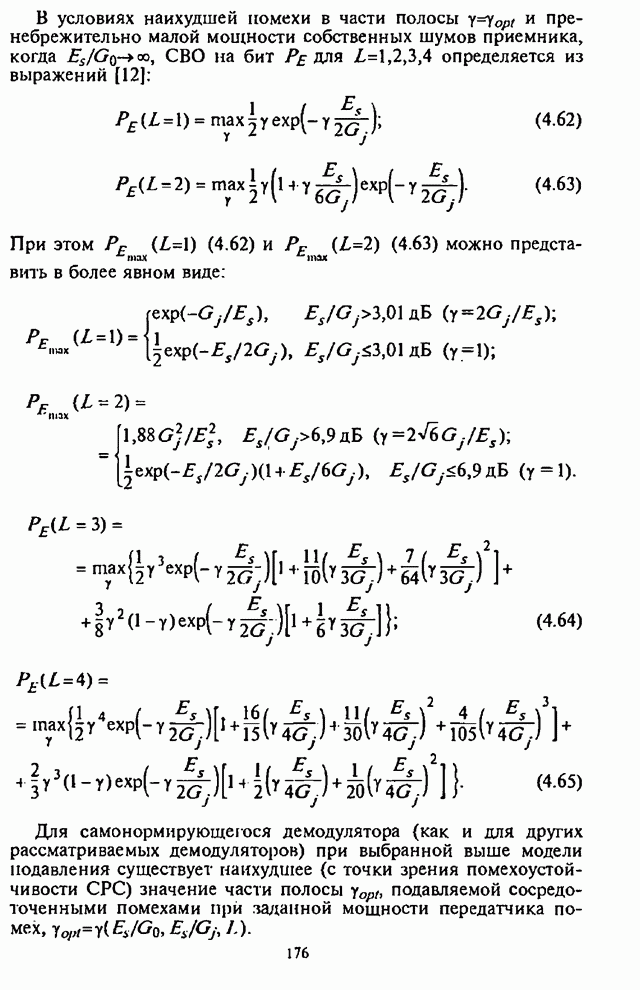| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
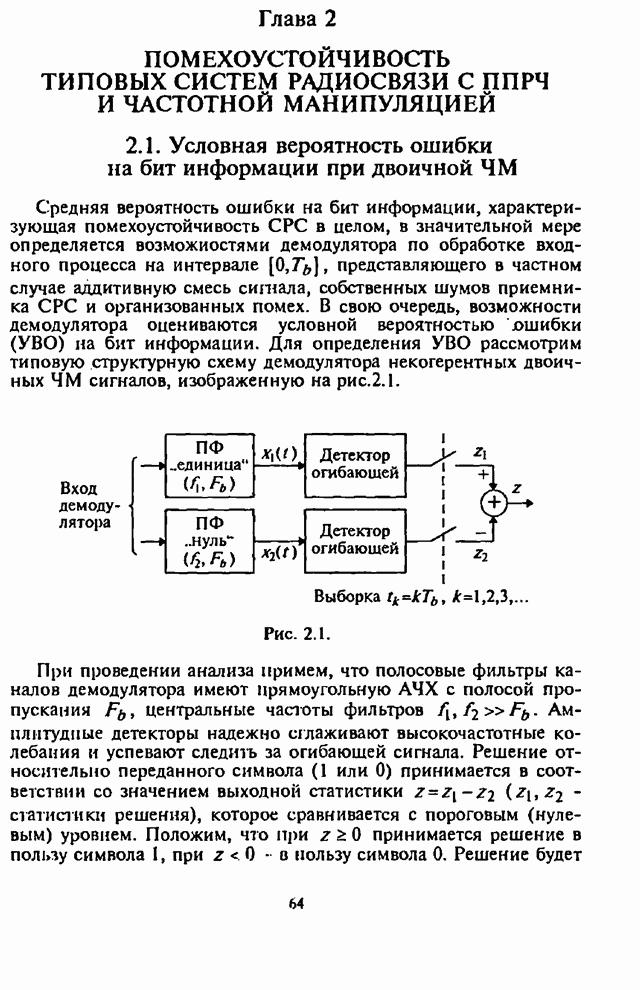
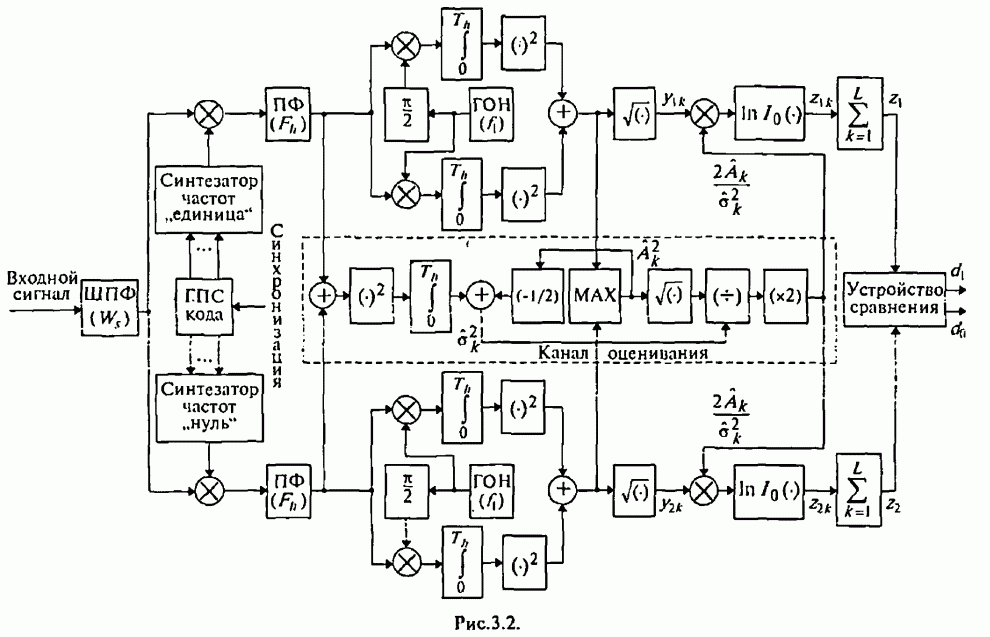
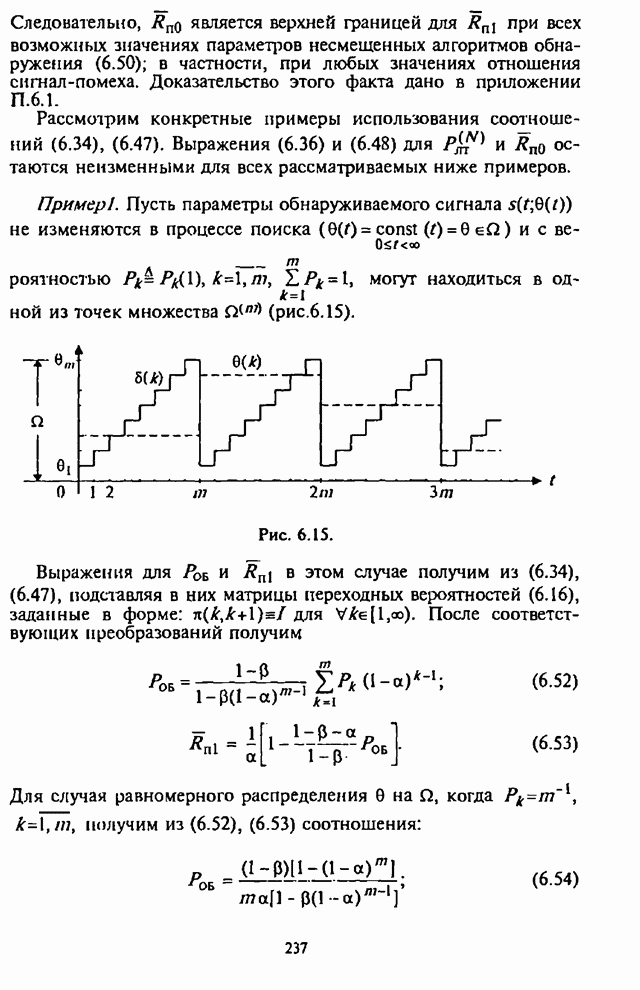
4.2. Помехоустойчивость демодулятора с линейным сложением выборок
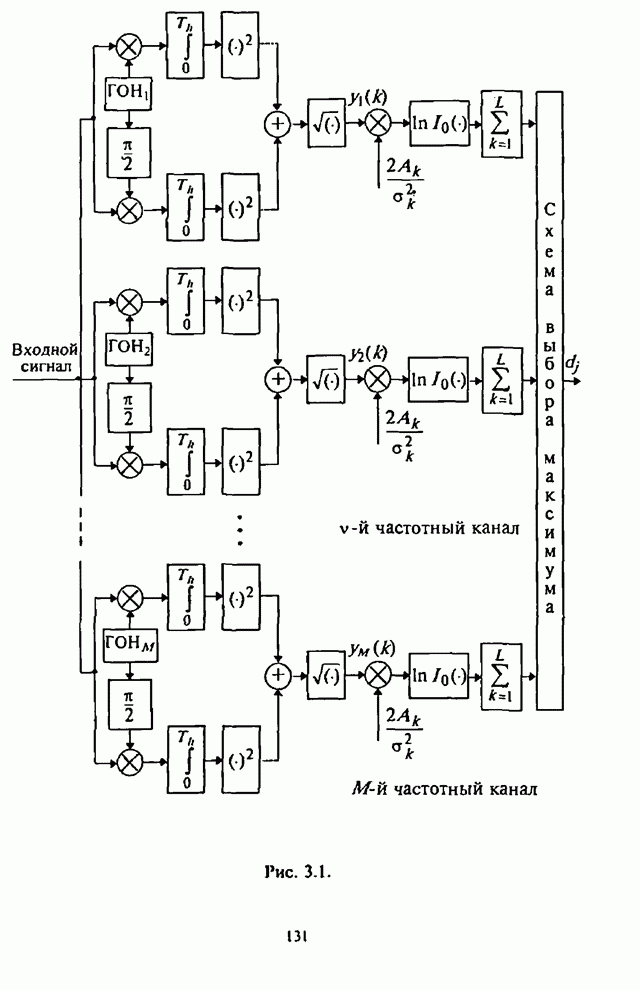
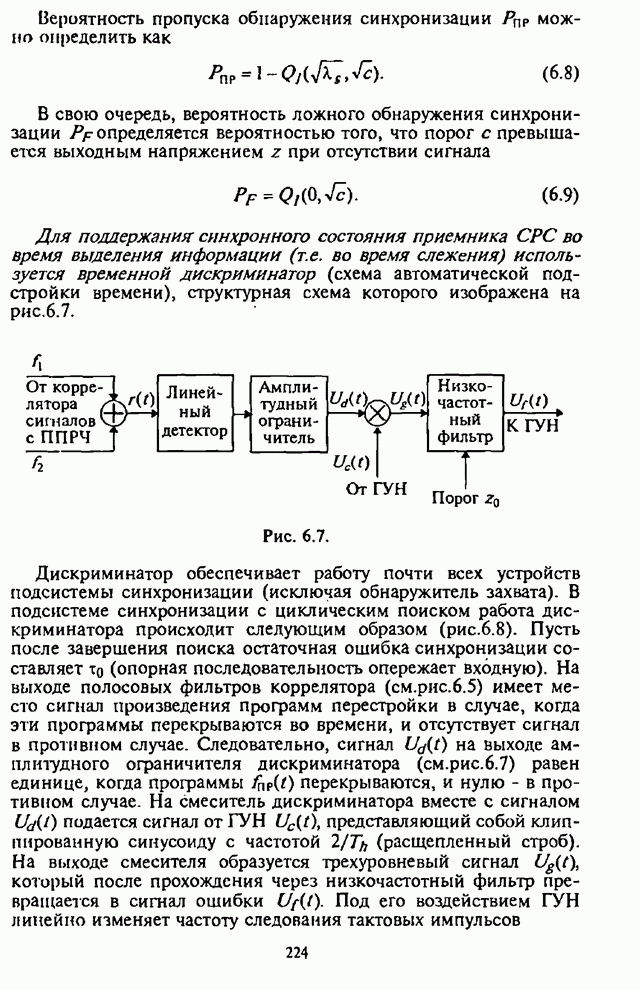
В соответствии со структурной схемой демодулятора (см. рис.4.1,а) выходная статистика алгоритма
![]() , (4.9)
, (4.9)
где
![]() (4.10)
(4.10)
Учитывая (4.5) и (4.7), выходные выборки КД огибающей ![]() и
и ![]() при
при ![]() , для канала «единица», в котором присутствует сигнал, и
канала «нуль», где нет сигнала, можно представить в виде:
, для канала «единица», в котором присутствует сигнал, и
канала «нуль», где нет сигнала, можно представить в виде:
при наличии помехи
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
в отсутствие помехи
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
В (4.11)-(4.14) обозначено: ![]() и
и ![]() - величины, характеризующие
элементы символа 1,
- величины, характеризующие
элементы символа 1, ![]() - случайная фаза, равномерно распределенная на интервале
- случайная фаза, равномерно распределенная на интервале
![]() ;
; ![]() .
.
Для определения СВО на бит PE при выходной статистике (4.9)
целесообразно использовать характеристическую функцию ![]() [10]
[10]
 (4.15)
(4.15)
где ![]() - дискретная случайная
величина, принимающая два значения (1 и 0),
- дискретная случайная
величина, принимающая два значения (1 и 0),
 (4.16)
(4.16)
Так как ![]() являются независимыми, то
определение функции
являются независимыми, то
определение функции ![]() (4.15) сводится к нахождению
(4.15) сводится к нахождению ![]() -й степени
характеристической функции любого из
-й степени
характеристической функции любого из ![]() , причем математическое ожидание
, причем математическое ожидание ![]() определяется
по независимым случайным величинам
определяется
по независимым случайным величинам ![]() и
и ![]() . При этом производится усреднение
по случайной величине
. При этом производится усреднение
по случайной величине ![]() , используя то свойство, что
характеристическая функция суммы случайных величин есть произведение
характеристических функций отдельных случайных величин. Затем осуществляется
усреднение по случайным величинам
, используя то свойство, что
характеристическая функция суммы случайных величин есть произведение
характеристических функций отдельных случайных величин. Затем осуществляется
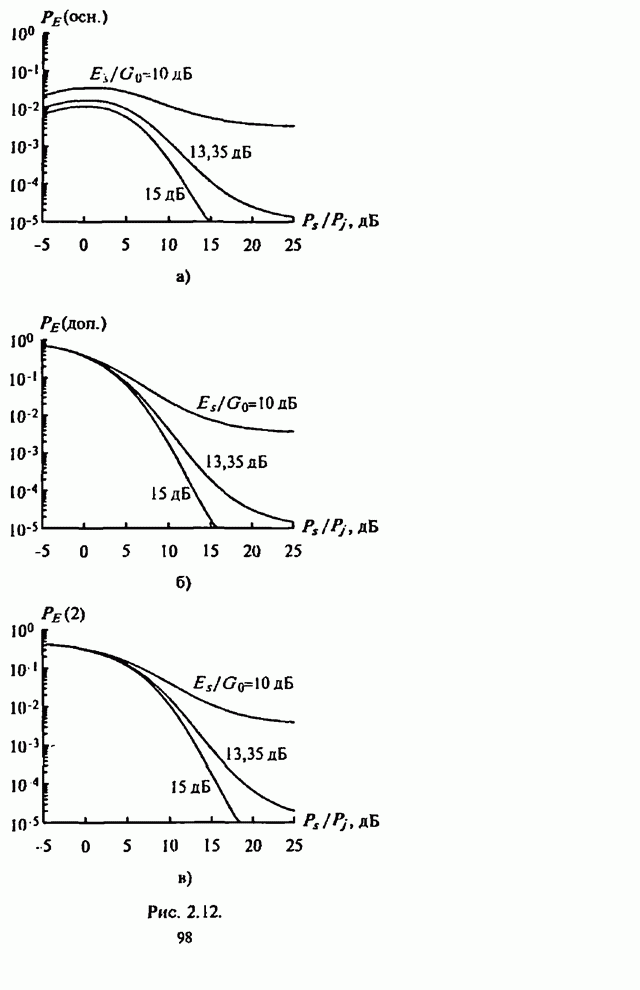
усреднение по случайным величинам ![]() и случайной фазе
и случайной фазе ![]() . Далее,
разлагая в степенной ряд экспоненциальные функции, включающие
. Далее,
разлагая в степенной ряд экспоненциальные функции, включающие ![]() в показатели степени, в явном
виде получим характеристическую функцию [10]
в показатели степени, в явном
виде получим характеристическую функцию [10]
 (4.17)
(4.17)
где
 (4.18)
(4.18)
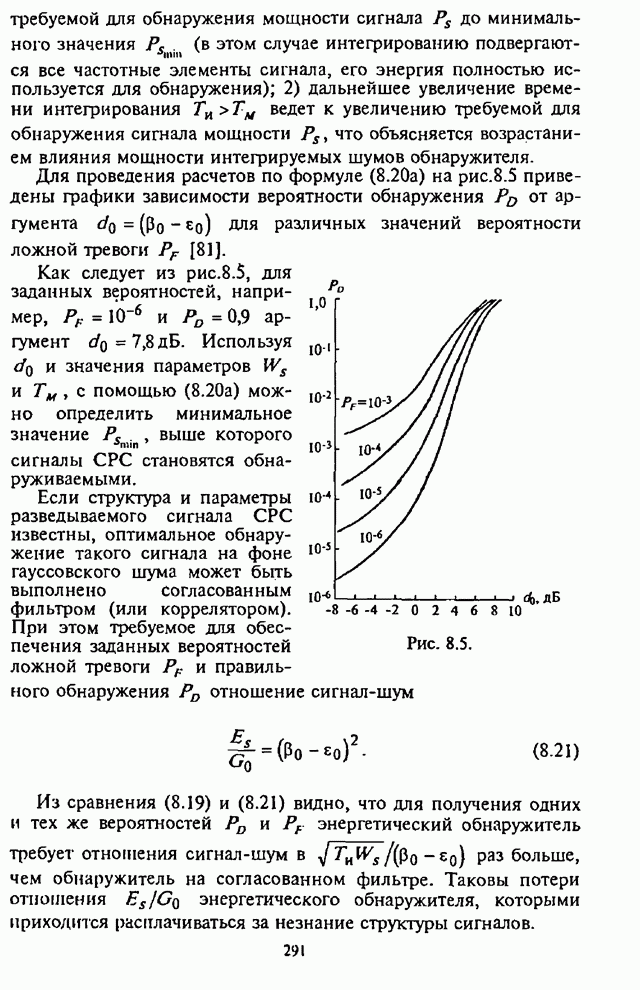
 (4.19)
(4.19)
Плотность распределения вероятности выходной статистики
![]() с
использованием характеристической функции определяется путем обратного
преобразования Фурье
с
использованием характеристической функции определяется путем обратного
преобразования Фурье
![]() (4.20)
(4.20)
Полученная таким образом плотность распределения вероятности
![]() интегрируется по отрицательным
значениям
интегрируется по отрицательным
значениям ![]() для получения СВО на бит
для получения СВО на бит
![]() (4.21)
(4.21)
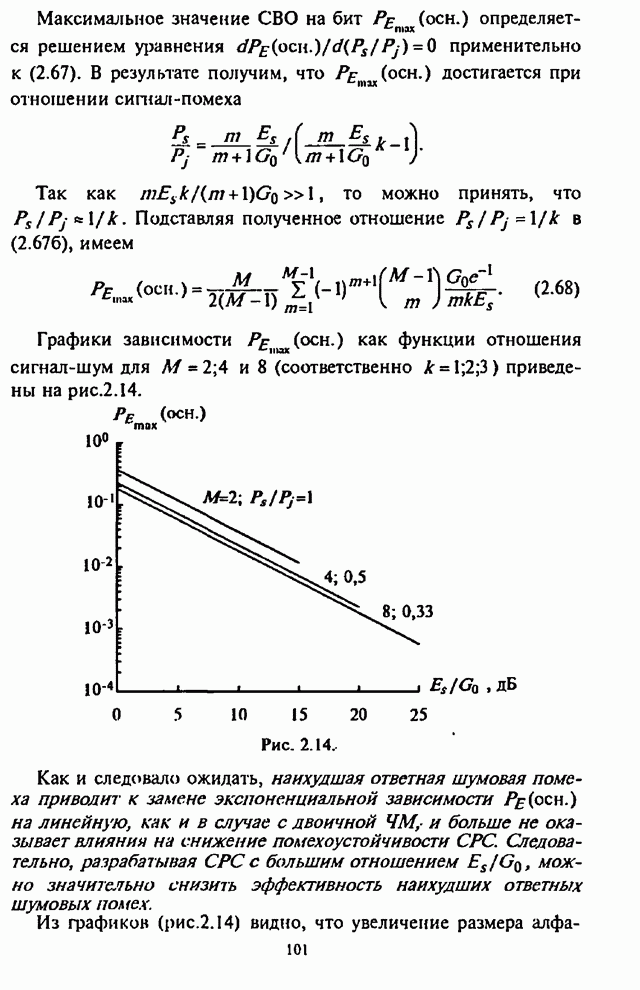
Следуя указанным преобразованиям, в [10] показано, что СВО ни бит в общем виде может быть представлена формулой
 (4.22)
(4.22)
где ![]()
![]()
![]() - коэффициенты разложения в элементарную
дробь.
- коэффициенты разложения в элементарную
дробь.
При ![]() коэффициенты разложения
коэффициенты разложения ![]() и
и ![]() равны нулю для всех
равны нулю для всех ![]() и
и ![]() . При
. При ![]() коэффициенты разложения
коэффициенты разложения
![]() имеют вид:
имеют вид:
 (4.23)
(4.23)
Коэффициенты ![]() при
при ![]() определяются из выражения
определяются из выражения
 (4.24)
(4.24)
В (4.23) и (4.24) обозначено: ![]() - символ Похгаммера,
- символ Похгаммера,
 (4.25)
(4.25)
при ![]()
![]() (4.26)
(4.26)
где ![]() - гамма-функция,
- гамма-функция,
![]() (4.27)
(4.27)
 (4.28)
(4.28)
Выражение (4.22) для СВО на бит ![]() является наиболее общим и
справедливым для любого числа скачков частоты
является наиболее общим и
справедливым для любого числа скачков частоты ![]() в течении одного бита
в течении одного бита ![]() .
.
Если принять, что скачки частоты отсутствуют, то при ![]() выражение приобретает
вид:
выражение приобретает
вид:
 (4.29)
(4.29)
При преобразовании формулы (4.22) учтено, что при ![]()
![]()
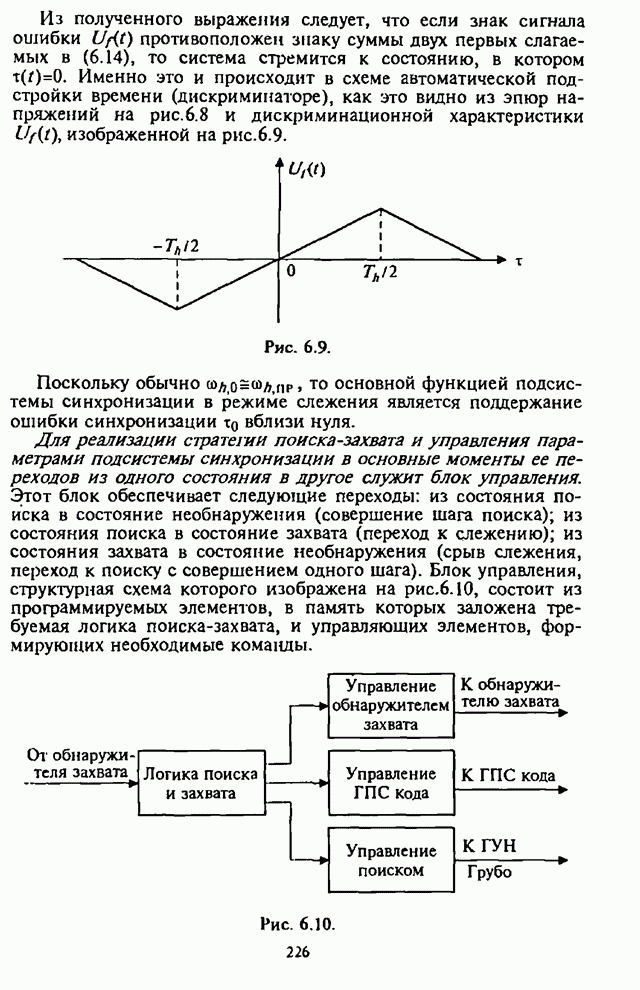
Учитывая, что  , СВО на бит
, СВО на бит ![]() при
при ![]()
 (4.30)
(4.30)
Выражение (4.30) представляет собой СВО на бит для СРС
с одним скачком частоты (![]() ) на двоичный разряд в условиях воздействия шумовой
помехи в части полосы и полностью соответствует полученной ранее зависимости
СВО на бит (см. (2.37)).
) на двоичный разряд в условиях воздействия шумовой
помехи в части полосы и полностью соответствует полученной ранее зависимости
СВО на бит (см. (2.37)).
Для случая малых собственных шумов приемного устройства
СРС, когда ![]() , точное выражение для СВО на
бит имеет вид [10]:
, точное выражение для СВО на
бит имеет вид [10]:
 (4.31)
(4.31)
где ![]() для всех
для всех ![]()

для всех ![]() .
.
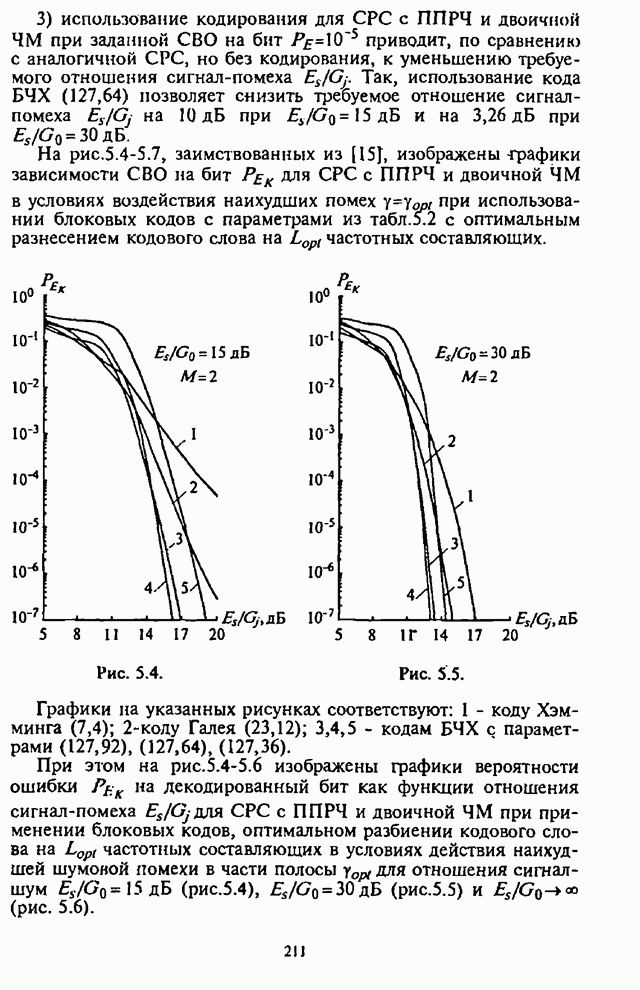
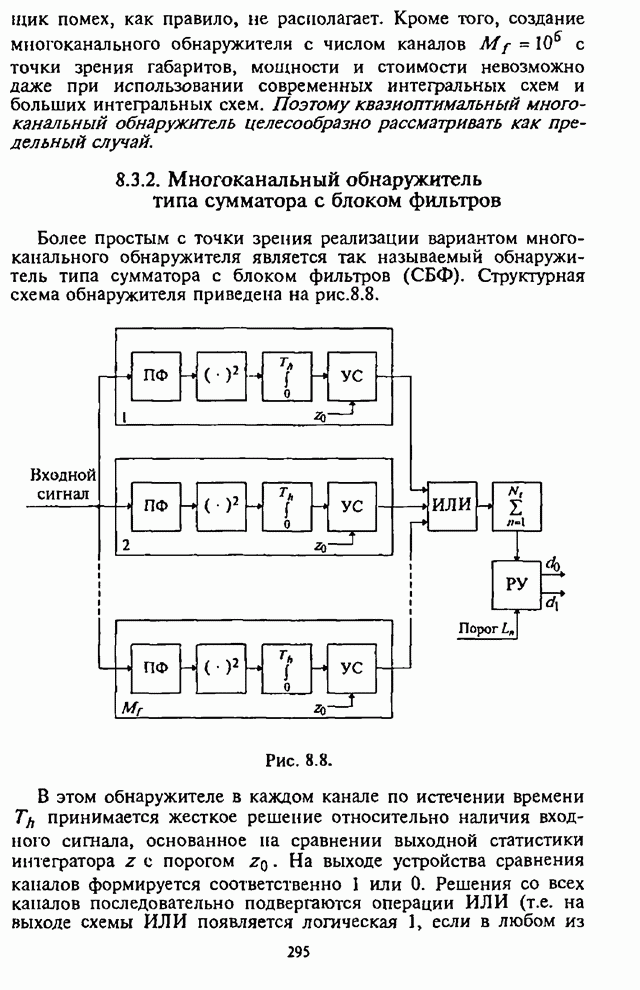
На основе приведенного анализа и полученных аналитических
выражений можно построить графические зависимости СВО на бит ![]() для различных исходных данных
в условиях воздействия шумовой помехи в части полосы. Используя результаты [10],
на рис.4.2-4.6 представлены графики СВО на бит
для различных исходных данных
в условиях воздействия шумовой помехи в части полосы. Используя результаты [10],
на рис.4.2-4.6 представлены графики СВО на бит ![]() и оптимального значения
и оптимального значения ![]() от обобщенных
параметров СРС и станции помех.
от обобщенных
параметров СРС и станции помех.
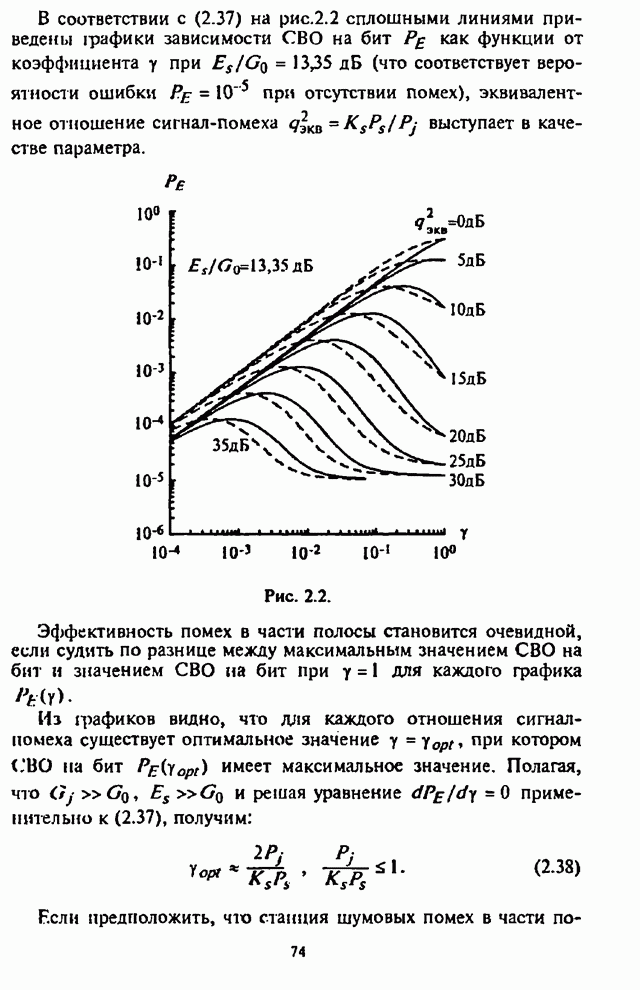
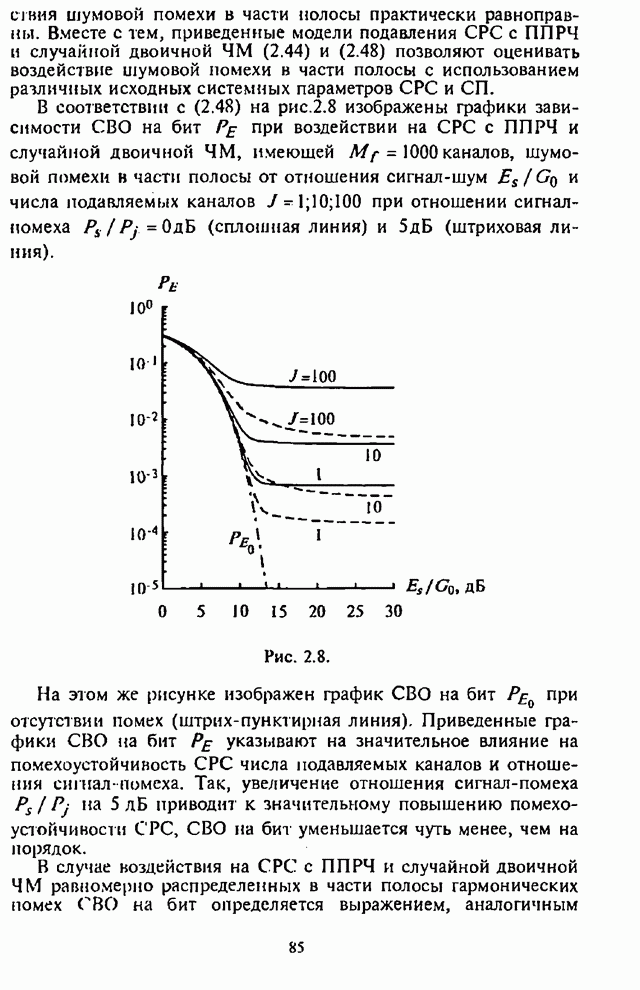
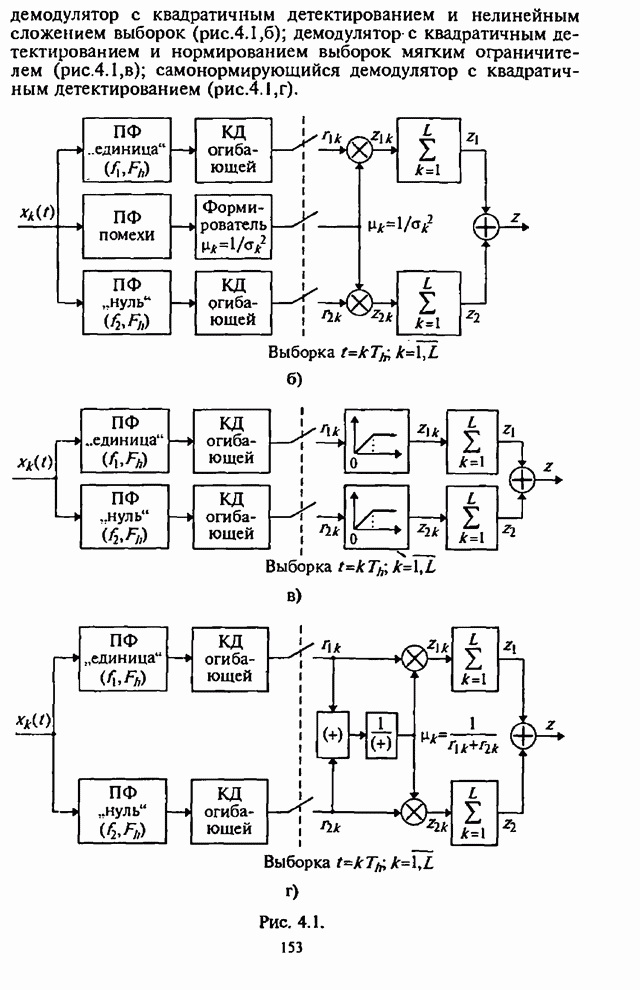
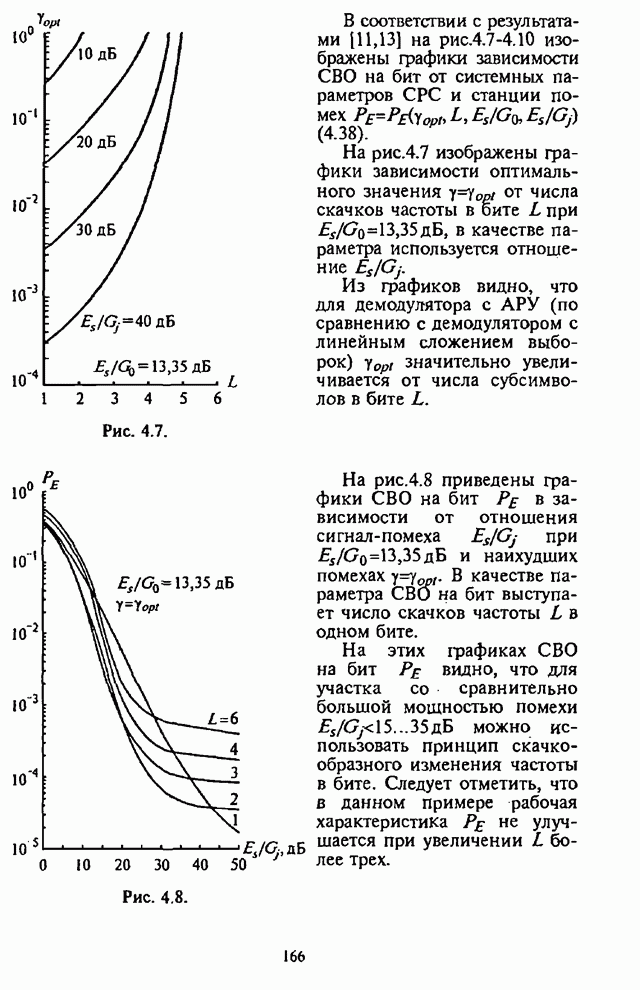
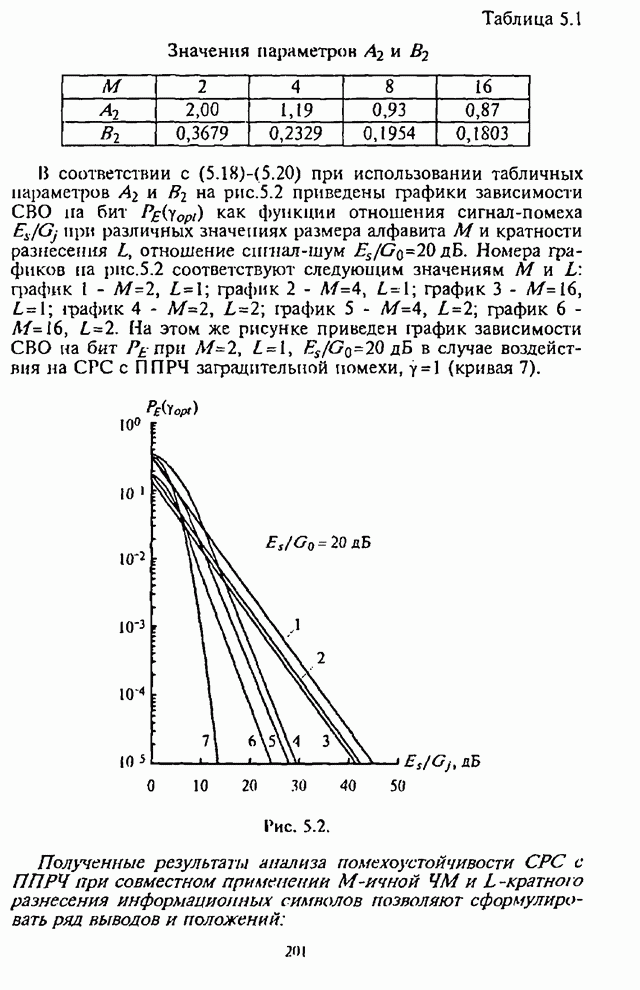
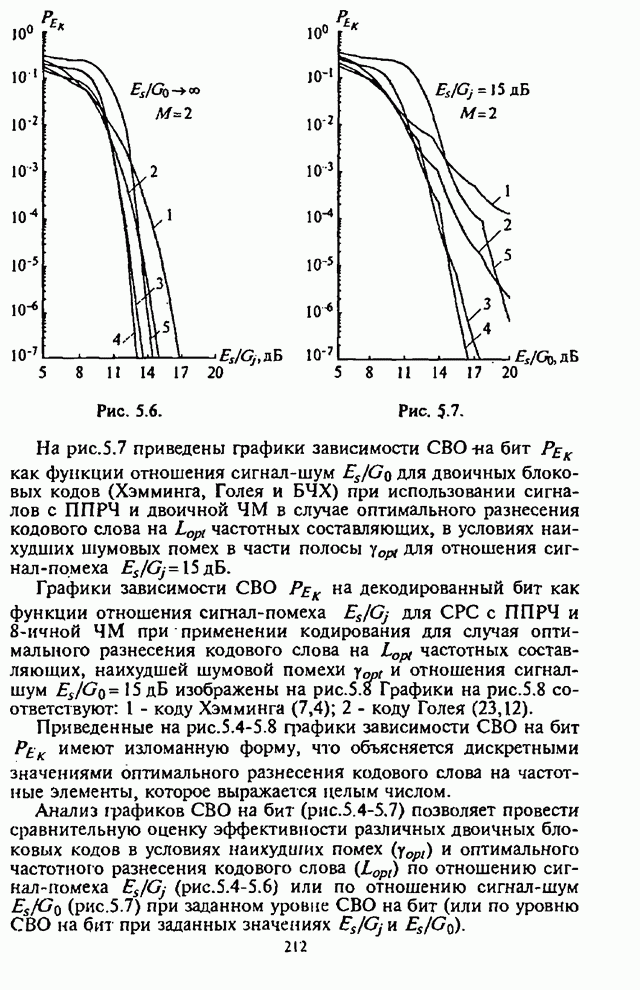
На рис.4.2 приведены графики СВО на бит ![]() как функции от части
подавляемой помехой полосы (коэффициента
как функции от части
подавляемой помехой полосы (коэффициента ![]() ) при
) при ![]() и числе скачков частоты
и числе скачков частоты ![]() , отношение сигнал-помеха
, отношение сигнал-помеха ![]() выступает в качестве
параметра.
выступает в качестве
параметра.

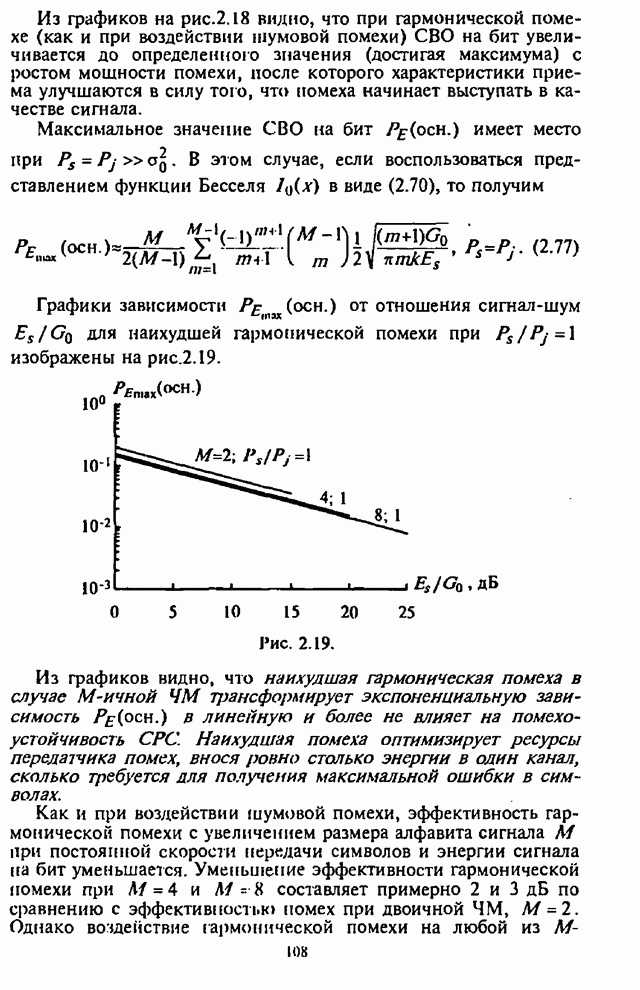
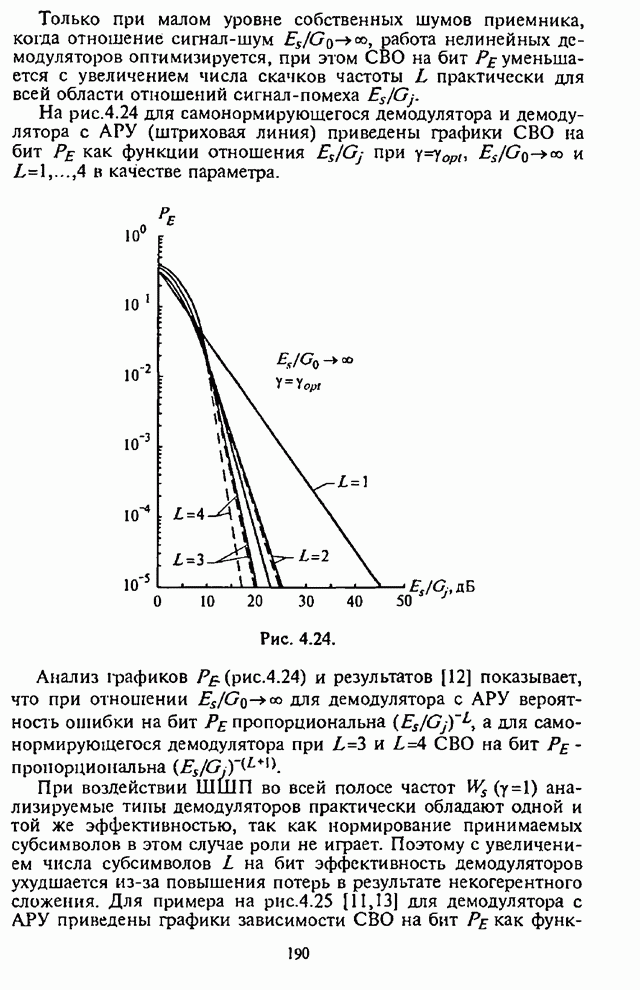
Рис. 4.2.
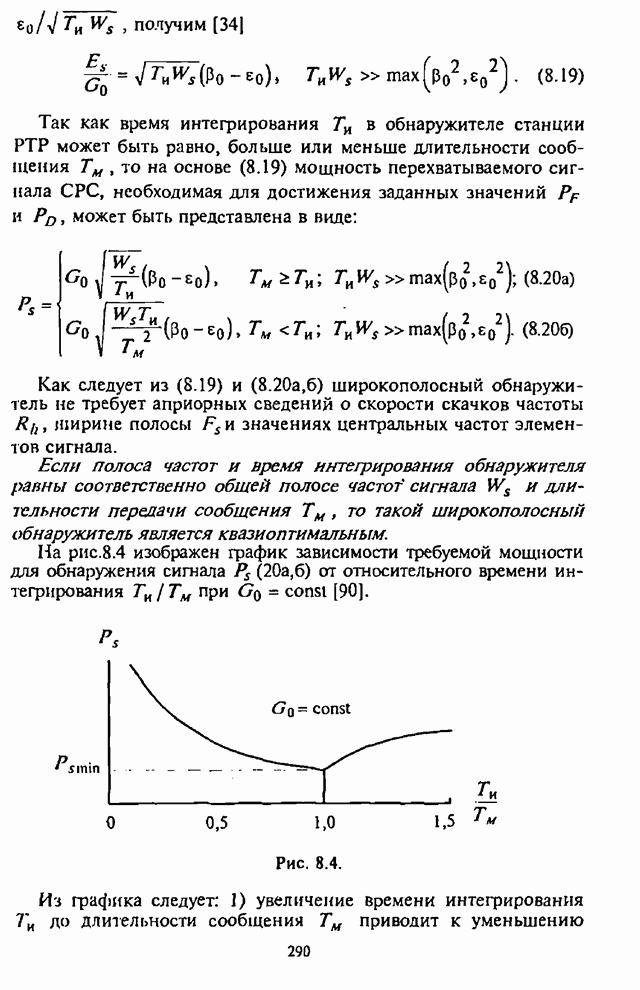
Из графиков на рис.4.2 видно, что для каждого отношения
![]() имеет место оптимальное
значение
имеет место оптимальное
значение ![]() , при котором СВО на бит
, при котором СВО на бит ![]() принимает
максимальное значение.
принимает
максимальное значение.

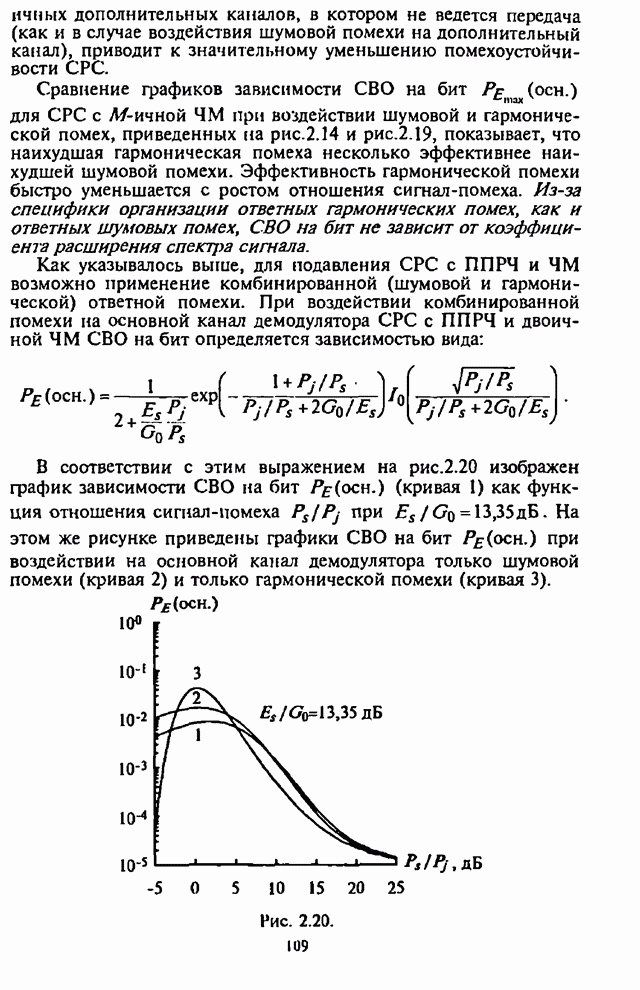
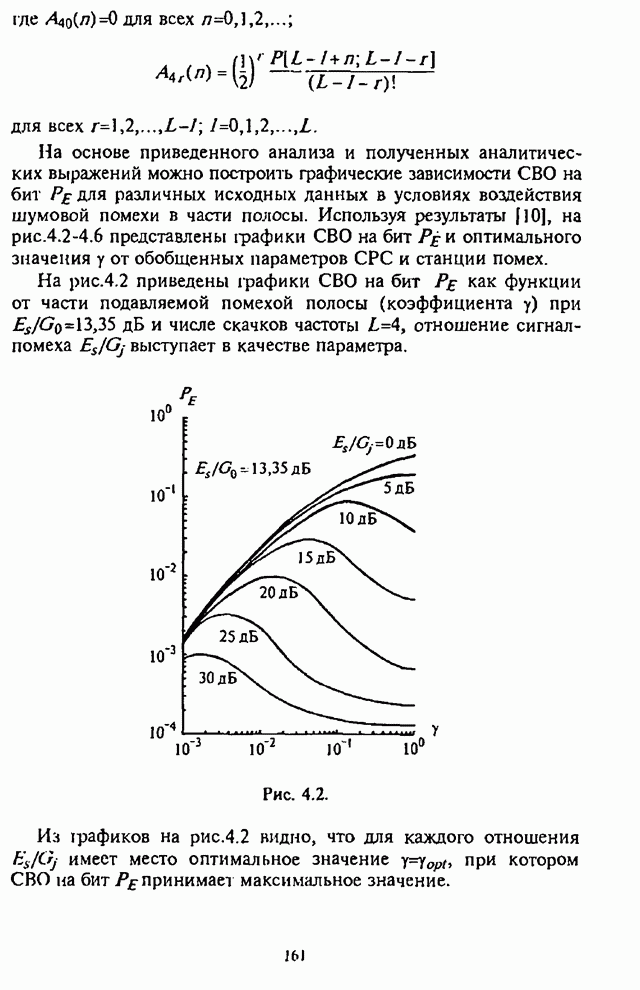
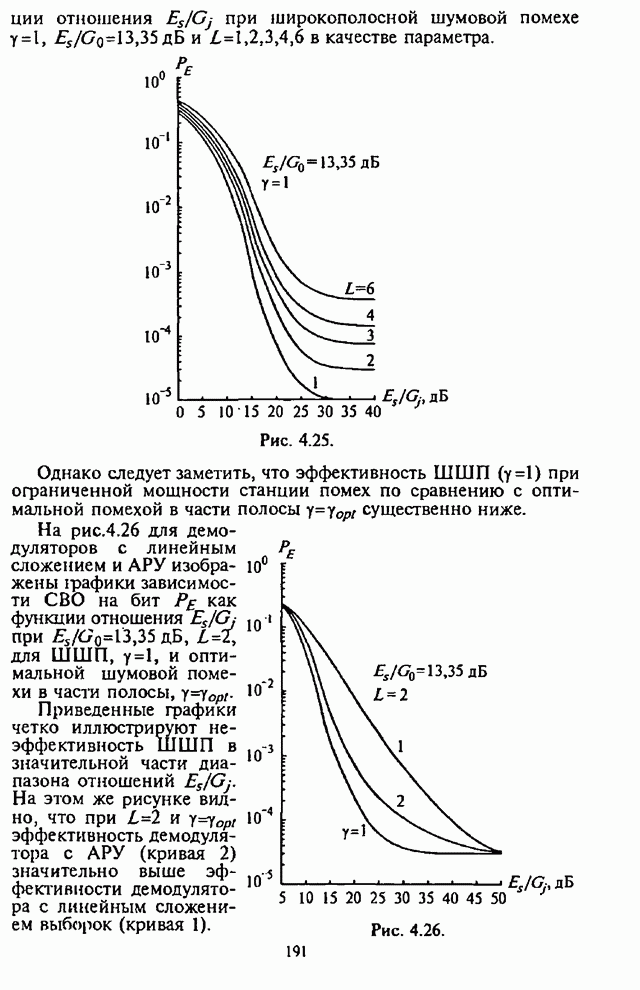
Рис. 4.3.
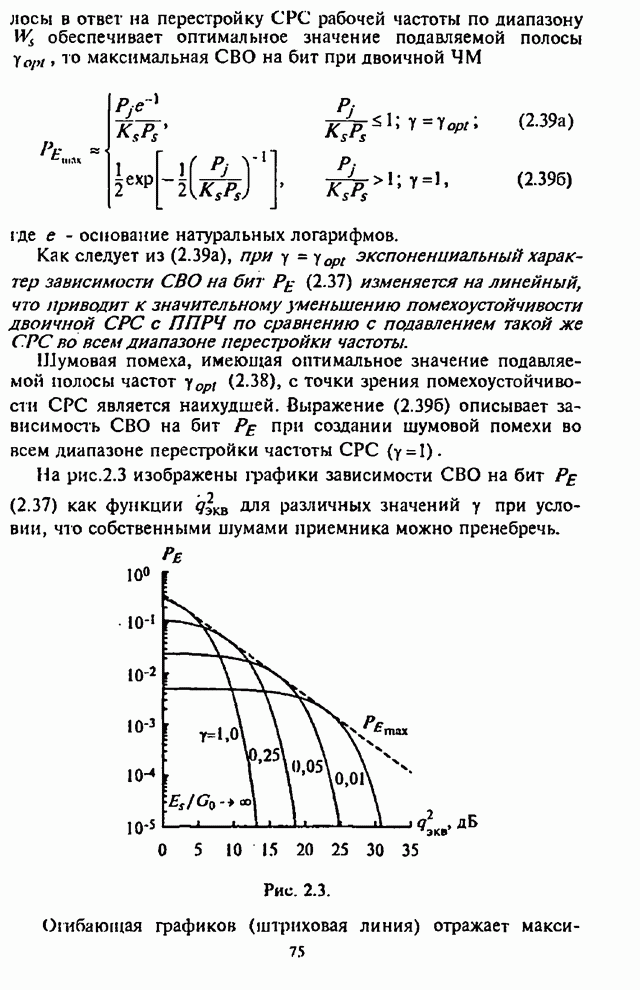
Графики зависимости оптимального значения части подавляемой
помехой полосы ![]() от числа скачков частоты
от числа скачков частоты ![]() при
при ![]() (что соответствует
(что соответствует ![]() в отсутствие помех и
в отсутствие помех и ![]() ) приведены на
рис.4.3, в качестве параметра используется отношение сигнал-помеха
) приведены на
рис.4.3, в качестве параметра используется отношение сигнал-помеха ![]() .
.
Из графиков видна сравнительно слабая зависимость ![]() от
от ![]() , а для
, а для ![]() оптимальное значение
оптимальное значение ![]() остается практически
постоянным для данного отношения
остается практически
постоянным для данного отношения![]() .
.

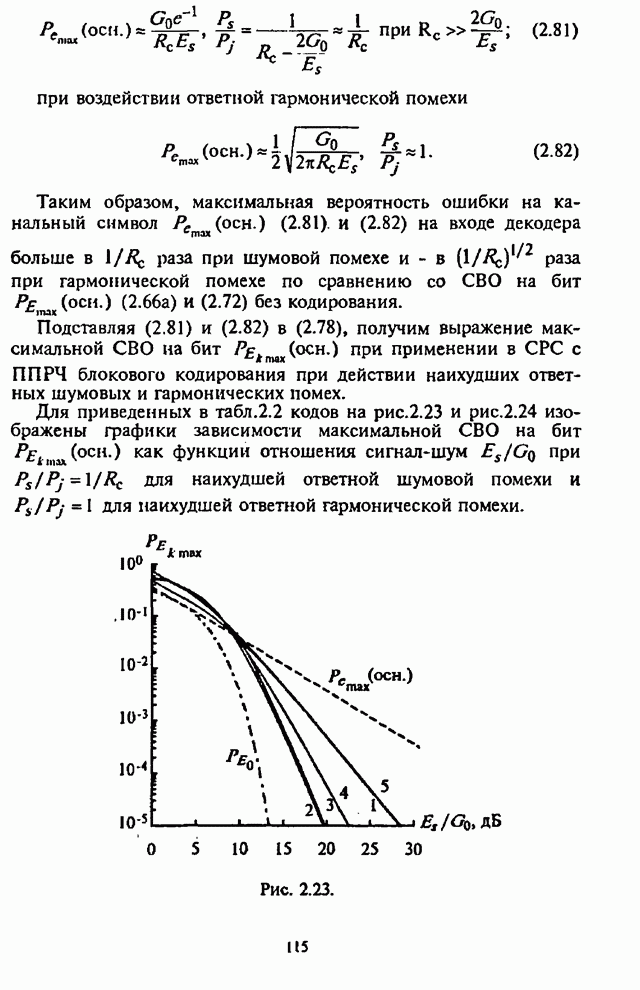
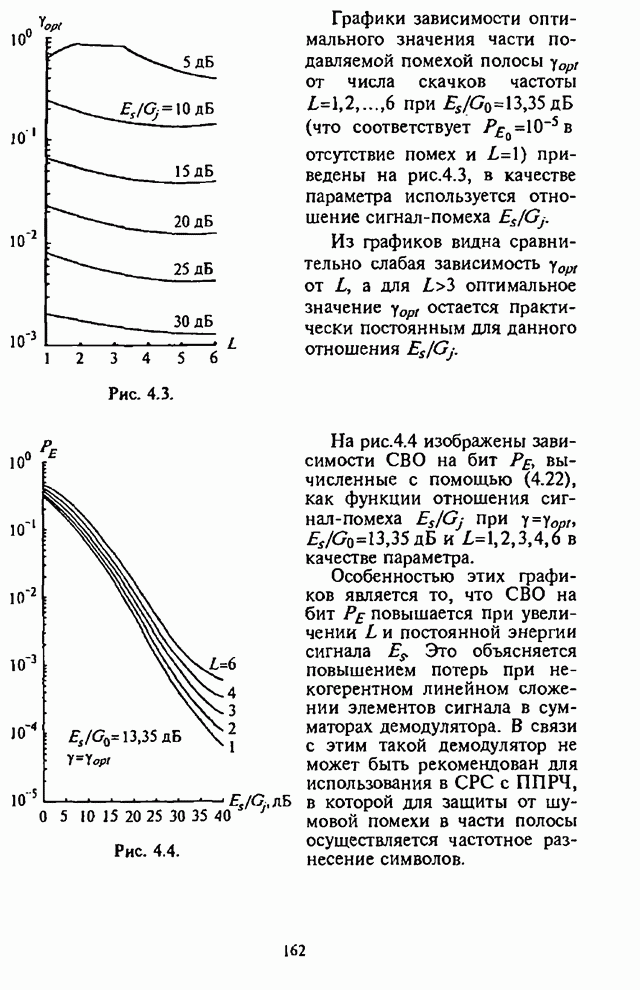
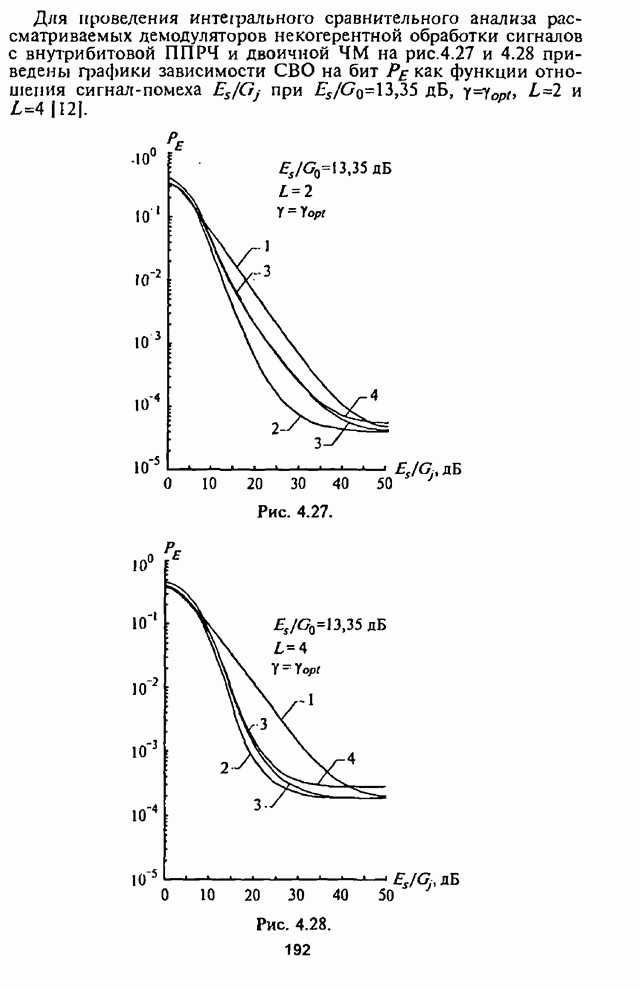
Рис. 4.4.
На рис.4.4 изображены зависимости СВО на бит ![]() вычисленные с помощью (4.22),
как функции отношения сигнал-помеха
вычисленные с помощью (4.22),
как функции отношения сигнал-помеха ![]() ; при
; при ![]() ,
, ![]() и
и ![]() в качестве
параметра.
в качестве
параметра.
Особенностью этих графиков является то, что СВО на бит
![]() повышается при увеличении
повышается при увеличении ![]() и постоянной энергии сигнала
и постоянной энергии сигнала ![]() . Это объясняется повышением
потерь при некогерентном линейном сложении элементов сигнала в сумматорах
демодулятора. В связи с этим такой демодулятор не может быть рекомендован для
использования в СРС с ППРЧ, в которой для зашиты от шумовой помехи в части
полосы осуществляется частотное разнесение символов.
. Это объясняется повышением
потерь при некогерентном линейном сложении элементов сигнала в сумматорах
демодулятора. В связи с этим такой демодулятор не может быть рекомендован для
использования в СРС с ППРЧ, в которой для зашиты от шумовой помехи в части
полосы осуществляется частотное разнесение символов.
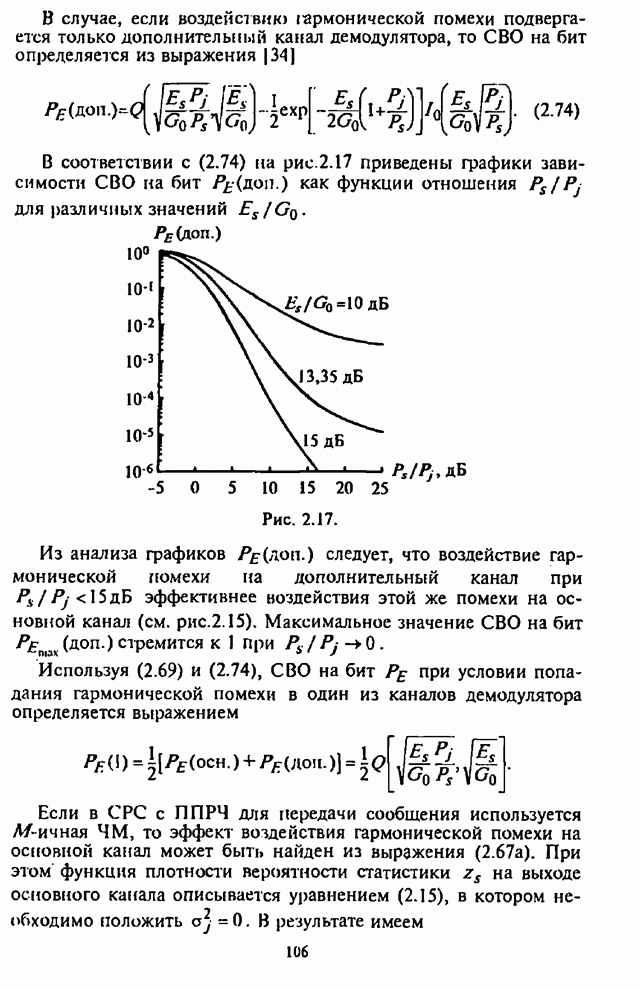
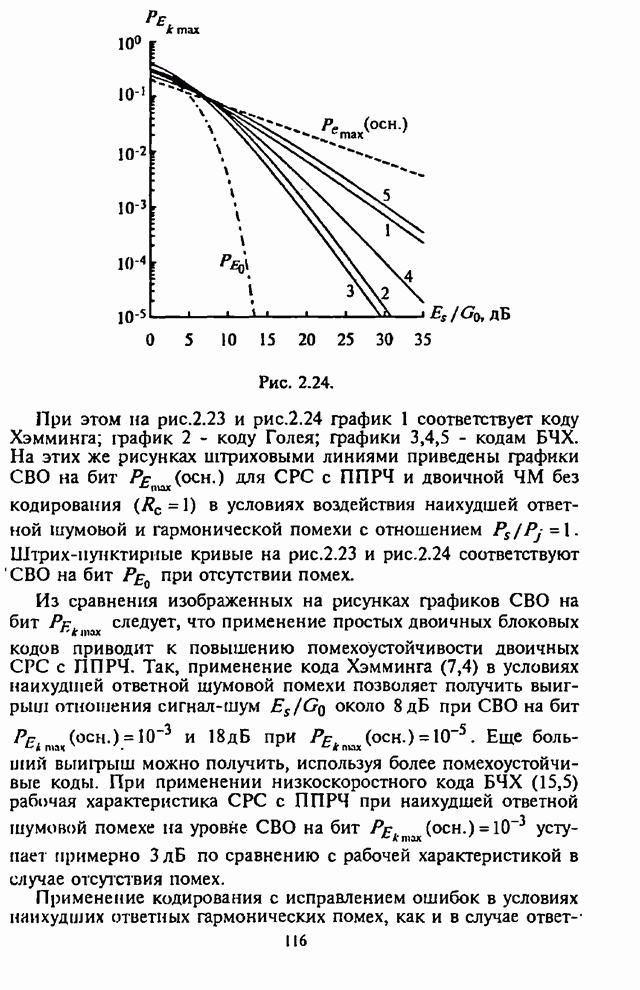
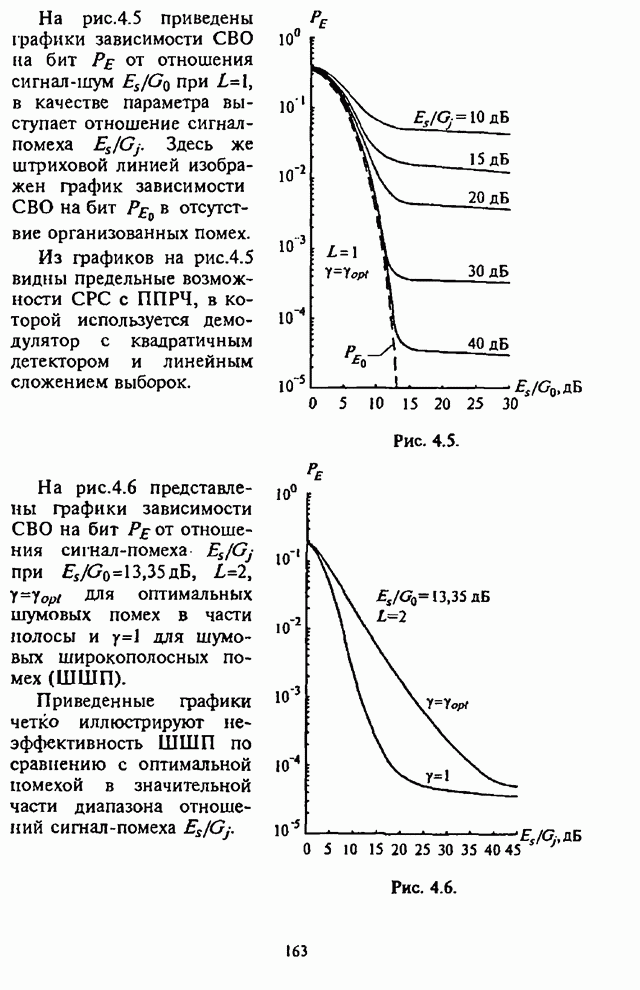
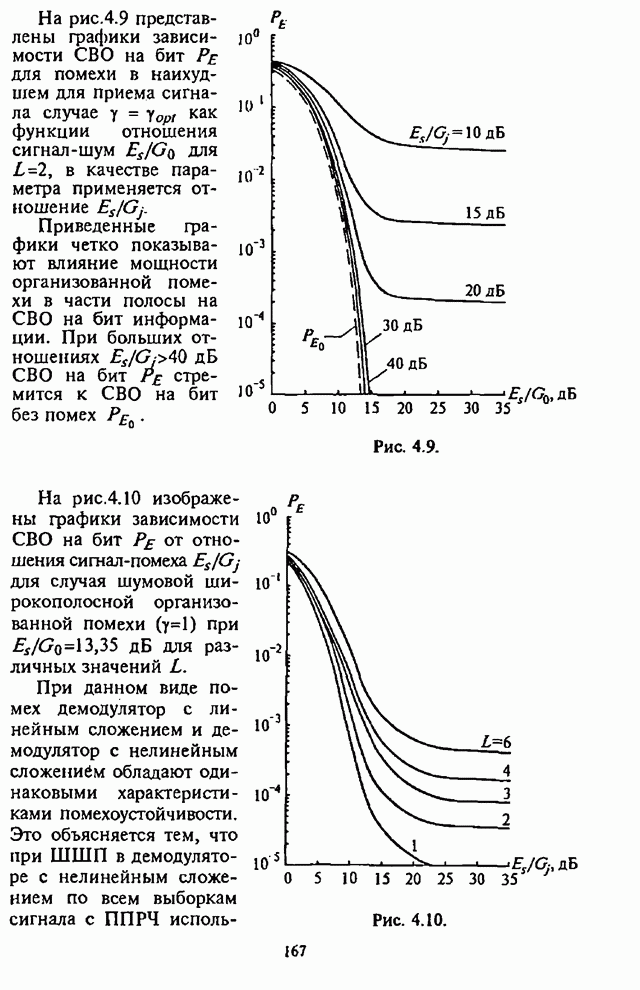
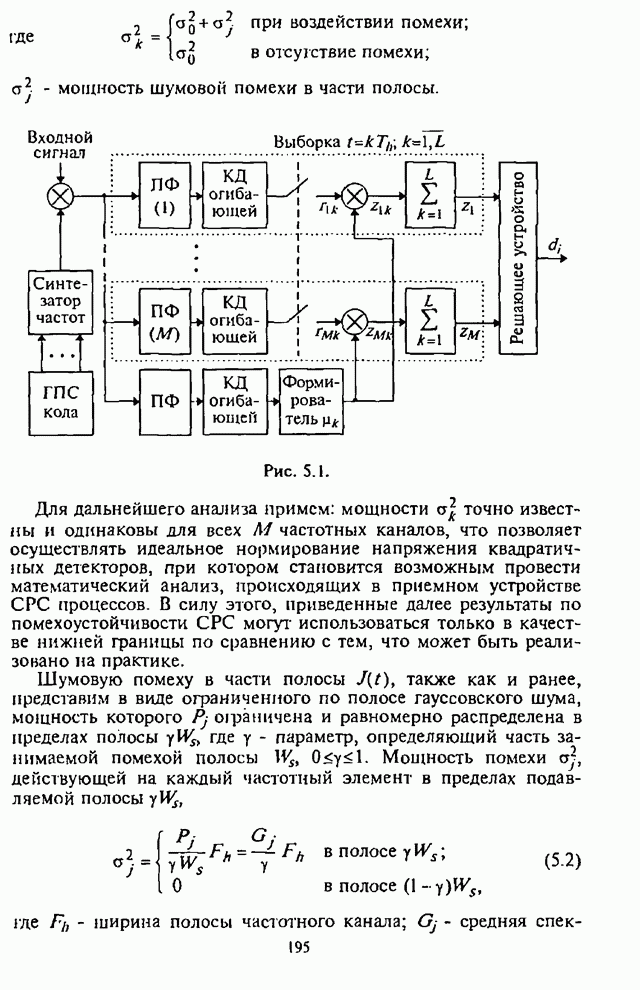
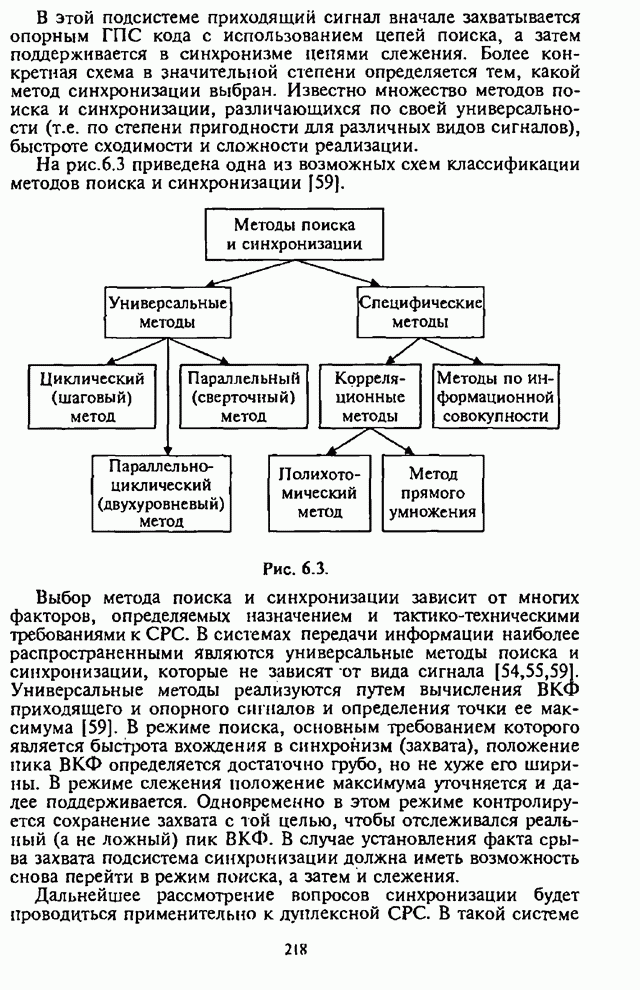
На рис.4.5 приведены графики зависимости СВО на бит ![]() от отношения сигнал-шум
от отношения сигнал-шум ![]() при
при![]() , в качестве параметра выступает
отношение сигнал-помеха
, в качестве параметра выступает
отношение сигнал-помеха ![]() . Здесь же штриховой линией
изображен график зависимости СВО на бит
. Здесь же штриховой линией
изображен график зависимости СВО на бит ![]() в отсутствие организованных
помех.
в отсутствие организованных
помех.
Из графиков на рис.4.5 видны предельные возможности СРС с ППРЧ, в которой используется демодулятор с квадратичным детектором и линейным сложением выборок.

Рис. 4.5.

Рис. 4.6.
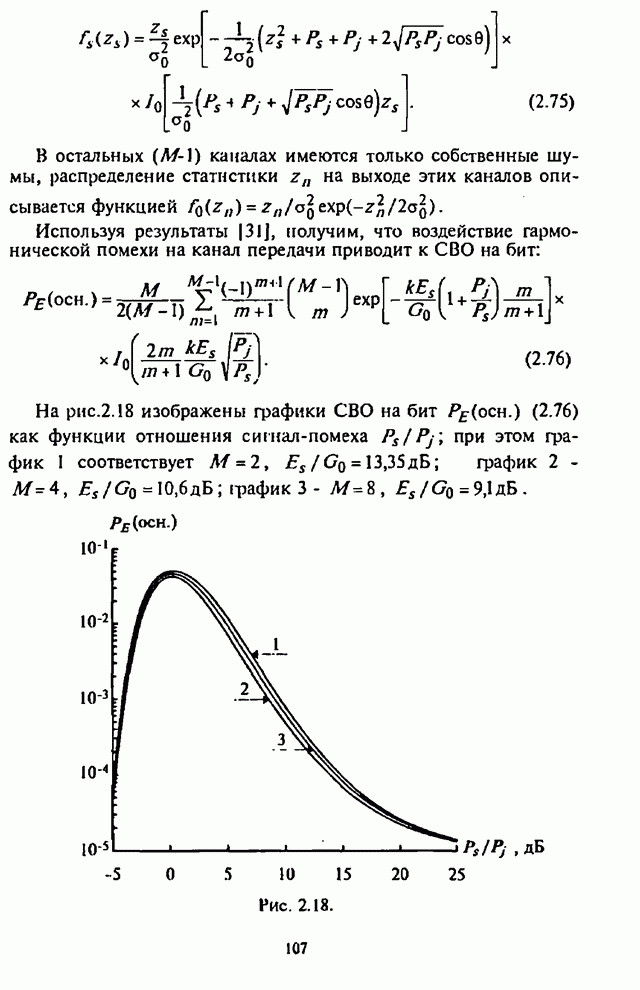
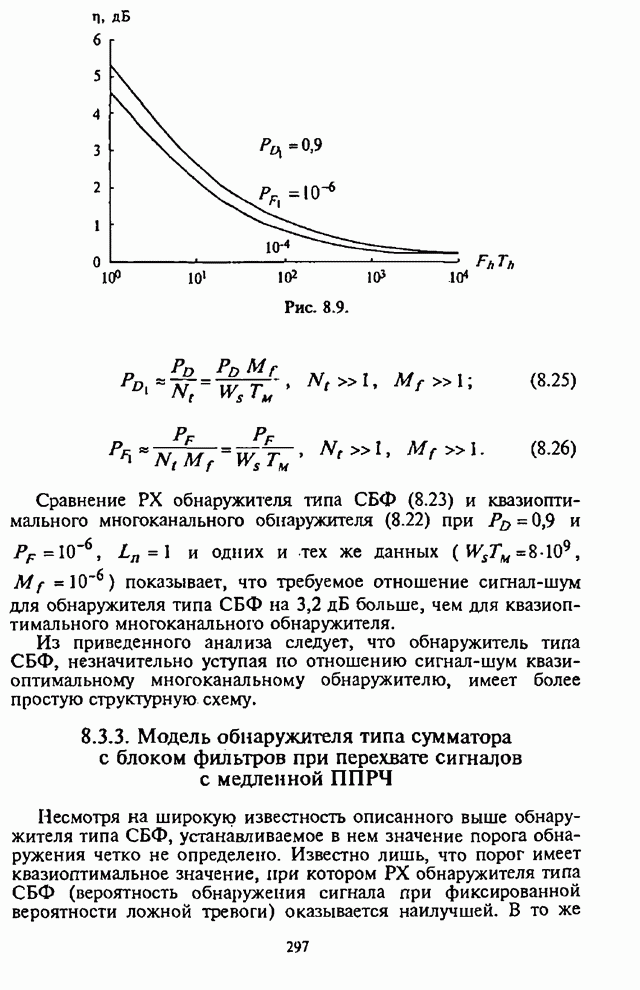
На рис.4.6 представлены графики зависимости СВО на бит
![]() от
отношения
сигнал-помеха
от
отношения
сигнал-помеха ![]() при
при ![]() ,
, ![]() ,
, ![]() оптимальных шумовых помех в
части полосы и
оптимальных шумовых помех в
части полосы и ![]() для
шумовых широкополосных помех (ШШП).
для
шумовых широкополосных помех (ШШП).
Приведенные графики четко иллюстрируют неэффективность
ШШП по сравнению с оптимальной помехой в значительной части диапазона отношений
сигнал-помеха ![]()
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
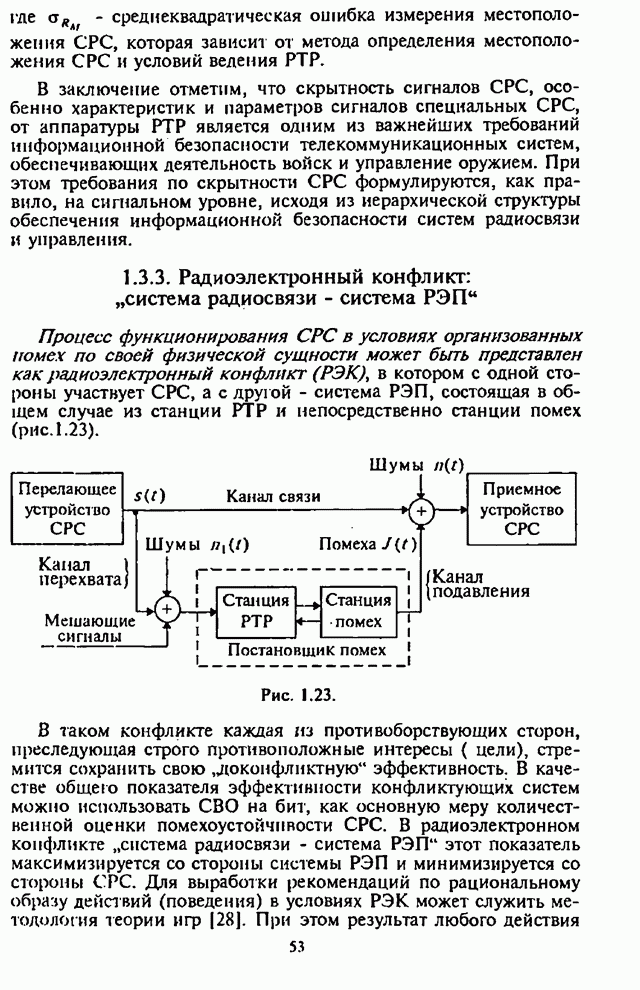
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
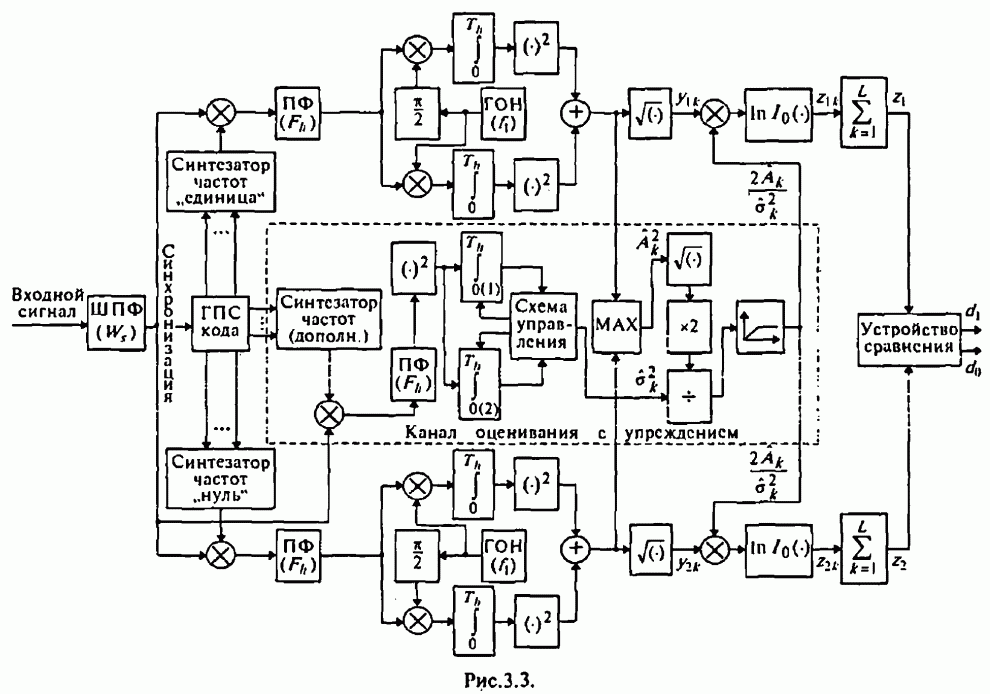
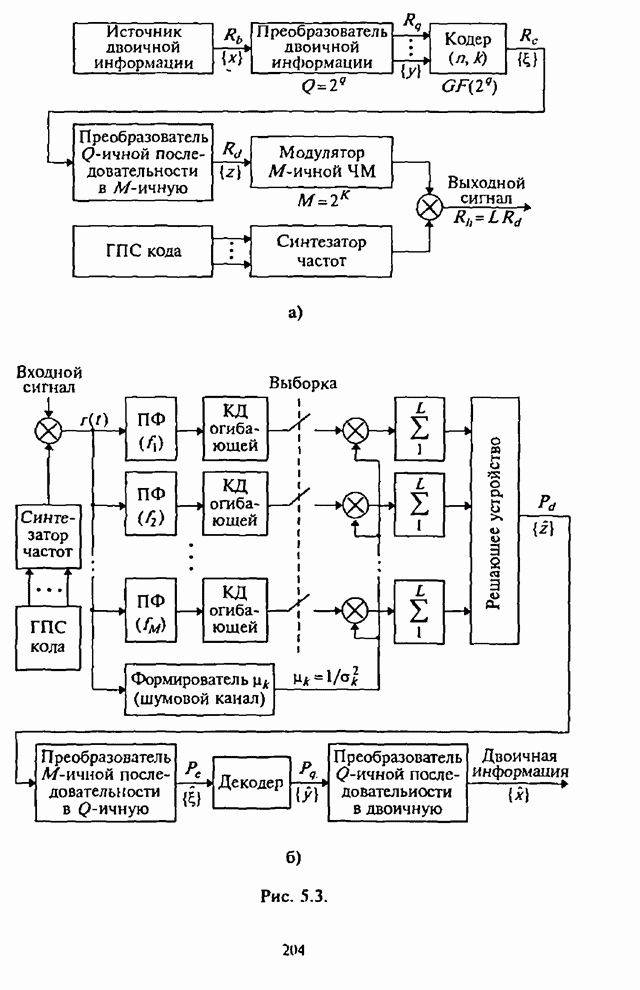
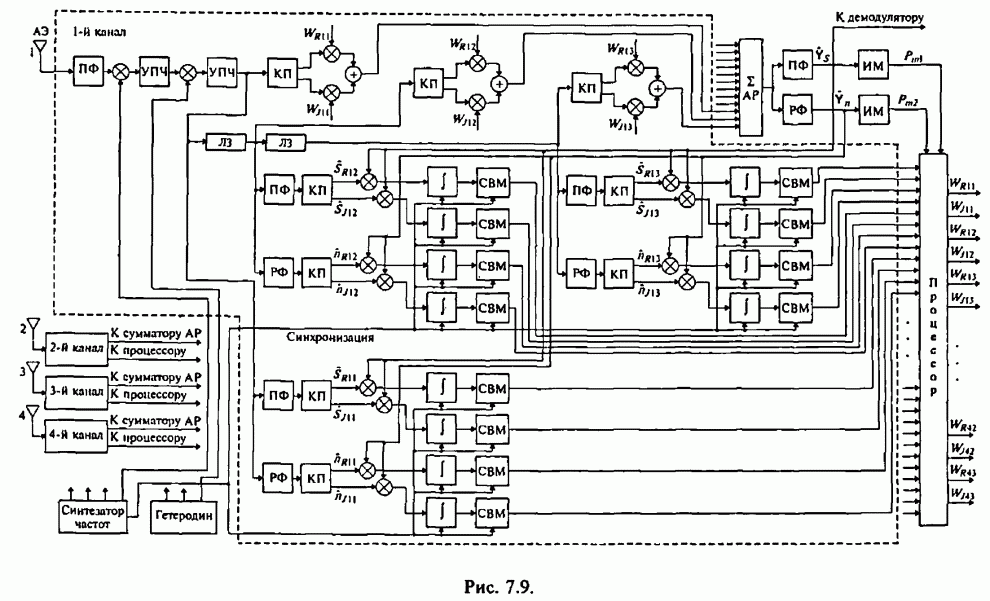
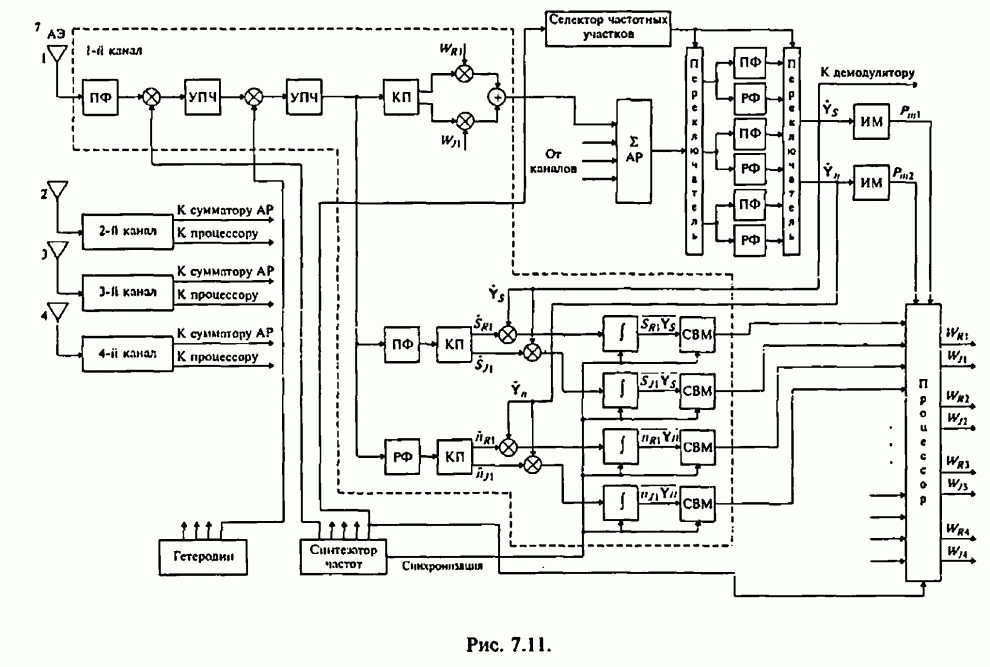
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
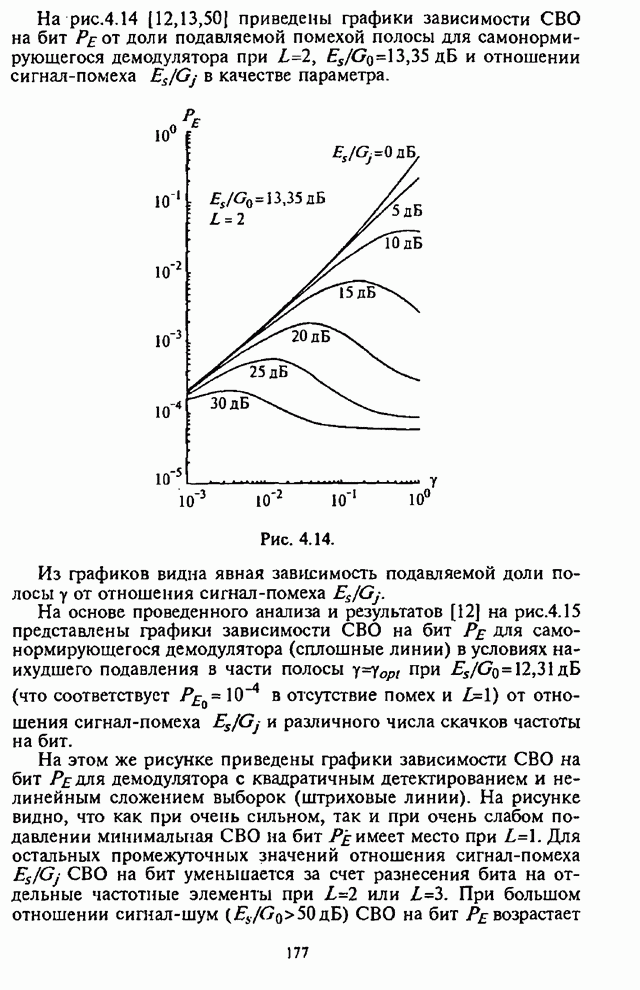
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
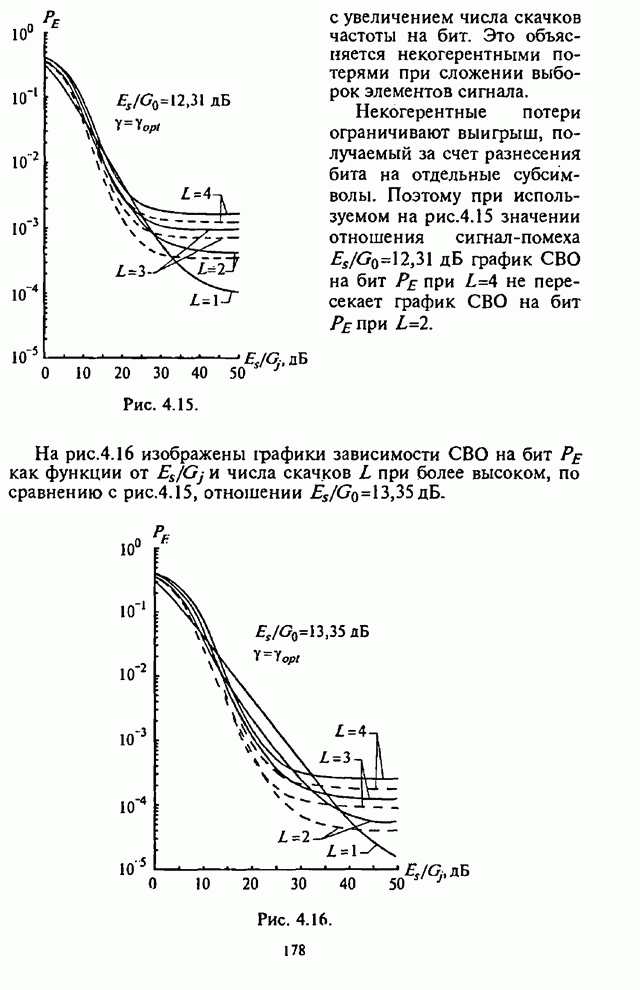
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
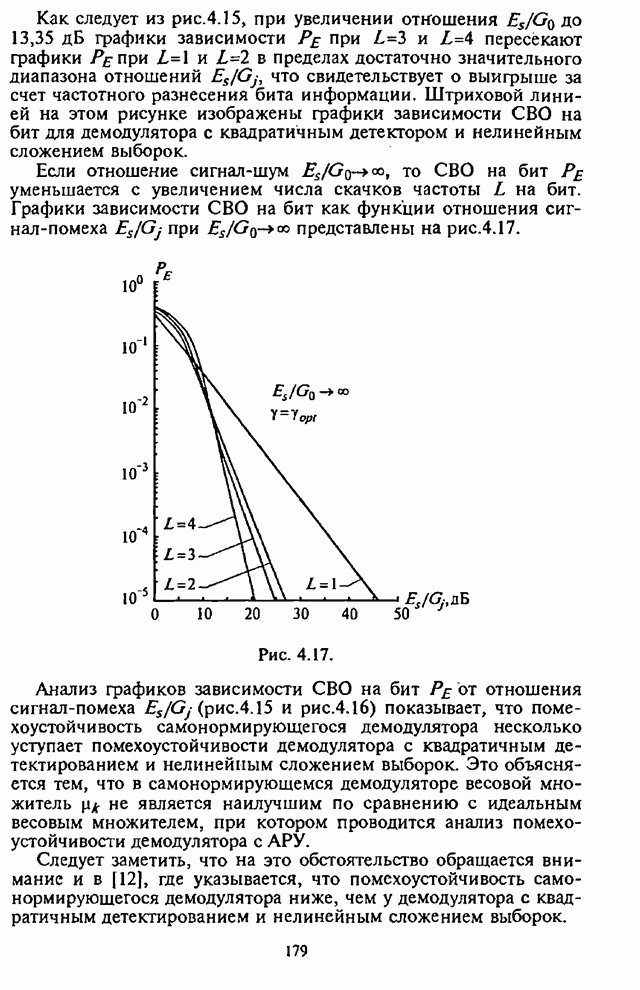
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
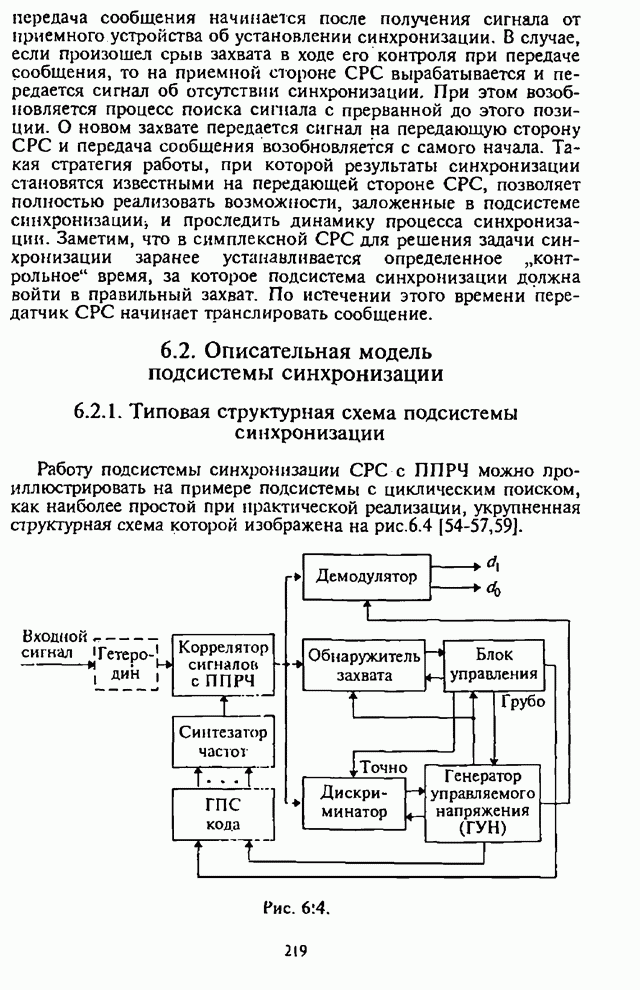
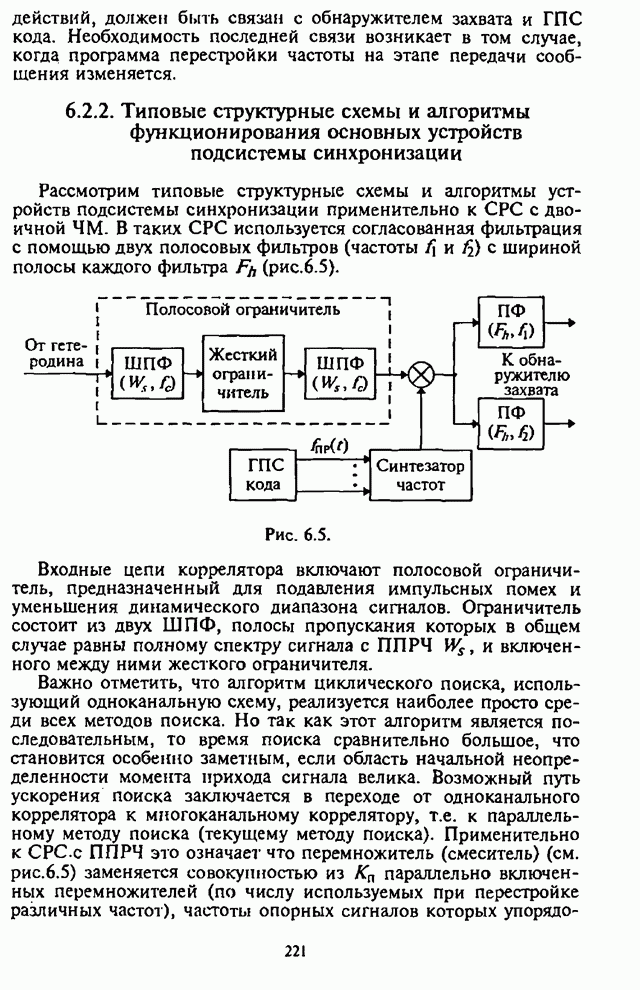
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
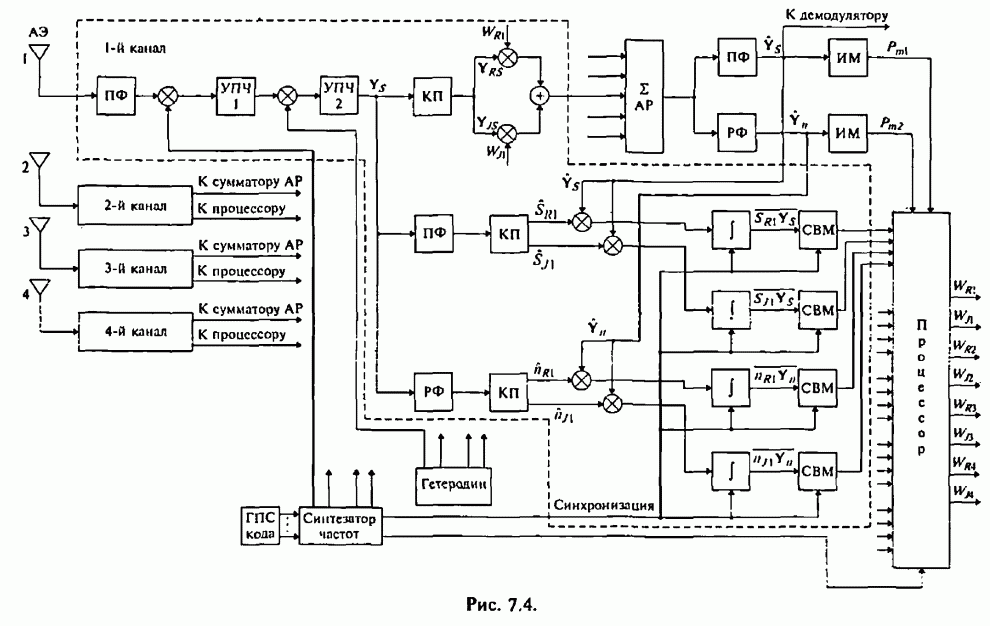
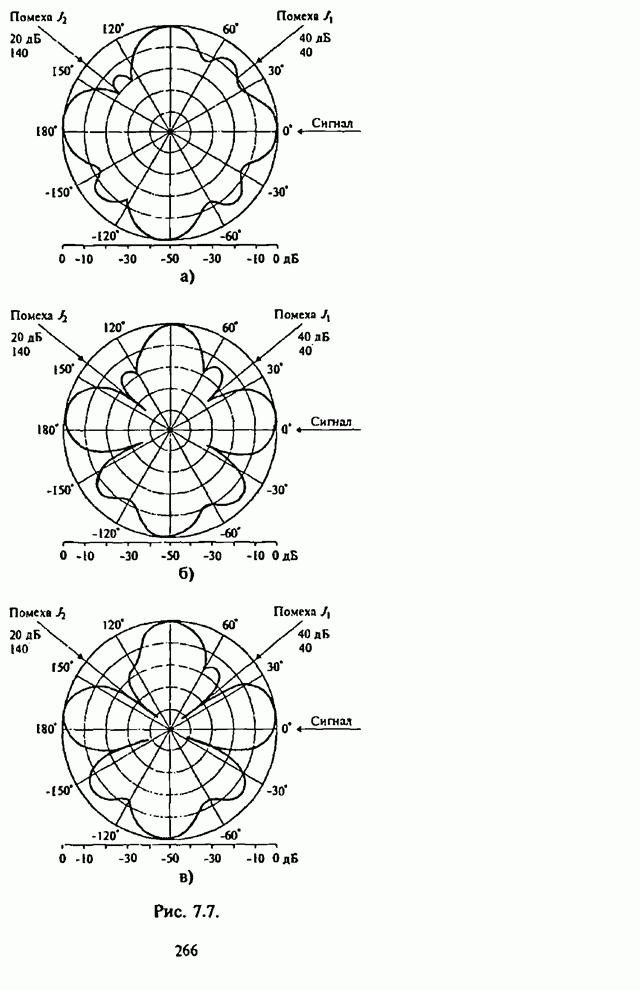
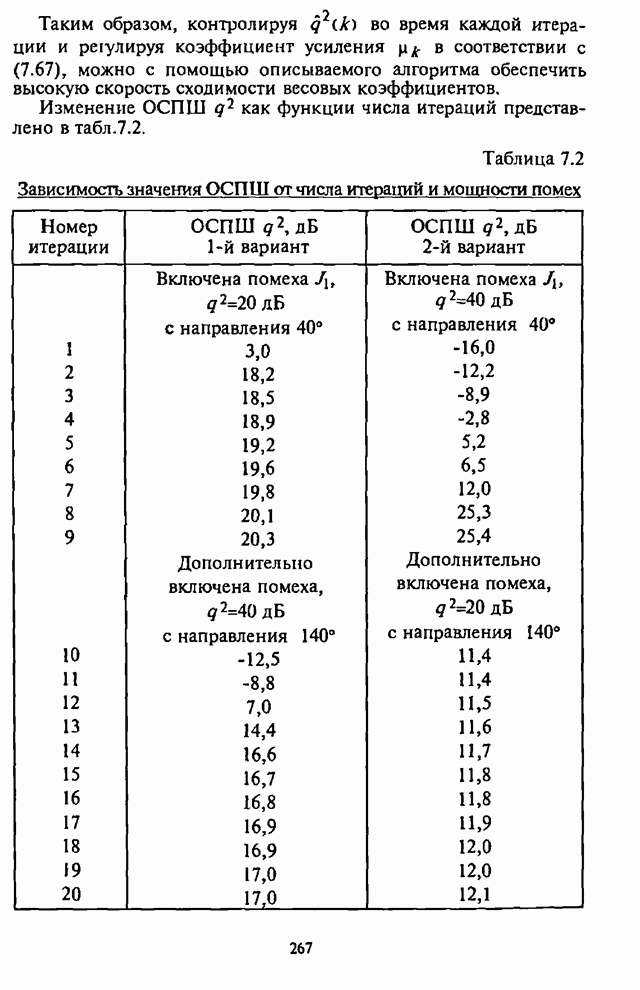
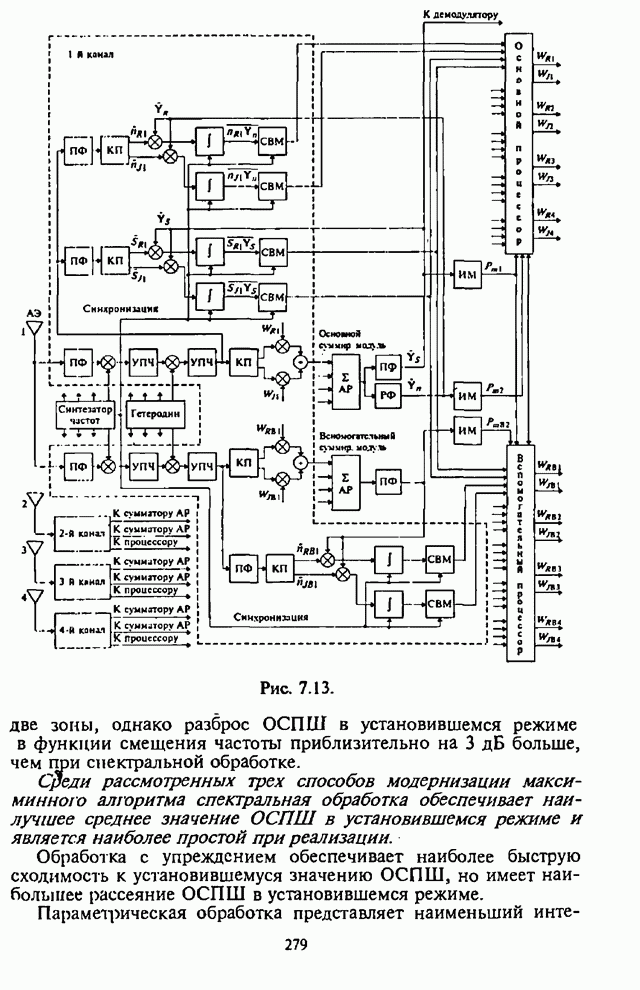
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
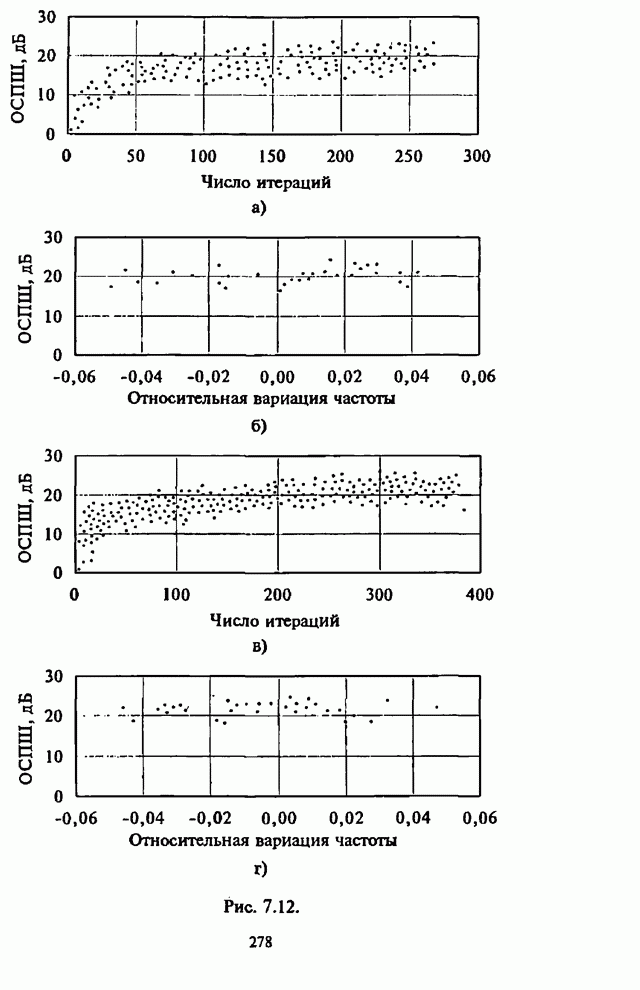
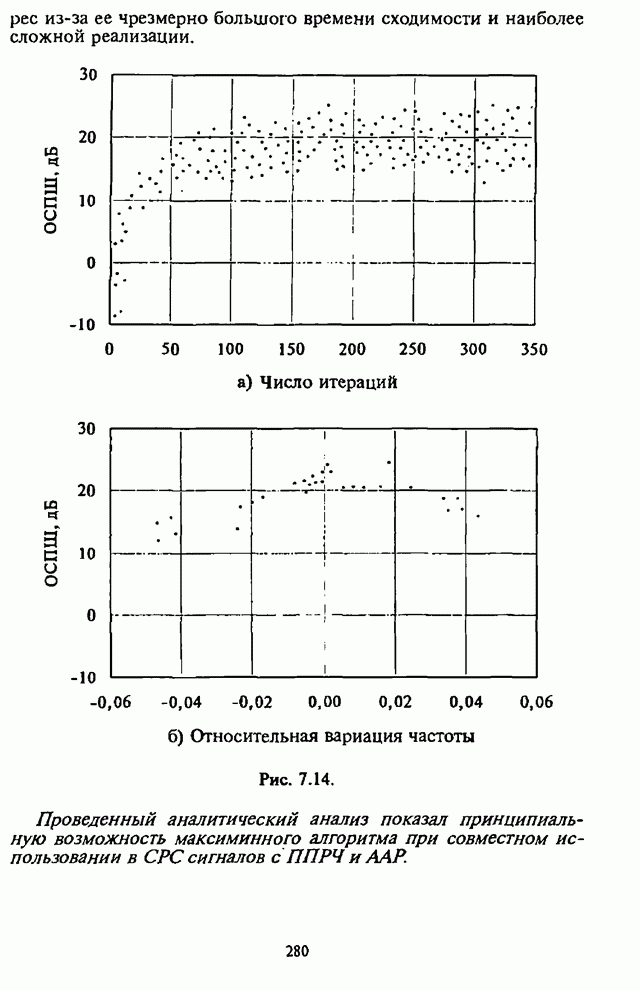
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
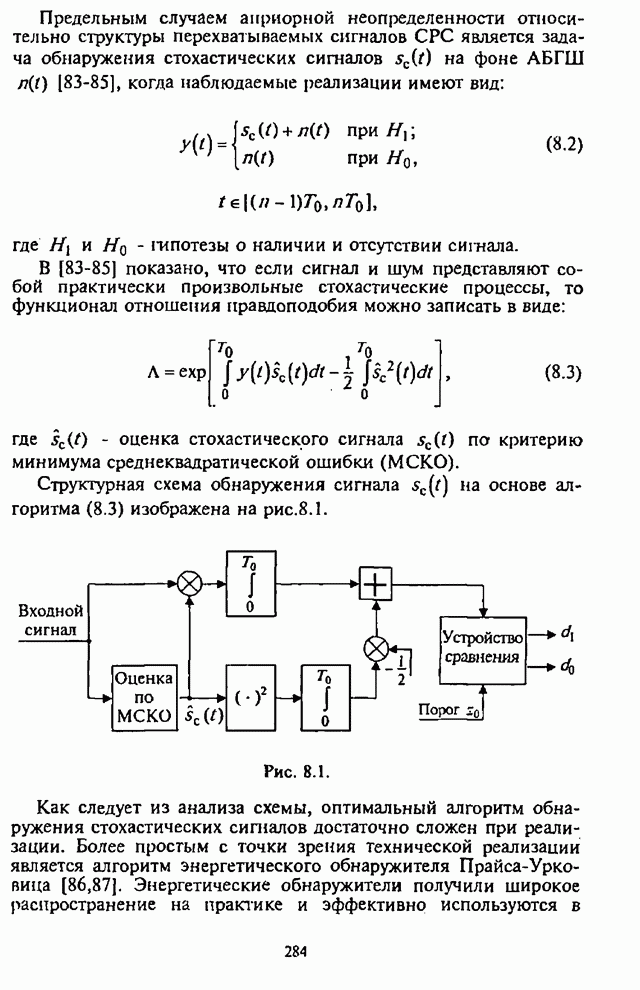
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
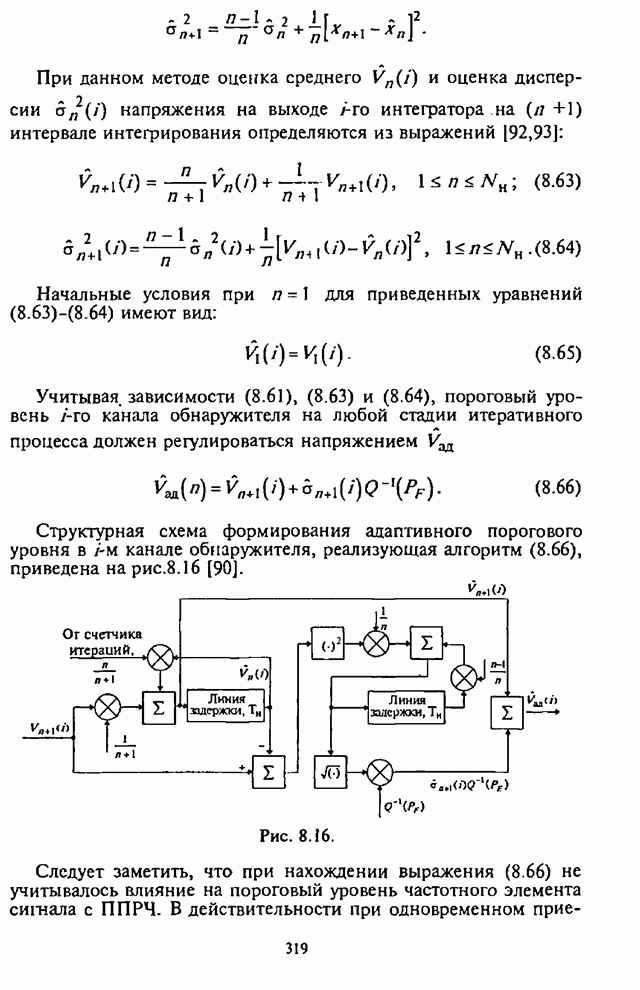
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
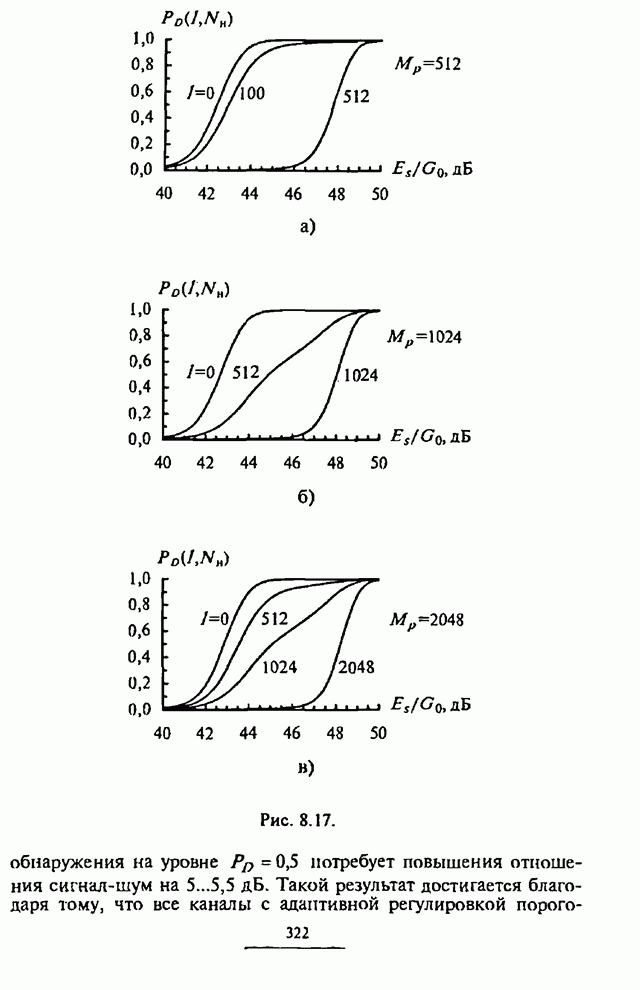
- 8.4.3. Вероятность обнаружения
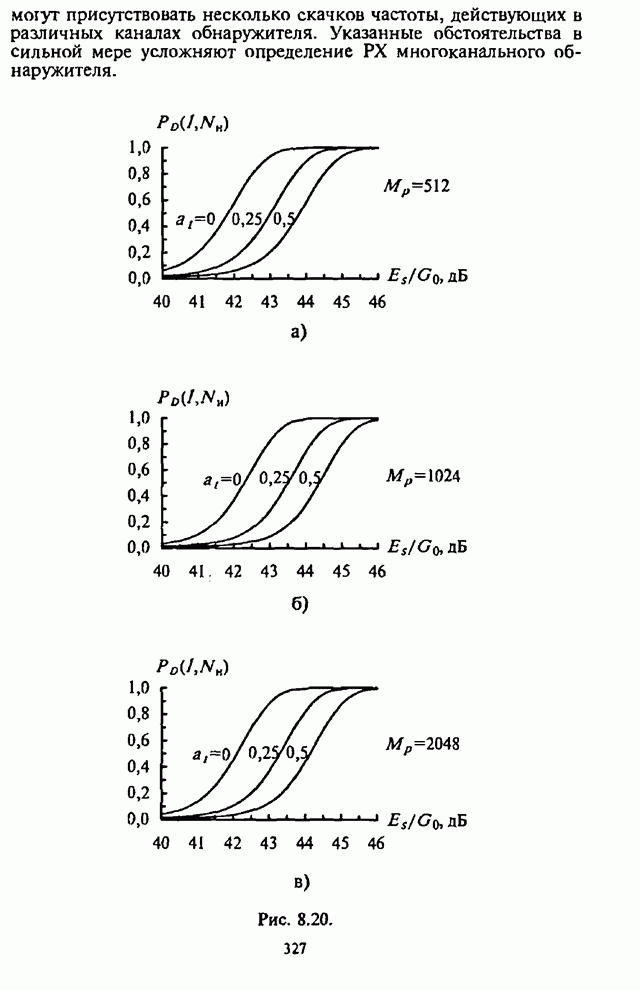
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
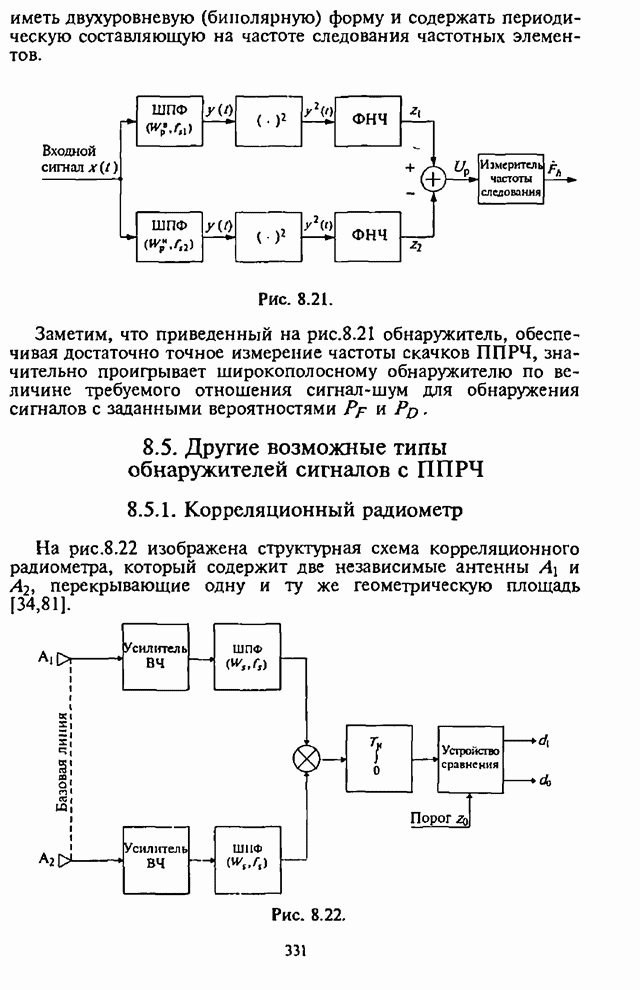
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
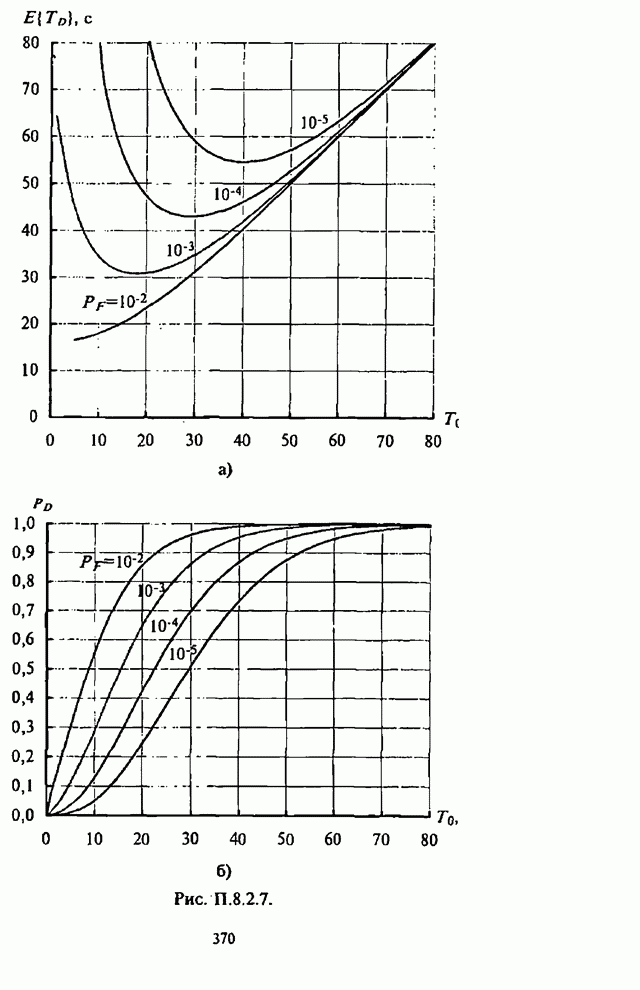
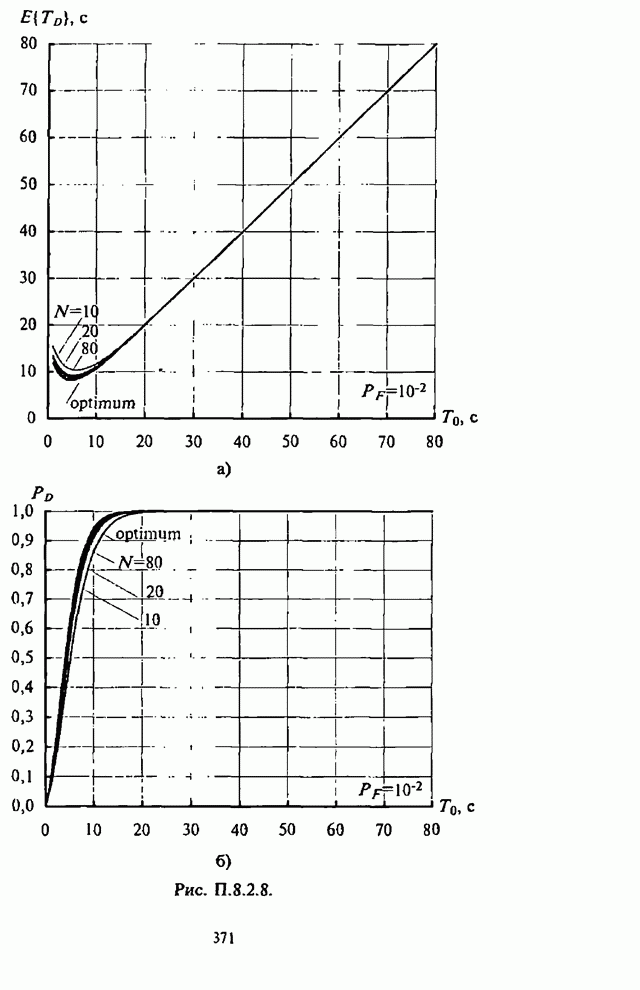
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ