| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П.8.1.2. Представление степенными рядами
Для
вычисления ![]() и
и
![]() - функций
применяются разложения в степенные ряды. Наиболее известны два варианта
разложения в степенные ряды функции
- функций
применяются разложения в степенные ряды. Наиболее известны два варианта
разложения в степенные ряды функции ![]() и два варианта - для функции
и два варианта - для функции ![]() [100]. Отметим, что
важно иметь отдельно выражения для
[100]. Отметим, что
важно иметь отдельно выражения для ![]() и при необходимости использовать именно
их, а не находить
и при необходимости использовать именно
их, а не находить ![]() и
затем вычитать ее из единицы, так как при этом можно уменьшить точность
вычисления. В [100] представлены следующие разложения:
и
затем вычитать ее из единицы, так как при этом можно уменьшить точность
вычисления. В [100] представлены следующие разложения:
 ; (П.8.1.17)
; (П.8.1.17)
 ; (П.8.1.18)
; (П.8.1.18)
 ; (П.8.1.19)
; (П.8.1.19)
 . (П.8.1.20)
. (П.8.1.20)
Основная
вычислительная сложность, связанная со степенным рядом, это исчезновение
значащих разрядов при вычислении ![]() или недостаточная точность, возникающая
при вычислении произведения большого числа на малое. Поэтому для вычисления
или недостаточная точность, возникающая
при вычислении произведения большого числа на малое. Поэтому для вычисления ![]() -го члена ряда
целесообразно использовать тождество
-го члена ряда
целесообразно использовать тождество
![]() , (П.8.1.21)
, (П.8.1.21)
а
![]() вычислять
приближенно по формулам, аналогичным формулам Стирлинга
вычислять
приближенно по формулам, аналогичным формулам Стирлинга
![]() , (П.8.1.22)
, (П.8.1.22)
где
![]() представляется
в виде непрерывной дроби следующим образом
представляется
в виде непрерывной дроби следующим образом
![]() .
.
Ошибка
округления при этом не превышает ![]() . Для
. Для ![]() значение
значение ![]() можно получить обычным способом.
можно получить обычным способом.
Теоретически
можно использовать любую формулу (П.8.1.17)-(П.8.1.20), однако на практике они
не всегда дают точный результат из-за потери значащих цифр при малых значениях
членов ряда. Поэтому, чтобы выбрать наиболее подходящее разложение, значения ![]() (или
(или ![]() ) оцениваются с помощью
границы Чернова
) оцениваются с помощью
границы Чернова
![]() , (П.8.1.23)
, (П.8.1.23)
где
 . (П.8.1.24)
. (П.8.1.24)
Граница Чернова удовлетворяет следующим неравенствам:
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
При
заданной величине абсолютной ошибки ![]()
![]() проверяется неравенство
проверяется неравенство ![]() . Если неравенство
выполняется, то
. Если неравенство
выполняется, то ![]() приравнивается
к нулю при
приравнивается
к нулю при ![]() ,
или единице при
,
или единице при ![]() .
Тем самым достигается требуемая точность без дополнительных вычислений. В
зависимости от того, где находится граница Чернова при данных значениях
.
Тем самым достигается требуемая точность без дополнительных вычислений. В
зависимости от того, где находится граница Чернова при данных значениях ![]() , выбирается та или
иная форма в разложении (П.8.1.17)-(П.8.1.20).
, выбирается та или
иная форма в разложении (П.8.1.17)-(П.8.1.20).
Ниже
приведена процедура выбора аппроксимирующих формул для ![]() [100]:
[100]:
1)
Если ![]() и
и ![]() , то
, то ![]() .
.
2)
Если ![]() и
и ![]() , то
, то ![]() .
.
3)
Если ![]() и
и ![]() , то рекомендуется
использовать (П.8.1.19).
, то рекомендуется
использовать (П.8.1.19).
4) В остальных случаях применять разложение (П.8.1.20).
При
расчете ![]() рекомендуется
следующая процедура выбора:
рекомендуется
следующая процедура выбора:
1)
Если ![]() и
и ![]() , то
, то ![]() .
.
2)
Если ![]() и
и ![]() , то
, то ![]() .
.
3)
Если ![]() и
и ![]() , то рекомендуется
использовать разложение (П.8.1.17);
, то рекомендуется
использовать разложение (П.8.1.17);
4) В остальных случаях используется разложение (П.8.1.18).
Рекуррентный алгоритм Макги. Представляя степенные ряды (П.8.1.17), (П.8.1.19) в виде:
![]() , (П.8.1.25)
, (П.8.1.25)
![]() . (П.8.1.26)
. (П.8.1.26)
Макги предложил рекуррентный алгоритм пересчета параметров по формулам [101]:
 (П.8.1.27)
(П.8.1.27)
при
начальных условиях ![]() .
.
Обозначим
через ![]() и
и ![]() частичные суммы рядов
(П.8.1.25) и (П.8.1.26) соответственно, а через
частичные суммы рядов
(П.8.1.25) и (П.8.1.26) соответственно, а через ![]() - требуемую относительную ошибку
вычисления
- требуемую относительную ошибку
вычисления ![]() и
и
![]() . С учетом
введенных обозначений можно сформулировать условия окончания итерационного
процесса.
. С учетом
введенных обозначений можно сформулировать условия окончания итерационного
процесса.
Процесс вычисления продолжается до тех пор, пока не будут выполнены условия
![]() (П.8.1.28)
(П.8.1.28)
для
вычисления ![]() и
и
![]() (П.8.1.29)
(П.8.1.29)
для
вычисления ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
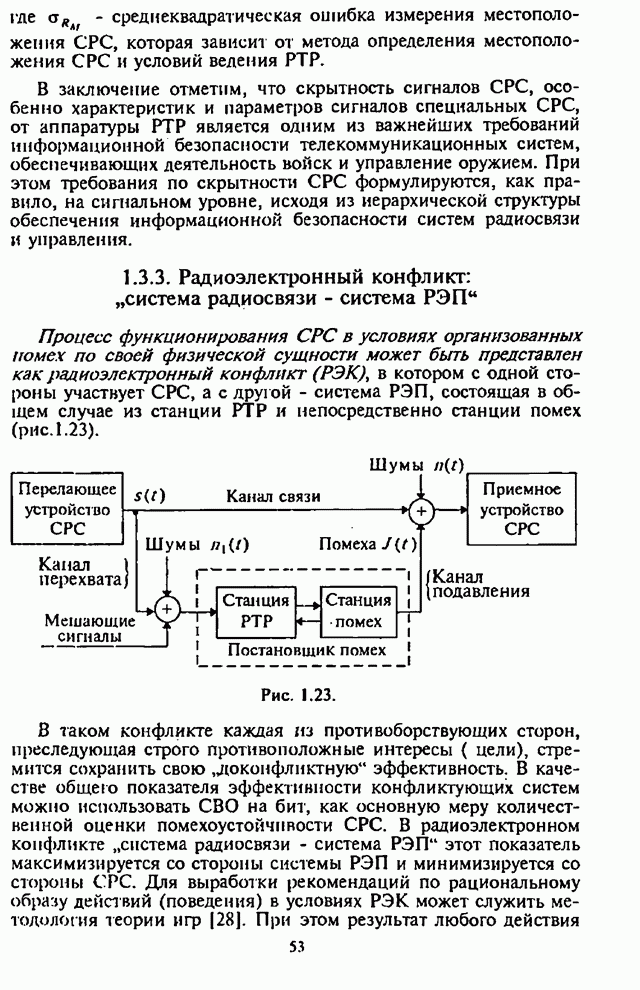
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
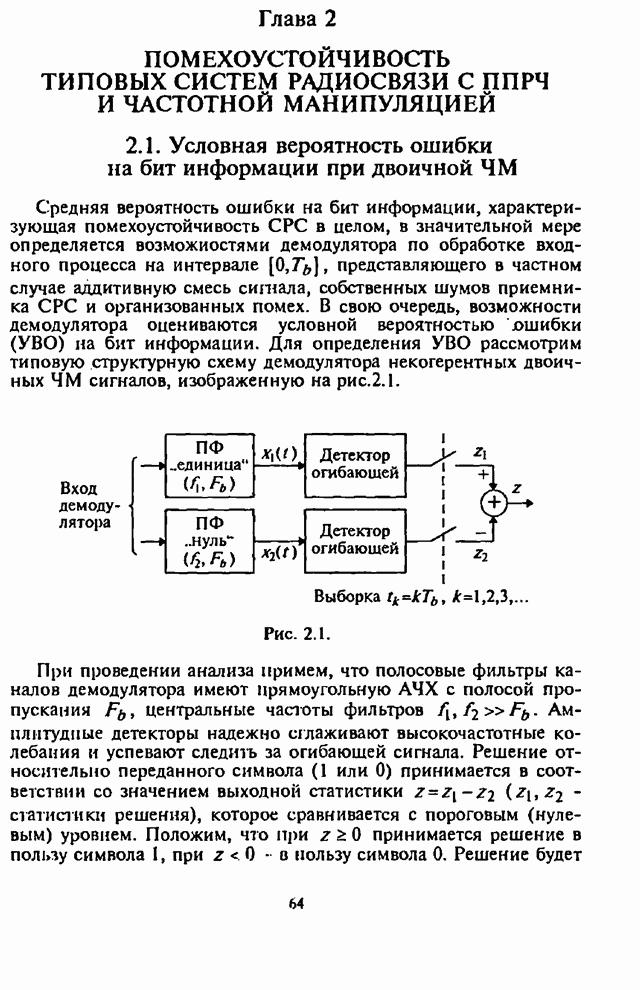
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ