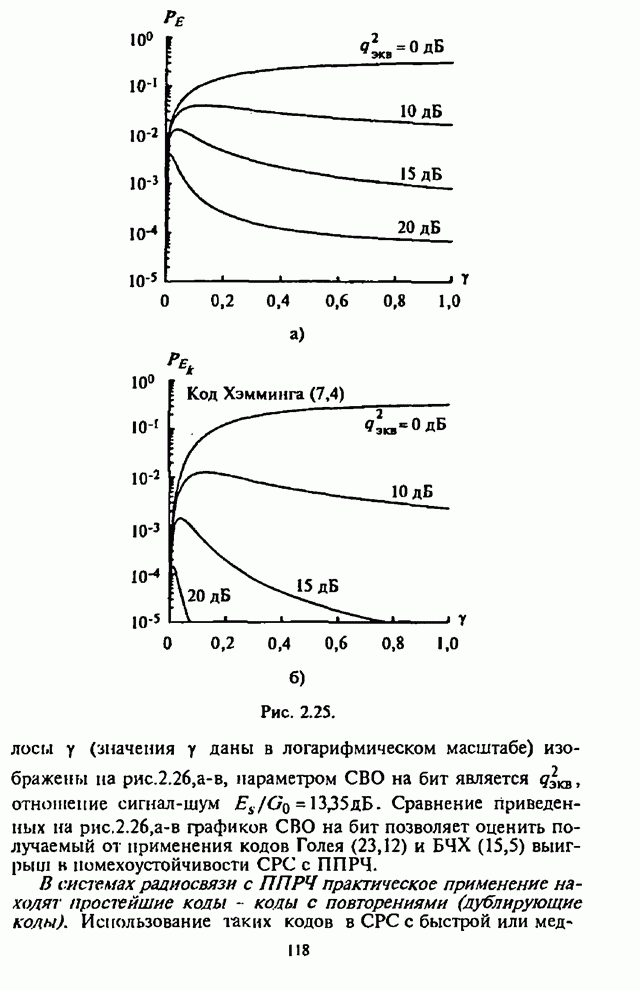
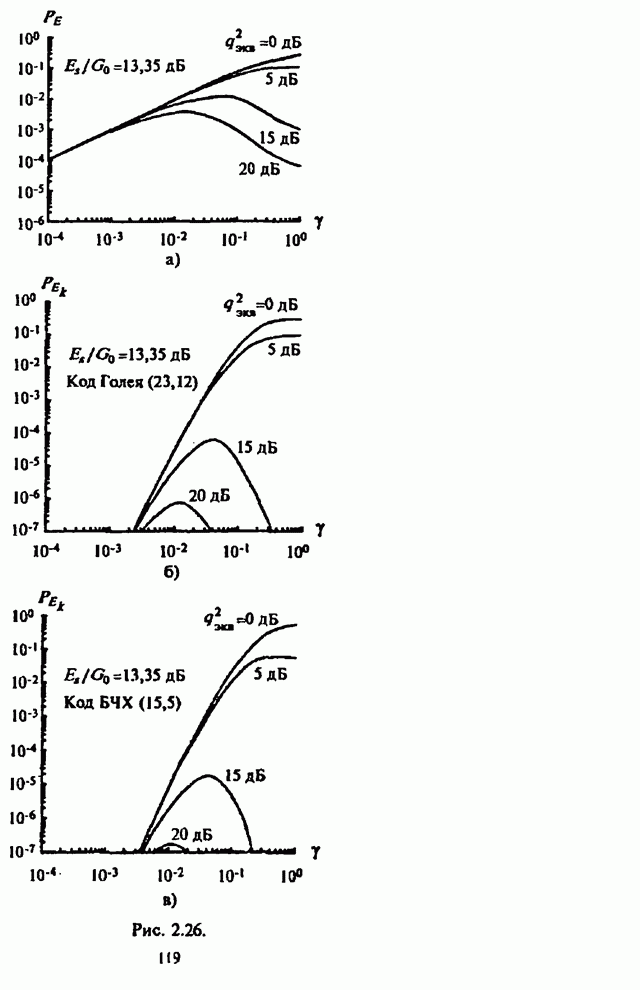
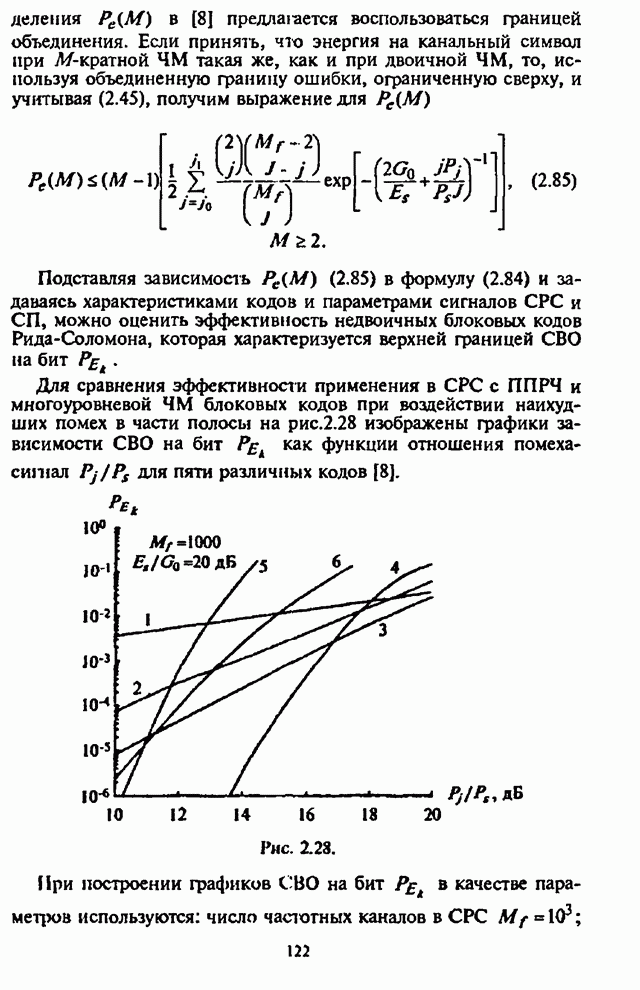
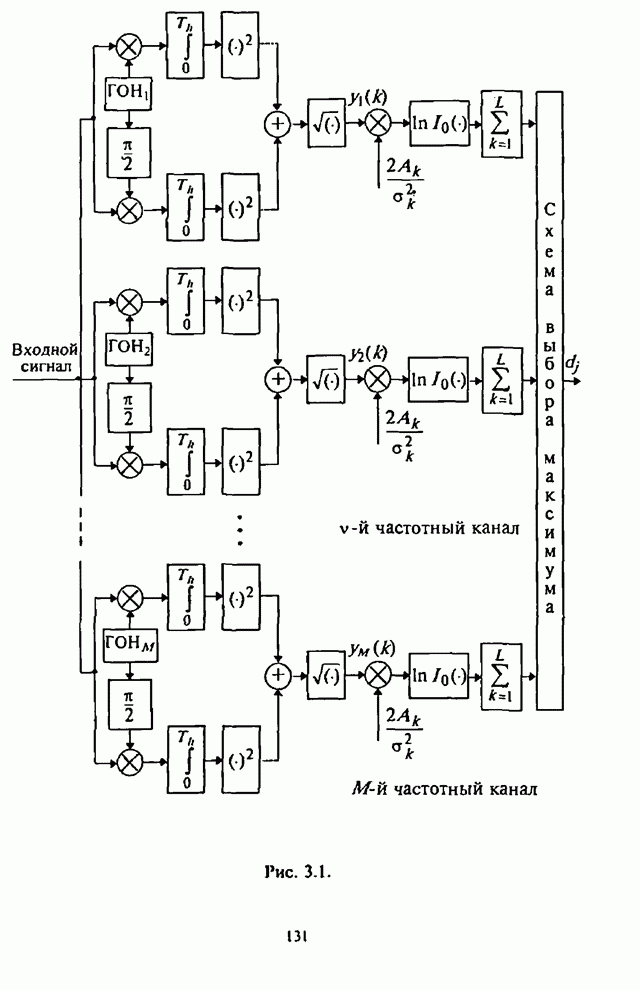
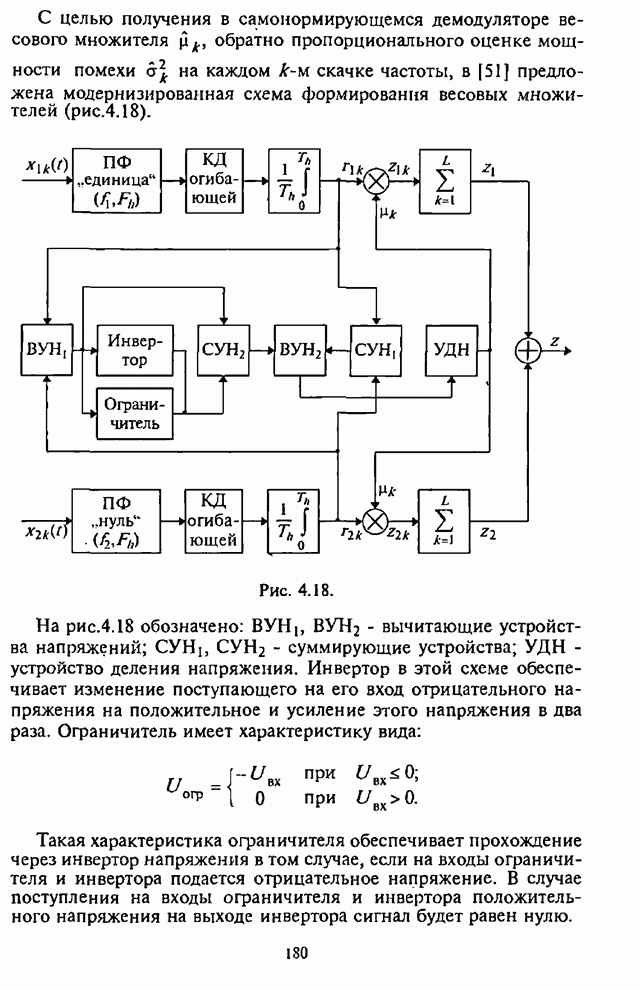
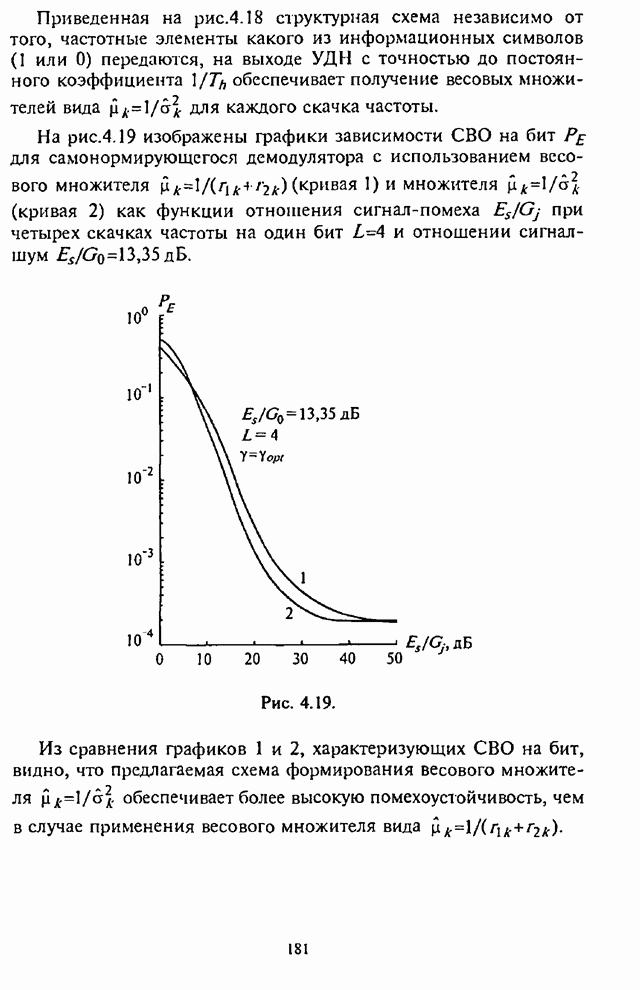
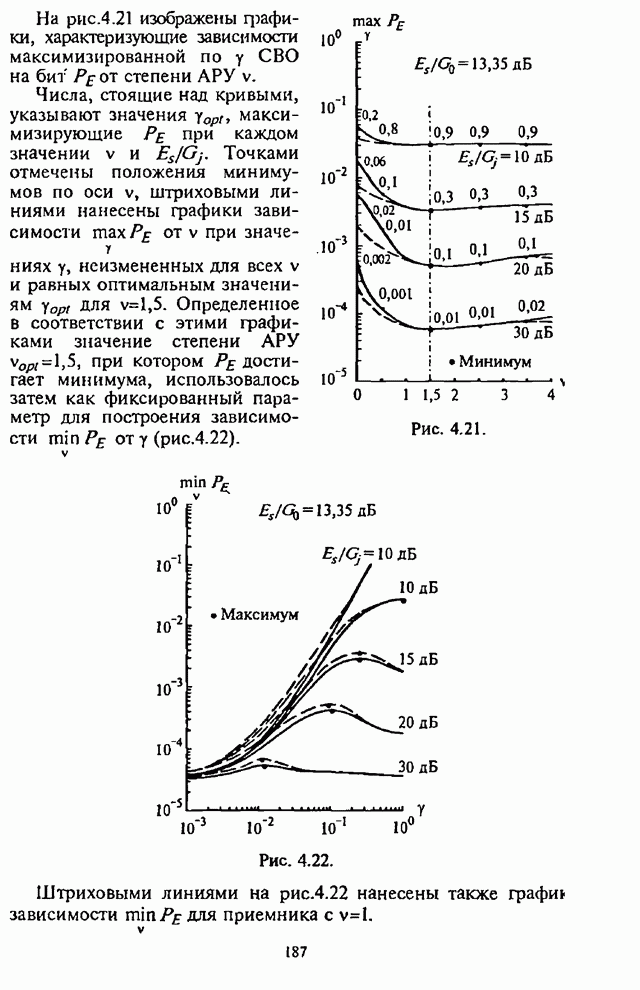
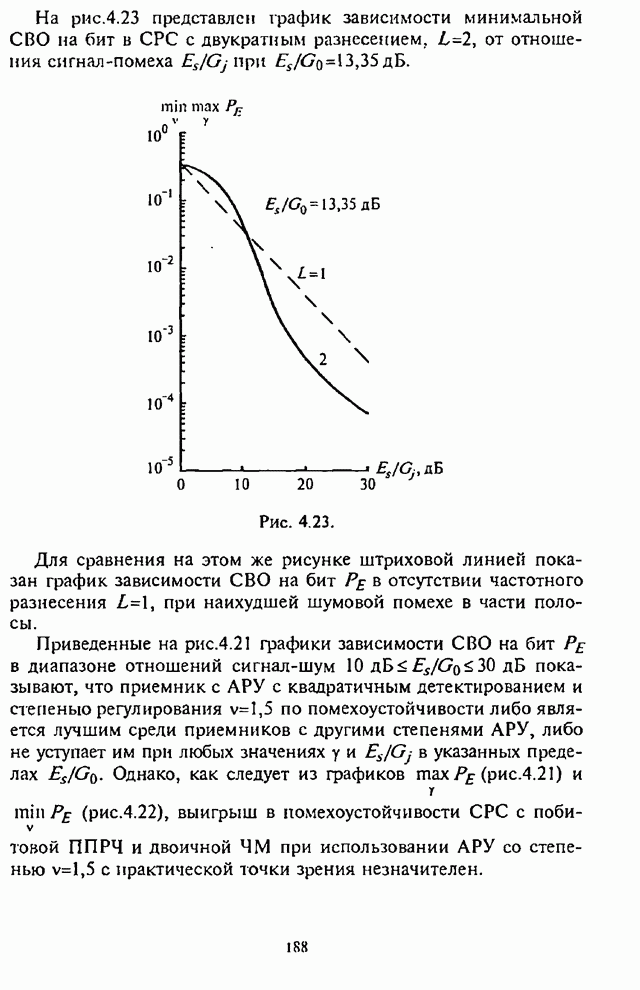
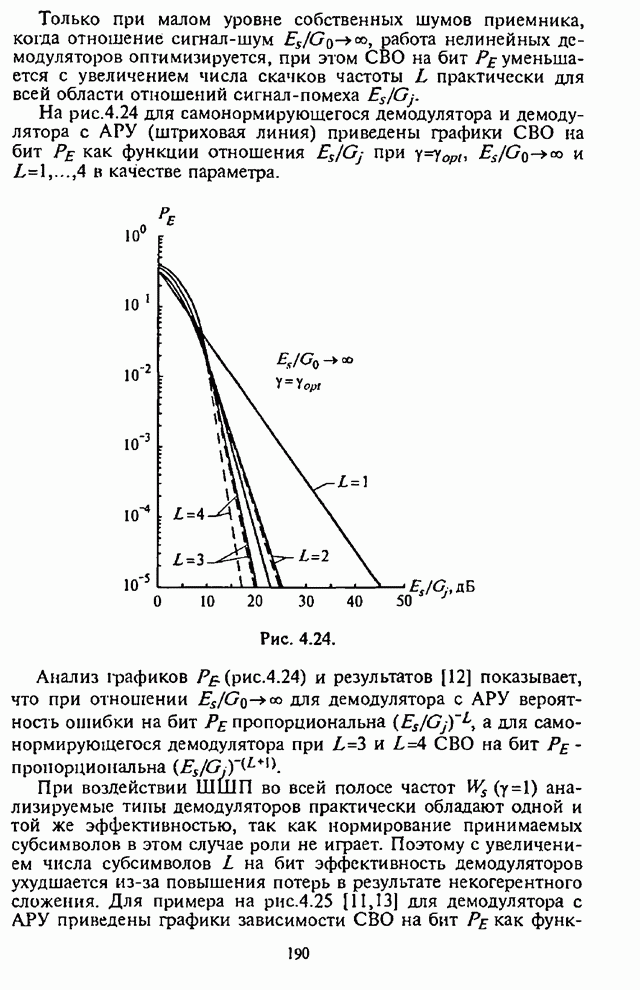
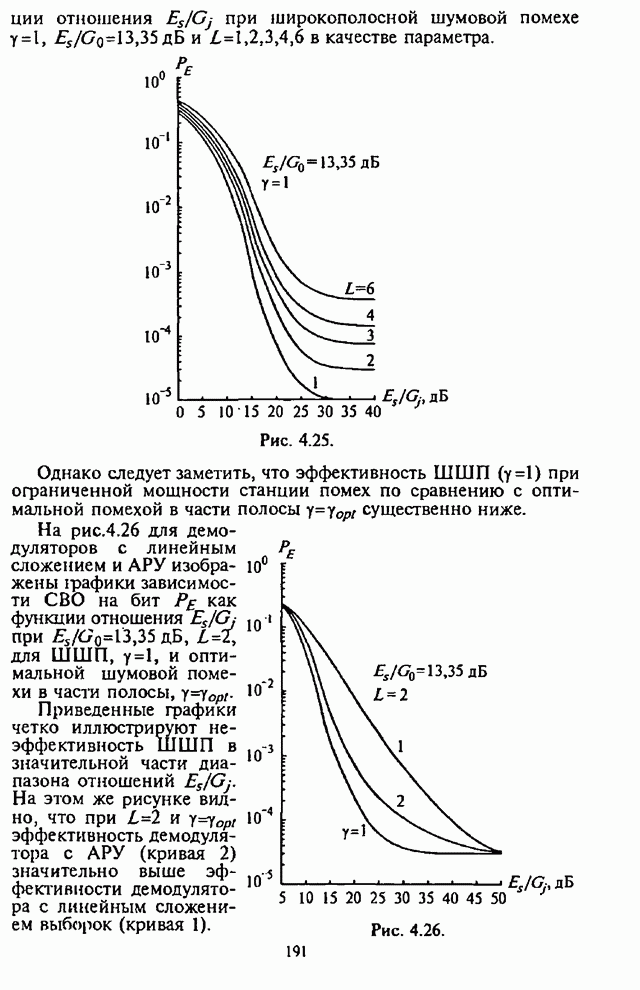
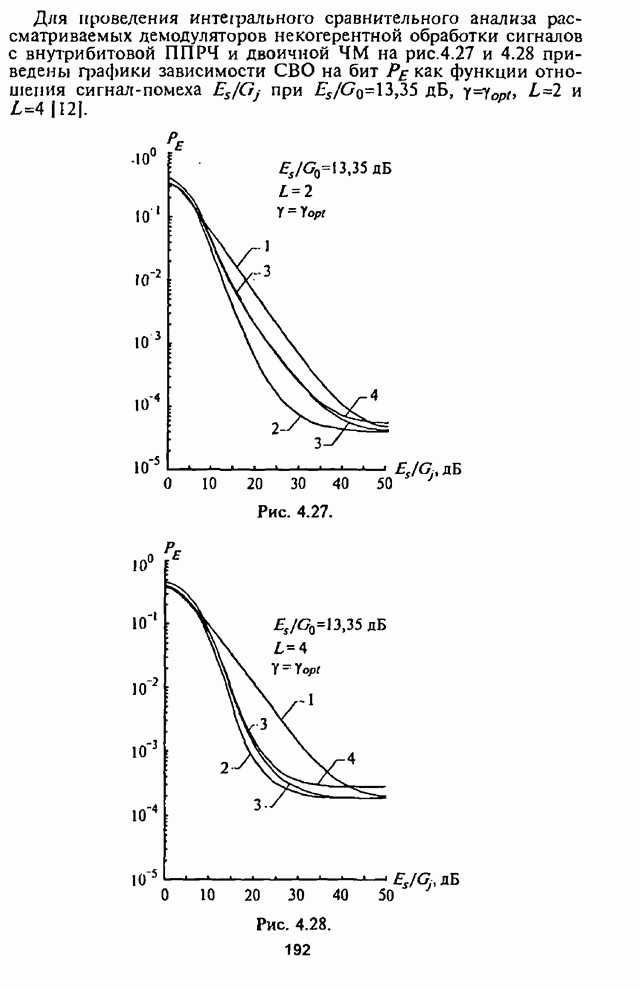
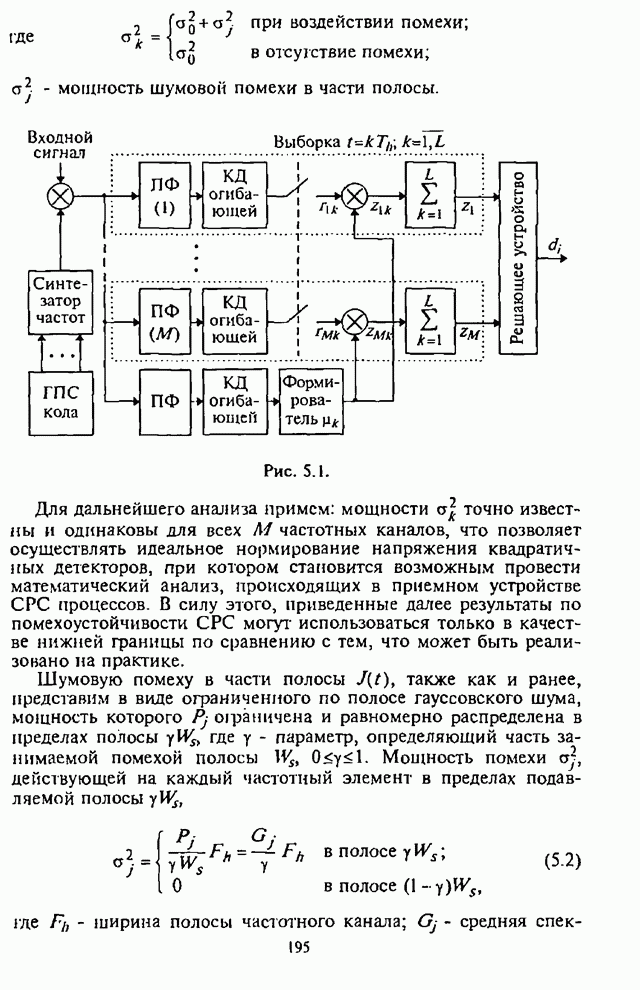
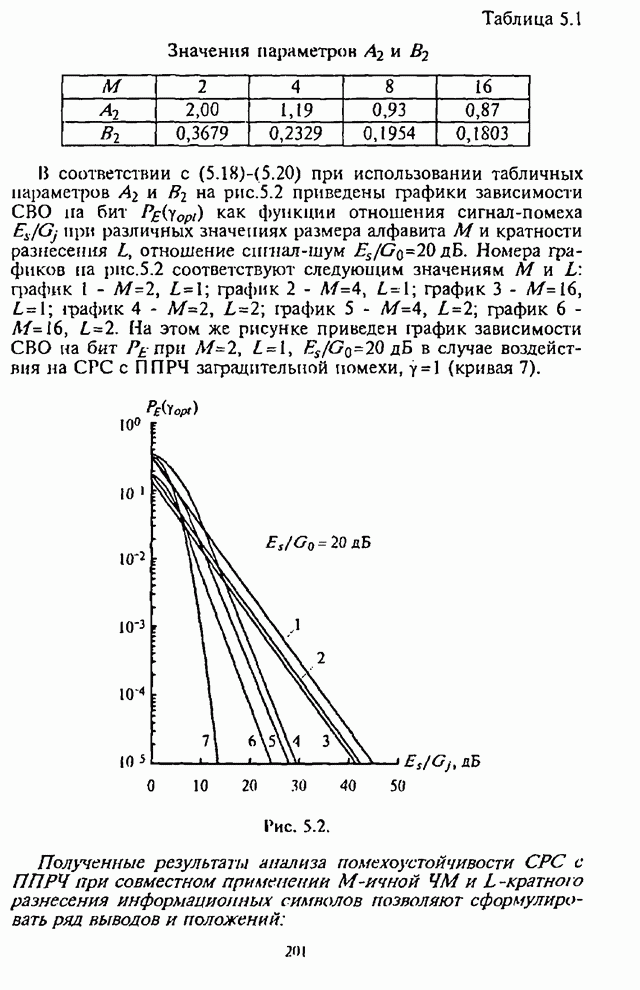
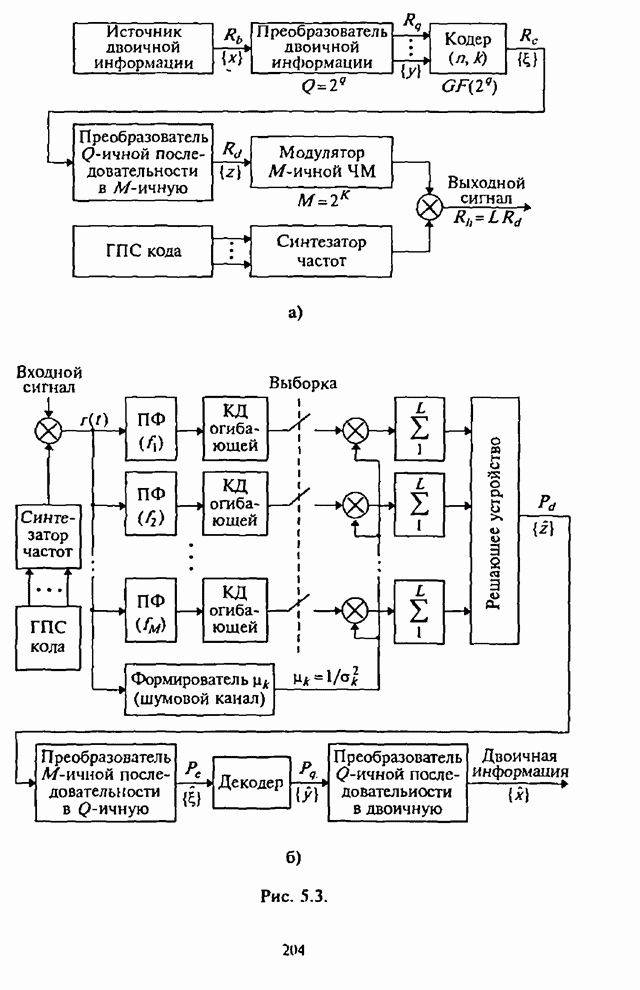
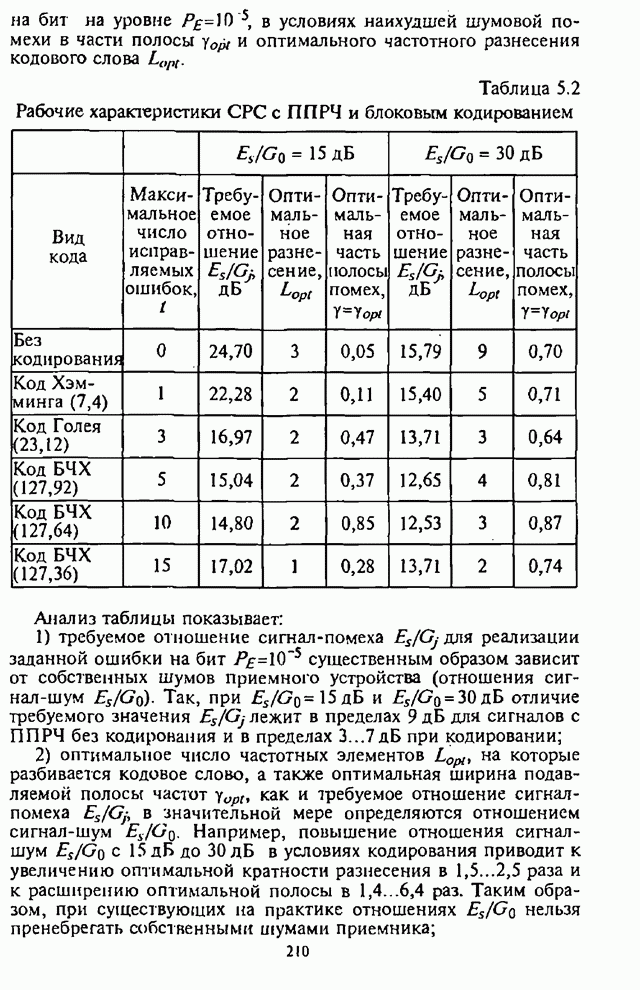
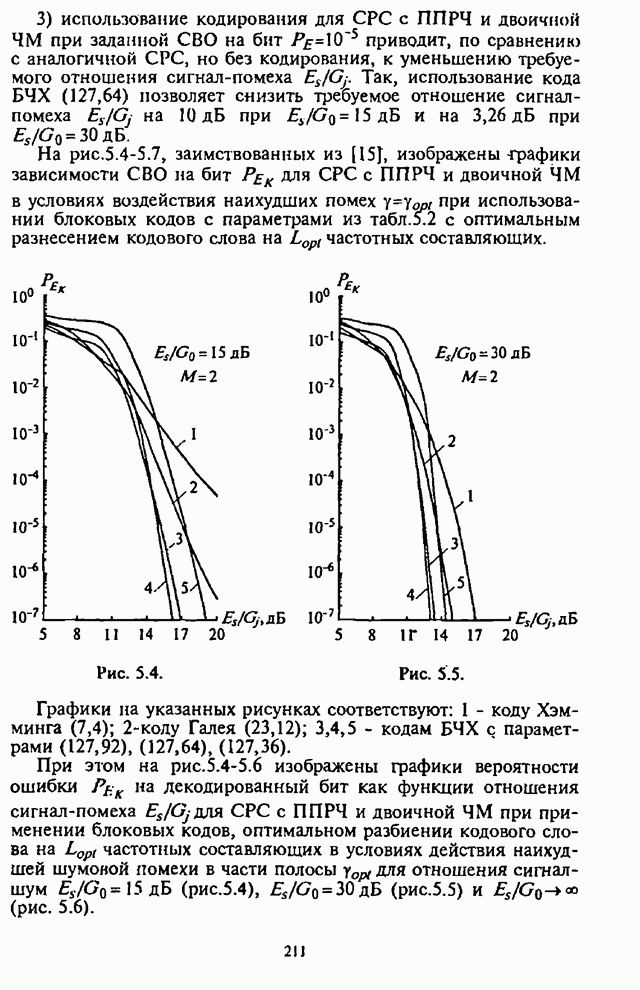
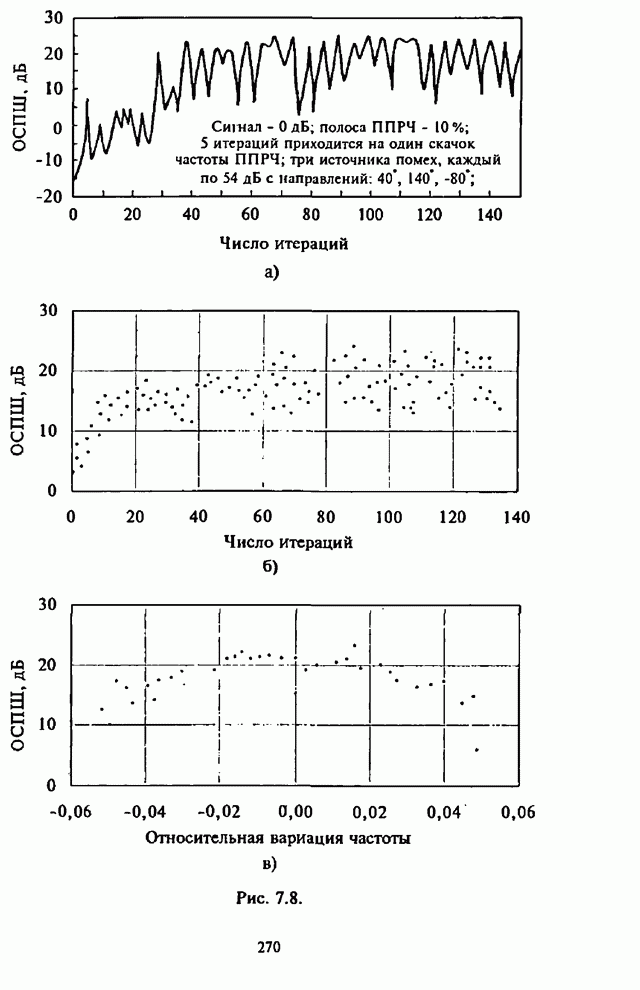
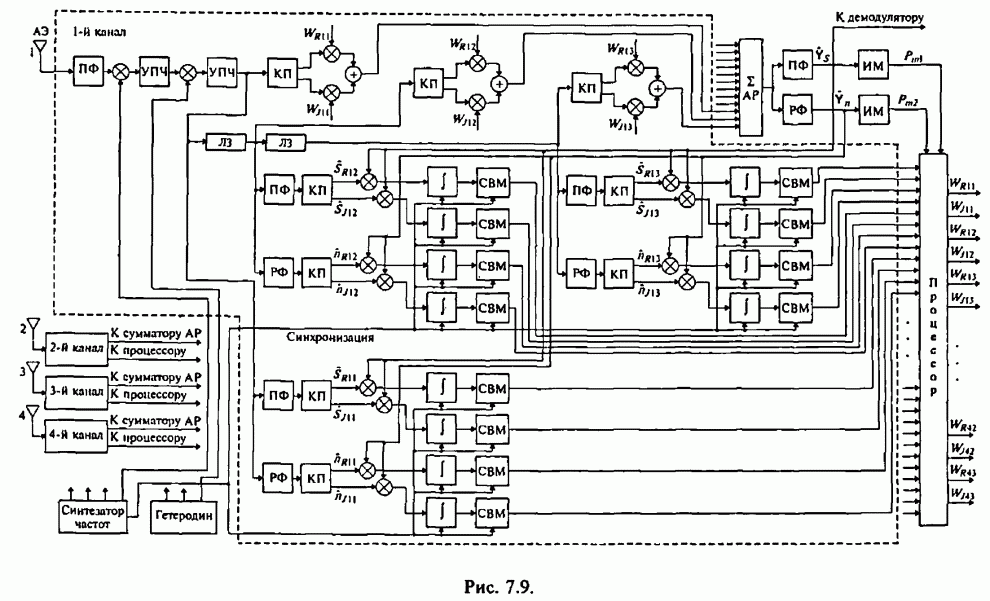
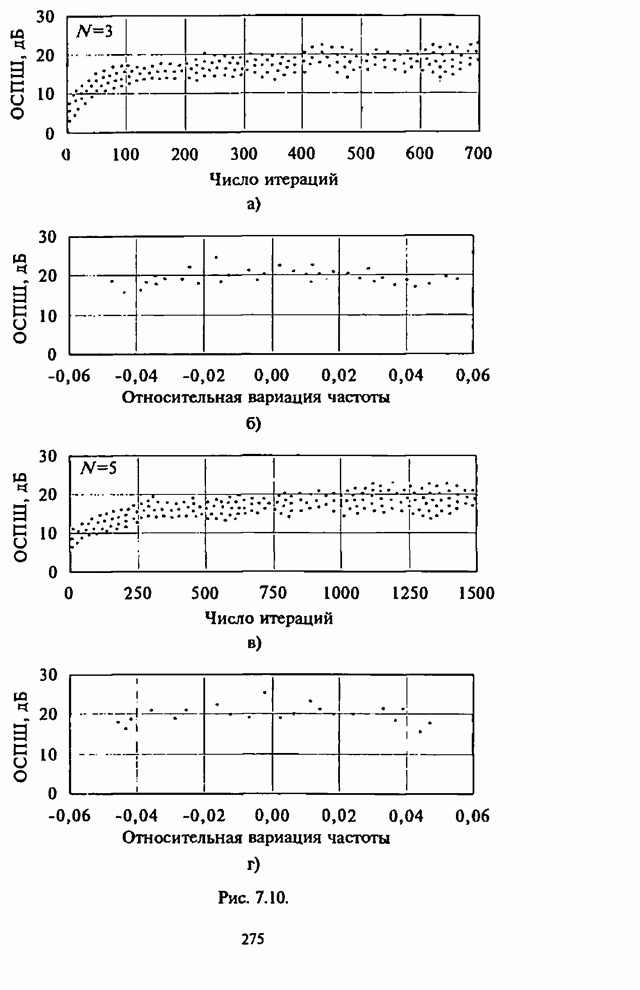
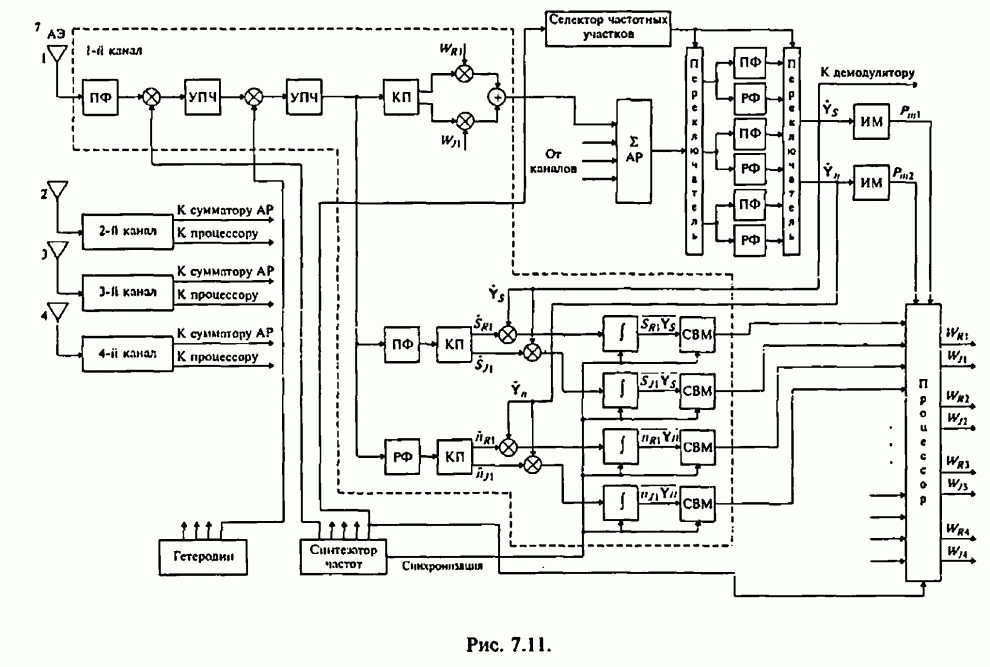
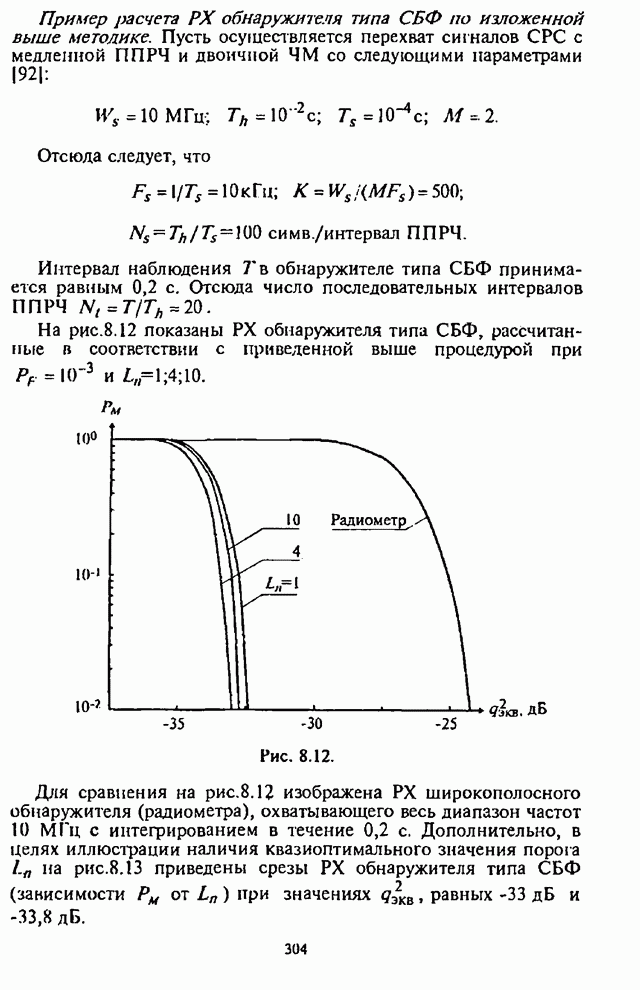
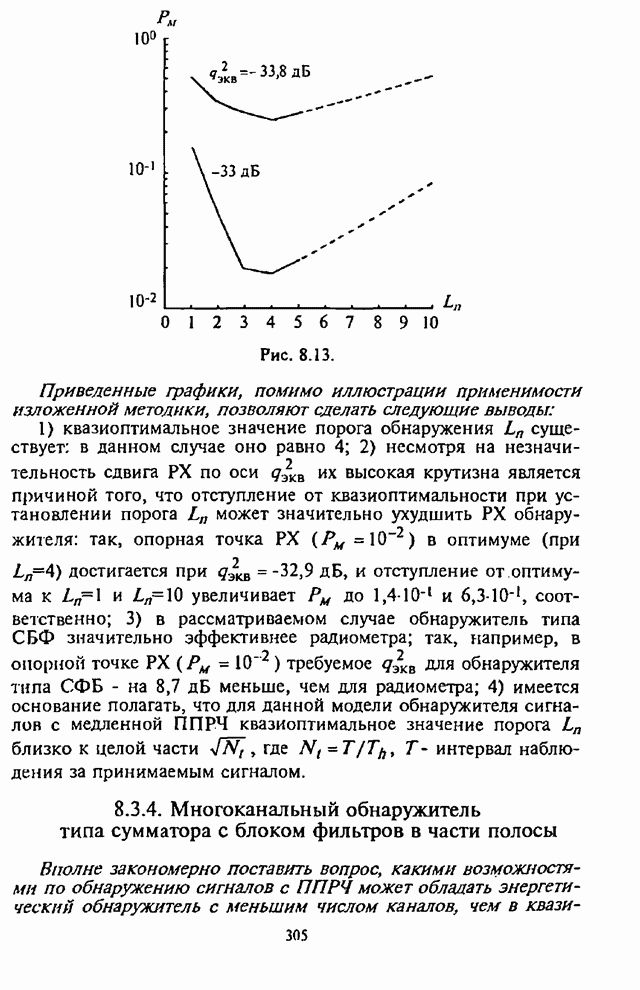
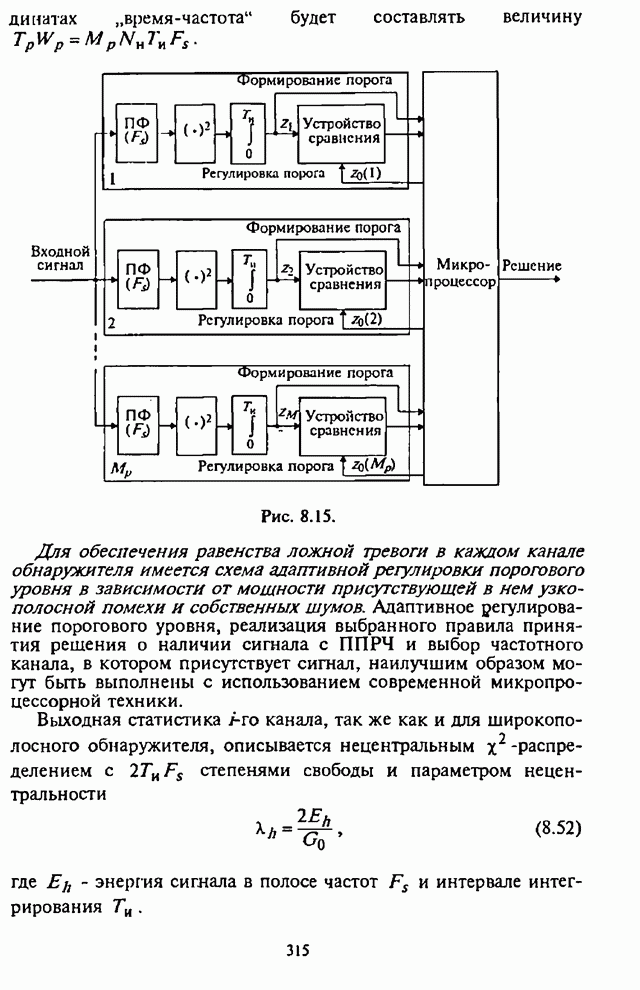
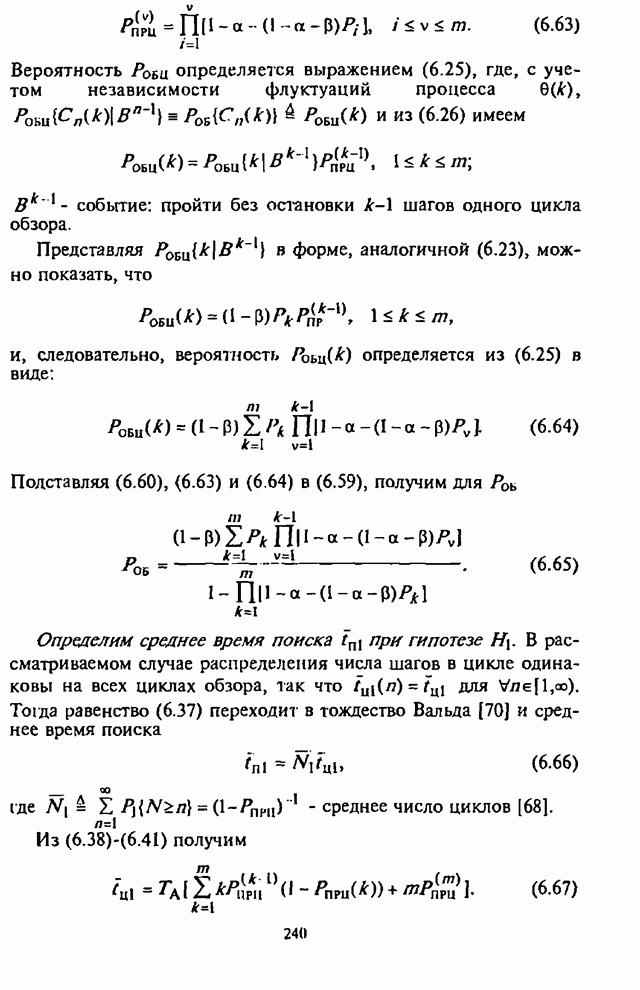| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П.8.1.3. Представление в виде рядов Неймана
Следуя
[102], примем за основу вычислительного алгоритма представление обобщенной ![]() -функции в виде ряда
Неймана (П.8.1.15), (П.8.1.16). Суть вычислительного метода заключается в
вычислении
-функции в виде ряда
Неймана (П.8.1.15), (П.8.1.16). Суть вычислительного метода заключается в
вычислении ![]() для
для
![]() и
и ![]() для
для ![]() посредством рекурсии модифицированной
функции Бесселя, применяемой в обратном порядке.
посредством рекурсии модифицированной
функции Бесселя, применяемой в обратном порядке.
При выводе алгоритма в [102] используется более общее разложение в ряд Неймана
![]() . (П.8.1.30)
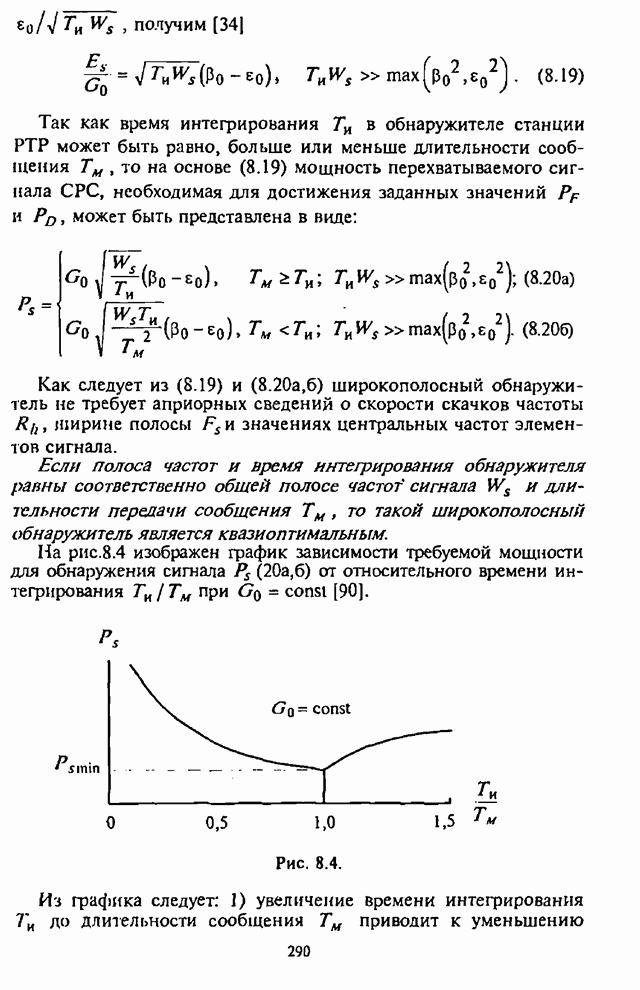
. (П.8.1.30)
Функции
данного вида образуют широкий класс, включающий в себя и ![]() ,
, ![]() при
при ![]() , а также разложение единицы
, а также разложение единицы
![]() . (П.8.1.31)
. (П.8.1.31)
Эти разложения вычисляются с помощью рекурсии бесселевых функций в обратном порядке
![]() , (П.8.1.32)
, (П.8.1.32)
начиная
с некоторого большого ![]() , при предположениях
, при предположениях ![]() и
и ![]() . Постоянная
. Постоянная ![]() находится из условия разложения в ряд
Неймана единицы (П.8.1.31). Возникающая ошибка связана с двумя источниками -
ошибкой усечения бесконечного ряда и ошибкой от переходных процессов,
возникающей при вычислении функций Бесселя по рекуррентным формулам из-за
неточного задания начальных условий в обратной рекурсии. При этом, как показано
в [102], ошибка переходных процессов мала по сравнению с ошибкой из-за усечения
ряда Неймана.
находится из условия разложения в ряд
Неймана единицы (П.8.1.31). Возникающая ошибка связана с двумя источниками -
ошибкой усечения бесконечного ряда и ошибкой от переходных процессов,
возникающей при вычислении функций Бесселя по рекуррентным формулам из-за
неточного задания начальных условий в обратной рекурсии. При этом, как показано
в [102], ошибка переходных процессов мала по сравнению с ошибкой из-за усечения
ряда Неймана.
Обозначим
через ![]() и
и ![]() функции,
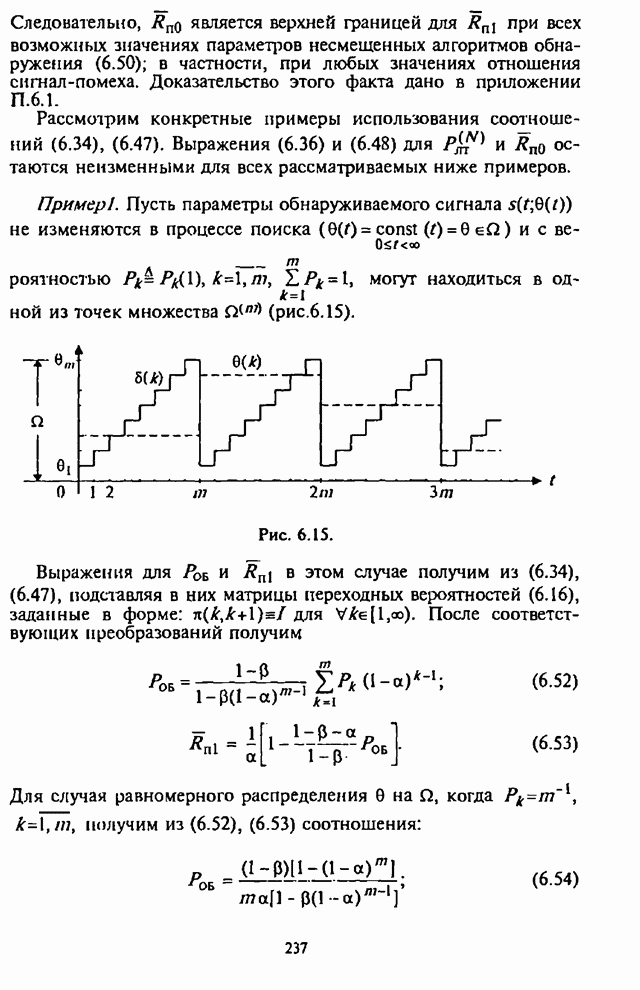
аппроксимирующие
функции,
аппроксимирующие ![]() и
и
![]() в результате
усечения рядов (П.8.1.30), (П.8.1.31), где вместо функций Бесселя используется
их аппроксимация, полученная в результате рекурсии в обратном порядке
в результате
усечения рядов (П.8.1.30), (П.8.1.31), где вместо функций Бесселя используется
их аппроксимация, полученная в результате рекурсии в обратном порядке
 (П.8.1.33)
(П.8.1.33)
С
учетом сделанных обозначений ![]() можно представить следующим образом
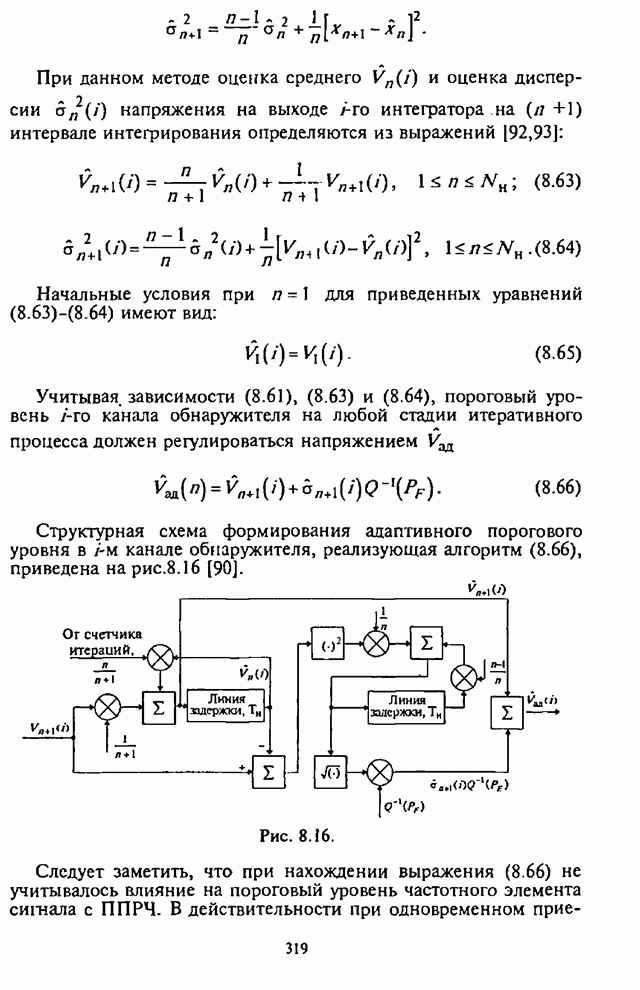
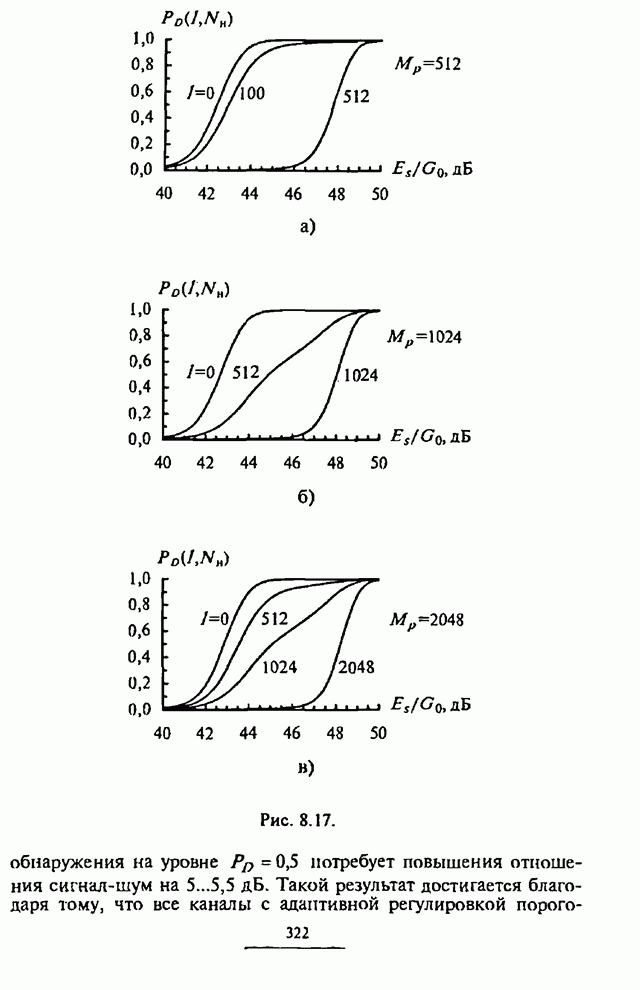
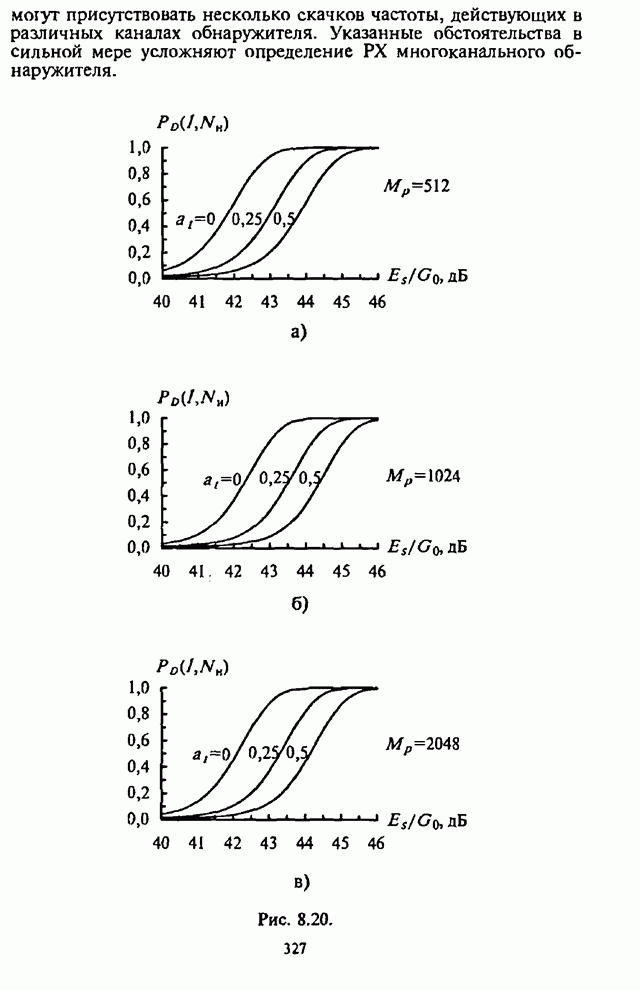
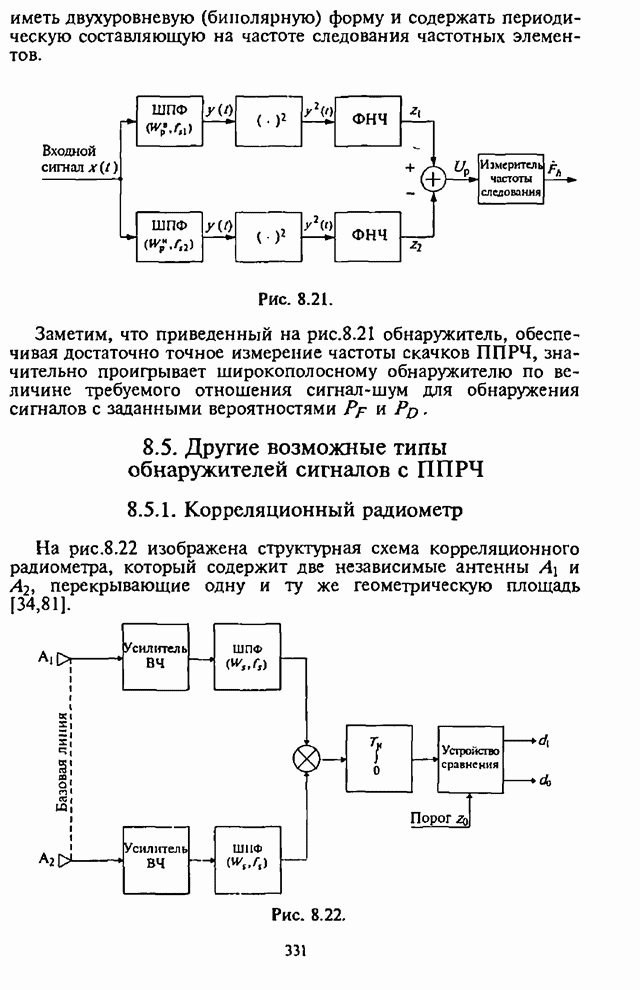
можно представить следующим образом
![]() . (П.8.1.34)
. (П.8.1.34)
Из (П.8.1.33) и (П.8.1.34) после преобразований получим рекуррентную формулу
![]() . (П.8.1.35)
. (П.8.1.35)
Формула
(П.8.34) позволяет рекуррентным образом получить ![]() при следующих начальных значениях
при следующих начальных значениях ![]() ,
, ![]() . Аналогичные рекуррентные
формулы можно получить и для
. Аналогичные рекуррентные
формулы можно получить и для ![]() . Поскольку
. Поскольку ![]() , то после
, то после ![]() итераций получим аппроксимацию для
итераций получим аппроксимацию для ![]() вида
вида
![]() . (П.8.1.36)
. (П.8.1.36)
Выражение
(П.8.1.34) применимо к ![]() в (П.8.1.15)
в (П.8.1.15) ![]() при подстановке
при подстановке
 (П.8.1.37)
(П.8.1.37)
и
к ![]() в
(П.8.1.16)
в
(П.8.1.16) ![]() при
подстановке
при
подстановке
 (П.8.1.38)
(П.8.1.38)
Обозначив
через ![]() ,
можем сформулировать алгоритм.
,
можем сформулировать алгоритм.
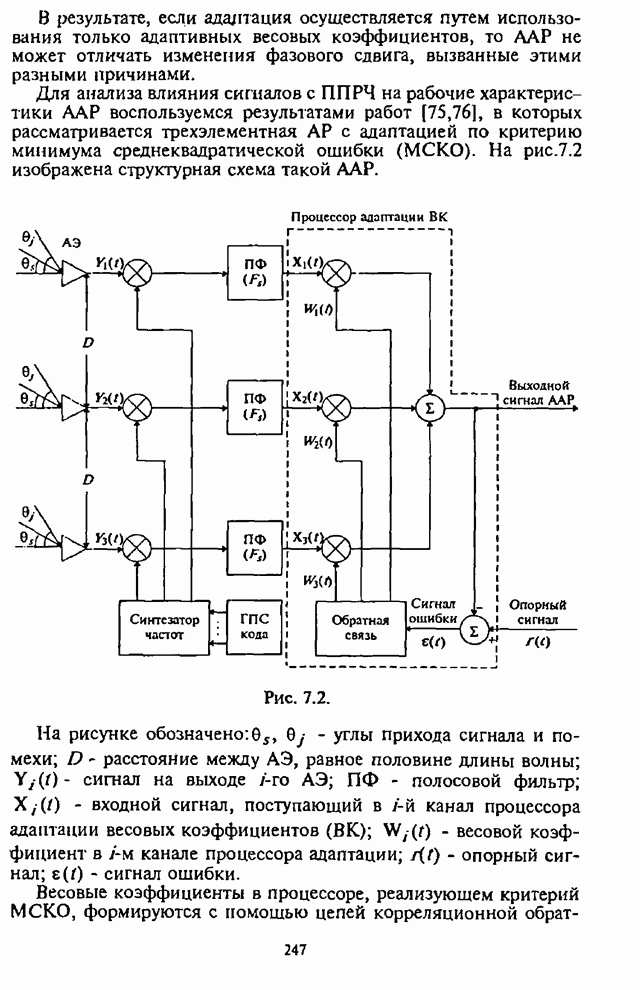
Алгоритм. На первом шаге вычислений задаются начальные значения
![]() . (П.8.1.39)
. (П.8.1.39)
Если
![]() , то
, то
 (П.8.1.40)
(П.8.1.40)
Рекуррентно пересчитываются
 (П.8.1.41)
(П.8.1.41)
Вычисления заканчиваются, если
![]() , (П.8.1.42)
, (П.8.1.42)
где
![]() - требуемая
погрешность в вычислении обобщенной
- требуемая
погрешность в вычислении обобщенной ![]() -функции.
-функции.
Окончательный результат определяется из выражения
 . (П.8.1.43)
. (П.8.1.43)
При
![]() имеем
имеем
 (П.8.1.44)
(П.8.1.44)
Величины
![]() и
и ![]() пересчитываются в
соответствии с (П.8.1.41). Условие окончания счета такое же, как и при
вычислении
пересчитываются в
соответствии с (П.8.1.41). Условие окончания счета такое же, как и при
вычислении ![]() .
.
Окончательный результат принимает вид:
 . (П.8.1.45)
. (П.8.1.45)
В
частном случае для ![]() начальные
условия имеют вид:
начальные
условия имеют вид:
 (П.8.1.46)
(П.8.1.46)
Рекуррентно
пересчитываются ![]() .
Остальные параметры пересчитываются в соответствии с (П.8.1.41)-(П.8.1.46).
.
Остальные параметры пересчитываются в соответствии с (П.8.1.41)-(П.8.1.46).
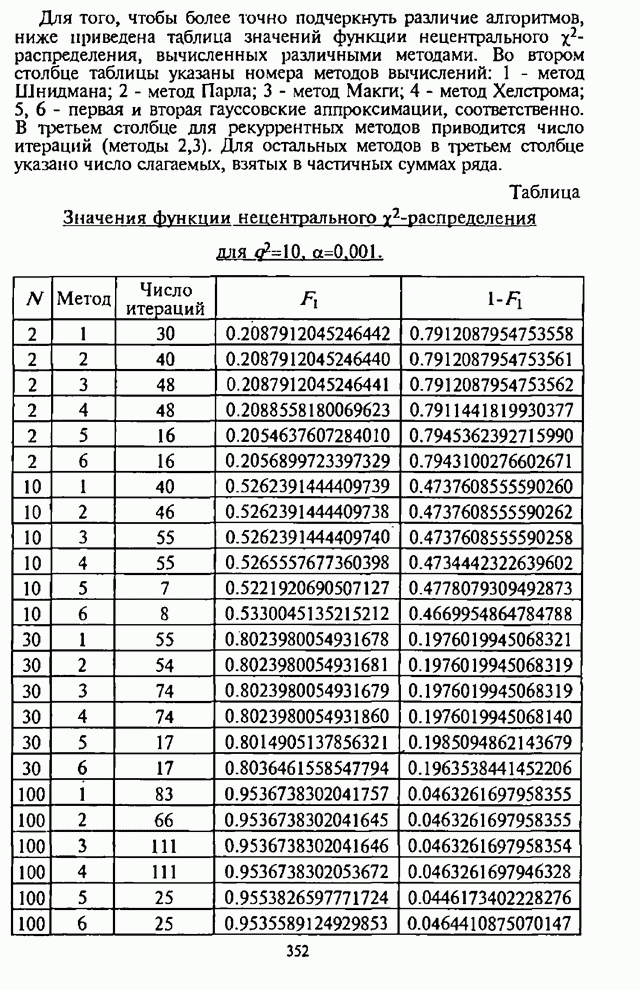
Ошибка
вычисления и условия останова. Общая относительная ошибка вычисления ![]() или
или ![]() определяется
относительной ошибкой частного
определяется
относительной ошибкой частного ![]() , которая равна сумме относительных ошибок
в
, которая равна сумме относительных ошибок
в ![]() и
и ![]() . Погрешность
вычисления
. Погрешность
вычисления ![]() и
и
![]() связана с
усечением ряда Неймана и неточностью задания начальных условий в обратной
рекурсии вычисления функций Бесселя. Суммарная относительная ошибка вычисления
знаменателя определяется из выражения
связана с
усечением ряда Неймана и неточностью задания начальных условий в обратной
рекурсии вычисления функций Бесселя. Суммарная относительная ошибка вычисления
знаменателя определяется из выражения
![]() . (П.8.1.47)
. (П.8.1.47)
Относительная ошибка вычисления числителя
 (П.8.1.48)
(П.8.1.48)
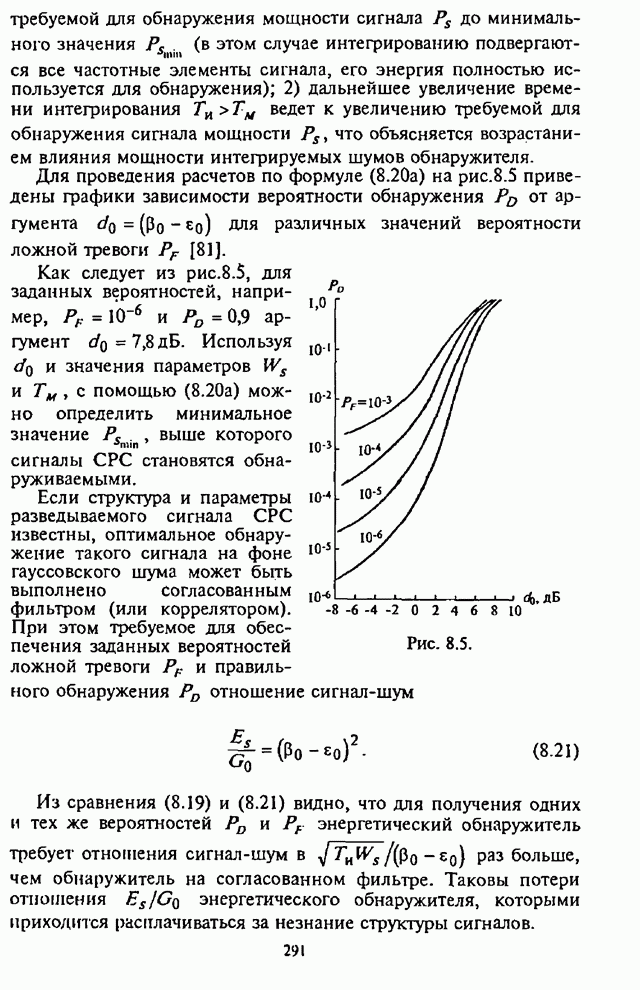
Из
сравнения (П.8.1.47) и (П.8.1.48) следует, что при ![]() относительная ошибка
знаменателя значительно преобладает над относительной ошибкой числителя.
Поэтому условие окончания счета определяется достижением заданной точности
вычисления знаменателя, которое для удобства задается в виде
относительная ошибка
знаменателя значительно преобладает над относительной ошибкой числителя.
Поэтому условие окончания счета определяется достижением заданной точности
вычисления знаменателя, которое для удобства задается в виде ![]() . В [103] рассмотрены и
другие условия окончания счета. Заметим, что все они приводят к одинаковому
числу итераций при заданной точности вычисления
. В [103] рассмотрены и
другие условия окончания счета. Заметим, что все они приводят к одинаковому
числу итераций при заданной точности вычисления ![]() -функции.
-функции.
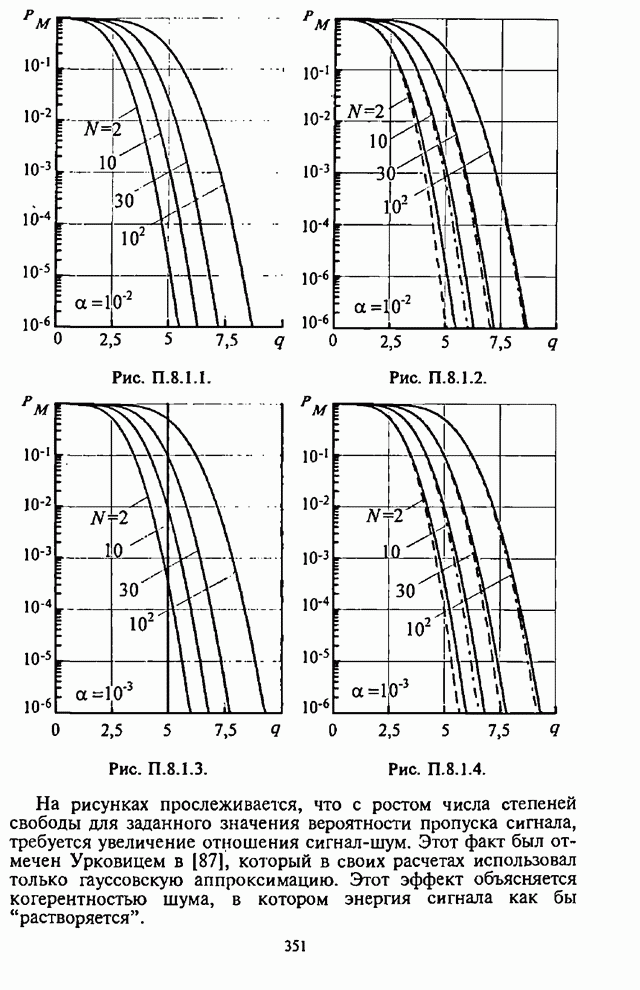
Границы
применимости алгоритма. В [102] отмечено, что алгоритм не эффективен для
больших значений ![]() .
Однако в [102] не приведены данные, касающиеся приемлемого значения
.
Однако в [102] не приведены данные, касающиеся приемлемого значения ![]() . В общем случае
существуют комбинации параметров
. В общем случае
существуют комбинации параметров ![]() , для которых алгоритм утрачивает
эффективность. Это объясняется тем, что результаты арифметических операций над
числами с плавающей точкой становятся больше или меньше допустимых в ЭВМ чисел,
прежде чем достигается требуемая точность. Эмпирические результаты показывают,
что минимальное значение
, для которых алгоритм утрачивает
эффективность. Это объясняется тем, что результаты арифметических операций над
числами с плавающей точкой становятся больше или меньше допустимых в ЭВМ чисел,
прежде чем достигается требуемая точность. Эмпирические результаты показывают,
что минимальное значение ![]() , при котором алгоритм работает,
определяется выражением [103]
, при котором алгоритм работает,
определяется выражением [103]
![]() , (П.8.1.49)
, (П.8.1.49)
где
![]() - наибольшее
число, представляемое в ЭВМ. Для достаточно больших
- наибольшее
число, представляемое в ЭВМ. Для достаточно больших ![]() алгоритм обеспечивает высокую
точность вычисления как в центральной части распределения, так и в «хвостовых»
частях.
алгоритм обеспечивает высокую
точность вычисления как в центральной части распределения, так и в «хвостовых»
частях.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Системы радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты: общие принципы
- 1.1. Краткая характеристика расширения спектра сигналов методом ППРЧ
- 1.1.1. Основные принципы и методы расширения спектра сигналов
- 1.1.2. Метод псевдослучайной перестройки рабочей частоты
- 1.1.3. Типовые структурные схемы систем радиосвязи с ППРЧ
- 1.2. Коэффициент расширения спектра сигнала и запас помехоустойчивости системы радиосвязи с ППРЧ
- 1.3. Общая характеристика помехозащищенности систем радиосвязи с ППРЧ
- 1.3.1. Помехоустойчивость систем радиосвязи с ППРЧ
- 1.3.2. Скрытность сигналов систем радиосвязи с ППРЧ
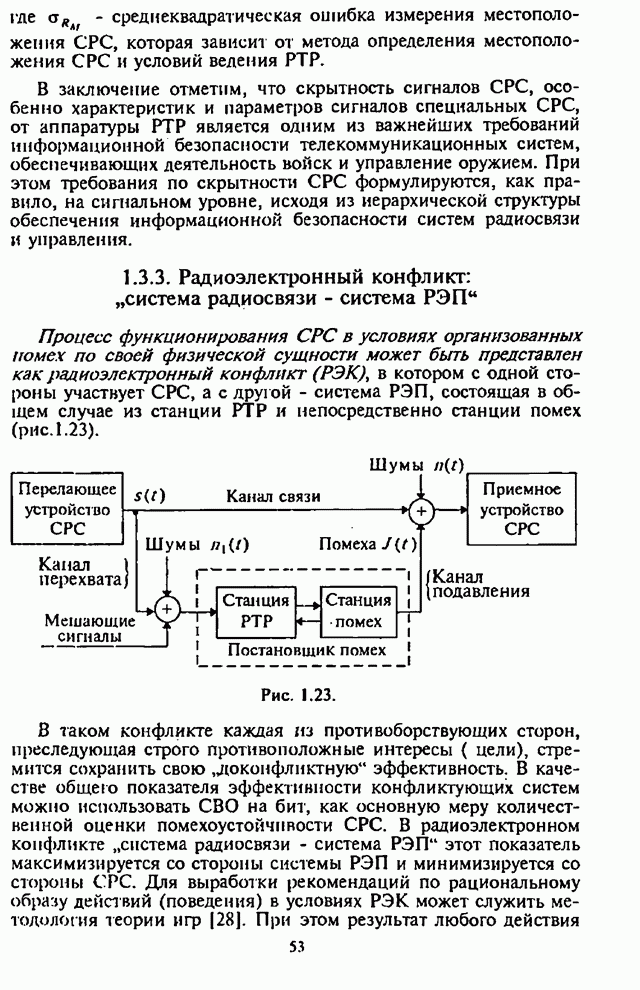
- 1.3.3. Радиоэлектронный конфликт: «система радиосвязи — система РЭП»
- 1.4. Модели и краткая характеристика основных видов помех
- Глава 2. Помехоустойчивость типовых систем радиосвязи с ППРЧ и частотной манипуляцией
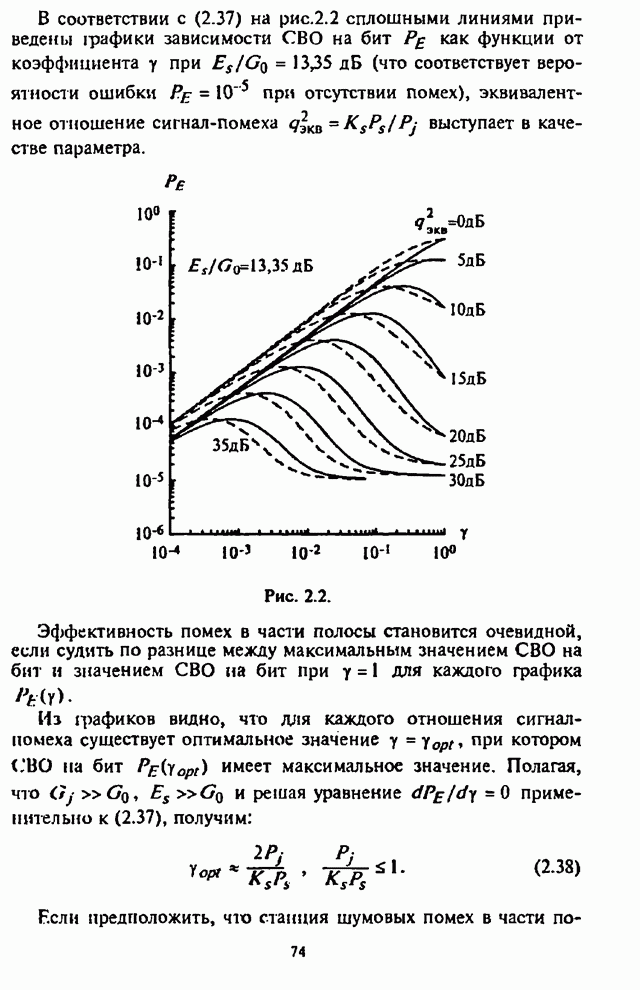
- 2.1. Условная вероятность ошибки на бит информации при двоичной ЧМ
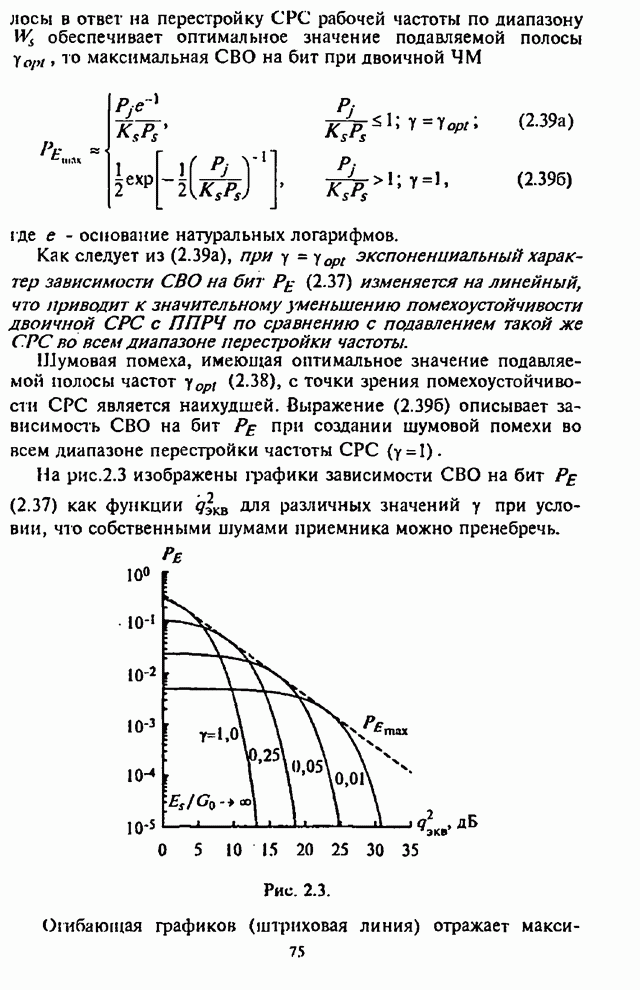
- 2.2. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и неслучайной ЧМ
- 2.3. Оценка воздействия шумовой помехи в части полосы на системы радиосвязи с ППРЧ и случайной двоичной ЧМ
- 2.4. Оценка воздействия ответных помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.1. Оценка временных возможностей станции ответных помех
- 2.4.2. Оценка воздействия ответных шумовых помех на системы радиосвязи с ППРЧ и ЧМ
- 2.4.3. Оценка воздействия ответных гармонических помех на системы радиосвязи с ППРЧ и ЧМ
- 2.5. Помехоустойчивость систем радиосвязи с ППРЧ, двоичной ЧМ и блоковым кодированием
- Глава 3. Синтез и анализ эффективности адаптивных алгоритмов различения сигналов с ППРЧ, частотной модуляцией и разнесением символов по частоте
- 3.1. Синтез оптимального адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и ЧМ
- 3.2. Квазиоптимальный адаптивный алгоритм различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3. Оценка помехоустойчивости синтезированного адаптивного алгоритма различения сигналов с внутрисимвольной ППРЧ и двоичной ЧМ
- 3.3.1. Случай «слабых» сигналов
- 3.3.2. Случай «сильных» сигналов
- Глава 4. Помехоустойчивость адаптивных алгоритмов демодуляции сигналов с внутрибитовой ППРЧ и двоичной частотной манипуляцией
- 4.1. Структурные схемы демодуляторов
- 4.2. Помехоустойчивость демодулятора с линейным сложением выборок
- 4.3. Помехоустойчивость демодулятора с нелинейным сложением выборок
- 4.4. Помехоустойчивость демодулятора с мягким ограничителем
- 4.5. Помехоустойчивость самонормирующегося демодулятора
- 4.6. Влияние адаптивной регулировки усиления на помехоустойчивость СРС
- 4.7. Сравнительный анализ помехоустойчивости демодуляторов сигналов с внутрибитовой ППРЧ и двоичной ЧМ
- Глава 5. Помехоустойчивость систем радиосвязи с ППРЧ при совместном применении частотной модуляции, разнесения символов по частоте и блокового кодирования
- 5.1. Помехоустойчивость систем радиосвязи с ППРЧ при M-ичной ЧМ и L-кратным разнесении символов по частоте
- 5.1.1. Условная вероятность ошибки на бит информации
- 5.1.2. Анализ средней вероятности ошибки на бит информации
- 5.2. Помехоустойчивость систем радиосвязи с ППРЧ, M-ичной ЧМ, блоковым кодированием и L-кратным частотным разнесением кодовых слов
- 5.2.1. Структурная схема системы радиосвязи
- 5.2.2. Средняя вероятность ошибки на бит информации
- 5.2.3. Анализ средней вероятности ошибки на бит информации
- Глава 6. Синхронизация в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 6.1. Назначение подсистемы синхронизации
- 6.2. Описательная модель подсистемы синхронизации
- 6.2.1. Типовая структурная схема подсистемы синхронизации
- 6.2.2. Типовые структурные схемы и алгоритмы функционирования основных устройств подсистемы синхронизации
- 6.3. Показатели и оценка эффективности циклических процедур поиска
- Приложение П.6.1. Верхняя граница среднего нормированного времени поиска
- Приложение П.6.2. Верхняя граница вероятности правильного обнаружения
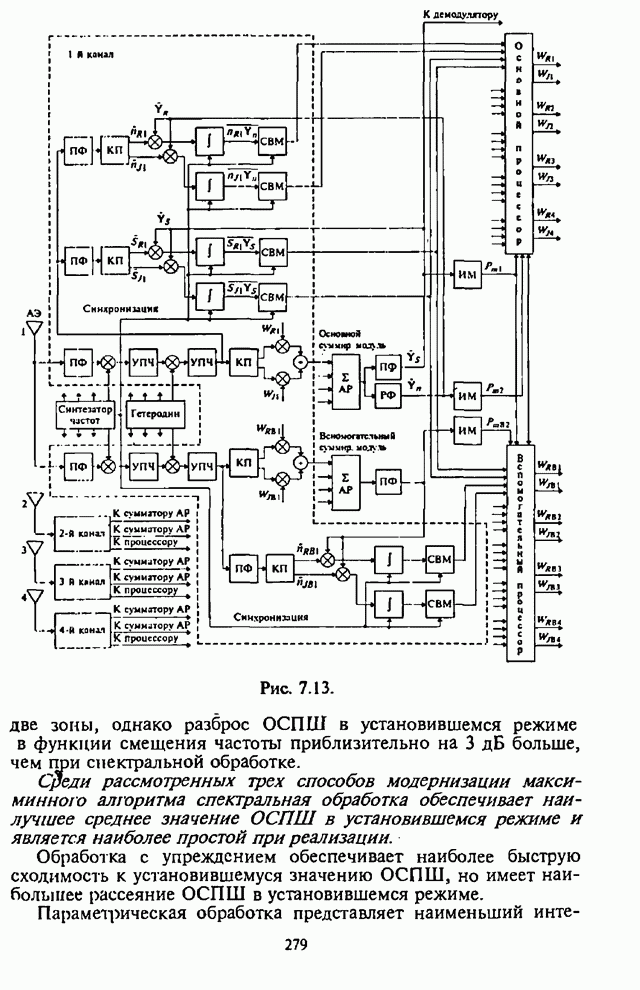
- Глава 7. Адаптивные антенные решетки в системах радиосвязи с псевдослучайной перестройкой рабочей частоты
- 7.1. Влияние сигналов с ППРЧ на характеристики адаптивной антенной решетки
- 7.2. Максиминный алгоритм обработки сигналов и помех
- 7.3. Реализация и возможности максиминного алгоритма
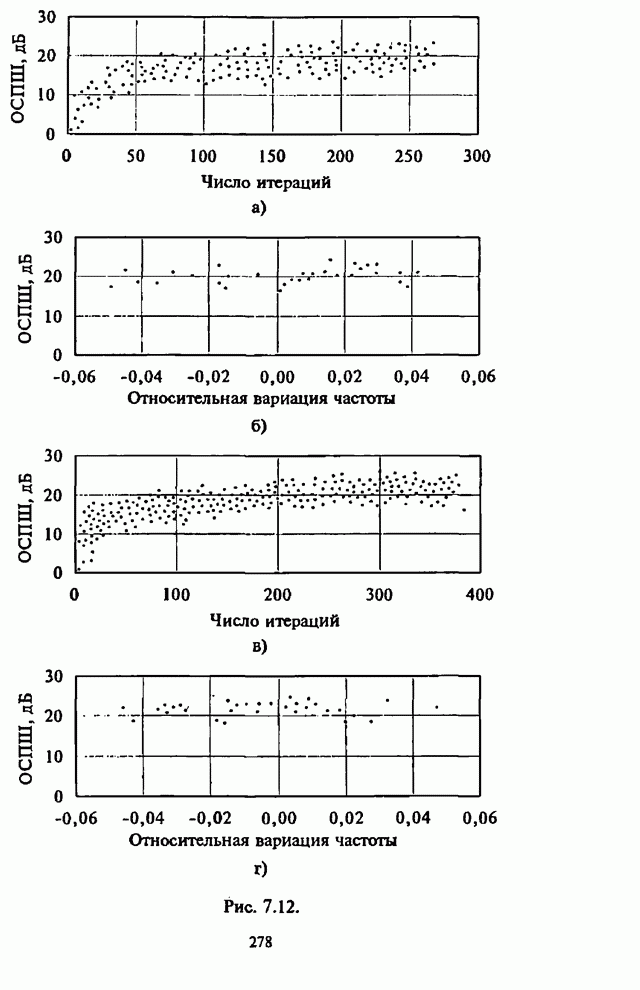
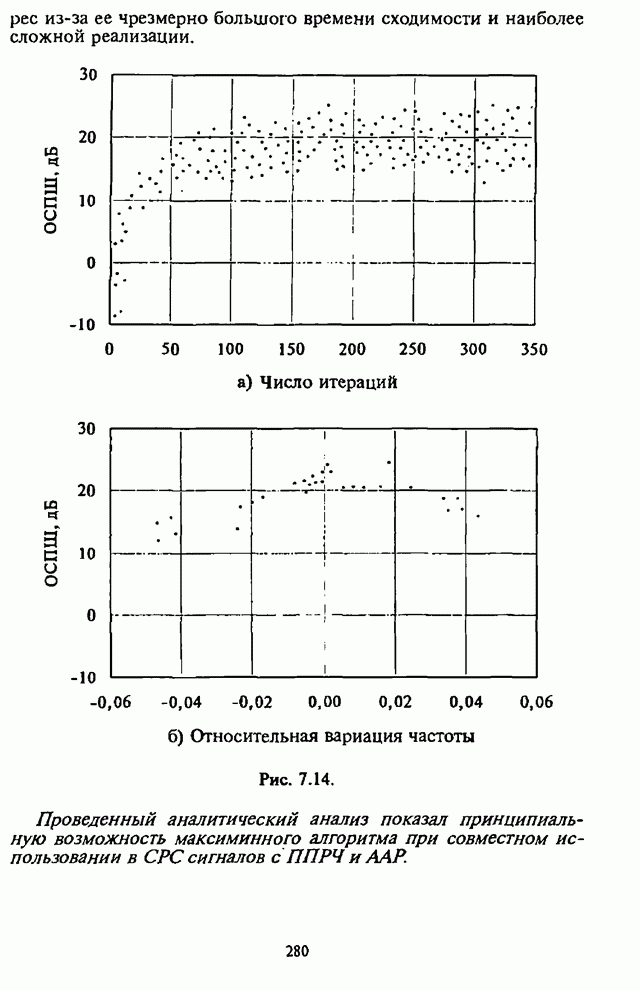
- 7.4. Модернизация максиминного алгоритма
- 7.4.1. Параметрическая обработка
- 7.4.2. Спектральная обработка
- 7.4.3. Обработка с упреждением
- Глава 8. Обнаружение сигналов с псевдослучайной перестройкой рабочей частоты
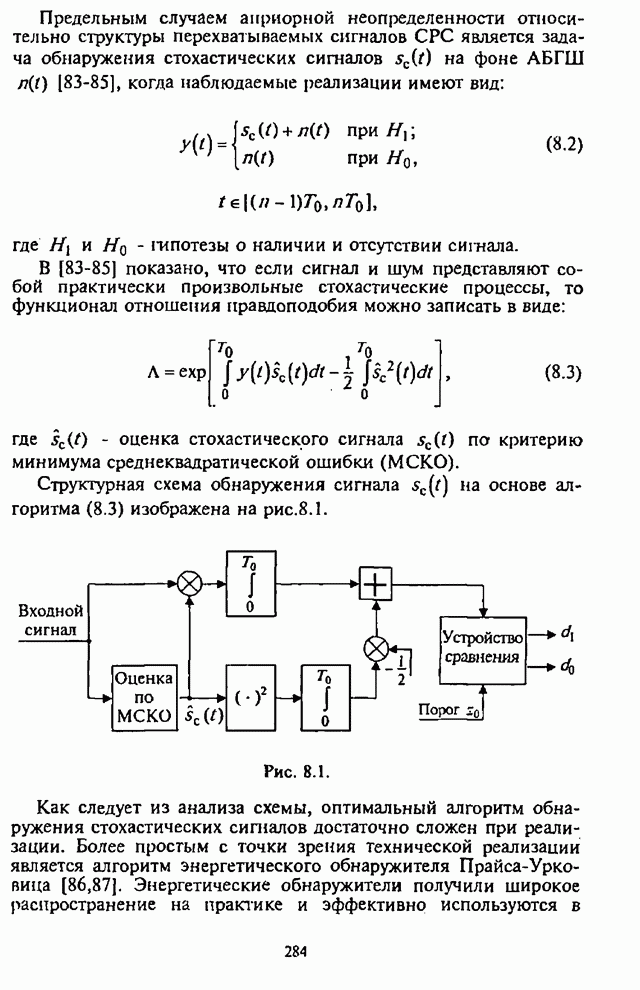
- 8.1. Обнаружение сигналов неизвестной структуры
- 8.2. Широкополосный энергетический обнаружитель
- 8.3. Многоканальные энергетические обнаружители
- 8.3.1. Квазиоптимальный многоканальный обнаружитель
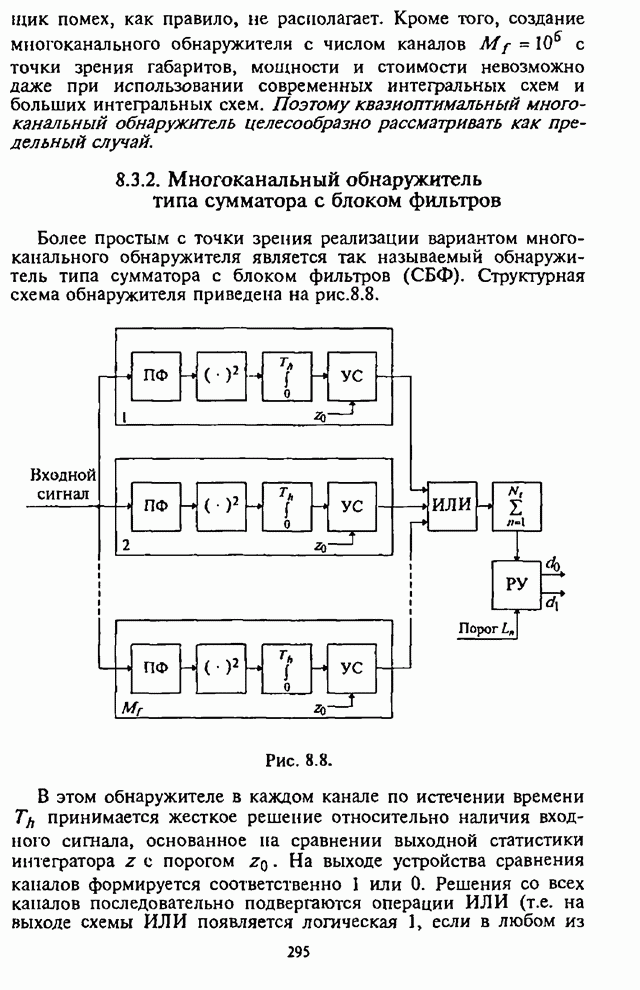
- 8.3.2. Многоканальный обнаружитель типа сумматора с блоком фильтров
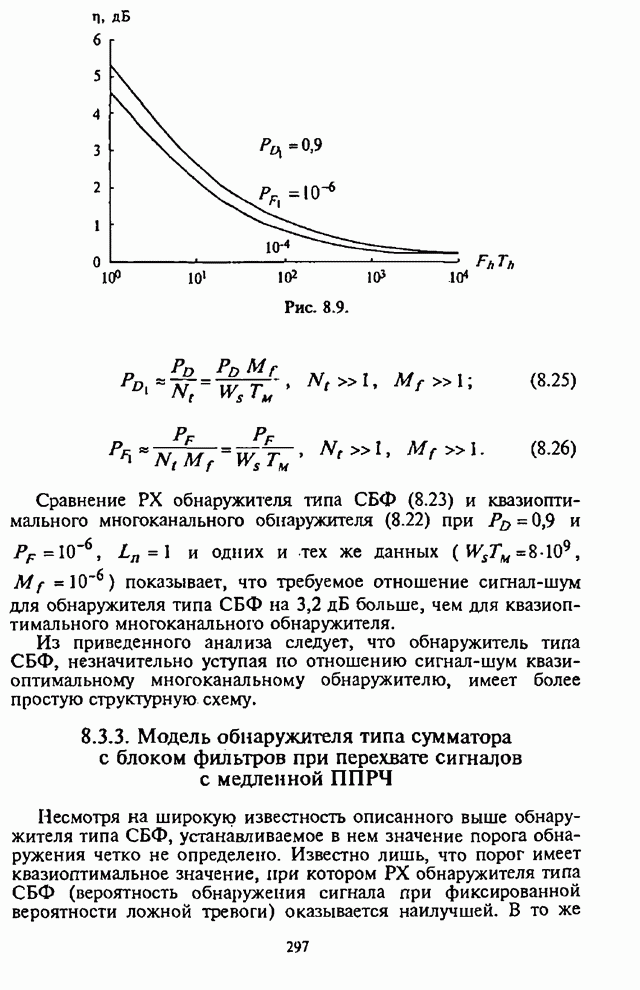
- 8.3.3. Модель обнаружителя типа сумматора с блоком фильтров при перехвате сигналов с медленной ППРЧ
- 8.3.4. Многоканальный обнаружитель типа сумматора с блоком фильтров в части полосы
- 8.3.5. Рассогласование по времени и частоте между характеристиками сигнала с ППРЧ и параметрами обнаружителя
- 8.4. Многоканальный адаптивный энергетический обнаружитель в условиях воздействия мешающих сигналов
- 8.4.1. Структурная схема многоканального адаптивного энергетического обнаружителя с регулировкой порогового уровня
- 8.4.2. Вероятность ложной тревоги и адаптивная регулировка порогового уровня
- 8.4.3. Вероятность обнаружения
- 8.4.4. Влияние рассогласования по времени на обнаружение сигналов
- 8.5. Другие возможные типы обнаружителей сигналов с ППРЧ
- 8.5.1. Корреляционный радиометр
- 8.5.2. Цифровой анализатор спектра
- 8.5.3. Метод вскрытия частотно-временной матрицы сигнала с ППРЧ
- Приложение П.8.1. Алгоритмы вычисления обобщенной Q-функции Маркума
- П.8.1.1. Постановка задачи
- П.8.1.2. Представление степенными рядами
- П.8.1.3. Представление в виде рядов Неймана
- П.8.1.4. Численное интегрирование
- П.8.1.5. Гауссовская аппроксимация
- П.8.1.6. Численные результаты
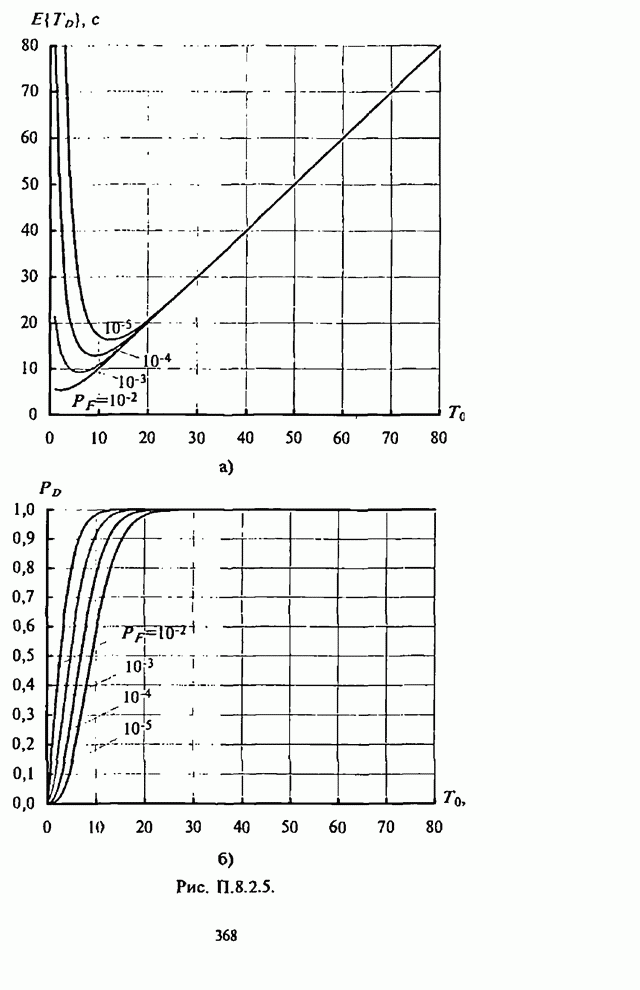
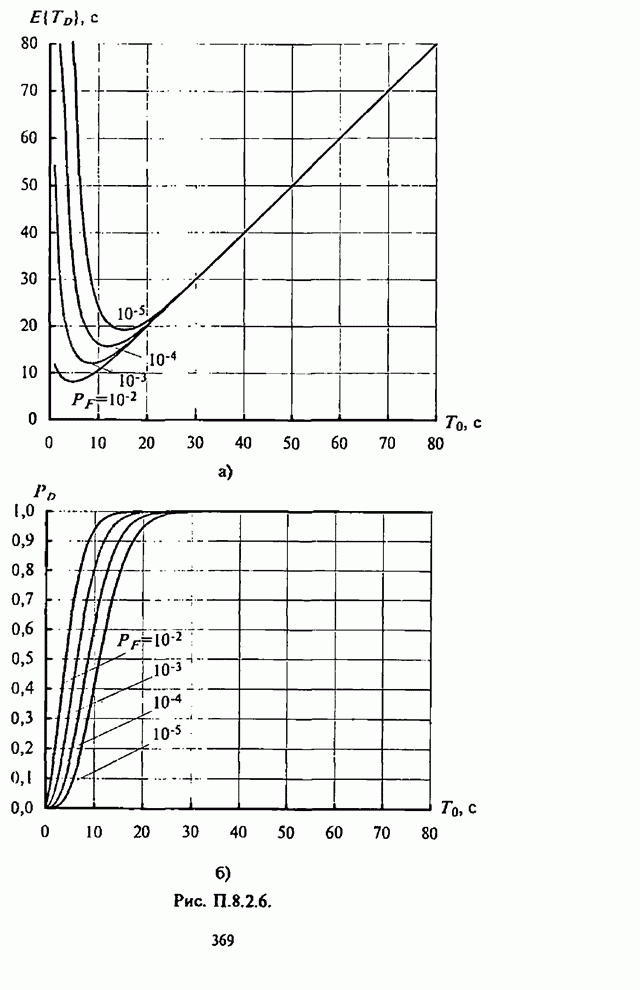
- Приложение П.8.2. Анализ вероятностно-временных характеристик алгоритмов обнаружения сигналов
- П.8.2.1. Вероятностно-временные характеристики основных видов обнаружителей
- П.8.2.2 Алгоритмы расчета вероятностно-временных характеристик основных видов обнаружителей
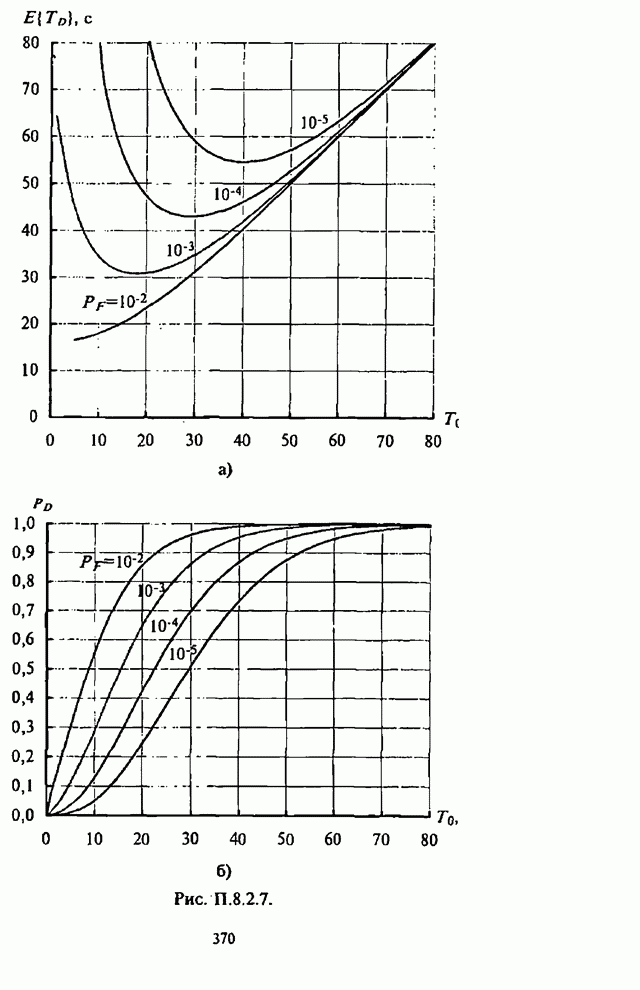
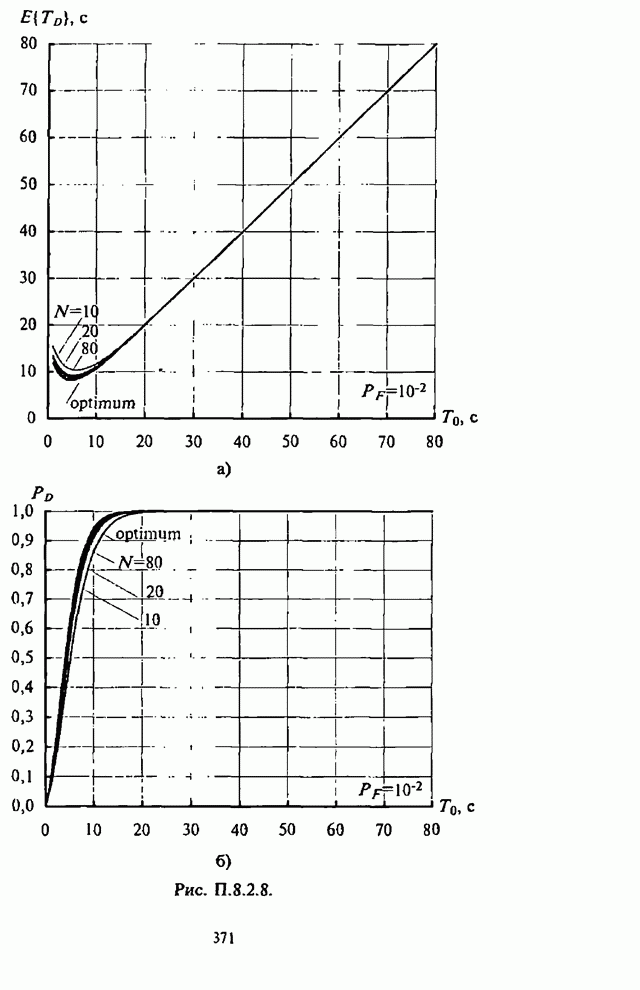
- П.8.2.3. Численные результаты
- СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
- ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ